Mechanophenotyping of 3D multicellular clusters using displacement arrays of rendered tractions

Significance

Epithelial tissue development, wound healing, and tumor progression are governed by mechanical interactions between groups of cells and the surrounding extracellular matrix. Multicellular clusters exert spatially heterogeneous deformations within 3D biomaterials, which confound existing analyses established for individual cells. Here, we demonstrate a scalable method to profile multicellular clusters based on how they locally pull, push, and twist the surrounding matrix. We validate this method using biochemical treatments that perturb cell–cell and cell–matrix interactions, which result in cluster disorganization and dissemination with distinct signatures of matrix deformation. This assay is implemented in a standardized well-plate format, which enables higher-throughput measurements of aberrant cell–matrix interactions and drug responses in human disease.

Abstract

Epithelial tissues mechanically deform the surrounding extracellular matrix during embryonic development, wound repair, and tumor invasion. Ex vivo measurements of such multicellular tractions within three-dimensional (3D) biomaterials could elucidate collective dissemination during disease progression and enable preclinical testing of targeted antimigration therapies. However, past 3D traction measurements have been low throughput due to the challenges of imaging and analyzing information-rich 3D material deformations. Here, we demonstrate a method to profile multicellular clusters in a 96-well-plate format based on spatially heterogeneous contractile, protrusive, and circumferential tractions. As a case study, we profile multicellular clusters across varying states of the epithelial–mesenchymal transition, revealing a successive loss of protrusive and circumferential tractions, as well as the formation of localized contractile tractions with elongated cluster morphologies. These cluster phenotypes were biochemically perturbed by using drugs, biasing toward traction signatures of different epithelial or mesenchymal states. This higher-throughput analysis is promising to systematically interrogate and perturb aberrant mechanobiology, which could be utilized with human-patient samples to guide personalized therapies.

Collective mechanical interactions between epithelial cells and three-dimensional (3D) extracellular matrix (ECM) shape embryonic tissue development, and their dysregulation can drive cancer progression or other disease states (1). In particular, the epithelial–mesenchymal transition (EMT) is associated with weakened cell–cell junctions and increased cell–matrix adhesions, driving tissue disorganization and dissemination (2). Remarkably, multicellular clusters cultured ex vivo in compliant 3D hydrogels can exhibit tissue-like form and function (3–7), representing a promising preclinical testbed for higher-throughput drug discovery and development (8, 9). However, existing assays for 3D mechanophenotyping have been limited to a few cells per experiment due to the need for high-resolution optics and labor-intensive image processing, as well as complex readouts of force generation (10). Rapid biophysical characterization of multicellular clusters in a 3D matrix could enable direct characterization and perturbation of disease state in human-patient samples, informing predictive and personalized therapies (11). Indeed, human circulating tumor-cell clusters have recently been observed with varying epithelial and mesenchymal states during metastatic breast cancer (12).

Traction force microscopy (TFM) resolves cell-generated deformations based on the motion of fluorescent tracer particles embedded within a compliant material (13). Early TFM studies measured cell–cell and cell–matrix interactions of multicellular epithelial clusters on planar two-dimensional (2D) substrates (14–21). More recently, TFM along with microrheological analyses have been utilized for 3D hydrogels, but have primarily focused on individual cells (22–33). Notably, epithelial cell lines exhibit more isotropic, spatially uniform tractions, while mesenchymal cell lines exhibit highly anisotropic tractions localized at the leading and trailing edge (22–24, 26, 28, 30, 31, 34). Nevertheless, it remains a formidable challenge to visualize 3D cell morphologies and tractions, particularly in a scalable experimental format (35). Most traditional TFM approaches require relatively high-resolution data on both cellular morphologies and material deformations, which poses significant experimental, workflow, and computational challenges. This issue is further exacerbated by also requiring knowledge of the underlying material properties to compute cellular tractions, which continues to be a significant challenge for fibrous and biologically remodeled extracellular materials (13).

Here, we demonstrate a high-content method to profile the spatially heterogeneous matrix deformations of multicellular clusters in a standard 96-well-plate format. We show that clusters exhibit collective tractions with distinct spatial signatures, which we visualize by tracking hundreds of thousands of embedded tracer particles to recover information-rich material-displacement fields. This Displacement Arrays of Rendered Tractions (DART) analysis was validated by inducing EMT in mammary epithelial cells cultured within a composite 3D hydrogel of silk fibroin and collagen I. Remarkably, we find that the progression from epithelial to mesenchymal states is associated with a successive loss of protrusive and circumferential tractions, as well as the formation of highly localized contractile tractions. Indeed, these emergent behaviors cannot be resolved by using conventional spatially averaged TFM metrics developed for individual cells. We further perturbed these cluster mechanophenotypes toward more mesenchymal or epithelial states using drugs that stabilize microtubules (e.g., Taxol) or inhibit epidermal growth factor receptor (EGFR) signaling (e.g., gefitinib). Since this approach does not rely on high-resolution 3D object detection, lower-numerical-aperture (NA) air objectives can be used to rapidly image a multiwell plate for higher-throughput volumetric image acquisition and analysis. This implementation of 3D TFM on a standardized platform could enable preclinical screening of human organoids to inform drug development and precision medicines.

DART

We designed a kinematics-based approach called DART metrics for characterizing the cell-induced matrix deformations without relying on a constitutive material model for the 3D biomaterial at hand. We previously demonstrated mean deformation metrics (MDM) to compute average values associated with the deformation fields of individual cells (29). However, we observed in these experiments that multicellular clusters applied spatially heterogeneous deformation fields over large volumes. Thus, the corresponding MDM regressed to null values due to spatial averaging. Moreover, this spatial averaging resulted in a loss of biologically interesting information associated with highly localized signatures in the cell-induced deformation field, making MDM unsuitable for analyzing collective deformations.

To compute the DART metrics, the particle displacement (${\mathit{u}}_i$) at positions (${\mathit{x}}_i$) was interpolated onto regularized grid points (${\mathit{x}}_{grid}$) in each image with a general spacing of 12 $\times \hspace{0.17em}12\hspace{0.17em}\times$ 12 voxels (3.84 $\times \hspace{0.17em}3.84\hspace{0.17em}\times$ 7.2 $\mathrm{\mu }$m) in the $x$, $y$, and $z$ directions, respectively. This grid spacing provided a good trade-off in terms of spatial resolution and computational throughput. For instance, choosing a grid spacing that was too large would smooth out the high spatial-frequency information from the displacement field and introduce errors in the analysis. Instead, choosing a grid spacing that was too small would make the displacement interpolation and subsequent postprocessing computationally very expensive. For this grid size of 12 $\times \hspace{0.17em}12\hspace{0.17em}\times$ 12 voxels, the displacement was sampled at $\sim$305,000 points in the volume of interest (2,048 $\times$ 2,048 $\times$ 126 voxels), which was more than three times the number of particles found in the image (usually between 80,000 and 100,000 particles), providing high-resolution reconstruction of the cell-induced displacement field at significantly reduced computational cost.

Let ${\mathit{u}}_{grid}$ be the displacement vector at the regularized grid points ${\mathit{x}}_{grid}$. A linear scattered interpolation scheme was utilized. The DART metrics computed kinematic quantities from the local deformation field of the cell cluster. Thus, only the displacement ${\mathit{u}}_{grid}$ at points ${\mathit{x}}_{grid}$ within a distance $d$ = 25 $\mathrm{\mu }$m from the cell-cluster surface was considered in computing the DART metrics, which was sufficient to capture most of the displacement data around each cluster. The displacements ${\mathit{u}}_{grid}$ at the points outside the search region were set to be zero. At each of the grid points ${\mathit{x}}_{grid}$, a unit vector ${\mathbf{n}}_{grid}$ originating from the centroid of the cell cluster (${\mathbf{r}}_o$) to the ${\mathit{x}}_{grid}$ was determined. By using the normal vector, the displacement ${\mathit{u}}_{grid}$ was then decomposed into radial ${\mathit{u}}_{grid}^r$ and hoop ${\mathit{u}}_{grid}^{\theta }$ displacement components as,

$$\begin{array}{cc}\hfill u_{grid}^r& =|{\mathbf{u}}_{grid}\hspace{0.17em}.\hspace{0.17em}{\mathbf{n}}_{grid}|\hfill \\ \hfill u_{grid}^{\theta }& =|{\mathbf{u}}_{grid}-\left({\mathbf{u}}_{grid}\hspace{0.17em}.\hspace{0.17em}{\mathbf{n}}_{grid}\right)\hspace{0.17em}{\mathbf{n}}_{grid}|.\hfill \end{array}$$ [1]

From $u_{grid}^r$ and $u_{grid}^{\theta }$, the regions where cells applied significant protrusive, contractile, and circumferential deformations were determined. These regions were found by binarizing the 3D matrix of $u_{grid}^r$ and $u_{grid}^{\theta }$ using thresholding operation with $u_{\text{significant}}$ as

$$\begin{array}{cc}\hfill u^{\text{protrusive}}& =\left\{\begin{array}{cc}1\hspace{1em}\hfill & \hspace{1em}\text{if}{u}_{grid}^r>u_{\text{significant}}\hfill \\ 0\hspace{1em}\hfill & \hspace{1em}\text{otherwise}\hfill \end{array}\right.\hfill \\ \hfill u^{\text{contractile}}& =\left\{\begin{array}{cc}1\hspace{1em}\hfill & \hspace{1em}\text{if}{u}_{grid}^r<-u_{\text{significant}}\hfill \\ 0\hspace{1em}\hfill & \hspace{1em}\text{otherwise}\hfill \end{array}\right.\hfill \\ \hfill u^{\text{circumferential}}& =\left\{\begin{array}{cc}1\hspace{1em}\hfill & \hspace{1em}\text{if}{u}_{grid}^{\theta }>u_{\text{significant}}\hfill \\ 0\hspace{1em}\hfill & \hspace{1em}\text{otherwise.}\hfill \end{array}\right.\hfill \end{array}$$ [2]

Since the DART analysis relies on binning cellular-displacement fields as either protrusive or contractile, the binary threshold parameter, $u_{\text{significant}}$, needed to be selected carefully. In particular, $u_{\text{significant}}$ should be above the noise floor, but should also not implicitly bias any given cluster toward either a contractile or protrusive (or both) phenotype. By systematically varying the threshold parameter, $u_{\text{significant}}$ across our control cell clusters, we found an optimal parameter value (SI Appendix, Fig. S4), which produced the most evenly distributed distribution of contractile displacement slices ($u_{\text{significant}}$ attains a global minimum in the SD for each cluster distribution). It should be noted that $u_{\text{significant}}$ represents the threshold value for binning displacements as either being contractile, protrusive, or both and was not an exclusion criteria for whether data were used or discarded in the DART analysis. However, to remove spurious white voxels in $u^{\text{protrusive}}$, $u^{\text{contractile}}$, and $u^{\text{circumferential}}$ produced from noise during particle tracking, these 3D matrix displacements were filtered to remove connected white components smaller than our 12-voxel grid-point spacing corresponding to a volume of 106.5 $\mathrm{\mu }{\mathrm{m}}^3$.

From $u^{\text{protrusive}}$, $u^{\text{contractile}}$, and $u^{\text{circumferential}}$, the relative localized regions where cells applied protrusive, contractile, and circumferential deformation was computed through DART. Here, the computation of contractile DART is described, but protrusive and circumferential DARTs are computed analogously. The volume about the center of the cell cluster in $u^{\text{contractile}}$ was divided into 16 equal subvolumes. The volume around each cell in $u^{\text{contractile}}$ was first divided into two, bottom and top, hemispheres. Each hemisphere was further divided into eight equal, $\pi /4$ apart, regions. Thus, each “slice” in the DART corresponded to a volumetric region in the real space around the cell cluster. The outer and inner slices in the DART board corresponded to the region in the lower (${\theta }_{el}\ge \pi$) and upper (${\theta }_{el}<\pi$) hemispheres of the $u^{\text{contractile}}$ region around each cell cluster. A slice was considered to be contractile if the corresponding region in $u^{\text{contractile}}$ had at least one white voxel signifying that the cell cluster applied significant contractile deformation in that region. The contractile quantification within each DART slice was binary. From the contractile DART, the number of contractile displacement slices was used as a metric to quantify how localized the contractile deformation was that the cell cluster applies. Similarly, the number of protrusive and circumferential displacement slices for each cell cluster was computed.

As the final part of our DART approach, a phenotype classifier was built to classify multicellular clusters into epithelial, mesenchymal, and transitory phenotypes using the Decision-TreeClassifier class from the Python Scikit library, a commonly used machine-learning tool. For classification, the decision tree utilized the number of contractile, protrusive, and circumferential displacement slices and shape anisotropy factor of a multicellular cluster. The decision-tree classifier had a maximum tree depth of five and a minimum number of leaf samples of five. The decision-tree model was trained with low tree depth and a high minimum number of leaf samples to prevent training data overfitting. The decision tree was trained on all multicellular clusters used in the analysis of the control dimethyl sulfoxide (DMSO) treatment condition. The accuracy of the decision tree on the training data was evaluated by using the normalized confusion matrix. A normalized confusion matrix C is defined such that C_i,j is the proportion of the observation known to be in the group $i$ and classified in the group $j$. The confusion matrix of a perfect classifier is equal to the identity matrix.

Results

DART Visualizes Spatially Heterogeneous Displacement Fields.

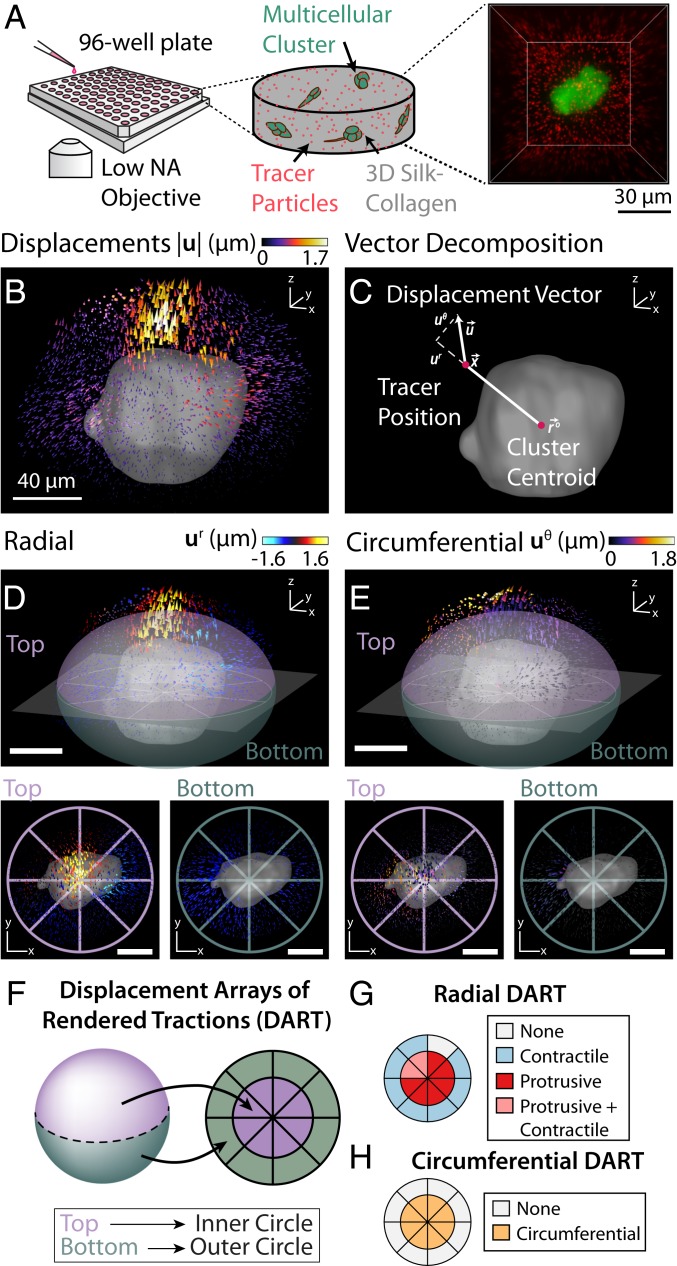
Collective cell–matrix interactions were characterized by embedding mammary epithelial cells (MCF-10A) in a composite hydrogel consisting of 7.5 mg/mL silk fibroin and 1 mg/mL collagen I (36) on a 96-well plate (Fig. 1A). These hydrogels had an elastic modulus of 600 Pa and a characteristic pore size of 2 $\mathrm{\mu }$m (SI Appendix, Fig. S1), which maintained epithelial cells as spherical clusters (“acini”) but was also permissive for local dissemination (SI Appendix, Fig. S2). These MCF-10A Snail–estrogen receptor (ER) cells were stably transfected to overexpress green fluorescent protein (GFP) in the cytoplasm, as well as an inducible ER construct for controlled EMT through the Snail transcription factor (37, 38). Cluster-induced deformations of the hydrogel were visualized by using our topological particle-tracking algorithm to map the displacement of 80,000 to 100,000 tracer particles around each cluster (39), after which the clusters were lysed to define a reference state. This case study focused on clusters cultured for 7 d, since EMT induction in this cell line typically occurs over several days or more (40). Prior to day 7, there remained a sizable number of individual cells, which were not the biological phenomena of interest. At longer times after day 7, the clusters grew large enough to interact mechanically through the 3D matrix, which would also complicate the traction analysis (SI Appendix, Fig. S2).

Fig. 1.

Schematic illustration of the experimental setup and DART metrics. (A) Experimental setup for high-throughput imaging to measure cell-induced matrix deformations. Multicellular clusters were grown inside a silk–collagen matrix with embedded 1-$\mathrm{\mu }$m red fluorescent tracer particles in a 96-well-plate setup. To achieve high-throughput imaging, clusters were imaged by using a spinning-disk confocal microscopy with a low-NA air objective. (B) The 3D cell-induced matrix deformations recovered by directly tracking tracer particles. (C) Matrix displacements $\overrightarrow{u}$ were decomposed into radial ($u^r$) and circumferential ($u^{\theta }$) components about the center of the cluster. (D, Upper) Radial displacements $u^r$ of the matrix around the cell cluster. (D, Lower) The surrounding volume is partitioned into top and bottom hemispheres, which were projected onto a 2D representation in Lower Left and Lower Right, respectively. (E, Upper) Circumferential displacements $u^{\theta }$ of the matrix around the cell cluster. (E, Lower) The surrounding volume is partitioned into top and bottom hemispheres, which are again projected onto a 2D representation in Lower Left and Lower Right. (F) Schematic mapping of 3D displacement fields onto a 2D DART representation. (G) Protrusive or contractile displacements with magnitude larger than $u_{\text{significant}}$ in the surrounding volume were represented by protrusive or contractile slices in the radial DART metrics. The top and bottom hemispheres map to the inner and outer slices of the DART, respectively. (H) Circumferential DART computed from E analogous to the method described in G. (Scale bars: 40 $\mathrm{\mu }$m.)

Multicellular clusters typically deformed the surrounding matrix in a spatially heterogeneous manner. For instance, a representative cluster exhibited inward (“contractile”) tractions around the periphery, but outward (“protrusive”) tractions near the top (Fig. 1B). Although visually pronounced, this heterogeneity is often averaged out in conventional TFM or kinematic metrics based on mean deformations around individual cells (22, 29) (SI Appendix, Fig. S3). In order to profile these spatial patterns, the displacement vector of a given tracer particle $\overrightarrow{u}$ due to matrix deformation was decomposed into radial $u^r$ and circumferential components $u^{\theta }$ relative to the center of the cluster (Fig. 1C). These discrete particle displacements were then interpolated onto a regularized grid in order to optimize computational throughput while maintaining adequate spatial resolution. Next, the volume around each cluster was subdivided into 16 equal subvolumes, with eight regions of equal volume in the top and bottom hemispheres, respectively (Fig. 1 D and E). For ease of visualization, we developed the DART analyses to map these 3D deformations onto a simpler, 2D representation. In each DART, the inner region of eight equal slices corresponds to the eight subvolumes in the top hemisphere, while the outer ring corresponds to the bottom hemisphere (Fig. 1 F and G). If the radial particle displacement within a given region exceeded a critical threshold ($u_{\mathrm{significant}}$) of 0.4 $\mathrm{\mu }$m (SI Appendix, Fig. S4), it was denoted as contractile, protrusive, or both (Fig. 1G). Similarly, if the circumferential displacement within a given region exceeded a certain threshold of 0.4 $\mathrm{\mu }$m, it was also noted (Fig. 1H). This DART displacement threshold, $u_{\text{significant}}$, was chosen to be at least five times above the intrinsic displacement noise floor and to produce an optimally even distribution of displacement slices in the DART control groups (SI Appendix, Fig. S4). The displacement noise floor obtained with our topology-based particle tracking (TPT) algorithm was 20.5 nm (39). Finally, the spatial heterogeneity of tractions was then quantified from the number of regions which exceeded the radial or circumferential displacement threshold.

Epithelial, Transitory, and Mesenchymal Clusters Exhibit Distinct Tractions and Morphologies.

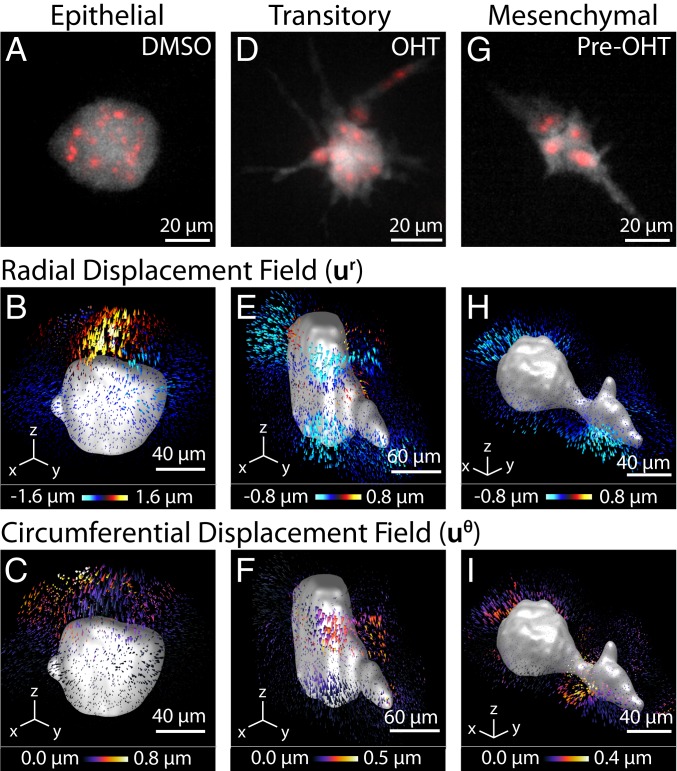
As a case study, three experimental conditions were characterized with multicellular clusters representing epithelial, transitory, and mesenchymal mechanophenotypes (SI Appendix, Fig. S5). MCF-10A Snail–ER cells were embedded as single cells within silk–collagen hydrogels and then imaged after 7 d. First, MCF-10A cells were maintained in an epithelial mechanophenotype by culturing with 0.05% DMSO, matching the concentration used to resuspend drug compounds. Epithelial cells organized into compact, roughly spherical multicellular acini (Fig. 2A). These clusters exerted localized protrusive and some circumferential deformations relative to the reference state after lysing, while the spatial distribution of contractile deformations varied across clusters (Fig. 2 B and C). Second, MCF-10A cells were induced to a transitory (EMT) mechanophenotype by Snail induction with 500 nM 4-hydroxytamoxifen (OHT) after embedding in the hydrogel. These transitory clusters exhibited significant protrusions (Fig. 2D), analogous to the budding outgrowths associated with branching morphogenesis. Moreover, these clusters exhibited uniformly distributed contractile deformations across the periphery with some circumferential deformations, but minimal protrusive deformations (Fig. 2 E and F). Third, MCF-10A cells were preinduced into a mesenchymal mechanophenotype by sustained treatment with 500 nM OHT for 72 h before embedding into the hydrogel (37). These clusters were highly elongated and spindle-like, with slightly decreased sizes due to slower proliferation after EMT (Fig. 2G). Mesenchymal clusters exhibited highly localized contractile deformations at only a few locations, consistent with front/back polarity, as well as minimal protrusive or circumferential deformations (Fig. 2 H and I).

Fig. 2.

Representative mechanophenotypes corresponding to epithelial, transitory, and mesenchymal states. (A, D, and G) Morphology of the cell clusters. The cytoplasm of the cell cluster is shown in gray (GFP), and the nucleus of the cells is shown in red (mCherry-H2B). Pre-OHT, OHT-pretreated. (B, E, and H) The 3D radial displacements, $u^r$, about the center of a cell cluster shown for a representative epithelial, mesenchymal, or transitory cell cluster. (C, F, and I) Corresponding 3D circumferential displacements, $u^{\theta }$, about the center of a cell cluster shown for a representative epithelial, mesenchymal, or transitory cell cluster.

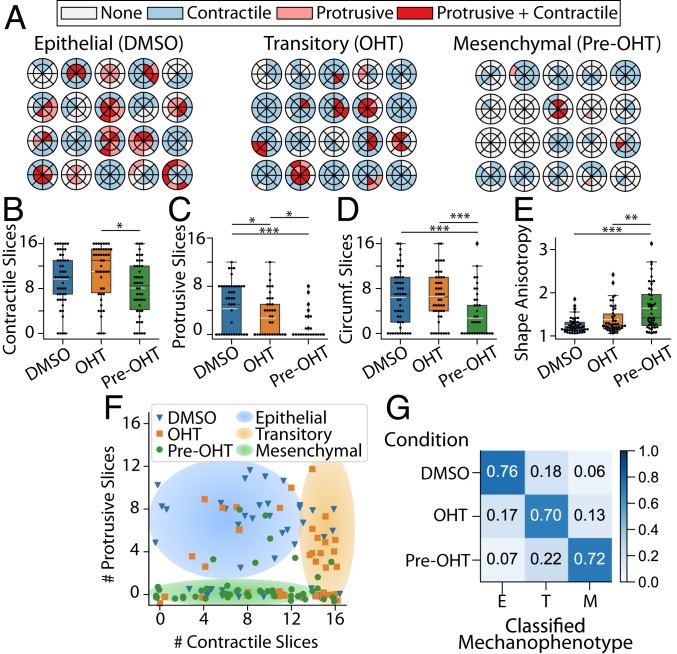
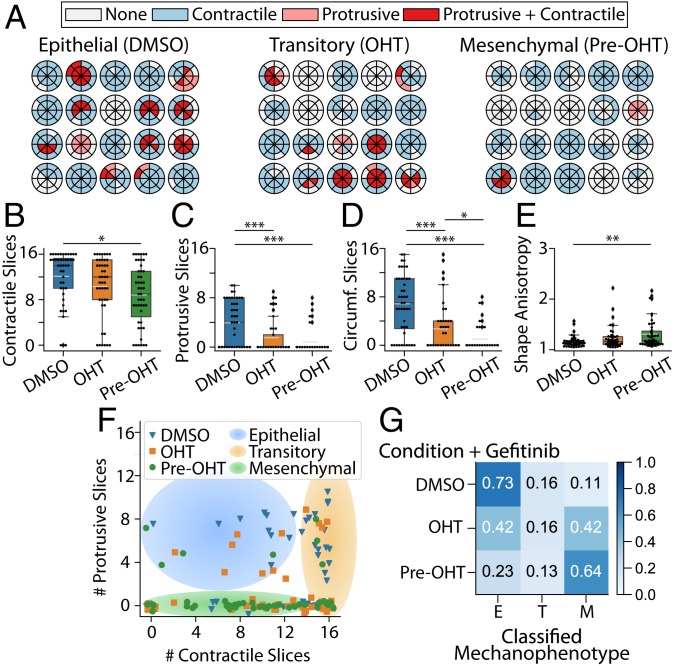
Representative DART analyses for clusters with epithelial, transitory, and mesenchymal mechanophenotypes captured these qualitative trends, although there existed appreciable heterogeneity across clusters. Epithelial and transitory clusters typically exerted numerous, spatially distributed contractile displacements ($\approx$10 or 11 slices), while mesenchymal clusters typically exerted fewer, localized contractile displacements ($\approx$8 slices or less) (Fig. 3 A and B). Next, epithelial clusters applied more protrusive displacements ($⪆$4 slices), which were considerably fewer for transitory and mesenchymal clusters (three and one slices, respectively) (Fig. 3 A and C). Moreover, epithelial and transitory clusters also exerted numerous circumferential displacements ($\approx$6 slices), while mesenchymal clusters showed fewer circumferential displacements ($\approx$3 slices) (Fig. 3D and SI Appendix, Fig. S6 A–C). Finally, epithelial and transitory clusters exhibited relatively compact morphologies (shape anisotropy $\approx$ 1), while mesenchymal clusters were more elongated ($\approx$ 1.6 or higher values) (Fig. 3E). These distinct cluster mechanophenotypes were compared based on their number of protrusive and contractile slices, revealing that epithelial clusters typically exhibited more protrusive deformations ($\approx$4 to 12 slices), while the distribution of contractile deformations varied (0 to 12 slices) (Fig. 3F). In comparison, transitory clusters typically exhibited fewer protrusive deformations (0 to 8 slices), but many distributed contractile deformations around the periphery ($\approx$13 to 16 slices) (Fig. 3F). Lastly, mesenchymal clusters exhibited minimal protrusive deformations ($\approx$0 slices) with a varying distribution of contractile deformations (0 to 16 slices) (Fig. 3F).

Fig. 3.

(A) Radial DARTS for 20 randomly selected clusters treated with DMSO, OHT, or pretreated with OHT (pre-OHT). (B) Boxplot of the number of contractile displacement slices. (C) Boxplot of the number of protrusive displacement slices. (D) Boxplot of the number of circumferential (Circumf.) displacement slices. (E) Boxplot for cell-morphology shape anisotropy. The white dashed line in the boxplots represents the mean value. *P $<$ 0.05; **P $<$ 0.01; ***P $<$ 0.001. (F) Scatter plot of raw data points for number of protrusive and contractile displacement slices ($P_s$ and $C_s$) for DMSO-treated, OHT-treated, or OHT-pretreated clusters. Jitter has been applied to the true positions of the raw data points to avoid points occlusion. The shaded regions are a guide to the eye to emphasize groupings of epithelial, transitory, or mesenchymal mechanophenotypes. (G) Normalized confusion matrix for the decision tree classifier using $C_s$, $P_s$, number of circumferential displacement slices (${\theta }_s$), and shape anisotropy ($SA$) metrics on the training data. E, epithelial; M, mesenchymal; T, transitory.

By using a decision tree, a commonly employed predictive classifier in computer science and machine learning, these three distinct mechanophenotypes were profiled based on contractile, protrusive, and circumferential deformations, as well as shape anisotropy (SI Appendix). Briefly, this analysis classified clusters based on a threshold number of protrusive slices (4.5), which was then refined based on shape anisotropy, number of circumferential slices, and contractile slices (SI Appendix, Fig. S7). We assessed and quantified the specificity and predictive capability of our decision tree via the standard machine-learning approach of using a confusion matrix. The classification via the confusion matrix showed 70% agreement between experimental condition and predicted mechanophenotype (epithelial, transitory, or mesenchymal), as shown in the on-diagonal entries of the confusion matrix (Fig. 3G). Moreover, 15 to 20% of clusters in each experimental condition were classified in an adjacent state (i.e., epithelial clusters classified as transitory, transitory clusters classified as epithelial or mesenchymal, etc.), corresponding to the neighboring off-diagonal entries of the confusion matrix (Fig. 3G). This classification may be attributed to biological heterogeneity, since MCF-10A cells can spontaneously undergo EMT, and EMT induction kinetics exhibit some variability (40). Nevertheless, classification across very dissimilar mechanophenotypes was relatively infrequent, at 6 to 7% (i.e., epithelial clusters classified as mesenchymal, or vice versa), corresponding to the entries at the top right and bottom left corners of the confusion matrix (Fig. 3G). Thus, epithelial, transitory, and mesenchymal clusters exhibit distinct morphologies and patterns of contractile, protrusive, and circumferential traction, which represent a characteristic “traction signature” or mechanophenotype.

Microtubule Stabilization with Taxol Enhances Protrusions and Localized Contractility.

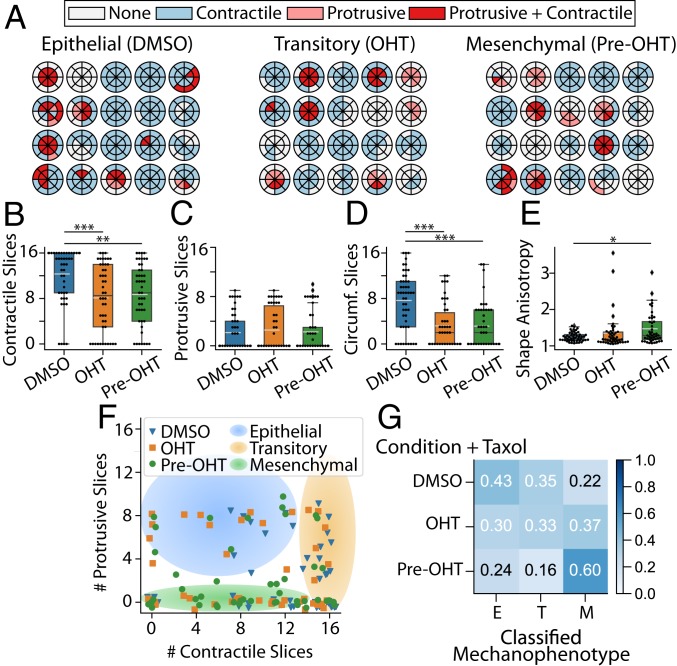
Cluster mechanophenotypes were perturbed by sublethal treatment with the microtubule-stabilizing agent Taxol, which can induce EMT (40). After 7 d of treatment with a sublethal dose of Taxol (4 nM) and 0.05% DMSO, clusters exhibited partially elongated morphologies reminiscent of the transitory mechanophenotype with OHT treatment only (SI Appendix, Fig. S8 A–C). Similarly, treatment with 4 nM Taxol and 500 nM OHT resulted in highly elongated morphologies reminiscent of the mesenchymal mechanophenotype after pretreatment of 500 nM OHT only (SI Appendix, Fig. S8 D–F). Pretreatment with 500 nM OHT and subsequent 4 nM Taxol resulted in unique cluster morphologies with slender, neuronal-like extensions (SI Appendix, Fig. S8 G–I). DART analysis of the cluster-induced matrix deformations corroborated these qualitative observations (Fig. 4A and SI Appendix, Fig. S6 D–F). For instance, Taxol- and DMSO-treated clusters typically exhibited more contractile slices ($\approx$12), fewer protrusive slices ($\approx$2), and more circumferential slices ($\approx$8), analogous to the transitory cluster mechanophenotype (Fig. 4 B–D and SI Appendix, SI Appendix, Fig. S6D). In comparison, Taxol- and OHT-treated clusters exhibited fewer contractile and circumferential slices ($\approx$8 and 2, respectively), analogous to the mesenchymal cluster mechanophenotype (Fig. 4 B and D and SI Appendix, Fig. S6E). Finally, Taxol- and OHT-pretreated clusters exhibited fewer contractile and circumferential slices ($\approx$8 and 2, respectively), as well as elevated shape anisotropy, also consistent with the mesenchymal cluster mechanophenotype (Fig. 4 B, D, and E and SI Appendix, Fig. S6F). Interestingly, Taxol- and OHT-treated or -pretreated clusters exhibited more protrusive slices ($\approx$2) than the comparable transitory and mesenchymal mechanophenotypes. Such behaviors may be attributed to actin- and microtubule-driven protrusions, which are associated with EMT (41). These outward protrusions may be stabilized by Taxol treatment, which inhibits microtubule depolymerization and impedes retraction (42). Overall, these trends were apparent on a plot of the contractile and protrusive slices per cluster, since Taxol- and DMSO-treated clusters were shifted rightward with more contractile slices (Fig. 4F) relative to the epithelial mechanophenotype in DMSO only (Fig. 3F). Moreover, Taxol- and OHT-treated or -pretreated clusters were shifted upward with more protrusive slices (Fig. 4F) relative to transitory and mesenchymal mechanophenotype with OHT treatment or pretreatment only (Fig. 3F). As a consequence, 35% of Taxol- and DMSO-treated clusters were classified as a transitory mechanophenotype (Fig. 3G). Similarly, 37% of Taxol- and OHT-treated transitory clusters were classified as a mesenchymal mechanophenotype (Fig. 3G). Finally, 60% of Taxol- and OHT-pretreated mesenchymal clusters were classified as a mesenchymal (OHT only) mechanophenotype (Fig. 3G). It should be noted that a significant percentage (24 to 43%) of Taxol-treated clusters were classified as an epithelial mechanophenotype, likely due to the increased number of protrusive slices (Fig. 3G). Thus, Taxol treatment biased clusters toward more transitory and mesenchymal mechanophenotypes by redistributing contractile and circumferential tractions, although protrusive tractions were also aberrantly enhanced relative to the previous experiments without Taxol.

Fig. 4.

(A) Radial DARTS for 20 randomly selected clusters treated with 4 nM Taxol combined with DMSO, OHT, or pretreatment with OHT (pre-OHT). (B) Boxplot of the number of contractile displacement slices. (C) Boxplot of the number of protrusive displacement slices. (D) Boxplot of the number of circumferential (Circumf.) displacement slices. (E) Boxplot for cell-morphology shape anisotropy. The white dashed line in the boxplots represents the mean value. *P $<$ 0.05; **P $<$ 0.01; ***P $<$ 0.001. (F) Scatter plot of raw data points for number of protrusive and contractile displacement slices ($P_s$ and $C_s$) for DMSO-treated, OHT-treated, or OHT-pretreated clusters. Jitter has been applied to the true positions of the raw data points to avoid points occlusion. The shaded regions are a guide to the eye to emphasize groupings of epithelial, transitory, or mesenchymal mechanophenotypes. (G) Normalized confusion matrix for the decision-tree classifier using $C_s$, $P_s$, number of circumferential displacement slices (${\theta }_s$), and shape anisotropy ($SA$) metrics on the training data. E, epithelial; M, mesenchymal; T, transitory.

EGFR Inhibition with Gefitinib Increases Heterogeneity of Transitory Clusters.

Lastly, cluster mechanophenotypes were perturbed by treatment with the EGFR inhibitor gefitinib, which ordinarily inhibits proliferation in epidermal growth factor (EGF)-dependent MCF-10A cells (43). Previously, cell lines expressing epithelial biomarkers were shown to be more sensitive to gefitinib and proliferated less in vitro and in vivo, while EMT was associated with resistance to gefitinib (44–46). Prior studies primarily focused on proliferation and apoptosis in bulk assays, with few higher-resolution measurements of migration and morphology. In these experiments, after 7-d treatment with 500 nM gefitinib (also a sublethal dose), DMSO-treated clusters exhibited compact morphologies consistent with the epithelial mechanophenotype (SI Appendix, Fig. S9 A–C). In comparison, gefitinib- and OHT-treated clusters exhibited both compact and elongated morphologies, reminiscent of epithelial and mesenchymal phenotypes (SI Appendix, Fig. S9 D–F). Finally, gefitinib- and OHT-pretreated clusters exhibited highly elongated morphologies, reminiscent of mesenchymal phenotypes (SI Appendix, Fig. S9 G–I). DART analysis revealed that gefitinib- and DMSO-treated clusters exhibited more contractile ($\approx$12), protrusive ($\approx$2), and circumferential ($\approx$8) slices with low shape anisotropy ($\approx$1) (Fig. 5 A–E and SI Appendix, Fig. S6G), consistent with an epithelial mechanophenotype. However, gefitinib- and OHT-treated clusters exhibited large variations in protrusive ($\approx$0 to 7) and circumferential ($\approx$0 to 5) slices relative to the transitory (OHT only) cluster mechanophenotype (Fig. 5 A, C, and D and SI Appendix, Fig. S6H). Overall, gefitinib- and OHT-pretreated clusters exhibited fewer contractile ($\approx$8), protrusive ($\approx$2), and circumferential ($\approx$2) slices with slightly increased shape anisotropy, analogous to a mesenchymal mechanophenotype (Fig. 5 A–E and SI Appendix, Fig. S6I). A plot of contractile and protrusive slices per cluster showed that gefitinib- and DMSO-treated clusters were located in the top left region associated with the epithelial (DMSO only) mechanophenotype. Similarly, gefitinib- and OHT-pretreated clusters were located at the bottom of the plot, associated with the mesenchymal (OHT pretreatment only) mechanophenotype. In comparison, the gefitinib- and OHT-treated clusters were widely dispersed toward the top and bottom of the plot (Fig. 5F). The decision-tree analysis revealed that 73% and 64% of gefitinib with DMSO- or OHT-pretreated clusters were classified as epithelial (DMSO only) and mesenchymal (OHT-pretreated) mechanophenotypes, respectively (Fig. 5F). Nevertheless, gefitinib- and OHT-treated clusters were mostly classified as either epithelial (42%) or mesenchymal (42%) mechanophenotypes, with relatively few clusters classified as transitory clusters (16%). Thus, gefitinib treatment did not significantly affect the DMSO- or OHT-pretreated cluster, which retained epithelial or mesenchymal mechanophenotypes, respectively. However, gefitinib and OHT treatment resulted in a mixed population of mostly epithelial and mesenchymal mechanophenotypes, with considerably fewer transitory clusters. This “switch-like” response may occur due to the strength of EGFR-dependent signaling relative to Snail-activated, EGFR-independent signaling (47), which will be characterized more in future work.

Fig. 5.

(A) Radial DARTS for 20 randomly selected clusters treated with 500 nM gefitinib combined with DMSO, OHT, or pretreatment with OHT (pre-OHT). (B) Boxplot of the number of contractile displacement slices. (C) Boxplot of the number of protrusive displacement slices. (D) Boxplot of the number of circumferential (Circumf.) displacement slices. (E) Boxplot for cell-morphology shape anisotropy. The white dashed line in the boxplots represents the mean value. *P $<$ 0.05; **P $<$ 0.01; ***P $<$ 0.001. (F) Scatter plot of raw data points for number of protrusive and contractile displacement slices ($P_s$ and $C_s$) for DMSO-treated, OHT-treated, or OHT-pretreated clusters. Jitter has been applied to the true positions of the raw data points to avoid points occlusion. The shaded regions are a guide to the eye to emphasize groupings of epithelial, transitory, or mesenchymal mechanophenotypes. (G) Normalized confusion matrix for the decision-tree classifier using $C_s$, $P_s$, number of circumferential displacement slices (${\theta }_s$), and shape anisotropy ($SA$) metrics on the training data. E, epithelial; M, mesenchymal; T, transitory.

Discussion and Conclusion

The DART analysis established here profiles multicellular cluster mechanophenotypes based on local displacements of tracer particles embedded in a 3D matrix, as well as cluster morphology. By combining these measurements into a machine-learning decision-tree structure, perturbations and transitions from one phenotype to another (e.g., epithelial to mesenchymal) as a function of drug treatment can be quantified in an automated fashion. This approach leverages previous developments in the machine-learning communities of reducing large, multivariable spatiotemporal datasets and binning them into a more intuitive scalar metric output. These measurements show that multicellular clusters exert a combination of protrusive, contractile, and circumferential deformations within a compliant 3D matrix relative to a reference state. Since these behaviors have not been previously characterized elsewhere, we do not have a well-defined “ground truth” for benchmarking these phenotypes. In principle, we could arbitrarily generate some deformation field as a “ground truth” in order to validate the DART classifier, but the relevance and scientific merit of this to our experimental results would be questionable. It should be noted that cluster morphology alone was insufficient to distinguish cluster phenotype across different experimental conditions. For example, the shape anisotropy of DMSO clusters was not significantly different from OHT clusters (Fig. 3E), although the OHT-pretreated clusters were more significantly elongated. Thus, high-resolution measurements of local matrix deformation can inform phenotypic classification for situations that are otherwise difficult to distinguish.

Our classification of multicellular cluster mechanophenotype directly considers spatial heterogeneity in the local 3D matrix deformation patterns. These observations of distinct spatial-displacement patterns were sufficient to classify 70% of cluster mechanophenotypes within a given experimental condition based on DMSO treatment, OHT treatment, or OHT pretreatment. It should be noted that some clusters were classified with a different mechanophenotype than would be expected from their experimental conditions. For instance, 17% of clusters treated with OHT were classified as an epithelial mechanophenotype, rather than transitory. Moreover, 18% of clusters treated with DMSO were classified as a transitory mechanophenotype rather than epithelial. It should be noted that single cells exhibit intrinsic, nongenetic heterogeneity from cell-cycle state, transcriptional noise, etc. This heterogeneity is likely compounded in multicellular clusters consisting of mechanically interacting cells. Indeed, we and others have shown that EMT can occur spontaneously based on local cell density in 2D monolayer culture (40, 48). Even relatively controlled EMT induction using this Snail–ER construct has some variability in the kinetics (37, 40). EMT is also regulated by the configuration of cell–cell adhesions, which will also result in heterogeneous tractions (49). Thus, the 70% value is reasonable given the underlying heterogeneity and plasticity of this cell type. In principle, other cell types may be “locked into” a more homogeneous mechanophenotype that could be profiled with near 100% agreement, but these cell types would not undergo EMT as readily. Further, we observed differences in tractions after treatment with EMT-inducing or -suppressing drugs, indicative of differences in drug sensitivity. Although computationally expensive, we envision that time-lapse imaging of clusters and associated tractions could further reveal how clusters interconvert between mechanophenotypes.

Clusters may also experience local differences in matrix properties, which could further amplify the measured phenotypic heterogeneity across different clusters. Fibrillar networks such as collagen I can be locally heterogeneous due to polydisperse fiber lengths and differences in connectivity, resulting in nonaffine deformations, nonlinear elasticity, and partially inelastic behavior (50). Moreover, clusters can locally degrade, deposit, or strain-stiffen the collagen I (30, 31, 51–53), as well as degrade silk fibroin (54). Our DART analysis only considers cluster-generated displacement fields relative to a reference state after the completion of the experiment and is agnostic to material properties, analogous with our previously demonstrated MDM analysis (29). Our measurements show that the spatial distribution of tractions are relatively consistent within experimental conditions, although they differ appreciably across conditions. In comparison, the magnitude of these displacements is relatively similar across experimental conditions, although we cannot discount some attenuation due to local alterations of matrix properties. An interesting possibility is that strong disagreement between cluster morphology and local displacements would indicate that matrix degradation or plastic deformation dominate over an elastic response, requiring additional corroboration. Improved constitutive equations could be used to determine cell-generated stresses (13), which could further improve our phenotypic classification. Differences in traction signature could potentially be driven by differences in ECM deposition. As an example, epithelial clusters exhibit “orbiting” motions as they deposit basement membrane around the periphery (55, 56). Our measurements of increased circumferential tractions in epithelial clusters are consistent with this mechanism. In future work, we envision additional characterization of local matrix microstructure and mechanics using optical tweezers (28, 31) or direct imaging of fibers (26).

In conclusion, DART establishes a quantitative and scalable framework to profile the heterogeneous matrix deformations of 3D multicellular clusters. Our analyses reveal that collective tractions are spatially nonuniform and cannot be captured using existing spherically symmetric (one-dimensional) analyses for individual cells or multicellular spheroids. We show that epithelial mechanophenotypes typically apply protrusive, circumferential, and contractile matrix deformations, while transitory mechanophenotypes after EMT exhibit mostly contractile and circumferential deformations that are widely distributed, and mesenchymal clusters exhibit localized contractility in only a few locations. We perturbed these behaviors using the microtubule stabilizer Taxol, which biases toward transitory or mesenchymal mechanophenotype, while also enhancing protrusions. In comparison, the EGFR inhibitor gefitinib drives clusters toward either epithelial or mesenchymal mechanophenotype in OHT-treated conditions, but has minimal effect on epithelial (DMSO) or mesenchymal (OHT-pretreated) mechanophenotypes. Thus, DART captures heterogeneity both within and across clusters in response to biochemical stimulation, with particular relevance for EMT in circulating tumor-cell clusters during cancer metastasis (12). We envision that DART can be implemented with a wide variety of 3D biomaterials at a 96-well-plate scale or beyond, enabling higher-throughput mechanophenotyping of organoids in 3D culture, including preclinical testing of human patient samples with personalized treatments.

Materials and Methods

Cell Culture and Matrix Preparation.

MCF-10A mammary epithelial cells stably transfected with an inducible Snail expression construct fused to an ER response element were a gift from D. A. Haber, Massachusetts General Hospital, Boston, MA (37). This cell line also overexpressed fluorescent proteins in the nucleus (mCherry-H2B) and cytoplasm (GFP) for live cell tracking. MCF-10A cells were routinely cultured in growth medium consisting of Dulbecco’s modified Eagle medium/F12 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid buffer (Fisher catalog no. 11330057) supplemented with 5% horse serum (Fisher catalog no. 16050122), 20 ng/mL Animal-Free Recombinant Human EGF (PeproTech catalog no. AF-100-15), 0.5 mg/mL hydrocortisone (Sigma catalog no. H0888), 100 ng/mL cholera toxin (Sigma catalog no. C8052), 10 $\mathrm{\mu }$g/mL insulin from bovine pancreas (Sigma catalog no. I1882), and 1% penicillin–streptomycin (Fisher catalog no. MT-30-002-CI).

Silk fibroin solution was extracted and purified from silkworm (Bombyx mori) cocoons (Treenway Silks), as described (36). Composite silk–collagen hydrogels were prepared through sonication-induced gelation initiation of silk fibroin, followed by the addition and neutralization of collagen I from rat tail tendon (Corning catalog no. 354249) to achieve a final hydrogel containing 7.5 mg/mL silk fibroin and 1 mg/mL collagen I (see SI Appendix for details). Briefly, silk fibroin was mixed into medium and then sonicated; 1 N sodium hydroxide was added in to achieve a final pH of 7.4; collagen I was mixed in well, followed by the addition of 5% 1-$\mathrm{\mu }$m fluorescent carboxylate-modified beads (Fluospheres; red 580/605); and, lastly, a single-cell suspension in medium was mixed in to yield 120,000 cells per mL.

Cells were embedded in 3D silk–collagen hydrogels with three experimental conditions: 1) Cells were cultured in 0.05% DMSO (the solvent used to suspend OHT) for 72 h in 2D culture, then embedded in 3D hydrogels with DMSO treatment. This condition served as the negative control and defined the “epithelial” mechanophenotype. 2) Cells were treated with 0.05% DMSO for 72 h in 2D culture, as in condition 1, then embedded in 3D hydrogels with 500 nM OHT (Sigma catalog no. H7904). This condition induces Snail expression through an ER construct (37) and defined the “transitory” mechanophenotype. 3) Cells were treated with OHT for 72 h in 2D culture to induce EMT and then embedded in 3D hydrogels with sustained OHT treatment to maintain Snail expression as a positive control, which defined the “mesenchymal” mechanophenotype.

Confocal Microscopy and Image Analysis.

Multicellular clusters and corresponding matrix displacements were imaged after 7 d of culture by using a Nikon Eclipse TiE fluorescence microscope with spinning-disk confocal head (Crest Optics X-light V2), with a light-guide coupled solid-state illumination system (Lumencor Spectra-X3), scientific complementary metal–oxide–semiconductor camera (Andor Neo), 20$\times$ Plan Apo objective (NA 0.75), GFP/fluorescein isothiocyanate Filter Set (Chroma catalog no. 49002), and tetramethylrhodamine isothiocyanate/DSRed Filter Set (Chroma catalog no. 49004). For the duration of time-lapse imaging, cells were maintained in a humidified environmental chamber at 37 °C and 5% ${\mathrm{C}\mathrm{O}}_2$. For matrix-displacement measurements, NIS Elements was used for automated image acquisition with z steps of 0.6 $\mathrm{\mu }$m from the bottom of the well to a height of 75 $\mathrm{\mu }$m under consistent exposure times, camera gain/gamma control, and aperture. All clusters analyzed were positioned in the center of the well and fully surrounded by 3D matrix, in order to avoid artifacts from longer-ranged mechanical interactions with the plate boundaries. The cluster centroids were uniformly distributed in $z$ throughout the imaging volume, and any clusters observed to adhere to the bottom were discarded. Visually, it was quite apparent when clusters mechanically interacted with the bottom, since they would preferentially disseminate downward through durotaxis, and so these clusters were not analyzed further. Further, manual inspection of DART plots across the remaining analyzed clusters confirmed that trends were consistent throughout the imaging volume at different heights. Images were acquired at 4-h intervals over a large number of wells ($n\hspace{0.17em}\approx$ 48 for each experiment) for a total of 16 h. In these experiments, cell cytoplasm was imaged in GFP and beads in the red fluorescent protein channel. At the end of time-lapse imaging, a reference state for the gel was obtained by lysing the cells within the hydrogels via sodium dodecyl sulfate. Since clusters remained relatively small at day 7 (<10 cells), every cell within the cluster was adherent to the surrounding ECM. Thus, every cell within the cluster was exposed at the periphery and would be lysed at the same time, regardless of experimental condition.

Measuring 3D Cell-Induced Deformations via TPT.

We utilized our previously developed TPT algorithm (39) to reconstruct the cell-induced 3D displacement fields by tracking individual fluorescent polystyrene microspheres (1 $\mathrm{\mu }$m) embedded as fiduciary markers in the silk–collagen matrix. The combination of light-emitting diode illumination-based spinning-disk confocal microscopy and low-NA objective for low-cost, high-throughput imaging of the 96-well-plate setup resulted in diminished signal-to-noise volumetric images. A custom image-segmentation and filtering routine was developed to allow precise and accurate localization and tracking using TPT for low-NA confocal imaging stacks (see SI Appendix for details).

Cell-Cluster Surface Segmentation.

The 3D cell-cluster surface was segmented from volumetric images of fluorescently labeled cytoplasm intensities (GFP channel). As a first step, the raw volumetric images were filtered by using a median filter with a $3\times 3\times 3$ voxel window to remove shot noise. Following, the images were filtered with a 3D Gaussian filter with $\sigma =2.5$. The images were then binarized by using adaptive image thresholding based on the local mean intensity (first-order statistics) in the neighborhood of each voxel. The sensitivity for the adaptive thresholding was manually set for each image to segment the cell clusters from the background appropriately. From the binary images, the small connected components having a total number of voxels <8,000 were set to an intensity value of 0 in the binary images. Morphological operations were performed to remove holes in the binary images (57). The volumes of the segmented binary images were increased by 1.6 $\mathrm{\mu }$m through a distance transform. Due to the large noise near the top and bottom of the volume, all of the voxels in the top and bottom eight z slices were set to 0 in the binarized images. The 3D triangulated cell-cluster surface was computed from the binary images by using MATLAB’s isosurface estimation at a target voxel value of 0.5. The triangulated cell-cluster surface mesh was smoothed by using accurate curvature flow smoothing (58). Finally, the centroid of the multicellular cluster was computed as the centroid of the segmented multicellular cluster from the binarized volumetric images of the fluorescent cell cytoplasm.

Statistical Analysis.

Experiments were repeated three times (external replicates), and a total of at least 40 clusters were analyzed per experimental condition. To compare DART and shape metrics across phenotype conditions, one-way repeated-measures (RM) ANOVA was used to check if the treatment data satisfied the Shapiro–Wilk normality test with P < 0.05. If the treatment data failed the Shapiro–Wilk normality test, Friedman RM ANOVA on ranks for comparing treatment differences was used. For all pairwise multiple comparisons, the Holm–Sidak posthoc test was used. The differences were considered to be statistically significant if P < 0.05. The statistical tests were performed by using SigmaPlot (Version 12.0).

In the figures, we used boxplots to visualize the distribution for each metrics. As per convention, boxplots show the data median, first quartile, third quartile, and data outliers marker through minimum and maximum values. The dots on the boxplots show the raw data values. The white dashed lines on the boxplots show the mean value. In the graphs, a statistically significant difference between two treatments is shown by a line connecting their boxplot with an annotation for the P value as follows: *P $<$ 0.05; **P $<$ 0.01; ***P $<$ 0.001.

Data Availability.

Code for DART Analysis is available at https://github.com/FranckLab/DART. Image data are available in ref. 59.