Summary
Multisite protein phosphorylation plays a critical role in cell regulation [1–3]. It is widely appreciated that the functional capabilities of multisite phosphorylation depend on the order and kinetics of phosphorylation steps, but kinetic aspects of multisite phosphorylation remain poorly understood [4–6]. Here we focus on what appears to be the simplest scenario, when a protein is phosphorylated on only two sites in a strict, well-defined order. This scenario describes the activation of ERK, a highly conserved cell signaling enzyme. We use Bayesian parameter inference in a structurally identifiable kinetic model to dissect dual phosphorylation of ERK by MEK, a kinase which is mutated in a large number of human diseases [4–6]. Our results reveal how enzyme processivity and efficiencies of individual phosphorylation steps are altered by pathogenic mutations. The presented approach, which connects specific mutations to kinetic parameters of multisite phosphorylation mechanisms, provides a systematic framework for closing the gap between studies with purified signaling enzymes and their effects in the living organism.
Results and Discussion
Multisite protein phosphorylation plays a critical role in signaling cascades regulating key cellular events, including the cell cycle and circadian rhythms [1–3]. Functional capabilities of multisite phosphorylation reactions depend on the order and kinetics of different phosphorylation steps [7,8]. Nevertheless, quantitative understanding of multisite phosphorylation kinetics remains elusive, even for the best studied examples [4–6]. This is largely due to the combinatorial complexity of multisite phosphorylation. Indeed, a protein with n phosphorylation sites can be found in 2n possible phosphostates, which may be connected by n! alternative pathways [9]. Here we focus on what appears to be the simplest multisite case, when a protein is phosphorylated on only two sites, and when the unphosphorylated and dually phosphorylated forms are connected by an ordered mechanism. Simple as it is, this case corresponds to the activation of the Extracellular Signal Regulated Kinase (ERK), a highly conserved signaling enzyme in metazoans [10].
ERK is activated when it is dually phosphorylated by MEK, a kinase that phosphorylates first the tyrosine and then the threonine within the TEY sequence in the regulatory loop of ERK [11]. Upon activation, ERK phosphorylates a broad spectrum of substrates including regulators of the cell cycle, cytoskeleton, and transcription. Mutations affecting either MEK or ERK are commonly associated with diseases, most notably cancers and developmental defects [12–17]. As a consequence, processes leading to ERK activation, such as ERK phosphorylation by MEK, or phosphorylation and activation of MEK itself, serve as successful drug targets in oncology [18]. While multiple mutations in MEK are known to affect the overall levels of dually phosphorylated ERK in vivo, their effects on the mechanism of ERK activation remain unknown [19–23]. Here we address this question using kinetic studies and Bayesian parameter inference.
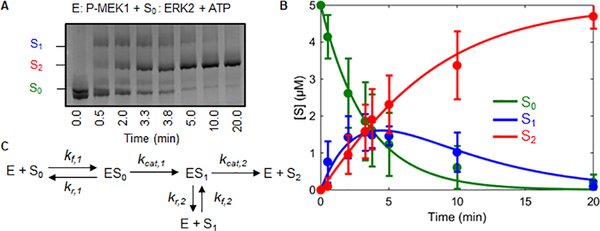
Our approach relies on transient kinetic analysis of ERK phosphorylation by MEK, using phostag gels to separate the unphosphorylated (S0), monophosphorylated (S1), and dually phosphorylated (S2) forms of ERK (Figures 1A, B) [24,25]. Kinetic data were analyzed via a mathematical model that describes ordered dual phosphorylation (Figure 1C). This is consistent with previous kinetic and structural studies showing that the tyrosine is phosphorylated before the threonine (Figures S3A–C) [26]. The species of this model correspond to the three phosphostates of ERK (S0–unphosphorylated ERK, S1–ERK phosphorylated on tyrosine, and S2–dually phosphorylated ERK), free enzyme (E), and two enzyme-substrate complexes (ES0 and ES1). The complex of MEK with monophosphorylated ERK can either dissociate or continue to dually phosphorylated product. Thus, this model contains both distributive and processive pathways, in which the two phosphorylations are carried out by either two separate enzyme molecules or the same molecule, respectively.
Figure 1. Determining kinetic parameters for MEK activation of ERK.
A) Kinetics of ERK phosphorylation by active wild type MEK. The three different ERK phosphostates were quantified via phostag gels. S0, S1, S2 represent unphosphorylated, monophosphorylated, and dually phosphorylated ERK respectively. B) Model fit to the kinetic data. The error bars indicate the standard deviation of the 12 replicates. The lines show a fit to the reduced model (Figure 2A) obtained using Bayesian inference. C) General model describing the mechanism by which a kinase phosphorylates a substrate with two ordered phosphorylation sites.
With two sets of association, dissociation, and catalysis rate constants for two sequential phosphorylations, the model has six parameters. We established that this model is structurally identifiable: given enough measurements, the values of these parameters can be identified from kinetic data (see SI). In practice, however, identifying parameters is extremely challenging, due to measurement noise and differences in the time scales of individual reactions [27,28]. As a consequence, parameter estimation commonly lead to ensembles of parameters that are equivalent in describing the data but are not readily suitable for mechanistic interpretation of the underlying dynamics. We ran into this challenge when we attempted to identify the six parameters of our model (Figure S2A).
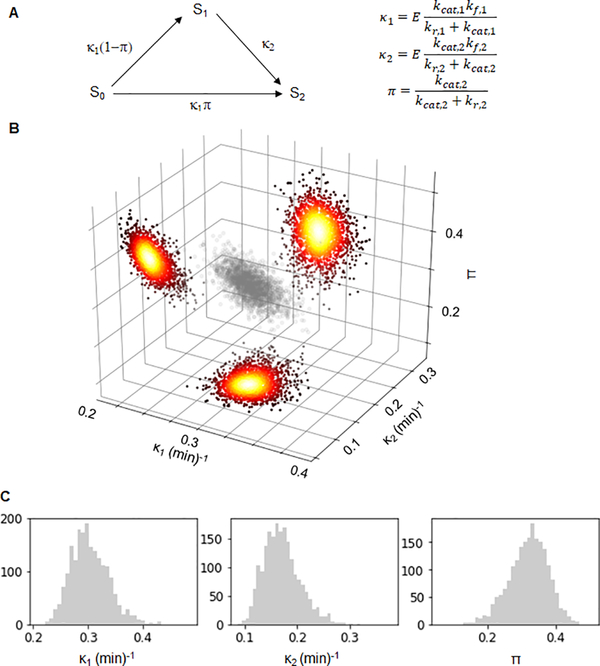
We noticed, however, that the ratio of total substrate to the Michaelis constant (KM = (kr + kcat)/kf) for each phosphorylation was below 1 (Figure S2B), indicating that we were not using a saturating substrate concentration. This observation agrees with previous biophysical measurements of MEK/ERK interactions in vitro that established that MEK and ERK bind with ~25 μM affinity, which is indeed greater than the maximal substrate concentration used in our experiments (5 μM) [29]. In this regime, the free enzyme concentration can be considered constant and equal to the total enzyme concentration (see SI). This justifies model reduction and leads to a simpler model with only three effective parameters (Figure 2A):
Figure 2. Bayesian analysis of ERK activation by wild type MEK.
A) The reduced three parameter model. The species S0, S1 and S2 correspond to different phosphostates of the substrate. The arrows and their labels denote rates of phosphorylation. The parameters κ1 and κ2 are the kinetic efficiencies of the first and second phosphorylation step, respectively, multiplied by the total amount of enzyme. The parameter π is the probability that both phosphorylations are carried out by the same enzyme. B) A scatter plot of 2000 parameter values sampled from the posterior distribution of Bayesian inference of the parameters corresponding to wild type MEK (grey). Accompanying the plot are heatmaps of the kernel density estimations of the 2D marginal distributions of the respective parameter pairs. C) Histograms of the Bayesian posterior samples for the three parameters (from left to right: κ1 (min)−1, κ2 (min)−1 and π). See also Table S1, Figures S1 and S2.
The first two parameters are products of enzyme concentration, which is controlled by experimental design, and kinetic efficiencies (kcat,1(2)/KM,1(2)) of the first and second phosphorylations. The third parameter can be interpreted as the probability that both phosphorylations are carried out by the same enzyme molecule, without an intervening dissociation step. This is a measure of processivity: the π = 0 limit corresponds to the fully distributive regime, when monophosphorylated ERK necessarily dissociates from MEK following the first phosphorylation step. When π = 1, monophosphorylated ERK remains associated with MEK and proceeds directly to the second phosphorylation step.
While the full model is nonlinear and must be solved numerically, the reduced model is linear and can be solved analytically, leading to compact expressions for the time-dependent concentrations of the three ERK phosphostates:
where Stot is the total substrate concentration. We established that the reduced model is also structurally identifiable (see SI). Based on this result, we used a Bayesian approach to parameter inference. This approach naturally accounts for measurement noise and yields a posterior distribution of parameters instead of their point or interval estimates [30]. We performed Bayesian inference of the three model parameters assuming a broad prior and used Markov Chain Monte Carlo methods to sample from the posterior distribution (see SI). As a result, the kinetic data gave rise to a sample from the posterior distribution in the three-dimensional parameter space (Figure 2B, Figure S1A). This approach is readily applicable for inferring kinetic parameters of mutants that are used in basic research or are associated with diseases (Figure 3A).
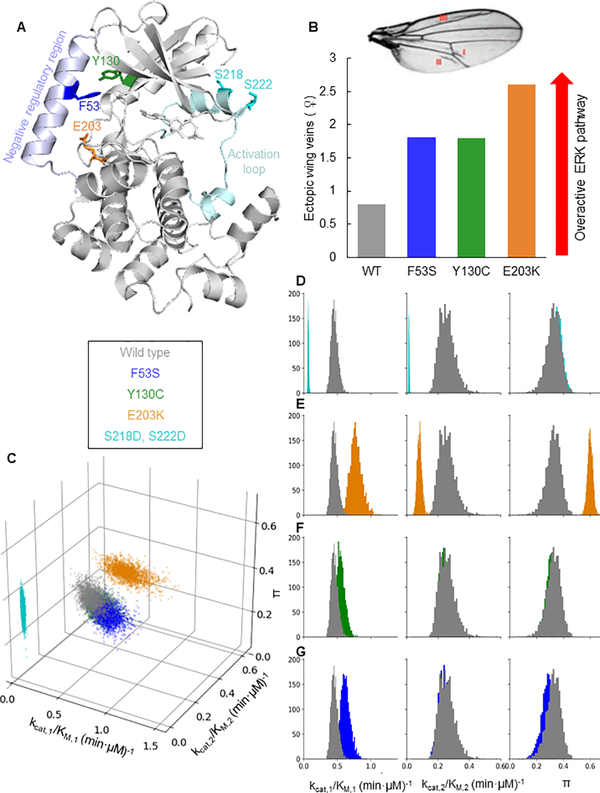
Figure 3. Mutations in MEK can be categorized based on kinetic parameters.
A) Positions of the mutations on MEK1 (PDB 3EQI [39]). The residues F53, Y130, and E203 are located between the interface of the negative regulatory helix and the kinase domain. S218 and S222 are located in the activation loop. B) Illustration of MEK mutant quantification of phenotype severity from previous study [41]. Overactivation of the ERK pathway leads to ectopic veins in fly wings. Shown are the number of ectopic veins in flies expressing the different MEK variants. C) A scatter plot showing parameter values sampled from the posterior distribution of the Bayesian inference for each MEK variant. The catalytic efficiency of the first phosphorylation is plotted on the front horizontal axis, the catalytic efficiency of the second phosphorylation on the right horizontal axis, and the processivity π on the vertical axis. Colors correspond to MEK variants. While the parameter values of the wild type MEK, F53S, and Y130C are indistinguishable, the parameter values for E203K and S218D, S222D are distinct. D-G) Histograms of the Bayesian posterior samples for the three parameters. Each histogram contains values for the parameter indicated by the column label and was obtained using Bayesian inference. Each histogram color corresponds to a MEK variant (cyan for S218D,S222D; orange for E203K; green for Y130C; blue for F53S). The grey histograms correspond to parameters for the wild type MEK. κ1 and κ2 are normalized by enzyme concentration to obtain kcat,1/KM,1 (min·μM)−1 and kcat,2/KM,2 (min·μM)−1. See also Figures S3 and S4.
In particular, the first phosphorylation step is commonly studied using ERK in which the threonine for the second phosphorylation is changed to alanine [31]. When we performed our analysis with this ERK mutant, we observed that the kinetic efficiency of the first phosphorylation is ~2-times higher when the second phosphorylation site is disrupted (Figures S1B–C). This highlights the importance of working with the wild type ERK to obtain biologically relevant rate constants. Furthermore, multiple studies have used phosphomimetic MEK variants rather than the wild type MEK activated by Raf [31–36]. In one of these variants (S218D,S222D), the two serines in the activation loop are changed to aspartates, mimicking the negative charge introduced by phosphorylation [31,37]. This variant is known to be less active than phosphorylated MEK, but its use simplifies experimental design. Indeed, when we repeated our Bayesian analysis of kinetic data obtained using this phosphomimetic MEK (Figure S4), we found that kinetic specificities for both phosphorylation steps are significantly lower than those for the dually phosphorylated wild type MEK (Figure 3C). However, the processivities of the wild type and phosphomimetic enzymes are essentially the same and significantly greater than zero, indicating that ~1/3 of ERK molecules are dually phosphorylated in a single enzyme/substrate encounter. This result can be understood by examining the definitions of κ1, κ2, and π. By decreasing the rate at which MEK binds to unphosphorylated and monophosphorylated ERK, the SSDD mutation could decrease the catalytic efficiencies of both phosphorylations while keeping the processivity constant.
Next, we analyzed the kinetic parameters of three MEK variants associated with human diseases. Each of these variants is characterized by a single amino acid substitution that disrupts the intramolecular contacts with the N-terminal negative regulatory region of MEK (Figure 3A) [38,39]. In parallel with the phosphorylation of serines within the activation loop, this region provides allosteric control of MEK activation. The E203K variant was identified in a human cancer, while the F53S and Y130C variants were found in humans with a broad spectrum of developmental abnormalities, including congenital heart defects and stunted growth [12,40]. Studies in fly and fish embryos suggest that the E203K substitution results in the most active MEK, based on the severity of disruptions to ERK-dependent morphogenetic processes [21,41]. For example, using ectopic veins in fly wings as an indicator for ERK pathway overactivation, Jindal et al. found that E203K causes a phenotype that is much stronger than the phenotypes caused by the F53S and Y130C variants (Figure 3B) [41]. Can these phenotypic differences be attributed to corresponding changes in the kinetic parameters of the mutant enzymes?
Our analysis of E203K MEK kinetic data (Figure S4) revealed that the catalytic efficiency of the first phosphorylation step is indeed strongly increased for E203K MEK, almost 2-fold when compared with the wild type enzyme (Figures 3C, E). This increase is accompanied by a pronounced reduction in the efficiency of the second phosphorylation step and a dramatic increase of processivity, indicating that more than half of ERK molecules are dually phosphorylated by the same enzyme. Thus, the processivity of MEK can be increased not only by crowded conditions and scaffolding proteins, as was suggested by earlier studies [35,36], but also by activating mutations (Figures 3C, E). Notably, however, the E203K mutation did not affect the ordering of the dual phosphorylation mechanism (Figures S3A–C).
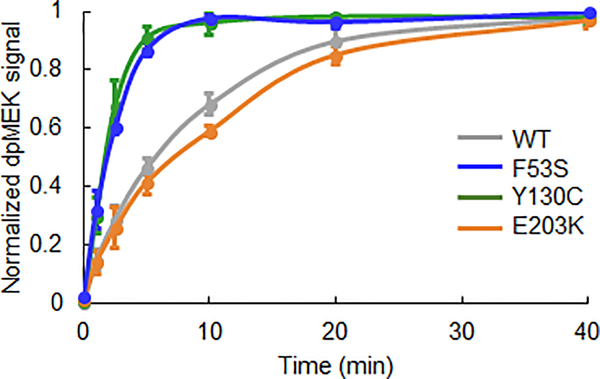
In contrast to the effects observed for E203K, kinetic parameters of ERK phosphorylation by the F53S and Y130C variants remain largely unchanged from the wild type MEK (Figures 3C, F, G, Figure S4). This is puzzling as these mutants show clear phenotypes in vivo and are associated with diseases (Figure 3B). To test if the phenotypic effects stem from changes in other processes, such as the activation of MEK itself, we analyzed the kinetics of MEK phosphorylation by Raf. This analysis revealed that both F53S and Y130C are activated significantly faster than wild type MEK (Figure 4). Interestingly, the activation kinetics of E203K MEK, are indistinguishable from those of the wild type MEK. Thus, our analysis reveals which of the multiple processes involved in multisite phosphorylation are affected by each mutation.
Figure 4. Quantification of MEK activation by Raf via Western Blot.
Raf activates the F53S and Y130C variants faster than it activates the wild type MEK and the E203K variant. The normalized dually phosphorylated (dp) MEK signal is an average of three experimental replicates and the error bars represent the standard error of the mean.
Together, this study takes a step towards closing the gap between work with purified signaling enzymes and their effects in the living organism. In particular, it has been proposed that distributive regime of ERK phosphorylation by MEK plays a key role in the emergence of switchlike responses in larger biochemical networks that contain the ERK phosphorylation reaction [42–45]. Our results establish that both distributive and processive pathways must be considered in analyzing the emergence of these systems-level effects for both wild type enzymes and their pathogenic variants.
While kinetic parameters may be estimated using a wide variety of approaches [46], we used model reduction and Bayesian inference because they are well-suited to our particular goals of systematic comparison of MEK variants. Specifically, our attempts to estimate parameters of the original model failed to constrain the values of individual rate constants and identified a large ensemble of six-dimensional parameter vectors that provide equivalent fit to data (Figure S2A). Importantly, the values of the effective parameters computed on the basis of this ensemble were highly constrained, which gave us the ability to compare the kinetics of the various MEK mutants using Bayesian inference with the analytically solvable reduced model. We believe that rationally reduced models will continue to play a key role in establishing a deeper understanding of cell regulation systems, including their quantitative responses to mutations of constituent proteins.
STAR Methods
LEAD CONTACT AND MATERIALS AVAILABILITY
Further information and requests for materials, resources and reagents, including the plasmids generated in this study, should be directed to and will be fulfilled by the Lead Contact, Stanislav Shvartsman (stas@princeton.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Plasmids
The pET-28a plasmid containing N-terminally His6-tagged human MEK (His6-MEK) was obtained as a gift from E. Goldsmith (UT Southwestern). This plasmid is under the T7 promoter and is under the control of the lac operon. All plasmids containing MEK mutations were mutagenized from the His6-MEK plasmid. For site-directed mutagenesis, His6-MEK was PCR amplified with forward and reverse primers containing the desired mutations (Table S1). For the PCR, high fidelity Pfu Ultra II Fusion HS DNA polymerase (Agilent Technologies) was incubated with 10ng His6-MEK plasmid, 1μM each of the primers, 250μM dNTP, and 1x PFU Ultra II buffer (Agilent Technologies). The solution underwent 25 polymerase chain reaction cycles at 55°C denaturing temperature and 2 minutes extension time. The PCR product was digested with DpnI, then transformed into competent DH5α cells, prepared using the Mix & Go! E.coli Transformation Kit (Zymo). Individual colonies were picked and grown in 5mL LB medium supplemented with 50 μg/ml Kanamycin at 37°C overnight. The plasmid was purified via QIAprep Spin Miniprep Kit (Qiagen). Mutations were confirmed via Sanger sequencing (Genewiz).
Recombinant protein purification
Rat His6-ERK was purified as previously described [21]. Plasmids containing the desired mutations were transformed into BL21 DE3 cells (NEB BioLab) for protein expression. 50mL cultures of E. coli BL21 cells expressing His6-ERK were grown in LB supplemented with 100μg/uL Ampicillin overnight at 37°C and inoculated into 2L of terrific broth with 100 μg/uL Ampicillin at 37°C and 250 r.p.m. After the OD600 reached ~0.8, protein expression was induced by adding 0.5mM final concentration of isopropyl β-D-1- thiogalactopyranoside (IPTG). The growth temperature was reduced to 20°C and the agitation lowered to 180 r.p.m. for overnight expression. The culture was harvested the next morning by centrifugation at 4°C at 3000g with Beckman J2-MI centrifuge with JA-10 rotor. Cells were lysed on ice using 0.25mg/mL lysozyme in 40mL lysis buffer (50mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES) pH 7.2, 500mM NaCl and 1x protease inhibitor (Sigma Aldrich) for 30 minutes. After lysozyme digestion, the lysate was tip sonicated using Fisher Scientific Model FB50 with CL-18 tip at 35% output on ice with 1 min on and 1 min off for 15 times for further lysis. The lysate was centrifuged at 8000 g with a Beckman Coulter Allergra 25R centrifuge with TA-10–250 rotor for 10 min at 4°C. The supernatant was applied to 1mL His-FF crude column (GE) using the ÄKTA pure protein purification system (GE) with a 0.5mL/min flow rate. The column was washed with 15% elution buffer (50mM HEPES pH 7.2, 500mM NaCl, 250mM imidazole) for 3 column volumes. Then 1.5mL fractions were collected as the proteins were eluted with a 15–100% gradient over 20 column volumes. The purities of the proteins were confirmed to be greater than 90% by Coomassie-stained SDS-PAGE gels. The purified protein was exchanged into the phosphorylation buffer (50mM HEPES pH 7.2, 100mM NaCl, 20mM MgCl2, 5% glycerol) and concentrated using the Vivaspin 20, 30kDa concentrator (Satorius) to 1.5mg/mL. Protein concentrations were determined to be 1.50mg/mL ±0.05mg/mL by determining the A280 using Nanodrop (Thermo Scientific Nanodrop lite) with an extinction coefficient of 42230 cm−1M−1. 25μL aliquots were flash-frozen using liquid N2 and stored at −80°C until use.
Human His6-MEK variants were expressed in E. coli BL21 DE3 cells supplemented with 50 μg/uL Kanamycin and purified using the same procedure as described above except that the MEK variants were determined to be 0.50mg/mL±0.05mg/mL by determining the A280 using Nanodrop with an extinction coefficient of 23620 cm−1M−1. All protein measurements were expressed as mean±SD from 4 measurements. All exctinction coefficeints were calcualted using the protein sequence and Northwestern Center for Biotechnology’s Peptide Property Calculator.
METHOD DETAILS
ERK phosphorylation by MEK
To prepare activated MEK, 6.5μM of MEK was added to a master mix containing the phosphorylation buffer, 5mM ATP, and 0.05μM of active human c-Raf (Millipore). The reaction mixture was incubated in a 30°C for 1.5 hours. To ensure that MEK was fully activated, we took aliquots throughout the 1.5 hours and ran the samples using phos-tag gel electrophoresis as described below to ensure that the non-phosphorylated form had fully disappeared. We performed Western Blot against dually phosphorylated MEK (1:4000 dilution, Cell Signaling Technology, Cat#9121, RRID: AB_331648) with Alexa Fluor 647 conjugates as the secondary antibody (1:2000 dilution, Invitrogen Cat#A-31573, RRID: AB_2536183) to ensure complete phosphorylation. To initiate the MEK-ERK reaction, 0.67μM of activated MEK was then added to a master mix containing phosphorylation buffer, 5mM ATP, and 5μM ERK. The enzyme to substrate ratio was chosen to ensure that the reaction ran to completion within a reasonable timeframe. Time points were chosen to best capture the dynamics of the peak concentration of the monophosphorylated form. Time point samples were collected by adding 4uL of the reaction to 1.5uL of 4x SDS loading buffer (250mM Tris-HCl pH 6.8, 10% SDS, 0.01% bromophenol blue, 40% glycerol, 2.86M β-mercaptoethanol) at 0.0, 0.5, 2.0, 3.3, 3.7, 5.0, 10.0, and 20.0 minutes. The samples were heated at 60°C for 10 minutes to break the disulfide bonds. For phosphomimetic MEK (S218D,S222D MEK), 2.5μM of phosphomimetic MEK was added and aliquots were taken out at 0.0, 1.0, 2.0, 3.3, 5.0, 10.0, 20.0, and 40.0 minutes.
Phos-tag gel
5uL of each sample was loaded onto Wako SuperSep Phos-tag 12.5% 17 well gel (Wako, Cat#195–17991) and ran at 175V for 160 minutes with Tris/Glycine/SDS running buffer (Bio-Rad). To visualize the gel bands, the gel was stained with Coomassie R staining solution (0.05% w/v Coomassie Brilliant Blue R, 25% isopropanol and 10% acetic acid) for 30 minutes before destaining with 10% acetic acid until the bands were clearly visible. The phos-tag gels were imaged using the Bio-Rad ChemiDoc MP Imaging System. The intensities of the bands were quantified using ImageJ’s (ImageJ, RRID: SCR_003070) ‘gels’ tool to measure the area of the peak.
MEK activation by Raf-1
0.05μM of active human c-Raf (Millipore) was added to 6.5μM of MEK in the phosphorylation buffer containing 5mM ATP. The reaction mixture was incubated in a 30°C water bath and 4μL aliquots were taken at 0.0, 1.0, 2.5, 5.0, 10.0, 20.0 and 40.0 minutes and added to 1.5μL of 4x SDS loading buffer to quench the reaction. The samples were heated at 60°C for 10 minutes to break the disulfide bonds. 5μL of each sample was loaded onto a 15-well Any kD Mini-PROTEAN TGX Precast Protein Gel (Bio-Rad) and ran at 200V for 45 minutes. The proteins were transferred onto a TransBlot Turbo LF PDVF membrane (Bio-Rad) using the TransBlot Turbo system (Bio-Rad). The membrane was then pre-incubated in 4% w/v milk powder in PBST (1x PBS + 0.1% Tween-20) for one hour. The membrane was then incubated in 4% milk containing primary antibody against dually phosphorylated MEK (1:4000 dilution, Cell Signaling Technology) overnight. After three 15-minutes washes in PBST, the membrane was switched into 4% milk containing the secondary antibody donkey Alexa Fluor 647 anti-rabbit conjugate (1:2000 dilution, Invitrogen) for 1 hour. After another three 15-minutes washes in PBST, the membrane was imaged using the Bio-Rad ChemiDoc MP Imaging System. The intensities of the bands were quantified using ImageJ’s ‘gels’ tool to measure the areas under the peaks.
Phosphorylation ratio by mass spectrometry
From a reaction of ERK phosphorylation by activated MEK E203K, 20μL of sample was collected at 3 minutes 15 seconds. The reaction was stopped by adding the sample to 60 μL 10M Urea. To remove salts and glycerol, a TCA precipitation was performed with the following procedure: 8 μL of chilled 0.15% N-Laurylsarcosine sodium and 8 μL of chilled 100% TCA were added to the sample on ice and mixed by inverting the tube a few times. After 15 minutes, the sample was centrifuged at 4°C for 10 minutes and the supernatant was removed. 0.4mL of 100% methanol was added and the solution was vortexed for 10 seconds. The supernatant was removed after centrifugation and another 0.4mL of 100% methanol was added, the solution vortexed, centrifuged and the supernatant removed. The resulting protein pellet was air dried and subsequently resolubilized in 10 μL of 6M guanidine hydrochloride (GuHCl).
Synthetic AQUA peptides were ordered from JPT Peptide Technologies. These peptides have heavy arginine incorporated (+10.00826859 Da) and correspond to the tryptic peptides of the pY-phosphorylated, and the pT-phosphorylated forms of ERK. 3uL of each AQUA (14μM in HPLC water) was added to the sample and the sample was diluted to 2M GuHCl with 10mM EPPS ph8.5 and digested overnight at 22°C with 10ng/ μL lysC (Wako, 2μg/ μL stock in HPLC water). The next morning, the sample was further diluted to 0.5M GuHCl with 10mM EPPS pH 8.5 and an additional 10ng/ μL LysC and 20 ng/ μL Trypsin (Promega) were added. The sample was incubated overnight at 37°C. All solvent was removed in vacuo and resuspended in 5% phosphoric acid. To desalt, stage-tip was performed, and the sample was resuspended in 40 μL 10% TFE, 1% TCA. 1μL was analyzed by LC-MS.
The Orbitrap Fusion Lumos (Thermo Fisher) was coupled with an Easy nLC 1200 high pressure liquid chromatography HPLC (Thermo Fisher) with an autosampler. For each run, injected peptides were separated on a 100μm inner diameter microcapillary column with ~0.5cm of 5μm BEH C18 beads (Waters) and 30cm of ~1.7μm BEH C18 beads (Waters). A 16–36% ACN gradient in 0.125% formic acid and 2% DMSO was applied over 40 minutes at 350nL/min. Ion transfer tube was maintained at 300°C and electrospray ionization was enabled by applying a voltage of 2.6 kV through a microtee at the inlet of the microcapillary column. The mass spectrometer was operated in data dependent mode with a survey scan using the Orbitrap at a resolution setting of 120k with a scan range of 500 – 850 m/z with an RF Lens (%) of 30, AGC target of 1.0E6 and a maximum injection time of 100 ms. Charge states between 2+ and 6+ were included. A dynamic exclusion window of 5 seconds with a mass tolerance of +/− 10 ppm was used. Peptides were fragmented using 30% HCD collision energy. MS2 spectrum was acquired using the Orbitrap at a resolution of 15k with an AGC target of 5.0e4 and a maximum injection time of 250 ms.
The Gygi Lab GFY software licensed from Harvard was used to convert mass spectrometric data from the Thermo RAW file to the mzXML format, and to correct erroneous assignments of peptide ion charge state and monoisotopic m/z. We used RawFileReader libraries from Thermo, version 4.0.26 to convert the raw files into mzXML file format. Assignment of MS2 spectra was performed using the SEQUEST algorithm by searching the data against the appropriate proteome reference dataset acquired from UniProt (Homo sapiens with Proteome ID UP000005640, Organism ID 9606, Protein count 74349; Escherichia coli (strain K12) with Proteome ID UP000000625, Organism ID 83333, Protein count 4391; both downloaded in June,2017) including 114 common contaminants like human Keratins and Trypsin [47,48]. The target-decoy strategy was used to construct reversed sequences in order to estimate the false discovery rate on the peptide level [49]. SEQUEST searchers were performed using a 20ppm precursor ion tolerance where both n and c-termini were required to be consistent with the protease specificity of Lys-C and Trypsin. Fragment ion tolerance in the MS2- spectrum was set at 0.02 Th. N-ethyl maleimide (+125.047679 Da) was set as a static modification on cysteine residues. Oxidation of methionine (+ 15.99492 Da), heavy arginine (+10.00826859 Da), and phosphorylation at serine, tyrosine, and threonine (+79.9663304104 Da) were set as variable modifications. A peptide level MS2 spectral assignment false discovery rate (FDR) of 0.5% was obtained by applying the target decoy strategy with linear discriminant analysis. The linear discriminant analysis used the following features: SEQUEST parameters XCorr and ΔXCorr, charge state, peptide length and absolute peptide mass accuracy. Forward peptides within three standard deviation of the theoretical m/z of the precursor were used as the positive training set. All reverse peptides were used as the negative training set. Peptides of at least seven amino acids were rank ordered by linear discriminant analysis score and were filtered to the desired cutoff. Peptides were assigned to proteins and filtered with 0.5% FDR on the protein level using the “picked” protein FDR approach [50]. Protein redundancy was removed by assigning peptides to the minimal number of proteins which can explain all observed peptides.
The elution profiles of the pT and the pY tryptic peptides were extracted using Xcalibur Qual Browser (Thermo), focusing on the base peak with m/z of range 741.99–742.00 (sample) and 745.32–745.34 (AQUA). The 3+ tryptic peptide of the mono phosphorylated ERK has a theoretical m/z of 741.99507 and the corresponding AQUA with heavy arginine has a theoretical m/z of 745.33116. The extracted information was processed in Excel (Microsoft). Despite an equal amount of the pY- and pT- phosphorylated AQUA were spiked into the sample, the two peptides have different detection signal because of their difference in flyability. We therefore normalized the peak intensity of the sample to the corresponding maximum peak intensity of the AQUA and smoothen the chromatogram by taking the 5-point moving average. The area under the curve for each of the four peaks was calculated using the trapezoidal method and the ratio between the sample and the AQUA calculated for both the pT- and the pY-phosphorylated peptides. The MS2 spectrum corresponding to the pY- and the pT-phosphorylated peptides with labeled information were extracted using the SuperDig tool from the Gygi Lab GFY software. The mass spectrometry proteomics data have been deposited to the ProteomeXchange Consortium via the PRIDE partner repository with the dataset identifier PXD016580 [51,52].
Kinetic modeling
Equations 1–6 describe the kinetics of dual phosphorylation of a substrate S by an enzyme E. The substrate exists in 3 different phosphostates, S0, S1, and S2, where the index indicates whether the substrate has been phosphorylated 0, 1, or 2 times. Both S0 and S1 bind reversibly to the enzyme E, forming complexes ES0 and ES1, respectively. At t = 0, all substrate is in the S0 state and all enzyme molecules are free.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Equations 7–8 describe the conservation laws for substrate and enzyme, respectively.
| (7) |
| (8) |
Reduced model
Since Stot << (kr,1 + kcat,1)/kf,1 and Stot << (kr,2 + kcat,2)/kf,2, we can use the pseudosteady-state approximation to get the following system of three linear equations:
| (9) |
| (10) |
| (11) |
where KM,1 = (kr,1 + kcat,1)/kf,1 and KM,2 = (kr,2 + kcat,2)/kf,2.
To simplify notation, we introduce κ1 = Etotkcat,1/KM,1, κ2 = Etotkcat,2/KM,2, and π = kcat,2/(kr,2 + kcat,2). Eqs. 9–11 become:
| (12) |
| (13) |
| (14) |
and have the following solutions:
| (15) |
| (16) |
| (17) |
Identifiability
To determine if the parameter values of the reduced model (Equations 12–14) could be recovered from data, we tested their structural identifiability using the time course data consisting of multiple trials of the measurable output (S0,S1,S2). A model is structurally identifiable if there is a subset of the parameter space such that any parameter can be uniquely determined from noise-free measurable output. Establishing structural identifiability is a first step before inferring parameters. We found that the model is structurally identifiable using the differential algebra method [53] as implemented in the software DAISY [54].
Bayesian parameter inference
This posterior distribution is proportional to the likelihood times the prior distribution of the parameters before any data is observed. We assumed that the distribution of the given measurements is governed by Equations 15–17 convoluted with Gaussian white noise. Thus, we infer κ1, κ2, and π, the three parameters in Equations 15–17, and the standard deviation σ, which is constant across observations. Measurements of the three states, and , are taken from n different replicates at 7 time points, so our sample space is for each of the MEK variants; the number of replicates was equal to 12 for wild type MEK and 5 for MEK variants with phosphomimetic or activating mutations.
If S is the analytic solution of Equations 15–17, a three dimensional real vector depending on the parameters, as well as on time t, gives rise to the likelihood via , where i indicates the replicate of the measurement, denotes the multivariate normal distribution with mean vector S(κ1,κ2,π,t) and covariance matrix σ2I3. We chose the prior distributions, κ1, κ2, σ~Unif(0,10), and π~Unif(0,1)asπ can only take parameters in this range.
We used PyStan distribution of the STAN software for Bayesian Analysis [55], which allows us to sample approximately from the posterior distributions using Markov Chain Monte Carlo methods. In our implementation, we used four chains with 500 warm-up draws and 500 post-warm-up draws, respectively.
QUANTIFICATION AND STATISTICAL ANALYSIS
MATLAB version R2016a was used for least squares fitting. The differentiable algebra method using the software DAISY was used to verify that the model is structurally identifiable [53,54]. The reduced ODE model is described in detail in the Reduced model section of the Method Details. Priors and likelihood of Bayesian inference are described in detail in the Bayesian parameter inference section of the Method Details. PyStan version 2.19 distribution of the statistical software STAN was used to access information on the posterior distribution via approximate sampling. STAN used Hamiltonian Markov Chain Monte Carlo to approximately sample from the posterior distribution. In total, N=2000 samples were drawn from four Markov chains. Each sample is a four dimensional real vector, containing the three biological parameters and the standard deviation of the Gaussian noise, denoted σ. From each chain, 500 warm-up draws were performed and discarded before drawing 500 further samples, which we then analyzed. For each of the four mutant MEK variants, we checked that the chains were sufficiently burnt in after the warmup phase by looking at trace plots and output statistics, in particular, the Rhat parameter and the effective sample size estimates. The resulting histograms for the marginal distributions of the three parameters of interest in are shown Figure 3D.
The parameter means reported by PyStan are as follows:
| Variant | Wild Type | Y130C | F53S | E203K | SSDD |
|---|---|---|---|---|---|
| κ1 | 0.29 | 0.36 | 0.41 | 0.64 | 0.17 |
| κ2 | 0.19 | 0.16 | 0.16 | 0.10 | 0.03 |
| π | 0.30 | 0.30 | 0.28 | 0.55 | 0.35 |
| σ | 0.10 | 0.07 | 0.09 | 0.11 | 0.12 |
Error bar definitions can be found in figure legends. The number of experimental replicates for the dual phosphorylation of ERK by wild type MEK is reported in the legend of Figure 1. The number of experimental replicates for the dual phosphorylation of ERK by the four mutant MEK variants is reported in the Bayesian parameter inference section of the Method Details. The number of experimental replicates for the phosphorylation of monophosphorylatable ERK by wild type MEK is reported in the legend of Figure S1. The number of experimental replicates for the activation of MEK by Raf is reported in the legend of Figure 4.
DATA AND CODE AVAILABILITY
Least squares fitting was performed using the lsqcurvefit routine in MATLAB version R2016a with the objective function described in the legend of Figure S2. Bayesian parameter inference was performed using PyStan version 2.19 distribution using Hamiltonian Markov Chain Monte Carlo methods with the details described in the Method Details. The mass spectrometry data for the phosphorylation ratio of ERK is available via ProteomeXchange with identifier PXD016580 [52].
Supplementary Material
Acknowledgements
We thank Henry Mattingly, Melanie Cobb, Natalie Ahn, Trudi Schüpbach, Jared Toettcher, Rebecca Burdine, Alexander Berezhkovskii for helpful discussions and E. Goldsmith for the wild type MEK and ERK constructs. H.A.H. gratefully acknowledges a sabbatical grant by EDGE to visit the Shvartsman lab and subsequent support of EPSRC and Royal Society URF. This work was supported by NIH grants R35GM128813 (M.W.) and R01GM086537 (S.Y.S.) and by the Lewis-Sigler collaboration fund (M.W. and S.Y.S.). E.Y. acknowledges support by the NIH HHS training grant T32GM007388. S.M. acknowledges support by the Hertz Foundation Fellowship and the NSF GRFP Fellowship. L.M. acknowledges support by the EPSRC grant EP/R513295/1.
Footnotes
Declaration of Interests
The authors declare no competing interests.
References
- 1.Salazar C, Brümmer A, Alberghina L, and Höfer T (2010). Timing control in regulatory networks by multisite protein modifications. Trends Cell Biol. 20, 634–641. [DOI] [PubMed] [Google Scholar]
- 2.Kageyama H, Kondo T, and Iwasaki H (2003). Circadian Formation of Clock Protein Complexes by KaiA, KaiB, KaiC, and SasA in Cyanobacteria. J. Biol. Chem. 278, 2388–2395. [DOI] [PubMed] [Google Scholar]
- 3.Cohen P (2000). The regulation of protein function by multisite phosphorylation - A 25 year update. Trends Biochem. Sci. 25, 596–601. [DOI] [PubMed] [Google Scholar]
- 4.Takahashi K, Tǎnase-Nicola S, and Ten Wolde PR (2010). Spatio-temporal correlations can drastically change the response of a MAPK pathway. Proc. Natl. Acad. Sci. U. S. A. 107, 2473–2478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Iwamoto N, D’Alessandro LA, Depner S, Hahn B, Kramer BA, Lucarelli P, Vlasov A, Stepath M, Böhm ME, Deharde D, et al. (2016). Context-specific flow through the MEK/ERK module produces cell- and ligand-specific patterns of ERK single and double phosphorylation. Sci. Signal. 9, 1–17. [DOI] [PubMed] [Google Scholar]
- 6.Atay O, and Skotheim JM (2017). Spatial and temporal signal processing and decision making by MAPK pathways. J. Cell Biol. 216, 317–330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ferrell JE, and Ha SH (2014). Ultrasensitivity part II: Multisite phosphorylation, stoichiometric inhibitors, and positive feedback. Trends Biochem. Sci. 39, 556–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Örd M, Möll K, Agerova A, Kivi R, Faustova I, Venta R, Valk E, and Loog M (2019). Multisite phosphorylation code of CDK. Nat. Struct. Mol. Biol. 26, 649–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Thomson M, and Gunawardena J (2009). Unlimited multistability in multisite phosphorylation systems. Nature 460, 274–277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Futran AS, Link AJ, Seger R, and Shvartsman SY (2013). ERK as a model for systems biology of enzyme kinetics in cells. Curr. Biol. 23, 972–979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Payne DM, Rossomando AJ, Martino P, Erickson AK, Her JH, Shabanowitz J, Hunt DF, Weber MJ, and Sturgill TW (1991). Identification of the regulatory phosphorylation sites in pp42/mitogen-activated protein kinase (MAP kinase). EMBO J. 10, 885–892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Rodriguez-Viciana P, and Rauen KA (2008). Biochemical Characterization of Novel Germline BRAF and MEK Mutations in Cardio-Facio-Cutaneous Syndrome. Methods Enzymol. 438, 277–289. [DOI] [PubMed] [Google Scholar]
- 13.Dentici ML, Sarkozy A, Pantaleoni F, Carta C, Lepri F, Ferese R, Cordeddu V, Martinelli S, Briuglia S, Digilio MC, et al. (2009). Spectrum of MEK1 and MEK2 gene mutations in cardio-facio-cutaneous syndrome and genotype-phenotype correlations. Eur. J. Hum. Genet. 17, 733–740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bromberg-white JL, Andersen NJ, and Duesbery NS (2012). Mek genomics in development and disease. Brief. Funct. Genomics 11, 300–310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rauen KA (2013). The RASopathies. Annu. Rev. Genomics Hum. Genet. 14, 355–369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jindal GA, Goyal Y, Burdine RD, Rauen KA, and Shvartsman SY (2015). RASopathies: Unraveling mechanisms with animal models. Dis. Model. Mech. 8, 769–782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sanchez-Vega F, Mina M, Armenia J, Chatila WK, Luna A, La KC, Dimitriadoy S, Liu DL, Kantheti HS, Saghafinia S, et al. (2018). Oncogenic Signaling Pathways in The Cancer Genome Atlas. Cell 173, 321–337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhao Y, and Adjei AA (2014). The clinical development of MEK inhibitors. Nat. Rev. Clin. Oncol. 11, 385–400. [DOI] [PubMed] [Google Scholar]
- 19.Emery CM, Vijayendran KG, Zipser MC, Sawyer AM, Niu L, Kim JJ, Hatton C, Chopra R, Oberholzer PA, Karpova MB, et al. (2009). MEK1 mutations confer resistance to MEK and B-RAF inhibition. Proc. Natl. Acad. Sci. U. S. A. 106, 20411–20416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Cagnol S, and Rivard N (2013). Oncogenic KRAS and BRAF activation of the MEK/ERK signaling pathway promotes expression of dual-specificity phosphatase 4 (DUSP4/MKP2) resulting in nuclear ERK1/2 inhibition. Oncogene 32, 564–576. [DOI] [PubMed] [Google Scholar]
- 21.Goyal Y, Jindal GA, Pelliccia JL, Yamaya K, Yeung E, Futran AS, Burdine RD, Schüpbach T, and Shvartsman SY (2017). Divergent effects of intrinsically active MEK variants on developmental Ras signaling. Nat. Genet. 49, 465–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Maust JD, Whitehead CE, and Sebolt-Leopold JS (2018). Oncogenic mutants of MEK1: A trilogy unfolds. Cancer Discov. 8, 534–536. [DOI] [PubMed] [Google Scholar]
- 23.Ordan M, Pallara C, Maik-Rachline G, Hanoch T, Gervasio FL, Glaser F, Fernandez-Recio J, and Seger R (2018). Intrinsically active MEK variants are differentially regulated by proteinases and phosphatases. Sci. Rep. 8, 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Kinoshita E, Kinoshita-Kikuta E, Takiyama K, and Koike T (2006). Phosphate-binding tag, a new tool to visualize phosphorylated proteins. Mol. Cell. Proteomics 5, 749–757. [DOI] [PubMed] [Google Scholar]
- 25.Kinoshita E, Kinoshita-Kikuta E, and Koike T (2009). Separation and detection of large phosphoproteins using phos-tag sds-page. Nat. Protoc. 4, 1513–1521. [DOI] [PubMed] [Google Scholar]
- 26.Piala AT, Humphreys JM, and Goldsmith EJ (2014). MAP kinase modules: The excursion model and the steps that count. Biophys. J. 107, 2006–2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Raue A, Karlsson J, Saccomani MP, Jirstrand M, and Timmer J (2014). Comparison of approaches for parameter identifiability analysis of biological systems. Bioinformatics 30, 1440–1448. [DOI] [PubMed] [Google Scholar]
- 28.Gutenkunst RN, Waterfall JJ, Casey FP, Brown KS, Myers CR, and Sethna JP (2007). Universally sloppy parameter sensitivities in systems biology models. PLoS Comput. Biol. 3, 1871–1878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Taylor CA, Cormier KW, Keenan SE, Earnest S, Stippec S, Wichaidit C, Juang Y-C, Wang J, Shvartsman SY, Goldsmith EJ, et al. (2019). Functional divergence caused by mutations in an energetic hotspot in ERK2. Proc. Natl. Acad. Sci. 116, 15514–15523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Filippi S, Barnes CP, Kirk PDW, Kudo T, Kunida K, McMahon SS, Tsuchiya T, Wada T, Kuroda S, and Stumpf MPH (2016). Robustness of MEK-ERK Dynamics and Origins of Cell-to-Cell Variability in MAPK Signaling. Cell Rep. 15, 2524–2535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Mansour SJ, Candia JM, Matsuura JE, Manning MC, and Ahn NG (1996). Interdependent domains controlling the enzymatic activity of mitogen activated protein kinase kinase 1. Biochemistry 35, 15529–15536. [DOI] [PubMed] [Google Scholar]
- 32.Burack WR, and Sturgill TW (1997). The activating dual phosphorylation of MAPK by MEK is nonprocessive. Biochemistry 36, 5929–5933. [DOI] [PubMed] [Google Scholar]
- 33.Ferrell JE, and Bhatt RR (1997). Mechanistic studies of the dual phosphorylation of mitogen-activated protein kinase. J. Biol. Chem. 272, 19008–19016. [DOI] [PubMed] [Google Scholar]
- 34.Prowse CN, Deal MS, and Lew J (2001). The Complete Pathway for Catalytic Activation of the Mitogen-activated Protein Kinase, ERK2. J. Biol. Chem. 276, 40817–40823. [DOI] [PubMed] [Google Scholar]
- 35.Aoki K, Yamada M, Kunida K, Yasuda S, and Matsuda M (2011). Processive phosphorylation of ERK MAP kinase in mammalian cells. Proc. Natl. Acad. Sci. U. S. A. 108, 12675–12680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Aoki K, Takahashi K, Kaizu K, and Matsuda M (2013). A quantitative model of ERK MAP kinase phosphorylation in crowded media. Sci. Rep. 3, 1541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Mansour SJ, Matten WT, Hermann AS, Candia JM, Rong S, Fukasawa K, Vande Woude GF, and Ahn NG (1994). Transformation of mammalian cells by constitutively active MAP kinase kinase. Science (80-. ). 265, 966–970. [DOI] [PubMed] [Google Scholar]
- 38.Fischmann TO, Smith CK, Mayhood TW, Myers JE, Reichert P, Mannarino A, Carr D, Zhu H, Wong J, Yang RS, et al. (2009). Crystal structures of MEK1 binary and ternary complexes with nucleotides and inhibitors. Biochemistry 48, 2661–2674. [DOI] [PubMed] [Google Scholar]
- 39.Berman HM, Battistuz T, Bhat TN, Bluhm WF, Bourne PE, Burkhardt K, Feng Z, Gilliland GL, Iype L, Jain S, et al. (2002). The protein data bank. Nucleic Acids Res. 28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Bentivegna S, Zheng J, Namsaraev E, Carlton VEH, Pavlicek A, Moorhead M, Siddiqui F, Wang Z, Lee L, Ireland JS, et al. (2008). Rapid identification of somatic mutations in colorectal and breast cancer tissues using mismatch repair detection (MRD). Hum. Mutat. 29, 441–450. [DOI] [PubMed] [Google Scholar]
- 41.Jindal GA, Goyal Y, Yamay K, Futran AS, Kountouridis I, Balgobin CA, Schüpbach T, Burdine RDC, and Shvartsman SY (2017). In vivo severity ranking of Ras pathway mutations associated with developmental disorders. Proc. Natl. Acad. Sci. U. S. A. 114, 510–515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Huang CYF, and Ferrell JE (1996). Ultrasensitivity in the mitogen-activated protein kinase cascade. Proc. Natl. Acad. Sci. U. S. A. 93, 10078–10083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Markevich NI, Hoek JB, and Kholodenko BN (2004). Signaling switches and bistability arising from multisite phosphorylation in protein kinase cascades. J. Cell Biol. 164, 353–359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Obatake N, Shiu A, Tang X, and Torres A (2019). Oscillations and bistability in a model of ERK regulation. J. Math. Biol. 291, 1–35. [DOI] [PubMed] [Google Scholar]
- 45.Eithun M, and Shiu A (2017). An all-encompassing global convergence result for processive multisite phosphorylation systems. Math. Biosci. 291, 1–9. [DOI] [PubMed] [Google Scholar]
- 46.Babtie AC, and Stumpf MPH (2017). How to deal with parameters for whole-cell modelling. J. R. Soc. Interface 14, 20170237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Eng Jimmy K., Ashley L. McCormack, and J.R. Y (1994). An Approach to correlate Tandem Mass Spectral Data of Peptides with Amino Acid Sequences in a Protein Database. J. Am. Soc. Mass Spectrom. 5, 976–989. [DOI] [PubMed] [Google Scholar]
- 48.Bateman A (2019). UniProt: A worldwide hub of protein knowledge. Nucleic Acids Res. 47, D506–D515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Elias JE, and Gygi SP (2007). Target-decoy search strategy for increased confidence in large-scale protein identifications by mass spectrometry. Nat. Methods 4, 207–214. [DOI] [PubMed] [Google Scholar]
- 50.Savitski MM, Wilhelm M, Hahne H, Kuster B, and Bantscheff M (2015). A scalable approach for protein false discovery rate estimation in large proteomic data sets. Mol. Cell. Proteomics 14, 2394–2404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Perez-Riverol Y, Csordas A, Bai J, Bernal-Llinares M, Hewapathirana S, Kundu DJ, Inuganti A, Griss J, Mayer G, Eisenacher M, et al. (2019). The PRIDE database and related tools and resources in 2019: Improving support for quantification data. Nucleic Acids Res. 47, D442–D450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Deutsch EW, Csordas A, Sun Z, Jarnuczak A, Perez-Riverol Y, Ternent T, Campbell DS, Bernal-Llinares M, Okuda S, Kawano S, et al. (2017). The ProteomeXchange consortium in 2017: Supporting the cultural change in proteomics public data deposition. Nucleic Acids Res. 45, D1100–D1106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ljung L, and Glad T (1994). On global identifiability for arbitrary model parametrizations. Automatica 30, 265–276. [Google Scholar]
- 54.Bellu G, Saccomani MP, Audoly S, and D’Angiò L (2007). DAISY: A new software tool to test global identifiability of biological and physiological systems. Comput. Methods Programs Biomed. 88, 52–61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Carpenter B, Gelman A, Hoffman MD, Lee D, Goodrich B, Betancourt M, Brubaker MA, Guo J, Li P, and Riddell A (2017). Stan: A probabilistic programming language. J. Stat. Softw. 76, 1–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Least squares fitting was performed using the lsqcurvefit routine in MATLAB version R2016a with the objective function described in the legend of Figure S2. Bayesian parameter inference was performed using PyStan version 2.19 distribution using Hamiltonian Markov Chain Monte Carlo methods with the details described in the Method Details. The mass spectrometry data for the phosphorylation ratio of ERK is available via ProteomeXchange with identifier PXD016580 [52].