Positional Strategies for Connection Specificity and Synaptic Organization in Spinal Sensory-Motor Circuits

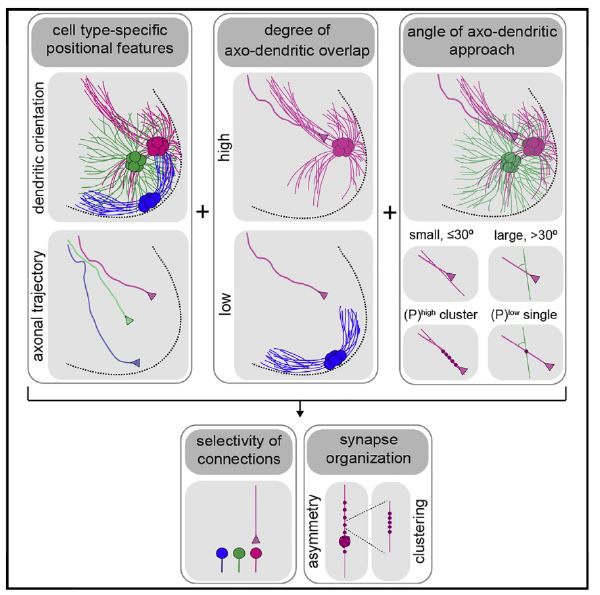
SUMMARY

Proprioceptive sensory axons in the spinal cord form selective connections with motor neuron partners, but the strategies that confer such selectivity remain uncertain. We show that muscle-specific sensory axons project to motor neurons along topographically organized angular trajectories and that motor pools exhibit diverse dendritic arbors. On the basis of spatial constraints on axo-dendritic interactions, we propose positional strategies that can account for sensory-motor connectivity and synaptic organization. These strategies rely on two patterning principles. First, the degree of axo-dendritic overlap reduces the number of potential post-synaptic partners. Second, a close correlation between the small angle of axo-dendritic approach and the formation of synaptic clusters imposes specificity of connections when sensory axons intersect multiple motor pools with overlapping dendritic arbors. Our study identifies positional strategies with prominent roles in the organization of spinal sensory-motor circuits.

In Brief

The study of axo-dendritic interactions between muscle-specific sensory and motor neurons revealed positional strategies for sensory-motor connectivity and synaptic organization. These strategies may have implications for defining the organization of neural circuits throughout the vertebrate CNS.

Graphical Abstract

INTRODUCTION

Elucidating the wiring maps of neuronal circuits provides a conceptual framework for understanding the integrative properties of the CNS (White et al., 1986). Recent advances in viral tracing and imaging have refined neural connectivity maps to unprecedented detail (Eichler et al., 2017; Kasthuri et al., 2015; Lerner et al., 2016; Markram et al., 2015). Despite our comprehensive knowledge of neuronal circuitry, the fundamental process by which a neuron selectively connects with its targets remains largely unknown. The interaction of complementary recognition tags expressed by pre- and post-synaptic partners (Sperry, 1963), which we will refer to as cell-cell recognition, has long been invoked as the main strategy to explain this process. This strategy implies the existence of an intricate recognition code that establishes connection selectivity, but in many brain regions it has been difficult to determine the identity and operational logic of presumed recognition determinants (Zipursky and Sanes, 2010).

Position-based strategies have also been implicated in the wiring of neuronal circuits. A number of studies support the notion that connectivity patterns are, in part, a reflection of the settling position of neuronal cell bodies (Bikoff et al., 2016; Hilde et al., 2016; Surmeli et al., 2011; Tripodi et al., 2011). Dendritic morphologies have also been suggested to constrain the number, type, and distribution of pre-synaptic inputs on post-synaptic neuronal partners (Brierley et al., 2012; Kostadinov and Sanes, 2015; Landgraf et al., 2003; Vlasits et al., 2016; Vrieseling and Arber, 2006). Moreover, positional features of axonal growth and segregation have been invoked as a strategy, independent of recognition programs, to explain how pre-synaptic neurons find their appropriate targets (Langen et al., 2015). These studies suggest that positional elements are critical in regulating the assembly and function of neuronal circuits.

Neuronal wiring has been studied extensively in the spinal sensory-motor (S-M) reflex arc. In this circuit, group la proprioceptive sensory neurons form monosynaptic connections with a selective set of motor neurons (MNs) (Baldissera et al., 1981; Eccles et al., 1957). Specifically, proprioceptive neurons form many connections with motor neurons that innervate the same (homonymous) muscle and fewer connections with motor neurons that supply synergistic muscles, while in principle they do not form connections with motor neurons (non-homonymous) that innervate muscles with antagonistic, or distinct function (Nichols, 1994). Patterns of S-M connection are largely conserved across limbed vertebrates (Hasan and Stuart, 1988; Hongo et al., 1984; Lichtman et al., 1984; Mendelson and Frank, 1991), and they are established early in development, primarily in an activity-independent manner (Mears and Frank, 1997; Mendelsohn et al., 2015). This has prompted suggestions that cell-cell recognition underlies the selectivity of these connections (Ladle et al., 2007). But, with the exception of a single repellent mechanism, in which plexinD1⁺ sensory axons are precluded from forming monosynaptic connections with sema3E⁺ motor neurons (Fukuhara et al., 2013; Pecho-Vrieseling et al., 2009), molecular mediators of S-M recognition have not been defined in this system.

Positional strategies also appear to have a role in establishing S-M connectivity patterns (Jessell et al., 2011; Tripodi and Arber, 2012). Genetic and anatomical evidence indicates that the settling position of motor neuron cell bodies imposes selectivity on S-M connections (Sürmeli et al., 2011). Cell body position provides an incomplete representation of overall neuronal territory, however, given that central neurons typically form elaborate dendritic arbors that differ in arborization in ways that reflect distinct neuronal identities (Jan and Jan, 2010). Moreover, input axons that project to a select neuronal target frequently originate from different positions within the CNS and follow distinct trajectories (Lemon, 2008). By implication, motor neuron dendritic and sensory axon morphologies could be prominent factors in a positional logic that serves as a determinant in the formation of selective neuronal connections. Whether these factors play a role in spinal S-M connectivity has yet to be explored.

To assess the roles of axo-dendritic morphologies in S-M connectivity, we used mouse genetics and recombinant viral methods to trace the spinal trajectories of muscle-specific proprioceptive sensory axons, and to map the planar orientations of dendrites originating from defined motor pools. We show that axonal and dendritic morphologies exhibit high positional organization. These organized positional features prompted us to explore how axo-dendritic geometry contributes to S-M connectivity. We identified types of axo-dendritic interactions and synaptic organization that can account for S-M connections with high accuracy. Our results suggest that positional factors play a prominent role in the organization of S-M circuits, which may have implications for defining how precise connections are established elsewhere in the vertebrate CNS.

RESULTS

Spinal Axonal Trajectories of Muscle-Specific Proprioceptors Are Topographically Organized

We first addressed the spinal trajectories of proprioceptive sensory axons by devising an intersectional assay that combines mouse genetics with viral tracing to permit selective labeling of muscle-specific proprioceptors. This assay relies on the expression of parvalbumin (PV) by proprioceptors (de Nooij et al., 2013; Lallemend and Ernfors, 2012). To prime reporter expression in proprioceptors a PV-directed FlpO recombinase (PV::FlpO) line was crossed with a Cre- and Flp-dependent tdTomato reporter animal [Ai65 (RCFL-tdT)] (Madisen et al., 2015). This was accompanied by muscle injection of self-com- plementary AAV1-Cre (scAAV1-Cre) virus to activate tdTomato expression in proprioceptive sensory neurons innervating selective muscles (Figure S1 A).

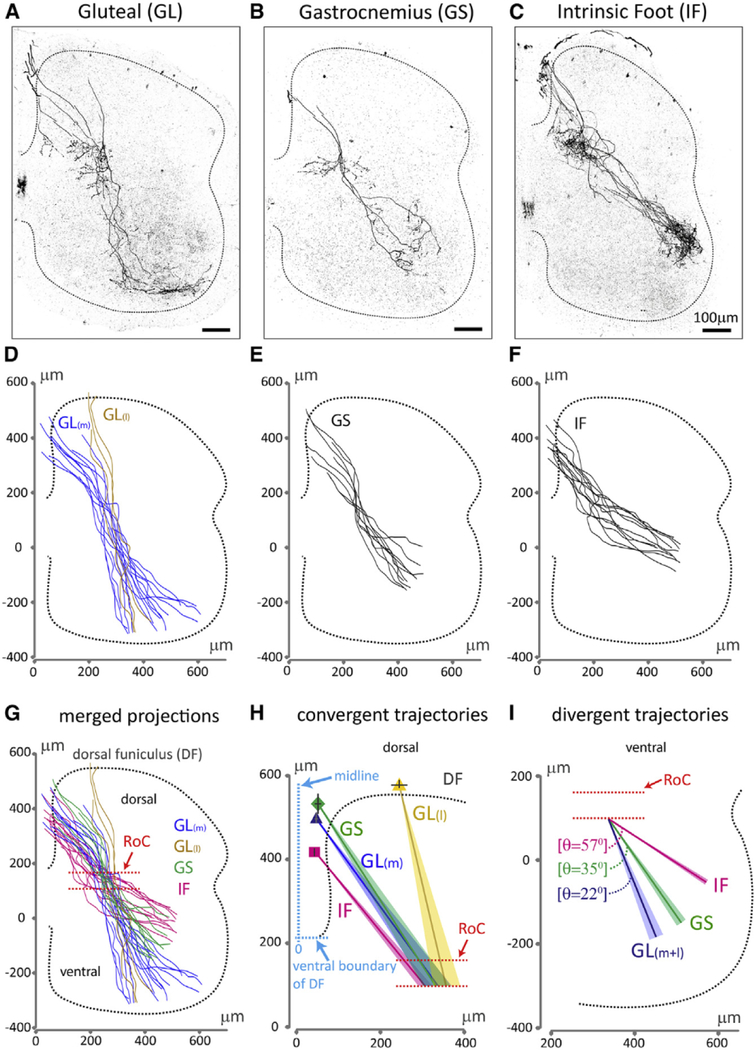
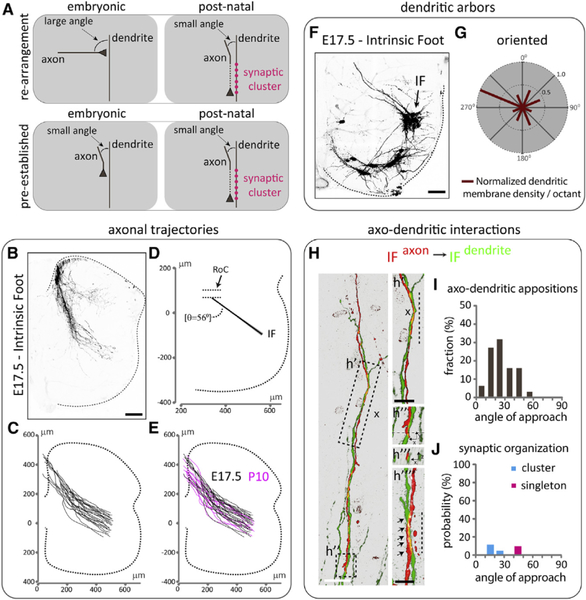
We focused on gluteal (GL), gastrocnemius (GS), and intrinsic foot (IF) proprioceptive sensory axons, given the distinct dorsoventral (DV) settling positions of their homonymous motor neuron targets (Sürmeli et al., 2011). Injection of scAAV1-Cre into GL, GS, or IF muscles of neonatal PV::FlpO^+/− ;Ai65^+/− mice resulted in selective and sparse labeling of primary sensory axons that enter the spinal cord at the dorsal funiculus (DF) and then project ventrally toward motor neurons (Figure 1A–1C). Reconstruction of GL-, GS-, or IF-labeled sensory axons revealed patterns of spatial segregation (Figures 1D–1G) in which GL, GS, or IF axons emerge from spatially restricted domains within the DF (Figure 1H), consistent with previous findings (Hongo et al., 1987). The emergence of GL axons from two points, medial (GL_(m)) and lateral (GL_(l)), in the DF may reflect the labeling of synergistic GL muscles (Figure 1H). Superimposition of GL_(m), GL_(l), GS, and IF axons revealed distinct medio-lateral (ML) trajectories toward a common region in the intermediate spinal cord where these axons converge (Figures 1G and 1H), which we define as a region of convergence (RoC) (Figures 1G–1I).

Figure 1. Spinal Axonal Trajectories of Muscle-Specific Proprioceptors in Wild-Type Mice.

(A-C) Representative spinal axonal projections from proprioceptive sensory neurons innervating distinct hindlimb muscles.

(D-F) Reconstruction of (D) GL_(m), GL_(l), (E) GS, and

(F) IF sensory axon trajectories.

(G) Overlay of axonal trajectories.

(H) Average sensory axon emergence points from the DF and axon trajectories from the DF to the region of convergence (RoC, red dotted lines). Emergence points (ML axis from the midline of the spinal cord, and DV axis of the DF): square, IF, (47 ± 2 μm, 218 ± 10 μm); dark-blue triangle, GL(_m), (52 ± 3 μm, 299 ± 13 μm); diamond, GS, (56 ± 8 μm, 327 ± 24 μm); yellow triangle, GL_(l), (254 ±19 μm, 388 ±10 μm).

(I) Sensory axon trajectory angles from the RoC to the ventral spinal cord relative to the ML axis (GL(m+l): 22° ± 2°, GS: 35° ± 2°, IF: 57° ± 1°). Dotted line depicts gray matter boundary. SEM of trajectories in (H) and (I) is shown as shaded colors. See Table S2 for experimental sample sizes.

Beyond the RoC, both GL_(m) and GL_(l) sensory axons followed a medial trajectory toward motor neurons, whereas GS and IF axons followed more lateral trajectories (Figure 1I). These trajectories appear topographically organized, with the spinal axons of sensory neurons supplying proximal muscles (GL) projecting medially, and the axons of sensory neurons innervating distal muscles (IF) projecting laterally, extending previous reports in cats (Hongo et al., 1987; Ishizuka et al., 1979).

Limb-Innervating Motor Pools Exhibit Diverse Patterns of Dendritic Arborization

We next assessed the dendritic pattern of defined motor pools by performing retrograde neuronal labeling from identified muscles in neonatal mice. Intra-muscular injection of recombinant scAAV6-GFP or rabies-ΔG-GFP viruses (collectively called Recombinant virus expressing GFP; Rv-GFP) were used to express GFP in distinct motor pools (see STAR Methods; Figure S1B). We focused on motor pools that exhibit distinct settling positions in the spinal cord (Figure S1G). These include the medially positioned GS and semitendinosus (ST) motor neurons and the laterally positioned tibialis anterior (TA) and GL motor neurons. In addition, we examined the motor neurons that supply IF muscles, located in the dorsal-most region of the lateral motor column (LMC) (McHanwell and Biscoe, 1981; Sürmeli et al., 2011).

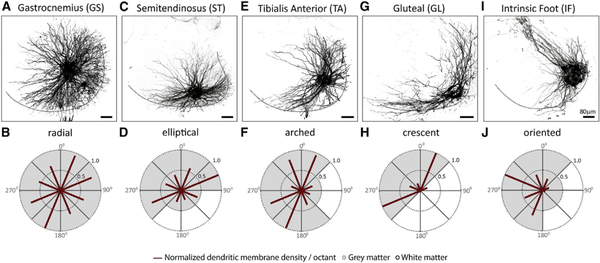
Injection of Rv-GFP into the GS (Figures 2A and 2B), ST (Figures 2C and 2D), TA (Figures 2E and 2F), GL (Figures 2G and 2H), or IF (Figures 2I and 2J) muscle revealed motor neurons with highly divergent dendritic arbors, ranging from near-radial for GS (Figure 2B) to an oriented pattern for IF motor neurons (Figure 2J). These data extend previous studies on motor neuron dendritic morphologies (Okado et al., 1990; Scheibel and Scheibel, 1971; Schoenen, 1982; Vrieseling and Arber, 2006).

Figure 2. Dendritic Arborization Patterns of Distinct Motor Pools in Wild-Type Mice.

Representative dendritic arbors of motor neurons (A, C, E, G, and I) innervating distinct hindlimb muscles. Radial plot quantification of normalized dendritic membrane density per octant (red bars) from the centroid of motor neurons of (B) GS, (D) ST, (F) TA, (H) GL, and (J) IF pools. Gray and white matter are depicted by shading in the plots. Black dotted line in (A), (C), (E), (G), and (I) depicts gray matter boundary. See Table S2 for experimental sample sizes.

Patterns of S-M Connectivity in Defined Reflex Circuits

The positional organization of axo-dendritic morphologies raises questions about their roles in regulating patterns of S-M connections. To address these questions, we first quantified the selectivity of sensory connections on motor neurons supplying distinct hindlimb muscles.

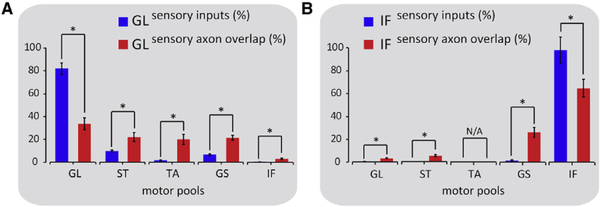
We used an anatomical assay that identifies synaptic contacts formed by muscle-specific sensory axons over the entire dendritic tree and somata of defined motor pools. This assay relies on the localization of cholera toxin subunit-B (CT-B) to vesicular glutamate transporter-1⁺ (vGluT1) sensory terminals (Sürmeli et al., 2011) and on the efficient labeling of motor neurons and their dendrites by scAAV6-GFP (Figure S1C). We first injected CT-B and scAAV6-GFP into hindlimb muscles to assess CT-B⁺ + vGluT1⁺ puncta on GFP⁺ motor neurons. We then summed the total number of CT-B⁺ + vGluT1⁺ puncta across all GFP⁺ motor neurons examined and expressed the number of puncta on each motor pool as a fraction of the total puncta across all motor neurons. This assay reveals the percentage of distribution of muscle-specific sensory inputs on distinct motor pools.

We focused on the GL and IF reflex arcs in which homonymous motor neurons occupy distinct ventral and dorsal positions within the LMC (Surmeli et al., 2011). We examined the degree of selectivity of GL sensory neurons for homonymous GL and non- homonymous ST, TA, GS, and IF motor neurons. We found that of the total GL sensory inputs on motor neurons 82% ± 5% were identified on GL, with small percentages distributed on ST (9.5 ± 1), TA (1.5 ± 0.5), GS (6.5 ± 0.5), and IF (0.5 ± 0.1) motor neurons (Figures 3A and S2A–S2E).

Figure 3. Axo-dendritic Overlap and Synapse Distribution in the GL and IF Reflex Circuits.

Histograms quantifying sensory input (CT-B⁺ + vGluT1⁺, blue bars) distribution and axo-dendritic overlap (tdTomato⁺ axons and GFP⁺ dendrites, red bars) between GL sensory axons and homonymous and non-homonymous motor neurons (A) and between IF sensory axons and homonymous and non- homonymous motor neurons (B). (A: axo-dendritic overlap (%): GLon GL: 33.5 ± 5, GLon ST: 22 ± 4, GL on TA: 20 ± 4.5, GL on GS: 21.5 ± 2, GL on IF: 3 ± 0.5; B: axo-dendritic overlap (%): IF on GL: 3.5 ± 0.3, IF on ST: 5.5 ± 0.8, IF on TA: N/A, IF on GS: 26 × 4.5, IF on IF: 65 ± 8). Asterisks represent p values < 0.05. N/A, not applicable. Error bars represent SEM. See Table S2 for experimental sample sizes.

Similarly, in the IF reflex circuit, 98% ± 11% of the total IF sensory synapses onto motor neurons were onto homonymous IF motor neurons, with limited percentages on non-homonymous GL (0.5 ± 0.2), and GS (1.5 ± 0.8) motor neurons, and no contacts on non-homonymous ST (0) or TA motor neurons (Figures 3B and S2F–S2I). The absence of IF inputs on TA motor neurons may reflect the positional segregation of IF and TA motor neurons across the rostro-caudal (RC) axis of the spinal cord (McHanwell and Biscoe, 1981) (Figure S1H).

These findings establish patterns of S-M connectivity in the GL and IF reflex circuits at the anatomical level and quantify a bias of connections for homonymous S-M pairs observed previously (Eccles et al., 1957; Mears and Frank, 1997; Surmeli et al., 2011).

Axo-dendritic Overlap Is Inadequate to Account in Full for Connection Selectivity

Synaptic densities have been shown to correlate with degrees of axon-dendritic overlap (Peters and Feldman, 1976; Rees et al., 2017). Having found such a relationship for synaptic distributions across homonymous motor neurons (Figure S4), we examined whether axo-dendritic overlap could account for the selectivity of connections in the GL and IF circuits (Li et al., 2007; Packer et al., 2013; Shepherd et al., 2005). To quantify the degree of axo-dendritic overlap, we co-injected scAAV1-Cre and scAAV6-GFP viruses into GL or IF muscles of PV::FlpO^+/− ;Ai65^+/− mice to simultaneously visualize tdTomato⁺ sensory axons and GFP⁺ motor neuron dendrites (Figure S1D). Next, we defined the spinal domain occupied by the GL or IF sensory axons. Within this domain, we summed the total amount of dendritic membrane from all motor pools examined and expressed the degree of overlap for each axo-dendritic pair as a fraction of the total dendritic membrane that intersects the defined domain of GL or IF sensory axons. This analysis quantifies the fraction of overlap between muscle-specific sensory axons and dendrites from distinct motor pools.

In the GL circuit, we found that the ratios of total dendritic membrane intersecting with GL sensory axons could not explain the synaptic percentages found between GL sensory and GL, ST, TA, and GS motor neurons (Figures 3A and S3A–S3D). In contrast, GL sensory axons exhibited minimal overlap with the dendrites of IF motor neurons, which could account for the low density of GL synaptic inputs found on IF motor neurons (Figures 3A and S3E).

Similar analysis in the IF circuit revealed significant overlaps of IF sensory axons with the dendrites of IF and GS motor neurons, but these were not sufficient to account for the percentages of IF inputs identified in these cases (Figures 3B, S3I, and S3H). In contrast, limited overlap was detected between IF sensory axons and the dendrites of GL and ST motor neurons, roughly approximating the minimal number or lack of IF synapses found for these motor neurons (Figures 3B, S3F, and S3G).

These results suggest that axo-dendritic overlap is inadequate to account in full for the selectivity of S-M connections, although it did eliminate some potential targets. Thus, axo-dendritic overlap may facilitate the task of selecting appropriate synaptic targets by reducing the number of potential post-synaptic partners.

The Angle of Axo-dendritic Approach Correlates with Connection Specificity and Synaptic Clustering

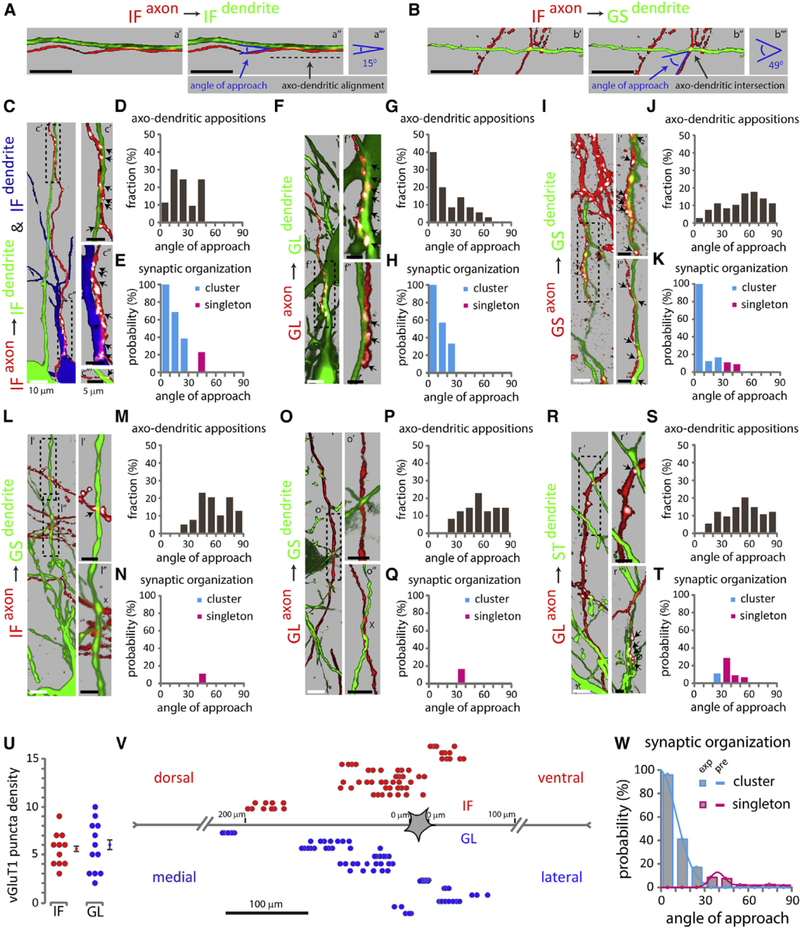
The inadequacy of axo-dendritic overlap to fully account for connectivity patterns prompted us to examine whether additional features of axo-dendritic geometry could be involved in connection selectivity. Our analysis revealed a notable difference in the angle by which sensory axons approach homonymous and non- homonymous motor neurons, most prominently exhibited in the IF reflex circuit (Figures S3I and S3H). IF sensory axons approach the dendrites of IF motor neurons at small angles (Figure 4A), whereas their approach to GS dendrites occurs at larger angles (Figure 4B). These observations raise the possibility that the angle of axo-dendritic approach might be related to connection specificity.

Figure 4. The Angle of Axo-dendritic Approach and Synaptic Organization in Defined Reflex Circuits.

Distribution of cluster and singleton synapses as a function of the angle of axo-dendritic approach. (A and B) Single confocal optical sections between IF axon on IF dendrite (a′), and IF axon on GS dendrite (b′). Green, motor neuron dendrite; red, sensory axon. Blue arrows point to angle of approach between IF axon on IF dendrite (a″), and IF axon on GS dendrite (b″). Dark gray arrows point to axo-dendritic alignment (shown with a dashed line) in (a″), and axo-dendritic intersection in (b″). (a″′ and b″′) indicate measured angle of approach between IF axon on IF dendrite (a″′), and IF axon on GS dendrite (b″′).

(C, F, I, L, O, and R) Maximum projection images of pseudo-color reconstructions of confocal optical sections. Green or blue, motor neuron; red, sensory axons; white, vGluT1⁺ puncta on sensory axons. Arrows indicate sensory axon + vGluT1⁺ + motor neuron appositions, x indicates absence of synapses from identified axo-dendritic appositions. 0 indicates lack of contact between sensory axon + vGlut1⁺ punctum and GFP⁺ dendrite, upon image rotation. (C) IF sensory axon on IF motor neuron dendrites; (c′ and c″) synaptic clusters; (c″′) singleton; (c″′) from a different section. (F) GL axon on GL dendrites; (f and f″) synaptic clusters; (f″) from a different section. (I) GS axon on GS dendrites; (¡′ and i″) synaptic clusters; (i″) from a different section. (L) IF axon on GS dendrites; (I′) singleton; (I″) no synaptic contact. (O) GL axon on GS dendrites; (o′ and o″) no synaptic contacts; (o″) from a different section. (R) GL axon on ST dendrites; (r′) singleton; (r″) cluster and lack of contact between sensory axon + vGlut1⁺ punctum and GFP⁺ dendrite; (r”) from a different section.

(D, G, J, M, P, and S) Histograms indicate the fraction (y axis) of angle (degrees) of approach (x axis) for different axo-dendritic appositions. IF axon on IF dendrite (D), GL axon on GL dendrite (G), GS axon on GS dendrite (J), IF axon on GS dendrite (M), GL axon on GS dendrite (P), and GL axon on ST dendrite (S).

(E, H, K, N, Q, and T) Histograms indicate the probability (y axis) of vGluT 1⁺ cluster (cyan) or singleton (magenta) as a function of the angle (degrees) of approach (x axis). IF axon on IF dendrite (E), GL axon on GL dendrite (H), GS axon on GS dendrite (K), IF axon on GS dendrite (N), GL axon on GS dendrite (Q), and GL axon on ST dendrite (T).

(U) Scatterplot of synaptic cluster size estimated from the number of consecutive vGluT1⁺ puncta within a pseudo-color reconstructed sensory axon opposed to a homonymous motor neuron. Error bars represent SEM.

(V) Spatial distribution of homonymous clusters, denoted by individual rows. Each circle represents a sensory axon + vGluT1⁺ + motor neuron apposition. Red circles, homonymous IF inputs; blue circles, homonymous GL inputs.

(W) Histograms (experimental data) and curves (predictions) depict the probability of cluster versus singleton synapse formation as a function of the angle (degrees) of axo-dendritic approach.

Values represent a pooled distribution of GL sensory with GL, ST, TA, GS, and IF motor neurons, GS sensory with GS motor neurons, and IF sensory with GL, ST, GS, and IF motor neurons (see also Table S1). Black dotted boxes in (C), (F), (I), (L), (O), and (R) depict angle of approach and synaptic organization fordistinct axo dendritic appositions. Black scale bar in (A) and (B), 10 n.m. See Table S2 for experimental sample sizes.

To test this possibility, we measured the angle of approach between individual IF sensory axons and dendrites of IF motor neurons (Figure 4C). We identified a total of 53 individual axo-dendritic appositions, of which 35 occurred at angles of 0°–30°, and 18 at angles of 31°−60° (Figure 4D; Table S1). This nearly 2 to 1 ratio indicates a bias of axo-dendritic appositions for angles ≤30° between IF sensory axons and IF motor neuron dendrites.

We next examined whether there is any relationship between the angle of axo-dendritic approach and synapse formation. Synaptic contacts were identified as vGluT1⁺ puncta on tdTomato⁺ sensory axons (Figure 4C). We found that of the 35 appositions identified at angles from 0° to 30°, 22 correlated with the detection of vGluT1⁺ synaptic contacts. In contrast, vGluT1 contacts were identified in only 3 of 18 appositions at angles from 31° to 60°, a 3.7-fold reduction compared to axo-dendritic approaches at 0°–30° angles (Table S1).

Additional analysis of synaptic contacts revealed a strong relationship between synaptic density and axo-dendritic angle. Synaptic inputs associated with axo-dendritic appositions in the range 0°–30° were organized into clusters of synapses on the same dendrite (Figure 4C, c′ and c″). IF synaptic clusters consisted on average of 5.5 ± 0.5 vGluT1⁺ appositions on individual dendrites (Figure 4U) distributed across ~20–120 μm of dendritic membrane (Figure 4V). In contrast, vGluT 1⁺ contacts identified at axo-dendritic angles >30° consisted of single synapses (singletons) (Figure 4C, c″′). There was a strict segregation in the angle of axonal approach between these two types of connections: those with approach angles ≤30° were invariably clusters and never singletons, whereas connections with angle >30° were invariably singletons and never clusters.

These results prompted us to quantify the probability of synaptic cluster or singleton formation as a function of the angle of axo-dendritic approach. These probabilities were determined by dividing the number of clusters or singletons by the total number of axo-dendritic appositions in 10° bins (Table S1). The probability of a cluster of synapses for near-parallel alignment (≤10°) was 100%, and this probability fell monotonically to 38.5% for angles near to but less than 30° (Figure 4E; Table S1). Singleton synapses only occurred at angles greater than 30° and with a low probability (Figure 4E; Table S1).

We also examined axo-dendritic appositions in homonymous GL and GS S-M pairs (Figures 4F and 4I). GL axons on GL dendrites, but not GS axons on GS dendrites, showed a bias to smaller approach angles, similar to IF axons on IF dendrites (Figures 4G and 4J; Table S1). The absence of angle bias for GS axons onto GS dendrites may be explained by the radial dendritic arbors of GS motor neurons (Figures 2A and 2B). Exploring the correlation between approach angles and synaptic organization in these circuits we again found a strict segregation, with clusters of synapses appearing exclusively for angles ≤30° and singletons appearing exclusively for angles >30° (Figures 4H and 4K; Table S1). As for the IF S-M connections, the probability of cluster formation was 100% for small angles and decreased as a function of approach angle (Figures 4H and 4K; Table S1).

We extended our study to include sensory axons and dendrites of non-homonymous motor neurons that exhibit significant overlap, such as IF axons and GS dendrites, as well as GL axons and GS, or ST dendrites (Figures 3B, 3A, and S3H, S3D, S3B). Unlike in the homonymous appositions, for these non-homonymous pairs the bias was to larger angles (Figures 4L, 4M, 4O, 4P, 4R, and 4S; Table S1). Furthermore, once again all connections with approach angles >30° were singletons (Figures 4N, 4Q, and 4T; Table S1). Interestingly, we also identified a single cluster between GL sensory axon on ST motor neuron dendrites, which occurred at an angle <30° (Figure 4R, r″, 4T; Table S1).

Our analysis reveals a strong correlation between approach angle and synapse number (Figure 4W; Table S1). Angles that range from parallel to 30° are associated with a high probability for synaptic clusters, a configuration typically observed between sensory axons and the dendrites of homonymous motor neurons. In contrast, angles >30° are correlated with the infrequent appearances of singleton synapses, an arrangement found between sensory axons with the dendrites of non-homonymous motor neurons. We next examined the implications of the angular correlation of synaptic organization for S-M connectivity.

Positional Factors Can Account for the Selectivity of S-M Connections

Although GL and IF sensory axons show higher degree of axodendritic overlap with their homonymous motor neurons, these preferences are significantly smaller than the degree of selectivity revealed by CT-B⁺ + vGluT1⁺ synapse counts (Figures 3A and 3B). We therefore tested whether the strong dependence of synaptic cluster and singleton synapses on approach angle in Figure 4W, when combined with our previous analysis of axo-dendritic overlaps, could account for the high degree of selectivity of sensory axons for their homonymous motor neurons.

We repeated the overlap analysis presented in Figure 3, but now including probabilities of clustered and singleton synapses as functions of axo-dendritic approach angle (Figure 4W). This was done using dendritic densities (Figure S1E) and axonal masks (Figure S1F) that were divided into 50 × 50 μm bins and computing average axo-dendritic approach angles within these bins. The angular dependences of synaptic cluster and singleton preferences were extracted from a curve fit to the experimental data (Figure 4W). This allowed us to compute the probability of an axon forming either cluster or singleton synapses with dendrites having a particular angular orientation within each bin.

In the GL circuit, axo-dendritic overlaps (Figures 5A–5E and magenta histograms in 5K) were then multiplied by these angular preference factors. This analysis yielded a significant improvement in connection selectivity (Figures 5F–5J and cyan histograms in 5K), with predicted GL sensory connections onto their both homonymous and non-homonymous motor neurons in good agreement with the measured CT-B⁺ + vGluT1⁺ synapse fractions (blue histograms in Figure 5K).

Figure 5. Positional Factors Can Account for S-M Connectivity Patterns in the GL and IF Reflex Circuits.

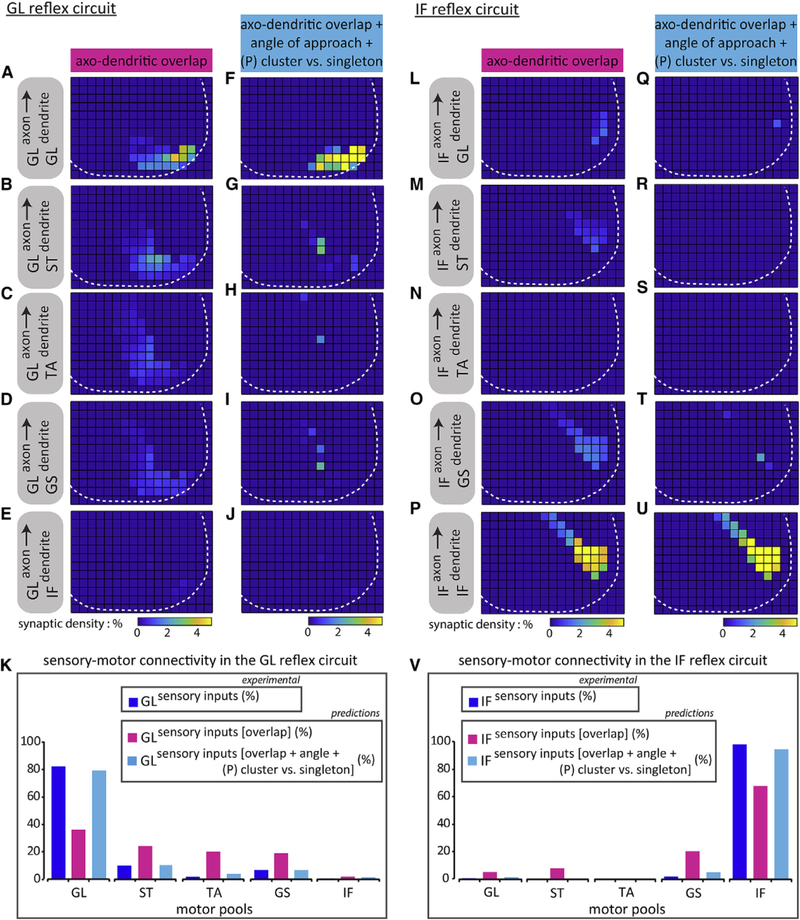
(A-E and L-P) Predicted patterns of connectivity based on axo-dendritic overlap between GL sensory axons on (A) GL, (B) ST, (C) TA, (D) GS, and (E) IF motor neurons, and IF sensory axons on (L) GL, (M) ST, (N) TA, (O) GS, and (P) IF motor neurons.

(F-J and Q-U) Same as (AHE) and (LHP), respectively, except with the addition of angular preference factors. GL sensory axons on (F) GL, (G) ST, (H) TA, (I) GS, and (J) IF motor neurons, and IF sensory axons on (Q) GL, (R) ST, (S) TA, (T) GS, and (U) IF motor neurons. White dotted line depicts gray matter boundary. Histograms summarizing (K) GL, or(V) IF sensory connectivity patterns across distinct motor pools. Sensory inputs histograms (blue) were derived from CT-B⁺ + vGluT1⁺ experimental data, as previously shown in Figure 3. Sensory inputs [overlap] histograms (magenta) are synaptic distributions (%) predicted using binned axo-dendritic membrane overlap data (K: GL on GL: 36, GL on ST: 24, GL on TA: 20, GL on GS: 18.5, GL on IF: 1.5; V: IF on GL: 5, IF on ST: 7.5, IF on TA: N/A, IF on GS: 20, IF on IF: 67.5). Sensory inputs [overlap + angle + (P) cluster versus singleton] histograms (cyan) are synaptic distributions (%) predicted incorporating binned axo-dendritic membrane overlap data and angular preference factors (K: GL on GL: 79, GL on ST: 10, GL on TA: 3.5, GL on GS: 6.5, GL on IF: 1; V: IF on GL: 1, IF on ST: 0, IF on TA: N/A, IF on GS: 4.5, IF on IF: 94.5). N/A, not applicable. See Table S2 for experimental sample sizes.

We next applied the same positional model to the IF circuit where a purely axo-dendritic overlap-based model predicted IF axons to IF dendrite connectivity well below what is experimentally observed (Figures 5L–5P and magenta histogram in 5V). Including the effect of the approach angle on the probability of cluster and singleton formation enhanced predicted connection percentages (Figures 5Q–5U and cyan histograms in 5V), putting them in good agreement with the measured CT-B⁺ + vGluT1⁺ synapse fractions (blue histograms in Figure 5V).

Moreover, we showed that axo-dendritic overlap can account for synaptic distributions of S-M synapses in homonymous circuits (Figures S4G–S4J). Adding angular factors to this computation generates predictions that are also in good agreement with synapse counts (Figures S5A–S5D), suggesting that positional factors can account for sensory input distribution on hom-onymous motor neurons.

We also used the overlap-plus-angle model to predict patterns of S-M connectivity in the GS reflex circuit (Figures S5E–S5I). The absence of experimentally derived synapse counts in the GS reflex circuit prevents us from evaluating these predictions. But, the predicted percentages for GS axons onto TA and ST motor neurons are in rough accord with the experimentally verified percentage for GL axons onto ST motor neurons (Figure 3A), so the synaptic predictions proposed here might represent fairly accurate patterns of synaptic connectivity in the GS reflex circuit.

The match between predicted values and experimental data suggests that patterns of S-M connectivity in the GL and IF reflex circuits can be explained by a positional model based on axo-dendritic morphology, overlap, and on an angle-dependent probability of forming clustered or singleton synapses. This positional model postulates that axonal approach angles play a causal role in synapse formation. This hypothesis raises a number of issues. First, small approach angles could be a result of, rather than a cause of, synaptic clustering. Given that our analysis was done at early postnatal stages (P7–P10), about a week after the formation of initial S-M connections (~E17.5) (Kudo and Yamada, 1987; Mears and Frank, 1997), it is possible that the axo-dendritic patterns we have reported are the result of an earlier process that involved sensory axons approaching the dendrites of motor neurons at unbiased angles. In this scenario, small approach angles would be the result of axo-dendritic re-arrangements occurring during development, as a consequence of synaptic cluster formation (Figure 6A). To address this issue, we repeated our analysis at an earlier developmental stage, between E17.5 and E18.5.

Figure 6. Axo-dendritic Morphologies and Interactions in the IF Reflex Circuit at Embryonic Stages of Wild-Type Mice.

(A) Schematics depicting different models of axodendritic configuration between IF sensory axons and IF motor neuron dendrites at embryonic and post-natal stages. Top: re-arrangement of axodendritic interactions results in angular reduction and synaptic cluster formation (magenta circles). Bottom: pre-established angular axo-dendritic interactions at embryonic and post-natal stages result in synaptic cluster formation (magenta circles).

(B) Representative spinal axonal projections from wild-type sensory neurons innervating intrinsic foot (IF) muscles labeled at E17.5 using a retrograde embryonic L5-L6 dorsal root fill. Black scale bar: 100μm.

(C) Reconstruction of IF sensory axons at E17.5.

(D) Average trajectory angle (56 ± 1°) of IF sensory axons from RoC toward the ventral spinal cord at E17.5. SEM of trajectory shown as shaded color.

(E) Overlay of reconstructed sensory axons. E17.5 spinal cords were scaled to the dimensions of a normalized P10 spinal cord (Figure 1F) for comparative analyses.

(F) Representative IF motor neuron dendritic arborization patterns labeled at E17.5 using a retrograde embryonic L5-L6 ventral root fill (note that some non-IF motor neurons, located in the ventral spinal cord, are also labeled). The dotted line represents the spinal cord boundary. Black arrow indicates IF motor neurons. Black scale bar: 80 μm.

(G) Radial plot quantification of normalized dendritic membrane density per octant (red bars) from the centroid of motor neurons of E17.5 IF pool.

(H) Maximum projection images of pseudo-color reconstructions of confocal optical sections. Green, IF motor neuron dendrites; red, IF sensory axon; white, vGluT1⁺ punctum on IF sensory axon. Arrows indicate sensory axon + vGluT1⁺ + motor neuron appositions. Vertical dotted line denotes axo-dendritic alignment. Black x indicates absence of synapses from identified axo-dendritic appositions, (h′), enlarged region showing axo-dendritic alignment and absence of vGluT 1⁺ puncta. (h″), region with presumptive IF sensory axon filopodium. (h″′) optical cross-section of Z stack encompassing presumptive filopodium denoted with a thin dotted line in (h″). (h″″) position of vGluT1⁺ synaptic cluster (image from a different section). White scale bar: 10 μm; black scale bar: 5 μm.

(I) Histogram indicating the fraction (y axis) of angle (degrees) of approach (x axis) for different axo-dendritic appositions.

(J) Histogram indicating the probability (y axis) of vGluTI⁺ cluster (cyan) or singleton (magenta) as a function of the angle (degrees) of approach (x axis).

See Table S2 for experimental sample sizes.

Another question that arises concerns the role of cell-cell recognition in the angular dependency of synaptic cluster formation. It is possible that this dependency is a secondary consequence of identity-dependent recognition signals that actually determine the selectivity of connections (Figure 7A). To address this issue, we examined the relationship between approach angle and synapse probability in the absence of motor pool identity.

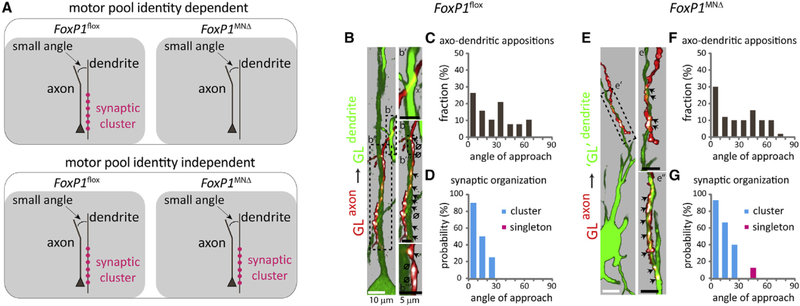
Figure 7. The Angle of Axo-dendritic Approach and Synapse Organization between GL sensory axons and ‘GL’ Motor Neuron Dendrites in FoxP1^MNΔ Mutants.

(A) Schematics depicting different models of axo-dendritic interactions at a small angle, and synaptic clusters between GL sensory axons and GL motor neuron dendrites at early post-natal stages in FoxP1^flox [PV::FlpO^+/−;Ai65^+/−] controls and FoxP1^MNΔ [PV::FlpO^+/−;Ai65^+/−] mutants. Top: the correlation between small approach angles and synaptic cluster formation (magenta circles) is dependent on motor pool identity. Bottom: the correlation between small approach angles and synaptic cluster formation (magenta circles) is independent of motor pool identity.

(B and E) Maximum projection images of pseudo-color reconstructions of confocal optical sections. Green, motor neurons; red, sensory axons; white, vGluT1 ⁺ puncta on sensory axons. Arrows indicate sensory axon + vGluT1⁺ + motor neuron appositions, x indicates absence of synapses from identified axo-dendritic appositions. 0 indicates lack of contact between sensory axon + vGlut1⁺ punctum and GFP⁺ dendrite, upon image rotation. (B) Control mice; GL sensory axon on GL motor neuron dendrites; (b′) axo-dendritic apposition and absence of synapse formation; (b″) synaptic cluster, and lack of contacts between sensory axons + vGlut1⁺ punctum and GFP⁺ dendrite; (b″′) example of close appositions but lack of contacts between sensory axon + vGlut1⁺ punctum and GFP⁺ dendrite. (E) Mutant mice; GL sensory axon on ‘GL’ motor neuron dendrites; (e′ and e″) synaptic clusters; (e″) from a different section. Black dotted boxes in (B) and (E) depict angle of approach and synaptic organization for distinct axo-dendritic appositions.

(C and F) Histograms indicate the fraction (y axis) of angle (degrees) of approach (x axis) for different axo-dendritic appositions.

(D and G) Histograms indicate the probability (y axis) of vGlut1⁺ cluster (cyan) or singleton (magenta) as a function of the angle (degrees) of axo-dendritic approach (x axis).

See Table S2 for experimental sample sizes.

Axo-dendritic Morphologies Are Established Early in Development

We reasoned that if muscle-specific sensory axons and motor neuron dendritic arbors exhibit similar positional patterns between ~E17.5 and ~P10, it is unlikely that positional rearrangements occur during this time window (Figure 6A). To this end, we focused on the IF reflex circuit and examined the morphologies of sensory axons and motor neuron dendrites at ~E17.5 and compared them with those at postnatal stages, as shown in Figures 1C and 2I.

To trace IF sensory axons and motor neuron dendrites embryonically, we performed dorsal and ventral root fills respectively, at L5-L6 levels of the spinal cord. At these segmental levels the majority of sensory axons originate from neurons innervating the IF muscles of hindlimbs (Surmeli et al., 2011). In addition, the identity of motor neurons can be inferred by their dorsal settling position in the spinal cord (Surmeli et al., 2011).

We first mapped the trajectory of spinal IF sensory axons and the dendritic arbors of IF motor neurons in ~E17.5 wild-type embryos. We found that IF sensory axons followed a lateral trajectory from the RoC to motor neurons that was similar to the trajectory of IF axons at postnatal stages (Figures 6B–6E, 1C, 1F, and 1I). We also found that IF motor neurons exhibited an oriented dendritic pattern, similar with the dendritic morphology of IF motor neurons at postnatal stages (Figures 6F, 6G, 2I, and 2J). Thus, axo-dendritic morphologies in the homonymous IF reflex circuit are established at embryonic stages.

We then examined angular patterns of IF axo-dendritic appositions at embryonic stages (Figure 6H). Of a total of 63 appositions, 41 occurred at angles from 0° to 30° and 22 at angles from 30° to 60° (Figure 6I; Table S1). This closely matches those results from early post-natal stages (Figure 4D; Table S1), indicating a consistency in angular patterns of appositions between these time points. We next asked whether there is any correlation between the angle of axo-dendritic approach and vGluT1 ⁺ puncta on labeled sensory axons. We detected only a limited number of vGlut1⁺ synapses due to the paucity of vGlut1⁺ puncta at these early stages of development. Despite this, we identified 3 clusters between 0° and 30° approach angles and 1 singleton between 30° and 60° angles (Figure 6J; Table S1), suggesting a similar pattern in angular dependency of synaptic organization as with early post-natal stages (Figure 4E; Table S1).

The scarcity of synapses at embryonic stages led us to consider loci where axons and dendrites are aligned in parallel to test whether small approach angles predict axo-dendritic alignment (Figures 4A and 6H, h′) that may precede synapse cluster formation. We detected a total of 27 axo-dendritic alignments all of which occurred at 0°−30° approach angles (Table S1). The probability of alignment was 100% for near parallel angles and 55% for angles approaching 30° (Table S1). The reduction of alignment probability as a function of the increase of approach angle is similar to the pattern of cluster probabilities at early post-natal stages (Figure 4E; Table S1). Moreover, in axo-dendritic interactions where a presumptive IF sensory axon filopodium extends along an IF motor neuron dendrite (Figure 6H, h″ and h″′), extensive axo-dendritic alignment was observed, but no co-localizing vGluT1⁺ puncta were detected, suggesting that small approach angles and axo-dendritic alignment precede synaptic cluster formation.

These results support a model in which patterns of axo-dendritic interactions are pre-established, with little rearrangement occurring between embryonic and early postnatal stages (Figure 6A).

Loss of Motor Pool Dendritic Diversity in FoxP1^MNΔ Mutants

We next examined the role of motor pool identity in the angular dependency of cluster formation. We reasoned that if the correlation between small approach angles and synaptic clustering is preserved in the absence of motor pool identity, this would suggest that it is independent of pool identity-specific programs of cell-cell recognition (Figure 7A).

The transcription factor FoxP1, through its ability to gate Hox gene function, controls the division between LMC and hypaxial motor column (HMC) characters (Dasen et al., 2008; Rousso et al., 2008). In FoxP1 mutants, the majority of LMC motor neurons acquire an HMC-like identity and lack motor pool specification programs as a result of a non-functional Hox network (Dasen et al., 2008; Rousso et al., 2008; Surmeli et al., 2011). The lack of pool identity in these mutants results in loss of putative pool-specific cell-cell recognition labels (Dasen et al., 2008). This permits us to examine whether the angular dependency of cluster formation is maintained in the absence of cell-cell recognition labels. We, thus, used mutants that lack FoxP1 expression selectively in motor neurons (Olig2::Cre;FoxP1^flox/flox, referred to as FoxP1^MNΔ mice), described previously (Surmeli et al., 2011).

We first examined whether the lack of motor pool identity in FoxP1^MNΔ mutants is accompanied by changes in dendritic morphologies. Injection of Rv-GFP into the GL, GS, or IF muscles of neonatal FoxP1^flox control animals revealed their distinctive crescent, radial, and oriented morphologies (Figures S6A, S6B, S6E, S6F, S6I, and S6J). In contrast, in FoxP1^MNΔ mice, the dendritic arbors of the ventrally scattered ‘GL’, ‘GS’, or ‘IF’ motor neurons (Surmeli et al., 2011) were aligned at the ventro-medial and ventro-lateral limits of the gray-white matter margins, with few dendrites extending into the central gray matter, in a crescent-like arrangement (Figures S6C, S6D, S6G, S6FI, S6K, and S6L). This arrangement is similar to the dendritic configuration exhibited by intercostal motor neurons within the HMC of both controls and mutants (Figures S6M–S6P). Thus, reversion of columnar identity from LMC to HMC-like leads to loss of motor pool dendritic diversity. These motor neurons now acquire a crescent-like dendritic pattern that resembles the dendritic morphology of HMC neurons.

Angle-Dependent Synaptic Clustering Occurs in the Absence of Motor Pool Identity

We next studied patterns of axo-dendritic interactions in FoxP1^MNΔ mutants. We focused on GL sensory axons and examined angular interactions and synaptic organization with the dendrites of the ventrally located ‘GL’ motor neurons.

To simultaneously label sensory axon and motor neuron dendrites we injected scAAV1-Cre and scAAV6-GFP into the GL muscle of FoxP1^MNΔ;PV::FlpO^+/− ;Ai65^+/− mutants. As controls we used FoxP1^flox;PV::FlpO^+/− ;Ai65^+/− littermates. We found that in mutants GL sensory axons project to the ventral-most regions of the spinal cord, where they appear to align with the lateral dendrites of ‘GL’ motor neurons, albeit with a lateral shift compared to controls (Figures S7A–S7C). Quantification showed that in both genetic backgrounds GL sensory axons emerge from similar locations within the DF and follow comparable angular trajectories from the DF to RoC (Figure S7D, left). Beyond the RoC, GL sensory axons in mutants project toward motor neurons at an angle that is laterally shifted compared to GL sensory axons in controls (Figure S7D, right). This finding may suggest a contribution of motor neuron identity in shaping sensory axonal trajectories (Baek et al., 2017). But despite this lateral shift, the overall distribution of CT-B⁺ + vGluT1⁺ sensory terminals on motor neurons is similar in both controls and mutants (Figure S7E), consistent with previous results (Surmeli et al., 2011).

We then studied angular appositions and synaptic organization in FoxP1^flox;PV::FlpO^+/− ;Ai65^+/− control and FoxP1^MNΔ;PV::FlpO^+/−;Ai65^+/− mutant littermates. The axo-dendritic appositions analyzed in mutants (Figures 7E and 7F; Table S1) closely matched those found in control animals (Figures 7B and 7C; Table S1). Further analysis in mutants revealed that all synapses found from 0° to 30° were organized in clusters, with a probability ranging from 93.3% for angles 0°−10° to 40% for 20°−30°. A single synapse was found at angles from 31°−60°, a 12.5% probability of singleton formation (Figure 7G; Table S1). Again, these values are close with the ones found in controls (Figure 7D; Table S1), suggesting that motor pool identity is dispensable for synaptic clustering at small angles.

DISCUSSION

Motor coordination requires the formation of specific monosynaptic connections between proprioceptive sensory axons and spinal motor neurons, but the principles that govern S-M selectivity have remained obscure. In particular, the contribution of axo-dendritic geometry in the formation of S-M connections has not been explored previously. We find that positional strategies based on spatial constraints in axo-dendritic relationships can account for the observed selectivity of connections. These findings suggest that positional factors are a key determinant in the organization of spinal S-M circuits.

The Angle of Axo-dendritic Approach as a Determinant of Connectivity and Synaptic Function

We observed that the probability of synapse formation in S-M circuits is related to the angle at which sensory axons approach motor neuron dendrites. What could be the mechanism of this dependency? To address this, we developed a model of axon growth and synapse formation (STAR Methods). The model posits an approach-angle dependent probability for an axon and dendrite to “associate,” leading to synaptic cluster formation. The model produces highly selective patterns of connection (Figure S5J). The model also suggests that multiple cluster formation may be enhanced when target dendrites have similar orientations, so that the growth cone does not need to reorient significantly to contact and align with other dendritic targets.

Our findings also provide an opportunity to examine Peters’ rule, that patterns of axon-dendritic overlap correlate with synaptic distribution and density (Peters and Feldman, 1976; Rees et al., 2017), in S-M circuits. We found that axo-dendritic overlap provides a bias for sensory axons to synapse onto their homonymous motor neurons, but that this is insufficient to account for the full selectivity seen in the data. On the basis of a strong correlation between the angle of axonal approach to a dendrite and the probability and number of synapses formed, we suggested that the angle of axo-dendritic approach could be an important positional factor for synapse formation. Combined with the observed dependence on approach angle, Peters’ rule significantly enhanced connection specificity between sensory axons and motor neurons with overlapping dendritic arbors. For both the GL and IF reflex circuits, the overlap-plus-angle model predicted patterns of S-M connectivity similar to the experimentally derived data.

The observed correlation between the angle of axo-dendritic approach and synapse formation raises questions about the significance of axo-dendritic approach angles in other circuits of the CNS. In the cerebellum, climbing fibers, originating from neurons of the inferior olive in the medulla, align with Purkinje cells and form hundreds of synaptic contacts that are organized into clusters (Rossi et al., 1993). In contrast, parallel fibers, originating from the cerebellar cortex, run orthogonally to the dendrites of Purkinje cells and form a limited number of singleton synapses (Napper and Harvey, 1988). It is possible, therefore, that synaptic organization in these cerebellar circuits adheres to similar axodendritic positional angles as observed in the spinal S-M system.

The Role of Cell-Cell Recognition in Small Approach Angles

A key question is whether the correlation between small approach angles and synaptic clustering involves programs of cell-cell recognition. We approached this question in two ways. First, we showed that axo-dendritic morphologies and patterns of angular interactions and synaptic organization are similar between post-natal and embryonic stages (Kudo and Ya- mada, 1987; Mears and Frank, 1997; Surmeli et al., 2011; Vrie- seling and Arber, 2006), arguing against potential axo-dendritic re-arrangements operating during development due to programs of cell-cell recognition. Second, we showed that in FoxP1^MNΔ mutants, in which motor neurons lack pool specification programs (Dasen et al., 2008; Rousso et al., 2008; Surmeli et al., 2011), the angular dependency of synaptic organization remains intact, indicating that pool-specific recognition labels are dispensable in this process. We also identified a synaptic cluster when sensory axons intersected the dendrites of motor neurons with the “wrong” identity at small angle (Figures 4R, r″, and 4T), further indicating that here pool-dependent recognition labels do not drive axo-dendritic interactions. The above findings together point to a mechanism of synaptic cluster formation and distribution that does not require cell-cell recognition but relies, instead, on the geometry of pre-established axo-dendritic morphologies.

Our hypothesis predicts that reorienting axo-dendritic interactions from large to small approach angles should increase the probability of synaptic cluster formation. In FoxP1^MNΔ mutants, the pool-identity deficient ‘GS’ motor neurons exhibit a reversion of dendritic morphology from radial to crescent-like, which is reminiscent of the dendritic pattern of ‘GL’ motor neurons in this genetic background (Figures S6A–S6H). This permitted us to test whether the reversion of ‘GS’ motor neuron dendrites results in a change of angular axo-dendritic interactions with respect to GL axons and ultimately whether this changes the probability of synaptic cluster formation. We found that in FoxP1^MNΔ;PV::FlpO^+/−;Ai65^+/− mutants, 15 of 59 of axo-dendritic appositions occurred at 0°–30° angles, a 5.3-fold increase compared to 2 of 42 appositions in FoxP1^flox;PV::FlpO^+/−;Ai65^+/− controls (Figures S8A, S8B, S8D, and S8E; Table S1). As predicted, the increase in small angular appositions was correlated with an increase in synaptic clusters. We detected a total of 10 synaptic clusters between 0° and 30° angles in mutants, with an 100% probability of cluster formation for near-parallel angles and 50% for angles between 20° and 30°, whereas no clusters were identified in control mice (Figures S8C and S8F; Table S1). All singleton synapses detected occurred at angles >30° in both genetic backgrounds (Figures S8C and S8F; Table S1). These findings show that reorienting axo-dendritic appositions toward small angles results in an increased probability of synaptic cluster formation, providing evidence for a causal effect of approach angles on synaptic organization. Unfortunately, very low survival rates for FoxP1^MNΔ;PV::FlpO^+/− ;Ai65^+/− mutants (~1 %), possibly due to unfavorable genetic modifiers), make it extremely challenging to collect sufficient numbers of animals for these experiments. Because we were only able to retrieve one mutant animal, we consider this result preliminary.

We also emphasize two caveats. First, the FoxP1^MNΔ mutation alters both programs of cell-cell recognition (Dasen et al., 2008) and axo-dendritic positioning. Genetic modifications that perturb either recognition or axo-dendritic positioning, but not both, would be better suited for tests of our hypothesis, but, to our knowledge, no such system has yet been identified (Arber, 2012). Second, it is currently unknown whether all programs of cell-cell recognition are absent in FoxP1^MNΔ mutants (Dasen et al., 2008). It is possible that generic, pool-independent recognition labels are still expressed in HMC-like motor neurons in this genetic background.

Conclusions

In this study, we suggest that one step in establishing S-M selectivity, the probability of synapse formation, may not depend on the identity of neuronal targets, but rather operates within the constraints imposed by recognition-independent positional programs. In this view, identity still functions to establish cell-type specific morphological features that bring sensory axons and motor neuron dendrites into favorable positions and orientations to increase the probability of synaptic cluster formation. Positional programs have also been shown to determine guidance of pre-synaptic axons to defined domains (Zlatic et al., 2003; Zlatic et al., 2009), settling position of target cell bodies (Bikoff et al., 2016; Hilde et al., 2016; Surmeli et al., 2011; Tripodi et al., 2011), and arborization patterns of target dendrites (Baek et al., 2017; Kostadinov and Sanes, 2015; Vrieseling and Arber, 2006), all of which operate to reduce the requirement of recognition signals to resolve selectivity of connections (Hassan and Hiesinger, 2015; Jessell et al., 2011; Tripodi and Arber, 2012). In cases where positional programs provide insufficient target resolution, recognition signals are likely required to distinguish the correct targets (Duan et al., 2014; Duan et al., 2018; Tan et al., 2015). This might explain the recognition signals that have been suggested to resolve connection selectivity in certain S-M circuits (Fukuhara et al., 2013; Vrieseling and Arber, 2006). In a broader context, however, our study has identified a recognition-independent mechanism by which axo-dendritic geometry and positioning can lead to highly selective connections.

STAR★METHODS

Detailed methods are provided in the online version of this paper and include the following:

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to the Lead Contact, Nikolaos Balaskas, at nb2529@columbia.edu.

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Olig2::Cre (MGI:3774124) (Dessaud et al., 2007), conditional FoxP1 (Feng et al., 2010), PV::FlpO (Jax 022730) (Madisen et al., 2015), tdTomato reporter Ai14 (Jax 007914) (Madisen et al., 2010) or Ai65 (Jax 021875) (Madisen et al., 2015), and ChAT::Cre (Jax 006410) (Rossi et al., 2011) mice were maintained on a mixed genetic background (129/C57BL6). In experiments with FoxP1 mice, FoxP1^+/flox, or Olig2::Cre; FoxP1^+/flox, or FoxP1^flox/flox were used as control (referred to as FoxP1^flox). In these genetic backgrounds, cell body position and dendritic patterns of motor neurons did not exhibit any notable differences. The FoxP1 and ROSA loci do not segregate according to Mendelian ratios due to genetic linkage. Only ~1 % of pups from FoxP1^flox/+;Ai65^+/−×Ai65^−/− intercrosses resulted in FoxP1^flox/+;Ai65^−/− mice. Genetically linked FoxP1^flox/+;Ai65^+/− animals were subsequently intercrossed to generate FoxP1^flox/flox;Ai65^−/− animals. Both male and female mice were used in this study and were maintained with standard husbandry and housing conditions. All experiments were performed in compliance with the National Institutes of Health Guidelines on the Care and Use of Animals and approved by the animal care and use committee at Columbia University.

METHOD DETAILS

Muscle injections using AAV, rabies virus, and tracers

For all viral and tracing experiments, postnatal day 3–5 pups were anesthetized on ice and a small incision in the skin was introduced to expose the select muscle. Injections were performed using pulled glass micropipettes and positive pressure. Spinal cord tissue was harvested 4–7 days post injection.

To label muscle-defined proprioceptive sensory axons, scAAN/1 -CMV-Cre (~1e10¹³ vg/ml) virus was injected into select muscles of mice with PV::FlpO^+/−;Ai65^+/−alleles. For GL and GS reflex circuits, analysis was mainly focused at L3 and L4 spinal segmental levels, whereas for IF, analysis was centered from L4 to L6 levels. The 1 serotype was chosen over serotype 6 due to higher efficiency in labeling sensory neurons. In the case of GL sensory neurons in Figure 1, a small fraction of input afferents was labeled in pilot experiments using scAAV9-CMV-Cre (~1e10¹³ vg/ml) in Pv::FlpO^+/−;Ai65^+/− mice.

To label motor neuron dendrites, scAAV6-CBh-GFP (~1e10¹² vg/ml) or rabies virus SAD-B19 ΔG-GFP (propagated as previously described (Zampieri et al., 2014)) were injected into muscles of wild-type, ChAT::Cre^+/−;Ai14^+/−, FoxP1^flox or FoxP1^MNΔ mice. The use of ChATr.Cre and Ai14 alleles facilitated the labeling of motor neurons and the assignment of spinal segmental levels. In the case of wild-type, FoxP1^flox or FoxP1^MNΔ mice an antibody against ChAT was used for labeling of motor neurons. In the case of GL motor neurons in Figure 2, a small fraction of dendrites was labeled in pilot experiments using scAAV6-CMV-Cre (~1e10¹² vg/ml) in Ai14 ^−/− mice.

To label muscle-defined proprioceptors and motor neuron dendrites, scAAN/1 -CMV-Cre and scAAV6-CBh-GFP viruses were injected into select muscles of PV::FlpO^+/−;Ai65^+/−, FoxP1^flox;PV::FlpO^+/−,Ai65^+/−or FoxP1^MNΔ;PV::FlpO^+/−;Ai65^+/− mice.

To assess sensory connectivity on motor pools, 1% cholera toxin subunit-B (CT-B) (as described in (Surmeli et al., 2011)), and scAAV6-CBh-GFP were injected into select muscles.

Injection specificity was assessed by the restriction of fluorescent dyes to defined muscles. In the case of ST muscle, due to the tight anatomical proximity of ST with synergistic semimembranosus and biceps femoris muscles that comprise the hamstring muscle group, and with adductor muscles, cross-labeling can occur. We therefore used the previously described cell body position of ST motor neurons across the ML and RC spinal levels to confirm specificity (McHanwell and Biscoe, 1981; Surmeli et al., 2011).

Embryonic sensory axon and motor neuron labeling

Embryonic day 17.5 or E18.5 spinal cords were dissected to expose the L5 and L6 dorsal and ventral roots, following dorsal and ventral laminectomy procedures, in oxygenated (95% O₂, 5% CO₂) Artificial Cerebrospinal Fluid (ACSF: (mM) 125 NaCI, 2.5 KCI, 1.25 NaH₂PO₄.H₂O, 26 NaHCO₃, 25 glucose, 0.4 ascorbic acid, 2 sodium pyruvate, 1 MgCI₂, 2 CaCI₂). Dorsal and ventral roots were labeled using tight fitted glass capillaries loaded with 10% Rhodamine- or 10% FITC-conjugated dextrans (3000 MW, Invitrogen) and incubated overnight in oxygenated (95% O₂, 5% CO₂) ACSF.

Tissue processing and immunohistochemistry

Approximately 4–7 days following viral or tracer muscle injection, pups were perfused first with 1xPBS, then followed by 4% paraformaldehyde (PFA, P6148 Sigma Aldrich). A ventral laminectomy was performed and the tissue was fixed overnight in 4% PFA at 4C. Spinal cords were removed from the vertebrate column and lumbar or thoracic level spinal cords were embedded in 4% low melting point agarose (LMP agarose, 16520–100 Invitrogen) and 80–100 μm transverse slices were cut using a Leica VT1000 vibratome. Vibratome slices were incubated, free-floating, with primary antibodies in 1xPBS, 1 % BSA and 0.3% Triton-X for 48 hr at 4C, washed three times with 1xPBS, and incubated for 24 hr with the appropriate secondary antibodies. Primary antibodies and working dilutions were: guinea pig anti-vGluT1 (1705:1:16,000; 1706:1:32,000; 1707:1:128,000 all this study), rabbit anti-dsRed (1:1,000, Clontech), goat anti-ChAT (1:200, Millipore), chicken anti-GFP (1:4,000, Abcam), rabbit anti-GFP (1:4,000, Invitrogen), sheep anti-GFP (1:4,000, AbD Serotec), goat anti-CT-B (1:8,000, List Biologicals), and mouse anti-CT-B (1:500, Abcam). Secondary antibodies used were all raised in donkey and conjugated to FITC (1:1,000), Cy3 (1:1,000), Cy5 (1:500), or Alexa Fluor 488 – conjugated (1:1,000) (Jackson Immunoresearch Laboratories).

Data analysis

Images were acquired on a Zeiss LSM-510 or LSM-880 meta confocal microscope using Zen software (Zeiss) and analyzed using Imaris software (Bitplane).

For sensory axon trajectory analysis, the position of muscle-defined proprioceptive axons were marked using the Imaris spot function in ~25 micron increments. The XY coordinates were then used to obtain mean trajectory angles from the emergence point in the DF to the RoC, and from the RoC to the axon terminal zone in the ventral horn. To determine the DV boundary of the RoC, the difference between the mean position of each sensory axon trajectory was calculated to identify the two points with the lowest degree of separation. To map the position of sensory axon emergence points, Cartesian co-ordinates were assigned to sensory axons that emerged from the DF using the Imaris spot function. All co-ordinates were scaled to a spinal cord hemi-section with gray-white matter boundary dimensions of 650 μm along the DV axis and 900 along the ML axis, with the central canal as the origin.

For dendritic radiality analysis, motor pools were divided into octants with the centroid representing the center of the motor pool. For each octant, the dendritic surface area outside of the cell body region was quantitated using the Imaris surface function, and normalized to the octant with the highest value.

For cell body position analysis, spheres were assigned to the center of motor neuron somata using the Imaris spot function. The Cartesian co-ordinates of each sphere were exported from Imaris and used to plot distribution contours on a normalized spinal cord hemi-section using a custom MATLAB script (Bikoff et al., 2016).

For muscle-defined sensory input distribution on non-homonymous motor pools, a color channel representing the co-localization of CT-B and vGluT1 was compared with a color channel representing the GFP signal using the Imaris co-localization function to estimate the distribution of CT-B + vGluT1 double positive sensory inputs on GFP-labeled motor pools. For muscle-defined sensory inputs on homonymous motor pools, CT-B + vGluT1 double positive sensory inputs were gated against CT-B-labeled motor neurons. Since CT-B also accumulates in motor neurons innervating the injected muscle, we used this property as an indicator for CT-B labeling efficiency. Each putative CT-B⁺ + vGluTT punctum was examined by manual inspection of serial optical sections to confirm apposition with a GFP- or CT-B-labeled dendrite, and assigned a sphere using the Imaris spot function.

For fine mapping of homonymous sensory input distribution, motor pools were divided into distinct dendritic or somatic compartments, and the number of CT-B⁺ + vGluT1⁺ puncta opposed to GFP⁺ motor neurons, as determined using the Imaris colocalization and spot functions as described above, was quantitated within each compartment. The CT-B⁺ + vGluT1⁺ puncta within each dendritic or somatic compartment were then expressed as a fraction (%) of the total puncta across the homonymous motor neurons.

To quantitate axo-dendritic overlap, a sensory axon mask corresponding to the territory occupied by muscle-defined sensory axons was created using the Imaris surface function. The sensory axon mask was used to identify intersecting dendrites from each motor pool. Renderings of axons and dendrites within the axon mask were modeled in Imaris and the surface area of each were used to calculate axo-dendritic overlap ratios.

For fine quantitation of axo-dendritic overlap within homonymous S-M pairs, the assay as described above was used, but it was modified to quantify the membrane surface area of distinct dendritic or somatic compartments of homonymous motor pools. Ratios of axo-dendritic surface overlap within each dendritic or somatic compartment were expressed as a fraction (%) of the total axo-dendritic surface overlap between defined sensory axons and homonymous motor neurons.

To visualize vGluT1 ⁺ synaptic clusters or singletons formed between muscle-identified sensory axons and motor neurons, optical sections of sparsely labeled sensory axons and motor neurons were pseudo-colored using Photoshop (Adobe) and imported into Imaris using the batch converter function prior to vGluTI co-localization analysis.

To examine the relationship between the angle at which sensory axons intersect motor neuron dendrites and synapse formation, the angle between sensory axon intersecting GFP⁺ motor neuron dendrites was measured within individual optical sections. The presence or absence of vGluTI at the site of intersection was determined, with single vGluTT appositions assigned as a singleton, and two or more consecutive vGluT1⁺ appositions classified as a cluster. The frequency of cluster and singleton formation was plotted in relation to 10 degree angular intervals. These data points were fit to mathematical curves to allow for more accurate extrapolations (Figure 4W). For the cluster probabilities the curve was exp(−0.5(0/12°)²), where θ is the angle (in degrees) between the axon and dendrite. Singleton probabilities were fit with 0.12exp(−0.5((0–39°)/5°)²) + 0.01(tanh((0–40°)/10°) + 1). The total angular factor was the probability of cluster formation, multiplied by 5 (the average number of vGluT 1⁺ puncta per cluster), plus the probability of singleton formation.

The effect of the angle of approach was determined by combining the angular factor with axo-dendritic overlap densities. To quantify the dendritic distribution of each motor pool, confocal images of immuno-stained spinal cord sections were first scaled to fit a normalized spinal cord to accommodate size differences between segmental levels, using the central canal as a point of reference. The ventral spinal cord was then divided into an array of 50 square micron elements, and the mean pixel intensity was determined using the Photoshop histogram function to approximate membrane density (Figure S1E). Sensory axon positions were determined using Cartesian co-ordinates using the Imaris spot function and assigned to the 50 square micron array to create a binary mask, which was mapped onto each motor pool membrane array (Figure S1F). The total amount of membrane, represented by the 50 square micron array, for each motor pool within each axon mask was then computed. The normalized sum of the membrane under each sensory axon mask provided an estimate of the degree of overlap with each motor pool examined. We also included in the analysis the overlap between sensory axons and motor neurons along the RC axis. RC motor pool segmental boundaries (Figure S1H) were estimated using data from McHanwell and Biscoe (1981). Overlaps computed in this manner were in good agreement with the results reported in Figures 3 and S4G–S4J. The results including angular factors were normalized for each sensory axon type to produce the synapse connection percentages in Figures 5 and S5.

Axon Model

Initially, a field of dendrites was created as in Figure S5J. An axon was then introduced at a given starting point at the boundary of the region. Axonal growth was simulated in steps of 1 μm of extension. The angle of axon growth fluctuated on each time step by an amount chosen from a zero-mean Gaussian with a standard-deviation of 0.5°. When an axon came within 3 μm of a dendrite, a probability was computed from the curves in Figure 4W either for making a singleton synapse or for becoming “associated” with the dendrite (this latter probability was calculated from the curve for clusters of synapses in Figure 4W). If neither of these options was chosen according to the computed probability, or if a singleton synapse formed, the axon continued to grow as before. If, on the other hand, the axon became associated with the dendrite, it grew parallel to the dendrite for 50 μm and created synapses at a rate of 1/10 per μm, as computed from a Poisson process. After the axon ran in this parallel direction for 50 μm, a “release” angle was chosen from a zero-mean Gaussian distribution with a standard deviation of 2°. The axon was then required to grow for another 60 μm before it could become associated with another dendrite. This prevented the axon from repeatedly being associated with the same dendritic branch. Axon growth simulated in this way was repeated over 1000 trials to measure selectivity. The panels in Figure S5J show two example runs.

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Guinea pig polyclonal anti-vGluT1 (CU1705)	This study	RRID: AB_2750940
Guinea pig polyclonal anti-vGluT1 (CU1706)	This study	RRID: AB_2665455
Guinea pig polyclonal anti-vGluT1 (CU1707)	This study	RRID: AB_2750941
Rabbit polyclonal anti-dsRed	Clontech	Cat#632496
Goat polyclonal anti-Choline Acetyltransferase	Millipore	Cat#AB144P
Chicken polyclonal anti-GFP	Abcam	Cat#AB13970
Rabbit polyclonal anti-GFP	Invitrogen	Cat#A11122
Sheep polyclonal anti-GFP	AbD Serotec	Cat#4745–1051
Goat polyclonal anti-Cholera Toxin, B-Subunit	List Biologicals	RRID: AB_10013220; Cat#703
Mouse monoclonal anti-Cholera Toxin, B-Subunit	Abcam	Cat#AB35988
Bacterial and Virus Strains
scAAV6-CBh-GFP	UNC Vector Core (VC)	scAAV6-CBh-GFP
scAAV6-CMV-Cre	This study	This study/ Custom UNC VC packaging
scAAVI -CMV-Cre	This study	This study/ Custom UNC VC packaging
scAAV9-CMV-Cre	This study	This study/ Custom UNC VC packaging
Rabies SAD-B19 ΔG-GFP	Wickersham et al., 2007	N/A
Chemical, Peptides, and Recombinant Proteins
Cholera Toxin B Subunit (low salt)	List Biologicals	Cat#104
Dextran, Fluorescein, 3000MW, Anionic, Lysine Fixable	Invitrogen	Cat#D-3306
Dextran, Tetramethylrhodamine, 3000MW, Anionic, Lysine Fixable	Invitrogen	Cat#D-3308
Experimental Models: Organisms/Strains
Olig2::cre	Dessaud et al., 2007	MGI:3774124
FoxP1 conditional	Feng etal., 2010	N/A
PV::FlpO	Madisen et al., 2015	Jax 022730
Ai65 (RCFL-tdT)	Madisen et al., 2015	Jax 021875
Ai14 (RCL-tdT)	Madisen et al., 2010	Jax 007914
ChAT::cre	Rossi et al., 2011	Jax 006410
Experimental Models: Cell Lines
HEK293	Sigma	Cat#85120602–1VL
B7GG	Zampieri et al., 2014	Ed Callaway
Oligonucleotides
FoxP1 Primer 1 5′ CTCCTAGTCACCTTCCCCAGTGC 3′	Feng et al., 2010	N/A
FoxP1 Primer 2 5′ G AAC ACT GT CG AAT G ACCCTGC 3′	Feng et al., 2010	N/A
Cre-F 5′ TTGCCGCGCCATCTGCCACCA 3′	This study	N/A
Cre-R 5′ CTAAT CG CC AT CTT CC AG 3′	This study	N/A
PVFlpO 16211 5′ TGTTTCTCCAGCATTTCCAG 3′	Madisen et al., 2015	N/A
PVFlpO 17564 5′ GGATGCTTGCCGAAGATAAG 3′	Madisen et al., 2015	N/A
PvFlpO 17566 5′ CTGAGCAGCTACATCAACAGG 3′	Madisen et al., 2015	N/A
RosaTomWT-F 5′ AAGGGAGCTGCAGTGGAGTA 3′	Madisen et al., 2010	N/A
RosaTomWT-R 5′ CCGAAAATCTGTGGGAAGTC 3′	Madisen et al., 2010	N/A
RosaTomMut-F 5′ GGCATTAAAGCAGCGTATCC 3′	Madisen et al., 2010	N/A
RosaTomMut-R 5′ CTGTTCCTGTACGGCATGG 3′	Madisen et al., 2010	N/A
Software and Algorithms
Imaris	Bitplane	N/A

Highlights.

• Sensory axonal and motor neuron dendritic morphologies show positional organization

• Axo-dendritic overlap reduces the number of potential post- synaptic partners

• The angle of axo-dendritic approach correlates with density of synapses

• A positional model predicts sensory-motor connectivity patterns with high accuracy