Deep Learning Based High-Resolution Reconstruction of Trabecular Bone Microstructures from Low-Resolution CT Scans using GAN-CIRCLE

Abstract

Osteoporosis is a common age-related disease characterized by reduced bone density and increased fracture-risk. Microstructural quality of trabecular bone (Tb), commonly found at axial skeletal sites and at the end of long bones, is an important determinant of bone-strength and fracture-risk. High-resolution emerging CT scanners enable in vivo measurement of Tb microstructures at peripheral sites. However, resolution-dependence of microstructural measures and wide resolution-discrepancies among various CT scanners together with rapid upgrades in technology warrant data harmonization in CT-based cross-sectional and longitudinal bone studies. This paper presents a deep learning-based method for high-resolution reconstruction of Tb microstructures from low-resolution CT scans using GAN-CIRCLE. A network was developed and evaluated using post-registered ankle CT scans of nineteen volunteers on both low- and high-resolution CT scanners. 9,000 matching pairs of low- and high-resolution patches of size 64×64 were randomly harvested from ten volunteers for training and validation. Another 5,000 matching pairs of patches from nine other volunteers were used for evaluation. Quantitative comparison shows that predicted high-resolution scans have significantly improved structural similarity index (p < 0.01) with true high-resolution scans as compared to the same metric for low-resolution data. Different Tb microstructural measures such as thickness, spacing, and network area density are also computed from low- and predicted high-resolution images, and compared with the values derived from true high-resolution scans. Thickness and network area measures from predicted images showed higher agreement with true high-resolution CT (CCC = [0.95, 0.91]) derived values than the same measures from low-resolution images (CCC = [0.72, 0.88]).

1. INTRODUCTION

Efficacy of in vivo computed tomography (CT) imaging modalities in most medical imaging applications depend on their spatial resolution, a determinant of the microstructural quality of the captured Tb network, outlining the scope of biological and clinical questions that can be addressed. Spatial resolution varies not only among different in vivo imaging modalities but also among different scanners of same modality, and low spatial resolution along with other modality specific factors such as signal to noise ratio (SNR), exposure time and radiation dose degrade the quality of the reconstructed CT image. Such degradation in CT image quality from high- to low-resolution scanners causes inconsistency in microstructural measurements in multi-site and longitudinal studies, where scanner mismatch across different study locations are evident.

Although, sophisticated hardware components such as high pitch detector, x-ray tube with fine focal spot etc. are capable of capturing high-resolution (HR) images, they contribute to high CT-machine cost, high radiation dose, and slow scan speed. Hence, HR image reconstruction using computational methods aiming to recover HR image from its low-resolution (LR) counterpart is an emerging research area. Several computational algorithms for HR image reconstruction are available in the literature which can be divided into two broad categories: (1) model-based reconstruction techniques, and (2) learning-based methods.

Model-based algorithms regulate the reconstruction process based on some prior assumption of the degradation scheme. ^1-3 On the other hand, learning-based methods accomplish the task by learning the non-linear mapping from low- to high-resolution images.^4-7 Recent progress in deep learning (DL) has established the capability of convolutional neural networks (CNN) in extracting HR features from LR images at low computational cost. Numerous DL based methods have shown promising results in HR reconstruction for different in vivo CT modalities.^8-14 Chen et al.⁸ proposed a deep densely connected network for super resolution (SR) reconstruction of magnetic resonance images. Chaudhury et al.⁹ proposed a three-dimensional (3D) CNN entitled “DeepResolve” that learns residual-based transformations between paired high- and low-resolution magnetic resolution image slices. Park et al.¹⁰ developed a CNN based SR CT image reconstruction technique that learns end-to-end mapping between paired low- and high- resolution image slices using the modified U-Net. Yu et al.¹¹ combined a single-slice CT SR network (s-CTSRN) with skip connections and a multi-slice CT SR network (m-CTSRN) to reconstruct SR CT images. Here, s-CTSRN improves the high frequency details extraction while m-CTSRN maintains the coherence between neighboring CT slices. Several generative adversarial network (GAN) based SR reconstruction techniques have also shown promising results.^15-21 Ledig et al. proposed a perceptual loss function as the weighted sum of adversarial and content loss, and used that as an objective for SR image reconstruction using GAN (SRGAN).¹⁵ Wang et al. used Residual-in-Residual Dense Block (RRDB) without batch normalization as the building block of SRGAN to eliminate noisy artifacts in reconstructed SR images using SRGAN.¹⁶ Wolterink et al. successfully enhanced the image quality by training an unsupervised GAN to learn the non-linear mapping from LR to HR images.¹⁷ You et al. trained a CT SR GAN entitled “GAN-CIRCLE” constrained by the identical, residual, and cycle consistency loss using paired two-dimensional (2D) HR and LR patches, where LR CT images were generated by adding noise to the down sampled HR CT images.¹⁸

In this paper, we investigate high resolution reconstruction techniques in the context of musculoskeletal imaging especially related to osteoporosis.^22,23 Osteoporosis is a common age-related disease characterized by reduced bone mineral density (BMD) and enhanced fracture-risk. Approximately, 40% of women and 13% of men suffer osteoporotic fractures in their lifetime. Osteoporotic hip fractures reduce life expectancy by 10-20%,²⁴ and increased life expectancy will increase fracture incidence to 6.3 million by 2050.²⁵ Dual-energy X-ray absorptiometry (DXA)-measured areal BMD is the clinical standard for diagnosis of osteoporosis. However, it is generally agreed that about 60% of bone’s mechanical competence is explained by variation in BMD,²⁶ and there are compelling evidences from histologic studies demonstrating the roles of bone microstructural degeneration in determining bone strength and fracture-risk.^27-29 Thus, valid and reliable measures of Tb microstructural features, associated with bone strength and fracture-risk, are of clinical significance.

Various topologic and geometric methods are available in literature to measure Tb micro-structure.^30-33 Vesterby et al. ³⁰ conceived a stereologic parameter, called star volume, which is the average volume of an object region that can be seen from a point inside that region unobscured in all directions. Hahn et al. ³¹ introduced the “trabecular bone pattern factor” which captures Tb connectivity in terms of the convexity property of the Tb surface defined as the ratio of the differences in perimeter and area under dilation. Hildebrand et al. ³² developed a 3-D structure model index, a function of global plate-to-rod ratio, based on the observation that the rate of volume change with respect to half thickness (or the radius) for platelike elements is different from that for rod-like elements. Feldkamp et al. ³³ showed that the makeup of TB networks can be expressed in terms of topological entities such as the 3-D Euler number. Saha and his colleagues have pioneered unique algorithms,^34-41 characterizing individual trabecular plates and rods, which have been adopted in a large number of studies.^34-57

Several 3D Tb imaging modalities, including magnetic resonance imaging (MRI)^26,42,58,59 and high-resolution peripheral quantitative computed tomography (HR-pQCT),^60-62 have been popularly applied in bone studies. Emerging multidetector-row CT (MDCT) scanners enable segmentation and measurement of Tb microstructures and overcome the major deficits of MRI and HR-pQCT modalities related to slow scan speed, limited field-of-view and failure to provide quantitative BMD. It has been demonstrated that microstructural measures are dependent on image resolution and other features.⁶³ A pertinent challenge with MDCT-based bone imaging emerges due to wide discrepancies in spatial resolution, and other imaging and reconstruction features from different vendors, and rapid upgrades in technology. It introduces a challenge related to data harmonization in large multi-site or longitudinal studies that typically involves data collection using different scanners. Often, research teams encounter a situation in longitudinal studies that a new and upgraded scanner substitutes the previous scanner in the middle of the study, which can result in an incomplete process for data acquisition and analysis, or a waste of previous data collected using the older machine. This results in a need for data harmonization, which will add immense value to the bone research community, enabling them to use data collected from multiple scanners, facilitating study design and improving fidelity of longitudinal studies that often face unavoidable situations of data collection from different scanners. In this paper, we present a deep learning-based optimized method for HR reconstruction of Tb microstructures from LR CT scans using GAN-CIRCLE,^18,19 and evaluate its performance in terms of image quality as well as clinically significant microstructural measures. Specifically, we compute different Tb microstructural measures such as thickness, spacing, and network area density from the LR and predicted HR CT scans, and examine their agreement with the reference values derived from true HR CT scans. DL network architecture, data acquisition protocols, post-processing steps, computation of microstructural measures, and statistical methods used for evaluation are elaborated in section 2. Experimental results are described in Section 3, and the conclusions are drawn in Section 4.

2. METHODOLOGY

In this section, we describe the deep learning network architecture developed for HR reconstruction of Tb image from the LR CT scan, followed by a brief description of the CT scan protocols on low- and high-resolution MDCT scanners as well as the steps for extracting matching pairs of LR and HR patches for training, validation, and testing. Finally, Tb microstructural measures examined in this paper are defined, and techniques adopted for statistical evaluation of these measures are discussed.

2.1. Deep Learning Network Architecture

A new deep learning network is designed and developed for HR reconstruction of Tb images capturing Tb microstructures from their LR CT scans using the basic principle of GAN-CIRCLE (Figure 1). GAN-CIRCLE is designed with two generator mappings G: X → Y and F: Y → X, where X is the set of LR CT scans and Y is the set of HR counterparts. The overall goal of this network is to learn the nonlinear process of the low-to-high resolution generator (G:X → Y), while synergistically regularizing with cycle-consistency, adversarial, and several other loss functions. The quality of the generator G is directly controlled using a supervision loss function L_SUP and, a discriminator D_Y and the associated adversarial loss function L_WGAN. The idea is that, during the learning process, both generator G and discriminator D_Y synergistically improve, simultaneously reducing both supervision and adversarial losses. To regularize the learning processes, a cycle-consistency check was added through a counter generator F: Y → X from HR to LR and a cycle-consistent loss function L_CYC. Similar to the case of generator G, the learning process of F is controlled using the supervision loss function L_SUP and the adversarial loss function L_WGAN associated with another discriminator D_X. An identity loss function L_IDT is used to regularize the training process which ensures that the network does not generate a significantly different output when a true HR patch is fed as an input to the LR-to-HR generator G. Finally, a joint sparsifying transformation loss function L_JST is used for simultaneously sparsifying predicted images and reducing noise, while preserving anatomical features by minimizing the difference from the true HR image. So, during training the network tries to minimize the following objective function:

$$L_{\text{GAN}-\text{CIRCLE}}=L_{\text{WGAN}}(D_Y,G)+L_{\text{WGAN}}(D_X,F)+{\lambda }_1{L}_{\text{CYC}}(G,F)+{\lambda }_2{L}_{\text{IDT}}(G,F)+{\lambda }_3{L}_{\text{JST}}(G)+L_{\text{SUP}}(G,F),$$

Figure 1.

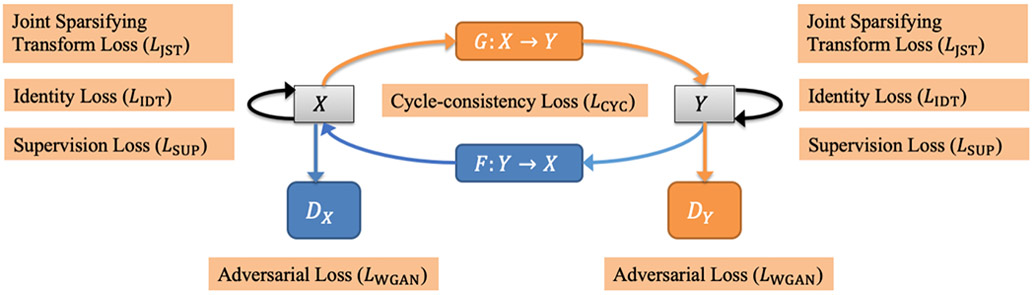
Basic modules of the GAN-CIRCLE used for HR CT image reconstruction. Here, X is the set of low-resolution CT scans, and Y is its high-resolution counterparts. The network consists of two basic GAN modules (Generator: G, Discriminator: D_Y) and (Generator: F, Discriminator: D_X), which are responsible for low-to-high and high-to-low resolution image reconstruction, respectively. Different loss functions are synergistically coupled to train the network, while constrained under the regularization terms related to cycle-consistency and identity loss to avoid overfitting.

where, λ₁, λ₂, and λ₃ are the weights for different losses.¹⁸

Network architectures of the generators G and F, and the discriminators D_X and D_Y are shown in Figure 2 and Figure 3 respectively. The Generator network is consisting of two sub-networks, a feature extraction network, and a reconstruction or up-sampling network. In the feature extraction network 12 non-linear SR blocks are concatenated, where each block consists of 3×3 convolution kernels, bias, leaky rectified linear unit (Leaky ReLU), and a dropout layer. Leaky ReLU is defined as follows: max(0, x) – α max(0, −x), where α denotes the slope of the function. At each convolutional layer same number of filters as suggested by You et al.¹⁸ is used. Stride within each convolution layer is set to 1 except for the first layer where the stride is 2; stride is the number of pixels with which the kernel slides horizontally or vertically. To capture the local as well as global features, outputs of the hidden layers in the feature extraction network are concatenated using a skip connection before feeding into the reconstruction network. The skip connection is used to prevent overfitting and training saturation. Reconstruction network follows a network in network architecture, where two parallel branches of CNNs are concatenated before up-sampling. Two SR blocks with 1×1 convolution kernel is used in the two parallel branches to reduce dimensionality while increasing the non-linearity of the network. After concatenating the outputs of the parallel branches, the image is up-sampled by a factor of 2 and finally, all the feature maps are fused to generate a residual image in the last convolution layer. For supervised training, residual image is combined with the input image to obtain the HR output image. Discriminator network is composed of 8 layers of convolution, bias, instance norm, and Leaky ReLU, followed by two fully-connected (FCN) layers with 1024 units and 1 unit. Each of the 8 convolution layers use a 4×4 convolution kernel with 64, 64, 128, 128, 256, 256, 512, and 512 filters respectively.

Figure 2.

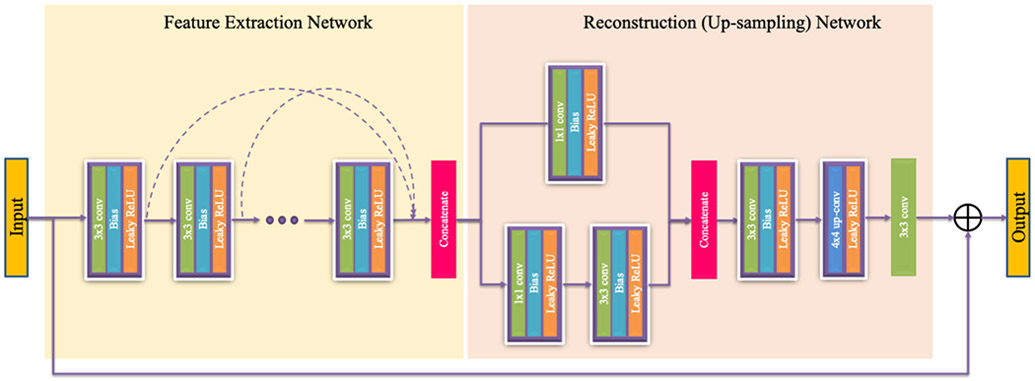
Architecture of a generator. Stride within each convolution layer is 1 except for the first layer where the stride is 2.

Figure 3.

Architecture of a discriminator. Here, n denotes the number of kernels in a convolutional layer, and s denotes the stride.

2.2. Dataset Description

Matching HR and LR ankle CT scans of human volunteers acquired on two different CT scanners with significantly different spatial resolution were used for training, validation, and testing of the GAN-CIRCLE-based HR reconstructor described in the previous section. Specifically, nineteen healthy volunteers (age: 26.2 ± 4.5 Y; 10 F) were recruited and the distal tibia of their left legs were scanned on two MDCT scanners. The study was conducted around the transition period of the MDCT scanner upgrade at the University of Iowa Comprehensive Lung Imaging Center (I-CLIC). The first MDCT distal scan on each volunteer was performed on a LR Siemens FLASH scanner, and then they were recalled and rescanned on a HR Siemens FORCE scanner after upgrade. The average time gap between the LR and HR scans was 44.6 ± 2.7 days, with the minimum and maximum gaps of 40 and 48 days, respectively. The human study was approved by The University of Iowa Institutional Review Board and all participants provided written informed consent. The CT scan protocols on the two scanners are described here.

FLASH scanner:

Single X-ray source spiral acquisition at 120 kV, 200 effective mAs, 1 sec rotation speed, pitch factor: 1.0, total effective dose equivalent: 170 μSv ≈ 20 days of environmental radiation in the U.S. Images were reconstructed at 200 μm slice-spacing using a normal cone beam method with a special U70u kernel.

FORCE scanner:

Single X-ray source spiral acquisition at 120 kV, 100 effective mAs, 1 sec rotation speed, pitch factor: 1.0, total effective dose equivalent: 50 μSv ≈ 5 days of environmental radiation in the U.S. Images were reconstructed at 200 μm slice-spacing and 150 μm pixel-size using Siemens’s special kernel Ur77u with Edge Technology.

For both scanners, Siemens z-UHR scan mode was applied, enabling Siemens double z sampling technology and achieving high structural resolution.

2.3. Data Processing, Training, and Validation

A Gammex RMI 467 Tissue Characterization Phantom (Gammex RMI, Middleton, WI) was scanned to calibrate CT Hounsfield numbers into BMD. First, both LR and HR CT scans were converted into BMD images using corresponding calibration phantom scans; then LR images were interpolated at 150 μm isotropic voxel size; and finally, HR images were registered to corresponding LR images. HR images were registered to the LR image in two-steps: first, cortical bone and Tb network of the HR image was manually registered to the LR image using ITK-SNAP registration toolkit.⁶⁴ In the second step, a rigid transformation, initialized by the transformation matrix from the manual registration step, was applied on the registered HR image for fine tuning. To improve the registration accuracy, region of interest (ROI) for registration cost function was defined as the distal tibia with a soft boundary. For training and testing purposes, pairs of low- and high-resolution matching patches of size 64×64 were randomly harvested from 30% peeled ROIs of registered LR and HR BMD images, and scaled to the unit interval of [0 1].

For training, weights of the convolution layers were initialized using the techniques proposed by He et al.⁶⁵ In the training process λ₁, λ₂, and λ₃ were set to 1, 0.5, and 0.001 respectively. Slope α of the leaky ReLU was set to 0.1 and drop out was applied to each convolution layer with p = 0.8. The network was trained for 500 epochs and took almost a day to train using Adam optimizer⁶⁶ with β₁ = 0.5 and β₂ = 0.9 and a learning rate of 1 × 10⁻⁴.

2.4. Computation of Tb Microstructural Measures

Tb measures examined in this paper are listed in Table 1. Each BMD image was processed through the following imageprocessing steps to compute different trabecular bone measures – (1) fuzzy skeletonization⁶⁹ and computation of trabecular network area density (Tb.NA) measure; (2) star-line analysis for computation of trabecular thickness (Tb.Th) and trabecular spacing (Tb.Sp) measures.⁶⁸ Note that all Tb measures were computed on 2D slices of LR, true HR and predicted HR images.

Table 1.

List of CT-derived trabecular bone measures examined in this paper. Nomenclatures of trabecular bone measures used by Bouxsein et al.⁶⁷ and Chen et al.⁶³ are followed here wherever possible.

Parameter (unit)	Description
Tb.NA (mm2/mm3)	Tb network area density, i.e., the average area of the medial surface of segmented bone per unit ROI
Tb.Th (μm)	Mean trabecular thickness computed by star-line analysis68
Tb.Sp (μm)	Mean trabecular spacing, i.e., the space between trabecular microstructures computed by star-line analysis68

2.5. Statistical Analysis

For quantitative evaluation, 2D measurements of Tb thickness, spacing, and network area were stacked to reconstruct a 3D representation of the measures. Summary statistics of each Tb measure from LR, true and predicted HR scans was computed in terms of mean and standard deviation over 100 randomly selected spherical ROIs of 12-pixel radius, fully confined within the 30% peeled ROI of each scan. Finally, linear and concordance correlation of the mean values of individual Tb measure from LR and predicted HR images with the reference mean values derived from true HR CT data was examined for each specimen.

3. EXPERIMENTS AND RESULTS

GAN-CIRCLE based HR Tb image reconstructor was trained and validated using matching low- and high-resolution CT scans of ten human volunteers, and the network was qualitatively as well as quantitatively evaluated on matching low- and high-resolution CT scans of nine other volunteers. Finally, improvement in both image quality and clinically significant Tb microstructural measures from LR to predicted HR scans were assessed w.r.t. the reference measures from true HR image.

Specifically, nine thousand matching pairs of low- and high-resolution patches from registered BMD images of ten volunteers were randomly harvested for training and validation of the HR Tb microstructure reconstructor. The set of 9,000 training samples was randomly split into 4:1 ratio for training and validation purposes. A different set of 5,000 pairs of matching LR and HR patches from the registered BMD images of nine other volunteers were used for testing and evaluation.

Results of deep learning-based HR reconstruction are illustrated in Figure 4. Figure 4 presents predicted HR images (middle row) from three LR images (left row); matching true HR images are shown in the right column for visual comparison. HR reconstruction of a full image slice was obtained by independently reconstructing non-overlapping 64×64 patches and stitching them together. No block effects are visible in the predicted HR images despite independent patch reconstruction. This observation suggests that cycle-consistency and other regularization constraints of the GAN-CIRCLE can avoid random patch-bias artifacts. To display the performance of the method at the level of Tb microstructures, one random patch is zoomed in for each example. It is observed by visually comparing matching zoomed in patches that the GAN-CIRCLE successfully performs a non-linear deblurring and filtering to reconstruct HR Tb microstructural features and resolution from blurred and noisy LR data.

Figure 4.

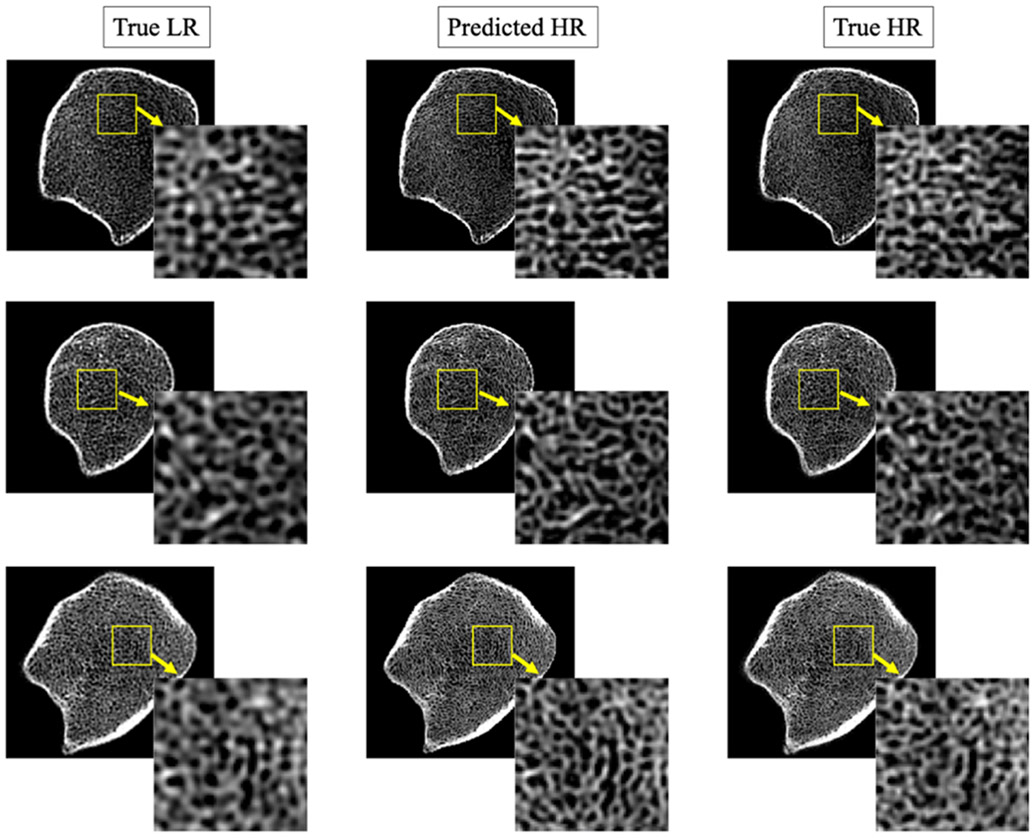
Results of HR prediction from LR trabecular bone CT scans using GAN-CIRCLE. Left-to-right columns: matching 2D image slices from true LR, predicted HR, and true HR CT data. LR and HR CT images of distal tibia were acquired on a Siemens FLASH and FORCE scanners, respectively. Three different rows represent images from three different human subjects.

The performance of the network was quantitatively evaluated using structural similarity (SSIM) index⁷⁰— a widely used method to estimate perceived quality of images and videos. For quantitative analysis, only 4,000 patches entirely lying inside the Tb were used, since the objective of this work was to predict HR microstructures from LR images. SSIM was computed between LR and true HR, as well as between predicted HR and true HR patches, and a paired t-test was conducted between these two sets of SSIM values. The results of the paired t-test suggest that the reconstruction network significantly improves (p < 0.01) the structural similarity with the true HR Tb microstructures.

For each test subject, agreement in the microstructural measurements from LR and predicted HR images with the reference measurements from true HR data was examined in terms of linear (r) and concordance correlation coefficients (CCC).

Mean and standard deviation (SD) of the r-values and CCCs for Tb.Th, Tb. Sp, and Tb.NA measures from nine test subjects are presented in Table 2. A paired t-test was conducted between the r-values from LR and true HR images, as well as predicted and true HR images for all three Tb measures, and the results showed no significant difference (p > 0.05) between the two sets of values. However, paired t-test on the CCC for each Tb measure showed that the measurements from predicted HR images had higher CCC with the reference values from true HR images compared to the values derived from the corresponding LR images. Most significant improvement in CCC was observed for Tb.Th (p < 0.0001) measure, where mean CCC between LR and true HR images was 0.66, while mean CCC between predicted and true HR images was 0.95. However, relatively smaller improvement in CCC was noticed for Tb.Sp (p < 0.01) and Tb.NA (p < 0.01) measure as compared to Tb.Th.

Table 2.

Results of linear and concordance correlation analyses for different Tb measures derived from LR, HR, and predicted HR images for individual subjects. Each cell shows mean ± SD of observed values of corresponding statistical metrics for different subjects.

	LR vs. True HR		Predicted HR vs. True HR
Tb Measures	Linear Correlation (r)	CCC	Linear Correlation (r)	CCC
Tb.Th (μm)	0.95 ± 0.02	0.66 ± 0.12	0.96 ± 0.01	0.95 ± 0.03
Tb.Sp (μm)	0.96 ± 0.02	0.93 ± 0.05	0.97 ± 0.02	0.95 ± 0.04
Tb.NA (mm2/mm3)	0.88 ± 0.07	0.83 ± 0.11	0.89 ± 0.07	0.88 ± 0.08

Measurements from nine test subjects were combined, and r-values, CCC among the microstructural measurements from LR and true HR images, as well as predicted HR and true HR images are reported in 3. For the combined analysis, all three Tb measures computed from LR and predicted HR images produced similar r-values with the reference measures from true HR scans. After combining Tb.Th values from all the test subjects, CCC between Tb.Th values from LR and true HR images was found to be 0.72 while for predicted and true HR CCC was 0.95. Figure 5 shows the linear correlation (a,b) and Bland-Altman (c,d) plot of combined Tb.Th measurements from nine test subjects. As can be seen from (c) and (d), mean difference between Tb.Th measurements from true and predicted HR images are significantly lower than the mean difference in Tb.Th values from LR and true HR images. This observation suggests that the proposed HR reconstructor successfully reduces the bias in Tb.Th measures from LR images. When combined, Tb.Sp and Tb.NA measures from LR images produced CCC of 0.97 and 0.88, respectively, with the values derived from true HR images, whereas the same measures from predicted HR images had CCC of 0.98 and 0.91 with the reference values. These results support our claim that the HR reconstructor successfully recovers the HR microstructural features from a LR CT image through non-linear deblurring and filtering.

Figure 5.

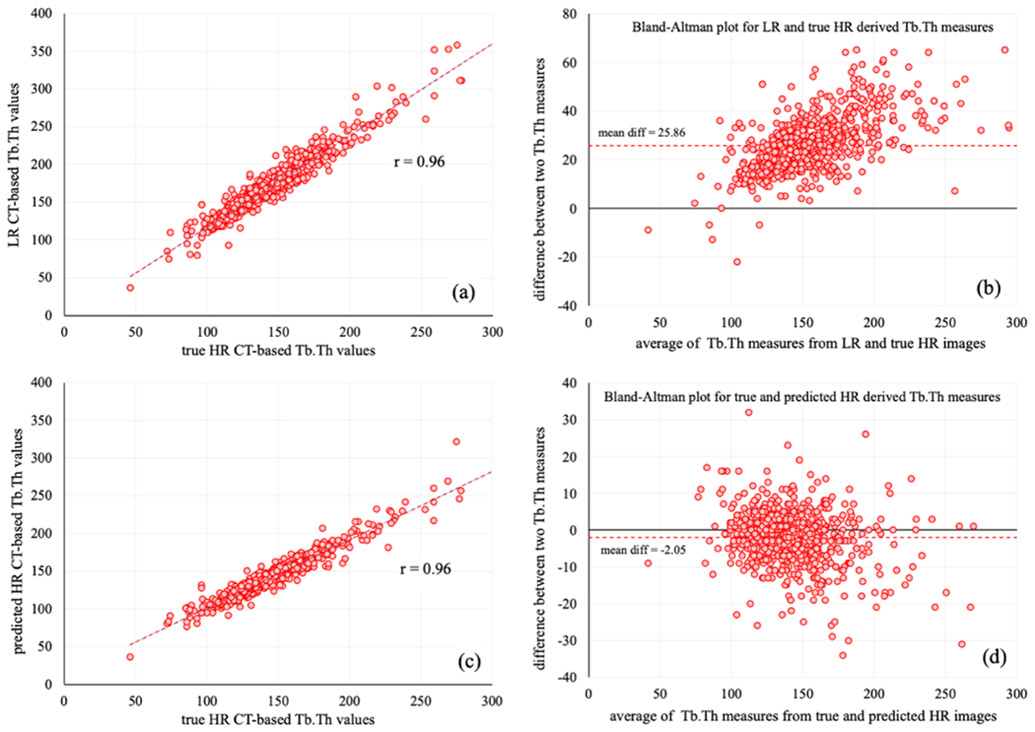
Linear correlation and Bland-Altman plots of Tb.Th measures from LR, HR, and predicted HR images of nine test subjects. (a) Linear correlation analysis among Tb.Th values from LR and true HR images. (b) Bland-Altman plot of measure difference between LR and true HR images. (c,d) Same as (a,b) but for true HR and predicted HR images.

4. CONCLUSIONS

In this paper, we have developed and evaluated a deep learning-based method for HR reconstruction of Tb microstructures from LR CT scans using GAN-CIRCLE. To the best of our knowledge, for the first time in biomedical imaging research, true matching LR and HR scans, collected from two different scanners, have been used for training and development of a HR reconstructor. Results of quantitative evaluative experiments on human ankle CT scans from two different scanners have been presented. The performance of the HR reconstructor has been evaluated both in terms of image quality, as well as clinically significant microstructural measures. Results of paired t-test have shown that SSIM values between predicted HR and true HR patches are significantly higher than the SSIM values between the LR and true HR patches. In general, Tb.Th, Tb.Sp, and Tb.NA measures derived from predicted HR images have shown higher agreement with the reference values computed from true HR scans as compared to the same measurements obtained from LR images. Furthermore, Bland-Altman plot of Tb.Th measures have shown that the deep learning network successfully reduces the fixed bias in Tb.Th values from LR images. These observations suggest that the new HR reconstructor will facilitate data harmonization to overcome challenges related to discrepancies in imaging facilities and features at different research performance sites and improve the fidelity of both cross-sectional and longitudinal study data, often collected using different scanners.

Table 3.

Results of linear and concordance correlation analysis of different Tb measures from LR, HR, and predicted HR images of nine test subjects combined together.

Tb Measures	LR – True HR		Predicted HR – True HR
	Linear Correlation (r)	CCC	Linear Correlation (r)	CCC
Tb.Th (μm)	0.96	0.72	0.96	0.95
Tb.Sp (μm)	0.98	0.97	0.98	0.98
Tb.NA (mm2/mm3)	0.91	0.88	0.92	0.91