External Validation of a Pharmacokinetic Model of Propofol for Target-Controlled Infusion in Children under Two Years Old

Abstract

Background

Previously, a linked pharmacokinetic-pharmacodynamic model (the Kim model) of propofol with concurrent infusion of remifentanil was developed for children aged 2–12 years. There are few options for pharmacokinetic-pharmacodynamic model of propofol for children under two years old. We performed an external validation of the Kim model for children under two years old to evaluate whether the model is applicable to this age group.

Methods

Twenty-four children were enrolled. After routine anesthetic induction, a continuous infusion of 2% propofol and remifentanil was commenced using the Kim model. The target effect-site concentration of propofol was set as 2, 3, 4, and 5 μg/mL, followed by arterial blood sampling after 10 min of each equilibrium. Population estimates of four parameters—pooled bias, inaccuracy, divergence, and wobble—were used to evaluate the performance of the Kim model.

Results

A total of 95 plasma concentrations were used for evaluation of the Kim model. The population estimate (95% confidence interval) of bias was −0.96% (−8.45%, 6.54%) and that of inaccuracy was 21.0% (15.0%–27.0%) for the plasma concentration of propofol.

Conclusion

The pooled bias and inaccuracy of the pharmacokinetic predictions are clinically acceptable. Therefore, our external validation of the Kim model indicated that the model can be applicable to target-controlled infusion of propofol in children younger than 2 years, with the recommended use of actual bispectral index monitoring in clinical settings that remifentanil is present.

Trial Registration

Clinical Research Information Service Identifier: KCT0001752

Graphical Abstract

INTRODUCTION

Total intravenous anesthesia is a popular method of general anesthesia. One of the techniques for employing total intravenous anesthesia is target-controlled infusion of propofol and short-acting opioids.

For adults, the pharmacokinetic and pharmacodynamic models that are commonly used for target-controlled infusion of propofol are the Marsh1 and Schnider models,2,3 which are both three-compartment models. However, these models are not well-suited for pediatric patients because of the difference in pharmacokinetic-pharmacodynamic parameters; considering their size, pediatric patients have a relatively larger volume of distribution and higher systemic clearance4 than adults have, and propofol has lower potency for them than for adults.5

Recently, our research group developed a model for target-controlled infusion of propofol with concurrent infusion of remifentanil in children between 2 and 12 years of age6 called the Kim model, which is currently being used in a few centers. The pharmacokinetic-pharmacodynamic parameters of the Kim model are shown in Table 1. However, there is limited choice of pharmacokinetic-pharmacodynamic model of propofol for children younger than 2 years of age,7,8,9 which has made performing target-controlled infusion in this population difficult. The study in which we established the Kim model involved an external validation step that included patients younger than 2 years; however, the external validation was not solely for this population and they were completely excluded when the model was designed. Therefore, whether the model would perform well in this population remains unclear.

Table 1. Pharmacokinetic-pharmacodynamic parameters of the Kim model.

Variables	Parameters	Estimate
PK	V1, L	1.69
	V2, L	27.2 + 0.93 × (weight − 25)
	Cl, L/min	0.89 × (weight/23.6)0.97
	Q, L/min	1.3
PD (intermediate)	E0	76.9
	Emax	35.4
	Ce50, μg/mL	3.78 − 0.183 × AGE
	γ	3.02
	ke0, /min	0.557
PD (final)	E0	79.9
	Emax	30.6
	Ce50, μg/mL	3.65 − 0.102 × AGE − 1.72 × REMI
	γ	3.02
	ke0, /min	0.557

PK = pharmacokinetic, PD = pharmacodynamic, V₁ = central volume of distribution, V₂ = peripheral volume of distribution, Cl = metabolic clearance, Q = inter-compartmental clearance, E₀ = baseline bispectral index value before propofol administration, E_max = minimum possible bispectral index value, C_e50 = C_e at 50% of the maximal propofol effect on Bispectral Index, AGE = age (yr), ã = steepness of the C_e versus bispectral index relationship, k_e0 = blood-brain equilibration rate constant, REMI = mean infusion rate of remifentanil throughout the operative period (bolus and infusion doses divided by the elapsed time from the first bolus to the end of infusion, ìg/kg/min).

In this study, we hypothesized that the Kim model could be applied to a population younger than 2 years. Therefore, we performed an external validation of the Kim model with concurrent infusion of remifentanil in children younger than 2 years.

METHODS

Study population

Pediatric patients younger than 2 years scheduled to undergo elective neurosurgery were enrolled. The exclusion criteria were as follows: history of a drug allergy or hypersensitivity to propofol; underlying cardiovascular disease, bradycardia, or hypotension; severe pulmonary, renal, or hepatic disease; hemodialysis treatment; body mass index greater than 35 kg/m²; or children whose parents declined their enrollment in the study.

As this is an exploratory study, we did not make specific calculation for sample size. Instead, we regarded 24 (six patients respectively for patients aged 0–6 months, 6–12 months, 12–18 months, and 19–24 months) participants would be sufficient. Thus, we planned to recruit a total of 28 children, considering 15% of dropout ratio.

Study protocol

On the day of surgery, the patients arrived in the operating room after appropriate fasting and without premedication. We omitted midazolam premedication, which was included in our original modeling,6 because it is not routine practice in our clinical setting. Monitoring of three-lead electrocardiogram (ECG), non-invasive blood pressure, peripheral pulse oximetry (S_pO₂), and end-tidal carbon dioxide (E_tCO₂) was performed using a Solar 8000 device (GE Medical, Milwaukee, WI, USA). Anesthesia was induced with 2% propofol (Fresofol MCT 2% 50 mL Inj.; Fresenius Kabi Austria GmBH, Graz, Austria) and remifentanil (Ultiva^TM 1 mg; GlaxoSmithKline, Parma, Italy). Propofol was loaded in a 50-mL Kovax-Syringe (Korea Vaccine, Ansan-si, Gyeonggi-do, Korea), and infusion was performed using a syringe pump (Pilot Anesthesia 2; Fresenius Vial, Brézins, France) that was controlled using target-controlled infusion software (Asan pump, ver. 2.1.3; Bionet Co., Ltd., Seoul, Korea) according to the Kim model. The initial target effect site concentration of propofol was set at 4.0 μg/mL, and the initial infusion rate of remifentanil was 0.2 μg/kg/min. After loss of consciousness, 0.6 mg/kg of rocuronium was administered to facilitate tracheal intubation. Arterial cannulation was performed to start invasive blood pressure monitoring and to enable intermittent blood sampling. The bispectral index (BIS; Covidien, Minneapolis, MN, USA) was also monitored to maintain adequate anesthetic depth and to evaluate the pharmacodynamic performance of the Kim model. We attempted to maintain the patients' BIS value between 40 and 60, and their blood pressure and heart rate between 80% and 120% of baseline by adjusting the target effect-site concentration of propofol and the infusion rate of remifentanil.

During surgery, the target effect-site concentration of propofol was set to 2, 3, 4, and 5 μg/mL to meet the clinical need as assessed by the anesthesiologist, which was followed by single arterial blood sampling after 10 minutes of equilibrium for measurement of actual plasma concentration of propofol. We regarded 10 minutes as sufficient for equilibrium because the blood–brain equilibration half-time is calculated as ln2/k_e0 ≒ 1.24 (minutes), and the pseudo steady-state occurs at approximately 4–5 fold the blood–brain equilibration half-time, which is approximately 5–6 minutes. We could not escalate and de-escalate for each of the set concentrations because drawing approximately seven to eight blood samples from children younger than 2 years was undesirable for ethical reasons. Rather than escalating the dose for sampling, we varied the order of blood sampling according to the clinical needs for propofol concentration. The total elapsed time and predicted plasma concentration of propofol at each sampling point were automatically recorded on a computer using the target-controlled infusion software. During the study period, the patients' blood pressure and heart rate were recorded at each point and were compared using a repeated-measures analysis of variance using SPSS software (ver. 22.0; SPSS Inc., Chicago, IL, USA). Input and output balance of fluids including crystalloids, colloids, blood products, estimated blood loss, urine output, and insensible losses were calculated and adjusted for patients' weight and duration of anesthesia.

Measurement of plasma concentration of propofol

Each of the blood samples collected in this study was placed into an Eppendorf tube^® (Eppendorf, Hamburg, Germany) within 30 minutes and centrifuged at 3,000 rpm for 10 minutes, and the supernatants were stored at −70°C. The plasma concentrations of propofol were measured using liquid chromatography-tandem mass spectrometry (LC-MS/MS) after liquid–liquid extraction with methyl tert-butyl ether (MTBE). A total of 200 μL of human plasma was mixed with 50 μL of internal standard (IS; 100 ng/mL, propofol-d¹⁷) and then extracted with 1 mL of MTBE. propofol-d¹⁷ was purchased from Cerilliant Corporation (Round Rock, TX, USA). Plasma samples were vortex mixed and centrifuged, and the organic phase was then evaporated to dryness at 40°C under a stream of nitrogen. The residue was reconstituted in 100 μL of 90% aqueous methanol and injected into the LC-MS/MS system. The analyte and IS were separated on a UHP ASB C18 column (100 × 2.1 mm, 1.9 µm, Agela Technologies, Wilmington, DE, USA) under gradient conditions. The mobile phases consisted of 0.1% ammonium hydroxide in 10 mM ammonium acetate and 0.1% ammonium hydroxide in acetonitrile. Negative electrospray ionization in multiple reaction monitoring (MRM) mode was employed. The MRM was based on an m/z transition of 177.1 > 177.1 for propofol and 194.2 > 194.2 for IS. The calibration curve was linear at the range of 10–2,000 ng/mL, and the correlation coefficients (r) were greater than 0.99 in all instances. The lower limit of the quantification of propofol was 10 ng/mL. The within-run precision and accuracy of the quality control samples (10, 30, 150, and 1,500 ng/mL) were less than 9.863% and 92.83%–96.93%, respectively. The between-run precision and accuracy of the quality control samples were less than 10.92% and 92.97%–98.73%, respectively. In the case of the samples with concentrations > 2,000 ng/mL, the samples were reanalyzed after dilution with blank plasma within the linear range. The dilution efficiency was also confirmed using dilution quality control samples (DiQC, 4,000 ng/mL) during analysis of the study samples, the precision and accuracy of which were 3.602% and 102.7%–110.6%, respectively.

External validation

We employed the concept of performance error (PE) by using the following equation, as previously described6,10:

$${PE}_{ij} = \frac{{measured}_{ij} - {predicted}_{ij}}{{predicted}_{ij}}$$

where predicted_ij is the j^th prediction of plasma concentration of propofol of the i^th patient, and measured_ij is the j^th actual measurement of plasma concentration of propofol of the i^th patient.

We took the following four parameters into account: inaccuracy, divergence, bias, and wobble. Inaccuracy was measured by obtaining the median absolute PE (MDAPE). For the i^th patient, MDAPE is defined as follows:

MDAPE_i = median {|PE_ij|, j = 1, …, N_i}

where N_i is the number of PEs in the i^th patient. The MDAPE is an absolute value that represents the size of the errors. Divergence for the i^th patient is defined as the slope obtained from the linear regression of that patient's |PE_ij|s against time:

$${Divergence}_i \left(\%/h\right) = 60 \times \frac{{\sum }_{j=1}^{N_i}\left|{PE}_{ij}\right| \times t_{ij} - \left({\sum }_{j=1}^{N_i}\left|{PE}_{ij}\right|\right) \times \left({\sum }_{j=1}^{N_i}{t}_{ij}\right)/N_i}{{\sum }_{j=1}^{N_i}{\left(t_{ij}\right)}^2 - {\left({\sum }_{j=1}^{N_i}{t}_{ij}\right)}^2/N_i}$$

where t_ij is the time (min) that the determination of the corresponding PE_ij was made. Divergence provides time-related trends of errors. Bias is determined as the median PE (MDPE). The MDPE for the i^th patient is defined as follows:

MDPE_i = median {|PE_ij|, j = 1, …, N_i}

Because the MDPE is a signed value, it represents the direction of errors. Wobble is a measure of the variability of the PE_ij in the i^th patient:

Wobble_i = median absolute deviation of {|PE_ij|, j = 1, …, N_i} from MDPE_i

After calculating all of the parameters for each patient, we calculated the population estimate. The pooled data approach was used as described in a previous study,10 with detailed calculations explained in the Supplementary Data 1.

The parameters were calculated using the fit4NM package (Ver. 4.5.2.; Eun-Kyeong Lee and Gyu-Jeong Noh, http://www.fit4nm.org, accessed on 15/03/2017). Bland–Altman plots for repeated measurements of the plasma propofol concentration were drawn using MedCalc^® (Ver. 17.2.; MedCalc Software bvba, Ostend, Belgium). Prediction probability, a type of correlation measurement, was calculated using Somer's d formula using fit4NM, with transformation of Somer's d from −1 to 1 scale to 0 to 1 scale.6,11

Ethics statement

This study was approved by the Institutional Review Board of Seoul National University Hospital (H-1509-131-708) and the Ministry of Drug and Food Safety (20150228285), and written informed consent was obtained from the parents and legal guardians. The study was registered prior to patient enrollment at http://cris.nih.go.kr (KCT0001752, principal investigator: Hee-Soo Kim, approved: 18/12/2015).

RESULTS

This study was designed so that blood samples would be collected at each of the propofol target effect-site concentrations (2, 3, 4, and 5 ìg/mL) for each child, which would obtain 96 blood samples from the 24 participants. However, one blood sample were unobtainable because of insufficient time during surgery to reach equilibrium. In total, 95 blood samples were obtained from the patients. Demographic data are shown in Table 2. The time-weighted average of the infusion rate of remifentanil (range) was 0.24 (0.04–0.47) ìg/kg/min.

Table 2. Demographic data (n = 24).

Variables		Values
Age, mon		11.0 ± 6.39
Height, cm		71.7 ± 8.9
Weight, kg		9.1 ± 2.1
Sex, M:F		13:11
Duration of surgery, min		206.7 ± 96.6
Characteristics of surgery
	Spine	18 (75)
	Brain	6 (25)

Data are shown as mean ± standard deviation or number (%).

M = male, F = female.

For the plasma concentration of propofol, individual bias ranged from −42.8% to 43.9%, whereas individual inaccuracy ranged from 3.03% to 43.9%. The prediction probability was 0.658 with a 95% confidence interval (CI) of 0.618–0.699.

The population estimates (95% CI) were shown in Table 3. Inaccuracy was less than 25% for both pharmacokinetics and pharmacodynamics. Analysis of the negative bias suggested that the plasma concentration of propofol was slightly overestimated but appropriate. Nonetheless, the calculated bias for the model was deemed acceptable considering the performance of previous models.1,12

Table 3. Comparison of pharmacokinetic performance of propofol infusion models for children (estimate 95% CI).

Variables	Kima	Kim6	Eleveldb,9
Range of age, yr	0–2	0.2–12	0–3
Bias, %	−0.96 (−8.62, 6.37)	−20.2 (−23.3, −18.1)	3.5
Inaccuracy, %	21.0 (15.1, 27.1)	30.4 (28.6, 32.7)	22.6
Divergence, %/hr	−17.4 (−26.2, −10.4)	19.1 (16.1, 22.7)
Wobble, %	12.8 (7.26, 18.2)	11.5 (9.63, 13.4)

^aThis study for children under two years of age; ^bCross-validated performance for ‘young age’ group (0–3 years of age).

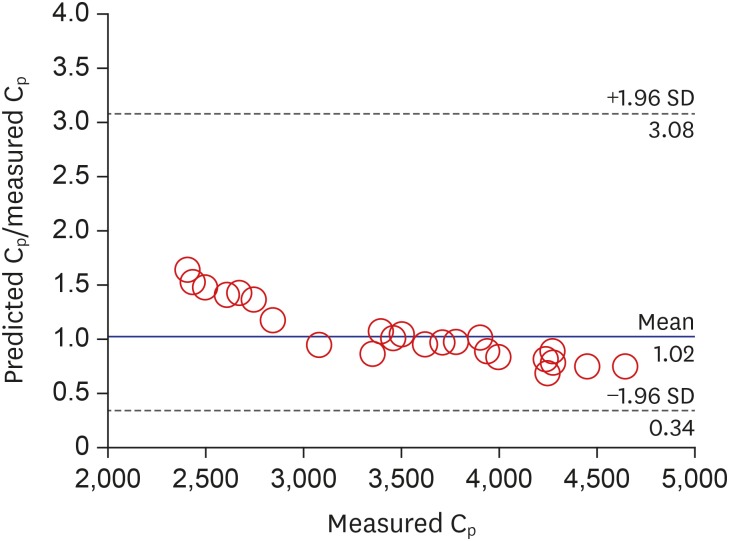
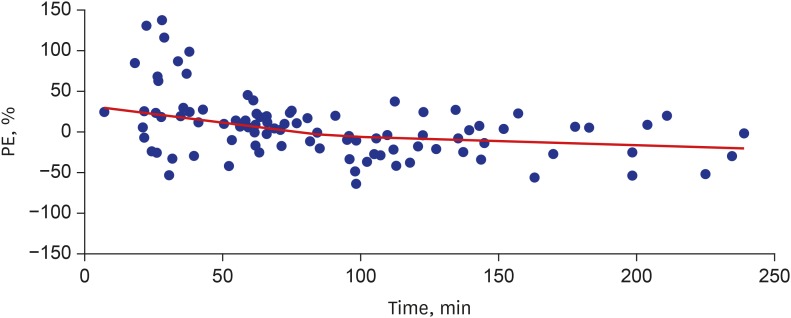
Fig. 1 shows a Bland–Altman plot with multiple measurements per subject for the plasma propofol concentrations. The PEs of propofol plasma concentration with respect to elapsed time are shown in Fig. 2.

Fig. 1. Bland-Altman plot with multiple measurements per subject. Bland-Altman plot with multiple measurements per subject of measured-to-predicted ratio of C_p (n = 95).

C_p = plasma concentration of propofol, SD = standard deviation.

Fig. 2. Performance error along time. PE of C_p along elapsed time (n = 95). The red line represents locally estimated scatterplot smoothing.

PE = performance error, C_p = plasma concentration of propofol.

There was a statistically significant decrement of heart rate and mean blood pressure as target plasma concentration increased. Mean (95% CI) of heart rate (beats/min) was 123 ± 18.6, 116.2 ± 10.8, 109.8 ± 10.2, and 109.2 ± 11.6 (P = 0.006), and mean (95% CI) of mean blood pressure (mmHg) was 72.3 ± 15.3, 69.1 ± 17.5, 60.6 ± 16.6, and 61.3 ± 11.3 (P = 0.005) for target concentration of 2,000 ng/mL, 3,000 ng/mL, 4,000 ng/mL, and 5,000 ng/mL, respectively.

The mean (95% CI) of input and output balance of fluids adjusted for patients' weight and anesthesia time was −1.47 (3.97) mL/kg/hr.

DISCUSSION

The results of this study showed that the Kim model is clinically acceptable for propofol use in children younger than 2 years, considering the model's inaccuracy and bias. Previous studies have considered an inaccuracy of less than 30% to be acceptable,13 and Eleveld et al.14 regarded inaccuracy of less than 20% as good performance, while more than 60% as poor performance. Also, even error of 20%–40% has not been shown to increase the rate of adverse events during target-controlled infusion.15 Previously established models have also been shown to have inaccuracies within this range for pediatric population.1,3,12,14,16,17

Most recently, Eleveld et al.9 announced a model for broad application, including ages starting from 1 weeks. The performance of the Kim model in children younger than two years old was compared with the performance of the Kim model in the original population and the performance of the model from Eleveld et al.9 in Table 3.6 The performance of our model on age 0 to 2 was similar to that of the new model of Eleveld for the age group of 0 to 3 years of age. In summary, with regard to bias and inaccuracy, the performance of the Kim model for young children is comparable to that of previous models.

The results of this study indicated that the performance of the Kim model was better for propofol plasma concentration in patients younger than 2 years compared to external validation in patients aged 2–12 years.6 This is quite surprising, since external validation in population of different age showed better performance than in population with similar age. More specifically, bias was almost zero in current validation while it was around −20% in previous validation, and inaccuracy were also better in current validation. In previous modeling study, almost linear weight-clearance relationship was observed, since the allometric exponent for clearance was 0.97, which is very close to 1. Authors of previous study described their overestimation of plasma concentration as a result of difference of their allometric exponent from a widely known value of 0.75, representing metabolic rate.6,18,19 However, in patients younger than two years old, it is repeatedly reported that allometric exponent should be somewhat different and we should not stick to 0.75.20,21,22,23 Rather, physiologically-based pharmacokinetic model is encouraged, especially in young population including infants and neonates.24 Therefore, we cannot simply assume that this model would perform better in the same age group it was originated. With these results, we can say that the fixed V₁ of 1.69L could have been underestimated and is more appropriate for children younger than two years.

The divergence and the wobble remained similar between the two populations (Table 3), suggesting that the time-affected variability and intra-individual variability did not differ, even though we did not simply escalate the concentration as done before at the modeling study.6

Heart rate and blood pressure showed statistically significant change for escalation of plasma concentration of propofol, still within normal range and without clinical implication.

Our study has some limitations. First of all, although the original Kim model is a linked pharmacokinetic-pharmacodynamic model, we validated only pharmacokinetic performance of the model. We recorded infusion of remifentanil throughout the study and monitored BIS, but we did not use midazolam as premedication, which was included in the original model. Therefore, we could not apply the same E₀ for calculation of predicted BIS, which made us impossible to perform external validation of pharmacodynamic performance. Second, we were unable to build a new model for this population because more frequent blood sampling was limited for children younger than 2 years, considering their total blood volume. For similar reason, we could not escalate and de-escalate the target concentration for each point to these patients due to limited number of blood sampling. Third, although we did not exclude neonates as candidates, children aged from 0 to 1 month were not included in this study, and the youngest were 2 months old. As pharmacokinetics of neonates are known to be different from that of infants,21 application of the Kim model to neonates should be done with more caution. Further study focused on neonates would give us more information about application of this model to neonates. Fourth, because we made four measurements for each patient, we were forced to determine MDPE and MDAPE as the mean of the middle two measurements. Finally, as we enrolled patients undergoing neurosurgery for most of the cases, blood loss and fluid balance should have been considered for more precise evaluation of performance. Especially, significant blood loss during surgery is reported to impair predictive performance of pharmacokinetic model of propofol in children.25 However, patients' input-output balance during surgery were not considered during validation. As mentioned in the results section, the balance was slightly negative, but relatively acceptable.

In conclusion, because its bias and inaccuracy in pharmacokinetic prediction are clinically acceptable, we can conclude that pharmacokinetic performance of the Kim model for propofol is acceptable for patients younger than 2 years old. We recommend using additional anesthetic depth monitoring such as the BIS in actual clinical settings since pharmacodynamic performance was still not validated in this age group.

SUPPLEMENTARY MATERIAL

Supplementary Data 1

Calculation of population estimates for median performance error, median absolute performance error, divergence and wobble