Explaining the efficiency of local health departments in the U.S.: an exploratory analysis

Abstract

No study to date has analyzed the efficiency at which local health departments (LHDs) produce public health services. As a result, this study employs data envelopment analysis (DEA) to explore the relative technical efficiency of LHDs operating in the United States using 2005 data. The DEA indicates that the typical LHD operates with about 28% inefficiency although inefficiency runs as high as 69% for some LHDs. Multiple regression analysis reveals that more centralized and urban LHDs are less efficient at producing local public health services. The findings also suggest that efficiency is higher for LHDs that produce a greater variety of services internally and rely more on internal funding. However, because this is the first study of LHD efficiency and some shortcomings exist with the available data, we are reluctant to draw strong policy conclusions from the analysis.

Introduction

Public health refers to the actions taken by society to advance the general health of the population as a whole. Nearly 3,000 local health department (LHDs), or public health departments, deliver public health services in almost every area of the U.S. According to Rawding and Wasserman [26; 87] the mission of a LHD “is to protect, promote, and maintain the health of the entire population of their jurisdiction”. In fact, just last year, LHDs across the U.S. took an active role with respect to the H1N1 virus with about one-third of all adults receiving their immunizations from public health staff.1

LHDs are organized in many different ways, with some servicing jurisdictions with 1,000 or fewer people as a separate agency of their municipal governments whereas others deliver public health services as independent, multi-county LHDs with populations of 1 million or more. LHDs expanded their scale and breadth of services over time in response to the particular needs and characteristics of the population in their jurisdictions [26]. LHDs vary dramatically in terms of capacity, authority, and resources. Although no standard exists, LHDs are expected to provide the following 10 essential public health services [23]:

1. Monitor health status and understand health issues facing the community.

2. Protect people from health problems and health hazards.

3. Give people information they need to make healthy choices.

4. Engage the community to identify and solve health problems.

5. Develop public health policies and plans.

6. Enforce public health laws and regulations.

7. Help people receive health services.

8. Maintain a competent public health workforce.

9. Evaluate and improve programs and interventions.

10. Contribute to and apply the evidence base of public health.

NACCHO [23] points out that the main sources of LHD funding include federal and state grants and funds (43%), local taxes (29%), Medicare and Medicaid reimbursements (11%), and fees (6%). Spending on public health services in the U.S. amounted to roughly $64 billion in 2007 [16]. While the precise mix of services differs across health departments, most local public health spending funds the surveillance and prevention of communicable diseases, testing and preservation of water quality, maintenance of sanitary conditions (e.g., approval of septic systems), ensuring of food protection (restaurant inspections), and providing of health information [23].

Very little is currently known about the efficiency at which local health departments produce public health services. In fact, no study to date has ever examined the efficiency at which LHDs in the U.S. produce local public health services, although several studies have examined cost differences across local departments or governments [e.g., 2, 6, 13, 22, 29, 30]. Perhaps analysts and policy-makers have not cared about efficiency because public health expenditures comprise less than 3% of all health care costs [16]. However, many experts believe that public health will take on an increasing role in the future given the threat of bioterrorism attacks, concerns over emerging diseases such as avian flu and SARS, and the seemingly growing burden from natural disasters such as Katrina [37].2 If so, a better understanding of the factors affecting the relative efficiency of local health departments may prove useful to public health policy-makers.

As a result, this paper uses data from a nationally representative survey by the National Association of County and City Health Officers (NACCHO) and data envelopment analysis (DEA) to measure the relative efficiency of 771 LHDs in 2005. The DEA indicates that the typical LHD operates with about 28% inefficiency although inefficiency ranges as high as 69% for some LHDs. Multiple regression analysis is then used to explore if various factors can explain these observed differences in inefficiency across the different LHDs. Among the findings, the regression results imply that more centralized and urban LHDs are less efficient at producing local public health services. In addition, the results suggest that efficiency is higher for LHDs that produce a greater variety of services internally and rely more on internal funding.

A simple description of data envelopment analysis3

The input-oriented technical efficiency measure is defined as the ratio of the optimal input bundle to the actual input bundle used in producing the given output bundle.4 This is a normative measure and to obtain the optimal input bundle we need to first specify the production technology. In this respect, the literature has primarily followed two approaches—stochastic frontier analysis (SFA) and data envelopment analysis (DEA).

The SFA approach is an econometric approach which requires the researcher to specify a functional form for the efficient frontier, as well as, the distributional assumptions for the inefficiency and error terms. For this approach, deviations from the efficient frontier are considered as resulting from inefficiency or random factors. The other approach, DEA, developed by Charnes, Cooper, and Rhodes [8], is based on mathematical programming and creates a piecewise-linear best practice frontier based on the observed data. DEA requires only a minimum number of regularity conditions to be satisfied with respect to the technology and does not require us to make arbitrary assumptions about the functional form of the production frontier. For this method, all deviations from the frontier are treated as inefficiency such that the DEA scores capture the relative efficiency of the decision making units (DMUs). We adopt DEA rather than SFA for estimating the technical efficiency of the local health departments since the functional form of the production frontier for LHDs and the distributional properties of the inefficiency and error terms are not known.

Since its introduction, DEA has been used in several studies concerning the health care sector with Brockett et al. [7], Bjorner and Keiding [5], and Bates et al. [3, 4] among the most recent. Hollingsworth et al. [18], Chilingerian and Sherman [9], Worthington [39] and Hollingsworth [17] provide comprehensive reviews of the literature on efficiency measurement in the health care sector using nonparametric methods. Further, DEA has been used for measuring the efficiency of government-operated health centers in other countries. For instance, Kirigia et al. [19] uses DEA to measure the technical efficiency of public health clinics in Kenya. Moreover, in New Zealand, the government has used DEA in practice since 1997 to identify efficient expenditure levels to set prices for hospital services at the diagnostic related group level [28].

Figure 1 can be used to explain the input oriented technical efficiency for a single-output, two-input case. Suppose that points A, B, C, D, E, F, and G represent input bundles of seven LHDs producing a single public health services output of level 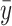(or more), using different combinations of two inputs, labor and capital. HBCDEJ represents the (piecewise linear) isoquant corresponding to output level 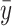and the area to the right bounded by HBCDEJ is the input requirement set 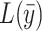. Clearly, points B, C, and D and E lie on the isoquant and represent efficient LHDs, whereas the points A, F, and G represent inefficient LHDs. Suppose that we are interested in evaluating the technical efficiency of the LHD represented by point A. In this case, it is possible to proportionately contract the input bundle to I and still produce the given amount of output. Hence comparison of the input bundle at A with the input bundle at I provides a measure of the input oriented technical efficiency for LHD A (i.e., 0I/0A). This is the Farrell input based technical efficiency measure [12]. As we can see, the measured efficiency will be <1 for the LHDs represented by A, F, and G, whereas it will be equal to 1 for the LHDs represented by B, C, D, and E.

Fig. 1.

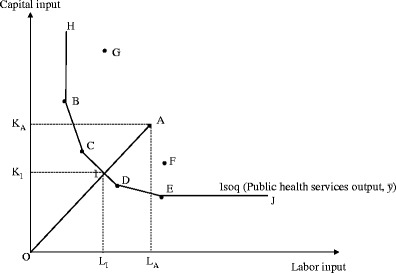
Input oriented technical efficiency

Conceptual model, sample, data, variables, and efficiency findings

This study treats the typical LHD as minimizing the quantity of inputs needed to provide a given variety of public health services to a fixed number of people in its local area. As a result of this conceptual framework, the variety of services and population serve as our output measures. While standard production theory normally relates inputs to outputs, Santerre [30] recently argues that population and variety of services serve as reasonable proxies for the scale and breadth of output given that public health services are not directly observable and measurable. For example, a greater population likely means more restaurant inspections by public health officials. Also, population is not an unreasonable proxy for output because, as mentioned in the introduction, public health refers to the actions taken for the health of the community as a whole.

Indeed, health economists often use patient indicators such as number of admissions or inpatient days to reflect output measures for hospital services [e.g., 10, 14]. However, not all public health needs may be the same across the various LHDs because of population heterogeneity. Therefore, controls for the heterogeneity of the population served by each LHD are specified in the second stage analysis.5

The National Association of County and City Health Officers (NACCHO) provides the data used in the forthcoming empirical analyses. NACCHO collected the data with a national survey of 2,864 local health departments (LHDs) in 2005 of which 2,300 or 80% responded to the questionnaire. The response rate was lowest for LHDs with populations under 25,000 (73%), around 83% for LHDs with populations between 25,000 and 74,999, relatively constant at about 90% for LHDs with population between 75,000 and 999,999 people and then 98% for LHDs with population over 1 million. Not all LHDs answered every question, however.

NACCHO lists up to 95 different public health services and identifies if the LHD provides internally or contracts out for each service and if that same type of service is provided by state, other local or nongovernmental agencies. The data source also identifies the number of services that are medical or clinical and those that are epidemiological or environmental in nature.6 Clinical services include immunizations, screening for diseases and conditions, treatment for communicable diseases, maternal and child health services such as family planning and prenatal care, and other medical care services including comprehensive primary care, home health care, oral health, and behavioral and mental health services. In contrast, epidemiological/environmental services include various epidemiology and surveillance activities, population-based primary prevention services (e.g., obesity or substance abuse), regulation, inspection and licensing services such as overseeing septic tank installation, public drinking water quality, or housing inspections, and other environmental health activities (e.g., hazardous waste disposal, pollution prevention, and land use planning). Because the labor intensity of clinical and environmental services may differ and thereby influence the degree of technical efficiency, they are treated as two separate outputs in the DEA. Only the variety of different clinical and nonclinical services produced internally by each LHD is treated as outputs. The percentage of services provided externally acts as an independent variable in the second stage analysis.7

Seven public health inputs are specified in the DEA. The five labor inputs are: the number of full-time equivalent (FTE) managers, nurses, sanitarians, clerical employees, and other employees. The percentage of employees with personal computers and the percentage with access to the internet represent the two measures of capital. Unfortunately, other measures of capital such as the market value of buildings and equipment are not provided by the data source.8

For the DEA analysis we allow for variable returns to scale and use the Banker, Charnes, and Cooper [1] model for measuring the input-oriented technical efficiency of a LHD. The basic DEA model was initially developed by assuming that all values of inputs and outputs are strictly positive. But in some situations, the inputs and outputs could be zeros and negatives. In our context, of the 2,300 responses reported by NACCHO, many observations had missing or zero values for some of our seven inputs and three output measures.

The implications of zero and missing values of outputs and inputs have been discussed in many studies. Thanassoulis [34] and Thanassoulis et al. [35] provide a detailed discussion of this issue. Zero outputs generally do not pose a problem in standard efficiency models because the output constraint corresponding to the zero output will always be feasible irrespective of the model orientation [35, p309].9 However, zero inputs introduce bias in DEA analysis because at least one unit with a zero input will always be VRS or CRS efficient regardless of the levels of its remaining inputs or outputs [35, p310]. In other words, when a DMU has a zero value of an input k, all peers of that DMU being assessed should also have a zero value on that input k. Thus, at least one DMU with zero value on input k will be a peer to the DMU being assessed and so will be Pareto-efficient irrespective of what values such a peer has on outputs or inputs other than k (even if they are using inefficiently large amounts of other inputs). This implies a restricted reference set for the units with zero inputs, since DMUs with zero values of an input will only be compared among themselves [35, p312]. Further, from a conceptual standpoint, health departments that can produce the given outputs with zero values of some inputs operate differently than those that require at least some amounts of those inputs to produce the same outputs. Hence, in a sense, these two groups do not face the same options of transforming inputs into outputs and so may face different technologies. [34, 35].

Because in our study—1) most zeros occur on the input side, 2) The production unit (public health department) having zero levels on some inputs operate different technology as production units with positive values on that input, and 3) the zero inputs may be related to the management decisions, including observations with zero values may bias the efficiency computations—therefore, they are excluded from the efficiency analysis. Hence only 771 of the 2,300 LHD-observations can be properly used in the DEA efficiency analysis.

Fortunately, not much of a difference is found when the smaller subsample of 771 LHDs is compared to the entire sample in terms of population size, demographic factors like percent white and Hispanic, the urban nature of the LHD’s jurisdiction, and the political boundaries of the LHD (e.g., town, city, or county). The LHDs in the smaller sample appear to be more populous and less rural on average but not in a statistical sense because of the relatively wide variation in the standard errors.10 Thus, this sample of 771 LHDs appears to be fairly representative of all LHDs operating in the U.S.

Before discussing the DEA findings, Table 1 provides some descriptive statistics for all of the variables used in the smaller DEA sample and the forthcoming multiple regression analysis. Some LHDs did not report figures for all of the explanatory variables specified in the multiple regression analysis, however. Note that population in the various LHDs ranges from 5 thousand to 5 million with the average LHD servicing nearly 200,000 people. The typical LHD offers internally 13 different clinical services and 23 different epidemiological/environmental services. Nearly 62% of the various services are produced externally. Also, note that most LHDs are organized at the county level and located in an urban setting.11

Table 1.

Descriptive statistics

	Number of observations	Mean	Standard deviation	Minimum value	Maximum value
Population	771	181,985	391,780	5,006	5,000,000
Internal clinical services	771	12.8	4.38	1	23
Internal non-clinical services	771	22.5	7.69	1	46
Managers	771	5.69	13.32	0.100	262.27
Nurses	771	20.43	31.06	0.100	307.58
Sanitarians	771	7.91	12.39	0.100	150
Clerical	771	22.80	39.06	0.400	400
Other	771	32.53	69.57	4.47E-08	871
Percent with personal computers	771	92.40	15.00	4	100
Percent with internet	771	31.13	25.56	1	100
Fraction services produced by other agencies	773	0.615	0.110	0	0.854
Percent state and federal funding	737	42.94	23.38	0	100
Percent White	769	81.80	16.05	10.46	99.50
Percent Hispanic	764	6.93	10.80	0	94.50
Town or City jurisdiction	773	0.109	0.312	0	1
County jurisdiction	773	0.613	0.487	0	1
City/County jurisdiction	773	0.155	0.362	0	1
Regional jurisdiction	773	0.120	0.326	0	1
Other jurisdiction	773	0.003	0.051	0	1
Urban area	773	0.479	0.500	0	1
Micropolitan area	773	0.238	0.426	0	1
Rural	773	0.283	0.451	0	1

To gain some knowledge about the insights that the subsequent DEA offers the analyst, Fig. 2 provides a glimpse at the relationship between the population size serviced by a LHD and the corresponding number of full-time equivalent employees for the 1,972 LHDs in the NACCHO sample with data reported for these two variables. Both variables are expressed as logarithms to compress the data for illustrative purposes. Not surprisingly, the scatter diagram shows larger populations require more full-time equivalent personnel. In fact, a simple regression equation confirms that the elasticity of full-time equivalent employees with respect to population equals approximately 0.88. That is, a 10% increase in population results in nearly 9% more employees, on average.

Fig. 2.

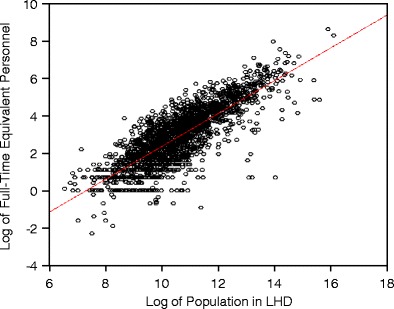
Scatter Diagram of Relationship between Population (in logs) serviced by each of the 1,972 LHDs and Full-Time Equivalent Personnel (also in logs)

Notice, however, that the number of full-time equivalent employees varies considerably at a particular population level. For example, the log of full-time equivalent personnel ranges from about −1 to 4 (or from 0.38 to 55 FTE employees) when the log of population equals 10 (or 22,000 people). This exercise shows that some LHDs produce with a vastly different amount of labor services than others do. We would like to identify those LHDs that can deliver a variety of clinical and non-clinical services to a particular level of population with a minimum amount of a potentially similar input mix. The first stage of the DEA will help determine which of the LHDs are able to provide a variety of services to its population in a relatively efficient manner (i.e., least amount of inputs). The second stage of the DEA will allow some insight into the external factors shaping the production behavior of LHD administrators in terms of technical efficiency.

Figure 3 shows the DEA findings for those same 1,972 LHDs. For this particular sample, small numbers have been added to the various outputs and inputs so those observations with missing (or zero) values can be used in the DEA.12 Accordingly, the results shown may be biased because a LHD with zeros for various inputs will be wrongly credited with efficiency when, instead, that LHD may not have employed that particular input because of an essentially different production process not involving that particular input. In any case, the findings of this DEA (which adds small numbers to avoid missing values) suggest that nearly 1,050 out of 1,972 LHDs can be considered as operating in a technically efficient manner when compared to the others in the sample (i.e., DEA score = 1).

Fig. 3.

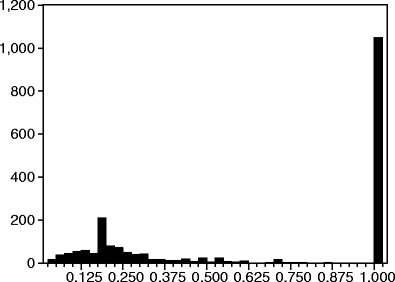
Relative efficiency of 1, 972 LHDs with imputed inputs and outputs

For the entire sample of 1,972 LHDs, the DEA score averages 0.65 which means that the typical LHD operates with about 35% relative inefficiency. LHDs with a DEA score of less than 1 could either increase their outputs with the same amount of inputs or produce the same amount of outputs with fewer inputs, at least compared to the benchmark or technically efficient LHDs. When the technically-efficient benchmark LHDs are eliminated from the calculations, the average DEA score drops to 0.25 with a median value of 0.20. In fact, the DEA score for this sample ranges as low as 0.03. Clearly, the degree of technical efficiency varies widely among the 923 under-performing LHDs in this sample, which is based upon adding arbitrarily small numbers so more observations can be used.13

Figure 4 reports the results from the DEA when those observations with missing values are eliminated from the analysis.14 According to these less biased findings, the typical LHD in the U.S. operates with about 28% relative inefficiency. The relative inefficiency ranges as high as 69% for some LHDs, however. The median efficiency score for the sample is 0.714. One hundred and eleven or 14.4% of the LHDs in the sample can be considered as the most efficient, meaning that it is not possible for those LHDs to reduce their inputs proportionally while still maintaining the level of public health services. These LHDs with a DEA score of 1 are capable of providing their population with a wide variety of services but with relatively less input usage compared to the others. Another 57 health departments have measured efficiency of more than 90% and can be considered as performing at a high level. That is, they operate closer to the production isoquant and not that far above it. In the next section we explore some of the reasons why the degree of technical inefficiency differs among these LHDs.

Fig. 4.

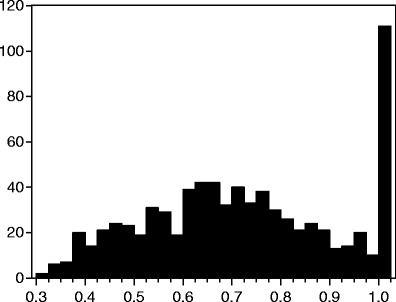
Relative efficiency of 771 LHDs with nonzero inputs and outputs

Second stage analysis explaining efficiency differences among LHDs

The previous section shows that efficiency differs considerably among the various LHDs. In this section, we use multiple regression analysis to explain some of the observed differences. It should be noted that our selection of independent variables in the second stage is limited by the variables available from the NACCHO survey but many of these same community and system characteristic variables are also specified by Mays et al. [21], Mays and Smith [22], and Santerre [30] in their evaluations of LHD performance.15 Five variables or sets of variables are specified in the regression analysis. First, since population represents one of the outputs, variables describing the degree of population heterogeneity seem to be relevant. A more heterogeneous population likely requires more inputs relative to output because varied needs must be satisfied. As a result, the racial and ethnic composition of the population served by each LHD is specified in the regression equation, as captured by percentages of the population that are white and Hispanic.

Second, the efficiency of public health services may also depend on spatial proximity. In fact, Santerre [29] argues that many local public health services act as density off-setting goods. That is, high neighborhood density generates increased negative externalities such as heightened antisocial behavior, faster spreading of communicable diseases, and more public health hazards due to improper sanitation. Consequently, a greater amount of resources may be needed relative to population in more congested areas. Thus, a set of dummy variables is included to control for the urban nature of the jurisdiction (urban, micropolitan, or rural) served by the LHD based upon the rural urban commuting area taxonomy with an urban area serving as the default category.

Third, recall that, in addition to population, the other two outputs in the DEA are the numbers of different clinical and nonclinical services provided by each LHD. However, the LHD may contract out for some services and some other public health services might be produced by higher levels of government or nongovernmental agencies. Therefore, to control for different levels of responsibility with respect to public health services across LHDs, the percentage of services provided externally is specified as an additional variable in the estimation equation. A direct relationship between the degree of external production and the DEA score might suggest that efficiency is improved through specialization. Oppositely, if economies of scope exist such that the same resources can produce a variety of services, an inverse relationship between the percentage of services provided externally and (internal) efficiency can be expected.

Fourth, some LHDs rely more on external funding from the state and federal governments than others. External funding may be associated with efficiency in two ways. First, greater funding from higher levels of government could result in a moral hazard problem such that the LHD faces less pressure to produce as efficiently as possible because of the financial cushion provided from outside sources. Second, greater external funding may simply reflect that public health problems are more severe in those particular LHDs. More severe problems require additional inputs. For both of these reasons, we would expect an inverse relationship between the percentage of external funding, which is specified in the estimation equation, and the degree of internal efficiency.

Fifth, a set of dummy variables are included to control for the type of jurisdiction served by each LHD (i.e., county, city/county, district/regional, or other with city/town as the omitted or default category). The degree of centralization may influence the efficiency at which public health services are delivered although the exact theoretical relationship is unclear. On the one hand, the Tiebout theory [36] argues that decentralization promotes efficiency. People shop for local public goods like public health by voting with their feet and this Tiebout-type competition forces public decision-makers to operate more efficiently. On the other hand, centralization could favor coordination and thereby enhance the efficiency of public health delivery. Finally, state dummy variables are specified in the estimation equation to control for any state policies that might create efficiency differences across the various LHDs in the sample.

The second stage of the analysis was to regress DEA scores on the aforementioned five sets of independent variables. Two methodological issues were addressed: First, as the DEA produced efficiency scores are truncated (scores range from 0 to 1 regardless of the actual variations among those who receive 0 and 1) and are serially correlated to one another (all scores are estimated relative to the leading performers on the efficiency frontier), a bootstrap simulation on the raw DEA scores was performed using Frontier Efficiency Analysis with R (FEAR, version 1.12) software [32, 33]. The bootstrap procedure produced bias-corrected efficiency scores between, but excluding 0 and 1. After simulation, the number of facilities with high efficiency scores was reduced. Second, as the regression residuals have a truncated distribution because the dependent variable (the DEA efficiency scores) are naturally bounded between 0 and 1, a truncated regression with random effects was performed. This model produces robust regression coefficients and standard errors of the independent variables [15]. For comparative purposes, ordinary least square results are also reported. Table 2 provides the multiple regression findings. The estimated coefficients and their associated t-statistics are shown opposite from each explanatory variable.

Table 2.

Multiple regression results: dependent variable = efficiency score

	Estimated coefficient (absolute value of t-statistic)
	Ordinary least squares	Truncated regression model
Constant	0.6459*** (5.02)	0.6678*** (15.05)
Fraction services produced by other agencies	−0.1706*** (3.77)	−0.1166** (2.37)
Fraction state and federal funding	−0.0004 (1.45)	−0.0004* (1.69)
Fraction White	0.0011*** (2.68)	0.0012*** (3.22)
Fraction Hispanic	0.00004 (0.06)	0.0006 (1.18)
County jurisdiction	−0.0525** (2.42)	−0.1117*** (5.87)
City/County jurisdiction	−0.0736*** (3.16)	−0.1178*** (5.49)
Regional jurisdiction	−0.0810*** (3.29)	−0.1335*** (5.79)
Other jurisdiction	−0.0692 (0.78)	−0.0620 (0.62)
Micropolitan area	0.0712*** (5.87)	0.0722*** (5.35)
Rural	0.1201*** (9.95)	0.1343*** (10.3)
Sigma		0.1365** (35.0)
Adjusted R2	0.334	0.416
Log of likelihood function	541.59	439.03
Number of observations	728	728

All models are specified with a set of 47 state dummy variables

***statistical significance at the 1% level

**statistical significance at the 5% level

*statistical significance at the 10% level

Both models essentially provide the same results regarding the relationship between the explanatory variables and the efficiency at which local public health services are delivered. First, the results suggest that LHDs are more efficient when they internally produce a greater variety of public health services, perhaps because of economies of scope. The coefficient estimate on the variable representing the fraction of services produced by other agencies can be used to calculate an elasticity estimate. The calculated elasticity suggests that a 10% increase in the fraction provided by external agencies is associated with nearly a 1% decline in internal efficiency.

Second, some evidence supports the premise that efficiency may be inversely related to the fraction of funding from higher levels of government. Interestingly, Varela et al. [38] recently discover that the efficiency of publicly-provided primary care services in Brazil is inversely correlated with the level of municipal dependence on intergovernmental grants. However, a calculated elasticity of 0.02 means that little economic significance should be attached to the influence of intergovernmental funding on efficiency. Third, racial but not ethnic composition appears to affect the efficiency at which public health services are delivered. According to the elasticity estimate of 0.14, a ten percent increase in the percentage of population that is white is associated with a 1.4% increase in efficiency.

Fourth, the level of centralization seems to matter greatly in terms of efficiency. The coefficient estimates on the county, city/county and regional dummy variables can be interpreted as implying that more centralized LHDs operate with, at least, 0.11 percentage points less efficiency than an otherwise comparable independent city or town jurisdiction. Finally, the empirical results indicate that LHDs in micropolitan and rural areas are 0.07 and 0.13 percentage points more efficient than LHDs in urban areas at producing local public health services. However, that difference may hold simply because of the social and health issues that emerge when people live in closer proximity to one another.

Conclusion

This paper offers the first, albeit exploratory, study on the relative efficiency of local public health departments in the U.S. The DEA finds that considerable variation in efficiency exists among LHDs. On average, the typical LHD operates with 28% inefficiency but some departments operate with inefficiency as high as 69%. The degree of inefficiency faced by LHDs seems to be particularly high especially when compared to hospitals for which measured efficiency averages around 85% [17]. While perhaps not much of a problem now, the inefficiency may take on greater meaning if LHDs assume more social responsibilities in the future as many policy-makers suspect.

The paper also finds that several factors are associated with the degree of inefficiency. LHDs appear to be more efficient when they provide internally a greater variety of services and when they are spending their own money. LHDs also seem to operate more efficiently when they are located in less congested areas, serve a predominately white population, and are run by a city or town.

We are reluctant to draw any policy implications from this study, however, for a number of reasons.16 First, our empirical analysis is confined to just 1 year of cross-sectional data. If the data ever become available it would be desirable to revisit this analysis with a panel data set. The panel data would help control for unobservable heterogeneity to some degree and also introduce a dynamic component into the analysis. Two, the analysis would be strengthened with expenditure data broken down by each type of service provided internally and externally. Third, data for other types of capital and non-labor inputs, more demographic and environmental data, and some measures of the quality of public health services for each LHD would add to the analysis. Indeed, measures of structural, process, and outcome quality are particularly important for the DEA given that less resources devoted to an activity, while potentially reflecting increased efficiency, may also reflect reduced levels of process quality or less “quality time” devoted to a particular activity.17

At least, this paper will serve as a template for a more ambitious study when that data become available. For now it is clear that substantial differences in efficiency exist across local health departments of the U.S. and we have some preliminary understanding about why those efficiency differences may exist.

Appendix 1: technical description of the DEA procedure used

Consider an industry producing a vector of s outputs y = (y ₁, y ₂,..., y _s) from a vector of m inputs x = (x ₁, x ₂,..., x _m). Let y _j represent the output vector and x _j represent the input vector of the j-th decision-making unit. Suppose that input- output data are observed for n DMUs. Then the technology set can be completely characterized by the production possibility set S = { (x, y): y can be produced from x } based on a few regularity assumptions of feasibility of all observed input- output combinations, free disposability with respect to inputs and outputs, and convexity.

The input-oriented technical efficiency measure is defined as the ratio of the optimal (i.e., minimum) input bundle to the actual input bundle of a DMU, for a given level of output, holding input proportions constant.18 The BCC—DEA [1] model for measuring the input-oriented technical efficiency of a DMU with the input-output bundle (x ₀, y ₀) is given by the model below

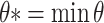Subject to

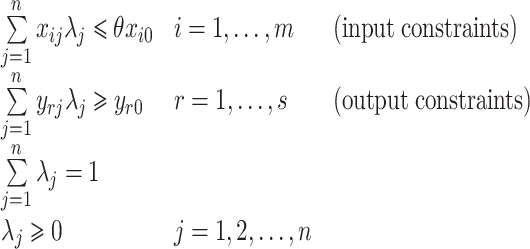1

As mentioned earlier, our conceptualized model involves three outputs (i.e., s = 3) and seven inputs (i.e., m = 7). Accordingly, the DEA model (1) has three output constraints and seven input constraints. In the above model, the output constraints ensure that the resultant output is no lower than what is actually being produced. An efficient DMU will have θ* = 1, implying that no equi-proportionate reduction in inputs is possible, whereas an inefficient DMU will have θ* < 1.

In model (1) above, the production process is allowed to exhibit variable returns to scale (VRS). In other words, we do not make the restrictive assumption of constant returns to scale (CRS). Rather, we allow the data to decide whether a particular health department operates under increasing, decreasing, or constant returns to scale.