Active learning strategies with COMBINE analysis: new tricks for an old dog

Abstract

The COMBINE method was designed to study congeneric series of compounds including structural information of ligand–protein complexes. Although very successful, the method has not received the same level of attention than other alternatives to study Quantitative Structure Active Relationships (QSAR) mainly because lack of ways to measure the uncertainty of the predictions and the need for large datasets. Active learning, a semi-supervised learning approach that makes use of uncertainty to enhance models’ performance while reducing the size of the training sets, has been used in this work to address both problems. We propose two estimators of uncertainty: the pool of regressors and the distance to the training set. The performance of the methods has been evaluated by testing the resulting active learning workflows in 3 diverse datasets: HIV-1 protease inhibitors, Taxol-derivatives and BRD4 inhibitors. The proposed strategies were successful in 80% of the cases for the taxol-derivatives and BRD4 inhibitors, while outperformed random selection in the case of the HIV-1 protease inhibitors time-split. Our results suggest that AL-COMBINE might be an effective way of producing consistently superior QSAR models with a limited number of samples.

Electronic supplementary material

The online version of this article (10.1007/s10822-018-0181-3) contains supplementary material, which is available to authorized users.

Introduction

The COMparative BINding Energy (COMBINE) method was introduced for the first time in 1995 by Ortiz et al. [1] to enable the study of congeneric series of compounds including the structural information of ligand–protein complexes. By extracting the decomposed protein–ligand interaction energies computed from structures of the complexes, the method allows to derive Quantitative Structure Active Relationships (QSAR) models using a regression algorithm (Partial Least Squares or PLS for instance). Since its introduction, several works have been published, for example [2–5], supporting the ability of the method to help understanding how compounds interact with their targets, explaining the different contributions to their potency, and to provide useful guidelines to design new molecules. Some of the latest examples include the study of type II dehydroquinase inhibitors by Peon et al. [6], the design of ligands against the severe acute respiratory syndrome (SARS) chymotrypsin-like protease [7] or the discovery of uncompetitive inhibitors of the glutamate racemase MurI from Helicobacter pylori [8]. However, although attempts have been made to keep the tool up with the times by incorporating new regression types [9] and implementing a comprehensive graphical user interface [10], the method has not received the same level of attention compared to other alternatives to study QSAR that provide better predictive ability and improved measurements of the uncertainty of the predictions [11–14]. These methods have, nonetheless, some challenges of their own. They may allow computational chemists to assess, up to a certain point, the reliability of their predictions, but do not offer any guidance about how to improve the performance of the models in the future if it is not satisfactory, which is often the case. On top of that, many times these algorithms work as some sort of black boxes [13] so that the interpretation of the results in a target-ligand context can be difficult. COMBINE analysis, on the other hand, provides a natural interpretation for potency contributions and allows exploiting such information to design new molecules all within the comfortable environment, for modellers and medicinal chemists, of the binding site.

Active learning (AL) is a semi-supervised learning approach that can be used to address some of the problems of the COMBINE method. AL strategies, by using an estimation of uncertainty for the predictions and an iterative learning scheme, enable building robust models with a fraction of the data that would be required with traditional approaches for the same accuracy. Several AL variants exist [15], each one with different strengths and weaknesses, but they all share the need to query the source of information, that is, to evaluate certain compounds for the sake of improving future model performance. This conceptual shift, meaning that the model not only casts predictions but it is also allowed to request more information as needed, is behind the consistently better performance shown by these methods [16, 17].

In this work, we propose to merge both technologies by introducing an uncertainty estimation component in COMBINE analysis and the possibility of using alternative modelling methods to partial least squares (PLS), such as support vector machine regression. For its evaluation, we have employed several diverse datasets, including a set of more than 90 BRD4 N-terminal domain inhibitors, a historical set containing inhibitors of the protease of the human immunodeficiency virus (HIV-PR) and a group of recently published Taxol derivatives [18–20].

Computational Methods

Data sets

• HIV-1 protease data sets (HIV-PR). The set includes a historical series of 48 protein–ligand complexes of HIV-1 protease inhibitors from Merck [21] that has been also employed in the past for testing COMBINE methodologies [5] (see Supporting Data Set 1).

• BRD4 N-terminal bromodomain (BD1) data set (BRD4-BD1). A series of 96 pyridinones [22] with BD1 inhibitory activity between 1.7 µM and 10 nM, was extracted from the Boehringer Ingelheim patent US 2015 0246919-A1 [22] (see Supporting Data Set 2).

• Taxanes data set. This set contains 62 Taxol analogues known to bind to the taxanes binding site in the microtubule with stabilizing effects [18–20] (see Supporting Data Set 3).

Protein–Ligand binding energy model

We have employed a version of the classic Molecular mechanics implicit solvent model surface access method [23], termed cMMISMSA, which includes corrections for hydrogen bonds [24] and Coulomb terms [25] and has been applied successfully in previous works [26, 27]. cMMISMSA (http://farmamol.uah.es/soft/cMMISMSA) allows calculating the binding energy of several ligands-protein complexes and decomposing the different contributions of each protein residue in the three parts of the scoring function: van der Waals, Coulomb and desolvation terms. Regarding the electrostatic calculations, we employed a dielectric constant value of four for HIV-PR, as described in Perez et al. [5], and a distance-dependent dielectric for the other datasets [28] (BRD4-BD1, Taxanes).

3D modelling of complexes

The sets of the HIV-PR inhibitors and Taxol derivatives were kindly provided by the authors of previous publications [5, 20]. In the case of the BRD4-BD1 inhibitors, the compounds were extracted from the patent [22] and pre-processed with the LigPrep module in the Schrodinger suite 2017v4. The crystal structure of the human BRD4-BD1 (PDB code 2OSS), was used for docking with Glide and the default parameters including the SP scoring function. Compounds then were parametrized using acpype.py [29], antechamber [30] and GAFF [31] and the resulting complexes were energy minimized (ncyc = 5000, maxcyc = 50,000, dx0 = 0.1, drms = 0.00001) using the GBSA implicit solvation model (igb = 1). The resulting AMBER topology (AMBER14 force field) and coordinates files were used as input for cMMISMSA ensuring force field compability between the minimization procedure and the COMBINE calculations.

Validation and performance metrics

Two metrics were chosen to validate and measure the evolution in performance of the models: the coefficient of determination (r²) and the mean squared error (MSE) between the predicted and the experimental pIC₅₀ values in the test set:

$${\text{r}}^2=1-\frac{{\sum }_{i=1}^n{(Y_i-{\widehat{Y}}_i)}^2}{\sum _{i=1}^n{(Y_i-{\overline{Y}}_i)}^2}$$

$$MSE=\frac{1}{n}\sum _{i=1}^n(Y_i-{\widehat{Y}}_i{)}^2$$

where n is the number of samples, ${\widehat{Y}}_i$ is the predicted value for sample i, $Y_i$ is the experimental pIC₅₀ value and ${\stackrel{-}{Y}}_i$ is the average of all experimental values.

However, in the case of the validation of the HIV-PR COMBINE model, and in agreement with the original publications [1, 5], we made use of the standard deviation of the error in the prediction (SDEP), which is defined as the square root of the mean squared error and q², which is equivalent to r² but in the context of cross-validation. Cross-validation was performed according to the original published protocol [5]: for 20 times, five compounds were extracted randomly from the original pool as test set and the correlation (q²) and SDEP were calculated and averaged to report a final value. For the “external set” validation, the first 33 compounds in the pool were used as training set, while the remaining 15 compounds were added to the test or external set [5].

COMBINE models

To reproduce the basic COMBINE scheme, the output from cMMISMSA was processed by a custom python notebook. The basic philosophy of this pioneering chemometric method is preserved by dividing the process in two parts: first, the different energy terms for each complex are calculated, and then a specific method, in this case support vector machine regression [16] (SVR), is applied to build the COMBINE model using the sklearn package [32]. In the case of the HIV-PR model and after an initial optimization procedure based on a standard 80%/20% training/test split cross-validation protocol using the r² and MSE values obtained for different combinations of parameters in the SVR (penalty C, kernel type and its parameters), we decided to employ a polynomial kernel of degree equal to 3 and a C value of 100, while for BRD4-BD1 inhibitors and the taxanes, a SVR with a linear kernel and penalty of one was used after following an analogous procedure.

Active learning strategies

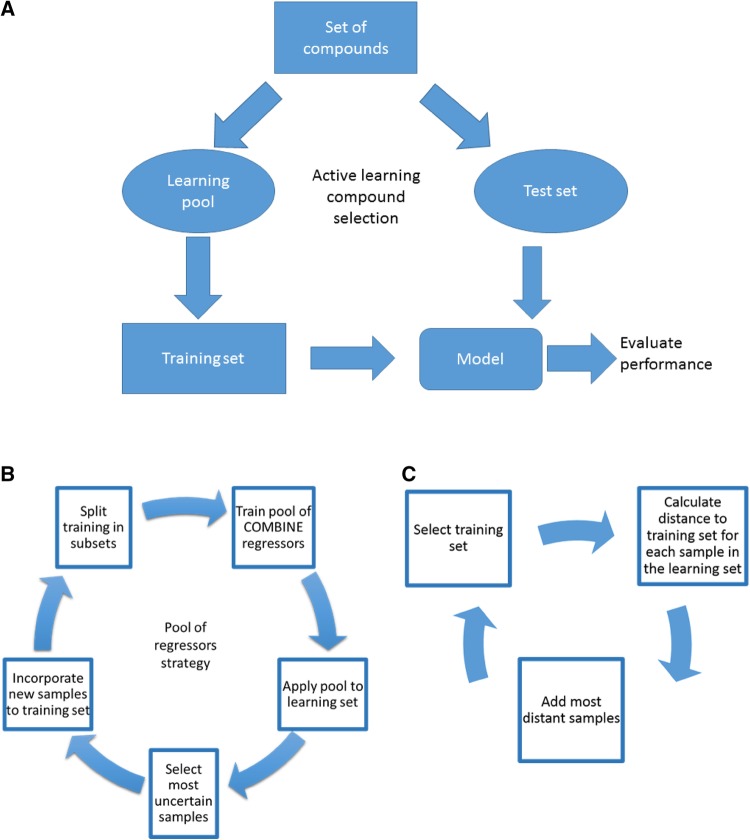
All strategies were implemented in a custom python notebook, which is included in Supplementary Information. The general workflow is shown in Fig. 1a. It starts by defining a test set, i.e. the final list of compounds that we would like to predict with maximum accuracy, and the learning pool, that is, a set with the different compounds available for selection to explore the series SAR, but with no information (label), and that could help to improve the performance of the current model if “synthesized and tested in a biological assay” (already done in our sets). Following, an initial training set is built with minimal information by randomly drawing samples from the learning pool (around 20%). Then, a strategy for selecting the next batch of compounds is chosen and the protocol continues till it runs out of samples in the learning pool. Three different strategies have been implemented in this work:

Fig. 1.

Diagram of the different Active Learning strategies employed in this work. a General workflow; b Pool of regressors; c Distance to the training set

• i.Pool of regressors. This strategy (Fig. 1b) consists in splitting at each iteration the training data in n subsets to build submodels that, then, are used to predict the outcome for every single sample in the remaining learning set. In this manner, there are n available predictions (as many as regressors trained with the subsets) per unlabelled sample in the learning pool, which are averaged and their variance used to represent the uncertainty of the predictions. In our case, a leave-one-out procedure was followed and the standard deviation of the predictions was used to rank the complexes for uncertainty selection.
• ii.Distance to the training set. Another approach (Fig. 1c) to measure the uncertainty of one particular sample involves calculating how distant is to all other samples in the training set. If the new sample is far from the others, the prediction is assumed to be less reliable since the sample probably lies outside the domain of applicability of the initial model. We have employed the Local Outlier Factor (LOF) method [33], which calculates the differences in the local density of a given point with up to 5 neighbours of the training set.
• iii.Random selection. This approach was meant to be a baseline for the AL strategies. At each iteration, the list of possible samples in the learning pool is shuffled randomly and the first 5 appended to the training set.

All protocols were run 25 times to collect statistics, adding 5 compounds to the training set at each iteration till the learning set is exhausted. In the case of the HIV-PR set, the training set in the Merck publication [21] was used as the learning pool, while the “prospective set”, also described in the paper, was selected as the test set (33 and 15 compounds respectively). The learning pool, for each experiment, was subsequently divided randomly in an initial training set of 20% of the data (7 complexes) and the rest of the learning pool with 80% of the data (28 ligands) available to improve the model at each iteration. For the BRD4-BD1 ligands and the taxanes, as the test set is not clearly defined, the full sets were split five times randomly in learning pool (80%)/test (20%) sets to assess the performance of the workflows (see Supplementary Information for full results). The learning set, once again, was split randomly in an initial training set (20%) and the rest of the learning set (80%) available for the following iterations.

Results and discussion

Validation of a reconstructed COMBINE model: performance of the HIV-PR inhibitors

Published COMBINE models available in the literature have not been validated using workflows which could be considered in agreement with modern “good practices” in the QSAR field. This may be related to the fact that COMBINE analysis predates most of these approaches. Therefore, to validate our reconstructed protocol, we employed equivalent metrics in order to be able to compare to the original publications [1, 5]: q² and SDEP (standard deviation of the error in the predictions) for cross-validation and SDEP for “external set” validation. Table 1 shows the results of our modelling efforts using this set and the new COMBINE workflow. Cross-validation metrics display a small improvement over the values reported by Perez et al. [5], however, the SDEP value in the external set is almost identical, confirming that our model presents an equivalent performance to the published one.

Table 1.

Results of the full COMBINE HIV-PR model validation

	HIV-PR from Perez et al. COMBINE AMBER model [5]	HIV-PR inhibitors	Taxanesa	BRD4-BD1 inhibitorsa
r2	0.89	0.85	0.94	0.81
q2	0.70	0.77	0.60	0.56
SDEPcv	0.72	0.63	0.91	0.36
SDEPext	0.83	0.82	–	–
r2ext	–	0.78	–	–

^aAverages using a 80%/20% training/test sets split and 20 times repeats. HIV-PR values were obtained as described in the text

Active learning in HIV-PR

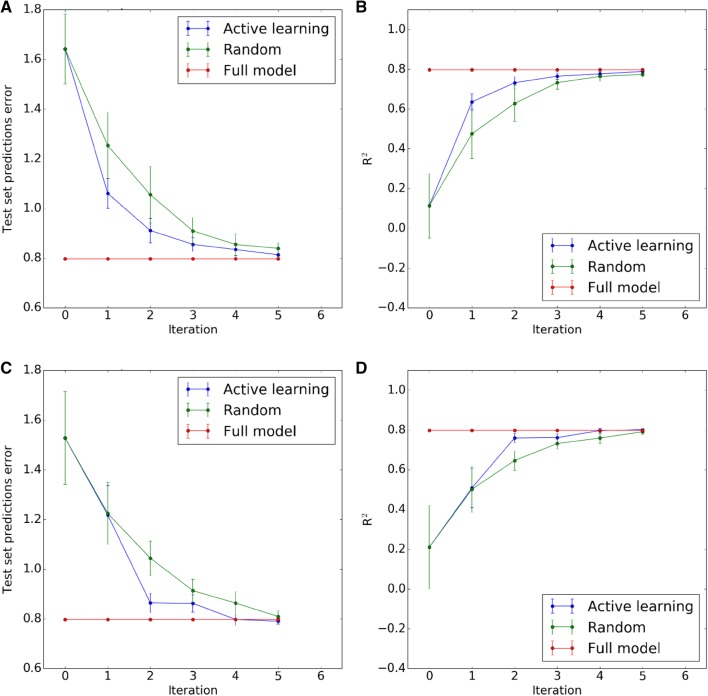
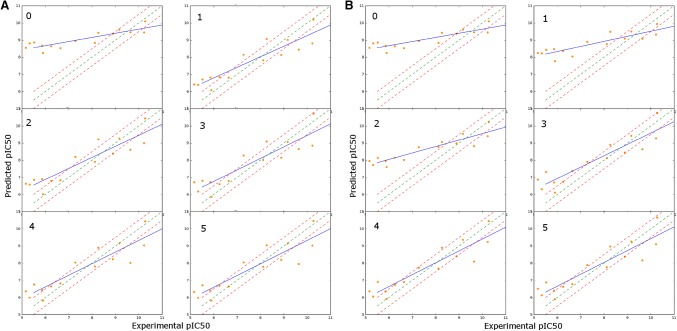
The reliability of the predictions from COMBINE models is usually difficult to assess. Several authors [28, 34, 35] have found inconsistencies in their performance depending on the parameters employed for energy calculations (e.g. dielectric constant), the binding modes of the compounds (e.g. lack of robust crystallographic evidence), the regression algorithm (e.g. PLS vs. SVM) and pre-treatment of the variables (e.g. scaling or feature selection). Motivated by this problem, we decided to introduce an approach to estimate the uncertainty of the predictions and, in this manner, implement a workflow that can guide practitioners to improve unsatisfactory or unreliable models. As a proof of concept, we selected the historical HIV-PR dataset, a set that contains 48 protease inhibitors with potencies ranging from 6 µM to 0.1 nM, and two simple uncertainty metrics: the distance to the training set and a pool of regressors (see methods section). Our simulation protocol, which consists of splitting the total learning pool in small batches of five compounds to be added iteratively to the training set, allows us to evaluate the evolution in the performance of the models using different strategies. As can be seen in Fig. 2, the active learning strategies based on both uncertainty estimators tested in this work outperform random selection of compounds and can produce models with less prediction error than their random counterparts with the same number of compounds in the training set. According to these results, the pool of regressors strategy seems also to obtain the best models, with a very promising first iteration compared to the other two models. To get some insight into the actual evolution of the models, we saved the individual results for the first run of the protocol for pool of regressors and random selection. Figure 3 shows the correlation of the experimental pIC₅₀ values of the molecules in the test set vs. the predicted ones at each iteration. The initial model (iteration 0) presents an almost random output which agrees with averaged r² and MSE values around 0 and 1.5 respectively (Fig. 2). Interestingly, after the first batch of compounds is added to the training set from the learning pool, the resulting model in the active learning strategy (pool of regressors) can produce much better correlated predictions (< r² > ~ 0.6 and < MSE > ~ 1.1, Fig. 2) while random selection produced a model with virtually no improvement compared to the initial training set. From the second iteration onwards, the gains produced by AL seem to be reduced progressively until it approaches the performance of the full model. On the contrary, with a random selection of compounds, and in this particular simulation, the workflow needed to reach iteration 3, that is, 15 extra compounds to have a similar performance to the model in the first iteration of AL with just five compounds more.

Fig. 2.

Performance of the active learning strategies in the HIV-1 protease inhibitors set. a Mean squared error at each iteration for the pool of regressors strategy vs. random selection and the full model. b Coefficient of determination at each iteration for the pool of regressors strategy vs. random selection and the full model. c Mean squeared error at each iteration for the distance to the training set strategy vs. random selection and the full model. d Coefficient of determination at each iteration for the distance to the training set strategy vs. random selection and the full model

Fig. 3.

Evolution of the models for each iteration in the HIV-PR simulation. a Pool of regressors. b Random selection. Green lines represent y = x; red lines mark ± 0.5 units from the green line (y = x + 0.5 and y = x-0.5); The resulting regression between the predicted values for the samples (orange dots) and the experimental values is plotted in blue

Overall performance of active learning

Propelled by these encouraging results we decided to expand our simulations to two other sets with very different properties: taxanes and BRD4-BD1. The taxanes set contains a series of complex natural product derivatives (macrocycles) but that has led to very successful COMBINE models in the past [19, 20]. The BRD4-BD1 set is made of a congeneric series of pyridinone derivatives designed to interact with the complex combination of flexible residues and the “dry” water molecules network in the binding site of the bromodomain that recognizes an acetyl-lysine residue [36]. These two binding sites have very different properties in terms of electrostatics and shape and were chosen to obtain a general overview of the performance of AL-COMBINE models beyond the HIV-PR set.

We first approached the taxanes set. An identical protocol to HIV-PR was followed with the exception of the number of iterations (8 in this case), the use of distance-dependent dielectric constant in the cMMISMSA model and the linear kernel and penalty value of 1 in the SVR (see methods). For splits 1 and 2 (Supp. Figs. 1, 3) both AL protocols outperform clearly random selection, while for splits 4 and 5, the advantage, although present, it is not that large. In the case of split 3, the performance is roughly equivalent to random selection. It is also worth noting that both AL workflows (pool of regressors and distance to the training set) tend to show the same trends in performance, being successful in the same splits, with a slight advantage for the pool of regressors.

Our aggregated results for this set (Supp. Fig. 1,3,5,7 and 9) show that the performance of the workflows depends more on the actual test set employed for the comparison (data split) than on the particular AL strategy employed. This can also be observed looking at the simulation results individually (Supp. Fig. 2, 4, 6, 8 and 10), where some more challenging test sets need significantly more data than others to produce equivalent results (e.g. split 2 vs. 3). However, it is also clear that AL tends to produce less variability in the results (smaller error bars) at each iteration when compared to random selection. This finding, together with the fact that AL outperforms 80% of the time random selection while it does not underperform, seems to support the use of AL strategies in the taxanes set.

Finally, we decided to employ the largest set, at least to our knowledge, ever used to build a COMBINE model, with 96 BRD4-BD1 inhibitors. Identical considerations to the taxanes set were taken into account: due to the size of the set, the number of iterations was set to 12, a linear kernel with a penalty of 1.0 was used for the SVR and the distance-dependent dielectric (default method in COMBINE) was employed.

Similarly to taxanes, we have found that the results tend to vary depending on the test set (split). AL performs best in split 4 and 5 (Supp. Figures 17 and 19), while in splits 1 and 3 (Supp. Figures 11 and 15) only one of the AL strategies seem to work (distance to the training set and pool of regressors respectively). In split 3 (Supp. Figure 15), AL performs equally to random selection. These numbers are, again, in agreement with the proportion of successful cases observed for the previous set. However, differences in the performance of AL are here less pronounced, probably due to the larger number of compounds in the set and the relatively lower complexity of the molecules. Another interesting observation is that the impact of AL seems to be more obvious in the first few iteration of the simulations (also observed in HIV-PR and taxanes) but, it also less evident (or negligible) if the initial training set, by chance, contains enough information to produce relatively reliable predictions of the test set (e.g. split 2 has r² values consistently above 0.1 for all simulations, see Supp. Figures 13 and 14).

One might wonder how the observed dependency on the “split” can be interpreted in the context of a typical drug discovery program. Ideally, the model should quickly learn the right features to give an optimal performance for the molecules designed in the late stages of the program, that is, potent compounds, but with any prior knowledge of how these molecules look like since the initial training set will contain low to medium potencies. In the case of HIV-PR, when a time-split of the data was used, the method reported significant improvements over random sampling, which would enable us to recommend the use of the AL-COMBINE protocol with small sets. However, when a time-split was not available (taxanes and bromodomain inhibitors), we obtained more erratic outcomes, oscillating from great improvements in most sets, to minor changes and, finally, no difference to random selection in a few cases. However, in no case we have observed worse performance than a random selection. In the abscent of any information about the connection between the present SAR in the training set, with the “future” SAR, that is, the interesting compounds to predict, we can conclude that the method does no harm (primum non nocere) and gives a decent probability of enhacing the models (70–80% in our test) with a very small computational cost. The decission of selecting the molecules from an AL-COMBINE approach or directly from the predicted potencies, could be guided by the uncertainty from the different metrics that we propose in this work. If we have been “gifted” with a very informative training set at the beginning of our program, we might decide not to spend precious compound synthesis resources and biological assay slots improving the performance of a model that is already fit for purpose.

Conclusions

In this work, we have assessed the possibility of building self-improved computational models by means of an automated ligand–protein modelling approach and an active learning strategy. Using three very diverse sets of ligands (protease inhibitors, bromodomain ligands and natural products derivatives) we have shown that the approach can be used to accelerate the process of obtaining reliable models with typically less data than random selection.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Abbreviations

AL

Active learning

PLS

Partial least squares

SVMR

Support vector machine regression

QSAR

Quantitative structure–activity relationships

COMBINE

COMparative binding energy analysis

cMMISMSA

Classic molecular mechanism implicit solvent model surface access

HIV

Human immunodeficiency virus

BRD4-BD1

Bromodomain-containing protein 4 N-terminal bromodomain