Kinetic Modeling of Local Epidemic Spread and Its Simulation

Abstract

The local epidemic spread in physical space is modeled using the kinetic equation. In particular, the infection occurs via the binary interaction between the uninfected and infected individuals. Then, the local epidemic spread can be modeled on the basis of the stochastic Boltzmann type equation. In this paper, the normalized virus titer inside the infected human body is defined as the function of the elapsed time, which is measured from the infection time. Consequently, the probability of the infection at the binary human interaction increases, as the normalized virus titer inside the human body increases, whereas the normalized virus titer inside the infected human body decreases, after the normalized virus titer reaches to its maximum value, namely, unity, in the characteristic time. Numerical results indicate that the propagation speed of the boundary between the infected and uninfected domains depends on such a characteristic time, strongly, when the Knudsen number and temperature are fixed. Such a dependency of the propagation speed of the boundary between the infected and uninfected domains on the characteristic time can be described by the Fisher–Kolmogorov–Petrovsky–Piscounov equation which is introduced from the stochastic Boltzmann type equation. Finally, we consider three types of the human behavior as plausible actions to the local epidemic spread.

Introduction

The epidemic spread sometimes does serious harms to humankind on the earth. In particular, the ebola virus [1], Zika virus [2], Severe Acute Respiratory Syndrome (SARS) corona-virus [3] and Middle East respiratory syndrome (MERS) corona-virus [4] caused serious harms to so many people. Regrettably, we cannot predict when and where new virus is generated and do harms to people, previously. Thus, the quantitative prediction of the epidemic spread is markedly significant to suppress harms by the virus at minimum. The most classical mathematical-model to demonstrate the epidemic spread was proposed by Kermack and McKendrick [5] as SIR model (S: susceptible, I: infected, R: removed/recovered). In SIR model, numbers of individuals in statuses S, I, and R are temporally evolved. Similarly, the extended model of SIR model, such as SIRS with the birth and death [6], SIRS model [7] and SIR model with other counterparts [8], were proposed. These SIR type models are simultaneous ordinary derivative equations in terms of the time ($t\in {\mathbb{R}}_{+}$). Thus, the epidemic spread in the physical space is not considered in SIR type models. To demonstrate the epidemic spread in physical space, the epidemic dynamics in the phase space $\left(t,\mathit{x}\right)$ (in ${\mathbb{R}}_{+}\times {\mathbb{X}}^3$, ${\mathbb{X}}^3\subseteq {\mathbb{R}}^3$) must be considered. Cardy and Grassberger [9] considered the epidemic spread on network in the physical space using SIR model and found the similarity between the epidemic spread and percolation on the network. In recent studies by Barrat and his coworkers [10–13], the epidemic spread on the basis of the complex network theory has been investigated. Additionally, the lattice gas cellular automaton analysis of the epidemic spread was proposed by Fuks and Lawniczak [14]. For example, the epidemic spread in Japan is calculated using 69 nodes (major cities), where the number of inhabitants is large, adequately. Two nodes are connected, when the distance between two cities is shorter than the critical value. The individuals move from one node to other nodes, when they are connected each other. Figure 1 shows the fraction of the infected individuals (number of infected individuals at a node/total number of individuals at a node) at $t=0$ and 10, in which t is the normalized time. At $t=0$, the infected individuals exist in Okayama city. Readers can easily understand that the number of nodes with high fraction of infected individuals increases, as the time passes from the frame at $t=10$. Theses studies of the epidemic spread in framework of the network theory or lattice gas cellar automaton are useful for understanding of the epidemic spread from a point (cell) to a point (cell) without tracing motions of infected individuals. Generally, the congested areas and depopulated areas sparsely exist in the country. Then, the epidemic spread from one node to the other node is reasonable approach. Meanwhile, we cannot explain the “local” epidemic spread inside a node using SIR model. Therefore, we must consider the local epidemic spread among individuals in the multi-agents system by tracing motions of individuals in order to investigate the local epidemic spread inside a node (city, village, county etc.).

Fig. 1.

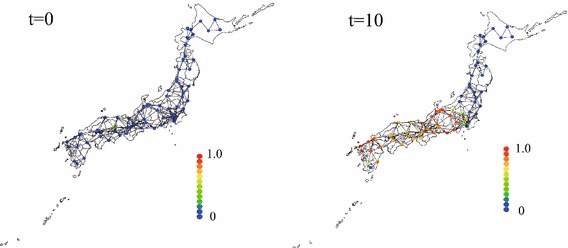
Fraction of infected individuals at 69 nodes (major cities) in Japan at $t=0$, 10 and 20. which are calculated by SIR model. Each nodes are connected when the distance between two nodes are less than the critical value

Remembering that the harmful virus is transferred from one individual to other individuals, the simulation of the local epidemic spread can be performed by tracing motion of individuals, who are infected or uninfected. Provided that infections from infected individuals to uninfected individuals occur via binary interactions, exclusively, binary interactions occur, when the distance between two individuals is less than the two times of the effective diameter of an individuals, in which the effective domain of an individual is expressed with the volume of a sphere with an effective diameter (d). Then, d must be determined to reflect a droplet infection together with the contact infection. Such a long range interaction can be expressed with an intermolecular potential [15]. After all, the local epidemic spread on the basis of such motions of individuals can be formulated by the “stochastic” Boltzmann type equation. The kinetic equation such as the stochastic Boltzmann type equation is certainly useful for a calculation of a large number of individuals, which is hard to trace of motion of each of individuals [16]. Here, readers remind that the phrase “stochastic” means that a small number of individuals also can be discussed in the framework of the kinetic theory [17].

A serious problem involved with SIR model is that transition rates such as $\text{S}\to \text{I}$ and $\text{I}\to \text{R}$ cannot be determined in the framework of the macroscopic scale. Provided that the infection status is expressed with the virus titer, we expect that a series of the infection process (uninfected $\to$ infected $\to$ recovery) can be understood with only one parameter, namely, the virus titer. A novelty of this paper is a kinetic modeling and computation of the epidemic spread using one parameter, namely, virus titer, whereas SIR type models distinguish individuals using three parameters (S, I and R). Readers readily understand SIR model allows the recovery of individuals, whose infection-interval is markedly shorter than the usual infection-term, because the transition of I $\to$ R can occur when a chosen random number $(\in [0,1])$ is smaller than the transition probability. Of course, an immunity is also another significant parameter to express the susceptibility of an individual toward the virus, which characterizes the probability of the infection of an individual. We, however, assume that the immunity is uniform for all the individuals to simplify our discussion. The virus tier, which is excited from zero by the binary interaction with the infected individual with some probability, is the state variable, which depends on the elapsed time after the infection. Then, the probability of the infection at the binary interaction is determined using the virus titer inside the infected individual. In particular, the normalized virus titer ($p\in \left[0,1\right]$) is defined as a function of the elapsed time ($\mathit{\tau }$), which is measured from the start time of the infection. Such a function must be determined to fit to real datum of the virus titer versus the elapsed time, as discussed by Beccam et al. [18], whereas the normalized virus titer is defined as a Gaussian function of the elapsed time to simplify our discussion. Therefore, the realistic function of the normalized virus titer is set as our future study.

Finally, the distribution function in the stochastic Boltzmann type equation is defined using variables such as t, $\mathit{x}$, $\mathit{v}$ ($\mathit{v}\in {\mathbb{V}}^3$: ${\mathbb{V}}^3\subseteq {\mathbb{R}}^3$: velocity space) and $p\left(\mathit{\tau }\right)$. The primary aim of this paper is the comprehension of the characteristics of the local epidemic spread at the initial stage, which changes in accordance with variations of parameters in the stochastic Boltzmann type equation. In particular, we consider the local epidemic spread at the initial stage in the framework of the kinetic theory. Therefore, we never postulate the epidemic spread via vehicles such as cars, trains or airplanes, which were discussed by Colizza et al. [12]. Hence, the time scale of the evolution of the virus titer and time scale of motion of individuals are set unspecified parameters, because we never specify the species of the virus. Additionally, we never mention to multi-epidemic-sources and restrict ourselves to single epidemic-source (domain) to simplify our discussion. In numerical analyses of the stochastic Boltzmann type equation, the direct simulation Monte Carlo (DSMC) method [19] on the basis of the null time counter (NTC) method by Bird [19] is applied. The DSMC method to solve the stochastic Boltzmann equation, which demonstrates the epidemic spread on the basis of the virus titer, is surely new approach to analyses of the epidemic spread, whereas the numerical algorithm in the DSMC is similar to conventional one [19] which has been used to solve the Boltzmann equation for reactive gases, because the Monte Carlo judgment of the transition of the uninfected individual to the infected individual is similar to the Monte Carlo judgment of the chemical reaction via a binary collision in reactive gases [19]. Here, readers must remind that we solve the “stochastic” Boltzmann type equation, in which the phrase “stochastic” means that Klimontovich’s distribution function [20] is considered in order to investigate effects of thermal fluctuations on the local epidemic spread. We introduce the Fisher–Kolmogorov–Petrovsky–Piscounov (FKPP) equation [21] from the stochastic Boltzmann type equation in order to calculate the propagation speed of the boundary between the infected and uninfected domains. Finally, the local epidemic spread via three types of extended human behaviors (stochastic lethal/quarantine without interactions, hypokinetia, and refugee-quarantine with interactions) in accordance with the local epidemic spread is investigated. One advantage of the kinetic model based on the virus titer over SIR model is that we can construct a flexible mathematical-model to reflect scenarios of actions of individuals in accordance with the virus titer of the infected individual (i.e, quarantine, refugee, hypokinesia etc.). In this paper, we primarily focus on the local epidemic spread owing to the thermal motion of individuals which does not postulate the intended velocity of pedestrians, because our aim of the study is an investigation of the local epidemic spread on the basis of the virus titer coupled with thermal motions of individuals in the framework of the kinetic theory. Thus, further advanced interaction models beyond the isotropic scattering in the binary collision between two pedestrians, which were proposed by Helbing [15] or Gipps and Marksjö [22], are not discussed in this paper, because the author considers that the investigation of the local epidemic spread, which includes the detailed dynamics of pedestrians, seems to be out of scope of this study. We, however, mention to the local epidemic spread, in which intended velocities of pedestrians are fixed to their constant values in “Appendix” in order to prove that the proposed kinetic model can be extended to more realistic model of the local epidemic spread in our future study. Finally, the Bhatnagar-Gross-Krook (BGK) like term is added to the stochastic Boltzmann equation to describe the relaxation of velocities of pedestrians toward their intended velocities.

This paper is organized as follows. In Sect. 2.1, the stochastic Boltzmann type equation for the local epidemic spread via the binary collision between the infected and uninfected individuals is formulated. In Sect. 2.2, the propagation speed of the boundary between the infected and uninfected domains is calculated from the FKPP equation, which is introduced from the stochastic Boltzmann type equation. In Sect. 2.3, DSMC analyses of the local epidemic spread are performed to investigate effects of parameters, which are used in the stochastic Boltzmann type equation, on the local epidemic spread. In Sect. 3, three types of the human behavior in accordance with the local epidemic spread are modeled and characteristics of three types of the human behavior in accordance with the local epidemic spread are investigated, numerically. Finally, we make concluding remarks in Sect. 4.

Stochastic Boltzmann Type Equation for Local Epidemic Spread and Its Numerical Analysis

The stochastic Boltzmann type equation for the local epidemic spread is formulated in Sect. 2.1. Afterwards, the FKPP equation is introduced from the stochastic Boltzmann type equation which is formulated in Sects. 2.1 and 2.2. Finally, numerical analyses of the stochastic Boltzmann type equation for the local epidemic spread are performed using the DSMC method in Sect. 2.3.

Formulation of Stochastic Boltzmann Type Equation for Local Epidemic Spread

The normalized virus titer inside the human body is expressed with p, in which $p=0$ corresponds to the uninfected state and $0<p$ corresponds to the infected state. Here, we remind that $p:=p\left(\mathit{\tau }\right)\in {\mathbb{R}}_{+}$ is a function of the elapsed time ($\mathit{\tau }$), once an individual is infected by the interaction with the infected individual at $t=t_p$ ($t,t_p\in {\mathbb{R}}_{+}$) such as

$$\begin{array}{c}\hfill p\left(\mathit{\tau }\right):=exp\left[-\frac{{\left(\mathit{\tau }-{\mathit{\tau }}_m\right)}^2}{2T_c}\right],\end{array}$$ 1

where $\mathit{\tau }:=t-t_p\in {\mathbb{R}}_{+}$ is the elapsed time, after the virus intrudes into the human body. From Eq. (1), $p(0)>0$ and $p\left(\mathit{\tau }\right)\in (0,1]$ is obtained. ${\mathit{\tau }}_m$ corresponds to the characteristic time, when the normalized virus titer reaches to the maximum value and $T_c$ is the variance of $p\left(\mathit{\tau }\right)$.

The time derivative of $p\left(\mathit{\tau }\right)$ is obtained as

$$\begin{array}{c}\hfill \frac{dp\left(\mathit{\tau }\right)}{dt}=\mathit{\psi }\left(\mathit{\tau }\right)=-\underset{c_p}{\underbrace{\frac{\mathit{\tau }-{\mathit{\tau }}_m}{T_c}}}p\left(\mathit{\tau }\right),\end{array}$$ 2

The motion of the individual is characterized by the translation in physical space ${\mathbb{X}}^3\subseteq {\mathbb{R}}^3$ and binary elastic collision (interaction) with another individual, which yields the change of the direction of his or her motion. Therefore, such a random change of the direction of motion via the binary elastic collision between two individuals seems to be implausible in our real society, because each of individuals tends to move toward his or her destination in accordance with his/her intended velocity. Meanwhile, we consider that such a random change of the direction of motion seems to be plausible, when children move in the classroom or campus of the school, as they like.

The virus inside the body of the infected individual intrudes into the body of the colliding partner in accordance with the following probability:

$$\begin{array}{c}\hfill \mathfrak{W}\le p\left(\mathit{\tau }\right),p\left(\mathit{\tau }\right)\in \mathbb{P},\left\{x\in \mathbb{P}|x\in \left(0,1\right]\cap x\in \mathbb{R}\right\},\end{array}$$ 3

where $\mathfrak{W}\in [0,1]$ is the white noise.

Equation (3) indicates that the probability of the virus-infection increases, as $p\left(\mathit{\tau }\right)$ increases. Thus, the probability of the virus-infection is low at the incubation period ($\mathit{\tau }\ll {\mathit{\tau }}_m$) or complete recovery period (${\mathit{\tau }}_m\ll \mathit{\tau }$).

The Klimontovich’s distribution function [20] is defined by

$$\begin{array}{cc}& f\left(t,\mathit{v},\mathit{x},p\left(\mathit{\tau }\right)\right):=\frac{1}{V_c}\sum _{i=1}^{N_c}{\mathit{\delta }}^3\left(\mathit{x}-{\mathit{x}}_i(t)\right){\mathit{\delta }}^3\left(\mathit{v}-{\mathit{v}}_i(t)\right)\mathit{\delta }\left(p-p_i\left(\mathit{\tau }\right)\right),\hfill \\ \hfill & \text{in}{\mathbb{R}}_{+}\times {\mathbb{V}}^3\times {\mathbb{X}}_v^3\times {\mathbb{P}}^{\prime },\left\{x\in {\mathbb{P}}^{\prime }|x\in [0,1]\cap x\in \mathbb{R}\right\},\hfill \end{array}$$ 4

where the subscript “i” is an index of the i-th individual, $N_c$ is the total number of individuals in ${\mathbb{X}}^3$, $V_c:=\left|{\mathbb{X}}_v^3\right|$ is the infinitesimal volume in $\mathit{x}\in {\mathbb{X}}_v^3$ (${\mathbb{X}}_v^3\subseteq {\mathbb{X}}^3$) and ${\mathbb{V}}^3\subseteq {\mathbb{R}}^3$: velocity space.

From above discussion, the stochastic Boltzmann type equation, which demonstrates the infection of the virus owing to the binary elastic collision between the infected and uninfected individuals, is formulated as:

$$\begin{array}{cc}& {\mathit{\partial }}_{t}f\left(t,\mathit{v},\mathit{x},p,s\right)+\mathit{v}·{\mathbf{\nabla }}_{\mathit{x}}f\left(t,\mathit{v},\mathit{x},p,s\right)+{\mathrm{\nabla }}_p\mathit{\psi }\left(\mathit{\tau }\right)f\left(t,\mathit{v},\mathit{x},p,s=1\right)\hfill \\ \hfill & =\mathfrak{Q}\left(f,f_1\right)=\mathfrak{A}{\int }_{p_1\in {\mathbb{P}}_1^{\prime }}{\int }_{{\mathit{v}}_1\in {\mathbb{V}}_1^3}{\int }_{\mathit{ϵ}\in \left[0,2\mathit{\pi }\right]}{\int }_{\mathit{\chi }\in \left[0,\mathit{\pi }\right]}\left(I_{10}^{11}+I_{10}^{10}+I_{01}^{11}+I_{01}^{01}+I_{00}^{00}+I_{11}^{11}\right)\hfill \\ \hfill {\tilde{E}}^{\mathit{\xi }}& \mathit{\sigma }sin\mathit{\chi }d\mathit{\chi }d\mathit{ϵ}{d}^3{\mathit{v}}_{1}d{p}_1,\hfill \\ \hfill I_{10}^{11}=& \left[f\left({\mathit{v}}^{\prime },p>0,s=1\right)f_1\left({\mathit{v}}_1^{\prime },p_1{|}_{\mathit{\tau }=0}>0,s_1=1\right)\right.\hfill \\ \hfill & \left.-f\left(\mathit{v},p>0,s=1\right)f_1\left({\mathit{v}}_1,p_1=0,s_1=0\right)\right]p\left(\mathit{\tau }\right){\mathit{\delta }}_{s,1}{\mathit{\delta }}_{s_1,0}\hfill \\ \hfill I_{10}^{10}=& \left[f\left({\mathit{v}}^{\prime },p>0,s=1\right)f_1\left({\mathit{v}}_1^{\prime },p_1=0,s_1=0\right)\right.\hfill \\ \hfill & \left.-f\left(\mathit{v},p>0,s=1\right)f_1\left({\mathit{v}}_1,p_1=0,s_1=0\right)\right]\left(1-p\left(\mathit{\tau }\right)\right){\mathit{\delta }}_{s,1}{\mathit{\delta }}_{s_1,0}\hfill \\ \hfill I_{01}^{11}=& \left[f\left({\mathit{v}}^{\prime }{,p|}_{\mathit{\tau }=0}>0,s=1\right)f_1\left({\mathit{v}}_1^{\prime },p_1>0,s_1=1\right)\right.\hfill \\ \hfill & \left.-f\left(\mathit{v},p=0,s=0\right)f_1\left({\mathit{v}}_1,p_1>0,s_1=1\right)\right]p_1\left({\mathit{\tau }}_1\right){\mathit{\delta }}_{s,0}{\mathit{\delta }}_{s_1,1}\hfill \\ \hfill I_{01}^{01}=& \left[f\left({\mathit{v}}^{\prime },p=0,s=0\right)f_1\left({\mathit{v}}_1^{\prime },p_1>0,s_1=1\right)\right.\hfill \\ \hfill & \left.-f\left(\mathit{v},p=0,s=0\right)f_1\left({\mathit{v}}_1,p_1>0,s_1=1\right)\right]\left(1-p_1\left({\mathit{\tau }}_1\right)\right){\mathit{\delta }}_{s,0}{\mathit{\delta }}_{s_1,1}\hfill \\ \hfill I_{00}^{00}=& \left[f\left({\mathit{v}}^{\prime },p=0,s=0\right)f_1\left({\mathit{v}}_1^{\prime },p_1=0,s_1=0\right)\right.\hfill \\ \hfill & \left.-f\left(\mathit{v},p=0,s=0\right)f_1\left({\mathit{v}}_1,p_1=0,s_1=0\right)\right]{\mathit{\delta }}_{s,0}{\mathit{\delta }}_{s_1,0}\hfill \\ \hfill I_{11}^{11}=& \left[f\left({\mathit{v}}^{\prime },p>0,s=1\right)f_1\left({\mathit{v}}_1^{\prime },p_1>0,s_1=1\right)\right.\hfill \\ \hfill & \left.-f\left(\mathit{v},p_1>0,s_1=1\right)f_1\left({\mathit{v}}_1,p_1\ge 0,s_1=1\right)\right]{\mathit{\delta }}_{s,1}{\mathit{\delta }}_{s_1,1}\hfill \end{array}$$ 5

where $\mathfrak{A}\in {\mathbb{R}}_{+}$ has the unit $\left[m/s\right]$ and fixed to 1 [m / s] in this paper, ${\mathit{\delta }}_{ij}$ is Kronecker’s delta function, and an index “s” in f(s) indicates the status of the infection, namely, $s=0$ (non-infection) and $s=1$ (infection). In Eq. (5), we assume that all the individuals have same mass (m) in order to simplify our discussion. An index “s” is, however, not a dependent parameter, because the status of the infection can be judged by the normalized virus titer, namely, $p(\mathit{\tau })=0$ (non-infection) and $p(\mathit{\tau })>0$ (infection) from Eq. (1). The subscription “1” indicates the collisional partner.

In the right hand side of Eq. (5), $\tilde{E}$ is defined as

$$\begin{array}{c}\hfill \tilde{E}=\sqrt{{\left|\tilde{\mathit{v}}\right|}^2+{\left|{\tilde{\mathit{v}}}_1\right|}^2},\end{array}$$ 6

where $\tilde{\mathit{v}}$ and $\widetilde{{\mathit{v}}_1}$ are normalized velocities by $C_{\infty }:=\sqrt{2R{\mathit{\theta }}_{\infty }}$ such as $\tilde{\mathit{v}}:=\mathit{v}/C_{\infty }$ and $\tilde{\mathit{v}}:={\mathit{v}}_1/C_{\infty }$ (R: gas constant, ${\mathit{\theta }}_{\infty }$: temperature).

From Eq. (5), the collision frequency depends on the total collisional energy, because an individual with the higher kinetic energy tends to access to another individual the more frequently, whereas the collision frequency in the Boltzmann equation depends on the relative velocity ($\left|\mathit{v}-{\mathit{v}}_1\right|$). Here, we are free from the geometric collisional mechanics, which is postulated in the Boltzmann equation. Additionally, $\mathit{\xi }\in \left[0,1\right]$ is a parameter, which expresses the dependency of the collision frequency on the total collisional energy. $\mathit{\sigma }$, $\mathit{\chi }\in \left[0,\mathit{\pi }\right]$ and $\mathit{ϵ}\in \left[0,2\mathit{\pi }\right]$ in the right hand side of Eq. (5) are the differential cross section ($\mathit{\sigma }=d^2/4$), deflection angle and scattering angle, respectively. Indeed, above isotropic scattering in the binary collision must be modified in order to demonstrate the characteristics of pedestrians, as discussed by Helbing [15].

From the left hand side of Eq. (5), $f\in C^1\left({\mathbb{X}}^3\right)\wedge f\in C^1\left({\mathbb{V}}^3\right)$ is postulated, although Klimontovich’s distribution function does not always satisfy the smoothness and continuity of f in both ${\mathbb{X}}^3$ and ${\mathbb{V}}^3$, whereas $\mathit{\psi }\in C^1\left({\mathbb{V}}^3\right)$ is always satisfied by $d_p\mathit{\psi }(p)=-c_p$ ($\because \left|c_p\right|<+\infty$) from Eq. (2).

Multiplying 1, p,...,$p^n$ ($n\in \mathbb{N}$) by both sides of Eq. (5) and integrating over ${\mathbb{V}}^3\times \mathbb{P}$, we obtain

$$\begin{array}{cc}& \frac{\mathit{\partial }{\mathit{\rho }}_p{\overline{p}}_0}{\mathit{\partial }t}+{\mathrm{\nabla }}_{\mathit{x}}·\left({\mathit{\rho }}_p{\overline{p}}_0\mathit{\delta }{\mathit{u}}_{p_0}\right)=G_{p_0},\hfill \\ \hfill & \frac{\mathit{\partial }{\mathit{\rho }}_p{\overline{p}}_1}{\mathit{\partial }t}+{\mathrm{\nabla }}_{\mathit{x}}·\left({\mathit{\rho }}_p{\overline{p}}_1\mathit{\delta }{\mathit{u}}_{p_1}\right)+c_p{\mathit{\rho }}_p{\overline{p}}_1=G_{p_1},\hfill \\ \hfill & \dots ,\hfill \\ \hfill & \frac{\mathit{\partial }{\mathit{\rho }}_p{\overline{p}}_n}{\mathit{\partial }t}+{\mathrm{\nabla }}_{\mathit{x}}·\left({\mathit{\rho }}_p{\overline{p}}_n\mathit{\delta }{\mathit{u}}_{p_n}\right)+c_p{\mathit{\rho }}_p{\overline{p}}_n=G_{p_n},\hfill \end{array}$$ 7

where $G_{p_n}:={\int }_{{\mathbb{V}}^3\times \mathbb{P}}{p}^n\mathfrak{Q}\left(f,f_1\right)d^3\mathit{v}dp$ is obtained as

$$\begin{array}{cc}\hfill G_{p_n}:=& {\int }_{{\mathbb{V}}^3\times \mathbb{P}}{p}^n\mathfrak{Q}\left(f,f_1\right)d^3\mathit{v}dp\hfill \\ \hfill =& {\int }_{p\in \mathbb{P}}{\int }_{\mathit{v}\in {\mathbb{V}}^3}{\int }_{p_1\in {\mathbb{P}}_1}{\int }_{{\mathit{v}}_1\in {\mathbb{V}}_1^3}{\int }_{\mathit{ϵ}\in \left[0,2\mathit{\pi }\right]}{\int }_{\mathit{\chi }\in \left[0,\mathit{\pi }\right]}\hfill \\ \hfill & p^{n}f\left({\mathit{v}}^{\prime }{,p|}_{\mathit{\tau }=0}>0,s=1\right)f_1\left({\mathit{v}}_1^{\prime },p_1>0,s_1=1\right)\hfill \\ \hfill & {\mathit{\delta }}_{s,0}{\mathit{\delta }}_{s_1,1}{p}_1\left({\mathit{\tau }}_1\right){\tilde{E}}^{\mathit{\xi }}\mathit{\sigma }sin\mathit{\chi }d\mathit{\chi }d\mathit{ϵ}{d}^3{\mathit{v}}_{1}d{p}_1{d}^3\mathit{v}dp,\hfill \end{array}$$ 8

and ${\mathit{\rho }}_p$, ${\overline{p}}_n$, $\mathit{\delta }{\mathit{u}}_{p_n}$ are defined as

$$\begin{array}{cc}\hfill {\mathit{\rho }}_p:=& {\int }_{{\mathbb{V}}^3\times \mathbb{P}}f{d}^3\mathit{v}dp={\overline{p}}_0,\hfill \\ \hfill {\overline{p}}_n:=& \frac{1}{{\mathit{\rho }}_p}{\int }_{{\mathbb{V}}^3\times \mathbb{P}}{p}^{n}f{d}^3\mathit{v}dp,\hfill \\ \hfill \mathit{\delta }{\mathit{u}}_{p_n}:=& \frac{1}{{\mathit{\rho }}_p{\overline{p}}_n}{\int }_{{\mathbb{V}}^3\times \mathbb{P}}{p}^n\mathit{v}f{d}^3\mathit{v}dp,\hfill \end{array}$$ 9

From Eqs. (7) and (8), the propagation velocity of the virus titer moment (${\mathit{\rho }}_p{\overline{p}}_n$) is $\mathit{\delta }{\mathit{u}}_{p_n}$. The number density of the infected individual ${\mathit{\rho }}_p$ increases via the collisional term $G_{p_0}$. Therefore, the propagation of the infected domain depends on $G_{p_0}$ together with the term ${\mathrm{\nabla }}_{\mathit{x}}·\left({\mathit{\rho }}_p{\overline{p}}_0\mathit{\delta }{\mathit{u}}_{p_0}\right)$.

In the left hand side of Eq. (7), terms $c_p{\mathit{\rho }}_p{\overline{p}}_n$ $(1\le n)$ satisfy

$$\begin{array}{cc}& c_p{\mathit{\rho }}_p{\overline{p}}_n<0\because c_p<0\left(0\le \mathit{\tau }<{\mathit{\tau }}_m\right)\wedge 0<{\mathit{\rho }}_p\wedge 0<{\overline{p}}_n,\hfill \\ \hfill & c_p{\mathit{\rho }}_p{\overline{p}}_n\ge 0\because c_p\ge 0\left({\mathit{\tau }}_m\le \mathit{\tau }\right)\wedge 0<{\mathit{\rho }}_p\wedge 0<{\overline{p}}_n\hfill \end{array}$$ 10

Equation (10) indicates that the virus titer moment increases at $0\le \mathit{\tau }<{\mathit{\tau }}_m$ and deceases at ${\mathit{\tau }}_m\le \mathit{\tau }$ owing to the time evolution of the virus in Eq. (1).

Provided that $f\left(\mathit{v},p\right)$ can be written as $f\left(\mathit{v},p\right)={\mathit{\varphi }}_v\left(\mathit{v}\right){\mathit{\varphi }}_p\left(p\right)$, the propagation velocity of the virus titer moment never depends on the distribution of p. We, however, conjecture that an individual with the larger kinetic energy can be a seed of the infection at the uninfected domain the more frequently. In later discussion on numerical results in Sect. 2.3, we confirm that $〈{\left|\mathit{\delta }{\mathit{u}}_{p_0}\right|}^2〉$ is surely larger than $〈{\left|\mathit{\delta }\mathit{u}\right|}^2〉$ at the boundary between the infected and the uninfected domains.

Besides with virus titer moments in Eq. (9), we define some moments such as

$$\begin{array}{cc}\hfill \mathit{\rho }:=& {\int }_{{\mathbb{V}}^3\times {\mathbb{P}}^{\prime }}f{d}^3\mathit{v}dp,\text{(density}\text{of}\text{individuals)}\hfill \\ \hfill \mathit{\delta }\mathit{u}:=& \frac{1}{\mathit{\rho }}{\int }_{{\mathbb{V}}^3\times {\mathbb{P}}^{\prime }}\mathit{v}f{d}^3\mathit{v}dp,\text{(thermally}\text{fluctuating}\text{flow}\text{velocity)}\hfill \\ \hfill \mathit{\theta }:=& \frac{1}{3\mathit{\rho }}{\int }_{{\mathbb{V}}^3\times {\mathbb{P}}^{\prime }}{v}^{2}f{d}^3\mathit{v}dp,\text{(temperature)}\hfill \\ \hfill \overline{p}:=& \frac{1}{\mathit{\rho }}{\int }_{{\mathbb{V}}^3\times {\mathbb{P}}^{\prime }}pf{d}^3\mathit{v}dp\text{(averaged}\text{normalized-virus}\text{titer)},\hfill \end{array}$$ 11

Analogy to FKPP Equation

In Sect. 2.1, we formulated general form of moment equations for the infected individuals from Eq. (5). On the other hand, moment equations for the uninfected individuals are formulated for individuals with $p=0$, namely, $p\in {\mathbb{P}}^{\prime }-\mathbb{P}$.

Multiplying 1 by both sides of Eq. (1) and integrating over $\left({\mathbb{P}}^{\prime }-\mathbb{P}\right)\times {\mathbb{V}}^3$, we obtain

$$\begin{array}{c}\hfill \frac{\mathit{\partial }{\mathit{\rho }}_{\mathrm{un}}}{\mathit{\partial }t}+{\mathbf{\nabla }}_{\mathit{x}}·\left({\mathit{\rho }}_{\mathrm{un}}\mathit{\delta }{\mathit{u}}_{\mathrm{un}}\right)=G_{\mathrm{un}}=-G_{p_0},\end{array}$$ 12

where $G_{\mathrm{un}}:={\int }_{({\mathbb{P}}^{\prime }-\mathbb{P})\times {\mathbb{V}}^3}\left(I_{01}^{11}+I_{01}^{01}+I_{00}^{00}\right)d\mathit{v}d\mathit{p}=-G_{p_0}$ is used. From Eqs. (7) and (12), we readily confirm the mass conservation, namely, ${\mathit{\partial }}_t\mathit{\rho }+{\mathrm{\nabla }}_{\mathit{x}}·\left({\mathit{\rho }}_p{\overline{p}}_0\mathit{\delta }{\mathit{u}}_{p_0}+{\mathit{\rho }}_{\mathrm{un}}\mathit{\delta }{\mathit{u}}_{\mathrm{un}}\right)=0$. The essence of the diffusion flux ($\mathfrak{J}$) is an expression of the separated velocity between ${\overline{p}}_0\mathit{\delta }{\mathit{u}}_{p_0}$ and $\mathit{\delta }{\mathit{u}}_{p_{\mathrm{un}}}$ with $\mathit{\delta }\mathit{u}$.

Using $\mathfrak{J}$, Eqs. (7) and (12) can be rewritten as

$$\begin{array}{cc}& \frac{\mathit{\partial }{\mathit{\rho }}_{p_0}}{\mathit{\partial }t}+{\mathbf{\nabla }}_{\mathit{x}}·\left({\mathit{\rho }}_{p_0}\mathit{\delta }\mathit{u}+\mathfrak{J}\right)=G_{p_0},\hfill \\ \hfill & \frac{\mathit{\partial }{\mathit{\rho }}_{\mathrm{un}}}{\mathit{\partial }t}+{\mathbf{\nabla }}_{\mathit{x}}·\left({\mathit{\rho }}_{\mathrm{un}}\mathit{\delta }\mathit{u}-\mathfrak{J}\right)=-G_{p_0},\hfill \end{array}$$ 13

where $\mathfrak{J}$ is defined using $\mathit{\delta }\mathit{u}:={\mathit{\rho }}^{-1}\left({\mathit{\rho }}_{p_0}\mathit{\delta }{\mathit{u}}_{p_0}+{\mathit{\rho }}_{\mathrm{un}}\mathit{\delta }{\mathit{u}}_{\mathrm{un}}\right)$ in Eq. (11) as

$$\begin{array}{c}\hfill \mathfrak{J}=\frac{{\mathit{\rho }}_{p_0}{\mathit{\rho }}_{\mathrm{un}}}{\mathit{\rho }}\left(\mathit{\delta }{\mathit{u}}_{p_0}-\mathit{\delta }{\mathit{u}}_{\mathrm{un}}\right).\end{array}$$ 14

In the framework of the Navier–Stokes–Fourier approximation, the diffusion flux is approximated as [23]

$$\begin{array}{c}\hfill {\mathfrak{J}}^{[1]}=-mD{\mathbf{\nabla }}_{\mathit{x}}{\mathit{\eta }}_{p_0}-\frac{\mathit{\rho }}{\mathtt{p}}{D}_{\mathtt{p}}{\mathbf{\nabla }}_{\mathit{x}}\mathtt{p},\end{array}$$ 15

where ${\mathit{\eta }}_{p_0}:={\mathit{\rho }}_{p_0}{\mathit{\rho }}^{-1}$ is the mass fraction of the number of infected individuals to the total number of individuals at $\mathit{x}$, D is the diffusion coefficient and $D_p$ is the pressure diffusion coefficient, m is a mass of the individual and $\mathtt{p}:=\mathit{\rho }R\mathit{\theta }$ is the static pressure.

$G_{p_0}$ can be written as

$$\begin{array}{c}\hfill G_{p_0}=k{\mathit{\rho }}_{p_0}{\mathit{\rho }}_{\mathrm{un}}=K_{01}{\mathit{\rho }}^2\left(1-{\mathit{\eta }}_{p_0}\right){\mathit{\eta }}_{p_0},\end{array}$$ 16

where $K_{01}$ is the transition rate by which the uninfected individuals change to infected individuals.

Setting $\mathit{\delta }\mathit{u}=\mathbf{0}$, $m=1$, $D_p=0$ and $D=$const. in ${\mathbb{X}}^3$, we obtain the following mass transport equation from Eqs. (13), (15) and (16):

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \frac{\mathit{\partial }{\mathit{\rho }}_{p_0}}{\mathit{\partial }t}-D\mathrm{\Delta }\frac{{\mathit{\rho }}_{p_0}}{\mathit{\rho }}=K_{01}{\mathit{\rho }}^2\left(1-{\mathit{\eta }}_{p_0}\right){\mathit{\eta }}_{p_0}.\end{array}\end{array}$$ 17

Equation (17) coincides with the Fisher-Kolmogorov-Petrovsky-Piscounov (FKPP) equation [24], when $\mathit{\rho }=1$, as follows

$$\begin{array}{c}\hfill \frac{\mathit{\partial }{\mathit{\eta }}_{p_0}}{\mathit{\partial }t}-D\mathrm{\Delta }{\mathit{\eta }}_{p_0}=K_{01}\left(1-{\mathit{\eta }}_{p_0}\right){\mathit{\eta }}_{p_0}.\end{array}$$ 18

Consequently, the epidemic spread has an analogy to the dynamics described by the FKPP equation, when forgoing assumptions used to obtain Eq. (18) from Eq. (5) is validated. On the other hand, Succi and his coworkers analyzed the FKPP equation with nonzero flow-flux, namely, $\mathit{\delta }\mathit{u}\ne \mathbf{0}$ using the lattice Boltzmann method (LBM) [25, 26]. The application of the LBM to the FKPP equation, which demonstrates the epidemic spread, is interesting issue in our future study, definitely.

The reaction–diffusion equation can be surely applied to the conventional SIR model using similar procedures mentioned above such as

$$\begin{array}{cc}& \frac{\mathit{\partial }{\mathit{\eta }}_{\mathrm{S}}}{\mathit{\partial }t}-D\mathrm{\Delta }{\mathit{\eta }}_{\mathrm{S}}=-K_{\mathrm{S}\to \mathrm{I}}{\mathit{\eta }}_{\mathrm{I}}{\mathit{\eta }}_{\mathrm{S}},\hfill \\ \hfill & \frac{\mathit{\partial }{\mathit{\eta }}_{\mathrm{I}}}{\mathit{\partial }t}-D\mathrm{\Delta }{\mathit{\eta }}_{\mathrm{I}}=K_{\mathrm{S}\to \mathrm{I}}{\mathit{\eta }}_{\mathrm{I}}{\mathit{\eta }}_{\mathrm{S}}-K_{\mathrm{I}\to \mathrm{R}}{\mathit{\eta }}_{\mathrm{I}},\hfill \\ \hfill & \frac{\mathit{\partial }{\mathit{\eta }}_{\mathrm{R}}}{\mathit{\partial }t}-D\mathrm{\Delta }{\mathit{\eta }}_{\mathrm{R}}=K_{\mathrm{I}\to \mathrm{R}}{\mathit{\eta }}_{\mathrm{I}},\hfill \end{array}$$ 19

where ${\mathit{\eta }}_{\mathrm{S}}\in {\mathbb{R}}_{+}$ (fraction of susceptible individuals), ${\mathit{\eta }}_{\mathrm{I}}\in {\mathbb{R}}_{+}$ (fraction of infected individuals), ${\mathit{\eta }}_{\mathrm{R}}\in {\mathbb{R}}_{+}$ (fraction of recovered individuals), and $K_{i\to j}\in {\mathbb{R}}_{+}$ is the transition rate from status “i” to “j”.

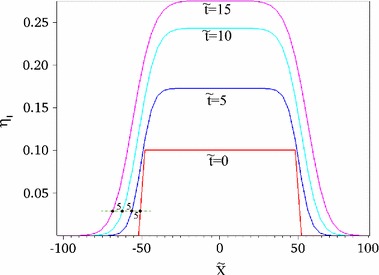
Figure 2 shows the time evolution of ${\mathit{\eta }}_{\mathrm{I}}$, which is obtained by solving Eq. (19) using $\tilde{D}=1$, ${\tilde{K}}_{\mathrm{S}\to \mathrm{I}}=0.25$ and ${\tilde{K}}_{\mathrm{I}\to \mathrm{R}}=0.1$, where all the physical quantities are normalized. Thus, the normalized quantities are denoted by $\stackrel{~}{}$. $\mathit{x}\in \mathfrak{X}\subseteq {\mathbb{X}}^2$ ($\mathit{x}\in \mathfrak{X}||\tilde{x}|\le 100\wedge |\tilde{y}|\le 100$) is considered as the numerical domain with the periodic boundary. The finite differential scheme is used to solve Eq. (19), whereas Succi [26] indicated that FKPP equation with the advection can be solved with better accuracy using the LBM rather than the finite differential scheme. Actually, we consider the directed flow of individuals in the process of the epidemic spread, as discussed in Sect. 3 and appendix. As an initial condition, ${\mathit{\eta }}_{\mathrm{S}}=0.9$, ${\mathit{\eta }}_{\mathrm{I}}=0.1$ and ${\mathit{\eta }}_{\mathrm{R}}=0$ in the domain ${\mathfrak{X}}_I$ ($\mathit{x}\in {\mathfrak{X}}_I|\sqrt{{\tilde{x}}^2+{\tilde{y}}^2}\le 50$), whereas ${\mathit{\eta }}_{\mathrm{S}}=1$ and ${\mathit{\eta }}_{\mathrm{I}}={\mathit{\eta }}_{\mathrm{R}}=0$ in the domain $\mathfrak{X}-{\mathfrak{X}}_I$. The infected domain expands, concentrically, as $\tilde{t}$ increases. Most of infected individuals at ${\mathfrak{X}}_I$ and $\tilde{t}=0$ change to recovered individuals at ${\mathfrak{X}}_I$ and $\tilde{t}=30$. Finally, most of infected individuals change to recovered individuals at $\tilde{t}=200$.

Fig. 2.

Time evolution of ${\mathit{\eta }}_{\mathrm{I}}$ obtained using Eq. (19)

The propagation speed of a traveling wave [24] which is obtained by Eq. (18) can be calculated by following procedures, when f in ${\mathbb{X}}^3$ is spherically symmetric, [27]

1. We set $\breve{\mathit{\varphi }}:={\mathit{\eta }}_{p_0}$ and $\breve{\mathit{\psi }}:=d{\mathit{\eta }}_{p_0}/dz$ using the definition $z:=r-ct$ ($r:={||\mathit{x}||}_{L_2}$).

2. Equation (18) can be rewritten using $\breve{\mathit{\varphi }}$ and $\breve{\mathit{\psi }}$ as

   $$\begin{array}{c}\hfill \frac{d}{dz}\left(\begin{array}{c}\breve{\mathit{\varphi }}\\ \breve{\mathit{\psi }}\end{array}\right)=\left[\begin{array}{c}\breve{\mathit{\psi }}\\ -\left(c/D\right)\breve{\mathit{\psi }}-\left(K_{01}/D\right)\left(1-\breve{\mathit{\varphi }}\right)\breve{\mathit{\varphi }}\end{array}\right]\end{array}$$ 20
3. Above system equation has two fixed points at $\left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=(0,0)$ and (1, 0). Jacobian matrix is obtained at $\left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=(0,0)$ and (1, 0) from Eq. (20), respectively, as

   $$\begin{array}{cc}\hfill J\left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=& \left(\begin{array}{cc}\frac{\mathit{\partial }{\breve{\mathit{\varphi }}}^{\prime }}{\mathit{\partial }\breve{\mathit{\varphi }}}& \frac{\mathit{\partial }{\breve{\mathit{\varphi }}}^{\prime }}{\mathit{\partial }\breve{\mathit{\psi }}}\\ \frac{\mathit{\partial }{\breve{\mathit{\psi }}}^{\prime }}{\mathit{\partial }\breve{\mathit{\varphi }}}& \frac{\mathit{\partial }{\breve{\mathit{\psi }}}^{\prime }}{\mathit{\partial }\breve{\mathit{\psi }}}\end{array}\right)=\left(\begin{array}{cc}0& 1\\ \frac{K_{01}}{D}\left(2\breve{\mathit{\varphi }}-1\right)& -\frac{c}{D}\end{array}\right)\hfill \\ \hfill =& \left\{\begin{array}{cc}\left(\begin{array}{cc}0& 1\\ -\frac{K_{01}}{D}& -\frac{c}{D}\end{array}\right)\hfill & \left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=(0,0),\hfill \\ \left(\begin{array}{cc}0& 1\\ \frac{K_{01}}{D}& -\frac{c}{D}\end{array}\right)\hfill & \left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=(1,0),\hfill \end{array}\right.\hfill \end{array}$$ 21

   where ${\breve{\mathit{\varphi }}}^{\prime }:=d\breve{\mathit{\varphi }}/dz$ and ${\breve{\mathit{\psi }}}^{\prime }:=d\breve{\mathit{\psi }}/dz$.
4. Two eigenvalues in Eq. (21) are obtained as

   $$\begin{array}{c}\hfill {\mathit{\lambda }}_{\pm }:=\left\{\begin{array}{cc}\frac{-c\pm \sqrt{c^2-4D{K}_{01}}}{2D}\hfill & \left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=(0,0)\hfill \\ \frac{-c\pm \sqrt{c^2+4D{K}_{01}}}{2D}\hfill & \left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=(1,0)\hfill \end{array}\right.\end{array}$$ 22
5. We assume that the boundary between two domains ${\mathbb{X}}_p^3$ ($\left\{\mathit{x}\in {\mathbb{X}}_p^3|{\mathit{\eta }}_{p_0}\left(\mathit{x}\right)\in (0,1]\right\}$) and ${\mathbb{X}}^3-{\mathbb{X}}_p^3$, namely, infected and uninfected domains, is expressed with $\left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=(0,0)$. The propagation speed of the boundary between such two domains must satisfy the following relation to yield the real value of ${\mathit{\lambda }}_{\pm }$ at $\left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=(0,0)$:

   $$\begin{array}{c}\hfill 2\sqrt{D{K}_{01}}\le c.\end{array}$$ 23

From item 5, the minimum value of the propagation speed of the boundary $\left(\breve{\mathit{\varphi }},\breve{\mathit{\psi }}\right)=(0,0)$ is equal to $2\sqrt{D{K}_{01}}$. In above numerical result of the reaction–diffusion equation of SIR model in Eq. (19), the propagation speed of the boundary between the infected and uninfected domains is defined by $2\sqrt{\tilde{D}{\tilde{K}}_{\mathrm{S}\to \mathrm{I}}}=1$. Figure 3 shows the time evolution of ${\mathit{\eta }}_{\mathrm{I}}$. The propagation speed of the boundary certainly coincides with unity, as shown in Fig. 3. Provided that D is independent of ${\mathit{\tau }}_m$ and $T_c$ in Eq. (1), the minimum propagation speed of the boundary between the infected and uninfected domains, namely, $2\sqrt{D{K}_{01}}$ depends on ${\mathit{\tau }}_m$ and $T_c$ via $K_{01}$ owing to Eq. (8). In this paper, we never refer to concrete form of $K_{01}$ owing to mathematical complexities, whereas later numerical results show that the propagation speed of the boundary domain strongly depends on ${\mathit{\tau }}_m$, when $T_c$ is fixed. From Eq. (8), we make a rough estimation of $K_{01}$ as $K_{01}\sim \mathfrak{K}p\left(\mathit{\tau }\right)$ ($\mathfrak{K}\in {\mathbb{R}}_{+}$). Figure 4 shows $\sqrt{K_{01}{{|}_{{\tilde{\mathit{\tau }}}_m=1/2}/K_{01}|}_{{\tilde{\mathit{\tau }}}_m=1}}=\sqrt{{p|}_{{\tilde{\mathit{\tau }}}_m=1/2\text{or}3/4}{/p|}_{{\tilde{\mathit{\tau }}}_m=1}}$ using ${\tilde{T}}_c=0.05$. $\sqrt{{p|}_{{\tilde{\mathit{\tau }}}_m=1/2}{/p|}_{{\tilde{\mathit{\tau }}}_m=1}}$ decreases from 42.5 at $\tilde{\mathit{\tau }}=0$ in the case of ${\tilde{\mathit{\tau }}}_m=1/2$, as $\tilde{\mathit{\tau }}$ increases. Similarly, $\sqrt{{p|}_{{\tilde{\mathit{\tau }}}_m=3/4}{/p|}_{{\tilde{\mathit{\tau }}}_m=1}}$ decreases from 8.91 at $\tilde{\mathit{\tau }}=0$ in the case of ${\tilde{\mathit{\tau }}}_m=3/4$, as $\tilde{\mathit{\tau }}$ increases. Then, we can understand that the propagation speed of the boundary domain between the infected and uninfected domains is markedly sensitive to ${\tilde{\mathit{\tau }}}_m$.

Fig. 3.

Time evolution of ${\mathit{\eta }}_{\mathrm{I}}$ obtained using Eq. (19)

Fig. 4.

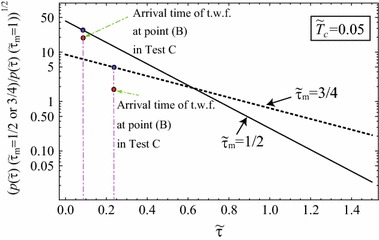
$\sqrt{{p|}_{{\tilde{\mathit{\tau }}}_m=1/2}{/p|}_{{\tilde{\mathit{\tau }}}_m=1}}$ versus $\tilde{\mathit{\tau }}$. Numerical results of ${\tilde{v}}_{\ast }{{|}_{{\tilde{\mathit{\tau }}}_m=1/2}/{\tilde{v}}_{\ast }|}_{{\tilde{\mathit{\tau }}}_m=1}$ [${\tilde{v}}_{\ast }$: normalized propagation speed of traveling wave front (t.w.f.)] and ${\tilde{v}}_{\ast }{{|}_{{\tilde{\mathit{\tau }}}_m=3/4}/{\tilde{v}}_{\ast }|}_{{\tilde{\mathit{\tau }}}_m=1}$

Numerical Analysis of Stochastic Boltzmann Type Equation for Local Epidemic Spread

All the physical quantities are normalized as

$$\begin{array}{cc}& \tilde{t}:=t/t_{\infty },\tilde{\mathit{x}}:=\mathit{x}/L_{\infty },t_{\infty }:=L_{\infty }/C_{\infty },\tilde{\mathit{\tau }}:=\mathit{\tau }/t_{\infty }\hfill \\ \hfill & \tilde{\mathit{\rho }}:=\mathit{\rho }/{\mathit{\rho }}_{\infty },\tilde{\mathit{u}}:=\mathit{u}/C_{\infty },\tilde{\mathit{\theta }}:=\mathit{\theta }/{\mathit{\theta }}_{\infty },\hfill \\ \hfill & \tilde{\mathit{v}}:=\mathit{v}/C_{\infty },\tilde{f}:=f/\left({\mathit{\rho }}_{\infty }{C}_{\infty }^3\right),C_{\infty }:=\sqrt{2R{\mathit{\theta }}_{\infty }},\hfill \end{array}$$

The initial velocity distribution function $f\left(t=0,\mathit{v},\mathit{x},p\left(\mathit{\tau }\right)\right)$ in ${\mathbb{R}}_{+}\times {\mathbb{V}}^3\times {\mathbb{P}}^{\prime }$ is assumed to follow the Maxwell–Boltzmann distribution in ${\mathbb{V}}^3$. Here, the distribution function in $x^3$-axis is assumed to be uniform. Of course, $\left(\mathit{v},\mathit{x}\right)\in {\mathbb{V}}^2\times {\mathbb{X}}^2$ might be more realistic to demonstrate local epidemic spread between the infected and uninfected individuals than $(\mathit{v},\mathit{x})\in {\mathbb{V}}^3\times {\mathbb{X}}^3$, when we exclude the interaction between two individuals inside three dimensional facilities (i.e., binary collision at the staircase.), whereas we consider $\left(\mathit{v},\mathit{x}\right)\in {\mathbb{V}}^3\times {\mathbb{X}}^3$, because the assumption of the uniformity along $x_3$-axis does not change the qualitative tendency of the local epidemic spread in $\left(x_1,x_2\right)$ space, markedly, as the two dimensional flow has been considered using not two dimensional collision between two discs but three dimensional collision between two spheres [28]. The reduction of the dimension will be easily done in accordance with the situation to be considered. Here, we set $\tilde{\mathit{x}}:=\left(\tilde{X},\tilde{Y},\tilde{Z}\right)$ and calculation domain as $\left(\tilde{X},\tilde{Y},\tilde{Z}\right)\in \mathfrak{X}\subseteq {\mathbb{X}}^3$, whereas we set $\mathit{\delta }\tilde{\mathit{u}}:=\left(\mathit{\delta }\tilde{u},\mathit{\delta }\tilde{v},\mathit{\delta }\tilde{w}\right)$ and $\mathit{\delta }{\tilde{\mathit{u}}}_{p_n}:=\left(\mathit{\delta }{\tilde{u}}_{p_n},\mathit{\delta }{\tilde{v}}_{p_n},\mathit{\delta }{\tilde{w}}_{p_n}\right)$. As an initial condition, we set $T_c/t_{\infty }=0.05$, $\tilde{\mathit{\rho }}=1$, ${\tilde{\mathit{u}}}_{\infty }=\mathbf{0}$, and $\text{Kn}={(\sqrt{2}\mathit{\pi }{d}^2{\mathit{\rho }}_{\infty }/m{L}_{\infty })}^{-1}=1.0$ (m: common mass of individuals). $N_c=100$ sample particles per a lattice are set, in which $61\times 61$ lattices equally spaced inside the calculation domain, $\mathfrak{X}$, $\left\{\tilde{x},\tilde{y}\in \mathfrak{X}|\tilde{x}\in \left[0,1\right],\tilde{y}\in \left[0,1\right]\right\}$. As the boundary condition on $\tilde{X}=0,1$ and $\tilde{Y}=0,1$, the periodic boundary condition is used in Tests A-1, 2, 3, 4, 5, B and C, whereas the specular boundary condition is used in Test A-6. At $\tilde{t}=0$, all the individuals inside the domain $\mathfrak{U}$, $\left\{\tilde{x},\tilde{y}\in \mathfrak{U}\subseteq \mathfrak{X}|\sqrt{{\left(\tilde{x}-0.5\right)}^2+{\left(\tilde{y}-0.5\right)}^2}<0.1\right\}$ are infected, simultaneously. In other words, all the individuals have $p\left(\tilde{\mathit{\tau }}=0\right)>0$ owing to Eq. (1) inside the domain $\mathfrak{U}$ at $\tilde{t}=0$, whereas individuals inside the domain $\mathfrak{X}-\mathfrak{U}$, who have $p=0$ at $\tilde{t}=0$, are uninfected. The schematic of the calculation domain ($\mathfrak{X}$) is shown in Fig. 5 (Table 1).

Fig. 5.

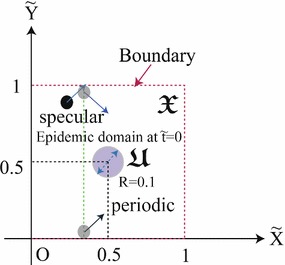
Schematic of calculation domain

Table 1.

Numerical tests

	${\tilde{\mathit{\tau }}}_m$	$\tilde{T}{|}_{t=0}$	$\mathit{\xi }$	$N_c$	B.C.
Test A-1	1	5	0.6	100	P
Test A-2	1	5	0.6	50	P
Test A-3	1	5	0.6	10	P
Test A-4	1	5	0	100	P
Test A-5	1	10	0.6	100	P
Test A-6	1	5	0.6	50	S
Test B	0.5	5	0.6	100	P
Test C	0.75	5	0.6	100	P

B.C. boundary condition, P periodic boundary, S specular boundary

Figure 6 shows the time evolution of $\overline{p}$ in Test A-1. The infected domain spreads at $0\le \tilde{t}\le 1.0$, concentrically, where the center of the concentric spread is, certainly, $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$. At ${\tilde{\mathit{\tau }}}_m=1.0$ in Eq. (1), p of the individual, who is infected at $\tilde{t}=0$, reaches to unity at $\tilde{\mathit{\tau }}=1$. Consequently, $\overline{p}$ increases toward $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ and reaches to 0.895 at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ at $\tilde{t}=1$, where we remind that $\overline{p}$ is not equal to unity at $\tilde{t}=1$, because individuals, who are infected at $\tilde{t}>0$ and have $p\left(\tilde{\mathit{\tau }}\right)<1$ owing to $\tilde{\mathit{\tau }}<1$, exist at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$. $\overline{p}\left(\tilde{X},\tilde{Y}\right)$ increases, as the distance from $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ decreases at $0\le \tilde{t}\le 1$, because the ratio of the number of individuals at $\left(\tilde{X},\tilde{Y}\right)$, who are infected at $0<\tilde{t}$ and uninfected, to the total number of individuals at $(\tilde{X},\tilde{Y})$ increases, as the distance from $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ decreases at $0\le \tilde{t}\le 1$. The uninfected domain, in which all the individuals are uninfected, corresponds to four corners of $\mathfrak{X}$ at $\tilde{t}=1.536$, whereas all the individuals in $\mathfrak{X}$ are infected at $\tilde{t}=1.842$. p of individuals, who are infected at $\tilde{t}=0$, decreases at ${\tilde{\mathit{\tau }}}_m=1<\tilde{t}$ from Eq. (1). Thus, $\overline{p}$ decreases toward $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, concentrically, as shown in frames at $\tilde{t}=1.842$, 2.16 and 3.072. Such a tendency of $\overline{p}$ certainly holds true for frames at $\tilde{t}=1.536$ and $t=3.792$, whereas such a tendency is indistinguishable, because we used common color contours in all the frames. Finally, all the individuals are infected in Test A-1. To avoid infections of all the individuals in $\mathfrak{X}$, $p\left(\tilde{\mathit{\tau }}\right)$ in Eq. (1) must be damped to zero, rapidly, before the interaction with the uninfected individuals. Such a situation can be obtained by using $p\left({\tilde{\mathit{\tau }}}_c\right)\ll 1$ (${\tilde{\mathit{\tau }}}_c$: inverse of the averaged collision frequency), when ${\tilde{\mathit{\tau }}}_m<{\tilde{\mathit{\tau }}}_c$. Next, we investigate the effect of ${\tilde{\mathit{\tau }}}_m$ on the local epidemic spread by considering Test B.

Fig. 6.

Time evolutions of $\overline{p}$ in Test A-1

Figure 7 shows the time evolution of $\overline{p}$ in Test B. The infected domain spreads, concentrically in a similar way to Test A. The propagation speed of $\overline{p}$ in Test B is higher than that in Test A-1. From Eq. (7), the propagation of the infected domain depends on the spatial propagation via ${\mathrm{\nabla }}_{\mathit{x}}{\mathit{\rho }}_0{\overline{p}}_0\mathit{\delta }{\mathit{u}}_{p_0}$ and generation of ${\mathit{\rho }}_0{\overline{p}}_0$ via $G_{p_0}$. We remind that $\overline{p}$ is related to ${\overline{p}}_0$, and $G_{p_0}$ increases, as $pf\left(p,s=1\right)$ increases, as shown by $I_{01}^{11}$ in the right hand side of Eq. (5). The increase in the propagation speed due to the decrease in ${\tilde{\mathit{\tau }}}_m$ is caused by the increase in $G_{p_0}$ due to the rapid increase in $p\left(\tilde{\mathit{\tau }}\right)$ as a result of the decrease of ${\tilde{\mathit{\tau }}}_m$ in Eq. (1) rather than the increase in $\mathit{\delta }{\mathit{u}}_{p_0}$, because our numerical results indicate that $〈\left|\mathit{\delta }{\tilde{\mathit{u}}}_{p_0}\left(\tilde{t}\right)\right|〉$ at the boundary between the infected and uninfected domains in Test A-1 is similar to that in Test B. Such a similarity between $〈\left|\mathit{\delta }{\tilde{\mathit{u}}}_{p_0}\left(\tilde{t}\right)\right|〉$ at the boundary between the infected and uninfected domains in Test A-1 and that in Test B indicates that D in Test A-1 is similar to that in Test B. In short, the difference between the propagation speed of the boundary domain between the infected and uninfected domains in Test A-1 and that in Test B is caused by the relation $K_{01}{{|}_{\mathrm{Test}\mathrm{A}-1}\ll K_{01}|}_{\mathrm{Test}\mathrm{B}}$ as a result of Eq. (23).

Fig. 7.

Time evolutions of $\overline{p}$ in Test B

Next, we consider on effects of velocity fluctuations via thermal fluctuations by comparing of $\overline{p}$, which are obtained in Tests A-1, 2 and 3. In the DSMC method to solve the stochastic Boltzmann type equation, the velocity fluctuations ($\mathit{\delta }\mathit{u}$) depend on the number of sample particles in a lattice (${\overline{N}}_c$), which is averaged during some time interval, such that [29]

$$\begin{array}{c}\hfill 〈\mathit{\delta }{\tilde{u}}^2〉=\frac{R\overline{\mathit{\theta }}}{{\overline{N}}_c},\end{array}$$ 24

where $\overline{\mathit{\theta }}$ is the temperature, which is averaged during some time interval.

Figure 8 shows snapshots of $\overline{p}$ in Tests A-1, A-2 and A-3 at $\tilde{t}=1.0$ (upper frames) and $\tilde{t}=1.536$ (lower frames). Figure 8 shows that there are not marked differences between contours of $\overline{p}$ in Test A-1 and those in Test A-2 at $\tilde{t}=1.0$ and 1.536, whereas there are marked differences between contours of $\overline{p}$ in Test A-1 and those in Test A-3 at $\tilde{t}=1.0$ and 1.536, because the infected domain never spreads concentrically in Test A-3. From Eq. (24), we can conjecture that $〈\mathit{\delta }{\tilde{u}}^2〉$ in Test A-1 is a half of that in Test A-2 and 1 / 10 times of that in Test A-3, because $\overline{\mathit{\theta }}$ is fluctuating around 5 at $0\le \tilde{t}$ in Tests A-1, 2 and 3. The dependency of the propagation speed of the boundary between the infected and uninfected domains on $\mathit{\delta }\tilde{u}$ is ignorable, because there are no marked differences among the area of the infected domain in Test A-1 and those in Tests A-2 and A-3 at $\tilde{t}=1$ and 1.536, as shown in Fig. 8. Consequently, the propagation speed of the boundary between the infected and uninfected domains strongly depends on the collisional term $G_{p_0}$ in Eq. (7), in other words, $K_{01}$ in Eq. (23).

Fig. 8.

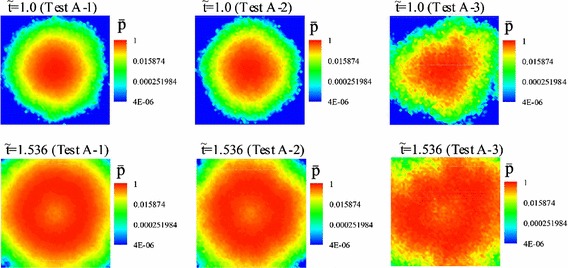
Snapshots of $\overline{p}$ in Tests A-1, A-2 and A-3 at $\tilde{t}=1.0$ (upper frames) and $\tilde{t}=1.536$ (lower frames)

Next, we investigate $\tilde{f}\left(p\right):={\int }_{{\mathbb{V}}^3}\tilde{f}\left(\tilde{t},\tilde{\mathit{x}},p\left(\tilde{\mathit{\tau }}\right),\tilde{\mathit{v}}\right)d{\mathit{v}}^3$, when $\tilde{t}$ and $\tilde{\mathit{x}}$ are fixed. We set $\mathrm{\Delta }p=0.0167$ in the range of $0<p\le 1$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ is the set of simple functions $\tilde{f}\left(\mathrm{\Delta }p\times i\right)$ ($i\in {\mathbb{Z}}_{+}$) on Lebesgue measure $p\in \left(i\times \mathrm{\Delta }p,(i+1)\times \mathrm{\Delta }p\right]$. Especially, $\tilde{f}\left(p=0\right)$, which corresponds to the ratio of the number of uninfected individuals to the total number of individuals at $\left(\tilde{X},\tilde{Y}\right)$, is Dirac measure at $p=0$. Figure 9 shows $\tilde{f}\left(p\right)$ versus p at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.0$ (upper-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.0$ (upper-middle frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.0$ (upper-right frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.92$ (lower-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.92$ (lower-middle frame), and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.92$ (lower-right frame), in Test A-1. $\tilde{f}\left(p\right)$ at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, which corresponds to a center of the concentric epidemic-domain, has a peak at $p=1$ and almost plateau discrete-distribution on Lebesgue measure in the range of $0.125\le p<1$ at $\tilde{t}=1$. Here, $\tilde{f}\left(p=1\right)$ corresponds to the number of individuals, who are infected at $\tilde{t}=0$, and $f\left(p<1\right)$ corresponds to the number of individuals, who are infected at $0<\tilde{t}\le 1$ in $\mathfrak{X}-\mathfrak{U}$. From $\tilde{f}(p)$ at $\tilde{t}=1$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, we can confirm that there exist a few individuals, who are infected at $0<t\le 1$ in $\mathfrak{X}-\mathfrak{U}$. $\tilde{f}(p)$ at $\tilde{t}=1$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ indicates that the bulk tendency $d_{p}f(p)<0$ is obtained in the range of $0\le p\le 0.25$. Consequently, there is no one, who is infected at $\tilde{t}=0$ in $\mathfrak{U}$, at $\tilde{t}=1$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$. $\tilde{f}\left(p=0\right)=1$ is obtained at $\tilde{t}=1$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$. In short, no one is infected at $\tilde{t}=1$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$.

Fig. 9.

$\tilde{f}(p)$ versus p at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.0$ (upper-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.0$ (upper-middle frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.0$ (upper-right frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.92$ (lower-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.92$ (lower-middle frame), and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.92$ (lower-right frame), in Test A-1

$\tilde{f}(p)$ at $\tilde{t}=1.92$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ indicates that the bulk tendency $d_{p}f(p)<0$ is obtained at $0\le p\le 0.125$ and $\tilde{f}(p)=0$ at $0.125<p$. As a result, most of individuals recovers at $\tilde{t}=1.92$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$. $\tilde{f}(p)$ at $\tilde{t}=1.92$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ indicates a concave form with one peak at $p=0$ and the other at $p=0.98$. Finally, $\tilde{f}(p)$ at $\tilde{t}=1.92$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ indicates the bulk tendency $d_p\tilde{f}(p)>0$ in the range of $0.256\le p\le 1$. As a result, $\tilde{f}(p)$ at $\tilde{t}=1.92$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ is similar to the mixture of $\tilde{f}(p)$ at $\tilde{t}=1.92$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ and $\tilde{f}(p)$ at $\tilde{t}=1.92$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$.

Next, we investigate $\tilde{f}\left(\tilde{\mathit{\tau }}\right):={\int }_{{\mathbb{V}}^3}\tilde{f}\left(\tilde{t},\tilde{\mathit{x}},p\left(\tilde{\mathit{\tau }}\right),\tilde{\mathit{v}}\right)d{\mathit{v}}^3$. We set $\mathrm{\Delta }\tilde{\mathit{\tau }}=0.02$ in the range of $0\le \tilde{\mathit{\tau }}\le 2$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ is the set of simple functions $\tilde{f}\left(\mathrm{\Delta }\tilde{\mathit{\tau }}\times i\right)$ ($i\in {\mathbb{Z}}_{+}$) on Lebesgue measure $\tilde{\mathit{\tau }}\in \left[i\times \mathrm{\Delta }\tilde{\mathit{\tau }},(i+1)\times \mathrm{\Delta }\tilde{\mathit{\tau }}\right)$. Then, $0\le \tilde{\mathit{\tau }}\le \mathrm{\Delta }\tilde{\mathit{\tau }}$ includes both uninfected individuals and infected individuals, whose elapsed time is in the range of $0\le \tilde{\mathit{\tau }}\le \mathrm{\Delta }\tilde{\mathit{\tau }}$. Figure 10 shows $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ versus $\tilde{\mathit{\tau }}$ at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.0$ (top-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.0$ (top-middle frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.0$ (top-right frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.23$ (middle-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.23$ (middle-middle frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.23$ (middle-right frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.47$ (bottom-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.47$ (bottom-middle frame), and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.47$ (bottom-right frame), in Test A-1. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.0$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ indicates that sixty percent of the total number of individuals, who are in $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ at $\tilde{t}=1.0$, are infected at $\tilde{t}=0$ and there is no one, who is infected at $\tilde{t}>0.44$, because of $f\left(\tilde{\mathit{\tau }}\le 0.56\right)=0$ at $\tilde{t}=1.0$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.0$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ indicates that there exist individuals, who are infected at $0.225\le \tilde{t}\le 0.775$, at $\tilde{t}=1.0$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$. Additionally, $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.0$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ has a maximum peak at $\tilde{\mathit{\tau }}=0.3$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.0$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ indicates that nobody is infected at $\tilde{t}=1.0$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.23$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ has a maximum peak at $\tilde{\mathit{\tau }}=1.23$, which means that most of individuals are infected at $\tilde{t}=0$, and finite values in the range of $0.725\le \tilde{\mathit{\tau }}\le 1.23$. Thus, individuals at $\tilde{t}=1.23$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ are infected at $0\le \tilde{t}\le 0.505$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.23$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ has finite values in the range of $0.265\le \tilde{\mathit{\tau }}\le 1.23$ and a maximum peak at $\tilde{\mathit{\tau }}=0.63$. We confirm that there exist individuals, who are infected at $\tilde{t}=0$, at $\tilde{t}=1.23$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, whereas there is no one, who is infected at $\tilde{t}=0$, at $\tilde{t}=1$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$. Thus, individuals at $\tilde{t}=1.23$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ are infected at $0\le \tilde{t}\le 0.965$. Additionally, we conjecture that $\tilde{f}\left(\tilde{\mathit{\tau }}=1\right)$ at $\tilde{t}=1.23$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ corresponds to $\tilde{f}\left(\tilde{\mathit{\tau }}=0.775\right)$ at $\tilde{t}=1.0$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.23$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ has finite values in the range of $0\le \tilde{\mathit{\tau }}\le 0.39$. Therefore, ninety percent of the total number of individuals, who are in $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ at $\tilde{t}=1.23$, are infected in the range of $0.89\le \tilde{t}\le 1.23$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.0$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ has a maximum value at $\tilde{\mathit{\tau }}=0.09$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ has finite values in the range of $0.97\le \tilde{\mathit{\tau }}\le 1.47$. Then, individuals at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ are infected in the range of $0\le \tilde{t}<0.5$. Forty six percent of individuals at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ are infected at $\tilde{t}=0$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ has finite values in the range of $0.5\le \tilde{\mathit{\tau }}\le 1.47$. Therefore, individuals at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ are infected in the range of $0\le \tilde{t}<0.97$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ has a maximum peak at $\tilde{\mathit{\tau }}=0.86$, which means that eight percent of individuals at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ are infected at $\tilde{t}=0.61$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ has finite values in the range of $0.2\le \tilde{\mathit{\tau }}\le 0.74$. Thus, individuals at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ are infected in the range of $0.73\le \tilde{t}<1.27$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at $\tilde{t}=1.47$ and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ has a maximum peak at $\tilde{\mathit{\tau }}=0.37$. Thus, eleven percent of the total number of individuals, who are in $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ at $\tilde{t}=1.47$, are infected at $\tilde{t}=1.1$.

Fig. 10.

$\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ versus $\tilde{\mathit{\tau }}$ at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.0$ (top-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.0$ (top-middle frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.0$ (top-right frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.23$ (middle-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.23$ (middle-middle frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.23$ (middle-right frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$, when $\tilde{t}=1.47$ (bottom-left frame), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$, when $\tilde{t}=1.47$ (bottom-middle frame), and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$, when $\tilde{t}=1.47$ (bottom-right frame), in the case of Test A-1

Next, we investigate effects of ${\mathit{\tau }}_m$ by considering $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ versus $\tilde{\mathit{\tau }}$ in Tests B and C. Figure 11 shows $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ versus $\tilde{\mathit{\tau }}$ at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ (point A), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ (point B) and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ (point C) (upper-left frame) and contour of $\overline{p}$ (upper-right frame) at $\tilde{t}=0.09$ in Test B. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ versus $\tilde{\mathit{\tau }}$ at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ (point A), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ (point B) and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ (point C) (lower-left frame) and contour of $\overline{p}$ (lower-right frame) at $\tilde{t}=0.33$ in Test C. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at point (A) in Test B indicates that all the individuals at point (A) are infected at $\tilde{t}=0$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at point (B) are finite at $\tilde{\mathit{\tau }}=0.05$ and 0.07. Then, most of individuals at point (B) are infected at $\tilde{t}=0.04$ and a few of individuals at point (B) are infected at $\tilde{t}=0.02$. Consequently, invasions of individuals from the domain $\mathfrak{X}-\mathfrak{U}$ to point (A) never occurs, whereas invasions of individuals from other points to point (B) seldom occur, because most of individuals are infected at $\tilde{t}=0.04$ at point (B). Such a tendency of the local epidemic spread in Test B is markedly different from that in Test A-1. The propagation speed of the boundary between the infected and uninfected domains in Test B is markedly higher than that in Test A. Then, the characteristic time of invasions of individuals from other points to point (B) is presumably longer than the characteristic time of the local epidemic spread in Test B. Consequently, invasions of individuals from other points to point (B) is suppressed in Test B. Similarly, invasions of individuals from $\mathfrak{X}-\mathfrak{U}$ to point (A) never occur at $\tilde{t}=0.09$. $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at point (A) in Test C also indicates that all the individuals at point (A) are infected at $\tilde{t}=0$, whereas $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ at point (B) are finite in the range of $0.08\le \tilde{\mathit{\tau }}\le 0.22$. Consequently, invasions of individuals from other points to point (B) in Test C occur more frequently than that does in Test B, because the propagation speed of the boundary between the infected and uninfected domains in Test C is lower than that in Test B. Consequently, the range of $\tilde{\mathit{\tau }}$, which yields $\tilde{f}\left(\tilde{\mathit{\tau }}\right)\ne 0$, namely, sum of Lebesgue measure, which yields $\tilde{f}\left(\tilde{\mathit{\tau }}\right)\ne 0$, becomes the longer, as ${\tilde{\mathit{\tau }}}_m$ becomes the longer. In summary, the ratio of the number of individuals, who are infected at other lattices (domains), to the total number of infected individuals at the specific lattice (domain) decreases, as ${\mathit{\tau }}_m$ decreases, because the local epidemic spread occurs inside the lattice rapidly via one or a few of invasions of the infected individuals from neighboring lattices, before some infected individuals reach to neighboring lattice, because the virus titer increases rapidly inside the lattice owing to small ${\mathit{\tau }}_m$ from Eq. (2). Figure 12 shows the sample particles (individuals), which are calculated using the DSMC method, in Test C (at $\tilde{t}=0.6$) and Test A-1 (at $\tilde{t}=0.88$). A sphere corresponds to one individual, where the diameter of a sphere is expressed with enlarged scale to help easy views of readers, and colors of spheres correspond to each values of p. The distribution of p in the neighborhood of the boundary between the infected and uninfected domains is almost uniform in Test C, as shown in the enlarged view in the upper-right frame, whereas individuals with different values of p coexist in the neighborhood of the boundary between the infected and uninfected domains in Test A-1, as shown in the enlarged view in the lower-right frame of Fig. 12. Consequently, we confirm that a small ${\tilde{\mathit{\tau }}}_m$ yields the rapid local epidemic spread via the binary collision between the infected and uninfected individuals, once a infected individual invades to the outside of the boundary between the infected and uninfected domains. Thus, the infected individual with the large velocity becomes a seed of the local epidemic spread, which will be confirmed in the discussion of $\mathit{\delta }{\mathit{u}}_{p_0}$ at the boundary between the infected and uninfected domains in Fig. 13. Consequently, such a higher velocity of the infected individuals at the boundary between the infected and uninfected domains attributes to the finite diffusion flux from Eq. (14) at the boundary between the infected and uninfected domains.

Fig. 11.

$\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ versus $\tilde{\mathit{\tau }}$ at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ (point A), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ (point B) and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ (point C) (upper-left frame) and contour of $\overline{p}$ (upper-right frame) at $\tilde{t}=0.09$ in Test B, and $\tilde{f}\left(\tilde{\mathit{\tau }}\right)$ versus $\tilde{\mathit{\tau }}$ at $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ (point A), $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ (point B) and $\left(\tilde{X},\tilde{Y}\right)=(0.5,0)$ (point C) (lower-left frame) and contour of $\overline{p}$ (lower-right frame) at $\tilde{t}=0.33$ in Test C

Fig. 12.

Snapshots of sample particles in Tests C (upper-left and right frames) at $\tilde{t}=0.6$ and in Test A-1 (lower-left and right frames) at $\tilde{t}=0.88$, where the color of a sphere corresponds to p

Fig. 13.

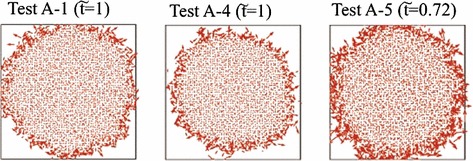
Snapshots of vector field $({\tilde{u}}_{p_0},{\tilde{v}}_{p_0})$ in Tests A-1 (left frame) and A-4 (middle frame) at $\tilde{t}=1.0$ and A-5 (right frame) at $\tilde{t}=0.72$

Toward further investigation of the propagation speed of the boundary between the infected and uninfected domains, we calculate the propagation speed of the traveling wave front in Tests A-1, B and C. The rough estimation of the propagation speed of the traveling wave front can be performed from Figs. 10 and 11 by calculating the arrival time of the wave front at point (B) $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.25)$ such as ${\tilde{v}}_{\ast }{|}_{{\tilde{\mathit{\tau }}}_m=1}=1.25$, ${\tilde{v}}_{\ast }{|}_{{\tilde{\mathit{\tau }}}_m=0.75}=2.5$ and ${\tilde{v}}_{\ast }{|}_{{\tilde{\mathit{\tau }}}_m=0.5}=12.5$. As a result, we obtain ${\tilde{v}}_{\ast }{{|}_{{\tilde{\mathit{\tau }}}_m=0.75}/{\tilde{v}}_{\ast }|}_{{\tilde{\mathit{\tau }}}_m=1}=2$ and ${\tilde{v}}_{\ast }{{|}_{{\tilde{\mathit{\tau }}}_m=0.5}/{\tilde{v}}_{\ast }|}_{{\tilde{\mathit{\tau }}}_m=1}=20$. Orders of such two ratios of the traveling wave front are similar to those calculated using Eq. (23), as shown in Fig. 4. Finally, the propagation speed of the traveling wave front depends on ${\tilde{\mathit{\tau }}}_m$ strongly, as predicted by discussions in Sect. 2.2.

Next, we investigate effects of the dependency of the local epidemic spread on $\mathit{\xi }$ in the collision term in Eq. (5) and $\tilde{\mathit{\theta }}$, respectively. Figure 13 shows snapshots of the vector field $({\tilde{u}}_{p_0},{\tilde{v}}_{p_0})$ in Tests A-1 (left frame) and A-4 (middle frame) at $\tilde{t}=1.0$ and A-5 (right frame) at $\tilde{t}=0.72$, where ${\tilde{\mathit{u}}}_{p_0}:=({\tilde{u}}_{p_0},{\tilde{v}}_{p_0},{\tilde{w}}_{p_0})$. The propagation speed of the boundary between the infected and uninfected domains in Test A-4 is slightly lower than that in Test A-1, whereas the propagation speed of the boundary between the infected and uninfected domains in Test A-5 is markedly higher than that in Test A-1. As a result, the increase in $\mathit{\xi }$ yields the slight increase in the propagation speed of the boundary between the infected and uninfected domains owing to the increase in the collision frequency, because the majorant collision frequency [30] is determined using $1<{\tilde{E}}_{max}$ in the DSMC calculation. Additionally, the increase in $\tilde{\mathit{\theta }}$ yields the increase in $〈\left|\mathit{\delta }{\mathit{u}}_{p_0}\right|〉$ at the boundary between the infected and uninfected domains, which leads to more rapid propagation of the boundary between the infected and uninfected domains in Test A-5 than that in Test A-1. The number of individuals with the large velocity, who determine the propagation speed of the boundary between the infected and uninfected domains, increases, as $\tilde{\mathit{\theta }}$ increases. Actually, we can confirm that the propagation speed of the boundary between the infected and uninfected domains depends on not $\mathit{\delta }\tilde{\mathit{u}}$ but $\mathit{\delta }{\tilde{\mathit{u}}}_{p_0}$ at the boundary between the infected and uninfected domains from Figs. 7 and 13. The increase in $〈\left|\mathit{\delta }{\mathit{u}}_{p_0}\right|〉$ at the boundary between the infected and uninfected domains owing to the increase in $\tilde{\mathit{\theta }}$ can be explained by the fact that D increases in accordance with the increase in $\tilde{\mathit{\theta }}$ due to $\tilde{D}\propto {\tilde{\mathit{\theta }}}^{\mathit{\xi }/2}$ in Eq. (14). Meanwhile, $K_{01}$ also increases in accordance with the increase in $\tilde{\mathit{\theta }}$, when $\mathit{\xi }>0$. Thus, it is still open problem whether the increase in the propagation speed of the boundary between the infected and uninfected domains via the increase in $\tilde{\mathit{\theta }}$ is caused by the increase in D or $K_{01}$ in Eq. (23). Meanwhile, the description of the relation between $\mathit{\delta }\tilde{\mathit{u}}$ and $\mathit{\delta }{\tilde{\mathit{u}}}_{p_0}$ at the boundary between the infected and uninfected domains is set as our future study. In Fig. 13, we find that $\left|\mathit{\delta }{\mathit{u}}_{p_0}\right|$ at the boundary between the infected and uninfected domains tend to be lager than $\left|\mathit{\delta }{\mathit{u}}_{p_0}\right|$ inside the infected domain. Such a tendency indicates that the virus tier is correlated to the velocity of the individual such as $f\left(p,\mathit{v}\right)=C\left(p,\mathit{v}\right){\mathit{\varphi }}_v\left(\mathit{v}\right){\mathit{\varphi }}_p(p)$ ($C\left(p,\mathit{v}\right)$) is the correlation function).

Finally, we investigate effects of the boundary condition on the local epidemic spread. Figure 14 shows snapshots of $\overline{p}$ at $\tilde{t}=1.0$ in Tests A-6 (upper-left frame) and A-1 (upper-right frame), and at $\tilde{t}=1.536$ in Tests A-6 (lower-left frame) and A-1 (lower-right frame). There are no marked differences between $\overline{p}$ in Test A-6 and $\overline{p}$ in Test A-1 at $\tilde{t}=1.0$ and 1.536. Consequently, effects of the boundary condition on the local epidemic spread are ignorable.

Fig. 14.

Snapshots of $\overline{p}$ at $\tilde{t}=1.0$ in Tests A-6 (upper-left frame) and A-1 (upper-right frame), and at $\tilde{t}=1.536$ in Tests A-6 (lower-left frame) and A-1 (lower-right frame)

From forgoing discussions on numerical results, we obtain some significant conclusions on the local epidemic spread as follows:

• (i)The propagation speed of the boundary between the infected and uninfected domains is dominated by both ${\tilde{\mathit{\tau }}}_m$ and $\tilde{\mathit{\theta }}$, exclusively.
• (ii)The boundary between the infected and uninfected domains spreads rapidly, when ${\tilde{\mathit{\tau }}}_m$ is small. Then, the infection with small ${\tilde{\mathit{\tau }}}_m$ can spread by a few invasions of infected individuals to the uninfected domain, when the interaction between the infected and uninfected individuals is allowable. Consequently, we must pay attention to the local epidemic spread with the small ${\tilde{\mathit{\tau }}}_m$ by suppressing movements of infected individuals not to invade to the uninfected domain. Of course, the local epidemic spread can be accelerated by the transport of the infected individuals to the uninfected domain using the vehicle, when ${\tilde{\mathit{\tau }}}_m$ is small.1
• (iii)The infected individual with the large velocity can invade to the uninfected domain, more frequently than those with the small velocity. The higher velocity of the infected individuals than that of the uninfected individuals at the boundary between the infected and uninfected domains yields the finite diffusion flux, which is expressed by Eq. (14). Then, the infected individual with the large velocity can be a seed of the infection in the uninfected domain, more frequently than those with the small velocity. Consequently, the virus titer p is correlated to $\left|\mathit{v}\right|$ in $f\left(t,p,\mathit{v},\mathit{x}\right)$. The diffusion flux resulted from the difference between such two velocities at the boundary between the infected and uninfected domains enables us to demonstrate the dynamics of the epidemic spread using the FKPP equation in Eq. (18). Actually, the dependency of the propagation speed of the traveling wave front (i.e., boundary between the infected and uninfected domains) on ${\tilde{\mathit{\tau }}}_m$ is described by Eq. (23) with some good accuracies.

Extension of Infection Process

In above discussion, the probability of the infection depends on $p>0$ (or $p_1>0$) and $\tilde{E}$, as shown in Eq. (5). Here, we consider the extension of the infection process of the virus by proposing three models. The first model (model A) is that the infected individuals with the normalized virus titer p are excluded from the calculation domain with the rate $\mathit{\mu }p$. In other words, infected individuals pass away or quarantined with the rate $\mathit{\mu }p$.

In the model A, the infected individuals with $p=1$ lead to death or being quarantined with the maximum probability.

Consequently, Eq. (5) is modified as

$$\begin{array}{cc}& \underset{\_}{\text{Model}\text{A (stochastic}\text{lethal/quarantine (without}\text{interactions)}\text{model)}}\hfill \\ \hfill \\ \hfill & {\mathit{\partial }}_{t}f\left(t,\mathit{v},\mathit{x},p,s\right)+\mathit{v}·{\mathbf{\nabla }}_{\mathit{x}}f\left(t,\mathit{v},\mathit{x},p,s\right)+{\mathrm{\nabla }}_p\mathit{\psi }\left(\mathit{\tau }\right)f\left(t,\mathit{v},\mathit{x},p,s=1\right)\hfill \\ \hfill & +\mathit{\mu }pf\left(t,\mathit{v},\mathit{x},p,s=1\right)=\mathfrak{Q}\left(f,f_1\right),\hfill \end{array}$$ 25

where $\mathit{\mu }\in {\mathbb{R}}_{+}$ corresponds to the force of mortality or quarantine. Provided that $\mathit{\mu }$ is equal to the inverse of the time interval $1/\mathrm{\Delta }t$, the infected individuals with $p=1$ always lead to death or being quarantined. In this paper, we restrict ourselves to the case of $\mathit{\mu }=1/\mathrm{\Delta }t$ to investigate effects of $\mathit{\mu }$ on the local epidemic spread.

As the time interval, four types of the time interval are considered such as $\mathrm{\Delta }\tilde{t}=2\times {10}^{-3}$ (Test D-1), $4\times {10}^{-3}$ (Test D-2), $5\times {10}^{-4}$ (Test D-3) and $1\times {10}^{-4}$ (Test D-4). Other initial conditions in Tests D-1, 2, 3 and 4 are quite sames as those in Test A-1. Figure 15 shows time evolutions of $\tilde{\mathit{\rho }}$ (top six frames), $\tilde{\mathit{\theta }}$ (middle six frames) and $\overline{p}$ (bottom six frames) in Test D-1. The infected individuals in $\mathfrak{U}$ pass away (or are quarantined), as shown in contours of $\tilde{\mathit{\rho }}$ at $\tilde{t}=0.0002$, 0.8 and 1.6. Meanwhile, the number of individuals, who pass away or are quarantined, is large along $\tilde{X}=0$ and $\tilde{Y}=0$, as shown in contours of $\tilde{\mathit{\rho }}$ at $\tilde{t}=2.4$ and 3.2. Finally, the infected individuals have disappeared at $\tilde{t}=8.8$. Therefore, Model A allows the survival of individuals, who are not infected, by arranging the force of mortality or quarantine, namely, $\mathit{\mu }$, as discussed later. $\tilde{\mathit{\theta }}$ fluctuates around 5 at $\tilde{t}=0.002$, whereas there emerges hot spots around $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ at $\tilde{t}=0.8$, 1.6 and 2.4. From contours of $\tilde{\mathit{\rho }}$ and $\tilde{\mathit{\theta }}$, we can confirm that $\tilde{\mathit{\theta }}$ is high in the domain, where $\tilde{\mathit{\rho }}$ is small, at $\tilde{t}=0.8$, 1.6, 2.4 and 3.2. The averaged temperature in the calculation domain, namely, $(1/V){\int }_{\mathfrak{X}}\tilde{\mathit{\theta }}{d}^3\mathit{x}$ (V: volume of the calculation domain), temporally decreases from $\tilde{t}=2.4$ to 3.2. Such a decrease in $\tilde{\mathit{\theta }}$ indicates that individuals with the higher kinetic energy tend to pass away or being quarantined the more frequently, because the infection rate via the binary collision increases in accordance with ${\tilde{E}}^{\mathit{\xi }}$, as shown in Eq. (5). Figure 15 shows that infected domain spreads concentrically at $\tilde{t}=0.8$, as shown in the contour of $\overline{p}$, whereas $\overline{p}$ is large locally at $\tilde{t}=1.6$, 2.4 and 3.2. We confirm that $\overline{p}$ is large in the domain, where $\tilde{\mathit{\rho }}$ is small, owing to the higher probability of the death or quarantine in accordance with the larger p in Model A. The infected individuals have disappeared at $\tilde{t}=8.8$, as shown by $\overline{p}=0$ in $\mathfrak{X}$ at $\tilde{t}=8.8$.

Fig. 15.

Time evolutions of $\tilde{\mathit{\rho }}$ (top six frames), $\tilde{\mathit{\theta }}$ (middle six frames) and $\overline{p}$ (bottom six frames) in Test D-1

Finally, we investigate effects of $\mathit{\mu }$ on the total number of uninfected individuals, namely, ${\tilde{\mathit{\rho }}}_t(\tilde{t}):={\tilde{\mathit{\rho }}}_t{(0)}^{-1}{\int }_{({\mathbb{P}}^{\prime }-\mathbb{P})\times {\mathbb{V}}^3\times \mathfrak{X}}\tilde{f}\left(t,p,\mathit{v},\mathit{x}\right)dp{d}^3\mathit{v}{d}^3\mathit{x}$. Figure 16 shows ${\tilde{\mathit{\rho }}}_t$ versus $\tilde{t}$ in Tests D-1, 2, 3 and 4, which are obtained using Model A.

Fig. 16.

${\tilde{\mathit{\rho }}}_t$ versus $\tilde{t}$ in Tests D-1, 2, 3 and 4, which are obtained using Model A

Figure 16 shows the result:

$$\begin{array}{cc}& \underset{\tilde{t}\to +\infty }{lim}{\tilde{\mathit{\rho }}}_t\left(\tilde{t}\right)=5.7\times {10}^{-2}(\text{Test}\text{D-1}).\hfill \\ \hfill & \underset{\tilde{t}\to +\infty }{lim}{\tilde{\mathit{\rho }}}_t\left(\tilde{t}\right)=2.6\times {10}^{-2}(\text{Test}\text{D-2}).\hfill \\ \hfill & \underset{\tilde{t}\to +\infty }{lim}{\tilde{\mathit{\rho }}}_t\left(\tilde{t}\right)=1.0\times {10}^{-1}(\text{Test}\text{D-3}).\hfill \\ \hfill & \underset{\tilde{t}\to +\infty }{lim}{\tilde{\mathit{\rho }}}_t\left(\tilde{t}\right)=4.5\times {10}^{-1}(\text{Test}\text{D-4}).\hfill \end{array}$$

These results indicate that ${lim}_{\tilde{t}\to +\infty }{\tilde{\mathit{\rho }}}_t\left(\tilde{t}\right)$ increases, as $\mathit{\mu }$ increases. Thus, the more rapid death or quarantine, which exhibits infected individuals to interact with others, yields the more uninfected individuals at $\tilde{t}\to +\infty$. Meanwhile, such a rapid death or quarantine via the increase in $\mathit{\mu }$ shows the rapid decrease of ${\tilde{\mathit{\rho }}}_t$ in the early term ($0\le \tilde{t}<0.6$), as shown in the enlarged view in Fig. 16. Indeed, we can understand that the rapid quarantine of the infected individuals via the early detection of the virus is significant to avoid the local epidemic spread.

In the second model (model B), the velocity of the infected individuals decreases in accordance with p such as

$$\begin{array}{c}\hfill \frac{d{\mathit{v}}_i}{dt}=-{\mathit{\zeta }}_p{p}_i\left(\mathit{\tau }\right){\mathit{v}}_i,i\in J\left\{x\in J|p_x\in \mathbb{P}\cap x\in \mathbb{N}\right\},(p\left(\mathit{\tau }\right)>0,\mathit{\zeta },{\mathit{\zeta }}_p\in {\mathbb{R}}_{+}),\\ \hfill \end{array}$$ 26

where ${\mathit{\zeta }}_p$ is the damping rate.

As a result of Eq. (26), Eq. (5) is modified as

$$\begin{array}{cc}& \underset{\_}{\text{Model}\text{B (hypokinesia}\text{model)}}\hfill \\ \hfill & {\mathit{\partial }}_{t}f\left(t,\mathit{v},\mathit{x},p,s\right)+\mathit{v}·{\mathbf{\nabla }}_{\mathit{x}}f\left(t,\mathit{v},\mathit{x},p,s\right)+{\mathrm{\nabla }}_p\mathit{\psi }\left(\mathit{\tau }\right)f\left(t,\mathit{v},\mathit{x},p,s\right)\hfill \\ \hfill & -p{\mathit{\zeta }}_p{\mathbf{\nabla }}_{\mathit{v}}·\mathit{v}f\left(t,\mathit{v},\mathit{x},p,s=1\right)=\mathfrak{Q}\left(f,f_1\right).\hfill \end{array}$$ 27

The total collisional energy ($\tilde{E}$) decreases owing to the decrease in the velocity of the infected individual in model B. Consequently, the infection rate via the binary collision decreases, as the damping rate of $\mathit{v}$, namely, $p{\mathit{\zeta }}_p$, increases in accordance with the increase in $p\left(\mathit{\tau }\right)$.

To investigate the characteristics of Model B, the local epidemic spread is calculated using ${\mathit{\zeta }}_p=10$, whereas initial conditions are quite same as those in Test A-1. Figure 17 shows time evolutions of $\tilde{\mathit{\rho }}$ (top six frames), $\tilde{\mathit{\theta }}$ (middle six frames) and $\overline{p}$ (bottom six frames), which are obtained using Model B. The infected domain spreads concentrically and the propagation speed of the boundary between the infected and uninfected domains at $0\le \tilde{t}\le 1$, which is obtained using Model B, is similar to that in Test A-1, as shown in contours of $\overline{p}$ in Figs. 5 and 17. The decrease in the kinetic energy of the infected individual yields the low temperature domain around $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ at $\tilde{t}=0.768$. Such a decrease in $\tilde{\mathit{\theta }}$ yields the decrease in the pressure, which attributes to the inflow of individuals, who exist in the high pressure domain, to the low pressure domain. Consequently, $\tilde{\mathit{\rho }}$ temporally increases around $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ at $0.768\le \tilde{t}$. Finally, the concentric contour of $\overline{p}$ at $\tilde{t}=1$ changes to the rhombus contour of $\overline{p}$ at $\tilde{t}=1.92$ owing to the periodic boundary condition. Indeed, Model B fails to delay the propagation of the boundary between the infected and uninfected domains, because the decrease in the kinetic energy of the infected individual yields the low pressure regime, which attracts uninfected individuals from the high pressure regime.

Fig. 17.

Time evolutions of $\tilde{\mathit{\rho }}$ (top six frames), $\tilde{\mathit{\theta }}$ (middle six frames) and $\overline{p}$ (bottom six frames), which are obtained using Model B with ${\mathit{\zeta }}_p=10$

Finally, in the third model, uninfected individuals try to go away from the gravitational center (${\mathit{x}}_G$) of infected individuals in accordance with the repulsive force (${\mathit{F}}_r$) and infected individuals are gathered to their gravitational center in accordance with the attractive force (${\mathit{F}}_a$). Such a situation still allows an interaction between infected and uninfected individuals. Therefore, gathering of the infected individuals is not complete quarantine, which removes existences of infected individuals with some probability from $\mathfrak{X}$ like Model A.

The repulsive and attractive forces are defined as

$$\begin{array}{cc}\hfill {\mathit{F}}_r:=& {\mathit{\kappa }}_r\frac{{\mathit{x}}_i-{\mathit{x}}_G}{\left|{\mathit{x}}_i-{\mathit{x}}_G\right|},\text{in}{\mathbb{X}}^3,{\mathit{\kappa }}_r\in {\mathbb{R}}_{+}\hfill \\ \hfill {\mathit{F}}_a:=& -{\mathit{\kappa }}_a\frac{{\mathit{x}}_i-{\mathit{x}}_G}{\left|{\mathit{x}}_i-{\mathit{x}}_G\right|},\text{in}{\mathbb{X}}^3,{\mathit{\kappa }}_a\in {\mathbb{R}}_{+}\hfill \\ \hfill {\mathit{x}}_G:=& \sum _{i\in J\left\{x\in J|p_x\in \mathbb{P}\cap x\in \mathbb{N}\right\}}{\mathit{x}}_i/\left|\bigcup _{i\in J\left\{x\in J|p_x\in \mathbb{P}\cap x\in \mathbb{N}\right\}}i\right|,\hfill \end{array}$$ 28

From Eq. (28), we obtain

$$\begin{array}{cc}\hfill \frac{d{\mathit{v}}_i}{dt}=& {\mathit{F}}_r,i\in K\left\{x\in K|p_x\in (\mathbb{P}\cap {\mathbb{P}}^{\prime })\cap x\in \mathbb{N}\right\}\hfill \\ \hfill \frac{d{\mathit{v}}_i}{dt}=& {\mathit{F}}_a,i\in J\left\{x\in J|p_x\in \mathbb{P}\cap x\in \mathbb{N}\right\}\hfill \end{array}$$ 29

As a result of Eq. (29), Eq. (5) is modified as

$$\begin{array}{cc}& \underset{\_}{\text{Model}\text{C (quarantine}\text{with}\text{interactions}\text{and}\text{refugee}\text{model)}}\hfill \\ \hfill & {\mathit{\partial }}_{t}f\left(t,\mathit{v},\mathit{x},p,s\right)+\mathit{v}·{\mathbf{\nabla }}_{\mathit{x}}f\left(t,\mathit{v},\mathit{x},p,s\right)+{\mathrm{\nabla }}_p\mathit{\psi }\left(\mathit{\tau }\right)f\left(t,\mathit{v},\mathit{x},p,s\right)\hfill \\ \hfill & +{\mathbf{\nabla }}_{\mathit{v}}·{\mathit{F}}_{r}f\left(t,\mathit{v},\mathit{x},p,s=0\right)+{\mathbf{\nabla }}_{\mathit{v}}·{\mathit{F}}_{a}f\left(t,\mathit{v},\mathit{x},p,s=1\right)\hfill \\ \hfill & =\mathfrak{Q}\left(f,f_1\right).\hfill \end{array}$$ 30

To investigate the characteristics of Model C, numerically, ${\mathit{\kappa }}_r=10$ and ${\mathit{\kappa }}_a=100$ are set. Other initial conditions are same as those in Test A-1. Figure 18 shows time evolutions of $\tilde{\mathit{\rho }}$ (top six frames), $\tilde{\mathit{\theta }}$ (middle six frames) and $\overline{p}$ (bottom six frames), which are obtained using Model C with ${\mathit{\kappa }}_r=10$ and ${\mathit{\kappa }}_a=100$. Contours of $\overline{p}$ in Fig. 18 indicates that the propagation speed of the boundary between the infected and uninfected domains, which is obtained using the Model C with ${\mathit{\kappa }}_r=10$ and ${\mathit{\kappa }}_r=100$, is lower than that in Test A-1 owing to refugees of uninfected individuals and swarming of infected individuals around $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$. The infected individuals try to go away from infected individuals at $\tilde{t}=1.0$, as confirmed by the vector fields of $\left(\tilde{u},\tilde{v}\right)$ in Fig. 19. Additionally, velocities of individuals around the boundary between the infected and uninfected domains is large at $\tilde{t}=2.16$ and 3.98, whereas individuals cluster toward $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ inside the boundary between the infected and uninfected domains. As a result, $\tilde{\mathit{\rho }}$ around $\left(\tilde{X},\tilde{Y}\right)=(0.5,0.5)$ temporally increases, whereas $\tilde{\mathit{\theta }}$ inside such a clustering domain temporally increases at $0.24\le \tilde{t}$, as shown in Fig. 18. Finally, all the individuals in $\mathfrak{X}$ are infected in Model C, although the propagation speed of the boundary between the infected and uninfected domains in Model C is lower than that in Test A-1.

Fig. 18.

Time evolutions of $\tilde{\mathit{\rho }}$ (top six frames), $\tilde{\mathit{\theta }}$ (middle six frames) and $\overline{p}$ (bottom six frames), which are obtained using Model C with ${\mathit{\kappa }}_r=10$ and ${\mathit{\kappa }}_a=100$

Fig. 19.

Vector fields $(\tilde{u},\tilde{v})$ at $\tilde{t}=1.0$, 2.16 and 3.98, which are obtained using Model C with ${\mathit{\kappa }}_r=10$ and ${\mathit{\kappa }}_a=100$

Concluding Remarks

The stochastic Boltzmann type equation was formulated to demonstrate the local epidemic spread in the local domain at the initial stage by focusing on the time evolution of the virus titer inside the infected individual. The propagation speed of the boundary between the infected and uninfected domains strongly depends on the characteristic time of the virus titer, namely, ${\mathit{\tau }}_m$, whereas the individual with the higher velocity becomes a seed of the local epidemic spread at the boundary between the infected and uninfected domains, the more frequently, as ${\mathit{\tau }}_m$ decreases. The analytical result of the propagation speed of the boundary between the infected and uninfected domains is obtained using the FKPP equation. The dependency of the propagation speed on ${\mathit{\tau }}_m$, which is analytically estimated using the FKPP equation, is numerically confirmed with some good accuracies. Additionally, the absolute value of the fluctuating flow velocity of infected individuals, namely, $〈\mathit{\delta }|{\mathit{u}}_{p_0}|〉$, at the boundary between the infected and uninfected domains increase in accordance with the increase in the initial temperature. The increase in $〈\mathit{\delta }|{\mathit{u}}_{p_0}|〉$ yields the increase in the propagation speed of the boundary between the infected and uninfected domains. Such an increase in the propagation speed of the boundary between the infected and uninfected domains owing to the increase in the initial temperature can be explained by increases in D and $K_{01}$ ($0<\mathit{\xi }$) in the framework of the FKPP equation, as shown in Eq. (23). The ratio of the number of individuals, who are infected at other lattices (domains), to the total number of infected individuals at the specific lattice (domain) decreases, as ${\mathit{\tau }}_m$ decreases, because the local epidemic spread occurs inside the lattice rapidly via one or a few of invasions of the infected individuals from neighboring lattices, before some infected individuals reach to neighboring lattice, because the virus titer increases rapidly inside the cell owing to small ${\mathit{\tau }}_m$. Meanwhile, the change of the velocity fluctuations via the change of the number of sample particles does not affect the propagation speed of the boundary between the infected and uninfected domains. The dependency of the collision frequency on the total kinetic energy of two interacting individuals indicates that the stronger dependency of the collision frequency on the total kinetic energy yields the faster propagation of the boundary between the infected and uninfected domains owing to the increase in $K_{01}$ ($\mathit{\xi }>0$). Finally, three types of the human behavior in accordance with the local epidemic spread was considered. In Model A, the more rapid death or quarantine of infected individuals, which is done not to interact with other uninfected individuals, yields the more uninfected individuals under $t\to +\infty$. In model B, the hypokinesia of infected individuals yields the concentration of individuals around the center of the infected domain. Consequently, Model B fails to delay the local epidemic spread owing to the increase in the collision frequency between the infected and uninfected individuals around the center of the infected domain. In Model C, the quarantine of the infected individuals inside the specific area was expressed with the attractive force, whereas the refugee of the uninfected individuals from the infected individuals was expressed with the repulsive force. Indeed, Model C succeeded the delay of the local epidemic spread, whereas the allowance of interactions between the infected and uninfected individuals leads to the result that all the individuals in the calculation domain are infected. Various types of the combination of Models A, B and C together with the realistic dynamics of pedestrians in “Appendix” are interesting in our future study together with the comparison of numerical results, which are obtained using our kinetic model, with real datum of the local epidemic spread.

Appendix: Local Epidemic Spread with Intended Velocities of Pedestrians

In this paper, we have considered the dynamics of pedestrians (individuals), who never have their intended velocities [15]. Additionally, we have assumed the isotropic scattering after the binary collision, which might be rough model to describe the characteristics of the dynamics of the pedestrians [15]. For example, the number of pedestrian, who go back to the direction, which has been walked, after the binary collision is presumably less than that of pedestrian, who go straight toward the intended direction after the binary collision. Therefore, we must set the weight on the small deflection angle in order to emphasize the grazing collision, which does not change intended velocities of colliding two pedestrian. Such stress on the small deflection angle is attained by changing a weighting parameter in the deflection angle in the Variable Soft Sphere (VSS) model [31]. Additionally, the kinetic equation beyond the stochastic Boltzmann equation (i.e., Enskog equation) must be considered to demonstrate packing effects via the high volume fraction in ${\mathbb{X}}^3$ occupied by pedestrian [32]. Finally, the sophistication of the collisional process in the local epidemic spread, which considers the characteristics of pedestrian, will be set as our future study.

Here, we mention to the effect of the intended velocities, briefly. The velocity of the individual with the index-i relaxes to intended velocities such as

$$\begin{array}{c}\hfill \frac{d{\mathit{v}}_i(t)}{dt}=\mathit{\nu }\left({\mathit{v}}_i^0-{\mathit{v}}_i(t)\right),\end{array}$$ 31

where ${\mathit{v}}_i^0$ is the intended velocities and $\mathit{\nu }$ is the relaxation rate.

From Eq. (31), we can formulate the stochastic Boltzmann equation with the relaxation to intended velocities such as

$$\begin{array}{cc}& {\mathit{\partial }}_{t}f\left(t,\mathit{v},\mathit{x},p,s\right)+\mathit{v}·{\mathbf{\nabla }}_{\mathit{x}}f\left(t,\mathit{v},\mathit{x},p,s\right)+{\mathrm{\nabla }}_p\mathit{\psi }\left(\mathit{\tau }\right)f\left(t,\mathit{v},\mathit{x},p,s=1\right)\hfill \\ \hfill & =\mathfrak{Q}\left(f,f_1\right)+\mathit{\nu }\left[{\mathit{\psi }}_0\left(t,\mathit{v},\mathit{x},p,s\right)-f\left(t,\mathit{v},\mathit{x},p,s\right)\right],\hfill \end{array}$$ 32

where ${\mathit{\psi }}_0\left(t,\mathit{v},\mathit{x},p,s\right)$ is defined as

$$\begin{array}{c}\hfill {\mathit{\psi }}_0\left(t,\mathit{v},\mathit{x},p,s\right):=\frac{1}{V_c}\sum _{i=1}^{N_c}{\mathit{\delta }}^3\left(\mathit{x}-{\mathit{x}}_i(t)\right){\mathit{\delta }}^3\left(\mathit{v}-{\mathit{v}}_i^0\right)\mathit{\delta }\left(p-p_i\left(\mathit{\tau }\right)\right).\end{array}$$ 33

The relaxation term in Eq. (32) is a form of the BGK model, whereas Eq. (32) indicates that the energy-momentum conservation violates. The author recommends readers to access to another type of the Boltzmann type equation proposed by Helbing [33], which demonstrates the collisional dynamics between two pedestrians by setting the intended velocity as a dependent variable in the distribution function.

In our numerical tests in Sects. 2.2 and 3, the initial distribution function is obtained using the Maxwell-Boltzmann distribution. Similarly, we consider the numerical condition at $\tilde{t}=0$, which is quite same as that in Test A-1. Additionally, we assume that the intended velocities of pedestrian are equal to those at $\tilde{t}=0$. Figure 20 shows $\overline{p}$ at $\tilde{t}=1.34$, which are obtained using Eq. (32), when $\tilde{\mathit{\nu }}=0.25$ (left frame), 0.5 (middle frame) and 1 (right frame), in which $\tilde{\mathit{\nu }}:=\mathit{\nu }{\tilde{t}}_{\infty }$. Figure 20 shows that the propagation speed of the boundary between the infected and uninfected domains decreases, as $\tilde{\mathit{\nu }}$ increases. As a result, we find that the intended velocity is a key parameter to determine the propagation of the boundary between the infected and uninfected domains.

Fig. 20.

$\overline{p}$ at $\tilde{t}=1.34$, which are obtained using Eq. (32), when $\mathit{\nu }=0.25$ (left frame), 0.5 (middle frame) and $\mathit{\nu }=1$ (right frame)

Next, we refer to the limiting case, in which $\tilde{\mathit{\nu }}$ is markedly large and the intended velocities of pedestrian are limited to two values, namely, $\left(\pm {\tilde{v}}_{\ell }^0,0,0\right)$. The number of pedestrians with the intended velocity $\left({\tilde{v}}_{\ell }^0,0,0\right)$ is same as that of pedestrians with $\left(-{\tilde{v}}_{\ell }^0,0,0\right)$. Of course, the intended velocity of each of pedestrians is fixed to its constant value, namely, $\pm {\tilde{v}}_{\ell }^0$, during the calculation.

Figure 21 shows time evolutions of $\overline{p}$, when ${\tilde{v}}_{\ell }^0=1$ and $\tilde{\mathit{\nu }}=100$ in Eq. (32), and initial numerical condition is quite same as that in Test A-1.

Fig. 21.

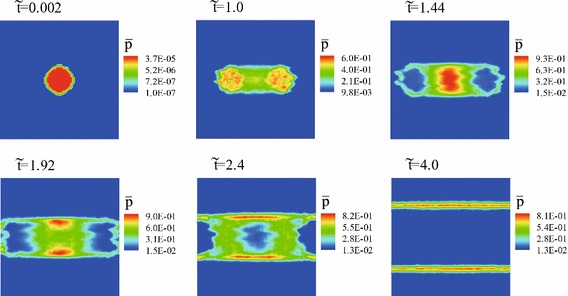
Time evolutions of $\overline{p}$, when ${\tilde{v}}_{\ell }^0=1$ and $\tilde{\mathit{\nu }}=100$ in Eq. (32), and initial condition is quite same as that in Test A-1

Three characteristics domains, $S_1$, $S_2$ and $S_3$, which are defined as

$$\begin{array}{cc}& \left\{\left(\tilde{x},\tilde{y}\right)\in S_1|{\left(\tilde{x}-0.3\right)}^2+{\left(\tilde{y}-0.5\right)}^2<{(0.1)}^2\right\},\hfill \\ \hfill & \left\{\left(\tilde{x},\tilde{y}\right)\in S_2|{\left(\tilde{x}-0.7\right)}^2+{\left(\tilde{y}-0.5\right)}^2<{(0.1)}^2\right\},\hfill \\ \hfill & \left\{\left(\tilde{x},\tilde{y}\right)\in S_3|\left(\tilde{x},\tilde{y}\right)\in T_1-\left(T_1\cap S_1\right)-\left(T_1\cap S_2\right)\right\},\hfill \\ \hfill & \text{where}\left\{\left(\tilde{x},\tilde{y}\right)\in T_1|\tilde{x}\in \left[0.3,0.7\right],\tilde{y}\in \left[0.4,0.6\right]\right\},\hfill \end{array}$$

are obtained at $\tilde{t}=1$. $\overline{p}$ in $S_1$ and $S_2$ is larger than that in $S_3$, whereas $\overline{p}=0$ in $\mathfrak{X}-S_1-S_2-S_3$. Consequently, the propagation of the boundary between the infected and uninfected domains in the $\tilde{Y}$-direction is suppressed owing to the intended velocities of pedestrians, namely, $\left(\pm 1,0\right)$, as confirmed by comparing of the contour of $\overline{p}$ at $\tilde{t}=1$ in Fig. 5 with that in Fig. 21.

Subsequently, four characteristic infected domains, $S_1^{\prime }$, $S_2^{\prime }$, $S_4$ and $S_5$, which are defined as

$$\begin{array}{cc}& \left\{\left(\tilde{x},\tilde{y}\right)\in S_1^{\prime }|{\left(\tilde{x}-0.2\right)}^2+{\left(\tilde{y}-0.5\right)}^2<{(0.1)}^2\right\},\hfill \\ \hfill & \left\{\left(\tilde{x},\tilde{y}\right)\in S_2^{\prime }|{\left(\tilde{x}-0.8\right)}^2+{\left(\tilde{y}-0.5\right)}^2<{(0.1)}^2\right\},\hfill \\ \hfill & \left\{\left(\tilde{x},\tilde{y}\right)\in S_4|\tilde{x}\in \left[0.4,0.6\right],\tilde{y}\in \left[0.4,0.6\right]\right\},\hfill \\ \hfill & \left\{\left(x,y\right)\in S_5|\left(\tilde{x},\tilde{y}\right)\in T_2-\left(T_2\cap S_1^{\prime }\right)-\left(T_2\cap S_2^{\prime }\right)-S_4\right\},\hfill \\ \hfill & \text{where}\left\{\left(\tilde{x},\tilde{y}\right)\in T_2|\tilde{x}\in \left[0.2,0.8\right],\tilde{y}\in \left[0.4,0.6\right]\right\},\hfill \end{array}$$

are obtained at $\tilde{t}=1.44$.

$S_1^{\prime }$ and $S_2^{\prime }$ are obtained as a result of time evolutions of $S_1$ and $S_2$ at $\tilde{t}=1$, respectively. Consequently, most of pedestrians in $S_1^{\prime }$ and $S_2^{\prime }$ recover from the infection, as confirmed by $\overline{p}\ll 1$ in $S_1^{\prime }$ and $S_2^{\prime }$. Meanwhile, $\overline{p}$ in $S_4$ approximates to its maximum value, namely, unity, at $\tilde{t}=1.44$.

Subsequently, two characteristic infected domains, $S_4^{\prime }$ and $S_4^{″}$, which are defined as

$$\begin{array}{cc}& \left\{\left(\tilde{x},\tilde{y}\right)\in S_4^{\prime }|\tilde{x}\in \left[0.4,0.6\right],\tilde{y}\in \left[0.6,0.65\right]\right\},\hfill \\ \hfill & \left\{\left(\tilde{x},\tilde{y}\right)\in S_4^{″}|\tilde{x}\in [0.4,0.6],\tilde{y}\in [0.35,0.4]\right\},\hfill \end{array}$$

are obtained at $\tilde{t}=1.92$.

$S_4^{\prime }$ and $S_4^{″}$ are obtained as a result of time evolutions of $S_4$ at $\tilde{t}=1.44$, respectively. In short, infected pedestrians (with $p>0$) in $S_4$ at $\tilde{t}=1.44$ induce infected pedestrians, who walk in $S_4^{\prime }$ or $S_4^{″}$ at $\tilde{t}=1.92$.

Subsequently, two characteristic infected domains, $S_4^{″\prime }$ and $S_4^{″″}$, which are defined as

$$\begin{array}{cc}& \left\{\left(\tilde{x},\tilde{y}\right)\in S_4^{″\prime }|\tilde{x}\in \left[0.3,0.7\right],\tilde{y}\in \left[0.66,0.67\right]\right\},\hfill \\ \hfill & \left\{\left(\tilde{x},\tilde{y}\right)\in S_4^{″″}|\tilde{x}\in \left[0.3,0.7\right],\tilde{y}\in \left[0.33,0.34\right]\right\},\hfill \end{array}$$

are obtained at $\tilde{t}=2.4$.

$S_4^{″\prime }$ and $S_4^{″″}$ are obtained as a result of time evolutions of $S_4^{\prime }$ and $S_4^{″}$ at $\tilde{t}=1.92$, respectively. In short, infected pedestrians (with $p>0$) in $S_4^{\prime }$ ($S_4^{″}$) at $\tilde{t}=1.92$ induce infected pedestrians, who walk in $S_4^{″\prime }$ ($S_4^{″″}$) at $\tilde{t}=2.4$. Of course, the propagation velocity of the infected domain in $\tilde{X}$-direction is overwhelming over that in $\tilde{Y}$-direction owing to the intended velocities of pedestrians, namely, $(\pm 1,0,0)$ and large $\mathit{\nu }$.

Finally, two characteristic infected domains, $S_4^{″″\prime }$ and $S_4^{″″″}$, which are defined as

$$\begin{array}{cc}& \left\{\left(\tilde{x},\tilde{y}\right)\in S_4^{″″\prime }|\tilde{x}\in \left[0,1\right],\tilde{y}\in \left[0.73,0.78\right]\right\},\hfill \\ \hfill & \left\{\left(\tilde{x},\tilde{y}\right)\in S_4^{″″″}|\tilde{x}\in \left[0,1\right],\tilde{y}\in \left[0.22,0.27\right]\right\},\hfill \end{array}$$

are obtained at $\tilde{t}=4.0$.

$S_4^{″″\prime }$ and $S_4^{″″″}$ are obtained as a result of time evolutions of $S_4^{″\prime }$ and $S_4^{″″}$ at $\tilde{t}=2.4$, respectively. In short, infected pedestrians (with $p>0$) in $S_4^{″\prime }$ ($S_4^{″″}$) at $\tilde{t}=2.4$ induce infected pedestrians, who walk in $S_4^{″″\prime }$ ($S_4^{″″″}$) at $\tilde{t}=4.0$. two characteristic infected domains $S_4^{″″\prime }$ and $S_4^{″″″}$ propagate to the positive and negative $\tilde{Y}$-directions, respectively, in accordance with the velocity fluctuations ($\mathit{\delta }{\mathit{u}}_{p_0}$) in $\tilde{Y}$-direction owing to the isotropic scatterings in binary collisions.

At last, we refer to the local epidemic spread, when intended velocities are ${\tilde{\mathit{v}}}_i^0=\left(\pm {\tilde{v}}_{\ell }^0=\pm 5,0,0\right)$. The number of pedestrians with the intended velocity $\left(v_{\ell }^0,0,0\right)$ is same as that of pedestrians with $\left(-v_{\ell }^0,0,0\right)$. The initial condition is quite same as that in Test A-1. Figure 22 shows contours of $\overline{p}$ (upper-left frame), $\tilde{\mathit{\rho }}$ (upper-middle frame) and $\tilde{\mathit{\theta }}$ (upper-right frame), when $\tilde{t}=0.168$, and contours of $\overline{p}$ (lower-left frame), $\tilde{\mathit{\rho }}$ (lower-middle frame) and $\tilde{\mathit{\theta }}$ (lower-right frame), when $\tilde{t}=0.96$. Certainly, the propagation speed of two characteristic infected domains, which correspond to $S_1$ and $S_2$ in the case of ${\tilde{v}}_{\ell }^0=1$, increases in accordance with the increase in ${\tilde{v}}_{\ell }^0$, as shown in upper-left frame of Fig. 22. Surely, two characteristic infected domains, which correspond to $S_4^{″″\prime }$ and $S_4^{″″″}$ in the case of ${\tilde{v}}_{\ell }^0=1$, are obtained at $\tilde{t}=0.96$. Such an increase in the propagation speed in $\tilde{Y}$-direction in accordance with the increase in ${\tilde{v}}_{\ell }^0$ is explained by the fact that the increase in ${\tilde{v}}_{\ell }^0$ yields the increase in the local temperature. For example, $\tilde{\mathit{\theta }}\in [0.055,0.095]$ is obtained, when ${\tilde{v}}_{\ell }^0=1$ and $\tilde{t}=4.0$, whereas $\tilde{\mathit{\theta }}\in [0.83,3.43]$ is obtained, when ${\tilde{v}}_{\ell }^0=5$ and $\tilde{t}=0.96$. The increase in the propagation speed of the boundary between the infected and uninfected domains in accordance with the increase in $\tilde{\mathit{\theta }}$ is surely confirmed in Fig. 13. Finally, we confirm that small patterns in contours of $\tilde{\mathit{\rho }}$ and $\tilde{\mathit{\theta }}$ appear at $\tilde{t}=0.168$, whereas such small patterns in contours of $\tilde{\mathit{\rho }}$ and $\tilde{\mathit{\theta }}$ change to large patterns at $\tilde{t}=0.96$. The large patterns in contours of $\tilde{\mathit{\rho }}$ at $\tilde{t}=0.96$ are self-organized in accordance with the local dense and sparse populations of pedestrians. The large spatial-patterns of $\tilde{\mathit{\rho }}$ and $\tilde{\mathit{\theta }}$ at $\tilde{t}=0.96$ change, temporally, as $\tilde{t}$ increases from $\tilde{t}=0.96$, whereas scales of the large patterns at $\tilde{t}=0.96$ are not enlarged, as $\tilde{t}$ increases from $\tilde{t}=0.96$. We, however, find that pattern formations in contours of $\tilde{\mathit{\rho }}$ and $\tilde{\mathit{\theta }}$ never yield patterns in contours of $\overline{p}$ at $\tilde{t}=0.96$.

Fig. 22.

Contours of $\overline{p}$ (upper-left frame), $\tilde{\mathit{\rho }}$ (upper-middle frame) and $\tilde{\mathit{\theta }}$ (upper-right frame), when $\tilde{t}=0.168$, and contours of $\overline{p}$ (lower-left frame), $\tilde{\mathit{\rho }}$ (lower-middle frame) and $\tilde{\mathit{\theta }}$ (lower-right frame), when $\tilde{t}=0.96$