Visibility of Quantization Errors in Reversible JPEG2000

Abstract

Image compression systems that exploit the properties of the human visual system have been studied extensively over the past few decades. For the JPEG2000 image compression standard, all previous methods that aim to optimize perceptual quality have considered the irreversible pipeline of the standard. In this work, we propose an approach for the reversible pipeline of the JPEG2000 standard. We introduce a new methodology to measure visibility of quantization errors when reversible color and wavelet transforms are employed. Incorporation of the visibility thresholds using this methodology into a JPEG2000 encoder enables creation of scalable codestreams that can provide both near-threshold and numerically lossless representations, which is desirable in applications where restoration of original image samples is required. Most importantly, this is the first work that quantifies the bitrate penalty incurred by the reversible transforms in near-threshold image compression compared to the irreversible transforms.

The highlights of this manuscript are as follows:

• A method to measure visibility of quantization error in reversible JPEG2000 is proposed.

• Near-threshold and lossless compression are enabled in a single scalable codestream.

• The impact of the nonlinearities in the reversible pipeline of JPEG2000 on near-threshold compression performance is quantified.

1. Introduction

Over the past several decades, there has been significant growth in digital media, leading to rapid development of methods for compact data representation, storage and transmission. Digital image compression is an important component of this effort, resulting in significant research interest over the past 40 years. In lossy image compression, significant bit-rate reductions are achieved by allowing a controlled level of error to be introduced into image data through quantization.

The growth of digital imaging has also resulted in the development of standardized image compression methods which enhance the compability and inter-operability of image communication systems. One of these international standards is JPEG2000 [1, 2]. Compared to earlier image compression standards, JPEG2000 provides better rate-distortion trade-off, especially at low bit-rates. Most importantly, it enables scalable compression, allowing codestreams which are progressive in quality, resolution, spatial location or component. Although some more recent image coding standards (e.g. HEVC intra [3]) achieve better rate-distortion performance than JPEG2000 at certain bit-rates, they do not posses the flexible scalability features offered by JPEG2000.

One of the goals of image compression research is to minimize the loss of perceptual quality as a result of quantization. Intensive research has been devoted to exploiting the properties of the Human Visual System (HVS) in image compression systems. In [4], an image compression method was proposed by Chou and Li, which uses a perceptually tuned subband image coding scheme to allow near-threshold image quality. More recently, several works have studied the perceptual properties of quantization error in the wavelet domain as well as incorporation of these models into JPEG2000 to achieve perceptually tuned compression: In [5], a model for detection of uniform quantization error in the wavelet domain was proposed by Watson et al. This model was later incorporated into JPEG2000 by Liu et al for quantization error control [6]. Zeng et al. provided a review of the visual optimization tools present within the JPEG2000 architecture at the time of the standardization in [7]. In [8], Chandler and Hemami performed psychovisual experiments with actual wavelet coefficients and uniform quantization to develop models, and incorporated these models into JPEG2000 to control quantization error during encoding. Richter and Kim [9] proposed a JPEG2000 encoder which was optimized using the multi-scale structural similarity (MS-SSIM) metric [10]. Tan et al. used a color perceptual distortion metric within a JPEG2000 compliant coder in [11]. In 2013, Han et al. [12] established quantization error models for the irreversible transform pipeline and deadzone quantization of JPEG2000. In that work, psychovisual experiments were conducted to measure visibility thresholds (VTs), defined as the maximum quantization stepsizes leading to distortions with a certain probability of detection. These VTs were then employed to control the quantization error, in order to achieve near-threshold JPEG2000 compression based on irreversible transforms. However, the work of Han et al. can only generate lossy codestreams, as the original image data can not be restored after the irreversible transforms. To address this shortcoming of the irreversible pipeline, the JPEG2000 standard offers an alternative reversible pipeline which uses reversible transforms. The reversible pipeline enables scalable compression all the way up to numerically lossless compression.

The contributions of this work are as follows: First, we introduce new methodology to measure the visibility of quantization error in reversible (i.e. integer-valued) wavelet and color transforms. Earlier works that modeled visibility of quantization error in wavelet transforms have all concentrated on irreversible transforms. Thus, these earlier methodologies are not immediately applicable to reversible transforms. Using this new methodology, we conduct psychovisual experiments to measure VTs which are then used to build a JPEG2000 encoder capable of keeping compression-induced distortion below the VT, adaptively for each image. Importantly, the proposed approach enables scalable codestreams that can yield near-threshold and numerically lossless representations of an image from a single codestream, which is desirable in applications where restoration of original image samples is required. In addition, the proposed encoder produces a codestream that can be decompressed using any JPEG2000 Part 1 compliant decoder. Perhaps most interestingly, the psychovisual experiments used to measure VTs for both the reversible and irreversible pipelines reveal that the nonlinearities which exist in the reversible pipeline have a profound impact on near-threshold compression performance. To the best of our knowledge, this is the first work that quantifies the loss (in bitrate) incurred by reversible transforms in near-threshold image compression.

The remainder of this paper is organized as follows: In Section 2, an introduction to the JPEG2000 Part 1 pipeline is provided. In Section 3, models of wavelet coefficients and quantization errors from the JPEG2000 reversible 5/3 discrete wavelet transform are established. Experiments used to measure the VTs, the resulting VTs, and the encoding procedure with the VTs are discussed in Section 4. Section 5 provides a comparison of the compression performance of the proposed method and the earlier irreversible scheme by Han et al. [12]. Finally, conclusions are provided in Section 6.

2. Background: JPEG2000 Encoding

The JPEG2000 Part 1 encoding procedure can be described as shown in Figure 1, where the deadzone quantization and the rate allocation steps are the only two sources of the compression distortion. Part 1 of the standard defines both a reversible encoding pipeline and an irreversible encoding pipeline. While the irreversible encoding pipeline is used in lossy compression, the reversible encoding pipeline enables both lossy as well as numerically lossless compression.

Figure 1:

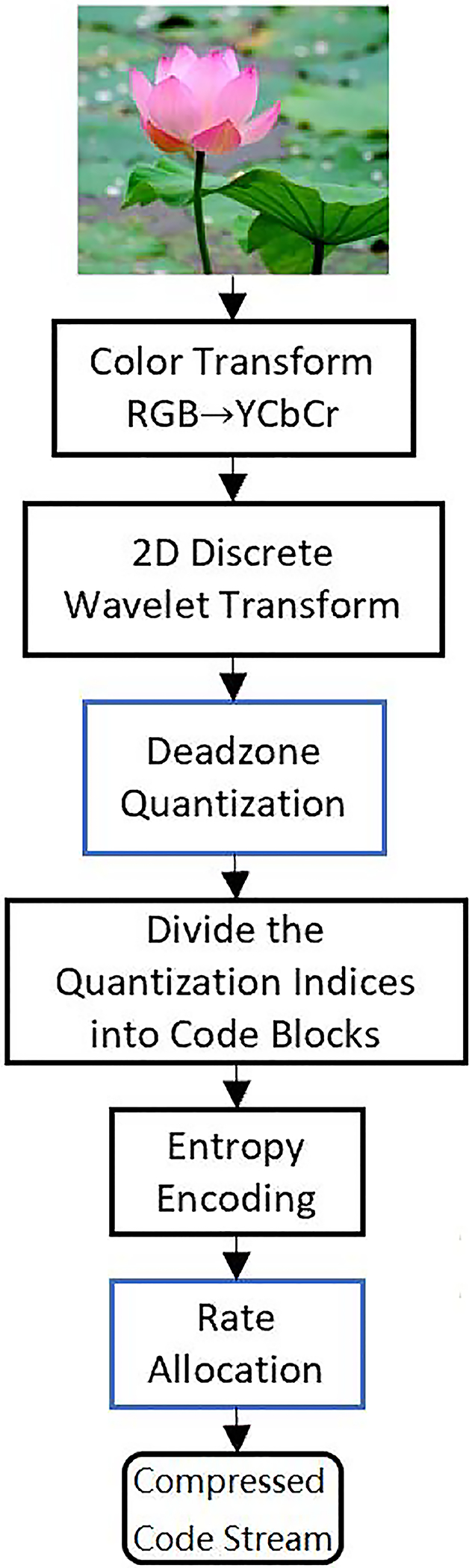
JPEG2000 Part I Encoding Procedure.

2.1. Multicomponent Transform (MCT)

As described in Figure 1, the first step in the encoding procedure is the multicomponent transform (MCT) (or color transform) which aims to decorrelate the RGB color channels by converting them to a luminance/chrominance representation. In the reversible pipeline, the reversible color transform (RCT) transforms the RGB color channels to a modified Y C_bC_r representation using the transform

$$\begin{gathered} \overline{Y}=\lfloor \frac{R+2G+B}{4}\rfloor \\ {\overline{C}}_{\text{b}}=B-G \\ {\overline{C}}_{\text{r}}=R-G \end{gathered}$$ (1)

where ⌊·⌋ denotes the floor operation. The RGB components can be recovered from the modified Y C_bC_r space by:

$$\begin{gathered} G=\overline{Y}-\lfloor \frac{{\overline{C}}_{\text{b}}+{\overline{C}}_{\text{r}}}{4}\rfloor \\ R={\overline{C}}_{\text{r}}+G \\ B={\overline{C}}_{\text{b}}+G. \end{gathered}$$ (2)

Because the components in both the RGB and the modified Y C_bC_r spaces are integers, which can be saved losslessly in computer systems, the RCT transform is reversible. On the other hand, the irreversible pipeline uses the well-known Y C_bC_r transform, referred to as the irreversible color transform (ICT) in JPEG2000. In contrast to the transforms used in the reversible pipeline, the values resulting from the ICT are floating point numbers, which due to finite computer precision, will result in inevitable loss of information when stored.

2.2. Discrete Wavelet Transform (DWT)

Following the color transform, each resulting component undergoes a 2-D discrete wavelet transform (DWT). Similar to the color transform, reversible and irreversible 2-D DWTs are defined for the reversible and irreversible encoding pipelines, respectively. The DWT used in the reversible pipeline is the reversible 5/3 DWT [13] whereas the irreversible 9/7 DWT [14] is used in the irreversible pipeline.

The 2-D DWTs implemented in JPEG2000 are separable transforms. The 1-D single-level reversible 5/3 DWT, which transforms pixels to coefficients in the high and low subbands, can be respectively expressed as:

$$\begin{gathered} y_h[n]=x[2n+1]-\lfloor \frac{x[2n]+x[2n+2]}{2}+\frac{1}{2}\rfloor \\ {y}_l[n]=x[2n]+\lfloor \frac{y_h[n]+y_h[n-1]}{4}+\frac{1}{2}\rfloor \end{gathered}$$ (3)

where x[n] denotes a sample in the pixel domain. y_h[n] and y_l[n] denote the resulting DWT coefficients in the high and low-pass subbands, respectively. The inverse transform is given as:

$$\begin{gathered} x[2n]=y_l[n]-\lfloor \frac{y_h[n]+y_h[n-1]}{4}+\frac{1}{2}\rfloor \\ x[2n+1]=y_h[n]+\lfloor \frac{x[2n]+x[2n+2]}{2}+\frac{1}{2}\rfloor . \end{gathered}$$ (4)

Similar to the RCT, the reversible 5/3 DWT defined by the Equations (3) and (4) is a reversible transform due to the rounding steps within the equations, which yield integer-valued coefficients. In contrast, the irreversible 9/7 DWT requires the use of floating point arithmetic.

It is important to emphasize that the RCT, reversible 5/3 DWT and their inverse counterparts in the reversible decoding pipeline are non-linear because of the floor operations, which is different from the transforms in the irreversible encoding and decoding pipelines.

2.3. Quantization

After the 2-D DWT, the resulting wavelet coefficients are quantized using a scalar deadzone quantizer [15]. Deadzone quantization is performed as follows:

$$q=Q(y)=\mathit{\text{sign}}(y)\cdot \lfloor \frac{\left|y\right|}{\Delta }\rfloor$$ (5)

where ⌊·⌋ denotes the floor operation. When the reversible pipeline is used in JPEG2000, a quantization step size of Δ = 1 must be used. Since the wavelet coefficients in this case are integers, this step size corresponds to no quantization, enabling perfect recovery of the wavelet coefficients at the decoder and leading to numerically lossless recovery of the image. It is important to emphasize that restricting the step size to Δ = 1 does not preclude lossy compression. Despite Δ = 1 used in the reversible pipeline, the encoder may discard bitplanes, resulting in lossy compression. In order words, lossy compression can be achieved by representing the integer quantization indices by a fewer number of bits. Removing the least-significant L bits in the integer representation corresponds to using a quantization step size of 2^L.

2.4. Rate-Allocation and Entropy Coding

The quantization indices are divided into rectangular codeblocks and each codeblock is compressed independently using a bitplane encoder. The bitplane coder compresses each bitplane starting from the most significant bitplane to the least significant bitplane. In the reversible pipeline, if the compressed data corresponding to all bitplanes of a codeblock are included in the final codestream, the codeblock can be recovered losslessly. However, if the compressed data corresponding to the L least significant bitplanes are excluded, an effective quantization with quantization step size 2^L has been applied to the codeblock leading to lossy compression. For lossy compression, the data rates alloted to each codeblock are determined through an optimization procedure which considers the distortion (conventionally, mean-squared-error (MSE)) as well as the bitrates corresponding to the compressed bitplane data from each codeblock. The final step is the formation of the codestream by assembling compressed data from the codeblocks into the final codestream.

3. Models of Wavelet coefficients and Quantization Errors for JPEG2000 Reversible 5/3 Discrete Wavelet Transform

In this paper, we focus on the reversible encoding pipeline of JPEG2000, and develop a rate allocation method based on HVS perception. In this scenario, the resulting wavelet coefficients, the effective quantization step sizes, and the quantization errors are all integers.

It is common in the literature to model the distribution of irreversible wavelet coefiicients in the LL subband using a Gaussian distribution [16]. For the reversible transform, we employ a discretized Gaussian distribution:

$$P(y)={\int }_{y-\frac{1}{2}}^{y+\frac{1}{2}}\frac{1}{\sqrt{2\pi {\sigma }^2}}\text{\hspace{0.17em}exp}\left[-\frac{x^2}{2{\sigma }^2}\right]dx$$ (6)

where y denotes an integer wavelet coefficient and σ² denotes the variance of the wavelet coefficients in the codeblock. Similarly, for the HL, LH, and HH subbands, the distribution of the wavelet coefficients of a codeblock is modeled using a discretized Laplacian distribution:

$$P(y)={\int }_{y-\frac{1}{2}}^{y+\frac{1}{2}}\frac{1}{\sqrt{2{\sigma }^2}}\text{\hspace{0.17em}exp}\left[-\frac{\sqrt{2}\left|x\right|}{\sigma }\right]dx.$$ (7)

Similar to the irreversible JPEG2000 pipeline, mid-point reconstruction [15] typically used in the dequantization of integer wavelet coefficients:

$$\widehat{y}=\overline{Q}(y)=\mathit{\text{sign}}(q)\cdot \lfloor (|q|+0.5)\times \overline{\Delta }\rfloor$$ (8)

where $\overline{\Delta }=2^L\Delta =2^L$ denotes the effective quantization step size for a coefficient missing its L least significant bits.

The distribution of the quantization error (y − ŷ) can be obtained using Equations (6), (7), and (8), given the values of σ² and $\overline{\Delta }$. Examples of the quantization error distributions for the LL and HL/LH/HH subbands are shown in Figures 2 and 3, respectively.

Figure 2:

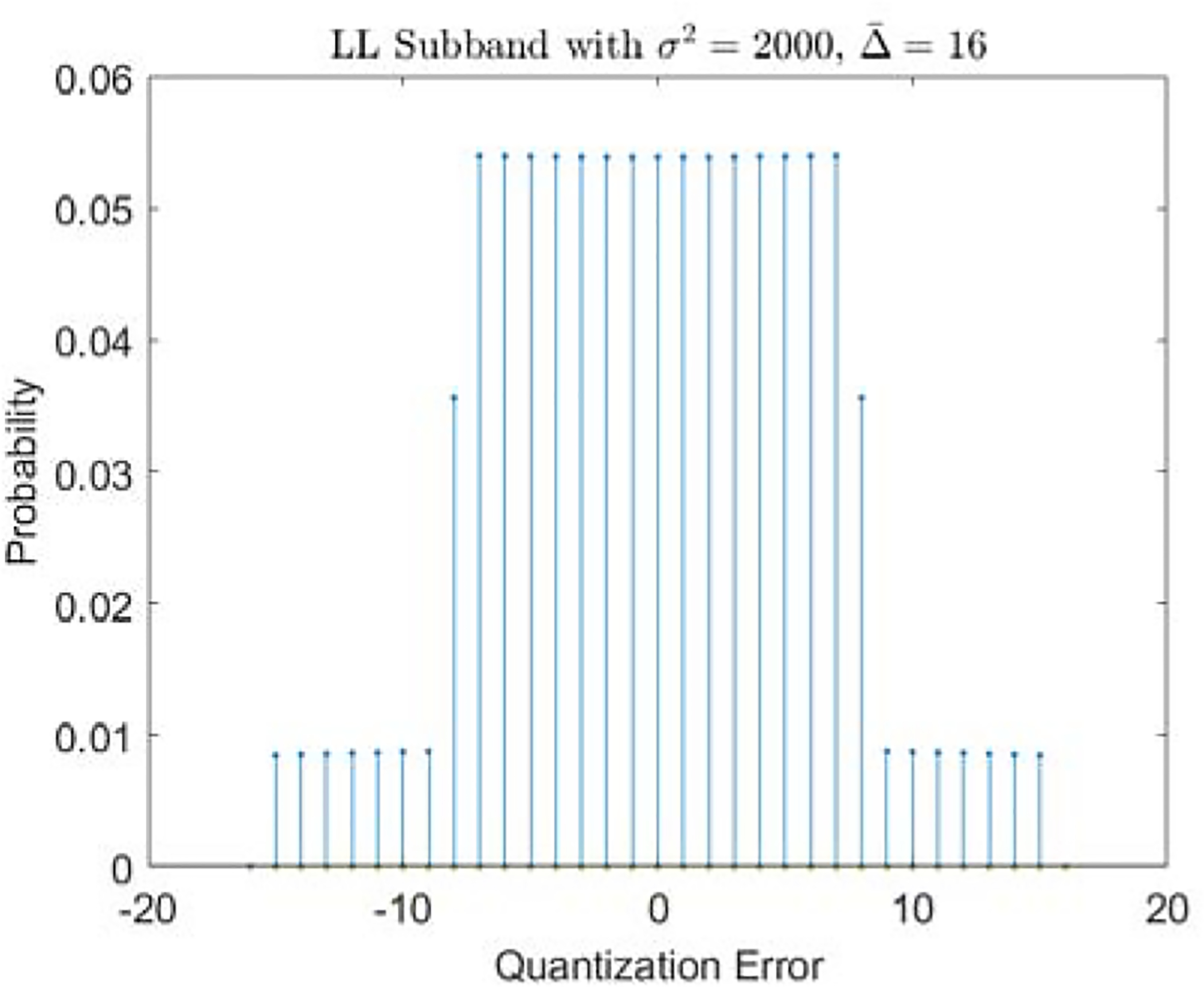
Quantization Error Distribution Example of the LL Subband.

Figure 3:

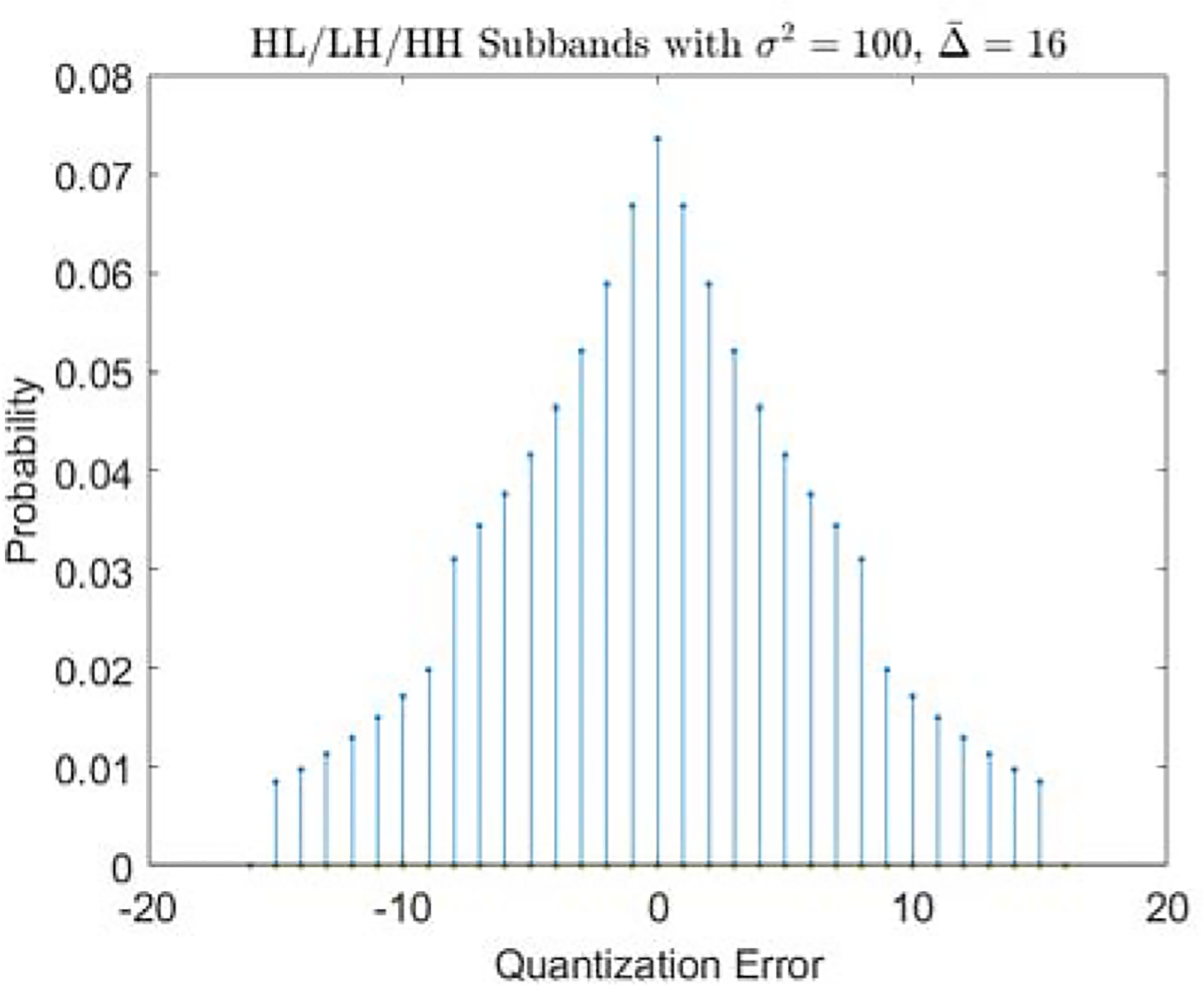
Quantization Error Distribution Example of the HL/LH/HH Subband.

4. Visibility Thresholds and the Encoding Procedure

The wavelet transform decomposes each component image into several subbands with different orientations and spatial frequencies. In order to quantitatively describe the HVS sensitivity to quantization errors, for a given subband of a given color component ($\overline{Y}$, ${\overline{C}}_{\text{b}}$, ${\overline{C}}_{\text{r}}$) we define the VT as the maximum possible error in a quantization step that leads to a Just-Noticeable Difference (JND) of the compression artifacts. Higher HVS sensitivity to a given subband of a given color component generally leads to a lower VT value. To measure the VT for a given subband, we perform psychovisual experiments following the bi-section search procedure described in Figure 4.

Figure 4:

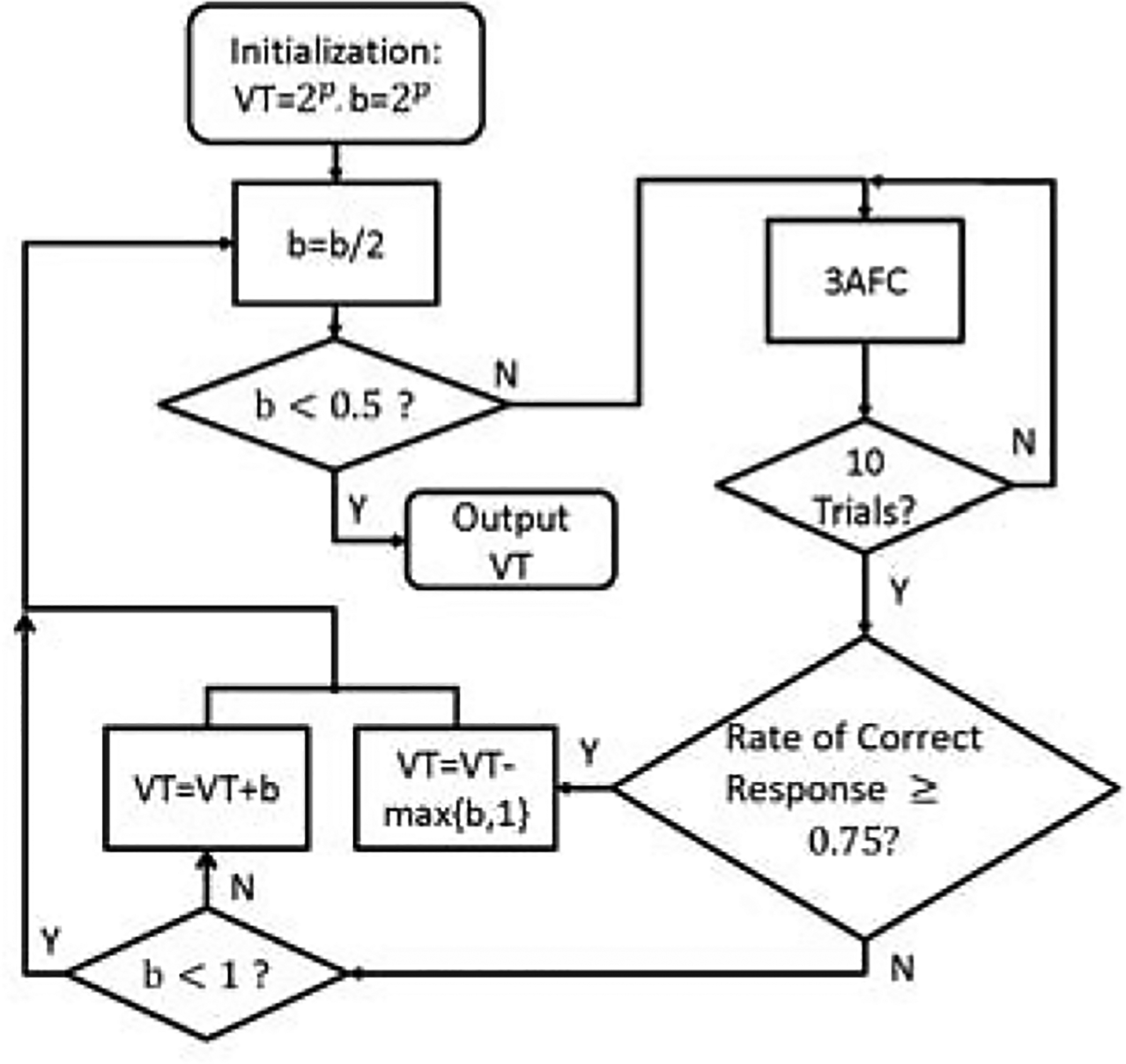
Flow chart of the psychovisual experiments to obtain VTs.

4.1. Psychovisual Experiments

The procedure described in Figure 4 uses bisection to determine a VT for a given subband. At each bi-section step, 10 trials of a 3-alternative-forced-choice (3AFC) test are conducted. All human subject studies were conducted in compliance with institutional review board guidelines. For each 3AFC trial, a human subject is presented with three 512 × 512 images, displayed side by side on a monitor in random order. Two of these images are with a constant pixel value. The third image contains a stimulus obtained from randomly generated compression distortion as described below. The subject is asked to pick the image which they perceive to be different among the three shown. After 10 trials, the rate of correct choice by the subject is calculated. If the correct rate is greater than 0.75, the VT is decreased; conversely, if the correct rate is less than 0.75, the VT is increased. This process is repeated until the bi-section stepsize is smaller than 1 (b < 1), after which the final VT is determined.

To generate compression distortion for a subband under test, an N×N codeblock of coefficients is first randomly generated according to the distribution in Equation (6) or Equation (7), depending on the subband. These coefficient values represent the unquantized originals. Here N = min{64, 512^−k} where k denotes the decomposition level of the subband. The codeblock is then inserted into the center of the subband and processed through the inverse reversible 5/3 DWT and inverse RCT synthesis chain to generate a 512×512 color image. This color image represents how the unquantized wavelet coefficients appear in the image domain. Next, the codeblock of coefficients is quantized/dequantized using the current VT value under consideration as the quantization step size. The resulting codeblock of reconstructed coefficients is inserted into the subband and processed through the inverse synthesis chain to generate another color image. This color image represents how the quantized wavelet coefficients, with the current stepsize, appear in image domain. The compression distortion is then the Difference between these two images, and is used as the stimulus. Examples of the stimuli containing quantization distortion for LL, HL, LH and HH wavelet subbands of the luminance component are shown in Figure 5. An example of a 3AFC trial containing two constant gray images and one stimulus image is shown in Figure 6.

Figure 5:

Examples of the Stimuli Containing Quantization Distortion (a: LL subband, b: HL Subband, c: LH Subband, d: HH Subband).

Figure 6:

An Example of Images Used in a 3AFC Trial to Measure the Visual Threshold.

It is important to emphasize that this procedure is different than that used for the irreversible pipeline in the literature [5, 8, 12]. Since the transforms in the irreversible pipeline are linear, the stimulus can be generated by directly generating the quantization error in wavelet domain, and processing it through the inverse irreversible 9/7 DWT and the inverse ICT synthesis chain. However the ”floor” operation in Equations (1) and (3) in the reversible pipeline introduce non-linearities which necessitates the new procedure described above. Moreover, as the non-linear operations for the low/high pass filtering of the 2-D reversible 5/3 wavelet transform in JPEG2000 are performed sequentially in each direction, we do not pool the VT measurements for HL and LH subbands at each decomposition level of a given color component.

In this work, measurement of the VTs was conducted on an ASUS PA-328Q monitor in a typical office environment with ambient light. The monitor dimensions were 3840×2160, with a pixel pitch of 0.1845 mm. The image brightness of the monitor was 350 cd/m². A fixed viewing distance of 60 cm and observation time of 10 seconds per trial was used for all experiments. Consistent with earlier results [12], it was observed that the resulting VTs were not very sensitive to the variance of the wavelet coefficients. Therefore, in order to reduce the time burden of the psychovisual experiments, these experiments were conducted at a single variance value for each subband, as shown in Table 1. These variance values were obtained by averaging the variances of codeblocks in different subbands over a natural image database, IRCCyN IVC Eyetracker Images LIVE Database [17]. All of the 29 natural images in the database were used.

Table 1:

Wavelet Coefficient Variances Used in the Psychovisual Experiments.

Subband	$\overline{\text{Y}}$	${\overline{\text{C}}}_{\text{b}}$	${\overline{\text{C}}}_{\text{r}}$
(HH, 1)	69.2	4.2	3.0
(HL/LH, 1)	165.4	7.4	6.0
(HH, 2)	491.7	26.9	22.6
(HL/LH, 2)	457.5	35.5	32.5
(HH, 3)	749.7	92.6	92.1
(HL/LH, 3)	589.9	77.7	75.7
(HH, 4)	908.0	165.6	160.2
(HL/LH, 4)	732.3	119.9	123.3
(HH, 5)	1156.7	255.9	228.1
(HL/LH, 5)	899.4	184.6	166.6
(LL, 5)	2496.9	563.4	514.1

4.2. Measured Visibility Thresholds

To determine the VTs for each subband, psychovisual experiments were conducted using 3 subjects. The results from these experiments are shown in Table 2. While individual VT measurements between the subjects show the inter-observer variability of the HVS as expected, the trends of the VT values from the three subjects are consistent across subbands and decomposition levels (i.e. lower decomposition levels and HH subbands usually get higher VT values).

Table 2:

Visibility Thresholds Measured by the Subjects for the Reversible 5/3 Transform (S1, S2 and S3 denote the results got from the 3 subjects, respectively).

Subband	$\overline{\text{Y}}$	${\overline{\text{C}}}_{\text{b}}$	${\overline{\text{C}}}_{\text{r}}$
	(S1/S2/S3)	(S1/S2/S3)	(S1/S2/S3)
(HH, 1)	∞/∞/∞	∞/∞/∞	∞/∞/∞
(HL, 1)	16/28/119	∞/∞/∞	∞/∞/∞
(LH, 1)	7/15/56	∞/∞/∞	∞/∞/∞
(HH, 2)	7/8/60	∞/∞/∞	∞/∞/∞
(HL, 2)	3/4/7	∞/∞/∞	∞/∞/∞
(LH, 2)	5/3/4	∞/∞/∞	∞/∞/∞
(HH, 3)	1/1/6	61/∞/∞	∞/∞/∞
(HL, 3)	2/1/3	8/11/∞	7/7/115
(LH, 3)	1/1/1	8/8/65	9/6/27
(HH, 4)	1/1/2	14/7/54	13/8/∞
(HL, 4)	1/1/1	5/16/12	7/4/14
(LH, 4)	1/1/2	3/7/15	7/4/14
(HH, 5)	1/1/1	14/9/13	4/4/13
(HL, 5)	1/1/1	4/5/2	1/4/6
(LH, 5)	1/1/1	4/3/6	2/3/6
(LL, 5)	1/1/1	3/2/4	1/1/3

When determining the final VTs for the validation experiments, we made the conservative choice by using the minimum of the VTs from the three subjects in each subband, which are shown in Table 3. In this table, the VTs which are infinity suggest that the corresponding subbands can be discarded without causing artifacts above the JND level in decompressed images. On the other hand, VTs which have a value of 1 suggest that any quantization error in these subbands will lead to artifacts in the decompressed image which will be visible beyond the target VT, thus no quantization should be used.

Table 3:

Visibility Thresholds for the Reversible 5/3 Transform.

Subband	$\overline{\text{Y}}$	${\overline{\text{C}}}_{\text{b}}$	${\overline{\text{C}}}_{\text{r}}$
(HH, 1)	∞	∞	∞
(HL, 1)	16	∞	∞
(LH, 1)	7	∞	∞
(HH, 2)	7	∞	∞
(HL, 2)	3	∞	∞
(LH, 2)	3	∞	∞
(HH, 3)	1	61	∞
(HL, 3)	1	8	7
(LH, 3)	1	8	6
(HH, 4)	1	7	8
(HL, 4)	1	5	4
(LH, 4)	1	3	4
(HH, 5)	1	9	4
(HL, 5)	1	2	1
(LH, 5)	1	3	2
(LL, 5)	1	2	1

4.3. Encoding Procedure

The proposed JND encoding is performed based on the JPEG2000 reversible encoding process as described in Section 2. The base quantization step in the deadzone quantizer is set to be 1, and the VTs in Table 3 are used in the rate allocation step in Figure 1.

Specifically, for a given codeblock, the minimum number of coding passes are included as required to ensure that the maximum quantization error falls below the VT for the wavelet coefficients with amplitudes smaller than or equal to the VT (i.e. for coefficients within the deadzone of the quantizer), and the maximum quantization error falls below a half of the VT for the wavelet coefficients with amplitudes larger than the VT (i.e. for coefficients outside the deadzone of the quantizer). All remaining coefficients are discarded. Alternatively, if numerically lossless restoration capability is also desired, the remaining coding passes can be includeed in one or more additional quality layers. Such a codestream would yield near-threshold restortation by decompression of the initial quality layers and numerically lossless restoration by decompression of the remaining quality layers.

5. Validation Experiments

Encoding and psychovisual validation experiments were conducted to demonstrate the efficacy of the proposed model. All images (n = 101) used in validation were sourced from the RAISE [18] raw color natural scene image database. Grayscale images were produced by extracting the luminance component from the color images. Examples of images used in validation are shown in Figure 7.

Figure 7:

Sample Test Images.

5.1. Encoding Validation

The reversible pipeline of the Kakadu V6.1 JPEG2000 encoder [19] was modified to incorporate the VTs measured as described in Section 4.2. The resulting system is compared to the irreversible pipeline of JPEG2000 Part I with the irreversible 9/7 wavelet transform, and the procedure described by Han et al. [12] to achieve near-threshold image quality. The VTs for the irreversible pipeline are also measured on the ASUS PA328Q monitor. In addition, numerically lossless compression results, which were obtained from the original JPEG2000 lossless compression method, are reported as a benchmark. All experiments used the Kakadu V6.1 JPEG2000 library [19]. It is important to emphasize that these three methods all use the unmodified Kakadu V6.1 JPEG2000 decoder, since all codestreams are compliant with Part 1 of the JPEG2000 standard.

Tables 4 and 5 show the bitrates and peak signal-to-noise ratios (PSNRs) obtained using grayscale and color images, respectively. Several interesting observations can be made based on the results presented in these tables. First, as expected, numerically lossless compression requires substantially higher bitrates than VT based visually lossless encoding. Additionally, by comparing the bitrates achieved using the VTs within the reversible and irreversible pipelines of the JPEG2000 Part 1 standard (denoted as ”RCT + reversible 5/3” and ”ICT + irreversible 9/7,” respectively, in the tables), it can be observed that the reversible pipeline requires considerably higher bitrates to achieve near-threshold visual quality in most cases. The average increase in bitrate is roughly 22% for grayscale images and 26% for color images.

Table 4:

Bitrate and PSNR Statistics - Grayscale Images.

	Bitrate (bpp)
Encoder	Mean	Maximum	Minimum
Lossless Encoding + RCT + Reversible 5/3	3.51	5.15	1.80
VT Encoding + RCT + Reversible 5/3	1.12	1.98	0.36
VT Encoding + ICT + Irreversible 9/7	0.92	2.03	0.13
VT Encoding + ICT + Irreversible 5/3	0.87	1.99	0.12
	PSNR (dB)
Encoder	Mean	Maximum	Minimum
Lossless Encoding + RCT + reversible 5/3	∞	∞	∞
VT Encoding + RCT + reversible 5/3	40.39	45.39	35.92
VT Encoding + ICT + irreversible 9/7	42.56	47.20	40.47
VT Encoding + ICT + irreversible 5/3	41.72	46.64	39.16

Table 5:

Bitrate and PSNR Statistics - Color Images.

	Bitrate (bpp)
Encoder	Mean	Maximum	Minimum
Lossless Encoding + RCT + Reversible 5/3	7.42	11.52	4.41
VT Encoding + RCT + Reversible 5/3	1.22	2.20	0.39
VT Encoding + ICT + Irreversible 9/7	0.97	2.12	0.13
VT Encoding + ICT + Irreversible 5/3	0.93	2.10	0.13
	PSNR (dB)
Encoder	Mean	Maximum	Minimum
Lossless Encoding + RCT + rev ersible 5/3	∞	∞	∞
VT Encoding + RCT + reversible 5/3	38.83	43.73	33.81
VT Encoding + ICT + irreversible 9/7	39.14	45.53	32.94
VT Encoding + ICT + irreversible 5/3	39.07	45.01	34.34

To further delinate the possible effects caused by the different wavelet kernels (5/3 vs 9/7) and the MCT kernels (RCT and ICT), experiments were also conducted using an irreversible 5/3 encoding pipeline, and the corresponding VTs measured on the ASUS PA328Q monitor. The psychovisual experiments to measure the VTs and to encode the images for this 5/3 irrversible pipeline followed Han et al.’s procedure. Results obtained using this approach, which are JPEG2000 Part 2 compliant, are denoted as ”ICT + irreversible 5/3” in Tables 4 and 5.

By comparing these results to those obtained using the ”ICT + irreversible 9/7”, it can be seen that the ”ICT + irreversible 5/3” requires similar bitrates to achive near-threshold quality, indicating that the bitrate increase in the ”RCT + reversible 5/3” is primarily due to the nonlinear rounding steps in the reversible pipeline, and not due to the different wavelet transform kernels.

5.2. Psychovisual Validation

Psychovisual validation experiments were performed using 10 subjects to ensure that the images produced by the encoders used in this work achieved the expected level of visual quality (i.e., the rate of correct choice not higher than 75%). The subjects participating in the validation experiments were different from those who participated in the VT measurement experiments. Repeated trials with different image patches from the above encoding and decoding experiments were included in a validation experiment. During each validation trial, three images are displayed on a monitor side-by-side in random order. Two images were never-compressed originals, and one was a decompressed image which had been compressed using a VT encoder. The subject was asked to identify the image which they believe is different among the three shown. These experiments were carried out using the same environment (i.e., ASUS PA-328Q monitor, viewing distance of 60 cm) as the design experiments; however, no limit was placed on decision time.

Tables 6 and 7 show the rate of correct choice obtained in these experiments using grayscale and color images, respectively. It can be seen that the rates of correct choice obtained in each of the three cases are comparable for both color and grayscale images. Furthermore, as expected, the rates of correct choice are below the 75% target (close around 50% on average) for all encoders. In most cases, the rates are significantly lower than 75%. The two extreme cases can be identified as Subject 4 and Subject 10, who were the least sensitive and the most sensitive, respectively, to quantization noise in the images. We postulate that masking effects [20], which were not considered in this work, lead to this additional improvement in visual quality. This suggests that future work may yield further enhancements in compression performance by incorporation of the masking effects into the proposed model.

Table 6:

The Rates of Correct Choice from 10 Subjects - Grayscale Images.

	RCT +	ICT +	ICT +
Subject	reversible 5/3	irreversible 5/3	irreversible 9/7
1	0.56	0.57	0.70
2	0.40	0.41	0.30
3	0.35	0.33	0.40
4	0.40	0.36	0.37
5	0.42	0.35	0.35
6	0.58	0.45	0.61
7	0.45	0.57	0.46
8	0.56	0.64	0.59
9	0.42	0.53	0.52
10	0.71	0.65	0.64
Mean/St. Dev.	0.49/0.11	0.49/0.12	0.49/0.14

Table 7:

The Rates of Correct Choice from 10 Subjects - Color Images.

	RCT +	ICT +	ICT +
Subject	reversible 5/3	irreversible 5/3	irreversible 9/7
1	0.66	0.57	0.66
2	0.44	0.40	0.36
3	0.45	0.36	0.41
4	0.36	0.44	0.43
5	0.45	0.36	0.40
6	0.66	0.74	0.65
7	0.67	0.39	0.42
8	0.41	0.64	0.55
9	0.51	0.67	0.52
10	0.73	0.45	0.74
Mean/St. Dev.	0.53/0.13	0.50/0.14	0.51/0.13

6. Conclusions

In this paper, we proposed a method for measuring the visibility thresholds when reversible color and wavelet transforms are employed. These thresholds were then incorporated into a JPEG2000 encoder to obtain images where compression artifacts were kept below a predetermined detectability threshold. Our proposed method enables progressive and scalable codestreams from near-threshold compression to numerically lossless compression, which is desirable in applications where restoration of original image samples is required. Notably, codestreams generated by the proposed method are compliant with Part 1 of the JPEG2000 standard. The performance of the proposed method was validated using psychovisual subjective testing. Most importantly, this is the first work that quantifies the loss in bitrate incurred by reversible transforms in near-threshold image compression compared to the irreversible transforms in JPEG2000. Our results reveal that this bitrate penalty is roughly 22% for grayscale and 26% for color images.