Optimizing nitroxide biradicals for Cross-Effect MAS-DNP: the role of g-tensors’ distance

Abstract

Nitroxide biradicals are common polarizing agents used to enhance the sensistivity of solid-state NMR experiments via Magic Angle Spinning Dynamic Nuclear Polarization (MAS-DNP). These biradicals are used to increase the polarization of protons through the Cross-Effect mechanism which requires two unpaired electrons with a Larmor frequencies difference greater than the one of protons. From their early conception the relative orientation of the nitroxide rings has been identified as a critical factor determining their MAS-DNP performance. However, the MAS leads to a complex DNP mechanism with time dependent energy level anti-crossings making difficult to pinpoint the role of relative g-tensors’ orientation. In this article, a single parameter called “g-tensors’ distance” is introduced to charaterize the relative orientation’s impact on the MAS-DNP field profiles. It is demonstrated for the first time how the g-tensors’ distance determines the nuclear hyperpolarization and depolarization properties of a given biradical. This provides a new critical parameter which paves the way for more efficient bis-nitroxides for MAS-DNP.

Graphical Abstract

Introduction

Nuclear Magnetic Resonance (NMR) provides unique microscopic information at the atomic scale for chemical and biological applications; even for solids when using Magic Angle Spinning (MAS) methods.¹ Nonetheless the well-known sensitivity issue limits some NMR applications. To overcome it, Dynamic Nuclear Polarization (DNP) was developed as a powerful approach that transfers the higher polarization from unpaired electron spins to the surrounding nuclei under appropriate microwave (μw) irradiation. The combination of MAS and DNP began in the mid 80’s^2–4 but emerged as a promising high-field method when gyrotrons were developed as stable high-power, high-frequency microwave sources.⁵ The commercialization of high magnetic field system (by modern standards) is now modifying and complementing the landscape of Solid-State NMR (ssNMR).⁶ In the past decades, MAS-DNP has witnessed successive instrumental and method developments with the uses of low/high temperature,^7–12 higher magnetic field (up to 21.1 T),¹³ faster spinning,¹⁴ and improved sample preparation.^15–18 Among these, the introduction of biradicals as polarization agents was an essential step. They enabled fast build-ups of high nuclear polarization using a low radical concentration and facilitated performing multi-dimensional experiments efficiently on challenging samples.^16,19–25 One cannot overstate the importance of the introduction of nitroxide biradicals such as TOTAPOL, bTbK and bTurea.^26–28 The last two examples, and their improved version TEKPol and AMUPol,^29–31 carefully control the relative orientation of the TEMPO moieties which enhances the Cross-Effect (CE) MAS-DNP mechanism.^27,28

The efficient CE polarization mechanism is active if the polarization agent consists of at least two interacting electron spins surrounded by interconnected nuclei. In addition, their corresponding EPR linewidth must be greater than the nuclear Larmor frequency. However the details of this mechanism under MAS were analysed well after the introduction and optimization of biradicals.^32–35 The simulations using a simple three-spin model (two electrons, a, b, and a nuclear spin, n) helped disentangling the impact of the different spin/experimental parameters on the polarization properties of a given biradicals. The mechanism for a three-spin system could be summed-up as:

• the μw irradiation creates a polarization difference between the electron spins, i.e. a gradient across the EPR line, later referred as |P_a−P_b|;^32–34

• this polarization difference is exchanged via the electron-electron dipolar coupling (and/or exchange interaction);^33,34,36

• it is transferred to the nucleus via a cross term involving the hyperfine coupling and the dipolar coupling (and/or exchange interaction) upon a degeneracy condition that generates an energy-conserving flip-flop-flip process, i.e the Cross effect; ^32–34,37

• the longitudinal relaxation mechanisms tend to bring the electron polarization P_a, P_b and the nuclear polarization P_n, back to their thermal Boltzmann equilibrium values.

At steady state, the electron polarization difference induces a nuclear polarization gain if |P_a−P_b| is greater than the nuclear polarization |P_n| or a loss in the opposite case. In a three-spin system, each of these phenomena are “distinct” and arise from periodic quasi instantaneous energy level anti-crossings dubbed as “rotor events”. With μw irradiation, this generally leads to an absolute nuclear polarization greater than the thermal Boltzmann equilibrium. Without μw it can lead to a nuclear polarization smaller than its Boltzmann thermal equilibrium value at steady state for bis-nitroxides. This effect, called depolarization,^36,38 has significant impact on the assessment of a biradical properties.^36,39,40 Under specific circumstances, a hyperpolarized state may be obtained in absence of μw irradiation.^38,40

The role of each electron-electron and electron-nuclear interaction has become clearer through steady state analysis.^34,36,40 Strong electron-electron interactions maintain biradicals’ performance at higher MAS frequencies and magnetic field, while generating faster polarization build-up.^33,39–42 Microwave irradiation strength increases |P_a−P_b| and too short (or too long) electron longitudinal relaxation reduces it. Improvement to the simulation codes to account for more electrons^38,41 or more nuclei^41,43 sheds light respectively on the impact of “MAS induced spectral diffusion”, and nuclear spin-diffusion. The simulations proved theoretically^34,43–45 the absence of the so-called nuclear diffusion barrier which was later proven experimentally.^46,47 Overall the understanding of MAS-DNP has bloomed into an almost textbook process.^21,45,48,49

Under these developments an ideal biradical would require strong dipolar coupling and moderate exchange interaction, compared to the nuclear Larmor frequency, and should consist of two radicals originating from different chemical species. These radicals should have EPR spectra with Larmor frequencies separated by the nuclei Larmor frequencies.³³ Such an ideal “hetero-biradical” has yet to be developed but some systems like Trityl-TEMPOs (TEMTRIPol-I⁴²), or BDPA-TEMPOs (HiTEKs¹³) are getting closer to it.

“Homo-biradicals” such as the bis-nitroxides, on the other hand, play an essential role in MAS-DNP as they are relatively stable and very efficient up to 14.1 T (at least).^39,50,51 Their g-tensors possess a large anisotropy that dominates the EPR spectrum. To be efficient, these homo-biradicals requires careful crafting of their relative orientation to generate CE mechanism. This tricky topic has yet to be clarified since this relative orientation helps to “separate” the Larmor frequencies of each of the nitroxides and mimic the “ideal” biradicals.

Earlier works have studied the impact of the relative orientation experimentally^28,52 and theoretically,³⁴ but recently Perras et al.⁵³ dedicated considerable computational effort to address this point. By scanning the Euler angles Ω=(α,β,γ) that define the g-tensors’ relative orientation, they showed how the scalar product of the y axis of the each g-tensors $(\overrightarrow{y}.{\overrightarrow{y}}_{\text{rot}})$,²⁸ controls the polarization gain, confirming previous experimental results.²⁸ The approach is remarkable albeit incomplete. Indeed, the relative orientation Ω has an impact on the MAS-DNP field profile (enhancement as a function of the magnetic field under MAS for a fixed μw frequency)^27,50 Consequently, for each relative orientation, the optimal field position differs. This adds a dimension to the problem that is explored here in order to better understand the influence of Ω on the polarization,⁵⁰ the depolarization^50,54 for bis-nitroxides.

In this article this multidimensional problem (4D) is reduced, under idealized conditions, to a 2D problem via a natural parameter: a tensor norm. To demonstrate this finding, we will first illustrate how Ω impacts the MAS-DNP field profile then show that the norm of the g-tensors difference can be used to predict the relative efficiency of a given biradical geometry, using an efficient simulation code previously developed.⁵⁰ This is rationalized by explaining how this g-tensors’ distance relates to overlapping Larmor frequencies offset and CE condition. Finally, we extend this approach to more realistic scenarios that includes the effect of anisotropic interactions, electron relaxation times and more nuclei.

Simulations parameters

Definitions

The nuclear polarization at thermal equilibrium, in presence and in absence of μw irradiation, are defined respectively as P_n,Boltzman, P_n,on, and P_n,off. The polarization gain ϵ_B and the depolarization ϵ_Depo are defined as:

$${ϵ}_B=P_{n,\text{on}}/P_{n,\text{Boltzman}},$$

$${ϵ}_{\text{Depo}}=P_{n,\text{off}}/P_{n,\text{Boltzman}}.$$

The ratio ϵ_on/off corresponds experimentally to the ratio of the NMR signal in presence and absence of μw irradiation

$${ϵ}_{\text{on}/\text{off}}=P_{n,\text{on}}/P_{n,\text{off}}.$$

This last ratio is routinely reported when quantifying the efficiency of nitroxides biradical, although it has been demonstrated in general that ϵ_B ≠ ϵ_on/off.^36,38,44

Numerical simulations

The MAS-DNP simulations have been carried out with the latest implementation of a previously published method for moderate electron-electron spin interaction, i.e. much smaller than the nuclear Larmor frequency/or EPR linewidth.^44,50 The “box” model uses N copies of a three-spin system (2 electrons, 1 proton) distributed in a box. These copies can be isolated or in interaction with each other. The “multi-nuclei” model simulates two electron spins in interaction with many protons. The MAS-DNP simulations use the same Hamiltonian^44,50 (reported in the SI) and the powder averaging is achieved using 987 Zaremba-Conroy-Cheng (ZCW) crystal orientations.^55–57

Except otherwise specified we used the following experimental conditions for the simulations: the temperature was set to 100 K, the MAS frequency was 8 kHz, the μw frequency was 395.175 GHz and the μw nutation frequency was 0.35 MHz.^50,58

The g-tensor principal values used in the simulations were [g_x, g_y, g_z] = [2.00924, 2.006082, 2.00204], the ¹⁴N hyperfine coupling values were $[A_x^{14\text{N}},A_y^{14\text{N}},A_z^{14\text{N}}]=[18,17,100]\text{MHz}.$.

In the first section of this manuscript, an idealized system is considered. First, one hyperfine coupling between electron a and nucleus 1 has been considered. For every crystal orientation, it was set to $[A_{a,1}^{\text{zz}}=0\text{MHz},A_{a,1}^{\pm }=0.2\text{MHz}]$. Second, the electron/electron dipolar coupling was considered null (D_a,b, = 0) and only an exchange interaction of J_a,b = 20 MHz was assumed. For this value, the dipolar/J rotor events are adiabatic.^33,34 Hence, the shape only results from the effect of the relative orientation Ω.

These two assumptions are unrealistic experimentally but a11ow the possibility of CE, dipolar/J, and Solid-Effect (SE) rotor events while making them independent of the crystal orientation considered. The relaxation times were also assumed isotropic with the electron relaxation times T_1,e and T_2,e, equal to 0.4 ms and 2.5 s respectively.^50,59–61 The nuclear relaxation time was assumed very long (T_1,n = 300 s) in order to reach the condition where the nuclear polarization is solely determined by the electron polarization difference.^34,48

In the realistic case, the bis-nitroxides possess properties similar as AMUPol, with a dipolar coupling D_ab, = 35 MHz, an exchange interaction J_a,b = −16 MHz, as previously reported^50,62 and, an anisotropic T_1e.^50,59,61 In addition, the nucleus is placed close to the electron spin a and coupled to it with a dipolar hyperfine coupling of 3 MHz. Consequently, its relaxation time is assumed short (T_1n = 0.1 s) as recently inferred.⁵⁰ The biradicals concentration was assumed to be equal to 10 mM. The box contained 32 biradicals with a minimal distance between two biradicals centre of mass is 2.8 nm. The nuclei model used identical parameters as in reference [50], i.e. 476 protons connected to electron a.

g-tensors’ distance

To correlate the polarization performance with a given g-tensor relative orientation, the g-tensors’ distance L_a,b is defined as the Frobenius norm of the tensor difference:

$$L_{a,b}(\Omega )=\Vert ({\widehat{g}}_a-{\widehat{g}}_b(\Omega )){\Vert }_{\text{Fro}}=\surd \text{Tr}\left[({\widehat{g}}_a-{\widehat{g}}_b{(\Omega ))}^{†}({\widehat{g}}_a-{\widehat{g}}_b(\Omega ))\right].$$

Where ${\widehat{g}}_a$ and ${\widehat{g}}_b(\Omega )$ represents the g tensors matrices for the relative orientation Ω = (α,β,γ). The norm accounts for both the effect of the relative orientations and the g-tensor’s anisotropy and is a natural quantity to define how two g-tensors relate. The g-tensor’s distance, L_a,b, is null if the two tensors are colinear and different from zero otherwise. It therefore quantifies the offset in the electron spins’ Larmor frequency induced by the relative orientation (vide infra), an essential parameter for the CE mechanism.

For a bis-nitroxides with g values [g_x, g_y, g_z] = [2.00924, 2.006082, 2.00204], L_a,b ∈ [0, 10.18 × 10⁻³]. The trivial case L_a,b(0,0,0) = 0 is not considered as it only generates SE.^34,37 Except otherwise specified, all angles are in degrees.

Impact of the g-tensors’ distance: an idealized model

In this section the role of L_a,b is examined using the idealized spin system that maintains the SE, CE mechanism, the latter dominating in general. The model is stripped of all anisotropic interaction except the g-tensors’ and the ¹⁴N hyperfine cou-plings. These hyperfine couplings are taken into account to give more accurate field profiles in g_z region; however, they remain very small compared to the EPR linewidth (nearly negligible). The exchange interaction was increased until the maximum enhancements were observed (see SI), indicating that the D/J rotor events are adiabatic.^33,34 In the model, the nuclear relaxation time is very long. Therefore, whenever a crystal orientation undergoes a CE rotor event, the nuclear polarization equates the maximum electron polarization difference observed during a rotor period at the quasi periodic steady-state.^34,36,45 In previous publications it was defined as |P_a − P_b|_max and corresponds to uniform norm over one rotor period of the electron-electron Zero-Quantum subspace polarization (See Fig. S1 for illustration and refs [34,36,45,48] for details). For simplicity, it is referred here as ‖P_a − P_b‖. At the quasi periodic steady-state, the nuclear polarization is given by

$$\left|P_n\right|=\Vert P_a-P_b\Vert$$

The first sub-section discusses the changes in the MAS-DNP field profile. The second, the dependence of ϵ_B, ϵ_Depo and ϵ_on/off upon L_a,b is introduced. Finally, the third part explains the underlying mechanism.

Effect of the relative orientation on the MAS-DNP Field Profile

To illustrate and discuss the effect of the g-tensors’ distance, four relative orientations are considered throughout this section to support the discussion. In black, Ω=[90,0,0], in red Ω=[0,90,0], in green Ω=[90,90,0] and in blue Ω=[90,90,90], span the accessible range of L_a,b(Ω). Their corresponding MAS-DNP field profiles, normalized, are represented in figure 1(a–d).

Fig. 1:

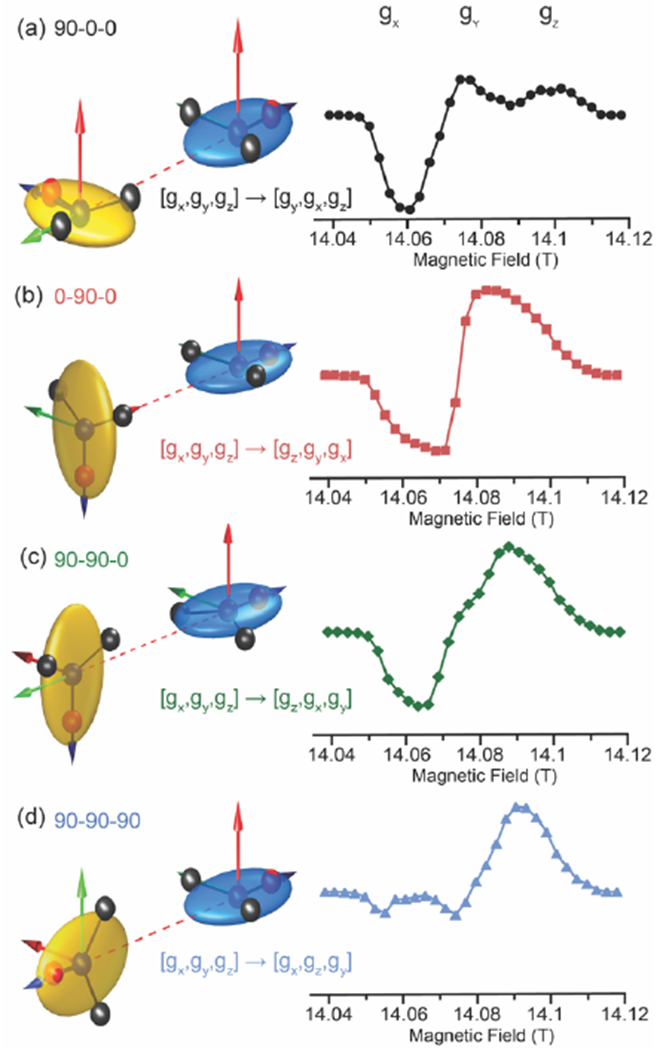
3D representation of four relative g-tensor orientations and their respective simulated MAS-DNP field profiles (a) Ω = [90,0,0], black circles; (b) Ω = [0,90,0], red squares, (c) Ω = [90,90,0], green diamonds, (d) Ω = [90,90,90], blue triangles. For illustration, the dipolar Euler angle is set to [0,−90,0]. Blue arrow = x axis, green arrow = y axis, and red arrow = z axis. On top of the MAS-DNP profile are indicated the “g_x, g_y, g_z” regions. The ZYZ convention is being used here assuming active rotation and the angles are in degrees.

1. corresponds to the relative orientation Ω = [90,0,0] and g-tensors’ distance L_a,b = 4.47×10⁻³. In this case, g_x and g_y are switched between electron a and b. The corresponding MAS-DNP field profile (right, black circles) is strongly asymmetric and the field value leading to the optimal DNP enhancement in the negative region at position B₀ = 14.06 T (g_x region)

2. corresponds to the relative orientation Ω = [0,90,0], L_a,b = 10.18×10⁻³. In this case, g_x and g_z are switched. Its MAS-DNP field profile (right, red squares) has an optimal DNP enhancement in the negative region at B₀ = 14.07 T and the profile is nearly symmetric.

3. corresponds to the relative orientation Ω = [90,90,0], L_a,b = 8.84×10⁻³ (right, green diamond). In this case, g_x, g_y and g_z are all permuted. Its MAS-DNP field profile is asymmetric leading to a maximum in the positive region. As compared to (b) the value is shifted towards higher field B₀ = 14.09 T.

4. corresponds to the relative orientation Ω = [90,90,90], L_a,b = 5.72 ×10⁻³ . In this case, only the g_y and g_z are switched. The MAS-DNP field profile is strongly asymmetric as in case (a). Unlike (a), the optimal DNP enhancement is positive, close to the high field (or g_z) region, B₀ = 14.095 T.

This first figure illustrates the influence of the relative orientation on the MAS-DNP field profile shape and the position of the maximum (absolute) enhancement. The optimal field position in this idealized system does not present any correlation with L_a,b (see Fig. S3), however the field profile tends to become more symmetric for larger L_a,b values. The shape of these MAS-DNP profile is analysed in the next paragraph with the following arguments:

• an electron polarization difference across the EPR line can exist if the two electrons spins’ polarization have different Larmor frequency when the w affects the polarization of one of them;

• this polarization difference can be transferred via the CE rotor events, i.e. during the rotor period, the electron Larmor frequency difference matches the nuclear Larmor frequency |Δv| = |(g_a − g_b)αB₀| = |v_a − v_b| = |v_n|.

• the CE MAS-DNP field profile presents a positive and negative side, a zero-crossing is observed close to the isotropic g value (g_iso ~ g_y).

In case (a), g_x and g_y were switched between the two nitroxides, while g_z points in the same direction for both nitroxides. As a consequence, only an irradiation in the g_x region can induce large ‖P_a − P_b‖ that can be transferred to the nuclei. A nuclear hyperpolarization is indeed observed in the gx region which corresponds to the ~14.06 T region. In the (b) case, g_x and g_z are switched while the g_y is conserved. Irradiating either on the g_x or g_z region can then lead to large polarization difference ‖P_a − P_b‖ and generate nuclear polarization enhancement. Consequently, the MAS-DNP profile is fairly symmetric. In case (c) all principal values are permuted, hence any irradiation in the x or z position generates large ‖P_a − P_b‖ and nuclear hyperpolarization, while the g_y corresponds to the field profile “zero” crossing. In the (d) case, only g_y and g_z are switched. Electron polarization difference can be created if the g_z region is irradiated, i.e. B₀ ~ 14.09 T and one should expect a maximum MAS-DNP in this region. This MAS-DNP field profile is similar to that observed experimentally observed for bTbK²⁷, TEKPOL⁵⁰ or ASYMPol^39,44 and whose structure is aimed at having Ω = [90,90,90].²⁷

The observations in Fig. 1 justify the need to extend the study and compute the MAS-DNP field profile for each relative orientation to find the optimal gains. Elsewise, the optimal relative orientation can be missed, and the problem be partially understood. A complete Euler angle scan is a CPU intensive (4D) problem that would require >1 year of simulations on a high-performance computer. In the following section that effort is avoided by taking advantage of the g-tensors’ distance (L_a,b). Computing the MAS-DNP field profile against L_a,b allows understanding how the ϵ_B, ϵ_Depo and ϵ_on/off relates the Euler angles in about 24 hours.

Correlation between the ϵ_B, ϵ_Depo and ϵ_on/off and the g-tensors’ distance

The impact of the g-tensors’ distance is probed through fifteen Ω values spanning L_a,b’s range. Some redundancy was kept in order to check the trends. The Ωs and L_a,b are reported in Table 1.

Table 1:

List of the fifteen relative orientations considered to span the g-tensors’ distance.

Ω = (α,β,γ),degrees			La,b × 103
45	0	0	3.16
90	0	0	4.47
90	60	90	4.95
90	90	90	5.72
60	70	90	6.23
60	90	70	6.98
45	90	90	7.44
90	90	45	7.44
60	90	45	8.02
135	90	45	8.55
0	90	90	8.84
90	90	0	8.84
45	90	0	9.53
135	90	0	9.53
0	90	0	10.18

For each L_a,b, the MAS-DNP field profiles were calculated and the corresponding maximum |ϵ_B|, |ϵ_on/off| and minimum ϵ_Depo were extracted and plotted against the g-tensors’ distance in Fig. 2. In this idealized case, only isolated biradicals (or three-spin systems) were considered.⁴⁴ Note that the position of |ϵ_B|’s and |ϵ_on/off|’s maxima coincide as ϵ_Depo is nearly constant across the MAS-DNP field profile.

Fig. 2:

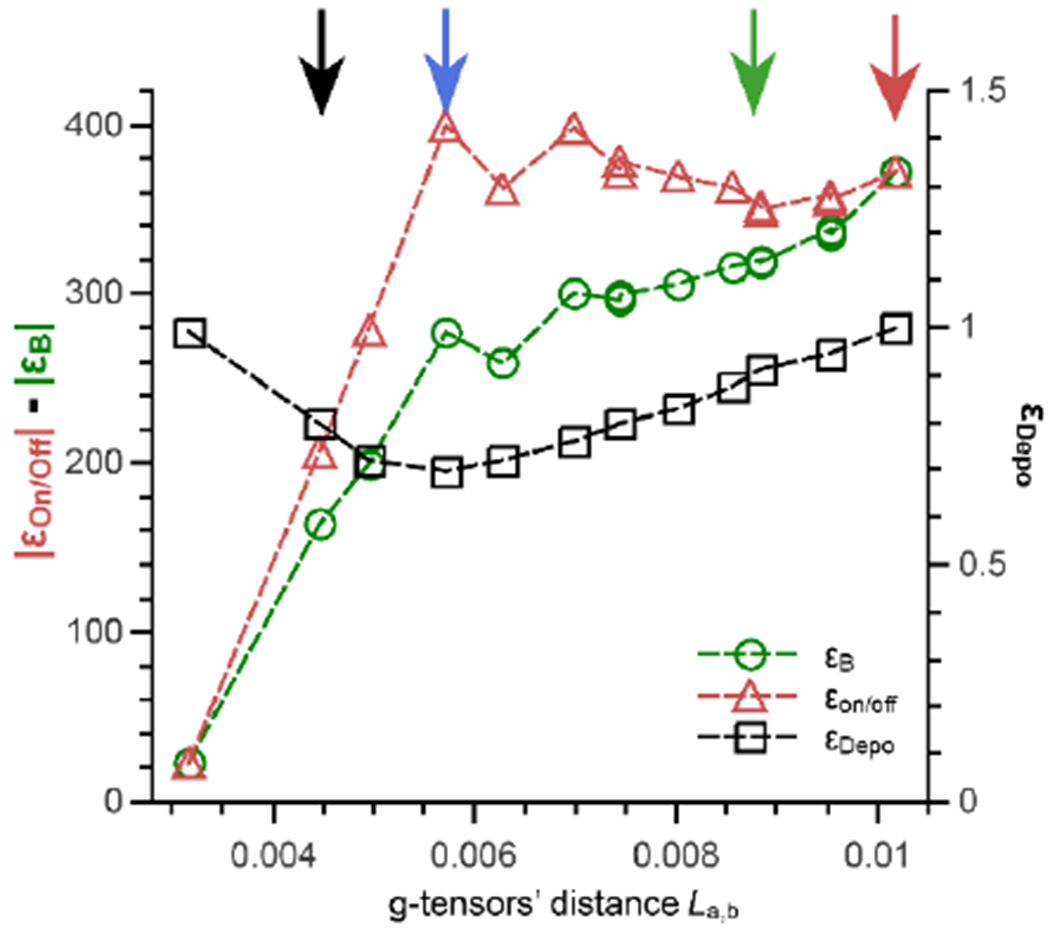
Evolution of the polarization gain |ϵ_B| (a, green circles), the depolarization ϵ_Depo (b, black diamonds) and the |ϵ_on/off| (c, red squares) as a function of the g-tensors’ distance. Lines are guide for the eye. The arrows point to the four illustrative orientations depicted in Fig. 1.

Fig. 2 provides information about the relations between all the ϵ’s and L_a,b. As a result the trend of |ϵ_B| simply increases with L_a,b. ϵ_Depo first decreases and then increases. Finally, |ϵ_on/off| increases steeply, and then plateaus. The plateau is reached at L_a,b ≈ 6 × 10⁻³, which corresponds to the maximum depolarization effect (or minimum ϵ_Depo). The correlation between |ϵ_B|,|ϵ_on/off| and L_a,b is not entirely smooth and can be attributed to the problem dimension reduction from 4D to a 1D here. Indeed, projections are often surjective operations which can generate “wiggles”. The trends are nonetheless clear. Increasing the bis-nitroxide g-tensors’ distance leads to better polarization gains. This is relation is remarkable and is unexpectedly simple. Beyond 6 × 10³, |ϵ_on/off| follows

$${ϵ}_{\text{on}/\text{off}}=\frac{{ϵ}_B}{{ϵ}_{\text{Depo}}}\approx \text{constant}$$

In this idealized model, |P_n| = ‖P_a − P_b‖ at steady state. This means that there is a direct correlation between ‖P_a − P_b‖ with and without μw irradiation determined by

$$\frac{|P_n{|}^{\text{on}}}{|P_n{|}^{\text{off}}}\approx \frac{\left|\right|P_a-P_b|{|}^{\text{on}}}{\left|\right|P_a-P_b|{|}^{\text{off}}}\approx \text{constant}$$

For L_a,b > 6 × 10⁻³, the g-tensors’ distance thus illustrates how the biradical geometry affects the electron polarization difference with or without μw irradiation. This result also generalizes a previous conclusion that a biradical that depolarizes cannot hyperpolarize well;³⁶ it extends it for any g-tensor orientations and not only for spin systems where the electron-electron interaction is not strong enough to ensure adiabatic dipolar/J rotor events.³⁶ For L_a,b below 6 × 10⁻³, the trends cannot be explained here simply. They are the object of the next section which analyses the underlying mechanism to answer the following questions: how does L_a,b impact the CE MAS-DNP mechanism? How does it impact the ability to create a large electron polarization gradient ‖P_a − P_b‖?

g-tensors’ distance and CE conditions

L_a,b relates to the measurement of the spatial similarity of the two g-tensors hence it quantifies what proportion of single crystal orientations have different Larmor frequencies. A good biradical must be able to maintain a large electron polarization difference that may be affected by |Δv|/v_n while transferring it to the nuclei when it periodically matches the CE condition |Δv|/v_n ≈ 1 (CE rotor events). This section is dedicated to the relation between the g-tensors’ distance with the CE conditions and with the electron polarization difference ‖P_a − P_b‖ under MAS.

First, the values of |Δv|/v_n under MAS were computed for a large set of single crystal orientations and the corresponding histograms are reported in Fig. 3. Sub-figures (a), (b), (c) and (d) were obtained for the four illustrative relative orientations (figure 1). Second, when under MAS as well, the proportion of crystal orientations that meet at least one CE rotor event is calculated and plotted against L_a,b in Fig. 4. To provide additional insights (|Δv|/v_n )_Mean is also reported in the same figure. Combined, Fig. 3 and Fig. 4 explain how the g-tensors’ distance affects the ϵ′ s.

Fig. 3:

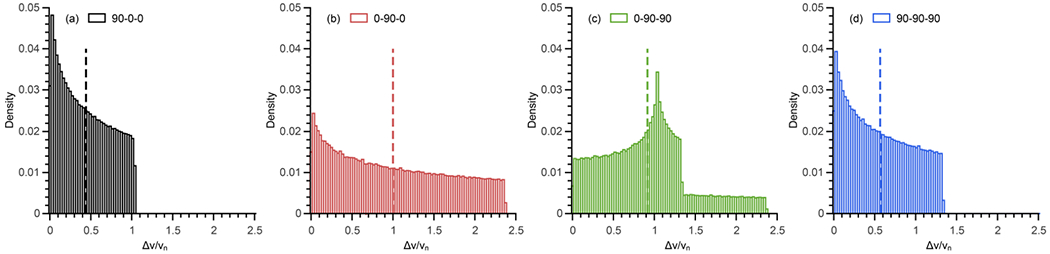
Histograms of the MAS offset |v_a − v_b|/v_n = |Δv|/v_n obtained after averaging 6715 ZCW single crystal orientations reported for the four illustrative relative orientations; (a) black for Ω = [90,0,0], (b) red Ω = [0,90,0], (c) green Ω = [90,90,0], (d) blue Ω = [90,90,90]. The dotted line represents the mean values (|Δv|/v_n)_Mean

Fig. 4:

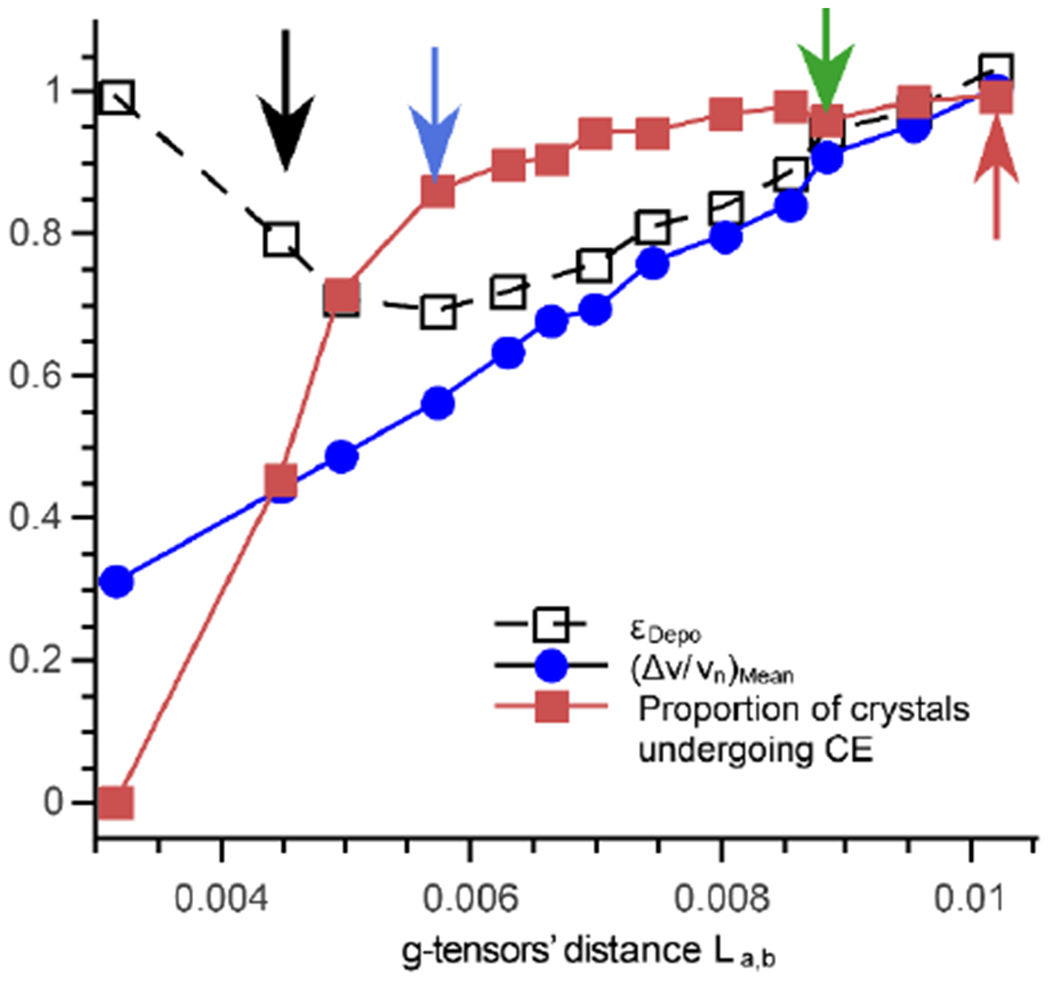
Blue circles, mean value of (|Δv|/v_n )_Mean, red squares proportion of orientation undergoing CE under MAS, black squares and dotted line, ϵ_Depo plotted against the g-tensors’ distance L_a,b. Black, red, green and blue arrows correspond to the four illustrative orientations.

Starting with the most efficient relative orientation, Fig. 3 case (b), there is a significant number of single crystal orientations have frequency separations beyond |Δv|/v_n = 1. |Δv|/v_n has the largest span of all four illustrative orientations, ranging from 0 to 2.4, and also the highest (|Δv|/v_n )_Mean ≈1. In addition, most of the single crystal orientations undergo CE rotor events (>99%, Fig. 4). Case (c), is also one of the best performing relative orientation (see Fig. 2) and shows similar properties. The single crystal orientations’ frequency differences span below and beyond 1. |Δv|/v_n has the same large span and a large (|Δv|/v_n)_Mean ≈ 0.88. Lastly, a vast majority of crystal orientations also undergo a CE rotor event, (96%, Fig. 4). Case (d) is a relative orientation with average polarization performance. It has more crystal orientations with |Δv|/v_n below than beyond 1, which only spans from 0 to 1.4. It has a lower mean value (|Δv|/v_n )_Mean ≈ 0.55. For this g-tensors’ distance, 86% of the crystal orientations contribute to the CE under MAS (Fig. 4). Finally, a poor performing biradical geometry, case (a), has a very small span with very few orientations beyond 1. Furthermore, only a small proportion of the crystal orientations are likely to encounter a CE rotor event: 45 % of them contribute to the MAS-DNP CE (Fig. 4) which here correlates with the reduced |Δv|/v_n span.

For case (b) and (c), a very large proportion of the single crystals can undergo a rotor event, which means that almost all orientations contribute to the CE mechanism. Consequently, |ϵ_B| and ϵ_Depo are solely determined by the electron polarization difference. Case (d) has slightly lower percentage of orientations meeting CE rotor events (86 %) and a smaller (|Δv|/v_n )_Mean~0.55. In that case, the |ϵ_B| and ϵ_Depo properties may result at once from a smaller electron polarization difference and the smaller proportion of CE contribution. In case (a), not only (|Δv|/v_n )_Mean is lower, but also fewer orientations contribute to the DNP mechanism via CE, 45% only. For this relative orientation, |ϵ_B| is low, and ϵ_Depo is high. The lower |ϵ_B| and (|Δv|/v_n )_Mean suggest here a lower electron polarization difference but the lack of depolarization can only be explained by the absence of CE rotor-events. Therefore, for this relative orientation, the reduced proportion of orientation undergoing CE rotor events is the main factor controlling the biradicals’ performance.

Detailing figure 4 one can first notice that (|Δv|/v_n )_Mean, and the proportion of orientation contributing to the CE have no direct relations. On the one hand, (|Δv|/v_n )_Mean, scales linearly with the g-tensors’ distance

$${\left(\frac{\left|\Delta v\right|}{v_n}\right)}_{\text{Mean}}\propto L_{a,b},$$

ranging from 0 to 1. The case (|Δv|/v_n )_Mean = 1 mimics the properties of the ideal “hetero-biradical”. On the other hand, the proportion of orientations leading to CE under MAS steep-ly increases to reach ~90 % for L_a,b > 6 × 10⁻³, and then slowly grows to > 99.4%. This is similar to ϵ_on/off’s behaviour reported in figure 2. Below 3.2 × 10⁻³, no CE and only SE can be obtained for isolated biradicals.

Figure 4 also re-reports ϵ_Depo’s dependence against L_a,b, which first decreases then increases. Here special attention should be given to the two extreme cases. When L_a,b is small, below 6 × 10⁻³, depolarization is weak to non-existent as a smaller proportion of single crystal orientations undergo CE rotor events. For L_a,b> 6 × 10⁻³, almost all orientations contribute to the CE and the polarization difference is the dominating factor. As ϵ_Depo scales linearly with L_a,b, there is a relation for bis-nitroxides on the segment [6 × 10⁻³, 10.18 × 10⁻³]

$${ϵ}_{\text{Depo}}\propto \Vert P_a-P_b{\Vert }^{\text{off}},{\left(\frac{|\Delta v|}{v_n}\right)}_{\text{Mean}},L_{a,b}$$

Since, |ϵ_on/off| is approximately constant in this range, (see Fig. 2), the polarization gain |ϵ_B|, the mean “frequency difference” and L_a,b are all proportionally related by

$$|{ϵ}_B|\propto \Vert P_a-P_b{\Vert }^{\text{on}},{\left(\frac{|\Delta v|}{v_n}\right)}_{\text{Mean}},L_{a,b}.$$

These simple relations are at the heart of the bis-nitroxides’ efficiency, all other parameters equal. High L_a,b is a desirable criterion to boost bis-nitroxides’ performance.

In summary, for sufficiently large L_a,b most orientations contribute to the CE; |ϵ_B| and ϵ_Depo are mostly determined by the electron polarization difference which correlates with L_a,b and (|Δv|/v_n )_Mean. When smaller, both the proportion of CE rotor events and (|Δv|/v_n )_Mean control |ϵ_B| and ϵ_Depo values. For any L_a,b values, |ϵ_on/off| seems only driven by the proportion of crystal orientations meeting CE rotor event. By designing biradicals that maximize (|Δv|/v_n )_Mean, it is therefore possible to generate better hyperpolarization and smaller depolarization. Such properties mimic the polarization difference observed in an “ideal” hetero-biradical when (|Δv|/v_n )_Mean=1 with the appropriate g-tensors’ distance.

These conclusions are drawn from an idealized spin system where the nuclear relaxation time is long and where the electron-electron interaction is isotropic. A fair assessment must account for all anisotropies, including the hyperfine, the electron dipolar coupling, the electron T_1e and in presence of a faster relaxing neighbouring nucleus. The impact of additional biradicals or nuclei is also discussed in the next section.

Impact of the g-tensors’ distance: extension to “realistic” model

The effect of the g-tensors’ distance is assessed using more realistic spin systems. The electron-electron dipolar coupling, the dipolar vector and the exchange interaction were taken from previous structure determination of AMUPol.^50,62 In addition, the model can consider isolated or interacting biradicals in a box (“box model”) or a two electron spins and many nuclei (“multi-nuclei model”).

Fig. 5 reports |ϵ_B|, ϵ_Depo and |ϵ_on/off| as a function of L_a,b. The dotted lines empty symbols represent the isolated 3-spin case and the full lines and symbols report the interacting one. The trends are identical to the idealized case. The |ϵ_B| increases with L_a,b in both cases, in an almost “linear” way. The ϵ_Depo also decreases first then increases for L_a,b > 6 × 10⁻³. |ϵ_on/off| goes first up and plateaus for L_a,b > 6 × 10⁻³ like in the idealized model. The same analysis applies for interacting case. |ϵ_B| and ϵ_Depo are lower in the interacting case due to the MAS induced spectral diffusion that originate from the inter-molecular D-rotor events which nearly compensate one another in ϵ_on/off.⁴⁴ The optimal field positions are reported in the figure S3.

Fig. 5:

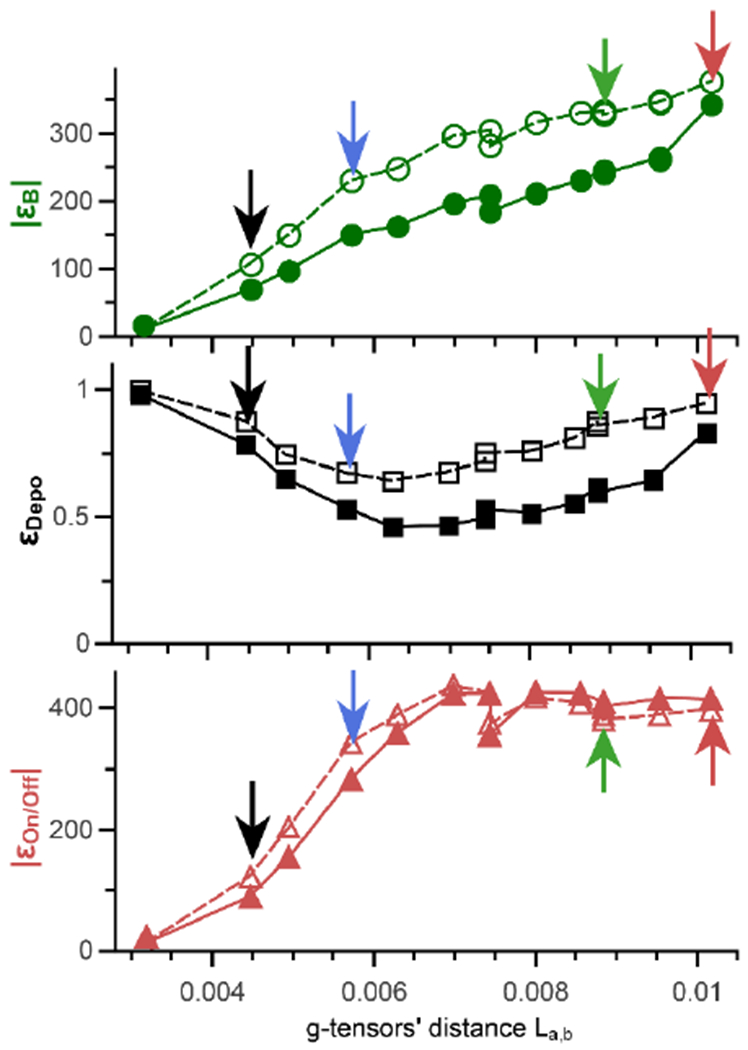
Relation between the polarization gain |ϵ_B| (a, green circles), the depolarization ϵ_Depo (b, black diamonds) and the |ϵ_on/off| (c, red squares) with the g-tensors’ distance. Lines are guide for the eye, dotted line corresponds to isolated 3-spins and full line interacting cases. The arrows point to the four illustrative orientations depicted in Fig. 1.

Therefore, the outcome of the first section are still relevant even when accounting for all known anisotropies. Additional simulations were carried out at other fields, 9.4 and 18.8 T, or different electron relaxation times and reveal the same behaviour (see SI), confirming the generality of the approach. However, for a given L_a,b value, the strength of the dipolar/exchange interaction, the orientation of the dipolar vector with respect to the g-tensors’ may additionally affect the MAS-DNP performance. Biradicals with identical L_a,b but different Euler angles may exhibit different performance that only numerical simulations may predict.

Finally, the box model results were combined with the multi-nuclei results to obtain the extrapolated ϵ′s as previously done and to determine the build-up times for the 15 relative orientations.⁵⁰ The results reported in figure Fig. 6 (a) shows for the extrapolated |ϵ_B|, ϵ_Depo and |ϵ_on/off|. They behave as in figure 5 but |ϵ_B| and |ϵ_on/off| are lower and ϵ_Depo is higher and are closer to the experimental values. Fig. 6 (b) shows that the build-up rate (1/T_b) increases with the g-tensors’ distance, on par with the fact that more crystal orientations contribute to the CE as the g-tensors’ distance increases. Overall figures 5 and 6 confirms the results of the idealized spin system while providing more realistic enhancement values.

Fig. 6:

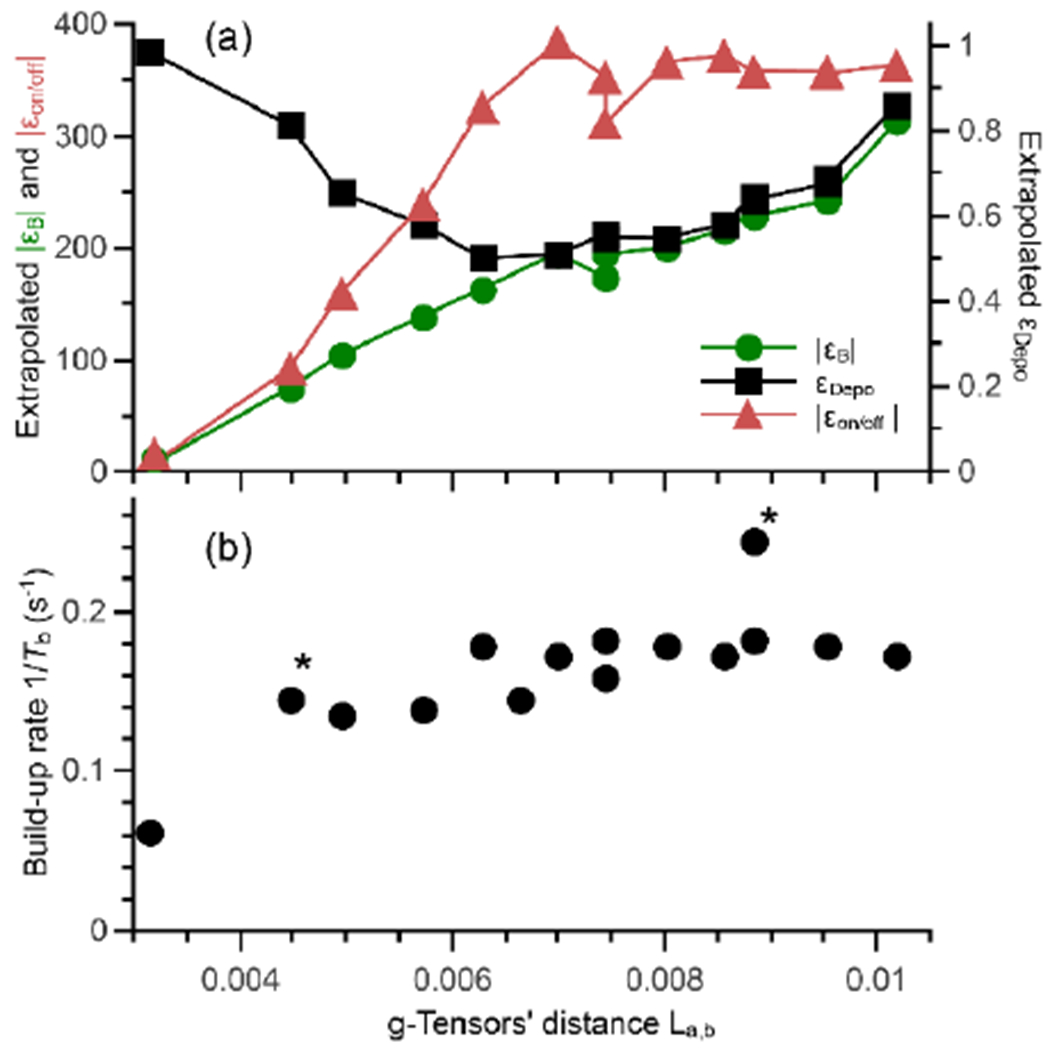
(a) Evolution of the polarization gain |ϵ_B| (a, green circles), the depolarization ϵ_Depo (b, black diamonds) and the |ϵ_on/off| (c, red squares) as a function of the g-tensors’ distance for the extrapolated case that combines the box model and the multi-nuclei one. Lines are guide for the eye. (b) Calculated build-up rate using the multi-nuclei model. The * indicates a bi-exponential behaviour.

These results can be compared to the recently obtained AMUPol and TEKPol structures.^50,62 The g-tensors’ distance for AMUPol is of L_a,b = 6 × 10⁻³ and for TEKPol L_a,b = 6.8 × 10⁻³. Both biradicals have a g-tensors’ distance that maximizes |ϵ_on/off| but do not reach the maximum g-tensors’ distance and potentially the maximum polarization levels.

Conclusions

The effect of the nitroxides’ relative orientation on the CE mechanism has been analysed with the assumption of moderate electron-electron interaction. The analysis revealed the effect of the g-tensor’s relative orientation on the MAS-DNP field profile: different g-tensors’ orientations lead to different optimal field positions (or μw frequencies). The effect of Euler angles can be factored into a norm, L_a,b, dubbed “g-tensors’ distance” which extensively simplifies the biradicals’ geometry optimization. Using an idealized bis-nitroxide system, the results are simple: when L_a,b is sufficiently large, here beyond 6x10⁻³, |ϵ_B| and ϵ_Depo increase linearly with L_a,b, while |ϵ_on/off| stays nearly constant. On the other hand when L_a,b is below 6x10⁻³, |ϵ_B| and|ϵ_on/off| decrease quickly with L_a,b while ϵ_Depo increases. Importantly, |ϵ_on/off| correlates with |ϵ_B|, which indicates that |ϵ_on/off| cannot be used alone to design new biradicals even if all other experimental geometric parameters are kept constant. the cross effect MAS-DNP mechanism requires both an electron polarization difference across the EPR line and orientations that generates CE rotor events. The analysis disentangled the g-tensors’ distance effects on each of them. In powder samples, that distance is proportional to the average electron spins’ Larmor frequency difference (|Δv|)_Mean and affects the proportion of orientations contributing to the CE. The CE rap-idly increases with the g-tensors’ distance and then plateaus for L_a,b > ~6x10⁻³. Above 6x10⁻³, the biradical’s properties are mostly determined by the ability to generate a large electron polarization difference across the EPR line, leading to the relationships: |ϵ_B| ∝ ϵ_Depo ∝ |Δv/v_n|_mean. While below 6x10⁻³, the smaller g-tensors’ distance leads to the reduction of crystal orientations contributing to the CE mechanism and the reduction of the electron polarization difference. Altogether they influence the enhancements leading to lower hyperpolarization but also less depolarization. Lastly, the behaviour of ϵ_on/off seems to only be correlated with the proportion of crystal orientations contributing to the CE under MAS.

These conclusions have been verified to a more realistic case that includes more spins and all known anisotropic interactions and relaxation times. Using the previously determined electron-electron interactions and relaxation times for AMUPol, very similar trends were observed compared to the ideal case. The build-up rates have been analysed and are controlled by the proportion of crystal orientations involved in CE rotor events, i.e. they get shorter for larger L_a,b. Finally, the AMUPol or TEKPol structure are compared to the trends and seems to be sub-optimal with respect to the g-tensors’ distance.

All in all, the g-tensors’ distance can be used to guide the design of more efficient homo-biradicals by maximizing |Δv/v_n|_mean. In particular, when |Δv/v_n|_mean = 1, the bis-nitroxides have similar electron polarization difference properties as compared to the ideal (and elusive) “hetero-biradical” mentioned in the introduction. This ideal biradical is obtained for (α,β,γ) = (0,90,0) but to date, no biradical matches this relative orientation. The closest published structure is dCdO which unfortunately seems to have a too large exchange interaction for CE.²⁸

This study confirms previous work that the β angle needs to be close to 90 degrees.^27,28,53 However it goes beyond and shows that when the changes in the MAS-DNP field profiles are considered, α and γ plays also an important role and should remain small to maximize L_a,b.

Based on these results, new biradicals structures can be designed by optimizing the g-tensors’ distance, the dipolar/exchange interaction, the relaxation time, as well as the solubility. This paves the way for new biradicals with potentially higher polarization gains, and short build-up times.