Potential Aggregation-Prone Regions in Complementarity-Determining Regions of Antibodies and Their Contribution Towards Antigen Recognition: A Computational Analysis

Abstract

Purpose

To analyze contribution of short aggregation-prone regions (APRs), which may self-associate via cross-β motif and were earlier identified in therapeutic mAbs, towards antigen recognition via structural analyses of antibody-antigen complexes.

Methods

A dataset of 29 publically available high-resolution crystal structures of Fab-antigen complexes was collected. Contribution of APRs towards the surface areas of the Fabs buried by the cognate antigens was computed. Propensities of amino acids to occur in APRs and to be involved in antigen binding were compared. Coincidence between APRs and individual CDR loops was examined.

Results

All Fabs in the dataset contain at least one APR in CDR loops and adjacent framework β-strands. The average contribution of APRs towards buried surface area of Fabs is 16.0 ± 10.7%. Aggregation and antigen recognition may be coupled via aromatic residues (Tyr, Trp), which occur with high propensities in both APRs and antigen binding sites. APRs are infrequent in the heavy chain CDR 3 (H3) loops (7%), but are frequent in H2 loops (45%).

Conclusions

Co-incidence of APRs with antigen recognition sites can potentially lead to the loss of function upon aggregation. Rational structure-based design or selection strategies are suggested for biotherapeutics with improved druggability while maintaining potency.

Electronic Supplementary Material

The online version of this article (doi:10.1007/s11095-010-0143-5) contains supplementary material, which is available to authorized users.

INTRODUCTION

Biotherapeutics, including monoclonal antibodies (mAbs) and their fragments, are an important segment of the pharmaceutical industry (1,2). Due to their ability to bind the targets with high specificity and affinity as well as near absence of non-mechanism toxicity due to off-target binding (3), mAb-based drugs offer attractive advantages over the small molecule therapeutics. On the other hand, these biotherapeutic drugs possess complex and conformationally heterogeneous molecular structures that are vulnerable to the changes in their environments and themselves. A complex series of processing steps between production to administration results in several physico-chemical stresses on the molecules (4). These stresses include high concentrations, variable temperatures, pH extremes, varying ionic strengths, shear stresses, and air-water as well as a variety of solid-liquid interfaces. As a result, potency and purity of the final drug product is impacted via multiple degradation pathways (5). Hence, there is considerable interest in the biopharmaceutical industry towards gaining fundamental understanding of the molecular properties that determine chemical, thermodynamic and long-term stability of biotherapeutic molecules.

Aggregation is the most common degradation pathway for biotherapeutics. Besides their potential to impact drug potency, aggregates are also considered a risk factor for immunogenicity (6). In particular, cross β-aggregates in biotherapeutics have the potential to be immunogenic (7). Hence, fundamental understanding as to why some molecules are more prone to aggregation than others would go a long way towards reducing or even eliminating this risk factor.

Aggregation is also a topic of intense research for proteins in general. Accumulating experimental evidence shows that specific regions of protein sequences, especially the ones with amyloidogenic properties, tend to drive aggregation (8–12). Early studies on small proteins and peptides have led to characterization of the physico-chemical properties of amyloid or amyloid-like aggregates associated with neurodegenerative diseases (13). The molecular trigger for these aggregates is the generation of the cross-β motif whose molecular structure was recently elucidated by Eisenberg lab (14,15). Formation of cross-β motif and amyloid-like aggregates in proteins is quite common. From a survey of the literature, we have found that experimental evidence is available for more than seventy different proteins showing aggregation via formation of the cross-β steric zipper motif (16), and even proteins in bacterial inclusion bodies can aggregate via this route (17). Short sequence regions that potentially drive aggregation have been detected in these proteins. These are called aggregation prone regions (APRs) (18). Typically, these APRs have unique features with respect to charge, hydrophobicity, aromaticity and secondary structural preference. A number of computational approaches have been developed to predict potential APRs in proteins (16). Most of these prediction methods use only the protein sequences as input to identify short APRs of 5–9 residues capable of forming amyloid-like fibrils (19). Other methods based on pattern recognition, three-dimensional profiles and molecular simulations are emerging (20–26).

The question of whether there are also APRs in mAbs led to our hypothesis that non-covalent aggregation in biotherapeutics has many parallels with that seen in proteins in general. Thioflavin T and Congo Red are the marker dyes commonly used for detecting amyloid-like aggregation because they bind the cross-β steric zipper motif (14). Aggregates formed by biopharmaceuticals, including therapeutic mAbs towards the end of their expiration dates, were reported to bind Thioflavin T and Congo Red (7,27).

Recently, we used TANGO (28) and PAGE (29) to identify the potential APRs in commercially available therapeutic mAbs (30). All therapeutic mAbs in our study contain several sequence regions that are strongly predicted to be aggregation prone (30). An interesting finding of our study is that some of these APRs are located in variable domains, primarily in complementarity-determining regions (CDRs) and adjoining framework β-strands (30). These parts of the antibody molecule also contribute significantly towards antigen binding. Hence, the above study indicated that there may be an undesirable link between aggregation tendency and molecular function in the therapeutic mAbs.

Here, we present a statistical survey based on high resolution crystal structures of Fab-antigen complexes available in the Protein Data Bank (31). These also include Fab-antigen complexes for commercially available therapeutic mAbs. We identify potential APRs in Fabs in our dataset using sequence-based prediction tools TANGO (28) and PAGE (29). The solvent-accessible surface area buried upon Fab-antigen complex formation is used as a parameter to gauge Fab-antigen interaction and the contribution of the potential APRs towards antigen recognition. In literature, protein-protein interactions have been commonly measured using approaches that rely on energetics (32,33) or contact residues (34) and the buried surface area (35) at the interfaces. The two approaches are closely related. In this study, we preferred to use buried surface area as a metric because it can be easily calculated. Moreover, it has been widely used in the study of protein-protein interactions (35–37).

All Fabs in our dataset contain at least one APR. In all but one Fab-antigen complex, the residues in these CDR-localized APRs also contribute towards antigen binding. Hence, we find that potential APRs may contribute significantly towards antigen binding. The aromatic residues, Tyr and Trp, occur with high propensities in both APRs and antigen binding sites. Incidence of APRs is not uniform in all CDR loops. In particular, APRs are less frequent in the heavy chain CDR 3 (H3) loops. On the other hand, APRs are found with the greatest frequencies in the heavy chain CDR 2 (H2) loops. Rational structure-based design strategies for therapeutic antibody candidates with both high potency and improved druggability are proposed.

MATERIALS AND METHODS

Dataset of Fab-Antigen Complexes

The term antigen is used throughout to refer to all binding partners of Fab in the complexes as defined by Janeway et al. (2004) (38). The complexes included in this study were collected from the Protein Data Bank (31) based on the following criteria. (a) The resolution is 2.5 Å or better. (b) Antigen is protein with at least 50 residues; complexes with small molecule haptens, polysaccharides, peptides and RNA as antigens are not included. (c) The complex has full Fab structure; complexes with Fv or single chain of antibody are not included. (d) The antibody sequences contained in complexes are non-redundant. This last criterion was hard to meet because the antibody sequences show high homologies when both variable and constant regions are included in the alignments. We retained one complex with best resolution from a set of complexes where both light chains and heavy chains of the Fabs showed greater than 90% sequence identity. The choice of 90% sequence identity is arbitrary. The average sequence identities for variable regions of Fab light and heavy chains in the final dataset are 60% and 55%, respectively. This indicates that we have a fair coverage of antibody sequence variation in our dataset. If more than one complex were present in the crystallographic asymmetric unit, only one copy is retained. (e) Catalytic antibodies are not included.

Our final dataset consists of 24 Fab-antigen complexes (resolution range: 1.2–2.5Å). We supplement this dataset with all the five available commercial Fab-antigen complexes. Among the five commercial Fab-antigen complexes, one complex (PDB ID: 1CE1) has an eight-residue-long peptide as antigen. Antigens in the other four complexes are proteins. These complexes satisfy the selection criterion on antigen type and size but not on resolution. The resolution for these structures varies from 1.9 Å to 2.61 Å. Overall, there are 29 complexes in our study with resolution range of 1.2–2.61 Å. This dataset compares favorably with the crystal structural datasets used in the previous studies of antibody-antigen complexes (32,35,36).

Definition of CDRs

Andrew Martin’s definition of complementarity-determining regions (CDRs) in antibody is followed (36). We chose this definition because it is based on antibody-antigen contact analysis, which shares similarity with our identification of recognition sites. Kabat numbering scheme is adopted (39).

Identification of Potential Aggregation-Prone Regions

The potential aggregation prone regions (APRs) are identified using a similar approach as described in our previous work (30). Two sequence-based prediction tools, viz. TANGO (28) and PAGE (29), are used to identify potential APRs. The aggregation propensity (lnπ) from PAGE is converted to Z score to identify the regions with statistically high aggregation propensity. The Z score of residue i is calculated as follows:

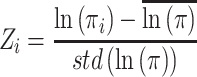1

where 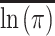is the average aggregation propensity of the sequence, and std(lnπ) is the standard deviation about average aggregation propensity.

We identify a region of sequentially consecutive residues as aggregation prone (APR) if any of the following criteria is satisfied:

• (i)The TANGO scores of five or more consecutive residues are ≥ 10%. Such APRs are assigned type 1 and are considered strong predictions.
• (ii)PAGE Z score is at least 1.96. Such APRs are assigned type 2 and are considered strong predictions.
• (iii)TANGO scores are ≥ 5% and PAGE Z score is ≥ 1. Such APRs are assigned type 3 and are considered weak predictions.

TANGO was reported to yield a success rate of 92% for peptides with TANGO score of 5% or greater (28). We use a more stringent cutoff of 10% to ensure APRs of type 1 are strongly predicted. APRs of type 2 are also strong predictions, as Z = 1.96 corresponds to 95% statistical confidence level. APRs of type 3 are weak predictions due to lower cut-off values.

As an example, Fig. 1 shows the TANGO and PAGE profiles for the light chain of the Fab in VEGF-blocking Fab—Neuropilin-1 complex (PDB ID: 2QQN). The types of APRs identified with the above criteria are labeled. This chain has all three types of APRs. APRs of type 3 are not frequent in our dataset. The APR at residue 131–136 is of both type 1 and type 2.

Fig. 1.

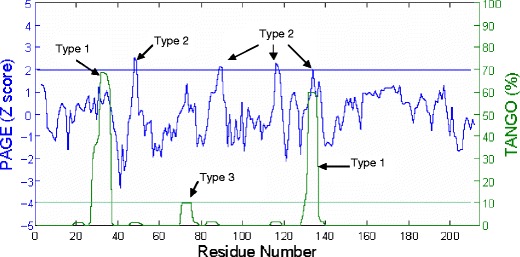
The TANGO and PAGE profiles for the light chain of the Fab in VEGF blocking Fab—Neuropilin-1 complex (PDB ID: 2QQN). X-axis shows residue number. Left Y-axis and blue curves are for PAGE Z score. Right Y-axis and green curve are for TANGO aggregation percentage. The blue horizontal line indicates PAGE Z score = 1.96. The green horizontal line indicates TANGO aggregation percentage = 10%. The peaks are labeled according to type of APRs (see Material and Methods).

We deliberately used two computational programs with substantially different algorithm philosophies. This ensures that identification of APRs in our dataset is not influenced by the peculiarities of the training sets and algorithms used in the development of computer programs. We note that APRs of type 1 and type 2 often overlap in our Fab sequences. The overlapping APRs are merged into single APRs in our data analysis.

Optimization of Antibody-Antigen Complex Structures

All structures of Fab-antigen complexes have been subjected to optimization. The optimization is performed using the modeling package Molecular Operating Environment (MOE) from Chemical Computing Group (http://www.chemcomp.com/). The optimization includes two major steps, viz., building the missing heavy atoms or residues (if any) and energy minimization.

Step One: Building the Missing Heavy Atoms and Residues

Each complex structure is first scanned for missing heavy atoms or residues. Complexes without missing atoms or residues are optimized via energy minimization only, and this step is skipped.

If the missing atoms in the complex are side-chain-heavy atoms, they are built using the rotamer library in MOE. The qualities of the side-chain models built in MOE are ranked based on energies, RMSD, and side-chain torsion angles. The side-chain model with first rank is chosen.

For those complexes with missing backbone atoms or residues, the full structures are built via homology modeling. The chain containing missing residues is the target to be built. The original structure of the target is used as primary structure template in homology modeling. An additional structural template is chosen such that it shares high overall sequence identity with the target sequence and contains coordinates for the missing residues. Thus, the additional template is applied only for the missing residues. In each homology modeling, 100 intermediate models are generated and ranked by Generalized Born/Volume Integral (GB/VI) scoring (40). The model with the best GB/VI score is chosen and further optimized via energy minimizations.

Step Two: Energy Minimizations of the Complexes

All-atom AMBER99 force field is used in energy minimization of each complex (41). A cut-off of 12 Å with switching started at 10 Å is applied to van der Waals as well as Coulombic interactions. Generalized Born-implicit solvation is employed. Interior and exterior dielectric values are 4 and 80, respectively.

Energy minimization is performed in two steps: (a) the hydrogen atom positions are optimized while heavy atoms kept harmonically tethered, and (b) all atoms are then energy minimized until gradient falls below 0.001. The optimized structures show less than 2 Å Cα RMSD with respect to the original structures.

Fab-Antigen Recognition Sites and Interface Areas

We use buried surface area to identify Fab-antigen recognition sites and gauge Fab-antigen interface. The buried surface area is referred to the surface area on both Fab and antigen that is accessible to solvent when Fab and antigen are separated but becomes inaccessible to solvent due to Fab-antigen complex formation. The solvent-accessible surface area (ASA) is calculated using the algorithm of Lee & Richards as implemented in the program Accelrys Discovery Studio (42). The probe of water solvent is 1.4 Å in radius.

The total buried surface area of a complex can be simply obtained as the sum of the ASA values of its isolated components minus that of the complex. Here, we calculate buried surface area in an equivalent hierarchical way in order to obtain the following quantities: (a) residues in Fab-antigen recognition sites, (b) total buried surface areas of the complex and contributions from its Fab and antigen components, (c) contribution of APRs in Fab to buried surface area, and (d) polar fraction of buried surface area.

Our hierarchical calculations start at atom level. First, the buried surface area of an atom is obtained as the difference between the ASA of that atom in isolated component and in the complex. Second, the buried surface area of a residue is calculated as the sum of the buried surface areas of all atoms in that residue. The binding sites are identified at residue level. A residue is considered as a Fab-antigen recognition/binding site if its buried surface area is ≥6 Ų. The cut-off of 6 Ų is arbitrary. We have also tried lower cut-off values of 3–5 Ų. The differences are minor. Third, the buried surface areas of Fab and antigen are the sums of those of binding residues in Fab and antigen, respectively. In a similar way, buried surface area of APRs in Fab is the sum of those of binding residues which also belong to APRs. Finally, total buried surface area of the complex is obtained as the sum of buried surface areas of Fab and antigen. Polar and non-polar buried surface areas are summed from polar and non-polar atoms, respectively. In our calculation, all carbon atoms are treated as non-polar. All oxygen and nitrogen atoms are considered polar. The sulfur atoms are considered non-polar if they are disulfide bonded. Otherwise, they are treated as polar.

We have also tried to identify the interface contact residues using the distance methods as employed by Tsai et al. (1996) (34). A residues pair is considered to be in contact between Fab and antigen if at least one heavy atom pair in the two residues is within a cut-off value (5Å). We obtained almost identical sets of binding site residues.

Hydrogen Bonds and Ion Pair Contacts

The program MOE is used to search hydrogen bond and ion pair contacts between Fab and antigen. The criteria for hydrogen bond proposed in Reference 43 is followed (43). The ion pair contact is inferred if a pair of nitrogen and oxygen atoms belonging to oppositely charged residues is within cut-off of 4.5 Å.

Propensity Value Calculations

Propensity P _bi of amino acid i to be a binding residue in Fab is calculated using the equation (44)

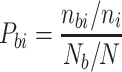2

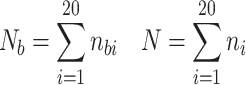3

where n _bi = number of amino acid i at binding sites of Fabs, n _i = total number of amino acids i in the heavy and light chains of the 29 Fabs in our dataset, N _b = total number of binding residues in Fabs, and N = total number of amino acids in heavy and light chains of the 29 Fabs.

Propensity P _ai of amino acid i to occur at APRs in Fab is calculated in similar way, using the equation

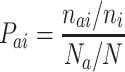4

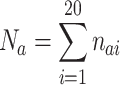5

where n _ai = number of amino acid i in APRs of Fab, N _a = total number of APR residues, and n _i and N have same meaning as in Eqs. 2 and 3.

RESULTS

Our dataset contains 29 Fab-antigen complexes taken from the Protein Data Bank (Table I). Twenty-four of these structures (Number 1–24 in Table I) are for non-commercial Fab-antigen complexes selected based on criteria outlined in Materials and Methods. The bottom five complexes in Table I are the commercially available Fab-antigen complexes. In all but one (PDB ID: 1CE1) case, the antigens in our dataset are proteins with at least 50 amino acid residues. Inclusion/exclusion of this complex does not impact our results significantly.

Table I.

List of Fab-Antigen Complexes

Number	PDB ID	Description	Resolution (Å)	R-Free
1	1FE8	Von Willebrand factor A3 domain/Fab fragment of IGG RU5 that inhibits collagen binding	2.03	0.264
2	1FNS	Von Willebrand factor A1 domain I546V mutant/the function blocking Fab NMC4	2	0.207
3	1H0D	Human angiogenin/Fab of mAb 26-2F	2	0.272
4	1IQD	Human factor VIII C2 domain/human monoclonal BO2C11 Fab.	2	0.253
5	1JPS	Tissue factor/humanized Fab D3h44	1.85	0.224
6	1KB5	Murine T-cell variable domain/Fab	2.5	0.221
7	1LK3	Engineered human interleukin-10 monomer/9D7 Fab fragment	1.91	0.24
8	1MLC	FAB D44.1/lysozyme	2.5	0.282
9	1OSP	Outer surface protein A of borrelia burgdorferi/Fab of a murine mAb	1.95	0.295
10	1UJ3	A humanized Fab fragment of anti-tissue-factor antibody/tissue factor	2.1	0.227
11	1WEJ	IgG1 Fab fragment (of E8 antibody)/horse cytochrome C	1.8	0.256
12	1YQV	Fab HyHEL5/lysozyme	1.7	0.234
13	1ZTX	West Nile virus envelope protein DIII/neutralizing E16 antibody Fab	2.5	0.282
14	2B2X	VLA1 RdeltaH I-domain/a quadruple mutant of the AQC2 Fab	2.2	0.272
15	2CMR	HIV-1 neutralizing antibody D5 Fab/the GP41 innter-core mimetic 5-helix	2	0.258
16	2DD8	SARS-CoV spike receptor-binding domain/neutralizing antibody	2.3	0.261
17	2FD6	Human urokinase plasminogen activator/urokinase receptor and an anti-upar antibody	1.9	0.276
18	2NXY	HIV-1 gp120 envelope glycoprotein(S334A)/CD4 and antibody 17b	2	0.231
19	2Q8B	Malaria antigen AMA1/growth-inhibitory antibody	2.3	0.256
20	2QQN	Neuropilin-1 b1 Domain/VEGF-blocking Fab	2.2	0.207
21	2R0L	Short form HGFA/Inhibitory Fab75	2.2	0.248
22	2VDR	Integrin alphaIIBbetaA3 headpiece/a chimeric fibrinogen gamma chain peptide	2.4	0.193
23	3D85	Crystal structure of IL-23/neutralizing Fab	1.9	0.214
24	3D9A	HyHel10 Fab/hen egg lysozyme	1.2	0.205
25	1BJ1	Vascular endothelial growth factor/neutralizing antibody	2.4	0.266
26	1CE1	Therapeutic antibody Fab/a synthetic peptide antigen	1.9	0.27
27	1N8Z	Extracellular domain of human HER2/therapeutic Fab	2.52	0.284
28	1SY6	Crystal structure of CD3γε heterodimer/therapeutic Fab	2.1	0.255
29	1YY9	Extracellular domain of the epidermal growth factor receptor/neutralizing Fab	2.61	0.289

Our study is based on analysis of 29 Fab-antigen complex crystal structures (listed above) with resolution range 1.2–2.61 Å. All the Fabs in this study are different. This dataset compares favorably with the previous studies of Fab-antigen complex crystal structure data analyses (32,35,36). For example, Jackson et al. (1999) had studied 15 Fab-antigen complexes with resolution range 1.8–3.0 Å (32). The dataset of Lo Conte et al. (1999) contained 19 Fab-antigen complexes with resolution range 1.8–3.0 Å (35). The study of MacCallum et al. (1996) was based on 26 Fab-antigen complexes with 1.8–3.1 Å (36)

Location of Potential Aggregation-Prone Regions

The multiple sequence alignments of light chains and heavy chains of Fabs are presented in Fig. 2a and b, respectively. The potential APRs obtained from TANGO (28) and PAGE (29) analysis are highlighted in Fig. 2 to facilitate direct comparison among the complexes. The APRs in variable domains (V_L and V_H) are primarily located in CDR loops and adjoining β strands. The APRs in constant domain (C_L and C_H) are well conserved in terms of location and composition. Each Fab in the complex contains 3–9 APRs with at least one of them being in CDR loops. These observations are consistent with our previous finding (30), even though different criteria are used here (see Materials and Methods section for details). In this study, we classify the APRs into types 1, 2, and 3. We consider APRs of types 1 and 2 to be strong predictions, while the type 3 APRs are weak predictions. Most of the APRs found in the CDRs and adjoining regions are of types 1 and 2. The APR “FTLTI” located in light chain framework region 2 for a few Fabs is of type 3. However, this APR is not involved in antigen binding.

Fig. 2.

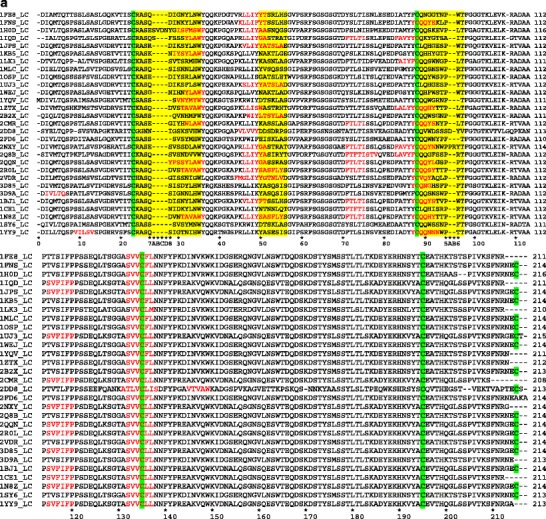
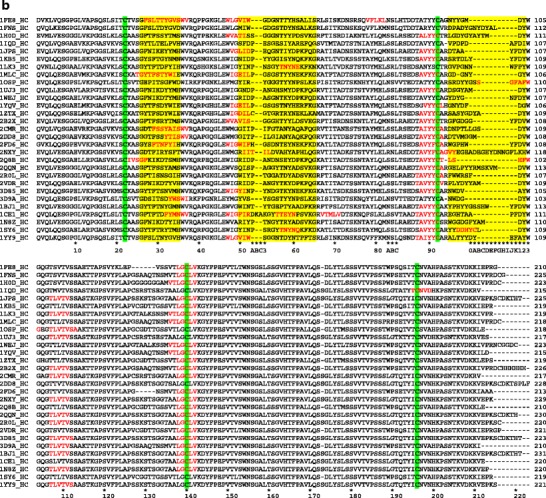
Multiple sequence alignments for (a) light and (b) heavy chains of the Fabs in our dataset. The Fab sequences are arranged in the same order as they are listed in Table I. All conserved Cys residues are highlighted in green. The CDRs are highlighted in yellow. The predicted APRs are shown in red letters. Kabat numbering is shown at the bottom of sequence alignment (39).

Contribution of CDR Localized APRs Towards Antigen Recognition

Table II (column 3 and 4) lists the buried surface area of Fab and antigen. Total buried surface area of a complex is the sum of buried surface areas of its two components, namely, Fab and antigen. Total buried surface areas (column3 + column4) of the 29 complexes range from 900 to 3,000 Ų, reflecting the general nature of protein-protein interfaces (35,37,45,46). Contributions from Fab and antigen to total buried surface area are close to half-and-half. The average total buried surface area for the complexes in our dataset is 1,915 ± 504 Ų, if we exclude therapeutic Fab-peptide complex (PDB ID: 1CE1). The buried surface area in this excluded complex is particularly small (926 Ų) due to the small size of peptide antigen.

Table II.

Buried Surface Area of Fabs, APRs in Fabs and Antigens in Fab-Antigen Complexes

Number	PDB ID	Fab (Å2)	Antigen (Å2)	APRs in Faba (%)	Number	PDB ID	Fab (Å2)	Antigen (Å2)	APRs in Faba (%)
1	1FE8	970	1,012	29.8	16	2DD8	895	906	6.0
2	1FNS	628	703	3.7	17	2FD6	679	732	22.4
3	1H0D	699	731	2.4	18	2NXY	695	703	22.2
4	1IQD	1,064	1,265	10.8	19	2Q8B	1,303	1,291	35.8
5	1JPS	1,229	1,229	5.7	20	2QQN	468	464	42.7
6	1KB5	1,489	1,435	13.7	21	2R0L	1,078	1,128	12.3
7	1LK3	919	952	10.8	22	2VDR	997	1,020	15.7
8	1MLC	718	810	33.3	23	3D85	720	755	8.7
9	1OSP	845	756	0.0	24	3D9A	878	921	9.5
10	1UJ3	1,140	1,113	5.4	25	1BJ1	933	1,040	2.5
11	1WEJ	627	715	13.2	26	1CE1	369	557	16.6
12	1YQV	825	923	19.1	27	1N8Z	1,153	1,270	29.2
13	1ZTX	755	808	20.2	28	1SY6	826	916	23.2
14	2B2X	1,480	1,500	17.2	29	1YY9	1,068	1,083	14.5
15	2CMR	1,188	1,186	18.5

^aPercent contribution towards buried surface area by the binding residues in Fab which also belong to APRs

Contribution of APRs towards antigen recognition is measured by their contributions to the surface area of Fab buried upon complex formation. Amino acid residues from CDR-localized APRs contribute towards antigen binding in 28 out of 29 Fab-antigen complexes in our dataset. The percentage contributions are shown in Table II (column 5). On average, 16.0 ± 10.7% (range: 0–42.7%) of buried surface area of Fabs can be attributed to APRs. The variation is large. For example, in case of the murine antibody Fab-protein A complex (PDB ID: 1OSP), the variable domain contains only one APR which falls in H3 loop but does not participate in antigen binding. In the case of the VEFG-blocking Fab—Neuropilin-1 complex (PDB ID: 2QQN), the contribution of APRs is the highest (42.7%). APRs contribute more than 10% to buried surface area of Fab in 20 out of the 29 complexes (69%). Among commercial antibodies, with the exception of the neutralizing Fab-VEGF complex (PDB ID: 1BJ1), APRs account for greater than 15% of buried surface area of Fab. Fig. 3 shows, as an example, the structure of the IGG RU5 Fab-Von Willebrand factor complex (PDB ID: 1FE8). In this case, 29.8% of buried surface area in Fab is attributed to binding residues that belong to APRs. These observations indicate aggregation may be coupled with antigen binding function of antibodies.

Fig. 3.

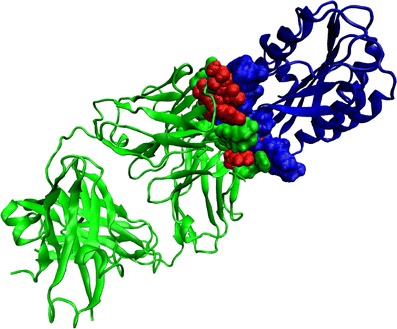
Ribbon representation for the structure of IGG RU5 Fab (green)-Von Willebrand factor (blue) complex (PDB ID: 1FE8). Only the binding residues in the Fab-antigen complex identified by our method are shown in CPK representation. Binding residues in Fab that also belong to APRs are shown in red color.

The polar fractions of buried surface areas of Fabs and the share of APRs towards these fractions are shown in Fig. 4a and b, respectively. Polar surface area calculated in this study consists of the buried surface areas from both neutral polar and charged atoms. On average, the Fab part of interface is 56 ± 7% polar. This value is similar to an earlier average value (49%) for antibody-antigen interfaces (35). The electrostatic and polar interactions have been known to be important factors in determining affinity and specificity of antibody-antigen complexes (47,48).

Fig. 4.

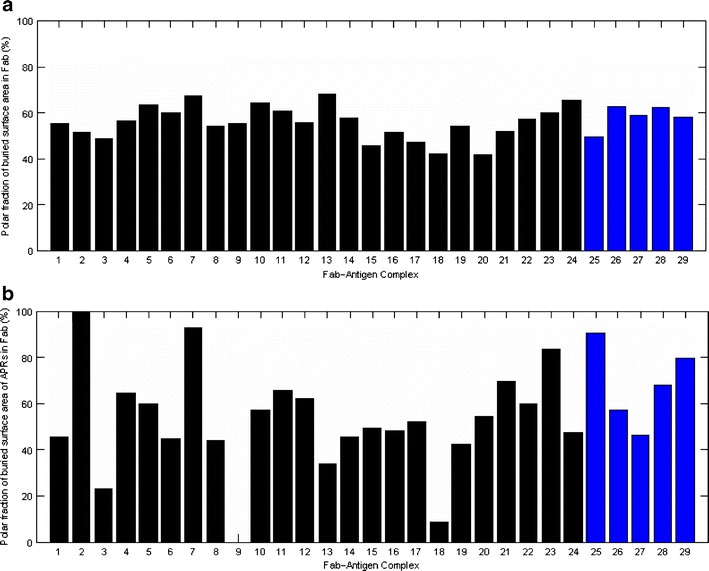
(a) Polar fraction of the buried surface area of Fabs for all complexes in our dataset. (b). Polar fraction of the buried surface area of APRs in Fab. The last five commercial Fab-antigen complexes are in blue color.

The APRs considered in the Fig. 4b are those found in the antigen-binding regions of Fabs. The average polar fraction of buried surface area of APRs is 55 ± 19% (range 9–93%) after excluding two outliers described below. This value is similar to that for Fabs. However, the variation is now wider. In case of murine antibody Fab-Protein A complex (Complex 9), the polar fraction for this complex is not available because none of the APRs contribute to the buried surface areas. For the Fab NMC4-Von Willebrand factor complex (Complex 2), the buried surface area of the APRs comes from only one binding residue (E92), which is hydrophilic, leading to 100% polar fraction. In four out of the five commercial Fab-antigen complexes, the APRs show greater than 50% polar fraction.

Propensity of Amino Acids to Occur in Binding Sites of Fabs and in APRs

Table III lists the antigen-binding residues of Fabs. The binding residues that also belong to APRs are highlighted in bold (Table III). The buried surface areas contributed by these binding residues are unequal. The binding residues are primarily located in CDR loops, with a few of them in the framework regions (FRs). Y49 in light chains is identified as a binding site residue in a few complexes. It immediately precedes L2 loops and, technically, falls in FR2. However, we pooled this residue with those in L2 in our analysis. Several residues in CDRs loops do not participate in antigen binding (Table IV). However, these non-binding residues may help CDR loops acquire the proper backbone conformations essential for binding (49).

Table III.

List of All Antigen Binding Residues in Fabs of Our Study

Number	PDB ID	L1			L2				L3			H1				H2					H3						Non-CDR
1	1FE8	D28	G30		Y49	Y50	R53		G91	G92	T93	T30	T31	Y32		W52	G53	D54	N56		Y96	Y97					S67 (LC)
		N31	Y32						N94	W96
2	1FNS	N30	Y32						E92	L94	W96					M50	W52	D54			A97	D98	Y99	G100
																S56	T57	D58			N100A	Y100B	Y100D
3	1H0D	N27D	Y28						S91	K92	E93	T33				T50	S52	S52A			L95	Y98	Y100B
		F32							V94	L96						G53	N56	Y58
4	1IQD	S29	S30		Y49	G50	T53		G92	T93	I96	Y27	E31	L32		S50	D52	E53			V95	P96	D97				Q1	V2 (HC)
		S31	Y32		R54	A55	T56					P33	H35			E56	I58				P98	D99	D101
5	1JPS	R27	D28		Y50	E56			H91	G92	E93	K30	E31			L50	D52	E53	Q54	N56	T96	A97	A98	Y100J
		K30	Y32						S94	P95	W96	Y32	Y33			T57	I58	Y59	Q64
6	1KB5	K27	Y30		Y49	N50	K52		H91	Y92	G93	S28	T30			Y53	Y54	G55	G56	I57	R96	T97	D98				D1 (LC)
		S31	Y32		T53	E56			T94	Y96		G31	Y32			S58	Y59	Q61	K64		L99	Y100	Y100J
7	1LK3	E27	S28		K50				S91	W92	N93	Y33				Y50	N52	N53	S54	Y56	V96	P97	G98				D1 (LC)
		T30	R32						G94	P95	L96					T57	N58	Y59	E61		N99	N100
8	1MLC	N32			Y50				S91	N92	S93	S30	T31			E50	L52	G53	S54		G95	D96	G98
									W94	R96		Y32	W33			S56	T57	Y58
9	1OSP	Y30	S31	R32	G50	T52	S53		Y91	W92		S31				Y53					R96	D97	Y98	Y99	G100		D66 (LC)
10	1UJ3	Q27	K30	F32	Y50	T52			H91	G92	E93	K30	D31			D52	A53	N54	H56		D95	S96	G97	Y98			D1 (LC)
									S94	Y96		Y32	Y33			S57	M58	Y59	Q64		D96	Y97	G98
11	1WEJ	H30	N31	Y32	N50	K52			W92			K30	D31	Y33		D52	A53	S54	N56
12	1YQV	N31	Y32		D50				W91	G92	R93	S30	D31	W33		E50	L52	S54	G55
																S56	T57	N58			G95	N96	Y97	D98			W47 (HC)
13	1ZTX	S30			W50				H91	Y92		Y27	T28	D31		L52	R56	R58			R94	S95	S97
									T93	T94		Y32	W33								Y98	G99	D100
14	2B2X	Q29	V30		Y49	L50	S52	Y53	W91	S92		T28	S30	R31		V50	S52	G53			R94	F96	G97				V2	W47 (HC)
		N31	H32		L54	A55	S56		N94	W96		Y32	T33			G54	H56	Y58			D98	Y100J	D101
15	2CMR	Y30	H31		K50				Y91	S92		S30	S31			I52	I53	F54	G55		D95	N96	P97				E73 (HC)
		W32							N93	Y94		Y32	A33			T56	A57	N58	Y59		T98	L100
16	2DD8	N27	S30						W91	S93	S94	S31	Y32	T33		T52	I53	L54			D95	T96	V97	M98
									D95A	Y96						I56	N58
17	2FD6	S31	Y32		K53				W91	N92		N31	Y33			W50	F52	D55	N56		W95	H98	W99
									Y93	F95						T57	E58	Y59
18	2NXY								W94	P95						I52	I53	L54			E99	E100B	G100C	E100D
																V56	H58				Y100E	D100F	N100G
19	2Q8B	D32	V34		Y49	Y50	I53		G91	R96		S25	G26	F27	K28	R50	D52	A53			L95	S96	H101	F102			E1	V2	Q3	L4	S74
					R54	Y55	T56					D31	T32	S33													S75	N76 (HC)
20	2QQN	Y28	S30						L92												E96	Y99	Y100				S67	G68 (LC)
		S31	Y32																		R100A	M100B
21	2R0L	D28	S30						S91	Y92	T93	N31	S32	H35		W50	Y52	T53	G54	G55	R94	F95	W96
		T31							T94	P96						A56	T57	D58	K64		W97	R98
22	2VDR	S30	N32		Y49	Y50			Y91	A92		D31	T32	Y33		R50	D52	N54			Y97	D98	Y99	Y100
					N53	D56			Q93	L94						Y56	K58
23	3D85	Y32			Y50				G91	H92	S93	T30	S31	N32		Y50	N52	Y53			N95	W96	D97	V98
									F94	F96		V33	H35			N54	T57	K58
24	3D9A	G30	N31		K49	Y50			S91	N92	S93	D27	T30	S31		Y50	Y53	S54			W96	D97
		N32			Q53				W94	Y96		D32	Y33			S56	Y58
25									Y91	S92					W50	N52	Y53	T54			Y95	P96	H97	Y98	Y99	G100
	1BJ1	Y32							V94	W96		N31	Y32	G33	E56	P57	T58				S100A	S100B	W100D
26									H91	192	S93
	1CE1	Y32			Y49	N50			R94	R96		Y33			F50	R52	K53				E95	G96	H97	A100
27		D28	N30		Y49	S50	F53					G26	F27	D31	R50	Y56					R94	W95	G96	G97	D98		R66(LC)	V2(HC)
	1N8Z	T31	A32		Y55	S56			H91	Y92	T94	T32	Y33		T57	R58					G99	F100	Y100A	Y102
28									W91	S92		T28	T30		Y50	N52	S53
	1SY6	S31	Y32		D50				S93	N94		R31	T33		R54	Y56	N58				D97	D98	Y100
29		Q27	S28						N91	N92	N93				W52	S53	G54	G55			T97	Y98	Y99
	1YY9	N32			Y50				W94	T96		T30	N31		N56	T57	D58				D100	Y100A					D1	(LC)

Table IV.

Contribution of Individual CDR Loop Towards Antigen Recognition

CDR Statistics	L1	L2	L3	H1	H2	H3	FR
Length of CDR loop (L)	12.0 ± 0.9	7.0 ± 0.0	9.0 ± 0.5	10.0 ± 0.0	16.9 ± 0.6	9.8 ± 3.0
Number of binding residues (Nb)	2.6 ± 1.2	2.0 ± 2.1	4.0 ± 1.4	3.1 ± 1.8	5.7 ± 2.3	4.7 ± 1.8	0.8 ± 1.4
Ratio 1 (%, Nb / L)	21.7	28.6	44.4	31.0	33.7	48.0
Percentage of buried surface area of Fab (SA buried)	12.3 ± 8.4	7.4 ± 7.5	17.3 ± 8.6	12.1 ± 8.3	23.5 ± 10.9	25.0 ± 13.8	2.3 ± 5.1
Ratio 2 (SA buried / Nb)	4.7	3.7	4.3	3.9	4.1	5.3
Number of hydrogen bonds and ion pairs	1.6 ± 1.6	0.7 ± 1.0	2.1 ± 1.7	1.8 ± 1.7	3.5 ± 2.6	3.1 ± 2.0

Fig. 5a and b compare the propensity of individual amino acid to occur in antigen-binding sites and in APRs in our dataset. Residues with propensity values above one are favored, while those with propensity values below one are disfavored. Our results are in general agreement with previous analysis on antibody-antigen interface (32,35). For example, Trp, Tyr and Arg, favored at antigen-binding sites in our analysis (Fig. 5a), are also the hot-spot residues for protein interfaces (50).

Fig. 5.

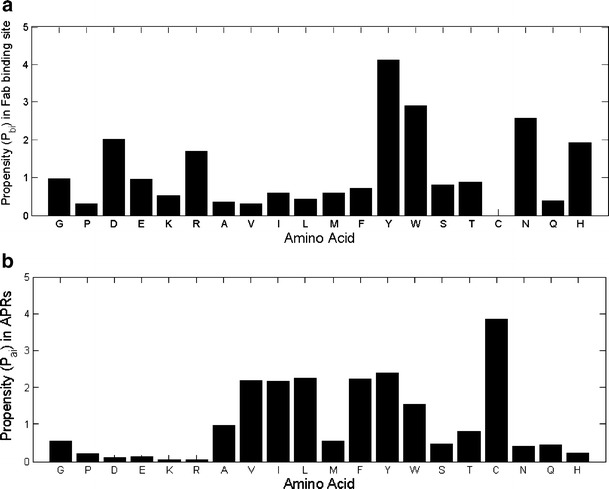
(a) Propensity (P_bi) of individual amino acid to occur at binding sites in Fab. (b) Propensity (P_ai) of individual amino acid to occur in APRs in Fab.

The APRs considered in propensity calculations are the APRs present in the overall sequences of Fabs including both variable (contributing towards binding) and constant domains (non-contributing ones) (Fig. 5b). Again our results are consistent with previous analyses of APRs (30,51,52). The aromatic residues (Tyr and Trp) and β-branched aliphatic residues Val, Ile, and Leu are favored in APRs. Charged residues are strictly avoided in APRs. Taken together, aromatic residues, Tyr and Trp, are favored both in antigen-binding sites and APRs. Hence, these residues may be the coupling agents between aggregation and antigen recognition.

Buried Surface Area Contributions and Coincidence of APRs with Individual CDR Loops

Fig. 6a shows the contribution of each CDR loop towards the buried surface area of the Fabs in the complexes. The average values along with the number of binding residues and CDR length are also presented in Table IV. The buried surface area values are very similar to those obtained by Wilson and Stanfield (1994) (53). On average, H3 loops contribute the most towards antigen binding (25 ± 13.8%, Table IV). The portion of residues that directly contact antigens is also the greatest (48%) for H3 loops. If the average buried surface area contribution for each loop is normalized by number of binding residues in the loop, H3 loops again have the greatest contribution (5.3% per residue). Consistently, the variability plots of antibody sequences and statistical studies of antigen-contacting residues have shown that H3 loops are important for antibody specificity (36,54,55).

Fig. 6.

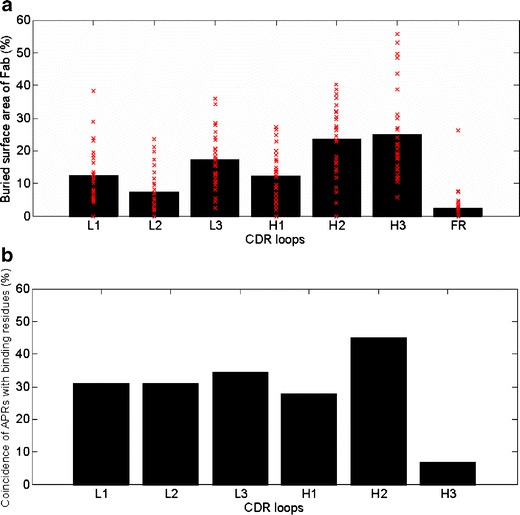
(a) Contribution of each CDR loop towards the buried surface area of Fab. Contributions from all framework regions (FR) are pooled and are shown as FR contribution. The bars show the average values over all complexes. The red crosses show the individual values for the 29 complexes. (b) Coincidence between APRs and binding residues in CDR loops. It is counted as one incidence if a CDR contains at least one binding residue which also belongs to an APR. For example, the coincidence between APRs and binding residues in L1 is 31%. This means L1 loops of 9 out of the 29 complexes (31%) contain at least one binding residue which also belongs to APR.

The average contribution of H2 loops is almost equal to that of the H3 loops (23.5 ± 10.9%; Table IV). H2 loops are the longest among CDR loops (16.9 ± 0.6 residues), and they contribute the most residues (5.7 ± 2.3) towards antigen binding (Table IV). The average buried surface area contribution by L3 loops is the third largest (17.3 ± 8.6%). Taken together, these three loops, namely, H3, H2 and L3, contribute approximately two-thirds (65.8 ± 17.7%, range: 19–100%) of the buried surface area of the Fabs. The shortest CDR loops, L2, also contribute the least (7.4 ± 7.5%, Table IV). In fact, these loops do not contribute towards the buried surface area of Fabs in seven (24%) complexes in our dataset (Fig. 6 and Table III). The overall contribution of the CDR loops in heavy chain (CDR loops: H1+H2+H3) towards buried surface area of Fab is 60.7 ± 11.3% (range 43–86%). Only in 6 out of 29 (approximately 21%) complexes, the heavy chain CDR loops contribute less than 50%. We have also counted the numbers of hydrogen bonds and ion pairs between Fab and antigen to study the specific interactions at Fab-antigen interfaces (Table IV). On average, the trend is the same. H2, H3 and L3 loops again make the greatest number of hydrogen bond and ion pair contacts with the antigens.

Fig. 6(b) plots the frequency of coincidence of APRs and binding residues in CDR loops. These values estimate the potential coupling between aggregation and antigen recognition for each CDR loop. Residues in APRs are also among the antigen-binding residues in CDR loops with an average frequency of 29.3 ± 12.5%. The two most important antigen-binding contributors, H2 and H3, show very different aggregation coupling frequencies. H2 loop has the highest APR incidence (44.8%), while H3 loop shows the lowest incidence (6.9%). The coincidences of APRs and binding residues in other CDR loops, L1, L2, L3 and H1, are similar (31.0 ± 2.8%).

DISCUSSION AND CONCLUSION

In the literature, there is increasing consensus that aggregation is an intrinsic property of proteins. In our previous work, we found that commercially available therapeutic mAbs contain short APRs similar to those seen in the amyloidogenic proteins (30). Interestingly, some of the potential APRs in mAbs overlapped with the CDR regions. However, that study could not tell if the APRs localized in the CDRs in those mAbs actually contributed to antigen recognition also. Present survey shows that CDR-localized potential APRs contribute significantly towards antigen recognition. This suggests the possibility of linkage between aggregation and loss of function in antibody-based therapeutics. This link is undesirable from the pharmaceutical point of view because therapeutic mAb drug substances as well as products are stored without their cognate antigens over long periods of time.

The link between aggregation and CDR loops has been previously reported based on experimental studies of domain antibodies (56). Moreover, APRs have been shown to overlap with protein-protein interfaces in general (57). Here, our survey seeks to understand the detailed characteristics of this link in the context of antibody-antigen recognition. Interestingly, we also observed that the APRs in Fc region of the mAbs lie close by but do not overlap with various protein (viz. F_cγ receptor(s), FcRn, Protein A and Protein G) binding sites. For example, APRs 269-VTCVV-274, 285-FNWYV-289 and 312-VVSVLTVL-319 lie close to but do not overlap with F_cγRIII and C1q binding sites in the crystal structure of the human antibody IgG1 b12 against HIV-1 (PDB code: 1HZH) (58).

Computational approaches towards identification of potential APRs utilize sequence (19,28,29,59,60) and structural (21) methods. In numerous instances, these predictions have been experimentally validated and used to design peptides and proteins with lower aggregation propensities (61,62). The sequence-based approaches have similar levels of accuracy as 3D profile-based ones (16). The sequence-based approaches are faster and require less computational resources as compared to the structural ones. These can be very useful in early discovery stage, where a large number of sequences are screened for potential leads. TANGO and PAGE are two such computational programs that require only the protein sequence as input. The prediction from TANGO relies on physicochemical rules behind β-sheet formation and assumes that the core of the aggregates is completely desolvated (28). It also takes into account the competition between other conformational states, such as α-helix, β-strand, turn, random coil and β-aggregates for the given sequence region. PAGE computes the aggregation propensity based on aromaticity, β-strand propensity, charge, solubility and hydrophobicity of the residues in window of 5–9 residues along the sequence (29). Both TANGO and PAGE have been used on a large number of peptides and small proteins and show high prediction accuracies. TANGO was found be more than 92% accurate in experimental validation studies (28). TANGO has also been used extensively by other groups (62–66). We used more than one program to identify APRs so that our results are not influenced by peculiarities of training sets and algorithms used. We noted good overlap between APRs of type 1 and type 2, indicating the general agreement between the two programs.

Molecular simulation techniques have also been used to study aggregation (22,23,25,26,67–69). This approach was recently applied to full-length antibody by Chennamsetty et al. (2009) (23,24). They have developed a technique named spatial-aggregation-propensity (SAP). SAP uses residue hydrophobicity and dynamical conformations collected from simulations to identify surface exposed hydrophobic patches. This concept is similar to the surface aggregation propensity used by Pechmann et al. (2009) (57). These surface-exposed hydrophobic patches can act as structural hot-spots for aggregation. These patches look for non-polar residues in close spatial vicinity on protein surfaces. The spatially vicinal residues do not have to be contiguous in amino acid sequence. Moreover, these surface patches are not necessarily potential cross β-aggregation sites. Hence, they are different from the cross β-motif-forming APRs identified by the sequence-based approaches. However, APRs also often contain hydrophobic β-branched aliphatic and aromatic residues. Hence, the APRs may overlap with the surface hydrophobic patches but not be completely equivalent to them. APRs can also be significantly polar, especially those containing Asn and Gln residues. The examples include yeast prion proteins sup35 and Ure2p and several neurodegenerative diseases, like Huntington’s disease (15,70–72). In the Fabs of our dataset, the APRs in L3 loops are polar (Fig. 2a). Overall, the APR and SAP approaches are complementary to each other.

To promote aggregation, an APR should have high intrinsic aggregation propensity, be conformationally unstable/flexible, be surface exposed or become exposed upon conformational transition and facilitate intermolecular interactions. Hence, three-dimensional structures are important for identifying which of the potential APRs could really initiate self-association. In a recent study, Hamada et al. (2009) studied the ability of individual β-strands to initiate amyloid-like fibril formation in β-lactoglobulin (73). They found that sequence regions with high intrinsic aggregation propensity still need at least local unfolding in the native structure to be able to seed aggregation. In light of this, one could postulate that the potential APRs in these surface-exposed CDR loops could seed aggregation in the therapeutic mAbs via self-association of Fabs. This process may be materially assisted by two factors: first, the mobility of the CDR loops is enhanced due to the absence of cognate antigens; second, the physico-chemical stresses may further perturb the native Fab structures locally.

Besides the strong experimental evidence for the existence of short sequentially contiguous cross β-aggregate- forming regions in general proteins, the available experimental evidence suggests that APRs may also play a similar role in biotherapeutic aggregation as well. Some of the evidence is discussed below.

1

Biopharmaceuticals at the end of expiration date were reported to form aggregates which bind Thioflavin T and Congo Red (27). Thioflavin T-binding is the characteristic of aggregates containing cross-β structures (7). Our previous analysis showed that the biopharmaceuticals reported by Maas et al. (2007) contain several TANGO/PAGE predicted APRs (See Table III in Reference 30) (30). Moreover, the TANGO/PAGE predicted APR 14-ALYLV-18 coincides with the experimentally proven fibril-forming segment 12-VEALYL-17 of insulin (21). Similar results were observed by us upon exposure of several different IgG2 mAbs to thermal stress (internal effort; data not shown).

2

Several experimental reports that study aggregation in the proteins and document the sequence changes in their variants (homologues or mutants) with reduced aggregation propensities were found to disrupt/mitigate the APRs predicted by TANGO and PAGE in our analyses. In particular, we cite three examples because of good agreement between the experiments and computational predictions. These are bovine growth hormone (74), amyloidogenic immunoglobulin light chain (75) and a human IgG1 mAb (23,24). We summarize our findings below; the details of these cases are presented in Supplementary Material. First, based on the experimental studies, Lehrman et al. have identified a sequence region 109–133 in bovine growth hormone (bGH) to be involved in aggregation (74). Our TANGO and PAGE analyses indicate the presence of APRs in this region (119-GILALM-124). The experimentally designed variants 8H-bGH and human growth hormone (hGH) differ in the sequence region 109–133 and show reduced aggregation propensity in the experiments of Lehrman et al. (74). Consistent with this observation, TANGO/PAGE spectra do not indicate an APR in this region for 8H-bGh and hGH. Second, Baden et al. (2008) have identified three non-conserved somatic mutations, I34N, Q42K and H87Y, which restore amyloidogenic immunoglobulin light chain AL-09 to its germline sequence κIO18/O8 (75). TANGO spectrum of AL-09 indicates a very strong APR containing I34 (32-YLIWY-36, TANGO aggregation score ∼90%). The PAGE spectrum shows an APR containing H87 (87-HCQQY-91). Both TANGO and PAGE did not find an APR involving the residues at the position 42. The corresponding TANGO spectra for both the germline sequence κIO18/O8 and the AL-09 mutants with reduced aggregation propensity indicate that APR 32-YLIWY-36 is substantially weakened for the germ line light chain due to the somatic disruption at position 34. However, APR 87-HCQQY-91 identified by PAGE remained unchanged. Third, L309K mutation in the C_H2 domain of intact IgG1 mAb studied by Chennamsetty et al. (2009) reduces its aggregation propensity as shown by turbidity and HPLC assays and improves its stability in DSC experiments (see Table I and Fig. 3 in Ref. 24) (24). This mutation actually disrupts a strong APR (302-VVSVLTVL-309) (TANGO aggregation score ∼90%) found in the Fc regions of IgG mAbs. This APR is well conserved among immunoglobulin Gs and was documented earlier (30). In all three cases, both TANGO and PAGE also detected additional APRs that were common between the proteins and their variants, indicating the potential for further reduction in aggregation propensities of the molecules.

3

Use of TANGO/PAGE predictions in combination with the molecular modeling can help identify positions/mutations to reduce aggregation propensities in the biotherapeutics. Recently, we observed that disruption of a TANGO-predicted strong APR in FR2-L2 region of an IgG2 mAb by a single point mutation reduced its aggregation propensity and improved solubility as indicated by biophysical experiments (in-house effort; data not shown).

Similar to small proteins and peptides, the potential APRs in the antibodies are also short sequence regions. Hence, one or a few changes in sequences that disrupt the CDR-localized APRs may significantly reduce aggregation propensity of the mAbs. From a product formulation and developability point of view, improvement in mAb stability and solubility is desirable. This may help improve expression levels in cell lines, facilitate high concentration dosage forms and increase shelf–life of the product. However, developability-related sequence mutations should not adversely impact the potency of the therapeutic mAbs. In this regard, the observed incidence of potential APRs in the CDR loops and adjacent framework β-strands is significant. Disruption of these APRs without affecting therapeutic mAb potency could be difficult and time-consuming without a rational approach. A structure-based input that simultaneously considers all these issues may lead to more “druggable” therapeutic candidates. The present study offers useful guidelines for drug candidate design and selection at early discovery and formulation stages:

1

Aromatic residues Tyr and Trp are favored both in APRs and CDRs (Fig. 5). Aromatic amino acids have been known to play an important role in directing molecular recognition, mostly because of their ability to form π-stacking interactions (76). Tyr is also frequently used in high affinity protein-protein interface design (77). Bogan et al. have reported that hot-spots of binding energy at protein interfaces are rich in Trp and Tyr (50). Hence, caution should be used when considering mutation of Tyr and Trp residues in mAb CDRs to alleviate aggregation because it could also impact mAb potency. Instead, mutation of a sequence neighbor to disrupt the APR’s amyloidogenic sequence pattern may be more appropriate.

2

The disruption of APRs should be performed in such a way that the CDR loop conformations, especially the conformations of residues that contribute substantially to antigen recognition, are not disturbed. Molecular models, crystal structures of Fab-antigen complexes and Alanine scanning experiments may help identify such binding hot-spot residues. Mutations affecting these residues should be avoided to preserve potency. On average, CDR loops H3, H2 and L3 contribute the most towards antigen recognition. H3 loops do contain fewer APRs, but this is not the case for H2 and L3 loops. While different binding site residues contribute unequally towards antigen recognition, there is still some risk that mutations in these loops could also impact potency of the mAb candidates. This is especially true at early discovery stages where Fab-antigen complex crystal structures are not yet available, antigen-binding residues are not well identified, and project time-lines are tight. On the other hand, L2 loops contribute the least towards antigen binding but often contain APRs (Fig. 6). Mutations aimed at disrupting the APRs in this region could help improve mAb stability without significantly impacting potency. Apart from L2 loops, L1 and H1 loops are the other regions where disruption of potential APRs can reduce mAb aggregation tendency and not impact the potency substantially.

3

Hydrophobic residues, especially Val, Ile and Leu, have high propensities for aggregation but not for antigen binding (Fig. 5). Hence, APR disruption via mutation of these residues to polar or charged residues should be considered, especially when these residues are close to the CDR regions and are surface exposed.

4

APR disruption in the constant regions of the mAbs can also reduce the aggregation propensity. However, in case of therapeutic mAbs, caution is advised because of the potential for drifting from germ-line sequences.

Electronic supplementary material

Below is the link to the electronic supplementary material.

ABBREVIATIONS

APR

aggregation-prone region

CDR

complementarity-determining region

Fab

fragment antigen binding

Fc

fragment crystallizable

FR

framework region

mAb

monoclonal antibody

PDB

Protein Data Bank