Skip to main content
PMC home page
Springer Nature - PMC COVID-19 Collection logoLink to Springer Nature - PMC COVID-19 Collection
. 2011 Jan 6;73(10):2305–2321. doi: 10.1007/s11538-010-9623-3

The Final Size of an Epidemic and Its Relation to the Basic Reproduction Number

Viggo Andreasen 1,2,✉
PMCID: PMC7088810  PMID: 21210241

Abstract

We study the final size equation for an epidemic in a subdivided population with general mixing patterns among subgroups. The equation is determined by a matrix with the same spectrum as the next generation matrix and it exhibits a threshold controlled by the common dominant eigenvalue, the basic reproduction number 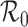Inline graphic: There is a unique positive solution giving the size of the epidemic if and only if 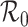Inline graphic exceeds unity. When mixing heterogeneities arise only from variation in contact rates and proportionate mixing, the final size of the epidemic in a heterogeneously mixing population is always smaller than that in a homogeneously mixing population with the same basic reproduction number 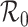Inline graphic. For other mixing patterns, the relation may be reversed.

Keywords: Heterogeneous mixing, Final size relation

References

  1. Anderson R. M., Donnelly C. A., Ferguson N. M., Woolhouse M. E. J., Watt C. J., et al. Transmission dynamics and epidemiology of BSE in British cattle. Nature (London) 1996;382:779–788. doi: 10.1038/382779a0. [DOI] [PubMed] [Google Scholar]
  2. Andreasen V. Instability in an SIR-model with age-dependent susceptibility. In: Arino O., Axelrod D., Kimmel M., Langlais M., editors. Mathematical population dynamics. Winnipeg: Wuerz Publ.; 1995. pp. 3–14. [Google Scholar]
  3. Andreasen V. Dynamics of annual influenza A epidemics with immuno-selection. J. Math. Biol. 2003;46:504–536. doi: 10.1007/s00285-002-0186-2. [DOI] [PubMed] [Google Scholar]
  4. Andreasen V., Frommelt T. A school-oriented, age-structured epidemic model. SIAM J. Appl. Math. 2005;65:1870–1887. doi: 10.1137/040610684. [DOI] [Google Scholar]
  5. Andreasen V., Sasaki A. Shaping the phylogenetic tree of influenza by cross-immunity. Theor. Popul. Biol. 2006;70:164–173. doi: 10.1016/j.tpb.2006.04.004. [DOI] [PubMed] [Google Scholar]
  6. Arinaminpathy N., McLean A. R. Antiviral treatment for the control of pandemic influenza: some logistical constraints. J. Roy. Soc. Interfaces. 2008;5:545–553. doi: 10.1098/rsif.2007.1152. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Arino J., Brauer F., van den Driessche P., Watmough J., Wu J. A final size relation for epidemic models. Math. Biosci. Eng. 2007;4:159–175. doi: 10.3934/mbe.2007.4.159. [DOI] [PubMed] [Google Scholar]
  8. Ball F. Deterministic and stochastic epidemics with several kinds of susceptibles. Adv. Appl. Probab. 1985;17:1–22. doi: 10.2307/1427049. [DOI] [Google Scholar]
  9. Boni M. F., Gog J. R., Andreasen V., Christiansen F. B. Influenza drift and epidemic size: the race between generating and escaping immunity. Theor. Popul. Biol. 2004;65:179–191. doi: 10.1016/j.tpb.2003.10.002. [DOI] [PubMed] [Google Scholar]
  10. Brauer F. Epidemic models with heterogeneous mixing and treatment. Bull. Math. Biol. 2008;70:1869–1885. doi: 10.1007/s11538-008-9326-1. [DOI] [PubMed] [Google Scholar]
  11. Corless R. M., Gonnet G. H., Hare D. E. G., Jeffrey D. J., Knuth D. E. On the Lambert W function. Adv. Comput. Math. 1996;5:329–359. doi: 10.1007/BF02124750. [DOI] [Google Scholar]
  12. Diekmann O., Heesterbeek J. A. P. Mathematical epidemiology of infectious diseases. Chichester: Wiley; 2000. [Google Scholar]
  13. Diekmann O., Heesterbeek J. A. P., Metz J. A. J. On the definition and the computation of the basic reproduction ratio R0 in models for infectious-diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
  14. Diekmann O., Heesterbeek J. A. P., Roberts M. G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface. 2010;7(47):873–885. doi: 10.1098/rsif.2009.0386. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Dwyer G., Dushoff J., Elkinton J. S., Levin S. A. Pathogen driven outbreaks in forest defoliators revisited: Building models from experimental data. Am. Nat. 2000;156:105–120. doi: 10.1086/303379. [DOI] [PubMed] [Google Scholar]
  16. Eames K. T. D., Keeling M. J. Modeling dynamic and network heterogeneities in the spread of sexually transmitted diseases. Proc. Natl. Acad. Sci. USA. 2002;99:13330–13335. doi: 10.1073/pnas.202244299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Elveback L. R., Fox J. P., Ackerman E., Langworthy A., Boyd M., Gatewood L. Influenza simulation-model for immunization studies. Am. J. Epidemiol. 1976;103:152–165. doi: 10.1093/oxfordjournals.aje.a112213. [DOI] [PubMed] [Google Scholar]
  18. Eubank S., Guclu H., Kumar V. S. A., Marathe M. V., Srinivasan A., et al. Modelling disease outbreaks in realistic urban social networks. Nature (London) 2004;429:180–184. doi: 10.1038/nature02541. [DOI] [PubMed] [Google Scholar]
  19. Ferguson N. M., Donnelly C. A., Anderson R. M. Transmission intensity and impact of control policies on the foot and mouth epidemic in Great Britain. Nature (London) 2001;413:542–548. doi: 10.1038/35097116. [DOI] [PubMed] [Google Scholar]
  20. Ferguson N. M., Cummings D. A. T., Cauchemez S., Fraser C., Riley S., et al. Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature (London) 2005;437:209–214. doi: 10.1038/nature04017. [DOI] [PubMed] [Google Scholar]
  21. Gart J. J. The mathematical analysis of an epidemic with two kinds of susceptibles. Biometrics. 1968;24:557–565. doi: 10.2307/2528318. [DOI] [PubMed] [Google Scholar]
  22. Getz W. M., Pickering J. Epidemic models—thresholds and population regulation. Am. Nat. 1983;121:892–898. doi: 10.1086/284112. [DOI] [Google Scholar]
  23. Gillespie J. H. Natural selection for resistance to epidemics. Ecology. 1975;56:493–495. doi: 10.2307/1934983. [DOI] [Google Scholar]
  24. Hethcote H. W., Yorke J. A. Gonorrhea transmission dynamics and control. Berlin: Springer; 1984. [Google Scholar]
  25. Keeling M. J. The effects of local spatial structure on epidemiological invasions. Proc. R. Soc. Lond. B. 1999;266:859–867. doi: 10.1098/rspb.1999.0716. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Kermack W. O., McKendrick A. G. Contributions to the mathematical theory of epidemics, 1. Proc. R.. Soc. A. 1927;115:700–721. doi: 10.1098/rspa.1927.0118. [DOI] [PubMed] [Google Scholar]
  27. Kiss I. Z., Green D. M., Kao R. R. The effect of contact heterogeneity and multiple routes of transmission on final epidemic size. Math. Biosci. 2006;203:124–136. doi: 10.1016/j.mbs.2006.03.002. [DOI] [PubMed] [Google Scholar]
  28. Kretzschmar, M., & Mikolajczyk, R. T. (2009). Contact profiles in eight European countries and implications for modelling the spread of airborne infectious diseases. PLOS One, 4. [DOI] [PMC free article] [PubMed]
  29. Lloyd A. L., May R. M. How viruses spread among computers and people. Science. 2001;292:1316–1317. doi: 10.1126/science.1061076. [DOI] [PubMed] [Google Scholar]
  30. Longini I. M., Nizam A., Xu S. F., Ungchusak K., Hanshaoworakul W., et al. Containing pandemic influenza at the source. Science. 2005;309:1083–1087. doi: 10.1126/science.1115717. [DOI] [PubMed] [Google Scholar]
  31. Ma J. L., Earn D. J. D. Generality of the final size formula for an epidemic of a newly invading infectious disease. Bull. Math. Biol. 2006;68:679–702. doi: 10.1007/s11538-005-9047-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. May R. M. Regulation of populations with nonoverlapping generations by microparasites—a purely chaotic system. Am. Nat. 1985;125:573–584. doi: 10.1086/284363. [DOI] [Google Scholar]
  33. Mills C. E., Robins J. M., Lipsitch M. Transmissibility of 1918 pandemic influenza. Nature (London) 2004;432:904–906. doi: 10.1038/nature03063. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Mossong J., Hens N., Jit M., Beutels P., Auranen K., et al. Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Med. 2008;5:381–391. doi: 10.1371/journal.pmed.0050074. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Newman M. E. J. Spread of epidemic disease on networks. Phys. Rev. E. 2002;66:016128. doi: 10.1103/PhysRevE.66.016128. [DOI] [PubMed] [Google Scholar]
  36. Pastor-Satorras R., Vespignani A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001;86(14):3200–3203. doi: 10.1103/PhysRevLett.86.3200. [DOI] [PubMed] [Google Scholar]
  37. Riley S., Fraser C., Donnelly C. A., Ghani A. C., Abu-Raddad L. J., et al. Transmission dynamics of the etiological agent of SARS in Hong Kong: Impact of public health interventions. Science. 2003;300:1961–1966. doi: 10.1126/science.1086478. [DOI] [PubMed] [Google Scholar]
  38. Tildesley M. J., Keeling M. J. Is R-0 a good predictor of final epidemic size: Foot-and-mouth disease in the UK. J. Theor. Biol. 2009;258:623–629. doi: 10.1016/j.jtbi.2009.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Volz E. Susceptible-infected-recovered epidemics in populations with heterogeneous contact rates. Eur. Phys. J. B. 2008;63:381–386. doi: 10.1140/epjb/e2008-00131-0. [DOI] [Google Scholar]
  40. Volz E. SIR dynamics in random networks with heterogeneous connectivity. J. Math. Biol. 2008;56:293–310. doi: 10.1007/s00285-007-0116-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Wallinga J., Teunis P., Kretzschmar M. Using data on social contacts to estimate age-specific transmission parameters for respiratory-spread infectious agents. Am. J. Epidemiol. 2006;164:936–944. doi: 10.1093/aje/kwj317. [DOI] [PubMed] [Google Scholar]

Articles from Bulletin of Mathematical Biology are provided here courtesy of Nature Publishing Group

RESOURCES