A spiking neural network model of spatial and visual mental imagery

Abstract

Mental imagery has long been of interest to the cognitive and neurosciences, but how it manifests itself in the mind and brain still remains unresolved. In pursuit of this, we built a spiking neural model that can perform mental rotation and mental map scanning using strategies informed by the psychology and neuroscience literature. Results: When performing mental map scanning, reaction times (RTs) for our model closely match behavioural studies (approx. 50 ms/cm), and replicate the cognitive penetrability of the task. When performing mental rotation, our model’s RTs once again closely match behavioural studies (model: 55–65°/s; studies: 60°/s), and performed the task using the same task strategy (whole unit rotation of simple and familiar objects through intermediary points). Overall, our model suggests: (1) vector-based approaches to neuro-cognitive modelling are well equipped to re-produce behavioural findings, and (2) the cognitive (in)penetrability of imagery tasks may depend on whether or not the task makes use of (non)symbolic processing.

Introduction

Mental imagery is the presence of a perception-like representation absent appropriate perceptual input (Kosslyn et al. 2006), and although the imagery debate has been long-running across both the cognitive and neurosciences (Kosslyn et al. 2006; Pylyshyn 2003), most of the effort has been spent on identifying neural correlates, rather than specifying how the cognitive processes underpinning mental imagery manifest themselves, computationally, in the brain. This is the aim of the present research. In particular, we created a spiking neuron model, dubbed MIM-1 (Mental Imagery Model 1), that can perform mental rotation and mental map scanning using cognitive strategies as described in the psychology literature.

Map scanning

Kosslyn et al. (1978) introduced the map scanning paradigm as a way of probing the underlying form of mental images. Participants memorized a map of an island with seven distinct, pictorial markers at various locations (e.g., a well, hut, tree). Once memorized, participants were given a location (verbally) and told to imagine its marker. After 5 s, they were verbally given a second location that might, or might not, be on the map. If the location was on the map, they were to mentally scan to the second location by envisioning a black dot “zipping” across the map. When they saw the black dot reach the center of the target, they pressed a button. If the second location was not in the map, they responded with a different button press. Overall, Kosslyn and colleagues found that the time required to scan between two locations scaled linearly with the distance between them, and that distance and reaction time (RT) were correlated at 0.97. To them, these findings supported the idea that mental images exhibited picture-like qualities that preserved metric distances.

This conclusion did not go unchallenged, however, with some claiming that the linear RTs were a function of task instructions, not properties inherent to mental images. In this vein, a counter-study by Pylyshyn (1981) used the same map scanning paradigm, only participants were also told there was a light source at each location, and a switch that could turn the source on or off. Here, participants were instructed to focus on a specific location, then told to imagine that the switch for a second location was flipped, and to respond when they saw the corresponding light turn on/off. Unlike Kosslyn and colleagues’ original study, RTs were not a function of the distance between the two locations, which lead to the conclusion that map scanning was cognitively penetrable (i.e., that one’s perceptual experience of the map was influenced by their cognitive states), and that the underlying mental representation used did not preserve metric distances.

Regardless of whether metric distances are preserved, the underlying representation does contain a spatial representation that outlines the location of objects. In this regard, there is some evidence that an object’s location is not precisely defined, but approximate (Denis et al. 1995), whereby the overall accuracy of the representation is mediated by one’s imagery abilities (Denis and Cocude 1997).

Whether the spatial representation is egocentric or allocentric remains to be seen; however, mental scanning does appear to invoke the right medial temporal lobe (Mellet et al. 2000), or MTL, which itself has been linked to allocentric spatial representations (Herweg and Kahana 2018). However, the MTL also appears to exhibit functional lateralization, with the right MTL being involved in perspective-taking and the left MTL being involved in viewpoint recognition (Lambrey et al. 2008; Burgess 2002). This fits with Kosslyn and colleagues’ theory that the right MTL involves processing coordinate data, as one would expect to occur during tasks such as perspective-taking, and the left MTL categorical information, such as recognizing/labelling specific viewpoints like “from above” (Kosslyn 1987; Kosslyn et al. 1989). Thus, it could be that case that MTL processes an allocentic representation that defines a small set of categorical locations, with each location being associated with a more detailed coordinate representation of what is present there (Lambrey et al. 2008; Burgess 2002). Under this view, the cognitive penetrability of mental map scanning would result from the sequence of categorical locations accessed during the task: if accessed sequentially along a specific trajectory en route to the target, then linear RTs should be observed; if the target location is immediately accessed via an attentional leap, then linear RTs should not be observed.

Mental rotation

With respect to mental rotation, Shepard and Metzler (1971) showed participants multiple pairs of irregularly shaped, three dimensional cube assemblies projected into two dimensions, and asked if the two images were mirrors of each other, or if one was a rotation of the other. Surprisingly, participant RTs for identifying rotations were directly proportional to the difference in angular rotation, a result that held regardless of whether the rotation occurred in the x–y plane or the depth plane. This suggested to the researchers that participants used picture-like mental imagery to form a three dimensional image of the cube assembly, then rotated that mental image as a whole unit.

Interestingly, mental rotation does not appear to depend on the visual system, as both congenitally blind and sighted but blindfolded participants have proven capable of completing the Shepard and Metzler paradigm (and producing the same linear RTs) when presented with haptic stimuli (Marmor and Zaback 1976). Research also suggests that rotation is, indeed, the dominate strategy used by participants (Cooper 1976), and that mental rotation is not cognitively penetrable (Borst et al. 2011). However, there is also evidence that a “whole unit” rotation is not always deployed, with complex and unfamiliar stimuli appearing to elicit a rotation of objects one part at a time, and simple and/or familiar objects a whole unit rotation (Bethell-Fox and Shepard 1988). To complicate matters further, there is also evidence suggesting that individuals store in memory a series of different orientations that objects are rotated into/out-of alignment with (Tarr and Pinker 1989; Tarr 1995), that flipping familiar objects in the depth plane is faster than rotating them in the x–y plane (Murray 1997), and that naming disoriented objects at 180 degrees is faster than at 120 degrees (Jolicoeur 1990).

In terms of the underlying representation, there is evidence that mental rotation tasks can be completed by leveraging a variety of different coordinate systems, though egocentric appears to dominate (Just and Carpenter 1985). Moreover, their representation and transformation appear to invoke different brain networks such that transformations occur when representations are passed from temporal regions to the parietal/occipital cortex (Kosslyn et al. 2006; Thompson et al. 2009; Zacks 2008). Some have theorized that this transformation is driven by motor regions (Cohen et al. 1996; Zacks 2008) and involves a continuous updating of the relationship between an object-centered and environment-centered frame of reference (Hegarty and Waller 2004; Zacks 2008), but the specific nature of this transformation is still not entirely understood. Conversely, it is understood that the spatial imagery involved in this transformation is distinct from both visual imagery and perception (Farah et al. 1988; Thompson et al. 2009).

Cognitive modelling in Nengo

MIM-1 was built using Nengo (Bekolay et al. 2014), an implemented neural architecture driven by the Neural Engineering Framework (NEF) and the Semantic Pointer Architecture (SPA).

In short, MIM-1 consists of a global imagery network that is comprised of three different, task-specific subnetworks. Taken together, MIM-1 models map scanning and mental rotation, and can perform each of these tasks without needing to be restarted, instead switching between them in response to user input.

Neural engineering framework (NEF)

The Neural Engineering Framework (NEF) concerns itself with how information can be represented and manipulated by neurons. More specifically: (i) how to move between the state-space of an input and the neuron-space of the brain, and (ii) how to perform transformations to representations.

Operating under the observation that neurons respond selectively in response to stimuli (that is, they possess tuning curves), if we have a state-space (e.g., a coordinate vector) at a given time, $\mathbf{x}(t)$, we can incorporate this selectivity by taking the dot product of the state-space and an encoding vector, ${\mathbf{e}}_i$, that details the preferred stimulus direction (e.g., 1 or $-1$) for neuron i, $⟨\mathbf{x}(t),{\mathbf{e}}_i⟩$; the closer the state-space vector is to the preferred stimulus direction, the stronger the neuron’s response (Bekolay et al. 2014; Eliasmith 2013; Kajić et al. 2017). We can model this response via scaling by a gain factor, ${\alpha }_i$, and adding a bias current, $J_i^{\mathit{bias}}$, which produces ${\alpha }_i⟨\mathbf{x}(t),{\mathbf{e}}_i⟩+J_i^{\mathit{bias}}$, which can then be applied to a leaky-integrate-and-fire (LIF) neuron model, $G_i$ (Bekolay et al. 2014; Eliasmith 2013; Kajić et al. 2017). Thus, the activity for neuron i at time t, or $a_i(t)$, is given by

$$\begin{array}{c}\hfill a_i(t)=G_i[{\alpha }_i⟨\mathbf{x}(t),{\mathbf{e}}_i⟩+J_i^{\mathit{bias}}],\end{array}$$ 1

where $[·]$ is the injected current and $G_i$ the neuron model that responds to said current (Bekolay et al. 2014; Eliasmith 2013; Kajić et al. 2017).

However, to facilitate downstream processing we also need the ability to move from neuron-space to state-space. Here, an estimate of the state-space, $\widehat{\mathbf{x}}$, can be produced by filtering spikes through a post-synaptic current model, h(t), and applying decoding weights, ${\mathbf{d}}_i$, that are derived from a least-squares solver that attempts to minimize the representational error of $\widehat{\mathbf{x}}$ (Bekolay et al. 2014; Eliasmith 2013; Kajić et al. 2017):

$$\begin{array}{c}\hfill \widehat{\mathbf{x}}(t)=\sum _i{a}_i(t)\ast [h(t){\mathbf{d}}_i].\end{array}$$ 2

Of course, all this is of little value if we cannot compute transformations, which is ultimately facilitated by a synaptic weight matrix, $\mathbf{W}$. If we label the pre-synaptic neuron as i and the post-synaptic neuron as j, then $W_{\mathit{ij}}$ is the synaptic weight for the connection, which is calculated as $W_{\mathit{ij}}={\alpha }_j⟨{\mathbf{e}}_j,{\mathbf{d}}_i⟩$ (Bekolay et al. 2014; Eliasmith 2013; Kajić et al. 2017). However, using decoding weights for pre-synaptic neurons simply passes the original state-space downstream. Fortunately, computing a transformation only requires using a least-squares solver to compute decoding weights for a transformed version of the original state-space, ${\mathbf{d}}_i^f$, thus producing $W_{\mathit{ij}}={\alpha }_j⟨{\mathbf{e}}_j,{\mathbf{d}}_i^f⟩$ (Bekolay et al. 2014; Eliasmith 2013; Kajić et al. 2017).

Semantic pointer architecture (SPA)

To facilitate symbolic processing, Nengo makes use of semantic pointers (denoted in lower-case bold), which are n-dimensional vectors that represent a “compressed” version of a larger semantic meaning (Eliasmith 2013). Cognitive processes can be implemented through binding and unbinding, which is done via circular convolution, denoted $⊛$. For example, if we wanted to compute the concept of a biped, we could convolve semantic pointers for legs and two: $\mathbf{biped}=\mathbf{legs}⊛\mathbf{two}$. If we then wanted to know how many legs a biped has, we would convolve the semantic pointer for biped with the involution (or pseudo-inverse) of the semantic pointer for legs, which will result in an approximation of the semantic pointer for two: ${\mathbf{legs}}^{\prime }⊛\mathbf{biped}\approx \mathbf{two}$. This binding and unbinding process can be repeated on more complicated constructs:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathbf{cat}& =\mathbf{legs}⊛\mathbf{four}+\mathbf{ears}⊛\mathbf{pointy}\hfill \\ \hfill {\mathbf{legs}}^{\prime }⊛\mathbf{cat}& ={\mathbf{legs}}^{\prime }⊛(\mathbf{legs}⊛\mathbf{four}+\mathbf{ears}⊛\mathbf{pointy})\hfill \\ \hfill & ={\mathbf{legs}}^{\prime }⊛\mathbf{legs}⊛\mathbf{four}+{\mathbf{legs}}^{\prime }⊛\mathbf{ears}⊛\mathbf{pointy}\hfill \\ \hfill & =\mathbf{four}+noise\hfill \\ \hfill & \approx \mathbf{four},\hfill \end{array}\end{array}$$ 3

which can ultimately be scaled to model complex cognitive processes (Eliasmith et al. 2012; Kajić et al. 2017).

SPA and cognitive architectures

One key advantage to modelling cognition with the SPA is its neural underpinnings. Symbolic architectures such as ACT-R (Anderson 1996) often fail to take into account neurobiology, and although recent work has helped close this divide (Borst et al. 2013), that the SPA is implemented in LIF neurons gives it an additional layer of cognitive plausibility that is typically absent from symbol-based architectures.

That said, the SPA is not the only neuron-based approach to cognitive modelling. Other architectures, for example LISA (Hummel and Holyoak 2003, 2005), have proven capable of performing complex cognitive processes such as analogical reasoning (Morrison et al. 2011); however, scaling is often an issue, with models requiring an unreasonably large amount of cortex (Eliasmith 2013). Conversely, the SPA only needs roughly 1 mm${}^2$ of cortex to bind two 500 dimensional vectors (Eliasmith 2013), which fits within the 9 mm${}^2$ boundary of local connectivity (Eliasmith 2013; Lund et al. 1993). In a related vein, there has also been recent work that merges topology with neural activity (Tozzi and Peters 2017), as well as work conceptualizing cognition as a continuous trajectory though high dimensional space (Mora-Sánchez et al. 2019). Both are interesting conceptualizations worth further inquiry, but currently lack a demonstrated ability to model complex cognitive processing, and to do so at scale.

However, the SPA does present a trade-off between cognitive flexibility and biophysical accuracy, though recent efforts such as BioSpaun (Eliasmith et al. 2016) have helped narrow this gap by incorporating more detailed neuron models. Nevertheless, there is a debate to be had over top-down versus bottom-up approaches to neuro-modelling (Eliasmith and Trujillo 2014), as well as evidence that low-level biophysical properties play a role in cognitive processing, such as attention (Zhang et al. 2019) and learning (Rao 2018).

Model

Overall, the goals for MIM-1 are as follows: (1) scan a mental map using either a scanning strategy, as per Kosslyn et al. (1978), or an attentional leap, as per Pylyshyn (1981). (2) Perform continuous, whole-unit rotations of both 3D and 2D objects in the x–y plane, and at a rate of 60°/s, as per Shepard and Metzler (1971). To this end, MIM-1 contains a variety of inter-connected subnetworks, each responsible for performing a specific task: rotation, scanning, and action selection.

We use simplified stimuli, rather than the detailed maps and complex cube assemblies typically used in behavioural studies (see Table 1). One rotation will be of a 3D cube, with a second rotation of the 2D letter M. The map that is scanned will be be populated with an alternating pattern of cubes and Ms (see Fig. 3).

Table 1.

MIM-1’s object semantic pointers

Semantic pointer	Graph label	Color	Texture	Spatial
$\mathbf{m}$	M	Blue	Smooth	Edges
	E	Blue	Smooth	Edges
	W	Blue	Smooth	Edges
	BE	Blue	Smooth	Edges
$\mathbf{cube}$	CUBE	Red	Rough	Edges

Fig. 3.

Map to be scanned. Here, an alternating sequence of 3D cubes and 2D letter Ms comprise the map. This map is ultimately divided into a $3\times 3$ grid, with each location semantic pointer being convolved with the semantic pointer for the object at said location. With respect to scanning, the network starts at the top left corner and scans across the to the top right corner. It then scans down from the top right corner to the bottom right corner, then from the bottom right corner to the bottom left corner, then up to the top left corner where it started. Finally, the network performs an attentional leap from the top left corner to location $\mathbf{six}$ (middle row, right column)

Semantic pointers

A key facet of both mental rotation and mental scanning are the spatial representations that define objects. This includes representations that define the structure of objects, as well as representations that define where objects fall within the larger world.

This work takes the view that the semantic pointer for an object contains an egocentric spatial representation, denoted ${\mathbf{obj}}_{\mathit{array}}$, which is a random sampling of ${\mathbb{R}}^3$ points from the object’s edges. However, objects are more than just a collection of points in space; they also have colour, texture, and a host of additional object properties. Thus, to more fully capture the semantics of objects, an object’s semantic pointer also contains a properties vector, ${\mathbf{obj}}_{\mathit{properties}}$, which is the superposition of the set, p, containing of all property-value convolutions associated with the object (e.g., $\mathbf{color}⊛\mathbf{red}$):

$$\begin{array}{c}\hfill {\mathbf{obj}}_{\mathit{properties}}=\sum _{i\in p}{\mathbf{property}}_i⊛{\mathbf{value}}_i\end{array}$$ 4

Overall, this produces

$$\begin{array}{c}\hfill \mathbf{obj}=\mathbf{spatial}⊛{\mathbf{obj}}_{\mathit{array}}+\mathbf{properties}⊛{\mathbf{obj}}_{\mathit{properties}}\end{array}$$ 5

where all semantic pointers are 528-dimensional and all except ${\mathbf{obj}}_{\mathit{array}}$ are selected from the unit sphere, with ${\mathbf{obj}}_{\mathit{array}}$ instead being comprised of 176 points in 3D space (selected from the object’s edges).

Representations that define where objects fall within the larger world are denoted ${\mathbf{A}}_i$. Consider Fig. 1. Here, we have a $N\times M$ map (top panel). This particular map—not used in our simulations—is divided into $N\times M$ sections (second panel), with each section being assigned a randomly generated semantic pointer that details that section’s location in the larger world (third panel). Each location semantic pointer is then convolved with the semantic pointer for the object that is present at that location (bottom panel). To generate a semantic pointer for ${\mathbf{A}}_i$, we sum all its elements, denoting the result ${\varphi }_i$. In the case of Fig. 1,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\varphi }_i=& \mathbf{one}⊛\mathbf{star}+\mathbf{two}⊛\mathbf{empty}+\mathbf{three}⊛\mathbf{diamond}\hfill \\ \hfill & +\mathbf{four}⊛\mathbf{star}+\mathbf{five}⊛\mathbf{empty}+\mathbf{six}⊛\mathbf{diamond}.\hfill \end{array}\end{array}$$ 6

Fig. 1.

The top panel shows an $N\times M$ map of an example world. The second panel shows that map partitioned into $N\times M$ sections. The third panel shows the assignment of randomly generated semantic pointers to each location. Bottom panel shows the binding of object semantic pointers to the appropriate location semantic pointer. The semantic pointer $\varphi$ for the map $\mathbf{A}$ is generated by summing all of the $\mathbf{location}⊛\mathbf{object}$ convolutions in $\mathbf{A}$

Of course, objects may not arrange themselves so neatly within this partition. For example, if a star spanned both location one and location four in Fig. 1, then the object semantic pointer that is convolved with each location semantic pointer would be a random sampling of 176 points from within that section of the map. How complex scenes are segmented and how objects are re-constructed across multiple locations is beyond the scope of this work, and may require alterations to the construction of $\mathbf{A}$.

Overall, we can regard $\mathbf{A}$ as a collection of ${\mathbb{R}}^3$ coordinate systems whereby each coordinate system is constrained to $[-1,1]$ and given a propositional code (i.e., the location semantic pointer). The larger idea is that multi-object scenes involve embedding objects within this $N\times M$ space, then forming object semantic pointers for each location in $\mathbf{A}$ by randomly sampling points from the object at that location.

MIM-1 network

An overview of MIM-1 can be seen in Fig. 2. Here, leaky-integrate-and-fire (LIF) neurons are organized into ensembles, which, depending on their activation, represent different state-spaces. Collections of ensembles can then be connected together to form a state, which specifically functions to represent semantic pointers. Groups of ensembles and states can then be wired together to form a network, which functions to perform a specific task.

Fig. 2.

MIM-1 network. Here, MIM-1 is comprised of three subnetworks: rotation, scanning, and action selection, plus a task state and a visual buffer state. Each subnetwork is responsible for performing a specific task, sending their output to the visual buffer for “rendering”. The action selection network serves two purposes: (1) to activate the appropriate subnetwork given the task input, and (2) to perform any actions requested by the subnetworks

MIM-1 is comprised of three subnetworks: one that performs mental rotation (rotation network), one that scans mental maps (scanning network), and one that selects actions based on instructions [action selection network, details for which can be found in Stewart et al. (2010)]. The rotation and scanning networks both connect to a state that functions as a visual buffer, with a task state connecting to the action selection network, thus allowing the imagery network to switch between different tasks without needing to re-build or restart the simulation.

Overall, a semantic pointer for a task instruction (e.g., $\mathbf{rotate}\mathbf{cube}$) is inserted into the task state. This state connects to the action selection network, itself selecting which semantic pointer is passed to which network (e.g., $\mathbf{cube}$ to the rotation network). The network will then complete the task, passing relevant information to the visual buffer for “rendering.”

To test MIM-1 we ran 5 simulations—each of which simulated 19 s of neural processing—and averaged across them to get an overview of performance. From $t=0$ to $t=1$, MIM-1 performed mental map scanning. From $t=1$ to $t=9$, it rotated the letter M in the x–y plane. From $t=10$ to $t=18$, it rotated cube in the depth plane. At all other times, MIM-1 was to remain idle. All connections have a 5 ms post-synaptic time constant.

Action selection network

The action selection network models the cortex $\to$ basal ganglia $\to$ thalamus $\to$ cortex loop involved in action selection, and is thoroughly detailed in Stewart et al. (2010). In short, however, the cortex connects to the basal ganglia, which inhibits the appropriate action. This results in a disinhibition of the corresponding areas of the thalumus, itself mapping to the cortical state resulting from the action (Stewart et al. 2010). Overall, this loops takes between 30 and 70 ms, depending on action complexity and the time constant of GABA (Stewart et al. 2010).

Map scanning network

As noted earlier, map scanning is cognitively penetrable such that one can shift attention across a trajectory (Kosslyn et al. 1978), or leap between two distant locations (Pylyshyn 1981). In pursuit of this, we first consider the map in Fig. 3, which is a $3\times 3$ grid with a cube or M embedded at each location.

We then take the semantic pointer for each object and convolve it with a randomly generated semantic pointer for each location within the map, which produces the spatial representation

$$\begin{array}{c}\hfill {\mathbf{A}}_{\mathit{scan}}=\left[\begin{array}{ccc}\mathbf{one}⊛\mathbf{cube}& \mathbf{two}⊛\mathbf{m}& \mathbf{three}⊛\mathbf{cube}\\ \mathbf{four}⊛\mathbf{m}& \mathbf{five}⊛\mathbf{cube}& \mathbf{six}⊛\mathbf{m}\\ \mathbf{seven}⊛\mathbf{cube}& \mathbf{eight}⊛\mathbf{m}& \mathbf{nine}⊛\mathbf{cube}\\ \end{array}\right]\end{array}$$ 7

that is is then converted into a semantic pointer, ${\varphi }_{\mathit{scan}}$, by summing all of its elements:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\varphi }_{\mathit{scan}}=& \mathbf{one}⊛\mathbf{cube}+\mathbf{two}⊛\mathbf{m}+\mathbf{three}⊛\mathbf{cube}\hfill \\ \hfill & +\mathbf{four}⊛\mathbf{m}+\mathbf{five}⊛\mathbf{cube}+\mathbf{six}⊛\mathbf{m}\hfill \\ \hfill & +\mathbf{seven}⊛\mathbf{cube}+\mathbf{eight}⊛\mathbf{m}+\mathbf{nine}⊛\mathbf{cube}.\hfill \end{array}\end{array}$$ 8

An overview of the network can be seen in Fig. 4. Here, a location state represents where attention is focused in the spatial representation (one, two, three, etc.), with its involution convolved with ${\varphi }_{\mathit{scan}}$ providing an approximation of the object at that location (cube or M). The object is then passed into a winner-take-all network (Stewart et al. 2011), which connects to the visual buffer. To move to a new location in ${\varphi }_{\mathit{scan}}$, a direction state represents a randomly generated semantic pointer for one of five movement directions (up, down, right, left, leap to [location]). This movement direction is convolved with the current location to generate a new semantic pointer that reflects a movement instruction (e.g., “move left from location three”). Finally, this instruction is then passed to the action selection network, which sends to the location state an updated location within ${\mathbf{A}}_{\mathit{scan}}$. Overall, we can view movement as a mapping between every location–direction convolution and a new location, $Move:\mathbf{location}⊛\mathbf{direction}\to \mathbf{new}\mathbf{location}$; however, because ${\mathbf{A}}_{\mathit{scan}}$ is allocentric, so too is this mapping (e.g., with respect to Fig. 3, the model would always go from $\mathbf{three}$ to $\mathbf{six}$ by moving $\mathbf{down}$, regardless of Fig. 3’s orientation relative to the viewer). Using this design, we can facilitate movement to any location from any other location, thus enabling map scanning across a trajectory, or via an attentional leap.

Fig. 4.

Scanning network. The location state (l) is where attention is currently focused in the map. When it is convolved with a direction (d), the action selection network produces a new location that is passed to the location state (i.e., attention shifts). When the involution of the location state is convolved with the map, it produces an approximation of the object at that location, which is passed through a winner-take-all network and sent to the visual buffer for “rendering”

Map scanning results

To test the network’s ability to both scan across a trajectory and perform an attention leap, we instructed the network to start at location 1 and scan: right for 200 ms, then down for 100 ms, left for 200 ms, up for 100 ms, then leap to location 6. This produced left to right scanning across the top row of Fig. 3 (locations $1\to 2\to 3$), then scanning down the far right column (locations $3\to 6\to 9$), across the bottom row from right to left (locations $9\to 8\to 7$), up the left column (locations $7\to 4\to 1$), then, finally, perform an attentional leap from location 1 to location 6. If the network was instructed to move in a way that was not possible (e.g., “move right from location 3”), it was to hold its current position until instructed otherwise.

Results can be seen in Fig. 5. Here, each coloured line represents a specific semantic pointer. The x-axis is time, and the y-axis represents the similarity between the representation formed by the neurons and each of the listed semantic pointers. For example, in the top panel of both figures, the representation formed by the neurons in the movement state is highly similar to the semantic pointer $\mathbf{right}$ from $t=0$ms to $t=200$ms, and is not similar to the other direction semantic pointers. This changes around $t=200$ms, however, when the representation becomes highly similar to $\mathbf{down}$ and not similar to the other directions semantic pointers.

Fig. 5.

Map scanning Cosine Similarities. Across all panels, each coloured line reflects a specific semantic pointer. The x-axis is time. The y-axis is the cosine similarity between the representation formed by the neurons and the listed semantic pointers. The top panel shows the direction state, with the network moving through the intended sequence of directions (right, down, left, up, leap to six). The middle panel shows the location state, with the network appropriately traversing the map ($1\to 2\to 3\to 6\to 9\to 8\to 7\to 4\to 1\to 6$), briefly holding its position at locations 3 and 7. The bottom panel shows the object that is extracted from each location, with the network correctly alternating between cubes and Ms

The middle panels show the location state. Here, the network is able to appropriately traverse the map (e.g., the network moved to location 2 when instructed to move right from location 1), including holding its position at locations $\mathbf{three}$ and $\mathbf{seven}$. Due to the 5 ms post-synaptic time constant between each connection in MIM-1, we can also see a slight delay between when a movement instruction is given and when the location is represented in the location state. Moreover, there is some noise after the network makes the attentional leap (everything after approx. 700 ms); however, the winner-take-all network is able to filter that noise, preventing any object semantic pointers from being passed to the visual buffer (bottom panel).

Concerning the visual buffer, the bottom panel also shows a slight delay between the location state and the visual buffer, and that the network is able to successfully extract the appropriate object from each location.

Putting it all together, the network is instructed to move attention right from location one. This sends attention to location two, from which it is instructed to again move right. This sends attention to location three; however, attention cannot move right from location three, so it holds until given a valid movement direction. This general process is repeated again for the remaining movement directions, with the object at each resulting location being passed to the visual buffer. In terms of RTs, the model takes approximately 50–75 ms to move between two locations and “render” the object, thereby producing linear RTs when using a scanning strategy. However, it is important to note that the network does not take planning into consideration. That is, we did not specifically intent for the network to traverse the path that it did; the path was simply a byproduct of the movement directions that we presented to the network. If we change the sequence of movement directions, or the amount of time they are presented for, the network with traverse a different path.

In terms of accuracy, all 5 simulations appropriately traverse the map, and all 5 extracted the correct object from each of the 10 locations visited.

Finally, the length of time the network was told scan in a particular direction was independent from the time it took for the network to move between two locations. Consider the first two instructions: $\mathbf{right}$ for 200 ms, then $\mathbf{down}$ for 100 ms. In both cases, the time it took to move from one location to another (middle panel of Fig. 5), be it from $\mathbf{one}$ to $\mathbf{two}$ or $\mathbf{six}$ to $\mathbf{nine}$ (for example), remained largely the same. This is because said movement time is dependent upon the time it takes to complete the location $\to$ instruction $\to$ action selection loop, and then extract the relevant object. This is also why the network spent more time at locations $\mathbf{three}$ and $\mathbf{seven}$; the network was instructed to move in a direction that was not possible (e.g., $\mathbf{three}⊛\mathbf{right}$), and therefore remained at the location until given a valid movement direction.

To confirm (i) that the network can successfully scan maps with different movement durations (i.e., not just 100 ms and 200 ms), and (ii) scan different paths than right, down, left, up, we ran another scanning experiment that had the network start at location 1 and scan down, right, up, then left, with each instruction being presented for 75 ms.

As seen in Fig. 6, the network scans down from 1 to 4, then across 5 and 6, then moves up to 3 where its briefly holds its location before scanning across 2 and back to its starting location at 1. As in Fig. 5, the network takes roughly 50 ms to move between two locations, and is able to extract from each location the appropriate semantic pointer. Moreover, because of the shorter movement duration, the network does not scan all the way down the vertical (i.e., $1\to 4\to 7$), instead moving $1\to 4$, then across the middle row.

Fig. 6.

Map scanning cosine similarities. In contrast to Fig. 5, each movement direction was presented for 75 ms, with the shorter time interval (x-axis) highlighting the delay produced by the 5 ms post-synaptic time constant (e.g., the location state is most similar to $\mathbf{four}$ around 0.125 s, but $\mathbf{m}$ is not present in the visual buffer until around 0.15 s)

Map scanning discussion

In Kosslyn et al. (1978)’s original study, participants took approximately 1.1 s to scan 2 cm and 1.9 s to scan 18 cm (the smallest and largest distances reported in the study). If we tentatively assume the 800 ms spent scanning between 2 and 18 cm reflects the rate of scanning independent of planning (and other cognitive processes involved in the task), then we get a rate of 50 ms/cm with 1 s spent on all non-scanning cognitive processes. Considering this independent scanning rate alongside the distances reported in Kosslyn et al. (1978), we get 100 ms for 2 cm and 900 ms for 18 cm, which, in both cases, is exactly 1 s off the study’s reported RTs. This tentatively suggests that MIM-1 is both cognitively and neurally plausible, and if it were expanded to account for additional cognitive processes involved in the task (e.g., planning) it would re-produce Kosslyn et al. (1978)’s RT results at 2 cm and 18 cm. However, although the spatial maps for $\mathbf{cube}$ and $\mathbf{m}$ contain points that fall between $-1$ and 1 on all axes, they are unit independent, which means the deeper question of how many locations comprise any given $\mathbf{A}$ still remains, though the aforementioned results suggest that an $N\times M$ cm mental map should result in an $\mathbf{A}$ that is divided into $N\times M$ locations, just as we proposed.

Importantly, there is a theoretical divide between direction-driven movement inputs such as “right,” and location-driven movement inputs such as “leap to [location].” The former is likely to be invoked in spatial navigation tasks that do not depend on landmarks, such as situated (route) planning, with the latter likely being invoked in those that do, such as prospective (route) planning (Hölscher et al. 2011). In the case of mental map scanning, the simplest explanation for the conflicting findings of Kosslyn et al. (1978) and Pylyshyn (1981) rests in whether task instructions elicited location-driven or direction-driven movement strategies. In Kosslyn et al. (1978), the salient aspect of the task instruction was a zipping black dot, which does not have attached to it any location (landmark) information, likely eliciting a direction-driven strategy. In contrast, the salient aspects in Pylyshyn (1981) were the light and the light switch, both of which contain location (landmark) information, likely eliciting a location-driven strategy.

Finally, the questions of how large the map (${\mathbf{A}}_{\mathit{scan}}$) can grow, and how many objects can be placed within it, still remain. In this vein, there are well documented complexity effects that mediate visuospatial memory—namely, the number of objects involved, the complexity of their arrangement, and the complexity of the recall path/sequence (Kemps 1999, 2001)—however, visuospatial memory is a related but imperfect proxy for mental map scanning, thus there may be additional mediating factors, such as one’s preference for visual or spatial imagery, or overall imagery ability.

Rotation network

Overall, the goal for this network is to demonstrate continuous rotations of both 2D and 3D objects (switching between cube and M as instructed), and at a rate of 60°/s. Unlike Shepard and Metzler (1971)’s original study, the network does not make same-different discriminations, and is currently limited to a whole-unit rotation strategy.

Central to the rotation network is the idea that transformations to objects occur when passed from a “representation network” in temporal regions to a “transformation network” in the parietal/occipital cortex (Kosslyn et al. 2006; Thompson et al. 2009; Zacks 2008). As seen in Fig. 7, the action selection network sends ${\mathbf{obj}}_{\mathit{array}}$ to the representation state and ${\mathbf{obj}}_{\mathit{properties}}$ to the properties state. The representation state then connects to 176 motor ensembles (one for each point in ${\mathbf{obj}}_{\mathit{array}}$), with these ensembles also receiving the motor inputs: $sin(t)$, $cos(t)$, and the axis of rotation ([1, 0, 0] for $\mathbf{cube}$ and [0, 0, 1] for $\mathbf{m}$). The rotation of each point $\mathbf{x}$ is computed via ${\mathbf{x}}^{\prime }=\mathbf{R}\mathbf{x}$ across each motor${}_i\to$ transformation connection, where $\mathbf{u}$ is the axis of rotation, t is the time since the start of a rotation, c is $cos(t)$, s is $sin(t)$, and $\mathbf{R}$ is

$$\begin{array}{c}\hfill \left[\begin{array}{ccc}c+u_x^2(1-c)& u_x{u}_y(1-c)-u_{z}s& u_x{u}_z(1-c)+u_{y}s\\ u_y{u}_x(1-c)+u_{z}s& c+u_y^2(1-c)& u_y{u}_z(1-c)-u_{x}s\\ u_z{u}_x(1-c)-u_{y}s& u_z{u}_y(1-c)+u_{x}s& c+u_z^2(1-c)\end{array}\right]\end{array}$$

This produces a rotated version of ${\mathbf{obj}}_{\mathit{array}}$ in the transformation state, which is then convoled with $\mathbf{spatial}$ and superimposed with ${\mathbf{obj}}_{\mathit{properties}}$ before being passed to the visual buffer.

Fig. 7.

Rotation network. Here, ${\mathbf{obj}}_{\mathit{array}}$ is passed to the representation state and ${\mathbf{obj}}_{\mathit{properties}}$ to the properties state. There are also 176 motor ensembles (one for each point in ${\mathbf{object}}_{\mathit{array}}$) that each receive $sin(t)$, $cos(t)$, and the rotation axis as input; and 176 representation $\to$ motor${}_i$$\to$ transformation connections that perform the rotation of each point. The rotated version of ${\mathbf{obj}}_{\mathit{array}}$ (T) is then convolved with $\mathbf{spatial}$ and superimposed with the object’s properties (P), then passed to the visual buffer

Rotation network results

To test the network’s ability to perform continuous, whole-unit rotations of both 2D and 3D objects, we instructed the network to rotate $\mathbf{m}$ about the z-axis from $t=1.0$ to $t=9.0$, and $\mathbf{cube}$ about the x-axis from $t=10.0$ to $t=18.0$.

Results for each object rotation can be seen in Figs. 8 and 9, respectively. In both instances, it takes roughly 5.5–6.5 s to complete one full rotation, resulting in a rotation rate of approximately $55\text{-}{65}^{\circ }$/s, with the properties state successfully representing the appropriate ${\mathbf{obj}}_{\mathit{properties}}$ value.

Fig. 8.

M rotation. All three panels show cosine similarity on the y-axis and time on the x-axis. The top panel shows the similarity between the semantic pointer represented in the transformation state and each of the object array semantic pointers. The middle panel shows the visual buffer and its representation’s similarity to $\mathbf{M}$ and $\mathbf{cube}$. The bottom panel shows the similarity between each ${\mathbf{obj}}_{\mathit{properties}}$ semantic pointer and the representation in the properties state. Tracking the transformation state, at t = 1 the network begins rotating M counter-clockwise, causing its similarity with ${\mathbf{m}}_{\mathit{array}}$ to decline until t = 4 when it reaches its lowest value after 180 degrees of rotation. The network then begins rotating the letter back into its upright position, causing the similarity with ${\mathbf{m}}_{\mathit{array}}$ to increase accordingly

Fig. 9.

Cube rotation. Same as Fig. 8, only for cube. Here, ${\mathbf{cube}}_{\mathit{array}}$ exhibits a similar waveform to that seen with ${\mathbf{m}}_{\mathit{array}}$, suggesting an elliptical rotation path

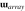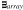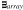Focusing in on $\mathbf{m}$’s rotation, we can see in the top panel of Fig. 8 that ${\mathbf{m}}_{\mathit{array}}$ correctly passes through (red), (green), and (purple) before returning to its canonical orientation. However, the sinusoids for and exhibit a triangular waveform, suggesting an elliptical rotation path, which we can be seen in Fig. 10.

Fig. 10.

A visual aid showing the x–y path the sampled point $(0.95,-0.80,0)$ traces during the rotation of M. Most noticeable are that (i) the neural representation of the y-axis is constrained to $[-0.2,0.2]$, and (ii) the point walks an elliptical path as opposed to circular one

This same pattern emerges during the cube rotation (Fig. 9), with ${\mathbf{cube}}_{\mathit{array}}$ exhibiting as similar waveform as ${\mathbf{m}}_{\mathit{array}}$ in Fig. 8, pointing to an elliptical rotation path like that seen during M’s rotation.

Rotation network discussion

With respect to rotation rates, each object takes approximately 5.5–6.5 s to move 360 degrees, which converts to a rotation rate of roughly $55\text{-}{65}^{\circ }$/s, fitting nicely alongside the ${60}^{\circ }$/s reported by Shepard and Metzler (1971). However, RTs used to derive the ${60}^{\circ }$/s rate include non-rotation cognitive processes (e.g., planning), which are thought to comprise roughly 20% of RTs (Shepard and Metzler 1971), thereby making our network’s rotation rate slower than behavioural studies. This discrepancy can be rectified by increasing the frequency of $sin(t)$ and $cos(t)$, which is a reasonable approach given the active role motor cortex oscillations play in facilitating movement (Richter et al. 2000), and mental rotation’s recruitment of the motor cortex, more generally (Cohen et al. 1996).

As noted, however, the rotation network is currently limited to whole-unit rotations. Prior research has shown that complex and/or unfamiliar stimuli can be rotated using a piecewise strategy that sees participants sequentially rotate parts of the object (Bethell-Fox and Shepard 1988), thus the question of how such a strategy is performed, neurally, remains.

One potential solution would be to introduce an inhibitory mechanism that prevents/permits the rotation of a subset of points in ${\mathbf{obj}}_{\mathit{array}}$. However, this disassociates object parts from the representation of the object (i.e., what constitutes the “top” of an object is not encoded in it’s semantic pointer); though, there is evidence that inhibitory neurons in the motor cortex are involved in some movement tasks (Putrino et al. 2010; Isomura et al. 2009), lending some credence to the inhibitory notion.

Conversely, a second potential solution would be to include object parts in an object’s semantic pointer, such as:

$$\begin{array}{c}\hfill {\mathbf{obj}}_{\mathit{array}}=\mathbf{top}⊛{\mathbf{top}}_{\mathit{array}}+\mathbf{bottom}⊛{\mathbf{bottom}}_{\mathit{array}}\end{array}$$ 9

where ${\mathbf{bottom}}_{\mathit{array}}$ and ${\mathbf{top}}_{\mathit{array}}$ are points sampled from the top and bottom of the object, and $\mathbf{obj}$ is constructed as per Eq. 5. Although this approach lends itself well to the SPA and could prove relevant to imagery tasks other than mental rotation, whether such a complex representation is practical remains to be seen, especially when object properties for each part of the object are factored in. Nevertheless, it’s potential application to tasks beyond mental rotation makes this approach an attractive one.

General discussion

Broadly construed, MIM-1 was able to perform mental scanning and rotation. It could switch between these tasks, produce RTs that are in line with behavioural results, and do so using known cognitive strategies. The use of a hybrid map in map scanning reflects theorized functionality in brain regions linked to the task, and the ability to scan across a trajectory, or perform an attentional leap, reflects its cognitive penetrability. The rotation network’s ability to move entire objects, both 2D and 3D, through intermediary points in both the depth and x–y plane parallels how familiar objects are rotated as a whole-unit. Moreover, motor region oscillations produce a constant rate of rotation, which matches the apparent impenetrability of the task.

All this being said, we are not the first to model mental imagery. For example, Rosenbloom (2011a) built a factor graph that used mental imagery to solve The Eight Puzzle boards by first storing the board in working memory, then applying a set of conditionals that mentally shifted the game pieces based off the state of the board. Although this graphical approach represents a notable advance in the cognitive architecture literature (Rosenbloom 2011b), it is largely disassociated from the underlying neural mechanisms that drive cognition.

In this vein, McKinstry et al. (2016) used a network of spiking neurons to control a robot (named Darwin XIII) that used reinforcement learning to perform the Shepard and Metzler (1971) mental rotation task. Overall, the authors found that Darwin XIII was able to successfully make same-different discriminations with a linear RT, and exhibited neural activation patterns associated with intermediate rotation angles (McKinstry et al. 2016). From this, the authors proposed that mental rotation could be rooted in learned associations, a view that is partially supported by the psychology literature [e.g., (Tarr and Pinker 1989; Tarr 1995)].

Our model, on the other hand, was designed in an attempt to bring together both the neural and cognitive mechanisms that underpin mental imagery, using them to perform multiple tasks. However, we stake no claims on the descriptive versus depictive imagery debate, though we do suggest vector-based approaches to neural-cognitive modelling are well equipped to re-produce behavioural results. Moreover, this work sheds light on some potentially interesting avenues of inquiry. First, it may be the case that cognitive penetrability in mental imagery depends on symbolic processing, as in the scanning network. Of course, one can slow rotation rates at will, but as noted above, one cannot speed rotation up beyond a certain point, which suggests the underlying neural architecture places limits on (at least some) non-symbolic processing, i.e. limits on motor processing constraining rotation rates.

Second, are spatial representations for objects constructed by randomly sampling points from the edges of objects? Edge detection has well established roots in visual perception (Marr and Hildreth 1980; Xie and Tu 2015), but objects are more than the sum of their edges, especially when properties such as colour are factored in. And how many points are sampled? Limited storage space in the brain suggests objects are not stored in their entirety, but what is the minimum number of points needed to accurately encode an object? Even more interestingly, when these objects are “rendered” in the visual buffer, are they rendered as stored (i.e., only the sampled points), or are the decompressed to render an entire object? If they are decompressed, do individual differences in imagery skills stem from individual differences in the efficiency, accuracy, and precision of this decompression process? Recent work on Spatial Semantic Pointers by Komer et al. (2019) suggests a potential answer to some of these questions, but their utility in mental imagery tasks is still largely unexplored.

Finally, how are these networks interconnected? They can probably work together to perform more complicated tasks, but how do they do so? Is there a larger meta-structure that routes information to-and-from the networks, integrating their inputs as needed? Or are there direct connections between them, processing information in a much more serialized way? Kosslyn et al. (2006) suggests that the visual buffer assumes a central role in this process, routing information between regions as needed, but how it does so is still somewhat ill-defined, at least computationally.

Overall, MIM-1 presents a step towards a deeper understanding of mental imagery and the computations that underpin it. Future work should look at fleshing out some of these computations while seeking to further integrate the networks.