Abstract
Working memory (WM) refers to a memory system with limited energy for short-term maintenance and plays an important role in cognitive functions. At present, research regarding WM mostly focuses on the coordination between neural signals in the signal microelectrode channel. However, how neural signals coordinate the coding of WM at the network level is rarely studied. Cross-frequency coupling (CFC) reflects the coordinated effect between different frequency components (e.g., theta and gamma) of local field potentials (LFPs) during WM. In this study, we try to map the changes that occur in the brain networks during WM at the level of CFC between theta-gamma of LFPs. First, a 16-channel brain network by using the CFC between theta-gamma of LFPs during WM was constructed. Then, the dynamic properties of the brain network during WM were analyzed based on graph theory. Experimental results show that the LFPs power increased at the WM state than at resting stat, but decreased across learning; the CFC between theta-gamma increased with learning days and phase-amplitude coupling (PAC) in the WM state was higher than that in free choice state and rest state; the changes of average degree, average shortest path length and global efficiency had significant difference on learning days. We can indicate that the CFC between theta-gamma in the network plays an important role in the WM formation. Furthermore, correct storage of WM information will not change local information transmission and the small-world attribute, while, it can increase the network connection and efficiency of information transmission.
Keywords: Working memory, Cross-frequency coupling, Brain network analysis, Complex network properties, Graph theory
Introduction
Working memory (WM) refers to the memory system with limited energy for short-term storage and processing of information, and WM plays an important role in many complex advanced cognitive activities, such as reading, understanding, reasoning and learning (Funahashi 2017; Christophel et al. 2017). Alzheimer’s disease (AD) is a progressive neurodegenerative disease, whose main clinical manifestation is WM impairment (Ateş et al. 2017; Davis et al. 2017; Haj and Antoine 2017). Therefore, the study of the WM mechanism is of great significance for WM impairment in AD and its clinical treatment. An investigation indicated that the medial prefrontal cortex (mPFC) plays an important role in many cognitive functions, especially in WM (Riga et al. 2016). Abnormal signal activity patterns in the mPFC can be one of causes of WM impairment (Bittner et al. 2015). Traditional research on WM mostly focuses on the coordination between multimode neural signals in the signal microelectrode channel (Li et al. 2014; Bai et al. 2014). Recently, brain network analysis method has become a novel method to explore the mechanism underlying WM (Liu et al. 2016; Vatansever et al. 2017). Research on WM mechanism at the network level can better reflect the information interaction and transmission, therefore, the network level storage of WM has been extensively studied. Investigations have shown the enhanced connection strength in mPFC network during spatial working memory tasks (Xie et al. 2014; Ouyang et al. 2014). Substantial evidence suggests that brain network properties can be used as biomarkers for predicting the task performance during WM tasks (Dai et al. 2014). Besides, research on the low-dimensional spike network based on sparse coding can reflect the information transfer efficiency of the network and provide support for quantitatively and effectively describing WM in the brain network (Carver et al. 2019). Graph theory is a mathematical approach to estimate the efficiency of information flow and widely used in the brain network analysis (Wheelock et al. 2018). For example, study based on the graph theory has demonstrated that electroencephalograph (EEG) networks during the encoding period of WM exhibit a significantly higher small-world topology which can promote the information flow between WM sub-networks (Toppi et al. 2018).
At present, the study of the WM mechanism can be divided into three levels: macrolevel, mesolevel and microlevel. At the macrolevel, the nonimplantable EEG is susceptible to external effects such as skin, hair, and motor interference, which will reduce the signal-to-noise ratio of the signals; at the microlevel, researches on the extracellular recording in primates and rodents mainly focused on the spiking activity of neurons during WM (Romo et al. 1999; Esmaeili and Diamond 2019). However, researches on the spiking activity at the microlevel cannot reflect the neural oscillations at different frequency bands in the brain network. At the mesolevel, LFPs obtained by using in vivo recording represent the linear sum of the postsynaptic potentials of the neural ensembles. The spatial resolution of LFPs is higher than that of EEGs, and the signal-to-noise ratio of an LFP is better than that of an electrocorticogram (ECoG) (Chen et al. 2018; Sorokin et al. 2017). Therefore, the LFPs are used to analyze the neural rhythmic oscillations.
Recently, studies have shown that theta (4–12 Hz) and gamma (30–100 Hz) oscillations play an important functional role in WM, respectively (Albouy et al. 2017; Lundqvist et al. 2018; Esmaeili and Diamond 2019). Theta rhythmic activity is thought to have a major function in memory processing (Decoteau et al. 2007). Study has shown that the synchronization of theta band can coordinate neural communication between multiple brain regions and contribute to the maintenance of short-term memories (Liebe et al. 2012). Besides, gamma oscillations have also been proved very important in memory processing. For example, gamma power has been suggested to reflect the spatial memory precision and involve in spatial memory processing (Stevenson et al. 2018). Meanwhile, evidences have been presented to demonstrate that cross-frequency coupling (CFC) between theta and gamma oscillations occurs frequently in WM (Nir et al. 2017; Zutshi et al. 2018; Wutz et al. 2018). Previous study has found that the CFC between theta and gamma coordinates communication between brain regions and is involved in memory processes (Lisman and Jensen 2013). Besides, the coupling of the theta and gamma will increase as a new human short-term memory is formed (Graetz et al. 2019). While the coupling of the theta and gamma in patients with mild brain injury will be lower than that of healthy people (Antonakakis et al. 2016).
CFC between theta and gamma oscillations can reflect the information interaction between different regions and different frequency band during WM. However, it still remains unclear whether theta-gamma coupling has any functional role during the learning and WM formation. Brain network analysis based on the graph theory can estimate the information transmission underlying WM and reveal the dynamic changes that occur in the brain network during learning of WM tasks. Therefore, combined the CFC and brain network methods, we try to map the changes that occur in the local mPFC networks during learning of a WM task at the level of CFC between theta and gamma oscillations. In this study, we recorded 16-channel LFPs in the mPFC of rats during WM in a T maze by using microelectrode implantation and constructed the brain network based on the CFC algorithm. The dynamic properties of the brain network during WM were analyzed by using complex network theory. This study provides a new method for exploring the WM mechanism from the perspective of brain network analysis.
Results
Behavioral performance
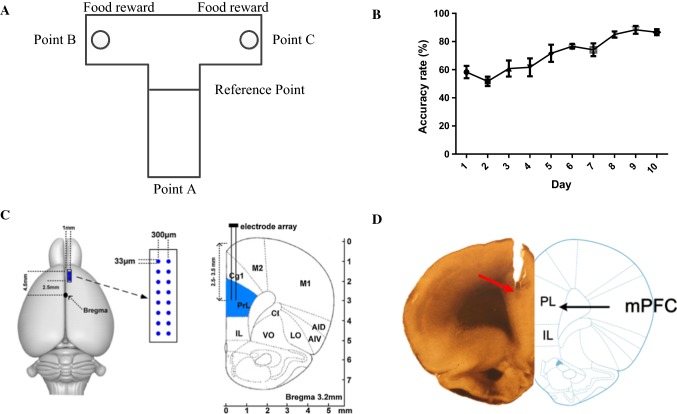
16-channel LFPs were recorded from mPFC as rats (n = 10) were trained to alternate two spatial locations to obtain a food reward in a T maze (Fig. 1A). Each trial of the spatial delayed alternation task consisted of a free choice phase and a delayed alternation phase. Only when the rats chose the different locations on the two runs can they obtained the food reward and recorded as correct. The change in the correct rate of the T maze training with learning days is shown in Fig. 1B. The correct rate of behavioral training increased gradually from 58.3 ± 10.8% on the first day to 86.7 ± 5.2% on the eighth day and to 88.3 ± 6.8%8 on the ninth day. The correct rate for two consecutive days reached more than 80%. This suggests that WM is formed after 10 days of training.
Fig. 1.
Behavioral performances. A The schematic of the delayed-alternation task on T maze. Rats were rewarded on the two goal locations (Point B or C) and at the starting area (Point A) after a goal choice. Each trial consisted of a sample run and a choice run. On the sample run, the rats can get reward by entering into either of arms. After a 5-s delay, the rats would have a choice run. Rats have to enter into the opposite arm to get food reward. B The correct rate of T maze training of 10 rats varied with time. The abscissa represents the number of learning days, and the ordinate represents the correct rate of T maze training. The correct rate increased significantly with an increase in learning days. (one-way ANOVA: , ****). C The schematic of the recording method. The microelectrode array consists of 16 electrodes (2 × 8, 33 μm diameter, 300 μm spacing, nickel–chromium, impedance < 1 MΩ). The number indicates the antero-posterior coordinates caudal to bregma. D Histological verification of the recording sites in mPFC
Histology
Extracellular electrophysiological recordings were made from the rat mPFC. The schematic of the recording method is shown in Fig. 1C. In order to verify the location of the microelectrode array, the histological sections of the recording sites from mPFC is shown in Fig. 1D.
Power changes in LFPs during the T maze task
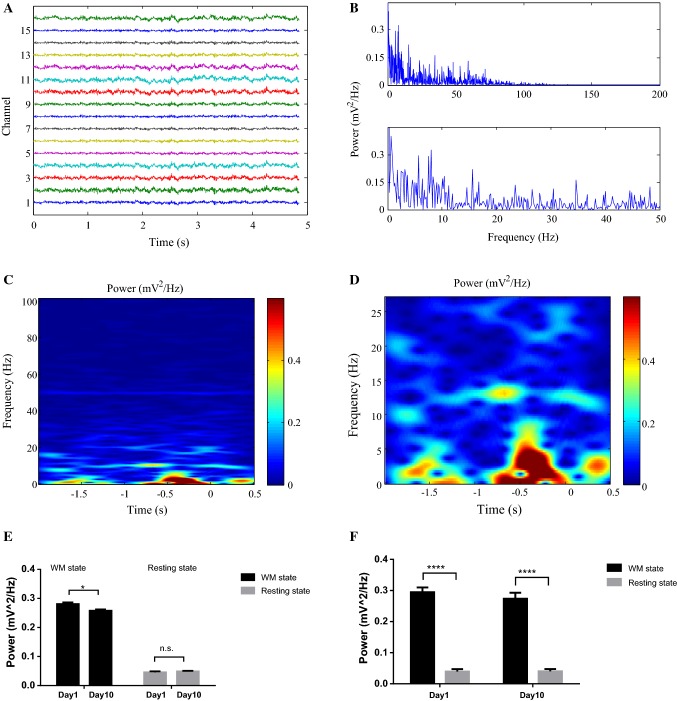
16-channel LFPs activities were recorded in the mPFC as rats performed the WM tasks on the T maze. The original LFPs were preprocessed to remove baseline drift and power–frequency interference to obtain zero-mean LFP signals without power–frequency interference in the time-domain and the frequency-domain (Fig. 2A, B). In Fig. 2A, the mean value of the 16-channel LFPs was zero, without baseline drift; in Fig. 2B, the frequency distribution of the LFPs was concentrated at 0–50 Hz, and there was no power–frequency interference at 50 Hz.
Fig. 2.
Power changes of LFPs in rat mPFC during WM tasks. A LFP signals in the time-domain after being preprocessed. B LFP signals in the frequency-domain after being preprocessed; the abscissa represents the LFPs frequency, and the ordinate represents the power spectrum of the LFPs. C Time–frequency power spectrum analysis of LFPs during WM period (10 rats, 100 trials, 16 channels average). The abscissa represents the time during the WM period (from 2 s before the reference point to the rats’ selection action in T maze), and the zero time is the selection reference point; the ordinate represents the frequency of LFPs. The colorbar represents the power of LFPs. D Low frequency power spectrum changes of the LFPs during WM period. E Comparison of the changes of LFPs power across the day 1 and day 10 of learning (10 rats, 40 trials from day 1 and day 10). The WM state were extracted from 2 s before the reference point to the rats’ selection action in the delayed alternation phase; the resting state was extracted from the 5-s delay between free choice and delayed alternation phases. Group results showed that the LFPs power at the WM state in the first day was significantly higher than in the last day, but there was no significant difference between the power at the rest state (independent sample t test, *, n.s.: no significant). F Comparisons of the changes of LFPs power in different learning days between the WM and resting state (10 rats, 40 trials from day 1 and day 10). Expert rats had learned the WM tasks at day 10. Group results showed the LFPs power at the WM state was significantly higher than that at the resting state both in day 1 and day 10 (paired sample t test, ****). (Color figure online)
After preprocessing, the LFPs were analyzed by time–frequency analysis (10 rats, 100 trials, 16 channels average). The changes in the LFP power with time during the WM period were analyzed (Fig. 2C, D). Figure 2C showed that the LFPs power at a low-frequency band during the WM tasks was higher than that at a high-frequency band. Meanwhile, the power of LFPs increased during the WM period and decreased after the selection reference point. Figure 2D represented the low frequency changes of power spectrum more clearly. The power of the low frequency LFPs also peaked near the reference point of selection. Furthermore, we analyzed the changes of LFPs power across learning (Fig. 2E). The LFPs power in first day was significantly higher than in last day at the WM state, however, there was no significant difference at the resting state. In addition, the changes of LFPs power in different learning days between the WM and resting state were analyzed (Fig. 2F). The LFPs power at the WM state was significantly higher than that at the resting state both in first day and last day. Taken together, these findings indicated that the LFPs power increased at the WM period than at resting stat, however, the LFPs power decreased when expert rats had learned the WM tasks.
The construction of a brain network based on the CFC algorithm
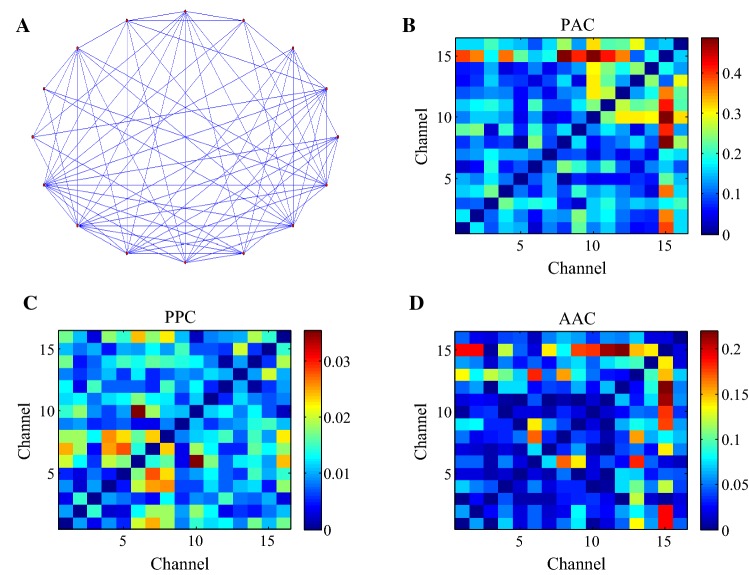
As the highly abstract of real systems, the complex network can be described by a set of nodes and edges (Bullmore and Sporns 2009). Graph theory is the most important mathematical method in the complex network analysis (Zhang et al. 2018). The construction and analysis of the complex network based on graph theory can help to understand the WM mechanism of the brain (Toppi et al. 2018). In this study, theta (4–12 Hz) and gamma (30–100 Hz) frequency band series were extracted from the preprocessed LFP signals by band filtering firstly. And then 16-channel electrodes were used as network nodes, and the CFC values between theta and gamma components of the LFPs during the WM were used as network edges. Based on the weighted network (Zheng et al. 2018; Supriya et al. 2016), the appropriate threshold was selected for the CFC edge matrix of theta-gamma to construct the brain network. If the CFC values of theta-gamma between the two nodes were greater than the threshold value, then there was a connection edge between the two nodes and the value of the connection edge was the CFC value; otherwise, there was no connection edge between the two nodes. We used three CFC algorithms including amplitude–amplitude coupling (AAC), phase–phase coupling (PPC), and phase amplitude coupling (PAC) to construct the brain network (Yeh et al. 2016; Tamburello and Mili 2015; Seymour et al. 2017). Taking the PAC algorithm as an example, the topology of the brain network based on the PAC of the theta phase and gamma amplitude is shown in Fig. 3A. There were connections between the nodes in the brain network, and no isolated nodes in the brain network. The number of edges connected by each node was approximately the same. The connectivity matrices of the brain network based on the CFC of theta-gamma during the WM period is shown in Fig. 3B–D. The distribution of the PAC and PPC values between the nodes in the brain network was more uniform (Fig. 3B, C). The AAC values between minority nodes were very strong, while the AAC values between majority nodes in the brain network were weak (Fig. 3D). The experimental results indicate that the nodes in the brain network based on the PAC and PPC of theta-gamma are closely related and each node has the same status in the network. Most nodes in the brain network based on the AAC of theta-gamma are sparsely connected and individual nodes closely related, which indicates that each node has a different status in the network.
Fig. 3.
The construction of the brain network based on the CFC of theta-gamma during the WM period. A The topology of the brain network based on the PAC of theta phase and gamma amplitude. The nodes in the network were 16-channel electrodes in the brain network, and the connections between the nodes were the PAC values of theta phase and gamma amplitude between the multichannel electrodes in the brain network. B The connectivity matrices of the brain network based on the PAC of theta-gamma during the WM period (10 rats, average over 100 trials). The WM period was chosen from 2 s before the reference point to the rats’ selection action in the T maze. The networks can show how much each node interacts with one another. The horizontal and vertical coordinates represent the channel index and the scaled color represents the connectivity strengths between nodes. C The connectivity matrices of the brain network based on the AAC of theta-gamma. D The connectivity matrices of the brain network based on the PPC of theta-gamma
The dynamic changes of the CFC
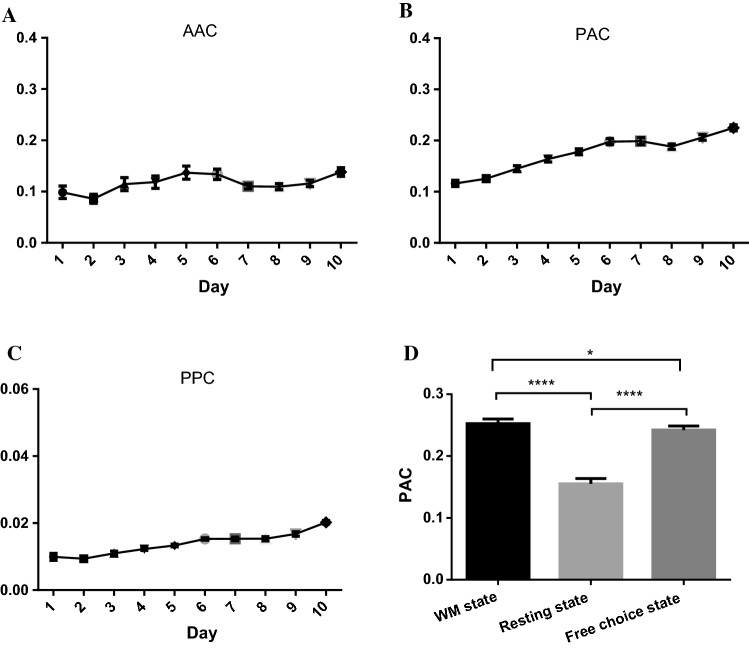
The changes in CFC values between the theta and the gamma components of the LFPs with learning days are shown in Fig. 4A–C. The AAC, PAC and PPC values between theta and gamma components of LFP signals increased significantly with an increase in learning days. The PAC between theta phase and gamma amplitude increased the fastest with an increase in learning days. Statistical differences in the AAC, PPC and PAC of 10 rats are shown in Table 1. The PAC values of theta phase and gamma amplitude were significantly different from the AAC and PPC values among the 10 rats. The average value of PAC was the largest, and the average value of PPC was the smallest. The results indicate that the coordination effect between theta and gamma components of LFP signals is involved in the formation of WM. The PAC values of theta and gamma increased the fastest in the process of WM, and the overall value of PAC was the largest, which means the modulation between the theta phase and the gamma amplitude may play an important role in the formation of WM.
Fig. 4.
The changes in CFC values of theta-gamma over the learning days (10 rats, 100 trials, average over 16 channels). A The changes in AAC between the theta amplitude and the gamma amplitude over the learning days. The AAC values between the theta amplitude and the gamma amplitude increased significantly with an increase in learning days (one-way ANOVA: , **). B The changes in PAC between the theta phase and the gamma amplitude over the learning days. The learning days had a significant effect on the PAC between the theta phase and the gamma amplitude. The PAC values increased significantly with an increase in learning days (one-way ANOVA: , ****). C The changes in PPC between the theta phase and the gamma phase over the learning days. The PPC values increased significantly with an increase in learning days (one-way ANOVA: , ****). D The comparison of PAC values of the brain network at the WM state, resting state and free choice state (10 rats, average over 168 correct trials). The time windows of the WM state and free choice state were extracted from 2 s before the reference point to the rats’ selection action in the delayed alternation phase and free choice phase respectively; the time window of the resting state was extracted from the 5-second delay between free choice and delayed alternation phases. The PAC values at the WM state and free choice state were both significantly higher than those in the resting state. In addition, the PAC values in the WM state were significant higher than those in the free choice state (one-way ANOVA: , **** and Bonferroni post hoc test: ****, *)
Table 1.
The comparisons of the AAC, PPC and PAC values of 10 rats
| ANOVA (one way)a | AACb | PACb | PPCb |
|---|---|---|---|
| Rat1 | 0.119 ± 0.093** | 0.161 ± 0.047 | 0.010 ± 0.008** |
| Rat2 | 0.121 ± 0.068** | 0.156 ± 0.045 | 0.0011 ± 0.005** |
| Rat3 | 0.114 ± 0.0979** | 0.164 ± 0.044 | 0.012 ± 0.003** |
| Rat 4 | 0.119 ± 0.0942** | 0.178 ± 0.044 | 0.013 ± 0.003** |
| Rat 5 | 0.131 ± 0.10** | 0.198 ± 0.045 | 0.015 ± 0.003** |
| Rat 6 | 0.110 ± 0378** | 0.145 ± 0.045 | 0.011 ± 0.005** |
| Rat 7 | 0.109 ± 0.047** | 0.188 ± 0.041 | 0.015 ± 0.050** |
| Rat 8 | 0.134 ± 0.079** | 0.175 ± 047 | 0.020 ± 0.004** |
| Rat 9 | 0.116 ± 0.049** | 0.206 ± 0438 | 0.017 ± 0.005** |
| Rat10 | 0.138 ± 0.064** | 0.199 ± 0.051 | 0.015 ± 0.004** |
| Average value | 0.116 ± 0.016** | 0.174 ± 0.036 | 0.013 ± 0.005** |
The values are the mean ± SD of AAC, PAC, PPC
**, compared to the values of PAC
aOne-way ANOVA, comparisons of the AAC, PPC and PAC values of 10 rats
bPost hoc t test
To further verify the modulation between the theta phase and the gamma amplitude during the WM formation, the PAC values between theta phase and gamma amplitude of the LFPs in the WM state, resting state and free choice state were compared and analyzed (Fig. 4D). The PAC values at the WM state and free choice state were significantly higher than those in the resting state. In addition, the PAC values in the WM state (WM need) were higher than those in the free choice state (no WM). It indicates that the PAC between the theta phase and the gamma amplitude of the LFPs increases during the time windows of choice, moreover, the PAC in the WM choice increases more obviously than in the free choices. The modulation between theta phase and gamma amplitude is involved in the formation of WM. The brain network based on the PAC of theta and gamma is used in the following analysis.
The dynamic changes of complex network properties
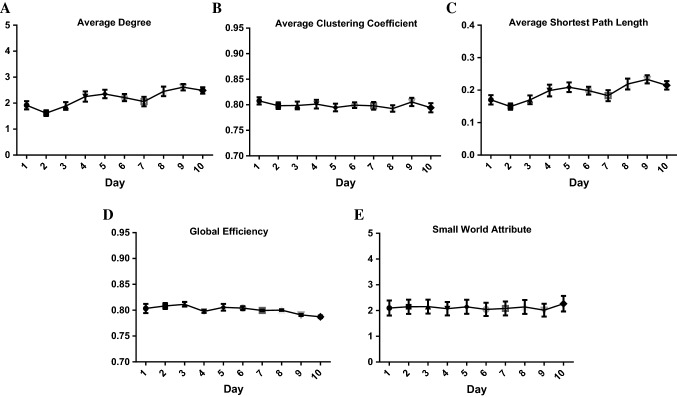
Based on the complex network theory, the dynamic changes in the complex network properties including: average degree, average clustering coefficient, average shortest path length, global efficiency and small-world attribute of the brain network based on the PAC algorithm during the WM tasks were analyzed (Fig. 5).
Fig. 5.
The complex network properties of the brain network based on the PAC algorithm during the WM tasks (10 rats, 100 trials). A Dynamic changes in the average degree of the brain network based on the PAC algorithm. The average degree of the brain network during the WM process increased significantly with an increase in learning days (one-way ANOVA: , ***). B Dynamic changes in the average clustering coefficient of the brain network based on the PAC algorithm. Learning days had no significant effect on the average clustering coefficients of the brain networks during WM. (one-way ANOVA: , ) C Dynamic changes in average shortest path length of the brain network based on the PAC algorithm. The average shortest path length of the brain network during the WM process increased significantly with an increase in learning days. (one-way ANOVA: , **). D Dynamic changes in the global efficiency of the brain network based on the PAC algorithm. The global efficiency of the brain network during the WM process decreased significantly with an increase in learning days. (one-way ANOVA: , **). E Dynamic changes in the small-world attribute of the brain network based on the PAC algorithm. There was no significant difference of the small-world attribute of the brain networks during WM in learning days (one-way ANOVA: , )
The average degree is the average of the weights among all the connected nodes. It represents the connection strength of the network. The greater the average degree is, the stronger the connection of the network is. Figure 5A showed that the average degree of the brain network increased significantly during the period of the first to the eighth days of learning, indicating that the connection of the network is enhanced. During the period of the ninth to the tenth days, the average degree of the brain network was unchanged, indicating that the connection of the network remains stable. The experimental results of the animal behavioral training showed that the correct rate could reach more than 80% for two consecutive days on the eighth day of learning, which means that the rats learned WM tasks in the T maze on the ninth day. Combining the results of the behavioral experiments and the analysis of the dynamic properties of the brain network, the average degree of the brain network may be closely related to the WM process, and the connection of the brain network during the process of WM is enhanced.
The average clustering coefficient can measure the local information transmission in the network and the ability of the network to defend against random attacks. With an increase in learning days, there was no significant difference in the average clustering coefficient of the network (Fig. 5B). This suggests that the learning days will not affect the local information transmission and the ability of the network to defend against random attacks.
The average shortest path length and the global efficiency represent the information transmission efficiency of the brain network. The shorter the average shortest path length is, the higher the information transmission efficiency of the network is. In contrast, the greater the global efficiency is, the higher the information transmission is. Figure 5C, D showed that the average shortest path length increased and the global efficiency decreased significantly with an increase in learning days, indicating that the information transmission efficiency of the brain network decreases with an increase in learning days. With an increase in learning days, the PAC values of the brain network increased significantly, which indicates that the coupling strength of theta phase and the gamma amplitude of the LFPs increases. WM may increase the amount of information in the brain network and decrease the efficiency of information transmission in the network.
The small-world attribute is the criterion for judging whether a constructed network has small world properties or not. Figure 5E showed that there was no significant difference in the small-world attribute of the network with an increase of learning days and all values of the small-world attribute were greater than 1. It suggests that the constructed brain networks in different learning days have the small-world attribute and learning days won’t affect the network attribute.
Discussion
In this study, we constructed a 16-channel brain network based on the CFC algorithm of theta and gamma components of LFPs during WM tasks and analyzed the dynamic properties of the brain network with learning days. The experimental results showed that there were significant differences of the CFC values and the complex network properties on learning days (Figs. 4 and 5).
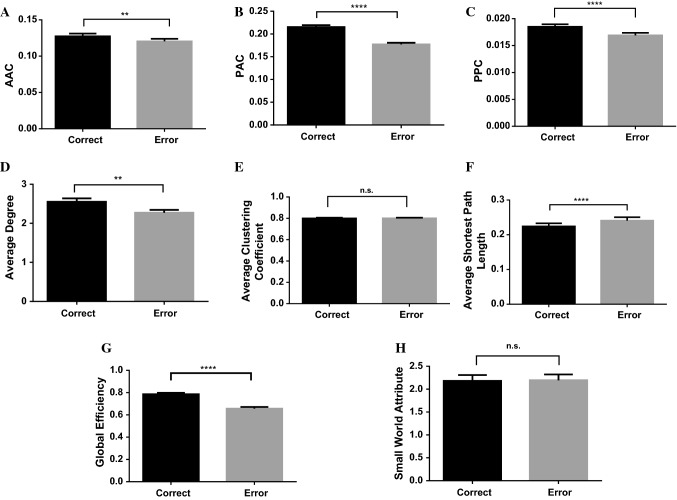
The CFC values between the theta-gamma components of the LFPs increased significantly with an increase in learning days. Previous study has found that the CFC between theta and gamma is involved in memory processes (Lisman and Jensen 2013). To identify if the increased theta-gamma coupling is associated with WM formation, we compared the CFC values in correct and error trials during WM tasks (Fig. 6A–C). We described 168 correct trials and 32 error trials from 10 expert rats which have learned the WM tasks in last 2 days (the ninth day and tenth day). Figure 6A–C showed that the CFC values in correct trials were significantly higher than those in error trials, which indicates that the CFC in the network contributes to correct storage of WM information. The results are in agreement with the previous reports.
Fig. 6.
The comparison of the CFC values and complex network properties during WM tasks. We described 168 correct trials and 32 error trials from 10 expert rats in last two days. A The comparison of the AAC values between theta phase and gamma amplitude of the LFPs in correct and error trials. The AAC values in correct trials were significantly higher than those in error trials (independent sample t test, **). B The comparison of the PAC values in the correct and error trials. The PAC values were significantly higher than those in error trials (independent sample t test, ****). C The comparison of the PPC values in correct and error trials. The PPC values were significantly higher than those in error trials (independent sample t test, ****). D The comparison of the average degree of the brain network based on the PAC algorithm in correct and error trials. The average degree of the brain network in correct trials was significantly higher than that in error trials (independent sample t test, **). E The comparison of the average clustering coefficient in correct and error trials. The average clustering coefficient in correct trials and error trials had no significant difference (independent sample t test, , n.s.: no significant). F The comparison of the average shortest path length in correct and error trials. The average shortest path length in correct trials was significantly lower than that in error trials (independent sample t test, ****). G The comparison of the global efficiency in correct and error trials. The global efficiency in correct trials was significantly higher than that in error trials (independent sample t test, ****). H The comparison of the small-world attribute in correct and error trials. The small-world attribute in correct trials and error trials had no significant difference (independent sample t test, )
In general, we try to map the changes that occur in the local mPFC networks during learning of the WM task at the level of CFC between theta and gamma components of the LFPs. Graph theory is a mathematical approach to estimate the efficiency of information flow and widely used in the brain network analysis (Wheelock et al. 2018). Evidence suggests that changes of the brain network properties can be used as biomarkers for predicting the task performance during WM tasks (Dai et al. 2014). In order to identify if the changes in the network that occurred during learning is associated with WM formation, the complex network properties based on the graph theory during WM tasks were compared in correct and error trials (Fig. 6D–H). Figure 6D showed that the average degree in correct trials were significantly higher than those in error trials. Since the average degree represents the connection strength of the network, we can indicate that the network connection is related to the correct storage of WM information. The average clustering coefficient represents the local information transmission in the network. Figure 6E showed the average clustering coefficient had no significance in correct and error trials, which indicates that the WM process won’t affect the local information transmission in the network. The average shortest path length and the global efficiency both represent the global information transmission efficiency of the brain network. Figure 6F, G showed that the average shortest path length in correct trials was lower than that in error trials and global efficiency in correct trials were significantly higher than those in error trials. We indicate that the correct storage of WM can increase the information transmission efficiency. Figure 6H showed that small-world attribution had no significance in correct and error trials and all values were greater than 1, indicating that the constructed brain networks in correct or error trails have the small-world attribution.
Taken together, the changes of average degree, the average shortest path length and the global efficiency in the network are associated with WM formation. Correct storage of WM information will not change local information transmission and the small-world attribute, while, it can increase the network connection and efficiency of information transmission.
Conclusion
In this study, we first recorded 16-channel LFP signals in the mPFC during WM tasks in the T maze by using multichannel in vivo recording technology and analyzed the power changes of the LFPs during WM. Second, the brain network was constructed by using the 16-channel electrodes as network nodes and the CFC values of theta and gamma components of LFPs as the connection between the nodes. Finally, we analyzed the dynamic changes in the CFC values and the complex network properties of the brain network during WM. The experimental results can be divided into tree aspects: the power changes of the LFPs during WM; the changes of CFC during WM; the changes of complex network properties. From the power changes of the LFPs, the power of LFPs increased at the WM period than at resting stat and peaked near the reference point of selection, however, the LFPs power decreased across learning. From the changes of the CFC, the CFC values between theta-gamma of LFPs increased significantly with an increase in learning days and the PAC values at the WM state were significantly higher than those in the free choice state and resting state. The modulation between theta phase and gamma amplitude plays an important role in the formation of WM. From the changes of the complex network properties, the changes of average degree, the average shortest path length and the global efficiency in the network are associated with WM formation. The network connection was enhanced and the information transmission efficiency decreased with an increase of learning days. Furthermore, correct storage of WM information will not change local information transmission and the small-world attribute, while, it can increase the network connection and efficiency of information transmission. This study tries to map the changes that occur in the brain networks during WM at the level of CFC between theta-gamma and provides innovative ideas for the coding mechanism of neural information in WM from the perspective of the graph theory and complex network properties.
Experimental procedure
Ethics statement
Behavioral training and electrophysiology recording methods were in accordance with the Guideline for the Care and Use of Laboratory Animals and were approved by the Biomedical Ethics Committee of Hebei University of Technology.
Electrophysiological recordings
Ten male Sprague–Dawley (SD) rats, aged 12–14 weeks and weighing 250–300 g, were bred in house and maintained on a 12:12 h light: dark schedule. Before the electrophysiological experiments, the SD rats were given a two-day food restriction (at least 85% of normal body weight). The electrophysiological experimental steps were as follows: (1) rats were anesthetized with chloral hydrate (350 mg/kg) throughout surgery; (2) the coordinates for the mPFC were determined according to the rat brain in stereotaxic coordinates (2.5–4.5 mm anterior to bregma, 0.2–1.0 mm lateral to midline, 2.5–3.0 mm from dura); (3) microelectrode arrays with 16 channels (2 × 8, 33 μm diameter, 300 μm spacing, nickel–chromium, impedance < 1 MΩ) were chronically implanted into the mPFC (Fig. 1C); (4) microelectrode arrays were affixed to the skulls using dental cement. After surgery, the rats were given 3–5 days to recover.
Training and data acquisition
The spatial delayed alternation task in a T maze based on a food reward was chosen as the WM paradigm for the rats. The T maze consists of a starting arm (point A), two target arms (point B and point C) that have the food reward, and the selection reference point (point O), shown in Fig. 1A. The rats’ intake of food was controlled to keep their weight at 85% of normal body weight. A total of 10 rats were given two training sessions per day (10 trials per session). Each trial of the T maze WM task included two phases: the free choice and the delayed alternation. Before the start of each task, rats were placed in the starting arm (point A), and the food reward was placed in the troughs of the target arms on both sides. At the beginning of the task, the rats were allowed to choose freely by opening the movable door in the departure area. Food rewards could be obtained from point A to the end of the target arm on either side. After feeding, the rats returned to the starting area and started again after a five-second delay. If the rats chose the target arm that they did not enter in the previous stage, they could get a food reward, and it was recorded as correct. In contrast, if the rats chose the same target arm that they had entered in the previous stage, they could not get a food reward. After the completion of a trial task, the rats returned to the starting area and waited for the next trial. Training continued until the correct rate was over 80% for two consecutive days.
During the training of the WM tasks in the T maze, we recorded the 16-channel neural data from the microelectrode arrays in the mPFC by using a Multichannel Neuroelectrophysiological Signal Recording System (OmniPlex/128, Plexon, USA). To extract the LFP data, the original neural signals were amplified (gain: 5000), filtered (0.3–500 Hz) and sampled at 1000 Hz.
Histology
We examined the positions of the recording electrode tips in the rat brain after the electrophysiological experiments. Firstly, all the rats were deeply anesthetized and transcardially perfused with phosphate buffered solution followed by 4% paraformaldehyde solution. Then the brain tissue was sliced at 150 μm and mounted on slides to visualize and photograph lesions. Lastly, the location of electrodes were verified histologically and plotted on standard diagrams compared with the brain atlas of rats.
Data analysis
Power spectrum estimation and time–frequency analysis
Power spectrum analysis can reflect the spectrum characteristics of signals. We chose fast Fourier transform (FFT) to analyze the frequency-energy distribution of multi-channel LFP signals. The formula of FFT is shown as:
| 1 |
where , is the angular frequency, is the signal frequency, is the signal time.
The time–frequency distribution of multi-channel LFPs was obtained by using short-time Fourier transform (STFT). The formula of STFT is shown as:
| 2 |
in which, is window function. The length of window function was chosen as 1000 ms, the moving step was chosen as 200 ms. The dynamic time–frequency distribution of LFPs in each channel was calculated during WM.
CFC algorithm
CFC can describe the coordination between different frequency components of the LFPs, including AAC, PPC and PAC. The CFC algorithm requires the following steps: first, extracting the instantaneous amplitude and phase of the signal by using a Hilbert transform; then calculating the CFC values with specific methods including AAC, PPC and PAC; and finally, comparing the differences among the AAC, PPC and PAC. The Hilbert transform decomposes signals in the time domain into adjacent frequency bands, and then converts each frequency band into complex signals in the frequency domain. After the Hilbert transform, the power of the signal does not change, but the phase is shifted by compared with the original signal. First, an analytic signal, , is defined below:
| 3 |
| 4 |
| 5 |
in which is the Hilbert transform of , is the amplitude of the signal in time step and is the instantaneous phase of the signal. Having the instantaneous phase and the amplitude of the signal, we can calculate different types of CFC.
AAC
The Pearson correlation coefficient is usually used to estimate AAC between signals. The specific formulas are as follows:
| 6 |
in which and represent the power densities of and , respectively. The Pearson correlation coefficient is between − 1 and 1. When , this means increases with an increase in ; when , this means increases with a decrease in . When , this means that there is no linear relationship between the two signals. The larger the Pearson correlation coefficient is, the stronger the correlation between the two signals is.
-
(2)
PPC
The Phase locking value (PLV) can measure the phase synchronism between two frequency bands. The description of PLV can be shown as follows:
| 7 |
in which is the length of the time sequence. The PLV value is between 0 and 1. A value of indicates that there is no coupling relationship between the two phases of the two signals, and a value of means a complete coupling between the phase of the two signals. The larger the PLV value is, the stronger the phase coupling between the two signals.
-
(3)
PAC
PAC of the amplitude of high-frequency activity to the phase of slower oscillations has been described in cognitive process and it is used to measure the modulation effect of the phase of one signal on the amplitude of another signal (Jafakesh et al. 2016). In this study, the modulation between theta phase and gamma amplitude of the multichannel LFP signals was studied by using PAC based on the PLV method. Assuming that two different signals are and , the instantaneous amplitude and the phase of and are extracted by the Hilbert transform.
| 8 |
| 9 |
The phase of is and the amplitude of is . The time series of was filtered on the frequency band of signal , which gave the value. By applying the Hilbert transform, we can get , which is the phase of . The PAC value of the two signals and can be obtained by using formula (8). The value of ranges from 0 to 1. The larger the value is, the stronger the coupling between and is. A value of indicates that there is no coupling between the two signals.
| 10 |
Complex network analysis
Graph theory is the most important mathematical tool in the field of complex network analysis. In graph theory, a complex network can be expressed as a graph. The graph consists of two sets: the vertex set and the edge set. The network topology properties are described as follows:
Degree
Degree is defined as the number of edges directly connected to nodes, which is the most important description of the statistical characteristics of nodes interconnection, and it reflects the characteristics of network evolution. The greater the degree of the node, the more important the node position in the network. The formula for calculating the degree of node is as follows:
| 11 |
-
(2)
Clustering coefficient
The clustering coefficient represents the possibility that neighbors of the node are neighbors to each other. This coefficient can measure the local information transmission of the network and reflect the ability of the network to defend against random attacks. The calculation formula is as follows:
| 12 |
in which is the ratio between the number of actual connected edges () and the maximum number of possible connected edges. The formula of the average clustering coefficient of the network is as follows.
| 13 |
-
(3)
Shortest path length and global efficiency
The shortest path length describes the optimal path for information transmission from the node to the node . describes the average shortest path length of the network between any two nodes in the network. The global efficiency is reciprocal to the average shortest path length .
| 14 |
| 15 |
-
(4)
Small-world attribute
Based on the complex network experiments, researchers have found that real networks are almost all small world networks, which also exists in the brain network (Bullmore and Sporns 2009). Evidence demonstrated that the neural network has a small-world network attribute, which was characterized by higher average clustering coefficient and shorter average shortest path length (Watts and Strogatz 1998). To quantify the small-world attribute of the network, the clustering coefficient and the shortest path length are unified as one index, , to measure the small-world attribute. In this equation, and . and are the average clustering coefficient of the real network and the random network, respectively. and are the average shortest path length of the real network and the random network, respectively. The network holds a small-world attribute if . The greater is, the stronger the small-world attribute is.
The average degree, average clustering coefficient, average shorted path length, global efficiency and small-world attribute are the basic characteristics of complex networks, reflecting the efficiency of WM information transmission in brain networks.
Statistical analysis
We recorded 16-channel LFPs activities from rat mPFC when they performed the WM task in T maze. In total, we described 100 trials from 10 rats in learning days and 168 correct trials and 32 error trials from 10 expert rats in last two days. Data in the text and figures are expressed as the mean ± SEM. The comparisons of the PAC values at the WM stat, resting state and free choice state were done by using Bonferroni post hoc test after one-way ANOVA. When comparing the correct rate of behavioral training, the CFC values and the complex network properties during learning days, a one-way ANOVA followed by post hoc t test was used. Independent sample t test and paired sample t test were used to compare two groups of data. The P value was considered statistically significant as follows: *, **, ***, ****.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Nos. 61571180 and 51737003).
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- Albouy P, Weiss A, Baillet S, et al. Selective entrainment of theta oscillations in the dorsal stream causally enhances auditory working memory performance. Neuron. 2017;94(1):193. doi: 10.1016/j.neuron.2017.03.015. [DOI] [PubMed] [Google Scholar]
- Antonakakis M, Dimitriadis SI, Zervakis M, et al. Altered cross-frequency coupling in resting-state MEG after mild traumatic brain injury. Int J Psychophysiol. 2016;102:1–11. doi: 10.1016/j.ijpsycho.2016.02.002. [DOI] [PubMed] [Google Scholar]
- Ateş FE, Cangöz B, Baskak B, et al. Frontal activity during a verbal emotional working memory task in patients with Alzheimer’s disease: a functional near-infrared spectroscopy study. Psychiatry Res Neuroimaging. 2017;261:29–34. doi: 10.1016/j.pscychresns.2016.12.013. [DOI] [PubMed] [Google Scholar]
- Bai W, Yi H, Liu T, et al. Incoordination between spikes and LFPs in Aβ1-42-mediated memory deficits in rats. Front Behav Neurosci. 2014;8:411. doi: 10.3389/fnbeh.2014.00411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bittner RA, Linden DEJ, Roebroeck A, et al. The when and where of working memory dysfunction in early-onset schizophrenia-A functional magnetic resonance imaging study. Cereb Cortex. 2015;25(9):2494–2506. doi: 10.1093/cercor/bhu050. [DOI] [PubMed] [Google Scholar]
- Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci. 2009;10(3):186. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Carver FW, Rubinstein DY, Gerlich AH, et al. Prefrontal high gamma during a magnetoencephalographic working memory task. Hum Brain Mapp. 2019;40(6):1774–1785. doi: 10.1002/hbm.24489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen H, Lei H, Xu Q. Neuronal activity pattern defects in the striatum in awake mouse model of Parkinson’s disease. Behav Brain Res. 2018;341:135–145. doi: 10.1016/j.bbr.2017.12.018. [DOI] [PubMed] [Google Scholar]
- Christophel TB, Klink PC, Spitzer B, et al. The distributed nature of working memory. Trends Cognit Sci. 2017;21(2):111. doi: 10.1016/j.tics.2016.12.007. [DOI] [PubMed] [Google Scholar]
- Dai Z, Yan C, Li K, et al. Identifying and mapping connectivity patterns of brain network hubs in Alzheimer’s disease. Cereb Cortex. 2014;25(10):3723. doi: 10.1093/cercor/bhu246. [DOI] [PubMed] [Google Scholar]
- Davis KE, Burnett K, Gigg J. Water and T-maze protocols are equally efficient methods to assess spatial memory in 3xTg Alzheimer’s disease mice. Behav Brain Res. 2017;331:54. doi: 10.1016/j.bbr.2017.05.005. [DOI] [PubMed] [Google Scholar]
- Decoteau WE, Thorn C, Gibson DJ, et al. Oscillations of local field potentials in the rat dorsal striatum during spontaneous and instructed behaviors. J Neurophysiol. 2007;97(5):3800–3805. doi: 10.1152/jn.00108.2007. [DOI] [PubMed] [Google Scholar]
- Esmaeili V, Diamond ME. Neuronal correlates of tactile working memory in prefrontal and vibrissal somatosensory cortex. Cell Rep. 2019;27(11):3167–3181. doi: 10.1016/j.celrep.2019.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Funahashi S. Working memory in the prefrontal cortex. Brain Sci. 2017;7(5):49. doi: 10.3390/brainsci7050049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graetz S, Daume G, Friese U, et al. Alterations in oscillatory cortical activity indicate changes in mnemonic processing during continuous item recognition. Exp Brain Res. 2019;237(2):573–583. doi: 10.1007/s00221-018-5439-4. [DOI] [PubMed] [Google Scholar]
- Haj ME, Antoine P. Describe yourself to improve your autobiographical memory: a study in Alzheimer’s disease. Cortex. 2017;88:165–172. doi: 10.1016/j.cortex.2017.01.004. [DOI] [PubMed] [Google Scholar]
- Jafakesh S, Jahromy FZ, Daliri MR. Decoding of object categories from brain signals using cross frequency coupling methods. Biomed Signal Process. 2016;27:60–67. doi: 10.1016/j.bspc.2016.01.013. [DOI] [Google Scholar]
- Li S, Ouyang M, Liu T, et al. Increase of spike–LFP coordination in rat prefrontal cortex during working memory. Behav Brain Res. 2014;261:297–304. doi: 10.1016/j.bbr.2013.12.030. [DOI] [PubMed] [Google Scholar]
- Liebe S, Hoerzer GM, Logothetis NK, et al. Theta coupling between V4 and prefrontal cortex predicts visual short-term memory performance. Nat Neurosci. 2012;15(3):456–462. doi: 10.1038/nn.3038. [DOI] [PubMed] [Google Scholar]
- Lisman JE, Jensen O. The theta-gamma neural code. Neuron. 2013;77(6):1002–1016. doi: 10.1016/j.neuron.2013.03.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Xia M, Dai Z, et al. Intrinsic brain hub connectivity underlies individual differences in spatial working memory. Cereb Cortex. 2016;27(12):1. doi: 10.1093/cercor/bhw317. [DOI] [PubMed] [Google Scholar]
- Lundqvist M, Herman P, Warden MR, et al. Gamma and beta bursts during working memory readout suggest roles in its volitional control. Nat Commun. 2018;9(1):394. doi: 10.1038/s41467-017-02791-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nir Y, Andrillon T, Marmelshtein A, et al. Selective neuronal lapses precede human cognitive lapses following sleep deprivation. Nat Med. 2017;23(12):1474–1480. doi: 10.1038/nm.4433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ouyang M, Li S, Tian X, et al. Functional connectivity among spikes in low dimensional space during working memory task in rat. PLoS ONE. 2014;9(3):e91481. doi: 10.1371/journal.pone.0091481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riga D, Matos MR, Glas A, et al. Optogenetic dissection of medial prefrontal cortex circuitry. Front Syst Neurosci. 2016;8:230. doi: 10.3389/fnsys.2014.00230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romo R, Brody CD, Hernández A, et al. Neuronal correlates of parametric working memory in the prefrontal cortex. Nature. 1999;399(6735):470–473. doi: 10.1038/20939. [DOI] [PubMed] [Google Scholar]
- Seymour RA, Rippon G, Kessler K. The detection of phase amplitude coupling during sensory processing. Front Neurosci. 2017;11:487. doi: 10.3389/fnins.2017.00487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorokin JM, Davidson TJ, Frechette E, et al. Bidirectional control of generalized epilepsy networks via rapid real-time switching of firing mode. Neuron. 2017;93(1):194–210. doi: 10.1016/j.neuron.2016.11.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stevenson RF, Zheng J, Mnatsakanyan L, et al. Hippocampal CA1 gamma power predicts the precision of spatial memory judgments. Proc Natl Acad Sci. 2018;115(40):10148–10153. doi: 10.1073/pnas.1805724115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supriya S, Siuly S, Wang H, et al. Weighted visibility graph with complex network features in the detection of epilepsy. IEEE Access. 2016;4:6554–6566. doi: 10.1109/access.2016.2612242. [DOI] [Google Scholar]
- Tamburello P, Mili L. New robust estimators of correlation and weighted basis pursuit. IEEE Trans Signal Process. 2015;63(4):882–894. doi: 10.1109/tsp.2014.2385664. [DOI] [Google Scholar]
- Toppi J, Astolfi L, Risetti M, et al. Different topological properties of EEG-derived networks describe working memory phases as revealed by graph theoretical analysis. Front Hum Neurosci. 2018;11:637. doi: 10.3389/fnhum.2017.00637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vatansever D, Manktelow AE, Sahakian BJ, et al. Angular default mode network connectivity across working memory load. Hum Brain Mapp. 2017;38(1):41–52. doi: 10.1002/hbm.23341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH. Collective dynamics of ‘small-world’networks. Nature. 1998;393(6684):440. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Wheelock MD, Rangaprakash D, Harnett NG, et al. Psychosocial stress reactivity is associated with decreased whole-brain network efficiency and increased amygdala centrality. Behav Neurosci. 2018;132(6):561. doi: 10.1037/bne0000276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wutz A, Loonis R, Roy JE, et al. Different levels of category abstraction by different dynamics in different prefrontal areas. Neuron. 2018;97(3):716–726. doi: 10.1016/j.neuron.2018.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie J, Bai W, Liu T, et al. Functional connectivity among spike trains in neural assemblies during rat working memory task. Behav Brain Res. 2014;274:248–257. doi: 10.1016/j.bbr.2014.08.027. [DOI] [PubMed] [Google Scholar]
- Yeh CH, Lo MT, Hu K. Spurious cross-frequency amplitude–amplitude coupling in nonstationary, nonlinear signals. Phys A. 2016;454:143–150. doi: 10.1016/j.physa.2016.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Li M, Wang R, et al. Abnormal brain white matter network in young smokers: a graph theory analysis study. Brain Imaging Behav. 2018;12(2):345–356. doi: 10.1007/s11682-017-9699-6. [DOI] [PubMed] [Google Scholar]
- Zheng W, Yu H, Ding W, et al. Changes in brain functional networks of insomniacs induced by magnetic stimulation at acupoints. IEEE Trans Appl Supercond. 2018;29(2):1–4. doi: 10.1109/TASC.2018.2882069. [DOI] [Google Scholar]
- Zutshi I, Brandon MP, Fu ML, et al. Hippocampal neural circuits respond to optogenetic pacing of theta frequencies by generating accelerated oscillation frequencies. Curr Biol. 2018;28(8):1–10. doi: 10.1016/j.cub.2018.02.061. [DOI] [PMC free article] [PubMed] [Google Scholar]