Global analysis of an epidemic model with vaccination

Abstract

In this paper, an epidemic dynamical model with vaccination is proposed. Vaccination of both newborn and susceptible is included in the present model. The impact of the vaccination strategy with the vaccine efficacy is explored. In particular, the model exhibits backward bifurcations under the vaccination level, and bistability occurrence can be observed. Mathematically, a bifurcation analysis is performed, and the conditions ensuring that the system exhibits backward bifurcation are provided. The global dynamics of the equilibrium in the model are also investigated. Numerical simulations are also conducted to confirm and extend the analytic results.

Introduction

Mathematical models have become important tools in analyzing the spread and control of infectious diseases [2]. Based on the theory of Kermack and Mckendrick [19], the spread of infectious diseases usually can be described mathematically by compartmental models such as $SIR,SIRS,SEIR,SEIRS$ models (where S represents the class of the susceptible population, E is the exposed class in the latent period, I is infectious class, R is the removed class, which has recovered with temporary or permanent immunity). In recent years, a variety of compartmental models have been formulated, and the mathematical analysis of epidemiology models has advanced rapidly, and the analyzed results are applied to infectious diseases [2, 18, 32]. Vaccination campaigns have been critical in attacking the spread of infectious diseases, e.g., pertussis, measles, and influenza. The eradication of smallpox has been considered as the most spectacular success of vaccination [44]. Although vaccination has been an effective strategy against infectious diseases, current preventive vaccine consisting of inactivated viruses do not protect all vaccine recipients equally. The vaccine-based protection is dependent on the immune status of the recipient [2, 32]. For example, influenza vaccines protect 70–90% of the recipients among healthy young adults and as low as 30–40% of the elderly and others with weakened immune systems (such as HIV-infected or immuno-suppressed transplant patients) (see, [14, 30, 44]).

Since vaccination is the process of administering weakened or dead pathogens to a healthy person or animal, with the intent of conferring immunity against a targeted form of a related disease agent, the individuals having the vaccine-induced immunity can be distinguished from the recovered individuals by natural immunity. Thus, vaccination can also be considered by adding some compartment naturally into the basic epidemic models. Over the past few decades, a large number of simple compartmental mathematical models with vaccinated population have been used in the literature to assess the impact or potential impact of imperfect vaccines for combatting the transmission diseases [1, 3, 11, 16, 20, 21, 23, 31, 43, 45]. In some of these studies (e.g., papers [16, 31, 43]), authors have shown that the dynamics of the model are determined by the disease’s basic reproduction number ${\mathfrak{R}}_0$. If ${\mathfrak{R}}_0<1$ the disease can be eliminated from the community; whereas an endemic occurs if ${\mathfrak{R}}_0>1$. Therefore, if an efficient vaccination campaign acts to reduce the disease’s basic reproduction number ${\mathfrak{R}}_0$ below the critical level of 1, then the disease can be eradicated. While in other studies, such as Alexander et al. [1] and Arino et al. [3], they have shown that the criterion for ${\mathfrak{R}}_0<1$ is not always sufficient to control the spread of a disease. A phenomenon known as a backward bifurcation is observed. Mathematically speaking, when a backward bifurcation occurs, there are at least three equilibria for ${\mathfrak{R}}_0<1$ in the model: the stable disease-free equilibrium, a large stable endemic equilibrium, and a small unstable endemic equilibrium which acts as a boundary between the basins of attraction for the two stable equilibria. In some cases, a backward bifurcation leading to bistability can occur. Thus, it is possible for the disease itself to become endemic in a population, given a sufficiently large initial outbreak. These phenomena have important epidemiological consequences for disease management. In recent years, backward bifurcation, which leads to multiple and subthreshold equilibria, has been attracting much attention (see, [1, 3, 4, 6, 11, 16, 17, 20, 21, 23, 24, 33, 34, 37, 40]). Several mechanisms with vaccination have been identified to cause the occurrence of backward bifurcation in paper [33].

In this paper, we shall investigate the effects of a vaccination campaign with an imperfect vaccine upon the spread of a non-fatal disease, such as hepatitis A, hepatitis B, tuberculosis and influenza, which features both exposed and infective stages. In particular, we focus on the vaccination parameters how to change the qualitative behavior of the model, which may lead to subthreshold endemic states via backward bifurcation. Global stability results for equilibria are obtained. The model constructed in this paper is an extension of the model in paper [31], including a new compartment for the latent class (an important feature for the infectious diseases eg. hepatitis A, hepatitis B, tuberculosis and influenza) and the disease cycle. It is one of the aims of this paper to strengthen the disease cycle to cause multiple endemic equilibria.

The paper is organized as follows. An epidemic model with vaccination of an imperfect vaccine is formulated in Sect. 2, and the basic reproduction number, and the existence of backward bifurcation and forward bifurcation are analyzed in Sect. 3. The global stability of the endemic equilibrium is established in Sect. 4. The paper is concluded with a discussion.

The model and the basic reproduction number

In order to derive the equations of the mathematical model, we divide the total population N in a community into five compartments: susceptible, exposed (not yet infectious), infective, recovered, and vaccinated; the numbers in these states are denoted by S(t), E(t), I(t), R(t), and V(t),  respectively. Let $N(t)=S(t)+E(t)+I(t)+R(t)+V(t)$. The flow diagram of the disease spread is depicted in Fig. 1.

Fig. 1.

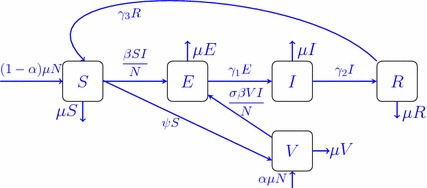
Flowchart diagram for model (2.1)

All newborns are assumed to be susceptible. Of these newborns, a fraction $\mathit{\alpha }$ of individuals are vaccinated, where $\mathit{\alpha }\in (0,1]$. Susceptible individuals are vaccinated at rate constant $\mathit{\psi }$. The parameter ${\mathit{\gamma }}_1$ is the rate constant at which the exposed individuals become infectious, and ${\mathit{\gamma }}_2$ is the rate constant that the infectious individuals become recovered and acquire temporary immunity. Finally, since the immunity acquired by infection wanes with time, the recovered individuals have the possibility ${\mathit{\gamma }}_3$ of becoming susceptible again. $\mathit{\beta }$ is the transmission coefficient (rate of effective contacts between susceptible and infective individuals per unit time; this coefficient includes rate of contacts and effectiveness of transmission). Since the vaccine does not confer immunity to all vaccine recipients, vaccinated individuals may become infected but at a lower rate than unvaccinated (those in class S). Thus in this case, the effective contact rate $\mathit{\beta }$ is multiplied by a scaling factor $\mathit{\sigma }$ ($0\le \mathit{\sigma }\le 1$, where $1-\mathit{\sigma }$ describes the vaccine efficacy, $\mathit{\sigma }=0$ represents vaccine that offers 100% protection against infection, while $\mathit{\sigma }=1$ models a vaccine that offers no protection at all). It is assumed that the natural death rate and birth rate are $\mathit{\mu }$ and the disease-induced death rate is ignored. Thus the total population N is constant. Since the model consider the dynamics of the human populations, it is assumed that all the model parameters are nonnegative.

Thus, the following model of differential equations is formulated based on the above assumptions and Fig. 1,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& {\displaystyle =(1-\mathit{\alpha })\mathit{\mu }N-\mathit{\mu }S-\frac{\mathit{\beta }SI}{N}-\mathit{\psi }S+{\mathit{\gamma }}_{3}R,}\hfill \\ \hfill {\displaystyle \frac{dV}{dt}}& {\displaystyle =\mathit{\mu }\mathit{\alpha }N+\mathit{\psi }S-\mathit{\sigma }\frac{\mathit{\beta }VI}{N}-\mathit{\mu }V,}\hfill \\ \hfill {\displaystyle \frac{dE}{dt}}& {\displaystyle =\frac{\mathit{\beta }SI}{N}+\mathit{\sigma }\frac{\mathit{\beta }VI}{N}-(\mathit{\mu }+{\mathit{\gamma }}_1)E,}\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\mathit{\gamma }}_{1}E-(\mathit{\mu }+{\mathit{\gamma }}_2)I,\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& ={\mathit{\gamma }}_{2}I-(\mathit{\mu }+{\mathit{\gamma }}_3)R,\hfill \end{array}\end{array}$$ 2.1

with nonnegative initial conditions and $N(0)>0$. System (2.1) is well posed: solutions remain nonnegative for nonnegative initial conditions. We illustrate here that there are limiting cases in system (2.1): if $\mathit{\sigma }=0$, the vaccine is perfectly effective, and $\mathit{\alpha }=\mathit{\psi }=0$, there is no vaccination, system (2.1) will be reduced to the standard SEIRS model in [28]; if ${\mathit{\gamma }}_3=0$ and the limit ${\mathit{\gamma }}_1\to \infty$, system (2.1) will be equivalent to an SVIR model in [31]. If we let $\mathit{\alpha }=0$ and ${\mathit{\gamma }}_3=0$, system (2.1) can be reduced to an SVEIR epidemic model in [16], where authors aim to assess the potential impact of a SARS vaccine via mathematical modelling. To explore the effect of the vaccination period and the latent period on disease dynamics, an SVEIR epidemic model with ages of vaccination and latency are formulated in paper [10]. In papers [10, 16, 28, 31], authors have shown that the dynamics of the model are determined by the disease’s basic reproduction number ${\mathfrak{R}}_0$. That is, the disease free equilibrium is globally asymptotically stable for ${\mathfrak{R}}_0\le 1$; and there is a unique endemic equilibrium which is globally asymptotically stable if ${\mathfrak{R}}_0>1$. If $\mathit{\psi }=0$ and limit ${\mathit{\gamma }}_1\to \infty$, system (2.1) will be reduced into an SIV epidemic model in [36], where authors investigate the effect of imperfect vaccines on the disease’s transmission dynamics. In [36], it is shown that reducing the basic reproduction number ${\mathfrak{R}}_0$ to values less than one no longer guarantees disease eradication. In this paper, we show that if a vaccination campaign with an imperfect vaccine and the disease cycle is considered, a more complicated dynamic behavior is observed in system (2.1). For example, the backward bifurcation occurs in system (2.1). In the following, first, it is easy to obtain that the total population N in system (2.1) is constant. To Simplify our notation, we define the occupation variable of compartments S, E, I, V,  and R as the respective fractions of a constant population N that belong to each of the corresponding compartments. We still write the occupation variable of compartments as S, E, I, V and R,  respectively. Thus, it is easy to verify that

$$\begin{array}{c}\hfill \mathcal{D}=\{(S,E,I,V,R)\in R_{+}^5:S+V+E+I+R=1\}\end{array}$$ 2.2

is positively invariant and globally attracting in $R_{+}^5$. It suffices to study the dynamics of (2.1) on $\mathcal{D}$. Thus, system (2.1) can be rewritten as the following system:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{dS}{dt}}& =(1-\mathit{\alpha })\mathit{\mu }-\mathit{\mu }S-\mathit{\beta }SI-\mathit{\psi }S+{\mathit{\gamma }}_{3}R,\hfill \\ \hfill {\displaystyle \frac{dV}{dt}}& =\mathit{\mu }\mathit{\alpha }+\mathit{\psi }S-\mathit{\sigma }\mathit{\beta }VI-\mathit{\mu }V,\hfill \\ \hfill {\displaystyle \frac{dE}{dt}}& =\mathit{\beta }SI+\mathit{\sigma }\mathit{\beta }IV-(\mathit{\mu }+{\mathit{\gamma }}_1)E,\hfill \\ \hfill {\displaystyle \frac{dI}{dt}}& ={\mathit{\gamma }}_{1}E-(\mathit{\mu }+{\mathit{\gamma }}_2)I,\hfill \\ \hfill {\displaystyle \frac{dR}{dt}}& ={\mathit{\gamma }}_{2}I-(\mathit{\mu }+{\mathit{\gamma }}_3)R.\hfill \end{array}\end{array}$$ 2.3

In the case $\mathit{\sigma }=0$, system (2.3) reduces to an SEIRS model without vaccination [28], where $R_0=\frac{\mathit{\beta }{\mathit{\gamma }}_1}{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}$, is considered as the basic reproduction number of the model. The classical basic reproduction number is defined as the number of secondary infections produced by a single infectious individual during his or her entire infectious period. Mathematically, the reproduction number is defined as a spectral radius $R_0$ (which is a threshold quantity for disease control) that defines the number of new infectious generated by a single infected individual in a fully susceptible population [39]. In the following, we shall use this approach to determine the reproduction number of system (2.3). It is easy to see that system (2.3) has always a disease-free equilibrium,

$$\begin{array}{c}\hfill P_0=(S^0,E^0,I^0,R^0,V^0)=(\frac{\mathit{\mu }(1-\mathit{\alpha })}{\mathit{\mu }+\mathit{\psi }},0,0,0,\frac{\mathit{\mu }\mathit{\alpha }+\mathit{\psi }}{\mathit{\mu }+\mathit{\psi }}).\end{array}$$

Let $x={(E,I,R,S)}^T.$ System (2.3) can be rewritten as

$$\begin{array}{c}\hfill x^{\prime }=\mathcal{F}(x)-\mathcal{V}(x),\end{array}$$

where

$$\begin{array}{c}\hfill \begin{array}{c}\mathcal{F}(x)=\left(\begin{array}{c}\mathit{\beta }SI+\mathit{\sigma }\mathit{\beta }IV\\ 0\\ 0\\ 0\end{array}\right),\mathcal{V}(x)=\left(\begin{array}{c}(\mathit{\mu }+{\mathit{\gamma }}_1)E\\ -{\mathit{\gamma }}_{1}E+(\mathit{\mu }+{\mathit{\gamma }}_2)I\\ -{\mathit{\gamma }}_{2}I+(\mathit{\mu }+{\mathit{\gamma }}_3)R\\ \mathit{\mu }S+\mathit{\beta }SI+\mathit{\psi }S-{\mathit{\gamma }}_{3}R-(1-\mathit{\alpha })\mathit{\mu }\end{array}\right).\hfill \end{array}\end{array}$$

The Jacobian matrices of $\mathcal{F}(x)$ and $\mathcal{V}(x)$ at the disease-free equilibrium $P_0$ are, respectively,

$$\begin{array}{c}\hfill \begin{array}{c}D\mathcal{F}(P_0)=\left(\begin{array}{ccc}F& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),D\mathcal{V}(P_0)=\left(\begin{array}{ccc}V& 0& 0\\ 0-{\mathit{\gamma }}_2& \mathit{\mu }+{\mathit{\gamma }}_3& 0\\ 0\mathit{\beta }{S}_0& -{\mathit{\gamma }}_3& \mathit{\mu }+\mathit{\psi }\end{array}\right),\hfill \end{array}\end{array}$$

where,

$$\begin{array}{c}\hfill \begin{array}{c}F=\left(\begin{array}{cc}0& \mathit{\beta }{S}_0+\mathit{\sigma }\mathit{\beta }{V}_0\\ 0& 0\end{array}\right),V=\left(\begin{array}{cc}\mathit{\mu }+{\mathit{\gamma }}_1& 0\\ -{\mathit{\gamma }}_1& \mathit{\mu }+{\mathit{\gamma }}_2\end{array}\right).\hfill \end{array}\end{array}$$

$F{V}^{-1}$ is the next generation matrix of system (2.3). It follows that the spectral radius of matrix $F{V}^{-1}$ is

$$\begin{array}{c}\hfill {\displaystyle \mathit{\rho }(F{V}^{-1})=\frac{\mathit{\beta }{\mathit{\gamma }}_1}{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}(S_0+\mathit{\sigma }{V}_0).}\end{array}$$

According to Theorem 2 in [39], the basic reproduction number of system (2.3) is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill R_{vac}& {\displaystyle =\frac{\mathit{\beta }{\mathit{\gamma }}_1}{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}(S_0+\mathit{\sigma }{V}_0)}\hfill \\ \hfill & {\displaystyle =R_0\frac{\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi })}{\mathit{\mu }+\mathit{\psi }}.}\hfill \end{array}\end{array}$$

The basic reproduction number $R_{vac}$ can be interpreted as follows: A proportion of $\frac{{\mathit{\gamma }}_1}{\mathit{\mu }+{\mathit{\gamma }}_1}$ of exposed individuals progress to the infective stage before dying; $\frac{1}{\mathit{\mu }+{\mathit{\gamma }}_2}$ represents the number of the secondary infection generated by an infective individual when he or she is in the infectious stage. Those newborns vaccinated individuals have generated the number $\frac{\mathit{\beta }{\mathit{\gamma }}_1}{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}\frac{\mathit{\mu }(1-\mathit{\alpha })}{\mathit{\mu }+\mathit{\psi }}$ of the secondary infection. Average vaccinated individuals with vaccination rate $\mathit{\psi }$ have generated the fraction $\frac{\mathit{\beta }{\mathit{\gamma }}_1}{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}\frac{\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi })}{\mathit{\mu }+\mathit{\psi }}$ of the secondary infection.

Equilibria and bifurcations

Now we investigate the conditions for the existence of endemic equilibria of system (2.3). Any equilibrium (S, V, E, I, R) of system (2.3) satisfies the following equations:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle }& (1-\mathit{\alpha })\mathit{\mu }-\mathit{\mu }S-\mathit{\beta }SI-\mathit{\psi }S+{\mathit{\gamma }}_{3}R=0,\hfill \\ \hfill {\displaystyle }& \mathit{\beta }SI+\mathit{\sigma }\mathit{\beta }IV-(\mathit{\mu }+{\mathit{\gamma }}_1)E=0,\hfill \\ \hfill {\displaystyle }& {\mathit{\gamma }}_{1}E-(\mathit{\mu }+{\mathit{\gamma }}_2)I=0,\hfill \\ \hfill {\displaystyle }& {\mathit{\gamma }}_{2}I-(\mathit{\mu }+{\mathit{\gamma }}_3)R=0,\hfill \\ \hfill & V=1-S-E-I-R.\hfill \end{array}\end{array}$$ 3.1

From the second and third equation of (3.1), we have $\mathit{\beta }{\mathit{\gamma }}_1(S+\mathit{\sigma }V)=(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2).$ Since $(S+\mathit{\sigma }V)<1$, this equation can be true only for $\mathit{\beta }{\mathit{\gamma }}_1>(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)$; hence, there exists no endemic equilibrium for $R_0\le 1$. For $R_0>1$, the existence of endemic equilibria is determined by the presence in (0, 1] of positive real solutions of the quadratic equation

$$\begin{array}{c}\hfill \begin{array}{c}\hfill P(I)=A{I}^2+BI+C=0,\end{array}\end{array}$$ 3.2

where,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill A& {\displaystyle =\mathit{\sigma }{\mathit{\beta }}^2(\mathit{\mu }+{\mathit{\gamma }}_3)+\frac{\mathit{\sigma }{\mathit{\beta }}^2(\mathit{\mu }+{\mathit{\gamma }}_2)(\mathit{\mu }+{\mathit{\gamma }}_3)}{{\mathit{\gamma }}_1}+\mathit{\sigma }{\mathit{\beta }}^2{\mathit{\gamma }}_2,}\hfill \\ \hfill B& {\displaystyle =\frac{\mathit{\beta }(\mathit{\mu }+{\mathit{\gamma }}_2)(\mathit{\mu }+{\mathit{\gamma }}_3)}{{\mathit{\gamma }}_1}[\mathit{\sigma }(\mathit{\mu }+\mathit{\psi })+\mathit{\mu }+{\mathit{\gamma }}_1]}\hfill \\ \hfill & +\mathit{\sigma }\mathit{\beta }{\mathit{\gamma }}_2(\mathit{\mu }+\mathit{\psi })+\mathit{\beta }{\mathit{\gamma }}_2{\mathit{\gamma }}_3(\mathit{\sigma }-1)-\mathit{\sigma }{\mathit{\beta }}^2(\mathit{\mu }+{\mathit{\gamma }}_3)\hfill \\ \hfill & +\mathit{\sigma }\mathit{\beta }(\mathit{\mu }+\mathit{\psi })(\mathit{\mu }+{\mathit{\gamma }}_3),\hfill \\ \hfill C& =\mathit{\mu }\mathit{\beta }(1-\mathit{\alpha })(\mathit{\mu }+{\mathit{\gamma }}_3)(\mathit{\sigma }-1)+(\mathit{\mu }+{\mathit{\gamma }}_3)(\mathit{\mu }+\mathit{\psi })[\frac{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}{{\mathit{\gamma }}_1}-\mathit{\sigma }\mathit{\beta }]\hfill \\ \hfill & {\displaystyle =\frac{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)(\mathit{\mu }+{\mathit{\gamma }}_3)(\mathit{\mu }+\mathit{\psi })}{{\mathit{\gamma }}_1}[1-\frac{\mathit{\beta }{\mathit{\gamma }}_1(\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi }))}{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)(\mathit{\mu }+\mathit{\psi })}]}\hfill \\ \hfill & {\displaystyle =\frac{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)(\mathit{\mu }+{\mathit{\gamma }}_3)(\mathit{\mu }+\mathit{\psi })}{{\mathit{\gamma }}_1}(1-R_{vac}).}\hfill \end{array}\end{array}$$ 3.3

From (3.2) and (3.3), we can see that the number of endemic equilibria of system (2.3) is zero, one, or two, depending on parameter values. For $\mathit{\sigma }=0$ (the vaccine is totally effective), it is obviously that there is at most one endemic equilibrium ($P^{\ast }(S^{\ast },E^{\ast },I^{\ast },R^{\ast },V^{\ast })$) in system. From now on we make the realistic assumption that the vaccine is not totally effective, and thus $0<\mathit{\sigma }<1$.

We notice that if $R_{vac}=1$, then we have

$$\begin{array}{c}\hfill {\displaystyle {\mathit{\psi }}_{crit}\stackrel{def}{=}\frac{R_0\mathit{\mu }[1+(\mathit{\sigma }-1)\mathit{\alpha }]-\mathit{\mu }}{1-\mathit{\sigma }{R}_0}.}\end{array}$$

Since all the model parameters are positive, it follows from (3.3) that $A>0$. Furthermore, if $R_{vac}>1$, then $C<0$. Since

$$\begin{array}{c}\hfill \frac{d{R}_{vac}}{d\mathit{\psi }}=-\frac{\mathit{\beta }{\mathit{\gamma }}_1}{(\mathit{\beta }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}\frac{\mathit{\mu }(1-\mathit{\sigma })(1-\mathit{\alpha })}{{(\mathit{\mu }+\mathit{\psi })}^2}<0.\end{array}$$

Thus, $R_{vac}$ is a continuous decreasing function of $\mathit{\psi }$ for $\mathit{\psi }>0$, and if $\mathit{\psi }<{\mathit{\psi }}_{crit}$, then $R_{vac}>1$ and $C<0$. Therefore, it follows that P(I) of Eq. (3.2) has a unique positive root for $R_{vac}>1$.

Now we consider the case for $R_{vac}<1.$ In this case, $C>0$, and $\mathit{\psi }\ge {\mathit{\psi }}_{crit}$. From (3.3), it is easy to see that $B(\mathit{\psi })$ is an increasing function of $\mathit{\psi }$. Thus, if $B({\mathit{\psi }}_{crit})\ge 0$, then $B(\mathit{\psi })>0$ for $\mathit{\psi }>{\mathit{\psi }}_{crit}$. Thus, P(I) has no positive real root which implies system have no endemic equilibrium in this case. Thus, let us consider the case $B({\mathit{\psi }}_{crit})<0$. In this case, let $\mathrm{\Delta }(\mathit{\psi })\stackrel{def}{=}{B}^2(\mathit{\psi })-4AC(\mathit{\psi })$. It is obvious that if $C({\mathit{\psi }}_{crit})=0$, then $\mathrm{\Delta }({\mathit{\psi }}_{crit})>0$. Notice that $B(\mathit{\psi })$ is an linear increasing function of $\mathit{\psi }$. Thus, there is a unique $\overline{\overline{\mathit{\psi }}}>{\mathit{\psi }}_{crit}$ such that $B(\overline{\overline{\mathit{\psi }}})=0,$ and thus $\mathrm{\Delta }(\overline{\overline{\mathit{\psi }}})<0.$ Since $\mathrm{\Delta }(\mathit{\psi })$ is a quadratic function of $\mathit{\psi }$ with positive coefficient for ${\mathit{\psi }}^2$, $\mathrm{\Delta }(\mathit{\psi })$ has a unique root $\overline{\mathit{\psi }}$ in $[{\mathit{\psi }}_{crit},\overline{\overline{\mathit{\psi }}}].$ Thus, for $R_{vac}<1$ we have $B(\mathit{\psi })<0$, $A>0,C\ge 0$, and $\mathrm{\Delta }(\mathit{\psi })>0$ for $\mathit{\psi }\in ({\mathit{\psi }}_{crit},\overline{\mathit{\psi }}).$ Therefore, P(I) has two possible roots and system (2.3) has two endemic equilibria $P_1^{\ast }(S_1^{\ast },E_1^{\ast },I_1^{\ast },R_1^{\ast },V^{\ast })$, $P_2^{\ast }(S_2^{\ast },E_2^{\ast },I_2^{\ast },R_2^{\ast },V^{\ast })$) for ${\mathit{\psi }}_{crit}<\mathit{\psi }<\overline{\mathit{\psi }}.$ From the above discussion, we have $B(\mathit{\psi })>0$ for $\mathit{\psi }>\overline{\overline{\mathit{\psi }}}$, and $\mathrm{\Delta }(\mathit{\psi })<0$ for $\mathit{\psi }\in (\overline{\mathit{\psi }},\overline{\overline{\mathit{\psi }}})$. Therefore, it follows that system (2.3) has no endemic equilibria for $\mathit{\psi }>\overline{\mathit{\psi }}$.

If $R_{vac}=1$, we have $C=0$. In this case, system has a unique endemic equilibrium for $B(\mathit{\psi })<0$ and no endemic equilibrium for $B(\mathit{\psi })>0.$

Summarizing the discussion above, we have the following Theorem:

Theorem 3.1

If $R_{vac}>1(i.e.,\mathit{\psi }<{\mathit{\psi }}_{crit})$, system (2.3) has a unique endemic equilibrium $P^{\ast }(S^{\ast },E^{\ast },I^{\ast },R^{\ast },V^{\ast })$; If there exists $R_{vac}<1(i.e.,\overline{\mathit{\psi }}>{\mathit{\psi }}_{crit})$, system (2.3) has two endemic equilibria $P_1^{\ast }(S_1^{\ast },E_1^{\ast },I_1^{\ast },R_1^{\ast },V_1^{\ast })$, $P_2^{\ast }(S_2^{\ast },E_2^{\ast },I_2^{\ast },R_2^{\ast },V_2^{\ast })$ for ${\mathit{\psi }}_{crit}<\mathit{\psi }<\overline{\mathit{\psi }}$ and has no endemic equilibria for $\mathit{\psi }>\overline{\mathit{\psi }}$; If $R_{vac}=1(i.e.,\mathit{\psi }={\mathit{\psi }}_{crit})$, system (2.3) has a unique endemic equilibrium $P^{\ast }(S^{\ast },E^{\ast },I^{\ast },R^{\ast },V^{\ast })$ for $B(\mathit{\psi })<0$ and no endemic equilibrium for $B(\mathit{\psi })>0.$

According to Theorem 2 of van den Driesche and Watmough [39], we have the following result.

Theorem 3.2

The disease-free equilibrium $P_0$ is locally asymptotically stable when $R_{vac}<1$ and unstable when $R_{vac}>1$.

In the following, we first give a global result of the disease-free equilibrium of system (2.3) under some conditions.

Theorem 3.3

If $R_0<1$, $P_0$ is globally asymptotically stable in the feasible positively invariant region.

Proof

Consider the following Lyapunov functional

$$\begin{array}{c}\hfill L={\mathit{\gamma }}_{1}E+(\mathit{\mu }+{\mathit{\gamma }}_1)I.\end{array}$$

By directly calculating the derivative of L along system (2.3) and notice that $S+\mathit{\sigma }V<1$, thus, we have

$$\begin{array}{c}\hfill \begin{array}{cc}{\displaystyle \frac{dL}{dt}}\hfill & {\displaystyle ={\mathit{\gamma }}_1\frac{dE}{dt}+(\mathit{\mu }+{\mathit{\gamma }}_1)\frac{dI}{dt}}\hfill \\ \hfill & {\displaystyle =\mathit{\beta }{\mathit{\gamma }}_1[S+\mathit{\sigma }V]I-(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)I}\hfill \\ \hfill & \le (\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)(R_0-1)I\le 0,\text{for}{R}_0\le 1.\hfill \end{array}\end{array}$$

It is easy to verify that the maximal compact invariant set in ${\displaystyle \{(S,E,I,R,V)\in \mathrm{\Omega }:\frac{dL}{dt}=0\}}$ is $\{P_0\}$ when $R_0\le 1$. The global stability of $P_0$ follows from the LaSalle invariance principle [22]. $\square$

From the above discussion, we know that system (2.3) may undergo a bifurcation at the disease-free equilibrium when $R_{vac}=1$. Now we establish the conditions on the parameter values that cause a forward or backward bifurcation to occur. To do so, we shall use the following theorem whose proof is found in Castillo-Chavez and Song [5], which based on the use of the center manifold theory [15].

For the following general system with a parameter $\mathit{\varphi }$.

$$\begin{array}{c}\hfill {\displaystyle \frac{dx}{dt}=f(x,\mathit{\varphi }):f:R^n\times R\to R^n,f\in C^2(R^n\times R).}\end{array}$$ 3.4

Without loss of generality, it is assumed that $x=0$ is an equilibrium for system (3.4) for all values of the parameters $\mathit{\varphi }$, that is, $f(0,\mathit{\varphi })=0$ for all $\mathit{\varphi }$.

Theorem 3.4

Assume that:

1. $A=D_{x}f(0,0)$ is the linearization matrix of system (3.4) around the equilibrium $x=0$ with $\mathit{\varphi }$ evaluated at 0. Zero is simple eigenvalue of A and all other eigenvalue of A have negative real parts;

2. Matrix A has a (non-negative ) right eigenvector $\mathit{\omega }$ and a left eigenvector v corresponding to the zero eigenvalue.

Let $f_k$ be the kth component of f and

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle a={\sum }_{k,i,j=1}^n{v}_k{\mathit{\omega }}_i{\mathit{\omega }}_j\frac{{\mathit{\partial }}^2{f}_k}{\mathit{\partial }{x}_i\mathit{\partial }{x}_j}(0,0),}\hfill \\ {\displaystyle b={\sum }_{k,i}^n{v}_k{w}_i\frac{{\mathit{\partial }}^2{f}_k}{\mathit{\partial }{x}_i\mathit{\partial }\mathit{\varphi }}(0,0).}\hfill \end{array}\end{array}$$

Then the local dynamics of system (3.4) around $x=0$ are totally determined by a and b.

• (i) $a>0,b>0.$ When $\mathit{\varphi }<0$ with $|\mathit{\varphi }|\ll 1$, $x=0$ is locally asymptotically stable and there exists a positive unstable equilibrium; when $0<\mathit{\varphi }\ll 1,x=0$ is unstable and there exists a negative and locally asymptotically equilibrium;
• (ii) $a<0,b<0.$ When $\mathit{\varphi }<0$, with $|\mathit{\varphi }|\ll 1$, $x=0$ is unstable; when $0<\mathit{\varphi }\ll 1,x=0$ is locally asymptotically stable and there exists a negative unstable equilibrium;
• (iii) $a>0,b<0.$When $\mathit{\varphi }<0$, with $|\mathit{\varphi }|\ll 1$, $x=0$ is unstable and there exists a locally asymptotically stable negative equilibrium; when $0<\mathit{\varphi }\ll 1,x=0$ is stable and a positive unstable equilibrium appears;
• (iv) $a<0,b>0.$ When $\mathit{\varphi }$ changes from negative to positive, $x=0$ changes its stability from stable to unstable. Correspondingly, a negative unstable equilibrium becomes positive and locally asymptotically stable.

Now by applying Theorem 3.4, we shall show system (2.3) may exhibit a forward or a backward bifurcation when $R_{vac}=1$. Consider the disease-free equilibrium $P_0=(S_0,0,0,0)$ and choose $\mathit{\beta }$ as a bifurcation parameter. Solving $R_{vac}=1$ gives

$$\begin{array}{c}\hfill \mathit{\beta }={\mathit{\beta }}^{\ast }=\frac{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)(\mathit{\mu }+\mathit{\psi })}{{\mathit{\gamma }}_1[\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi })]}\end{array}$$

Let $J_0$ denote the Jacobian of the system (2.3) evaluated at the DFE $P_0$ with $\mathit{\beta }={\mathit{\beta }}^{\ast }$. By directly computing, we have

$$\begin{array}{c}\hfill J_0(P_0,{\mathit{\beta }}^{\ast })=\left[\begin{array}{cccc}-\mathit{\mu }-\mathit{\psi }& 0& -{\mathit{\beta }}^{\ast }{S}_0& {\mathit{\gamma }}_3\\ 0& -(\mathit{\mu }+{\mathit{\gamma }}_1)& {\mathit{\beta }}^{\ast }{S}_0+\mathit{\sigma }{\mathit{\beta }}^{\ast }(1-S_0)& 0\\ 0& {\mathit{\gamma }}_1& -\mathit{\mu }-{\mathit{\gamma }}_2& 0\\ 0& 0& {\mathit{\gamma }}_2& -\mathit{\mu }-{\mathit{\gamma }}_3\end{array}\right].\end{array}$$

Let

$$\begin{array}{c}\hfill |\mathit{\lambda }-J_0(P_0,{\mathit{\beta }}^{\ast })|=0.\end{array}$$

It is easy to obtain that $J_0(P_0,{\mathit{\beta }}^{\ast })$ has eigenvalues given by

$$\begin{array}{c}\hfill {\mathit{\lambda }}_1=-(\mathit{\mu }+\mathit{\psi });{\mathit{\lambda }}_2=-(\mathit{\mu }+{\mathit{\gamma }}_3);{\mathit{\lambda }}_3=0;{\mathit{\lambda }}_4=-(2\mathit{\mu }+{\mathit{\gamma }}_1+{\mathit{\gamma }}_2).\end{array}$$

Thus, ${\mathit{\lambda }}_3=0$ is a simple zero eigenvalue of the matrix $J(P_0,{\mathit{\beta }}^{\ast })$ and the other eigenvalues are real and negative. Hence, when $\mathit{\beta }={\mathit{\beta }}^{\ast }$, the disease free equilibrium $P_0$ is a non-hyperbolic equilibrium. Thus, assumptions (A1) of Theorem 3.4 is verified. Now, we denote with $\mathit{\omega }=({\mathit{\omega }}_1,{\mathit{\omega }}_2,{\mathit{\omega }}_3,{\mathit{\omega }}_4)$, a right eigenvector associated with the zero eigenvalue ${\mathit{\lambda }}_3=0$.

Thus,

$$\begin{array}{c}\hfill \begin{array}{cc}& -(\mathit{\mu }+\mathit{\psi }){\mathit{\omega }}_1-{\mathit{\beta }}^{\ast }{S}_0{\mathit{\omega }}_3+{\mathit{\gamma }}_3{\mathit{\omega }}_4=0,\hfill \\ \hfill & -(\mathit{\mu }+{\mathit{\gamma }}_1){\mathit{\omega }}_2+[{\mathit{\beta }}^{\ast }{S}_0+\mathit{\sigma }{\mathit{\beta }}^{\ast }(1-S_0)]{\mathit{\omega }}_3=0,\hfill \\ \hfill & {\mathit{\gamma }}_1{\mathit{\omega }}_2-(\mathit{\mu }+{\mathit{\gamma }}_2){\mathit{\omega }}_3=0,\hfill \\ \hfill & {\mathit{\gamma }}_2{\mathit{\omega }}_3-(\mathit{\mu }+{\mathit{\gamma }}_3){\mathit{\omega }}_4=0.\hfill \end{array}\end{array}$$

Thus, we have

$$\begin{array}{cc}\hfill \mathit{\omega }=& (\frac{{\mathit{\gamma }}_2{\mathit{\gamma }}_3}{(\mathit{\mu }+{\mathit{\gamma }}_3)(\mathit{\mu }+\mathit{\psi })}-\frac{\mathit{\mu }(1-\mathit{\alpha })(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}{{\mathit{\gamma }}_1(\mathit{\mu }+\mathit{\psi })[\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi })]},\frac{\mathit{\mu }+{\mathit{\gamma }}_2}{{\mathit{\gamma }}_1},1,\hfill \\ \hfill & \frac{{\mathit{\gamma }}_2}{\mathit{\mu }+{\mathit{\gamma }}_3}).\hfill \end{array}$$

The left eigenvector $v=(v_1,v_2,v_3,v_4)$ satisfying $v\mathit{\omega }=1$ is given by

$$\begin{array}{c}\hfill \begin{array}{cc}& -(\mathit{\mu }+\mathit{\psi })v_1=0,\hfill \\ \hfill & -(\mathit{\mu }+{\mathit{\gamma }}_1)v_2+{\mathit{\gamma }}_1{v}_3=0,\hfill \\ \hfill & -{\mathit{\beta }}^{\ast }{S}_0{v}_1+{\mathit{\beta }}^{\ast }(S_0+\mathit{\sigma }(1-S_0))v_2-(\mathit{\mu }+{\mathit{\gamma }}_2)v_3+{\mathit{\gamma }}_2{v}_4=0,\hfill \\ \hfill & {\mathit{\gamma }}_3{v}_1-(\mathit{\mu }+{\mathit{\gamma }}_3)v_4=0.\hfill \end{array}\end{array}$$

From the above, we obtain that

$$\begin{array}{c}\hfill v=(0,\frac{{\mathit{\gamma }}_1}{\mathit{\mu }+{\mathit{\gamma }}_1},1,0).\end{array}$$

Let a and b be the coefficients defined as in Theorem 3.4.

Computation of $a,b$. For system (2.3), the associated non-zero partial derivatives of f (evaluated at the DFE $(P_0)$, $x_1=S,x_2=I,x_3=E,x_4=R.$) are given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill a& {\displaystyle =2v_2{\mathit{\omega }}_1{\mathit{\omega }}_3\frac{{\mathit{\partial }}^2{f}_2}{\mathit{\partial }S\mathit{\partial }I}(P_0,{\mathit{\beta }}^{\ast })+2v_2{\mathit{\omega }}_2{\mathit{\omega }}_3\frac{{\mathit{\partial }}^2{f}_2}{\mathit{\partial }E\mathit{\partial }I}(P_0,{\mathit{\beta }}^{\ast })+v_2{\mathit{\omega }}_3{\mathit{\omega }}_3\frac{{\mathit{\partial }}^2{f}_2}{\mathit{\partial }{I}^2}(P_0,{\mathit{\beta }}^{\ast })}\hfill \\ \hfill & {\displaystyle +2v_2{\mathit{\omega }}_3{\mathit{\omega }}_4\frac{{\mathit{\partial }}^2{f}_2}{\mathit{\partial }I\mathit{\partial }R}(P_0,{\mathit{\beta }}^{\ast })}\hfill \\ \hfill & {\displaystyle =\frac{2{\mathit{\beta }}^{\ast }{\mathit{\gamma }}_1}{\mathit{\mu }+{\mathit{\gamma }}_1}[\frac{{\mathit{\gamma }}_2{\mathit{\gamma }}_3(1-\mathit{\sigma })}{(\mathit{\mu }+{\mathit{\gamma }}_3)(\mathit{\mu }+\mathit{\psi })}-\frac{\mathit{\mu }(1-\mathit{\sigma })(1-\mathit{\alpha })(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}{{\mathit{\gamma }}_1(\mathit{\mu }+\mathit{\psi })[\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi })]}}\hfill \\ \hfill & {\displaystyle -\mathit{\sigma }\frac{(\mathit{\mu }+{\mathit{\gamma }}_3)(\mathit{\mu }+{\mathit{\gamma }}_2)+{\mathit{\gamma }}_1{\mathit{\gamma }}_2+{\mathit{\gamma }}_1(\mathit{\mu }+{\mathit{\gamma }}_3)}{{\mathit{\gamma }}_1(\mathit{\mu }+{\mathit{\gamma }}_3)}].}\hfill \\ \hfill b& {\displaystyle =v_2\sum _{j=1}^4{w}_i\frac{{\mathit{\partial }}^2{f}_2}{\mathit{\partial }{x}_j\mathit{\partial }{\mathit{\beta }}^{\ast }}(P_0,{\mathit{\beta }}^{\ast })}\hfill \\ \hfill & {\displaystyle =\frac{2{\mathit{\gamma }}_1}{\mathit{\mu }+{\mathit{\gamma }}_1}(S_0(1-\mathit{\sigma })+\mathit{\sigma })>0.}\hfill \end{array}\end{array}$$ 3.5

Since the coefficient b is always positive, according to Theorem 3.4, it is the sign of the coefficient a, which decides the local dynamics around the disease-free equilibrium $P_0$ for $\mathit{\beta }={\mathit{\beta }}^{\ast }$. If the coefficient a is positive, the direction of the bifurcation of system (2.3) at $\mathit{\beta }={\mathit{\beta }}^{\ast }$ is backward; otherwise, it is forward.

Thus, we formulate a condition, which is denoted by $(H_3):$

$$\begin{array}{cc}\hfill {\displaystyle \frac{{\mathit{\gamma }}_2{\mathit{\gamma }}_3}{(\mathit{\mu }+{\mathit{\gamma }}_3)(\mathit{\mu }+\mathit{\psi })}>}& {\displaystyle \frac{\mathit{\mu }(1-\mathit{\alpha })(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}{{\mathit{\gamma }}_1(\mathit{\mu }+\mathit{\psi })[\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi })]}}\hfill \\ \hfill & {\displaystyle +\frac{\mathit{\sigma }((\mathit{\mu }+{\mathit{\gamma }}_2)(\mathit{\mu }+{\mathit{\gamma }}_3)+{\mathit{\gamma }}_1{\mathit{\gamma }}_2+{\mathit{\gamma }}_1(\mathit{\mu }+{\mathit{\gamma }}_3))}{{\mathit{\gamma }}_1(1-\mathit{\sigma })(\mathit{\mu }+{\mathit{\gamma }}_3)}.}\hfill \end{array}$$

Thus, if $(H_3)$ holds, we have $a>0$, otherwise, $a<0$.

Summarizing the above results, we have the following theorem.

Theorem 3.5

If $(H_3)$ holds, system (2.3) exhibits a backward bifurcation at $R_{vac}=1$ (or equivalently $\mathit{\beta }={\mathit{\beta }}^{\ast }$). Otherwise, system (2.3) exhibits a forward bifurcation at $R_{vac}=1$ (or equivalently when $\mathit{\beta }={\mathit{\beta }}^{\ast }$).

Remark 1

From Theorem 3.5, it can follows that the occurrence of either a backward or forward bifurcation may be expected. In fact, in system (2.3), let $\mathit{\alpha }=0.3,\mathit{\mu }=0.00004566,\mathit{\beta }=0.4,\mathit{\psi }=0.01,{\mathit{\gamma }}_1=0.1,{\mathit{\gamma }}_2=0.05,{\mathit{\gamma }}_3=0.033,\mathit{\sigma }=0.15.$ It is easy to verify that the condition $(H_3)$ is satisfied. By applying Xpp plot software and choosing the above parameters, we can describe the backward bifurcation diagram of system (2.3) (see, Fig. 2). Let all parameter values be same as in Fig. 2, except $\mathit{\psi }$ is changed as 0.2. The condition $(H_3)$ is not satisfied and we have forward bifurcation diagram Fig. 3 at $R_{vac}=1$. So it is clear that there is one threshold value of $\mathit{\psi }$ say ${\mathit{\psi }}^{\ast }$ such that backward bifurcation occurs of $\mathit{\psi }<{\mathit{\psi }}^{\ast }$ and forward bifurcation occurs if $\mathit{\psi }>{\mathit{\psi }}^{\ast }$. Both of these bifurcation diagrams are obtained by considering $\mathit{\beta }$ as bifurcation parameter and later it is plotted with respect to $R_{vac}$.

Fig. 2.

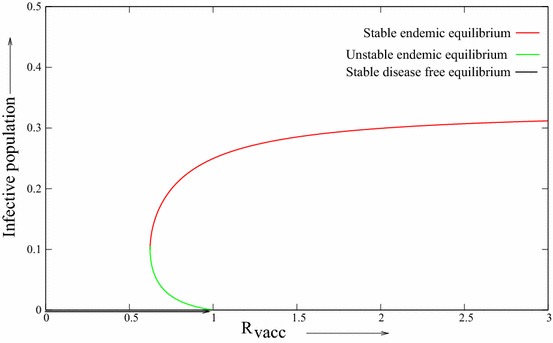
The backward bifurcation diagram for model (2.3)

Fig. 3.

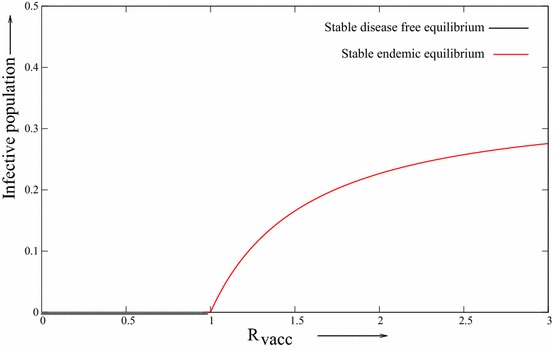
The forward bifurcation diagram for model (2.3)

Global stability of the endemic equilibrium

In this section, we shall investigate the global stability of the unique endemic equilibrium for $R_{vac}>1.$ Here we shall apply the geometric approach [25, 27, 38] to establish the global stability of the unique endemic equilibrium. In recent years, many authors [3, 16, 26, 28, 29] have applied this method to show global stability of the positive equilibria in system. Here, we follow the techniques and approaches in paper [3, 16] to investigate global stability of the endemic equilibrium in system (2.3). Here, we omit the introduction of the general mathematical framework of these theorems and only focus on their applications.

In the previous section, we have showed that if $R_{vac}>1$, system (2.3) has a unique endemic equilibrium in $\mathcal{D}$. Furthermore, $R_{vac}>1$ implies that the disease-free equilibrium $P_0$ is unstable (Theorem 3.2). The instability of $P_0$, together with $P_0\in \mathit{\partial }\mathcal{D}$, implies the uniform persistence of the state variables. This result can be also showed by using the same arguments from Proposition 4.2 in [27] and Proposition 2.2 in [29]. Hence, there exists a constant $0<\mathit{\delta }<1$ such that any solution of $\tilde{x}=(S,V,E,I,R)$ of system (2.3) with the initial conditions ${\tilde{x}}_0=(S(0),V(0),E(0),I(0),R(0))\in \mathrm{\Omega }$ satisfies

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}inf\tilde{x}>\mathit{\delta },\tilde{x}=(S,V,E,I,R).\end{array}$$

Thus, we first give the following result:

Proposition 4.1

System (2.3) is uniformly persist in $\mathcal{D}$ for $R_{vac}>1$ .

To prove our conclusion, we set the following differential equation

$$\begin{array}{c}\hfill \dot{x}=f(x),\end{array}$$ 4.1

where $f:\mathcal{D}(\subset R^n)\to R^n$, $\mathcal{D}$ is open set and simply connected and $f\in C^{\prime }(R^n)$.

Let

$$\begin{array}{c}\hfill {\displaystyle \overline{\mathit{\mu }}(Q)=P_f{P}^{-1}+P\frac{\mathit{\partial }{f}^{[2]}(x)}{\mathit{\partial }x}{P}^{-1},}\end{array}$$ 4.2

where, P(x) be a nonsingular $(\begin{array}{c}n\hfill \\ 2\hfill \end{array})\times (\begin{array}{c}n\hfill \\ 2\hfill \end{array})$ matrix-valued function, which is $C^1$ on $\mathcal{D}$ and $P_f(x)$ is the derivative of P(x) in the direction of the vector field f(x). ${\displaystyle \frac{\mathit{\partial }{f}^{[2]}(x)}{\mathit{\partial }x}}$ is also $(\begin{array}{c}n\\ 2\end{array})\times (\begin{array}{c}n\\ 2\end{array})$ matrix, the second additive compound of the Jacobian matrix $\mathit{\partial }f/\mathit{\partial }x.$ $\overline{\mathit{\mu }}$ is the $Lozinski\breve{i}$ measure with respect to a vector norm $|·|$. The following result comes from Corollary 2.6 in paper [25].

Theorem 4.1

Suppose that $(\mathrm{i})$ $\mathcal{D}$ is simply connected and ${\mathcal{D}}_0$ is a compact set which is absorbing with respect to system (4.1); $(\mathrm{ii})$ For some matrix P, there exists a positive constant $\mathit{\nu }$ such that $\overline{\mathit{\mu }}(Q)\le -\mathit{\nu }<0$ for all $x\in {\mathcal{D}}_0$. Then the unique equilibrium $x_0$ in system (4.1) is global asymptotically stable.

From Proposition 4.1, it is easy to verify that the condition $(\mathrm{i})$ in Theorem 4.1 holds. Therefore, to prove our conclusion, we only verify that $(\mathrm{ii})$ in Theorem 4.1 holds. According to paper [35], the Lozinski$\breve{i}$ measure in Theorem 4.1 can be evaluated as follow:

$$\begin{array}{c}\hfill \overline{\mathit{\mu }}(Q)=inf\{\mathit{\kappa }:D_{+}||z||\le \mathit{\kappa }||z||,\text{for}\text{all}\text{solutions}\text{of}\dot{z}=Pz\},\end{array}$$

where $D_{+}$ is the right-hand derivative.

Now we state our main result in this section.

Theorem 4.2

Suppose that the parameters in system (2.3) satisfy the following inequalities

$$\begin{array}{c}\hfill {\mathit{\gamma }}_3<{\mathit{\gamma }}_1,\mathit{\mu }+\mathit{\psi }>2{\mathit{\gamma }}_1,\mathit{\mu }>{\mathit{\gamma }}_1.\end{array}$$ 4.3

Then the unique equilibrium $P^{\ast }$ in system (2.3) is globally asymptotically stable for $R_{vac}>1$.

Proof

Let $f(x)={(f_1(x),f_2(x),f_3(x),f_4(x))}^T$, where $f_1(x)=(1-\mathit{\alpha })\mathit{\mu }-\mathit{\mu }S-\mathit{\beta }SI-\mathit{\psi }S+{\mathit{\gamma }}_{3}R,f_2(x)=\mathit{\mu }+\mathit{\psi }S-\mathit{\sigma }\mathit{\beta }VI-\mathit{\mu }V,f_3(x)=\mathit{\beta }SI+\mathit{\sigma }\mathit{\beta }IV-(\mathit{\mu }+{\mathit{\gamma }}_1)E,f_4(x)={\mathit{\gamma }}_{1}E-(\mathit{\mu }+{\mathit{\gamma }}_2)I,$ and $x={(S,V,E,I)}^T$. Then, the Jacobian matrix of system (2.3) can be written as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\displaystyle \frac{\mathit{\partial }f}{\mathit{\partial }x}=\left[\begin{array}{cccc}-\mathit{\psi }-\mathit{\beta }I-\mathit{\mu }-{\mathit{\gamma }}_3& -{\mathit{\gamma }}_3& -{\mathit{\gamma }}_3& -\mathit{\beta }S-{\mathit{\gamma }}_3\\ \mathit{\psi }& -\mathit{\sigma }\mathit{\beta }I-\mathit{\mu }& 0& -\mathit{\sigma }\mathit{\beta }V\\ \mathit{\beta }I& \mathit{\sigma }\mathit{\beta }I& -{\mathit{\gamma }}_1-\mathit{\mu }& \mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V\\ 0& 0& {\mathit{\gamma }}_1& -{\mathit{\gamma }}_2-\mathit{\mu }\end{array}\right].}\end{array}\end{array}$$

The second additive compound [25](see, “Appendix”) of Jacobian matrix is the $6\times 6$ matrix given by

$$\begin{array}{c}\hfill \begin{array}{cc}{\displaystyle \frac{\mathit{\partial }{f}^{[2]}}{\mathit{\partial }x}}\hfill & =-diag\left(\begin{array}{c}\mathit{\psi }+\mathit{\beta }I(1+\mathit{\sigma })+2\mathit{\mu }+{\mathit{\gamma }}_3\hfill \\ \mathit{\psi }+\mathit{\beta }I+2\mathit{\mu }+{\mathit{\gamma }}_1+{\mathit{\gamma }}_3\hfill \\ \mathit{\psi }+\mathit{\beta }I+2\mathit{\mu }+{\mathit{\gamma }}_2+{\mathit{\gamma }}_3\hfill \\ {\mathit{\gamma }}_1+\mathit{\sigma }\mathit{\beta }I+2\mathit{\mu }\hfill \\ {\mathit{\gamma }}_2+\mathit{\sigma }\mathit{\beta }I+2\mathit{\mu }\hfill \\ {\mathit{\gamma }}_1+{\mathit{\gamma }}_2+2\mathit{\mu }\hfill \end{array}\right)\hfill \\ \hfill & +\left[\begin{array}{cccccc}0& 0& -\mathit{\sigma }\mathit{\beta }V& {\mathit{\gamma }}_3& \mathit{\beta }S+{\mathit{\gamma }}_3& 0\\ \mathit{\sigma }\mathit{\beta }I& 0& \mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V& -{\mathit{\gamma }}_3& 0& \mathit{\beta }S+{\mathit{\gamma }}_3\\ 0& {\mathit{\gamma }}_1& 0& 0& -{\mathit{\gamma }}_3& -{\mathit{\gamma }}_3\\ -\mathit{\beta }I& \mathit{\psi }& 0& 0& \mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V& \mathit{\sigma }\mathit{\beta }V\\ 0& 0& \mathit{\psi }& {\mathit{\gamma }}_1& 0& 0\\ 0& 0& \mathit{\beta }I& 0& \mathit{\sigma }\mathit{\beta }I& 0\end{array}\right].\hfill \end{array}\end{array}$$

Let

$$\begin{array}{c}\hfill P=\left[\begin{array}{cccccc}{\displaystyle \frac{1}{E}}& 0& 0& 0& 0& 0\\ 0& {\displaystyle \frac{1}{E}}& 0& 0& 0& 0\\ 0& 0& 0& {\displaystyle \frac{1}{E}}& 0& 0\\ 0& 0& {\displaystyle \frac{1}{I}}& 0& 0& 0\\ 0& 0& 0& 0& {\displaystyle \frac{1}{I}}& 0\\ {\displaystyle \frac{1}{E}}& 0& 0& 0& 0& {\displaystyle \frac{1}{I}}\end{array}\right].\end{array}$$

Set ${\displaystyle Q=P_f{P}^{-1}+P\frac{\mathit{\partial }{f}^{[2]}}{\mathit{\partial }x}{P}^{-1}}$, where $P_f$ is the derivative of P in the direction of the vector field f. Thus, we have

$$\begin{array}{c}\hfill P_f{P}^{-1}=-diag(\dot{E}/E,\dot{E}/E,\dot{E}/E,\dot{I}/I,\dot{I}/I,\dot{I}/I).\end{array}$$

From (2.3), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{\dot{E}}{E}}& =(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}-\mathit{\mu }-{\mathit{\gamma }}_1\hfill \\ \hfill {\displaystyle \frac{\dot{I}}{I}}& ={\mathit{\gamma }}_1\frac{E}{I}-\mathit{\mu }-{\mathit{\gamma }}_2\hfill \end{array}$$

Thus, we obtain that

$$\begin{array}{cc}\hfill Q& {\displaystyle =P_f{P}^{-1}+P\frac{\mathit{\partial }{f}^{[2]}}{\mathit{\partial }x}{P}^{-1}}\hfill \\ \hfill & =\left[\begin{array}{cccccc}{Q}_{11}& 0& {\mathit{\gamma }}_3& {\displaystyle -\mathit{\sigma }\mathit{\beta }V\frac{I}{E}}& {\displaystyle (\mathit{\beta }S+{\mathit{\gamma }}_3)\frac{I}{E}}& 0\\ \mathit{\sigma }\mathit{\beta }I& Q_{22}& -{\mathit{\gamma }}_3& {\displaystyle (\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}}& 0& {\displaystyle (\mathit{\beta }S+{\mathit{\gamma }}_3)\frac{I}{E}}\\ -\mathit{\beta }I& \mathit{\psi }& Q_{33}& 0& {\displaystyle (\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}}& {\displaystyle \mathit{\sigma }\mathit{\beta }V\frac{I}{E}}\\ 0& {\displaystyle {\mathit{\gamma }}_1\frac{E}{I}}& 0& Q_{44}& -{\mathit{\gamma }}_3& -{\mathit{\gamma }}_3\\ 0& 0& {\displaystyle {\mathit{\gamma }}_1\frac{E}{I}}& \mathit{\psi }& Q_{55}& 0\\ 0& 0& 0& \mathit{\beta }I& \mathit{\sigma }\mathit{\beta }I& Q_{66}\end{array}\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill Q_{11}& {\displaystyle =-(\mathit{\psi }+\mathit{\beta }I+\mathit{\mu }+\mathit{\sigma }\mathit{\beta }I+{\mathit{\gamma }}_3)+{\mathit{\gamma }}_1-(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E},}\hfill \\ \hfill Q_{22}& {\displaystyle =-(\mathit{\psi }+\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3)-(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E},}\hfill \\ \hfill Q_{33}& {\displaystyle =-(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu })-(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E},Q_{44}=-(\mathit{\psi }+\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3)-{\mathit{\gamma }}_1\frac{E}{I}}\hfill \\ \hfill Q_{55}& {\displaystyle =-(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu })-{\mathit{\gamma }}_1\frac{E}{I},Q_{66}=-({\mathit{\gamma }}_1+\mathit{\mu })-{\mathit{\gamma }}_1\frac{E}{I}.}\hfill \end{array}$$

As in [3, 16], we define the following norm on ${\mathbb{R}}^6$:

$$\begin{array}{c}\hfill ||z||=max\{U_1,U_2\},\end{array}$$ 4.4

where $z\in {\mathbb{R}}^6$, with components $z_i,i=1,\dots ,6$ and

$$\begin{array}{cc}& U_1(z_1,z_2,z_3)\hfill \\ \hfill & =\left\{\begin{array}{c}max\{|z_1|,|z_2|+|z_3|\},\text{if}sgn(z_1)=sgn(z_2)=sgn(z_3)\hfill \\ max\{|z_2|,|z_1|+|z_3|\},\text{if}sgn(z_1)=sgn(z_2)=-sgn(z_3)\hfill \\ max\{|z_1|,|z_2|,|z_3|\},\text{if}sgn(z_1)=-sgn(z_2)=sgn(z_3)\hfill \\ max\{|z_1|+|z_3|,|z_2|+|z_3|\},\text{if}-sgn(z_1)=sgn(z_2)=sgn(z_3)\hfill \end{array}\right.\hfill \end{array}$$

and let

$$\begin{array}{cc}& U_2(z_4,z_5,z_6)\hfill \\ \hfill & =\left\{\begin{array}{c}|z_4|+|z_5|+|z_6|,\text{if}sgn(z_1)=sgn(z_2)=sgn(z_3)\hfill \\ max\{|z_4|+|z_5|,|z_4|+|z_6|\},\text{if}sgn(z_1)=sgn(z_2)=-sgn(z_3)\hfill \\ max\{|z_5|,|z_4|+|z_6|\},\text{if}sgn(z_1)=-sgn(z_2)=sgn(z_3)\hfill \\ max\{|z_4|+|z_6|,|z_5|+|z_6|\},\text{if}-sgn(z_1)=sgn(z_2)=sgn(z_3)\hfill \end{array}\right.\hfill \end{array}$$

Now we demonstrate the existence of some $\mathit{\kappa }>0$ such that

$$\begin{array}{c}\hfill D_{+}||z||\le -\mathit{\kappa }||z||.\end{array}$$ 4.5

By linearity, if this inequality is true for some z, then it is also true for $-z$. Similar to analyzing methods in paper [3, 16], our proof is subdivided into eight separate cases, based on the different octants and the definition of the norm (4.4). To facilitate our analysis, we use the following inequalities:

$$\begin{array}{cc}\hfill U_1(t)& \ge |z_2|,|z_3|,|z_2+z_3|,\hfill \\ \hfill U_2(t)& \ge |z_4|,|z_5|,|z_6|,|z_5+z_6|,|z_4+z_5+z_6|,\hfill \end{array}$$

for all $z={(z_1,z_2,z_3,z_4,z_5,z_2,z_6)}^T\in {\mathbb{R}}^6.$

Case 1. Let $U_1(z)>U_2(z)$,$z_1,z_2,z_3>0$ and $|z_1|>|z_2|+|z_3|.$

Then we have $||z||=z_1$ and $U_2(z)<z_1$. Taking the right derivative of $||z||$, we have

$$\begin{array}{cc}\hfill D_{+}||z||& ={\dot{z}}_1\hfill \\ \hfill & {\displaystyle =-(\mathit{\psi }+\mathit{\beta }I(1+\mathit{\sigma })+\mathit{\mu }+{\mathit{\gamma }}_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}-{\mathit{\gamma }}_1)z_1}\hfill \\ \hfill & {\displaystyle +{\mathit{\gamma }}_3{z}_3-\mathit{\sigma }\mathit{\beta }V\frac{I}{E}{z}_4+(\mathit{\beta }S+{\mathit{\gamma }}_3)\frac{I}{E}{z}_5}\hfill \\ \hfill & {\displaystyle \le -(\mathit{\psi }+\mathit{\beta }I(1+\mathit{\sigma })+\mathit{\mu }+{\mathit{\gamma }}_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}-{\mathit{\gamma }}_1)|z_1|}\hfill \\ \hfill & {\displaystyle +{\mathit{\gamma }}_3|z_3|+\mathit{\sigma }\mathit{\beta }V\frac{I}{E}|z_4|}\hfill \\ \hfill & {\displaystyle +(\mathit{\beta }S+{\mathit{\gamma }}_3)\frac{I}{E}|z_5|.}\hfill \end{array}$$

Since $|z_1|>|z_3|,|z_4|,|z_5|\le U_2(z)<|z_1|$, and $|z_1|=||z||$, thus, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill D_{+}||z||& {\displaystyle \le {\mathit{\gamma }}_1|z_1|-(\mathit{\psi }+\mathit{\beta }I(1+\mathit{\sigma })+\mathit{\mu })|z_1|+{\mathit{\gamma }}_3\frac{I}{E}|z_5|}\hfill \\ \hfill & {\displaystyle \le ({\mathit{\gamma }}_1-(\mathit{\psi }+\mathit{\beta }I(1+\mathit{\sigma })+\mathit{\mu })+max\{{\mathit{\gamma }}_1,{\mathit{\gamma }}_3\frac{I}{E}\})||z||.}\hfill \end{array}\end{array}$$ 4.6

Case 2. Similarly, it is easy to verify that Eq. (4.6) also holds for $U_1>U_2$ and $z_1,z_2,z_3<0$ when $|z_1|>|z_2|+|z_3|.$

Thus, if we require that $2{\mathit{\gamma }}_1<\mathit{\psi }+\mathit{\mu }$ holds, then the inequality (4.5) holds for case 1 and case 2.

Case 3. Let $U_1(z)>U_2(z)$, $z_1,z_2,z_3>0$ and $|z_1|<|z_2|+|z_3|.$ Thus, we have $||z||=|z_2|+|z_3|=z_2+z_3$ and $U_2(z)<|z_2|+|z_3|.$ So,we have

$$\begin{array}{cc}\hfill D_{+}||z||& ={\dot{z}}_2+{\dot{z}}_3\hfill \\ \hfill & {\displaystyle =-(1-\mathit{\sigma })\mathit{\beta }I{z}_1-(\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E})z_2}\hfill \\ \hfill & {\displaystyle -(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}}\hfill \\ \hfill & {\displaystyle +{\mathit{\gamma }}_3)z_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}(z_4+z_5+z_6)+{\mathit{\gamma }}_3\frac{I}{E}{z}_6}\hfill \\ \hfill & {\displaystyle \le -(1-\mathit{\sigma })\mathit{\beta }I|z_1|-(\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E})|z_2|}\hfill \\ \hfill & {\displaystyle -(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}+{\mathit{\gamma }}_3)|z_3|}\hfill \\ \hfill & {\displaystyle +(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}|(z_4+z_5+z_6)|+{\mathit{\gamma }}_3\frac{I}{E}|z_6|.}\hfill \end{array}$$

Using the inequalities $|z_6|,|z_4+z_5+z_6|\le U_2(z)<|z_2|+|z_3|$, from the above, we obtain that

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill D_{+}||z||& {\displaystyle \le -(\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3)|z_2|-(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3)|z_3|+{\mathit{\gamma }}_3\frac{I}{E}|z_6|}\hfill \\ \hfill & {\displaystyle \le (max\{{\mathit{\gamma }}_1,{\mathit{\gamma }}_3\frac{I}{E}\}-(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3))||z||.}\hfill \end{array}\end{array}$$ 4.7

Case 4. By linearity, Eq. (4.7) also holds for $U_1>U_2$ and $z_1,z_2,z_3<0$ when $|z_1|<|z_2|+|z_3|.$

Thus, if we require that ${\mathit{\gamma }}_1<{\mathit{\gamma }}_3+\mathit{\mu }$ holds, then the inequality (4.5) holds for case 3 and case 4.

Case 5. Let $U_1(z)>U_2(z)$, $z_1<0<z_2,z_3$ and $|z_1|>|z_2|.$ Thus, we have $||z||=|z_1|+|z_3|,$ and $U_2(z)<|z_1|+|z_3|$. By directly calculating, we obtain that

$$\begin{array}{cc}\hfill D_{+}||z||& =-{\dot{z}}_1+{\dot{z}}_3\hfill \\ \hfill & {\displaystyle =(\mathit{\psi }+\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3-{\mathit{\gamma }}_1+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E})z_1-{\mathit{\gamma }}_3{z}_3-{\mathit{\gamma }}_3\frac{I}{E}{z}_5}\hfill \\ \hfill & {\displaystyle +\mathit{\psi }{z}_2-(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}{z}_3+\mathit{\sigma }\mathit{\beta }V\frac{I}{E}(z_4+z_5+z_6)}\hfill \\ \hfill & {\displaystyle \le -(\mathit{\psi }+\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3-{\mathit{\gamma }}_1+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E})|z_1|-{\mathit{\gamma }}_3|z_3|+{\mathit{\gamma }}_3\frac{I}{E}|z_5|}\hfill \\ \hfill & {\displaystyle +\mathit{\psi }|z_2|-(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}|z_3|+\mathit{\sigma }\mathit{\beta }V\frac{I}{E}|z_4+z_5+z_6|}\hfill \end{array}$$

Using the inequalities $|z_5|,|z_4+z_5+z_6|\le U_2(z)<|z_1|+|z_3|$ , we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill D_{+}||z||& {\displaystyle \le -(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3+\mathit{\beta }S\frac{I}{E})|z_1|+{\mathit{\gamma }}_1|z_1|+{\mathit{\gamma }}_3\frac{I}{E}|z_5|}\hfill \\ \hfill & {\displaystyle -(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+\mathit{\beta }S\frac{I}{E})|z_3|}\hfill \\ \hfill & {\displaystyle \le (max\{{\mathit{\gamma }}_1,{\mathit{\gamma }}_3\frac{I}{E}\}-(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+\mathit{\beta }S\frac{I}{E}))||z||.}\hfill \end{array}\end{array}$$ 4.8

Case 6. By linearity, Eq. (4.8) also holds for $U_1>U_2$ and $z_2,z_3<0<z_1,$ when $|z_1|<|z_2|.$

Thus, if we require that ${\mathit{\gamma }}_1<\mathit{\mu }$ holds, then the inequality (4.5) holds for case 5 and case 6.

Case 7. Let $U_1(z)>U_2(z)$, $z_1<0<z_2,z_3$ and $|z_1|<|z_2|.$ Thus, we have $||z||=|z_2|+|z_3|=z_2+z_3$ and $U_2(z)<|z_2|+|z_3|$. Thus, we have

$$\begin{array}{cc}\hfill D_{+}||z||& ={\dot{z}}_2+{\dot{z}}_3\hfill \\ \hfill & {\displaystyle =(\mathit{\sigma }-1)\mathit{\beta }I{z}_1-(\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E})z_2+{\mathit{\gamma }}_3\frac{I}{E}{z}_5}\hfill \\ \hfill & {\displaystyle -(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}{z}_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}(z_4+z_5+z_6)}\hfill \\ \hfill & {\displaystyle \le (1-\mathit{\sigma })\mathit{\beta }I|z_1|-(\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E})|z_2|+{\mathit{\gamma }}_3\frac{I}{E}|z_5|}\hfill \\ \hfill & {\displaystyle -(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E})|z_3|+(\mathit{\beta }S+\mathit{\sigma }\mathit{\beta }V)\frac{I}{E}|z_4+z_5+z_6|}\hfill \end{array}$$

Using the inequalities $,|z_5|,|z_4+z_5+z_6|\le U_2(z)<|z_2|+|z_3|,$ and $|z_1|\le |z_2|$, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill D_{+}||z||& {\displaystyle \le -(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3)|z_2|+{\mathit{\gamma }}_3\frac{I}{E}|z_5|-(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3)|z_3|}\hfill \\ \hfill & {\displaystyle \le (max\{{\mathit{\gamma }}_1,{\mathit{\gamma }}_3\frac{I}{E}\}-(\mathit{\sigma }\mathit{\beta }I+\mathit{\mu }+{\mathit{\gamma }}_3))||z||.}\hfill \end{array}\end{array}$$ 4.9

Case 8. By linearity, Eq. (4.9) also holds for $U_1>U_2$ and $z_2,z_3<0<z_1,$ when $|z_1|<|z_2|.$

Thus, if we require that ${\mathit{\gamma }}_1<{\mathit{\gamma }}_3+\mathit{\mu }$ holds, then the inequality (4.5) holds for case 7 and case 8.

Therefore, from the discussion above, we know that if inequalities (4.3)hold, then there exists $\mathit{\kappa }>0$ such that $D_{+}||z||\le -\mathit{\kappa }||z||$ for all $z\in {\mathbb{R}}^4$ and all nonnegative S, V, E and I. All conditions in Theorem 4.1 can be satisfied when inequalities (4.3) hold. Therefore, by Theorem 4.1, we can determine that if inequalities (4.3) hold, then the unique endemic equilibrium of system (2.3) is globally stable in $\mathcal{D}$ for $R_{vac}>1$.

$\square$

Remark 2

In Sect. 3, we have shown that system (2.3) exhibit a backward bifurcation for $R_{vac}\le 1$. As stressed in [3], for cases in which the model exhibits bistability, the compact absorbing set required in Theorem 4.1 does not exist. By applying similar methods in [3], a sequence of surfaces that exists for time $\mathit{ϵ}>0$ and minimizes the functional measuring surface area may be obtained. Therefore, the global dynamics of system (2.3) in the bistability region can be further investigated as it has been done in paper [3].

Discussion

In this paper, an epidemic model with vaccination has been investigated. By analysis, it is showed that the proposed model exhibits a more complicated dynamic behavior. Backward bifurcation under the vaccination level conditions, and bistability phenomena can be observed. The global stability of the unique endemic equilibrium in the model is demonstrated for $R_{vac}>1$. Note that the model (2.3) can be solved in an efficient way by means of the multistage Adomian decomposition method (MADM) as a relatively new method [8, 9, 12, 13]. The MADM has some superiority over the conventional solvers such as the R-K family. To illustrate the various theoretical results contained in this paper, the effect of some important parameter values on the dynamical behavior of system (2.3) is investigated in the following.

Now we consider first the role of the disease cycle on the backward bifurcation. If ${\mathit{\gamma }}_3=0$, [i.e., the disease cycle-free in model (2.3)], then the expression for the bifurcation coefficient, a, given in Eq. (3.5) reduces to

$$\begin{array}{c}\hfill {\displaystyle a=-\frac{2{\mathit{\beta }}^{\ast }{\mathit{\gamma }}_1}{\mathit{\mu }+{\mathit{\gamma }}_1}[\frac{\mathit{\mu }(1-\mathit{\alpha })(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}{{\mathit{\gamma }}_1(\mathit{\mu }+\mathit{\psi })(\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi }))}+\frac{\mathit{\mu }+{\mathit{\gamma }}_2}{{\mathit{\gamma }}_1}\mathit{\sigma }+\frac{{\mathit{\gamma }}_2}{\mathit{\mu }}\mathit{\sigma }+\mathit{\sigma }]<0.}\end{array}$$

Thus, the backward bifurcation phenomenon of system (2.3) will not occur if ${\mathit{\gamma }}_3=0.$ This is in line with results in papers [16, 31], where the disease cycle-free model (2.3) has a globally asymptotically stable disease-free equilibrium if the basic reproduction number is less than one.

Differentiating a, given in Eq. (3.5), with respect to ${\mathit{\gamma }}_3$ gives

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathit{\partial }a}{\mathit{\partial }{\mathit{\gamma }}_3}=\frac{2{\mathit{\beta }}^{\ast }{\mathit{\gamma }}_1{\mathit{\gamma }}_2}{\mathit{\mu }+{\mathit{\gamma }}_1}[\frac{\mathit{\mu }(1-\mathit{\sigma })+\mathit{\sigma }(\mathit{\mu }+\mathit{\psi })}{(\mathit{\mu }+\mathit{\psi }){(\mathit{\mu }+\mathit{\gamma })}^2}]>0.}\end{array}$$

Hence, the bifurcation coefficient, a is an increasing functions of ${\mathit{\gamma }}_3$. Thus, the feasibility of backward bifurcation occurring increases with disease cycle.

Now we consider the role of vaccination on the backward bifurcation. Let $\mathit{\alpha }=\mathit{\psi }=\mathit{\sigma }=0$, then the expression for the bifurcation coefficient, a, given in Eq. (3.5), is reduces to

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill a& {\displaystyle =\frac{2{\mathit{\beta }}^{\ast }{\mathit{\gamma }}_1}{\mathit{\mu }+{\mathit{\gamma }}_1}[\frac{{\mathit{\gamma }}_2{\mathit{\gamma }}_3}{\mathit{\mu }(\mathit{\mu }+{\mathit{\gamma }}_3)}-\frac{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}{{\mathit{\gamma }}_1\mathit{\mu }}]}\hfill \\ \hfill & {\displaystyle <\frac{2{\mathit{\beta }}^{\ast }{\mathit{\gamma }}_1}{2\mathit{\mu }+{\mathit{\gamma }}_1+{\mathit{\gamma }}_2}(\frac{{\mathit{\gamma }}_2}{\mathit{\mu }}-(1+\frac{\mathit{\mu }}{{\mathit{\gamma }}_1})(1+\frac{{\mathit{\gamma }}_2}{\mathit{\mu }}))}\hfill \\ \hfill & {\displaystyle <-\frac{2{\mathit{\beta }}^{\ast }{\mathit{\gamma }}_1}{2\mathit{\mu }+{\mathit{\gamma }}_1+{\mathit{\gamma }}_2}(1+\frac{\mathit{\mu }+{\mathit{\gamma }}_2}{{\mathit{\gamma }}_1})}\hfill \\ \hfill & <0.\hfill \end{array}\end{array}$$

Thus, the backward bifurcation phenomenon of system (2.3) will not occur if $\mathit{\alpha }=\mathit{\psi }=\mathit{\sigma }=0$ (i.e., the model (2.3) will not undergo backward bifurcation in the absence of vaccination). This is also in line with results in paper [26], where the vaccination-free model (2.3) has a globally asymptotically stable equilibrium if the basic reproduction number $R_0$ is less than one. Furthermore, the impact of the vaccine-related parameters ($\mathit{\psi },\mathit{\sigma }$) on the backward bifurcation is assessed by carrying out an analysis on the bifurcation coefficient $a$ as follows. Differentiating a, given in Eq. (3.5), partially with respect to $\mathit{\psi },$ gives

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{\mathit{\partial }a}{\mathit{\partial }\mathit{\psi }}}& {\displaystyle =-\frac{2{\mathit{\beta }}^{\ast }{\mathit{\gamma }}_1(1-\mathit{\sigma })}{\mathit{\mu }+{\mathit{\gamma }}_1}[\frac{{\mathit{\gamma }}_2{\mathit{\gamma }}_3}{(\mathit{\mu }+{\mathit{\gamma }}_3){(\mathit{\mu }+\mathit{\psi })}^2}}\hfill \\ \hfill & +\frac{\mathit{\mu }(1-\mathit{\alpha })(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)[\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\mu }+2\mathit{\psi })]}{{\mathit{\gamma }}_1{(\mathit{\mu }+\mathit{\psi })}^2{[\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi })]}^2}]\hfill \\ \hfill & <0.\hfill \end{array}\end{array}$$

Thus, the backward bifurcation coefficient, a is a decreasing function of the vaccination rate $\mathit{\psi }$. Hence, the possibility of backward occurring decreases with increasing vaccination rate ( i.e., vaccinating more susceptible individuals decrease the likelihood of the occurrence of backward bifurcation).

Differentiating the bifurcation coefficient a, given in Eq. (3.5), partially with respect to $\mathit{\sigma }$ gives

$$\begin{array}{c}\hfill {\displaystyle \frac{\mathit{\partial }a}{\mathit{\partial }\mathit{\sigma }}=\frac{2{\mathit{\beta }}^{\ast }{\mathit{\gamma }}_1}{\mathit{\mu }+{\mathit{\gamma }}_1}{M}_1,}\end{array}$$

with

$$\begin{array}{cc}\hfill M_1=& {\displaystyle -(\frac{{\mathit{\gamma }}_2{\mathit{\gamma }}_3}{(\mathit{\mu }+{\mathit{\gamma }}_3)(\mathit{\mu }+\mathit{\psi })}+\frac{\mathit{\mu }(1-\mathit{\alpha })(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)(\mathit{\mu }+\mathit{\psi }+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi }))}{{\mathit{\gamma }}_1(\mathit{\mu }+\mathit{\psi }){[\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi })]}^2}}\hfill \\ \hfill & {\displaystyle +\frac{\mathit{\mu }+{\mathit{\gamma }}_2}{{\mathit{\gamma }}_1}+\frac{{\mathit{\gamma }}_2}{\mathit{\mu }+{\mathit{\gamma }}_3}+1).}\hfill \end{array}$$

Thus, the bifurcation coefficient, a is a decreasing function with respect to $\mathit{\sigma }$. That is, the likelihood of backward bifurcation occurring decreases with increasing vaccine efficacy. Let $\mathit{\alpha }=0.3,\mathit{\mu }=0.00004566,\mathit{\beta }=0.4,\mathit{\psi }=0.005,{\mathit{\gamma }}_1=0.1,{\mathit{\gamma }}_2=0.05,{\mathit{\gamma }}_3=0.033.$ By direct calculating, it is easy to verify that $M_1$ is negative and also condition $(H_3)$ is satisfied. Figure 4 depicts the backward bifurcation occurring phenomena with lower vaccine efficacy with $\mathit{\sigma }=0.15$; Fig. 5 depicts the likelihood of backward bifurcation occurring with higher vaccine efficacy $\mathit{\sigma }=0.45$.

Fig. 4.

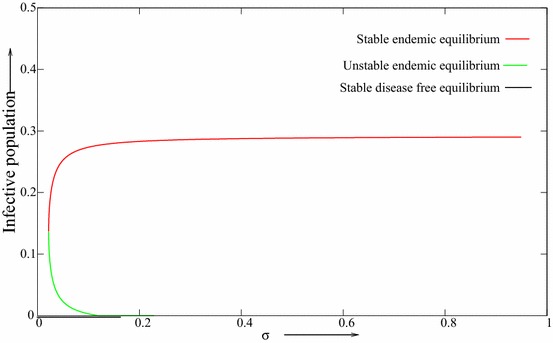
The backward bifurcation diagram with respect to vaccine efficacy $\mathit{\sigma }=0.15$

Fig. 5.

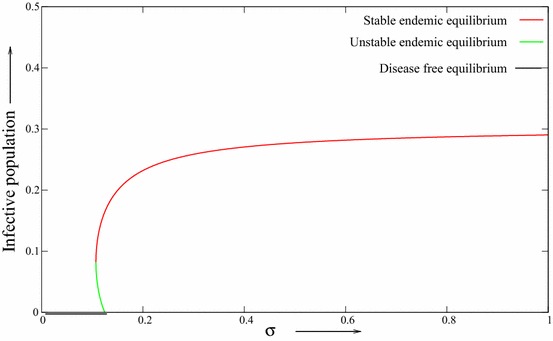
The backward bifurcation diagram with respect to vaccine efficacy $\mathit{\sigma }=0.45$

In addition, it is obvious that our expression for the basic reproduction number in system (2.3), i.e.,

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle R_{vac}=\frac{\mathit{\beta }{\mathit{\gamma }}_1}{(\mathit{\mu }+{\mathit{\gamma }}_1)(\mathit{\mu }+{\mathit{\gamma }}_2)}\frac{\mathit{\mu }(1-\mathit{\alpha })+\mathit{\sigma }(\mathit{\mu }\mathit{\alpha }+\mathit{\psi })}{\mathit{\mu }+\mathit{\psi }}}\hfill \end{array}\end{array}$$

is independent of the loss rate of immunity ${\mathit{\gamma }}_3$. From the above analysis, we have found that the dynamics of the model are not determined by the basic reproduction number, and the phenomena of the backward bifurcation in system may occur. Moreover, it is found that the occurrence feasibility is increasing with the loss rate of immunity ${\mathit{\gamma }}_3$.

From the following expression,

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{d{R}_{vac}}{d\mathit{\psi }}=-R_0\frac{\mathit{\mu }(1-\mathit{\sigma })(1-\mathit{\alpha })}{{(\mathit{\mu }+\mathit{\psi })}^2}<0,\frac{d{R}_{vac}}{d\mathit{\alpha }}=-R_0\frac{\mathit{\mu }(1-\mathit{\sigma })}{\mathit{\mu }+\mathit{\psi }}<0,}\hfill \end{array}\end{array}$$

it is easy to see that the policy of vaccinations with imperfect vaccines can decrease the the basic reproduction number $R_{vac}$. Thus, the imperfect vaccine may be beneficial to the community. This is also a positive point, sice it is know that the use of some imperfect vaccine can sometime result in detrimental consequences to the community [3, 20].

At last, we must point out that although the system (2.3) with (2.2) is well posed mathematically, we acknowledge the biological reality that the fraction of the constant total population which occupies a compartment can only be within the subset Q of rational values within $R_{+}^5$, and furthermore only within a sub-subset of values within Q belonging to n / N where n belongs to the integers $Z\in [0,N]$. In addition, we also point out that the analysis of the model (2.1) may become somewhat different if disease fatalities and more complex vital dynamics are included, in particular, if the population size is no longer constant. In the future, we may investigate many various modeling possibilities to simulate a real world biological process based on model (2.1). On the other hand, we note that the population in our model (2.1) is assumed to be homogeneously mixed. In fact, different individual may have different number of contacts. Thus, a complex network-based approach on diseases transmission may be closer to a realistic situation [7, 41, 42]. In the future, we shall investigate dynamics of the proposed model based on a complex network.

Appendix

The second additive compound matrix $A^{[2]}$ for a $6\times 6$ matrix $A=(a_{ij})$ is

$$\begin{array}{c}\hfill A^{[2]}=\left(\begin{array}{cccccc}{a}_{11}+a_{22}& a_{23}& a_{24}& -a_{13}& -a_{14}& 0\\ a_{32}& a_{11}+a_{33}& a_{34}& a_{12}& 0& -a_{14}\\ a_{42}& a_{43}& a_{11}+a_{44}& 0& a_{12}& a_{13}\\ -a_{31}& a_{21}& 0& a_{22}+a_{33}& a_{34}& -a_{24}\\ -a_{41}& 0& a_{21}& a_{43}& a_{22}+a_{44}& a_{23}\\ 0& -a_{41}& a_{31}& -a_{42}& a_{32}& a_{33}+a_{44}\end{array}\right)\end{array}$$