Stretching Single Collagen Fibrils Reveals Nonlinear Mechanical Behavior

Abstract

The mechanical properties of collagen fibrils play an important role in cell-matrix interactions and are a manifestation of their molecular structure. Using a, to our knowledge, novel combination of uniaxial, longitudinal straining and radial nanoindentation, we found that type I collagen fibrils show a pronounced nonlinear behavior in the form of strain stiffening at strains from 0 to 15%, followed by strain softening at strains from 15 to 25%. At the molecular scale, this surprising phenomenon can be explained by the combination of unfolding of disordered domains and breaking of native cross-links at different stages of strain. Fibrils cross-linked artificially by glutaraldehyde do not show such a behavior, and nanoindentation allowed us to measure the mechanics of the overlap and gap regions in the D-banding individually. The results could have consequences for our understanding of matrix mechanics and the influence of excessive glycation, which has been linked with age-related diseases such as diabetes. Furthermore, the simplicity of the straining method could be attractive in other areas of biophysics at the nanometer scale because it does not require any bespoke instrumentation and is easy to use.

Significance

Collagen fibrils are the basic building blocks of multicellular animal tissue outside of cells. Their structure and physical properties affect how cells behave and thereby can affect the health of the organism. We thus need to understand mechanical collagen fibril properties at the individual fibril level. In this study, we present results of mechanical measurements on single fibrils using a novel approach, which is simple but, at the same time, offers unparalleled spatial resolution. The data underpin our understanding of collagen fibril mechanics, and we can draw conclusions from it about their internal structure. This could be used in the future to develop new medical treatments for diseases such as diabetes.

Introduction

The main function of collagen fibrils is to be a scaffold for adherent cells and to provide overall strength, shape, and integrity to tissues and organs (1,2). However, it is becoming increasingly clear that collagen fibrils are not just passive components. They provide mechanical cues that influence cell behavior (3). For example, stem cell differentiation is known to be directed by matrix elasticity (4). Apart from the obvious significance in cell-matrix interaction, such effects could be harnessed in biomaterial designs by tuning the fibril mechanics as required. The mechanical properties of the matrix could also be a promising target for novel medical treatments.

To determine single fibril mechanics, some form of mechanical testing is required. At the microscopic scale of collagen fibrils, this requires bespoke techniques because fibrils have diameters ranging from only a few tens to a few hundred nanometers. This makes them inaccessible to conventional, off-the-shelf mechanical-testing instrumentation. To address this challenge, atomic force microscopy (AFM)-based force experiments (5, 6, 7) and dedicated micro- and nanomechanical devices have been developed in the past (8, 9, 10). Also, optical tweezers have been used to strain fibril bundles to extract the elastic modulus (11).

An additional complication is that some of the most important types of collagens such as type I collagen fibrils are not uniform but possess a particular substructure on the nanometer scale called D-banding (12, 13, 14). In AFM images, the D-banding consists of alternating peaks (called overlaps), which are ∼5 nm high, and valleys (called gaps). The D-banding commonly has a periodicity of D ≈ 67 nm (14). There is evidence that the morphology of the D-banding influences cell adhesion (15) and plays a role in the overall mechanical properties of the fibrils. However, investigations that focus on the subtle differences in the structure and properties of overlaps and gaps are scarce (16, 17, 18, 19).

From a simplified point of view of continuum mechanics, overlaps and gaps can be treated as alternating, connected “blocks” (Fig. 1 a) whose mechanical properties ultimately have to be determined independently. Currently, the only direct method to measure these at a high-enough spatial resolution is nanoindentation by AFM (16). Here, the AFM tip is employed as a nano-size indenter to penetrate a small distance into the fibril (Fig. 1 b). The resulting deflection of the tip is then recorded (Fig. 1 c). Because the spring constant of the tip is known, a force-distance curve is obtained whose slope represents the stiffness (N/m) of the fibril at that location. This stiffness represents a convolution of tensile and compression mechanical properties in the longitudinal and radial directions, respectively (Fig. 1 b). Using suitable contact and indentation models, elastic parameters of the fibrils can then be determined from the stiffness (20,21).

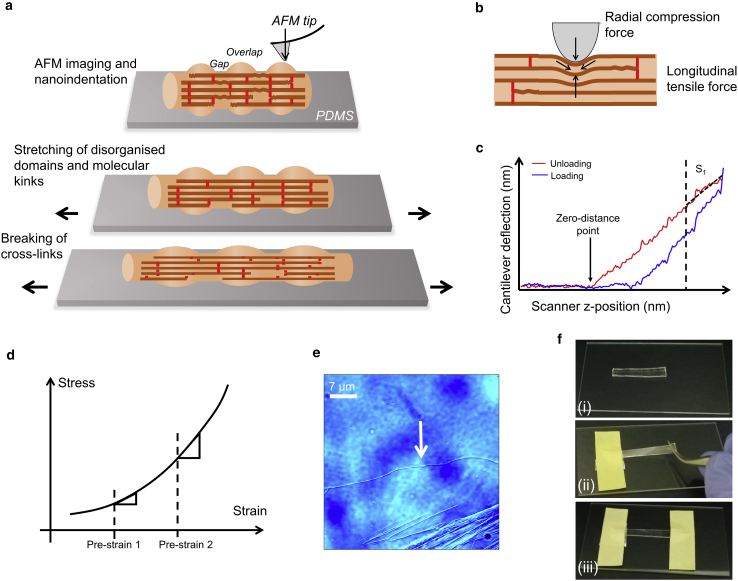
Figure 1.

Stretching of collagen fibrils and analysis of indentation data. Fibrils deposited on a polydimethylsiloxane (PDMS) foil are shown in (a). When the foil is stretched macroscopically, the fibrils are strained along longitudinally, leading to the straightening of disordered domains and breaking of cross-links. AFM imaging and nanoindentation are performed at different strains to determine the stiffness of fibrils at a resolution sufficient to resolve overlaps and gaps. A simplified model of nanoindentation is shown in (b). The AFM tip represents a hard indenter that penetrates a small distance into the sample, thereby probing a convolution of the radial compression stiffness and the longitudinal tensile stiffness of the fibril. The prestraining of the fibrils longitudinally on the foil (a) has the same effect as increasing the longitudinal tensile force but not the radial compression force (b). The slope of the top quarter of the unloading branch, S₁, of the indentation force-versus-distance curve (c) provides the indentation stiffness. The “zero-distance point,” where the AFM tip just touches the surface, is defined by the inflection point of the unloading curve. Determining the indentation stiffness at different prestrains of the foil (d) effectively probes the longitudinal stress-strain curve of the fibrils at a much greater strain range than possible by nanoindentation alone. An optical microscopy image of a collagen fibril on the PDMS foil is shown in (e). Foil stretching is shown in (f): (i) shows the foil before stretching in which fibrils are deposited, (ii) shows the manual stretching of foil, and (iii) shows the adhesive tape keeping the foil stretched. To see this figure in color, go online.

AFM nanoindentation has been performed extensively with fibrils from a variety of sources and under different conditions (16,17,19,21, 22, 23, 24, 25, 26), typically providing elastic moduli in the GPa range for dehydrated fibrils and the MPa range for hydrated fibrils. However, AFM nanoindentation relies on several assumptions and has limitations (20,21) such as the “10% rule,” which states that the indentation depth should not be greater than 10% of the indented object height; otherwise, the influence of the underlying substrate would be too high (25). With fibril diameters of around 100 nm, this limits the indentation depth to ∼10 nm, which means that the effective longitudinal tensile strain applied during the indentation is even less than that (Fig. 1 b). Apart from the fact that such small strains are difficult to control even with the high precision of an AFM, it would be desirable to apply higher strains to fibrils because the constituent building blocks, the tropocollagen molecules, have lengths of the order of 300 nm, and processes such as the unfolding of disordered domains could occur on a similar length scale, which cannot be captured by nanoindentation alone.

In this work, a novel, to our knowledge, approach was employed to expand the strain range: AFM nanoindentation was combined with prestraining individual collagen fibrils longitudinally by stretching a flexible foil on which fibrils are deposited (Fig. 1 a). Collagen fibrils adsorb readily onto hydrophobic surfaces such as polymers (27). Because collagen fibrils adhere very strongly to the foil, they are stretched along with it. We have used this foil-stretching technique in the past to investigate how the D-banding geometry changes upon stretching, but we did not combine it with nanoindentation (28). Such experiments were reported in a recent study in which fibrils were adsorbed on PDMS foils and stretched using a motorized stage (19). With this method, it was found that fibrils become stiffer with strain.

We used a similar approach here to investigate this phenomenon further. The great advantage of combining nanoindentation with stretching is that fibril stiffness can be determined at several prestrains, thereby probing small segments of the longitudinal stress-strain curve along an expanded range (Fig. 1 d) while at the same time preserving the inherently high spatial resolution of nanoindentation. This is not possible by nanoindentation or uniaxial tensile testing alone, and the increased strain range compared to earlier nanoindentation studies helps to gain a unique insight into fibril nanomechanics that would otherwise be inaccessible.

Materials and Methods

Sample preparation

Type I collagen fibrils were obtained from wild-type, adult rat tail tendon, which was a byproduct of teaching lab courses. All local laws and regulations pertinent to research with vertebrate tissue were observed. Approval was not required for this study. First, the skin was removed to expose the underlying tendon. Pieces of the tendon were extracted using a scalpel and were kept in a phosphate-buffered saline solution (Sigma-Aldrich Company, Dorset, UK) for a maximum of 4 months at 4°C. To prepare a sample, a piece of tendon was rinsed in deionized (DI) water and drawn manually on the foil with a pair of tweezers. Because fibrils are very sticky, drawing the tendon over the foil leaves a “trail” of bundles and individual fibrils behind, which can easily be identified by AFM imaging (21). The foils used were small, rectangular pieces cut out from a 1- to 2-mm-thick PDMS slab (see “PDMS Foil Preparation” below) with a scalpel. The sample was subsequently dried using a stream of nitrogen.

Cross-linking

To prepare fibrils with an increased amount of cross-links, we exposed them to glutaraldehyde (GA; Sigma-Aldrich), a well-established and strong protein cross-linking agent (29). Pieces of tendons dissected from a rat tail tendon were manually loosened and lightly pulled apart using tweezers. The piece of tendon was then washed in DI water and resuspended in a phosphate-buffered saline solution, with either 2 or 4% GA, for 40 h at 37°C. Then, the piece of cross-linked tendon was rinsed in DI water to remove excess GA and was subjected to sample preparation as described above.

PDMS foil preparation

Polydimethylsiloxane (PDMS) foils were prepared by mixing Sylgard 184 polymer with the Sylgard 184 cross-linking agent (Dow Corning, Midland, MI) to a 10:1 mass ratio (30). The mixture was poured into a glass petri dish to obtain foils of a 1- to 2-mm thickness. The mixture was then cured at room temperature for at least 48 h. Curing under such conditions allows the resulting PDMS foils to achieve ∼150% longitudinal strains without tearing (30).

Stretching

Once fibrils were deposited on a roughly 3-cm-long PDMS strip, one end was affixed on a glass microscope slide with standard household adhesive tape. The other end of the PDMS strip was pulled manually, stretching the strip to at least 50% visually observable macroscopic strain, and then taped on the microscope slide (Fig. 1 f). The sample was maintained in this state for at least 12 h before any AFM measurements to avoid any creep during subsequent imaging and analysis.

AFM

Tapping-mode imaging and nanoindentation were performed using a Dimension Icon AFM (Bruker, Billerica, MA) with two different tips: Budget Sensors Tap300-G probes (Windsor Scientific, Slough, UK), with a nominal spring constant of 40 N/m and a nominal resonance frequency of 350 kHz (Tip A), and Budget Sensors Tap150-G probes (Windsor Scientific), with a nominal spring constant of 5 N/m and a nominal resonance frequency of 150 kHz (Tip B). Each tip had a nominal apex radius of less than 10 nm. All measurements were performed on fibrils of at least 100 nm in diameter, and all fibrils were imaged subsequent to nanoindentation to ensure that no plastic imprint of the tip had been left on the surface of the fibril. All measurements were performed in air under ambient conditions (humidity ≈ 30%, temperature ≈ 23°C).

Nanoindentation measurements to obtain the stiffness of collagen fibrils were performed on ∼2-μm-long segments of the fibrils using the “Point and Shoot” mode of the Nanoscope 8.10 AFM operating software. The “Point and Shoot” mode allows the user to arbitrarily determine several locations in a previously mapped height image where a force curve is to be taken. Force-distance measurements (Fig. 2) were performed with Tip A on three randomly chosen locations close to each other. A maximal force of 150 nN was applied to ensure that no plastic deformation of the fibrils would take place. For our experiments, a loading rate of 1 Hz was chosen except when otherwise indicated.

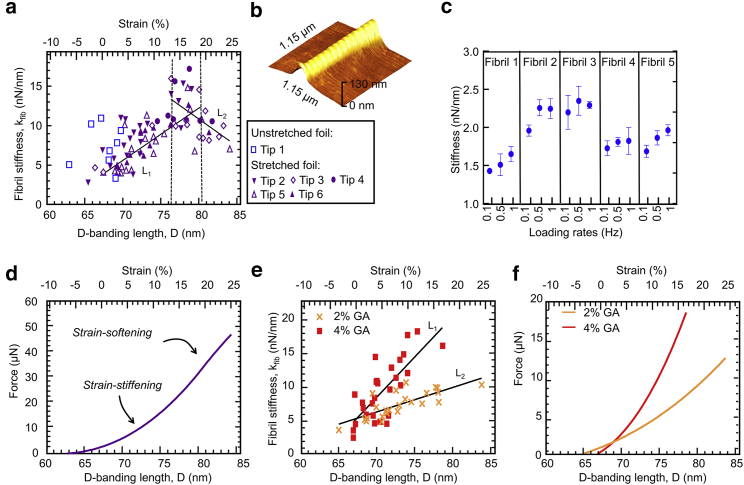
Figure 2.

Native collagen fibrils. (a) Fibril stiffness as a function of strain is shown. All measurements were performed in the air and at ambient conditions with the same type of AFM tip (Tip A; see Materials and Methods). Each data point represents one individual fibril. The linear fit L₁ of the data in the interval 60 nm < D < 80 nm is as follows: slope = 0.51 nN/nm², R² = 0.62. The linear fit L₂ of the data in the interval 76 nm < D < 85 nm is as follows: slope = −0.68 nN/nm², R² = 0.26. (b) An AFM topography image of fibril section is shown. (c) Stiffness of five different unstrained fibrils were acquired at the loading rates of 1, 0.5, and 0.1 Hz. Error bars represent the standard deviation of 3 measurements. (d) The reconstructed force-versus-strain curve was obtained from integrating L₁ and L₂ over strain. The inflection point marks the transition from strain stiffening to strain softening. Artificially cross-linked fibril stiffness as a function of strain is shown in (e) and cross-linked with 2% GA and 4% GA solutions. The linear fit L₁ of the 2% GA data is as follows: slope = 1.2 nN/nm², R² = 0.59. The linear fit L₂ of the 4% GA data is as follows: slope = 0.36 nN/nm², R² = 0.58. The reconstructed force-versus-strain curve showing the expanded strain range of up to 26% is shown (f). To see this figure in color, go online.

To differentiate overlap regions from the gap regions, the tapping-“Force-volume mode” was used with Tip B. The “Force-volume mode” provides force-distance measurements in a two-dimensional array along with topography information. First, a tapping-mode image was taken. Then, a map of 64 × 64 indentation curves were taken on a 1.15 × 1.15 μm area, which means at least four force curves were taken within any single D-banding period. The loading rate was 5 Hz, and the maximal force applied to the fibril was 150 nN.

Data analysis

Gwyddion Image Processing Software was used for image analysis (available at http://gwyddion.net/). To determine the fibril stiffness from a force curve, a linear fit was performed on the top quarter of the tip deflection-versus-scanner z-position curve as shown in Fig. 1 c. The slope of this regression line is directly proportionate to the radial stiffness of the fibril (21). The three slope values from the force curves on a single fibril were then averaged.

When the tip is in contact with the fibril, a series arrangement of two springs with the tip spring constant k_tip and fibril spring constant k_fib is formed, resulting in a total spring constant k_tot. Using the series rule for ideal springs, the sought quantity k_fib is then

$$k_{fib}=\frac{k_{tip}\times k_{tot}}{k_{tip}-k_{tot}}.$$ (1)

The tip spring constant, k_tip, was obtained by performing a force curve on a hard substrate to determine the optical lever deflection sensitivity and then thermal tuning of the cantilever using the “thermal tune” function of the Nanoscope AFM operating software.

The D-banding length, D, for a given fibril was determined by dividing a specific distance by the number of peaks along that distance. The minimal number of peaks used was 10. The fibril strain is then given by

$$\text{Strain}=\frac{D-D_0}{D_0}\times 100,$$ (2)

where D₀ is the average D-banding length of unstretched fibrils.

A MATLAB script (The MathWorks, Natick, MA) was used to reconstruct a stiffness map from a force-volume map by following the same process as described earlier (21). Using Gwyddion, an average stiffness profile for each fibril was obtained from these stiffness maps. The peaks and troughs were identified, and their corresponding stiffnesses were averaged to obtain the average overlap and gap stiffness—k_overlap and k_gap, respectively—for each fibril.

Results and Discussion

Macroscopic prestraining expands the strain range of nanoindentation

To prestrain fibrils, they are first deposited on a highly stretchable substrate, here a PDMS foil. Because they naturally adhere very strongly to the foil, stretching the latter leads to a longitudinal, uniaxial strain of the fibrils themselves. Then, AFM nanoindentation is performed. For the purpose of this study, relative changes of the stiffness of fibrils as they are strained were investigated. As long as all measurements are performed with the same tip (or tips of the same size) and the same indentation depth, the effect of the geometry of the tip cancels out, and it is not necessary to determine quantitative, mechanical parameters such as elastic moduli, which would require the use of indentation models and thereby potentially introduce additional uncertainties.

Fibril D-banding can be used as a marker for individual fibril strain

Stretching the foil manually by a given amount does not necessarily mean that the actual strain of an individual fibril on the foil is exactly the same. Fibrils can lie in random directions on the foil, and more significantly, because collagen fibrils have a greater longitudinal tensile strength than the foil, they could hold it back locally to a certain extent or slip on the foil. Hence, to determine the actual fibril strain, the D-banding length of individual fibrils was taken as a precise in situ measure of strain on a per-fibril basis, as determined by AFM imaging (28).

Native fibrils show strain stiffening followed by strain softening

Fig. 2 a shows the stiffness, k_fib, of individual, native fibrils as a function of their individual D-banding length. No correlation was found between the diameter and stiffness. Also, k_fib did not depend on the maximal applied force in the range from 25 to 150 nN. That is, the unloading branch of the curve in Fig. 1 c was always linear, irrespective of the righthand end point of the curve.

Although the data scatter considerably, reflecting the natural variation of k_fib of different fibrils, an overall trend can be observed: the stiffness, k_fib, increases from ∼2 to 14 nN nm⁻¹ with strains up to ∼15% (strain stiffening), then decreases again to ∼8 nN nm⁻¹ with strains up to 25% (strain softening). The overall trend is highlighted with the two trendlines, L₁ and L₂.

From the stiffness-versus-strain data (Fig. 2 a), a force-versus-strain curve can be reconstructed (Fig. 2 d) by the integration of the former with a force of zero (integration constant of zero) at the lowest strain. The result is similar to the curves often observed in polymeric and, especially, elastomeric materials. The exemplary AFM topography image (Fig. 2 b) taken at a high strain confirms that the overall integrity and structure (D-banding) of fibrils is preserved.

The fibrils in Fig. 2 a were probed with a loading rate of 1 Hz. Collagen fibrils are viscoelastic (31), which means that the measured stiffness could be dependent on the loading rate. In our experiments, there was no significant difference between loading rates of 1 and 0.5 Hz (Fig. 2 c). However, a lower stiffness was measured when fibrils were indented at a rate of 0.1 Hz. Such a tendency is common in the mechanical testing of elastomers and can readily be explained by the particular dynamics of slow, molecular rearrangements in a viscoelastic material (32). Although it would be interesting to further explore collagen fibril viscoelasticity at low loading rates, it is outside the scope of our work, and the data in Fig. 2 c suggest that loading rates of 1 Hz (for a given indentation depth) are on the “safe” side for determining elastic properties.

Strain stiffening (Fig. 2 a) could be explained by molecular straightening (Fig. 1 a). There are domains within the fibrils where the molecules are more disordered and allow for straightening while still, overall, preserving the number and locations of intermolecular, native cross-links. This is typical behavior for elastomers. As more and more of the disordered sections are straightened, the resistance of the fibril to an external tensile force increases. At some point, when most of the disordered sections are straightened, the stiffness reaches a maximum, and further strain starts to break cross-links (Fig. 1 a). This then allows molecules to slide against each other, manifesting itself in a lower resistance to the external tensile force and leading to the strain-softening part of the curve (Fig. 2 a).

The experiments in Fig. 2 were performed with different AFM tips of the same type and nominal geometry (tip material, spring constant, tip shape). According to theoretical indentation models, the measured indentation stiffness scales with the square root of the projected tip-sample contact area (21), which means the stiffness is effectively dependent on tip shape and indentation depth. However, in Fig. 2 a, the data for k_fib do not show any obvious correlation with different tips (the indentation depth was always the same), and, if anything, the natural fibril-to-fibril variation of the data is greater than the variation between different tips. It can therefore be concluded that the error introduced by using different tips of the same type is not significant, and hence, measurement sets taken with different tips can be compared quantitatively.

Fig. 2 e shows stiffness-versus-strain of fibrils exposed to 2 and 4% GA solution, respectively. As for native fibrils, an increase in stiffness was observed, but a strain-softening behavior could not be detected. The increase in stiffness is higher for fibrils exposed to a more-concentrated GA solution.

GA is a strong protein cross-linking agent. It is conceivable, and it has been shown in earlier experiments, that GA exposure increases the intrafibrillar cross-link density and hence can lead to an increase in fibril stiffness (29). Overall, the observations indicate that, with the model of Fig. 1 a, GA results in more cross-links. In this case, disordered sections straighten upon strain as for native fibrils, but after most of these sections are straightened, the sheer number of cross-links prevents strain softening. Some cross-links may well break, as in the case of native fibrils, but this is not sufficient to result in a noticeable strain-softening behavior.

These experimental results agree with stress-strain simulations performed on collagen fibrils with different cross-linking densities (33). In those simulations, fibrils with a low cross-link density strain stiffen up to a small yield strain and then strain soften (33). However, highly cross-linked fibrils strain stiffen up to a greater yield strain and then exhibit a brittle-like fracture.

To see the D-banding, the experiments had to be performed in air, that is, with (at least partially) dehydrated fibrils, which raises the question of how representative the results are for fibrils under physiological conditions. In terms of mechanical properties, the biggest difference is that fibrils appear much softer in water than in air, which has been shown consistently in numerous studies, including nanoindentation as well as uniaxial, longitudinal testing (7,21,26,34), and is attributed to significant water uptake of hydrated fibrils. This in itself does not invalidate our experimental observations (Fig. 2 a) or their interpretation (Fig. 1 a). The simplistic picture is that water inside fibrils acts as a “lubricant” or “cushion” between the collagen molecules and facilitates molecular sliding, thereby leading to a lower stiffness (continuum model of water). However, it is also known that, on the few-nanometer scale, water molecules form structured networks, especially between hydrophilic molecules, and contribute in much more complex (and, to date, largely unknown) ways to protein interactions (35). In this network model of water, it is conceivable that it acts more like a “glue” between protein molecules. The exact molecular mechanisms of collagen reorganization under the load and the role of water in the fibrillar context are beyond the scope of this work. However, the fact that strain stiffening of collagen fibrils was also observed in water in a recent study (19) suggests that our results are at least qualitatively representative. Whether strain softening also happens in water is unknown, but according to our interpretation of cross-link breaking, it is plausible.

Resolving the stress-strain curve for overlaps and gaps

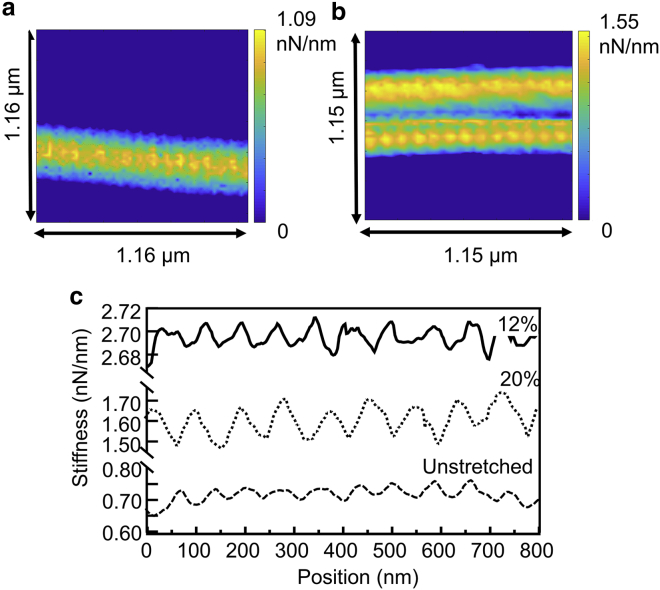
As mentioned above, the distinguishing advantage of the approach shown here is that the spatial resolution of nanoindentation by AFM is preserved. Hence, tests that probe overlaps and gaps independently are possible. To this end, force-volume mapping was used, which is, essentially, a grid of many force-distance curves in a given area of the sample (21). Fig. 3, a and b show two stiffness maps of unstrained and highly strained fibrils, respectively, in which the D-banding pattern is clearly visible. Fig. 3 c shows an example of longitudinal line profiles through the stiffness maps, showing an overall stiffness increase from 0 to 12% strain and then a decrease from 12 to 20% strain.

Figure 3.

(a) Stiffness map of an unstrained fibril. (b) The stiffness map of a fibril strained up to 20% is shown. (c) The line profiles of the stiffness of an unstrained, 12%-strained, and 20%-strained fibril. To see this figure in color, go online.

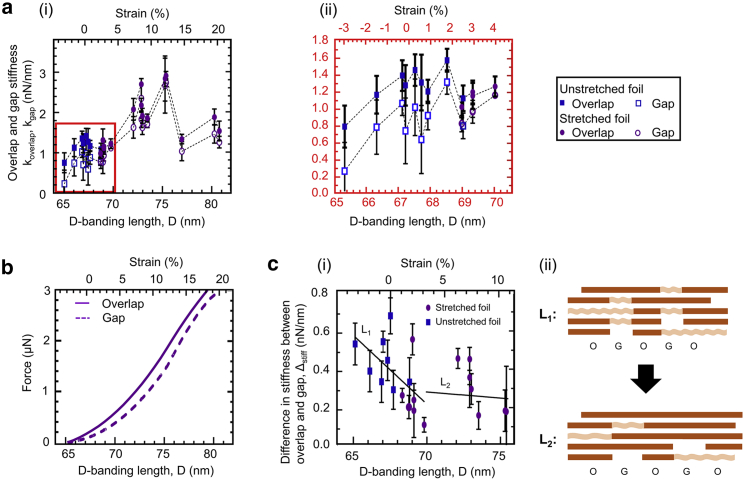
Fig. 4 a shows that overlap and gap stiffness—k_overlap and k_gap, respectively—individually follow the same general trend. Fig. 4 a ii shows a zoom into data points on the bottom left of Fig. 4 a i for clarity. Both overlap and gap strain stiffen up to roughly 12% strain and then strain soften. Furthermore, the overlap always appears stiffer than the gap region, which is in agreement with the literature (16). Fig. 4 b is a reconstruction of the force-versus-strain curves from Fig. 4 a (note: because the reconstruction is performed by integration of the stiffness data with an arbitrary integration constant, the vertical position of the force-versus-strain curves has no significance).

Figure 4.

Overlaps and gaps of fibrils resolved. All measurements were performed in air and at ambient conditions with the same type of AFM tip (Tip B; see Materials and Methods). (a) Stiffness as a function of strain (i) in the interval of 65 nm < D < 81 nm and (ii) in the interval of 65 nm < D < 72 nm is shown. (b) Reconstructed longitudinal force-versus-strain curves showing the expanded range of more than 20% are shown. (c) The difference in stiffness between the gap and the overlap as a function of strain for the strain-stiffening behavior is shown. (i) The linear fit L₁ for data points in the interval 65 nm < D < 70 nm are as shown: slope = −0.07 nN/nm², R² = 0.33. The slope is significantly different from 0: p-value = 0.03. The linear fit L₂ for data points in the interval 70 nm < D < 76 nm are as follows: slope = −0.006 nN/nm², R² = 0.008. The slope is not significantly different from 0: p-value = 0.82. (ii) The number of disordered sections is greater in the gap (G), which, therefore, strain stiffens faster (L₁) than the overlap (O). At a certain strain, there is not such an excess of disordered sections in the gap anymore (L₂), and the strain stiffening in gaps and overlaps is similar. Error bars represent the standard deviations of 10 measurements per data point. To see this figure in color, go online.

Fig. 4 c shows the difference of the overlap and the gap stiffnesses, Δ_stiff, determined from Fig. 4 a i for the strain-stiffening region (strains <12%). Here, a linear regression and statistical analysis of lower (L₁) versus higher strains (L₂) reveals that, at a lower strain, Δ_stiff decreases with increasing strain, whereas at a higher strain, Δ_stiff remains essentially constant.

This observation indicates that overlaps and gaps become mechanically and structurally more similar with increasing strain. The most plausible interpretation for our observations is that, in native, unstrained fibrils, the gap contains more disordered sections than the overlap (L₁, Fig. 4 c ii), making the gap softer. Upon straining, disordered sections in both overlaps and gaps straighten. However, because there are initially more disordered sections in the gap, their “concentration” decreases faster upon straining relative to the concentration in the overlap. This leads the gap to stiffen faster than the overlap and thus to the observed reduction of Δ_stiff in L₁. In L₂, the “oversupply” of disordered sections has almost vanished so that the overlap and gap appear to have similar stiffness within the accuracy of the measurement. Above a 12% strain, however, not enough data points are available to determine the dependence of Δ_stiff on strain.

Conclusions

To summarize, a novel, to our knowledge, approach is presented, which significantly expands the strain range of tensile tests on single collagen fibrils while preserving the nanometer scale resolution. It can be implemented readily by most labs at low cost and effort. It was found that individual fibrils undergo strain stiffening followed by strain softening depending on the cross-link density. Moreover, the slightly different stress-strain behavior of the gap compared with the overlap corroborates the hypothesis that the gap is molecularly more disordered than the overlap. A possible reason for this could be that the gap and hence the D-banding have evolved to take up strain so that fibrils are not structurally disrupted when a mechanical load is applied to them.

An aspect that we did not investigate in this work is reversibility. Biological tissues such as tendons are often subject to cyclic, mechanical loading, for example, in locomotion. Such macroscopic loading-unloading cycles must translate somehow to the microscopic scale of collagen fibrils. The obvious question would be whether the nonlinear behavior shown in Fig. 2 a is fully reversible, and, if not, how cyclic loading affects the stress-strain behavior. Our interpretation (Fig. 1 a) suggests that although strain stiffening may be reversible, strain softening may not. This is because the latter is due to the breaking of intermolecular cross-links, a process that can be considered to be irreversible.

Ultimately, the stress-strain behavior of collagen fibrils as integral constituents of the extracellular matrix is most significant in cell biology. Cells take mechanical cues from the extracellular matrix, which can direct their behavior and their differentiation routes (4). Furthermore, in cancer progression, the structure and mechanical properties of the matrix have a crucial significance and are even thought to regulate metastasis (36). This means that it is the extracellular matrix itself that could be a new and promising target for therapeutic intervention. At the more technological level, the results also have implications in the design of novel, collagen-based tissue scaffolds in tissue engineering. In principle, the fibrillary components of such synthetic scaffolds should at least exhibit a similar strain-stiffening behavior as shown here with strains of up to 15%, especially because artificial collagen scaffolds reconstructed from collagen monomers are not normally cross-linked. Here, the stretching method presented could help in determining the right cross-link level and possibly, because of its low cost and simple set-up, even be used in quality control.

Author Contributions

E.G. and P.M. conceived the experiments, analyzed the data, and interpreted the results. E.G. performed the experiments. E.G. and P.M. wrote the manuscript and designed the figures.

Editor: Wendy Shaw.