Chromatin Compaction Leads to a Preference for Peripheral Heterochromatin

Abstract

A layer of dense heterochromatin is found at the periphery of the nucleus. Because this peripheral heterochromatin functions as a repressive phase, mechanisms that relocate genes to the periphery play an important role in regulating transcription. Using Monte Carlo simulations, we show that an interaction that attracts euchromatin and heterochromatin equally to the nuclear envelope will still preferentially locate heterochromatin to the nuclear periphery. This observation considerably broadens the class of possible interactions that result in peripheral positioning to include boundary interactions that either weakly attract all chromatin or strongly bind to a randomly chosen 0.05% of nucleosomes. The key distinguishing feature of heterochromatin is its high chromatin density with respect to euchromatin. In our model, this densification is caused by heterochromatin protein 1’s preferential binding to histone H3 tails with a methylated lysine at the ninth residue, a hallmark of heterochromatin. We find that a global rearrangement of chromatin to place heterochromatin at the nuclear periphery can be accomplished by attaching a small subset of loci, even if these loci are uncorrelated with heterochromatin. Hence, factors that densify chromatin determine which genomic regions condense to form peripheral heterochromatin.

Significance

We propose an experimentally testable, density-based mechanism for the positioning of peripheral heterochromatin. The observation that the increased density of a phase can target the contents of the phase to a surface has important implications for biological phenomena beyond the nuclear periphery.

Introduction

The spatial organization of chromatin in interphase eukaryotic cells is typified by a layer of dense, transcriptionally repressed heterochromatin adjacent to the nuclear periphery. This peripheral heterochromatin is visible by both electron (1) and fluorescent (2) microscopy and is present in most eukaryotes (with some notable exceptions (3)). Genes segregated to the nuclear periphery typically experience a repression of their expression (4, 5, 6, 7, 8) (though this also has exceptions (9)). The highly conserved nature of peripheral heterochromatin suggests that it is a fundamental feature of nuclear architecture. Furthermore, differences in radial organization of heterochromatin could be useful as a diagnostic (10), could play a role in cell differentiation (3), and—in at least the case of the rod cells of nocturnal mammals—is used for tasks such as focusing light (11).

The DamID technique (12,13) involves fusing a bacterial adenine methyltransferase to lamin B1, so that adenine methylation labels DNA regions in contact with lamin B1. These regions, which were found at the nuclear periphery (13,14), are called lamina-associated domains (LADs). The genomic position of LADs are correlated with regions of low gene density, genes with low expression levels, regions of pericentric heterochromatin, and regions with high levels of the epigenetic marks H3K9me2/3 (14,15). However, the mechanisms that bring the LADs in contact with the nuclear periphery remain poorly understood (15,16).

Knockouts of lamin A and lamin C—proteins that form the fibrous layer at the periphery—lead to a loss of peripheral heterochromatin (3) and a loss of peripheral positioning for tested LADs. Several additional proteins, including CEC-4, Yin Yang 1, emerin, heterochromatin protein 1 (HP1), and lamin B receptor, have been shown to play a role attaching LADs to the nuclear periphery in some cell types. A review of factors implicated in position LADs is given by Steensel (15). Cabianca et al. found that cec-4 and mrg-1 independently regulate attachment of heterochromatin to the nuclear periphery in Caenorhabditis elegans, with the former providing a weak attraction and the latter anchoring heterochromatin to the periphery in an H3K9me3 (trimethylation of the ninth lysine of a nucleosome’s histone 3 protein)-independent manner (17). However, the full combination of factors that are required for positioning to the nuclear periphery remains poorly understood. For example, (3) shows that the presence of lamin B receptors can cause peripheral heterochromatin in the absence of lamin A and C. Plants, which lack lamins altogether, still have peripheral heterochromatin (18). Given that LADs cover roughly a third of the human genome and peripheral heterochromatin is found in almost all eukaryotes, it is desirable to find a more general explanation for the relocation of heterochromatin regions to the nuclear periphery.

In this article, we propose that the chromatin density difference between heterochromatin and euchromatin is capable of supplying the specificity that causes heterochromatin to localize to the nuclear periphery. Using Monte Carlo simulations, we show that a nonspecific interaction with the nuclear envelope that is equally attractive of heterochromatin and euchromatin leads to peripheral heterochromatin formation. This envelope-chromatin interaction need only affect a small fraction of the genome for this effect to occur.

The higher chromatin density of heterochromatin (that is, the higher DNA and associated protein content per unit volume) is a defining feature of heterochromatin that leads to its darker appearance in stained electron microscopy. Indeed, with 5.5–7.5 times as much DNA per unit volume (19), heterochromatin is one of the most prominent features of nuclear organization. Our observations suggest that any compacted region of chromatin will preferentially segregate to the nuclear periphery. In this article, we focus on compaction due to the preferential binding of HP1 to nucleosomes with the epigenetic mark H3K9me3. We focus on H3K9me3 because it is widely recognized as being associated with heterochromatin. Reduction in the H3K9 methylation state in the vicinity of a loci can cause its release from the nuclear periphery (20, 21, 22). Global reduction of H3K9me3 leads to the loss of peripheral heterochromatin (16). Although not the only source of density heterogeneity, this mark is a good starting point for understanding the heterochromatin densification and positioning in the nucleus.

Previous simulations relied on a specific attraction to the nuclear periphery for periodic regions (23), regions based on chromatin immunoprecipitation for lamins (24), or heterochromatic regions (25) to recover a three-dimensional model of the genome. Our study investigates which regions are intrinsically predisposed for lamin association in the presence of a nonselective peripheral attraction. In particular, we focus on the compaction of chromatin due to HP1-H3K9me3 binding and how the resulting compaction determines which genomic regions are found at the nuclear periphery. We demonstrate the ability of interactions that are not specific to heterochromatin to selectively reorganize the nucleus, even when these interactions are relatively weak or sparsely applied.

Methods

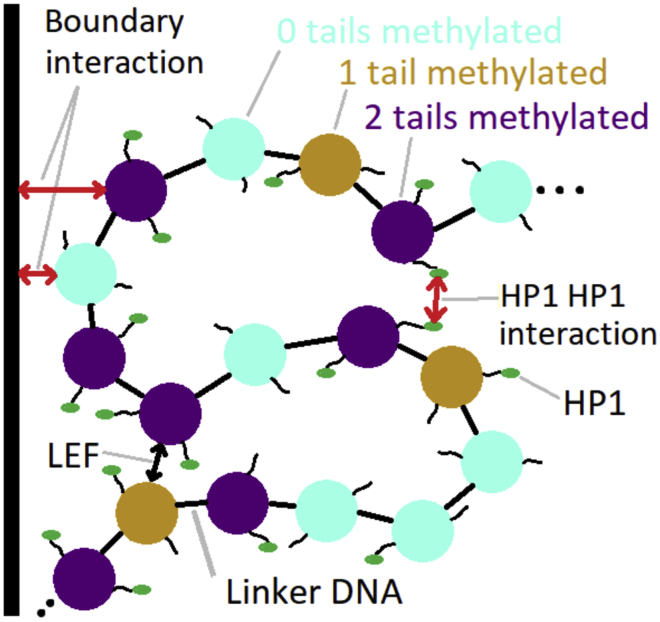
The phase segregation of heterochromatin and euchromatin occurs on the size scale of roughly a micron. Because of computational limitations, simulations of this scale are necessarily coarse grained. Our approach is to start with a coarse-grained model of chromatin and add a few key interactions so that the consequences of each of these interactions can be investigated. Fig. 1 provides a cartoon summary of the interactions included, each of which is introduced below.

Figure 1.

Cartoon representing the interactions included in the simulation. Nucleosomes may have neither (cyan), one (tan), or both (purple) of their tails marked with H3K9me3. Marked tails are more likely to be bound by HP1 (green oval). Interactions include HP1-HP1 binding, loop extrusion factors (LEFs), and a nonspecific attraction to the nuclear boundary. To see this figure in color, go online.

Chromatin polymer

Each computational bead in our simulation corresponds to a single nucleosome, roughly 200 bp of DNA. At this length scale, the mechanics of human chromatin is dominated by the geometry of 147 bp of DNA being wrapped around a histone octomer to form the nucleosome, separated from the following nucleosome by a roughly 50-bp long linker DNA strand. The histone octomers introduce kinks into the otherwise straight DNA backbone. These kinks, in conjunction with the natural flexibility of the linker DNA subject to thermal fluctuations, results in a Kuhn length of ${\ell }_k=38\text{nm}$ (26). The Kuhn length is defined such that for a long chromatin chain, the square of the end to end distance of the chromatin is $\langle {\overrightarrow{R}}_{ee}^2\rangle \approx {\ell }_k{L}_{link}$, where L_link is the cumulative linker length of the chromatin (i.e., L_link = (16.5 nm)N_nuc, where N_nuc is the number of nucleosomes). We incorporate this result into our previous model (27) of chromatin by modeling DNA as a worm-like chain with a persistence length of ${\ell }_p={\ell }_k/2=19\text{nm}$, with beads spaced a path length 16.5 nm apart.

Boundary interaction

For computational purposes, we model a single chromosome, namely chromosome 18 of human genome assembly 19, with 390,387 nucleosome beads. Interphase chromosomes do not spread over the entire nucleus but have been observed to segregate into separate chromosome territories (28). Therefore, we simulate chromosome 18 inside a 1.8 μm cube in which a single face of the cube is designated as the confining nuclear periphery. This approximates the geometry of chromosome 18 within its chromosome territory interacting with the nuclear boundary, as indicated by the inset of Fig. 2. Chromosome 18 was chosen because it has been found in a peripheral chromosome territory in multiple cell lines and species (29,30).

Figure 2.

Rendering of a simulation of a single chromosome confined to a territory with nonspecific attraction to the left boundary. Inset in lower left indicates approximate size in comparison to a 6-μm cartoon nucleus. Each bead represents a nucleosome with neither (cyan), one (tan), or both (purple) of its histone 3 tails trimethylated. Beads are only shown if they are in a 344 nm (12 discretization bins)-wide slice in the middle of the simulation box. Scale bar, 100 nm. To see this figure in color, go online.

For simulations with all nucleosomes attracted to the boundary, we apply an attraction energy of:

$$E_{bind}=\sum _{i\in \text{beads}}\{\begin{array}{cc}-0.3{\mathrm{k}}_{\mathrm{B}}\mathrm{T}& x_i\le \Delta \\ 0& \text{otherwise}\end{array},$$

where Δ = 28.7 nm is the discretization length (27). This potential is chosen to represent any short-range interaction below the resolution, Δ, of the simulation. For simulations with only a fixed number of nucleosomes attached to the boundary, we require that these nucleosomes reside within Δ of the left boundary after being brought there during simulation initialization. The number of beads bound N was chosen to be 75, 100, 150, and 300 with four replicates of each. We allow the beads to rearrange themselves on the surface by moving around within the 28.7-nm wide layer.

Compaction due to epigenetic modifications

Each nucleosome bead can have neither, one, or both of its histone 3 tails marked with H3K9me3. We designate the methylation state of each nucleosome based on the chromatin immunoprecipitation sequencing (ChIP-seq) signal for the mark (31) with a threshold applied such that half of all tails are marked. This is roughly consistent with the combined, measured levels of trimethylation (and to a lesser extent, dimethylation), which account for 20–30% and 30–40% of the tails, respectively (32,33). The methylation pattern is held constant throughout the simulation.

The source of densification of chromatin into heterochromatin in our model is a 4.0 k_BT oligomerization potential of HP1 coupled with a 1.53 k_BT preference for HP1 to bind histone tails marked with H3k9me3 over those without the mark. These values are based on binding curves (34) that were analyzed in (35) to determine these energetic parameters. The effects that this condensing potential has on heterochromatin, as well as the counterbalancing effects of general repulsive forces, are explored in (27). Here, we choose the chemical potential of HP1 to be −1 k_BT so that it binds roughly half of histone tails. Consistent with (27), we use a repulsion of $1.92\times {10}^{-3}\frac{{\mathrm{k}}_{\mathrm{B}}\mathrm{T}}{n{m}^3}\varphi \left(1-\varphi \right),$ where ϕ is the local volume density of chromatin. For our present purposes, it is sufficient that these interactions result in the condensation of genomic regions that are rich in H3K9me3, leaving genomic regions low in the mark to spread out through the remaining available space.

Loop extrusion factors

Loop extrusion factors (LEFs) reorganize chromatin architecture by attaching to the chromatin at two adjacent locations and then walk in opposite directions along the strand to extrude a loop of chromatin (36). The walking of the LEFs along the chromatin is inhibited in a directionally dependent manner at CTCF binding sites (36). In this way, LEFs increase the contact probability for pairs of loci that are close to each other on the genome, particularly if they are found between convergently oriented CTCF cites.

We incorporate LEFs into our simulation by requiring pairs of beads that are held together by a LEF remain spatially colocated. To determine which pairs of beads are held together by LEFs, we follow (37) by running a Gillespie algorithm in which LEFs stochastically walk along and fall off the chromatin and are inhibited in a directionally dependent manner by CTCF binding sites whose locations we take from (38). We assume a LEF concentration of one per 120 kb and a processivity of 120 kb. These numbers are chosen in accordance with the best fit values found in previous studies (39). As we are using a equilibrium Monte Carlo simulation, we first run the Gillespie algorithm to equilibrium and then take the pairs of beads held together by the LEFs from the end of the Gillespie algorithm into the Monte Carlo simulation where they remain fixed. The presence of LEFs was not found to qualitatively affect our results with respect to the formation of peripheral heterochromatin (see Fig. S1). That our conclusions about peripheral heterochromatin do not change when LEFs are excluded demonstrates their generality.

Monte Carlo implementation

The Monte Carlo algorithm used is an updated version of that presented in (27). The condensing HP1-based interaction, as well as a general steric repulsion, are carried out using density-based coarse graining, in which the interactions are dependent on the local density of nucleosomes, ${\varphi }_c$, and the local density of histone tails bound by HP1, ρ, are each calculated using a Δ = 28.7 nm discretization. The energy of oligomerization of HP1 molecules (which causes their bound nucleosomes to coalesce) is included with an energy term proportional to −ρ². The simulation contains no explicit steric interactions. The repulsive and volume exclusion effects are included via an energy term proportional to ${\varphi }_c^2$ as well as a hard limit of ${\varphi }_c<22.7\text{nucleosomes}/{\Delta }^3$. This density-based coarse-graining approach (40) greatly accelerates the Monte Carlo sampling used to equilibrate the structure by both reducing the computation needed to make a Monte Carlo move and softening the potentials of interaction. These effects greatly increase the probability that each move is accepted.

The same set of Monte Carlo move types from (27) were used, the most important of which is a crank-shaft move type, which rotates a section of chromatin about the axis running though its ends. In addition, a “spider” move, which is described in Fig. S2, allows semiflexible sections of DNA that are bound together by LEFs to move in a coordinate manner. To accelerate the equilibration, Monte Carlo moves are allowed to cross over each other. Equilibration of the Monte Carlo algorithm is treated in the Supporting Material of (27). Because this article includes interactions with the boundary as well as the action of LEFs, we need to ensure that these interactions do not introduce insurmountable energy barriers that prevent the simulation from equilibrating in the roughly 10 billion crank-shaft moves used. To this end, we ensure that LEF-bound nucleosomes are able to traverse the simulation confinement. To ensure that the observed peripheral heterochromatin was not an artifact of the initial condition followed by poor sampling, we first ran the simulation without the boundary interaction on so that heterochromatin formed away from the periphery and then turned on the boundary interaction (see Fig. S3). Also available in the Supporting Materials and Methods is the contact probability as a function of genomic distance (Fig. S4) along with a comparison to Hi-C data for chromosome 18 (36).

The FORTRAN code for our Monte Carlo algorithm and the PYTHON code for the Gillespie algorithm are available on our GitHub page (https://github.com/SpakowitzLab/wlcsim/tree/MS2019_peripheral) and our lab’s website.

Results

Nonspecific binding to lamina

The exact nature of the interaction(s) that bind chromatin to the nuclear periphery is unknown. That there must be at least some attraction between the two is clear. The boundary condition preventing the chromatin polymer from leaving the nuclear confinement requires the density of chromatin to approach zero outside of the confinement. Without an attraction between the chromatin and its confinement, this boundary condition, in combination with the connectivity of the DNA polymer, would lead to a region of reduced chromatin density adjacent to the boundary. In fact, in the simple model of chromatin as a long, flexible, noninteracting random walk in a spherical confinement, the density of chromatin as a function of radial distance r would be proportional to sin² (πr/r_confine)/r², which trends to zero at the confinement. However, the opposite is observed, with dense heterochromatin typically being found at the nuclear boundary. This implies that there must be interaction(s) holding chromatin in proximity to the nuclear confinement.

The boundary interaction potential need not be specific to heterochromatin but can be equally attractive of all chromatin. To demonstrate this, we introduce an attractive potential of 0.3 k_BT for each nucleosome (i.e., independent of its methylation state or HP1 binding status) when they are within 28.7 nm of the nuclear envelope. The 28.7-nm width is chosen to represent the coarse-grained effect of any short range potentials, defined as potentials with a range at or below the resolution of the simulation, which is set by the discretization. This particular choice for the width is not critical for our results as width could be compensated for with a higher attractive potential.

Fig. 2 shows a single snapshot of the chromatin simulation with the nonspecific attraction applied to the left side of the confinement box. Peripheral heterochromatin in the form of dense, H3K9me3-rich beads (purple) forms along the attractive side of the confinement. The formation of this methylation-rich layer is a general feature and is not sensitive to the exact parameters chosen for the simulation, provided that a sufficiently strong nonspecific attraction to the boundary is present. Also visible are regions of heterochromatin that are not in contact with the nuclear confinement, consistent with observations from microscopy. The cubical hard boundaries that prevent beads from leaving the box are meant to approximate the chromosome being confined to a single chromosome territory. Actual chromosomes are not strictly segregated into their respective territories but are able to mix to some degree. Hence, any effects of hard boundaries are artifacts of the simulation.

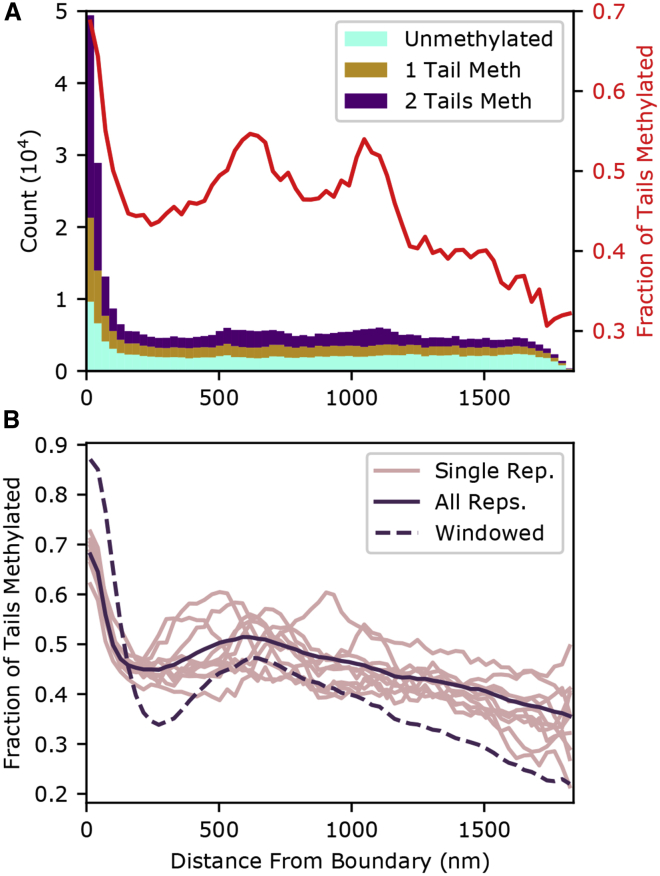
We quantify the configuration shown in Fig. 2 by plotting the composition of the simulation as a function of x position in Fig. 3, showing a large number of nucleosomes found within a few discretization bins of the confinement boundary. This high average density of the peripheral heterochromatin is caused by the synergistic effects of the HP1-based condensation and the attractive chromatin-boundary potential. The roughly 10-fold nucleosome density enrichment of the peripheral heterochromatin over the euchromatin is a bit higher than the 5.5–7.5-fold enrichment measured in heterochromatin (19), but this is consistent with observations of particularly dense chromatin reported at the periphery (41). This dense peripheral chromatin is notably enriched in H3K9me3, demonstrating that a nonspecific binding can specifically enrich the periphery in the mark.

Figure 3.

Upper: a stacked histogram showing the number of nucleosomes (left vertical axis) as a function of distance from the attractive boundary based on the single configuration shown in Fig. 2. Nucleosomes are categorized depending on whether zero (cyan), one (tan), or both (purple) of their H3 tails are trimethylated at the ninth lysine. The width of each histogram bar is a single discretization length (28.7 nm). The red curve indicates the fraction of tails methylated (right vertical axis). Lower: light curves: fraction of tails methylated averaged over five Monte Carlo configurations. Bold curve: overall fraction of tails that were marked for 50 configurations (10 replicates, five Monte Carlo configurations each). Dashed curve: fraction of tails within an H3K9me3-rich genomic region is shown. A bead is defined as being in an H3K9me3-rich region if >50% of the tails in the surrounding 101 nucleosome-wide window (50 in either direction) have the mark. To see this figure in color, go online.

Also visible in Fig. 3 are dense, H3K9me3-rich heterochromatic regions in the interior of the simulation. The existence of nonperipheral heterochromatin is consistent with microscopy (1,42). Note that relative density of these regions, which are also visible in Fig. 2, is underestimated in Fig. 3 because they will only be present in a small part of any plane parallel to the boundary and so are partially averaged out.

The structure of chromatin is stochastic and continuously changing with considerable cell-to-cell variability. The configurations presented in Figs. 2 and 3 are but a single snapshot of a single simulation. To capture the variability inherent in this structure, we ran the Monte Carlo simulation 10 times with different initial conditions and allowing the positions of LEFs to vary. The fraction-methylated profile for the final configurations of each of these simulations is shown in Fig. 3 B by the light curves. The overall fraction of tails methylated, calculated using the data from five Monte Carlo configurations from each of the 10 replicates, is shown by the solid curve in Fig. 3 B. An increased fraction methylated adjacent to the attractive boundary in all curves indicates the presence of H3K9me3-rich peripheral heterochromatin. Regions of nonperipheral heterochromatin—similar to those observed in Figs. 2 and 3—are stochastically incorporated throughout the interior of the confinement, increasing the variance in the fraction methylated. We interpret the observed secondary peak in the methylation fraction as follows. In the absence of a boundary-chromatin attraction, the natural tendency of random walks to avoid boundaries would result in a higher density near the center of the confinement. This higher density would lead to a higher methylation fraction as was observed in our previous simulations (27). In that case, the heterochromatin was held near the center of the confinement by a corona of euchromatin to which it was attached. In this simulation, the central peak of nonperipheral heterochromatin does not appear to be completely eliminated by the introduction of a peak near the boundary.

Window averaging

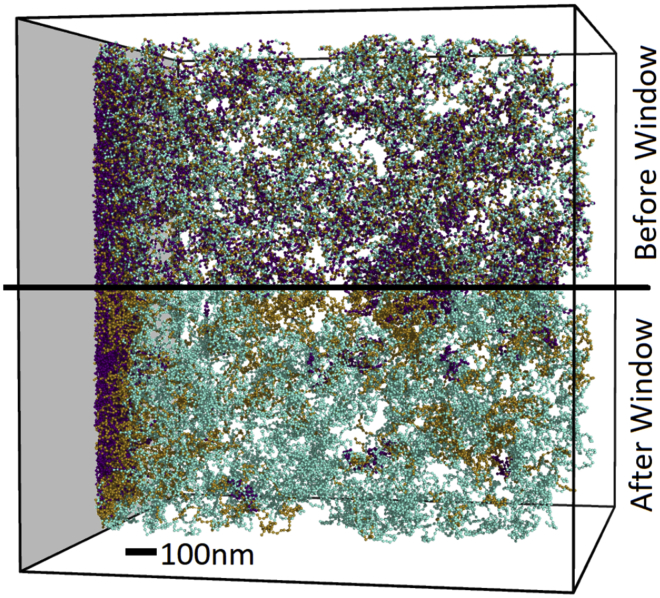
The left end of the solid curve in Fig. 3 B indicates that 66% of the tails in the immediate vicinity of the boundary are methylated (compared with an overall fraction of 50%). The remaining 44% unmethylated tails—despite their epigenetic marking—reside in peripheral heterochromatin. Many of these are unmethylated tails that lie within otherwise highly methylated genomic regions in the ChIP-seq-based methylation profile. Similarly to the strategy we employed in (27), we applied a window average of the surrounding 20 kb. Fig. 4 shows that it is not the methylation level of nucleosomes themselves (displayed by the coloring in the top of Fig. 4) but the overall methylation of the genomic region (bottom of Fig. 4) that determines peripheral positioning.

Figure 4.

The top half of the image shows our chromatin simulation with the following nucleosome coloring for the number of tails marked with H3K9me3 used in Fig. 3: neither (cyan), one (tan), and both (purple). The bottom half shows the mirror image of the top half, except the nucleosomes are recolored according the average methylation level of a 101-nucleosome window, with coloring indicating less than 53.0% of tails marked (cyan), 53.0–70.5% of tails marked (tan), and greater than 70.5% (purple). Scale bar, 100 nm. To see this figure in color, go online.

To quantify the proclivity for methylation-rich genomic regions to be found at the boundary, we performed a window average of the methylation state (with a window spanning 50 nucleosomes on either side of the nucleosome of interest) and then reclassified the beads into H3K9me3-rich regions if more than half of the histone tails were methylated and lean regions if fewer than half the tails were methylated. The fraction of nucleosomes classified as being in methylation-rich regions is shown by the dashed line in Fig. 3 B. Over 80% of chromatin found near the attractive boundary is considered enriched by this definition. This proportion rises to over 98% if we only require a third of the tails be methylated. This degree of selectivity is quite significant considering that the attractive potential at the boundary is agnostic to the methylation state of the chromatin.

Random attachments

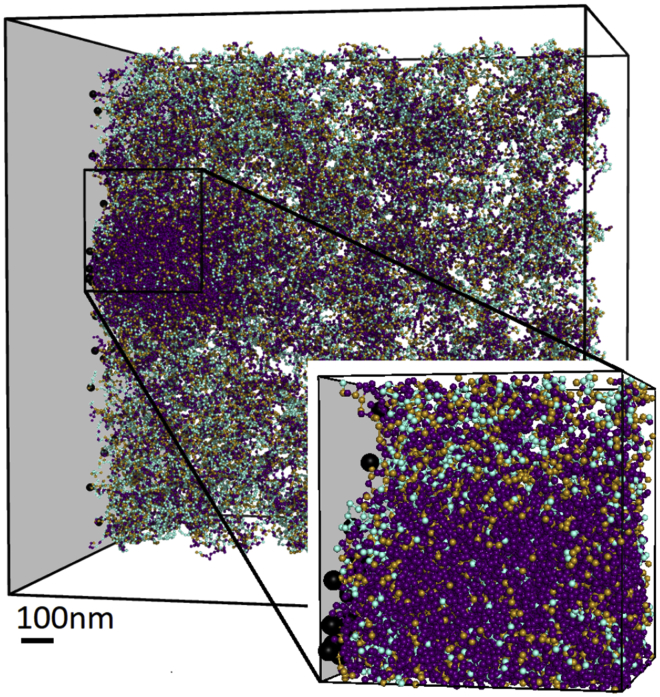
The nonspecific interaction with the nuclear confinement that is introduced in the simulation that produced Fig. 2 was applied equally to all nucleosomes. Although general attraction between chromatin and the nuclear confinement is sufficient to produce peripheral heterochromatin, it is not necessary. To demonstrate this, we replace the chromatin-boundary potential in our simulation with a requirement that 150 randomly chosen nucleosomes are attached to the boundary, as shown in Fig. 5.

Figure 5.

Simulation in which 150 randomly chosen points (black dots) are attached to the boundary. Zoomed inset is included for clarity. Note that the general attraction used in Fig. 2 is no longer applied. Scale bar, 100 nm. To see this figure in color, go online.

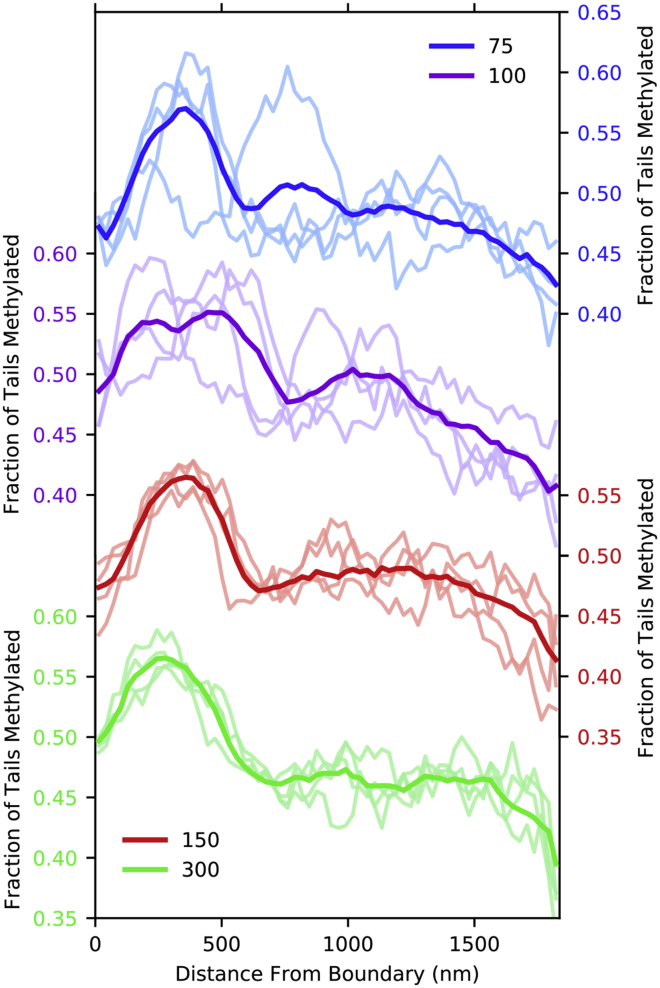
Fig. 6 shows the fraction of tails that are methylated for the simulations with a varying number of beads attached to the boundary as well as condition-wide averages. As few as 150 attachments are required to cause heterochromatin to consistently form in the vicinity of the attachment boundary in all replicates. Simulations with only 100 or 75 attached nucleosomes also had an increased probability of heterochromatin forming on the boundary.

Figure 6.

Fraction of tail methylated for configurations in which 75–300 beads are “bound” by requiring them to be within the first discretization. Profiles of single simulation snapshots are shown in light curves. Overall compositions for four replicates times five snapshots each are indicated in bold face of the same color. To see this figure in color, go online.

We emphasize that the 150 points in Fig. 5 were chosen randomly and are not correlated with the epigenetic state. These randomly selected attachments are still able to cause an H3K9me3-rich phase to form near the boundary. We observe several differences in the qualitative nature of the peripheral heterochromatin in the case of all beads being weakly attracted to the boundary (as in Figs. 2, 3, and 4) versus the case of randomly attached beads (Fig. 5; (6)). In the former, a layer of heterochromatin formed in the first few discretization bins adjacent to the boundary. In the latter, the droplets of heterochromatin, which are found in the interior region of the former case, are relocated to within 500 nm of the boundary. We do not intend to make a judgment about which of these cases (or perhaps a combination of them in a manner reminiscent of (17)) is most realistic in vivo, only to show that either is sufficient to explain the presence of peripheral heterochromatin.

Correlation with DamID

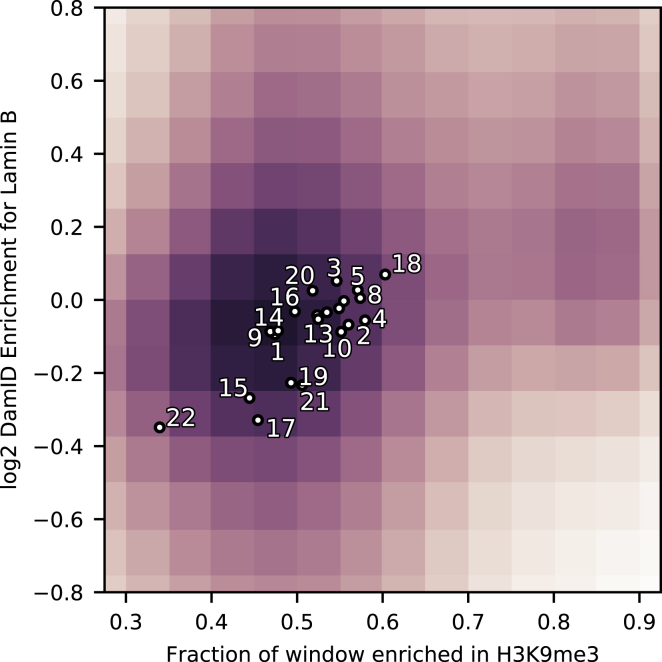
In the model we present, H3K9me3 densifies chromatin, which can then be relocated to the nuclear periphery by nearly any attractive interaction. This observation is consistent with genomic locations high in H3K9me3 being correlated with DamID data for lamin B, which is found in the fibrous layer at the nuclear periphery. Indeed, such a correlation was observed in (14,43), providing the inspiration for this work. Guelen’s analysis (14) focused on the H3K9me3 (and other genomic markers) in the vicinity of the boundaries of LADs, which were identified as regions of enriched lamin B contact with well-defined boundaries. For our present purpose, we are interested not in the boundaries of LADs per se, but the overall correlation between lamin B contact and H3K9me3 measured by ChIP-seq. We therefore present a reanalysis of this correlation in Fig. 7. The density of DamID data points is indicated by the coloring of the background, with darker regions corresponding to more data points. The horizontal position of each point is determined by the fraction of the 20-kb genomic window surrounding the loci that has a ChIP-seq signal greater than the average ChIP-seq signal. The chromosome-wide averages are displayed by dots.

Figure 7.

Lamin B contact is correlated with H3K9me3. The shading of the background shows the density of DamID-based lamin B data points (14) and the postwindow, postcutoff ChIP-seq signal for H3K9me3 (46) of the surrounding 20 kb. Dots show average DamID enrichment for corresponding chromosomes versus the average H3K9me3 ChIP-seq signal for the entire chromosome, excluding centromeres. Sex chromosomes are excluded. Unlabeled chromosomes near the center are 12, 11, 6, and 7 from left to right. The figure is cropped for space purposes. To see this figure in color, go online.

The shading in Fig. 7 shows a correlation between H3K9me3 and lamin B contact (person r = 0.178, p < 10⁻¹⁵). In particular, there is a group of H3K9me3-rich data points (at around x = 0.8) with a notably enriched lamin B contact, consistent with the hypothesis of regions of H3K9me3-induced peripheral heterochromatin.

Also notable is the correlation (person r = 0.801, p = 7.6 × 10⁻⁶) between chromosome-wide H3K9me3 level and lamin B contact. Chromosome 18, which is the focus of our simulations, has both the highest ChIP-seq score and (apart from the sex chromosomes) the highest DamID enrichment. This is consistent with fluorescence in situ hybridization observations that found that chromosome 18 associates with the nuclear periphery (29). Although correlation does not imply causation, the chromosome-wide correlation in Fig. 7, along with the density-driven mechanism described in this article, suggests that H3K9me3-induced densification may also position entire chromosome territories. The biological function of the chromosome positioning could be related to the difference in gene content, with chromosomes with lower gene content being enriched in lamin contact (see Fig. S5).

Details of lamin B DamID versus H3K9me3 comparison

The DamID method (12,13,44,45) identifies log2 enrichment of lamin B contact at specified loci containing the GATC motif; it is this enrichment (14) that we compare to ChIP-seq data (46) for H3K9me3. We use each of the enrichment values from all eight data sets provided by (14) for chromosomes 1–22. The liftOver tool (47,48) was used to convert the locations of each of these data points to genome assembaly hg19.

We first process the H3K9me3 ChIP-seq signal (46) by dividing it into 200-bp bins, roughly corresponding to nucleosomes. To prevent the correlation with ChIP-seq from being dominated by a small number of strongly enriched points that may be the result of biases in the ChIP-seq protocol, we apply a cutoff to the ChIP-seq signal and divide by the cutoff to put data points on a 0–1 range. This cutoff is chosen such that the postcutoff average is one half. Based on our previous simulation work (27), we would expect the H3K9 methylation state of the surrounding roughly 20 kb of chromatin to determine whether any particular GATC motif will be found in heterochromatin. We therefore perform a window average of beads 1 kb (50 bins) to either side of the loci of interest. A 2D histogram of the resulting DamID window-averaged ChIP-seq data is then performed, with the height of the histogram corresponding to the shading in Fig. 7.

To calculate the chromosome-wide averages, we averaged the postcutoff but prewindow-averaged ChIP-seq data over the entirety of each chromosome (irrespective of DamID locations), excluding centromeric regions. The average of all DamID data points is used to give the DamID value of each chromosome. We note that because the entire chromosome except the centromere is included in the average, the dot for each chromosome is not exactly the same as the average of the points that determined the shading of Fig. 7. The chromosome-wide average is meant to represent the chromosome’s total H3K9me3 enrichment and therefore attraction of the respective chromosome territory to the boundary.

Although a correlation between H3K9me3 and lamin B contact is visible in Fig. 7, we emphasize that the H3K9me3-HP1 interaction is far from the only mechanism that could densify chromatin and thereby cause peripheral organization. For example, polycomb proteins, variation in nucleosome positioning, histone tail acetylation, and supercoiling may also play a role in selectively condensing chromatin. Further muddling the correlation between H3K9me3 and lamin B contact is the difference in cell line between the two data sets, NHLF and Tig3, respectively, though both are human lung fibroblast cell lines.

Discussion

Using Monte Carlo simulations, we have shown that a nonspecific attractive force that pulls chromatin to the nuclear periphery can result in a peripheral layer of chromatin that is specifically enriched in H3K9me3. At least as important as this simulation result is the intuition it supplies for when and why peripheral heterochromatin should occur. The only difference in our simulation between nucleosomes that are marked by H3K9me3 and those that are not is that HP1 binding is more energetically favorable for the former. In turn, the only effect of HP1 is to oligomerize, causing tails that it is bound to (typically methylated ones) to condense into a dense state (i.e., heterochromatin). For genomic regions low in H3K9me3, the entropic benefit of the freedom to move about the nucleus overpowers the condensing tendency of HP1. Without any interactions with the nuclear boundary, the heterochromatin will tend to form in the center of the confinement surrounded by euchromatin as in (27). Indeed, rod cells in the eyes of nocturnal mammals display an “inverted” organization with heterochromatin in the interior (11,25). In simulations with inert boundaries (27), this organization occurs because 1) a layer of semidense chromatin surrounds heterochromatin, pushing it away from boundaries, and 2) spreading hetrochromatin against the confinement would increase the surface area and therefore the associated surface energy of the heterochromatin phase.

If a sufficiently strong attractive force pulls chromatin to the nuclear boundary, then heterochromatin, which has a greater chromatin content per unit volume than euchromatin, will experience a greater energetic interaction with the boundary and therefore preferentially be relocated to the nuclear periphery. An alternative way to conceptualize the effect of a nonspecific binding potential is to reason that an attractive boundary creates a layer of higher chromatin density. Heterochromatin, which has already given up entropy to condense, has less entropy to lose when it is incorporated into this boundary layer. Our Monte Carlo simulations show that a strong binding force that pulls a random subset of loci to nuclear periphery is also sufficient to explain peripheral heterochromatin. This result can be rationalized by arguing that when a small number of H3K9me3-rich nucleosomes are pulled to the boundary, they pull the other beads in their phase along with them. In contrast, if a small number of H3K9me3-low loci are relocated to the boundary, they are incorporated either into or alongside the peripheral heterochromatin and do not pull the rest of the H3K9me3-low beads—for whom they do not have a particularly strong attraction—along with them.

Given the above arguments, we would expect a sufficiently strong nonspecific attraction to cause heterochromatin to relocate to the periphery. We further argue that, given the rather low bar for such an interaction, it is not altogether surprising that one (or perhaps many) exist, which is why we see peripheral heterochromatin in most eukaryotes. Indeed, we see that if as few as 150 randomly chosen loci in chromosome 18 are bound to the periphery, this is enough to cause its heterochromatin to form adjacent to the boundary. At a single such binding location for every 0.5 Mb, this is roughly an order of magnitude fewer then the average gene density of the human genome (using the rough estimate of 20,000 genes in the human genome). Alternatively, such an interaction could apply to more than 150 loci with a weaker binding affinity.

The HP1-H3K9me3 interaction is unlikely to be the only mechanism causing densification of chromatin. Variations in other marks such as histone tail acetylation (48) and H3K27me (21) may also contribute to the peripheral placement of chromatin in this way. Indeed, our hypothesis predicts that any mechanism compacting chromatin (epigenetic or otherwise) should cause preferential localization to the nuclear periphery, affording a route for experimentally testing our hypothesis.

The ability to relocate heterochromatin need not apply only to the nuclear periphery. Any nuclear object to which chromatin is attracted or to which some loci are anchored could act as a condensation surface for heterochromatin. Aside from the nuclear confinement, the most prominent such object is the nucleolus. It is therefore not surprising that the nucleolus is also typically surrounded by heterochromatin. Indeed, although LADs are primarily known for their peripheral localization, they are also associated with the nucleolus (15).

Throughout this article, we argue that an interaction with the nuclear periphery (or nucleolus) need not be specific to heterochromatin to cause heterochromatin to be relocated there. Although not strictly necessary, it is entirely possible that heterochromatin-specific interactions with the nuclear envelope exist in at least some organisms. For example, a protein may have evolved to preferentially attach H3K9me3-marked histones or HP1 to the lamina. What we have shown is that a significantly less restrictive set of proteins or mechanisms—almost anything that attracts or binds DNA or any chromatin protein to the periphery—would suffice. Even in the presence of heterochromatin-specific interactions, it is important to recognize the contribution of nonspecific, density-based interactions for a number of reasons: 1) even in a cell where a heterochromatin-specific interaction causes peripheral heterochromatin, any other mechanism that condenses a region of the genome can cause the region to be relocated to existing heterochromatin, which in turn could cause the region to be silenced; 2) observing that some factor causes the formation of peripheral heterochromatin (or that knocking out the factor eliminates it) does not necessarily mean that the factor has any specificity for heterochromatin; and 3) the search for additional mechanisms that bring heterochromatin to the periphery can be broadened to include ones without specificity for heterochromatin.

Conclusions

In this article, we investigate the effect of an attractive boundary for a system in which H3K9me3-specific HP1 binding causes the formation and densification of heterochromatin. We find that an attractive force between chromatin and the nuclear environment causes peripheral heterochromatin to form along the nuclear periphery. The interaction with chromatin need not be specific to regions high in H3K9me3 for genomic regions high in the mark to be enriched in heterochromatin. In our simulations, the formation of a dense H3K9me3-rich phase at the nuclear periphery is not sensitive to the details of the chromatin chain nor its interaction with the nuclear boundary. Peripheral heterochromatin is generated in the presence of a weak attraction between the periphery and all chromatin as well as when only a random subset of chromatin is bound to the periphery. In the latter case, heterochromatin is found to systematically form at the nuclear periphery even when less than 0.05% of all the nucleosomes are bound to the boundary, demonstrating the ability of a relatively small number of interactions to rearrange the entire nuclear structure.

We focus on heterochromatin formation based on the presence of H3K9me3. We found that the level of methylation of the 101-nucleosome-long genomic region centered at a nucleosome was indicative of whether that nucleosome would be found in proximity to the nuclear boundary. Applying the 101-nucleosome window average to ChIP-seq methylation data (46), we show that it is indeed correlated with lamin B contact (14), as expected for peripheral heterochromatin. In our simulations, we have assumed a fixed H3K9me3 profile based on ChIP-seq data (31). However, the spreading of the mark to neighboring nucleosomes has been observed (49), suggesting a cycle in which both H3K9me3 causes peripheral organization, and the heavily H3K9-methylated environment of peripheral heterochromatin methylates nucleosomes that are relocated there. This is of great interest for future work.

Finally, we emphasize that although the interaction we introduce here is based on HP1 binding to H3K9me3-marked tails, this need not be the only source of chromatin compaction. Our results suggest that peripheral relocation can result from any interaction that densifies chromatin, epigenetic or otherwise, natural or experimentally induced.

Author Contributions

Q.M. implemented code, ran simulations, and performed analysis. Q.M., B.B., and A.J.S. wrote the manuscript.

Editor: Tamar Schlick.