Abstract
Migratory cells exhibit a variety of morphologically distinct responses to their environments that manifest in their cell shape. Some protrude uniformly to increase substrate contacts, others are broadly contractile, some polarize to facilitate migration, and yet others exhibit mixtures of these responses. Prior studies have identified a discrete collection of shapes that the majority of cells display and demonstrated that activity levels of the cytoskeletal regulators Rac1 and RhoA GTPase regulate those shapes. Here, we use computational modeling to assess whether known GTPase dynamics can give rise to a sufficient diversity of spatial signaling states to explain the observed shapes. Results show that the combination of autoactivation and mutually antagonistic cross talk between GTPases, along with the conservative membrane binding, generates a wide array of distinct homogeneous and polarized regulatory phenotypes that arise for fixed model parameters. From a theoretical perspective, these results demonstrate that simple GTPase dynamics can generate complex multistability in which six distinct stable steady states (three homogeneous and three polarized) coexist for a fixed set of parameters, each of which naturally maps to an observed morphology. From a biological perspective, although we do not explicitly model the cytoskeleton or resulting cell morphologies, these results, along with prior literature linking GTPase activity to cell morphology, support the hypothesis that GTPase signaling dynamics can generate the broad morphological characteristics observed in many migratory cell populations. Further, the observed diversity may be the result of cells populating a complex morphological landscape generated by GTPase regulation rather than being the result of intrinsic cell-cell variation. These results demonstrate that Rho GTPases may have a central role in regulating the broad characteristics of cell shape (e.g., expansive, contractile, polarized, etc.) and that shape heterogeneity may be (at least partly) a reflection of the rich signaling dynamics regulating the cytoskeleton rather than intrinsic cell heterogeneity.
Significance
Migratory cells exhibit a diverse set of shapes and behaviors. To understand the source of this diversity, we develop a computational approach to study the dynamics of a Rho GTPase signaling model. Rho GTPases influence cell shape and polarity through cytoskeletal regulation. We hypothesize that much of the broad shape diversity found in imaging studies may be the result of cells exploring a complex regulatory landscape rather than a result of differences between cells. Results show that known GTPase signaling can produce a variety of distinct regulatory phenotypes for a fixed parameter set. Thus, although numerous factors influence cell morphology, GTPase dynamics on their own can explain much of the broad variation in signaling that eventually affects cell shape.
Introduction
It is well documented that similar cells from a single population exhibit different morphologies (shape in particular (1,2)) and behaviors (amoeboid versus mesenchymal migration (3)). Where does this diversity come from? One possibility is that the cells are functionally different, possibly differing in their gene expression, protein activity levels, or cytoskeletal factors that determine the cells’ structure. Another is that the cells are similar but that we observe their exploration of a complex morphological state space. In this article, we utilize a new, to our knowledge, computational modeling approach to assess whether and to what extent the dynamics of a crucial class of cytoskeletal regulators, the Rho GTPases, may explain shape diversity in migratory cells.
Numerous factors will influence cellular morphology. Biophysical properties such as membrane tension and cortical stiffness will affect bulk cell characteristics. Keratocyte morphology, for example, can be explained exclusively by interactions between F-actin force production and resistive membrane tension (4,5). Genetic factors will strongly influence cell morphology; neurons and migratory cells are vastly different, and epithelial to mesenchymal transitions significantly alter a cell’s morphology. Environmental structure will influence cell morphology as well (two-dimensional (2D) versus three-dimensional (3D) environments or fibrous versus nonfibrous environments). Cytoskeletal signaling will also play a role by regulating cellular remodeling.
With all of these influential factors, one might expect a nearly continuous space of diverse morphologies. This does not, however, appear to be the case. At a high level, genetics seems to predispose cells to take on particular characteristics (e.g., neuronal versus epithelial versus migratory). Within these broad classes, cells seem to exhibit a discrete collection of morphologies. For example, cultured Drosophila hemocytes can be classified as a heterogeneous mixture of five discrete shapes (normal, elongated, large ruffled, teardrop, and large smooth) (6). Drosophila BG-2 (our main focus here) cells were shown to exhibit seven shapes varying in size and type of polarization (2). Melanoma cells in 3D matrices can exhibit either mesenchymal or amoeboid modes of migration and also demonstrate a mixture of six different shapes (star, spindle, teardrop, ellipse, small round, and large round) (7).
This discrete, relatively restricted set of morphologies has led to the proposition (8) that there may be a common mechanism underpinning cell shape determination that gives rise to a relatively simple morphological landscape where biophysical and environmental forces act to tune the landscape. Here, we demonstrate that Rho GTPase signaling, which is known to be central to cytoskeletal regulation (9), can explain much of the heterogeneity observed in cell populations and thus may be a core element of this common mechanism.
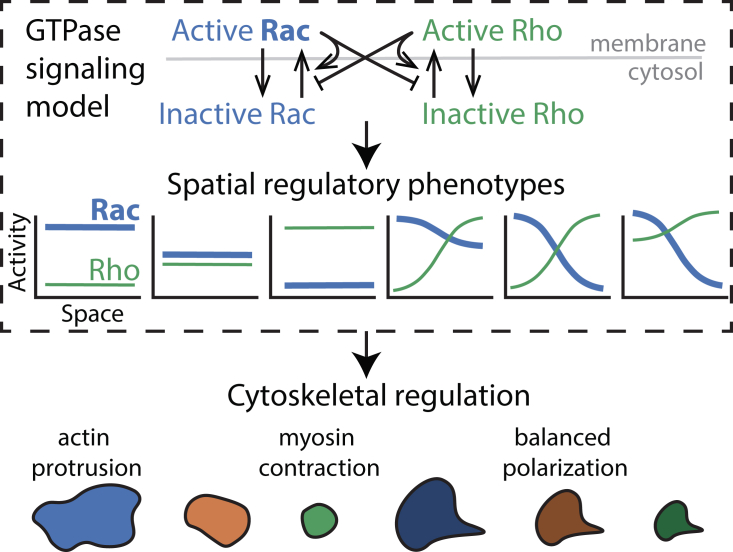
Rho GTPase proteins are known to be central regulators of cytoskeletal remodeling across eukaryotic species (10) and contribute to cell migration in many animal model organisms (9). Cell shape, protrusiveness, polarization (2), and mode of migration (3,11) have all been causally linked to Rac1 and RhoA GTPase activity levels (henceforth Rac and Rho). Broadly, Rac activity is associated with actin polymerization and cellular protrusion, whereas Rho activity is associated with actomyosin contraction (9,12). For this reason, GTPase activity levels have been linked to cell shape (Fig. 1). Cells that have high levels of Rac and little Rho are spread out and flat, those that have low levels of Rac and high Rho are contracted, and those with more balanced Rac and Rho levels are more neutrally sized, being neither obviously protrusive nor contractile (2). Additionally, polarized shapes are, in many cases, characterized by spatially distinct zones of GTPase signaling: a Rac-dominated protrusive front and Rho-dominated contractile rear (13, 14, 15, 16) (reviewed in (17)).
Figure 1.
Overview of the model and modeling approach. A schematic of the mutual antagonism, autoactivation, and biochemical conservation Rac and Rho GTPase signaling model investigated here is shown. Rac and Rho GTPases exist in active, membrane-bound, slowly diffusing forms and in inactive, cytosolic, quickly diffusing forms. For this model, we analyze the types of spatial GTPase activation profiles (regulatory phenotypes) that arise from PDE simulations (shown in the six plots in the dashed box). We do not explicitly model cytoskeletal remodeling or 2D cell morphology. Rather, we rely on prior literature that has demonstrated links between cell shapes and GTPase signaling through cytoskeletal regulation. For example, Rac-dominated cells expand and protrude because of actin assembly, Rho-dominated cells contract because of myosin-based contraction, and spatially organized Rac and Rho signals lead to polarized cells. The bottom row of cartoons depicts different shapes that would naturally be linked to different GTPase signaling profiles. The box around the GTPase model and spatial activation profiles indicates that this is the focus of this article, whereas the shape morphologies outside of this box are inferred and not directly modeled. To see this figure in color, go online.
Given their central role in regulating the cytoskeleton, Rho GTPases have been the source of intense investigation since their discovery. Nearly three decades of research (9) have led to a picture in which these proteins sit at the center of larger signaling network involving interactions with a host of signals (18), the extracellular matrix (19), mechanical forces (20), and membrane tension (21). In addition, Rho GTPases have been demonstrated to regulate each other’s activity; they mutually antagonize each other (18,22) and autoactivate themselves (23). Here, we use mathematical modeling to explore the consequences of these feedback mechanisms between Rho GTPases (independent of the larger signaling web and the myriad physical interactions) on the types of spatial distributions of protein activation that form the foundation of cytoskeletal regulation.
Mathematical and computational modeling have long been used to investigate the role of GTPases on cell dynamics (see, for example, (24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34) along with (35, 36, 37, 38, 39) for reviews). The “wave-pinning” (WP) model (40, 41, 42) of GTPase dynamics demonstrated that the combination of nonlinear feedback (such as autoactivation or mutual antagonism) along with mass-conserved (un)binding dynamics explains many aspects of polarization. More recently, (43) showed that this same combination produces protein distributions indicative of a restricted set of observed cell morphologies. Here, we extend this work and use computational modeling to demonstrate that known GTPase dynamics explain a wider diversity of activation profiles then previously shown.
In this article, we use computational modeling to investigate the role of Rho GTPase dynamics in generating a variety of spatial regulatory phenotypes that are associated with cell morphology. Rather than consider the full myriad of biophysical, genetic, and environmental factors that affect cells, we focus on the influence of regulatory Rho GTPase signaling and ask how much of the observed diversity in cell morphology could be explained by signaling dynamics alone? Furthermore, we focus on observations from Drosophila BG-2 cells (2), which provide a representative sample of stable morphologies commonly observed in many cell types. To be clear, shape is a complicated morphological feature of a cell. For this article, we will focus on two aspects of shape: presence versus absence of polarity and whether the cell is predominantly spreading, contracting, or in a more balanced configuration. We focus on these two features because they represent broad characteristics at the level of the whole cell rather than more detailed or spatially localized characteristics that likely arise from a myriad of interacting processes. We will therefore not consider other features such as ruffling, nuclear location, presence of filopodia, or the many other physical features that contribute to cell shape.
This approach will, of course, limit the scope of results. Cell shape and migration can be explained independently of Rho GTPase signaling in some cases (e.g., keratocytes), and some cells exhibit highly dynamic morphologies that are hallmarks of feedback between signaling and remodeling. Further, the partial differential equation (PDE) modeling approach here is intended to study gross cell characteristics such as size and polarity, although alternative PDE systems could, in principle, model more refined characteristics such as ruffling or filopodia. Nonetheless, this approach yields insights into how GTPase signaling influences cell shape and demonstrates the rich diversity that may arise without these added complexities.
Results show that well-established cross talk interactions between Rac and Rho generate a surprising diversity of spatial protein activation profiles in one dimension and two dimensions. Specifically, a single parameter set can generate complicated multistability in which three homogeneous and three distinct polarized states (all stable) coexist, each of which would be naturally associated with an observed morphology (e.g., a cell with a GTPase distribution that is polarized but dominated by Rac activation throughout would be associated with a large, protrusive, and polarized cell; see Fig. 1 for a schematic). Our computational approach also reveals that the parameter space is structured and that multistable parameter sets are mostly polarizable. This observation leads to the main biological hypothesis of this article: much of the variance in cell shape within a population of cells may be a result of those cells exploring a rich GTPase signaling regulatory landscape rather than being a reflection of intrinsic differences between the cells (e.g., model parameters). Further, this work highlights how well-known Rho GTPase signaling dynamics can act as a central element for generating regulatory phenotypes that influence shape in a variety of cells.
The study is organized as follows. In the detailed Methods, we describe the mathematical details of the model, computational approach, and numerical simulations. In Results, we introduce the GTPase signaling model (Model Background and Description) and summarize the novel, to our knowledge, computational approach (Computational Approach) used to assess the model’s dynamics. We next describe the model’s predictions (The Combination of Mutual Antagonism, Autoactivation, and Biochemical Conservation Leads to a Wide Array of Spatial GTPase Regulatory Phenotypes That Match Known Cell Morphologies), parameter space characterization (Parameter Space Characterization), and the results of numerical bifurcation analysis (Numerical Bifurcation Analysis). In Discussion, we conclude the work. There are also four figures and three simulation videos collected as Supporting Material.
Methods
Here, we describe the spatial mutual antagonism and autoactivation model of GTPase dynamics and provide more detail about our computational approach.
PDE model
A system of reaction-diffusion PDEs is used to model Rac and Rho GTPase activity in the cell. We track the activity of active Rac ((z, τ)) and Rho ((z, τ)) and inactive Rac ((z, τ)) and Rho ((z, τ)). Active forms are bound to and diffuse in the cell membrane, whereas inactive forms are free to diffuse in the cytosol. We consider the spatial domain to be a one-dimensional (1D) slice along the cell’s diameter and assume no-flux boundary conditions. The PDEs governing the GTPase dynamics on z ∈ [0, L] and for time τ ∈ [0, ∞) are
| (1a) |
| (1b) |
| (1c) |
| (1d) |
with no-flux boundary conditions
| (1e) |
Here, DR and Dρ are the diffusion coefficients for active Rac and Rho, and and are the diffusion coefficients of the inactive forms, respectively. Because the active forms are membrane bound, the corresponding diffusion coefficients are much smaller than the inactive forms’ diffusion coefficients. We assume that the inactivation rates, kR and kρ, do not depend on Rac and Rho activity. Instead, we assume that mutual antagonism and autoactivation occur through the activation rates, and Aρ:
| (1f) |
Here, the activation rates are comprised of increasing or decreasing Hill functions with exponent n. The parameters and prescribe the strength of the autoactivation and mutual antagonism, respectively, and is the basal rate of activation in the absence of feedback. The parameters rR,ρ and describe the amount of GTPase needed to reach the half-maximal autoactivation and antagonistic effect on the other GTPase, respectively.
Because the GTPases simply switch between active and inactive forms yet are not created nor destroyed, the activity levels of Rac and Rho must satisfy conservation statements. Indeed, adding and integrating over the domain Eqs. 1a, 1b, 1c, and 1d gives
| (1g) |
Here, and are the mean Rac and Rho activity levels.
To reduce the number of parameters in the model, we scale the GTPase amounts by the corresponding half-maximal autoactivation parameter, time by the deactivation rate of Rac, and space by the cell length:
| (2) |
Under this scaling, the equations become
| (3a) |
| (3b) |
| (3c) |
and
| (3d) |
with x ∈ [0, 1] and t ∈ [0, ∞). The scaled activation rates are
| (3e) |
and the activity levels satisfy the conservation statements
| (3f) |
The scaled parameters are
where ∗ = R or ρ.
Finally, to reduce the complexity of the model, we restrict our attention to the case aR = aρ = a, bR = bρ = b, sR = sρ = s, cR = cρ =c and set k = 1 throughout. We also assume that the diffusion coefficients in the active state and in the inactive state are similar between Rac and Rho GTPases so that DR =Dρ = D and that = Di.
Well-mixed model
In the well-mixed model, we ignore space and consider GTPase activity to be homogeneous within the cell. This reduces the equations to a system of four ordinary differential equations (ODEs), describing the temporal dynamics of GTPase activity.
| (4a) |
| (4b) |
| (4c) |
and
| (4d) |
Note that this system can be reduced to a system of two ODEs, which is more readily studied (for example, in the phase plane), using the fact that the total amount of each GTPase is assumed to be constant. This means that the amount of inactive GTPase, Ri and ρi, can be calculated as Ri = RT − R and ρi = ρT − ρ. The reduced well-mixed model is therefore
| (4e) |
| (4f) |
The steady states of the well-mixed model correspond to homogeneous steady states (HSSs) of the PDE model.
Local perturbation analysis
The local perturbation analysis (LPA), discussed in further detail in (37,44, 45, 46, 47), is an approximation method that facilitates the prediction about how a spatial reaction-diffusion model will respond to spatially heterogeneous perturbations. Specifically, this method is used to assess how an HSS of a PDE system comprised of fast and slow diffusing variables will respond to a spatially localized pulse-like perturbation. The fast or slow diffusion discrepancy is then exploited to describe the evolution of that pulse-like perturbation by a collection of ODEs that describe the evolution of concentrations near to (local variables) and away from (global variables) the perturbation.
Applying this reduction method and using conservation to further simplify the system yields the following equations describing the evolution of the global (R, ρ) and local variables (, ):
| (5a) |
| (5b) |
| (5c) |
and
| (5d) |
Here, the functions AR and Aρ capture the mutual antagonism and autoactivation as before.
This LPA ODE system is used in two ways. First, it is simulated to determine whether a sufficiently large perturbation will yield a response. To do this, we set the initial conditions of the global variables R, ρ to their HSS values (determined by simulating the well-mixed system) and then apply different initial conditions to the local variables and . If the values of and diverge to a new value different from the HSS, this indicates a response has occurred. Otherwise, if the values of and converge back to the HSS, the system is stable with respect to that perturbation. We thus systematically apply an array of perturbations to determine if the system will respond to any of them.
In addition to simulating the LPA ODEs directly, we also apply bifurcation analysis to them to assess parameter space structure with respect to one or two of the parameters (Figs. 3 a and 7). See subsequent sections for further detail on this approach.
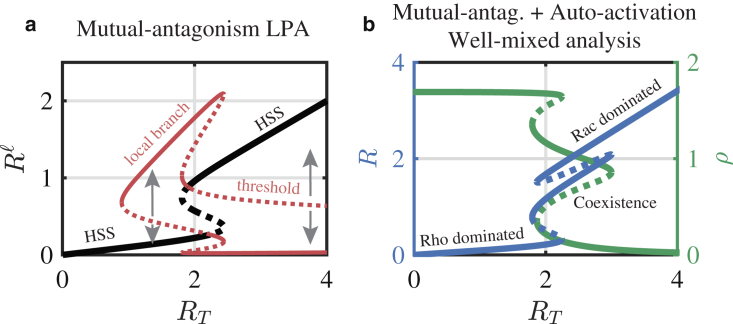
Figure 3.
Bistability, tristability, and polarization. (a) LPA bifurcation analysis of the mutual antagonism model (a = 0, similar to results in (43)) is shown. The global (black curve) and local solution branches (red curve) are shown along with their stability (solid, stable; dashed, unstable). A region of well-mixed bistability is enclosed in a larger region where stimulus induced polarization is possible (via a perturbation across a threshold). Gray arrows illustrate how a local perturbation may induce a response. A perturbation from the HSS may drive system to the local branch or may be insufficient to induce a response. In the former case, the LPA predicts that the perturbation will grow to the local branch driving pattern formation. Note also that as the parameter RT changes, the global branch changes stability at the points where the local branch bifurcates, indicating the possibility for spontaneous pattern when the HSS becomes linearly unstable. Parameters are b = 1, c = 0, s = 0.5, n = 3, and ρT = 2. (b) Well-mixed bifurcation analysis of the mutual antagonism and autoactivation model (a > 0) is shown. Tristability is possible with both autoactivation and mutual antagonism. The middle branch is referred to as the coexistence HSS, with both Rac and Rho activity are at moderate levels. Parameters are a = 1.8, b = 4, c = 0, s = 0.5, n = 3, and ρT = 2. To see this figure in color, go online.
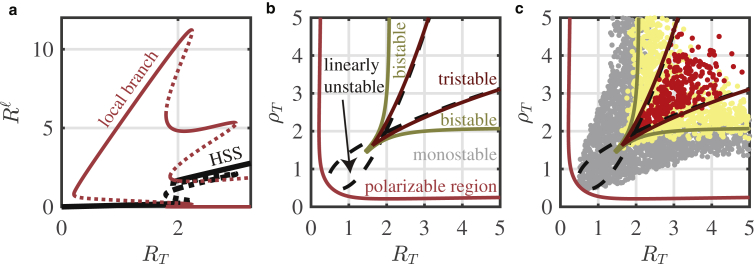
Figure 7.
LPA bifurcation diagrams confirms parameter space structure. (a) The Rac global (black) and local (red) solution branches are plotted with their stability (stable → solid; unstable → dashed) with respect to RT. (a) The tristable regime sits within a region of polarizability. As in Fig. 3a, perturbations across thresholds (dashed red lines) may induce polarization as the local perturbation grows to a value (solid red lines) that differs from the background HSS (black curve). (b) Two-parameter bifurcation diagram of (a) with respect to ρT is shown. The region of tristability sits within a larger region of bistability, which sits within a larger region of polarizability. The red curve is a continuation of the fold bifurcation with the lowest RT of the local solution branch from (a). The dark red and dark yellow curves are fold continuations from the well-mixed branch. The black dashed curves are the continuation of Turing bifurcations (the branch points where the local solution branches bifurcate from the global HSS solution branch). See Methods for further details of the bifurcation analysis. (c) A slice of the 5D parameter space from the PDE screen (Fig. 5, d–f) is plotted in the (RT, ρT) plane. To match the parameters used to produce the bifurcation diagram in (a) and (b), only polarizable parameter sets with 1.3 < a < 2.3, 3.5 < b < 4.5, and 0 < c < 0.025 from the PDE screen are plotted. Red points: tristable and polarizable parameter sets. Yellow points: bistable and polarizable. Gray points: monostable and polarizable. Parameters used are listed in Numerical Bifurcation Analysis. To see this figure in color, go online.
Computational approach details
We want to understand how GTPase dynamics depend on the parameters in the mutual antagonism and autoactivation model. To efficiently produce a near-uniform sample of the five-dimensional (5D) parameter space of interest, {(a, b, c, RT, ρT) ∈ 5 | 0 ≤ a, b, RT, ρT ≤ 5 and 0 ≤ c ≤ 0.25}, we used MATLAB’s (The MathWorks, Natick, MA) Latin hypercube sampling command with N = 106 sample points and the default settings. For each parameter set, we then successively used well-mixed analysis, LPA, and PDE numerics to understand the spatial GTPase dynamics. Note that the restriction of c < 0.25 is made because larger values of c produce uninteresting, monostable dynamics as a result of the dynamics becoming more linear in nature.
First, we used the well-mixed model to find the HSSs of the PDE system. To determine the HSSs, it is sufficient to determine the steady states of the well-mixed model. To do so, we used a Latin hypercube sampling method to generate 50 initial conditions (R0, ρ0) in the range 0 ≤ R0 ≤ RT and 0 ≤ ρ0 ≤ ρT. Using these initial conditions, we then numerically solved the well-mixed model forward in time to t = 100 for each initial condition (IC). Using the value at t = 100 as a new initial condition, we repeated this integration three times in an effort to improve the accuracy of the steady state. Next, we classified each parameter set as monostable, bistable, or tristable based on the number of unique (within a tolerance = 10−6) steady states found for each parameter set. Because the computational method (MATLAB’s uniquetol function) can only distinguish steady states within a fixed numerical tolerance, it is possible that the method reports the wrong number of steady states instead of the true number of steady states. For example, some parameter sets that are classified as bistable may truly be monostable despite the computational method finding two nearby steady states that differ only slightly more than the chosen numerical tolerance. For the same reason, the method may report more than three steady states for a given parameter set. In this case, the parameter set may indeed have more than three parameter sets, or it may not. Morever, we expect multistability (i.e., more than three steady states) with the mutual antagonism and autoactivation circuit for very select parameter values. We found 285 parameter sets (out of 106) to have more than three steady states. We ignored these parameter sets for our investigation because they are relatively rare (and therefore likely not representative of dynamics) in the parameter space sampled.
Second, we used LPA to determine whether the parameter set could support a polarized regulatory phenotype. For each parameter set, we use the LPA ODEs to characterize the LPA stability of each of the HSS. If all eigenvalues of the Jacobian matrix of the LPA ODE system evaluated at an HSS all have negative real part, the HSS is called LPA stable. If at least one of eigenvalues has positive real part, the HSS is called LPA unstable. For those HSSs that are LPA stable, we simulated a spatially localized pulse by perturbing the initial conditions of the local variables in the LPA ODE system. That is, we chose initial conditions for the local variables in the LPA ODE system and to be perturbations from the HSS, (Rss, Riss, ρss, ρiss), and for the global variables to be the HSS values. We considered both large and small multiplicative perturbations for initial conditions for the local variables. Large perturbations were defined as = 10Rss and = Rss/10, and small perturbations as = 2Rss and = Rss/2 (similar for Rho). We considered all 16 possible combinations of these local perturbations as initial conditions and recorded whether the LPA ODE system returned to the HSS or was attracted to a different steady state. If the LPA ODE system is attracted to a different steady state that is not another one of the other HSSs found by well-mixed analysis for any of the HSSs found for a given parameter set, we called that parameter set “polarizable (stimulus required)” (as in Fig. 6, a–c; Table 1). Moreover, we distinguished between those parameter sets that are polarizable with stimuli of different sizes as in Fig. 6, g–i. Those parameter sets that are polarizable with a small stimulus are shown as yellow points in Fig. 6, g–i, and those parameter sets that are polarizable with a large stimulus are shown as black points in Fig. 6, g–i. Those parameter sets that have at least one HSS that is LPA unstable are considered “polarizable (linearly unstable)” (Table 1) and are shown as red points in Fig. 6, g–i.
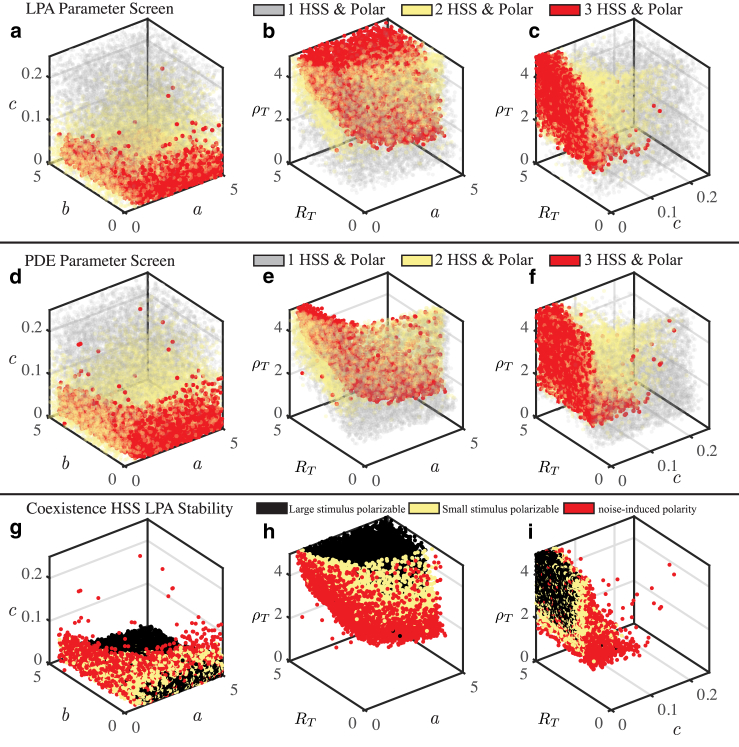
Figure 6.
Unsupervised simulation screen reveals a nested parameter space structure. Each point represents a sample from the Latin hypercube sample, so that each point has unique values of a, b, c, RT, and ρT. Each panel shows a 3D projection of the 5D parameter space. (a–c) The LPA parameter screen reveals parameter space structure, with tristable polarizable (red) parameter sets nested inside bistable polarizable (yellow) parameter sets nested inside a large region of monostable polarizable (gray) parameter sets. Nonpolarizable monostable parameter sets are not plotted. These parameter sets would fill out the empty space in (a)–(c). (d–e) The PDE Parameter Screen confirms the parameter space structure predicted by the LPA (plotting conventions as in a–c). (g–i) For each tristable parameter set, the level of stimulus (none, small, large) required to elicit a polarization response from the coexistence HSS is shown. For yellow points, a stimulus double or half the value of the HSS active protein concentration yields a response. For black points, a stimulus greater than 10 times or one-tenth the value of the HSS concentration yields a response. When the coexistence HSS is LPA unstable (red points), any perturbation away from the coexistence HSS may result in polarization. Other parameters are s = 0.5 and n = 3. To see this figure in color, go online.
Table 1.
Well-Mixed, LPA, and PDE Parameter Screen Results
| Parameter Sets | Polarizable (Stimulus Required) | Polarizable (Linearly Unstable) | Not Polarizable | ||
|---|---|---|---|---|---|
| LPA Screen | Monostable | 890,309 | 66.3% | 10.4% | 23.3% |
| Bistable | 90,305 | 55.7% | 44.3% | 0% | |
| Tristable | 19,101 | 84.3% | 15.7% | 0% | |
| PDE Screen | Monostable | 890,309 | 18.8% | 8.0% | 73.2% |
| Bistable | 90,305 | 30.6% | 36.6% | 32.8% | |
| Tristable | 19,101 | 22.7% | 11.3% | 66% |
From an initial 106 parameter sets, the number of mono-, bi-, and tristable sets was determined (285 parameter sets were omitted; see Computational Approach Details for details). “Polarizable (stimulus required)” refers to parameter sets that require a sufficiently large perturbation from an HSS to polarize. “Polarizable (linearly unstable)” refers to those parameter sets that are LPA unstable (LPA Screen) or those parameter sets that are unstable with respect to noise around one or more HSSs in the PDE Screen. “Not Polarizable” refers to parameter sets that did not polarize using our numerical parameters and initial conditions.
Third, we repeated the parameter screen with PDE numerics. With PDE numerics, we sought to determine 1) whether or not a given HSS is observable (stable with respect to noise) and 2) whether a polarized pattern is a steady state of the PDE system. To assess 1, we used each HSS as an initial condition but added noise to the active GTPase forms R and ρ and checked for a polarized pattern. Noisy initial conditions were generated by uniformly choosing two random numbers r1 and r2 from the interval (−0.1, 0.1) and adding r1 to the HSS R-value and r2 to the HSS ρ-value. We maintained mass conservation by subtracting r1 from the HSS Ri-value and r2 from the HSS ρi-value. If one or more HSSs were unstable with respect to noise, we called this parameter set “polarizable (linearly unstable)” (as in Table 1). To assess 2, we generated a polarized initial condition with R = RT and ρ = 0 for 0 ≤ x ≤ 0.5, R = 0 and ρ = ρT for 0.5 < x ≤ 1, Ri = RT/2, and ρi = ρT/2. If a polarized pattern results, we say this parameter set is “polarizable (stimulus required)” (as in Table 1); otherwise, we say this parameter set is not polarizable. For all PDE numerics, we used MATLAB’s pdepe function with default parameters Δx = 1/200, Δt = 1/400, and integrated until time t = 400. To check whether a polarized pattern results, we computed the absolute difference between the maximum and minimum for both GTPases. If this absolute difference is sufficiently large (tolerance = 0.01), we consider the pattern to be polarized.
Numerical bifurcation analysis
Here, we describe the methods used to produce Figs. 3 and 7. All numerical continuation was performed using MatCont (48) in MATLAB.
We applied standard numerical bifurcation analysis to the LPA ODEs (4.5) with a = 0 to produce Fig. 3 a. Bifurcation analysis of the well-mixed model ((4a), (4b), (4c), (4d), (4e), (4f)) was applied with a > 0 to produce Fig. 3 b. We produced Fig. 7 a using the LPA ODEs ((5a), (5b), (5c), (5d)) with parameters as in Fig. 3 b. Note that 1) the local branches (shown in red) have a fold (saddle node) bifurcation for small values of RT, 2) the global HSS branch (shown in black) has fold bifurcations (seen clearly as the points where the blue curve changes direction and stability in Fig. 3 b), and 3) Turing bifurcations where the local branches bifurcate from the global HSS solution branch (black curves).
To gain more insight into the structure of the broader parameter space, we performed a two-parameter bifurcation analysis to track the critical bifurcations found in Fig. 7 a. Results are shown in Fig. 7 b and copied over to Fig. 7 c without change to compare with results from the PDE simulation screen. We produced the boundary of the polarizable region (the red curve in the two-parameter bifurcation diagram in Fig. 7 b) by numerically continuing the fold bifurcation on the local branch with the lowest RT from Fig. 7 a in the RT-ρT plane. We numerically continued the fold bifurcations from the global branch in Fig. 7 a to produce the curves that bound the bistable and tristable regimes in Fig. 7, c and d. These fold bifurcations each form an unbounded “triangle” in the RT-ρT plane with a cusp bifurcation at the lower left corner. Those points in the intersection of these two “triangles” form the tristable regime (bounded by dark red curves), and those points in one “triangle,” but not the other, form the bistable regime. Finally, to produce the linearly unstable loop (black dashed curve) in Fig. 7 c, we numerically continued the Turing bifurcations from Fig. 7 a.
Numerical methods for PDE simulations
To produce Fig. 4, we used MATLAB’s pdepe function with default parameters, Neumann boundary conditions, Δx = 1/400, Δt = 1/1000 and integrated until time t = 1000. We used homogeneous initial conditions for active and inactive GTPases, with a local perturbation added or subtracted from the homogeneous initial condition for 0 ≤ x ≤ 0.1. To ensure mass conservation, the area of any perturbation added to the active forms is subtracted from the inactive forms: R = Rss + Rperturb for 0 ≤ x ≤ 0.1, R = Rss otherwise; ρ = ρss + ρperturb for 0 ≤ x ≤ 0.1, ρ = ρss otherwise; Ri = RT − Rss − Rperturb/10; and ρi = ρT − ρss − ρperturb/10. In Fig. 4 a, Rss = 1.4230, ρss = 0.0764, Rperturb = 4.2362, and ρperturb = −0.0764; Fig. 4 b, Rss = 1.3655, ρss = 1.3856, Rperturb = 4.8109, and ρperturb = −1.3856; Fig. 4 c, Rss = 0.0740, ρss = 1.4422, Rperturb = −0.0740, and ρperturb = −1.4422; Fig. 4 d, Rss = 1.4230, ρss = 0.0764, Rperturb = −0.0082, and ρperturb = 4.4212; Fig. 4 e, Rss = 0.0740, ρss = 1.4422, Rperturb = 17.7256, and ρperturb = −1.4422; and Fig. 4 f, Rss = 0.0740, ρss = 1.4422, Rperturb = 4.3759, and ρperturb = −0.0178.
Figure 4.
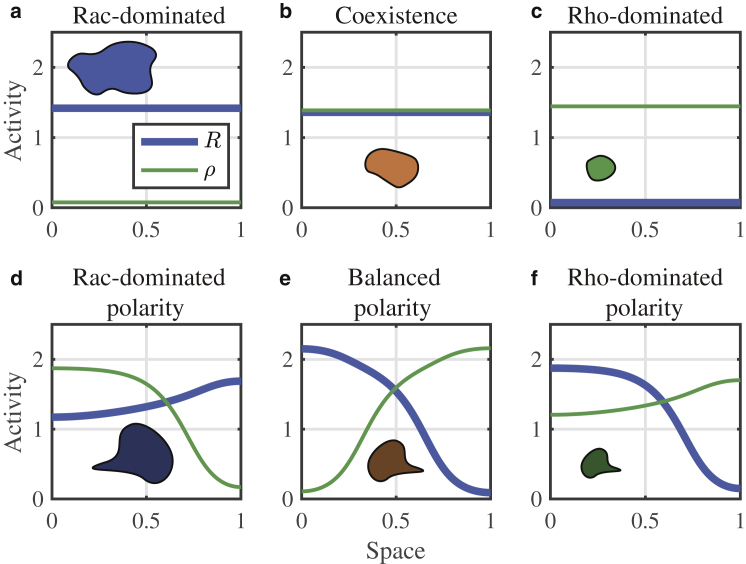
Example PDE simulations of diverse protein activation states from a single parameter set. (a) Rac-dominated HSS is shown. (b) Coexistence HSS is shown. (c) Rho-dominated HSS is shown. (d) Rac-dominated polarity is shown. (e) Balanced polarity is shown. (f) Rho-dominated polarity is shown. All panels are simulated from the same parameter set: a = 3.8941, b = 0.4476, c = 0.0223, RT = 1.8466, ρT = 1.8678, s = 0.5, n = 3, D = 0.01, and Di = 10 (chosen as a representative set from the parameter screen in Parameter Space Characterization). Inset cartoons link GTPase activity distributions to a different cell morphology (e.g., large nonpolar in a or small and polarized in f). For details on numerical methods and initial conditions, see Numerical Methods for PDE Simulations. To see this figure in color, go online.
To produce the 2D simulations in Fig. 5, we used a time-dependent finite element method, implemented in FEniCS (49), to simulate the analogous 2D version of (6a), (6b), (6c), (6d) in a circular domain of area 1. For time stepping, we used an implicit-explicit scheme (Crank-Nicolson for time stepping, with an explicit reaction term), similar to the method used in (50). A triangular mesh was generated for each simulation with the FEniCS parameter “mesh resolution” = 40, Δt = 0.001, and the total time t = 50. Parameters and initial conditions are as in Fig. 4, d–f for Fig. 4, a, b, and c, respectively, except Rperturb = 4.3759 for Fig. 4 b. Initial perturbations were applied in a π/2 radians sector pointing “north.” Inactive GTPase activity levels were adjusted correspondingly to maintain mass conservation upon local perturbation (Fig. 5 b uses different initial conditions than Fig. 4 e because there is insufficient inactive GTPase activity to apply a perturbation of the same amplitude over the quarter circle and maintain positive mass).
Figure 5.
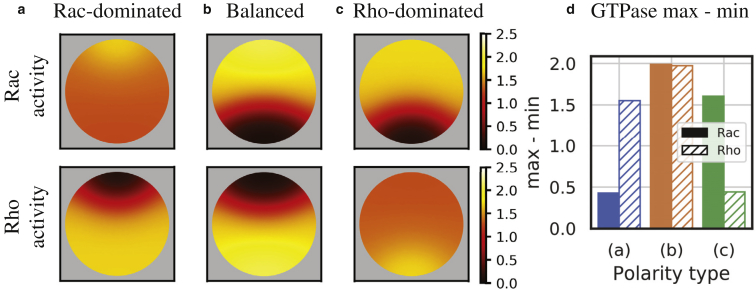
Example PDE simulations of diverse GTPase regulatory phenotypes from a single parameter set in a 2D domain. Top panels: steady-state Rac activity; bottom panels: steady-state Rho activity. (a) Rac-dominated polarity is shown. (b) Balanced polarity is shown. (c) Rho-dominated polarity is shown. (d) Quantification of GTPase spatial gradient strength for each regulatory phenotype is shown (the difference between maximal GTPase activity and minimal GTPase activity from each panel). Parameters are the same as in Fig. 4. See Videos S1, S2, and S3 for animations. For details on numerical methods and initial conditions, see Numerical Methods for PDE Simulations. To see this figure in color, go online.
Data availability
All code and data (including code to make the figures) are available as an archived GitHub repository at https://doi.org/10.6084/m9.figshare.9176252.
Results
Our goal here is to study the consequences of known GTPase dynamics (Fig. 1) to determine the extent to which they may generate a variety of spatial activation profiles, referred to as “regulatory phenotypes,” that can influence cell shape. Toward this end, we study a spatiotemporal model of GTPase dynamics that incorporates the primary known characteristics of Rac and Rho dynamics: autoactivation, mutual antagonism, and conservation (Fig. 1). Numerous past investigations have studied the temporal dynamics of this canonical mutual antagonism and autoactivation system (51, 52, 53). This study differs from such prior studies of this motif in two ways. First, it focuses on spatial dynamics in the context of cell polarity. Second, we incorporate biochemical conservation, which is known to be a vital aspect of Rho GTPase dynamics that leads to the formation of new spatiotemporal behaviors such as wave-pinning (32,40, 41, 42,54). To characterize the spatiotemporal behaviors of this mutual antagonism, autoactivation, and conservation system in a systematic fashion, we use a multifaceted approach combining well-mixed analysis, LPA (37,44, 45, 46, 47), and PDE simulation with unsupervised parameter space screening (Fig. 2).
Figure 2.
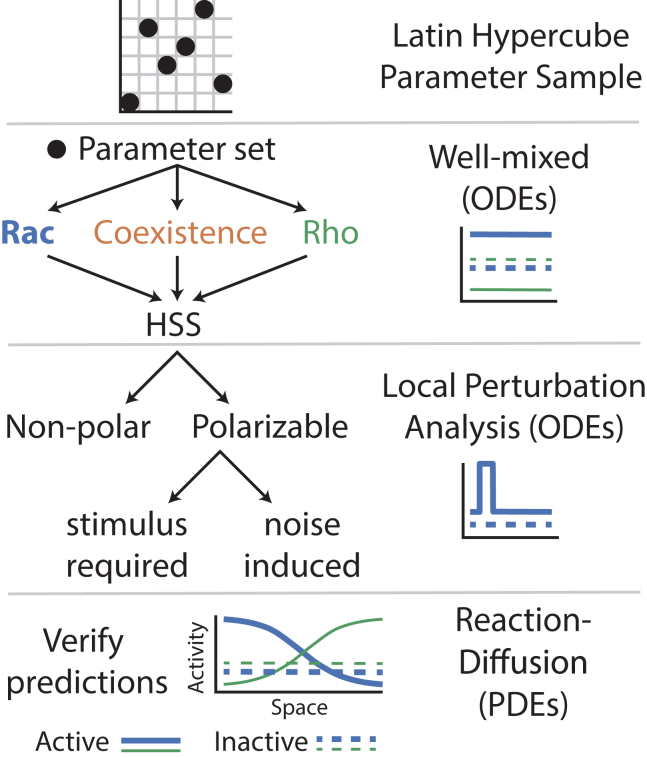
Overview of computational approach to assess the GTPase signaling model’s dynamics and parameter space structure. Latin hypercube sampling is used to obtain a computationally efficient sample of five-dimensional (5D) parameter space. For each parameter set, we use well-mixed analysis (based on ODE integration) to first determine the number and possible homogeneous steady states (HSSs). Next, we use the local perturbation analysis (LPA) to efficiently assess the nonlinear stability of each HSS and classify each parameter set as nonpolar or polarizable. Polarization may result from a spatially localized stimulus (depicted as a pulse-like stimulus from the HSS) or from noise (if the HSS is linearly unstable). Lastly, we use numerical simulations of the reaction-diffusion PDEs to verify the predictions of the well-mixed and LPA methods. To see this figure in color, go online.
Note that although our intention is to investigate links between GTPase signaling dynamics and cell morphology, we have chosen not to simulate full moving and deforming cells. Instead, we approach this problem from the perspective of investigating spatial GTPase activity, which has been causally linked to morphology ((2,9,12, 13, 14, 15, 16, 17), etc.). For this reason, we associate GTPase activity levels to cell shape (Fig. 1) through known cytoskeletal regulation pathways. Full dynamic cell simulations would require numerous assumptions that are, at this point, not well informed by data (to our knowledge). For example, although it is known that Rac and Rho activity are associated with protrusive and contractile forces in isolation, what happens when both are highly activated in a region of the cell? When a cell expands because of protrusion, is cell volume or membrane surface area conserved? How does tension influence signaling (if at all)? To focus on the role of signaling in influencing morphology, we consider only static cell phenotypes (fixed domains from a modeling and simulation perspective) and leave these questions for subsequent studies.
Model background and description
This study is inspired by and bridges two primary bodies of literature regarding cell polarity regulation and multistability in gene regulation. Studies of cell polarity (40, 41, 42, 43) have revealed that the combination of GTPase conservation and either mutual antagonism or autoactivation leads to a novel type of dynamic referred to as wave-pinning (WP). These WP dynamics are characterized by reaction-diffusion traveling waves that become “pinned” in the domain, generating a region of high GTPase activity and a region of low GTPase activity. These regions form a polarized pattern with “front” and “rear” corresponding to regions of high and low activity, respectively. Fig. 3 a demonstrates (using a relatively new method, the LPA, which is described further in Methods) that the combination of mutual antagonism and GTPase conservation can lead to a set of spatial Rho GTPase activation profiles including uniformly Rac-activated, uniformly Rho-activated, or polarized states. In this figure, the black bifurcation branch illustrates well-mixed solutions of this model (and their stability) as a function of the amount of total Rac in the mutual antagonism system (RT). In LPA terms, this is referred to as a “global branch” because it represents solutions that are globally uniform. The red branch provides information about spatial pattern formation. In short (further details about the LPA can be found in the explanatory article (46)), the mere presence of these red branches indicates the potential for pattern formation. These are referred to as “local branches” in LPA terms because they provide information about how the system will respond to spatially localized, pulse-like perturbations. The solid red branches represent different states that a spatially localized, pulse-like perturbation can attain, and the dashed red lines represent response thresholds that a perturbation must exceed to elicit a response. For example, consider the roughly RT = 1.5 state. Here, there is a single HSS. However, the red branches indicate that if a perturbation is applied that raises the local activation levels above the dashed red line, they will be attracted to the solid red line. This indicates the potential for a patterning response because one part of the spatial domain may achieve a higher activation level than the rest of the domain. Further inspection of Fig. 3 a thus suggests that there is a regime of parameter space where polarized states coexist with both low-Rac and high-Rac well-mixed steady states (see (43) for a complete bifurcation diagram).
The cell polarity literature has not considered the consequences of both autoactivation and mutual antagonism jointly acting on the formation of polarized signaling patterns. On the other hand, the simple tristable circuit comprised of mutual antagonism and autoactivation has been extensively studied in gene expression literature (51, 52, 53). Fig. 3 b illustrates a typical well-mixed bifurcation diagram showing the well-known tristability in this system (i.e., for intermediate values of RT, there are three stable HSSs). Much of this literature has focused on temporal aspects of this system and, because much of this work is related to gene regulation, does not consider the consequences of biochemical conservation.
We study the spatiotemporal consequences of all three of these elements (mutual antagonism, autoactivation, and biochemical conservation) regulating cell dynamics, all of which are pertinent to GTPase signaling. Toward this end, we thus consider a PDE model of this system utilizing standard Hill function representations of feedback pathways:
| (6a) |
| (6b) |
| (6c) |
and
| (6d) |
Here, we model the GTPase activity in a 1D domain (0 ≤ x ≤ 1) with no-flux boundary conditions, representing an averaged cross section of a cell without the distinction of membrane and cytosol (motivated by previous work that explains how an averaged 1D model is sufficient to account for cell geometry, the membrane, and the cytosol (38)). R(x, t) and ρ(x, t) are the slowly diffusing (D) membrane-bound active forms of Rac and Rho GTPase, and Ri(x, t) and ρi(x, t) are the freely diffusing (Di) cytosolic inactive forms. Because the GTPases simply switch between active and inactive forms with no production or degradation on the timescales of interest, the total amount of each GTPase is conserved: and . The activation rates (terms in parenthesis) capture the feedback between GTPases: a is the strength of the autoactivation, b is the strength of the mutual antagonism switch, s gives the value of GTPase for which half-maximal mutual antagonism occurs, c is the baseline activation rate of GTPase, and n prescribes the “steepness” of each Hill function (as n → ∞, these functions approach sharp on-off switches). For simplicity, the parameters a, b, c, s, and n are assumed to be the same for Rac and Rho, and the system has been nondimensionalized so that the half maximum of the autoactivation Hill function is 1 and the deactivation rates are 1. See Methods for full model details.
Computational approach
The goal of this study is to broadly characterize the different steady-state spatial distributions of activated GTPase concentrations arising from this model. Rather than simply choose a representative parameter set to study, we have developed an efficient approach to map spatiotemporal regimes of behavior of this system throughout parameter space. This is a multifaceted approach that combines the use of well-mixed analysis, LPA (a relatively new nonlinear perturbation analysis method), and PDE simulation to perform an unsupervised screen of parameter space.
To characterize the model behavior, we use Latin hypercube sampling to generate a computationally efficient sample of high-dimensional parameter space (Fig. 2). For each parameter set, we utilize three methods of analysis that provide increasingly more refined information about the model’s dynamics. 1) Well-mixed analysis is used to determine what kinds of spatially HSSs are present, e.g., Rac dominated, coexistence, or Rho dominated. 2) The LPA is used to rapidly assess whether nonuniform steady states (e.g., polarization) are expected. This is a highly efficient approximate nonlinear perturbation analysis that predicts whether the model responds to a sufficiently large perturbation and give rise to a spatial pattern. 3) Finally, PDE simulation is used to check for and determine the nature of pattern formation. This multifaceted approach combines all three methods into a coherent computational framework. For a detailed description of each of these methods, see Methods.
The combination of mutual antagonism, autoactivation, and biochemical conservation leads to a wide array of spatial GTPase regulatory phenotypes that match known cell morphologies
Before broadly characterizing the parameter space dynamics of this model, we first illustrate the types of states this system elicits and discuss how those map onto previously observed cell morphologies. For a single parameter set, a system comprised of mutual antagonism and autoactivation can elicit three or even four distinct, stable well-mixed states. Alternatively, either of these feedback mechanisms in conjunction with biochemical conservation is known to yield coexistence of uniform and polarized steady states (43). We thus hypothesize that the combination of all three may yield a variety of diverse stable spatial protein distributions, each of which corresponds to a distinct cell morphology.
PDE simulation results for select parameter sets show that this is indeed the case (Fig. 4). Fig. 4, a–f demonstrate that for a single parameter set, three possible HSSs, along with multiple polarized states, are stable. Each of these regulatory phenotypes can be associated with a cell morphology through known cytoskeletal regulation, as shown by the inset cartoons in Fig. 4. Given the propensity for Rac to generate protrusion and Rho contraction, Rac-dominated states would be associated with large spreading cells, and Rho-dominated states with small contracting cells. Alternatively, the state in which both are at moderate levels would be associated with a balanced rest state that is neither overly protrusive nor contractile. Importantly, this simple system can give rise to each of these protein distributions for a single parameter set.
Surprisingly, these results also show that in addition to producing multiple well-mixed states, a single parameter set can produce multiple distinct polarized states. Fig. 4, d–f illustrate that for a single parameter set, multiple polarized patterns are stable. The heterogeneous states Fig. 4, d–f would be associated with a polarized cell that protrudes on one side and contracts on the other. Although each of those three states are polarized, they are distinct. In the case of Fig. 4 d, a uniformly high-Rac but still polarized state would be associated with a large, broadly protrusive but polarized morphology. The uniformly low-Rac, polarized state in Fig. 4 f would be associated with a smaller, more contracted polarity state. Finally, the more balanced polarity state in Fig. 4 e would correspond to an intermediate polarized state. Importantly, each of these polarity states stems from a single parameter set.
Each of the three polarity states are the endpoint of numerical simulations and thus they should be stable attracting states. To verify this, we performed additional PDE simulations. For the fixed parameter set (the ones used in Fig. 4), we simulated a collection of 25 initial conditions representing pulse-like perturbations of a homogeneous state. Each consisted of a uniform profile on the interval 0.1 < x ≤ 1 with either an elevated or depressed value for the active Rac or Rho on the interval 0 ≤ x ≤ 0.1. Five different values of Rac and Rho perturbations were considered respectively, leading to 25 total perturbations. PDE simulation results (Figs. S1–S3) show that with this array of initial conditions, each of the six steady states shown in Fig. 4 occur for multiple initial conditions, suggesting that these six steady states are attractors. This does not, of course, rule out the existence of other steady-state solutions.
To further illustrate that these polarized patterns are stable attracting states, we numerically simulated the PDE system in a circular 2D domain. For the same set of parameters in Fig. 4, multiple polarized GTPase distributions are stable in a circular 2D domain. Fig. 5 shows the steady-state spatial GTPase activities in a Rac-dominated (Fig. 5 a), balanced (Fig. 5 b), and Rho-dominated (Fig. 5 c) polarization pattern (the HSSs from Fig. 4, a–c are easily obtained and are therefore not shown). Quantifying the difference between the maximal and minimal Rac and Rho GTPase activity illustrates (Fig. 5 d) the steepness of the polarized gradient for each of the observed polarities matching the distributions found in the 1D simulations shown in Fig. 4. See Videos S1, S2, and S3 for animations of the polarization patterns in Fig. 5, a–c. With additional mathematical modeling to incorporate relevant biophysical properties and cellular behavior, it could be possible to connect the active GTPase distributions to cell shape changes; however, we leave this challenging task to future studies.
In conclusion, this simple model combining known aspects of GTPase regulation gives rise to a variety of possible steady-state protein distributions, both homogeneous and heterogeneous. Furthermore, a single parameter set can give rise to a variety of possible steady states. This has both theoretical and biological consequences. Theoretically, these results demonstrate that simple signaling dynamics can give rise to a much more diverse set of spatial activation profiles than previously thought. Biologically, these results suggest that it is possible for a population of identical cells to exhibit a wide diversity of morphologies. That is, two cells may look different not because they have different underlying “parameters” but because they simply ended up in different parts of the underlying state space generated by a single (or similar) set of parameters.
Parameter space characterization
We analyze the full structure of the parameter space for the GTPase signaling model (Fig. 6, details in Computational Approach Details). We generated a sample of 106 parameter sets through Latin hypercube sampling so that each parameter set is a unique combination of five model parameters: a, b, c, RT, and ρT. Well-mixed analysis is used to classify each parameter set based on the number of linearly stable HSSs present as monostable, bistable, or tristable. As expected, we find that each of these three regimes are present: ∼89% of the parameter sets are monostable, 9% bistable, and 2% tristable (Table 1). In the bistable case, the two HSSs are, respectively, either Rac or Rho dominated (i.e., Fig. 4, a and c). In the tristable case, both these are present along with a balanced state, namely, the coexistence HSS, in which Rac and Rho are at uniform and comparable levels (Fig. 4 b). We note that the relative sparsity of multistable parameter sets largely results from multistability being restricted to lower values of the basal activation rate (c; see Fig. 6 a) and that a lower ceiling on that parameter could significantly affect these fractions. Nonetheless, monostability is most prevalent as expected.
We next assessed the capacity for polarization in these mono-, bi-, and tristable parameter regimes. Specifically, we simulated the evolution of a spatially localized pulse-like perturbation using the LPA ODEs and assessed whether it was possible for that perturbation to achieve a stable “local” state (see Methods for further detail). This approach essentially allows us to determine whether the GTPase activity has the capacity to respond to a spatial stimulus for a given parameter set and, if so, whether that response requires a sufficiently large stimulus or results from linear instability. This analysis indicates a large proportion of parameter sets may have the potential to elicit additional polarization states; 76.7% of monostable, 100% of bistable, and 100% of tristable parameter sets are polarizable (Table 1). These results suggest that all multistable parameter sets may have the capacity for polarity. We say “may” because the results of the LPA are only approximate and require numerical PDE simulations for verification (see subsequent results). Nonetheless, LPA predicts that polarization is common in the sampled parameter ranges and is more prevalent among multistable parameter sets than monostable parameter sets.
Visualization of the parameter space structure using the LPA simulation screen results (Fig. 6, a–c) reveals why the multistable parameter sets are all predicted to be polarizable. Each panel of Fig. 6 shows a 3D scatter plot obtained from projecting the 5D Latin hypercube sample of parameter space to three dimensions. Each point represents a parameter set with unique values of a, b, c, RT, and ρT color coded as indicated in the legend. For example, in Fig. 6, a, d, and g, each point has unique RT- and ρT-values, but these dimensions are not shown in the plot. The parameter space of this model has a clear nested structure. The nucleus of this parameter space (red points indicate tristability with polarization) is a regime in which a fixed parameter set can give rise to multiple regulatory phenotypes. This is nested in a parameter regime in which heterogeneity is more restricted (yellow points indicate bistability with polarization). This is, in turn, nested within a much more widespread and ubiquitous parameter regime in which polarity is possible but in which each parameter set emits only a single HSS along with polarity (gray points indicate monostability with polarization). Thus, consistent with the quantification results in Table 1 and prior analysis (43), the multistable parameter regimes appear to lie within a broader polarizable regime.
Note that those parameter sets which are monostable and nonpolarizable are not shown in Fig. 6. These parameter sets fill out the rest of the “empty space” in Fig. 6, a–c and appear to be most distant from the multistable nucleus. Additionally, Fig. 6 contains red points (representing tristable polarizable parameter sets) that appear isolated from the bulk of similar parameter sets. The apparent isolation could result from 1) the 3D projection of 5D data, 2) an unusual 5D combination of parameters, or 3) numerical thresholding errors (see Computational Approach Details) in determining the number of steady states (i.e., mistakenly classifying these as tristable parameter sets when they are really mono- or bistable). Despite these rare isolated points, the parameter space structure appears to have a clear nested structure.
To verify the predictions of the LPA, we repeated the parameter screen with full PDE numerics. Previous studies have suggested that the LPA predicts that parameter regimes in which polarization or pattern formation occurs are larger than they are in the actual PDEs (45). In other words, the LPA overestimates the regions of parameter space that produce interesting behavior such as polarization (or other pattern formation in other systems). It would thus be most efficient to use the LPA to pare down the number of parameter sets for which PDE simulations are performed. However, this approach has not been fully validated, and thus, we simulate the PDEs for all parameter sets. For each parameter set, we assessed whether or not each HSS is stable with respect to noise and whether a polarized pattern can be found. Specifically, to assess whether each HSS is stable or unstable, we added noise to each HSS as an initial condition and observed the response. To determine if a particular parameter set will polarize in response to a sufficiently strong perturbation, we used a polarized pattern as an initial condition and assessed whether the system evolved to a polarized or homogeneous state (details in Computational Approach Details). Although there are differences between the PDE and LPA results, the qualitative conclusions are consistent (Fig. 6, d–f). First, an array of individual parameter sets can still give rise to diverse steady-state spatial distributions of protein activation. Second, the nested parameter space structure is still observed. Third, polarization appears to be more common in multistable regimes than monostable regimes.
The main discrepancy between the PDE and LPA results is that there are many parameter sets in which the LPA predicts polarization is possible but in which PDE simulations do not achieve polarity. This discrepancy appears to be most prominent in the tristable and polarizable case, in which the PDE analysis suggests that a large proportion of tristable parameter sets do not give polarized patterns, whereas the LPA screen suggests all tristable parameter sets are polarizable (66% of tristable parameter sets are not polarizable in the PDE screen, whereas 0% are not polarizable in the LPA screen; see Table 1). Inspection of Fig. 6, b and e suggests that there is a particular region of the tristable parameter space that the LPA appears to falsely predict is polarizable. More generally, further mining of the LPA and PDE screen results shows that approximately 48.74% of parameter sets predicted to polarize by the LPA fail to do so when simulating the PDEs with our limited set of initial conditions and fixed diffusion coefficients. However, effectively all parameter sets that polarize in PDE simulations are predicted to do so by the LPA; the LPA failed to predict polarization of only 0.0494% of parameter sets that actually polarize in PDE simulations. Combined, these results demonstrate that the LPA is conservative in its prediction of interesting dynamics in the sense that it detects essentially all dynamically interesting parameter sets but generally predicts regimes of behavior to be larger than they are for the PDEs.
Based on the discrepancy between the LPA and PDE results and the general interest in this parameter regime that generates a rich state space, we next focused on the regime predicted to be tristable and polarizable by the LPA. Specifically, we assessed (Fig. 6, g–i) whether the coexistence HSS of tristable parameter set was linearly unstable (red points) and thus would polarize in response to any stimulus, stable but easy to polarize with a relatively small stimulus (yellow points), or strongly stable, requiring a large stimulus for polarization (black points). The LPA unstable points form a “shell” around the LPA stable points, suggesting that it is more difficult for the system to polarize if its parameters are further into the tristable regime. We quantitatively analyzed the apparent nested structure by calculating the distribution of distances from parameter sets of interest to the center of mass of the entire parameter sample (Fig. S4). The LPA unstable points appear to be further from the center of mass in parameter space than the LPA stable points, indicating that the LPA stable points form the nucleus of parameter space. Interestingly, comparison of Fig. 6, b, e, and h shows that the “hard to polarize” tristable sets match up with those that were falsely predicted to polarize by the LPA. This suggests that parameter sets that reside deeper in the tristable regime are more stable against spatial perturbations and that this point is the source of the discrepancy between the PDE and LPA results.
In conclusion, these results reveal that polarization is fairly ubiquitous throughout parameter space. The parameter space has a well-defined nested structure in which some regions yield more diversity of states (e.g., the number of possible steady states for a given parameter set) than others. These results also demonstrate that the diversity of potential morphological states shown in Figs. 4 and 5 is not an artifact of a single parameter set, but rather is indicative of an entire regime of behavior that lies at the very core of this parameter space. Finally, these results also demonstrate the power of this approach to mapping the structure of the parameter space of this model. Although there are discrepancies between the LPA (which is much more computationally efficient) and PDE (which is more accurate) approaches, the qualitative conclusions are generally consistent.
Numerical bifurcation analysis
To supplement the computational approach, we used numerical bifurcation analysis to study the bifurcation structure of this model. This alternative approach provides 1) another method to study parameter space structure, 2) a direct comparison to bifurcation analysis in previous work (43), and 3) validation for our computational approach.
To perform this analysis, we first convert the GTPase model to a system of LPA ODEs. The numerical continuation package MatCont (48) is then used to perform a bifurcation analysis of that reduced system. This allows us to directly compare the dynamics of this system to that of the simpler systems consisting of only mutual antagonism or autoactivation in (43). Results show that the structure of the bifurcation diagram (Fig. 7 a) is qualitatively similar to that of the mutual antagonism model (Fig. 3 a) in the sense that regimes of coexisting multistability and polarization are present. However, the inclusion of autoactivation can result in tristability (Fig. 7, a and b), which does not occur in a model with only mutual antagonism.
Comprehensive bifurcation analysis with respect to all model parameters of this system is beyond the scope of this article. Bifurcation analysis does provide an alternative approach to demonstrate the presence of rich regimes of behavior with diverse, coexisting GTPase activation states that map onto different cell morphologies.
Motivated by the previously observed nested parameter space structure and by the previous bifurcation analysis in (43), we next examined the bifurcation structure in the (RT, ρT) plane (Fig. 7 b). We again found the nested parameter space structure with the region of polarizability encompassing both the bistable and tristable regimes (see Methods for details on Fig. 7 b).
Lastly, as additional verification of the parameter space structure, we projected a slice of the data from the PDE parameter screen (Fig. 5, d–f) onto the two-parameter bifurcation diagram (Fig. 7 d). The red points indicate tristable and polarizable parameter sets, yellow points are those parameter sets that are bistable and polarizable, and the gray points are those parameter sets that are monostable and polarizable. We find agreement between the two-parameter bifurcation diagram and the parameter screen, further validating our computational approach. We do note once again that although the agreement is not perfect, the regimes of behavior predicted to yield interesting dynamics by the LPA are generally larger than actual regimes found through brute-force PDE simulation. Thus, the LPA appears to capture all interesting regimes of behavior, though it does overpredict the size of those regimes.
In conclusion, numerical bifurcation results confirm the nested parameter space structure and coexistence of polarization in the monostable, bistable, and tristable regimes that was found using the LPA and PDE parameter screens. Moreover, the LPA bifurcation structure in Fig. 7 a has similar qualities to that in Fig. 3 a, suggesting that the addition of autoactivation to the previously studied mutual antagonism and conservation system (as in (43)) adds to the structure of the parameter space rather than fundamentally altering it. The addition of autoactivation leads to the genesis of a tristable and polarizable parameter regime nested within the bistable and polarizable regime that forms the nucleus of the parameter space.
Discussion
Past quantification of cell shape diversity among various types of cells has revealed three essential observations. First, cells exhibit a restricted and discrete set of morphologies. Second, cells of different types (within migratory cell types, at least) exhibit the same set of morphologies. Third, cells of the same type can exhibit diverse cell shapes despite being derived from the same lineage. Our work here provides a hypothesis for how this landscape of discrete cell morphologies may arise from a diverse set of GTPase regulatory phenotypes and how seemingly similar cells can exhibit the full spectrum of that diversity.
In this study, we used computational modeling and analysis to demonstrate that the simple and well-known dynamics of Rho GTPase signaling can generate a wide variety of regulatory phenotypes. Of course, a myriad of factors—including genetic, regulatory, biophysical, and environmental factors—will jointly influence a cell’s morphology. However, Rho GTPases are well-known cytoskeletal regulators whose activity levels have been causally linked to cell shape (2). We thus conclude that this variety of regulatory phenotypes may explain a significant amount of cell shape diversity found in cellular populations. The simple reaction-diffusion model including autoactivation, mutual antagonism, and biochemical conservation recovers at least six GTPase activity profiles associated with different morphologies observed in recent studies (2) (although it does not capture fine-scale signaling or shape details such as ruffled or spiky shapes, as seen in these studies). Interestingly, it is not simply the case that different regions of parameter space yield different regulatory phenotypes. Rather, individual states of the model (i.e., parameter sets) can yield a variety of different regulatory phenotypes.
These results suggest that 1) Rho GTPase dynamics can explain much of the diversity of cell shapes observed experimentally and 2) diverse regulatory phenotypes may arise even in the absence of any intrinsic differences between cells. The dynamics of Rho GTPase regulation can thus explain both the presence of the discrete morphological landscape observed in a variety of cell populations, as well as how populations of seemingly similar cells from the same source can explore that full landscape.
To facilitate exploration of the dynamics of this spatial model of GTPase dynamics, we further developed a computational approach to efficiently and broadly explore the model’s parameter space to determine where different types of regulatory phenotypes would be expected to appear. Thus, rather than pick a representative parameter set, we explored the entirety of parameter space to determine the full scope of dynamics possible. Results reveal a highly structured parameter space where different parameter regimes exhibit varying levels of diversity of regulatory phenotypes. In particular, the model’s parameter space has a nested structure in which the nucleus is comprised of parameter sets that can individually give rise to multiple spatial protein activation states that correspond to a variety of different shapes. A lower diversity of states is found further from the nucleus of this nested parameter space.
These results confirm conclusions of large-scale statistical analyses of cell shape data sets that have shown the presence of cell shape “attractors” (2) and hypothesized that transitions between these attractors may be driven by environmental perturbations that affect GTPase signaling (6). They further demonstrate that the simple, well-established cross talk interactions between Rac and Rho can produce the majority of those observed “attractors.” Thus, although a number of other factors undoubtedly influence morphology, these central cytoskeletal regulators are sufficient to produce much of the observed heterogeneity.
The structured parameter space we observe also has similar properties to the structure found in prior mathematical analyses of spatiotemporal GTPase dynamics. In (43) and (55), bifurcation analyses illustrated a similar nested structure to parameter space. Results here differ from those of prior studies in two important ways. First, we explore a more complete model of Rho GTPase cross talk that accounts for both autoactivation and mutual antagonism rather than only one of these mechanisms. Including the combination of these interactions is responsible for the increased heterogeneity observed in model results. Without both these feedback mechanisms, the regulatory phenotypes found are more limited (43). Second, we have utilized an unsupervised parameter space screening (similar to that found in (56, 57, 58, 59)) method based on LPA to generate a more comprehensive understanding of the model’s dynamics and structure.
Further work is needed to understand the link between cell signaling and cell morphology. We have focused only on the core signaling dynamics of Rho GTPases to assess the types of spatial protein distributions that those dynamics generate. We did not consider the myriad of complex interactions and feedback mechanisms between cytoskeletal regulation, remodeling, adhesion, cytoskeletal flows, membrane mechanics, etc. Thus, in one sense, we assess the maximal scope of heterogeneity that could be explained through signaling alone. Full spatial cell simulations based on these GTPase distributions in two dimensions (60, 61, 62, 63) or three dimensions (64) or those that more accurately capture the cytosolic-membrane binding dynamics of GTPase signaling (65,66) are needed to further investigate how these factors would influence cell morphology. Alternatively, extensions to account for the broader signaling network (e.g., (67)) regulating cytoskeletal remodeling will also be required to understand how other molecular regulators (GEFs and GAPs, for example) affect morphology.
Despite these limitations, this study demonstrates that the known regulatory interactions between these proteins can (at a qualitative level) generate the full landscape of regulatory phenotypes that are associated with cell morphologies found in imaging studies. Furthermore, detailed analysis of the model’s parameter space structure shows that these regulatory phenotypes coexist in parameter space, explaining how similar cells of the same fate drawn from a single population can exhibit a wide variety of differing morphologies. More generally, these results suggest Rho GTPases may play a significant role in regulating cell shape and, given their ubiquity in migratory cells, may be a foundational part of a common mechanism regulating cell shape in different cell types.
Author Contributions
C.Z. and W.R.H. designed the research. C.Z. performed the research and analyzed data. C.Z. and W.R.H. wrote the manuscript.
Acknowledgments
This work was supported by a National Science Foundation grant DMS1562078 (to W.R.H.) and a Natural Sciences and Engineering Research Council of Canada Postdoctoral Fellowship Award (to C.Z.). This work was conducted in part using the resources of the Advanced Computing Center for Research and Education at Vanderbilt University, Nashville, TN.
Editor: Ruth Baker.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2020.01.035.
Supporting Material
References
- 1.Bakal C., Aach J., Perrimon N. Quantitative morphological signatures define local signaling networks regulating cell morphology. Science. 2007;316:1753–1756. doi: 10.1126/science.1140324. [DOI] [PubMed] [Google Scholar]
- 2.Sailem H., Bousgouni V., Bakal C. Cross-talk between Rho and Rac GTPases drives deterministic exploration of cellular shape space and morphological heterogeneity. Open Biol. 2014;4:130132. doi: 10.1098/rsob.130132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Byrne K.M., Monsefi N., Kholodenko B.N. Bistability in the Rac1, PAK, and RhoA signaling network drives actin cytoskeleton dynamics and cell motility switches. Cell Syst. 2016;2:38–48. doi: 10.1016/j.cels.2016.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rubinstein B., Jacobson K., Mogilner A. Multiscale two-dimensional modeling of a motile simple-shaped cell. Multiscale Model. Simul. 2005;3:413–439. doi: 10.1137/04060370X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nickaeen M., Novak I.L., Mogilner A. A free-boundary model of a motile cell explains turning behavior. PLoS Comput. Biol. 2017;13:e1005862. doi: 10.1371/journal.pcbi.1005862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yin Z., Sadok A., Bakal C. A screen for morphological complexity identifies regulators of switch-like transitions between discrete cell shapes. Nat. Cell Biol. 2013;15:860–871. doi: 10.1038/ncb2764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cooper S., Sadok A., Bakal C. Apolar and polar transitions drive the conversion between amoeboid and mesenchymal shapes in melanoma cells. Mol. Biol. Cell. 2015;26:4163–4170. doi: 10.1091/mbc.E15-06-0382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yin Z., Sailem H., Bakal C. How cells explore shape space: a quantitative statistical perspective of cellular morphogenesis. BioEssays. 2014;36:1195–1203. doi: 10.1002/bies.201400011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ridley A.J. Rho GTPase signalling in cell migration. Curr. Opin. Cell Biol. 2015;36:103–112. doi: 10.1016/j.ceb.2015.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Boureux A., Vignal E., Fort P. Evolution of the Rho family of ras-like GTPases in eukaryotes. Mol. Biol. Evol. 2007;24:203–216. doi: 10.1093/molbev/msl145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang B., Lu M., Ben-Jacob E. The three-way switch operation of Rac1/RhoA GTPase-based circuit controlling amoeboid-hybrid-mesenchymal transition. Sci. Rep. 2014;4:6449. doi: 10.1038/srep06449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nobes C.D., Hall A. Rho GTPases control polarity, protrusion, and adhesion during cell movement. J. Cell Biol. 1999;144:1235–1244. doi: 10.1083/jcb.144.6.1235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wong K., Pertz O., Bourne H. Neutrophil polarization: spatiotemporal dynamics of RhoA activity support a self-organizing mechanism. Proc. Natl. Acad. Sci. USA. 2006;103:3639–3644. doi: 10.1073/pnas.0600092103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Xu J., Wang F., Bourne H.R. Divergent signals and cytoskeletal assemblies regulate self-organizing polarity in neutrophils. Cell. 2003;114:201–214. doi: 10.1016/s0092-8674(03)00555-5. [DOI] [PubMed] [Google Scholar]
- 15.Lin B., Holmes W.R., Levchenko A. Synthetic spatially graded Rac activation drives cell polarization and movement. Proc. Natl. Acad. Sci. USA. 2012;109:E3668–E3677. doi: 10.1073/pnas.1210295109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Machacek M., Hodgson L., Danuser G. Coordination of Rho GTPase activities during cell protrusion. Nature. 2009;461:99–103. doi: 10.1038/nature08242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Rappel W.J., Edelstein-Keshet L. Mechanisms of cell polarization. Curr. Opin. Syst. Biol. 2017;3:43–53. doi: 10.1016/j.coisb.2017.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Guilluy C., Garcia-Mata R., Burridge K. Rho protein crosstalk: another social network? Trends Cell Biol. 2011;21:718–726. doi: 10.1016/j.tcb.2011.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Discher D.E., Janmey P., Wang Y.L. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 20.Vogel V., Sheetz M. Local force and geometry sensing regulate cell functions. Nat. Rev. Mol. Cell Biol. 2006;7:265–275. doi: 10.1038/nrm1890. [DOI] [PubMed] [Google Scholar]
- 21.Houk A.R., Jilkine A., Weiner O.D. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell. 2012;148:175–188. doi: 10.1016/j.cell.2011.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Martin E., Ouellette M.H., Jenna S. Rac1/RhoA antagonism defines cell-to-cell heterogeneity during epidermal morphogenesis in nematodes. J. Cell Biol. 2016;215:483–498. doi: 10.1083/jcb.201604015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Goryachev A.B., Leda M. Many roads to symmetry breaking: molecular mechanisms and theoretical models of yeast cell polarity. Mol. Biol. Cell. 2017;28:370–380. doi: 10.1091/mbc.E16-10-0739. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ma L., Janetopoulos C., Iglesias P.A. Two complementary, local excitation, global inhibition mechanisms acting in parallel can explain the chemoattractant-induced regulation of PI(3,4,5)P3 response in dictyostelium cells. Biophys. J. 2004;87:3764–3774. doi: 10.1529/biophysj.104.045484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chau A.H., Walter J.M., Lim W.A. Designing synthetic regulatory networks capable of self-organizing cell polarization. Cell. 2012;151:320–332. doi: 10.1016/j.cell.2012.08.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Park J., Holmes W.R., Levchenko A. Mechanochemical feedback underlies coexistence of qualitatively distinct cell polarity patterns within diverse cell populations. Proc. Natl. Acad. Sci. USA. 2017;114:E5750–E5759. doi: 10.1073/pnas.1700054114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Holmes W.R., Park J., Edelstein-Keshet L. A mathematical model coupling polarity signaling to cell adhesion explains diverse cell migration patterns. PLoS Comput. Biol. 2017;13:e1005524. doi: 10.1371/journal.pcbi.1005524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tang K., Boudreau C.G., Khadra A. Paxillin phosphorylation at serine 273 and its effects on Rac, Rho and adhesion dynamics. PLoS Comput. Biol. 2018;14:e1006303. doi: 10.1371/journal.pcbi.1006303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Holmes W.R., Liao L., Edelstein-Keshet L. Modeling the roles of protein kinase Cβ and η in single-cell wound repair. Mol. Biol. Cell. 2015;26:4100–4108. doi: 10.1091/mbc.E15-06-0383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Holmes W.R., Golding A.E., Edelstein-Keshet L. A mathematical model of GTPase pattern formation during single-cell wound repair. Interface Focus. 2016;6:20160032. doi: 10.1098/rsfs.2016.0032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Simon C.M., Vaughan E.M., Edelstein-Keshet L. Pattern formation of Rho GTPases in single cell wound healing. Mol. Biol. Cell. 2013;24:421–432. doi: 10.1091/mbc.E12-08-0634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chiou J.G., Ramirez S.A., Lew D.J. Principles that govern competition or co-existence in Rho-GTPase driven polarization. PLoS Comput. Biol. 2018;14:e1006095. doi: 10.1371/journal.pcbi.1006095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wu C.F., Chiou J.G., Lew D.J. Role of competition between polarity sites in establishing a unique front. eLife. 2015;4:e11611. doi: 10.7554/eLife.11611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Howell A.S., Jin M., Lew D.J. Negative feedback enhances robustness in the yeast polarity establishment circuit. Cell. 2012;149:322–333. doi: 10.1016/j.cell.2012.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Iglesias P.A., Devreotes P.N. Navigating through models of chemotaxis. Curr. Opin. Cell Biol. 2008;20:35–40. doi: 10.1016/j.ceb.2007.11.011. [DOI] [PubMed] [Google Scholar]
- 36.Verkhovsky A.B. Cell polarization: mechanical switch for a chemical reaction. Curr. Biol. 2012;22:R58–R61. doi: 10.1016/j.cub.2011.12.012. [DOI] [PubMed] [Google Scholar]
- 37.Edelstein-Keshet L., Holmes W.R., Dutot M. From simple to detailed models for cell polarization. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013;368:20130003. doi: 10.1098/rstb.2013.0003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Holmes W.R., Lin B., Edelstein-Keshet L. Modelling cell polarization driven by synthetic spatially graded Rac activation. PLoS Comput. Biol. 2012;8:e1002366. doi: 10.1371/journal.pcbi.1002366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Holmes W.R., Edelstein-Keshet L. A comparison of computational models for eukaryotic cell shape and motility. PLoS Comput. Biol. 2012;8:e1002793. doi: 10.1371/journal.pcbi.1002793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mori Y., Jilkine A., Edelstein-Keshet L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophys. J. 2008;94:3684–3697. doi: 10.1529/biophysj.107.120824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mori Y., Jilkine A., Edelstein-Keshet L. Asymptotic and bifurcation analysis of wave-pinning in a reaction-diffusion model for cell polarization. SIAM J. Appl. Math. 2011;71:1401–1427. doi: 10.1137/10079118X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Jilkine A., Marée A.F.M., Edelstein-Keshet L. Mathematical model for spatial segregation of the Rho-family GTPases based on inhibitory crosstalk. Bull. Math. Biol. 2007;69:1943–1978. doi: 10.1007/s11538-007-9200-6. [DOI] [PubMed] [Google Scholar]
- 43.Holmes W.R., Edelstein-Keshet L. Analysis of a minimal Rho-GTPase circuit regulating cell shape. Phys. Biol. 2016;13:046001. doi: 10.1088/1478-3975/13/4/046001. [DOI] [PubMed] [Google Scholar]
- 44.Grieneisen V. University of Utrecht; Utrecht, the Netherlands: 2009. Dynamics of Auxin Patterning in Plant Morphogenesis. [Google Scholar]
- 45.Holmes W.R. An efficient, nonlinear stability analysis for detecting pattern formation in reaction diffusion systems. Bull. Math. Biol. 2014;76:157–183. doi: 10.1007/s11538-013-9914-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Holmes W.R., Mata M.A., Edelstein-Keshet L. Local perturbation analysis: a computational tool for biophysical reaction-diffusion models. Biophys. J. 2015;108:230–236. doi: 10.1016/j.bpj.2014.11.3457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Mata M.A., Dutot M., Holmes W.R. A model for intracellular actin waves explored by nonlinear local perturbation analysis. J. Theor. Biol. 2013;334:149–161. doi: 10.1016/j.jtbi.2013.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Dhooge A., Govaerts W., Sautois B. New features of the software MatCont for bifurcation analysis of dynamical systems. Math. Comput. Model. Dyn. Syst. 2008;14:147–175. [Google Scholar]
- 49.Alnæs M., Blechta J., Logg A. The FEniCS project version 1.5. Archive of Numerical Software. 2015;3:9–23. [Google Scholar]
- 50.Liu Y. University of British Columbia; 2019. Analysis of pattern formation in reaction-diffusion models for cell polarization. Master’s thesis.https://open.library.ubc.ca/collections/ubctheses/24/items/1.0378329 Available from. [Google Scholar]
- 51.Guantes R., Poyatos J.F. Multistable decision switches for flexible control of epigenetic differentiation. PLoS Comput. Biol. 2008;4:e1000235. doi: 10.1371/journal.pcbi.1000235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wu F., Su R.Q., Wang X. Engineering of a synthetic quadrastable gene network to approach Waddington landscape and cell fate determination. eLife. 2017;6:e23702. doi: 10.7554/eLife.23702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Holmes W.R., Reyes de Mochel N.S., Nie Q. Gene expression noise enhances robust organization of the early mammalian blastocyst. PLoS Comput. Biol. 2017;13:e1005320. doi: 10.1371/journal.pcbi.1005320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Otsuji M., Ishihara S., Kuroda S. A mass conserved reaction-diffusion system captures properties of cell polarity. PLoS Comput. Biol. 2007;3:e108. doi: 10.1371/journal.pcbi.0030108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Trong P.K., Nicola E.M., Grill S.W. Parameter-space topology of models for cell polarity. New J. Phys. 2014;16:065009. [Google Scholar]
- 56.Wang Y., Ku C.J., Altschuler S.J. Identifying network motifs that buffer front-to-back signaling in polarized neutrophils. Cell Rep. 2013;3:1607–1616. doi: 10.1016/j.celrep.2013.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Nguyen L.K., Degasperi A., Kholodenko B.N. DYVIPAC: an integrated analysis and visualisation framework to probe multi-dimensional biological networks. Sci. Rep. 2015;5:12569. doi: 10.1038/srep12569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Huang B., Lu M., Onuchic J.N. Interrogating the topological robustness of gene regulatory circuits by randomization. PLoS Comput. Biol. 2017;13:e1005456. doi: 10.1371/journal.pcbi.1005456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Yue H., Camley B.A., Rappel W.J. Minimal network topologies for signal Processing during collective cell chemotaxis. Biophys. J. 2018;114:2986–2999. doi: 10.1016/j.bpj.2018.04.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Vanderlei B., Feng J.J., Edelstein-Keshet L. A computational model of cell polarization and motility coupling mechanics and biochemistry. Multiscale Model. Simul. 2011;9:1420–1443. doi: 10.1137/100815335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Strychalski W., Adalsteinsson D., Elston T.C. Simulating biochemical signaling networks in complex moving geometries. SIAM J. Sci. Comput. 2010;32:3039–3070. doi: 10.1137/090779693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Camley B.A., Zhao Y., Rappel W.J. Crawling and turning in a minimal reaction-diffusion cell motility model: coupling cell shape and biochemistry. Phys. Rev. E. 2017;95:012401. doi: 10.1103/PhysRevE.95.012401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Alonso S., Stange M., Beta C. Modeling random crawling, membrane deformation and intracellular polarity of motile amoeboid cells. PLoS One. 2018;13:e0201977. doi: 10.1371/journal.pone.0201977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Cusseddu D., Edelstein-Keshet L., Madzvamuse A. A coupled bulk-surface model for cell polarisation. J. Theor. Biol. 2018;481:119–135. doi: 10.1016/j.jtbi.2018.09.008. Published online September 8, 2018. [DOI] [PubMed] [Google Scholar]
- 65.Rätz A., Röger M. Turing instabilities in a mathematical model for signaling networks. J. Math. Biol. 2012;65:1215–1244. doi: 10.1007/s00285-011-0495-4. [DOI] [PubMed] [Google Scholar]
- 66.Rätz A., Röger M. Symmetry breaking in a bulk-surface reaction-diffusion model for signalling networks. Nonlinearity. 2014;27:1805–1827. [Google Scholar]
- 67.Kim T.H., Monsefi N., Cho K.H. Network-based identification of feedback modules that control RhoA activity and cell migration. J. Mol. Cell Biol. 2015;7:242–252. doi: 10.1093/jmcb/mjv017. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All code and data (including code to make the figures) are available as an archived GitHub repository at https://doi.org/10.6084/m9.figshare.9176252.