Molecular Simulation of Mechanical Properties and Membrane Activities of the ESCRT-III Complexes

Abstract

The endosomal sorting complex required for transport (ESCRT) machinery carries out the membrane scission reactions that are required for many biological processes throughout cells. How ESCRTs bind and deform cellular membranes and ultimately produce vesicles has been a matter of active research in recent years. In this study, we use fully atomistic molecular dynamics simulations to scrutinize the structural details of a filament composed of Vps32 protomers, a major component of ESCRT-III complexes. The simulations show that both hydrophobic and electrostatic interactions between monomers help maintain the structural stability of the filament, which exhibits an intrinsic bend and twist. Our findings suggest that the accumulation of bending and twisting stresses as the filament elongates on the membrane surface likely contributes to the driving force for membrane invagination. The filament exposes a large cationic surface that senses the negatively charged lipids in the membrane, and the N-terminal amphipathic helix of the monomers not only acts as a membrane anchor but also generates significant positive membrane curvature. Taking all results together, we discuss a plausible mechanism for membrane invagination driven by ESCRT-III.

Significance

Using atomistic simulations, we demonstrate that a key component (Vps32) of the ESCRT-III complex features intrinsic bending and twist, which suggests that the accumulation of bending and twisting stresses as the filament elongates on the membrane surface likely provides the driving force for membrane invagination. The simulations also demonstrate that the N-terminal helix of Vps32 drives the formation of local positive mean curvature, which balances the negative curvature of invagination produced by the spiral scaffold. The study illustrates how molecular simulations can be used to identify protein mechanical properties and protein-membrane interactions that are critical to the generation of large-scale membrane deformations, and the approach is applicable to other membrane remodeling processes.

Introduction

Cell membranes adopt a broad range of shapes to facilitate the specific functions of various membrane compartments (1,2). For example, protein-induced membrane bending and remodeling drives numerous biological processes including cell division, growth, and cell-cell communication (3, 4, 5, 6, 7, 8). The endosomal sorting complex required for transport (ESCRTs) proteins are cytosolic factors that are involved in fundamental cellular processes including organelle biogenesis (9,10), sorting cargo into intraluminal vesicles of multivesicular endosomes (11, 12, 13), cytokinesis (14, 15, 16), plasma membrane and lysosome repair (17, 18, 19), and the formation and scission of intraluminal vesicles (20, 21, 22, 23), among many others (24, 25, 26, 27, 28, 29, 30, 31, 32). ESCRTs are of particular interest because the membrane curvature they induce results in budding away from the cytoplasm (Fig. 1 a), which is topologically opposite as compared to the vesicles formed by other proteins such as clathrin, COP-I, and COP-II (24,33, 34, 35, 36, 37). The core ESCRT machinery is composed of five complexes: ESCRT-0, -I, -II, and -III and the Vps4 AAA ATPase. During intralumenal vesicle formation at multivesicular endosomes, ESCRT-II provides the architecture that directs ESCRT-III assembly, which functions together with Vps4 to trigger membrane remodeling (28,30,38). ESCRT-III complexes are heteropolymers of multiple subunits, including Vps20, Vps32, Vps24, and Vps2, which assemble into conformationally dynamic assemblies that can appear as striking spiral structures (23,25) at the membrane surface (Fig. 1 b).

Figure 1.

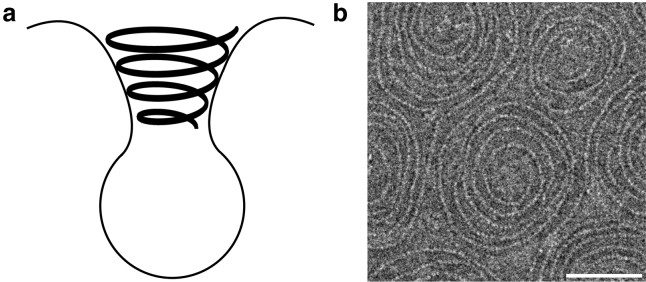
(a) Schematic showing Vps32, major component of ESCRT-III, polymerizes into spiral structure that lies in the inside of the membrane invagination, opposite in topology to other proteins involved in vesicle formation, such as clathrin, dynamin, and CHMP1B (45). (b) An electron microscopy image illustrates the spiral structures formed by ESCRT-III (23); the scale bar represents 50 nm.

The mechanisms by which the ESCRT-III polymers induce membrane deformation and ultimately membrane fission remain unclear, and several hypotheses have been put forward (25,39). Fabrikant et al. (40) analyzed the energetics of membrane scission for the “Dome model,” in which the authors proposed that ESCRT-III complexes self-assemble into a dome-like structure within a preformed membrane bud, generated by another ESCRT-III subunit. The outer surface of the dome has a strong affinity to membranes containing anionic lipids, which results in narrowing of the membrane neck and ultimately leads to membrane fission. Another recently proposed framework is commonly referred to as the membrane buckling model (41). In this scenario, ESCRT-III spiral polymers act as deformable springs, which accumulate strain by lateral compression while growing in a confined area. The out-of-plane buckling of the spiral generates the invagination of the membrane; subsequently, as a result of interactions with other ESCRT-III subunits or the Vps4 ATPase, the spirals disassemble, leading to release of the stored elastic energy that enables vesicle scission (23).

The essential element of the discussed mechanistic models concerns the interplay of mechanical deformation of the filament and membrane deformation mediated by protein-membrane interactions. Therefore, to further examine these competing mechanistic ideas, it is essential to characterize the mechanical properties of the ESCRT-III filament, the filament-membrane interface, as well as interactions and local membrane deformations that stabilize this interface. For example, it is of interest to establish whether the filament has any significant intrinsic tendency to bend and twist, which potentially modifies the protein-membrane interface (42); if so, accumulation and release of mechanical strain as the filament continues to grow on the membrane surface might constitute an important driving force required for membrane deformation during the fission process.

Such information, however, is not explicitly available from experimental studies because of the lack of high-resolution characterization of the filament on the membrane surface. For example, several high-resolution crystal structures are available for the key component of the ESCRT-III filament (43,44); in particular, Tang et al. (44) determined an active conformation of the ESCRT-III subunit, Vps32, at a resolution of 1.6 Å without the autoinhibitory C-terminal tail. The arrangement of the protein in the crystal lattice provides hints for the protein-protein interactions that stabilize the filament structure; locations of patches of cationic amino acids also lead to concrete hypotheses regarding the protein-membrane interface, which was supported by mutagenesis studies. However, whether the proposed protein-protein and protein-membrane interface remain stable under the physiological condition requires an explicit examination. Moreover, the mechanical properties of the filament and local membrane deformation coupled with filament-membrane interaction are not available from these previous studies.

In this work, using Vps32 as the key ESCRT-III component, we employ atomistic molecular dynamics (MD) simulations to address these key unanswered questions. First, we investigate protein-protein interfaces in one-dimensional filament structures in solution and also identify the residues that are responsible for the structural stability of the filament. We then analyze the mechanical properties of the one-dimensional filament, including the intrinsic bend and twist, and compute the relevant elastic moduli; the results can be used as a benchmark for developing coarse-grained models at either particle or continuum levels that aim to predict the interaction between the filament and lipid membrane at much longer length scales. Next, we study the filament-membrane interface using a Vps32 trimer model and identify structural motifs that stabilize the protein-membrane interface as well as the local membrane deformation induced by the protein binding. Taking all the results together, we discuss a plausible mechanism for membrane invagination driven by a spiral Vps32 filament.

Methods

The protein monomer structure is based on the crystal structure of Vps32 determined by Tang et al. (44) (Protein Data Bank: 5FD7); as discussed further below, the Vps32 structure was chosen over the CHMP1B system (45) because CHMP1B filaments interact with lipid membranes with the opposite binding topology. The coordinates of the ${\alpha }_0$ helix (residue no. 1–11) and those for residues 12–18 and residues of 141–150 of the ${\alpha }_4$ helix (see sequence listed in Fig. 2 a) are not available in the crystal structure. The missing coordinates for these residues are generated using a homology model with the Chimera software (46). This modeled protein monomer is then used to generate one-dimensional filament structures containing six monomers based on the lattice parameters in the crystal structure (Fig. S1; (44)).These protein filament models are used to investigate the stability of the protein-protein interface in aqueous solution and scrutinize the potential protein-membrane interfaces. While building those models, the ${\alpha }_0$-helix, which is amphipathic in nature, is oriented such that it does not overlap with the neighboring proteins and is available for anchoring the filament on the membrane surface (see below).

Figure 2.

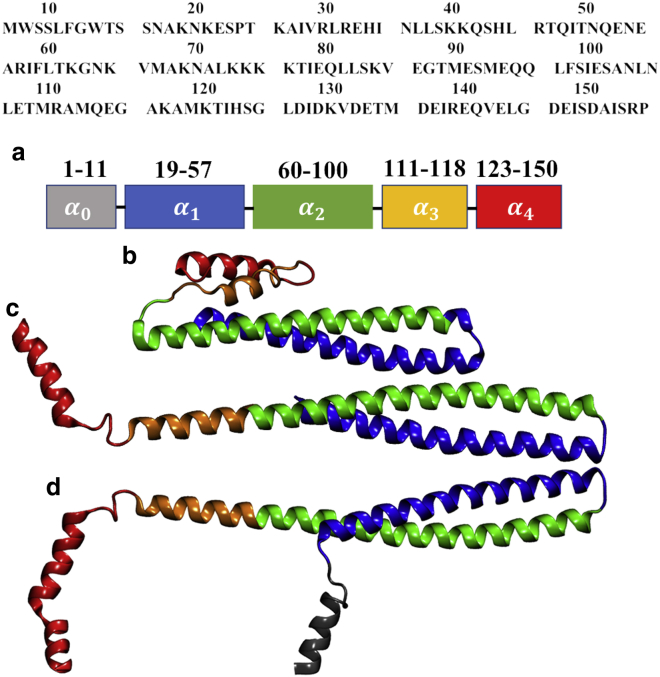
(a) The amino acid sequence and the number of residues in different helices of the Vps32 protein. The crystal structure of the Vps32 protein in the (b) folded and (c) extended configuration is shown. (d) Shown is the modeled structure of full-length Vps32 used in the current simulation, which includes residues 1–17 and 140–150, which are missing in the crystal structure. To see this figure in color, go online.

Fully atomistic molecular dynamics (MD) simulations are performed to study the structural and mechanical properties of the protein filaments in solution. A one-dimensional protein filament is placed at the center of the simulation box. The protein is then solvated using TIP3P water molecules (47). The protein monomer has a total charge of +1 unit, thus Cl⁻ ions are added to achieve overall charge neutrality. Additionally, appropriate numbers of Na⁺ and Cl⁻ ions are added to maintain the physiological salt concentration of 150 mM. Periodic boundary conditions are employed along all three principle directions. The CHARMM36 force field (48) is used to describe all the components throughout this work. The particle mesh Ewald (49) method is used to compute electrostatic interactions, and a switching function is used to reduce the van der Waals force smoothly to zero between 1.0 and 1.2 nm. The solvated system is first energy minimized using the conjugate gradient method to remove bad contacts between the solute and solvent atoms. This step is followed by a short NVT simulation in which a harmonic restraint is initially applied to the protein atoms and then gradually released during the course of the equilibration. This NVT-equilibrated system is then subject to NPT equilibration at the atmospheric pressure and 303 K temperature, during which no atoms are restrained. The pressure and temperature of the system during equilibration are controlled by a Berendsen barostat (50) with a time constant of 5 ps and a velocity-rescale thermostat (51) with a time constant of 1 ps, respectively; during the production run, the Berendsen barostat is replaced by the Parrinello-Rahman barostat (52) with a time constant of 1 ps. The LINCS algorithm (53) is used to constrain covalent bonds involving hydrogen atoms to enable an integration time step of 2 fs. All simulations are performed using the GROMACS simulation package (54).

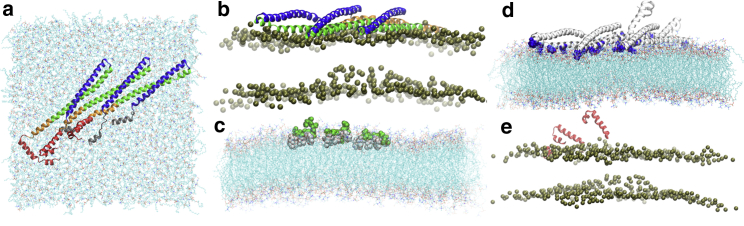
For the analysis of a protein-membrane interface, a protein trimer is placed at 1.1 nm from the top of a lipid membrane composed of 70% zwitterionic POPC (1-palmitoyl-2-oleoyl-glycero-3-phosphocholine) and 30% anionic POPS (1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-L-serine) lipids. We consider two different protein orientations: one with the ${\alpha }_1$ helix closer to the membrane surface and another with the elongated helix composed of ${\alpha }_2$ and ${\alpha }_3$ helices closer to the membrane surface to investigate the favorable protein-membrane interface. To help better sample protein insertion and equilibrate lipid distributions around the protein, the protein-membrane simulations are performed in three steps. First, a protein trimer is placed on top of a highly mobile membrane mimetic model (55) membrane with a 1.7 times higher area-per-lipid value and equilibrated for 75 ns under the constant area condition. The protein readily inserts into the membrane in this step, which is followed by 75 ns of standard NPT equilibration. In the final stage, the organic solvent, 1,1-dichloroethane, in the highly mobile membrane mimetic model is removed and the short lipid tails are regrown to their full length using CHARMM-GUI (56, 57, 58). Then the entire system is equilibrated for another 75 ns at the atmospheric pressure and 303 K temperature using a Parrinello-Rahman barostat and Nose-Hoover thermostat, respectively. The details of the system sizes for different simulations are summarized in Table S1.

Results

Protein-protein interface in the filament assembly

The crystal structure used here (44) indicates a highly elongated (or open) conformation of the Vps32 monomer that differs significantly from a homology model proposed by Henne et al. (59), in which Vps32 adopts a compact configuration consisting of four $\alpha$-helices (Fig. 2, a and b). The ${\alpha }_1$- and ${\alpha }_2$-helices are similar in both the compact and open structures. However, ${\alpha }_2$- and ${\alpha }_3$-segments are distinct $\alpha$-helices in the compact configuration, whereas they are combined into an extended single helix in the open conformation. In solution, Vps32 is conformationally dynamic and the structure interchanges between the compact and open forms (44). The observation that Vps32 adopts the open conformation in the crystalline state suggests that this conformation is also featured in the Vps32 filament in solution. This is supported by the observation that all monomers in the periodic one-dimensional filament model remain in the open conformation throughout the 100-ns-long simulation (Fig. 3 a).

Figure 3.

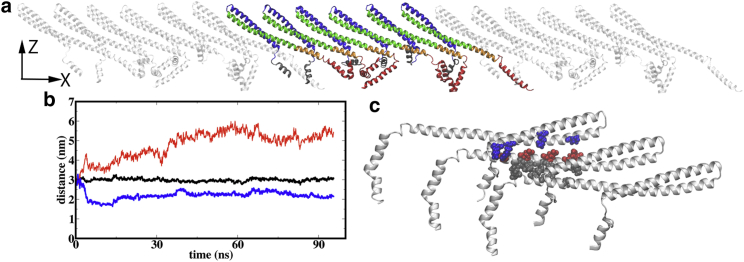
(a) An equilibrated structure of a one-dimensional Vps32 filament, which contains six protein monomers and is periodic along the x direction. (b) Examples of distances between two neighboring ${\alpha }_4$-helices and the distance between two neighboring ${\alpha }_1$-helices (black) as functions of simulation time are shown. See the main text for details. (c) Hydrophobic and electrostatic interactions between neighboring monomers (see the main text for details) are shown. Gray, red, and blue represent the hydrophobic, negatively charged, and positively charged residues, respectively. To see this figure in color, go online.

To scrutinize the protein-protein interface in the one-dimensional filament, we calculate the interhelix distances between neighboring monomers. As shown in Figs. 3 b and S2, distances between each pair of the neighboring ${\alpha }_1$-, ${\alpha }_2$-, and ${\alpha }_3$-helices are close to a constant value of 3.0 nm, suggesting that the core structure of the filament is rigid. However, the ${\alpha }_4$-helices are flexible, and their positions in the filament are not well defined. The ${\alpha }_4$-helix randomly binds with the neighboring ${\alpha }_4$ helices during the course of the simulation as highlighted in Fig. 3 a; as a result, the distance between neighboring ${\alpha }_4$-helices varies significantly between 2 and 5 nm (Figs. 3 b and S2). Evidently, ${\alpha }_4$-helix does not contribute to the stability of the one-dimensional Vps32 filament.

The ${\alpha }_0$-helices maintain the helical structure and orient freely throughout the simulation without binding with neighboring monomers; this is consistent with their expected role in membrane anchoring as discussed below. Therefore, the filament is largely stabilized by interactions among the neighboring ${\alpha }_1$-, ${\alpha }_2$-, and ${\alpha }_3$-helices, which feature both hydrophobic and electrostatic contacts as illustrated in Fig. 3 c: hydrophobic residues Met87, Ile94, Ala97, Leu101, and Met104 of ${\alpha }_2$ strongly interact with the hydrophobic residues Met107, Met114, Ile117, and Leu121 of ${\alpha }_3$ of the neighboring monomer, and positively charged residues Lys21, Arg25, and Lys36 of ${\alpha }_1$ and Lys69 of ${\alpha }_2$ interact with the negatively charged residues Glu85, Glu88, Glu95, Glu102, and Glu109 of ${\alpha }_2$ of the neighboring monomer.

Filament mechanical properties

To probe the intrinsic bend and twist of the Vps32 filament, we simulate a finite filament consisting of 21 monomers. As shown in Fig. 4 a, the equilibrated filament structure exhibits a significant degree of twist (∼11°) and bending, ∼20° along the “in plane” (xz plane) and ∼44° along the “perpendicular plane” (xy plane) of the filament (see Appendix I); the estimated radius of curvature for the central part of the filament is 30.5 ± 9.6 nm (see Fig. S10), which falls in the range estimated in experiments based on electron microscopy images (23,41,59). The elastic moduli for stretch, bending, and twist (torsion) are computed using the law of equipartition of energy, which was used recently to compute mechanical properties of an actin filament (60).

Figure 4.

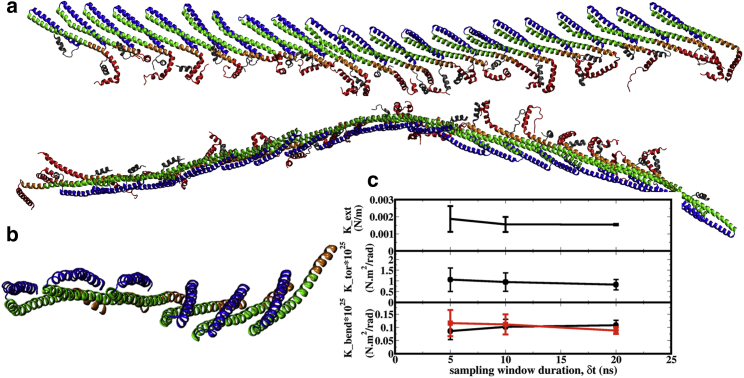
(a) Top (top) and side (bottom) view of an equilibrated protein filament that contains 21 protein monomers without periodicity along x. (b) A zoomed-in view for a few monomers to illustrate the twist in the filament is shown. (c) Stretch, twist, and bending moduli of the filament computed as functions of sampling window duration (see Appendix I) are shown. To see this figure in color, go online.

The elongation or stretch modulus of the one-dimensional filament is ∼0.16 × 10⁻² N/m, which is ∼30 times lower than that of an actin filament (∼4.4 × 10⁻² N/m) (61), suggesting that the Vps32 filament is much more flexible than the actin filament. The Vps32 spirals should be radially compressible because of this relatively high flexibility, as observed in the experiment (41). The torsional or twist modulus of the filament is ∼0.8 × 10⁻²⁵ N ⋅ m² ⋅ rad⁻¹, which is ∼40 times higher than that of an actin filament (∼0.2 × 10⁻²⁶ N ⋅ m² ⋅ rad⁻¹) (62). The high value of the twist modulus is due to the larger protein-protein interface, which is stabilized by strong electrostatic and hydrophobic interactions as discussed earlier. The bending modulus of the filament (∼0.1 × 10⁻²⁵ N ⋅ m² ⋅ rad⁻¹) is approximately one order of magnitude lower than that of an actin filament (∼0.7 × 10⁻²⁵ N ⋅ m² ⋅ rad⁻¹) (63). The lower bending modulus of the Vps32 filament is consistent with its lower persistence length (∼260–800 nm) estimated from the experiment (23,41) as compared to an actin filament (∼17 μm) (64). The spontaneous bending helps drive the filament to adopt a spiral configuration as observed in a transmission electron microscopy image of the filament (23).

Membrane-protein interface

The Vps32 trimer remains stable and is readily absorbed on the membrane surface as shown in Fig. 5 a. Each monomer maintains its elongated open form similar to the crystal structure and solution simulations. Independent simulations are carried out keeping the elongated ${\alpha }_2$- and ${\alpha }_3$-helices closer to the membrane surface in one case and with the ${\alpha }_1$-helix closer to the membrane surface in the other case (Fig. S3, a and b). Although the protein trimer remains adsorbed on the membrane surface in both simulations, the binding is visibly stronger when the elongated ${\alpha }_2$- and ${\alpha }_3$-helices are in contact with the membrane as reflected by the considerably larger number of protein-membrane contacts (Fig. S3 c). This finding is consistent with the recent experimental result of Buchkovich et al. (65) that the mutation of cationic residues in ${\alpha }_1$ to anionic amino acids led to minor decrease in the membrane-binding activity of Vps32; this is expected because ${\alpha }_1$-helices are not in contact with the membrane as they remain on top of the ${\alpha }_2$-helices (Fig. 5 b). By contrast, charge inversion of cationic residues in the ${\alpha }_2$- and ${\alpha }_3$-helices, including Lys60, Lys64, Lys68, Lys71, Lys79, Lys112, and Lys115, led to significantly decreased membrane-binding activity of the Vps32 filament; these residues are indeed in close contact with the membrane in the preferred protein-membrane interface observed in the current MD simulations (Fig. 5 d).

Figure 5.

(a) An equilibrated structure of a Vps32 trimer (represented in ribbon) absorbed on the membrane surface. (b) The ${\alpha }_2$- (green) and ${\alpha }_3$- (brown) helices are adsorbed on the membrane surface; only phosphorus atoms of the lipid heads are shown for clarity. For the analysis of an alternative binding mode, see the Supporting Materials. (c) ${\alpha }_0$-helices (white and green spheres) of the trimer are inserted into the membrane. The hydrophobic residues (white spheres) are closer to the membrane center compared to the hydrophilic residues (green spheres), which are closer to the membrane top surface. (d) The positively charged lysine residues 60, 64, 68, 71, 79, 112, and 115 (blue spheres) are strongly adsorbed on the membrane surface. (e) Only one of the three ${\alpha }_4$-helices (red) is adsorbed on the membrane surface, which is represented by phosphorous atoms (bile color). To see this figure in color, go online.

For the remaining two α-helices, ${\alpha }_0$ and ${\alpha }_4$, experimental results (65) suggested that the ${\alpha }_0$-helix is required for membrane binding of Vps32; deletion of the N-terminal helix completely abolished the ability of Vps32 to bind to the membrane. As discussed above, the ${\alpha }_0$-helix does not engage in interaction with other protein motifs and therefore is readily available for membrane binding. As shown in Fig. 5 c, all three amphipathic ${\alpha }_0$-helices are inserted into the membrane such that the hydrophobic residues of ${\alpha }_0$ pack well with the hydrophobic core of the membrane, in agreement with the experimental observation. By contrast, as shown in Fig. 5 e, only one out of three ${\alpha }_4$-helices is adsorbed on the membrane surface during the simulation; qualitatively similar behaviors are seen in two other independent MD simulations. Therefore, the interaction between ${\alpha }_4$ with the anionic membrane is not as strong as those of the ${\alpha }_2$- and ${\alpha }_3$-helices, probably because of the presence of negatively charged residues (Asp127, Glu128, Asp131, Glu132, Glu135, Glu138, Asp141, Glu142, and Asp145) in ${\alpha }_4$.

In the crystal structure, favorable electrostatic interactions between the negatively charged residues of ${\alpha }_4$ and positively charged residues of ${\alpha }_2$ stabilize the two-dimensional structure shown in Fig. S4. In the presence of a membrane surface, however, the positively charged lysine residues 64, 68, and 71 of ${\alpha }_2$ are adsorbed on the membrane surface as shown in Fig. 5 d and also suggested by Buchkovich et al. (65). Thus, these lysine residues are not available for bridging between protofilaments in a membrane environment, suggesting that alternative two-dimensional structures such as spiral filaments are favored on the membrane surface; as discussed in (23), the distance between neighboring protofilaments is also likely longer than what the crystalline environment implies because of the presence of the ${\alpha }_5$-helix. We also investigated if the ${\alpha }_4$-helices of one protofilament can bind to the ${\alpha }_1$-helices of the neighboring protofilament because the latter do not bind to the membrane surface. As shown in (Fig. S5), after equilibration, several ${\alpha }_4$-helices move away from the ${\alpha }_1$-helices, suggesting that interaction between them is not strong.

Protein-induced membrane curvature

Generation of intralumenal vesicles requires maintaining a balance of competing positive and negative membrane curvatures (59,65). The membrane curvature at the bottom and inside of an invagination is negative, but the membrane curvature at the rim of the invagination is positive. Buchkovich et al. (65) proposed that the helical nature of the ESCRT-III can stabilize the negative curvature of an invagination and thus the insertion of its N-terminal amphipathic containing hydrophobic residues should promote a competing or opposing positive curvature. To verify this hypothesis, we carry out simulations to investigate if the N-terminal of Vps32 is capable of generating local positive curvature in the membrane.

As discussed in previous work (66), periodic boundary conditions discourage membrane curvature development with small membrane patches. Therefore, we adopt a membrane ribbon protocol (66) (see Fig. S6) that features only periodicity in the y direction, whereas membrane edges are formed in the x direction; the length of the x dimension is taken to be substantially longer, ∼32.5 nm, which allows membrane bending without significant end effects.

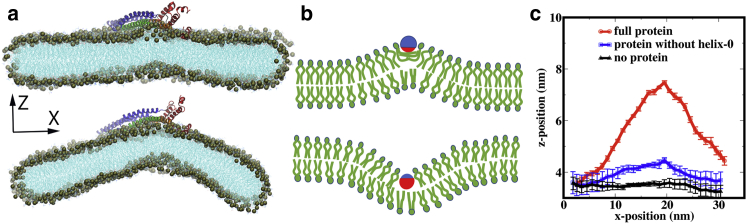
During the simulation, the membrane ribbon gradually adapts a positively curved structure within 20 ns (Fig. 6 a, top$\to$bottom), and the curvature is maintained for the rest of the 85 ns simulation. The curvature formation is likely due to insertion of the amphipathic ${\alpha }_0$ helices inside the membrane as suggested by Zimmerberg and Kozlov (67). Unlike the BAR proteins, which induce membrane curvature mainly because of their intrinsic concave morphologies, the amphipathic helices induce curvature by directly interacting with lipids and changing their packing and orientation with respect to the membrane surface. The nature of the membrane curvature (i.e., positive or negative curvature) depends on the chemical nature of the amphipathic helix as illustrated in Fig. 6 b. If the hydrophilic interactions are stronger than the hydrophobic interactions, then the hydrophilic part remains close to the membrane surface to gain access of the hydrophilic lipid heads and solvent, with the hydrophobic part inserting shallowly into the membrane to interact with the hydrophobic lipid tails. In this scenario, the proximal lipid tails change their orientation such that a positive mean curvature is formed as shown in Fig. 6 b (top). However, if the hydrophobic interactions are much stronger than the hydrophilic interactions, then the helix enters much deeper inside the membrane and lipid molecules change their orientations toward a negative mean curvature as shown in Fig. 6 b (bottom); note that the latter scenario was discussed mainly with theoretical analyses (68,69) rather than direct experimental observation. As shown in Fig. 5 c, the hydrophilic residues of Vps32 ${\alpha }_0$-helices remain close to the membrane surface; thus, the hydrophobic residues also remain relatively far from the membrane center. Hence, the mechanism shown at the top of Fig. 6 b applies, leading to a positive mean curvature as indeed observed in the membrane ribbon simulations.

Figure 6.

(a) Initial configuration of the Vps32 trimer-membrane complex for membrane curvature simulation (see the main text for details). A significant positive mean curvature is generated in the membrane by the protein. (b) A schematic diagram of the positive (top) and negative (bottom) mean curvature formation mechanism is shown. The green, blue, and red colors represent the lipid, hydrophilic part of the amphipathic object, and hydrophobic part of the amphipathic object, respectively. (c) Shown is the z position of the membrane midplane (averaged along the y direction) as a function of the x position showing large mean curvature in the presence of the Vps32 trimer, much less curvature when ${\alpha }_0$-helices are removed from the protein, and no curvature in the absence of the protein on the membrane surface. See the main text for details. To see this figure in color, go online.

To further verify that the positive membrane curvature generated by the Vps32 protein is mainly due to the insertion of its amphipathic ${\alpha }_0$-helix, several control simulations are carried out; these include a membrane ribbon without any protein and a simulation with the same Vps32 trimer on top of a membrane ribbon but with the ${\alpha }_0$-helices removed. As shown in Fig. 6 c, the protein-free membrane ribbon features a flat profile on average, and the trimer without the ${\alpha }_0$-helices also features a substantially reduced curvature compared to the original trimer model. These observations further validate the simulation protocol and support the critical role of the ${\alpha }_0$-helices in generating the local positive mean curvature.

Discussion

The simulation results show that the ${\alpha }_0$-helices indeed spontaneously insert into the membrane because of their amphipathic nature. The hydrophobic residues of the inserted ${\alpha }_0$-helices perturb the tail orientations of the proximal lipids, causing a pressure imbalance between the two leaflets that leads to a strong local positive curvature on the membrane; this is consistent with the hypothesis (65) that the ESCRT-III N-terminal helices generate positive curvature to balance the negative curvature of invagination produced by the spiral scaffold.

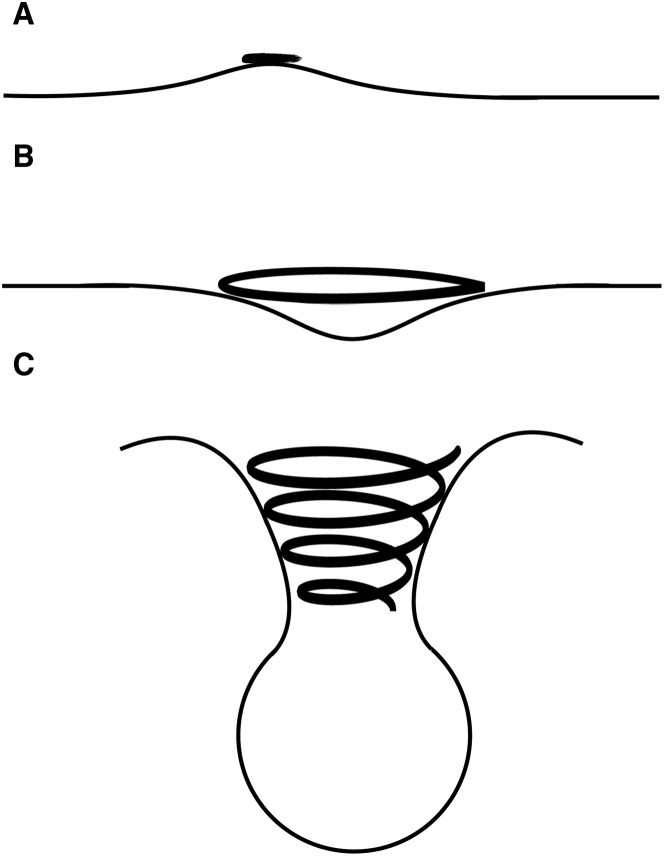
Based on these findings, we propose a plausible mechanism for how ESCRT-III filament formation drives membrane deformation (Fig. 7). As the filament initially grows on the membrane surface into a circular ring, the local positive curvature generated by the ${\alpha }_0$-helices might induce a negative curvature at the center of the circular ring. To test this hypothesis, we have performed a pair of exploratory simulations for a larger membrane ribbon with two protein trimers on top and separated by a certain distance: ∼25 nm in one case and ∼50 nm in the other, which can be considered as two ends of the chord of a circular ring (Fig. 8, a and b). Because of the much larger system sizes, only 20 ns of simulations have been collected for each case, and much longer simulations likely require coarse-grained simulations, which we will report separately.

Figure 7.

A cartoon representation of a plausible mechanism of membrane curvature development catalyzed by Vps32 filaments. (a) Initial adsorption of Vps32 induces local positive curvature because of the insertion of the N-terminal helix; (b) adsorption of a ring of Vps32 polymers induces a negative curvature at the center of the circular ring; (c) as the Vsp32 filament continues to elongate, bending and twisting deformations of the filament lead to the formation of a three-dimensional (3D) helical spiral that creates the neck of the invagination.

Figure 8.

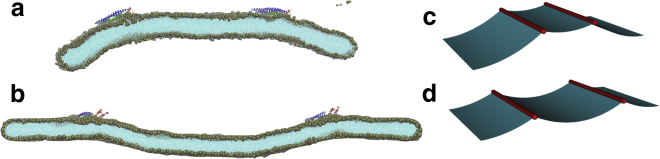
Exploratory atomistic simulation of membrane deformation with two Vps32 trimers separated by (a) ∼25 nm and (b) ∼50 nm on a membrane ribbon. (c and d) Results of a continuum mechanics analysis that illustrate the effect of two filaments separated by different distances on the shape of the membrane are shown; the spontaneous curvature is zero outside of the region of the filament, shown here in red. See Appendix II for details. Three-dimensional (3D) rendering is done using the software package MayaVi(74). To see this figure in color, go online.

These exploratory simulations nevertheless provide interesting hints: when the distance between the trimers is relatively short (∼25 nm), the positive mean curvature generated by one trimer compensates the positive mean curvature generated by the other, leading to flattening of the region between the two trimers (Fig. 8 a). As the distance between the trimers is increased to ∼50 nm, a negative mean curvature is induced at the center as a combined effect of two positive mean curvatures generated by the individual trimers (Fig. 8 b), suggesting that a complete circular ring would likely generate a stronger negative mean curvature (Fig. 8, c and d), a result in fact supported by a continuum mechanics analysis (see Appendix II). We note that the amount of lipids encircled by the ring of diameter ∼50 nm corresponds to a ∼12-nm-radius vesicle, which is the typical size of vesicles generated by ESCRT-III polymers as observed in yeast (25).

As the filament continues to grow, it spontaneously generates a twist in the structure as revealed in our simulations. The intrinsic twist in the filament causes the cationic membrane-binding interface formed by Lys60, Lys64, Lys68, Lys71, Lys79, Lys112, and Lys115 residues to gradually move away from the membrane surface as can be visualized in Fig. S7. Because the twist modulus of the filament is high, as discussed above, the filament no longer grows on a flat membrane surface; rather, it bends down the membrane to achieve a more energetically favorable membrane-filament interface. Because of the relatively low bending modulus of the filament and strong filament-membrane interaction, the filament prefers to grow in a three-dimensional (3D) helical spiral, which creates the neck of the invagination (Fig. 7 c).

The typical distance between the neighboring helical turns of the spiral is lower than 20 nm (23); hence, the local positive curvature generated by an individual helical turn is cancelled out by the neighbors, thereby generating a flat neck of the invagination as shown in Fig. 8 c. However, a positive membrane curvature should still exist at the rim of invagination because the local effect of the outermost helical turn cannot be completely cancelled out. This positive membrane curvature at the rim stabilizes the invagination by balancing the negative mean curvature generated by the 3D spiral scaffold.

In summary, we have performed MD simulations to study atomistic resolution structural properties of a Vps32 filament and its mechanical properties, which were not readily available from experiments. Vps32 adopts an open configuration in the filament assembly in solution, and the filament is stabilized by both electrostatic and hydrophobic interactions across the monomer-monomer interface. The filament prefers to bind with the membrane via elongated ${\alpha }_2$- and ${\alpha }_3$-helices rather than via ${\alpha }_1$-helices, likely because of the larger number of positively charged lysine residues present in the former. The N-terminal helices serve the dual role of anchoring the protein on the membrane surface and generating a local positive mean curvature in the membrane. The protofilament exhibits an intrinsic bend and twist, and the competition between these mechanical deformations and protein-membrane bending constitutes an important driving force for the membrane deformations required for the ESCRT-driven vesicle fission process.

We end by highlighting that we have focused here on a single-component filament model consisting of yeast Vps32 (snf7p). Thus, the results regarding protein-protein interaction in the filament and protein-membrane interactions are likely different from those of other ESCRT-III subunits. For example, another well-characterized ESCRT-III protein, CHMP1B/Did2, was shown to feature much more extensive protein-protein interactions in the copolymer formed together with IST1 (45). However, it is well appreciated that CHMP1B and Vps32 differ in many respects. Most notably, Vps32 functions during inward membrane bending, whereas CHMP1B has largely been implicated in outward membrane bending (45). Therefore, they likely feature different protein-protein and protein-membrane interactions. Additionally, Vps32 filaments have been shown to be highly dynamic, capable of undergoing rapid subunit exchange (70). Thus, the head/tail type of protomer binding mode studied here appears to be more consistent with such inherent dynamics, as compared to the tight interlocking arrangement involving six protomers as observed for CHMP1B (45). Finally, we note that recent studies (71,72) suggested that Vps32 filament alone did not appear to generate major membrane curvature, whereas copolymers with other ESCRT components led to remarkable 3D helical membrane tubes. However, our previous work (38) demonstrated that ESCRT-II/Vps20-nucleated Vps32 polymers strongly prefer association with highly bent membranes over flat membranes. These contrasting findings emphasize how various factors, including protein concentration and filament nucleation, may influence the membrane curvature sensing and membrane remodeling activities of ESCRT polymers, clearly warranting further analysis. Along this line, going beyond the single-component filament model analyzed here represents an exciting challenge that almost certainly requires an integrated experimental and computational approach.

Author Contributions

Q.C., S.E.S., and A.A. designed the project. T.M. conducted the molecular simulations. T.M. and Q.C. analyzed the simulation data. W.L. and S.E.S. conducted the continuum mechanics analyses. T.M., Q.C., S.E.S., and A.A. wrote the article.

Editor: D. Peter Tieleman.

Appendix I: Calculation of Protofilament Mechanical Properties

The relevant mechanical properties are analyzed using the simulation of a restraint-free and finite protofilament consisting of 21 monomers (see Fig. S8 for the simulation setup).

The extensional spring constant is calculated using the equipartition theorem. A small fluctuation, l, around the equilibrium length, $\langle L\rangle$, of the filament generates a restoring force, $F=-K_{ext}\left(l/\langle L\rangle \right)$, where K_ext is the extensional spring constant or stretch modulus per 1 μm length (60) ($K_{ext}=k_{ext}\left(\langle L\rangle /1\mu \mathrm{m}\right)$, where K_ext is the normally defined extensional spring constant). The restoring energy is defined by $E_{ext}=-\int Fdl\text{'}=K_{ext}{l}^2/2\langle L\rangle$. Using the equipartition theorem, $K_{ext}\langle l^2\rangle /2\langle L\rangle =k_{B}T/2$, giving rise to $K_{ext}=\langle L\rangle k_{B}T/\langle l^2\rangle$, where $\langle l^2\rangle ={\langle {\left(L\left(t\right)-{\langle L\left(t\right)\rangle }_{\delta t}\right)}^2\rangle }_{\delta t}$ and k_B is the Boltzmann constant. The sampling window duration is δt and ${\langle \cdots \rangle }_{\delta t}$ denotes the average over a time $\left(t-\delta t/2<t<t+\delta t/2\right)$.

For a small twist in the filament, θ_t, the restoring torque, $\tau =-K_{tor}\left({\theta }_t/\langle L\rangle \right)$, where K_tor is the torsional or twist modulus per unit length (60) (i.e., $K_{tor}=k_{tor}\langle L\rangle$, where k_ext is the normally defined torsional spring constant). The restoring torque energy is defined by$E_{tor}=-\int \tau d{\theta }_t\text{'}=K_{tor}{\theta }_t^2/2\langle L\rangle$. Using the equipartition theorem, $K_{tor}=\langle L\rangle k_{B}T/\langle {\theta }_t^2\rangle$, where $\langle {\theta }_t^2\rangle ={\langle {\left({\theta }_t\left(t\right)-{\langle {\theta }_t\left(t\right)\rangle }_{\delta t}\right)}^2\rangle }_{\delta t}$. Similarly, the bending modulus is $K_{bend}=\langle L\rangle k_{B}T/\langle {\theta }_b^2\rangle$, where $\langle {\theta }_b^2\rangle ={\langle {\left({\theta }_b\left(t\right)-{\langle {\theta }_b\left(t\right)\rangle }_{\delta t}\right)}^2\rangle }_{\delta t}$.

The twist or torsional angle, θ_t, of the filament is defined as the angle between two vectors $V_{t1}^p$ and $V_{t2}^p$, which are yz-plane projections of vectors $V_{t1}$ and $V_{t2}$ (defined below), respectively (Fig. 9, illustrated using cartoon). The filament can bend along the plane containing the proteins and along the plane perpendicular to it as well. Thus, to calculate the in-plane bending modulus, we define the bending angle θ_b as the angle between xz-plane projections of two vectors $V_{b1}$ and $V_{b2}$ (Fig. 9), defined below. Similarly, for the perpendicular-plane bending modulus, the bending angle θ_b is defined as the angle between xy-plane projections of two vectors $V_{b1}$ and $V_{b2}$ (Fig. 9). For the filament, $V_{t1}$ is defined from the center of ${\alpha }_3$-helix to the center of ${\alpha }_2$-helix of a monomer; $V_{t2}$ is an analogous vector but defined in the opposite direction; that is, it is defined from the center of ${\alpha }_2$-helix to the center of ${\alpha }_3$-helix of another monomer (Fig. 9). The vector $V_{b1}$ is defined as joining the center of ${\alpha }_2$- and ${\alpha }_3$-helices of a monomer and the center of corresponding helices in the neighboring monomer. The time series for the twist and bending angles are shown in Fig. S9. The moduli are calculated for different sampling window durations, $\delta t$ = 5, 10, and 20 ns, to check for convergence.

Figure 9.

A schematic showing different vectors for calculating bend and twist angles of the filament. The α-helices in each monomer are shown schematically as rectangles with the same color coding as Fig. 2. To see this figure in color, go online.

Appendix II: Membrane with Lines of Spontaneous Curvature

We consider the Helfrich energy (73) describing the energetics of a lipid bilayer initially in the shape of a rectangular sheet of length 2L and width 2W as follows:

$$\mathcal{E}=\underset{\Omega }{\int }\frac{B}{2}{\left(2H-C_0\right)}^2+\overline{B}{\kappa }_{G}dS,$$ (A1)

where $2H=c_1+c_2$ is the mean curvature and ${\kappa }_G$ is the Gaussian curvature, $\Omega$ denotes the membrane surface, and dS is the surface area element. We parameterize the surface by arclength $s\in \left[-L,L\right]$ in the $\hat{\mathit{x}}$ direction and $y\in \left[-W,W\right]$ in the $\hat{\mathit{y}}$ direction, and we denote the membrane position by $\mathit{X}\left(s,y\right)=\left(X\left(s\right),y\right)$, with $X\left(0\right)=0$. $C_0$ is the spontaneous curvature, which we will assume to be zero outside of two thin parallel bands aligned with the $\hat{\mathit{y}}$ axis, each placed a distance S away from the center of the sheet at s = 0.

Given that the membrane is thin, we expect it to be roughly inextensible; thus, we conveniently define the tangent angle $\varphi \left(s\right)$ such that ${\mathit{X}}_s=\text{cos}\left(\varphi \right)\hat{\mathit{x}}+\text{sin}\varphi \left(s\right)\hat{\mathit{y}}$. Then $2H={\varphi }_s$ (and ${\kappa }_G=0$ in two dimensions). In this case, the energy may be written as follows:

$$\mathcal{E}=\underset{-L}{\overset{L}{\int }}\frac{B}{2}{\left({\varphi }_s-C_0\left(s\right)\right)}^{2}ds.$$ (A2)

A variational derivative of the energy with respect to ϕ reveals the simple expression at equilibrium as follows:

$${\varphi }_{ss}-C_0\text{'}\left(s\right)=0.$$ (A3)

The membrane is now assumed to be flat far from the region of forcing, which requires the application of a moment at the far edge ($s=L$). The boundary conditions for the above are then $\varphi \left(0\right)=0$ (by symmetry) and $\varphi \left(L\right)=0$. The resulting solution is

$$\varphi \left(s\right)=\varphi \left(0\right)+{\int }_0^s{C}_0\left(s\text{'}\right)ds\text{'}-\frac{s}{L}{\int }_0^L{C}_0\left(s\right)ds.$$ (A4)

If the support of the spontaneous curvature is very small, the mathematical idealization $C_0\left(s\right)=c_0\delta \left(s-S\right)$, where δ is the Dirac delta function, results in a very clean result. In this case, we have ${\varphi }_s=0$ for $s\ne S$, and ${\left[{\varphi }_s\right]}_S=c_0$, where ${\left[{\varphi }_s\right]}_S={\varphi }_s\left(S^{+}\right)-{\varphi }_s\left(S^{-}\right)$ is the jump in ${\varphi }_s$ at $s=S$, resulting in the following:

$$\varphi \left(s\right)=\{\begin{array}{cc}-c_{0}s/L,& s<S\\ -c_{0}s/L+c_0,& s>S\end{array}.$$ (A5)

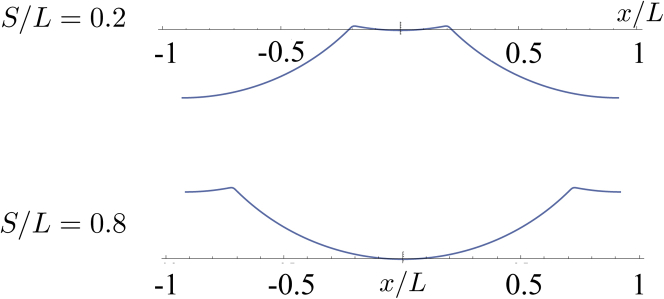
We have recovered an intuitive result: the energy-minimizing membrane shape is that of two circular regions (with constant bending moment) glued together. This configuration distributes the bending moment evenly throughout each section. Clamping at the far end, and the curvature at the point S, dictates whether the point s = 0 is above or below the region of forcing: simple geometry indicates that the crossover value of S is L/2. Fig. 10 displays the resulting physical shapes for two different filament locations ($S/L=0.2$ and $S/L=0.8$) with $c_0=-1$, and indeed we see that the effects on the membrane depend on the position of activity, as observed in the MD simulations (Fig. 8, a and b).

Figure 10.

Predicted membrane shapes for two different values of S/L with $c_0=-1$. To see this figure in color, go online.