LEARNING 3D WHITE MATTER MICROSTRUCTURE FROM 2D HISTOLOGY

Abstract

Histological analysis is typically the gold standard for validating measures of tissue microstructure derived from magnetic resonance imaging (MRI) contrasts. However, most histological investigations are inherently 2-dimensional (2D), due to increased field-of-view, higher in-plane resolutions, ease of acquisition, decreased costs, and a large number of available contrasts compared to 3-dimensional (3D) analysis. Because of this, it would be of great interest to be able to learn the 3D tissue microstructure from 2D histology. In this study, we use diffusion MRI (dMRI) of a squirrel monkey brain and corresponding myelin stained sections in combination with a convolution neural network to learn the relationship between the 3D diffusion estimated axonal fiber orientation distributions and the 2D myelin stain. We find that we are able to estimate the 3D fiber distribution with moderate to high angular agreement with the ground truth (median angular correlation coefficients of 0.48 across the unseen slices). This network could be used to validate dMRI neuronal structural measurements in 3D, even if only 2D histology is available for validation. Generalization is possible to transfer this network to human stained sections to infer the 3D fiber distribution at resolutions currently unachievable with dMRI, which would allow diffusion fiber tractography at unprecedented resolutions. We envision the use of similar networks to learn other 3D microstructural measures from an array of potential common 2D histology contrasts.

1. INTRODUCTION

Diffusion magnetic resonance imaging (dMRI) has proven a valuable tool in the neuroscience community due to its ability to infer tissue composition, microstructure, and structural connectivity of the brain [1, 2]. In the white matter, diffusion of water molecules is sensitive to the size, shape, and orientation of extra and intra-cellular tissue components [3], making it possible to infer the distribution of axonal fiber orientations in each dMRI voxel from a set of diffusion measurements, a model typically referred to as the fiber orientation distribution (FOD). These fiber orientation estimates can be used to reconstruct the structural connections between brain areas in a process known as fiber tractography [4–6]. However, tractography has been shown to have several fundamental limitations [7, 8], and validating the accuracy and reproducibility of these techniques is critical for them to become reliable medical and research tools.

Towards this end, the gold standard for validating dMRI (and a number of other contrasts) is in comparison to histology. For example, validation has been performed by (A) comparing tractography against histological tracers injected into the brain [9–11], (B) comparing estimated fiber orientations against myelin or axon stains [12–14], and (C) comparing diffusivity measures against cell or neuronal densities [15]. However, these studies have been limited to 2D analysis of tissue sections imaged with bright field microscopes. Very few studies have performed 3D validation [16, 17] due to limited field-of-view, time, and costs associated with 3D acquisitions. In contrast, 2D light microscopy is relatively inexpensive, can cover an entire tissue slice at high in-plane resolution, can be acquired on dozens to hundreds of sections of the same brain, and can be stained for a number of contrasts associated with tissue microstructure (for example, myelin, Nissl, tracers, etc.).

With this in mind, it would be of great interest to the neuroimaging community to be able to learn the 3D tissue microstructure from 2D histology. Thus, in this study, we use ex vivo diffusion MRI of a squirrel monkey brain and corresponding myelin stained sections in combination with a convolutional neural network (CNN) to learn the relationship between the 3D diffusion estimated FOD and the 2D myelin stain. This network can be used to validate dMRI structural measurements in 3D. Additionally, this pre-trained network could be transferred to human stained sections to infer the 3D fiber distribution at resolutions currently unachievable with dMRI, allowing fiber tractography at unprecedented resolutions. We envision the use of similar networks to learn other 3D microstructural measures from an array of potential common 2D brightfield contrasts.

2. METHODS

Here, we aim to use 2D myelin-stained micrographs, from which traditionally only 2D orientation information is extracted, in order to estimate the 3D fiber structure in these locations (Figure 1).

Fig. 1. The problem.

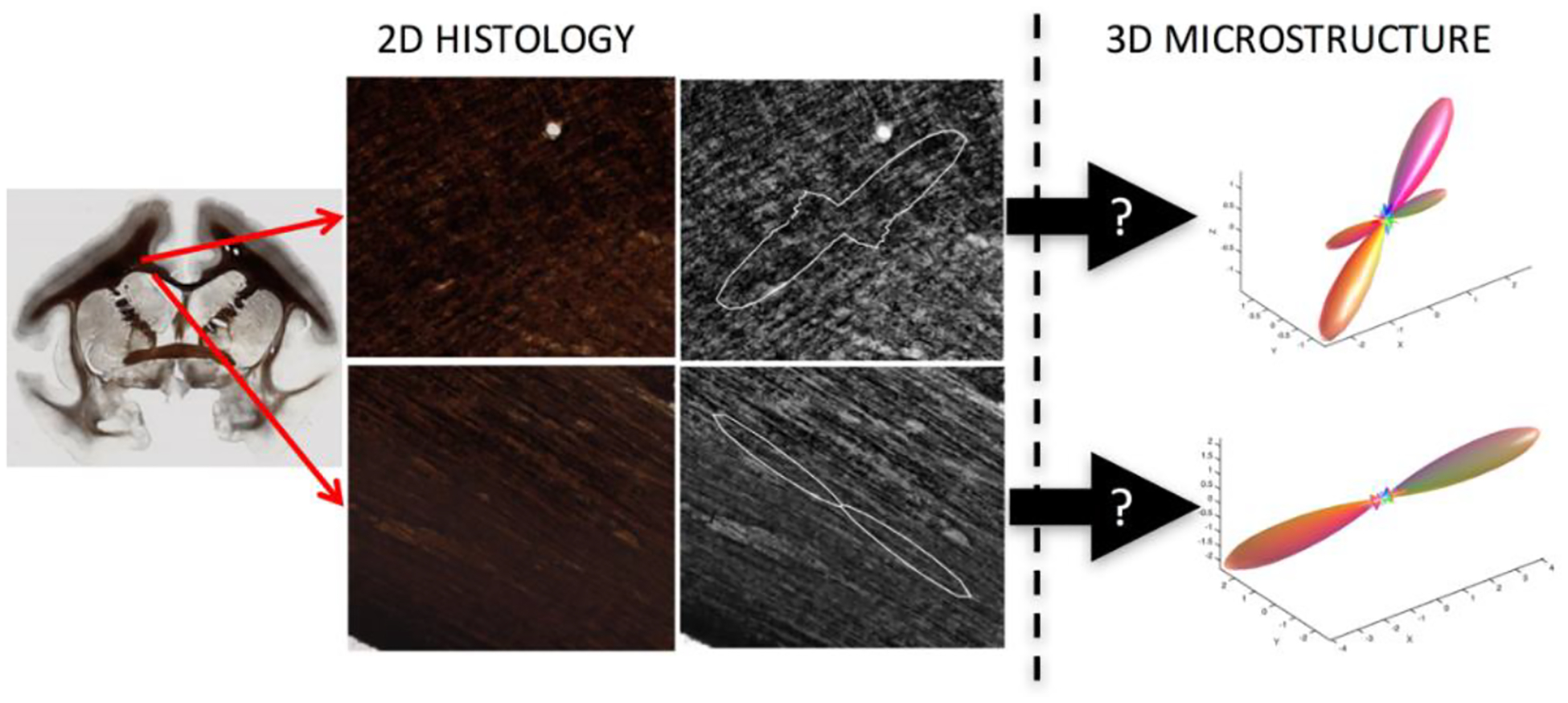
Conventional micrographs are inherently 2D representations of the underlying tissue. Here, we aim to use Brightfield microscopy of myelin-stained tissue to estimate the 3D fiber orientation distribution

5.1. Data acquisition - MRI

MRI experiments, histological methods, and data registration were performed on an ex vivo squirrel monkey brain following the procedures described in [18, 19]. Briefly, ex vivo imaging was performed a Varian 9.4 T magnet, with diffusion weighted scans acquired using a PGSE multi-shot spin-warp imaging sequence (TR = 4.6 s, TE = 42 ms, 32 gradient directions, b ≈ 1000s/mm², 300 μm voxel, 192×128×115 matrix). Diffusion processing was performed in “histology” space after registration (see below) using constrained spherical deconvolution [20] for voxel-wise reconstruction, resulting in diffusion FODs reconstructed in histology space.

5.2. Data acquisition - Histology

Following scanning, the brain was frozen and cut serially on a microtome in the coronal plane at 50 um thickness. Every 6th section (150um) was mounted and stained with a gallyas silver stain [21] to identify myelinated axons. Whole-slide brightfield microscopy was performed using a Leica SCN400 Slide Scanner at 20× magnification, resulting in a maximum in-plane resolution of 0.5 um/pixel. To ease computation and memory burdens images were down-sampled to 2 um/pixel to serve as input to the network. Finally, a multi-step registration procedure was utilized [22] that involves 2D affine and 2D non-rigid transformations to an intermediate “frozen tissue block space”, followed by 3D affine and 3D non-rigid transformations to MRI data. Deformation fields produced by registration steps allow transfer of any set of data to any desired space for comparisons [18], in this study, we chose to process dMRI data in histology space, resulting in high resolution myelin images aligned with corresponding dMRI derived FoDs.

5.3. The network

We use a CNN architecture that consists of four 2D convolutional layers (Figure 2). The input is a “patch” of the high-resolution myelin image of size 256×256 pixels. The patch has a corresponding dMRI FoD, represented using spherical harmonic (SH) basis functions, in this case using 6^th order SH of size 1×28.The C1, C2, C3, C4 layers consist 128×128, 64×64, 32×32 and 16×16 feature maps. For all 2D convolutional layers the kernel size was set to (3, 3) and strides at (2, 2). All 2D convolutional layers were activated by ‘Relu’ followed by batch normalization and 2D max pooling was used except for C1 where only max pooling was used. The C4 layer was flattened and a dropout of 0.5 was used while connecting to a fully connected layer of 28 neurons which is equivalent to the output of the network a set of 6^th order SH coefficients.

Fig. 2. CNN architecture.

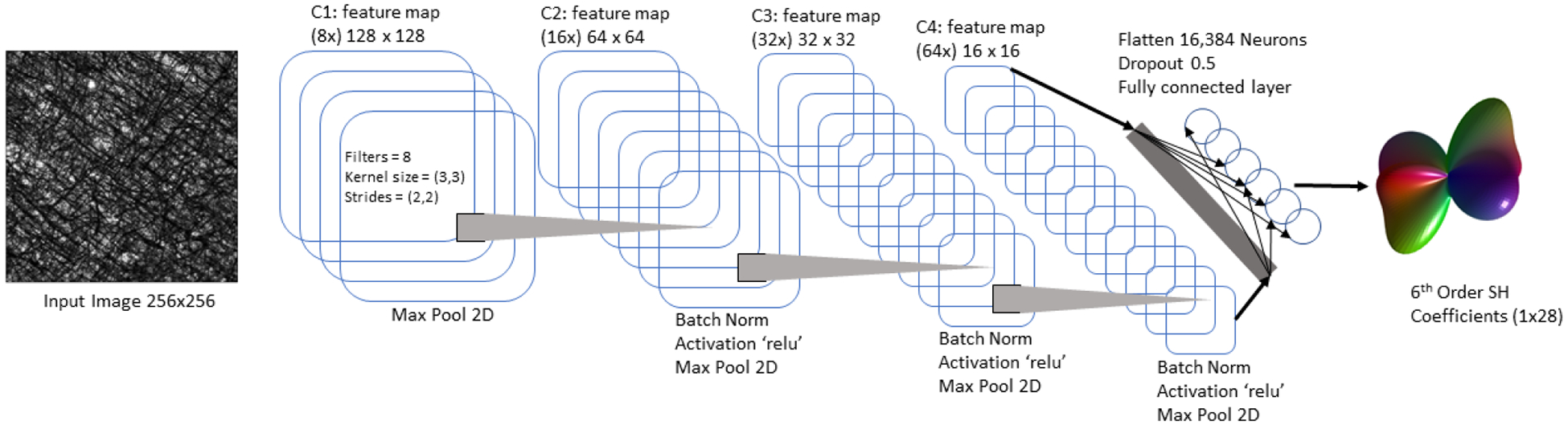
This architecture begins with a single input patch of size 256×256x with a corresponding output of 6^th order SH coefficients (1×28). The network consists of four convolutional layers with subsequent down-sampling and flattened towards the end to a fully connected dense layer. Relu activation, batch normalization and max pooling have been used for all convolutional layers.

Ten myelin-stained micrographs were utilized in this study. Nine slices were used for the training and the validation of the CNN and a single slice was completely withheld for testing of the CNN. From these images, a total of 248,304 patches were generated with corresponding outputs. 30,000 of these were randomly selected for validation of the network to prevent over-fitting of the network. This leads to the training data being set at 218,304 patches. The CNN was trained with the loss function of ‘mean squared error’. The optimizer of the network was used as ‘RMSProp’. Batch size was set to 1000 as feeding more patches were not possible due to limitation of GPU memory. The network was trained for 50 epochs after which it attained convergence as per cross-validation criteria. A Nvidia 1080 Ti GPU was used to train the network.

3. RESULTS

Figure 3 shows the results of applying this network to the unseen myelin-stained section. The CNN iterated through 50 epochs, minimizing the mean squared error (MSE) of SH coefficients. MSE for the unseen slice (Figure 3, A) are on the order of that seen during training. The converged network attained MSE of 0.025, which is close to the median shown for the hidden slice. Additionally, the estimated 3D FODs show a range of agreement with ground truth, with ACCs ranging from negative to nearly perfect (Figure 3, B), with a median value of 0.48, indicating moderate predication ability. Example myelin-stained patches, the ground truth FODs, and predicted FODs are shown for varying levels of reconstruction accuracy (Figure 3, C–F).

Fig. 3. Estimated 3D FODs show moderate to high agreement with ground truth.

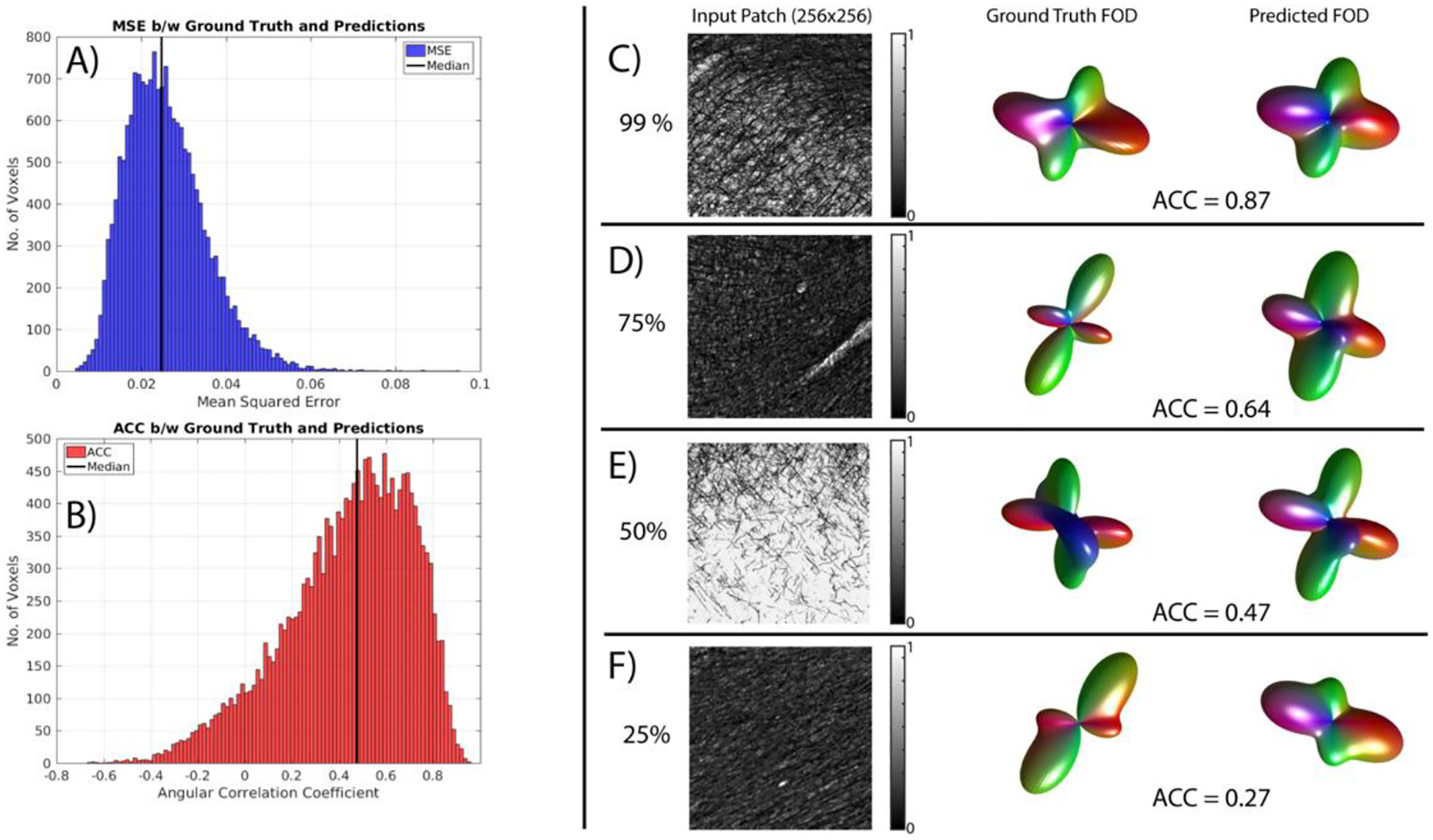
The CNN minimizes the MSE of SH coefficients between ground truth and predictions (A), resulting in ACC values with median correlations of 0.49. Example myelin-stained patches, ground truth FODs and predicted FODs are shown for varying levels of reconstruction accuracy (C-F).

Figure 4 visualizes the predicted and ground truth FODs reconstructed across the full unseen slice. Visualizing across a larger FOV shows spatial consistency in predictions, in agreement with expected anatomy and dMRI FODs. This suggests the possibility of utilizing this approach for fiber tractography on 2D images. While many regions show high prediction power (Figure 4, left), this technique can result in largely inaccurate FOD reconstructions in others (Figure 4, right).

Fig. 4. Estimating 3D FODs performed across an entire slice.

Predicted FODs (top) from 2D histology are shown along with the ground truth fiber geometries (bottom) for two regions. One exhibiting high agreement (left) with the ground truth, the other with a lower agreement (right).

4. DISCUSSION

Recently, deep learning approaches have proven valuable in the field of diffusion MRI, demonstrating the ability to accurately predict FODs from the diffusion signal [23], and harmonizing signal across scanners [24, 25], lending insight into the relationship between the signal and tissue microstructure. In this study, we have used a CNN to estimate 3D fiber distributions from inherently 2D micrographs. To the best of our knowledge, this study is the first attempt to extract 3D features from 2D histology.

Although results varied across the brain, many predicted fiber geometries showed moderate to high agreement with the ground truth distributions. This analysis and network structure could potentially be used to estimate other 3D tissue microstructure features from the large number of available 2D histological resources, atlases, and databases. For example, it may be possible to estimate cell or neuron densities, diameters, segment lengths, orientations, and undulations, among other microstructural features that may be clinical indicators of pathologies or diseases. This would be critical to diffusion MRI validation studies, in addition to a variety of other MRI contrasts.

Alternatively, this methodology could be used to reconstruct the 3D structural connections of a human brain, at spatial resolutions surpassing those feasible with current clinical and pre-clinical scanners. For example, an existing myelin-stained atlas of the human brain could be utilized, and processed using the current methodology, resulting in 3D fiber distributions at ~500um isotropic resolution, characterizing volumes much smaller than the typical 2.5 mm resolution. Smaller voxels may alleviate partial volume affects and the crossing fiber problem [26–28], potentially improving the accuracy of tractography and improving our understanding of the human connectome.

There are several potential improvements to the current study, as well as future areas of exploration. The next step will be to include additional slices from the same monkey, as well as incorporate, test, or train on multiple subjects from existing atlases or databases [18, 19]. Successful generalization to new subjects would lend significant confidence in applying this to unseen brains or new species, for example the human brain. Finally, we recognize that the low ACC in many regions of the brain may be due to ambiguities associated with determining whether a fiber is going-into or coming-out-of the 2D plane, both of which may intuitively look similar in a 2D projection image. Implementing a loss function that is invariant to the through-plane orientation may lead to better reconstructions, although the network would not be able to identify whether the axon distribution is oriented into or out of plane. Successful implementation of this network would require some form of post-processing of FODs to ensure spatial continuity. This could possibly be solved by “flipping” certain FODs in the through-plane direction so that they were consistent with their neighbors in a way similar to 2D phase unwrapping.

5. CONCLUSION

We have implemented a deep learning approach in order to extract 3D microstructural measures from inherently 2D microscopy images. Specifically, we trained a CNN to estimate the 3D fiber distribution from myelin-stain brightfield micrographs, with moderate to high accuracy throughout most of the brain. Spatial coherence suggests that this technique could be performed on consecutive 2D slices to perform 3D fiber tractography, potentially at resolutions much higher than that possible with current dMRI practices, and possibly on new unseen brains or specimens – for example the human brain. There is potential to use this, and similar, techniques to estimate a number of 3D metrics from 2D histological contrasts.