Revealing Electronic Signature of Lattice Oxygen Redox in Lithium Ruthenates and Implications for High-Energy Li-ion Battery Material Designs

Abstract

Anion redox in lithium transition metal oxides such as Li₂RuO₃ and Li₂MnO_3, has catalyzed intensive research efforts to find transition metal oxides with anion redox that may boost the energy density of lithium-ion batteries. The physical origin of observed anion redox remains debated, and more direct experimental evidence is needed. In this work, we have shown electronic signatures of oxygen-oxygen coupling, direct evidence central to lattice oxygen redox (O²⁻/(O₂)ⁿ⁻), in charged Li_2-xRuO₃ after Ru oxidation (Ru⁴⁺/Ru⁵⁺) upon first-electron removal with lithium de-intercalation. Experimental Ru L₃-edge high-energy-resolution fluorescence detected X-ray absorption spectra (HERFD-XAS), supported by ab-initio simulations, revealed that the increased intensity in the high-energy shoulder upon lithium de-intercalation resulted from increased O-O coupling, inducing (O-O) σ*-like states with π overlap with Ru d-manifolds, in agreement with O K-edge XAS spectra. Experimental and simulated O K-edge X-ray emission spectra (XES) further supported this observation with the broadening of the oxygen non-bonding feature upon charging, also originated from (O-O) σ* states. This lattice oxygen redox of Li_2-xRuO₃ was accompanied by a small amount of O₂ evolution in the first charge from differential electrochemistry mass spectrometry (DEMS) but diminished in the subsequent cycles, in agreement with the more reduced states of Ru in later cycles from Ru L₃-edge HERFD-XAS. These observations indicated that Ru redox contributed more to discharge capacities after the first cycle. This study has pinpointed the key spectral fingerprints related to lattice oxygen redox from a molecular level and constructed a transferrable framework to rationally interpret the spectroscopic features by combining advanced experiments and theoretical calculations to design materials for Li-ion batteries and electrocatalysis applications.

Graphical Abstract

1. Introduction

The redox process of positive electrode materials largely dictates the energy density and cycling stability of the Li-ion batteries. Conventional positive electrode materials including LiCoO₂ and LiNi_xMn_yCo_zO₂, with layered structures, hinge on the reversible redox couples of 3d transition metals including Co³⁺/Co⁴⁺,^1–2 Ni²⁺/Ni⁴⁺ (or Ni³⁺/Ni⁴⁺)^3–4 and Mn³⁺/Mn⁴⁺,^5–6 accompanied by lithium (de-)intercalation, delivering a capacity of around 140 mAh/g,^1–6 upon charging to 4.3 V with respect to Li metal (V_Li). This redox process is rooted in the electronic structure of lithium early transition metal oxides. Due to their large electronegativity difference, oxygen 2p-states lie well below the transition metal d-states, hence, the Fermi level has a predominantly metallic character, and the transition metals mainly undertake the burden of the redox reaction.^7–9 For most transition metals, this cationic redox scenario usually provides one electron per metal site and poses significant limitations on the energy density of positive electrode materials for mobile devices and automotive applications.⁹ However, as we move from early to late transition metals, or to higher valence metal states via lithium de-intercalation, we increase the electronegativity of the transition metal species.¹⁰ This results in a larger degree of energetic overlap between the metal d-states and the oxygen p-states, and therefore a more covalent interaction between the transition metal and oxygen.^{8–9, 11} In this scenario a direct extraction/replenishment of the electron density from the oxygen density of states can occur.^{7–8, 12} This scenario is usually referred to as anionic redox, in contrast with conventional cationic redox. The notion of anion redox arose for the first time in LiCoO₂ in the 1990s, where oxygen release was observed upon charging up to 4.4 V_Li.¹³ Ceder et al.¹² explained this finding using density functional theory (DFT) calculations in which both metal and oxygen contribute to the redox processes at high potentials.¹² Within the 3d metals family, going from early transition metals to late transition metals, this oxygen charge compensation mechanism is augmented due to a more covalent metal-oxygen framework¹².

Li-rich layered oxides, Li₂MO₃ (M = Ru, Ir, Mn),^{8, 11, 14–22} have been studied extensively and offer much higher energy density than LiMO₂ by providing more lithium for (de-)intercalation. These oxides can be written generally as Li(Li_1/3M_2/3)O₂, with 1/3 of the transition metal sites within the transition metal layer occupied by Li. This Li excess allows a higher transition metal valence (4+) , compared to LiMO₂ (3+), and therefore leads to more overlap between transition metal and oxygen states, resulting in a highly covalent MO bonding.^{7, 10, 12} These reported Li-rich metal oxides can be divided into two classes. The first class is represented by oxides derived from Li₂MnO₃,^{17–18, 21, 23–37} which exhibits a relatively poor reversibility attributed to oxygen redox (oxidation) into molecular oxygen, leading to oxygen loss. Although Li₂MnO₃ can yield a first cycle discharge capacity higher than 200 mAh/g, upon charging to 4.8 V_Li,^{25, 29–32, 34–35} it suffers from a poor cycling performance.^{23, 29–31} Considerable oxygen loss occurs upon charging Li₂MnO₃^17,32, where 0.125 oxygens can be released per unit of extracted Li³⁰. The Li₂MnO₃ derived compounds such as Li(Li_xMn_yNi_zCo_1-x-y-z)O₂ (Li-rich Mn-rich NMC) introduce additional redox couples (Ni²⁺/Ni⁴⁺ and Co³⁺/Co⁴⁺) that may boost both cationic and lattice oxygen redox, reaching a reversible capacity of around 300 mAh/g.^36–38 Although their cycling stability is much improved compared to pure Li₂MnO₃ electrodes, they still suffer from a significant voltage decay over subsequent cycles³⁷, and the oxygen redox contribution to the redox process is diminished upon extended cycling.³⁷ The second group of Li-rich metal oxides is derived from noble metals including Li₂RuO₃^{11, 39–41} and Li₂IrO_3,^42–43 which show reversible capacities with a two-electron transfer process and a high cycle life. For example, Tarascon and co-workers^{15–16, 39–40} have shown that Li₂Ru_1-xMn_xO₃ and Li₂Ru_1-xSn_xO₃ deliver first discharge capacities as high as 250 mAh/g,^{16, 39–40} and capacity retention of higher than 80 % after 100 cycles.^{16, 39} It has been proposed that the capacity corresponding to the second electron transfer results from reversible lattice oxygen oxidation into peroxo- and superoxo- like species in the bulk.^{11, 16, 39–40}

The mechanism giving rise to the reversible capacities associated with the lattice oxygen redox is not well understood. Unambiguous experimental evidence or an electronic structure signature for lattice oxygen redox for these Mn-, Ir- and Ru- based oxides is missing. There are primarily two schools of thought on the physical origin of lattice oxygen redox in Li-rich oxides. The first class of proposed mechanisms argues that anion redox induces the formation of (O₂)ⁿ⁻ peroxo-like species,^{11, 39–41, 43} and the redox couple O²⁻/(O₂)ⁿ⁻ can proceed reversibly upon cycling. A certain M-O bond covalency is required for reversible oxidation of the anion as proposed by Doublet, Tarascon and coworkers.^{11, 41} Tarascon et al. have proposed the existence of peroxo-like O₂ⁿ⁻ species for Li_2-xRuO₃ at 4.6 V_Li during the first cycle via X-ray photoelectron spectroscopy (XPS) studies.^{16, 39} The formation of such peroxo-like species is accompanied by Ru reduction which is referred to as a reductive coupling mechanism.^{11, 40} The Ru⁶⁺ species are stabilized by modifying the coordination sphere of Ru through oxygen-oxygen bond formation and the transfer of extra electrons to the transition metal for reduction, eventually forming Ru⁵⁺-(O₂)²⁻ peroxo-species or Ru⁴⁺-(O₂)⁻ superoxo-species. However, we should note that the XPS measurement has a penetration depth of only 5 nm to 10 nm⁴⁴. Therefore, the evidence provided by XPS is from the surface and subsurface of the materials which is likely not representative of the bulk. Moreover, the XPS fingerprint is not clear and cannot be unequivocally assigned to peroxo-like species, but might also come from surface electrolyte decomposition products. Hence, there is no unambiguous experimental evidence from an electronic structure perspective to support this proposed redox process. The formation of peroxo-like species is further demonstrated and visualized by McCalla et al.⁴³ using high-resolution transmission electron microscopy and neutron diffraction in delithiated Li_2-xIrO₃, where an O-O bond distance of around 2.4 Å has been shown.⁴³ In addition, Saubanère et al.¹¹ have reported from crystal orbital overlap population (COOP) analysis that the covalent bonding between Ru-O stabilizes the peroxo-like species in Li_2-xRuO₃ upon oxidation. In contrast, the Mn-O bond has less covalency, resulting in further oxidation of peroxo-like species and eventually evolving molecular oxygen. This idea has also been further explored by Bruce and coworkers.³⁶ Their O K-edge resonant inelastic X-ray scattering (RIXS) study on Li-rich Mn-rich NMC showed an increased intensity of the elastic peak (around 531 eV) upon charging to around 4.4 V_Li, a fingerprint they assigned to formation of oxygen-localized electron holes.³⁶ However, the rationale for such an assignment remains unclear. Moreover, there is no strong indication of true peroxide or superoxide species formation since there is no clear Raman signal from 800 cm⁻¹ to 1100 cm⁻¹ in ex-situ charged Li-rich NMC samples,³⁶ the characteristic wavenumber range for metal peroxide and superoxides.³⁶ Bruce and coworkers have concluded that the reversibility of anionic redox relies on more delocalized O holes, which require more delocalized M-O bonds from higher M-O covalency.

In the second school of thought, the oxygen redox of Li-rich oxides is attributed to the reversible oxidation and reduction of the non-bonding oxygen density of states created by Li-O-Li configuration,^45–46 unique to Li-excess or disordered oxides. Due to the high ionicity of Li-O interaction, the oxygen 2p orbital bond with lithium resembles a lone-pair non-bonding oxygen, and its density of states lies at a higher electron energy level compared to the corresponding ones of transition metal bonded oxygen (bonding oxygen), thus providing a more facile electron transfer from oxygen.⁴⁵ Therefore, oxygen redox can be represented as a redox couple of O²⁻/O⁻, where electron density is directly taken from non-bonding oxygen 2p states. However, there is no unequivocal experimental evidence that oxygen redox proceeds as a redox couple of O²⁻/O⁻ without oxygen sub-lattice distortion. This mechanism is further extended by Gent and Chueh^{38, 47}, where they proposed that anionic redox is a dynamic process, requiring synergistic transition metal migration and O²⁻/O⁻ redox couple. In-situ X-ray diffraction (XRD) and RIXS³⁸ on Li-rich and Mn-rich NMC (Li_1.2Mn_0.54Ni_0.13Co_0.13O₂) demonstrated that the oxygen redox and the transition metal migration are coupled. The oxygen-bonded transition metal migrates to a tetrahedral site, creating non-bonding oxygen 2p states on the de-coordinated oxygen. Similar to what Seo et al.⁴⁵ have proposed, this non-bonding oxygen can perform O²⁻/O⁻ redox, coupled with continuous transition metal migration. In particular, a RIXS feature with an emission energy of 523.7 eV, different from the 525 eV emission feature for conventional O²⁻ species, could be assigned to the anionic redox state in both Li-ion and Na-ion battery electrodes.^{38, 48} However, although further theoretical study shows that this specific RIXS feature corresponds to excitations into unoccupied O-2p states, e.g., oxidized oxygen because 2p orbitals of O²⁻ are full occupied, a simple extension of a peroxide model into transition-metal oxide material remains questionable⁴⁹.

In this study, we find unambiguous evidence of lattice oxygen redox upon lithium deintercalation from Li₂RuO_3. By coupling hard and soft X-ray absorption (XAS) and X-ray emission spectroscopy (XES) experimental studies with ab-initio Bethe-Salpeter equation (BSE) spectroscopy calculations⁵⁰, we capture the redox processes of both oxygen and ruthenium in Li_2-xRuO₃ upon the first charge, which contrasts the redox process of conventional battery materials including LiCoO₂ and LiNi_1/3Mn_1/3Co_1/3O₂. This detailed characterization of the redox process allows us to qualify different previously proposed hypotheses and experimental studies regarding lattice oxygen redox. Furthermore, combining the redox process with differential mass spectrometry (DEMS) measurements, we evaluate the reversibility of the anionic redox of Li₂RuO₃ and discuss the implications for the design of high-energy positive electrode materials leveraging anionic redox.

2. Result and Discussion

Electronic signatures of oxygen-oxygen coupling in Li_2-xRuO₃

XAS and XES on the charged oxide-only pellet electrodes, without conductive carbon and binder, revealed electronic structure evidence of oxidation of non-bonding oxygen in Li_2-xRuO₃. Both O K-edge XAS total fluorescence yield (TFY) and Ru L₃-edge high-energyresolution fluorescence detected (HERFD)-XAS of the pristine electrode (Li₂RuO₃) were composed of two major peaks (c.a. 528.8 eV and 530.8 eV for the O K-edge in Figure 1(a) and 2841.1 eV and 2843.6 eV for the Ru L₃-edge in Figure 1(b)). Ab-initio theoretical calculations with OCEAN^50–51 using the pristine Li₂RuO₃ structure (C2/c)^52–53 resulted in simulated O K-edge (Figure 1(a)) and Ru L₃-edge (Figure 1(b)) spectra that agree well with the experimental spectral fingerprints of the pristine electrode. Furthermore, these calculations also enabled us to visualize the electron densities corresponding to specific excited state features. The low-energy peak can be attributed to a t_2g feature, having a metal 4d_xy (degenerate with 4d_yz and 4d_zx) orbital with a π overlap with O 2p states, whereas the high-energy peak can be attributed to the e_g* states, comprising the σ* overlap between transition metal 4d_x2-y2 states and O 2p states, as shown in Figure 1(c). Here we should note that the computed spectra have slightly larger t_2g and e_g splitting compared to the experimental spectra, which indicates we have an overestimation of the ligand field. Moreover, as we might note that in the pristine experimental Ru L₃-edge XAS spectra of Li₂RuO₃ (Figure 1(b)), there is a small high-energy shoulder which is not understood, which might potentially come from mixed oxidation states^54–56, and/or surface reacting with moisture undergoing proton and lithium ions exchange.⁵⁷ Worth notably, this feature has never been reported by previous Ru L₃-edge measurements of Ru-based oxides⁵⁸ and complexes^54–55 since they were limited by the significant core-hole lifetime broadening and therefore such small feature was not resolved, which requires further studies.

Figure 1:

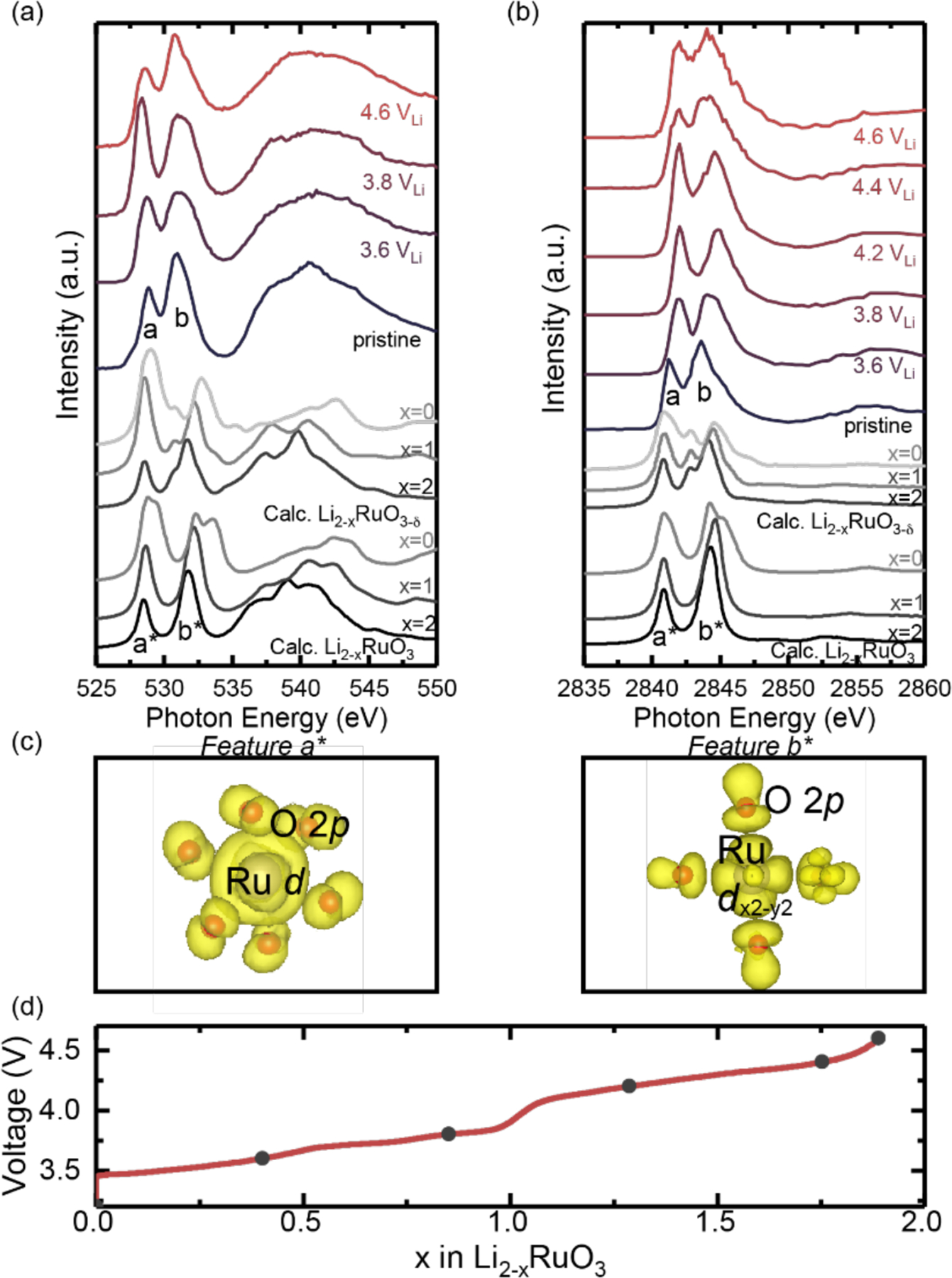
(a) O K-edge XAS collected in TFY mode, and (b) Ru L₃-edge HERFD-XAS spectra of Li_2-xRuO₃ pellets as a function of charging potential (3.6 V_Li, 3.8 V_Li, 4.2 V_Li, 4.4 V_Li, and 4.6 V_Li). Corresponding simulated spectra of the Li₂RuO₃, Li₁RuO₃, Li₀RuO₃ as well as Li₂RuO₃-_δ, Li₁RuO₃-_δ, Li₀RuO₃-_δ (δ =1/4), are also shown for comparison, representing the structures with oxygen vacancies. The calculated O K-edge and Ru L₃-edge spectra are shifted by 528 eV and 2884 eV, respectively, to allow for a direct comparison with the experimental spectra. The computed features labeled “a*” and “b*” match with the experimental features “a” and “b” in the pristine Li₂RuO₃. (c) Visualization of charge densities that corresponds to a* and b* of the computed spectra of pristine Li₂RuO₃; a* can be assigned to the t_2g feature comprised of Ru d- manifolds and O 2p state with a π overlap, and b* can be assigned to e_g* feature composed of Ru 4d_x2-y2 and O 2p orbitals with a σ* overlap. (d) The voltage profile of Li_2-xRuO₃ pellets in the first cycle show two major plateaus at 3.6 V_Li and 4.2 V_Li in line with previous works.^{16, 39–40} The closed black circles indicate the voltages where the ex-situ samples were collected. The fitted peak intensities of t_2g and e_g peak at each state of charge is shown in Figure S1, and the fitted peaks for O K-edge and Ru L-edge are shown in Figure S2 and S3, respectively.

Upon charging, the low-energy t_2g peak intensity (integrated area) gradually increased up to 3.8 V_Li, and then decreased, relative to that of the high-energy e_g feature, in both O K-edge XAS (Figure 1(a) and Figure S1(a)) and Ru L-edge HERFD XAS (Figure 1(b) and Figure S1(b)). The increase of the t_2g peak integrated area up to 3.8 V_Li, which corresponds to the first lithium de-intercalation per formula from Li₂RuO₃ in the low-voltage plateau as shown in Figure 1(d), can be attributed to the removal of approximately one t_2g electron upon oxidation of Ru⁴⁺ to Ru⁵⁺ in Li_2-xRuO₃. Similar spectroscopic changes have been reported for oxides relying predominantly on cationic redox including LiCoO₂^59–60 and LiNi_1/3Mn_1/3Co_1/3O₂⁶¹, where the metal L-edge shifts monotonically and the pre-peak area in O K-edge XAS increased,^59–61 marking the removal of the electron from transition metal d states upon lithium de-intercalation. On the other hand, upon charging to voltages greater than 3.8 V_Li, the e_g feature in both Ru L₃-edge and O K-edge spectra were found to grow relative to the low-energy t_2g peak and broaden considerably on the high-energy side (Figure 1(a), (b), and Figure S1). Through DFT calculations, we determined the most energetically favorable structures at different lithium contents of Li_2-xRuO₃ by enumerating all possible configurations (computational details shown in Methods section). Simulated Ru L₃-edge (Figure 2(a) and (b)) and O K-edge (Figure S4) spectra of Li_2-xRuO₃ revealed the appearance of a high-energy shoulder in the vicinity of the e_g feature for Li_0.5RuO₃ and Li₀RuO₃, which could potentially account for the broadening observed in the experimental spectra Aided by a charge density visualization at the shoulder peak energy, we assigned this feature to a stronger oxygen-oxygen (O-O) σ* − like antibonding states with a π* overlap with transition metal d-manifolds (Figure 2(b)). This combined experimental and simulated approach for the Li_2-xRuO₃ revealed electronic structure evidence for the antibonding state of oxygen-oxygen coupling associated with lattice oxygen redox in bulk proposed previously from DFT studies.¹¹

Figure 2:

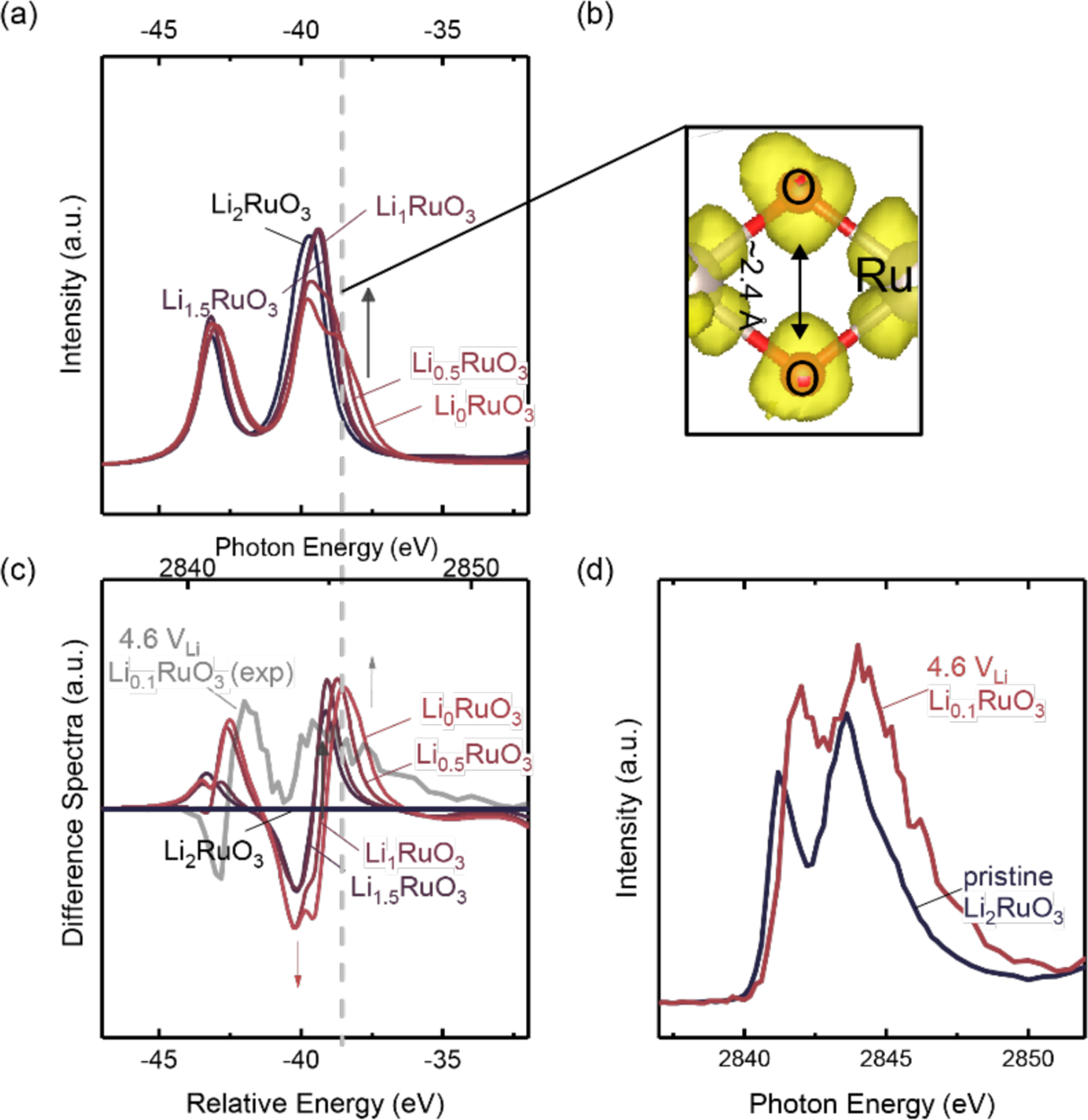
(a) Calculated Ru L₃-edge HERFD XAS and (c) calculated and experimental difference spectra of Li_2-xRuO₃. Upon delithiation, an additional peak appears at a photon energy just above the e_g feature. The electron density of this excitation shows it to be an (O-O) σ*-like feature hybridized with Ru d-manifolds due to oxygen cage distortion and shortening of the O-O bond from 2.8 Å to 2.4 Å upon delithiation, as shown in the schematic in (b). (d) Experimental Ru L₃-edge HERFD XAS of Li_2-xRuO₃ charged to 4.6 V_Li (red) and pristine Li_2-xRuO₃ (black), where a broadening of e_g peak was observed with higher intensity at higher photon energy, matching with the observation in the computed spectra, and can be attributed to the creation of (O-O) σ*-like feature. The voltage profile determined from the DFT-calculated structure of Li_2-xRuO₃ is shown in comparison with the experimental profile in Figure S5.

Theoretical spectra simulations of other candidate structures show that the experimentally observed changes in the O K- and Ru L-edge XAS spectra cannot be solely explained by introducing oxygen vacancies in Li_2-xRuO₃, which is known to evolve oxygen gas at voltages around 4.2 V_Li,⁴⁰ nor by true peroxo (d_O-O ≈1.5 Å )⁶² or superoxo- (d_O-O ≈1.2 Å – 1.3 Å)⁶³ species of oxygen with bond length of less than 1.8 Å . The high-energy peak shoulder observed in the experimental XAS spectra of Li_2-xRuO₃ obtained from the 4.2 V_Li plateau cannot be explained by the presence of lattice oxygen vacancies. The simulated O K-edge (Figure 1(a) and Figure S6) and Ru L₃-edge (Figure 1(b) and Figure S7) of Li_2-xRuO_3-δ with δ = 0.25 oxygen vacancies per formula unit in the bulk led to additional features between the t_2g and e_g peaks, as well as a significant decrease in the intensity of the e_g relative to the t_2g feature, which were not clearly experimentally observed (Figure 1(a), (b) and Figure S1). Moreover, we have also performed a test calculation on Ru L-edge XAS of a surface Ru atom surrounded by surface oxygen vacancies as in Figure S7(d), and a similar trend as the bulk oxygen vacancy calculations was also observed. Here, we saw a more intense feature between t_2g and e_g peaks and more depressed e_g peaks due to larger degree of Ru reduction, compared to the cases with bulk oxygen vacancies. (Figure S7(a)) However, we cannot rule out the presence of oxygen vacancy formation as we have also observed a slight rise of the feature between e_g and t_2g, and this observation could potentially coming from oxygen vacancies formed in the oxides upon charging, but the additional features at high photon energy cannot be solely explained by oxygen vacancy formation. Previous computational work on Li_2-xRuO₃ and Li_2-xIrO₃ showed the presence of distorted oxygen cages with an oxygen distance around 2.4 Å,^{40, 43} and refined neutron diffraction data in chemically delithiated Li_2-xIrO₃ samples also confirmed an oxygen-oxygen distance of around 2.4 Å.⁴³ This O-O bond distance does not support the presence of true peroxide or superoxide species. We performed Ru L₃-edge and O K-edge spectra simulations by reducing the oxygen-oxygen bond distance from 2.4 Å to 1.8 Å in Li₀RuO₃ where we forced two oxygen atoms closer together while keeping the position of other atoms the same. This led to increased high-energy shoulder intensities for both Ru L₃-edge and O K-edge, indicating a stronger oxygen-oxygen coupling, as shown in Figure S8 and Figure S9(a). However, a further reduction of the O-O bond distance from 1.8 Å to 1.2 Å, so to form a true superoxide, led to a drastic reduction in the e_g intensity compared to the t_2g peak. This could be the result of reduced σ overlap between Ru 4d and O 2p states coming from a smaller O-Ru-O bond angle associated with shorter O-O bonds. As such changes were not observed in the experimental XAS data in Figure 1, the formation of peroxo-like and superoxo-like species with an O-O bond length less than 1.8 Å in bulk Li_2-xRuO₃ (1≤x≤2) is also not likely based on our combined experimental and simulated study. Moreover, as we force the O-O bond distance from 2.4 Å to 1.8 Å and 1.2 Å, we induced an energy penalty of above 3 eV respectively, which also indicates that from an energetic standpoint, forming such short O-O bond distance in Li_2-xRuO₃ is not possible.

The oxygen-oxygen coupling in Li_2-xRuO₃ (1≤x≤2) is further supported by O K-edge valence XES, which probes the projected occupied local density of state (DOS) with O-2p symmetry. The XES spectra of the pristine electrode in Figure 3(a) and Figure 3(b) consisted of three major features: one major peak centered at ≈523 eV and two shoulders located at ≈521 eV and ≈526 eV, respectively. When comparing these, on a binding energy scale, with valence band XPS data from Li₂RuO₃, similar features are observed with different relative intensities due to different selection rules dictating valence XES and XPS (Figure 3(a)).⁶⁴ In line with previous work on perovskite materials that have comparable O K-edge XES spectra⁶⁴, we assign the major XES peak to non-bonding oxygen, and the high- and low-energy shoulders to anti-bonding and bonding Ru-O bonds, respectively.⁶⁴ This assignment is supported by the DFT projected DOS of Ru 4d and oxygen 2p in Figure 3(a), where the high-energy shoulder reflects Ru-O bonding states (≈ 6 eV in the DOS) with a predominantly oxygen character, the low-energy shoulder reflects anti-bonding Ru-O states with mostly metal character (≈1 eV in the DOS), and the center peak indicates non-bonding oxygen states without significant contribution of Ru d-electrons (≈2.5 eV in the DOS). Here, we should note that the center non-bonding peak position of computed ground-state DOS had some discrepancies with experimental O K-edge XES spectra (Figure 3(a)). When charging Li_2-xRuO₃ up to 3.8 V_Li, there was no significant change observed for the O K-edge XES spectra (Figure 3(b)), in agreement with corresponding simulated O K-edge XES spectra of Li_2-xRuO₃ (0 ≤ x ≤ 1) in Figure 3(c). The O K-edge XES indicates that there is no oxygen participation upon first lithium removal. In contrast, upon charging Li_2-xRuO₃ to 4.2 V_Li and beyond a spectral broadening was observed (Figure 3(b)), indicative of changes to the probed oxygen states. This broadening was also found in the ab-initio calculated XES spectra of Li_0.5RuO₃ and Li₀RuO₃ (Figure 3(c)), especially for the oxygen non-bonding peak. Here we should note that for OCEAN simulation of O K-XES, since no core-hole effect is considered, the energy is referenced to the Fermi level, and the relative energy scale is the same as E-E_f scale. Using the crystal orbital overlap population (COOP), in line with previous work,^{11, 41, 65–66} the broadening in the oxygen non-bonding feature can be attributed to an increased O-O antibonding character (by showing negative COOP intensity) in the energy range where we observed the broadening in computed spectra (from −2 eV to 0 eV vs. the Fermi level) in Figure 4(d). Furthermore, by visualizing the charge density in the same energy range, we observed that the charge density also resembled a (O-O) σ* interaction with a nodal plane in the middle as shown in Figure 3(d). This finding further supports the formation of oxygen-oxygen coupling upon charging Li_2-xRuO₃ in the high-voltage plateau of 4.2 V_Li. The peak broadening in the XES data most likely came from the (O-O) σ* antibonding states (Figure 3(d)). These states are different from those with an additional π* participation from Ru 4d electrons which are responsible for the increased intensity at the high-energy shoulder found in the XAS spectra (Figure 2). Here, we captured the creation of both “non-bonding” (O-O) σ* in the O K-edge XES (Figure 3(d)) in contrast with “anti-bonding” (O-O) σ* with metal (Ru) π* contribution in XAS, shown in the charge density in Figure 2(a). Furthermore, such broadening in the experimental XES spectra was not observed in charged Li_1-xCoO₂ (Figure S12) and Li_1-xNi_1/3Mn_1/3Co_1/3O₂ (Figure S12). Their largely unchanged peak widths indicate the absence of lattice oxygen-oxygen coupling (Figure 4(e)). However, broadening in the XES spectra was observed in substituted Li_2-xRu_1-yM_yO₃ such as Li_2-xRu_0.μmn_0.5O₃ (Figure 4(e) and Figure S12) as well as Li_2-xMnO₃ derived materials including Li-rich Mn-rich NMC probed by RIXS,³⁶ where the central peak of the RIXS spectra broadened upon charging. This broadening in O K-edge XES appears concurrently with changes in the O K-edge absorption, including broadening and the creation of an additional feature around 531 eV, but not in metal L-edges as in Ru cases.³⁸ This observation is in agreement with previous COOP analysis performed by Saubanère et al. on Li₂MnO₃,¹¹ where upon lithium deintercalation, a stronger O-O coupling exists, inducing (O-O) π and σ states. However, contrary to the present Ru case, the (O-O) σ* states of Li₂MnO₃ have no Mn contribution,¹¹ and therefore the additional states did not appear in Mn L-edge spectra of the charged electrodes from previous experiemtnal measurement, where upon charging, the Mn L-edge spectra of Li_2-xMnO₃ did not show significant change.⁶⁷ This suggested that for the Ru-based material, the (O-O) σ* is stabilized through π overlap with Ru d-manifolds because of the much more delocalized d states. In contrast, for the Mn scenario, this (O-O) σ* is not coordinated with any transition metal, and oxygen is released due to more weakened metal oxygen coordination. This observation suggests that strongly covalent Ru-O bonds is critical to enable lattice oxygen-oxygen coupling.^{11, 41}

Figure 3:

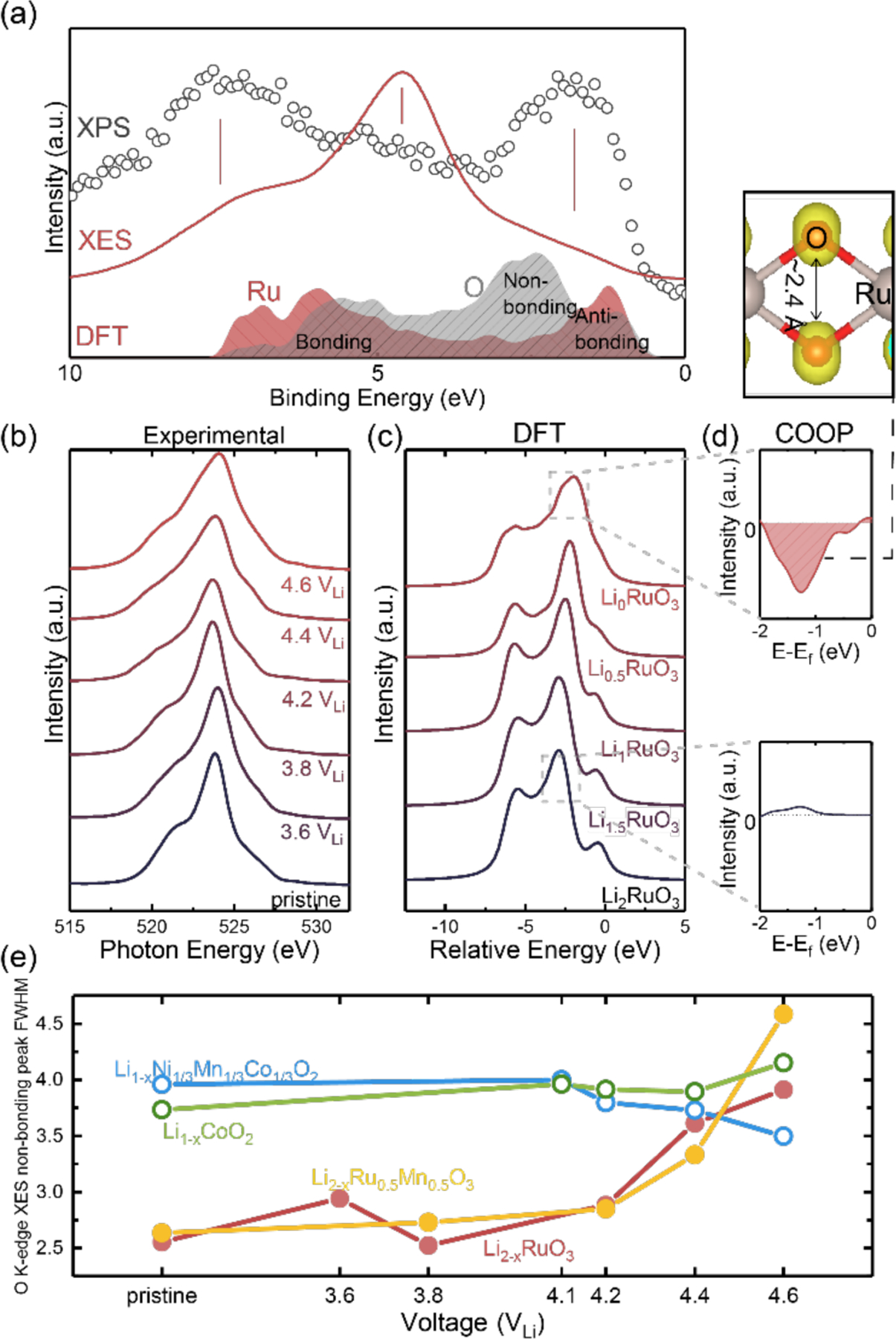
(a) Alignment of the O K-edge XES to XPS valence band measurement on the binding energy scale and comparison of ground-state DFT projected orbital-wise density of state calculation for Ru 4d and O 2p_. In the XES spectra the three features can be assigned to bonding, non-bonding, anti-bonding oxygen states from low to high photon energy, respectively. (b) O K-edge XES of Li_2-xRuO₃ as a function of state of charge. (c) Simulated O K-edge XES of Li_2-xRuO₃ as a function of lithium content, where peak broadening was noted for Li_0.5RuO₃ and Li₀RuO₃. (d) Crystal orbital overlap population (COOP) of Li_2-xRuO₃ (bottom x = 0 and top x = 2), where, upon delithiation, Li₀RuO₃ showed a stronger O-O σ* feature around the non-bonding region in the experimental and computed spectra compared to the fully-lithiated case of Li₂RuO₃. (e) Non-bonding peak full width at half maximum (FWHM) as a function of charging potential of different positive electrode materials: LiCoO₂ (LCO), LiNi_1/3Mn_1/3Co_1/3O₂ (NMC), Li₂RuO₃ (LRO) and Li₂Ru_0.5mMn_0.5O₃(LRMO). The materials claimed to have anionic redox (closed symbol) were observed to have significant peak broadening upon charging in contrast with LCO and NMC (open symbol), which utilize predominantly cationic redox activity upon oxidation. Here, the FWHM was extracted based on the width at the half height of the most predominant peak (non-bonding peak) as the other shoulder peaks are much smaller than non-bonding peak, thus we assume that the shoulder peaks evolution will not have significant effect on the FWHM of the center non-bonding peak, the FWHM extraction procedure is also shown schematically in Figure S10. The ground-state projected DOS of the fully lithiated and delithiated Li_2-xRuO₃ is shown in Figure S11 (a) and (b), respectively, and the COOP analysis of full energy range of Li₂RuO₃ and Li₀RuO₃ is shown in Figure S11(c). Raw XES data of LCO, NMC and LRMO is shown in Figure S12 and more detailed analysis is shown in Figure S13.

Figure 4.

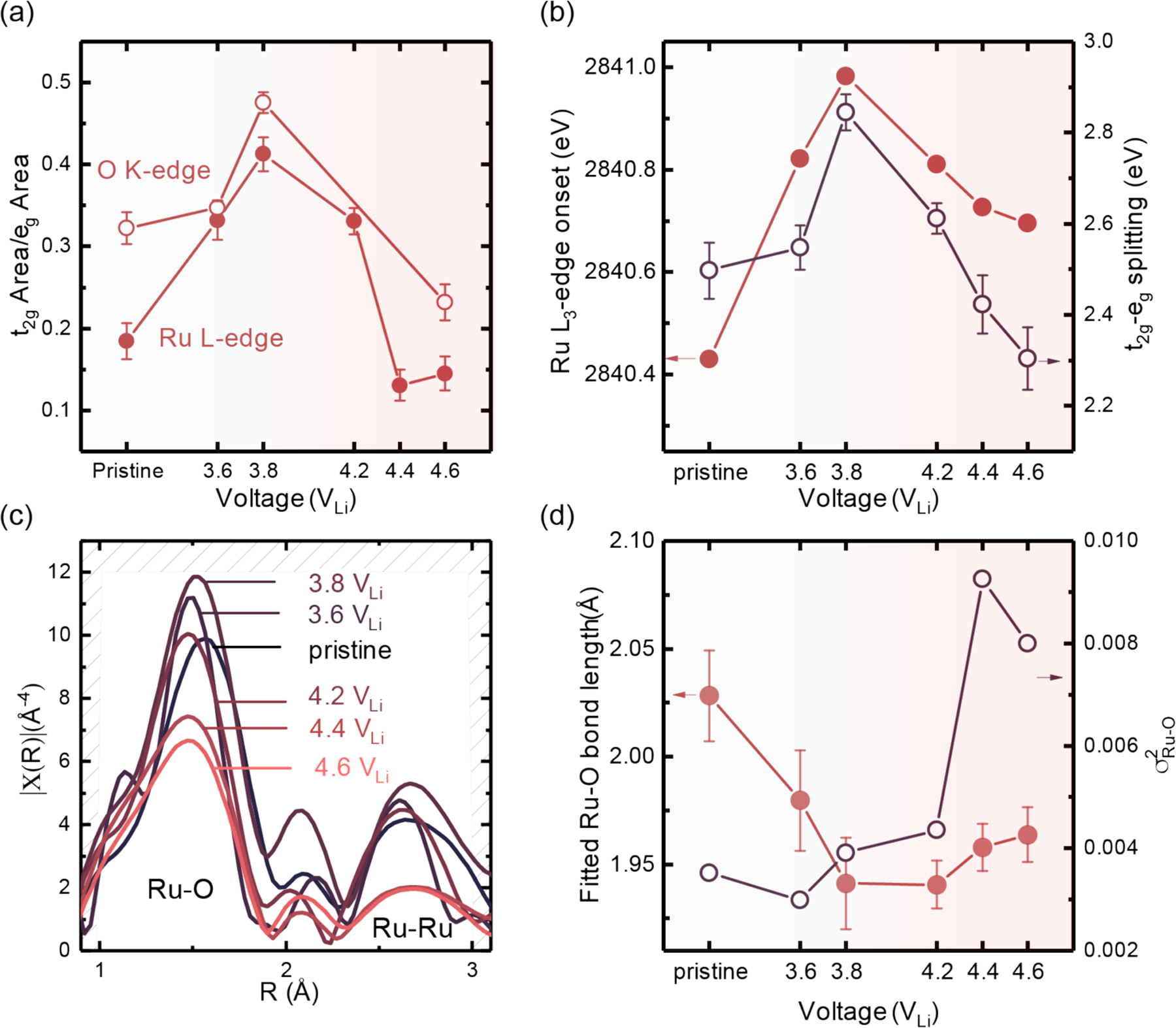
(a) Ratio of integrated peak area of the t_2g peak (feature a in Figure 1) and e_g peak (feature b in Figure 1) of O K-edge (open circle) and Ru L-edge (closed circle) from XAS spectra. Detailed fitting results are shown in Figure S1–S3. (b) Ru L-edge edge shift (closed circle) and t_2g (feature a in Figure 1) and e_g (feature b in Figure 1) features splitting (open circle). (c) Raw EXAFS data, Fourier-transformed χ(R) as a function of R (reduced distance) of Li_2-xRuO₃ in the first charge as a function of state of charge including 3.6 V_Li, 3.8 V_Li, 4.2 V_Li, 4.4 V_Li, and 4.6 V_Li, showing two major features, one centered around 1.5 Å (reduced distance), representing Ru-O interaction, and another centered around 2.6 Å (reduced distance), representing Ru-Ru interaction. The k-range for Fourier transformation is 1 Å ⁻¹ to 11 Å ⁻¹. (d) Fitted Ru-O bond length (closed circle) and Debye-Waller factor $\left({\sigma }_{Ru-o}^2\right)$ from Ru K-edge EXAFS shown in Figure 2(c). In the first plateau, Ru is monotonically oxidized with increasing t_2g and e_g splitting, accompanied by Ru-O bond contraction. Upon charging to 4.2 V_Li, Ru metal is slightly reduced with less t_2g and e_g splitting, and there is an increase in the Ru-O bond length and disorder in the system. The raw EXAFS data in k-space and fitting results are shown in Figure S15 and S16, and the summary of the EXAFS fitting parameter is shown in Table S1. Summary of alternative EXAFS fitting parameter by only using the first coordination shell is shown in Table S2.

Moreover, the broadening observed in the O K-edge XES spectra cannot be explained by the creation of oxygen vacancies in the structure as shown by the simulated O K-XES spectra of Li_2-xRuO_3-δ (δ=1/4) in Figure 3(c) and Figure S6, where only a small shift of the nonbonding peak towards lower energy was observed, whereas in the experimental spectra a positive shift was observed for Li_2-xRuO_3-δ upon charging. In addition, such broadening also cannot come from the formation of true peroxo- or superoxo- species with O-O bond length less than 1.8 Å. Simulated XES spectra of Li₀RuO₃ with equilibrium O-O bond distance of 2.4 Å and shortened distance of 1.8 Å and 1.2 Å in Figure S9(b) reveal distinctive new peak features in the simulated XES spectra for the 1.2 Å case, potentially coming from fingerprints of σ, π, π * of the O-O bonding, which were clearly not observed experimentally in this case. Our experimental and simulated XAS and XES revealed unambiguous electronic structure signatures for lattice oxygen redox in form of oxygen-oxygen coupling upon first charge of Li_2-xRuO₃ on the 4.2 V_Li plateau, which include 1) the growth of the e_g peak shoulder in the O K-edge and Ru L₃-edge XAS spectra originated from the (O-O) σ*-like states with π overlap with Ru d-manifolds and 2) the broadening of non-bonding oxygen originated from the (O-O) σ* states (without Ru d hybridization). Simulated XAS data further revealed that such O-O coupling in Li_2-xRuO₃ has an oxygen-oxygen distance not smaller than 1.8 Å, namely much longer than those in true molecular oxygen dimers, peroxide and superoxide, which is in agreement with previous proposal by Doublet et al.⁴¹ that the fully de-coordinated oxygen couples can escape from the lattice.

XAS Spectroscopy evidence of reductive coupling in Li_2-xRuO₃

We further examined the electronic structure signature for the reductive coupling in Li_2-xRuO₃,^{11, 39, 41} in which the reduction of Ru is accompanied by the oxidation of lattice oxygen (or lattice oxygen-oxygen coupling) in the 4.2 V_Li plateau. Upon charging Li_2-xRuO₃ to 3.8 V_Li, the ratio of the integrated peak intensities between the t_2g and e_g features, in both Ru L₃-edge and O K-edge XAS spectra (Figure 4(a)), indicated electron removal from the t_2g states upon oxidation of Ru. This assignment is supported by simulated Ru L₃-edge (Figure 2(b)) and O K-edge XAS spectra (Figure S4) of Li_2-xRuO₃ obtained from BSE calculations, which show the increase of the low-energy t_2g peak relative to the high-energy e_g peak with de-intercalation of one lithium per formula unit from Li₂RuO₃ to LiRuO_3. Ru oxidation within the 3.8 V_Li plateau is further evidenced by positive shifts in the edge photon energy of the Ru L₃-edge (Figure 4(b)) and Ru K-edge XAS (Figure S14), greater energy splitting between t_2g and e_g features in Ru L₃-edge XAS (Figure 4(b)) coming from larger ligand fields associated with higher oxidation states^54–56, and shortened Ru-O bonds obtained from the extended X-ray absorption fine structure (EXAFS) analysis of the Ru K edge in Figure 4(c), matching with previous observations from Mori et al.⁵⁸ Upon further charging within the 4.2 V_Li plateau, the ratio of integrated peak intensities of t_2g to e_g features in both Ru L₃-edge and O K-edge XAS spectra began to decrease (Figure 4(a)), accompanied by negative shifts in the onset energy of the Ru L₃ edge (Figure 4(b)) and K edge (Figure S14), as well as a smaller energy splitting between t_2g and e_g features in Ru L-edge XAS(Figure 4(b)), indicative of Ru reduction. The trend observed in the Ru L₃-edge shift (Figure 4(b)) is consistent with other metrics to estimate Ru oxidation states used in previous work⁶⁸. For example, the centroid and the pre-peak position of Ru L₃-edge shifted towards higher photon energies during charging up to 3.8 V_Li, and towards lower energies at 4.2 V_Li and above (Figure S17). Such trend of energy splitting between t_2g and e_g is also evidenced from the computed Ru L₃-edge XAS spectra (Figure 2(a)) where as we remove the first Li⁺, the crystal field splitting increases slightly, and then decreases after removing the second Li⁺ per formula unit. Therefore, experimental Ru L₃- and O K-edge XAS data of Li_2-xRuO₃ during the first charge along with simulated XAS spectra support the simultaneous Ru reduction and oxygen-oxygen coupling in the 4.2 V_Li plateau reported previously as reductive coupling.^{11, 39–40, 43} Similarly, slight reduction of Ir has been reported by Hong et al.⁴⁷ using Ir L-edge XAS, accompanied by proposed lattice oxygen oxidation in fully de-intercalated Sn-substituted Li_xIr_ySn_1-yO₃ (x = 0, y = 0.5 and 0.75).⁴⁷ While the Ru oxidation state reduction in the 4.2 V_Li plateau did not yield a statistically significant increase in the Ru-O bond length from Ru K-edge EXAFS (Figure 4(d)), the Debye-Waller factor $\left({\sigma }_{Ru-o}^2\right)$ associated with the Ru-O bond was increased markedly at 4.2 V_Li and above, indicating increased variances of Ru-O bond length and angles as well as a distorted Ru-O cage, which requires further study.

The XAS spectral evidence of reductive coupling at the 4.2 V_Li plateau during the first charge was diminished in subsequent cycles. The voltage profile of Li_2-xRuO₃ in the subsequent charges was also markedly different from the first cycle. In fact, the first charge distinct voltage plateaus at 3.8 V_Li and 4.2 V_Li were replaced by a sloppy voltage profile with an average potential of around 3.6 V_Li in subsequent cycles, as shown in Figure 5(a). During the third charge, the Ru L₃-edge onset energy was found to increase monotonically with increasing lithium de-intercalation. This is in contrast to behavior during the first charge with first an increase and then a decrease in the edge onset energy (Figure 5(a) and Figure 4(b)), characteristic of reductive coupling (reduction of Ru) with an enhanced oxygen-oxygen interaction. This observation suggests that reductive coupling, and potentially oxygen-oxygen coupling, is substantially diminished in subsequent cycles, and Ru redox was largely responsible for reversible capacities. This postulate is supported by a much lower photon energy onset at comparable lithium content in Li_2-xRuO₃ in the third charge (Figure 5(a) bottom panel) compared to the first charge (Figure 5(a) top panel). Further support comes from the DEMS in Figure 5(b), where an irreversible oxygen redox (oxygen oxidation) generated oxygen in the first charge at around 4.2 V_Li, but in subsequent cycles oxygen evolution fell below the detection limit. The amount of oxygen evolution can only be translated to a molar oxygen deficiency fraction of 2 %. From the DEMS measurement, we can also capture the first onset of CO₂ evolution at ≈3.9 V_Li, potentially due to residual Li₂CO₃ from the synthesis precursor.^69–70 Upon charging to 4.2 V_Li, lattice oxygen redox was accompanied by pronounced electrolyte oxidation to generate CO₂ evolution (2.0 % mole fraction), which was also reduced considerably in subsequent cycles. Previous online electrochemistry mass spectrometry (OEMS)^{4, 71} on NMC and Li-rich NMC has attributed part of the CO₂ evolution to singlet oxygen evolved from electrolyte decomposition at the cathode surface. Even by attributing all the CO₂ evolution to the oxide lattice (although this is unlikely), we would only create around 0.4 mol of oxygen vacancies (0.8 mol of electron transfer) per formula unit of oxide during the 4.2 V_Li plateau. Accounting for the charge associated with the simultaneous Li-removal in this stage (≈ 0.8 mol Li⁺ and e⁻), oxygen and CO₂ evolution alone cannot explain the reduction of transition metal within the high-voltage plateau observed in Ru L₃- and O K-edge XAS in Figure 4 (a) and (b), and Figure 5(a) in the first charge. As a result, during the first cycle, the redox process proceeded with Ru^4+/5+ accompanied by oxygen-oxygen coupling and transition metal reduction, whereas in subsequent cycles the high reversibility of Li_2-xRuO₃ most likely relied heavily on reversible Ru redox of Ru^3.x+/Ru⁵⁺ (where x is closer to 1 than 0), which surprisingly resembles the trends found in 3d transition metal systems in both Li-rich and Na-ion compounds^{37, 48}

Figure 5:

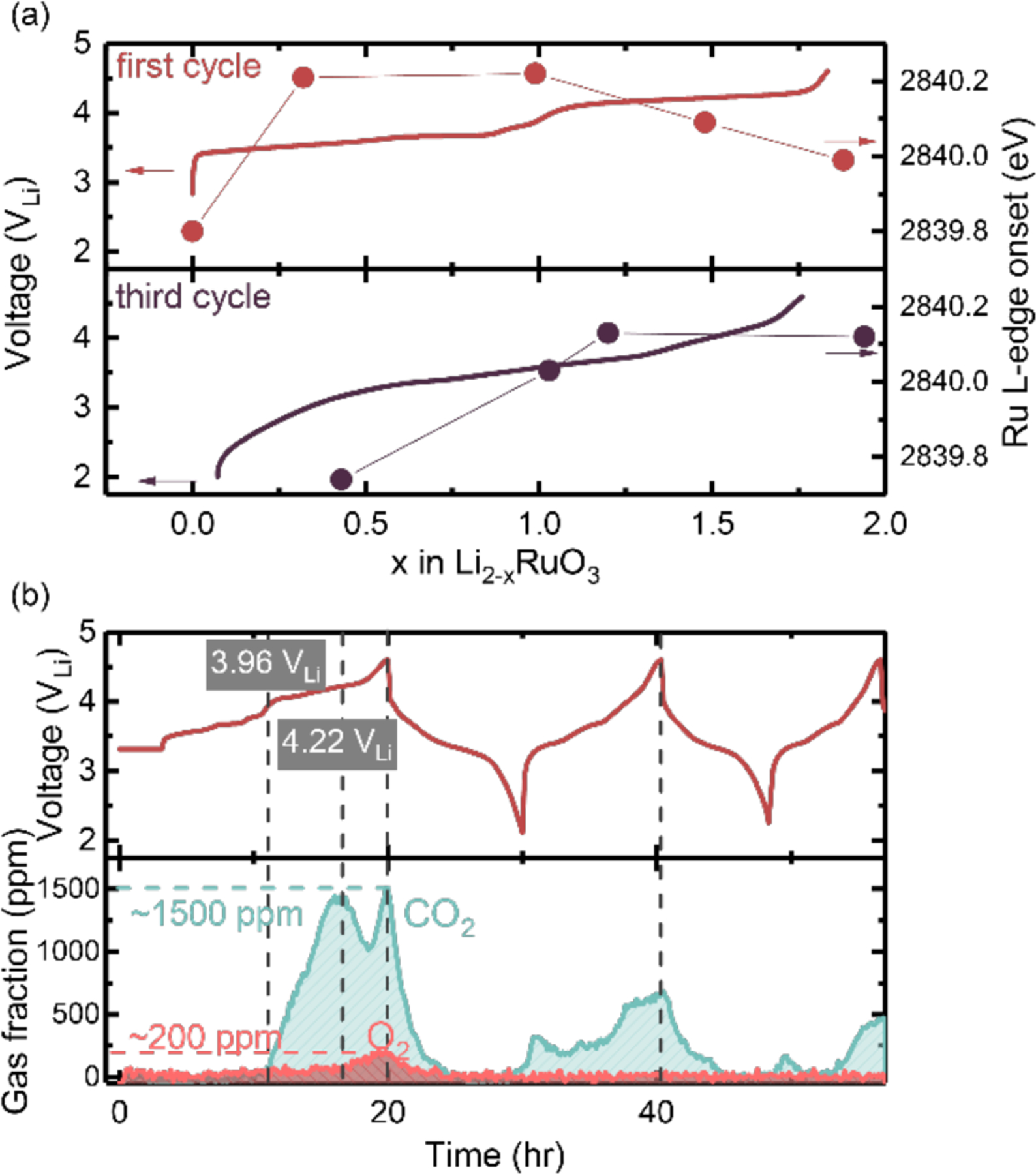
(a) Voltage profiles of Li₂RuO₃ composite electrodes during the first (dark red) and third (purple) charge cycle with current density of 16.35 mA per gram of fully lithiated oxide (g_oxides) or 0.088 mA per cm² of the electrode cross-section (cm_geo²), and the Ru-L₃ HERFD XAS edge onset of the corresponding composite electrodes as a function of lithium content indicated in filled circle (Figure S18). The lithium content was calculated based on the current applied and time of charge/discharge process and the charge transferred during the 5 h potential holding at the end-of-charge, which can be translate to how many lithium ions per formula unit (de-)intercalate upon cycling. (b) Differential electrochemistry mass spectrometry (DEMS) of Li₂RuO₃ during the first three cycles, where on the top panel is the voltage profile with a current density of 16.35 mA/g_oxides (0.049 mA/cm_geo²) and the bottom panel is the CO₂ and O₂ evolution as a function of time during the first three cycles.

Implications in oxygen redox reported for other oxides

The electronic structure signature of oxygen-oxygen coupling associated with lattice oxygen oxidation in Li_2-xRuO₃ revealed that non-bonding oxygen is primarily being oxidized,⁴⁵ giving rise to characteristic features in the O K-edge and Ru L₃-edge XAS as well as to the O K-edge XES. The oxidized non-bonding species can be formed through oxygen sublattice distortion which also has a transition metal (Ru) coordination, where this intermediate O-O dimer-like species can be stabilized through metal oxygen covalency,^{11, 40} in contrast with Mn-based oxides exhibiting anionic redox.^{47, 67} The electronic fingerprints and the physical origin proposed in this work can be applied to explain spectroscopic data of Li-excess materials reported previously. For charged Li_xIr_ySn_1-yO₃, the appearance of an additional spectral feature, i.e. at ≈523 eV in O K-edge XES and at ≈531 eV in O K-edge XAS, as well as the broadening of the e_g feature (≈531 eV) for charged Li₂IrO₃ have been previously attributed to oxygen redox without any specific electronic structure details. Similarly, for Li₂MnO₃ and its derivative materials including Li-rich Mn-rich NMC, researchers have observed similar increased intensities at the high-energy peak of ≈531 eV of O K-edge^{36, 38}. This peak has been proposed to be the fingerprint of oxygen redox, but no specific physical origin has been assigned to it. Based on this work, this feature can be assigned to the π/σ states of (O-O) bonding from enhanced oxygen coupling, providing electronic structure details for oxygen redox. While spectral changes of Ir L-edge XAS and O K-edge XAS spectra of Li_xIr_ySn_1-yO₃ are expected to be similar to those of Ru found in this work (Figure 1), previous Ir L-edge measurements^{47, 72} suffered from significant peak broadening due to the much shorter core-hole lifetime of Ir⁷³ and failed to detect any spectroscopic changes. High-energy resolution L-edge XAS is critical to follow any changes in such 4d and 5d transition metal oxides. Importantly, in Li₂MnO₃⁶⁷ and Li-rich Mn-rich NMC³⁸, even though similar changes have been observed in O K-edge spectra, no simultaneous broadening or additional peak is reported in the Mn L-edge upon charging,⁶⁷ which suggest that this (O-O) peroxo-like state did not have any metallic contribution, and therefore is more prone to oxygen evolution compared to metal-hybridized peroxo-like species as in Li₂RuO_3. Similarly, an emerging peak at ≈531 eV was observed in the O K-edge XAS of charged Li_1.2Ti_0.4M_0.4O₂ (M = Fe, Mn)⁷⁴ and Li_1.3Nb_0.3M_0.4O₂ (M = Fe, Mn)⁷⁵, while minimal differences were noted for transition metal L edges,^74–75 indicating the (O-O) coupled states in these compounds are not hybridized with the transition metal, resulting in lower capacity retention compared to Ru and Ir-based materials.

The observed electronic structure fingerprints for oxygen redox in Li₂RuO₃ and implications are discussed with respect to different proposed mechanisms for oxygen redox in the literature. The finding on oxidation of non-bonding oxygen can be related to the DFT studies of oxygen redox in Li₂MnO₃, Li₂Ru_0.5Sn_0.5O₃ and Li-excess disordered rocksalt reported by Seo and Ceder,⁴⁵ where the oxidation of non-bonding oxygen (the oxygen bound to Li) was proposed. However, similar to what Tarascon, Doublet and coworkers claim,^{11, 40} we argue that the strong hybridization between Ru and O₂ⁿ⁻ is critical to stabilize the oxidized oxygen species otherwise oxygen-oxygen coupling would form molecular oxygen, causing capacity loss (irreversible oxygen redox). In addition, transition metal migration can create under-coordinated oxygen, which can facilitate the coupling between transition metal migration and oxygen redox in Li-rich Mn-rich NMC (Li_1.2Mn_0.54Ni_0.13Co_0.13O₂) observed by Gent and Chueh.³⁸ Nevertheless, such oxygen, without transition metal coordination, is prone to be released and would not contribute to capacities in later cycles, as shown by hard XAS data from Hu et al.³⁷, where the capacity contribution from oxygen redox of such materials is diminished to 50 mAh/g in the 83^rd cycle compared to 120 mAh/g in the first cycle.³⁷ Moreover, we show that in such covalent oxides with a 4d transition metal, even though stable (O-O) coupling can be formed in the first charge, the capacity attributed to oxygen redox can be overwhelmed by a more significant contribution from cation redox in subsequent cycles.

3. Conclusions

In this work, by combining O K-edge XAS, Ru L₃-edge HERFD-XAS and O K-edge XES spectroscopy with ab-initio theoretically calculated spectra, we have captured and rationalized electronic structure fingerprints that reveal an enhanced O-O coupling in Li_2-xRuO₃ in the 4.2 V_Li plateau during the first charge after removing ≈ 50 % of the lithium. This observation provides direct evidence central to lattice oxygen redox (O²⁻/(O₂)ⁿ⁻) in charged Li_2-xRuO₃ after Ru oxidation (Ru⁴⁺/Ru⁵⁺). Such oxygen-oxygen coupling (lattice oxygen redox) of Li_2-xRuO₃ was also accompanied with simultaneous Ru reduction that cannot be solely explained by oxygen vacancy formation in the oxides at high potentials. Upon the first charge, the lattice oxygen redox is accompanied by a small amount of O₂ evolution in the first charge (captured by DEMS), which is diminished in subsequent cycles. This observation is in agreement with the changes in Ru L₃-edge HERFD-XAS. Ru was found to be in a more reduced state in later cycles despite similar lithium content, indicating that the Ru redox contributed more to discharge capacities in later cycles than in the first cycle. This study has provided theoretical insights on previously reported spectroscopic features in resonant inelastic X-ray scattering spectroscopy and O K-edge XAS across different materials families exhibiting anionic redox. This work highlights the importance of combining with the state-of-the-art core-level measurements and ab-initio excited-state Bethe-Salpeter equation calculations in order to interpret the spectroscopic features. The presented approach can be used as a transferable framework to monitor the spectroscopy changes of metal oxides undergoing redox/electrochemical reactions for Li-ion and electrocatalysis applications.

4. Methods

Experimental methods

Solid-state synthesis

The pristine Li₂RuO₃ was synthesized through the solid-state route previously undertaken by Goodenough et al.⁷⁶ and Tarascon et al.⁴⁰ Li₂CO₃ and RuO₂ precursors are first dried under air flow at 300 °C for 4 h. The precursors were then mixed in stoichiometric amounts, but with a Li excess of 10 %, with a mortar and a pestle for 1 h in a argon-filled glovebox (H₂O, O₂ < 0.1ppm). The resultant powder was pelletized under 1 MPa and calcined and sintered at 1000 °C and 900°C under air with heating rate of 2 °C/min for 24 h and 48 h, respectively, with intermediate grinding. The phase purity of Li₂RuO₃ is confirmed through X-ray diffraction (XRD) with PANalyt’cal X’Pert PRO (Figure S19).

Positive electrode preparation

The pellet electrode was prepared by pelletizing around 48 mg of active material using 6 mm diameter pressing die set (Across International) for 15 mins. The pellets were then sintered under air at 900 °C for 6 hours. The cooling and heating rates were 2 °C/min. The pellet electrodes were then broken into pieces of around 3 mg each and dried in vacuum under 120 °C overnight before being transferred into an Argon-filled glovebox (<0.5 ppm of H₂O and O₂). The pellet electrodes were used for the X-ray measurements to remove any ambiguities introduced by conductive carbon and binder.

Composite electrodes were prepared by mixing active material (80 % mass fraction), 10 % acetylene black (AB) and 10 % polyvinylidene fluoride (PVDF) (Kynar) dispersed in N-Methyl-2-pyrrolidone (NMP) with Fritsch Minimill 23 homogenizer. The slurry was then blade-coated onto an aluminum sheet with a gap of 5 μm. The composite electrodes were punched into 1.27 cm disc and pressed at 5.7×10⁴ kg/cm² under a hydraulic press, to embed the powder into the aluminum disc. Finally, the electrodes were completely dried at 120 °C under vacuum for 12 h before being transferred into Argon-filled glovebox (<0.5 ppm of H₂O and O₂). The active loading of the composite electrodes for the cycling experiments is around 3 mg/cm². Composite electrodes for DEMS experiments were prepared with a slurry dispersed in less NMP to make a more viscous slurry. The resultant slurry was then blade-coated onto a stainless steel 304 mesh with an opening of 20 μm with a wire diameter of 0.2 mm with an aluminum sheet underneath, and with a gap of 15 μm. The electrodes were then dried and separated from the aluminum sheet underneath and punched into 15 mm diameter discs. The DEMS electrodes were pressed at 4.11×10⁴ kg/cm² under a hydraulic press. Finally, the electrodes were completely dried at 120 °C under vacuum for 12 h before being transferred into an Argon-filled glovebox (<0.5 ppm of H₂O and O₂). The active loading of the composite electrodes for the DEMS experiments was around 5.27 mg/cm², which is higher than the loading of composite electrodes for XAS measurements to ensure that enough gaseous species were evolved to be detected during cycling.

Electrochemical measurements

Electrochemical behavior of the pellet electrodes was confirmed by galvanostatic measurements in two-electrode cells (Tomcell type TJ-AC). Cells were assembled in an argon-filled glovebox (<0.5 ppm of H₂O and O₂) and comprised a lithium metal foil as the negative electrode and the positive electrode, separated by two pieces of polypropylene separator (2500 Celgard), impregnated with 150 μL of LP57 (1M LiPF₆ in a 3:7 ethylene carbonate (EC): ethylmethyl carbonate (EMC) electrolyte (BASF)). After assembly, the cells rested for 6 h prior to measurement and then were charged with different end-of-charge potentials (3.6 V_Li, 3.8 V_Li, 4.2 V_Li, 4.4 V_Li, and 4.6 V_Li) at a rate of ≈1.64 mA/g. This rate of charge corresponds to a rate of C/100 based on the theoretical capacity calculated assuming one lithium extraction per Li₂RuO₃. The cell was held at the end-of-charge potential for 5 h before disassembly inside the glovebox. The composite electrode was charged in a two-electrode coin cell (Hohsen CR2016) with Li metal foil as the negative electrode. The positive and negative electrodes were separated by two pieces of polypropylene separator (2500 Celgard), impregnated with 100 μL of LP57. The coin cells were charged at a rate of C/10 (16.35 mA/g) with different end-of-charge potential (first cycle: 3.6 V_Li, 3.8 V_Li, 4.2 V_Li and 4.6 V_Li, third cycle: 3 V_Li, 3.4 V_Li, 4 V_Li, and 4.6 V_Li). The cells were held at the end-of-charge potential for 5 h before being disassembled inside the glovebox. The collected pellets and composite electrodes were rinsed in 1 mL EMC solution with stirring for 24 h to remove the residual electrolyte and electrolyte decomposition products on the surface. The pellets and composite electrodes were then dried in vacuum for 4 h before further characterization using XAS and XES.

Differential electrochemistry mass spectrometry measurements

The DEMS setup was constructed in-house based on the design reported by McCloskey et al.⁷⁷ and used for the detection of gas evolution including CO₂ and O₂ in the head space of the electrochemistry cell along with pressure monitoring. Details on the DEMS setup and cell design are documented in Harding et al.⁷⁸ The cell volume is around 6.7 cm³ for the measurement and Argon (Airgas, 99.999 % pure, O₂, H₂O, CO₂ < 1 ppm ) was used as a carrier gas. The DEMS cells were prepared inside an argon-filled glovebox (<0.5 ppm of H₂O and O₂) and comprised a lithium metal foil as the negative electrode and the DEMS positive electrodes, separated by two pieces of polypropylene separator (2500 Celgard), impregnated with 150 μL of LP57. The cell was first pressurized with argon to around 150 kPa and allowed to rest for 8 h prior to electrochemical measurements to check for any potential leakage. DEMS measurement started 4 h after pressurization with a time interval of 10 min of collecting the gas from the headspace to obtain a CO₂ evolution background from evaporated EMC fragments. The gas evolution profile upon charge/discharge as a function of time presented in this work were already background subtracted by fitting the gas evolution profile collected in the open circuit voltage stage after pressurizing with a polynomial function. The electrochemical measurements were carried out at a current density of 16.35 mA/g (0.088 mA/cm²) for charge and discharge (corresponding to a C/10 rate), and a time interval of 10 min was set between each DEMS sequence.

Synchrotron measurements

After rinsing and drying, the dried pellet electrodes were mixed with sucrose or BN powder to make 10 mm pellets. The pellets were wrapped around with Kapton tape for protection during transportation for hard X-ray absorption measurements.

High-energy resolution fluorescence detected Ru L₃-edge XAS was conducted at the Stanford Synchrotron Radiation Lightsource (SSRL) at SLAC National Accelerator Laboratory. The measurements were performed with a high-resolution tender x-ray spectrometer developed on a dispersive Johansson geometry in a 500 mm Rowland circle using a Si(111) analyzer.⁷⁹ The spectrometer recorded in dispersive mode the overall Ru Lα emission line; for extracting the HERFD spectrum, the peak intensity of the Lα emission line is plotted as a function of the incident photon energy. By using the Si(111) monochromator of SSRL beamline 6–2, an overall energy resolution of 0.6 eV was achieved enabling the sharpening of the Ru-L₃ XAS features when compared to conventional x-ray absorption spectroscopy, i.e., total fluorescence yield or transmission mode XAS (comparison shown in Figure S20). The incident beam was about 400 μm × 800 μm (FWHM) and the photon flux ≈ 10¹² sec⁻¹. The dried electrode material was mixed with sucrose to minimize any self-absorption effects across the very intense Ru L₃-edge resonances, resulting in pressed pellets with an active material mass fraction concentration of 0.5 %.

Ruthenium K-edge EXAFS was conducted at beamline 20-BM-B of the Advanced Photon Source (APS) at Argonne National Laboratory in transmission mode with an active materials mass fraction of 10 %, diluted with boron nitride. A Ru metal foil was used as reference. O K-edge XAS and XES were conducted at the Advanced Light Source (ALS) on beamline 8.0.2. All spectroscopy data were normalized and processed using the ATHENA software package.⁸⁰

Computational Methods

DFT calculations

We used the Perdew-Burke-Enzerhof (PBE)⁸¹ formulation of the density functional and projected augmented wave (PAW) potentials implemented in Vienna Ab-initio Simulation Package (VASP)^82–84, with Dudarev’s rotationally invariant Hubbard-type U⁸⁵ applied on the transition metal where we applied a U_eff = 4 eV on Ru 4d orbital as reported from previous work.^{11, 45} A k-point per reciprocal atom of 8000 was used. The delithiated structures were generated with a primitive cell with 4 formula unit of Li₂RuO₃, where for each different lithium content, the most energetically favorable configuration was taken. The voltage profile calculated using the energetics from the delithiated structures is shown in Figure S5, where the computed voltage profile matched relatively well with experimental charging curve. However, we should note that to compute the true ground-state at each lithium content along the convex hull, a cluster expansion approach should be employed.⁸⁶ The surface calculations in Figure S7(d) was conducted with VASP using a stoichiometric slab model with slab thickness of 5 Å and a vacuum thickness of 10 Å to avoid any spurious interactions across the periodic boundary. For simplicity, a surface orientation of (001) was chosen for the test, and a k-point grid of 7 × 7 × 1 was used. We fully relaxed the surface structure before the OCEAN calculations.

The XAS and XES simulations were performed with the OCEAN 2.5.2 code^50,51, which combines ground-state density-functional theory and the Bethe-Salpeter equation (BSE) to account for the core-hole presence and to properly capture the spin-orbit interactions of transition metals. The ground-state charge density and wave functions used in the core-hole screening and BSE calculations were obtained using Quantum Espresso.⁸⁷ Norm-conserving pseudopotentials from the ABINIT⁸⁸ distribution were used. The k-point grid used to solve the Kohn-Sham states was typically 6×6×3 for the pristine Li₂RuO₃ (24 atom cell). Similar values were used for all structures. The screening calculations used a 2×2×2 k-point grid. The number of unoccupied bands used for the BSE calculation was 250, and the screened core-hole potential calculation included 750 bands. A spectral broadening of 0.5 eV was applied and dipole and quadrupole transitions were considered. To enable easy spectroscopic feature comparison, the core-level shift was not turned on for the OCEAN calculations. Given the polycrystalline type of our samples, all simulated spectra were obtained by averaging the contribution from all photon polarizations.