Persistent spatial patterns of interacting contagions

Abstract

The spread of infectious diseases, rumors, fashions, and innovations are complex contagion processes, embedded in network and spatial contexts. While the studies in the former context are intensively expanded, the latter remains largely unexplored. In this paper, we investigate the pattern formation of an interacting contagion, where two infections, A and B, interact with each other and diffuse simultaneously in space. The contagion process for each follows the classical susceptible-infected-susceptible kinetics, and their interaction introduces a potential change in the secondary infection propensity compared to the baseline reproduction number $R_0$. We show that the nontrivial spatial infection patterns arise when the susceptible individuals move faster than the infected and the interaction between the two infections is neither too competitive nor too cooperative. Interestingly, the system exhibits pattern hysteresis phenomena, i.e., quite different parameter regions for patterns exist in the direction of increasing or decreasing $R_0$. Decreasing $R_0$ reveals remarkable enhancement in contagion prevalence, meaning that the eradication becomes difficult compared to the single-infection or coinfection without space. Linearization analysis supports our observations, and we have identified the required elements and dynamical mechanism, which suggests that these patterns are essentially Turing patterns. Our work thus reveals new complexities in interacting contagions and paves the way for further investigation because of its relevance to both biological and social contexts.

I. INTRODUCTION

After entering the new millennium, infectious diseases appear to be more active than ever, along with many new emerging pathogens. Well-known examples include Severe Acute Respiratory Syndrome in 2003 [1,2], influenza A (H1N1) in 2009 [3], Middle East Respiratory Syndrome coronavirus in 2012 [4], Ebola in 2013 [5], and the continuing H7N9 of avian influenza virus [6], etc. To understand contagion processes, mathematical models are an essential tool and have a long tradition in scientific communities that can date back to Bernuolli's work on the smallpox vaccination in 1760 [7]. Until now, the modeling effort has been fruitful at all levels [8,9], ranging from conceptual models [10,11] that capture the generic features of contagions, network models [12–15] that focus on the underlying structure of population or commuting patterns to the sophisticated computational models [16,17], where a variety of high-resolution data, like demographics, transportation, epidemiological features, and behavioral response [18], are incorporated.

One important research line aims to understand realistic yet more complicated contagion scenarios, where, e.g., more than one infection is considered that circulates simultaneously in the population. This sort of interacting contagions is motivated by the fact that the spread of different infections in the real world is not entirely independent; they often influence each other [19,20]. Well-known examples include the case of pneumonia bacterium like Streptococcus pneumoniae and viral respiratory illness (e.g., seasonal influenza) where they mutually facilitate each other's propogation [21,22], and the coinfection between human immunodeficiency virus and a host of other infections [23–27]. The interaction among different infections can be either competitive [28–34] (they suppress each other's circulation) or cooperative [35–42] (they support each other). The mean-field treatment and percolation studies of structured population reveal a rich spectrum of new dynamical features that are unexpected in the classic scenario of single infection. For example, when different infections are competing, both one-infection-dominance and coexistence are possible, depending on the properties of involved infections and the underlining networks [28]. By contrast, in cooperative contagions discontinuous outbreak transition appears [35,36], along with many interesting spreading features such as the higher chance of outbreak in clustered networks [37], first-order phase transitions in the contagion prevalence [40], etc.

Although these studies provide new insights into the temporal dynamics of interacting contagions, their spatial behavior is largely unknown [43]. The investigation of the spatial role is indispensable for a full comprehension of contagion complexities [44,45], not only for its conceptual significance but also for its practical relevance to the real world [46]. Abundant empirical evidence reveals nontrivial dynamical properties in spatial epidemiology, such as traveling waves [47], infection patterns [48], and even the spatiotemporal chaos [49]. A major modeling effort is devoted to the studies of traveling waves in spatial domains, like the Black Death in Europe or the rabies epizootic in France [44]. The emergence of infection patterns, however, receives much less attention, yet a few mechanisms are proposed for their generation [50,51]. These studies mainly focus on the single infection cases by incorporating additional compartments and/or additional dynamical processes. To our knowledge, there is rare work discussing the spatial dynamics of interacting contagions, especially the possibility of pattern emergence. A preliminary effort studies the spatial dynamics of two interacting contagions, assuming all individuals are of identical mobilities; novel propagation modes are revealed, like receding fronts and standing waves [40]. However, in realistic cases, individuals in different states are generally of different mobilities, depending on the individual's state. For example, healthy people normally move faster than the sick, who might prefer staying at home or in the hospital for recovery. So what is the generic spatial dynamics when more than one infection proliferates in the population? This question is also of particular interest in the ecology community, where different diffusivities of species are thought to be responsible for the emergence of patchiness [52]. In addition, recent works show that multiplex networks as the underlying medium provide another mechanism for generating patterns even if all species are of the same mobility [53–56].

In this work, we study the dynamical properties of two interacting susceptible-infected-susceptible (SIS) infections in a spatially extended context within the reaction-diffusion (RD) framework, see Fig. 1. When the susceptible individuals are assumed to diffuse faster than the infected, we find infection patterns in a wide range of parameters. Counterintuitively, neither competition nor cooperation between the two infections is required for pattern formation, implying a rather loose precondition for their emergence. Our linearization analysis provides a good prediction, where positive eigenvalues imply instability modes, corresponding to the pattern formation.

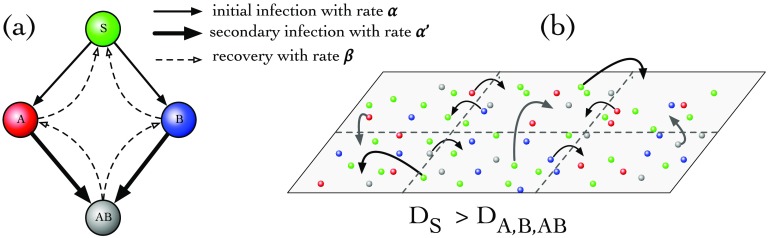
FIG. 1.

The model of interacting contagions. (a) Mean-field model (without space): Consider two infections, A and B, that circulate in a population. Four states are then possible for host individuals: susceptible S, partially infected A or B, and the coinfected state AB. In the contagion process, S becomes partially infected (A/B) with an initial infection rate $\alpha$ by contacting the infected; the partially infected individuals can be further be infected by the other infection to be doubly infected (AB) with the secondary infection rate ${\alpha }^{\prime }$. All infected individuals recover with rate $\beta$. (b) Spatially interacting contagions: When subpopulations are coupled through their spatial neighborhood, the diffusion captures the local mobility of individuals and thus also the infections they carried. Generally, the mobility of a given individual depends on its state; e.g., in epidemic spread, susceptible people statistically move faster than infected individuals, who might prefer to stay at home or in the hospital for recovery. Mathematically, this is captured by $D_S>D_{A,B,AB}$ within the RD framework described by Eq. (2).

The paper is organized as follows. In Sec. II, we first briefly introduce the mean-field treatment of interacting contagions and then define the spatial model in the RD framework. Main results are shown in Sec. III, where the impact of contagion interactions, the baseline reproduction number, and the mobilities of different states are studied. Special interest goes to the pattern hysteresis in Sec. IV. The dynamical mechanism is discussed in Sec. V. Finally, we summarize our work in Sec. VI.

II. MODEL DESCRIPTION

A. Mean-field model without space

As in Ref. [40] we shall only consider the case of two infections, A and B, each of SIS-type contagion dynamics. For a single SIS-type infection, host individuals can be susceptible (S) or infected (I); the transmission happens via $S+I\to 2I$ and recovery by $I\to S$, with infection rate $\alpha$ and recovery rate $\beta$, respectively. The dynamics of SIS therefore captures a class of contagions where recovered individuals confer no immunity. In a well-mixed population, one can write down the kinetic equations for $S\left(t\right)$ and $I\left(t\right)$; an outbreak happens only if the so-called basic reproduction number $R_0\equiv \alpha /\beta >1$ and the population is contagion-free otherwise.

When generalized to the case of two infections [see Fig. 1(a)], a host could then be in one of four states (S, A, B, AB), corresponding to being susceptible, infected with A only, infected with B only, and infected with both, respectively. In the transmission dynamics, we distinguish two infection rates: the initial rate ${\alpha }_A$ (${\alpha }_B$), with which infection A (B) transmits to a susceptible S individual, and the secondary rate ${\alpha }_{AB}$ (${\alpha }_{BA}$), with which a secondary infection transmits to a host who is already infected with A (B). To simplify, we assume uniform recovery rate $\beta$. With these, the mean-field (MF) dynamics is

$$\begin{array}{ccc}\hfill \dot{S}& =& -{\alpha }_{A}S(I_A+I_{AB})-{\alpha }_{B}S(I_B+I_{AB})+\beta (I_A+I_B),\hfill \\ \hfill {\dot{I}}_A& =& {\alpha }_{A}S(I_A+I_{AB})-{\alpha }_{AB}{I}_A(I_B+I_{AB})+\beta (I_{AB}-I_A),\hfill \\ \hfill {\dot{I}}_B& =& {\alpha }_{B}S(I_B+I_{AB})-{\alpha }_{BA}{I}_B(I_A+I_{AB})+\beta (I_{AB}-I_B),\hfill \\ \hfill {\dot{I}}_{AB}& =& {\alpha }_{AB}{I}_A(I_B+I_{AB})+{\alpha }_{BA}{I}_B(I_A+I_{AB})-2\beta I_{AB}.\hfill \end{array}$$ (1)

Here $S$, $I_A$, $I_B$, and $I_{AB}$ denote the densities of individuals in the states S, A, B, and AB, respectively. The precise meaning of ${\alpha }_{AB}$ is the rate that a host already infected with A can be further infected with B and vice versa. One can then conveniently defines the cooperativity coefficients $C_A={\alpha }_{AB}/{\alpha }_B$ ($C_B={\alpha }_{BA}/{\alpha }_A$), measuring the infection A–(B) induced change in the secondary infection rate for the other. When A and B cooperate, the secondary infection is easier, i.e., $C_{A,B}>1$; $C_{A,B}<1$ implies competitive contagions, such as the case of cross-immunity; and if $C_{A,B}=1$, then the two infections are neutrally interacting, essentially decoupled in their contagion processes. Without considering birth and death processes in the population, the four densities are in conservation, i.e., $S+I_A+I_B+I_{AB}=1$. For simplicity, here we adopt symmetrical parameters, i.e., ${\alpha }_A={\alpha }_B=\alpha$ for the initial infections, ${\alpha }_{AB}={\alpha }_{BA}={\alpha }^{\prime }$ for the secondary infections, which implies $C_A=C_B={\alpha }^{\prime }/\alpha \equiv C$.

In Ref. [40], this mean-field model has been systematically studied, and the main findings are as follows: for strong cooperation ($C>2$), the contagion shows backward bifurcations [57], i.e., first-order dynamical phase transitions with two different thresholds in $R_0$, one for outbreak at 1, and the other for eradication at $2\sqrt{C-1}/C<1$; for competitive or weakly cooperative scenarios ($C<2$), the contagion transitions are qualitatively the same as the traditional single infection, showing continuous outbreak transitions. General asymmetrical parameters do not change the results qualitatively. For details we refer to Ref. [40].

B. Spatially interacting contagions

When the spatial dimension is incorporated [Fig. 1(b)], the dynamics is conveniently described by the RD system [44] as [in the 1 dimensional (1D) domain]

$$\begin{array}{ccc}\hfill {\partial }_{t}S(x,t)& =& f_S+D_S{\partial }_x^{2}S,\hfill \\ \hfill {\partial }_t{I}_A(x,t)& =& f_A+D_A{\partial }_x^2{I}_A,\hfill \\ \hfill {\partial }_t{I}_B(x,t)& =& f_B+D_B{\partial }_x^2{I}_B,\hfill \\ \hfill {\partial }_t{I}_{AB}(x,t)& =& f_{AB}+D_{AB}{\partial }_x^2{I}_{AB}.\hfill \end{array}$$ (2)

The first terms in the right-hand side $f_{S,A,B,AB}$ are reactions, representing the intrinsic contagion dynamics, the same as the right-hand side of Eq. (1); the second terms are the diffusion, capturing the local mobilities of individuals potentially capable of carrying the infections to their neighboring regions, with $D_{S,A,B,AB}$ being the corresponding diffusion coefficients. The simplest case, where $D_S=D_A=D_B=D_{AB}$, has been studied in Ref. [40] and mainly focuses on the properties of traveling waves. There, apart from the classic scenario of forward movements, the backward propagation also emerges, together with the possibility of standing waves being expected. These new modes come from the competition between the reactions and the diffusion in Eq. (2).

In the following studies, we consider a more general setting, where the individuals' mobilities depend on their states; therefore the diffusion coefficients are not all identical any more. To simplify, we only differ the diffusion of the infected from the susceptible's and do not further distinguish those partially infected and the doubly infected, i.e., $D_A=D_B=D_{AB}=D_I\ne D_S$. As mentioned above, the mobilities of the infected individuals are generally lower than the healthy, and therefore we assume $D_S>D_I=1$ if not stated otherwise. In Appendix, the linearization analysis of Eq. (2) is conducted, where positive eigenvalues mean the instability of the homogeneous solutions, providing indicators for patterns to emerge.

In numerical simulations, the RD system is approximated as diffusively coupled ordinary differential equations and is solved with the fourth-order Runge-Kutta method, with the spatial resolution and time step being 1 [and $1\times 1$ in the 2 dimensional (2D) domain] and 0.01, respectively [58]. Random initial conditions are adopted whereby for each site $x$, a random number in the range of (0, $\epsilon$) is chosen for the densities of $I_{AB}(x,0)$ with $I_{A,B}(x,0)=0$, and $S(x,0)=1-I_{AB}(x,0)$ for the density conservation. $\epsilon ={10}^{-6}$ is used, meaning the population is almost contagion free but with many tiny infection seeds introduced. The specific value of $\epsilon$ or additional seeding in $I_{A,B}(x,0)$ does not qualitatively change the pattern dynamics. A periodic boundary condition is used throughout the study.

To monitor the process of pattern emergence, we introduce a spatial heterogeneity quantity:

$$\begin{array}{c}\hfill h\left(t\right)=\sqrt{\frac{1}{L_1}{\int }_0^{L_1}{\sum }_{j=1}^4{[X_j(x,t)-\langle X_j\left(t\right)\rangle ]}^{2}dx}\end{array}$$ (3)

in 1D continuous space or

$$\begin{array}{c}\hfill h\left(t\right)=\sqrt{\frac{1}{L_1{L}_2}{\int }_0^{L_2}{\int }_0^{L_1}{\sum }_{j=1}^4{(X_j(x,y,t)-\langle X_j\left(t\right)\rangle )}^{2}dxdy}\end{array}$$ (4)

in 2D continuous space, with $L_{1,2}$ being the size of the domain and $X_{1,2,3,4}=\left\{S,I_A,I_B,I_{AB}\right\}$. $\langle X_j\left(t\right)\rangle$ is the average density of each component over the whole domain. In our practice, we compute the heterogeneity according to the discrete version

$$\begin{array}{c}\hfill h\left(t\right)=\sqrt{\frac{1}{N}{\sum }_{i=1}^N{\sum }_{j=1}^4{[X_j^i\left(t\right)-\langle X_j\left(t\right)\rangle ]}^2},\end{array}$$ (5)

where $N$ is the number of local sites. By definition, a homogeneous solution (no pattern) means $h\to 0$, and the heterogeneous cases (pattern emergence) have $h>0$. Note that, in the single SIS infection, a well-known fact is that no positive eigenvalue is detected, and the homogeneous state with $h(t\to \infty )=0$ is the only stable solution.

III. PATTERN FORMATION

We start with 1D space and random initial conditions, where we can see the spatiotemporal evolution of infection patterns as illustrated in Fig. 2, which shows an example in a supercritical region ($R_0=2$), but without any cooperation or competition ($C=1$) at the moment. Without proper data in hand for an estimate, we assume $D_S=10$, which means that the susceptible individuals move faster by an order of magnitude than the infected.

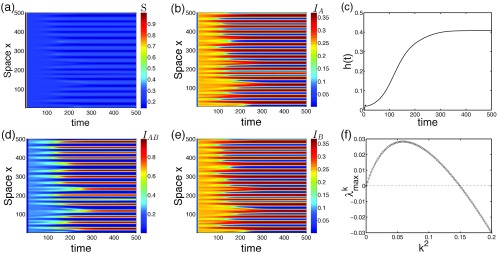
FIG. 2.

Emergence of infection patterns in 1D space. Starting with a perturbed contagion-free state (random initial conditions), strongly and weakly infected regions segregate from each other as time goes by [(a), (b), (d), and (e)]. Note that, due to the symmetrical parameters for the two infections, the resulting patterns of $I_A$ and $I_B$ are also in symmetry as $t\to \infty$, even though their initial conditions are not. (c) The spatial heterogeneity $h\left(t\right)$ gradually increases and then tends to saturation thereafter. (f) Among all Fourier modes, there are some unstable ${\lambda }_{\max }^k>0$, which trigger the spatial instability, in line with the patterns shown here. Parameters: $R_0=2$, $C=1$, $D_S=10$, $D_I=1$.

As we can see, patterns emerge as the strongly and weakly infected regions are gradually formed and segregated. A close comparison shows that the four densities are well correlated, where the density landscapes of A, B, and AB overlap, but the density distribution of S is opposite, as expected. In particular, the infection patterns of A and B are asymptotically identical $I_A(x,t)=I_B(x,t)$ when $t\to \infty$. By incorporating this symmetry, Eq. (2) can be reduced into

$$\begin{array}{ccc}\hfill {\partial }_{t}S(x,t)& =& -2\alpha S(I+I_{AB})+2\beta I+D_S{\partial }_x^{2}S,\hfill \\ \hfill {\partial }_{t}I(x,t)& =& \alpha S(I+I_{AB})-C\alpha I(I+I_{AB})+\beta (I_{AB}-I)+D_I{\partial }_x^{2}I,\hfill \\ \hfill {\partial }_t{I}_{AB}(x,t)& =& 2C\alpha I(I+I_{AB})-2\beta I_{AB}+D_I{\partial }_x^2{I}_{AB},\hfill \end{array}$$ (6)

where $I(x,t)=I_A(x,t)=I_B(x,t)$. For this reason, in the latter part we will adopt the overall density of infection A (${\rho }_{{}_A}=I_A+I_{AB}$) as our observable to illustrate the pattern, but we have to bear in mind that the results apply exactly to infection B since ${\rho }_{{}_A}={\rho }_{{}_B}$ (${\rho }_{{}_B}=I_B+I_{AB}$) after the transient. Note that, due to the difference in diffusivities, the overall density of a given location is in general not conserved anymore, i.e., $S\left(x\right)+I_A\left(x\right)+I_B\left(x\right)+I_{AB}\left(x\right)\ne 1$. The pattern formation process is captured in the increasing trend of spatial heterogeneity $h\left(t\right)$.

By analyzing the eigenvalues of the linearized system, there is indeed a positive eigenvalue region for some Fourier modes, which implies pattern formation and therefore supports our observations. From Fig. 2(f), the spatial scale can be estimated through the relation

$$\begin{array}{c}\hfill \mathrm{wavelength}=2\pi /k,\end{array}$$ (7)

where $k$ is a wave number and the value is 25.7–31.4 units when $k^2$ is chosen between 0.04 and 0.06 around the peak. This estimated length scale well matches the pattern scale here (500 units/16 bars $\approx 31.3$). The system exhibits a rich spectrum of dynamical properties, which we will discuss in details in the following part.

A. Impact of contagion interaction

The first concern is the role of contagion interaction—characterized by the cooperativity coefficient $C$. We might suppose that it is due to the contagion interaction that induces pattern formation. Strong cooperation or competition may be preferred. But this is not actually the case.

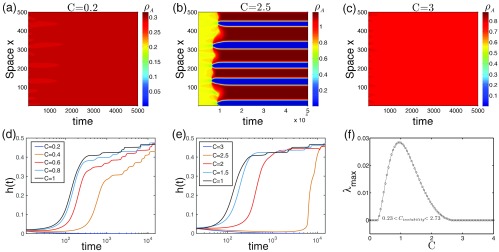
Figure 3 shows that too-competitive (small $C$) or too-cooperative (large $C$) interaction hinders the emergence of a pattern (e.g., $C=0.2$ and $C=3$). More evidence is illustrated in the evolution of $h\left(t\right)$ for a couple of cases with different $C$ [Figs. 3(d) and 3(e)]. As we see, the increasing trend of $h\left(t\right)$ becomes slower or just ceases when the interaction $C$ deviates gradually from 1 at both sides. These suggest that the most favored case for pattern emergence occurs at an intermediate interaction (here, coincidentally, the neutral scenario). The maximal eigenvalues ${\lambda }_{\max }$ clearly show that only a bounded range of $C$ supports the emergence of patterns, and they peak around $C=1$ [Fig. 3(f)]. While the positive sign of ${\lambda }_{\max }$ indicates the possibility of pattern formation, their absolute value determines the speed of segregation process. So for those with small positive eigenvalues, pattern formation takes a long time, like the one in Fig. 3(b). Note that the specific value of $C$ for the most favored cases is not necessarily at 1; generally, it depends on the reproduction number $R_0$, a larger $R_0$ reduces the value, and vice versa. Further studies show that when $C$ deviates from the most favored case, the peaked mode $k$ becomes smaller; accordingly, the pattern scale increases [according to Eq. (7)], as one can compare the number of bars in Fig. 3(b) and in Fig. 2.

FIG. 3.

The impact of contagion interactions. Upper row: The spatiotemporal evolution of overall density of infection A (${\rho }_{{}_A}=I_A+I_{AB}$) for $C=0.2,2.5,3$, which shows that strong competition, e.g., $C=0.2$ in (a) or strong cooperation like $C=3$ in (c) actually inhibits patterns. (b) A case with a relatively strong interaction ($C=2.5$) that takes a long time to develop patterns. Lower row: $h\left(t\right)$ for a couple of interaction $C$ indicates that patterns are most likely to happen in the case of $C\simeq 1$ [(d) and (e)]; any deviation to a smaller or larger value will delay or just fail to have the formation process. (f) Eigenvalue analysis shows that the pattern appears within $0.23<C_{\mathrm{instability}}<2.73$, where ${\lambda }_{\max }>0$ and the peak is around $C=1$, in line with the observations here. Parameters: $R_0=2$, $D_S=10$, $D_I=1$. Random initial conditions are used in (a)–(e).

Generally, an outbreak is the precondition of pattern formation; the presence of competition between two infections inhibits each other's outbreaks and therefore also suppresses patterns. Counterintuitively, the cooperative interaction is also shown to impair pattern emergence, yet strong cooperation is always believed to facilitate outbreaks. A more confusing observation is that the intermediate interaction cases like the neutral one are the most likely scenario for patterns. These cases are usually believed to be weakly or noninteracting; the dynamics of the two infections are almost decoupled just as the single infection case, and no any pattern should be expected. This argument is, however, not true because the two contagion processes are not completely decoupled even when $C=1$, as we will discuss later.

B. Impact of the baseline reproduction number $R_0$

Now we turn to two traditional control parameters—the reproduction number $R_0$, which measures the baseline contagion capability of a given infection, and the mobilities.

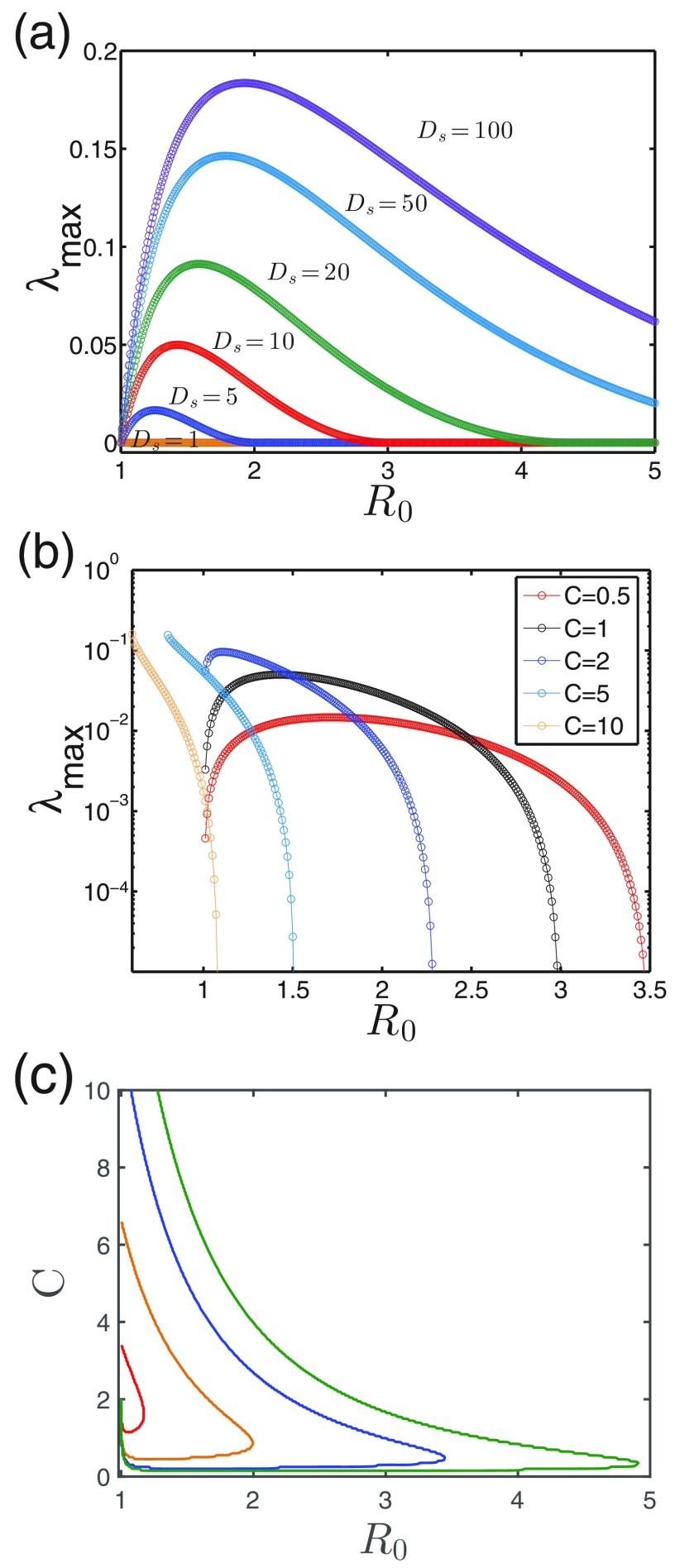
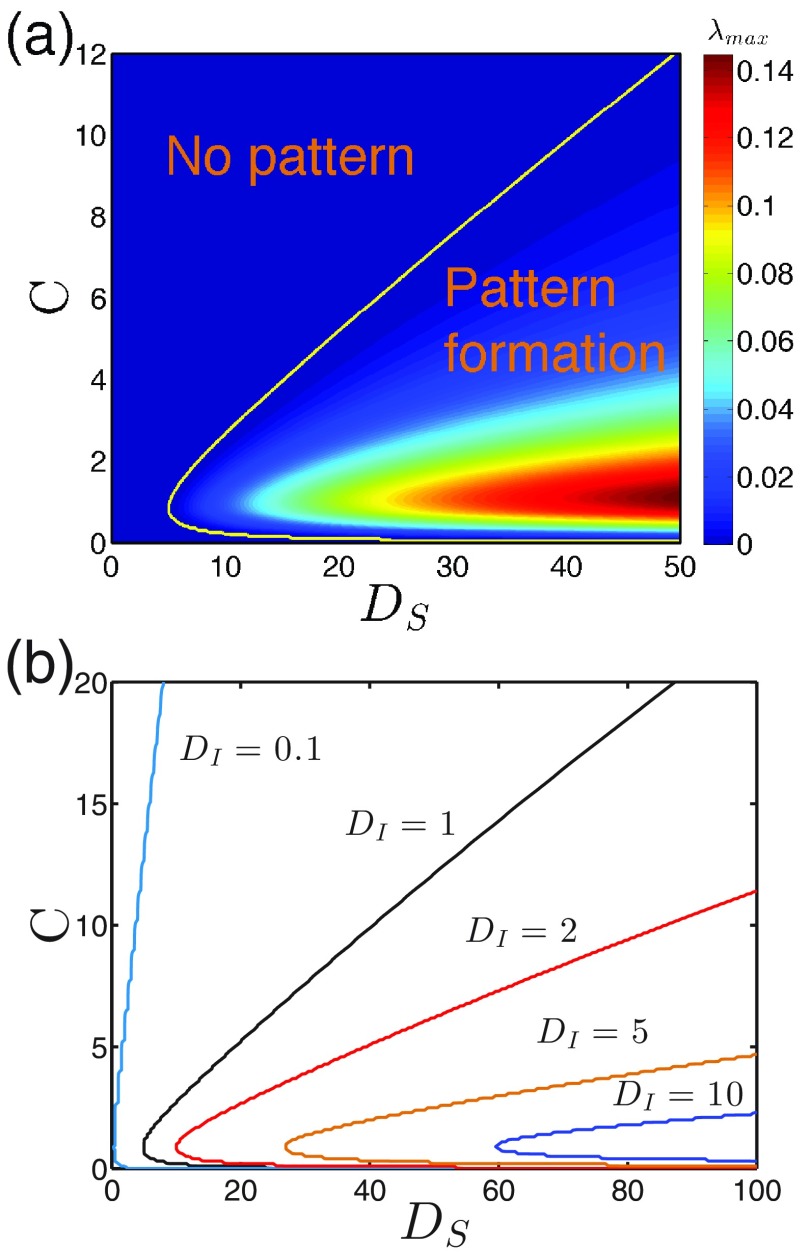
Figures 4(a) and 4(b) show the impact of $R_0$ on pattern formation for a couple of diffusion coefficients $D_S$ and interaction levels $C$. There is an upper threshold in $R_0$ for pattern transitions in all cases, above which the prevalence ${\rho }_{{}_{A,B}}$ is homogeneous. This means that, similarly to contagion interaction $C$, a bounded range is present for patterns. This range expands as $D_S$ becomes larger, but the upper threshold reduces as $C$ increases.

FIG. 4.

The impact of baseline reproduction number. (a) ${\lambda }_{\max }$ versus $R_0$ for different $D_S$ by fixing $C=1$. (b) ${\lambda }_{\max }$ versus $R_0$ for different $C$ by fixing $D_S=10$. (c) Boundaries for a couple of $D_S$ in $R_0\text{-}C$ parameter space, where the left side allows for pattern (${\lambda }_{\max }>0$) and the right side corresponds to no pattern (${\lambda }_{\max }=0$). Similarly to the impact of the interaction strength $C$, there is also an upper threshold of $R_0$ for the pattern emergence, above which patterns disappear. Parameter: $D_I=1$.

Figure 4(c) summarizes these observations in a more compact way. Notice that whenever the pattern becomes less likely to emerge (approaching the boundaries), the pattern scale increases. A close observation shows that for weakly cooperative or competitive cases ($C<2$) where outbreak phase transitions are continuous in the MF treatment, patterns are not allowed for $R_0<1$; this result is incorrect because the eigenvalues are computed based on the equilibrium of MF treatment (see Appendix), which could be different when patterns are present. Similar issue arises in strong cooperative cases ($C>2$), where the lower boundaries can be much reduced compared to the MF ones, which will be discussed in Sec IV.

C. Impact of mobilities

While Figs. 4(a) and 4(c) indicate that a higher mobility of the susceptible individuals facilitates pattern formation, Fig. 5(a) further provides the phase diagram by fixing the mobility of the infected ($D_I=1$). It shows that patterns tend to disappear when $C$ deviates from the intermediate values or $D_S$ becomes smaller. The former observation is consistent with the above results whereby the most favored cases for patterns occur at intermediate interactions. The latter observation suggests that a higher mobility of the susceptible is beneficial to the pattern emergence. In principle, a large-enough $D_S$ can always produce patterns no matter how strong the interaction between the two infections (either large or small $C$).

FIG. 5.

The impact of mobilities. (a) ${\lambda }_{\max }$ shown in $D_S\text{-}C$ space, where the boundary line separates the regions with (${\lambda }_{\max }>0$) and without (${\lambda }_{\max }=0$) pattern formation. $D_I=1$ fixed. (b) Boundaries for a couple of $D_I$; the left sides are regions allowing patterns. Parameter: $R_0=2$.

Figure 5(b) shows the impact of the infected mobilities, where we can see that increasing $D_I$ shrinks the pattern regions. This means for those cases where the infected individuals still move a lot, a pattern is less likely to appear. Actually, what really matters here is the ratio of the two diffusion coefficients; these boundaries are all well collapsed by rescaling the $x$ axis as $D_S/D_I$ if $C$ is not too large (see Supplementary Figure S1) [59]. This is because their absolute values simply set scale, and it is the ratio of $D_S/D_I$ that shifts the peaked wave-vector mode $k$, namely the pattern scales. Notice that for the limiting case of $D_I=0$, where the infections become completely localized, the spreading is blocked and there is no nontrivial patterns expected. All together, pattern formation favors the condition when the susceptible people diffuse a lot and at the same time the infected move relatively less (i.e., large ratio $D_S/D_I$), which prevents a too-large pattern scale from exceeding the domain size.

IV. PATTERN HYSTERESIS

A main concern for the contagion phenomena is prevalence. Here we address the following question: Compared to the case without space [described by Eq. (1)], what is the impact of the embedded space on the overall prevalence of outbreaks?

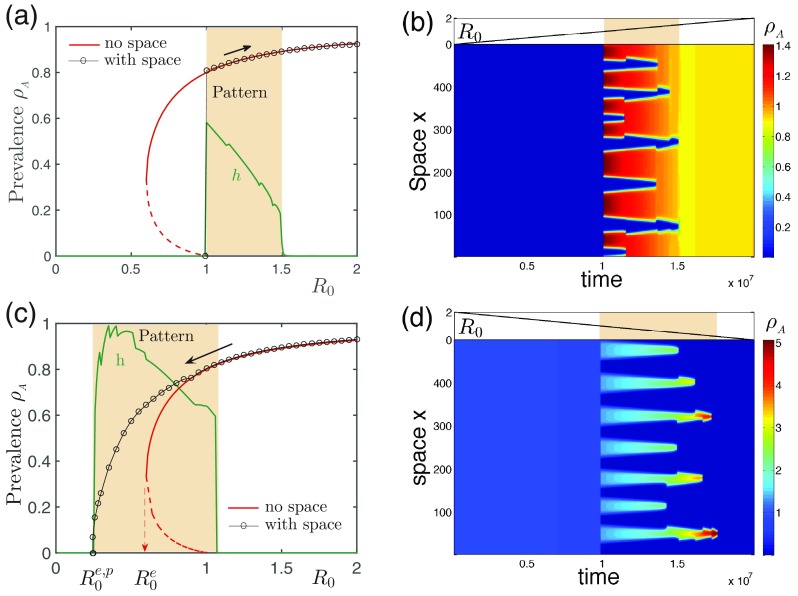
To achieve this aim, we first focus on the cooperative cases and slowly increase the reproduction number $R_0$ of the noisy system from zero, to trigger an outbreak, to a large value; then we decrease $R_0$ (e.g., by vaccination programs) for contagion eradication, and we examine the prevalence in the whole process. In numerical simulations, we start from the equilibrium state under the initial $R_0$, the increasing (decreasing) rate of $R_0$ is set ${10}^{-7}$ per time unit, and random perturbations within (0, $\epsilon$) are constantly imposed to trigger patterns or outbreaks in the density of $I_{AB}(x,t)$ for each site per time unit; accordingly, $S(x,t)$ minus the same $\epsilon$ for the density conservation. Here $\epsilon$ is also taken as ${10}^{-6}$. An interesting dynamical property we identified is the hysteresis phenomena, as shown in Fig. 6. In the direction of increasing $R_0$ [Figs. 6(a) and 6(b)], outbreak transition remains the same for both cases (with and without space), where the outbreak thresholds are identical at $R_0\approx 1$ and the two outbreaks share the same prevalence. Immediately after the outbreak, pattern is formed. Further increase in $R_0$ interestingly does not destroy the patterned infection as the theoretic prediction that when $R_0>1.08$ for $C=10$ [see Fig. 4(b)] patterns should become unstable. Instead, the pattern disappears until $R_0>1.5$, as shown by $h\left(t\right)$. The presence of pattern does not alter the overall outbreak size in this direction.

FIG. 6.

Pattern hysteresis. The pattern hysteresis emerges when we increase the parameter $R_0$ (upper row) and then decrease it (lower row). Left column [(a) and (c)]: The average prevalence as a function of $R_0$ with and without (MF cases) space in both directions; the patterns present in the shaded region are indicated by a nonzero heterogeneity $h$. Right column [(b) and (d)]: The corresponding spatiotemporal evolution of patterns. The parameter $R_0$ is changed slowly enough (subplots at the top) to have stable patterns. Pattern hysteresis is defined by two sets of pattern regions [1–1.5 in (a) and (b) and 1.08–0.25 in (c) and (d)]. The lower panels show that the presence of patterns leads to a much more difficult eradication because $R_0^{e,p}<R_0^e$, close to zero, which is bad for containment. Parameter: $C=10$ with tiny conservative noise kept in the system (see the text).

In the opposite direction [Figs. 6(c) and 6(d)], the pattern is not permitted at the beginning with $R_0=2$. By decreasing the reproduction number, pattern emerges until $R_0\approx 1.08$, predicted by the eigenvalue analysis. An amazing phenomenon happens when we further decrease $R_0$ so the eradication of the two infections now occurs not at $R_0^e$ but at a much smaller threshold, $R_0^{e,p}$ (“p” indicates the presence of patterns). This means that a persistent prevalence is present compared to the MF case (without space) in this less-infectious region. An intuitive explanation can be found in Fig. 6(d), where the coinfected individuals are now clustered in a few spatial spots in quite high densities; the two infections support each other, making their survival at a rather small $R_0$. Here the number of segregated bars decreases in both cases as time goes by [Fig. 6(b) and 6(d)], indicating that the pattern scale increases as the patterns become less likely, in line with the above observations.

Taken together, by varying $R_0$ in two directions, the pattern regions are quite different, only sharing a small overlap. This process is reminiscent of hysteresis in statistical physics, and hence we term the phenomenon pattern hysteresis. In the standard hysteresis, like first-order phase transitions, the critical behavior is depicted by a different transition point along each direction, and the hysteresis is defined typically by two different thresholds. In pattern hysteresis, however, the critical behavior along each direction is defined by a set of two thresholds for a pattern region, and the hysteresis is defined by two different sets of thresholds. As shown, pattern hysteresis results in persistent prevalence, and, to eradicate infections, an unusually high amount of effort is required.

Unexpectedly, even for neutral ($C=1$) and competitive ($C<1$) contagions, hysteresis is still present. For example, we compute the cases with $C=1$ and 0.5 by decreasing $R_0$ and find that the eradication threshold $R_0^{e,p}$ is around 0.7 and 0.9, respectively (see Supplementary Figure S2) [59], smaller than the cases without space, where $R_0^e=1$ for the eradication. Strikingly, the higher prevalence than MF value in these noncooperative cases are observed for all patterned regions, not only the patterned range within $R_0<1$ as shown in Fig. 6(c). Due to the hysteresis-induced deviation from the MF prevalence, the computation of eigenvalues is not exact when only using the MF prevalence without considering moving direction. True pattern regions with hysteresis are wider than the ones computed based on the fixed points in the MF treatment, as shown in Fig. 4.

V. DYNAMICAL MECHANISM

Until now, we see the emergence of patterns and provide a theoretic analysis by computing the eigenvalues of the linearized system. But still there is a lack of mechanism analysis, from which we may build a theory.

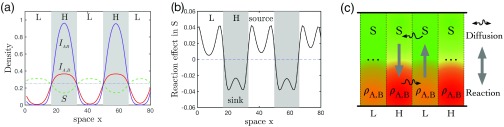
To this aim, we first plot all four density distributions of the stationary pattern, see Fig. 7(a), from which we see that these densities are segregated within high (H) and low (L) density regions, and the distribution tendency for S and for those infected are just reversed. To understand how these density profiles come to be possible, we look into the contributions from the two different dynamical parts—the reaction and diffusion. We find an aggregation process behind [Fig. 7(b)]: In L regions, where the density of S is higher than the neighboring regions, the reaction ${\rho }_{{}_{A,B}}\to S$ instead further increases its density to be even higher; a similar process happens in H regions, where the high density of infected gets higher by the underlining reaction process $S\to {\rho }_{{}_{A,B}}$. The diffusion processes, however, always dilute any high density in its neighborhood to counterbalance the density aggregation. Therefore, the two contributions are just opposite.

FIG. 7.

Dynamical mechanism. (a) Density profiles arranged within the high (H) and low (L) infected density regions in the 1D domain. The dotted-dashed line is the MF value (i.e., without space) of S for reference. (b) The effect of reactions in the dynamics of S [i.e., $f_S$ in Eq. (2)]. The positive reaction contribution (source) is to increase the density of S, whereas the negative one (sink) is to increase the infected at the expense of S instead. (c) The scheme of dynamical flows between two neighboring regions: The net reaction within the H regions is from the susceptible S of a low density to the infected ${\rho }_{{}_{A,B}}$ of a high density to be even higher and is reversed in the L regions—an aggregation process (the thick vertical arrows). Diffusion is always from high-density regions to low-density regions (the curved arrows). In such a way, a dynamical loop is formed, maintaining stable patterns. Same settings as in Fig. 2, and profiles in (a) are plotted after 1000 time units.

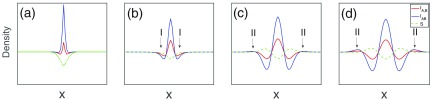
Bearing this in mind, Fig. 8 shows how instabilities trigger occurrence of patterns, which can be summarized as follows:

• (1)Starting from an equilibrium state, set the densities of both infections a bit higher in the center to seed the instability, and the density of S is accordingly lower than the equilibrium for conservation [Fig. 8(a)].
• (2)Immediately after this perturbation, the densities of infected decrease for their deviation from the equilibrium, and therefore the reactions of $I_{AB}\to I_{A,B}\to S$ dominate. As $D_S>D_I$, a substantial amount of S quickly replenishes in the lateral regions (region I), and soon the density of S becomes relatively higher [Fig. 8(b)].
• (3)Then the aggregation process starts, where S steadily increases in region I via ${\rho }_{{}_{A,B}}\to S$; the reverse happens in the center where ${\rho }_{{}_{A,B}}$ increases. The increase of S in lateral regions combined with its diffusion causes further increase of all densities in the wider outside regions and because $D_S>D_I$, $I_{A,B,AB}>S$ at some points [region II in Fig. 8(c)].
• (4)This then triggers another aggregation process in region II for $I_{A,B,AB}$ to build up [Fig. 8(d)]. In such a way, the patterning process sweeps the whole domain and these periodic profiles steadily grow until the stationary state is reached, as shown in Fig. 7(a).

FIG. 8.

Onset of pattern formation. Panels (a)–(d) show the occurrence of pattern formation triggered by a perturbation. The initial conditions of the evolution are from equilibrium state ($S^{*}=I_A^{*}=I_B^{*}=I_{AB}^{*}=1/4$, for the chosen parameters) except for the center site at the 1D domain with a length of 60 units shown here. Parameters: $R_0=2$, $C=1$, $D_S=10$, $D_I=1$.

Based on these observations, the occurrence of patterns can be decomposed into two essential processes: (i) the triggered alternating profiles, where S and $I_{A,B,AB}$ start to take the lead in turns such as in Fig. 8(b) and 8(c), and (ii) the aggregation process. While the former is naturally driven by the diffusion difference, the latter is critical for further growth and is summarized in Fig. 7(c). There the reactions happen within each local site for aggregation, and diffusion occurs between neighboring sites for dilution. Once an alternating profile is triggered between neighboring sites, the reaction dominates over the diffusion at the beginning for the growth of the profiles. As diffusion becomes stronger later, the two eventually are balanced in the form of a sustainable dynamical loop, and a stationary pattern is then reached.

Note that such a dynamical loop is impossible for single infections, and therefore patterns cannot be expected. In simulations of such a case in a similar setting, we can also see a profile like Fig. 8(b) because process (i) is still present, but further growth is absent because there is no similar process with the aggregation mechanism in its dynamics. The system becomes homogeneous eventually.

The impact of physical parameters on pattern formation can be understood by discussing their influence on the stability of this dynamical loop as follows:

• (a)$C\to 0$ or $C\to \infty$ breaks the loop's sustainability. $C\to 0$ means the termination of the secondary infection process, and this breaks down the reaction into two single-infection processes, $S\to I_{A,B}$. Since the aggregation dynamics is absent for a single infection, no pattern is expected. $C\to \infty$, on the contrary, leads to an overwhelming fraction in ${\rho }_{{}_{A,B}}$, while others, especially the density of S, become quite low in H regions. As such, the inadequate supply of S for the reaction to produce ${\rho }_{{}_{A,B}}$ makes the loop collapse, and patterns thus also fail to exist. This explains why too-competitive or -cooperative interactions fail to generate patterns and an intermediate $C$ provides the most favored condition for patterns.
• (b)For a large $C$, however, there are two strategies one can think of to keep the loop working: either a large $D_S$ that provides a quick supply of S from the neighborhood or a small $D_I$ where the loss of ${\rho }_{{}_{A,B}}$ by dilution is so slow that the reaction $S\to {\rho }_{{}_{A,B}}$ is almost turned off and even a very low density of S is enough to keep the loop working. This explains why pattern emergence favors large $D_S$ and small $D_I$ and why the ratio $D_S/D_I$ is essential.
• (c)The impact of $R_0$ is similar to $C$ and affects both initial and secondary infection processes. $R_0\to 0$ terminates the whole reaction, $R_0\to \infty$ by contrast, and results in an imbalance between S and ${\rho }_{{}_{A,B}}$; therefore a bounded pattern range of $R_0$ is explained. Also as expected, when a larger $R_0$ is used, the value of $C$ for the most favored conditions decreases for moderate densities of ${\rho }_{{}_{A,B}}$, and vice versa.
• (d)As the dynamical loop is endangered by tuning parameters, this always means an inadequate supply of either S or ${\rho }_{{}_{A,B}}$. As a consequence, the width of the L/H regions tends to increase for accumulating the minority species to sustain the loop. This is why the less likely cases for pattern are always accompanied by increased length scales. And once the pattern scale exceeds the domain size, patterns disappear.

At first glance, this mechanism is seemingly different from the Turing mechanism [60], where activator and inhibitor species are well defined and fixed [44]. Interestingly, in our system either the susceptible or the infected plays both roles; for example, in the H regions, the infected are activators to themselves but are inhibitors to S, while in the L regions, S plays the role of activator to its own but of inhibitor to the infected instead. So the activator and inhibitor are not fixed but spatially alternating, region L/H dependent. Even so, we argue that the patterns here still belong to Turing mechanism, because they are consistent with the general criterion “local activation with lateral inhibition” [61,62]. Wherever a dynamical loop emerges, the aggregation process increases the local activator and then is followed by the inhibition by others in its lateral regions. The striking similarity to Turing patterns can be seen in the 2D domain (Fig. 9).

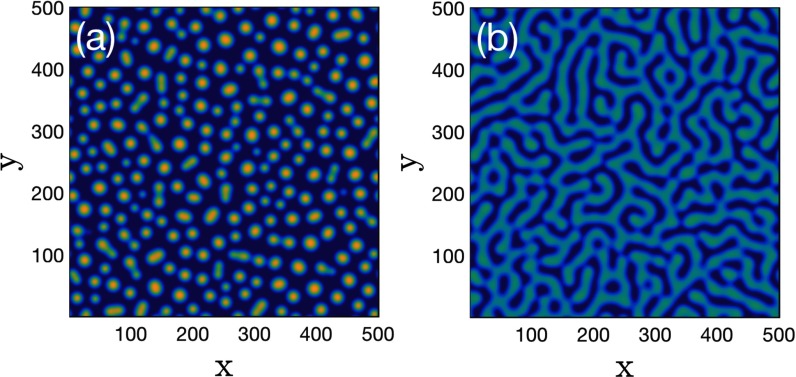
FIG. 9.

Typical patterns in the 2D domain. (a) Spot pattern ($R_0=1.5$) and (b) strip pattern ($R_0=2.2$). Random initial conditions and 500 time units transient are used. Dark blue indicates weakly infected regions. Parameters: $C=1$, $D_S=10$.

VI. DISCUSSION AND CONCLUSION

In the real world, hundreds or even thousands of different infectious strains simultaneously circulate around and they potentially interact with each other. In this study, we investigate the generic contagion scenario of two interacting infections in the spatial context. Compared with the trivial dynamics of single SIS-type infections, the presence of more than one infection reveals new complexities in the form of infection patterns. Their emergence does not require any peculiar infection-infection interaction; instead, the pattern formation favors a mild condition where too-strong cooperation or competition is absent. Dynamical mechanism analysis reveals an aggregation phenomenon along with a dynamical loop. This mechanism is rooted in the intrinsic dynamics when two infections are engaged, and too-strong baseline infection or infection-infection interaction destroys this loop. Among other observations, one finding of particular interest is the pattern hysteresis, i.e., the pattern formation is not only determined by the system parameters but also depends on its evolution history. Since our model is simple enough, only involving two classic SIS infections, we expect some empirical evidence to be found in the future.

The consequence of pattern formation is straightforward whereby the infection is now spatially segregated; some locations are of high prevalence while their neighborhoods could be much less infected or contagion free, even though the whole system is in the outbreak phase. When the patterns emerge, the clustering of the infected individuals leads to persistent survival of the infections in the form of pattern hysteresis. As a consequence, much more effort, if it is not impossible, is required to eradicate infectious diseases compared to the scenario without space (e.g., within a single city) or the single-infection case.

Here we choose infectious diseases as the context, where our findings are bad news for health departments and the public, because minimizing or eradicating infections is the primary task, and this becomes more difficult for interacting contagions. In some other contexts, however, such as social contagions, a higher prevalence is usually desired. For example, companies want to sell more products or technologies to their customers, politicians try to convince more people of their political opinions, and bloggers want to make their messages have a wider readership and more retweets. In those cases, the implications of our study, which supports higher and persistent prevalence, are good news.

Our results together with previous related works [35–40] show that the contagion dynamics of two infections is fundamentally different from the classic scenario based on a single infection. These observations of “more is different” [63] suggest that realistic contagions could be far more complex than the picture captured by most of previous modeling efforts. Besides, our work highlights that the spatial dimension is capable of harboring unexpected amount of complexities in the contagion processes, which has largely been underestimated in past research. In this sense, our work could act as a helpful starting point for a more systematic investigation, while many open questions remain, such as the contagion dynamics of more general cases with arbitrary number of infections and how to relate the plain-spaced pattern dynamics to a networked modern world, where heterogeneous transportation systems are often present [46]. Other important issues include devising effective strategies for containment [64] and maximization strategies in some other contexts.

APPENDIX: LINEARIZATION STABILITY ANALYSIS

To theoretically analyze the pattern emergence of Eq. (2), here we follow the standard procedure of linearization stability analysis [44]. Let there be a steady, spatially homogeneous state ($S^{*},I_A^{*},I_B^{*},I_{AB}^{*}$), which could be an outbreak solution or a contagion-free fixed point of Eq. (1), depending on the parameters. The emergence of patterns can be studied by posing perturbations into the system and monitoring their evolution, i.e., $(\delta S,\delta I_A,\delta I_B,\delta I_{AB})=(S-S^{*},I_A-I_A^{*},I_B-I_B^{*},I_{AB}-I_{AB}^{*})$. The evolution of the linearized system can be formulated by

$$\begin{array}{ccc}\hfill \frac{\partial }{{\partial }_t}\left(\begin{array}{c}\delta S\\ \delta I_A\\ \delta I_B\\ \delta I_{AB}\end{array}\right)& =& \left(\begin{array}{cccc}\frac{\partial f_s}{{\partial }_S}+D_S\frac{{\partial }^2}{{\partial }_{x^2}}& \frac{\partial f_s}{{\partial }_{I_A}}& \frac{\partial f_s}{{\partial }_{I_B}}& \frac{\partial f_s}{{\partial }_{I_{AB}}}\\ \frac{\partial f_A}{{\partial }_S}& \frac{\partial f_A}{{\partial }_{I_A}}+D_I\frac{{\partial }^2}{{\partial }_{x^2}}& \frac{\partial f_A}{{\partial }_{I_B}}& \frac{\partial f_A}{{\partial }_{I_{AB}}}\\ \frac{\partial f_B}{{\partial }_S}& \frac{\partial f_B}{{\partial }_{I_A}}& \frac{\partial f_B}{{\partial }_{I_B}}+D_I\frac{{\partial }^2}{{\partial }_{x^2}}& \frac{\partial f_B}{{\partial }_{I_{AB}}}\\ \frac{\partial f_{AB}}{{\partial }_S}& \frac{\partial f_{AB}}{{\partial }_{I_A}}& \frac{\partial f_{AB}}{{\partial }_{I_B}}& \frac{\partial f_{AB}}{{\partial }_{I_{AB}}}+D_I\frac{{\partial }^2}{{\partial }_{x^2}}\end{array}\right)\left(\begin{array}{c}\delta S\\ \delta I_A\\ \delta I_B\\ \delta I_{AB}\end{array}\right).\hfill \end{array}$$ (A1)

Next, we make Fourier transformation,

$$\begin{array}{ccc}\hfill \delta S^k& =& \int \delta S(x,t)e^{-i\mathbf{k}·\mathbf{x}}dx,\hfill \end{array}$$ (A2)

$$\begin{array}{ccc}\hfill \delta I_A^k& =& \int \delta I_A(x,t)e^{-i\mathbf{k}·\mathbf{x}}dx,\hfill \end{array}$$ (A3)

$$\begin{array}{ccc}\hfill \delta I_B^k& =& \int \delta I_B(x,t)e^{-i\mathbf{k}·\mathbf{x}}dx,\hfill \end{array}$$ (A4)

$$\begin{array}{ccc}\hfill \delta I_{AB}^k& =& \int \delta I_{AB}(x,t)e^{-i\mathbf{k}·\mathbf{x}}dx,\hfill \end{array}$$ (A5)

where $\mathbf{k}$ is the wave vector. With this operation we reduce the PDEs into ODEs. Inserting the above forms into Eq. (A1), for a given Fourier mode $k=\left|\mathbf{k}\right|$, we then have

$$\begin{array}{ccc}\hfill \frac{d}{dt}\left(\begin{array}{c}\delta S^k\\ \delta I_A^k\\ \delta I_B^k\\ \delta I_{AB}^k\end{array}\right)& =& \left(\begin{array}{cccc}\frac{\partial f_s}{{\partial }_S}-k^2{D}_S& \frac{\partial f_s}{{\partial }_{I_A}}& \frac{\partial f_s}{{\partial }_{I_B}}& \frac{\partial f_s}{{\partial }_{I_{AB}}}\\ \frac{\partial f_A}{{\partial }_S}& \frac{\partial f_A}{{\partial }_{I_A}}-k^2{D}_I& \frac{\partial f_A}{{\partial }_{I_B}}& \frac{\partial f_A}{{\partial }_{I_{AB}}}\\ \frac{\partial f_B}{{\partial }_S}& \frac{\partial f_B}{{\partial }_{I_A}}& \frac{\partial f_B}{{\partial }_{I_B}}-k^2{D}_I& \frac{\partial f_B}{{\partial }_{I_{AB}}}\\ \frac{\partial f_{AB}}{{\partial }_S}& \frac{\partial f_{AB}}{{\partial }_{I_A}}& \frac{\partial f_{AB}}{{\partial }_{I_B}}& \frac{\partial f_{AB}}{{\partial }_{I_{AB}}}-k^2{D}_I\end{array}\right)\left(\begin{array}{c}\delta S^k\\ \delta I_A^k\\ \delta I_B^k\\ \delta I_{AB}^k\end{array}\right).\hfill \end{array}$$ (A6)

The instability of small perturbations in wave-vector mode $\mathbf{k}$ is then determined by the maximal value of the resulting eigenvalues ${\lambda }_{1,2,3,4}^k$. A nontrivial pattern appears if any mode of the perturbations is linearly unstable, i.e., ${\lambda }_{\max }={max}_k\left({\lambda }_{\max }^k\right)=max\left({\lambda }_{1,2,3,4}^k\right)>0$. The above analysis can be conveniently extended into a higher spatial dimension without changing the statement at all.

When we want to study the impact of any parameter on the pattern dynamics, we compute the ${\lambda }_{\max }$ as a function of those parameters which are supposed to be already incorporated in (A6). Figure 3(f) shows such an example to examine the role of contagion interaction $C$ in pattern formation. Similar computations are conducted for Figs. 4(a) and 4(b). A bit more complicated case is Fig. 5(a), where the eigenvalue ${\lambda }_{\max }$ is now a function of both $C$ and $D_S$, and the value of ${\lambda }_{\max }$ is color coded. Since the system is conserved when the mode $k\to 0$ as described by Eq. (1), we can easily prove that ${\lambda }_{\max }=0$ rather than negative values for those cases without pattern. To divide the region in Fig. 5(a), it is therefore proper to set a threshold with a small value, say, ${10}^{-5}$, to separate the pattern formation region (${\lambda }_{\max }>{10}^{-5}$) from the region without pattern (${\lambda }_{\max }<{10}^{-5}$). The location of the boundary could shift slightly when using a different threshold, and this shift is undetectable as long as the threshold value is small enough. In Fig. 5(b), we only plot the boundary lines for different mobilities of infected $D_I$, and with these curves, we can study the impact of $D_I$ on the region available for pattern. Figure 4(c) is obtained in a similar way as in Fig. 5(b): by plotting the boundaries in the $R_0\text{-}C$ parameter space for a couple of $D_S$.