Abstract
There continues to be a critical need for developing data-informed computational modeling techniques that enable systematic evaluations of mitral valve (MV) function. This is important for a better understanding of MV organ-level biomechanical performance, in vivo functional tissue stresses, and the biosynthetic responses of MV interstitial cells (MVICs) in the normal, pathophysiological, and surgically repaired states. In the present study, we utilized extant ovine MV population-averaged 3D fiducial marker data to quantify the MV anterior leaflet (MVAL) deformations in various kinematic states. This approach allowed us to make the critical connection between the in vivo functional and the in vitro experimental configurations. Moreover, we incorporated the in vivo MVAL deformations and pre-strains into an enhanced inverse finite element modeling framework (Path 1) to estimate the resulting in vivo tissue pre-stresses (σCC≅σRR≅ 30kPa) and the in vivo peak functional tissue stresses (σCC≅510 kPa, σRR≅740 kPa). These in vivo stress estimates were then cross-verified with the results obtained from an alternative forward modeling method (Path 2), by taking account of the changes in the in vitro and in vivo reference configurations. Moreover, by integrating the tissue-level kinematic results into a downscale MVIC microenvironment FE model, we were able to estimate, for the first time, the in vivo layer-specific MVIC deformations and deformation rates of the normal and surgically repaired MVALs. From these simulations, we determined that the placement of annuloplasty ring greatly reduces the peak MVIC deformation levels in a layer-specific manner. This suggests that the associated reductions in MVIC deformation may down-regulate MV extracellular matrix maintenance, ultimately leading to reduction in tissue mechanical integrity. These simulations provide valuable insight into MV cellular mechanobiology in response to organ- and tissue-level alternations induced by MV disease or surgical repair. They will also assist in the future development of computer simulation tools for guiding MV surgery procedure with enhanced durability and improved long-term surgical outcomes.
Keywords: finite element (FE) inverse modeling, structural constitutive models, collagen fiber recruitment, mitral valve surgical repair, cell mechanotransduction
1. Introduction
The mitral valve (MV) is one of the four heart valves, which lies in between the left atrium and the left ventricle. Its major components include the anterior and posterior leaflets, annulus (forming a junction between the left ventricle and atrium), chordae tendineae, and papillary muscles, which form a connection to the left ventricle. The closure of the MV is maintained by the coaptation and contact of the two leaflets as supported by the chordae tendineae, and their delicate dynamic interactions with the left atrium and the left ventricle in turn regulate the overall function and the unidirectional blood flow through the heart.
Interests in an improved understanding of MV function have rapidly grown in the past two decades, associated with extensive developments of both experimental and computational modeling methodologies. Recent advances in the field include investigations of the mechanical properties of MV leaflets through material characterization and modeling (Grashow et al. 2006a; Grashow et al. 2006b; May-Newman et al. 1995; Zhang et al. 2016), quantification of in vivo dynamic kinematics (Eckert et al. 2009; Rausch et al. 2011; Sacks et al. 2006; Sacks et al. 2002), image-based finite element (FE) biomechanical modeling of the MVs (Kunzelman et al. 1993; Lee et al. 2015a; Prot et al. 2007; Votta et al. 2008; Wang et al. 2013), among others.
Several studies (Braunberger et al. 2001; Flameng et al. 2003; Flameng et al. 2008; Gillinov et al. 2008) have shown that excessive tissue stress and the resulting strain-induced tissue remodeling and damage may be primary etiological factors for the significant number of MV repair failures. Moreover, these undesirable stress-induced changes in the mitral valve interstitial cell (MVIC) metabolism and the consequent collagen biosynthesis are likely associated with the limited durability of MV repair. Thus, there is a critical need for developing reliable and predictive computer simulation tools, which allow for systematic evaluations of MV function at the normal, pathophysiological, and surgically repaired states. Such development requires the essential connection of the MV organ-level biomechanical performance to in vivo tissue stresses and the phenotypic and biosynthetic responses of the MVICs. The development of these advanced modeling tools will be beneficial to better clinical management of mitral valve disease with improved long-term surgical outcomes.
Yet, despite the promise of computational approaches for simulating MV function, a fundamental question still remains: what is the proper choice and what are the effects of the reference configuration? This question is also associated with the determination of the residual and pre-stresses, as well as the zero-stress state (Chuong et al. 1986a; Fung 1991). Such an important piece of information is closely related to the determination of tissue homeostasis for the normal MV function. Moreover, the underlying cellular biosynthetic function of the MVICs has been found to be closely linked to the MVIC deformation (Lee et al. 2015b). Yet, while most of the detailed knowledge of MV comes from in-vitro experimental studies, there are no methods developed to translate these findings to in-vivo function. Without such approaches, we cannot correctly simulate in vivo MV function, nor make the connection of cell and tissue behaviors to the tissue-level remodeling.
Thus, the overall objective of this study was to make the important quantitative connection between the MV in vivo functional state and in vitro experimental configuration (as first reported by Amini et al. (Amini et al. 2012)) at both the tissue and cellular levels. This was accomplished by estimating the in vivo MV tissue mechanical behaviors using an inverse FE modeling technique extended from (Lee et al. 2015b). Further, we utilized these results to, for the first time, simulate the in vivo layer-specific MVIC deformations and deformation rates using a downscale FE simulation framework (Lee et al. 2015b), and how they change with surgical repair
2. Methods
2.1. Overview of the study.
For the analysis of MV deformations, we defined the following kinematic states (Fig. 1a):
β0 – the in vitro reference configuration wherein tissue mechanical properties and in vitro MVIC deformations were acquired.
β1 – the excised, unloaded state where the MV was removed from the heart and placed in the phosphate buffered saline solution.
β2 – the in vivo reference configuration, defined as the time point associated with the onset of ventricular contraction (OVC, Fig. 2b), where the MV leaflets were just coapted.
βt – the in vivo loaded state at time t, with the MV under transvalvular pressure (Fig. 2b).
Figure 1 –
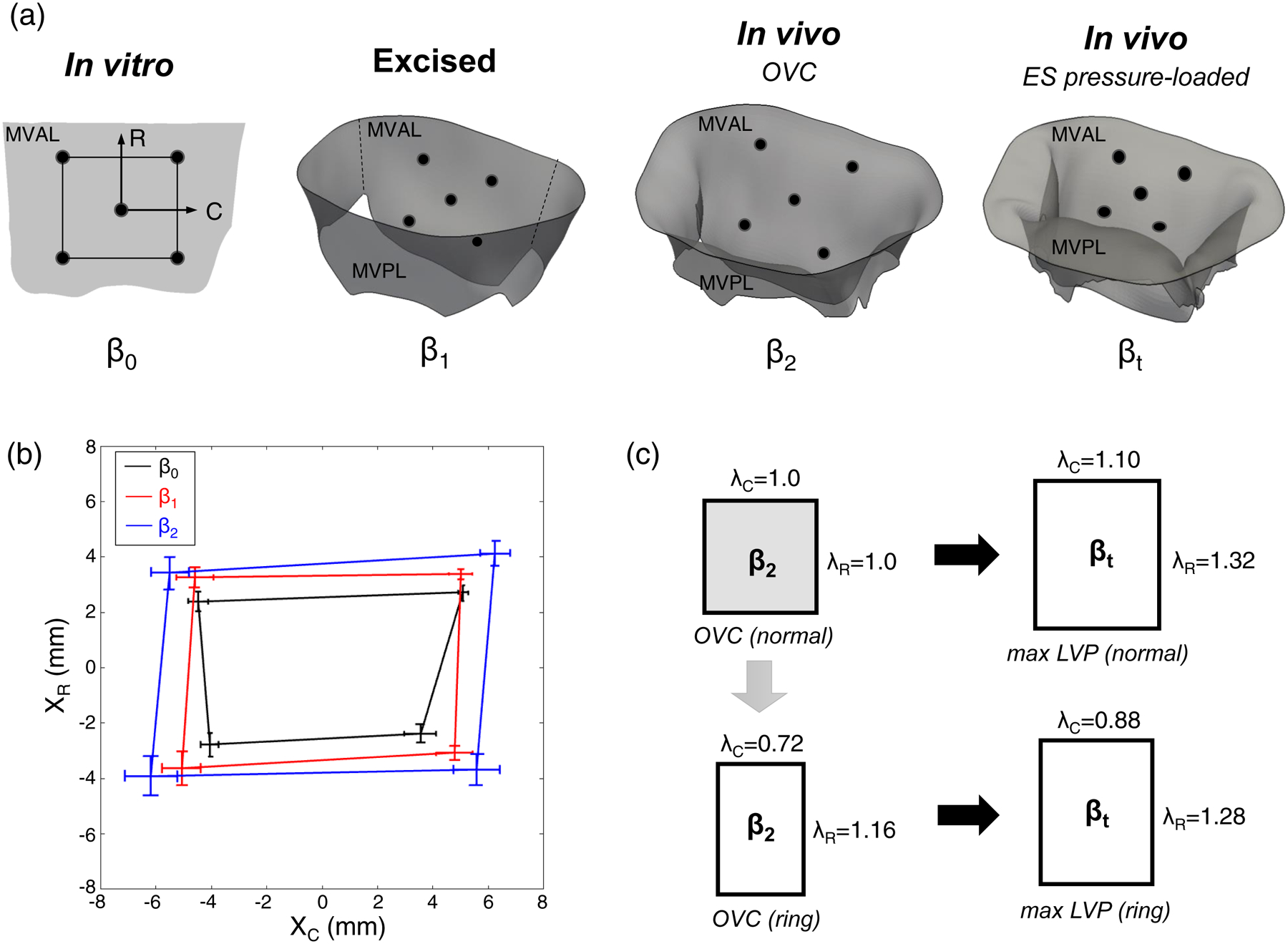
(a) Schematic diagram of the key kinematic states used in the present study (ES: end-systolic), (b) Results of population-averaged fiducial marker positions (mean ± SEM, n=6) as shown on the projected 2D plane at key kinematic states. Note that XC and XR denote marker coordinates on the projected plane along the circumferential and radial directions, respectively, and (c) illustration of the surgical repair effect on the functional strains in the central region of the MVAL previously quantified in (Amini et al. 2012), as utilized in the MVIC simulations for both normal and surgically repaired MVs.
Figure 2 –
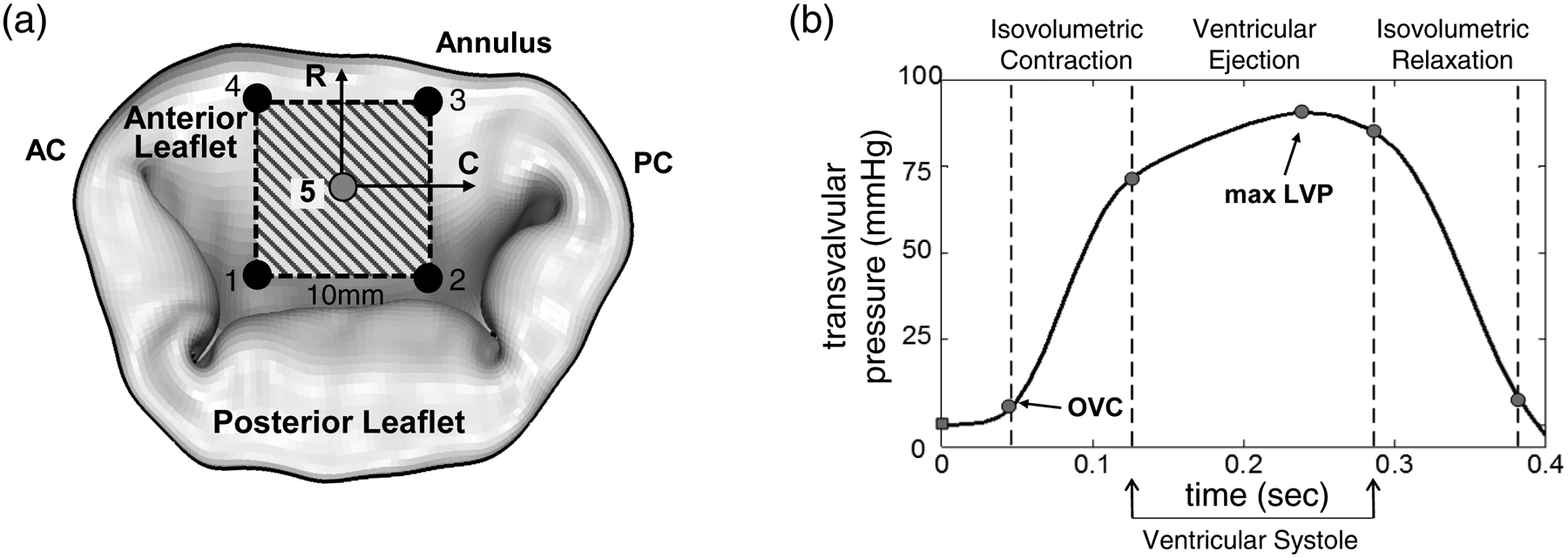
(a) Schematic of mitral valve leaflets and the arrangement of 5 sonocrystal transducers on the central region of the MVAL, (b) an illustration of the measured transvalvular pressure over one representative cardiac cycle, which was applied as pressure loading conditions for the FE simulations of the MVAL. The corresponding time points for in vivo reference configuration β2 and maximum pressure-loaded state βt,maxLVP were marked on the pressure-time curve. (LVP: left ventricular pressure).
For each of the above configurations, the coordinates of the 5 fiducial (sonocrystal) markers (Fig. 2a) were determined either by sonomicrometry array localization (SAL) (for β2, and βt, see Section 2.2) under in vivo settings or using direct 2D measurements for β0 and β1 with a low magnification, wide field microscope in in vitro experiments. Next, we determined specimen-averaged fiducial marker positions, which is one of the novelties of this work, so that representative kinematics could be utilized (Section 2.3). We then employed two computational/modeling approaches to estimate the in vivo stresses of the MV tissues (Section 2.4). The first approach (Path 1) was based on an enhanced inverse FE modeling framework, which adopted a simplified constitutive model (to reduce the computational demands of the intensive FE calculations for the parameter estimation) to characterize the in vivo MV tissue mechanical properties, and to calculate the in vivo tissue stresses with and without considerations of the quantified pre-strains (Section 2.4.2). In the second approach (Path 2), the deformation gradient tensors with respect to both the in vitro experimental configuration and the in vivo reference state were directly applied to a full structural constitutive model to calculate the corresponding tissue stresses (Section 2.4.3). In Path 2, we took into explicit account of the effects of changes in the reference configurations on collagen fiber orientation and recruitment in the fitting to the tissue’s respective biaxial mechanical testing data.
The purpose of introducing this additional forwarding modeling approach (Path 2) was threefold: (i) to cross-verify the in vivo MV tissue-level stress estimations obtained by the inverse modeling approach (Path 1), (ii) to provide richer information about alterations in collagen fiber architecture and recruitment mechanisms due to the change in the reference configurations, and (iii) most importantly, to make the connection between the in vitro measured tissue mechanical properties to those derived in vivo. Finally, to investigate the relations between MVIC and tissue-level mechanical stimuli in the normal and surgically altered MVs, we adopted previously developed MVIC model along with the quantified MV leaflet deformations to simulate the in vivo MVIC deformations and deformation rates of the four histologically distinct MV leaflet layers (Section 2.5). These novel findings shed light on the adaptions of local cellular biomechanical behaviors in response to surgery-induced changes in the organ- and tissue-level mechanical and geometrical environment.
2.2. In vivo sonocrystal data collection.
In vivo sonocrystal data acquired from the previous study (Amini et al. 2012) were utilized for analyses of MVAL deformation and for the subsequent in vivo MVAL tissue stress estimations. Briefly, 9 male Dorsett sheep (35–45 kg) were used in compliance with guidelines for the care and use of laboratory animals (NIH Publication No. 85–23, revised 1985). With a sterile left lateral thoracotomy, 2-mm hemispherical piezoelectric transducers were sutured with 6–0 polypropylene sutures to the central region of the MV anterior leaflet in a 10-mm square array (Fig. 2a), and the 3D coordinate of each transducer was determined at an interval of 5 ms (Gorman et al. 1996) with transvalvular pressure continuously monitored during cardiac cycles (Fig. 2b). In this study, 3D positional data of the first group (n=6) with 4 corner sonocrystal (fiducial) markers were used for deformation analysis as presented in Section 2.3. The data of the second group (n=3) with 5 fiducial markers were employed in the in vivo tissue stress estimation in Section 2.4.
2.3. In vivo MVAL deformation analysis.
To obtain better representative kinematic information from each of the kinematic states (Fig. 1a), the extant sonocrystal data were assigned a numeric value based on the surgical placement on the anterior leaflet (Fig. 2a). The corner sonocrystals (#1~#4) formed a quadrilateral unit, with midpoints on opposing sides of the quadrilateral unit connected to form bisecting vectors. These bisecting vectors formed the plane upon which transformed coordinates were projected, and the formed vectors were rotated to optimize orthogonality by minimizing the angle between the vectors and the X- and Y- axes (which became the radial and circumferential axes for a transformed coordinate system). Next, all coordinates were transformed into a new coordinate system, and projected onto a two-dimensional plane. A single cardiac cycle was selected (Fig. 2b), starting with the OVC time point (β2). Each time point during the cardiac cycle was normalized, interpolating as necessary, so that each cycle could be easily compared and averaged between different data sets. For all sets of data, the transformed coordinates were averaged at each time point over the normalized cardiac cycle to form the representative cardiac responses. In order to further calculate the in-surface deformations and strains of the MVAL tissue, a 4-node bilinear finite element was used based on the average sonocrystal marker positions, following previously developed approaches (Sacks et al. 2006).
2.4. Estimations of in vivo MVAL tissue stresses.
In order to estimate the in vivo stresses of the MV tissue, we adopted two computational/analytical modeling approaches. The first approach (Path 1) utilized an enhanced inverse FE modeling framework with a simplified structural model. The second approach (Path 2) used analytical modeling with direct applications of the deformation gradient tensors to a full structural constitutive model considering the changes in the reference configurations. In the subsequent sections, we first introduce the constitutive relations for a full structural model (FSM), which was used in the forward modeling approach (Path 2), and for its simplified form that was adopted in the inverse modeling-based stress estimation approach (Path 1). Then, the results of the two approaches for the estimated in vivo MVAL tissue stress are presented.
2.4.1. Structural constitutive models for the MVAL tissue.
Previously developed constitutive models, that represented the underlying microstructural micromechanics, were adopted (Fan et al. 2014; Sacks et al. 2016; Zhang et al. 2016). In brief, MVAL tissue is idealized as a fiber-reinforced composite material with contributions of the mechanical responses from distinct collagen and elastin fiber networks and the non-fibrous ground matrix. Within the representative volume element (RVE), the strain energy function Ψ of an incompressible, full structural model (FSM) was defined as the sum of each constituent’s contribution, and the corresponding 2nd Piola-Kirchhoff stress tensor SFSM is computed based on a pseudo-hyperelasticity incompressible formulation (Fung 1993) by
| (1), |
where the notations and definitions of the model parameters are provided in Nomenclature. Moreover, is the consequence of the incompressibility condition, and the penalty parameter ρ = −μmC33 is derived from the plane-stress condition (S33 = 0). Note that when Γ is symmetric about a local direction, Eqn. 1 will have an axis of material symmetry in that direction.
Although the above constitutive model has richer information about the underlying collagen fiber architecture and recruitment, estimating 12 parameters using a genetic algorithm-based global optimization procedure, which requires intensive calculations, is computationally intractable. Thus, we utilized the simplified model to reduce computational demands with no loss of model fidelity for in vivo stress estimation in Path 1. This simplified structural model (SSM) has an exponential ensemble fiber stress-strain relation for the collagen fibers and assumes that elastin fiber’s contribution could be idealized by the neo-Hookean matrix component (Fan and Sacks 2014; Lee et al. 2015c). The corresponding 2nd-PK stress tensor SSSM has the form:
| (2), |
where c0, c1 and μm are the three material parameters to be characterized for the MVAL tissue, and Ecutoff is the cutoff ensemble fiber strain beyond which the ensemble fiber stress-strain relationship becomes linear to avoid unlimited exponential growth of the stress (Lee et al. 2015c). Here, Ecutoff was set to a level where the ensemble fiber stress is about 1.5 MPa (Zhang et al. 2016). Based on our numerical studies, both simplified and full structural models produce equivalent responses at the fiber ensemble and tissue levels (c.f. Section 3.2 and Fig. 8).
Figure 8 –
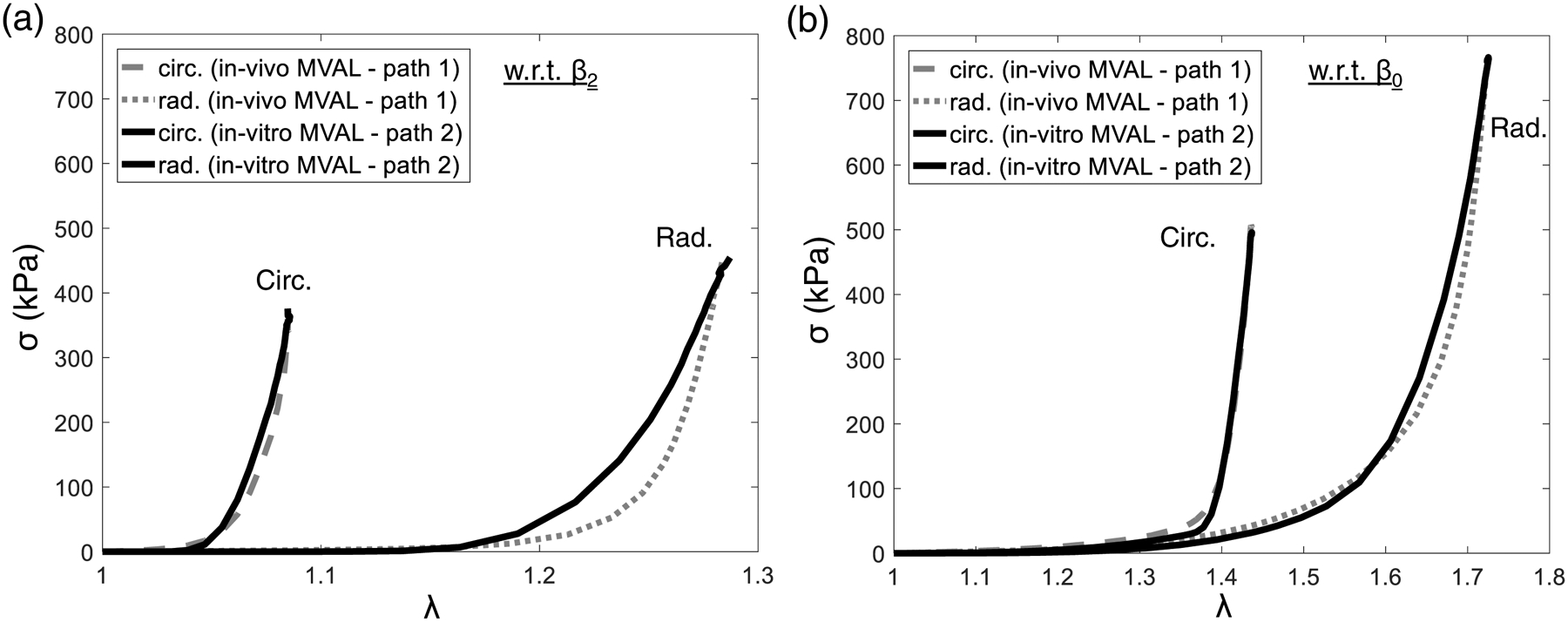
Comparisons of the predicted stresses between inverse modeling algorithms (using representative in vivo ovine MV specimen data for Path 1, dashed and dotted lines) and forward modeling approaches (representative in vitro ovine MV specimen data for Path 2, solid lines), with respect to: (a) in vivo reference configuration (state β2), and (b) in vitro reference configuration (state β0).
2.4.2. In vivo stress estimation — Path 1: an inverse FE modeling approach.
In this in vivo stress estimation approach we employed an inverse FE modeling framework (Fig. 3), extended from the previous version for estimations of the in vivo functional properties of the MVAL tissue between the β2 and βt states (Lee et al. 2014). In brief, the MVAL surface was obtained based on a single 5-node element along with the 3D positional data at state β2. The reconstructed MVAL surface was then discretized into 40×40=1,600 shell (S4) elements. Employing affine collagen fiber kinematics (Gilbert et al. 2006; Lee et al. 2015d), element-by-element local material axis μC and collagen fiber dispersion σC (inset in Fig. 3) were then determined by mapping the collagen fiber architecture as measured by the small angle light scattering (SALS) technique (Sacks et al. 1997). Moreover, to simulate the MVAL tissue’s mechanical behavior over the cardiac cycle, the simplified structural model (Eq. (2)) was implemented in the user material subroutine UMAT for implicit dynamics (quasi-static application with an initial time step size of 10−6 and automatic time step size adjustment) in ABAQUS 6.14 (Simulia, Dassault Systèmes). Displacement boundary conditions, as interpolated from the 5 fiducial markers’ 3D positional data, were applied on the nodes along the four edges of the MVAL surface. To mimic the MV leaflet closing behavior, transvalvular pressure p(t) (Fig. 2b) was prescribed across the transmural section of the MVAL surface. A global optimization procedure, based on the genetic algorithm (GA), was performed to determine the optimal parameter set xopt by minimizing the errors between the FE predicted deformed surfaces and the time-varying MVAL surfaces reconstructed from the in vivo sonocrystal data
| (3), |
where x = {μm, c0, c1}T is a vector of the three estimated parameters, f(x) is the objective function to be minimized in the GA-based global optimization, ndata=40 is the number of time points over the cardiac cycle, ui is a 5,043×1 vector collecting all the nodal displacements of the MVAL surface nodes at time i, whereas its subscript denotes the in vivo reconstructed surface or the FE predicted surface, and ||·|| stands for the Euclidean norm.
Figure 3 –
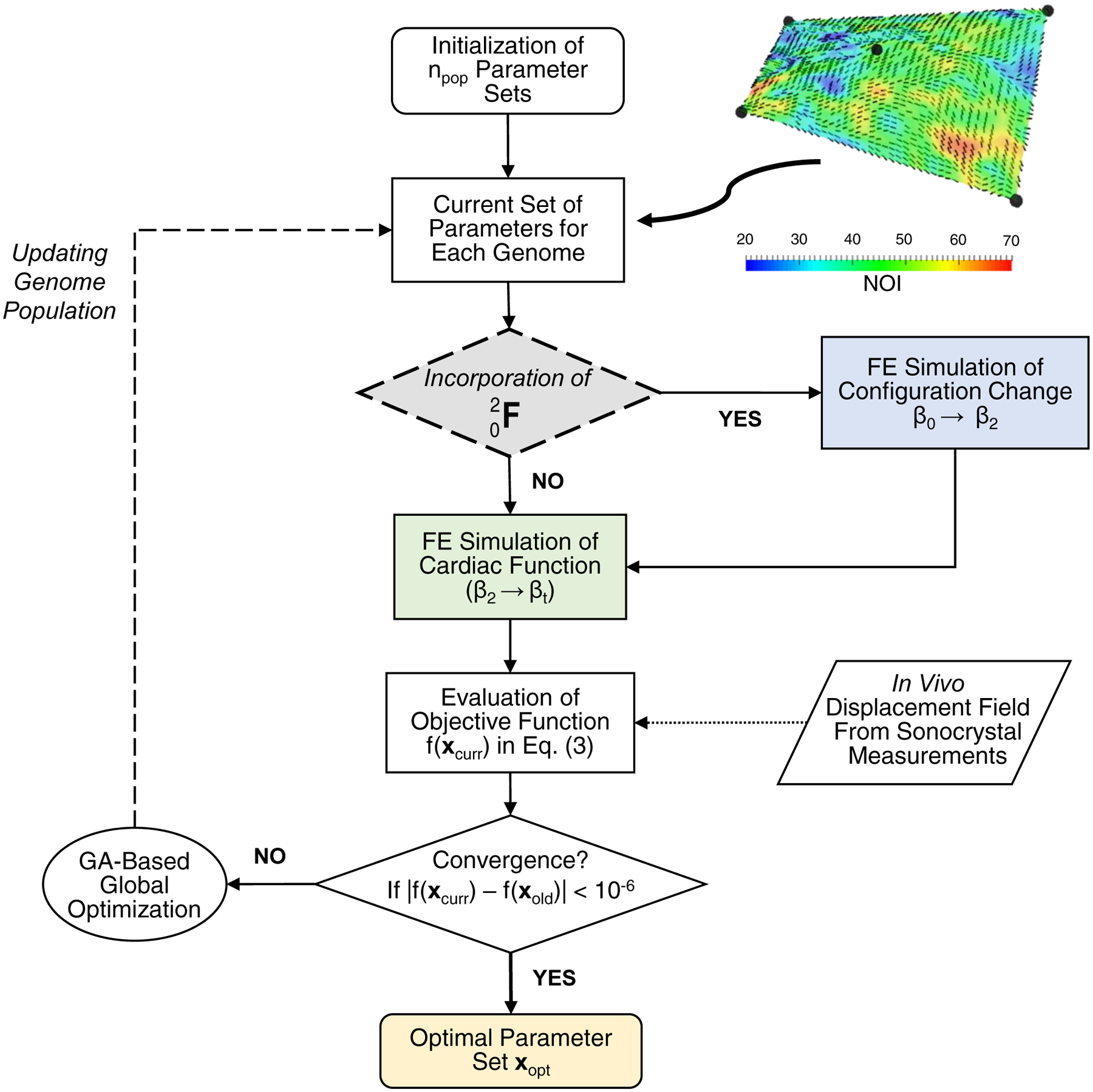
Flowchart diagram of the inverse modeling approach (Path 1) for estimating in vivo functional mechanical properties of the MVAL tissue using genetic algorithm-based global optimization with and without incorporation of the pre-strains due to the change between the in vitro and in vivo reference configurations (from state β0 to state β2). The inset demonstrates the corresponding FE model of the MVAL surface with 40×40 thin-shell elements combined with the mapped collagen fiber architecture. Note that NOI = (90 – OI) / 90 * 100% and OI=orientation index represents the degree of collagen fiber alignment derived from the measured data (Lee et al. 2014; Sacks et al. 1997).
In order to further account for the effects of pre-strains on the characterization of the MVAL mechanical properties with respect to state β0, we enhanced this Path 1 inverse FE modeling pipeline by implementing the following two-step simulations (Figure 4):
Step-1: A simulation that incorporated the dimensional changes from the in vivo state (β2) to the in vitro configuration (β0) was carried out by prescribing the inverse of the quantified to obtain the stress-free configuration of the MVAL FE model at the in vitro reference configuration (Fig. 4a) and nodal displacement field.
Step-2: A two-stage simulation was performed to incorporate the pre-strain effects (Fig. 4b). The recorded displacement field from Step-1 was reversed in time sequence and gradually applied on all the nodes to recover the geometry at state β2. Hence, the quantified pre-strains could be intrinsically embedded in the MVAL FE model. At the second simulation state, the previous inverse modeling procedure was conducted to estimate the model parameters with respect to state β0 (in vivo reference configuration).
Finally, the in vivo MVAL tissue stresses were obtained by simulating one cardiac cycle by using the optimal parameter set, and then compared with those obtained by using the forward modeling approach in Path 2 (Section 2.4.3). Note that the following assumptions were made in the inverse modeling-based FE simulations:
The region of interest (ROI) was considered as the central region (~10mm × ~10 mm) of the MVAL as delimited by the sonocrystal marker array (Fig. 2a).
Only the functional, quasi-static behaviors of the MVAL tissue were considered (Grashow et al. 2006a; Grashow et al. 2006b), with any viscous or time-dependent effects ignored.
The mean MVAL regional tissue stresses were obtained by averaging the predicted stress field over all the 1600 elements in the ROI of the MVAL (Lee et al. 2014).
Figure 4 –
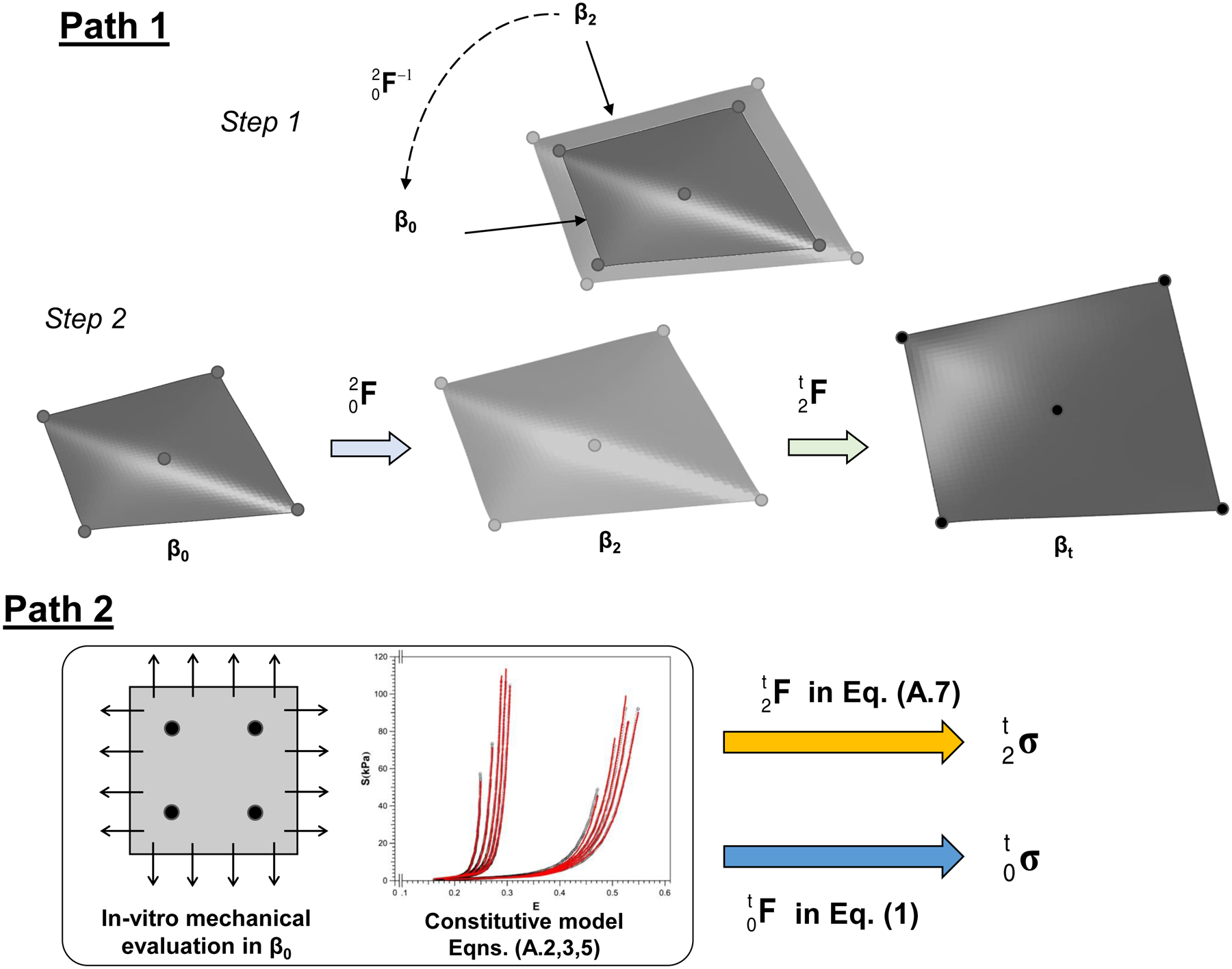
(Top) Illustrative diagrams of the two-step simulation procedure for the enhanced inverse FE modeling framework in Path 1: a simulation of the dimensional changes from β2 to β0, and a two-stage simulation for incorporating the quantified pre-strains with the inverse modeling framework from β0 to β2, and then to βt. Stresses were determined by averaging over 1,600 MVAL surface elements of the region of interest delimited by the ROI based on the FE simulation results. (Bottom) Schematic diagram of the forward (analytical) modeling approach in Path 2 and the corresponding equations used for the fitting of ovine biaxial testing data and for estimations of in vivo tissue stresses. Stresses were calculated at the center of the sonocrystal marker array.
2.4.3. In vivo stress estimation — Path 2: a forward (analytical) modeling approach.
In the previous section, a simplified version of the structural constitutive model was adopted in the inverse FE modeling framework for computational feasibility. In order to gain better insight into the roles of the underlying collagen fiber architecture in the MV function, we used the full structural model in the forward (analytical) modeling approach (Path 2, Figure 4) for estimating the ovine MVAL tissue stresses, which were then compared with those obtained by the inverse modeling approach for verification purpose.
We first employed an in-house program in Mathematica (Wolfram Research Corp.), developed in our group (Sacks et al. 2016) based on the differential evolution algorithm for estimating the FSM parameters (Eq. (1)) by fitting the stress-strain relations to the in vitro measured biaxial mechanical data. In brief, the initial parameters were taken from the best fit of previous studies (Lee et al. 2015c). The seeds for the genetic algorithm were uniform distributed in an 11-orthotope centered at the initial guess. The range of seeds, referred to the length of the orthotope, was taken to be ±3 standard deviations of the previous best-fit parameters. In performing parameter estimation, we first examined the equi-biaxial loading protocol (P11:P22 = 1:1), which approximates the physiological loading conditions, and fit only the matrix and the elastin components to the low stress region (<7 kPa), which occur before the recruitment of collagen fibers. Here, Pij refers to the i,jth component of the 1st Piola-Kirchhoff stress tensor. Next, the collagen fiber component was fit to the full equi-biaxial tension loading protocol keeping the elastin parameters unchanged. This reduced the number of parameters to seven (ηc, μC, σC, μD, σD, Elb, Eub) and five (μm, , , a, b) for these two fitting steps, respectively. Once a reliable estimate of the parameters was obtained, the ranges of parameter seeds were reduced to be within ±1 standard deviations, and the inner 3 protocols (P11:P22 = 3:4, 1:1, 4:3) were fit, followed by all the testing protocols (P11:P22 = 1:2, 3:4, 1:1, 4:3, 2:1) to obtain the final estimated parameter set for all the ovine MVAL specimens.
After the model parameters were obtained, the Cauchy stress tensor of the MVAL tissue over one cardiac cycle with respect to the in vivo (β2) reference configuration was analytically calculated (Eq. (A.7)) using the in vivo MVAL deformation gradient tensor , followed by the push-forward operation , where . Similarly, tissue stresses with respect to the in vitro (β0) reference configuration were obtained by using the deformation gradient tensor , where . The stress-strain relationships over one cardiac cycle obtained in Path 2 for representative in vitro ovine MV specimen were compared with those as estimated in Path 1 for representative in vivo ovine MV specimen (Fig. 8a–b).
2.5. Downscale linking to MVIC deformation.
To connect the underlying MVIC responses to tissue-level mechanical stimuli, we utilized the downscale FE simulation framework for the MVIC microenvironment developed previously (Lee et al. 2015b). Briefly, one RVE model (100μm × 100μm, Fig. 6a) was constructed for each of the four MVAL tissue layers, namely atrialis (A), spongiosa (S), fibrosa (F) and ventricularis (V). MVICs were considered as uniformly distributed ellipsoidal inclusions (Fig. 6b), with cell dimensions, cell density and cell orientations in accordance with multi-photon microscopy (MPM) imaging data (Carruthers et al. 2012a; Lee et al. 2015b). For modeling the mechanical behavior of the RVE, the simplified structural constitutive model (Eq.(2)) was employed for the extracellular matrix (ECM), which accounts for layer-specific volume fractions (from histology results) and layer-specific collagen microstructural architecture (from MPM data). For the MVIC regions, the Saint-Venant Kirchhoff material model was used with previously characterized MVIC stiffness (Lee et al. 2015b). FE simulations were performed by prescribing the tissue-level deformations as equivalent displacement boundary conditions on all the edge nodes of the RVE model. Predictions of the deformation field were then analyzed to evaluate the overall in vivo layer-specific MVIC deformations, denoted by the nuclear aspect ratio (NAR) and the time derivative d(NAR) / dt. Such a dimensionless indicator is defined as the ratio of the MVIC circumferential dimension LC to its transmural dimension LT (Fig. 6b),
Figure 6 –
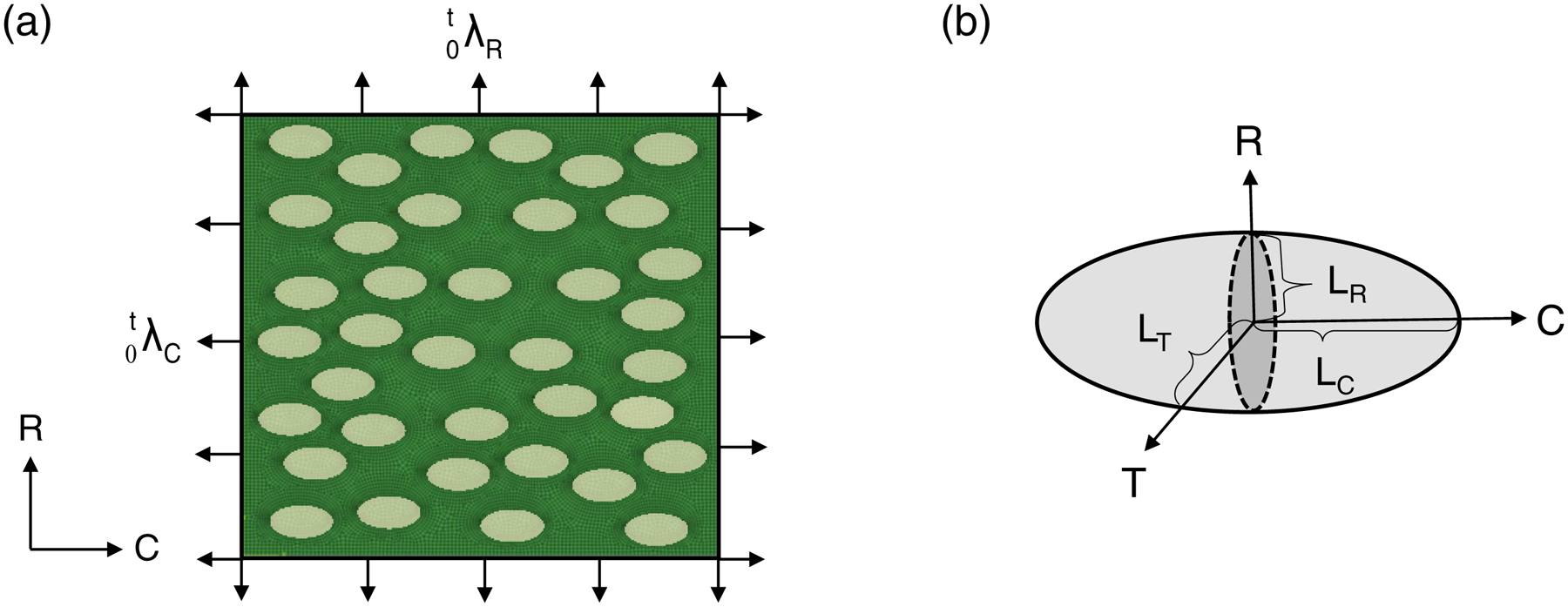
(a) Schematic of the MVIC microenvironment model (Lee et al. 2015b) on the circumferential-radial plane with applied tissue-level deformations as displacement boundary conditions, and (b) an ellipsoidal geometry for describing MVIC deformations with the dimensions of three major/minor axes as LC, LR, and LT along circumferential, radial, and transmural directions, respectively.
As a main part of the surgical repair technique for treating patients with mitral regurgitation (MR), ring annuloplasty attempts to restore the MV apparatus to its normal annular size and shape, and to facilitate more natural leaflet coaptation (Carpentier 1983). Although surgical repair has been more commonly adopted in the past two decades for treating MV disease compared to traditional valve replacement, unsatisfyingly frequent failures of surgical repair still remain a clinical issue. Such surgical repair failures have been shown to be closely related to excessive tissue stresses and the resulting tissue damage and remodeling (Braunberger et al. 2001; Eckert et al. 2009; Flameng et al. 2008; Gillinov et al. 2008). Therefore, to further investigate the surgical repair effect associated with the annuloplasty ring, we employed MVAL kinematic deformations, as quantified from the sonocrystal data with an implanted flat ring from our previous study (Amini et al. 2012), in the MVIC microenvironment simulations. The tissue-level principal stretches of the ring-repaired MVALs were obtained by adjusting those stretches of the normal MVALs to reflect the functional deformations of the repaired MVALs (Fig. 1c):
| (4), |
where the subscript J=C,R stands for the principal stretch in the circumferential or radial direction, respectively. Then, the modified tissue-level stretches were used as the prescribed displacement boundary conditions for the MVIC microenvironment FE model to simulate the layer-specific deformations and deformation rates similar to the procedure as described for the normal MVALs.
3. Results
3.1. Average sonocrystal marker positions and MVAL deformations.
Average 3D positions of the corner fiducial markers at states β0, β1, and β2 were obtained using the proposed analysis technique (Fig. 1b, Table 1). The resulting average in-surface deformation gradient tensors of the MVAL between each pair of these kinematic states were:
| (5). |
Note that changes in the reference configurations result primarily in circumferential and radial directions stretches with relatively small amount of shear deformations. Specifically, we found a ~12% circumferential stretch and a ~23% radial stretch from the excised state (β1) to the in vitro reference configuration (β0), whereas ~18% circumferential and ~10% radial stretches were observed between the in vivo reference configuration (β2) to the excised state (β1). Combining these results, relatively isotropic pre-strains for the MVAL were quantitatively determined to be ~32% and ~35% pre-stretches along the circumferential and radial directions, respectively. There results are in good agreement with the novel findings in our previous study (Amini et al. 2012) which used a single sonocrystal dataset and chose the minimum left ventricular pressure as the in vivo reference configuration; in this study, choosing the onset ventricular contraction as the in vivo reference configuration and using population-averaged sonocrystal 3D positions allow for more systematic investigations of the MVAL function in vivo.
Table 1 –
Average 3D positions (mean ± SEM, n=6) of the four corner fiducial markers at three kinematic states (C: circumferential, R: radial, and T: transmural)
| Marker Position | State β0 | State β1 | State β2 | |
|---|---|---|---|---|
| Fiducial Marker 1 | XC | 5.06±0.17 mm | 4.97±0.43 mm | 6.22±0.55 mm |
| XR | 2.71±0.29 mm | 3.39±0.21 mm | 4.13±0.47 mm | |
| XT | 0 mm | −0.23±0.46 mm | 0.27±0.29 mm | |
| Fiducial Marker 2 | XC | −4.51±0.37 mm | −4.64±0.67 mm | −5.55±0.68 mm |
| XR | 2.41±0.37 mm | 3.28±0.39 mm | 3.44±0.59 mm | |
| XT | 0 mm | 0.23±0.46 mm | −0.27±0.29 mm | |
| Fiducial Marker 3 | XC | −4.07±0.33 mm | −5.09±0.69 mm | −6.22±0.95 mm |
| XR | −2.76±0.42 mm | −3.62±0.61 mm | −3.89±0.72 mm | |
| XT | 0 mm | −0.23±0.46 mm | 0.27±0.29 mm | |
| Fiducial Marker 4 | XC | 3.52±0.59 mm | 4.76±0.68 mm | 5.54±0.84 mm |
| XR | −2.36±0.33 mm | −3.06±0.26 mm | −3.67±0.59 mm | |
| XT | 0 mm | 0.23±0.46 mm | −0.27±0.29 mm |
3.2. Estimations of MVAL in vivo stresses.
In vivo functional mechanical properties of the MVAL tissue were characterized using in vivo kinematic data in conjunction with the proposed inverse modeling technique (Path 1), and the SSM model parameters (mean ± SEM, n=3, second animal study group) with and without considerations of the quantified pre-strains were obtained (Table 2). The estimated in vivo stresses at peak pressure loading of the representative MVAL tissue (MVAL-1) without the pre-strain effect were σCC=~360 kPa and σRR=~450 kPa, whereas the estimated stresses with the pre-strain effect were σCC=~510 kPa and σRR=~740 kPa (Fig. 7). Here, we used subscripts CC and RR to denote the stress directions along the circumferential and radial directions, respectively. The inherent pre-stresses in the MVAL tissue due to changes in the reference configurations from state β0 to state β2 (λC=1.323 and λR=1.346) were determined to be σCC=30.4 kPa, and σRR=20.5 kPa, which are relatively small compared to the estimated tissue stresses under the peak pressure loading.
Table 2 –
Estimated SSM model (Eq. (2)) parameters for ovine MVAL tissue (n=3, second animal study group) using the in vivo inverse FE modeling technique, with and without consideration of the quantified pre-strains
| Without the pre-strain effect (from state β2 to state βt) | μm (kPa) | c0 (kPa) | c1 |
| MVAL-1 | 3.51 | 0.00233 | 33.66 |
| MVAL-2 | 4.33 | 0.00192 | 28.04 |
| MVAL-3 | 2.65 | 0.00041 | 23.54 |
| mean | 3.49 | 0.0016 | 28.41 |
| SEM | 0.49 | 0.0006 | 2.93 |
| With the pre-strain effect (from state β0 to state βt) | μm (kPa) | c0 (kPa) | c1 |
| MVAL-1 | 3.42 | 1.05×10−5 | 24.21 |
| MVAL-2 | 4.52 | 2.81×10−6 | 27.23 |
| MVAL-3 | 2.83 | 0.42×10−6 | 25.18 |
| mean | 3.59 | 3.61×10−6 | 25.53 |
| SEM | 0.49 | 3.45×10−6 | 0.88 |
Figure 7 –
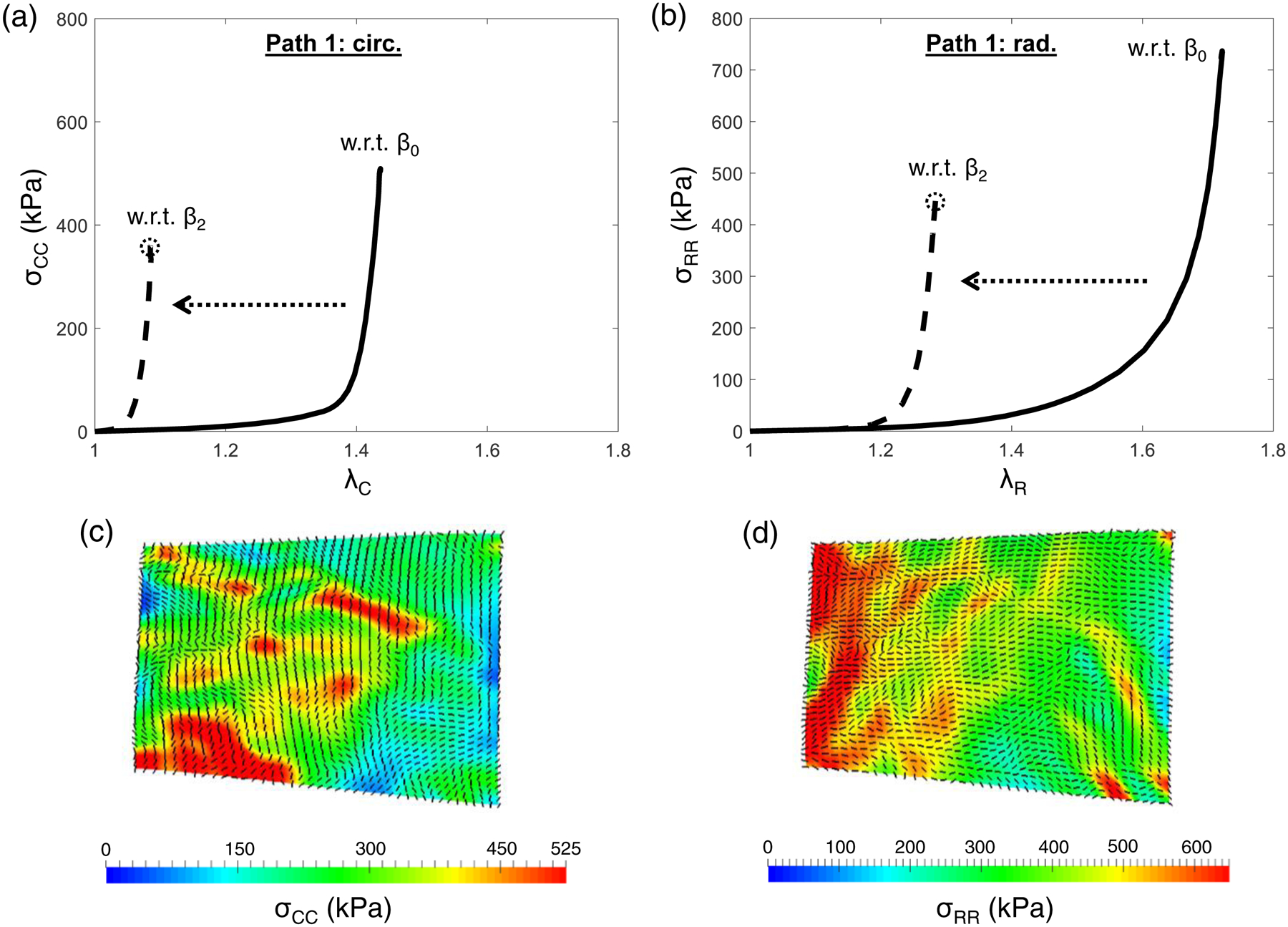
Predicted in vivo stresses of the representative MVAL tissue (MVAL-1) by inverse modeling algorithms (Path 1) with and without consideration of the quantified pre-strains: (a) in the circumferential direction, and (b) in the radial direction. (c-d) The corresponding principal stress contour and principal stress directions over the MVAL surface at the maximum LVP with respect to state β2.
For the forwarding modeling in Path 2, we first fit the full structural model to the acquired biaxial mechanical testing data. Good fits of the in vitro biaxial mechanical data (only the equi-biaxial tension loading protocol was shown for clarity in Fig. 5a) was found (Specimen #1, r2 = 0.989, Table 3). Note that the changes in the reference configurations from β0 to β2 were incorporated in the fitting procedure by using the quantified , which will influence both Γ(θ0;μc,σc) and fiber recruitment behaviors. Details about how the underlying structural function and micromechanics of the FSM, including fiber orientation density function (Fig. 5b) and the fiber recruitment function D(x; μD, σD, Elb, Eub) (Fig. 5c) were altered due to the change in the reference configurations, are provided in Appendix A.
Figure 5 –

(a) Fitting of the in vitro equi-biaxial tension loading data of the representative MVAL tissue (Specimen #1) for estimating the model parameters of the modified full structural constitutive model considering the change in the referential configurations (r2 = 0.989), (b) effects of the changes in referential configurations on (b) fiber orientation density function (ODF), and (c) fiber recruitment density function with a fiber oriented along the circumferential direction, associated with forward modeling based in vivo MVAL tissue stress estimation (Path 2).
Table 3 –
Estimated FSM model (Eqn. 1) parameters for the MVAL tissue (n=6, first animal study group) by fitting to in vitro biaxial mechanical testing data incorporating changes in the referential configuration.
| Tissue ID # | ηm (Pa) | (kPa) | (kPa) | a | b | ηf (MPa) | μc (deg.) | σc (deg.) | μD | σd | 0Elb | 0Eub |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 9.33 | 32.55 | 11.65 | 2.89 | 2.89 | 106.8 | −27.6 | 8.52 | 0.555 | 0.032 | 0.3 | 0.621 |
| 2 | 23.16 | 171.1 | 6.09 | 2.89 | 2.98 | 179.4 | −10.0 | 13.2 | 0.648 | 0.013 | 0.402 | 0.684 |
| 3 | 6.79 | 24.02 | 4.84 | 3.00 | 3.00 | 176.3 | −26.0 | 6.65 | 0.697 | 0.013 | 0.451 | 0.733 |
| 4 | 8.76 | 25.11 | 14.48 | 2.31 | 2.96 | 162.1 | 8.7 | 18.5 | 0.639 | 0.034 | 0.338 | 0.696 |
| 5 | 10.48 | 39.60 | 7.19 | 2.67 | 3.00 | 177.3 | 24.8 | 7.52 | 0.675 | 0.013 | 0.413 | 0.694 |
| 6 | 5.73 | 85.91 | 1.73 | 2.98 | 2.71 | 156.1 | 18.7 | 22.5 | 0.711 | 0.022 | 0.422 | 0.703 |
| mean | 10.71 | 63.05 | 7.66 | 2.79 | 2.92 | 159.7 | −1.9 | 12.8 | 0.655 | 0.021 | 0.388 | 0.689 |
| SEM | 2.59 | 23.55 | 1.89 | 0.11 | 0.04 | 11.24 | 22.6 | 6.49 | 0.023 | 0.009 | 0.057 | 0.037 |
Next, to cross-verify the in vivo stress estimates from the inverse modeling in Path 1, we compared representative specimen results from both (Fig. 8a–b). Note here that these results are from difference valves. Although some discrepancies were observed in the predicted stress-strain curves, such as the radial stress-strain response with respect to state β2 (Fig. 8a), the estimated in vivo MVAL tissue stresses with respect to both state β0 and state β2 by using the two approaches were in general very good agreement. Further details on the impact of this finding are provided in the Discussion.
3.3. Simulated layer-specific MVIC deformation and deformation rate in vivo.
By applying the in vivo tissue-level deformations as displacement boundary conditions on the MVIC microenvironment model, we quantitatively determined the in vivo layer-specific NARs (with peak values–A: 3.77, S: 3.46, F: 4.91, V: 3.41) and the deformation rates (with peak values–A: 15.0 1/sec, S: 11.2 1/sec, F: 22.9 1/sec, V: 8.73 1/sec) (Fig. 9a–b). Our numerical predictions showed substantially larger NAR and d(NAR)/dt values in the fibrosa layer, which confirm the fibrosa layer’s underlying microstructure of highly dense collagen fibers along the circumferential for bearing the primary loading during MV function.
Figure 9 –
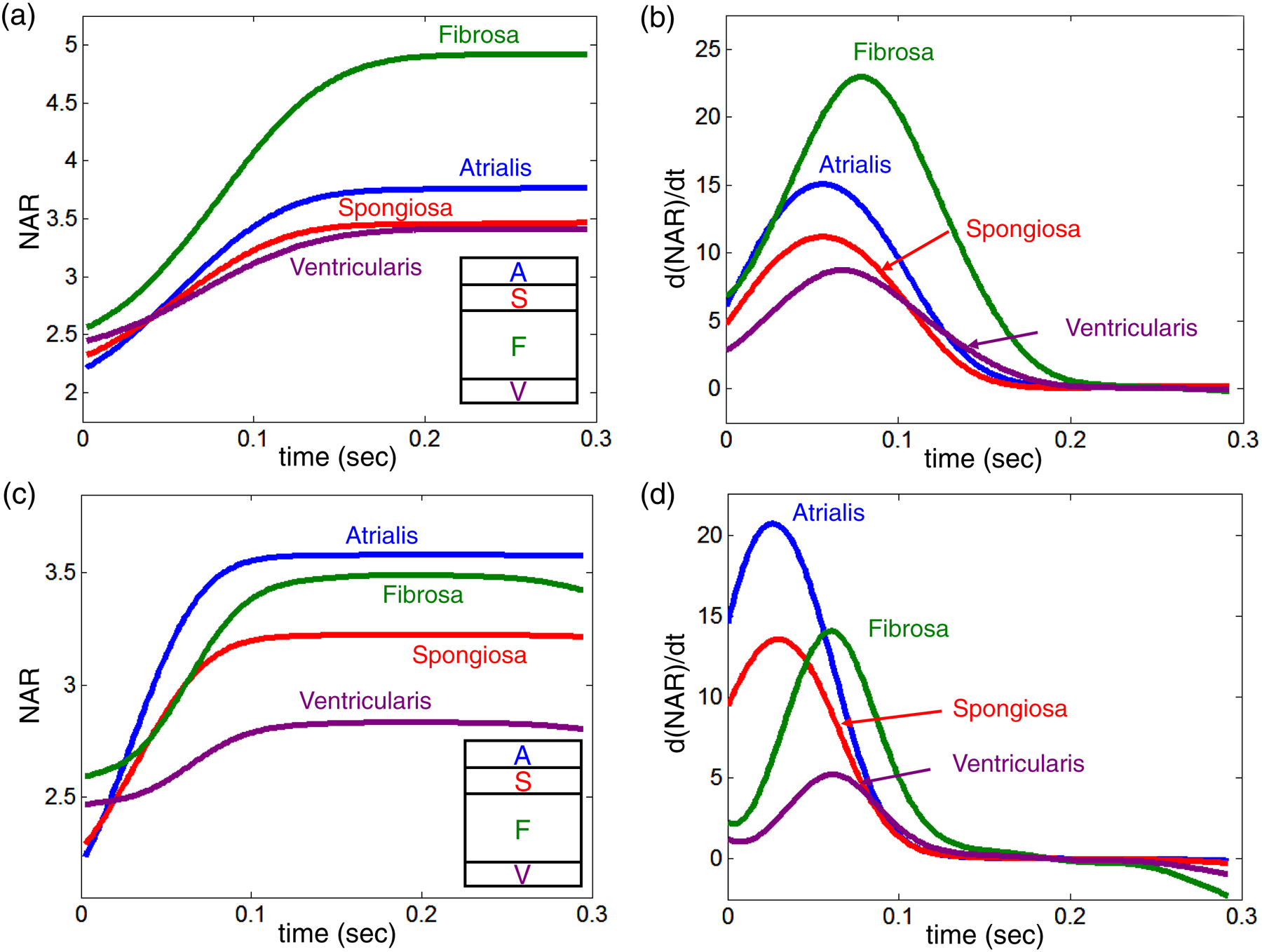
Predicted layer-specific NARs versus time for the MVs: (a) MVIC deformations (normal MV), (b) MVIC deformation rates (normal MV), (c) MVIC deformations (repaired MV), and (d) MVIC deformation rates (repaired MV). The inlet shows the hierarchy of the four MVAL tissue layers from the atrial surface to the ventricular surface)
Using the kinematic data for surgical repair and following similar FE simulation procedure, we were able to investigate the effects of annuloplasty ring on the MVIC deformation patterns (Fig. 9c–d). Note that geometry changes (Fig. 1c), induced by flat annuloplasty ring, lead to notable reductions in fibrosa NARs from 4.91 to 3.49 (Fig. 10) and ventricularis NARs from 3.41 to 2.83, and relatively smaller decreases in atrialis NARs from 3.76 to 3.58 and spongiosa NARs from 3.45 to 3.22 (Fig. 9a&c). Moreover, the highest deformation rate shifted from the fibrosa layer as for the normal MVAL (Fig. 9b) to the atrialis layer as for the repaired counterpart (Fig. 9d).
Figure 10 –
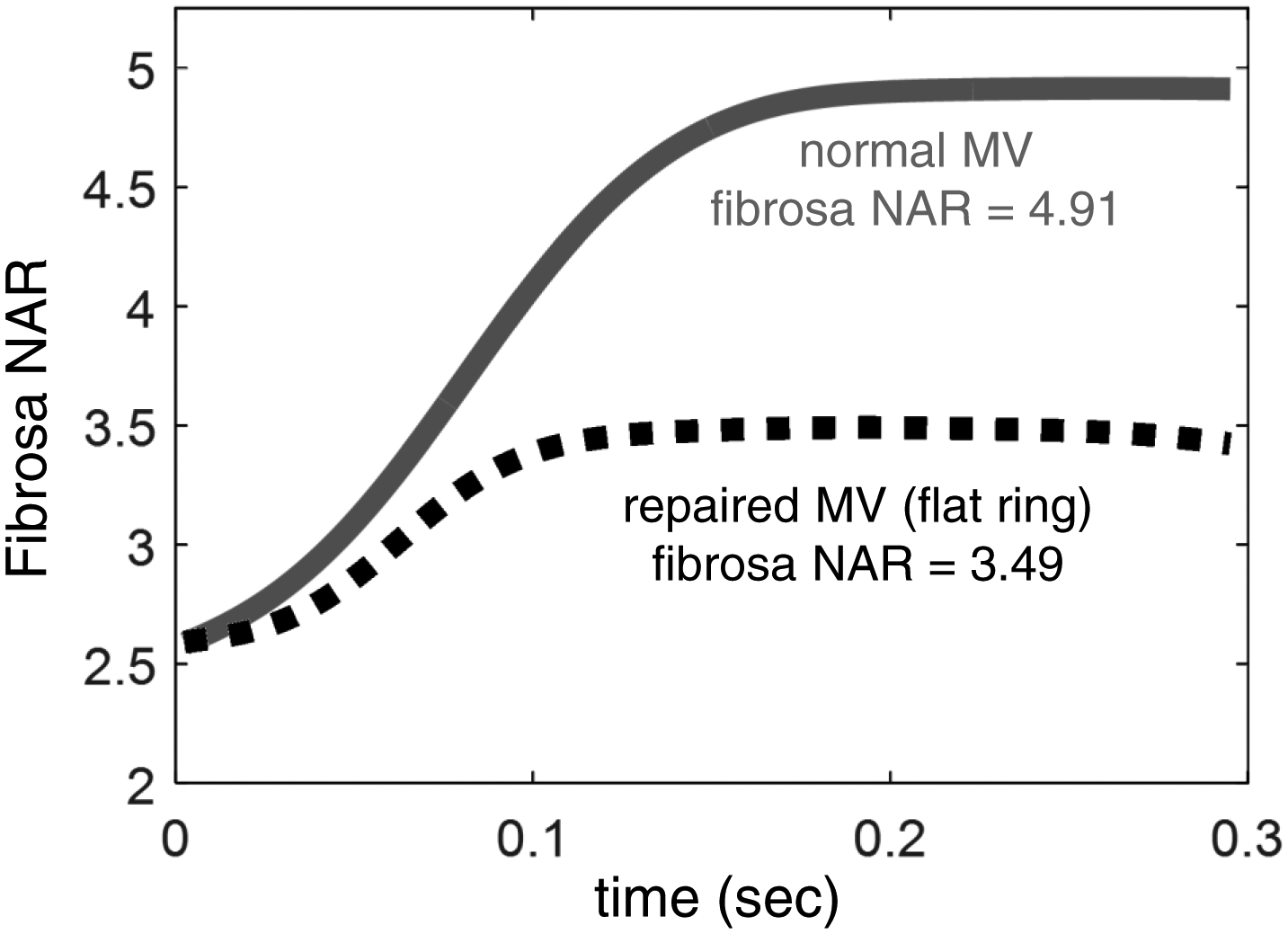
Comparison of the predicted fibrosa MVIC deformation between the normal MV and the repaired MV, demonstrating the remarked reduction of fibrosa layer NAR value (from 4.91 to 3.49) due to changes in the annular geometry/dimension induced by the flat annuloplasty ring.
4. Discussion
4.1. Overall findings.
Utilizing the population-averaged 3D positions at kinematic states β0, β1, and β2 (Fig. 1b), we were able to, for the first time, quantitatively link the in vitro tissue’s behaviors to the in vivo functioning MV. This is important for future extensions to in vivo biomechanical modeling of the MV since all knowledge of the cellular and tissue-level behaviors are acquired and most available in vitro. As for quantitative comparisons, our estimated MVAL tissue stresses (σCC=~510 kPa and σRR=~740 kPa with pre-strain effect and σCC=~360 kPa and σRR=~450 kPa without the pre-strain effect) were in a similar range to those predicted stresses in literature, such as our previously developed high-fidelity in vitro MV FE model: σMVAL=~400 kPa (Lee et al. 2015c), an in vivo MV model based on 3D ultrasound images: σMVAL=~390 kPa (Prot et al. 2009), a human MV model: σMVAL=~340 kPa (Wang and Sun 2013), among others.
In addition, as another novel aspect of this study we quantified the pre-stresses for the MVAL tissues by integrating the quantified pre-stretches (λC=1.323, λR=1.346) with the inverse modeling-based FE simulations. We found that the resulting pre-stresses and are relatively small (<10%) compared to the estimated in vivo functional stresses. These pre-stress results, while small in magnitude, indicate that the long toe-region of the MV stress-strain behavior, typically observed in vitro (Grashow et al. 2006a), is completely absorbed by the pre-strains (Fig. 7a–b). This implies that it is the elastin fiber network is primarily responsible for the pre-strain, whereas collagen fibers subsequently engage in bearing the majority of the MV’s physiological loading. While elastin may help modulate very compliant bending behavior of the MV, this pre-strain appears to be the major function of the two orthogonal elastin fiber networks (Lee et al. 2015d). Although the role of elastin has been well observed in many soft tissues (especially arterial tissues (Cardamone et al. 2009; Dahl et al. 2008)), the exact functional role of elastin fibers in other tissues, such as heart valve tissues, is often unclear. Thus, an important finding herein provides important insight into the functional role of the MV elastin fiber network.
Regarding the minor discrepancies of the estimated MVAL in vivo tissue stresses between the proposed two approaches (Fig. 8a–b), it should be carefully noted that these are from two different valve specimens. Thus, the level of agreement is actually quite remarkable, and further suggest that the approaches developed and utilized in the present study are reliable. However, caution should always be used in in-vivo/in-vitro comparisons due to the many possible sources of errors, such as the effects of tissue excision and preconditioning used in in-vitro tissue testing protocols. Moreover, the predicted Cauchy stresses representing the estimated values at the center of the marker array in Path 2 differ from the averaging process (over 1,600 MAVL surface elements) for the ROI delimited by the markers in Path 1. Nevertheless, our numerical results suggest, at least for valvular tissues, that in vitro mechanical testing data of preconditioned tissues, with the concept of preconditioning suggested by Fung in late 1980s (Chuong et al. 1986b; Fung et al. 1991) and theoretically addressed by Lanir (Nevo et al. 1994), produces a reasonable approximation to tissue’s responses at the in vivo state, and that the pseudo-elastic assumption is valid for representing the tissue’s physiological responses.
Lastly, regarding the two-step simulation procedure in our enhanced inverse FE modeling framework (Figure 4, Section 2.4.2), the distinctions between our approach and existing simulation methodologies in the biomechanical modeling literature (Prot et al. 2016; Rausch et al. 2013) are two-fold: (i) the pre-strain components in our study were determined based on the specimen averaged kinematic data and related information, rather than pre-assumed values, and (ii) the MVAL geometry associated with the in vitro reference configuration (state β0) was obtained from the computational mesh derived from the kinematic data with respect to the in vivo reference configurations rather than derived from medical image data. Another notable feature of our modeling procedure is the ability to make the direct connection between the in vitro mechanical testing configuration and the resulting tissue-level and cellular mechanical data to in vivo MV modeling.
4.2. Underlying collagen fiber micromechanical behaviors and ovine tissue variability.
Variations of the mechanical properties observed in the three ovine specimens were examined by performing FE simulations of equi-biaxial tension protocol by using their respective estimated SSM model parameter (Fig. 11a–b). This was necessary since each MV underwent different strain paths in-vivo, preventing direct comparisons of the measured strain vs. computed stresses. Our results showed a slightly larger specimen variability in the predicted circumferential stress than in the predicted radial stress. Nevertheless, these results demonstrated the reproducibility of our inverse FE modeling technique for characterizing the in vivo MVAL tissue properties. In addition, by using the estimated SSM model parameters c0 and c1 of the mean MVAL tissue response (Table 2), we were able to seek for the equivalent fiber recruitment parameters in the FSM model (assuming ηc=159.7 MPa and ensuring same ensemble stress-strain relation). This allowed us to investigate the changes in the underlying micromechanical behaviors of collagen fiber networks due to the alteration in the referential configurations , including the ensemble fiber stress-strain relation (Fig. 11c) and the collage fiber recruitment function (Fig. 11d) as a function of the collagen fiber ensemble strain Eens. These results showed a clear shift of both the Sens-Eens curve and the fiber recruitment function, at the microscopic level, as well as the changes in the peak and shape of the recruitment function D(Eens) due to the pre-strain effects. This micromechanics-based interpretation helped to provide insightful information about the adaptions of the underlying collagen fiber network in response to the changes in tissue-level mechanical loading/deformation. Integration of such information will become very beneficial when applying the developed techniques to the biomechanical modeling of the MV under clinical settings to evaluate valve performance at pathophysiological and surgically repaired conditions.
Figure 11 –
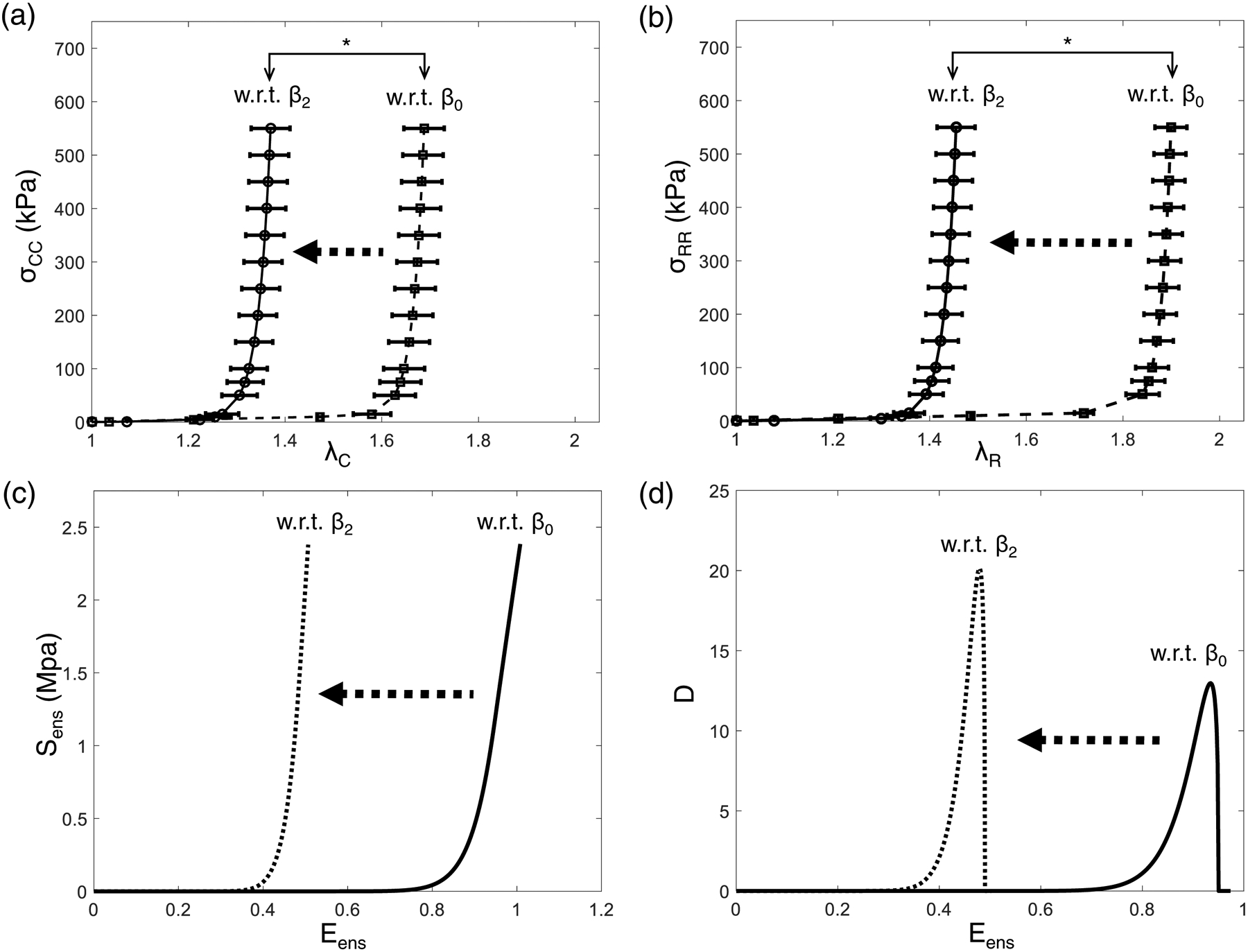
Predicted Cauchy stresses of the MVAL tissue specimens (mean ± SEM, n=3) under equi-biaxial tension loading with respect to state β0 and state β2 in the (a) circumferential direction and (b) radial direction (* indicates p < 0.001). Effects of changes in the referential configurations on the micromechanical behaviors of collage fiber networks: (c) ensemble fiber stress-strain relation, and (d) fiber recruitment density function D(Eens) as a function of Eens.
4.3. In vivo MVIC deformation and the implication of MV annuloplasty surgical repair.
A novel aspect of this study was to, for the first time, predict the in vivo MVIC deformations (Fig. 9a–b), which demonstrated substantial layer-specific variations in the MVIC deformation level and the deformation rate during isovolumetric contraction. The relation between cellular deformations and tissue strain has become more appreciated in the heart valve mechanobiology research (Balachandran et al. 2006; Balachandran et al. 2009; Lee et al. 2015b; Sakamoto et al.; Zhang et al. 2016). Our recent study demonstrated that MVIC deformations can be simulated in the context of appropriate ECM models within the layered MV leaflet. Yet, these studies all relied on in vitro approaches alone. The present study is an attempt to make the in vivo estimates possible by combining the present kinematic analysis approach. It should be noted that our approach accounts for the presence of pre-strain, which has been found for the MV and recently in the aortic valve (Aggarwal et al. 2016). Accounting for these significant effects is clearly a necessary step in understanding cellular responses to organ-level stimulation.
Interestingly, from these numerical studies we determined that the MVICs residing in the fibrosa layer of the normal MV experienced the largest deformation and the highest deformation rate during systolic closure (Fig. 9a–b). This was primarily due to its layer-specific microstructural compositions, i.e., highly dense collagen fibers along the circumferential direction, level of material anisotropy, and ECM architecture. Moreover, the atrialis layer, which is composed of radially aligned elastin fibers for sustaining majority of the tissue-level loading along the radial direction, had relatively larger deformation and higher deformation rate compared to the rest of two MVAL tissue layers (Fig. 9a–b). These findings, in supplement to our previous in situ MVIC study (Lee et al. 2015b), provided insightful information about the coupling between tissue micromechanics and cellular mechanical behavior and about their contributions to the overall organ-level MV function in response to external mechanical stimuli.
Regarding our investigations of the flat ring effect on the MVIC deformations (Fig. 9c–d), it is interesting to note that such surgical ring-induced geometry changes (28% circumferential contraction and 16% radial expansion at the OVC state and 12% circumferential contraction and 28% radial expansion at the max LVP state) resulted in notable reduction of the fibrosa NARs from 4.91 to 3.49 (Fig. 10) and relatively smaller decrease in atrialis NARs from 3.76 to 3.58 (Fig. 9a and Fig. 9c). These numerical findings suggest that layer-specific fiber compositions, ECM mechanical properties, and microstructure are the primary drivers for subtle re-distributions of the external pressure over the four MVAL tissue layers. They are also responsible for the alteration in the interactions among the MV, the left ventricular and the left atrium in order to maintain the overall MV function associated with ring-induced annular geometry restrictions.
Such surgery- or disease-induced growth and remodeling (G&R) mechanisms of cellular mechanical responses were also observed in the bovine animal studies of the pregnancy effects on the significant MVAL tissue mass growth and cellular changes (Pierlot et al. 2014; Pierlot et al. 2015; Wells et al. 2012). This important piece of information at the cellular level together with collagen biosynthesis and tissue adaption and tissue-level stresses obtained from predictive organ-level FE simulations (Lee et al. 2015c) could be used in the future for assessment of the existing annuloplasty rings. This could also be helpful for designing individual-optimized annuloplasty that would not only restore the functional geometry of the MV annulus but could also achieve the MV homeostasis that resemble their MV normal counterparts. These future extensions will ultimately be beneficial for improving the long-term surgical outcomes of MV repair for treating patients with functional or ischemic mitral regurgitation.
4.4. Study limitations and perspectives.
In the present work, we used extant sonocrystal data to obtain specimen-averaged 3D positional data for in-surface strain analyses of the MVAL, for the in vivo tissue property characterization, and for functional tissue stress estimations. One associated issue is that although the sonomicrometry array localization technique (Gorman et al. 1996) provides an excellent spatial and temporal resolution for acquiring the 3D positions of the fast-moving heart valves, it cannot be used in routine clinical studies. We are thus currently resorting to semi-automatic image segmentation techniques (Bouma et al. 2016; Jassar et al. 2011) and a spline-based valve leaflet strain calculation approach (Aggarwal et al. 2016; Aggarwal et al. 2015) recently developed in our groups for evaluations of the in vivo leaflet surface strains and the quantification of the pre-strains of the functioning MV. This ongoing extension will also help to better understand the biomechanical behaviors of the entire MV leaflets rather than the delimited region of the MV anterior leaflet.
Second, the constitutive models utilized were based on a pseudo-hyperelasticity formulation, ignoring any time-dependent responses. This appears to be a quite reasonable assumption, according to previous studies (Grashow 2005; Grashow et al. 2006a; Liao et al. 2005; Liao et al. 2007), where it was determined that healthy mitral valve tissues have no physiologically meaningful viscous or related significant viscoelastic properties. This has been shown over a range of strain rates measured in vivo (Sacks et al. 2006) so that MV tissues should be considered functionally elastic. However, more sophisticated constitutive models, which account for the G&R mechanisms, would be needed for understanding of disease progression, pregnancy-induced growth and remodeling (Pierlot et al. 2014; Pierlot et al. 2015) (Rego et al. 2016), and/or surgery-induced mechanobiological changes of the tissue’s mechanical properties and microstructure.
Finally, our novel predictions of the in vivo layer-specific MVIC deformations provide valuable insight into the cellular mechanobiology in response to the tissue-level deformation as well as to the mechanical stimuli induced by the implanted annuloplasty ring. However, there is currently no technique or imaging modality available under clinical settings that allows for systematic measurements of the in vivo MVIC geometry dimensions and deformations. There is an essential need, as part of future extensions, to extend our previous in situ study (Carruthers et al. 2012b; Lee et al. 2015b) or facilitate a new in vitro device to acquire necessary data for thorough validations of our MVIC predictions for normal, diseased and surgically repaired MVs.
4.5. Conclusions.
In summary, we first analyzed the previously acquired sonocrystal data of the normal MVAL to obtain the population-averaged 3D marker positional information. Such kinematic information was then used to quantify the MVAL deformations at various kinematic states as well as to quantitatively determine the MVAL pre-strains (~32% circumferential pre-stretch and ~35% radial pre-stretch). These results allowed us to make the important connection between the in vivo functional state and the in vitro reference configurations. Such connections are critical for detailed biomechanical modeling, as it allowed us to connect in-vitro information to the in-vivo functional state. Moreover, we incorporated the quantified MVAL deformations and the pre-strains into the inverse FE modeling framework (Path 1) for characterizing the in vivo mechanical properties of the MVAL tissue, and for estimating the resulting pre-stresses (, ) and the in vivo functional tissue stresses (σCC≅510 kPa, σRR≅740 kPa). These in vivo tissue stress estimates were then cross-verified with the analytical calculations (Part 2) by taking account of the change in reference configurations. By further integrating the tissue-level deformations with a downscale MVIC microenvironment FE model, we were able to, for the first time, simulate the in vivo layer-specific MVIC deformations and deformation rates in the normal and repaired MVs. From these results we can speculate that diminished cell deformations induced post-repair may play an important role in MV tissue deterioration as observed in post repaired states. Thus, approaches developed herein can provide valuable insight into the MV remodeling at the cellular levels in response to disease- or surgery-induced changes at the organ- and tissue-level mechanical loading/deformation. Integration of such information within a multiscale biomechanical modeling framework will ultimately assist in the simulation-guided surgical repair with improved long-term surgical outcomes.
Acknowledgments
Support from the National Institutes of Health (NIH) grants R01 HL119297, HL63954, HL103723, and HL73021 is gratefully acknowledged. Dr. Chung-Hao Lee was in part supported by the start-up funds from the School of Aerospace and Mechanical Engineering (AME) at the University of Oklahoma, and the American Heart Association Scientist Development Grant Award (16SDG27760143).
Appendix A. Modifications of the full structural constitutive model to account for a change in the referential configurations for structural model parameters
The formulation described in this appendix allows for handling the changes in tissue geometry at the reference state due to mechanisms, such as preconditioning, layer separation, removal of tissue component via enzyme degradation and others. The framework is also applicable to employed in vitro measured mechanical properties for in vivo modeling of the MV. Several key assumptions were considered:
Changes are due to alterations in the reference configuration only; the mass fractions of tissue constituents remain unchanged and the internal mechanical energy remains zero.
Changes of tissue dimensions and internal architecture are in accordance with the collagen fiber affine assumption (Chandran et al. 2006; Lee et al. 2015d). Thus, the configurational change is homogeneous and can be described by tissue-level deformation gradient tensor.
Changes associated with alterations of referential configurations result only in collagen fiber orientation, degree of fiber undulation (fiber recruitment), and tissue dimensions.
Structural parameters of the tissue are most conveniently obtained in state β0, which refers to in vitro reference configuration, and the tissue Helmholtz strain energy function Ψ is defined in state β2 for in vivo modeling of the MVAL tissue at any pressure-loaded state βt. Hence, our goal here is to seek the expressions with the quantified structural parameters at state β2.
In the formulations below, we first adopted the following notations:
| (A.1), |
where is the effective Green strain of the collagen fiber ensemble at state βt with respect to β0, and n=[cos(θ0),sin(θ0)]T is the unit vector in which the collagen fiber orients in the in vitro reference configuration.
A.1. Changes in the collagen fiber orientation density function (ODF).
The assumption of fiber affine deformation can be described by the relation dx=FdX, which maps the material line segment dX at the undeformed configuration to the corresponding deformed configuration dx via the homogeneous tissue-level deformation gradient tensor F. Let us restrict our discussion on planar soft biological tissues, the fiber ODF at state β2 can be related to the measured ODF Γ0(θ0;μc,σc) at state β0 by adopting Nanson’s relation in finite strain theory (Fan and Sacks 2014):
| (A.2), |
where ; the statistical distribution parameters are μc and μc at state β0. The fiber orientation angle at state β2 is determined by the relation below (Gilbert et al. 2006; Lee et al. 2015c; Lee et al. 2015d):
| (A.3). |
The modified collagen fiber ODF Γ2(θ2) due to the change in the referential configurations, resulting in the pre-strains , is depicted in Fig. 5b.
A.2. Changes in the collagen fiber ensemble formulation.
Next, let us consider an ensemble collection of collagen fibers with varying fiber slack strain and use a fiber recruitment function at the ensemble level to account for a range of fiber slack strains as referred to state β0 by:
| (A.4), |
where Beta(α,β) is the Beta distribution function with shape parameters α and β.
For the recruitment parameters to be recast with respect to state β2, we seek for the modified fiber recruitment function D2 with the same Beta distribution parameters and by using the mapping from in vitro reference configuration (β0) to in vivo reference configuration (β2) below
| (A.5). |
The modified fiber recruitment function associated with collagen fiber oriented along the circumferential direction (θ0=0°) due to the change in the referential configurations as described by the pre-strains is depicted in Fig. 5c.
Finally, the resulting expression for the ensemble fiber stress-strain relationship with respect to state β2 can be obtained
| (A.6). |
A.3. Complete formulation of the tissue strain energy function with respect to state β2.
Therefore, we can facilitate in vivo modeling and stress estimation using the final form of tissue stress-strain relationship
| (A.7) |
where , , , . with the fiber orientation angle with respect to state β2 as determined n′(θ2)=[cos(θ2),sin(θ2)]T by Eq. (A.3).
Nomenclature: Notations and definitions of the parameters in the full structural constitutive model.
| Parameter | Definition |
|---|---|
| Ψc | Strain energy function component of the collagen fiber network |
| Ψe | Strain energy function component of the elastin fiber networks |
| Ψm | Strain energy function component of non-fibrous matrix |
| C=FTF | Right-Cauchy deformation tensor |
| E=(C−I)/2 | Green-Lagrange strain tensor |
| I | 2nd-rank identity tensor |
| I4=nc∙Cnc | Square of the circumferential stretch associated with elastin fibers |
| I6=nR∙CnR | Square of the radial stretch associated with elastin fibers |
| Eens(θ0)=n(θ0)∙En(θ0) | Ensemble fiber strain of the individual collagen fiber in the direction of n(θ) |
| Sens | Ensemble fiber stress calculated based on the ensemble fiber stress-strain relation |
| Ecutoff | Cutoff limit of ensemble fiber strain beyond which the ensemble fiber stress-strain relationship becomes linear |
| n(θ0) | Unit vector of collagen fiber orientation w.r.t. β0 |
| nc=n(0°) | Unit vector of elastin fiber orientation along the circumferential direction w.r.t. β0 |
| nR=n(π) | Unit vector of elastin fiber orientation along the radial direction w.r.t. β0 |
| μm | Shear modulus of the non-fibrous matrix represented by a neo-Hookean material |
| ηc | Collagen fiber modulus |
| Elastin fiber modulus of the elastin fibers along the circumferential direction | |
| Elastin fiber modulus of the elastin fibers along the radial direction | |
| a | Exponent of the elastin ensembles along the circumferential direction |
| b | Exponent of the elastin ensembles along the radial direction |
| Γ(θ;μC,σC) | Orientation density function of the collagen fiber network with a mean fiber direction μC and a standard deviation σC |
| D(x;μD,σD,Elb,Eub) | Fiber recruitment distribution function with a mean μD, a standard deviation σD and a lower-bound limit Elb at which collagen fiber recruitment begins and a upperbound limit Eub at which collagen fiber is fully recruited |
Footnotes
Conflict of Interests
None of the authors have a conflict of interests with the present work.
References
- Aggarwal A, Pouch AM, Lai E, Lesicko J, Yushkevich PA et al. (2016) In-vivo heterogeneous functional and residual strains in human aortic valve leaflets J Biomech 49:2481–2490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aggarwal A, Sacks MS (2015) A framework for determination of heart valves’ mechanical properties using inverse-modeling approach Lect Notes Comput Sci 9126:285–294. [Google Scholar]
- Amini R, Eckert CE, Koomalsingh K, McGarvey J, Minakawa M et al. (2012) On the in vivo deformation of the mitral valve anterior leaflet: Effects of annular geometry and referential configuration Ann Biomed Eng 40:1455–1467. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balachandran K, Konduri S, Sucosky P, Jo H, Yoganathan A (2006) An ex vivo study of the biological properties of porcine aortic valves in response to circumferential cyclic stretch Ann Biomed Eng 34:1655–1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balachandran K, Sucosky P, Jo H, Yoganathan AP (2009) Elevated cyclic stretch alters matrix remodeling in aortic valve cusps: Implications for degenerative aortic valve disease Am J Physiol Heart Circ Physiol 296:H756–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouma W, Lai EK, Levack MM, Shang EK, Pouch AM et al. (2016) Preoperative three-dimensional valve analysis predicts recurrent ischemic mitral regurgitation after mitral annuloplasty Ann Thorac Surg 101:567–575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Braunberger E, Deloche A, Berrebi A, Abdallah F, Celestin JA et al. (2001) Very long-term results (more than 20 years) of valve repair with carpentier’s techniques in nonrheumatic mitral valve insufficiency Circulation 104:I8–11. [PubMed] [Google Scholar]
- Cardamone L, Valentin A, Eberth JF, Humphrey JD (2009) Origin of axial prestretch and residual stress in arteries Biomech Model Mechanobiol 8:431–446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpentier A (1983) Cardiac valve surgery--the “french correction” J Thorac Cardiovasc Surg 86:323–337. [PubMed] [Google Scholar]
- Carruthers CA, Alfieri CM, Joyce EM, Watkins SC, Yutzey KE et al. (2012a) Gene expression and collagen fiber micromechanical interactions of the semilunar heart valve interstitial cell Cell Mol Bioeng 5:254–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carruthers CA, Good B, D’Amore A, Liao J, Amini R et al. Alterations in the microstructure of the anterior mitral valve leaflet under physiological stress. In: ASME 2012 Summer Bioengineering Conference, 2012b. American Society of Mechanical Engineers, pp 227–228. [Google Scholar]
- Chandran PL, Barocas VH (2006) Affine versus non-affine fibril kinematics in collagen networks: Theoretical studies of network behavior J Biomech Eng 128:259–270. [DOI] [PubMed] [Google Scholar]
- Chuong CJ, Fung YC (1986a) On residual stress in arteries J Biomech Eng 108:189–192. [DOI] [PubMed] [Google Scholar]
- Chuong CJ, Fung YC (1986b) Residual stress in arteries In: Schmid-Schonbein G, Woo SLY, Zweifach B (eds) Frontiers in biomechanics. Springer-Verlag, New York, pp 117–129. [Google Scholar]
- Dahl KN, Ribeiro AJ, Lammerding J (2008) Nuclear shape, mechanics, and mechanotransduction Circ Res 102:1307–1318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eckert CE, Zubiate B, Vergnat M, Gorman JH 3rd, Gorman RC et al. (2009) In vivo dynamic deformation of the mitral valve annulus Ann Biomed Eng 37:1757–1771. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan R, Sacks MS (2014) Simulation of planar soft tissues using a structural constitutive model: Finite element implementation and validation J Biomech 47:2043–2054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flameng W, Herijgers P, Bogaerts K (2003) Recurrence of mitral valve regurgitation after mitral valve repair in degenerative valve disease Circulation 107:1609–1613. [DOI] [PubMed] [Google Scholar]
- Flameng W, Meuris B, Herijgers P, Herregods M-C (2008) Durability of mitral valve repair in barlow disease versus fibroelastic deficiency J Thorac Cardiovas Surg 135:274–282. [DOI] [PubMed] [Google Scholar]
- Fung YC (1991) What are the residual stresses doing in our blood vessels? Ann Biomed Eng 19:237–249. [DOI] [PubMed] [Google Scholar]
- Fung YC (1993) Biomechanics: Mechanical properties of living tissues. 2nd edn Springer Verlag, New York. [Google Scholar]
- Fung YC, Liu SQ (1991) Changes of zero-stress state of rat pulmonary arteries in hypoxic hypertension J Appl Physiol 70:2455–2470. [DOI] [PubMed] [Google Scholar]
- Gilbert TW, Sacks MS, Grashow JS, Woo SL, Badylak SF et al. (2006) Fiber kinematics of small intestinal submucosa under biaxial and uniaxial stretch J Biomech Eng 128:890–898. [DOI] [PubMed] [Google Scholar]
- Gillinov AM, Blackstone EH, Nowicki ER, Slisatkorn W, Al-Dossari G et al. (2008) Valve repair versus valve replacement for degenerative mitral valve disease J Thorac Cardiovas Surg 135:885–893.e882. [DOI] [PubMed] [Google Scholar]
- Gorman JH 3rd, Gupta KB, Streicher JT, Gorman RC, Jackson BM et al. (1996) Dynamic three-dimensional imaging of the mitral valve and left ventricle by rapid sonomicrometry array localization J Thorac Cardiovasc Surg 112:712–726. [DOI] [PubMed] [Google Scholar]
- Grashow JS (2005) Evaluation of the biaxial mechanical properties of the mitral valve anterior leaflet under physiological loading conditions. Master’s Thesis, University of Pittsburgh [Google Scholar]
- Grashow JS, Sacks MS, Liao J, Yoganathan AP (2006a) Planar biaxial creep and stress relaxation of the mitral valve anterior leaflet Ann Biomed Eng 34:1509–1518. [DOI] [PubMed] [Google Scholar]
- Grashow JS, Yoganathan AP, Sacks MS (2006b) Biaixal stress-stretch behavior of the mitral valve anterior leaflet at physiologic strain rates Ann Biomed Eng 34:315–325. [DOI] [PubMed] [Google Scholar]
- Jassar AS, Brinster CJ, Vergnat M, Robb JD, Eperjesi TJ et al. (2011) Quantitative mitral valve modeling using real-time three-dimensional echocardiography: Technique and repeatability Ann Thorac Surg 91:165–171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kunzelman KS, Cochran RP, Chuong C, Ring WS, Verrier ED et al. (1993) Finite element analysis of the mitral valve J Heart Valve Dis 2:326–340. [PubMed] [Google Scholar]
- Lee C-H, Amini R, Sakamoto Y, Carruthers CA, Aggarwal A et al. (2015a) Mitral valves: A computational framework In: Multiscale modeling in biomechanics and mechanobiology. Springer, pp 223–255. [Google Scholar]
- Lee C-H, Carruthers CA, Ayoub S, Gorman RC, Gorman JH et al. (2015b) Quantification and simulation of layer-specific mitral valve interstitial cells deformation under physiological loading J Theor Biol 373:26–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee CH, Amini R, Gorman RC, Gorman JH 3rd, Sacks MS (2014) An inverse modeling approach for stress estimation in mitral valve anterior leaflet valvuloplasty for in-vivo valvular biomaterial assessment J Biomech 47:2055–2063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee CH, Rabbah JP, Yoganathan AP, Gorman RC, Gorman JH 3rd et al. (2015c) On the effects of leaflet microstructure and constitutive model on the closing behavior of the mitral valve Biomech Model Mechanobiol 14:1281–1302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee CH, Zhang W, Liao J, Carruthers CA, Sacks JI et al. (2015d) On the presence of affine fibril and fiber kinematics in the mitral valve anterior leaflet Biophys J 108:2074–2087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao J, Yang L, Grashow J, Sacks MS Collagen fibril kinematics in mitral valve leaflet under biaxial elongation, creep, and stress relaxation In: Society for Heart Valve Disease Third Biennial Meeting, Vancouver, 2005. SHVD. [Google Scholar]
- Liao J, Yang L, Grashow J, Sacks MS (2007) The relation between collagen fibril kinematics and mechanical properties in the mitral valve anterior leaflet J Biomech Eng 129:78–87. [DOI] [PubMed] [Google Scholar]
- May-Newman K, Yin FC (1995) Biaxial mechanical behavior of excised porcine mitral valve leaflets Am J Physiol 269:H1319–1327. [DOI] [PubMed] [Google Scholar]
- Nevo E, Lanir Y (1994) The effect of residual strain on the diastolic function of the left ventricle as predicted by a structural model J Biomech 27:1433–1446. [DOI] [PubMed] [Google Scholar]
- Pierlot CM, Lee JM, Amini R, Sacks MS, Wells SM (2014) Pregnancy-induced remodeling of collagen architecture and content in the mitral valve Ann Biomed Eng 42:2058–2071. [DOI] [PubMed] [Google Scholar]
- Pierlot CM, Moeller AD, Lee JM, Wells SM (2015) Pregnancy-induced remodeling of heart valves Am J Physiol Heart Circ Physiol 309:H1565–1578. [DOI] [PubMed] [Google Scholar]
- Prot V, Haaverstad R, Skallerud B (2009) Finite element analysis of the mitral apparatus: Annulus shape effect and chordal force distribution Biomech Model Mechanobiol 8:43–55. [DOI] [PubMed] [Google Scholar]
- Prot V, Skallerud B (2016) Contributions of pre-strains, hyperelasticity, and muscle fiber activation on mitral valve systolic performance Int J Numer Meth Biomed Eng. [DOI] [PubMed] [Google Scholar]
- Prot V, Skallerud B, Holzapfel G (2007) Transversely isotropic membrane shells with application to mitral valve mechanics. Constitutive modelling and finite element implementation Int J Numer Methods Eng 71:987–1008. [Google Scholar]
- Rausch MK, Bothe W, Kvitting JP, Goktepe S, Miller DC et al. (2011) In vivo dynamic strains of the ovine anterior mitral valve leaflet J Biomech 44:1149–1157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rausch MK, Famaey N, Shultz TO, Bothe W, Miller DC et al. (2013) Mechanics of the mitral valve: A critical review, an in vivo parameter identification, and the effect of pre-strain Biomech Model Mechanobiol 12:1053–1071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rego BV, Wells SM, Lee CH, Sacks MS (2016) Mitral valve leaflet remodelling during pregnancy: Insights into cell-mediated recovery of tissue homeostasis J R Soc Interface 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sacks MS, Enomoto Y, Graybill JR, Merryman WD, Zeeshan A et al. (2006) In-vivo dynamic deformation of the mitral valve anterior leaflet Ann Thorac Surg 82:1369–1377. [DOI] [PubMed] [Google Scholar]
- Sacks MS, He Z, Baijens L, Wanant S, Shah P et al. (2002) Surface strains in the anterior leaflet of the functioning mitral valve Ann Biomed Eng 30:1281–1290. [DOI] [PubMed] [Google Scholar]
- Sacks MS, Smith DB, Hiester ED (1997) A small angle light scattering device for planar connective tissue microstructural analysis Ann Biomed Eng 25:678–689. [DOI] [PubMed] [Google Scholar]
- Sacks MS, Zhang W, Wognum S (2016) A novel fibre-ensemble level constitutive model for exogenous cross-linked collagenous tissues Interface focus 6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakamoto Y, Buchanan RM, Adams JS, Guilak F, Sacks MS Modeling the functional role of valve interstitial cell stress fibers Journal of Biomechanical Engineering. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Votta E, Caiani E, Veronesi F, Soncini M, Montevecchi FM et al. (2008) Mitral valve finite-element modelling from ultrasound data: A pilot study for a new approach to understand mitral function and clinical scenarios Philos Transact A Math Phys Eng Sci 366:3411–3434. [DOI] [PubMed] [Google Scholar]
- Wang Q, Sun W (2013) Finite element modeling of mitral valve dynamic deformation using patients-pecific multi-slices computed tomography scans Ann Biomed Eng 41:142–153. [DOI] [PubMed] [Google Scholar]
- Wells SM, Pierlot CM, Moeller AD (2012) Physiological remodeling of the mitral valve during pregnancy Am J Physiol Heart Circ Physiol 303:H878–892. [DOI] [PubMed] [Google Scholar]
- Zhang W, Ayoub S, Liao J, Sacks MS (2016) A meso-scale layer-specific structural constitutive model of the mitral heart valve leaflets Acta biomaterialia 32:238–255. [DOI] [PMC free article] [PubMed] [Google Scholar]


