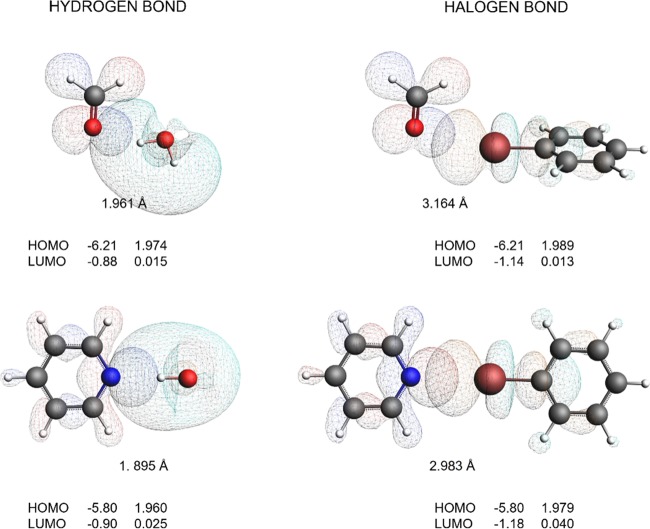
Abstract
Halogen bonds are highly important in medicinal chemistry as halogenation of drugs, generally, improves both selectivity and efficacy toward protein active sites. However, accurate modeling of halogen bond interactions remains a challenge, since a thorough theoretical investigation of the bonding mechanism, focusing on the realistic complexity of drug–receptor systems, is lacking. Our systematic quantum-chemical study on ligand/peptide-like systems reveals that halogen bonding is driven by the same bonding interactions as hydrogen bonding. Besides the electrostatic and the dispersion interactions, our bonding analyses, based on quantitative Kohn–Sham molecular orbital theory together with energy decomposition analysis, reveal that donor–acceptor interactions and steric repulsion between the occupied orbitals of the halogenated ligand and the protein need to be considered more carefully within the drug design process.
1. Introduction
Halogen bonding (XB) is commonly defined as the interaction occurring between the electrophilic region on a halogen atom and a nucleophilic region on another atom.1 The first concrete approach to halogen bonding was suggested in the 50’s of the last century when Mulliken theorized that a charge transfer (CT) process was the basis of the UV absorption spectra observed for iodine in both acetone and aromatic solvents.2 He was the first to consider these systems as Lewis acid–base pairs, in which orbital interactions would mediate the CT from the base to the acid, the halogen.3 Such phenomena, based on spectroscopic observations, were then confirmed by the work of Odd Hassel about CT complexes.4
In 2005, Clark et al. proposed a different understanding of halogen bonding by the so-called σ-hole model.5 Starting from a BLYP NBO analysis on halomethanes, the theory assumes the presence of a positive electrostatic potential surface, calculated on the halogen atom, to be the driving force of XB. Albeit still using the Lewis acid–base definition, it treats XB as a noncovalent electrostatic interaction, ignoring the importance of the CT phenomena proposed by Mulliken. Similarly, hydrogen bonding (HBs) have been considered as electrostatic noncovalent bonds for a long time, mainly because of their relatively weak bond strength.6 However, both experimental and theoretical studies have already pointed out the covalent contribution to their interaction mechanism.7−9
Interestingly, for both XBs and HBs, ab initio calculations confirm the involvement of stabilizing molecular orbital (MO) interactions10,11 and the CT mechanism.12,13 Thus, electrostatics cannot be the only driving force of halogen bonding, and even exchange–repulsion, induction, and dispersive effects are important.14,15 Electrostatics, indeed, are not enough to explain bond directionality16 or to predict the structure of the complex in a variety of cases for which the final geometry cannot be rationalized by σ-hole.17 Predicting the stability and geometry of XBs deserves great attention in drug design,18,19 where accurate analyses can improve the predictive power of computations. There is an increasing need for modeling drug–receptor XBs appropriately, as the latter has turned out to be the key to selectivity and efficacy toward a wide range of protein therapeutic targets.20,21 One of the first and most representative examples of XBs in medicinal chemistry derives from the work of Sandler et al., by which it was possible to elucidate the interaction mechanism of the iodinated thyroid hormones (T3 and T4) and the related selectivity toward the nuclear receptors TRα and TRβ.22 Not surprisingly, many computational methods have been developed to improve XB modeling.23,24 The σ-hole model has been extensively used to give indications about the ideal interaction geometry between halogenated ligands and simple backbone monopeptide (N-methyl-acetamide) or sidechain models,25 but generally by paying more attention to the electrostatic properties of ligands rather than to the chemical–structural complexity of the protein target.26 Moreover, in the available protein databases, only a few ligands adopt the bond geometries classically predicted by σ-hole theory,27,28 indicating the concrete necessity of a more accurate and reproducible XB model for drug design.
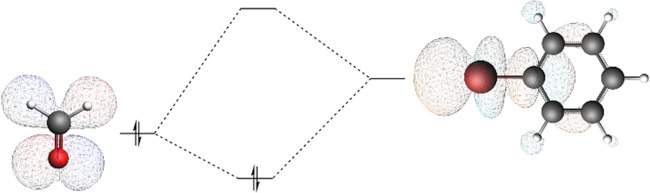
In the present work, we provide a deeper understanding of the XB mechanism in ligand–protein systems, by means of Kohn–Sham MO theory and quantitative energy decomposition analysis (EDA). Starting from the simplest model of interaction (Figures 1 and 2), we inspected the effect of the local backbone environment on the XB complex geometry and energy. Bromobenzene (PhBr) was used as the basic model of halogenated ligands. In fact, after a “chemical structure search” on the Protein Data Bank database,29 67.33% of the latter showed at least a halobenzene moiety (including also fluorine). Among the elements that are able to donate XBs, bromine was chosen due to its atomic properties, ranging between chlorine and iodine, although its relative abundance in the available crystal structures is 4 times lower than that of chlorine (Cl 76.36%, Br 18.52%, I 5.10%). Based on the insights emerging from our analyses, we support the potential use of bromine in drug design. Finally, we have investigated the resemblances between halogen bonding and hydrogen bonding.
Figure 1.
Molecular orbital interactions between a carbonyl electron donor and a halogenated benzene electron acceptor forming a halogen bond complex.
Figure 2.
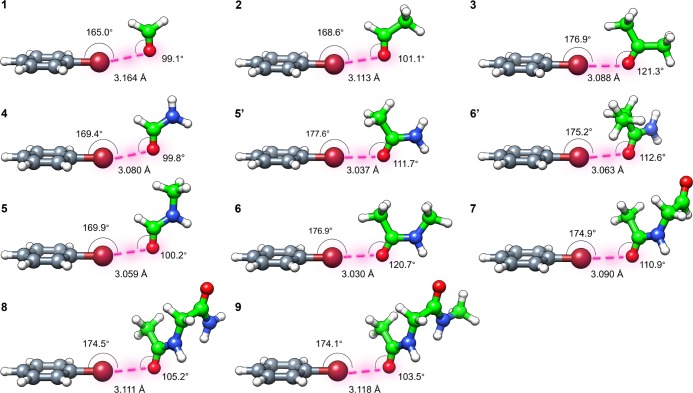
Optimized three-dimensional (3D) models used in the present work; XB interaction angles and bond distances are reported.
2. Methodology
2.1. Computational Settings
Density functional theory (DFT) calculations were performed with the Amsterdam density functional 2018.105 (ADF).30−32 Optimized geometries and energies were calculated in the gas phase. The dispersion-corrected BLYP-D3(BJ) functional was used33,34 for all energies and geometries. The Kohn–Sham molecular orbitals (KS MOs) were constructed from a linear combination of Slater-type orbitals (STOs), having correct cusp behavior and long-range decay. The TZ2P basis set was used.35 This is a triple-ζ quality basis set for all atoms, augmented with two sets of polarization functions: 2p and 3d on H, 3d and 4f on C and O, and 5d and 6f on Br. Such combination has been reported to be accurate in reproducing the structural and energy properties of related noncovalent bonds.36,37 Neither frozen core approximation nor symmetry constraints were used. Three-dimensional (3D) molecular structures were generated by the ADF program. All of the plots were obtained using GNUPLOT 4.6.38 The PyFrag 2019 program was used to perform energy calculations as a function of distances and angles.39 Two-dimensional structures were drawn using Marvin Sketch,40 ChemDraw Professional 16.0,41 and Chimera 1.11.2 software.
2.2. Energy Decomposition Analysis (EDA)
Energy decomposition analysis is a valuable method to separate individual energetic terms.42,43 The bond energy of complexes was decomposed into the strain (or preparation) energy ΔEStrain and the interaction energy ΔEInt
| 1 |
ΔEStrain is the energy necessary to deform the optimized separated monomers into their geometry in the final complex. The term ΔEInt accounts for the effective interaction energy between monomers in the complex state and can be further decomposed into four physically meaningful terms
| 2 |
The term ΔVElstat represents the classical electrostatic interactions between charge distributions related to the deformed monomers. The orbital interaction energy term, ΔEOi, contains charge transfer (donor–acceptor interactions) and polarization effects (electron density redistribution on one monomer in the presence of the other monomer). The Pauli repulsion ΔEPauli accounts for the destabilization due to the overlap between the monomers’ occupied orbitals and is responsible for steric repulsion. The term ΔEDisp is added for dispersion corrections.
2.3. Voronoi Deformation Density (VDD) Charge
VDD charge accumulation, ΔQA, has been calculated for halogen bonding as the change in electron density between the isolated monomers 1 and 2 and the complex, giving indications about charge transfer processes44
| 3 |
A positive VDD charge corresponds to the loss of electrons, whereas a negative charge is related to the gain of electrons.
3. Results and Discussion
3.1. Bonding Energies and Geometries
The bonding energy and the geometry of each complex presented in Scheme 1 were calculated to understand how the gradual substitution at the carbonyl acceptor toward realistic model systems affects the mutual orientation of the XB partners and the overall stability. The local protein environment and even small geometrical deformations of the target site, in fact, can be crucial for the perfect fit of the ligand and its bound-state stability. Solvation and entropic contributions were not considered, to evaluate only the intrinsic nature of halogen bonding as related to the chemical partners.
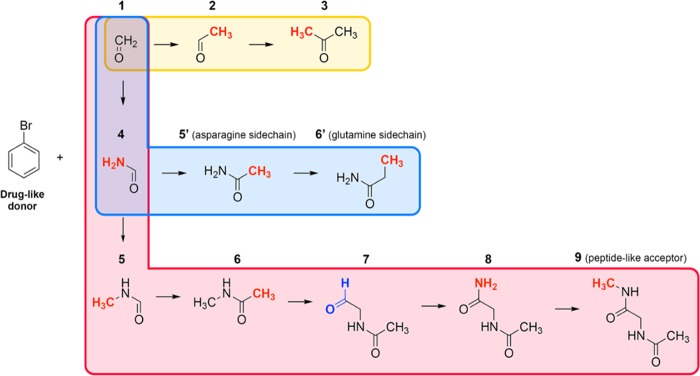
Scheme 1. Schematic Representation of the Halogen-Bond Donor and Halogen-Bond Acceptors in This Study.
Either methyl and amino (−CH3 and −NH2, highlighted in red) or formyl (−CHO, highlighted in blue) groups were added stepwise to formaldehyde. Each set is distinguished by different background colors (1 → 3 yellow; 1 → 6′ light blue; and 1 → 9 light red).
In Table 1, the bond energy and different geometrical parameters are reported (see also Supporting Information (SI 1–2) for cartesian coordinates). The results clearly indicate that the stepwise functionalization of the carbonyl acceptor leads to an observable variation of energies and geometries. ΔEBond becomes more stabilizing almost linearly with the insertion of −CH3 and −NH2 groups for each complex set (1 → 3, 1 → 9, and 1 → 6′), reaching the largest values for complexes 3 (−2.48 kcal mol–1), 6 (−2.79 kcal mol–1), and 6′ (−3.19 kcal mol–1), respectively, while it becomes weaker when a formyl moiety is added to form complex 7 (−2.65 kcal mol–1). Data reveal, at the first instance, that the presence of the second peptide bond, close to the XB pair, is involved in complex stability (Table 1, complexes from 7 to 9). The Br–O distance follows the same trend of ΔEBond only for set 1 → 3, that is, it becomes shorter with a more stable ΔEBond. In set 1 → 9, it shortens proportionally from complex 1 (3.164 Å) to complex 6 (3.034 Å), but after the insertion of the formyl group it slightly elongates, reaching, finally, a value of 3.118 Å in complex 9. In complex 6′, yielding the strongest ΔEBond value among the overall set, the bond length shows some increase as well (3.063 Å). These values are consistent with previous benchmarks on available crystal structures.28
Table 1. Geometrical Features and Bonding Energies of Bromobenzene in Complex with XB Acceptors Used in our Studya.
| set | complex | Br···O (Å) | ωBrOC (deg) | θCArBrO (deg) | φBrOCN (deg)b | ΔEBond (kcal mol–1)c |
|---|---|---|---|---|---|---|
| 1–3 | 1 | 3.164 | 99.1 | 165.0 | 180.0 | –2.10 (−1.85) |
| 2 | 3.113 | 101.1 | 168.6 | 180.0 | –2.29 (−2.02) | |
| 3 | 3.088 | 121.3 | 176.9 | 175.0 | –2.48 (−2.18) | |
| 1–9 | 1 | 3.164 | 99.1 | 165.0 | 180.0 | –2.10 (−1.85) |
| 4 | 3.080 | 99.8 | 169.4 | 180.0 | –2.47 (−2.16) | |
| 5 | 3.059 | 100.2 | 169.9 | 181.1 | –2.60 (−2.30) | |
| 6 | 3.030 | 120.7 | 176.9 | 168.7 | –2.79 (−2.47) | |
| 7 | 3.090 | 110.9 | 174.9 | 136.1 | –2.65 (−2.35) | |
| 8 | 3.111 | 105.2 | 174.5 | 127.8 | –2.68 (−2.37) | |
| 9 | 3.118 | 103.5 | 174.1 | 125.2 | –2.71 (−2.39) | |
| 1–6′ | 1 | 3.164 | 99.1 | 165.0 | 180.0 | –2.10 (−1.85) |
| 4 | 3.080 | 99.8 | 169.4 | 180.0 | –2.47 (−2.16) | |
| 5′ | 3.037 | 111.7 | 177.6 | 179.6 | –2.79 (−2.46) | |
| 6′ | 3.063 | 112.6 | 175.2 | 217.1 | –3.19 (−2.83) |
Computed at BLYP-D3(BJ)/TZ2P.
For the complex set 1 → 3, values refer to dihedral angles represented by BrOCH (1) and BrOCCH3 (2, 3).
In parentheses, the counterpoise corrected energy. The basis superposition error of monomers is reported in SI 3.
The ideal CArBrO angle θ (Figure 3) has been reported in the literature to be 175–180°.23 Comparison of the most stable complexes (3, 6, and 6′) highlights that, although they retain almost the same linear angle (176.9 and 175.2°), their respective energies are different. For 6 and 6′ this is due to the difference in the dispersion energy term, while complex 3 shows a lower stability because of any contribution (Figure 4). Therefore, a more linear XB does not necessarily implicate a stronger XB. The θ angle, indeed, neglects the effect of substituents on stability. The BrOC angle, ω, ranges on average between 99 and 121°. The dihedral angle between bromine, carbonyl oxygen, carbonyl carbon, and its main geminal N atom (−H for formaldehyde and −CH3 for acetaldehyde or acetone), φ, can change significantly as new moieties are added to the acceptor structure. Interestingly, complexes 7, 8, 9, and 6′ feature the highest variability of φ compared to the other systems, by negative and positive deviations from planarity (180°), respectively (136.1, 127.8, 125.2, and 217.1°). This geometrical feature indicates how the carbonyl bond plane is oriented toward the halogen atom: when a formyl group is added to complex 6, the main axis of the carbonyl bond is rotated drastically clockwise (φ ≪ 180°), while in the −CH3-functionalized complex 6′ it is rotated anticlockwise (φ ≫ 180°) (vide infra). For both, the oxygen lone pair (LP) orientation with respect to the halogen atom changes significantly, and even the resulting energy variation is different. The ΔEBond reaches the strongest energy for the 6′ complex (−3.19 kcal mol–1), giving preliminary suggestions about the higher stability of the Gln sidechain-mediated XB. The inclusion of the formyl moiety (complex 7), on the other hand, leads to destabilization. These findings imply the existence of different forces determining the interaction mechanism.
Figure 3.
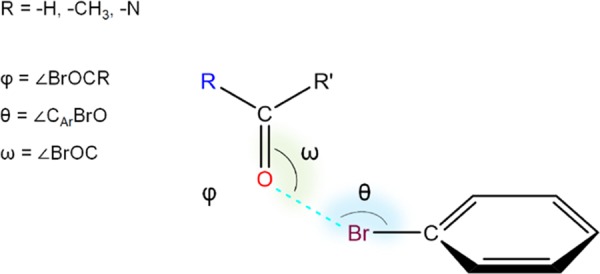
Representation of the halogen-bonding angles.
Figure 4.
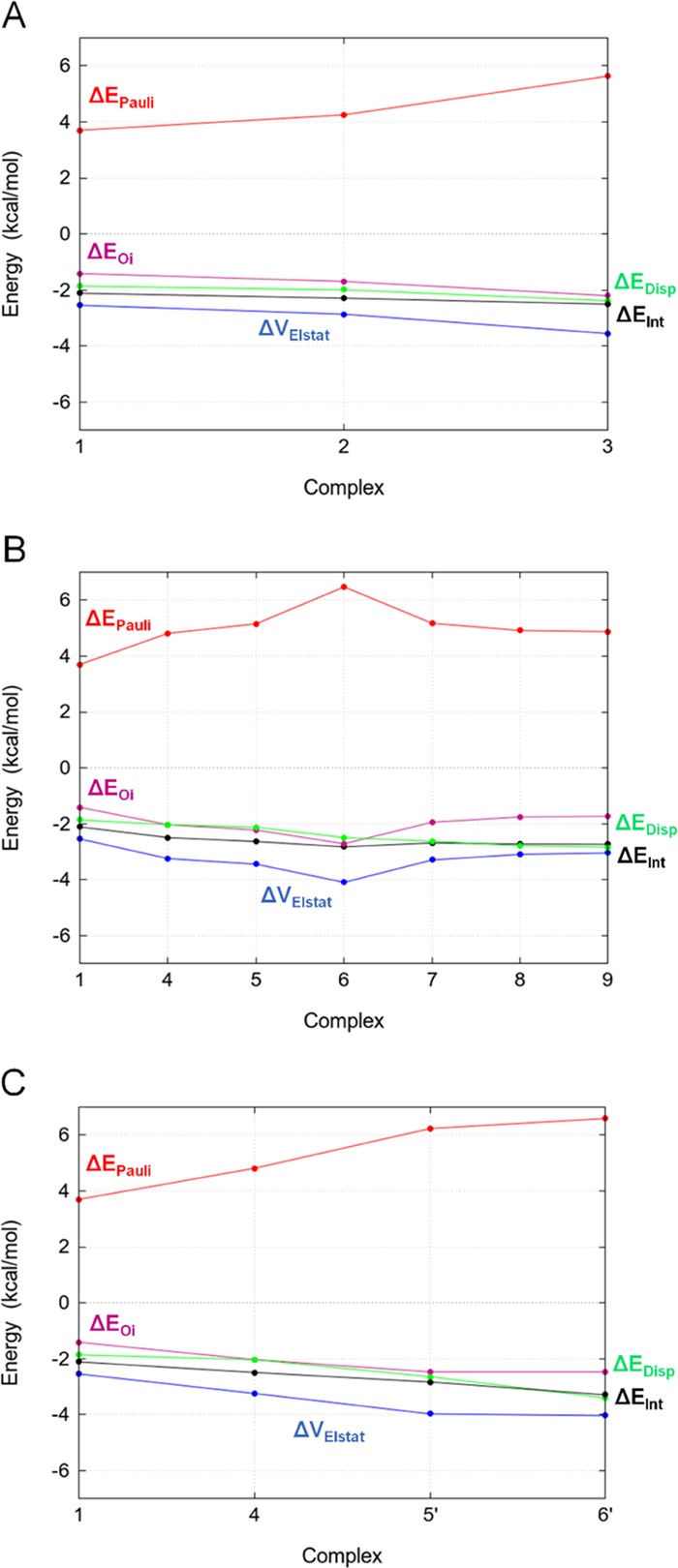
EDA for XB complex sets 1 → 3 (A), 1 → 9 (B), and 1 → 6′ (C).
3.2. Nature of the Halogen Bond
Energy decomposition analysis in combination with the Kohn–Sham molecular orbital theory offers a thorough understanding of the electronic mechanism involved in the stability of each XB complex set (SI 4).
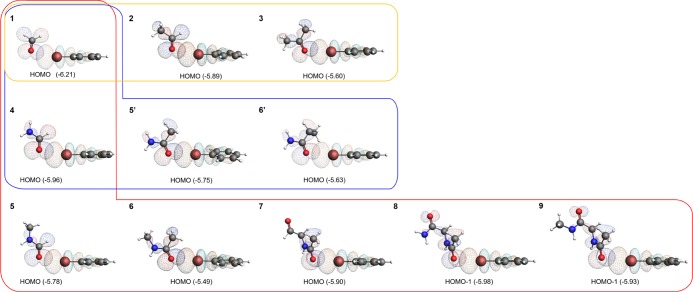
For set 1 → 3, the stepwise addition of methyl groups leads to an increase of all contributions to ΔEInt (Figure 4A). In magnitude, electrostatics is the most stabilizing component, whereas Pauli repulsion is highly destabilizing. However, ΔVElstat cannot provide the observed negative ΔEInt alone, because, if other favorable components were excluded, it would be largely canceled out by ΔEPauli. Both ΔEOi and ΔEDisp contribute significantly to the interaction energy. The electrostatic interaction energy shows a strong correlation with the orbital interaction energy. It can be seen that their gradient is almost equal for each pair of points shown in Figure 4 (ΔΔVElstat ≈ ΔΔEOi). The change in orbital interaction depends on the energies of the interacting orbitals. In general, the smaller the highest occupied molecular orbital (HOMO)–lowest unoccupied molecular orbital (LUMO) gap, the stronger the orbital interactions. The larger charge on the acceptor when going from 1 to 3 results in the destabilization of the oxygen LP orbital (see also Figures 5 and 6), thereby decreasing the HOMO–LUMO gap and thus yielding a stronger ΔEOi.
Figure 5.
Optimized complexes, MOs and related energies (in eV). Each set is distinguished by different colors (1 → 3 yellow; 1 → 6′ blue; and 1 → 9 red).
Figure 6.
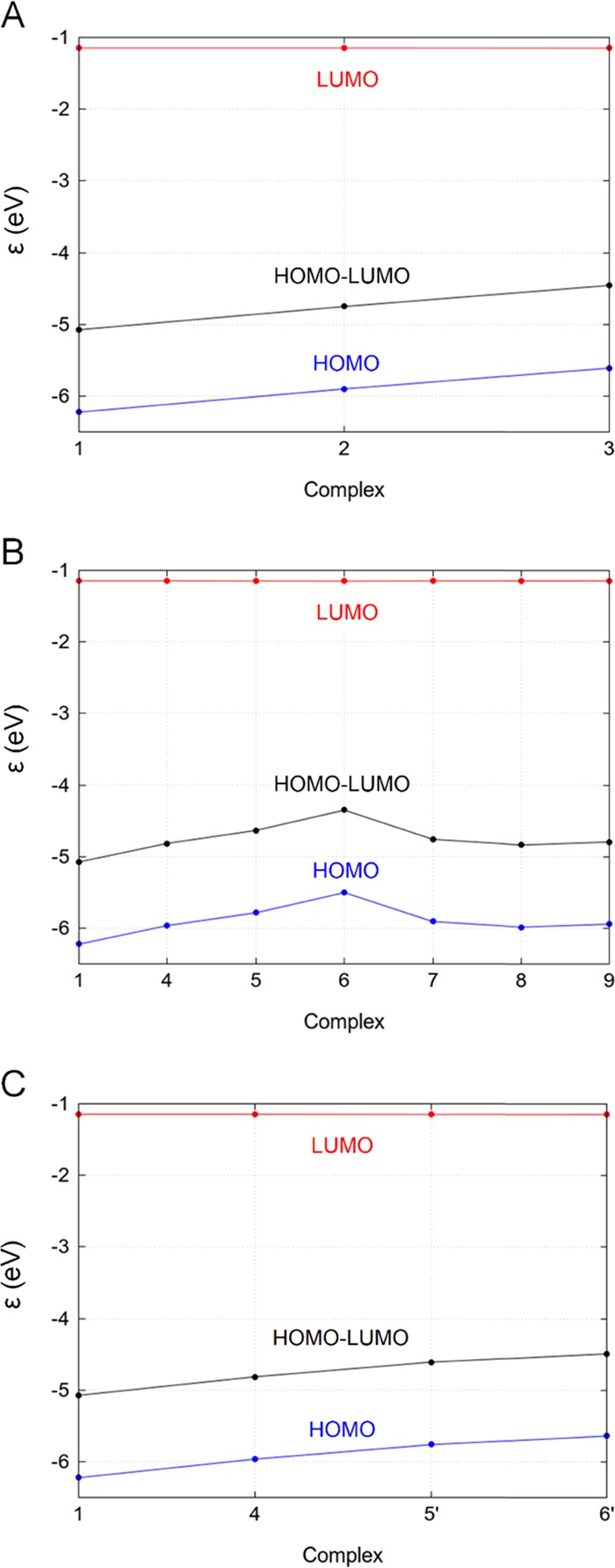
Energy (in eV) of the interacting HOMO and LUMO, for sets 1 → 3 (A), 1 → 9 (B), and 1 → 6′ (C); for complexes 8–9, values refer to HOMO – 1.
Analysis of set 1 → 9 is consistent with previous results (Figure 4B). All of the components increase their contribution up to the largest value (6), where ΔEOi equals even ΔEInt. After the inclusion of the formyl moiety, all of the contributions decrease, with the only exception of ΔEDisp. When the new peptide bond is formed, the other components reach a plateau. ΔEInt becomes more stabilizing due to dispersion effects, and also because of the considerable decrease in Pauli repulsion destabilization observed after the insertion of the formyl group. Contributions from the orbital and electrostatic interactions are still correlated. They become less stabilizing concerted with the clockwise reorientation of the LP located on the peptide carbonyl (Table 1, φ).
Acetamide and propanamide (5′, 6′, Scheme 1) represent very simple models of sidechain acceptors: Asn and Gln, respectively. ΔEInt is more stabilizing for the Gln. ΔEPauli is increasingly destabilizing stepwise along the entire set, while ΔEDisp is more stabilizing. ΔEOi and ΔVElstat are approximately constant between 5′ and 6′ (Figure 4C). The −CH3 and −NH2 stepwise functionalization is determinant in improving the overall stability, as already observed for the series formaldehyde–acetaldehyde–acetone (set 1 → 3), but the higher stabilization observed for the Gln sidechain is due to dispersive effects only because the β methyl group improves neither the electrostatics nor the orbital interaction, i.e., when considering the Gln sidechain as a potential acceptor, the stabilization observed is only due to dispersion effects, while in the case of the Asn sidechain all of the components are affected. The Gln is more favored than the Asn sidechain in forming XBs, following the better dispersion given by the β carbon. It is reasonable to assume that a linear alkyl elongation of acetamide would not affect the XB stability in terms of ΔEOi and ΔVElstat. There is no indication in these systems for any substantial C–H···Br hydrogen bonding, which would show up as a slight elongation of the C–H bond due to the donor–acceptor interaction of the Br lone-pair orbital with the σ*CH acceptor orbital. Such a C–H elongation does not occur (see SI 5). On the contrary, there is a (very minor) contraction of the C–H bond upon complexation.
Our calculations give concrete evidence of how the nearby local chemical environment of any potential acceptor can influence the ligand–protein XBs, acting on each energy component. To further elucidate the role of MO interactions in halogen bonding, we performed an extensive KS MO analysis.
3.3. Kohn–Sham Molecular Orbitals and Charge Transfer
In Figure 5, it is possible to see the overlap between the main interacting LUMO of bromobenzene (XB donor) and the HOMO of the XB acceptors. The LUMO energy of bromobenzene is constant, and, on the other moiety, the HOMO, which mainly consists of an oxygen LP, follows a certain trend, yielding different ΔεHOMO–LUMO values (Figure 6). εHOMO increases when going from acceptor 1 to acceptor 3, from 1 to 6 and from 1 to 6′, reflecting the observed ΔEBond trends and energy minima. As can be seen in Figure 5, the oxygen LP orbital on the acceptors overlaps significantly with the virtual orbital on Br. The introduction of another peptide bond into complex 6 (complexes 7–9) stabilizes the εHOMO by 0.49 eV. The carbonyl bond axis rotates clockwise, and a weaker ΔEOi contribution is observed for complexes 7, 8, and 9. The oxygen’s LP orbital of complexes 8 and 9, in fact, occupies a lower (more stabilized) energy level (HOMO – 1), and the HOMO is located on the other oxygen atom. Based on the significant contribution of ΔEOi to the total XB energy, and the good correlation between ΔEOi and the LP energy level (HOMO), we can conclude that MO interactions play an important role in halogen bonding. To further validate this observation, charge transfer mechanisms were explored by gross population analysis and VDD charges (Table 2 and Figure 7).
Table 2. Gross Populations (in Electrons) of Main Interacting MOs.
| complex | LUMO | HOMO |
|---|---|---|
| 1 | 0.013 | 1.989 |
| 2 | 0.017 | 1.987 |
| 3 | 0.021 | 1.985 |
| 4 | 0.019 | 1.984 |
| 5 | 0.021 | 1.983 |
| 5′ | 0.023 | 1.985 |
| 6 | 0.024 | 1.984 |
| 6′ | 0.021 | 1.990 |
| 7 | 0.018 | 1.992 |
| 8 | 0.016 | 1.993a |
| 9 | 0.016 | 1.994a |
Values refer to HOMO – 1.
Figure 7.
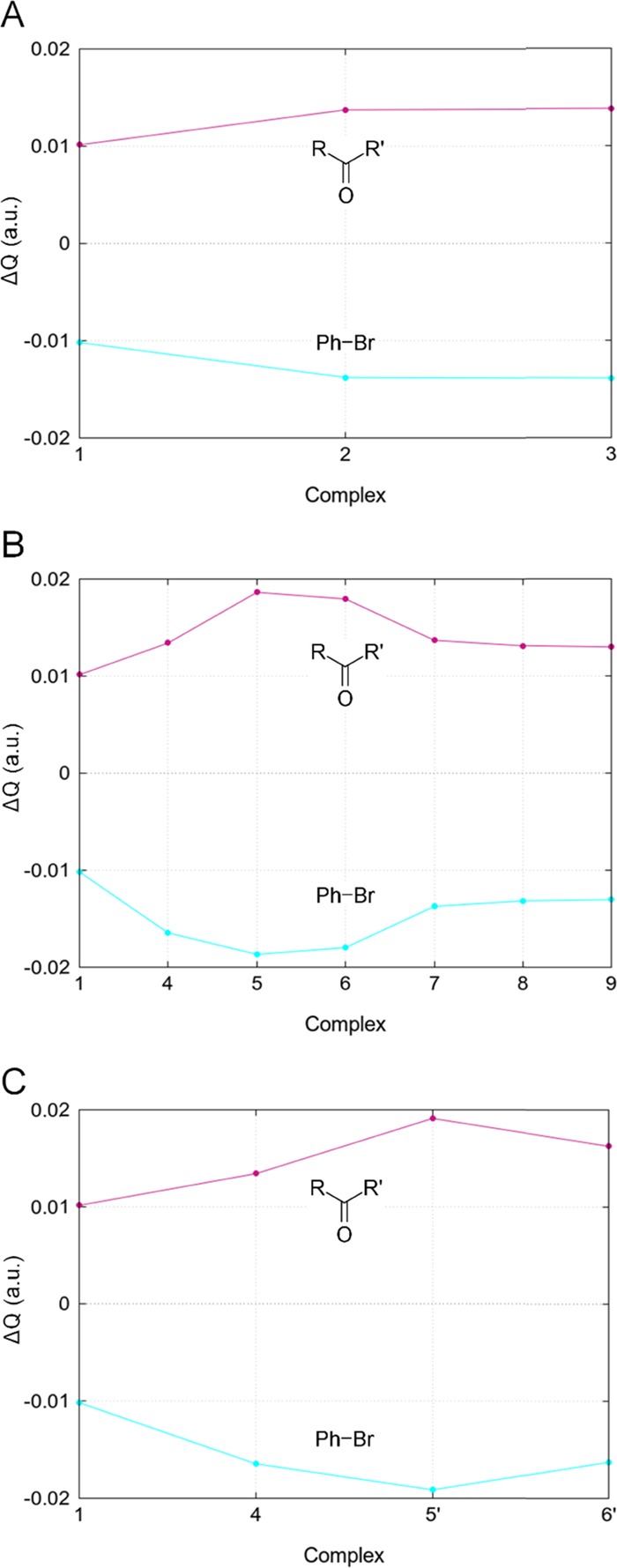
VDD charges (in au) of the halogen-bond acceptor and donor for sets 1 → 3 (A), 1 → 9 (B), and 1 → 6′ (C) due to the halogen-bond formation (eq 3).
Gross population values give a measure of how many electrons migrate from the LP orbital of the XB acceptor toward the lowest unoccupied MOs of the XB donor (charge transfer). Values are consistent with the existence of a CT process for any XB complex. The gross populations increase for the LUMO and decrease for the HOMO when −CH3 and −NH2 groups are added to the XB acceptor. The opposite behavior is observed in the presence of the second peptide bond. Indeed, the LUMO population decreases for complex 7 and is kept constant for complexes 8 and 9, where only the HOMO population changes slightly. The VDD charge analysis reported in Figure 7 gives further insight into the electron density flow from the XB acceptor to the donor. In all of the complexes, the carbonyl compound VDD charge ΔQ is positive (it donates electrons), while the bromobenzene is always negative (it accepts electrons). As the methyl and amino groups are added to the system, acceptor and donor charges become respectively more positive and more negative, conversely when introducing another peptide bond.
In set 1 → 6′, ΔεHOMO–LUMO becomes smaller with the methyl group insertion, but ΔQ of the Asn sidechain acceptor (5′) is more negative than Gln (6′), indicating a less efficient CT in the latter case. Consistently, the greater XB length observed in 6′ (3.063 vs 3.032 Å, Table 1) leads to a smaller HOMO–LUMO overlap, compared to complex 5′ (S2 = 0.008 in 5′, S2 = 0.005 in 6′). The CT is strongly evident when considering the series formaldehyde–acetaldehyde–acetone (1–3), in which −CH3 groups are added stepwise at both sides of the carbonyl moiety and the LUMO population increases. In accordance, ΔεHOMO–LUMO (Figure 6) becomes smaller when going from 1 to 3. ΔεHOMO–LUMO, gross population analysis, and VDD charges resemble the same general trend, confirming the involvement of CT in XB stability and its dependence on the local chemical environment of the Lewis pair. Noteworthily, structural isomer pairs (5–5′, 6–6′) show that substituents’ position affects the electronic distribution significantly since their ΔεHOMO–LUMO, gross populations, and VDD charges are different for each complex, despite each member sharing the same atoms with its analogue. In general, we found that protein methyl and amino building blocks improve the charge donation and the stability of the complex, differently from the proximal peptide bond carbonyl, which tends to lower it.
3.4. Halogen Bonds vs Hydrogen Bonds
XBs and HBs share two features: (1) a common bond acceptor, i.e., an electronegative atom with a partial negative charge acting as the XB or HB acceptor, and (2) directionality. In the previous sections, we have defined the presence of CT mechanisms mediated by MO interactions. Here we address the importance of XB directionality and the main differences compared to HB. In Figure 8, the most relevant HOMOs of formaldehyde are reported. Any of these orbitals could overlap in space with the main LUMO of the donor, yielding some interaction. As can be seen in Figure 8, all three orbitals can have a good overlap with the LUMO of the XB donor. However, the energy difference between the HOMO and lower-lying orbitals is very large. For example, the orbital energy goes down by 3.67 eV when moving from the HOMO to HOMO – 1, which amounts to an increase in the gap between the occupied MO and the LUMO of more than 72%. As a result, the HOMO–LUMO interaction is stronger than the [HOMO – 1]–LUMO interaction.
Figure 8.
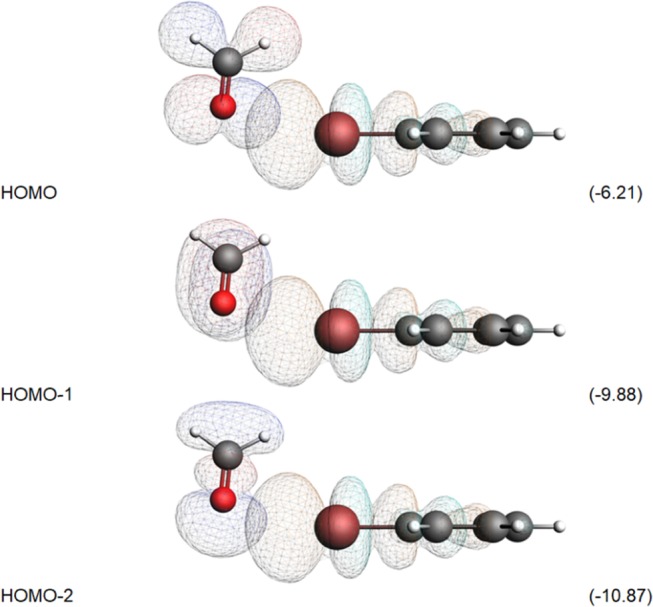
Directionality and energy (in eV) of the most relevant HOMOs in the formaldehyde XB complex.
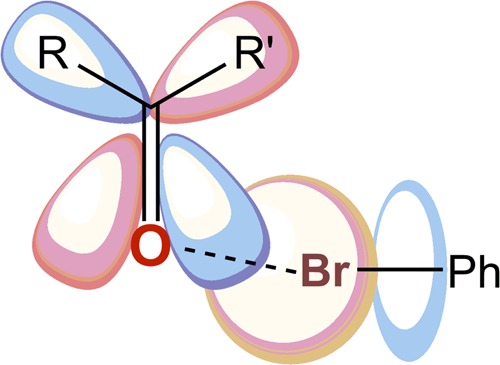
The major overlap involves an LP of the oxygen oriented toward the halogen atom following the BrOC angle, ω, close to 120° (Figure 1). A similar depiction was already provided in the literature for HBs and can be reliably related to the so-called “orthogonality” between HBs and XBs in ligand–protein systems,45 i.e., the peptide carbonyl can engage both at one time, following the directionality of its LPs.
With a view to validate the common nature of HBs and XBs, we have calculated the geometry and energy of the complexes obtained using pyridine and formaldehyde as bond acceptors (having different LP directionality) and water and bromobenzene as bond donors. The calculated geometries and MOs reported in Figure 9 confirm that XBs and HBs can have a similar bonding mechanism.
Figure 9.
XB/HB pair comparison. HOMO and LUMO energies (in eV) along with their gross population (in electrons) and the bond lengths between O/N and H/Br (in Å).
For each pair, donor–acceptor orbital overlap occurs exactly in the same direction of the LP HOMO. The bond distances are considerably smaller for the HB complexes. The gross populations reveal a similar charge transfer picture: the LP orbitals lose electron density, which is being transferred to the opposing virtual orbital on hydrogen (HB) or the halogen (XB). The gross populations for HBs and XBs are of the same order of magnitude.
EDA discloses similarities between HBs and XBs in a more quantitative manner (Table 3). ΔEBond and ΔEInt attribute more stability to the HBs than XBs. Energy components are more stabilizing for the pyridine than the formaldehyde acceptor in any complex pair, because of the higher LP orbital. Their relative contribution to the overall energy is approximately equal, independently of the complex considered. ΔEPauli and ΔVElstat give the highest contribution, followed by ΔEOi and ΔEDisp. Even in these cases, the electrostatic interaction and Pauli repulsion are not the only determining factors for the total interaction energy. Interestingly, ΔEOi shares the same order of magnitude with ΔVElstat, being generally more than one-half of the latter. The dispersion interaction is relatively more important for the XBs than for the HBs.
Table 3. EDA (in kcal mol–1) for HB and XB Complexes, Computed at the BLYP-D3(BJ)/TZ2P Level of Theory.
| complex | ΔVElstat | ΔEPauli | ΔEOi | ΔEDisp | ΔEint | ΔEBonda |
|---|---|---|---|---|---|---|
| HOH···O=CH2 | –7.56 | 7.43 | –4.02 | –1.21 | –5.36 | –5.27 (−4.94) |
| HOH···NC5H5 | –13.01 | 13.73 | –7.15 | –1.70 | –8.13 | –7.90 (−7.50) |
| PhBr···O=CH2 | –2.54 | 3.70 | –1.41 | –1.86 | –2.11 | –2.10 (−1.85) |
| PhBr···NC5H5 | –6.44 | 9.36 | –3.60 | –2.70 | –3.38 | –3.33 (−2.99) |
In parentheses, the counterpoise corrected energy.
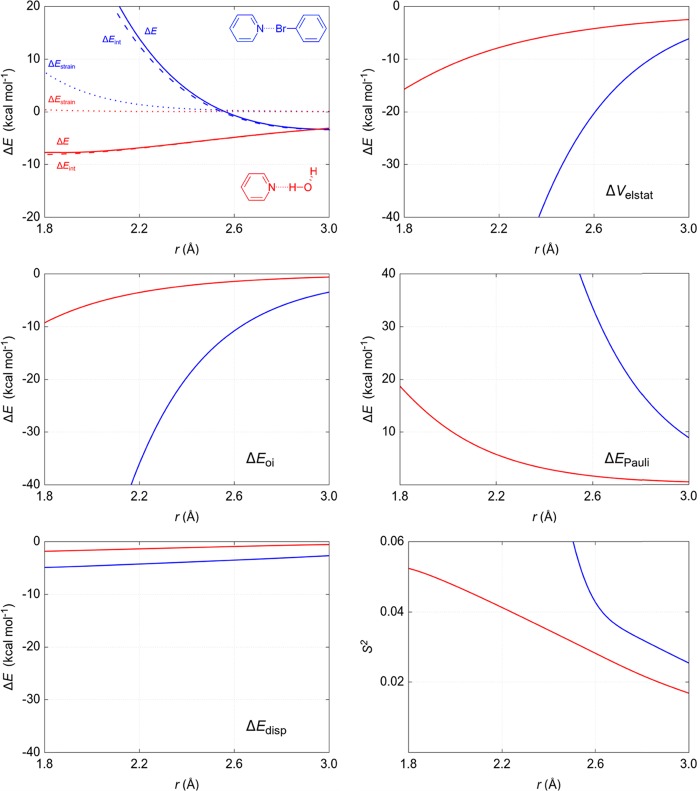
The effect of the bond donors on any energetic component is greater than the effect of the bond acceptors, especially if comparing bromobenzene and water as bound to the pyridine acceptor. The bond distance in a HB complex is ∼1.5 times shorter than in the analogous XB. However, the |ΔεHOMO–LUMO| is smaller for the XB than the HB because the LUMO is more stabilized in bromobenzene than in water. Also, the MO interaction is more favorable for HB than XB, and the bond length is shorter. To analyze these aspects, we calculated the interaction energy profile of the HB and XB complexes by varying the distance between N and Br/H from 3.0 to 1.8 Å in 20 geometry optimization steps (0.06 Å per step). The angles ∠CArBrN and ∠NHO were kept constant. The results are reported in Figure 10 (see SI 6 for coordinates). In both HB and XB, electrostatics and orbital interactions are the most important stabilizing components. Note that all individual contributions, as functions of the atom pair distance, are more favorable in halogen bonding, except for ΔEPauli and ΔEStrain, which are less destabilizing in hydrogen bonding. The interaction energy gets stronger with shorter distances in HB, while in XB it quickly becomes destabilizing at ∼2.5 Å, indicating that shorter bond lengths are not allowed. Indeed, both Pauli repulsion and strain energy are 20 times more destabilizing in XB than in HB.11 XB is clearly more favored than the latter one in terms of electrostatics, orbital interactions, and dispersion at any distance. However, the strong Pauli repulsion, due to the overlap between the monomers’ filled orbitals, prevents the monomers from getting closer to each other.
Figure 10.
Energy terms and the largest overlap are represented as functions of the distance between the acceptor N and donors Br (XB complex in blue) or H (HB complex in red), computed at the BLYP-D3(BJ)/TZ2P level of theory.
3.5. Directionality of Halogen Bonds
Bonding directionality is crucial for understanding the basis of XB stability, as the orbital overlap and, therefore, the orbital interaction are strongly affected by the relative orientation of the monomers. The σ-hole theory models directionality by computing the electrostatic potential surface of the halogen atom in the isolated monomer. Based on this, the perpendicular orientation of the XB atom pair (θ = 90°, Figure 3) should be highly disfavored because of the electrostatic repulsion occurring between the negative charge density of the acceptor and the negative belt on the halogen. This model follows the classical chemical interpretation of repulsion occurring when strongly electronegative atoms approach each other. However, DFT calculations on perpendicular geometries, performed by Huber et al. in 2013,16 provided results that are highly inconsistent with this conclusion.
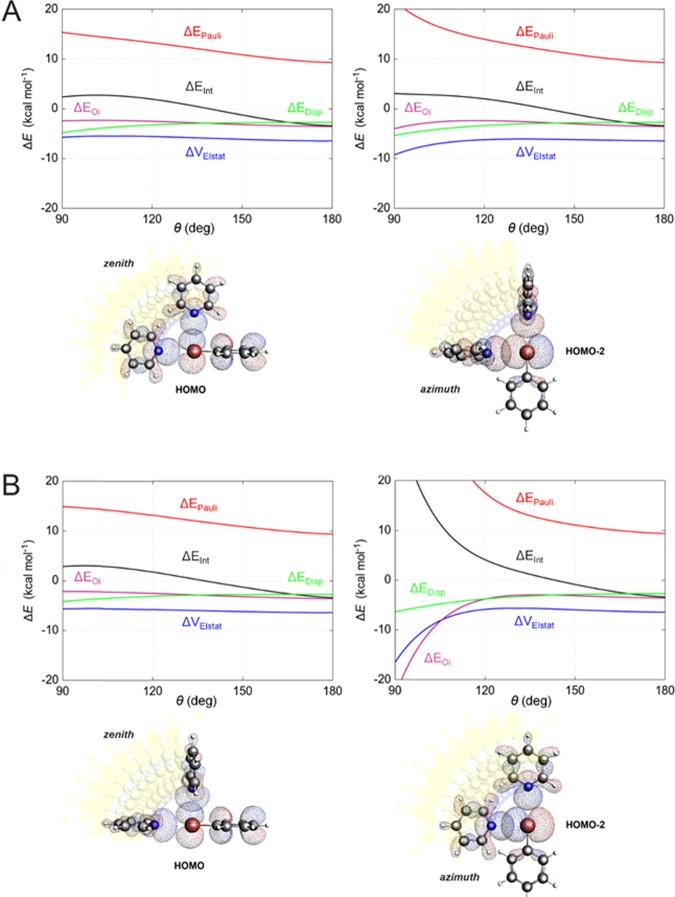
To understand the directionality of XBs for medicinal chemistry, the pyridine–bromobenzene complex model was used. Pyridine Lewis base is not a natural protein component, but its electron LP is highly directional and lies on the same plane of the bromine atom, making pyridine suitable for the specific correlation between stability and directionality. The geometry of the complex was reoptimized by starting from two possible orientations of the pyridine plane with respect to the phenyl ring, namely, transverse and coplanar (Figure 11, panels A and B). The θ angles, corresponding to the minimum energy structures of the two constrained optimizations, were almost linear (178.2 and 179.3° respectively), and the bond lengths were 2.986 and 2.983 Å. The transverse and coplanar optimized structures differed in energy only by 0.05 kcal mol–1, validating the usage of both in the subsequent step. For each structure, we performed single-point energy calculations and energy decomposition analysis, as a function of the zenith and azimuthal angle θ, ranging from 180 to 90° in 10 steps (coordinates in SI 7). As expected, ΔEInt is unfavorable for θ ∼ 90–140°, independently of the case considered. The azimuth angle variation leads to more destabilization than the zenith angle. ΔEDisp is linearly more favorable in any condition. ΔVElstat and ΔEOi are almost constant for the zenith angle, while they even become more stabilizing for the azimuth angle variation. In any case, the complex is highly destabilized in the perpendicular orientations (Figure 11) because ΔEPauli increases, reaching the highest contribution for the coplanar/azimuth θ angle complex combination. Why does Pauli repulsion increase? As shown in Figure 11, depending on the angle considered, a different HOMO of the bromobenzene overlaps with the HOMO of pyridine. Such orbitals are the HOMO and HOMO – 2, for the zenith and azimuthal angle, respectively. In general, for the most stable geometries, the HOMOs of the donor and acceptor do not overlap significantly and ΔEInt is favorable. Independently of the case considered, in fact, for θ = 180°, S2 is always less than 10–5 (SI 7, pages 54-63-72-82). However, when θ decreases, the overlap becomes greater by several orders of magnitude compared to the initial state. Specifically, for θ = 90°, S2 is always larger than 10–3. The big HOMO–HOMO overlap causes strong Pauli repulsion and, finally, an unfavorable interaction energy is observed.
Figure 11.
Energy terms and MOs represented as functions of the zenith/azimuth θ angle between N, Br, and aromatic C, computed at the BLYP-D3(BJ)/TZ2P level of theory (A, transverse orientation; B, coplanar orientation).
As mentioned above, regarding the azimuth angle in Figure 11, the electrostatic interactions and orbital interactions are more stabilizing at perpendicular geometries than at the linear ideal ones. Indeed, this result is in total contrast with the σ-hole model—which, conversely, predicts destabilizing electrostatics for perpendicular XBs—and extremely pronounced for the coplanar complex (Figure 11B), where the orbital interactions are even stronger than electrostatics.
4. Conclusions
In the present study, we have investigated the effect of substituents on peptide halogen-bond (XB) acceptors, by means of the Kohn–Sham molecular orbital (MO) theory and energy decomposition analysis (EDA), giving the basis for more accurate ligand–protein interaction models. We find that peptide methyl and amino building blocks improve the stability of XB complexes by electrostatics, dispersion, and charge transfer from the Lewis base to the halogenated Lewis acid. Conversely, the inclusion of a peptide carbonyl, adjacent to the XB pair, decreases the stability of the XBs. Our results point out the great influence of the protein backbone environment in both the complex geometries and energies. The most used N-methyl-acetamide acceptor model (complex 6), indeed, is not appropriate when describing ligand–peptide XBs. The inclusion of the dihedral angle φ dependence into our analysis provides a deeper understanding of the XB donor–acceptor orientation, by accurately describing the approach of the halogen atom toward the peptide bond plane. Moreover, we have found φ to be highly dependent on the chemical environment, whereas the widely used θ angle shows only little dependence.
We have also compared the stability and geometry of XBs to HBs, as a function of the atom pair distance. Our EDA on donor–acceptor model systems of XBs and HBs reveals that XBs and HBs share the same interaction mechanism, based on the subtle interplay of electrostatics, donor–acceptor orbital interactions, and dispersion, consistent with previous comparative studies. However, it was found that XBs are less stable than HBs, with bond lengths longer than HBs, because of a stronger Pauli repulsion. Our findings demonstrate the need to incorporate quantum effects in molecular modeling approaches for drug design. Finally, the directionality of XBs was thoroughly investigated using a pyridine–bromobenzene model. The zenith and azimuth θ angles were explored in a range between 180 and 90°, starting from either a transverse or a coplanar orientation of the pyridine with respect to the bromobenzene ring. The electrostatic interactions appear to be always more favorable for the perpendicular than for the linear states, in total disagreement with the σ-hole model. Indeed, the only term responsible for the destabilization of the interaction energy is the Pauli repulsion arising from the HOMO–HOMO overlap between the lone pair of the XB acceptor and the π lone pairs of the XB donor. Thus, the directionality of XBs is ascribed to the Pauli repulsion and not to any electrostatic repulsion.
This work has provided an insightful understanding of the halogen bonding mechanism in ligand–peptide systems, by means of an accurate quantum-chemical modeling methodology, comprising all underlying physicochemical factors required within a typical drug design process. Our findings will support the implementation of DFT-based forcefields, aimed at modeling even large ligand–protein systems more accurately. Indeed, the proposed strategy is highly suitable to the context of molecular docking, molecular dynamics, and all of those computational methods by which the correct prediction or rationalization of ligand binding states can make the difference to the identification of new powerful therapeutic candidates.
Acknowledgments
We thank Cedric Koolen, M.Sc. and Joep Wals, B.Sc. for their contribution to this work. Furthermore, we thank Daniela Rodrigues Silva, M.Sc. and Dr. Tanja Sergeieva for their insightful discussions. We thank the Netherlands Organization for Scientific Research (NWO) for financial support and L.d.A.S. for the scholarship from the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES Grant 88881.190191/2018-01). G.P. would like to acknowledge financial support from the Hungarian Scientific Research Fund (OTKA) K111862.
Glossary
Abbreviations
- Asn
asparagine
- CT
charge transfer
- EDA
energy decomposition analysis
- Gln
glutamine
- HB
hydrogen bond
- KS
Kohn–Sham
- LP
lone pair
- MO
molecular orbital
- STO
Slater-type orbital
- VDD
Voronoi deformation density
- XB
halogen bond
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.9b00946.
Cartesian coordinates of optimized monomers; cartesian coordinates of optimized complexes; basis superposition errors (BSSEs) for optimized complexes; energy decomposition analysis of XB complexes; intramolecular and intermolecular hydrogen bonds; cartesian coordinates of constrained complexes; cartesian coordinates of constrained angle complexes (PDF)
Author Contributions
All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Desiraju G. R.; Ho P. S.; Kloo L.; Legon A. C.; Marquardt R.; Metrangolo P.; Politzer P.; Resnati G.; Rissanen K. Definition of the Halogen Bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. 10.1351/PAC-REC-12-05-10. [DOI] [Google Scholar]
- Mulliken R. S. Structures of Complexes Formed by Halogen Molecules with Aromatic and with Oxygenated Solvents1. J. Am. Chem. Soc. 1950, 72, 600–608. 10.1021/ja01157a151. [DOI] [Google Scholar]
- Mulliken R. S. Molecular Compounds and Their Spectra. III. The Interaction of Electron Donors and Acceptors. J. Phys. Chem. A 1952, 56, 801–822. 10.1021/j150499a001. [DOI] [Google Scholar]
- Hassel O. Structural Aspects of Interatomic Charge-Transfer Bonding. Nobel Lect. Chem. 1970, 1963–1970, 314–329. 10.1126/science.170.3957.497. [DOI] [PubMed] [Google Scholar]
- Clark T.; Hennemann M.; Murray J. S.; Politzer P. Halogen Bonding: The σ-Hole. J. Mol. Model. 2007, 13, 291–296. 10.1007/s00894-006-0130-2. [DOI] [PubMed] [Google Scholar]
- Perlstein J. The Weak Hydrogen Bond In Structural Chemistry and Biology (International Union of Crystallography, Monographs on Crystallography, 9) By Gautam R. Desiraju (University of Hyderabad) and Thomas Steiner (Freie Universität Berlin). Oxford University Press: Oxford and New York. 1999. ISBN 0-19-850252-4. J. Am. Chem. Soc. 2001, 123, 191–192. 10.1021/ja0047368. [DOI] [Google Scholar]
- Isaacs E. D.; Shukla A.; Platzman P. M.; Hamann D. R.; Barbiellini B.; Tulk C. A. Covalency of the Hydrogen Bond in Ice: A Direct X-Ray Measurement. Phys. Rev. Lett. 1999, 82, 600–603. 10.1103/PhysRevLett.82.600. [DOI] [Google Scholar]
- van der Lubbe S. C. C.; Fonseca Guerra C. Hydrogen-Bond Strength of CC and GG Pairs Determined by Steric Repulsion: Electrostatics and Charge Transfer Overruled. Chem. - Eur. J. 2017, 23, 10249–10253. 10.1002/chem.201701821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Lubbe S. C. C.; Fonseca Guerra C. The Nature of Hydrogen Bonds: A Delineation of the Role of Different Energy Components on Hydrogen Bond Strengths and Lengths. Chem. - Asian J. 2019, 14, 2760–2769. 10.1002/asia.201900717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang C.; Danovich D.; Mo Y.; Shaik S. On The Nature of the Halogen Bond. J. Chem. Theory Comput. 2014, 10, 3726–3737. 10.1021/ct500422t. [DOI] [PubMed] [Google Scholar]
- Wolters L. P.; Bickelhaupt F. M. Halogen Bonding versus Hydrogen Bonding: A Molecular Orbital Perspective. ChemistryOpen 2012, 1, 96–105. 10.1002/open.201100015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grabowski S. J. Hydrogen and Halogen Bonds Are Ruled by the Same Mechanisms. Phys. Chem. Chem. Phys. 2013, 15, 7249–7259. 10.1039/c3cp50537e. [DOI] [PubMed] [Google Scholar]
- Mitoraj M. P.; Michalak A. Theoretical Description of Halogen Bonding – an Insight Based on the Natural Orbitals for Chemical Valence Combined with the Extended-Transition-State Method (ETS-NOCV). J. Mol. Model. 2013, 19, 4681–4688. 10.1007/s00894-012-1474-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stone A. J. Are Halogen Bonded Structures Electrostatically Driven?. J. Am. Chem. Soc. 2013, 135, 7005–7009. 10.1021/ja401420w. [DOI] [PubMed] [Google Scholar]
- Thirman J.; Engelage E.; Huber S. M.; Head-Gordon M. Characterizing the Interplay of Pauli Repulsion, Electrostatics, Dispersion and Charge Transfer in Halogen Bonding with Energy Decomposition Analysis. Phys. Chem. Chem. Phys. 2018, 20, 905–915. 10.1039/C7CP06959F. [DOI] [PubMed] [Google Scholar]
- Huber S. M.; Scanlon J. D.; Jimenez-Izal E.; Ugalde J. M.; Infante I. On the Directionality of Halogen Bonding. Phys. Chem. Chem. Phys. 2013, 15, 10350 10.1039/c3cp50892g. [DOI] [PubMed] [Google Scholar]
- Santos L. A.; da Cunha E. F. F.; Ramalho T. C. Toward the Classical Description of Halogen Bonds: A Quantum Based Generalized Empirical Potential for Fluorine, Chlorine, and Bromine. J. Phys. Chem. A 2017, 121, 2442–2451. 10.1021/acs.jpca.6b13112. [DOI] [PubMed] [Google Scholar]
- Halogen Bonding I: Impact on Materials Chemistry and Life Sciences; Metrangolo P.; Resnati G., Eds.; Topics in Current Chemistry; Springer International Publishing, 2015. [Google Scholar]
- Cavallo G.; Metrangolo P.; Milani R.; Pilati T.; Priimagi A.; Resnati G.; Terraneo G. The Halogen Bond. Chem. Rev. 2016, 116, 2478–2601. 10.1021/acs.chemrev.5b00484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jedwabny W.; Dyguda-Kazimierowicz E. Revisiting the Halogen Bonding between Phosphodiesterase Type 5 and Its Inhibitors. J. Mol. Model. 2019, 25, 29 10.1007/s00894-018-3897-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward R. A.; Colclough N.; Challinor M.; Debreczeni J. E.; Eckersley K.; Fairley G.; Feron L.; Flemington V.; Graham M. A.; Greenwood R.; Hopcroft P.; Howard T. D.; James M.; Jones C. D.; Jones C. R.; Renshaw J.; Roberts K.; Snow L.; Tonge M.; Yeung K. Structure-Guided Design of Highly Selective and Potent Covalent Inhibitors of ERK1/2. J. Med. Chem. 2015, 58, 4790–4801. 10.1021/acs.jmedchem.5b00466. [DOI] [PubMed] [Google Scholar]
- Sandler B.; Webb P.; Apriletti J. W.; Huber B. R.; Togashi M.; Lima S. T. C.; Juric S.; Nilsson S.; Wagner R.; Fletterick R. J.; Baxter J. D. Thyroxine-Thyroid Hormone Receptor Interactions. J. Biol. Chem. 2004, 279, 55801–55808. 10.1074/jbc.M410124200. [DOI] [PubMed] [Google Scholar]
- Scholfield M. R.; Zanden C. M. V.; Carter M.; Ho P. S. Halogen Bonding (X-Bonding): A Biological Perspective: Halogen Bonding (X-Bonding). Protein Sci. 2013, 22, 139–152. 10.1002/pro.2201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ford M. C.; Ho P. S. Computational Tools To Model Halogen Bonds in Medicinal Chemistry. J. Med. Chem. 2016, 59, 1655–1670. 10.1021/acs.jmedchem.5b00997. [DOI] [PubMed] [Google Scholar]
- Wilcken R.; Zimmermann M. O.; Lange A.; Joerger A. C.; Boeckler F. M. Principles and Applications of Halogen Bonding in Medicinal Chemistry and Chemical Biology. J. Med. Chem. 2013, 56, 1363–1388. 10.1021/jm3012068. [DOI] [PubMed] [Google Scholar]
- Wilcken R.; Zimmermann M. O.; Lange A.; Zahn S.; Boeckler F. M. Using Halogen Bonds to Address the Protein Backbone: A Systematic Evaluation. J. Comput.-Aided Mol. Des. 2012, 26, 935–945. 10.1007/s10822-012-9592-8. [DOI] [PubMed] [Google Scholar]
- Auffinger P.; Hays F. A.; Westhof E.; Ho P. S. Halogen Bonds in Biological Molecules. Proc. Natl. Acad. Sci. U.S.A. 2004, 101, 16789–16794. 10.1073/pnas.0407607101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sirimulla S.; Bailey J. B.; Vegesna R.; Narayan M. Halogen Interactions in Protein–Ligand Complexes: Implications of Halogen Bonding for Rational Drug Design. J. Chem. Inf. Model. 2013, 53, 2781–2791. 10.1021/ci400257k. [DOI] [PubMed] [Google Scholar]
- Berman H. M.; Westbrook J.; Feng Z.; Gilliland G.; Bhat T. N.; Weissig H.; Shindyalov I. N.; Bourne P. E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. 10.1093/nar/28.1.235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- te Velde G.; Bickelhaupt F. M.; Baerends E. J.; Fonseca Guerra C.; van Gisbergen S. J. A.; Snijders J. G.; Ziegler T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. 10.1002/jcc.1056. [DOI] [Google Scholar]
- Fonseca Guerra C.; Snijders J. G.; te Velde G.; Baerends E. J. Towards an Order- N DFT Method. Theor. Chem. Acc. 1998, 99, 391–403. 10.1007/s002140050353. [DOI] [Google Scholar]
- Amsterdam Modeling Suite Making Computational Chemistry Work. https://www.scm.com/ (accessed Oct 04, 2019).
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Becke A. D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Snijders J. G.; Vernooijs P.; Baerends E. J. Roothaan-Hartree-Fock-Slater Atomic Wave Functions. At. Data Nucl. Data Tables 1981, 26, 483–509. 10.1016/0092-640X(81)90004-8. [DOI] [Google Scholar]
- Brauer B.; Kesharwani M. K.; Kozuch S.; Martin J. M. L. The S66x8 Benchmark for Noncovalent Interactions Revisited: Explicitly Correlated Ab Initio Methods and Density Functional Theory. Phys. Chem. Chem. Phys. 2016, 18, 20905–20925. 10.1039/C6CP00688D. [DOI] [PubMed] [Google Scholar]
- van der Wijst T.; Lippert B.; Swart M.; Fonseca Guerra C.; Bickelhaupt F. M. Differential Stabilization of Adenine Quartets by Anions and Cations. J. Biol. Inorg. Chem. 2010, 15, 387–397. 10.1007/s00775-009-0611-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- gnuplot. https://gnuplot.sourceforge.net/ (accessed Apr 11, 2019).
- Sun X.; Soini T. M.; Poater J.; Hamlin T. A.; Bickelhaupt F. M. PyFrag 2019—Automating the Exploration and Analysis of Reaction Mechanisms. J. Comput. Chem. 2019, 40, 2227–2233. 10.1002/jcc.25871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MarvinSketch. https://docs.chemaxon.com/display/docs/MarvinSketch (accessed Apr 11, 2019).
- PerkinElmer | For The Better. https://www.perkinelmer.com/it/ (accessed Apr 11, 2019).
- Ziegler T.; Rauk A. On the Calculation of Bonding Energies by the Hartree Fock Slater Method. Theor. Chim. Acta 1977, 46, 1–10. 10.1007/BF02401406. [DOI] [Google Scholar]
- Bickelhaupt F. M.; Baerends E. J.. Kohn-Sham Density Functional Theory: Predicting and Understanding Chemistry. In Reviews in Computational Chemistry; John Wiley & Sons, Ltd, 2007; pp 1–86. [Google Scholar]
- Fonseca Guerra C.; Handgraaf J.-W.; Baerends E. J.; Bickelhaupt F. M. Voronoi Deformation Density (VDD) Charges: Assessment of the Mulliken, Bader, Hirshfeld, Weinhold, and VDD Methods for Charge Analysis. J. Comput. Chem. 2004, 25, 189–210. 10.1002/jcc.10351. [DOI] [PubMed] [Google Scholar]
- Voth A. R.; Khuu P.; Oishi K.; Ho P. S. Halogen Bonds as Orthogonal Molecular Interactions to Hydrogen Bonds. Nat. Chem. 2009, 1, 74–79. 10.1038/nchem.112. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.