A model for epidemic dynamics in a community with visitor subpopulation

Highlights

• •With a model consisting of SIR and SIS models, we affirm claims in previous works.
• •We derive different basic reproduction numbers looking at varying perspectives.
• •We discuss the biological meanings of these basic reproduction numbers.
• •All the basic reproduction numbers coincide with respect to the critical condition.
• •Relevant public health policies are proposed based on our findings.

Abstract

With a five dimensional system of ordinary differential equations based on the SIR and SIS models, we consider the dynamics of epidemics in a community which consists of residents and short-stay visitors. Taking different viewpoints to consider public health policies to control the disease, we derive different basic reproduction numbers and clarify their common/different mathematical natures so as to understand their meanings in the dynamics of the epidemic. From our analyses, the short-stay visitor subpopulation could become significant in determining the fate of diseases in the community. Furthermore, our arguments demonstrate that it is necessary to choose one variant of basic reproduction number in order to formulate appropriate public health policies.

1. Introduction

As the world becomes more of a global village with advances in technology and easier accessibility to different places, it is very crucial to consider side effects like the spread of diseases. The history of man is replete with stories of epidemics invading groups of people, sometimes resulting in mortality. In the long run, such diseases can disappear and recur in the future or become less deadly due to people getting immune. Some notable epidemics in history include the “Spanish” flu (1918–1919) as well as the Black Deaths (1346–1350) which invaded Europe from Asia and recurred for three decades afterwards before getting eliminated (Brauer, 2017).

It is a well established fact that ‘globetrotters’ contribute significantly to the global movement of microbes as they serve as a crucial sentinel population. The displacement of people due to social and political unrest as well as the natural migration of disease vectors to new areas also contribute to the worldwide spread of diseases (Wilson, 2010, WHO, 2018).

Infectious diseases do not respect border restrictions as their spread is magnified by rapid urbanization, globalization of trade and travels as well as unpredictable climate change and complexities in societal behavior (MacIntyre et al., 2016; Walters et al., 2018). All of these factors have practically removed the barriers which prevent epidemic transmission among humans and between humans and animals (Farrar et al., 2016).

In the work presented by Parikh et al. (2013), a synthetic population model of the Washington DC metro area was extended to include leisure and business travelers classified as transients. The final size of the epidemic among residents was found to be remarkably higher when transients were included in the simulation of a flu-like disease outbreak. According to Chowell et al. (2016), it is crucial to formulate reliable models that embody the basic transmission characteristics of specific pathogens and social scenarios. They further stated that improved models are required to capture the variation in early growth dynamics of real epidemics in order to gain better understanding of the dynamics as they reviewed trends in modeling and classifying early epidemic progression.

In considering the emerging diseases of wildlife, Tompkins et al. (2015) show that the key drivers of such diseases are agents from domestic sources and human-assisted exposure to infectious agents from wild populations. Talking about swine fever otherwise known as hog cholera, wild boar populations are known to serve as reservoir for the disease thereby constituting a great challenge for domestic pig farmers, veterinarians and other stakeholders (Mur, Sánchez-Vizcaíno, Fernández-Carrión, Jurado, Rolesu, Feliziani, Laddomada, Martínez-López, 2018, Postel, Austermann-Busch, Petrov, Moennig, Becher, 2018). It then becomes a daunting public health challenge to prevent contacts between wild boar and local pig populations.

Epidemiologists are always concerned about the outbreak of diseases and increasing global travels can easily increase their worries. For instance, as of March 2015, Japan was confirmed to be totally free of measles. However, that status changed when a new wave of measles infections was reportedly started by a tourist in Okinawa Prefecture in March 2018 (Mizumoto, Kobayashi, Chowell, 2018, Diseases, 2018). The threat of measles is a serious one because it has about the highest basic reproduction number R ₀ among the most commonly known infectious diseases (van den Driessche, 2017). It has been established that R ₀ is a very vital threshold parameter that theoretically determines whether a disease is eliminated or becomes endemic after it is introduced into a given population. In fact, it is widely believed to be one of the most important contributions of mathematics to the field of epidemiology (Diekmann, Heesterbeek, Roberts, 2010, Heffernan, Smith, Wahl, 2005, van den Driessche, Watmough, 2002). Heffernan et al. (2005) gave a concise summary of prevalent approaches for formulating R ₀ from deterministic models as well as relevant data. They also looked closely at the use of R ₀ in evaluating diseases like severe acute respiratory syndrome (SARS) and avian influenza as well as some livestock and vector-borne diseases. van den Driessche (2017) applied the theoretical concepts of R ₀ to various disease models, namely the West Nile virus in birds, anthrax in animals, cholera and Zika in humans.

Basically, R ₀ is concerned with the initial trend of infective populations in ideal situations where very small number of infective individuals appear and are always surrounded by susceptible individuals. Before such infectives lose their infectivity, the density of susceptibles is assumed to be unchanged. In such a biological context, the basic reproduction number is defined as the expected number of new cases of an infection caused by an infected individual, in a population consisting of susceptible contacts only.

Following this biological definition, a mathematical theory is used to derive the basic reproduction number as the spectral radius of a specific matrix which is called the ”next generation matrix” (NGM) for a system of ordinary differential equations governing epidemic dynamics (see Cushing, Diekmann, 2016, Diekmann, Heesterbeek, Britton, 2013 for a complete reference, or see van den Driessche, 2017 for a recent review). In the frequently referred paper by van den Driessche and Watmough (2002), very helpful results were obtained for disease control having investigated the actual definition of R ₀ based on a compartmental system of ordinary differential equations. Diekmann et al. (2010) highlighted the NGM as the foundation for the mathematical definition of R ₀. As such, their work attempted to demystify issues surrounding the formulation of NGMs since R ₀s are basically defined as the spectral radii of such matrices. We should recognize that, as described above, the basic reproduction number is defined both biologically/conceptually and mathematically as the supremum for the expected number of secondary cases in epidemic dynamics, whereas it is clear that the index R ₀ could be important and useful to characterize the threat of infectious diseases.

In this paper, we emphasize the role of R ₀ from some specific viewpoints in theoretical discussions. We examine R ₀ focused on (i) transmission of disease within and to the resident population and (ii) transmission of disease within and to the short-stay visitor population. Such residents and visitors may be considered to be either humans or animals as a variety of situations can be considered. The R ₀ focused on residents can be considered as the most standard case as it may be a bit difficult to really estimate the impact of short-stay visitors in the spread of diseases. The R ₀ focused on short-stay visitors is very important when the residents are considered as some vectors in the community which can easily spread diseases to visitors. That way, we can make inferences by combining different R ₀s. Besides we shall demonstrate that R ₀ only deals with the initial behavior of infections because the overall behavior is governed by the model under consideration.

2. Assumptions, modeling, and model

We consider a community consisting of residents and short-stay visitors. Our focus is on the dynamics of epidemics over a short period of time such that the total population size of the community is taken to be constant, ignoring any change due to birth and death within the period of interest. Also, the resident and visitor populations are respectively constant. We assume that all immigrating visitors are susceptible and likely to be infected during their stay in the community. In addition, infected visitors can carry on their normal activities during their stay thus still appearing susceptible until they leave the community.

Following the stated assumptions, we consider the following model governing the epidemic dynamics:

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{x}_r}{dt}}& =& -x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)\hfill \\ \hfill {\displaystyle \frac{d{y}_r}{dt}}& =& x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)-\rho y_r;\hfill \\ \hfill {\displaystyle \frac{d{z}_r}{dt}}& =& \rho y_r;\hfill \\ \hfill {\displaystyle \frac{d{x}_v}{dt}}& =& -x_v({\beta }_{vr}{y}_r+{\beta }_{vv}{y}_v)+M-{\displaystyle \frac{x_v}{x_v+y_v}}E;\hfill \\ \hfill {\displaystyle \frac{d{y}_v}{dt}}& =& x_v({\beta }_{vr}{y}_r+{\beta }_{vv}{y}_v)-{\displaystyle \frac{y_v}{x_v+y_v}}E,\hfill \end{array}$$ (1)

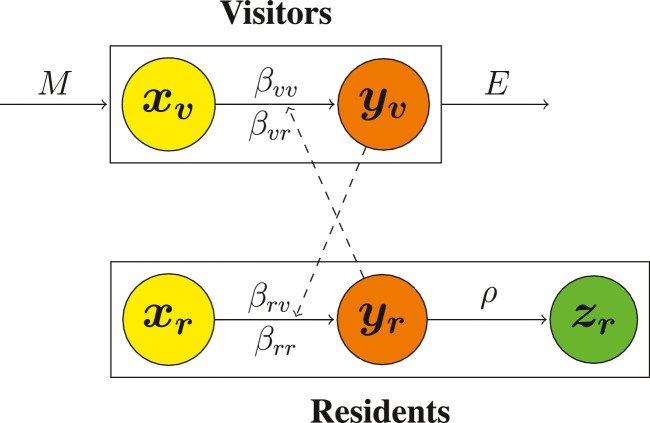
where the variables x_r, y_r, z_r, x_v, and y_v are the susceptible resident, the infective resident, the recovered resident, the susceptible visitor, and the infective visitor population sizes respectively in the community at time t. The infection coefficients β_rr, β_vr, β_rv and β_vv are positive constants. They represent transmissions from infective to susceptible individuals, respectively from resident to resident, from resident to visitor, from visitor to resident, and from visitor to visitoras shown in Fig. 1 .

Fig. 1.

The scheme of the model for the epidemic dynamics of a community with short-stay visitor subpopulation.

Based on the simplest modeling assumption, the interactions among individuals within the community follow the concept of complete (perfect) mixing. Therefore, the disease transmission is given by mass-action terms like in the case of the classical Kermack–Mckendrick epidemic dynamics model (for example, see Diekmann, Heesterbeek, Britton, 2013, Keeling, Rohani, 2008, Martcheva, 2015). ρ is the recovery rate of the resident population. M is the flux (velocity) of visitor immigration, while E is the flux of visitor emigration.

To complete the model, we take the above-mentioned assumptions into account such that

$$x_r\left(t\right)+y_r\left(t\right)+z_r\left(t\right)=N_r;x_v\left(t\right)+y_v\left(t\right)=N_v,$$

where the total resident population size N_r and the total visitor population size N_v are constant independent of time. Hence, from the equations for the x_v, y_v compartments of the model, we get

$${\displaystyle \frac{d{x}_v}{dt}}+{\displaystyle \frac{d{y}_v}{dt}}=M-E=0.$$

With these relations from the assumptions of constant subpopulation sizes, we can get the following closed three-dimensional system in terms of (x_r, y_r, y_v):

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d{x}_r}{dt}}& =& -x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v);\hfill \\ \hfill {\displaystyle \frac{d{y}_r}{dt}}& =& x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)-\rho y_r;\hfill \\ \hfill {\displaystyle \frac{d{y}_v}{dt}}& =& (N_v-y_v)({\beta }_{vr}{y}_r+{\beta }_{vv}{y}_v)-{\displaystyle \frac{M}{N_v}}{y}_v.\hfill \end{array}$$ (2)

3. The dynamics without cross infection

3.1. The resident subpopulation

If there is no cross infection such that ${\beta }_{vr}=0$ and ${\beta }_{rv}=0$ in the system (1), the epidemic dynamics with respect to the resident subpopulation follows the classical Kermack–Mckendrick SIR model (see Diekmann, Heesterbeek, Britton, 2013, Keeling, Rohani, 2008, Martcheva, 2015 or any other textbooks of mathematical biology/epidemiology). Going by the well-known nature of the SIR model, we see that $(x_r,y_r,z_r)\to (x_r^{*},0,N_r-x_r^{*})$ with some $x_r^{*}>0$ as t → ∞ for the initial condition given by $(x_{r0},y_{r0},z_{r0})=(N_r-y_{r0},y_{r0},0)$ with y _r0 > 0. The final size of the epidemic, that is, $N_r-x_r^{*}$ ( > 0) is implicitly determined by

$$N_r-x_r^{*}=\frac{\rho }{{\beta }_{rr}}\ln {\displaystyle \frac{x_{r0}}{x_r^{*}}}.$$ (3)

The basic reproduction number can be defined by

$${\mathcal{R}}_{rr}=\frac{{\beta }_{rr}{N}_r}{\rho },$$ (4)

which is expressed by the product of the expected duration of infectivity of each infective resident 1/ρ, the resident-resident transmission coefficient β_rr, and the resident subpopulation size N_r. When ${\mathcal{R}}_{rr}\le 1,$ the infective population size y_r decreases monotonically towards 0. When ${\mathcal{R}}_{rr}>1,$ the temporal variation of y_r shows a peak signifying an outbreak after a period of increase from a sufficiently small initial value $y_r\left(0\right)=y_{r0}>0$.

3.2. The visitor subpopulation

The visitor population without cross infection mathematically corresponds with the classical Kermack–Mckendrick SIS model. Now, let us consider such an initial condition that 0 < y_v(0) ≪ 1 and x_v(0) ≈ N_v. Then, for dy_v/dt in (2),

$${\frac{d{y}_v}{dt}|}_{t=0}\approx ({\beta }_{vv}{N}_v-\frac{M}{N_v})y_v.$$

Thus, when the right hand side is positive, that is, if $\left({\beta }_{vv}{N}_v^2\right)/M>1,$ the infective population size y_v increases in an initial period. So we can obtain the basic reproduction number

$${\mathcal{R}}_{vv}=\frac{{\beta }_{vv}{N}_v^2}{M},$$ (5)

which appears as the product of the expected duration of each visitor’s stay in the community N_v/M, the visitor-visitor transmission coefficient β_vv, and the visitor subpopulation size N_v. If ${\mathcal{R}}_{vv}<1,$ the infective population size decreases in an initial period. Furthermore, from (2), we can get

$$\frac{d{y}_v}{dt}={\beta }_{vv}{y}_v\left\{N_v\right(1-\frac{1}{{\mathcal{R}}_{vv}})-y_v\}$$ (6)

such that if ${\mathcal{R}}_{vv}\le 1,$ dy_v/dt < 0 for any t > 0. So, y_v is monotonically decreasing if ${\mathcal{R}}_{vv}\le 1$ such that y_v → 0 as t → ∞. Otherwise, if ${\mathcal{R}}_{vv}>1,$ $y_v\to y_v^{*}=N_v(1-1/{\mathcal{R}}_{vv})>0$ as t → ∞.

When ${\mathcal{R}}_{vv}\le 1,$ the disease is eventually eliminated from the visitor population due to the outflow of infective visitors which outweighs the inflow of susceptible visitors. In contrast, when ${\mathcal{R}}_{vv}>1,$ the disease becomes endemic, that is, the disease remains at any given time after its invasion in the population. In other words, the recruitment of infective visitors from the inflow of susceptible visitors compensates for the outflow of infective visitors.

Since the disease is endemic in the visitor subpopulation when ${\mathcal{R}}_{vv}>1,$ it eventually disperses throughout the resident subpopulation when there is cross infection from visitors to residents, that is, when β_rv > 0. Even if ${\mathcal{R}}_{rr}\le 1,$ cross infections with β_vr > 0 and β_rv > 0 cause disease outbreak within the resident subpopulation when ${\mathcal{R}}_{vv}>1$. In other words, when there are cross infections, disease outbreak necessarily occurs within the resident subpopulation as far as ${\mathcal{R}}_{vv}>1$. Consequently, if ${\mathcal{R}}_{rr}>1$ or ${\mathcal{R}}_{vv}>1,$ disease outbreak occurs in the resident subpopulation in the presence of cross infections, that is, when β_vr > 0 and β_rv > 0. Hereafter, with the effect of cross infection, we shall focus on the case when ${\mathcal{R}}_{rr}<1$ and ${\mathcal{R}}_{vv}<1$.

4. Equilibrium states

There is no oscillatory solution for the system (2). It is easily seen that y_r and y_v are positive and finite at any finite time t for any y_r(0) > 0 and y_v(0) > 0. Since dx_r/dt < 0 for any positive x_r, y_r, and y_v, x_r is monotonically decreasing in time though it cannot become negative because it is bounded below by zero. Thus x_r(t) > 0 for any t > 0 and any x_r(0) > 0. If y_r(0) > 0 and y_v(0) > 0, indeed we have

$$\frac{1}{x_r}{\displaystyle \frac{d{x}_r}{dt}}=-({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)$$

and

$$x_r\left(t\right)=x_r\left(0\right)\exp [-{\int }_0^t{\beta }_{rr}{y}_r\left(T\right)+{\beta }_{rv}{y}_v\left(T\right)dT].$$

So, x_r must always converge to a non-negative value. Hence, it can be easily proven that both of y_r and y_v also converge to non-negative values. Therefore, (x_r, y_r, y_v) always attains some kind of equilibrium state, which excludes the possibility of oscillatory solutions.

From the equations in (2), we can obtain the following result:

Lemma 4.1

For the system (2) , there are possible equilibria $(x_r^{*},0,0)$ for $x_r^{*}\ge 0$ and $(0,0,N_v(1-1/{\mathcal{R}}_{vv}))$ . The latter equilibrium exists when and only when ${\mathcal{R}}_{vv}>1$ .

Next, by the arguments given in Appendix A, we can get the following result about feasible equilibrium values for (2):

Theorem 4.2

For the system (2) ,

• 1. y_r → 0 as t → ∞;
• 2. $(x_r,y_r,y_v)\to (x_r^{*},0,0)$ with $x_r^{*}\ge 0$ as t → ∞ if ${\mathcal{R}}_{vv}\le 1$ ;
• 3. $(x_r,y_r,y_v)\to (0,0,N_v(1-\frac{1}{{\mathcal{R}}_{vv}}\left)\right)$ as t → ∞ if ${\mathcal{R}}_{vv}>1$ when β_rv > 0.

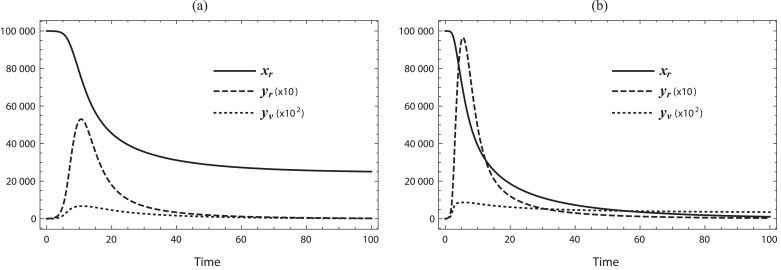
As shown in Fig. 2 (b), if ${\mathcal{R}}_{vv}>1,$ all residents would have experienced the infection in the end while there is always a portion of infective visitors, this gives rise to an endemic situation. On the other hand, as we see in Fig. 2(a), if ${\mathcal{R}}_{vv}<1,$ there is a portion of susceptible residents who would not have experienced the infection in the end. Also, the visitor population would have no infected individuals in the end. Here, the disease disappears from the community in the long run. It should be noted that the value of the basic reproduction number ${\mathcal{R}}_{vv}$ clearly determines the epidemic size for the resident subpopulation.

Fig. 2.

Numerical examples of temporal variation of system (2). (a) $({\mathcal{R}}_{rr},{\mathcal{R}}_{vv},{\mathcal{R}}_{vr},{\mathcal{R}}_{rv})=(0.75,0.50,0.05,32.73)$; (b) $({\mathcal{R}}_{rr},{\mathcal{R}}_{vv},{\mathcal{R}}_{vr},{\mathcal{R}}_{rv})=(0.75,1.50,0.08,56.69)$. Commonly, $N_r=100000.00,N_v=100.00,\rho =0.14,M=20.00,$$(x_r\left(0\right),y_r\left(0\right),y_v\left(0\right))=(99990.0,10.0,0.0)$. ${\mathcal{R}}_{vr}:={\beta }_{vr}{N}_v/\rho ,$${\mathcal{R}}_{rv}:={\beta }_{rv}{N}_r{N}_v/M$.

For the system (2) with cross infections, we could not obtain any equation(s) like (3) to determine the final size of the epidemic. However, we can get the following analytical estimation going by the proof shown in Appendix B:

Theorem 4.3

As for the state $(x_r^{*},0,0)$ feasible for the system (2) when ${\mathcal{R}}_{vv}\le 1,$ the value $x_r^{*}$ necessarily satisfies $x_r^{*}<x_r^{\mathrm{upper}}$ defined by

$$x_r^{\mathrm{upper}}:=(\frac{1}{{\mathcal{R}}_{rr}}+\frac{M}{\rho N_v}\frac{1-{\mathcal{R}}_{vv}}{{\mathcal{R}}_{rr}})N_r.$$ (7)

The value x_r cannot approach any value beyond $x_r^{\mathrm{upper}}$ from any initial state with y_r(0) > 0 or y_v(0) > 0.

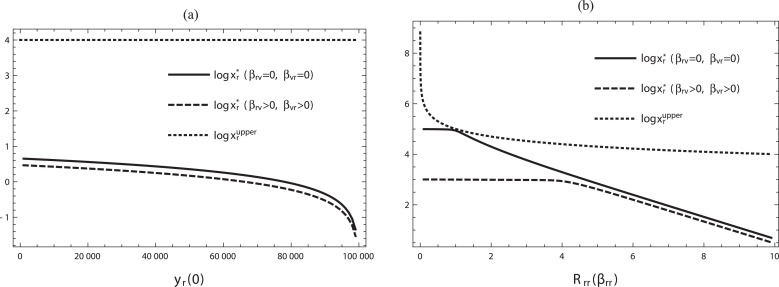
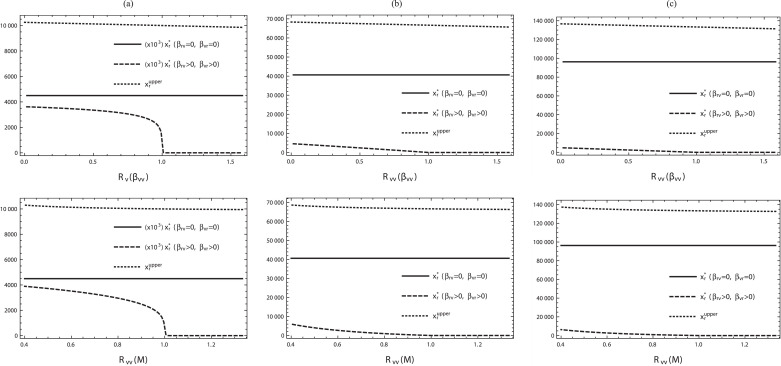
This result can be confirmed by the numerical calculations shown in Figs. 3 and 4 .

Fig. 3.

The dependence of the final size of susceptible resident population $x_r^{*}$ on the initial size of infective resident population y_r(0) and on β_rr. (a) ${\beta }_{rr}=2.0\times {10}^{-5},$${\mathcal{R}}_{rr}=10.0,$$(x_r\left(0\right),y_r\left(0\right),y_v\left(0\right))=(N_r-y_{r0},y_{r0},0.0)$; (b) $(x_r\left(0\right),y_r\left(0\right),y_v\left(0\right))=(99990.0,10.0,0.0)$. The horizontal axis in (b) shows the value of ${\mathcal{R}}_{rr}$ which is a function of β_rr as given by (4). Commonly, $N_r=100000.0,$$N_v=100.0,$$\rho =0.2,$$M=0.5,$${\beta }_{vr}=1.6\times {10}^{-4},$${\beta }_{rv}=1.0\times {10}^{-5},$${\beta }_{vv}=4.0\times {10}^{-5},$${\mathcal{R}}_{vv}=0.8,$${\mathcal{R}}_{vr}=0.08,$${\mathcal{R}}_{rv}=200.0$.

Fig. 4.

The dependence of the final size of susceptible resident population $x_r^{*}$ on β_vv and on M. (a) ${\beta }_{rr}=2.0\times {10}^{-5},$${\mathcal{R}}_{rr}=10.0$; (b) ${\beta }_{rr}=3.0\times {10}^{-6},$${\mathcal{R}}_{rr}=1.50$; (c) ${\beta }_{rr}=1.5\times {10}^{-6},$${\mathcal{R}}_{rr}=0.75$. The horizontal axes show the values of ${\mathcal{R}}_{vv}$ which is a function of β_vv for the upper figures with $M=0.5$ and that of M for the lower ones with ${\beta }_{vv}=4.0\times {10}^{-5}$ as given by (5). Commonly, $N_r=100000.0,$$N_v=100.0,$$\rho =0.2,$${\beta }_{vr}=1.6\times {10}^{-4},$${\beta }_{rv}=1.0\times {10}^{-5},$${\mathcal{R}}_{vr}=0.08,$${\mathcal{R}}_{rv}=200.0,$$(x_r\left(0\right),y_r\left(0\right),y_v\left(0\right))=(99990.0,10.0,0.0)$.

Although the critical value $x_r^{\mathrm{upper}}$ given in Theorem 4.3 is independent of the initial condition of the system (2), the numerical result given in Fig. 3(a) explicitly indicates that the final size $x_r^{*}$ itself depends on the initial condition. This is similar to a characteristic of the standard Kermack–McKendrick SIR model. Also, the numerical results given in Fig. 4 indicates that the final size $x_r^{*}$ is significantly affected by interactions with the visitor subpopulation as mathematically implied by Theorem 4.2.

5. The basic reproduction numbers

We discuss in this section how the different basic reproduction numbers can be mathematically derived for the model (2). Subsequently, going by their meanings from the perspective of modeling, we examine how they are different and what nature they have in common (for such possibly different formulas for basic reproduction number, see the arguments in Brauer, Castillo-Chavez, Mubayi, Towers, 2016, Cushing, Diekmann, 2016, van den Driessche, 2017).

5.1. The basic reproduction numbers in terms of each subpopulation

At first, let us consider a public health policy geared towards controlling the disease among residents. Then, it is necessary to evaluate the basic reproduction number which is defined as the index about the possibility of the disease spread within the resident population. As shown in Appendix C, making use of the NGM with the theory given by van den Driessche and Watmough (2002), van den Driessche et al. (2008), we can derive the following basic reproduction number for the model (2) when ${\mathcal{R}}_{vv}<1$:

$$R_{0\mid r}={\mathcal{R}}_{rr}(1+\frac{{\mathcal{R}}_{vv}}{1-{\mathcal{R}}_{vv}}\mathcal{B})={\mathcal{R}}_{rr}+\frac{{\mathcal{R}}_{rv}{\mathcal{R}}_{vr}}{1-{\mathcal{R}}_{vv}}$$ (8)

with

$$\mathcal{B}=\frac{{\beta }_{rv}{\beta }_{vr}}{{\beta }_{rr}{\beta }_{vv}};{\mathcal{R}}_{vr}=\frac{{\beta }_{vr}{N}_v}{\rho };{\mathcal{R}}_{rv}=\frac{{\beta }_{rv}{N}_v{N}_r}{M},$$

where $\mathcal{B}$ expresses the ratio of the infectivity between residents and visitors (inter-subpopulation infection) to the infectivity within subpopulations (intra-subpopulation infection). Larger $\mathcal{B}$ means that infections between subpopulations are more significant than those within them. ${\mathcal{R}}_{rv}$ can be regarded as the expected number of infective residents that a single infective visitor can produce, assuming that every contact to the resident is always to the susceptible. It appears as the product of the expected duration of each visitor’s stay in the community N_v/M, the visitor-resident transmission coefficient β_rv, and the resident subpopulation size N_r. Conversely, the expected number of infective visitors that a single infective resident can produce, assuming every contact to the visitor is always to the susceptible, is ${\mathcal{R}}_{vr}$ which is expressed by the product of the expected duration of the infectivity of each infective resident 1/ρ, the resident-visitor transmission coefficient β_vr, and the visitor subpopulation size N_v.

The basic reproduction number R _0∣r can be translated based on its conceptual definition as similarly argued in (Cushing and Diekmann, 2016): The formula (8) can be rewritten as

$$R_{0\mid r}={\mathcal{R}}_{rr}+{\mathcal{R}}_{rv}\sum _{k=0}^{\infty }{\mathcal{R}}_{vv}^k{\mathcal{R}}_{vr}\text{for}{\mathcal{R}}_{vv}<1.$$

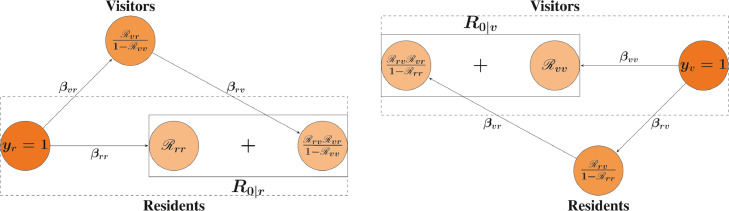
As illustrated in Fig. 5 , the first term ${\mathcal{R}}_{rr}$ means the expected number of secondary infective residents produced by the initial single infective resident, which may be regarded as the secondary cases arising from direct infection. In contrast, the second term adds the expected number of secondary infective residents produced by the infective visitors who can be regarded to have the source of their infection traced back only along the line of infective visitors to the initial single infective resident. From the biological definitions of ${\mathcal{R}}_{vr},$ ${\mathcal{R}}_{vv},$ and ${\mathcal{R}}_{rv},$ the initial single infective resident is expected to produce ${\mathcal{R}}_{vr}$ infective visitors, and subsequently each of these infective visitors is expected to produce ${\mathcal{R}}_{vv}$ infective visitors. Looking at the furtherance of the infection process only within the visitor subpopulation caused by the initial single infective resident, the simple addition of those new infective visitors produced by the cascade of infections results in ${\mathcal{R}}_{vr}+{\mathcal{R}}_{vv}{\mathcal{R}}_{vr}+{\mathcal{R}}_{vv}^2{\mathcal{R}}_{vr}+\cdots$. Then since ${\mathcal{R}}_{rv}$ is the expected number of infective residents produced by a single infective visitor, we see that the product of ${\mathcal{R}}_{rv}$ and this sum can be consequently regarded as the expected number of secondary infective residents produced by the infective visitors who can have the root of their infection traced back to the initial single infective resident.

Fig. 5.

Decomposition of the basic reproduction numbers R_0∣r and R_0∣v defined by (8) and (9).

We remark that ${\mathcal{R}}_{0\mid r}\to \infty$ as ${\mathcal{R}}_{vv}$ increases towards 1. This could be regarded as reasonable because we have clarified in the previous sections that the whole resident subpopulation is necessarily infected if ${\mathcal{R}}_{vv}>1$. Indeed, applying this translation about the meaning of the formula (8) for the case when ${\mathcal{R}}_{vv}\ge 1,$ the basic reproduction number would be divergent due to the divergence of the sum ${\mathcal{R}}_{vr}+{\mathcal{R}}_{vv}{\mathcal{R}}_{vr}+{\mathcal{R}}_{vv}^2{\mathcal{R}}_{vr}+\cdots$. It should be remarked that such divergence of the basic reproduction number does not mean that the actual basic reproduction number would be divergent. It simply means that the supremum for the expected number of secondary cases in the epidemic dynamics does not exist, so that the situation could be regarded as highly threatening as the disease spreads in the resident subpopulation. This is the same for the situation with ${\mathcal{R}}_{vv}>1$ as mentioned above.

In contrast, when we consider a public health policy for controlling the disease among visitors, it is necessary to evaluate the basic reproduction number R _0∣v which is defined as the index about the possibility of the disease spread in the visitor population. The process for deriving R _0∣v is similar to that of R _0∣r (Appendix C):

$$R_{0\mid v}={\mathcal{R}}_{vv}(1+\frac{{\mathcal{R}}_{rr}}{1-{\mathcal{R}}_{rr}}\mathcal{B})={\mathcal{R}}_{vv}+\frac{{\mathcal{R}}_{rv}{\mathcal{R}}_{vr}}{1-{\mathcal{R}}_{rr}}={\mathcal{R}}_{vv}+{\mathcal{R}}_{vr}\sum _{k=0}^{\infty }{\mathcal{R}}_{rr}^k{\mathcal{R}}_{rv}\text{for}{\mathcal{R}}_{rr}<1.$$ (9)

A similar translation is applicable for (9) like the one for R _0∣r (see Fig. 5). We remark again that ${\mathcal{R}}_{0\mid v}\to \infty$ as ${\mathcal{R}}_{rr}$ increases towards 1, which can be interpreted as a consequence due to the divergence of the sum ${\mathcal{R}}_{rv}+{\mathcal{R}}_{rr}{\mathcal{R}}_{rv}+{\mathcal{R}}_{rr}^2{\mathcal{R}}_{rv}+\cdots$ for R_rr ≥ 1. This scenario is different from the previous one because the infective residents eventually disappear in the end for R_rr > 1 after every resident is infected and recovers. However, we need to recall that the basic reproduction number is defined as the expected number of secondary cases in the conceptually supremum case for the subsequent infections. Thus, this result can be understood as the case when the basic reproduction number of the resident subpopulation corresponding to ${\mathcal{R}}_{rr}$ is kept beyond 1. As such, the visitor subpopulation is regarded as always being exposed to infective residents by cross infection (which corresponds to the divergence of the above-mentioned sum). This situation could indicate that the threat of disease spread in the visitor subpopulation is enormous.

Note that the basic reproduction numbers R _0∣r and R _0∣v may be specifically called ‘type reproduction numbers’ as in the terminology of (Heesterbeek, Roberts, 2007, Roberts, Heesterbeek, 2003) because we are interested only in the total number of expected secondary infections in each subpopulation originating from an infective individual within the same subpopulation (also see Lewis, Shuai, van den Driessche, 2019, Smith, McKenzie, Snow, Hay, 2007, van den Driessche, 2017, Yakob, Clements, 2013).

5.2. Comparison of the basic reproduction numbers

The basic reproduction numbers R _0∣r and R _0∣v are basically different but have a common critical nature shown in the following theorem:

Theorem 5.1

The condition R _0∣r < 1 holds if and only if R _0∣v < 1.

Therefore the condition R _0∣r > 1 holds if and only if R _0∣v > 1. This theorem can be easily proven by the definitions of R _0∣r and R _0∣v given by (8) and (9). As a special case, we can consider the critical condition $R_{0\mid r}=1$ and $R_{0\mid v}=1,$ which lead to the following corollary:

Corollary 5.1.1

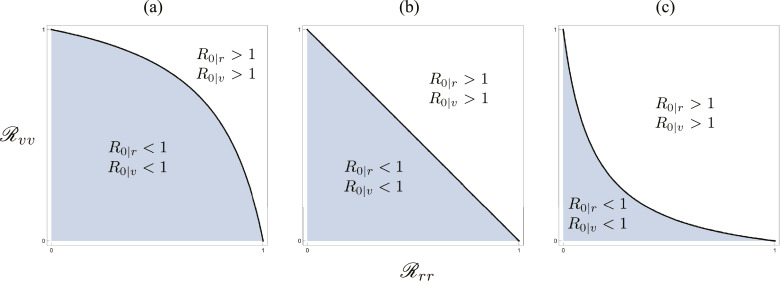
There is a set of values ${\mathcal{R}}_{rr}$ and ${\mathcal{R}}_{vv}$ each less than 1, say $({\mathcal{R}}_{rr},{\mathcal{R}}_{vv})=({\mathcal{R}}_{rr}^{*},{\mathcal{R}}_{vv}^{*}),$ such that $R_{0\mid r}=1$ and $R_{0\mid v}=1$ . The set is defined by

$$({\displaystyle \frac{1}{{\mathcal{R}}_{rr}^{*}}}-1)({\displaystyle \frac{1}{{\mathcal{R}}_{vv}^{*}}}-1)=\mathcal{B}\text{for}{\mathcal{R}}_{rr}<1\text{and}{\mathcal{R}}_{vv}<1.$$

The dependence of R _0∣r and R _0∣v on ${\mathcal{R}}_{rr}$ and ${\mathcal{R}}_{vv}$ is shown in Fig. 6 . It is quite clear from the figure that even if ${\mathcal{R}}_{rr}<1$ and ${\mathcal{R}}_{vv}<1,$ as far as there is cross infection, the basic reproduction number for each subpopulation can become greater than unity simultaneously. Furthermore, Fig. 6 explicitly shows that as the effect of cross infection becomes stronger (i.e., for larger $\mathcal{B}$), the basic reproduction numbers are more likely to become greater than unity.

Fig. 6.

Classification of the region $({\mathcal{R}}_{rr},{\mathcal{R}}_{vv})$ in terms of the values of R_0∣r and R_0∣v. (a) $\mathcal{B}<1$; (b) $\mathcal{B}=1$; (c) $\mathcal{B}>1$. The boundary corresponds to the set of $({\mathcal{R}}_{rr},{\mathcal{R}}_{vv})=({\mathcal{R}}_{rr}^{*},{\mathcal{R}}_{vv}^{*})$ defined in Corollary 5.1.1 with Theorem 5.1.

Now, as derived in Appendix C, we can consider an additional basic reproduction number given by

$$\begin{array}{cc}\hfill R_{0\mid c}& =\frac{{\mathcal{R}}_{rr}+{\mathcal{R}}_{vv}+\sqrt{{({\mathcal{R}}_{rr}+{\mathcal{R}}_{vv})}^2-4{\mathcal{R}}_{rr}{\mathcal{R}}_{vv}(1-\mathcal{B})}}{2}\hfill \\ & =\frac{{\mathcal{R}}_{rr}+{\mathcal{R}}_{vv}+\sqrt{{({\mathcal{R}}_{rr}+{\mathcal{R}}_{vv})}^2+4({\mathcal{R}}_{rv}{\mathcal{R}}_{vr}-{\mathcal{R}}_{rr}{\mathcal{R}}_{vv})}}{2}.\hfill \end{array}$$ (10)

Although this basic reproduction number R _0∣c may be the one formally derived by the NGM for the system (2), the formula (10) could not be translated by the conceptual definition of basic reproduction number as we did for R _0∣r and R _0∣v. Hence, in this paper we use R _0∣c only as a reference index for the other basic reproduction numbers.

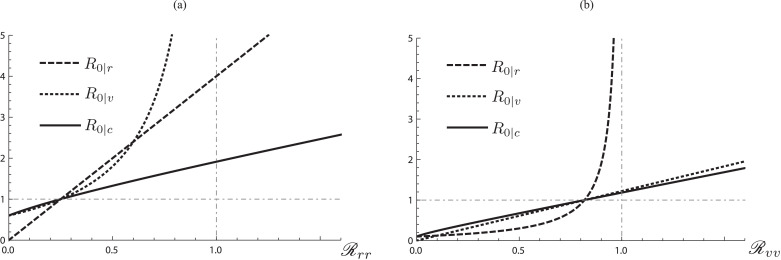
As numerically shown in Fig. 7 , although the three basic reproduction numbers R _0∣r, R _0∣v, and R _0∣c have different values from each other, the critical condition is identical.

Theorem 5.2

The condition R _0∣c < 1 holds if and only if R _0∣r < 1 (i.e., R _0∣v < 1) when ${\mathcal{R}}_{rr}<1$ and ${\mathcal{R}}_{vv}<1$ .

Fig. 7.

Differences in the values of R_0∣r, R_0∣v and R_0∣c given by (8), (9) and (10) with $\mathcal{B}=2.0$. (a) ${\mathcal{R}}_{vv}=0.6$; (b) ${\mathcal{R}}_{rr}=0.1$. The three curves intersect when they take the value of unity.

As mentioned in (Cushing and Diekmann, 2016) and other literature, independent of the formula of the basic reproduction number, the critical condition that it is equal to unity is mathematically identical as long as it is well-defined.

Corollary 5.2.1

The condition $R_{0\mid c}=1$ is mathematically equivalent to the condition $R_{0\mid r}=1$ ( $R_{0\mid v}=1$ ).

Moreover, we can find the following mathematical result about their order (Appendix D):

Corollary 5.2.2

When R _0∣r < 1 and R _0∣v < 1, R _0∣c > R _0∣r and R _0∣c > R _0∣v . When R _0∣r > 1 or R _0∣v > 1, R _0∣c < R _0∣r and R _0∣c < R _0∣v .

It is clearly undetermined which is the larger between R _0∣r and R _0∣v because from (8) and (9), they are symmetric in terms of ${\mathcal{R}}_{rr}$ and ${\mathcal{R}}_{vv}$. Their relative values therefore depend on the values of ${\mathcal{R}}_{rr}$ and ${\mathcal{R}}_{vv}$. In contrast, the above corollary shows that R _0∣c is necessarily larger than R _0∣r and R _0∣v when R _0∣r < 1 and R _0∣v < 1, where either R _0∣r or R _0∣v is less than unity if and only if the other is less than unity as we see in Theorem 5.1. When R _0∣r > 1 or R _0∣v > 1, R _0∣c is necessarily smaller than R _0∣r and R _0∣v.

From the standpoint that the basic reproduction numbers R _0∣r and R _0∣v are more practical compared to R _0∣c, we can remark that R _0∣c, which would be frequently/conventionally used as the mathematically derived basic reproduction number, appears to overestimate the basic reproduction number for each subpopulation when it is smaller than unity while underestimating it when it is larger than unity.

When a disease is imported into the community by tourists or other short term visitors, R _0∣r can be reasonably measured in a bid to protect the residents. Actually, the features of the residents could be identified more easily than those of the visitors. In contrast, R _0∣v could be important and have to be practically evaluated from the standpoint of a specific kind of visitor subpopulation. For instance, when the visitors are prone to a particular kind of disease to which the residents in the community are characteristically immune though they can facilitate its spread. Furthermore, since the basic reproduction number R _0∣c corresponds to the expected number of secondary cases summed up for both resident and visitor subpopulations, it would be an unsatisfactory overestimation for discussing the prevention, the intervention, or the containment of the spread of a transmissible disease in the kind of community we consider. Moreover, R _0∣c is quite tricky to estimate given the contrasting peculiarities of the two subpopulations: the attributes of residents are relatively easier to measure compared to those of visitors who are only around in the community for a short period.

6. Concluding remarks

It is obvious that some kind of control measures need to be put in place to mitigate the effects of disease transmission in a community with visitor population. The most obvious measure might be to control the visitor population size, N_v. However, it would be equally effective to control the flux, that is, the inflow and outflow, M and E. A sufficiently large M (and E) means the duration of stay N_v/M ≪ 1 so as to make ${\mathcal{R}}_{vv}=\left({\beta }_{vv}{N}_v^2\right)/M\ll 1$ which guarantees the suppression of disease spread. For the purpose of clarity, a large M implies large visitor movements. As stated earlier, reducing the visitor population size will be very effective although it is in general quite difficult to achieve within a country except in conserved areas. For transnational human movements, visa application processes can be tightened but in a world of growing globalization, that might be counterproductive.

The dynamics of swine fever, which is endemic and of major concern in the global hog business, is a very good example which corresponds to our model since there is the possibility of cross infection within and between domestic pig and wild boar populations such that we have β_rr > 0, β_vr > 0, β_rv > 0 and β_vv > 0. It is established that the disease is transmitted both directly as stated earlier and indirectly (through polluted carcasses, food waste, or vehicles and equipment). For pig farm holders, the value of the basic reproduction number R _0∣r is very critical. To make sure it is kept as low as possible, the following are very crucial: vaccination (though there are still knowledge gaps) and control measures like proscription of swill feeding, isolation of pigs before introduction into stock, culling and thorough disinfection of all hogs on affected farms, proper disposal of carcasses, homogenized strict import approach for live pigs and pork, management of wild boars and prevention of contacts between local pigs and wild boars (Mur, Sánchez-Vizcaíno, Fernández-Carrión, Jurado, Rolesu, Feliziani, Laddomada, Martínez-López, 2018, Postel, Austermann-Busch, Petrov, Moennig, Becher, 2018, Sánchez-Cordón, Montoya, Reis, Dixon, 2018).

For the model we considered, the basic reproduction number can be viewed from different perspectives depending on the focus of public health policy makers. Any mathematical variant of the basic reproduction number, namely R _0|r and R _0|v, can be said to be the supremum of the expected number of secondary infections which keeps changing with the effects of new infections.

6.1. Effects of cross infection

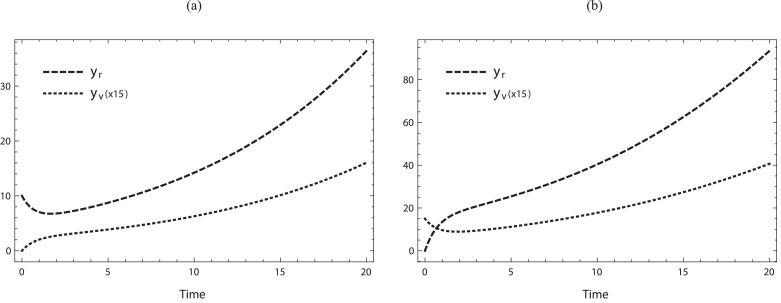
From the results obtained in the previous sections, we can say that even when ${\mathcal{R}}_{rr}$ and ${\mathcal{R}}_{vv}$ are small, there could be disease outbreak in the subpopulations given sufficiently high cross infections. This implies that even without outbreak in isolation, when the subpopulations have contacts with each other, there is always a likelihood of outbreak. Such a case is numerically demonstrated by Fig. 8 for our model (2). Due to the small values of ${\mathcal{R}}_{rr}$ and ${\mathcal{R}}_{vv},$ it is likely that the infective population size decreases in an initial period within the subpopulation where the initial infective appears. However, since the basic reproduction number can go beyond unity when there is cross infection, an outbreak of disease appears after a time lag. This kind of time lag in the temporal variation later leading to disease outbreak would likely cause delays in policy/social/sanitary measures against disease invasion in the community.

Fig. 8.

Numerical examples of the temporal variation of the system (2). (a) $(x_r\left(0\right),y_r\left(0\right),y_v\left(0\right))=(99990.0,10.0,0.0)$; (b) $(x_r\left(0\right),y_r\left(0\right),y_v\left(0\right))=(100000.0,0.0,1.0)$. Commonly, $\mathcal{B}=2.0,$${\mathcal{R}}_{rr}=0.4,$${\mathcal{R}}_{vv}=0.5,$${\mathcal{R}}_{rv}=16.90,$${\mathcal{R}}_{vr}=0.02,$$R_{0\mid r}=1.200,$$R_{0\mid v}=1.167,$$R_{0\mid c}=1.084$.

To measure the contribution of cross infection on the basic reproduction number for each subpopulation, we may use the following indices:

$$\begin{array}{cc}\hfill {\xi }_r& :=\frac{R_{0\mid r}-{\mathcal{R}}_{rr}}{{\mathcal{R}}_{rr}}=\frac{R_{0\mid r}}{{\mathcal{R}}_{rr}}-1=\frac{{\mathcal{R}}_{rv}{\mathcal{R}}_{vr}}{1-{\mathcal{R}}_{vv}}\frac{1}{{\mathcal{R}}_{rr}}\text{for}{R}_{0\mid r};\hfill \\ \hfill {\xi }_v& :=\frac{R_{0\mid v}-{\mathcal{R}}_{vv}}{{\mathcal{R}}_{vv}}=\frac{R_{0\mid v}}{{\mathcal{R}}_{vv}}-1=\frac{{\mathcal{R}}_{rv}{\mathcal{R}}_{vr}}{1-{\mathcal{R}}_{rr}}\frac{1}{{\mathcal{R}}_{vv}}\text{for}{R}_{0\mid v}.\hfill \end{array}$$

It can be easily found that if ${\mathcal{R}}_{vv}>{\mathcal{R}}_{rr},$ then ξ_r > ξ_v. This means that the effect of cross infection on the resident subpopulation is more serious as the isolated visitor subpopulation has the larger basic reproduction number for the disease. Conversely, we can say that the effect of cross infection on the visitor subpopulation is more serious when the isolated resident subpopulation has the larger basic reproduction number for the disease. Intuitively, these results are very much acceptable.

6.2. Application for malaria

Malaria is a disease of global relevance as it has been a key concern in almost 100 countries of the world. Interestingly, it is preventable but its control has proven to be something which requires serious attention as drug-resistant strains of the plasmodium species, the cause of malaria, have been known to emerge. Ineffective vaccination programmes have also been known to result to more fatal outbreaks of this disease transmitted by the female Anopheles mosquitoes to humans after being infected when they bite infective humans (Cowman et al., 2016).

In order to apply our model for malaria, humans can be viewed as residents while mosquitoes can be regarded as visitors. The recruitment of mosquitoes can be seen as their influx into the visitor subpopulation while the effective elimination of mosquitoes by the use of insecticides or through other means can be taken as leading to their outflux from the visitor subpopulation. Notably, for malaria, there are generally no direct human-human and mosquito-mosquito transmissions, so intra-subpopulation infections do not exist, that is, ${\beta }_{rr}={\beta }_{vv}=0$. Then, we have

$$R_{0\mid r}=R_{0\mid v}=\frac{{\beta }_{rv}{N}_v{N}_r}{M}\frac{{\beta }_{vr}{N}_v}{\rho }={\mathcal{R}}_{rv}{\mathcal{R}}_{vr}.$$ (11)

Managing β_vr and β_rv implies taking some measures to control mosquitoes as they both have direct effects in the outbreak of malaria. N_r and N_v also have direct effect, but more attention should be paid to the latter because of its square order contribution on the basic reproduction numbers. If we can control the mosquito density N_v so that R _0∣v < 1, the outbreak of malaria could be successfully suppressed. This argument could be extended to other vector-borne diseases like Dengue fever, Lyme disease, West Nile fever, etc.

Taking a different standpoint where we consider mosquitoes as residents and humans as visitors, for example, the case of some explorers in a mosquito infested environment, the expected duration of stay N_v/M appears very crucial. A sufficiently short duration of stay could help manage the epidemic effectively. Also, an enough low contact rate with the mosquito population would be very vital. This can be achieved by control measures like the use of insecticide-treated nets (ITN) and mosquito repellents. Another control measure might be the use of vaccination by the visitors to make them immune to being infected.

6.3. Application for avian influenza

Horimoto et al. (2005) predicted that a new influenza pandemic would occur following outbreaks of the H5 and H7 subtypes of avian influenza A in birds and humans. Infection in humans was known to occur through very close contact with birds which had been infected while bird to bird infections were obviously easier. Using the concept of the basic reproduction number, Liu et al. (2015) investigated the dynamics of a bird-to-human transmission model with regards to human psychology vis-à-vis avian influenza. Their outcome shows that if there is an outbreak, “the saturation effect within avian population and the psychological effect in human population cannot change the stability of equilibria but can affect the number of infected humans”. Liu and Fang (2015) formulated a two-host dynamic model for H7N9 virus infection in both bird and human populations. Critical transmission parameters were computed using nationwide surveillance data of infections in mainland China. The analysis of their model shows that the long term prevention of human H7N9 infections is necessitated by culling infected birds.

From the perspective of our model, we take humans as residents and birds as short-stay visitors such that β_rr ≈ 0, β_vr ≈ 0, β_rv > 0 and β_vv > 0 since human-to-bird influenza transmissions are almost impossible and human-to-human infections are quite rare. So, we have $\mathcal{B}=0$ and $R_{0\mid v}={\mathcal{R}}_{vv}$. Otherwise, taking domesticated birds as residents and wild birds as short-stay visitors, we have β_rr > 0, β_vr ≈ 0, β_rv > 0, and β_vv > 0. In this case, $\mathcal{B}=0$ and $R_{0\mid r}={\mathcal{R}}_{rr}$.

Just like in the case of malaria, one effective control measure for avian influenza would be to ensure that infected birds are kept away as much as possible since ${\mathcal{R}}_{vv}$ depends on the square value of the bird population density. For wild birds that migrate seasonally to a local community, measures can be taken to keep them off. For poultry and other possible local hosts of avian influenza, screening or culling as established by (Liu and Fang, 2015) can help in preventing the disease outbreak in the local community.

6.4. Relationship with metapopulation dynamics

In the past couple of decades, most papers related to theoretical/mathematical studies of the global spread of transmissible diseases were focused on the mobility of humans over various populations or patches (see Arino, van den Driessche, 2006, Colizza, Vespignani, 2008, Gong, Small, 2018, Saito, Nishiura, Higuchi, 2018, Soriano-Paños, Lotero, Arenas, Gómez-Gardeñes, 2018, Wang, Wu, 2018 and references therein). Frequently, such movements correspond to migration as opposed to temporary visits for a finite period as we consider in our case, or to human transportation on a large spatial scale during relatively long trips. Our scenario of short visits does not fully capture the metapopulation framework in most of those previous works but the interaction between the resident and visitor subpopulations has some semblance of metapopulation behavior. Indeed, the two subpopulations may be regarded as patches between which diseases can spread. This may be said to display some metapopulation dynamics in the context of modern trends in social networks (Hackl, Dubernet, 2019, Wang, Wang, Wu, 2018) while metapopulation dynamics have been generally based on a spatially heterogeneous structure of population distribution (Arino, van den Driessche, 2006, Ball, Britton, House, Isham, Mollison, Pellis, Scalia Tomba, 2015, North, Godfray, 2017).

In this paper, we have considered a community under epidemic interaction with short-term visitors. We do not explicitly consider metapopulation dynamics although the visitors in our model can be regarded as the epidemic agents in terms of interaction between “patches” in a metapopulation. In this sense, the analysis of our model can be regarded as being about the likelihood of the spread of a transmissible disease in a community which corresponds to a patch. It is necessary to discuss such a likelihood over a metapopulation especially when an transnational or global-scale outbreak is concerned, whereas even in such a case, each local community in the metapopulation must consider the likelihood of spread within the community in order to prevent or contain it as mentioned in the last part of Section 5.2. This paper could be regarded as a mathematical modeling work devoted to such a problem.

Appendix A. Proof for Theorem 4.2

• 1.
  Suppose that $y_r\to y_r^{*}>0$. Then, if $x_r\to x_r^{*}>0,$ we have

  $${\displaystyle \frac{d{x}_r}{dt}}\approx -x_r^{*}({\beta }_{rr}{y}_r^{*}+{\beta }_{rv}{y}_v)<0\text{for}t\gg 1.$$

  This is contradictory to the precondition for x_r to converge to a positive value. Therefore, x_r → 0 as t → ∞. Then we have $d{y}_r/dt\approx -\rho y_r^{*}<0$ for t ≫ 1. Since this is contradictory again, we conclude that y_r → 0.
• 2.
  Since y_r → 0 as t → ∞, we have

  $$\begin{array}{cc}\hfill {\displaystyle \frac{d{y}_v}{dt}}& \approx {\beta }_{vv}{y}_v(\frac{{\beta }_{vv}{N}_v^2-M}{{\beta }_{vv}{N}_v}-y_v)\text{for}t\gg 1\text{when}{\beta }_{vv}>0;\hfill \\ \hfill {\displaystyle \frac{d{y}_v}{dt}}& \approx -\frac{M}{N_v}{y}_v\text{for}t\gg 1\text{with}{\beta }_{vv}=0.\hfill \end{array}$$ (A.1)

  From these results, we can easily find that, if $({\beta }_{vv}{N}_v^2-M)/\left({\beta }_{vv}{N}_v\right)\le 0$ with β_vv > 0, that is, if ${\mathcal{R}}_{vv}\le 1,$ then dy_v/dt < 0 for t ≫ 1 so that y_v → 0 as t → ∞. Also, y_v → 0 as t → ∞ when ${\beta }_{vv}=0$.

  These arguments show that, when ${\mathcal{R}}_{vv}\le 1,$ all infective visitors end up leaving the community such that $(x_r,y_r,y_v)\to (x_r^{*},0,0,0)$ with $x_r^{*}\ge 0$ as t → ∞.

• 3.
  If $({\beta }_{vv}{N}_v^2-M)/\left({\beta }_{vv}{N}_v\right)>0$ with β_vv > 0, that is, if ${\mathcal{R}}_{vv}\le 1,$ then (A.1) corresponds to a logistic equation. This implies that

  $$y_v\to y_v^{*}=\frac{{\beta }_{vv}{N}_v^2-M}{{\beta }_{vv}{N}_v}>0\text{as}t\to \infty .$$

  Thus, for y_r → 0 as t → ∞, we have

  $$\frac{d{x}_r}{dt}\approx -{\beta }_{rv}{x}_r{y}_v^{*}\text{for}t\gg 1.$$
  Hence, when β_rv > 0, we see that x_r → 0 as t → ∞. These arguments prove that

  $$(x_r,y_r,y_v)\to (0,0,\frac{{\beta }_{vv}{N}_v^2-M}{{\beta }_{vv}{N}_v})\text{as}t\to \infty .$$

This result can also be supported by the local stability analysis. We can easily get the following Jacobian matrix for the system (2) about the equilibrium point $(x_r^{*},y_r^{*},y_v^{*})=(0,0,({\beta }_{vv}{N}_v^2-M)/\left({\beta }_{vv}{N}_v\right))=(0,0,N_v(1-1/{\mathcal{R}}_{vv}))$ :

$$J(0,0,N_v(1-\frac{1}{{\mathcal{R}}_{vv}}\left)\right)=\left(\begin{array}{ccc}-{\beta }_{rv}{N}_v(1-\frac{1}{{\mathcal{R}}_{vv}})& 0& 0\\ {\beta }_{rv}{N}_v(1-\frac{1}{{\mathcal{R}}_{vv}})& -\rho & 0\\ 0& \frac{M{\beta }_{vr}}{{\beta }_{vv}{N}_v}& -N_v(1-\frac{1}{{\mathcal{R}}_{vv}})\end{array}\right),$$ (A.2)

which has eigenvalues $-{\beta }_{rv}{N}_v(1-1/{\mathcal{R}}_{vv}),$ $-\rho ,$ and $-N_v(1-1/{\mathcal{R}}_{vv})$. This establishes that, if ${\mathcal{R}}_{vv}>1,$ the equilibrium point $(0,0,N_v(1-1/{\mathcal{R}}_{vv}))$ exists locally asymptotically stable. In the same way, making use of the eigenvalue analysis about the Jacobian matrix for the linearization of (2), it can also be proven that the equilibrium point (0,0,0) is unstable if ${\mathcal{R}}_{vv}>1$.

Appendix B. Proof for Theorem 4.3

Now, let us consider the case that ${\mathcal{R}}_{vv}\le 1,$ when $(x_r,y_r,y_v)\to (x_r^{*},0,0)$ with $x_r^{*}>0$ as t → ∞, being proved by Theorem 4.2. We can derive the following Jacobian matrix about the point $(x_r^{*},y_r^{*},y_v^{*})=(x_r^{*},0,0)$ with $x_r^{*}>0$:

$$J(x_r^{*},0,0)=\left(\begin{array}{ccc}0& -{\beta }_{rr}{x}_r^{*}& -{\beta }_{rv}{x}_r^{*}\\ 0& {\beta }_{rr}{x}_r^{*}-\rho & {\beta }_{rv}{x}_r^{*}\\ 0& {\beta }_{vr}{N}_v& {\beta }_{vv}{N}_v-\frac{M}{N_v}\end{array}\right)$$ (B.1)

which can be evaluated using the bottom right 2 × 2 matrix

$$\mathcal{J}=\left(\begin{array}{cc}{\beta }_{rr}{x}_r^{*}-\rho & {\beta }_{rv}{x}_r^{*}\\ {\beta }_{vr}{N}_v& {\beta }_{vv}{N}_v-\frac{M}{N_v}\end{array}\right)$$ (B.2)

whose characteristic equation is given by

$${\lambda }^2-\left(\text{tr}\mathcal{J}\right)\lambda +\text{det}\mathcal{J}=0,$$ (B.3)

where

$$\text{tr}\mathcal{J}=\frac{\rho }{N_r}({\mathcal{R}}_{rr}{x}_r^{*}-N_r)-\frac{M}{N_v}(1-{\mathcal{R}}_{vv})$$

and

$$\det \mathcal{J}=\frac{\rho M}{N_r{N}_v}[{\mathcal{R}}_{rr}({\mathcal{R}}_{vv}-\mathcal{B}{\mathcal{R}}_{vv}-1)x_r^{*}+N_r(1-{\mathcal{R}}_{vv})]$$

with

$$\mathcal{B}=\frac{{\beta }_{rv}{\beta }_{vr}}{{\beta }_{rr}{\beta }_{vv}}.$$

This $\mathcal{B}$ expresses the ratio of the infectivity between residents and visitors (inter-subcommunity infection) to the infectivity within subcommunities (intra-subcommunity infection).

From the theory of local stability, the point $(x_r^{*},0,0)$ is unfeasible if $\text{tr}\mathcal{J}>0$ or $\det \mathcal{J}<0$. The condition $\text{tr}\mathcal{J}>0$ gives

$$x_r^{*}>(\frac{1}{{\mathcal{R}}_{rr}}+\frac{M}{\rho N_v}\frac{1-{\mathcal{R}}_{vv}}{{\mathcal{R}}_{rr}})N_r.$$ (B.4)

For $\det \mathcal{J}<0,$ we have

$$x_r^{*}>\frac{1-{\mathcal{R}}_{vv}}{{\mathcal{R}}_{rr}[\mathcal{B}{\mathcal{R}}_{vv}+(1-{\mathcal{R}}_{vv})]}{N}_r.$$ (B.5)

Since the right side of (B.4) is greater than that of (B.5), we can conclude that if (B.4) is satisfied, then $(x_r^{*},0,0)$ with $x_r^{*}>0$ is unfeasible. So we define the critical value $x_r^{\mathrm{upper}}$ by the right side of (B.4), that is, by (7). Consequently from these arguments, the point $(x_r^{*}0,0)$ with $x_r^{*}>x_r^{\mathrm{upper}}$ is unfeasible. Thus, the feasible equilibrium state $(x_r^{*},0,0)$ with $x_r^{*}>0$ must satisfy $x_r^{*}<x_r^{\mathrm{upper}}$.

Appendix C. Derivation of R_0|r, R_0|v, and R_0|c

In order to obtain the basic reproduction number R _0∣r which is the index of the possibility of the disease spread within the resident subpopulation, following the theory given by (van den Driessche, Watmough, 2002, van den Driessche, Watmough, Brauer, 2008), we arrange (2) at first as follows:

$$\begin{array}{cc}{\displaystyle \frac{d{y}_r}{dt}}\hfill & =x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)-\rho y_r;\hfill \\ {\displaystyle \frac{d{y}_v}{dt}}\hfill & =(N_v-y_v)({\beta }_{vr}{y}_r+{\beta }_{vv}{y}_v)-\frac{M}{N_v}{y}_v;\hfill \\ {\displaystyle \frac{d{x}_r}{dt}}\hfill & =-x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v),\hfill \end{array}$$ (C.1)

then decompose it into the recruitment terms of new infections for the resident and the other terms as follows:

$$\frac{d\mathit{X}}{dt}=\mathit{F}\left(\mathit{X}\right)-\mathit{V}\left(\mathit{X}\right),$$ (C.2)

where $\mathit{X}={\left(y_r\left(t\right)y_v\left(t\right)x_r\left(t\right)\right)}^{\text{T}}$. F represents the recruitment rate of new infections, and V represents the other factors related to the epidemic dynamics, so that

$$\begin{array}{cc}\hfill \mathit{F}& :=\left(\begin{array}{c}{x}_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)\\ 0\\ 0\end{array}\right);\mathit{V}:=\left(\begin{array}{c}\rho y_r\\ -(N_v-y_v)({\beta }_{vr}{y}_r+{\beta }_{vv}{y}_v)+\frac{M}{N_v}{y}_v\\ x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)\end{array}\right).\hfill \end{array}$$ (C.3)

Next, we have the Jacobian matrices of F and V about X:

$$\begin{array}{cc}\hfill D\mathit{F}\left(\mathit{X}\right)& :=\left(\begin{array}{ccc}{\beta }_{rr}{x}_{r0}& {\beta }_{rv}{x}_{r0}& {\beta }_{rr}{y}_{r0}+{\beta }_{rv}{y}_{v0}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right);\hfill \\ \hfill D\mathit{V}\left(\mathit{X}\right)& :=\left(\begin{array}{ccc}\rho & 0& 0\\ -{\beta }_{vr}(N_v-y_{v0})& -{\beta }_{vv}(N_v-2y_{v0})+{\beta }_{vr}{y}_{v0}+\frac{M}{N_v}& 0\\ {\beta }_{rr}{x}_{r0}& {\beta }_{rv}{x}_{r0}& {\beta }_{rr}{y}_{r0}+{\beta }_{rv}{y}_{v0}\end{array}\right).\hfill \end{array}$$

At the disease-free equilibrium X ₀ ≔ (0  0  N_r)^T, they become

$$\begin{array}{c}\hfill D\mathit{F}\left({\mathit{X}}_0\right):=\left(\begin{array}{ccc}{\beta }_{rr}{N}_r& {\beta }_{rv}{N}_r& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right);D\mathit{V}\left({\mathit{X}}_0\right):=\left(\begin{array}{ccc}\rho & 0& 0\\ -{\beta }_{vr}{N}_v& -{\beta }_{vv}{N}_v+\frac{M}{N_v}& 0\\ {\beta }_{rr}{N}_r& {\beta }_{rv}{N}_r& 0\end{array}\right).\end{array}$$

Taking the top left hand corner 2 × 2 matrices in each of the two matrices, we have

$$\begin{array}{cc}\hfill \mathcal{F}& :=\left(\begin{array}{cc}{\beta }_{rr}{N}_r& {\beta }_{rv}{N}_r\\ 0& 0\end{array}\right);\mathcal{V}:=\left(\begin{array}{cc}\rho & 0\\ -{\beta }_{vr}{N}_v& -{\beta }_{vv}{N}_v+\frac{M}{N_v}\end{array}\right).\hfill \end{array}$$

Then, the next generation matrix (NGM) is obtained by

$$\mathcal{K}={\mathcal{FV}}^{-1}=\left(\begin{array}{cc}\frac{N_r[{\beta }_{rr}(M-{\beta }_{vv}{N}_v^2)+{\beta }_{rv}{\beta }_{vr}{N}_v^2]}{\rho (M-{\beta }_{vv}{N}_v^2)}& \frac{{\beta }_{rv}{N}_r{N}_v}{M-{\beta }_{vv}{N}_v^2}\\ 0& 0\end{array}\right).$$ (C.4)

The basic reproduction number R _0∣r is given by the maximum absolute value of the eigenvalues of (C.4), that is,

$$R_{0\mid r}=\max \left\{0,|\frac{N_r[{\beta }_{rr}({\beta }_{vv}{N}_v^2-M)-{\beta }_{rv}{\beta }_{vr}{N}_v^2]}{\rho ({\beta }_{vv}{N}_v^2-M)}|\right\}.$$

Therefore we get the following basic reproduction number for the model (2):

$$R_{0\mid r}=\left|\frac{{\mathcal{R}}_{rr}{\mathcal{R}}_{vv}(1-\mathcal{B})-{\mathcal{R}}_{rr}}{{\mathcal{R}}_{vv}-1}\right|={\mathcal{R}}_{rr}|1+\frac{{\mathcal{R}}_{vv}}{1-{\mathcal{R}}_{vv}}\mathcal{B}|.$$ (C.5)

Since we consider only the case that ${\mathcal{R}}_{vv}<1,$ we obtain (8) as R _0∣r.

To derive R _0∣v, we should change the decomposition of (C.1) because we now consider the basic reproduction number which is the index of the possibility of the disease spread within the visitor subpopulation. The decomposition into F and V should be such that the recruitment terms of new infections for the visitor and the other terms are as follows, differently from (C.3):

$$\begin{array}{cc}\hfill \mathit{F}& :=\left(\begin{array}{c}0\\ (N_v-y_v)({\beta }_{vr}{y}_r+{\beta }_{vv}{y}_v)\\ 0\end{array}\right);\mathit{V}:=\left(\begin{array}{c}-x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)+\rho y_r\\ \frac{M}{N_v}{y}_v\\ x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)\end{array}\right).\hfill \end{array}$$

In the way same with that for R _0∣r, the NGM $\mathcal{K}$ is obtained as

$$\mathcal{K}=\left(\begin{array}{cc}0& 0\\ \frac{{\beta }_{vr}{N}_r{N}_v}{\rho -{\beta }_{rr}{N}_r}& \frac{N_v^2[{\beta }_{vv}(\rho -{\beta }_{rr}{N}_r)+{\beta }_{rv}{\beta }_{vr}{N}_r]}{M(\rho -{\beta }_{rr}{N}_r)}\end{array}\right).$$ (C.6)

Therefore, the basic reproductive number R _0∣v given by the maximum absolute value of the eigenvalues of (C.6) is expressed as follows:

$$R_{0\mid v}=\left|\frac{{\mathcal{R}}_{rr}{\mathcal{R}}_{vv}(1-\mathcal{B})-{\mathcal{R}}_{vv}}{{\mathcal{R}}_{rr}-1}\right|={\mathcal{R}}_{vv}|1+\frac{{\mathcal{R}}_{rr}}{1-{\mathcal{R}}_{rr}}\mathcal{B}|.$$

Since we consider only the case that ${\mathcal{R}}_{rr}<1,$ we obtain (9) as R _0∣v.

In order to derive the basic reproduction number for the whole community R _0∣c, we should change the decomposition of (C.1), because the decomposition into F and V should be such that the recruitment terms of new infections come from both residents and visitors, differently from those for R _0∣r and R _0∣v:

$$\begin{array}{cc}\hfill \mathit{F}& :=\left(\begin{array}{c}{x}_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)\\ (N_v-y_v)({\beta }_{vr}{y}_r+{\beta }_{vv}{y}_v)\\ 0\end{array}\right);\mathit{V}:=\left(\begin{array}{c}\rho y_r\\ \frac{M}{N_v}{y}_v\\ x_r({\beta }_{rr}{y}_r+{\beta }_{rv}{y}_v)\end{array}\right).\hfill \end{array}$$

Then the NGM $\mathcal{K}$ is now obtained as

$$\mathcal{K}=\left(\begin{array}{cc}\frac{{\beta }_{rr}{N}_r}{\rho }& \frac{{\beta }_{rv}{N}_r{N}_v}{M}\\ \frac{{\beta }_{vr}{N}_v}{\rho }& \frac{{\beta }_{vv}{N}_v^2}{M}\end{array}\right).$$ (C.7)

Since the characteristic equation of the matrix (C.7) can be expressed as

$$f\left(\lambda \right)={\lambda }^2-({\mathcal{R}}_{rr}+{\mathcal{R}}_{vv})\lambda +{\mathcal{R}}_{rr}{\mathcal{R}}_{vv}(1-\mathcal{B})=0,$$ (C.8)

we can easily find that the basic reproductive number R _0∣c given by the maximum absolute value of the eigenvalues of (C.7) becomes (10):

$$\begin{array}{cc}\hfill R_{0\mid c}& =\max \left\{\left|\frac{{\mathcal{R}}_{rr}+{\mathcal{R}}_{vv}\pm \sqrt{{({\mathcal{R}}_{rr}+{\mathcal{R}}_{vv})}^2-4{\mathcal{R}}_{rr}{\mathcal{R}}_{vv}(1-\mathcal{B})}}{2}\right|\right\}\hfill \\ & =\frac{{\mathcal{R}}_{rr}+{\mathcal{R}}_{vv}+\sqrt{{({\mathcal{R}}_{rr}+{\mathcal{R}}_{vv})}^2-4{\mathcal{R}}_{rr}{\mathcal{R}}_{vv}(1-\mathcal{B})}}{2}.\hfill \end{array}$$

Appendix D. Proofs for Theorem 4.3, Corollaries 5.2.1 and 5.2.2

For R _0∣c < 1, it is necessary and sufficient that $\text{tr}\mathcal{K}<2$ and f(1) > 0 for the characteristic equation of the NGM $\mathcal{K},$ given by (C.8). Since we are considering the case that ${\mathcal{R}}_{rr}<1$ and ${\mathcal{R}}_{vv}<1,$ we can easily find that necessarily $\text{tr}\mathcal{K}={\mathcal{R}}_{rr}+{\mathcal{R}}_{vv}<2$. Next, we can find that the condition f(1) > 0 is equivalent to R _0∣r < 1. Therefore, it is shown that R _0∣c < 1 if R _0∣r < 1. The converse is also true. Then the proof of Theorem 5.2 is established, and Corollary 5.2.1 also follows. Going by Theorem 5.1, the theorem and the corollary hold also for R _0∣v.

To prove Corollary 5.2.2, we show from the characteristic equation (C.8) that f(R _0∣r) < 0. If so, it is guaranteed that R _0∣c > R _0∣r. Indeed, since ${\mathcal{R}}_{rr}{\mathcal{R}}_{vv}(1-\mathcal{B})={\mathcal{R}}_{rr}-R_{0\mid r}(1-{\mathcal{R}}_{vv})$ from (8), we can find that

$$f\left(R_{0\mid r}\right)=R_{0\mid r}^2-({\mathcal{R}}_{rr}+{\mathcal{R}}_{vv})R_{0\mid r}+{\mathcal{R}}_{rr}{\mathcal{R}}_{vv}(1-\mathcal{B})=(R_{0\mid r}-1)(R_{0\mid r}-{\mathcal{R}}_{rr}).$$

Since $f\left({\mathcal{R}}_{rr}\right)=-{\mathcal{R}}_{rr}{\mathcal{R}}_{vv}\mathcal{B}<0,$ it is necessarily satisfied that ${\mathcal{R}}_{rr}<R_{0\mid r},$ that is, $R_{0\mid r}-{\mathcal{R}}_{rr}>0$. So, given R _0∣r < 1, we have f(R _0∣r) < 0 so that R _0∣c > R _0∣r. Going by Theorem 5.2, it is also established that R _0∣v < 1. This completes the proof.