Spatial dynamics of airborne infectious diseases

Abstract

Disease outbreaks, such as those of Severe Acute Respiratory Syndrome in 2003 and the 2009 pandemic A(H1N1) influenza, have highlighted the potential for airborne transmission in indoor environments. Respirable pathogen-carrying droplets provide a vector for the spatial spread of infection with droplet transport determined by diffusive and convective processes. An epidemiological model describing the spatial dynamics of disease transmission is presented. The effects of an ambient airflow, as an infection control, are incorporated leading to a delay equation, with droplet density dependent on the infectious density at a previous time. It is found that small droplets ($\sim 0.4\mathrm{\mu }\mathrm{m}$) generate a negligible infectious force due to the small viral load and the associated duration they require to transmit infection. In contrast, larger droplets ($\sim 4\mathrm{\mu }\mathrm{m}$) can lead to an infectious wave propagating through a fully susceptible population or a secondary infection outbreak for a localized susceptible population. Droplet diffusion is found to be an inefficient mode of droplet transport leading to minimal spatial spread of infection. A threshold air velocity is derived, above which disease transmission is impaired even when the basic reproduction number R₀ exceeds unity.

Highlights

► We model the spatial spread of airborne diseases by pathogen-carrying droplets. ► The importance of an ambient airflow on the infection dynamics is examined. ► Infection results from direct contact between droplets and susceptible individuals. ► A threshold air velocity, above which disease transmission is impaired, is derived. ► Droplet convection can cause secondary infections in the absence of infected people.

1. Introduction

The temporal dynamics of infectious disease transmission is well documented (Anderson and May, 1991), however, the spatial spread of infection and the mechanisms driving it are less well understood. Spatial dynamics of respiratory diseases has received much attention in recent years following the rapid global spread of both Severe Acute Respiratory Syndrome (SARS) (Hufnagel et al., 2004) and pandemic influenza (2009) A(H1N1) (Balcan et al., 2004). Large-scale geographic models are typically implemented by superimposing a transportation network on local infection dynamics (Keeling and Rohani, 2002, Colizza et al., 2006). Smaller scale models often implement reaction-diffusion equations to describe random movements within populations (Noble, 1974, Murray et al., 1986). Such models have been shown to exhibit traveling-wave solutions whose existence depends on the basic reproduction number R ₀ (Källén et al., 1985, Mendez, 1998). However, few models address the mode of disease transmission that underlies the spatial dynamics.

For some respiratory infections, such as influenza, three modes of transmission have been identified: airborne, droplet and contact transmission (Weber and Stilianakis, 2008). All three modes result from the generation of respiratory droplets by an infected person during an expiratory event (e.g. coughing, sneezing). Droplet and contact transmission require relatively close contact between the infected and susceptible individuals for efficient disease transmission. Therefore, spatial spread via these routes of transmission must be driven by human movement. In contrast, the airborne spread of a pathogen may be attributed to the movement of both people and fine aerosol droplets suspended in the air and their associated airborne residence time and pathogen load. Furthermore, the airborne route is the primary mode of transmission for other respiratory diseases, such as tuberculosis, and its contribution to the spatial spread of infection is of paramount importance.

The relative importance of the three modes of transmission is difficult to quantify; however, recent experience with SARS and influenza outbreaks has highlighted the potential for airborne transmission in indoor environments. Evidence of the airborne transmission of respiratory infections has been documented in hospital ward settings (Wong et al., 2010), housing complexes (Yu et al., 2004) and on board commercial airliners (Moser et al., 1979). In particular, the importance of indoor airflows has been established (Li et al., 2007), with large air flow rates resulting in lower disease transmission (Nielsen, 2009). However, the threshold air velocity above which disease transmission is impaired is as yet unknown. A comprehensive knowledge and understanding of the mechanisms driving such transmission is vital for the implementation of adequate infection controls in indoor public environments such as schools, hospitals and long-term care facilities.

Airborne transmission is mediated by fine aerosol droplets small enough to remain suspended in air for prolonged periods, and large enough to contain non-negligible pathogen load. The standard epidemiological models operate on the assumption that contact between susceptible and infected persons is necessary for disease transmission (Keeling and Rohani, 2007). However, the pathogen-carrying droplets emitted by an infected individual during an expiratory event are the disease vector and the standard models should be adjusted to reflect this. Such models have been used to describe the spatial spread of fungal spores over a vineyard (Burie et al., 2006) and to model disease spread following the point release of an infectious agent (Reluga, 2004).

A zero-dimensional model for the temporal development of an epidemic driven by expiratory droplets (in particular, respirable droplets) was developed in Stilianakis and Drossinos (2010). The model is built on the concept of an infectious cloud surrounding each infected individual, an idea also considered in Eichenwald et al. (1960). In this work we investigate the airborne spread of an infection in a closed spatial environment within which the human population is confined for a prolonged period of time. For example, such outbreaks have been documented in public settings including prisons (Awofeso et al., 2001, Gómez-Pintado et al., 2010), boarding schools (Rose, 1980), long-term care facilities (Dharan et al., 2009) and on board large cruise ships (Miller et al., 2000, Ward et al., 2010). In the absence of intervention measures, such outbreaks can persist for many weeks. We extend the zero-dimensional model to include the spatial dynamics of airborne-droplet transmission (also known as aerosol transmission) and investigate how an ambient airflow can influence disease spread. Accordingly, we neglect transmission by droplet spray, a close-contact transmission mode that occurs via direct deposition onto a susceptible's mucous membranes, and by (physical) contact transmission. Furthermore, we consider transmission only by respirable expiratory droplets, droplets whose post-evaporation diameter is less than $10\mathrm{\mu }\mathrm{m}$, neglecting transmission by inspirable droplets, droplets whose post-evaporation diameter is between 10 and $100\mathrm{\mu }\mathrm{m}$. We follow Nicas et al. (2005) and take the droplet post-evaporation diameter to be half the pre-evaporation diameter. Inspirable droplets contribute to disease transmission by inhalation almost immediately after generation (e.g., during the first breath) as they are considerably larger than respirable droplets and they gravitationally settle very fast. As in the case of droplet spray, transmission by inspirable droplets occurs only at close contact.

2. A one-dimensional spatial model for airborne transmission

Consider a population of susceptible, infected and recovered individuals. Let $S(x,t)$ be the density of susceptibles, $I(x,t)$ the density of infected and $R(x,t)$ the density of recovered individuals, with $N(x,t)=S+I+R$ being the total population density and $n(t_0)={\int }_{x}N(x,t_0)\mathit{dx}$ representing the total number of people in the spatial domain at any time $t_0\ge 0$. Henceforth, all densities refer to spatial densities, unless otherwise noted, and airborne droplets refer to respirable droplets. It is assumed that infected individuals continuously generate a cloud of pathogen carrying aerosol droplets and we let $D(x,t)$ be the (number) density of active droplets, which we define as droplets that are both airborne and have a nonzero pathogen load.

The zero-dimensional model, which constitutes the basis of the one-spatial dimension model, is derived in Stilianakis and Drossinos (2010). A general one-dimensional evolution equation to model the spatial spread of disease due to the continuous motion of people and droplets takes the form

$$\frac{\partial C_i}{\partial t}=-\frac{\partial Q_i}{\partial x}+{\Psi }_i(x,t),$$

for each species $i\in [S,I,R,D]$, where $C_i(x,t)$ represents the density of species i, the flux $Q_i(x,t)$ is the rate at which species i passes the point x at time t and ${\Psi }_i(x,t)$ is a source term representing the creation (or destruction) of species i. The density of susceptibles will decrease through contact with pathogen-carrying (respirable airborne) droplets and subsequent infection. The density of infected people will increase accordingly. Furthermore, it will decrease at the rate that individuals recover ${\mu }_i$, where $1/{\mu }_i$ is the disease infectivity period. Thus

$${\Psi }_S=-\frac{{\beta }_d}{N}\mathit{DS},{\Psi }_I=\frac{{\beta }_d}{N}\mathit{DS}-{\mu }_{i}I,{\Psi }_R={\mu }_{i}I,$$

where ${\beta }_d$ is the transmission rate per droplet of diameter d. A detailed derivation of the transmission terms is provided in Stilianakis and Drossinos (2010). The dynamics of the airborne droplets is determined by generation and annihilation processes. The droplet density at any point is proportional to the density of infected individuals and increases at the rate ${\kappa }_d$ that pathogen-loaded droplets are shed. Moreover, the active droplet density will decrease as droplets are removed through gravitational settling and inhalation (by the person who generated it or another population member) and via pathogen inactivation. Thus

$${\Psi }_D={\kappa }_{d}I-{\alpha }_{d}D,$$

where ${\alpha }_d$ is the droplet removal rate and $1/{\alpha }_d$ the droplet infectivity period.

We assume that human movement can be modeled as a diffusive process (Noble, 1974, Keeling and Rohani, 2007, Murray, 2003) and the associated flux is given by Fick's law as

$$Q_j=-D_p\frac{\partial C_j}{\partial x}\mathrm{for}j=S,I,R,$$

where the minus sign is interpreted as the tendency of people to move from high density areas to low density areas and D _p is the diffusivity of the human population. For real world situations, movement of the general population might also be modeled by including a convective term, whereby human motion would be faster and in a specified direction. However, movement in such facilities as prisons and long-term care facilities is more restricted and sporadic and a diffusive flux better models such a scenario. In addition, restricting movement to a diffusive process is more convenient to investigate if droplets can drive the transmission process.

The droplet flux Q _D depends on environmental characteristics. Droplets are generated through expiratory events (e.g. coughing, sneezing) with an initial velocity. Average expiration velocities are 11.7 ms⁻¹ and 3.9 ms⁻¹ for coughing and speaking respectively (Chao et al., 2009). For respirable droplets, the droplet relaxation time, the time required to adjust the droplet velocity to a new condition of forces, is of the order $\sim {10}^{-7}-{10}^{-4}\mathrm{s}$. Therefore, the droplet velocity rapidly tends to the carrier-gas (air) velocity. The exhaled air flow has been modeled as a continuous turbulent round jet (Wang et al., 2005, Parienta et al., 2011). For a steady-state turbulent jet, small droplets, which follow the instantaneous fluid streamlines, may reach relatively large distances from the source (more than 8 m after 100 s). However, it was argued in Zhu et al. (2006), where the air flow within a calm room was calculated via a Computational Fluid Dynamics software, that droplets smaller than $30\mathrm{\mu }\mathrm{m}$ diameter would disperse within the room without significant influence of gravity or inertia. Accordingly, we consider that the initial velocity of the exhaled respirable droplets is the underlying fluid velocity, namely either the ambient air velocity or zero in its absence. For convenience, we henceforth refer to the ambient airflow as the ventilation. This airflow could be naturally induced (e.g. a draft through an open window) or be the result of an artificial indoor ventilation system.

It follows that, in an enclosed space with no ventilation, airborne droplets will be transported by molecular diffusion alone and $Q_D=-D_d\partial D/\partial x$, where D _d is the molecular droplet diffusivity. Molecular (Brownian) diffusivity may be safely ignored for droplets larger than $0.5\mathrm{\mu }\mathrm{m}$ diameter. We retain it in the formal derivation of the flux equations to allow the simulation of nanodroplets, to allow for turbulent droplet diffusion in the presence of an external turbulent flow, and to render the numerical solution of the parabolic differential equations stable. In a ventilated environment airborne droplets will also be convected by the ambient airflow. The appropriate flux is $Q_D=\mathit{vD}-D_d\partial D/\partial x$, where D _d is the turbulent diffusivity, and v the average, constant air ventilation velocity. The one-dimensional droplet flux is an idealized approximation. In reality, the air flow is unlikely to be at a constant unidirectional velocity, and ventilation may simply mix droplet and air particles around within the domain. A higher dimensional spatial model is required to describe such complex flow characteristics. However, the one-dimensional model can be a good approximation for environments where air is predominantly in one direction, for example a draft of air blowing through a room.

Assuming the diffusion coefficients of both people and droplets are constant the model is

$$\frac{\partial S}{\partial t}=-{\beta }_d\frac{\mathit{DS}}{N}+D_p\frac{{\partial }^{2}S}{\partial x^2},$$ (1)

$$\frac{\partial I}{\partial t}={\beta }_d\frac{\mathit{DS}}{N}-{\mu }_{i}I+D_p\frac{{\partial }^{2}I}{\partial x^2},$$ (2)

$$\frac{\partial N}{\partial t}=D_p\frac{{\partial }^{2}N}{\partial x^2},$$ (3)

$$\frac{\partial D}{\partial t}={\kappa }_{d}I-{\alpha }_{d}D-v\frac{\partial D}{\partial x}+D_d\frac{{\partial }^{2}D}{\partial x^2},$$ (4)

and the density of recovered individuals is obtained from $R=N-(S+I)$. Eqs. (1), (2), (3), (4) reduce to the model equations proposed in Stilianakis and Drossinos (2010) for infectious disease transmission by respirable droplets without contact transmission with zero ventilation velocity and diffusion coefficients.

We consider the spread of a pathogen in the domain $0\le x\le l$. We assume that people are confined to the interval $[0,l]$ and prescribe zero-flux conditions at the boundaries (the subscript x denotes partial differentiation with respect to x)

$$S_x(0,t)=S_x(l,t)=0,I_x(0,t)=I_x(l,t)=0,N_x(0,t)=N_x(l,t)=0.$$

The boundary conditions for droplets would be expected to depend on the type of ventilation present. We assume that droplets are removed from the system when they reach the end of the domain (physically this could be, for example, through a wall vent or an open window). One option is then to place an artificial boundary at the end of the domain x=l so that droplets effectively travel through the boundary unhindered. This is referred to as a transparent boundary condition. For convection-diffusion problems such a condition would take the form Wesseling (2000)

$$D_t(l,t)+{\mathit{vD}}_x(l,t)=0.$$

However, for a small diffusion coefficient, the boundaries are sufficiently far from the region of interest that, for the timescales of interest, droplets never reach them by diffusive processes alone. Therefore, it is sufficient to assume that droplets can be transported out of the domain by convection alone and we set the diffusive flux at the boundaries to zero

$$D_x(0,t)=D_x(l,t)=0.$$

In our simulations we compared the use of the transparent and diffusive boundary conditions and found that, as expected, solutions were identical. Therefore, we present only those performed with the zero diffusive flux condition.

The prescribed boundary conditions prevent the entrance or exit of people. Therefore, people are free to move about the domain but cannot leave it. Consequently, the total number of people in the domain will be constant for all time

$$n(t_0)={\int }_0^{l}N(x,t_0)\mathit{dx}=n_0,\forall t_0\ge 0.$$

Initial conditions must also be prescribed to distribute people throughout the domain at t=0. Since the total number of people in the domain is constant for all time, n ₀ is determined from the initial distribution

$$n_0={\int }_0^{l}N(x,0)\mathit{dx}={\int }_0^l[S(x,0)+I(x,0)]\mathit{dx},$$ (5)

where we assume the initial number of recovered (immune) people is identically zero, $R(x,0)=0$. Initially, we assume that no droplets are present and are generated for $t>0$ by the infected population. We consider two possibilities for the initial distribution of the human population. The total population can be uniformly distributed throughout the domain (Noble, 1974), which we henceforth refer to as a (spatially) homogeneous initial condition. This corresponds to a constant initial total population density

$$N_{\mathrm{homo}}(x,0)=\frac{n_0}{l}.$$

In this scenario, N will be constant for all time, with $N(x,t)=n_0/l$. Alternatively, people can be randomly distributed throughout the domain yielding a (spatially) heterogeneous initial condition. The latter case presents an opportunity to investigate whether droplets generated by infected individuals at one point in the domain can infect susceptible individuals at other locations, i.e., whether infection can occur without direct physical contact of a susceptible with an infected individual.

2.1. Scaling and non-dimensionalization

We scale all population densities with the uniform density $n_0/l$. The droplet scale is chosen by balancing droplet generation and removal processes such that, the number of droplets is approximately proportional to the number of infected people and the constant of proportionality is the ratio of the droplet generation and removal rates. We scale x with the length of the domain and choose the droplet removal time as the characteristic time scale, since this represents the time the droplet is airborne and capable of causing infection. Therefore, we scale

$$S,I,N\sim \frac{n_0}{l},D\sim \frac{{\kappa }_d}{{\alpha }_d}\frac{n_0}{l},x\sim l,t\sim \frac{1}{{\alpha }_d}.$$ (6)

The dimensionless equations are

$$\frac{\partial S}{\partial t}=-\lambda R_0\frac{\mathit{DS}}{N}+{\eta }_p\frac{{\partial }^{2}S}{\partial x^2},$$ (7)

$$\frac{\partial I}{\partial t}=\lambda R_0\frac{\mathit{DS}}{N}-\lambda I+{\eta }_p\frac{{\partial }^{2}I}{\partial x^2},$$ (8)

$$\frac{\partial N}{\partial t}={\eta }_p\frac{{\partial }^{2}N}{\partial x^2},$$ (9)

$$\frac{\partial D}{\partial t}=I-D-\nu \frac{\partial D}{\partial x}+{\eta }_d\frac{{\partial }^{2}D}{\partial x^2},$$ (10)

where

$$R_0=\frac{{\beta }_d{\kappa }_d}{{\alpha }_d{\mu }_i},\lambda =\frac{{\mu }_i}{{\alpha }_d},\nu =\frac{v}{{\alpha }_{d}l},{\eta }_{d,p}=\frac{D_{d,p}}{{\alpha }_d{l}^2}.$$

The dimensionless parameters and the characteristic time scales of the model are summarized in Table 1 . The parameter R ₀ is the basic reproduction number, which describes the spread of disease through a completely susceptible population in the initial stages of an outbreak. $\lambda$ is the ratio of the droplet removal time scale ${\tau }_r$ to the disease infectivity time ${\tau }_i$ and represents the fraction of the total disease infectivity period for which a droplet is capable of causing infection. The dimensionless coefficient of the convection term $\nu ={\tau }_r/{\tau }_c$ represents the ratio of the droplet-removal time to the convection time. Similarly, the dimensionless number ${\eta }_d={\tau }_r/{\tau }_d$ represents the ratio of the removal time to the diffusion time. Boundary and initial conditions in dimensionless form are given by

$$S_x(0,t)=S_x(1,t)=0,S(x,0)=S_0(x),$$

$$I_x(0,t)=I_x(1,t)=0,I(x,0)=I_0(x),$$

$$N_x(0,t)=N_x(1,t)=0,N(x,0)=S_0(x)+I_0(x),$$

$$D_x(0,t)=D_x(1,t)=0,D(x,0)=0,$$

where the functions $S_0(x)$ and $I_0(x)$ are prescribed initial population-density distributions. The dimensionless form of the initial population density, Eq. (5), is

$${\int }_0^{1}N(x,0)\mathit{dx}={\int }_0^1[S(x,0)+I(x,0)]\mathit{dx}=1.$$

For the homogeneous case, with constant initial population density $N_{\mathrm{homo}}(x,0)=1$, this implies

$$S(x,0)+I(x,0)=1.$$

Table 1.

Characteristic time scales and derived dimensionless parameters.

Time scale (s)		Dimensionless parameter
${\tau }_i=\frac{1}{{\mu }_i}$	Disease infectivity
${\tau }_t=\frac{{\alpha }_d}{{\beta }_d{\kappa }_d}$	Disease transmission	$R_0\equiv \frac{{\beta }_d{\kappa }_d}{{\alpha }_d{\mu }_i}=\frac{{\tau }_i}{{\tau }_t}$
${\tau }_r=\frac{1}{{\alpha }_d}$	Droplet removal (droplet infectivity)	$\lambda =\frac{{\mu }_i}{{\alpha }_d}=\frac{{\tau }_r}{{\tau }_i}$
${\tau }_c=\frac{l}{v}$	Convective	$\nu =\frac{v}{{\alpha }_{d}l}=\frac{{\tau }_r}{{\tau }_c}$
${\tau }_{d,p}=\frac{l^2}{D_{d,p}}$	Diffusion (droplet, person)	${\eta }_{d,p}=\frac{D_{d,p}}{{\alpha }_d{l}^2}=\frac{{\tau }_r}{{\tau }_{d,p}}$

3. Model parameters for an influenza outbreak

We apply the one-dimensional model to numerically study the spatial and temporal dynamics of a model for an influenza epidemic. Most of the required parameters are taken from Stilianakis and Drossinos (2010); the parameters specific to the spatial dynamics and droplet size are discussed in the following, and parameter values used in the numerical simulations are summarized in Table 2 .

Table 2.

Parameter values.

Parameter		Value
${\mu }_i$	Infection recovery rate	0.2 per day
c	Contact rate	13 per day
${\rho }_p$	Pathogen concentration in the lung fluid	3.71×106 pathogens cm−3
B	Breathing rate	24 m3 per day
Vcl	Personal-cloud volume of an infected person	8 m3
pd	Infection probability by an inhaled pathogen	0.052
${\tau }_{\mathit{ct}}$	Characteristic breathing (contact) time	20 min
${\beta }_p$	Transmission rate per inhaled pathogen	0.028 per day
v	Air velocity	0.2 m s−1
Dturd	Turbulent diffusivity of droplet	10−3 m2 s−1
Dp	Diffusivity of people	10−5 m2 s−1
${\mu }_p$	Pathogen inactivation rate	8.64 per day
l	Domain length	2000 m
Parameters dependent on droplet size
d	Droplet diameter (post-evaporation)	$d_1=4\mathrm{\mu }\mathrm{m}$
		$d_2=0.4\mathrm{\mu }\mathrm{m}$
Vd	Pre-evaporation (spherical) droplet volume	$V_{d_1}=2.68\times {10}^{-10}{\mathrm{cm}}^3$
		$V_{d_2}=2.68\times {10}^{-13}{\mathrm{cm}}^3$
$N_p^0$	Initial number of pathogens per droplet	$N_p(d_1)=9.95\times {10}^{-4}$
		$N_p(d_2)=9.95\times {10}^{-7}$
qd	Inhaled droplet deposition probability	$q_{d_1}=0.88$
		$q_{d_2}=0.2$
${\beta }_d$	Transmission rate per inhaled droplet	${\beta }_{d_1}=2.45\times {10}^{-5}$ per day
		${\beta }_{d_2}=5.57\times {10}^{-9}$ per day
${\kappa }_d$	Droplet production rate	${\kappa }_{d_1}=4.1\times {10}^5$ per day
		${\kappa }_{d_2}=6.14\times {10}^5$ per day
${\theta }_d$	Gravitational settling rate	${\theta }_{d_1}=28.80$ per day
		${\theta }_{d_2}=0.39$ per day
${\alpha }_d$	Droplet removal rate	${\alpha }_{d_1}=37.44$ per day
		${\alpha }_{d_2}=9.03$ per day
Dd	Molecular diffusivity of droplet	$D_{d_1}=6.2\times {10}^{-12}{\mathrm{m}}^2{\mathrm{s}}^{-1}$
		$D_{d_2}=8.34\times {10}^{-11}{\mathrm{m}}^2{\mathrm{s}}^{-1}$

The effect of droplet size on disease spread is investigated by choosing two characteristic respirable-droplet sizes of post-evaporative diameters $d_1=4\mathrm{\mu }\mathrm{m}$ and $d_2=0.4\mathrm{\mu }\mathrm{m}$. As mentioned earlier, the post-evaporative diameter is taken to be half the emitted pre-evaporative diameter. Droplet generation rates ${\kappa }_d$ are based on the number of pathogen loaded droplets emitted during a cough. Generations rates per cough are taken as ${\kappa }_{d_1}=160{\mathrm{day}}^{-1}$ (Nicas et al., 2005) and ${\kappa }_{d_2}=240{\mathrm{day}}^{-1}$ (Morawska et al., 2009), the latter based on a cough volume of 400 cm${}^3$. The daily generation rates are obtained by considering a 200-fold increase for a sneeze (Nicas et al., 2005), and a total of 11 sneezes and 360 coughs per day (Atkinson and Wein, 2008).

In the model presented here, the infectious agent is not the droplet but the pathogens it carries. Therefore, the transmission rate per droplet ${\beta }_d$ will depend the transmission rate per pathogen, ${\beta }_d={\beta }_p{q}_d{N}_p^0$, where q _d is the probability of deposition in the human respiratory tract and $N_p^0(d)$ is the number of pathogens in a droplet of diameter d. In turn, the transmission rate per pathogen ${\beta }_p$ is determined from the contact rate c _d of a susceptible with a droplet and the probability p _d that such a contact will result in successful transmission ${\beta }_p=c_d{p}_d$. In order to derive the contact rate with a droplet we assume that each infected person is surrounded by a droplet cloud with volume V _cl. It is further assumed that a susceptible individual comes in contact with a droplet through breathing during an encounter with this droplet cloud. If the average breathing rate is B and ${\tau }_{\mathit{ct}}$ is a characteristic time of breathing during the encounter then the contact rate c _d can be expressed as $c_d=c(B/V_{\mathit{cl}}){\tau }_{\mathit{ct}}$, where c is the average number of total contacts a susceptible individual has per unit time. The transmission rate per droplet is thus

$${\beta }_d=c\frac{B}{V_{\mathit{cl}}}{\tau }_{\mathit{ct}}{p}_d{q}_d{N}_p^0,$$

and the number of pathogens per droplet can be determined by $N_p^0=V_d{\rho }_p$, where V _d is the volume of the (spherical) pre-evaporative droplet and ${\rho }_p$ is the pathogen concentration of the lung fluid. Using the parameters of Table 2, the transmission rate per pathogen is calculated as 0.028 per day and the transmission rate per droplet thus evaluates to ${\beta }_{d_1}=2.45\times {10}^{-5}$ per day and ${\beta }_{d_2}=5.57\times {10}^{-9}$ per day.

The droplet removal rate is determined by three distinct processes: gravitational settling of the droplet, inactivation of the pathogen load (which effectively removes the droplet) and the inhalation of the droplet by population members. Following Stilianakis and Drossinos (2010) the removal rate can be expressed as

$${\alpha }_d={\theta }_d+{\mu }_p+(1+c{\tau }_{\mathit{ct}})\frac{B}{V_{\mathit{cl}}}{q}_d,$$ (11)

where ${\theta }_d$ is the gravitational settling rate of the droplet and ${\mu }_p$ is the inactivation rate of airborne pathogens. Gravitational settling rates are size dependent and we take ${\theta }_{d_1}=28.8$ per day and ${\theta }_{d_2}=0.39$ per day (Drossinos and Housiadas, 2006). This implies that, in the absence of other removal processes, a droplet with diameter $d_1=4\mathrm{\mu }\mathrm{m}$ will settle under gravity in a tranquil environment in approximately 50 min. Decreasing the droplet diameter by an order of magnitude results in the droplet remaining airborne for approximately 2.56 days. The pathogen inactivation rate ${\mu }_p$, assumed to be independent of size, is taken to be 8.64 per day (Hemmes et al., 1960) and a droplet is effectively removed through pathogen inactivation in under 3 h. Therefore, pathogen inactivation is a crucial process for the removal of smaller droplets that could, theoretically, take days to settle under gravity alone. Taking both gravitational settling and pathogen inactivation processes into account, droplets remain airborne and infectious for 38.5 min (d ₁) and 2.66 h (d ₂). The inclusion of removal through inhalation, the last term on the right-hand-side of Eq. (11), has negligible influence on these times (removal times of 35 min or 2.46 h for $d=d_1$ or $d=d_2$ respectively) and we approximate the droplet removal rate by ${\alpha }_d={\theta }_d+{\mu }_p$.

Droplet diffusivity will depend on the presence or absence of ventilation. In an unventilated environment, with $v\approx 0\mathrm{m}{\mathrm{s}}^{-1}$, the molecular diffusivity of droplets is calculated as $D_{d_1}=6.2\times {10}^{-12}{\mathrm{m}}^2{\mathrm{s}}^{-1}$ and $D_{d_2}=8.34\times {10}^{-11}{\mathrm{m}}^2{\mathrm{s}}^{-1}$ (Drossinos and Housiadas, 2006). For an air-conditioned environment with standard wall-mounted air-conditioners a typical airflow velocity is v=0.2 m s⁻¹ (Zhu et al., 2006) and we take this to be constant throughout the entire domain. Under such conditions the flow will invariably be turbulent and the droplet diffusivity will be several orders of magnitude larger. We estimate the turbulent diffusivity of both droplet classes to be $D_d^{\mathit{tur}}={10}^{-3}{\mathrm{m}}^2{\mathrm{s}}^{-1}$.

Human diffusivity, motion, can be crudely estimated from $D_p\approx x^2/t$, where x is a characteristic distance traveled in a time t. For the spatial spread of a disease through a geographically open population typical distances traveled per hour are in the range 18–42 m (Noble, 1974, Bertuzzo et al., 2010, Lou and Zhao, 2011). We expect that movement would be more restricted in a closed environment, for example a prison or long-term care facility, and we estimate that people diffuse approximately 10 m per hour yielding $D_p\approx {10}^{-5}{\mathrm{m}}^2{\mathrm{s}}^{-1}$. Intuitively, we estimate the spatial size of such environments to be of the order 10³  m and fix our domain length at l=2000 m.

4. Droplet dynamics

4.1. Characteristic time scales

The time scale of disease transmission ${\tau }_t={\alpha }_d/{\beta }_d{\kappa }_d$ is determined from droplet properties and is thus dependent on droplet size. We estimate ${\tau }_t(d_1)\approx 3.72$  days and ${\tau }_t(d_2)\approx 2640$  days. Clearly, the time required by the smaller droplet to transmit disease will result in minimal disease transmission for the duration of the infectivity period (approximately 5 days for influenza).

Droplet dynamics are greatly influenced by their (post-evaporative) diameter as this determines the residence time in air of an individual droplet, its infectivity properties and its pathogen load. The dynamics are described by three different timescales (Table 1), two of which, ${\tau }_r$ (droplet removal time scale) and ${\tau }_d$ (droplet diffusion time scale), are dependent on droplet size. The convective timescale ${\tau }_c$ represents the time it takes for the ambient airflow to carry the droplet the entire length of the domain. If l is of the order of ${10}^1-{10}^3\mathrm{m}$ then typical convection times are ${\tau }_c=O({10}^2-{10}^4)$  s and, clearly, convection is a fast process relative to the disease dynamics with ${\tau }_c⪡{\tau }_t$. Intuitively, this implies that lower ventilation velocities, which increase the convection time ${\tau }_c$, result in greater disease transmission. The droplet-removal (droplet infectivity) time scale is the inverse of the size-dependent droplet removal rate ${\alpha }_d$ with ${\tau }_r(d_1)\approx 38.46$  min and ${\tau }_r(d_2)\approx 2.66$  h. Thus, since ${\tau }_r(d_1)<{\tau }_r(d_2)$ we have that ${\nu }_{d_1}<{\nu }_{d_2}$ and convection effects, for a constant air-ventilation velocity, are stronger for smaller droplets since they remain airborne longer and can be carried further from their point of origin. Furthermore, $\nu$ is inversely proportional to the length l and convection will thus exert greater influence on droplet dynamics over shorter domains as droplets will be rapidly transported the entire length of the domain.

The droplet diffusion time scales depend on the presence or absence of an ambient airflow. For an unventilated environment, typical Brownian diffusion time scales will be ${\tau }_d(d_1)\sim {10}^9-{10}^{13}$ days and ${\tau }_d(d_2)\sim {10}^8-{10}^{12}$ days for $l\sim {10}^1-{10}^3\mathrm{m}$. In a ventilated environment, we estimate the time scale of turbulent diffusion to be ${\tau }_d^{\mathit{tur}}\sim 1-{10}^4$ days. Thus, for the short term spread of infection, since droplets are only airborne for $O(1\mathrm{h})$ and ${\tau }_r⪡{\tau }_d$, diffusion is an insufficient mechanism to transport droplets throughout the domain with the largest influence occurring at very short lengths and with non-zero airflow. However, over such lengths contact and droplet transmission are more likely to drive disease transmission.

From the preceding discussion on droplet timescales it is evident that, in a ventilated environment, droplets are rapidly transported out of the domain and disease transmission is comparatively too slow to result in substantial infection. For larger domains convection times can be significantly increased and the transmission of infection will become more efficient (e.g. ${\tau }_c\approx 3.5$ days for l=60,000 m). We estimate $R_0=1.34$ and $\lambda =0.005$ for $d_1=4\mathrm{\mu }\mathrm{m}$ and $R_0=0.0019$ and $\lambda =0.022$ for $d_2=0.4\mathrm{\mu }\mathrm{m}$. The lower value of R ₀ for $d=d_2$ is the result of the small viral load of the droplet which determines the magnitude of the transmission rate per droplet ${\beta }_d$, Table 2. Thus, the larger generation rates associated with smaller droplets do not result in greater transmission.

4.2. Droplet delay equation

For a ventilated environment we can neglect droplet diffusion and Eq. (10) becomes a first order equation. We consider the solution for the particular initial condition $D(x,0)=0$. The characteristic curves satisfy

$$\frac{\mathit{dt}}{\mathit{dx}}=\frac{1}{\nu },$$

which yields

$$t=\frac{(x-x_{⁎})}{\nu },$$ (12)

for any $x=x_{⁎}$ at t=0. Along each characteristic curve D will satisfy

$$\frac{\mathit{dD}}{\mathit{dx}}+\frac{1}{\nu }D=\frac{1}{\nu }I\left(x,\frac{x-x_{⁎}}{\nu }\right),$$

This first order linear equation can be easily solved for D(x) to obtain

$$D(x)=\frac{e^{-x/\nu }}{\nu }\left({\int }_0^x{e}^{\xi /\nu }I\left(\xi ,\frac{\xi -x_{⁎}}{\nu }\right)d\xi -{\int }_0^{x_{⁎}}{e}^{\xi /\nu }I\left(\xi ,\frac{\xi -x_{⁎}}{\nu }\right)d\xi \right).$$

The parameter x _⁎ can be eliminated using Eq. (12) yielding

$$D(x,t)=\frac{1}{\nu }{\int }_{x-\nu t}^x{e}^{-(x-\xi )/\nu }I\left(\xi ,t-\frac{x-\xi }{\nu }\right)d\xi .$$

This solution is only valid far from the boundaries, for $\nu t<x<1$, however, it provides an intuitive idea of the droplet dynamics. The role of droplets in disease transmission is thus to introduce a delay into the classic SIR system. Disease transmission at time t depends on the density of infected individuals at a previous time $t-((x-\xi )/\nu )$. The integral also describes how the convection of droplets influences the spatial spread of the disease. It describes the force of infection that individuals at position $\xi$ exert on those at x and as $|x-\xi |\to \infty$ the droplet density vanishes and no infection will occur. Thus, the transmission risk decays with distance from the source of infection. A corresponding equation can be derived for the diffusion-only scenario showing similar behavior and its derivation is outlined in Appendix A.

4.3. Stability of a homogeneous population density

We derive stability criteria for the homogeneous case where the total population density is uniformly distributed throughout the domain and N=1. For the basic disease-free state $(S,I,D)=(\mathrm{1,0},0)$, the evolution of small perturbations $(\widehat{S},\widehat{I},\widehat{D})$ are governed by the linearized equations

$${\widehat{S}}_t=-\lambda R_0\widehat{D}+{\eta }_p{\widehat{S}}_{\mathit{xx}},$$

$${\widehat{I}}_t=\lambda R_0\widehat{D}-\lambda \widehat{I}+{\eta }_p{\widehat{I}}_{\mathit{xx}},$$

$${\widehat{D}}_t=\widehat{I}-\widehat{D}-\nu {\widehat{D}}_x+{\eta }_d{\widehat{D}}_{\mathit{xx}}.$$

We consider perturbations proportional to $e^{\mathit{ikx}+\omega t}$, where $\omega$ and k are the frequency and wavenumber, respectively. On substitution into the linearized system we obtain a quadratic equation for $\omega$

$${\omega }^2+\omega (i\nu k+M+L)-\lambda R_0+\mathit{ML}+i\nu \mathit{kM}=0,$$

where, for convenience, we define

$$M=\lambda +{\eta }_p{k}^2,L=1+{\eta }_d{k}^2.$$

This has solution

$$\omega (k)=-i\frac{\nu k}{2}-\frac{(M+L)}{2}\left[1\pm \sqrt{1+\frac{4\lambda R_0-4\mathit{ML}-{\nu }^2{k}^2}{(M+L{)}^2}+2i\frac{\nu k(L-M)}{(L+M{)}^2}}\right].$$ (13)

The disease-free state will be unstable when the real part $\mathfrak{R}\{\omega (k)\}>0$ and disturbances with wavenumber k will grow. Defining the square root in Eq. (13) as $p+\mathit{iq}$, with $p>0$ and both p and q real, we can write

$$\mathfrak{R}\{\omega \}=-\frac{(M+L)}{2}(1\pm p),$$

where for instability we require $p>1$. Now, equating real and imaginary parts yields

$$p^2-q^2=1+\frac{4\lambda R_0-4\mathit{ML}-{\nu }^2{k}^2}{(M+L{)}^2},q=\frac{\nu k(L-M)}{p(L+M{)}^2}.$$

Solving for q in terms of p we obtain

$$F(p)=p^2-\frac{{\nu }^2{k}^2(L-M{)}^2}{p^2(L+M{)}^4}=\frac{(M+L{)}^2+4\lambda R_0-4\mathit{ML}-{\nu }^2{k}^2}{(M+L{)}^2}.$$

Since F(p) is a monotonic increasing function of p the condition for instability can be expressed as $F(p)>F(1)$ which yields

$$R_0>\frac{\mathit{ML}}{\lambda }\left[1+\frac{{\nu }^2{k}^2}{(M+L{)}^2}\right].$$ (14)

We calculate ${\eta }_p=5.77\times {10}^{-9}$ and ${\eta }_d=3.57\times {10}^{-15}$ and, since ${\eta }_d⪡{\eta }_p⪡1$, we can approximate Eq. (14) by

$$R_0>1+{\nu }^2\frac{k^2}{(\lambda +1{)}^2}.$$

Clearly, $R_0>1$ is a necessary condition for instability and it follows that the infection will always die out for $d=d_2$, regardless of whether ventilation is present or not, since $R_0=0.0019⪡1$. In an unventilated environment, $\nu =0$, the larger airborne droplets will be transported by diffusion alone and the uniform state is unstable at all wavenumbers when $R_0>1$ and the infection will spread. In a ventilated environment, $\nu >0$, disturbances with a wavenumber satisfying

$$k<\frac{(\lambda +1)}{\nu }\sqrt{R_0-1}=k_{\mathrm{crit}}$$ (15)

will be unstable. This result shows that the basic homogeneous disease-free state is stable to short wavelength perturbations ($k\to \infty$) and only becomes unstable at long wavelengths ($k\to 0$). The stability diagram is sketched in Fig. 1 . Clearly, R ₀ must exceed unity for the onset of instability and, for fixed $R_0>1$, the critical wavenumber decreases with increasing $\nu$, which physically corresponds to increasing the ventilation velocity and thereby reducing the time it takes for droplets to traverse the domain. Therefore, increasing $\nu$ has a stabilizing effect, by reducing the number of unstable modes that will be amplified.

Fig. 1.

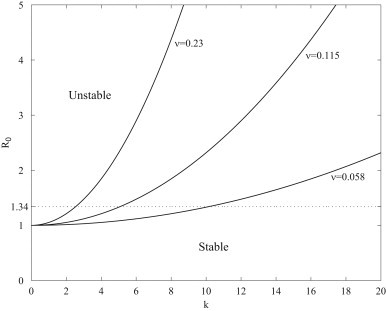
Stability diagram for a homogeneously distributed population.

For a velocity of v=0.2 m s⁻¹, the critical wavenumber is $k_{\mathrm{crit}}=2.54$ and perturbations with wavelength satisfying $\Lambda >{\Lambda }_{\mathrm{crit}}=2\pi /k\approx 2.47$ will be amplified. Significantly, all permissible wavelengths ($\Lambda <1$) for our domain $x\in (\mathrm{0,1})$ are stable and therefore an arbitrary perturbation to the disease-free state will decay. Reducing the ventilation velocity decreases ${\Lambda }_{\mathrm{crit}}$ and unstable modes become permissible within the domain and any arbitrary perturbation will grow in time. The analysis indicates that, for a fixed size domain, increasing the ventilation velocity can mitigate the effects of a respiratory disease.

5. Numerical Results

We examined the spatial dynamics of the model for droplet size $d_1=4\mathrm{\mu }\mathrm{m}$ considering both homogeneous and heterogeneous initial population-density distributions. The system (7), (8), (9), (10) was solved using a fully implicit finite difference scheme implemented in Matlab^®.

5.1. An unventilated environment

In an unventilated environment, with $\nu =0$, the spatial spread of disease will solely depend on the diffusion of people or droplets. Droplet diffusion is a slow process, for example a $4\mathrm{\mu }\mathrm{m}$ droplet will diffuse approximately 5.7 mm while airborne. In the same time a person could diffuse over 7 m. Therefore, the spatial spread of disease will be driven by the diffusion of people as droplets are essentially stationary relative to the human population. Mathematically, this observation follows immediately from the inequality ${\eta }_d⪡{\eta }_p$. We first consider the disease spread when a localized infected density is introduced to a uniformly distributed susceptible population. We find that, for small times ($t\sim 5\approx 3\mathrm{h}$), droplet density rapidly increases until $D(x,t)\approx I(x,t)$ and subsequently droplets and infected dynamics are indistinguishable. This occurs once droplet generation and removal processes are essentially balanced. This indicates that there is no separation between droplets and infected individuals and close contact is required for efficient transmission. At larger times the localized infectious peak is observed to grow in amplitude, Fig. 2 (a). An outbreak in a closed population could be expected to persist for many weeks. However, times in excess of $t=2000\approx 53$ days are unrealistic for an influenza epidemic. At such times the model predicts the formation of two infectious traveling pulses, propagating in opposite directions. Accordingly, the density of susceptibles evolves into a wave front slowly infiltrating the completely susceptible population ahead of the front, Fig. 2(b). There are several reasons why this behavior is observed. Firstly, the idealized case of a homogeneous population, where the infected population is surrounded by a constant source of susceptibles is uncharacteristic of a true human population distribution. In the absence of susceptible individuals the density of infected individuals would rapidly decay, Fig. 3 . Secondly, once an outbreak is identified within the closed population, interventions such as isolation, quarantine or treatment would be imposed to limit the impact of the outbreak. Diffusion models used to describe the larger scale geographic spread of disease display such traveling wave behavior, with transportation networks simulated using larger diffusion coefficients and timescales of the order of years being considered (Noble, 1974, Murray et al., 1986).

Fig. 2.

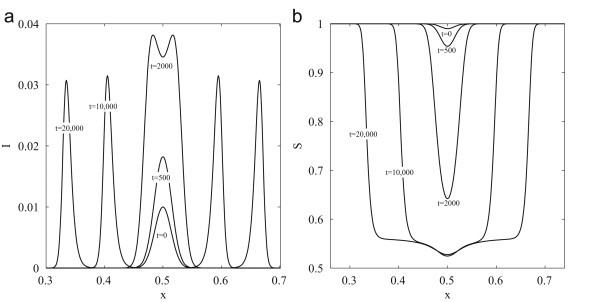
Model dynamics of airborne-influenza transmission driven by the diffusion of people, with droplet diameter $d_1=4\mathrm{\mu }\mathrm{m}$. Initial conditions are $I_0(x)=0.01e^{-k^2(x-0.5{)}^2}$, $S_0(x)=1-I_0(x)$ with wavenumber k=50. (a) Density of infected individuals. (b) Density of susceptible individuals. All variables are dimensionless and scaled following (6).

Fig. 3.

Model dynamics of influenza transmission driven by the diffusion of people, with droplet diameter $d_1=4\mathrm{\mu }\mathrm{m}$. The graph shows the densities of susceptible (solid line) and infected (dashed line) individuals with initial condition $I_0(x)=(25/\sqrt{\pi })e^{-k^2(x-0.4{)}^2}$, $S_0(x)=(25/\sqrt{\pi })e^{-k^2(x-0.5{)}^2}$ and wavenumber k=50. All variables are dimensionless and scaled following (6).

Disease spread resulting from a heterogeneous initial distribution, where localized densities of infected and susceptible individuals are placed in different regions of the domain, is considered in Fig. 3. As before, the droplet density rapidly approaches the density of infected individuals and the two densities are thereafter indistinguishable from each other. We find that, even with very close contact between the two groups, diffusion is too slow a process to effectively transmit infection. In the absence of a susceptible population, and since ${\eta }_p⪡1$, the density of infectious individuals at any point $x=x_0$ will decay via $I(t)=I_0(x_0)e^{-\lambda t}\to 0$ as $t\to \infty$. The lifetime of the infected population is thus $1/\lambda$ which (dimensionally) corresponds to the disease infectivity time scale ${\tau }_i$ of 5 days. The infected population recovers before diffusion has time to effectively transmit the infection, ${\tau }_i⪡{\tau }_p$. To conclude, in the absence of an ambient airflow, diffusion is an inefficient mechanism for the spatial spread of disease which will, presumably, be driven by contact and droplet transmission during close contact events.

5.2. A ventilated environment

In a ventilated environment, with $\nu >0$, the infection dynamics are determined by the droplet size, the ambient air velocity and the length of the spatial domain. For a fixed droplet size and domain length, the wavenumbers that satisfy Eq. (15) are determined solely by the ventilation velocity v. As discussed in Section 4.3, when v=0.2 m s⁻¹, all permissible wavenumbers are stable. The evolution of an arbitrary perturbation under such conditions is shown in Fig. 4 . Droplets generated by the infectious population are rapidly transported out of the domain causing minimal infection as they travel through the susceptible population, since the convective timescale is much less than that required for transmission ${\tau }_c⪡{\tau }_t$, and the infectious curve decays.

Fig. 4.

Model dynamics of an influenza outbreak driven by the convection of droplets, with respirable droplet diameter $d_1=4\mathrm{\mu }\mathrm{m}$ and ventilation velocity v=0.2 m s⁻¹. Initial conditions are $I_0(x)=0.01e^{-k^2(x-0.2{)}^2}$, $S_0(x)=1-I_0(x)$ with k=30. (a) Density of infected individuals. (b) Density of droplets. All variables are dimensionless and scaled following (6).

If we rewrite (15), we find that the basic-state will be stable to an arbitrary perturbation provided the ventilation velocity satisfies

$$v>\frac{{\alpha }_{d}l(\lambda +1)}{2\pi }\sqrt{R_0-1}=v_{\mathrm{crit}}.$$

For parameter values listed in Table 2 we find that $v_{\mathrm{crit}}=0.08\mathrm{m}{\mathrm{s}}^{-1}$ and ventilation velocities of this magnitude and above are sufficient to prevent the spatial spread by the airborne route for a uniformly distributed population. However, we emphasize that this is an approximate value obtained for the relatively small diffusion of people and neglecting the possibility of contact and/or droplet transmission. In addition, the true air velocity will depend on the distance from the ventilation source, with larger velocities closer to the source. The unstable evolution of an arbitrary perturbation when v=0.01 m s⁻¹ is shown in Fig. 5 . An infectious pulse can be seen to propagate through the susceptible population in the direction of positive air flow. Droplet and infected densities are qualitatively similar and only slightly out of phase with each other, with droplets propagating ahead of the infectious pulse. Dynamically this implies that, for small air velocities, the dynamics of droplets and infectious individuals are closely coupled and only separate from each other at sufficiently high velocities.

Fig. 5.

Model dynamics of an influenza outbreak driven by the convection of droplets, with respirable droplet diameter $d_1=4\mathrm{\mu }\mathrm{m}$ and ventilation velocity v=0.01 m s⁻¹. Initial conditions are $I_0(x)=0.01e^{-k^2(x-0.2{)}^2}$, $S_0(x)=1-I_0(x)$ with k=30. (a) Densities of infected individuals (solid line) and droplets (dashed line). (b) Density of susceptible individuals. All variables are dimensionless and scaled following (6).

Finally, we consider the spatial transmission of infection resulting from a heterogeneous initial population distribution, where infected and susceptible populations are placed at separate locations in the domain, Fig. 6 . For small times, $t\sim 10\approx 6$  h, the infected population generate droplets which are subsequently transported in the direction of positive air flow. A secondary curve for infectious individuals forms when droplets encounter the susceptible population, $t=100\approx 2.5$ days. At later times these secondary cases produce droplets of their own and a secondary peak in the droplet curve can be observed, $t=500\approx 13$ days. The amplitude of the secondary curve for infectious individuals is obviously influenced by the initial distance between the infectious and susceptible populations. At large times, $t=1000\approx 26$ days, it is clear that the amplitudes of both curves for infectious individuals decay. This behavior results from the decay of the initial infectious population through recovery and the subsequent reduction in droplets being convected towards the susceptible region. This demonstrates that it is possible for infection to occur in the absence of an infected population and purely as the result of the airborne non-diffusive transport of aerosol droplets.

Fig. 6.

Model dynamics of an influenza outbreak driven by the convection of droplets, with respirable droplet diameter $d_1=4\mathrm{\mu }\mathrm{m}$ and ventilation velocity v=0.2 m s⁻¹. The graphs show the density of susceptibles (solid line) on the right vertical axis. The densities of infected individuals (dashed line) and droplets (dotted line) are shown on the left vertical axis. Initial conditions are $I_0(x)=(25/\sqrt{\pi })e^{-k^2(x-0.4{)}^2}$, $S_0(x)=(25/\sqrt{\pi })e^{-k^2(x-0.6{)}^2}$ and with k=50. All variables are dimensionless and scaled following (6).

6. Discussion

In this work we developed a model for the spatial spread of an airborne infection driven by pathogen-carrying droplets. Two droplet diameter values, $d_1=4\mathrm{\mu }\mathrm{m}$ and $d_2=0.4\mathrm{\mu }\mathrm{m}$, were considered that are representative of experimentally determined droplet size distributions. Droplet dynamics are governed by generation and removal processes, the latter being dominated by gravitational settling and pathogen inactivation. Inactivation is a particularly crucial removal process for smaller droplets that could remain airborne for days. Smaller droplets are found to be a weak disease vector. Their relatively large generation rates do not result in greater transmission due to the small viral load and the associated duration required to transmit infection. Transmission is, thus, dominated by the larger droplets.

A delay equation was derived for the droplet density as a function of the infected population density. The role of droplets in disease transmission is to introduce a delay into the system, with disease transmission at a given time dependent on the number of infected individuals present at a previous time. The equation also highlights how droplet-driven transmission decays with distance from the source of infection.

The relative importance of diffusive and convective processes in the spatial spread of infection was investigated. Two initial population distributions were considered: spatially homogeneous or heterogeneous. In both cases droplet diffusion is shown to be a slow process with disease spread, in an unventilated environment, driven by human movement. This result follows from the observation that the time require for droplets to diffuse is significantly greater than that for humans, ${\tau }_p⪡{\tau }_d$. In the homogeneous scenario and for long time scales, the model displays the classic infectious wave propagating through a susceptible population, following an initial transient state until a balance is achieved between droplet generation and removal processes. In contrast, human diffusion is an insufficient mechanism to transmit disease in the heterogeneous scenario, with the infected population recovering before encountering susceptible individuals, ${\tau }_i⪡{\tau }_d$. However, the inclusion of ventilation effects and the subsequent transport of droplets from the source of infection can result in a secondary outbreak if susceptible individuals are encountered. This signifies that infection is possible without direct contact between susceptible and infected individuals. Furthermore, it was shown that increasing the velocity above a critical value can impair disease transmission in a homogeneously distributed population as droplets will be rapidly transported out of the domain causing minimal infection since the time required for transmission is large relative to the convective time scale ${\tau }_c⪡{\tau }_t$.

The use of ventilation to prevent disease transmission is well-accepted by both society and science. However, little work has been done on implementing control strategies based on this knowledge. Identifying optimum air velocities for indoor environments could mitigate transmission and reduce the disease burden in health-care facilities, schools and other densely populated locations. The model presented here indicates that, in a fixed size environment, the distribution of sick/healthy individuals and the ambient air velocity are the primary factors to consider when analyzing such an intervention.

Appendix A. Solution of the droplet equation with diffusion

In the absence of ventilation effects the droplet equation (10) takes the form

$$\frac{\partial D}{\partial t}=-D+I+{\eta }_d\frac{{\partial }^{2}D}{\partial x^2},$$ (A.1)

and for convenience, we consider the solution on an infinite domain as droplet diffusion is a sufficiently slow process that boundaries do not interfere with the solutions, Fig. 2, Fig. 3. We let $D(x,0)=\varphi (x)$ denote the initial droplet density and assume a solution of the form

$$D(x,t)=H(t)G(x,t),$$

which yields

$$\frac{\partial G}{\partial t}+\frac{G(x,t)}{H(t)}\frac{\mathit{dH}}{\mathit{dt}}=-G(x,t)+\frac{I(x,t)}{H(t)}+{\eta }_d\frac{{\partial }^{2}G}{\partial x^2}\mathrm{with}H(t)\ne 0.$$

We choose H(t) to satisfy

$$\frac{\mathit{dH}}{\mathit{dt}}=-H,\Rightarrow H(t)=e^{-t},$$

and the function $G(x,t)$ then satisfies the inhomogeneous diffusion equation

$$\frac{\partial G}{\partial t}=f(x,t)+{\eta }_d\frac{{\partial }^{2}G}{\partial x^2},$$

where $f(x,t)=I(x,t)/H(t)$ and with initial condition $G(x,0)=\varphi (x)$. Following Kevorkian (2000), the solution for $G(x,t)$ will be of the form

$$G(x,t)=u(x,t)+v(x,t),$$

where u and v are the solutions of the simplified diffusion equations

$$u_t={\eta }_d{u}_{\mathit{xx}}+\mathit{f(x,t)},v_t={\eta }_d{v}_{\mathit{xx}},$$

$$u(x,0)=0,v(x,0)=\varphi (x).$$

These equations can easily be solved to obtain

$$u(x,t)={\int }_0^t{\int }_{-\infty }^{\infty }\frac{1}{\sqrt{4\pi {\eta }_d(t-t\prime )}}\exp \left(-\frac{(x-x\prime {)}^2}{4{\eta }_d(t-t\prime )}\right)f(x\prime ,t\prime )\mathit{dx}\prime \mathit{dt}\prime ,$$

$$v(x,t)=\frac{1}{\sqrt{4\pi {\eta }_{d}t}}{\int }_{-\infty }^{\infty }\exp \left(-\frac{(x-x\prime {)}^2}{4{\eta }_{d}t}\right)\varphi (x\prime )\mathit{dx}\prime ,$$

and the solution of (A.1) is then

$$D(x,t)=e^{-t}{\int }_0^t{\int }_{-\infty }^{\infty }\frac{1}{\sqrt{4\pi {\eta }_d(t-t\prime )}}\exp \left(-\frac{(x-x\prime {)}^2}{4{\eta }_d(t-t\prime )}\right)\frac{I(x\prime ,t\prime )}{H(t\prime )}\mathit{dx}\prime \mathit{dt}\prime +e^{-t}\frac{1}{\sqrt{4\pi {\eta }_{d}t}}{\int }_{-\infty }^{\infty }\exp \left(-\frac{(x-x\prime {)}^2}{4{\eta }_{d}t}\right)\varphi (x\prime )\mathit{dx}\prime .$$