New method for comparing DNA primary sequences based on a discrimination measure

Abstract

We introduce a new approach to compare DNA primary sequences. The core of our method is a new measure of pairwise distances among sequences. Using the primitive discrimination substrings of sequence S and Q, a discrimination measure DM(S, Q) is defined for the similarity analysis of them. The proposed method does not require multiple alignments and is fully automatic. To illustrate its utility, we construct phylogenetic trees on two independent data sets. The results indicate that the method is efficient and powerful.

1. Introduction

With the completion of the sequencing of the genomes of human and other species, the field of analysis of genomic sequences is becoming very important tasks in bioinformatics. Comparison of primary sequences of different DNA strands remains the upmost important aspect of the sequence analysis. So far, most comparison methods are based on string alignment (Pearson and Lipman, 1988, Lake, 1994): a distance function is used to represent insertion, deletion, and substitution of letters in the compared strings. Using the distance function, one can compare DNA primary sequences and resolve the questions of the homology of macromolecules. However, it is not easy to use for long sequences since it is realized with the aid of dynamic programming, which will be slow due to the large number of computational steps.

In the past two decades, alignment-free sequence comparison (Vinga and Almeida, 2003) has been actively pursued. Some new methods have been derived with a variety of theoretical foundations. One category out of these methods is based on the statistics of word frequency within a DNA sequence (Sitnikova and Zharkikh, 1993, Karlin and Burge, 1995, Wu et al., 1997, Wu et al., 2001, Stuart et al., 2002, Qi et al., 2004). The core idea is that the more similar the two sequences are, the greater the number of the factors shared by two sequences is. The earliest publication using frequencies statistics of k-words for sequence comparison dates from 1986 (Blaisdell, 1986). Three years after, Blaisdell (1989) proved that the dissimilarity values observed by using distance measures based on word frequencies are directly related to the ones requiring sequence alignment. In recent years, many researchers employ the k-words and the Markov model to obtain the information about the biological sequences (Pham and Zuegg, 2004, Pham, 2007, Kantorovitz et al., 2007, Helden, 2004, Dai et al., 2008).

Another category does not require resolving the sequence with fixed word length segments. It can be further divided into three groups. In the first group, researchers represent DNA sequence by curves (Hamori and Ruskin, 1983, Nandy, 1994, Randic et al., 2003a, Randic et al., 2003b, Zhang et al., 2003, Liao, 2005, Li et al., 2006; Qi et al., 2007, Yu et al., 2009), numerical sequences (He and Wang, 2002), or matrices (Randic, 2000, Randic et al., 2001). According to the representation, some numerical characterizations are selected as invariants of sequence for comparisons of DNA primary sequences. The advantage of these methods is that they provide a simple way of viewing, sorting and comparing various gene structures. But how to obtain suitable invariants to characterize DNA sequences and compare them is still a question need our attention.

The second group corresponds to iterated maps. Jeffrey (1990) proposed the chaos game representation (CGR) as a scale-independent representation for genomic sequences. The algorithm exploited iterative function systems to map nucleotide sequences into a continuous space. Since then, alignment-free methods based on CGR have aroused much interest in the field of computational biology. Further studies by Almeida et al. (2001) showed that CGR is a generalized Markov chain probability table which can accommodate non-integer orders, and that CGR is a powerful sequence modelling tool because of its computational efficiency and scale-independence (Almeida and Vinga, 2002, Almeida and Vinga, 2006, Almeida and Vinga, 2009). Such alignment-free methods have been successfully applied for sequence comparison, phylogeny, detection of horizontal transfers, detection of oligonucleotides of interest, meta-genomic studies (Deschavanne et al., 1999, Pride et al., 2003, Sandberg et al., 2003, Teeling et al., 2004, Chapus et al., 2005, Wang et al., 2005, Dufraigne et al., 2005, Joseph and Sasikumar, 2006).

The third group is based on text compression technique (Li et al., 2001, Chen et al., 2004, Cilibrasi et al., 2004). If one sequence which is given the information contained in the other sequence is significantly compressible, the two sequences are considered to be close. There are also some important methods which are based on compression algorithm but do not actually apply the compression, such as Lemple–Ziv complexity and Burrows–Wheeler transform (Otu and Sayood, 2003, Mantaci et al., 2007, Mantaci et al., 2008, Yang et al., 2010).

In this paper, we propose a new sequence distance for the similarity analysis of DNA sequences. Based on the properties of primitive discrimination substrings, we construct a discrimination measure (DM) between every two sequences. Furthermore, as application, two data sets ($\mathrm{\beta }\text{-globin}$ genes and coronavirus genomes) are prepared and tested to identify the validity of the method. The results demonstrate that the new method is powerful and efficient.

2. Discrimination measure

DNA sequences consist of four nucleotides: A (adenine), G (guanine), C (cytosine), and T (thymine). A DNA sequence, of length n, can be viewed as a linear sequence of n symbols from a finite alphabet $\mathcal{A}=\{\mathrm{A},\mathrm{C},\mathrm{G},\mathrm{T}\}$. Let S and Q be sequences defined over $\mathcal{A}$, l(S) be the length of S, S(i) denotes the ith element of S and S(i, j) is the substring of S composed of the elements of S between positions i and j (inclusive).

Definition 1

S(i, j) is called a discrimination substring (DS) that distinguishes S from Q if $S(i,j)\overline{\in }Q$, particularly, if S(i, j) does not include any other DSs distinguishing S from Q, we call S(i, j) a primitive discrimination substring (PDS) that distinguishes S from Q.

The set of PDSs that distinguish S from Q is denoted by $\mathrm{\Delta }(S,Q)$. Similarly, $\mathrm{\Delta }(Q,S)$ expresses the set of PDSs that distinguish Q from S. Note that every sequence has its own identity, hence $\mathrm{\Delta }(S,Q)$ is usually different from $\mathrm{\Delta }(Q,S)$. For example for S=acctac and Q=gtgact, we can obtain that $\mathrm{\Delta }(S,Q)=\{\mathit{cc},\mathit{ta}\}$ and $\mathrm{\Delta }(Q,S)=\{\mathit{gt},\mathit{tg},\mathit{ga},\mathit{act}\}$.

Suppose $u\in \mathrm{\Delta }(S,Q)$ and l(u)=k, then we can get $u(1,k-1)\in Q$ (otherwise $u(1,k-1)\in \mathrm{\Delta }(S,Q)$, which conflicts with the minimum of u). Therefore the larger the k is, the more the same elements both S and Q have and correspondingly the smaller the degree of discrimination that S distinguishes from Q is. On the other hand, if the number of appearances of u in sequence S is t, we obviously note that the smaller the t is, the smaller the degree of discrimination that S distinguishes from Q is. From the above description, we construct the following discrimination measure that one sequence distinguishes from another sequence.

Definition 2

$\mathit{DM}(S_1\to S_2)$ denotes the discrimination measure that S ₁ distinguishes from S ₂

$$\mathit{DM}(S\to Q)=\sum _{u\in \mathrm{\Delta }(S,Q)}t/[(l(S)-k+1){\log }_2(k+1)]\text{,}$$

$$\mathit{DM}(Q\to S)=\sum _{v\in \mathrm{\Delta }(Q,S)}t\prime /[(l(Q)-k\prime +1){\log }_2(k\prime +1)]\text{,}$$

in which $v\in \mathrm{\Delta }(Q,S)$, $l(v)=k\prime$ and the number of appearances of v in sequence Q is $t\prime$.

Definition 3

The discrimination measure of sequences S and Q is

$$\mathit{DM}(S,Q)=\sqrt{(\mathit{DM}(S\to Q){)}^2+(\mathit{DM}(Q\to S){)}^2}\text{.}$$

For the function DM to be a distance, it must satisfy (a) $\mathit{DM}(x,y)>0$ for $x\ne y$; (b) DM(x,x)=0; (c) DM(x,y)=DM(y,x) (symmetric); and (d) $\mathit{DM}(x,y)\le \mathit{DM}(x,z)+\mathit{DM}(z,y)$ (triangle inequality). Apparently, DM satisfies distance conditions (a)–(c). It is not obvious that it also satisfies (d). The following proposition answers this.

Proposition 1

DM(x,y) satisfies the triangle inequality, that is $\mathit{DM}(x,z)\le \mathit{DM}(x,y)+\mathit{DM}(y,z)$.

Proof

Suppose s is an arbitrary element of $\mathrm{\Delta }(x,z)$. If s is also contained in $\mathrm{\Delta }(x,y)$, clearly we can obtain that $\mathit{DM}(x\to z)\le \mathit{DM}(x\to y)+\mathit{DM}(y\to z)$. If there exists an element $t\in \mathrm{\Delta }(x,z)$, and t is not contained in $\mathrm{\Delta }(x,y)$, then we can derive $t\in \mathrm{\Delta }(y,z)$, therefore the triangle inequality $\mathit{DM}(x\to z)\le \mathit{DM}(x\to y)+\mathit{DM}(y\to z)$ still comes into existence. Similarly, we can prove that $\mathit{DM}(z\to x)\le \mathit{DM}(y\to x)+\mathit{DM}(z\to y)$.

Let $a=\mathit{DM}(x\to z)$, $b=\mathit{DM}(z\to x)$, $c=\mathit{DM}(x\to y)$, $d=\mathit{DM}(y\to x)$, $e=\mathit{DM}(y\to z)$, $f=\mathit{DM}(z\to y)$, we need to show

$$\sqrt{a^2+b^2}\le \sqrt{c^2+d^2}+\sqrt{e^2+f^2}\text{.}$$

Since

$$\sqrt{a^2+b^2}\le \sqrt{(c+e{)}^2+(d+f{)}^2}\text{,}$$

it is sufficient to prove the following inequality:

$$\sqrt{(c+e{)}^2+(d+f{)}^2}\le \sqrt{c^2+d^2}+\sqrt{e^2+f^2}\text{.}$$

This is equivalent to, by squaring both sides of the above inequality,

$$\mathit{ce}+\mathit{df}\le \sqrt{(c^2+d^2)(e^2+f^2)}\text{.}$$

To prove this inequality, we just need to prove

$$(\mathit{ce}+\mathit{df}{)}^2\le (c^2+d^2)(e^2+f^2)\text{,}$$

i.e. $2\mathit{cedf}\le e^2{d}^2+c^2{f}^2.$ Obviously, this inequality comes into existence. Therefore,

$$\sqrt{a^2+b^2}\le \sqrt{c^2+d^2}+\sqrt{e^2+f^2}\text{.}$$

Hence DM(x,y) satisfies the triangle inequality.  □

3. Results and discussion

In this section, we apply the discrimination measure to analyze two sets of DNA primary sequences. The similarities among these species are computed by calculating the discrimination measure between every two sequences. The smaller the discrimination measure is, the more similar the species are. That is to say, the discrimination measures of evolutionary closely related species are smaller, while those of evolutionary disparate species are larger. Fig. 1 illustrates the basic processes of the DM algorithm. The first set we select includes 10 $\mathrm{\beta }\text{-globin}$ genes, whose similarity has been studied by many researchers using their first exon sequences (Randic et al., 2003a, Randic et al., 2003b, Liu and Wang, 2005). Here we will analyze these species using their complete $\mathrm{\beta }\text{-globin}$ genes. Table 1 presents their names, EMBL accession numbers, locations and lengths.

Fig. 1.

The flow diagram of our method.

Table 1.

The full DNA sequences of $\mathrm{\beta }\text{-globin}$ gene of 10 species.

Species	Database	Accession	Location	Length (bp)
Human	EMBL	U01317	62187–63610	1424
Goat	EMBL	M15387	279–1749	1471
Opossum	EMBL	J03643	467–2488	2022
Gallus	EMBL	V00409	465–1810	1346
Lemur	EMBL	M15734	154–1595	1442
Mouse	EMBL	V00722	275–1462	1188
Rat	EMBL	X06701	310–1505	1196
Gorilla	EMBL	X61109	4538–5881	1344
Bovine	EMBL	X00376	278–1741	1464
Chimpanzee	EMBL	X02345	4189–5532	1344

In Table 2 , we present the similarity/dissimilarity matrix for the full DNA sequences of $\mathrm{\beta }\text{-globin}$ gene from 10 species listed in Table 1 by our new method. Observing Table 2, we note that the most similar species pairs are human–gorilla, human–chimpanzee and gorilla–chimpanzee, which is expected as their evolutionary relationship. At the same time, we find that gallus and opossum are the most remote from the other species, which coincides with the fact that gallus is the only nonmammalian species among these 10 species and opossum is the most remote species from the remaining mammals. By further study of the values in the table, we can gain more information about their similarity.

Table 2.

The similarity/dissimilarity matrix for 10 $\mathrm{\beta }\text{-globin}$ genes based on DM.

Species	Human	Goat	Oposs.	Gallus	Lemur	Mouse	Rat	Gorilla	Bovine	Chimp.
Human	0	0.2394	0.2683	0.2803	0.2233	0.2484	0.2489	0.0294	0.2438	0.0297
Goat		0	0.2761	0.2844	0.2502	0.2634	0.2570	0.2474	0.1130	0.2471
Oposs.			0	0.2895	0.2828	0.2728	0.2698	0.2701	0.2785	0.2733
Gallus				0	0.2827	0.2778	0.2838	0.2895	0.2805	0.2896
Lemur					0	0.2591	0.2502	0.2223	0.2545	0.2201
Mouse						0	0.1863	0.2548	0.2606	0.2530
Rat							0	0.2562	0.2628	0.2558
Gorilla								0	0.2472	0.0167
Bovine									0	0.2483
Chimp.										0

Another usage of the similarity/dissimilarity matrix is that it can be used to construct phylogenetic tree. The quality of the constructed tree may show whether the matrix is good and therefore whether the method of abstracting information from DNA sequences is efficient. Once a distance matrix has been calculated, it is straightforward to generate a phylogenetic tree using the NJ method or the UPGMA method in the PHYLIP package (http://evolution.genetics.washington.edu/phylip.html). In Fig. 2 , we show the phylogenetic tree of 10 $\mathrm{\beta }\text{-globin}$ gene sequences based on the distance matrix DM, using NJ method. The tree is drawn using the DRAWGRAM program in the PHYLIP package. From this figure, we observe that (1) gallus is clearly separated from the rest, this coincides with real biological phenomenon; (2) human, gorilla, chimpanzee and lemur are placed closer to bovine and goat than to mouse and rat, this is in complete agreement with Cao et al. (1998) confirming the outgroup status of rodents relative to ferungulates and primates.

Fig. 2.

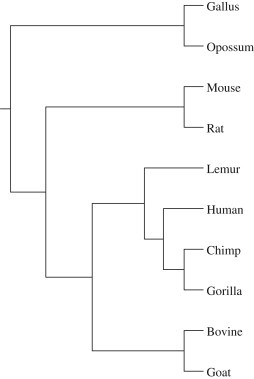
The phylogenetic tree for 10 species using the full DNA sequences of $\mathrm{\beta }\text{-globin}$ gene based on DM.

Next, we consider inferring the phylogenetic relationships of coronaviruses with the complete coronavirus genomes. The 24 complete coronavirus genomes used in this paper were downloaded from GenBank, of which 12 are SARS-CoVs and 12 are from other groups of coronaviruses. The name, accession number, abbreviation, and genome length for the 24 genomes are listed in Table 3 . According to the existing taxonomic groups, sequences 1–3 form group I, and sequences 4–11 belong to group II, while sequence 12 is the only member of group III. Previous work showed that SARS-CoVs (sequences 13–24) are not closely related to any of the previously characterized coronaviruses and form a distinct group IV.

Table 3.

The accession number, abbreviation, name, and length for each of the 24 coronavirus genomes.

No.	Accession	Abbreviation	Genome	Length (nt)
1	NC_002645	HCoV-229E	Human coronavirus 229E	27,317
2	NC_002306	TGEV	Transmissible gastroenteritis virus	28,586
3	NC_003436	PEDV	Porcine epidemic diarrhea virus	28,033
4	U00735	BCoVM	Bovine coronavirus strain Mebus	31,032
5	AF391542	BCoVL	Bovine coronavirus isolate BCoV-LUN	31,028
6	AF220295	BCoVQ	Bovine coronavirus Quebec	31,100
7	NC_003045	BCoV	Bovine coronavirus	31,028
8	AF208067	MHVM	Murine hepatitis virus strain ML-10	31,233
9	AF201929	MHV2	Murine hepatitis virus strain 2	31,276
10	AF208066	MHVP	Murine hepatitis virus strain Penn 97-1	31,112
11	NC_001846	MHV	Murine hepatitis virus	31,357
12	NC_001451	IBV	Avian infectious bronchitis virus	27,608
13	AY278488	BJ01	SARS coronavirus BJ01	29,725
14	AY278741	Urbani	SARS coronavirus Urbani	29,727
15	AY278491	HKU-39849	SARS coronavirus HKU-39849	29,742
16	AY278554	CUHK-W1	SARS coronavirus CUHK-W1	29,736
17	AY282752	CUHK-Su10	SARS coronavirus CUHK-Su10	29,736
18	AY283794	SIN2500	SARS coronavirus Sin2500	29,711
19	AY283795	SIN2677	SARS coronavirus Sin2677	29,705
20	AY283796	SIN2679	SARS coronavirus Sin2679	29,711
21	AY283797	SIN2748	SARS coronavirus Sin2748	29,706
22	AY283798	SIN2774	SARS coronavirus Sin2774	29,711
23	AY291451	TW1	SARS coronavirus TW1	29,729
24	NC_004718	TOR2	SARS coronavirus	29,751

In Fig. 3 , we present the phylogenetic tree belonging to 24 species based on the distance matrix DM, using UPGMA method. The tree is viewed using the DRAWGRAM program. As shown in Fig. 3, four groups of coronaviruses can be seen from it: (1) The group I coronaviruses, including TGEV, PEDV and HCoV-229E tend to cluster together; (2) BCoV, BCoVL, BCoVM, BCoVQ, MHV, MHV2, MHVM, and MHVP, which belong to group II, are grouped in a monophyletic clade; (3) IBV, belonging to group III, is situated at an independent branch; (4) the SARS-CoVs from group IV are grouped in a separate branch, which can be distinguished easily from other three groups of coronaviruses. The tree constructed based on DM algorithm is quite consistent with the results obtained by other researchers (Zheng et al., 2005, Song et al., 2005, Liu et al., 2007, Li et al., 2008). The emphasis of the present work is to provide a new method to analyze DNA sequences. From the above applications, we can see that our method is feasible for comparing DNA sequences and deducing their similarity relationship.

Fig. 3.

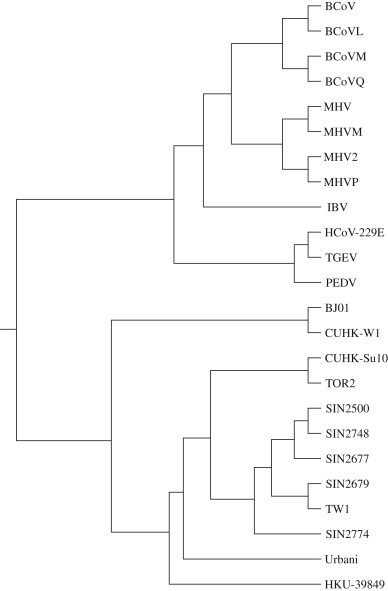
The phylogenetic tree for 24 coronavirus using whole genomes based on DM.

4. Conclusion

In this paper, we propose a new method for the similarity analysis of DNA sequences. It is a simple method that yields results reasonably and rapidly. Our algorithm is not necessarily an improvement as compared to some existing methods, but an alternative for the similarity analysis of DNA sequences. The new approach does not require sequence alignment and graphical representation, and besides, it is fully automatic. The whole operation process utilizes the entire information contained in the DNA sequences and do not require any human intervention. The application of the DM algorithm to the sets of $\mathrm{\beta }\text{-globin}$ genes and coronavirus genomes demonstrates its utility. This method will also be useful to researchers who are interested in evolutionary analysis.