Coinfection can trigger multiple pandemic waves

Abstract

Sequences of epidemic waves have been observed in past influenza pandemics, such as the Spanish influenza. Possible explanations may be sought either in mechanisms altering the structure of the network of contacts, such as those induced by changes in the rates of movement of people or by public health measures, or in the genetic drift of the influenza virus, since the appearance of new strains can reduce or eliminate herd immunity. The pandemic outbreaks may also be influenced by coinfection with other acute respiratory infections (ARI) that increase transmissibility of influenza virus (by coughing, sneezing, running nose). In fact, some viruses (e.g., Rhinovirus and Adenovirus) have been found to induce “clouds” of bacteria and increase the transmissibility of Staphylococcus aureus. Moreover, Rhinovirus and Adenovirus were detected in patients during past pandemics, and their presence is linked to superspreading events. In this paper, by assuming increased transmissibility in coinfected individuals, we propose and study a model where multiple pandemic waves are triggered by coinfection with ARI. The model agrees well with mortality excess data during the 1918 pandemic influenza, thereby providing indications for potential pandemic mitigation.

1. Introduction

Recent studies provide empirical evidence of epidemic waves in past flu pandemics, as in the Spanish influenza of the 1918–1919 (Chowell et al., 2006a, Chowell et al., 2006b; Ferguson et al., 2006, Mills et al., 2004). Mortality excess data and hospitalization data available for most part of the US, some UK cities and other European cities, such as Copenhagen and Geneva, show the occurrence of more than just a single pandemic wave, with intervals between waves amounting, in some instances, to several months.

As it was readily recognized, such behaviors pose a serious challenge to the simplest and most popular pandemic models. Of course, natural and political barriers can alter the structure of the contact networks, by possibly reducing interactions between infected and susceptible individuals, and thus delaying the course of the epidemics. While this effect may explain pandemic waves in wide areas (such as the US), its influence is much weaker when narrower areas are considered (e.g., at city level). Moreover, possible effects of containment/mitigation strategies may not be disregarded (Bootsma and Ferguson, 2007, Hatchett et al., 2007), especially for more recent outbreaks. Other explanations for pandemic waves should be sought in the genetic variation of the influenza virus (Castillo-Chavez et al., 1989, Andreasen et al., 1997, Boni et al., 2004), i.e., the appearance of new strains that could reduce or eliminate acquired immunity. However, the presence of more than one strain in the same pandemic outbreak has not been observed yet. Exogenous time changes in transmission rates, such as seasonal forcing, is a further candidate explanation (Colizza et al., 2006, Colizza et al., 2007). While the role of seasonal forcing as a trigger of steady oscillations for endemic diseases, as measles, is well established (Fine and Clarkson, 1982), and factors underlying the winter seasonality of influenza have been suggested (Hemmes et al., 1960), the phenomenon can hardly be taken as a robust explanation of waves of pandemic flu (at least at local scale).

Alternative explanations can be advanced in a coinfection scenario (May and Nowak, 1995, Adler and Losada, 2002). For instance, can other acute respiratory infections (ARI), such as Rhinovirus and Adenovirus, be responsible for increasing transmissibility (e.g., by coughing, sneezing, running nose) of pandemic influenza? If this is the case, coinfection with ARI could also be responsible for epidemic waves, for instance when the dynamics of the influenza pandemic and the ARI are not synchronized. Recent works support this hypothesis. In fact, the presence of respiratory pathologies not directly linked to the pandemic virus has been detected in most of past pandemic episodes. In particular, Rhinovirus and Adenovirus were detected in patients during past pandemic events (Lloyd-Smith et al., 2005, Brundage, 2006). Moreover, superspreading episodes (Lloyd-Smith et al., 2005), potentially linked to coinfection events, were detected in all these cases (Brundage, 2006). Superspreading events in SARS might also be caused by coinfection with other respiratory viruses (Bassetti et al., 2005a). The mechanism was also identified as responsible for increased transmission of Staphylococcus aureus (Bassetti et al., 2005b). Additional (though indirect) support to the coinfection scenario can be drawn from a recently advanced proposal (Edwards et al., 2004), according to which alteration of the lung airway surface properties by inhaled nontoxic aerosols is an effective strategy to contain the amount of exhaled bioaerosol, thus mitigating the spread of airborne infectious diseases.

In this paper, we model the role of ARI in the transmission dynamics of a pandemic outbreak by coupling an SIR model for flu with an SIS model for ARI. While it is not difficult to develop models exhibiting wave-like behavior, the proposed model does not require any “ad-hoc” mechanism, such as the introduction of time-varying transmission rates. Most notably, with a minimum number of extra parameters it supplies an empirically testable conjecture, perhaps worthy to be considered in future studies.

The model proves amenable to theoretical treatment. Specifically, we can provide the expression for the effective reproduction number of epidemic flu, and show how this is affected by coinfection. Next, we show that multiple waves are possible during the course of a single pandemic episode, and exhibit the exact conditions for this to occur: the increased transmissibility in coinfected individuals and non-synchronicity in the time course of the two infections. With no need for introducing diffusion structures (see Flahault et al., 2006) and non-constant transmission rates (e.g., depending on different strains), the model accounts for the multiple epidemic waves observed in past pandemics, such as the Spanish influenza.

2. The coinfection model for pandemic influenza

We consider a coinfection model of an infectious disease, evolving according to an SIR epidemic model (e.g., pandemic influenza), with another respiratory infectious disease, evolving according to an SIS model (e.g., Rhinovirus). We assume that the effect of the latter on the dynamics of the former is to increase transmissibility (e.g., by coughing, sneezing, running nose, etc.).

2.1. Modeling ARI

There are more than 100 recognized serotypes (plus some not typed yet) of Rhinovirus, the principal cause of common cold, and thus it is unlikely to develop full immunity (Goldmann, 2001). In fact, a sero-epidemiologic study of Rhinovirus infections at different ages found that newborns had antibodies to approximately 20% of 56 serotype (Hamparian et al., 1970). Moreover, Rhinovirus can be contracted from three to eight times a year for children and from three to five times a year for adults (Goldmann, 2001). It is thus reasonable to model ARI through a SIS model.

As regards the onset of ARI, common colds, like most ARI, are more common in winter or, in the tropics, during the rainy season. This frequency has been found to vary, depending on the etiology of the infection; Rhinovirus infection is more frequent in fall and spring (Fox et al., 1985), while Coronavirus infection tends to occur more frequently in winter (Reed, 1981). A review on common cold is given in Heikkinen and Jrvinen (2003).

2.2. Epidemic transmission model

Individuals are assumed to move among the following epidemiological states: $s_S$, susceptible to both diseases, $s_I$, susceptible to influenza and affected by ARI, $i_S$, affected by influenza and susceptible to ARI, $i_I$ affected by both diseases, $r_S$ recovered from influenza and susceptible to ARI and $r_I$ recovered from influenza and affected by ARI, according to the flow diagram in Fig. 1 . Let $S_S$, $S_I$, $I_S$, $I_I$, $R_S$, $R_I$ denote the relative frequencies of individuals in the classes, with $S_S+S_I+I_S+I_I+R_S+R_I=1$. Individuals susceptible to both diseases (class $S_S$) can acquire influenza and progress to class $I_S$ at the per-capita rate $\beta I_S+\rho I_I$ or acquire ARI and move to class $S_I$ at the per-capita rate $\alpha (S_I+I_I+R_I)$, where $\beta$ is the influenza transmission rate per person per unit of time (i.e., the average number of effective contacts per unit time) for the individuals affected by influenza only, $\rho$ is the influenza transmission rate per person per unit of time for the coinfected individuals, and $\alpha$ is the ARI transmission rate per person per unit of time. Individuals susceptible to influenza and affected by ARI (class $S_I$) progress to class $I_I$ at the per-capita rate $\beta I_S+\rho I_I$ (the same rate of class $S_S$ since we assume changes in transmissibility and not in susceptibility) or move to class $S_S$ at the per-capita rate $\delta$, where $1/\delta$ is the average duration of infectivity of individuals affected by ARI. Individuals affected only by influenza (class $I_S$) recover from influenza at the per-capita rate $\gamma$ or move to class $I_I$ at the per-capita rate $\alpha (S_I+I_I+R_I)$, where $1/\gamma$ is the average duration of infectivity of individuals affected by influenza. Coinfected individuals (class $I_I$) recover from influenza at the rate $\gamma$ or move to class $I_S$ at rate $\delta$. Individuals recovered from influenza and susceptible to ARI (class $R_S$) move to class $R_I$ at the rate $\alpha (S_I+I_I+R_I)$. Finally, individuals recovered from influenza and affected by ARI (class $R_I$) move to class $R_S$ at the rate $\delta$. The full transmission model is described by the following system of ordinary differential equations:

$$\left\{\begin{array}{c}{\dot{S}}_S(t)=-\alpha [S_I(t)+I_I(t)+R_I(t)]S_S(t)+\delta S_I(t)\hfill \\ \phantom{{\dot{S}}_S(t)=}-[\beta I_S(t)+\rho I_I(t)]S_S(t)\hfill \\ {\dot{S}}_I(t)=+\alpha [S_I(t)+I_I(t)+R_I(t)]S_S(t)-\delta S_I(t)\hfill \\ \phantom{{\dot{S}}_I(t)=}-[\beta I_S(t)+\rho I_I(t)]S_I(t)\hfill \\ {\dot{I}}_S(t)=-\alpha [S_I(t)+I_I(t)+R_I(t)]I_S(t)+\delta I_I(t)\hfill \\ \phantom{{\dot{I}}_S(t)=}+[\beta I_S(t)+\rho I_I(t)]S_S(t)-\gamma I_S(t)\hfill \\ {\dot{I}}_I(t)=+\alpha [S_I(t)+I_I(t)+R_I(t)]I_S(t)-\delta I_I(t)\hfill \\ \phantom{{\dot{I}}_I(t)=}+[\beta I_S(t)+\rho I_I(t)]S_I(t)-\gamma I_I(t)\hfill \\ {\dot{R}}_S(t)=-\alpha [S_I(t)+I_I(t)+R_I(t)]R_S(t)+\delta R_I(t)\hfill \\ \phantom{{\dot{R}}_S(t)=}+\gamma I_S(t)\hfill \\ {\dot{R}}_I(t)=+\alpha [S_I(t)+I_I(t)+R_I(t)]R_S(t)-\delta R_I(t)\hfill \\ \phantom{{\dot{R}}_I(t)=}+\gamma I_I(t)\hfill \end{array}\right)\text{.}$$ (1)

To assume that coinfection leads to increased transmissibility means considering $\rho >\beta$ in system (1). Initial times for influenza and ARI will be denoted by $t_0$ and $t_0^{\mathrm{ari}}$, respectively.

Fig. 1.

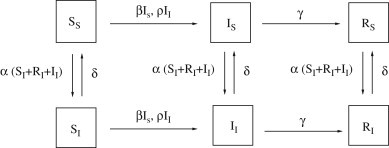
Representation of the flow of individuals among epidemiological classes.

2.3. Reproduction numbers

The basic reproduction number $R_0$ is the threshold parameter which determines whether or not the introduction of an infectious agent leads to an epidemic outbreak (Diekmann and Heesterbeek, 2000). It is essentially the average number of secondary cases a single infected individual will cause in a population with no immunity to the disease (Anderson and May, 1992). When $R_0<1$ the infection will die out with certainty, otherwise an epidemic outbreak will occur and, in general, the larger the value of $R_0$, the harder it is to control the epidemic.

It is trivial to check that for the ARI the threshold parameter is given by

$$R_0^{\mathrm{ari}}=\frac{\alpha }{\delta }\text{.}$$ (2)

In fact, the ARI is modeled by a classical SIS where the susceptible class is given by the sum of $S_S$, $I_S$ and $R_S$ classes, while the infected class is given by the sum of $S_I$, $I_I$ and $R_I$ classes. The condition $\alpha >\delta$ ensures the endemic persistence of ARI in a completely susceptible population.

As regards influenza, its dynamics is not described by a classical SIR model (with exception of the case $\rho =\beta$, which we do not consider) and its threshold condition depends on the dynamics of ARI. In particular, we will see that an influenza outbreak can be induced by the presence of ARI even though $\beta /\gamma$ (the basic reproduction number of influenza in absence of ARI) is less than 1. Most importantly, at least a second epidemic wave, due to coinfection with ARI, can be induced after a first outbreak.

System (1) admits the following equilibria:

• (a)
  in absence of ARI:

  $$(S_S,S_I,I_S,I_I,R_S,R_I)=(S^{\star },0,0,0,1-S^{\star },0)\text{,}$$ (3)
• (b)
  with ARI at the endemic equilibrium:

  $$(S_S,S_I,I_S,I_I,R_S,R_I)=(S^{\star }\delta /\alpha ,S^{\star }(1-\delta /\alpha )\text{,}0,0,(1-S^{\star })\delta /\alpha ,(1-S^{\star })(1-\delta /\alpha ))\text{,}$$ (4)

  where $S^{\star }\in (0,1]$ is the proportion of individuals susceptible to influenza.

$S^{\star }=1$ means a completely susceptible population and this case corresponds to the beginning of the pandemic influenza epidemics (i.e., $S^{\star }=S^{\star }(t_0)=1$) in absence of ARI (Eq. (3)) or when ARI is at its endemic state (Eq. (4)), which implies $t_0^{\mathrm{ari}}<t_0$. The case $0<S^{\star }<1$ can be interpreted as the equilibrium at the end of an epidemic wave (i.e., $S^{\star }=S^{\star }(\overline{t})$ for $\overline{t}⪢t_0$, eventually $\overline{t}\to +\infty$) generated by influenza alone in absence of ARI (Eq. (3)) or when ARI is at its endemic state (Eq. (4)), for instance when $t_0^{\mathrm{ari}}>\overline{t}$. The basic reproduction number (or effective reproduction number, depending on the context) $R_0$ in the two equilibria (3), (4) has been computed by employing the next-generation operator technique (Diekmann and Heesterbeek, 2000) (details for computing $R_0$ at the equilibrium (4) are given in Appendix A, equilibrium (3) can be treated in a similar way).

For the equilibrium (3) we obtain:

$$R_0=S^{\star }\beta /\gamma \text{,}$$ (5)

and for the equilibrium (4) we obtain:

$$R_0=S^{\star }\left[\frac{\beta }{\gamma }\frac{\delta }{\alpha }+\frac{\rho }{\gamma }\left(1-\frac{\delta }{\alpha }\right)\right]=S^{\star }\left[\frac{\beta }{\gamma }\frac{1}{R_0^{\mathrm{ari}}}+\frac{\rho }{\gamma }\left(1-\frac{1}{R_0^{\mathrm{ari}}}\right)\right]\mathrm{with}\rho >\beta \text{.}$$ (6)

Eqs. (5), (6) have a straightforward interpretation: when the basic reproduction number of ARI $\alpha /\delta$ is below 1, ARI is not persistent, thus no coinfection can occur, and the appropriate basic reproduction number for flu is the standard SIR threshold $S^{\star }\beta /\gamma$ (i.e., $\beta /\gamma$ in a fully susceptible population). On the other hand, when the basic reproduction number of ARI $\alpha /\delta$ is above 1, then a substantial part of the population can be infected with ARI at the onset of the influenza epidemics. In this case a typical influenza infective individual would cause, during his/her whole period of infectivity, $\beta /\gamma$ new infections if he/she is not coinfected with ARI, which occurs with probability $S^{\star }\delta /\alpha$ and $\rho /\gamma$ if he/she is coinfected with ARI, which occurs with probability $S^{\star }(1-\delta /\alpha )$.

From Eq. (6) it follows that for each value of $R_0^{\mathrm{ari}}>1$, it does exist a threshold value $\overline{\rho }(R_0^{\mathrm{ari}})$ such that $R_0>1$. Moreover, $\overline{\rho }(R_0^{\mathrm{ari}})$ is a decreasing function of $R_0^{\mathrm{ari}}$ and

$$\underset{R_0^{\mathrm{ari}}\to +\infty }{\lim }\overline{\rho }(R_0^{\mathrm{ari}})=\gamma /S^{\star }\mathrm{and}\underset{R_0^{\mathrm{ari}}\to 1^{+}}{\lim }\overline{\rho }(R_0^{\mathrm{ari}})=+\infty \text{.}$$

This has two noteworthy consequences. First, for $S^{\star }=1$ a sufficiently large endemic infective fraction of ARI is capable to trigger an epidemic outbreak of influenza even if $\beta /\gamma <1$. Second, even if an influenza outbreak has arrived to its end with $0<S^{\star }<1$, a sufficiently large increase of the infective fraction of ARI toward its endemic state is capable to trigger a further pandemic wave. As expected, larger values of $\rho$ are required for lower vales of $R_0^{\mathrm{ari}}$ (see Fig. 2 ).

Fig. 2.

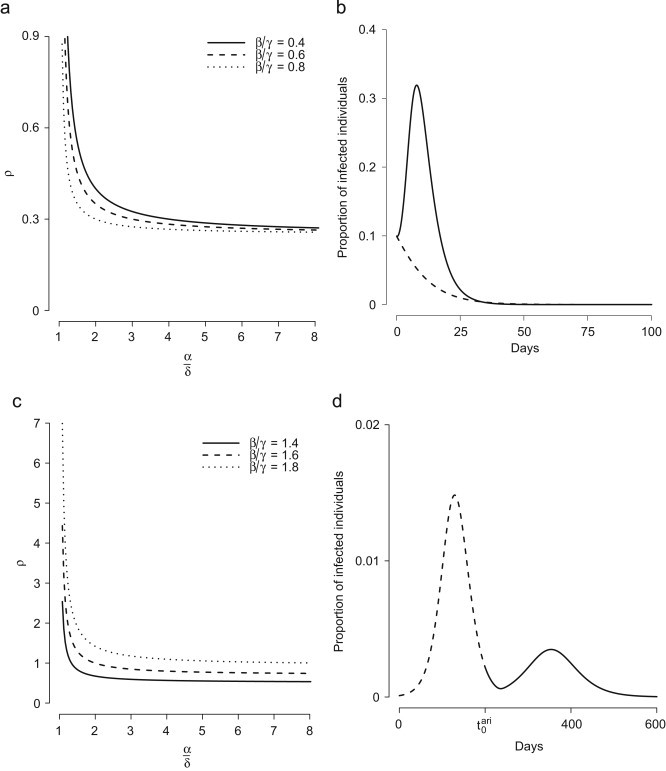
(a) Threshold value $\overline{\rho }(R_0^{\mathrm{ari}})$ for different values of $\beta /\gamma$ (keeping fixed $\gamma =0.25$) and $S^{\star }=1$. (b) For $S^{\star }=1$, $\beta =0.2$ and $\gamma =0.25$, dashed line represents the proportion of infected individuals in the absence of ARI, while solid line represents the proportion of infected individuals in presence of ARI ($\alpha =1$, $\delta =0.25$, $\rho =0.8$, $t_0=t_0^{\mathrm{ari}}=0$). (c) As in (a) but for $S^{\star }<1$ (at the end of the first epidemic wave). (d) For $S^{\star }<1$, dashed line represents the proportion of infected individuals before the onset of ARI, while solid line represents the proportion of infected individuals after the onset of ARI. Parameters employed: $\beta =0.3$, $\gamma =0.25$, $\alpha =1$, $\delta =0.25$, $\rho =0.8$, $t_0=0$ and $t_0^{\mathrm{ari}}=200$.

2.4. Sequences of epidemic waves

In the previous sections, we argued that a second epidemic wave can be generated after ARI has reached its endemic equilibrium. However, a full sequence of epidemic waves can be generated throughout the growing phase of the dynamics of ARI.

Let us consider the fraction of individuals infected by ARI $J(t)=S_I(t)+I_I(t)+R_I(t)$, the fraction of individuals susceptible to influenza $S(t)=S_S(t)+S_I(t)$ and the proportion of individuals susceptible to influenza but affected by ARI among total susceptibles to flu $x(t)=S_I(t)/S(t)$. From Eq. (1) it follows that the dynamics of $x(t$) is described by the following forced linear differential equation:

$$\dot{x}(t)=\alpha J(t)-(\delta +\alpha J(t))x(t)\text{.}$$ (7)

Therefore, we can express $x$ in terms of $J:x(t)=x(J(t))$. The following equation, which can be computed by applying the same technique employed for obtaining Eqs. (5), (6) and where we omit explicit dependence on $t$, represents the effective reproduction number1 :

$$R_e=\left(\frac{\beta }{\gamma }\frac{\gamma +\delta }{\gamma +\delta +\alpha J}+\frac{\rho }{\gamma }\frac{\alpha J}{\gamma +\delta +\alpha J}\right)S_S+\left(\frac{\beta }{\gamma }\frac{\delta }{\gamma +\delta +\alpha J}+\frac{\rho }{\gamma }\frac{\gamma +\alpha J}{\gamma +\delta +\alpha J}\right)S_I=S[A(J)(1-x(J))+B(J)x(J)]\text{.}$$ (8)

The previous formula illustrates the action of a typical infective in the phases that typically occur at the end of an epidemic wave ($I_S\approx 0$ and $I_I\approx 0$), and clearly shows the avenue through which epochs of increasing prevalence of ARI (i.e., increasing $J$) can favor further epidemics. The quantities $A(J)$ and $B(J)$ are reproduction numbers themselves: $A(J)$ characterizes the situation where the susceptible pool is fully composed by individuals free from ARI, whereas $B(J)$ characterizes the situation where the susceptible pool is fully composed by individuals infected by ARI. Both $A(J)$ and $B(J)$ are increasing in $J$. Moreover $B(J)>A(J)$ holds for all $J$ and as $J$ increases the composition of the susceptible pool is modified by increasing the percentage of susceptible with ARI. Therefore $R_e$ is an increasing function of the prevalence of ARI, suggesting that even if at the end of an epidemic wave $R_e$ is below 1, it may well go above threshold at subsequent times as a consequence of the growing dynamics of ARI.

Eq. (8) can be approximated in terms of the total number of individuals infected by ARI $J$ and the total number of individuals susceptible to influenza $S$, thus obtaining $R_e=R_e(J,S)$. In fact, in all epidemiologically meaningful circumstances the following relationships hold: $S_S\approx S(1-J)$ and $S_I\approx \mathit{SJ}$ (see Appendix B). Thus, equation $R_e(J,S)=1$ can be written as

$$\text{JS}(\alpha \rho +\gamma (\rho -\beta ))+S\beta (\gamma +\delta )-J\alpha \gamma =\gamma (\gamma +\delta )\text{,}$$ (9)

which is a hyperbole in $S$ and $J$. Since $S$ is non-increasing and $J$ is non-decreasing (if $J(t_0)<1-\delta /\alpha$), Eq. (9) allows the computation of the minimum number of susceptible individuals $S_m^{\star }$ required for inducing an epidemic wave. By setting $J=1-\delta /\alpha$, which is the proportion of individuals infected by ARI at the endemic equilibrium, we get

$$S_m^{\star }=\frac{\gamma (\alpha -\delta )+\gamma (\gamma +\delta )}{\rho (\alpha -\delta )+\beta (\gamma +\delta )+\gamma (\rho -\beta )(1-\delta /\alpha )}\text{,}$$ (10)

which, for $\beta =\rho$, corresponds to $\gamma /\beta$, as for classical SIR models. Eqs. (9), (10) allow splitting the phase plan $(J,S)$ into three regions: $R_e>1$, $R_e<1$ and no waves, as shown in Fig. 3a . All trajectories end in the segment $E=\{(J,S):J=1-\delta /\alpha ,S\in [0,S_m^{\star }]\}$. Let us suppose that $S(t_0)\in (\gamma /\beta ,1]$. If $\beta =\rho$, $S_m^{\star }$ is squeezed over $\gamma /\beta$ (and region $R_e<1$ disappears) and trajectory can cross the line $R_e=1$ only once. If $\rho >\beta$, the curve can be crossed many times, accounting for sequences of epidemic waves. Let us suppose that $S(t_0)\in (S_m^{\star },\gamma /\beta ]$ (this requires that $\rho >\beta$). In this case influenza alone cannot generate an outbreak (since $S(t_0)\beta /\gamma <1$) but epidemic waves (possibly more than one) can be generated as a consequence of coinfection if the infected fraction with ARI is increasing over time. A simulated example is shown in Fig. 3b–d.

Fig. 3.

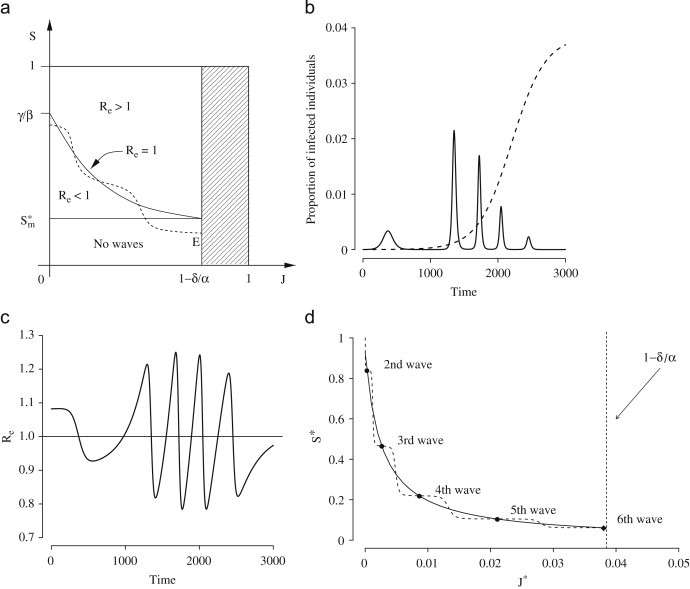
(a) Regions in the phase plan $(J,S)$ induced by Eqs. (9), (10) and example of trajectory accounting for epidemic waves induced by ARI (dashed line). (b) Proportion of individuals infected by influenza (solid line) and by ARI (dashed line) over time. A “very small” epidemic wave, not shown here, arises at $t\approx 3300$. Parameters employed: $\beta =0.27$, $\gamma =0.25$, $\alpha =0.104$, $\delta =0.1$, $\rho =100$, $t_0=t_0^{\mathrm{ari}}=0$. (c) Effective reproduction number (see Eq. (8)) over time for simulation in (b). (d) Solid line represents the possible solutions of the equation $R_e(J,S)=1$ (Eq. (9)) and filled circles represent actual pairs of values $(J,S)$ at the beginning of each wave in (b) (but for the first one, which is not a solution of $R_e(J,S)=1$). Diamond refers to the 6th (not shown) wave. Dashed line represents the trajectory of $(J(t),S(t))$.

2.5. Analysis of the Spanish influenza

We fit model (1) to the time series $\{m_t{\}}_{t=1}^{\mathrm{T}}$ of weekly mortality excess during the Fall 1918 and Winter 1919 waves of the 1918–1919 Spanish pandemic in Birmingham, Cardiff, Coventry, Leicester, Liverpool, London, Manchester, Newcastle upon Tyne, Nottingham, Portsmouth and Sheffield.2

By assuming that coinfection does not affect induced mortality we approximated the excess of mortality at time $t$ by the following equation:

$$m_t\approx {\tilde{m}}_t=\epsilon (I_S(t)+I_I(t))\text{.}$$ (11)

Parameters values and procedure employed for their computation are reported in Table 1 . $1/\gamma$ was sampled from a gamma distribution in order to obtain an average infectious period of influenza approximately between 2 and 4 days (Ferguson et al., 2005, Longini et al., 2005). $1/\delta$ was sampled from a gamma distribution in order to obtain an average infectious period of ARI approximately between 7 and 10 days (Heikkinen and Jrvinen, 2003). Variability in the average duration of infectious periods of both influenza and ARI allowed us to estimate confidence intervals for all the other epidemiological parameters. Moreover, we assumed $t_0^{\mathrm{ari}}>t_0$. Since the basic reproductive number $R_0$ of the fall wave can be estimated from the data through the equation $R_0=1+r/\gamma$, where $r$ is the intrinsic growth rate, and $R_0$ for system (1) in absence of ARI is $\beta /\gamma$ (see Eq. (5)), we estimated the transmission rate of influenza as $\beta =r+\gamma$. We fix the initial number of infected individuals by influenza and by ARI to 1. The other model parameters, namely transmission rate for ARI, $\alpha$, transmission rate for influenza in coinfected individuals, $\rho$, death rate, $\epsilon$, initial time for influenza, $t_0$, and initial time for ARI, $t_0^{\mathrm{ari}}$ were estimated through least squares fitting to the number of influenza deaths over time. By sampling $\gamma$ and $\delta$ from their respective gamma distributions, 500 different model realizations were employed to estimate confidence intervals for the model parameters.

Table 1.

Model parameters

Parameter	Description	Mean value	95% CI	Procedure
$N$	Number of individuals	8664693		Fixeda
$1/\gamma$	Average duration of flu infectious period	2.94 days	(1.79, 4.34)	Sampledb
$1/\delta$	Average duration of ARI infectious period	8.47 days	(6.82, 10.04)	Sampledc
$r$	Intrinsic growth rate of the fall wave	$0.2{\mathrm{days}}^{-1}$		Estimatedd
$\beta$	Transmission rate of flu	$0.54{\mathrm{days}}^{-1}$	(0.43, 0.76)	Computed as $r+\gamma$
$\alpha$	Transmission rate of ARI	$0.96{\mathrm{days}}^{-1}$	(0.79, 1.09)	Fitted
$\rho$	Transmission rate of flu for coinfected individuals	$1.6{\mathrm{days}}^{-1}$	(1.44, 2.25)	Fitted
$\epsilon$	Mortality rate	$0.0069{\mathrm{days}}^{-1}$	(0.0041, 0.0142)	Fitted
$t_0$	Initial time of flu	$-1.86\mathrm{weeks}$	$(-2.35,-1.22)$	Fitted
$t_0^{\mathrm{ari}}$	Initial time of ARI	16.56 weeks	(15.52, 17.65)	Fitted
$R_0$	Reproduction number of the fall wave	1.58	(1.36, 1.86)	Computed as $\beta /\gamma$

^aSee Smallman-Raynor et al. (2002).

^bSampled from a gamma distribution with shape parameter 20 and scale parameter 0.15.

^cSampled from a gamma distribution with shape parameter 111.8421 and scale parameter 0.076.

^dEstimated by fitting the cumulative number of cases with an exponential model.

Fig. 4 a shows the comparison between the observed data and the model predictions (coefficient of determination: $R^2=0.82$, 95% CI (0.79, 0.84)). Some of the discrepancies between the fit and the data can of course be due to phenomena not accounted for by the model. This may well be the case for the observed difference in slope in the decay phase of the first wave. The poor fit observed may be due to military demobilization at the end of the first world war (Ferguson et al., 2006) that makes the data uncompliant with any classical SIR model (by eliminating these points from the computation, we obtain an average estimate of $R^2=0.93$). The discrepancy in the height of the first peak can be better explained as an effect of our choices—namely, to have estimated the transmission parameter, $\beta$, from the intrinsic growth rate $r$, instead of leaving it as a free parameter to be estimated by least squares fit.

Fig. 4.

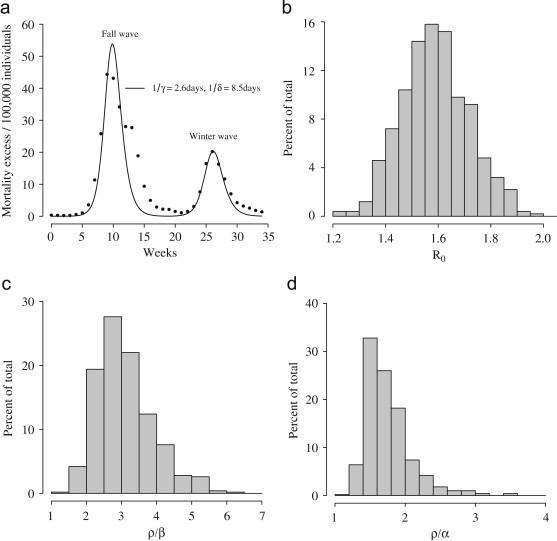
(a) The best-fit solution obtained by fitting model (1) to the GB data (filled circles, initial time 24 August 1918). (b) Distribution of $R_0$. (c) Distribution of $\rho /\beta$. (d) Distribution of $\rho /\alpha$.

The average value of the reproduction number of influenza for the first wave is $R_0=1.58$ (see Fig. 4b). Transmission parameter for class $I_I$ is in average 3.1 times that of class $I_S$ (see Fig. 4c) and 1.7 times that of ARI (see Fig. 4d). The cumulative attack rate is estimated to be 63% at the end of the first wave and 85.4% at the end of the second wave. Proportion of deaths is estimated to be slightly lower than 1%.

It is worth noticing that we tried to fit the proposed model to the Summer 1918 (data not shown) and Fall 1918 waves but the results were unsatisfactory. In fact, the Summer wave is characterized by a higher reproductive number ($R_0=1.89$, by assuming $1/\gamma =2.94$ days) and a much lower mortality excess with respect to the fall wave. However, the introduction of a specific induced mortality rate for coinfected individuals ${\epsilon }_c$ in Eq. (11) (i.e. by assuming $m_t\approx {\tilde{m}}_t=\epsilon I_S(t)+{\epsilon }_c{I}_I(t))$ allowed us to obtain a fit which compares reasonably well with actual data.

3. Conclusions

Mathematical models have been employed to study the spatio-temporal spread of influenza (Rvachev and Longini, 1985, Flahault et al., 1988, Viboud et al., 2003) and evaluate the impact of different containment/mitigation strategies (Longini et al., 2004, Longini et al., 2005, Germann et al., 2006, Ferguson et al., 2005, Ferguson et al., 2006, Colizza et al., 2007). A review is given in Riley (2007). We have employed a simple compartmental model with homogeneous mixing to describe the transmission dynamics during the Spanish flu pandemic. The model accounts for sequences of epidemic waves induced by coinfection with another acute respiratory infection during its growth phase.

While simple, the model appears compatible with historical data. However, many area of improvement can be identified.

Compartments for symptomatic and asymptomatic individuals can be introduced. In fact, the occurrence of asymptomatic cases for influenza is well known. Moreover, differences between the two classes in influenza transmission are suspected. This can drastically affect the outcomes of the model—for example, the estimated value of attack rate.

Increased susceptibility to influenza in individuals affected by ARI may well represent an extra factor for the spread of influenza, in addition to the one (increased influenza transmission in coinfected individuals) that we have considered throughout the paper.

Introduction of increased induced mortality in coinfected individuals would help considerably in the explanation of historical data. Yet it encounters a major obstacle in the lack of (specific) reliable data needed to estimate induced mortality parameters. However, introduction of induced mortality in coinfected individuals in Eq. (11), and its estimates by least squares do allow good fits of the Summer and Fall waves.

More realistic models can also be derived by adding compartments for latent, hospitalized individuals and by considering age structured populations.

Despite its simplicity, however, if significant evidence of the importance of coinfection in enhancing the transmissibility of flu—here only hypothesized—should be found in the future, this would open further avenues to pandemic mitigation.

Good fits of the mortality data may as well be obtained by more parsimonious models—for example, by introducing an “ad-hoc” time-varying transmission rate allowing an increase in transmissibility during the pandemic course. Yet, the advantage of the coinfection model is that it is based on an empirically testable hypothesis. Moreover, by adding a minimal number of extra parameters, it can provide useful policy indications as regards pandemic mitigation.

Sequences of epidemic waves can also be obtained by considering multiple ARI. In fact, more than one kind of ARI has been found in patients affected by influenza in past pandemics.

Another mechanism potentially inducing sequences of pandemic waves is the change of the transmissibility rate of ARI $(\alpha )$ for coinfected individuals, for example through a mechanism of increased transmissibility similar to the one we have assumed for the transmissibility of influenza.

Finally, we have shown that sequences of epidemic waves can be generated during the exponential growth phase of ARI. The number of epidemic waves that can be generated is a decreasing function of $R_0^{\mathrm{ari}}$, and no more than two waves should be generated, provided that $R_0^{\mathrm{ari}}$ is large enough. Future work will be devoted to investigating this hypothesis.

Appendix A. Computing $R_0$

Let us consider the Jacobian $J$ of the system (1) restricted to the influenza infectious classes $I_S$ and $I_I$, at the equilibrium (4). It can be written as

$$J=T+\Sigma -D\text{,}$$ (12)

where

$$T=S^{\star }\left(\begin{array}{cc}\hfill \beta \delta /\alpha \hfill & \hfill \rho \delta /\alpha \hfill \\ \hfill \beta (1-\delta /\alpha )\hfill & \hfill \rho (1-\delta /\alpha )\hfill \end{array}\right)$$

is a matrix whose elements are all real positive numbers, and they correspond to the transmission rates of the influenza;

$$\Sigma =\left(\begin{array}{cc}\hfill -\alpha (1-\delta /\alpha )\hfill & \hfill \delta \hfill \\ \hfill \alpha (1-\delta /\alpha )\hfill & \hfill -\delta \hfill \end{array}\right)$$

is a real matrix with positive off-diagonal elements corresponding to transition between the influenza infectivity classes;

$$D=\left(\begin{array}{cc}\hfill \gamma \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \gamma \hfill \end{array}\right)$$

is a real positive diagonal matrix which elements represent the recovery rates for the influenza.

Note that all the elements of the matrix

$$-(\Sigma -D{)}^{-1}=\frac{1}{\gamma (\gamma +\alpha )}\left(\begin{array}{cc}\hfill \delta +\gamma \hfill & \hfill \delta \hfill \\ \hfill \alpha (1-\delta /\alpha )\hfill & \hfill \alpha (1-\delta /\alpha )+\gamma \hfill \end{array}\right)$$

are real positive, so it is possible to estimate $R_0$ as the dominant eigenvalue of the next-generation operator $K$ defined as

$$K=-T(\Sigma -D{)}^{-1}=\frac{S^{\star }}{\gamma (\gamma +\alpha )}\left(\begin{array}{cc}\hfill [\beta (\delta +\gamma )+\rho (\alpha -\delta )]\delta /\alpha \hfill & \hfill [\beta \delta +\rho (\alpha -\delta +\gamma )]\delta /\alpha \hfill \\ \hfill [\beta (\delta +\gamma )+\rho (\alpha -\delta )](1-\delta /\alpha )\hfill & \hfill [\beta \delta +\rho (\alpha -\delta +\gamma )](1-\delta /\alpha )\hfill \end{array}\right)\text{.}$$

Since $\det (K)=0$, it follows that the dominant eigenvalue of $K$ is

$$R_0=S^{\star }\left[\frac{\beta }{\gamma }\frac{\delta }{\alpha }+\frac{\rho }{\gamma }\left(1-\frac{\delta }{\alpha }\right)\right]\text{.}$$

Similar arguments allow the calculation of Eqs. (5), (8).

Appendix B. Approximating $S_I(t)$ and $S_S(t)$

In what follows we show that $S_S(t)\approx S(t)(1-J(t))$ and, consequently, that $S_I(t)\approx S(t)J(t)$ in all epidemiologically meaningful circumstances.

B.1. Approximation for small values of $R_0^{\mathrm{ari}}$

Let us consider Eq. (7). By assuming a small enough value of $R_0^{\mathrm{ari}}$, that is by taking the limit $R_0^{\mathrm{ari}}\to 1^{+}$, we can suppose that:

• (1) $\dot{x}(t)\approx 0$, since exchanges rate between classes $S_I(t)$ and $S_S(t)$ is determined by ARI;
• (2) $J(t)\approx 0$, since in general $J(t)<1-1/R_0$ if $J(t_0^{\mathrm{ari}})<1-1/R_0$.

Thus we can obtain the following relationship for $x(t)$:

$$x(t)\approx \frac{J(t)}{J(t)+1}$$

and by considering the first-order Taylor expansion of $x(t)$ about $J(t)=0$ we obtain

$$x(t)\approx J(t)\text{,}$$

that is $S_I(t)\approx S(t)J(t)$ and, consequently, $S_S(t)\approx S(t)(1-J(t))$.

B.2. Global dynamics of $x(t)$ and $J(t)$

More in general, let us consider the equation system

$$\left\{\begin{array}{c}\dot{J}(t)=(\alpha -\delta -\alpha J(t))J(t),\hfill \\ \dot{x}(t)=\alpha J(t)-(\delta +\alpha J(t))x(t).\hfill \end{array}\right)$$ (B.1)

The first equation describes the dynamics of the class of individuals infected by ARI, whose explicit solution is the following logistic function:

$$J(t)=\frac{J_0(1-1/R_0^{\mathrm{ari}})}{J_0-(J_0-1+1/R_0^{\mathrm{ari}}){\mathrm{e}}^{-\delta (R_0^{\mathrm{ari}}-1)t}}\text{.}$$

The second equation is Eq. (7). The system (B.1) admits two equilibria, namely $(0,0)$ and $(J_e,J_e)$, where $J_e=1-1/R_0^{\mathrm{ari}}$. It is easy to show that the latter is globally asymptotically stable (see the phase plan in Fig. B1 , considering that $\dot{J}(t)>0$ if $R_0^{\mathrm{ari}}>1$ and $\dot{x}(t)>0$ if $x(t)<\alpha J(t)/(\alpha J(t)+\delta )$, and $\dot{x}(t)<0$ otherwise). Moreover, let us define the quantity $C(t)=x(t)/J(t)$. The following equation holds:

$$\dot{C}(t)=\alpha (1-C(t))\text{,}$$

whose explicit solution $C(t)=1-(1-C_0){\mathrm{e}}^{-\alpha t}$ globally converges to $C^{\infty }=1$. This means that convergence to the equilibrium $(J_e,J_e)$ is obtained along the bisector axis $x=J$ (see Fig. B1), independently from $R_0^{\mathrm{ari}}$. Moreover, convergence is faster for large values of $\alpha$ or when $x(t_0)\approx J(t_0)$ (that results in $C_0=1$), that is in all epidemiologically meaningful circumstances. This means that the following approximations for $S_I(t)$ and $S_S(t)$ hold: $S_I(t)\approx S(t)J(t)$ and, consequently, $S_S(t)\approx S(t)(1-J(t))$.

Fig. B1.

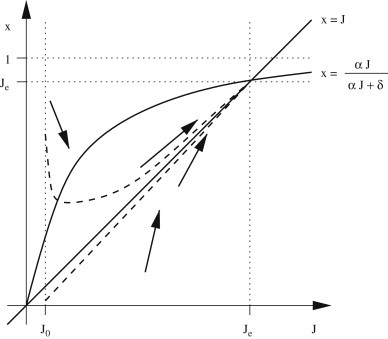
In the phases plan $(J,x)$ trajectories (dashed lines) tend to $(J_e,J_e)$ along the bisector $x=J$.