Sexual transmission and the probability of an end of the Ebola virus disease epidemic

Highlights

• •WHO erroneously declared the end of Ebola, many of which caused by sexual transmission.
• •We computed the probability of the end of an Ebola, accounting for sexual transmission and under-ascertainment.
• •Calculating the probability of the end of epidemic outperformed the existing 42-day criteria of the WHO.
• •Waiting time to declare the end of Ebola depends on the sexual behaviors.
• •With substantial sexual transmissions, ascertaining the end of epidemic could even take 1 year.

Abstract

The criteria of zero Ebola cases defined by the World Health Organization did not explicitly account for the sexual transmission and led to multiple recrudescent events in West Africa from 2015 to 2016, partly indeed caused by sexual transmission from survivors. We devised a statistical model to compute the probability of the end of an Ebola virus disease epidemic, accounting for sexual transmission and under-ascertainment of cases. Analyzing the empirical data in Guinea, Liberia and Sierra Leone, the performance of the proposed model was compared with the existing criteria comprising a fixed waiting time of 42 days since the last case testing negative or burial. We showed that the waiting time can vary depending on the sexual behaviors of survivors and their adherence to refraining from unprotected sex is likely one of the key factors in determining the absence of additional cases after declaration. If the proportional weight of sexual transmission among all secondary transmission events was substantial, ascertaining the end could even require waiting 1 year from the purported last case. While our proposed method offers an objectively interpretable probability of the end of an epidemic, it highlights that the computation requires a good knowledge of sexual contact.

1. Introduction

Ebola virus disease (EVD), caused by Ebola virus, also referred to as Ebola haemorrhagic fever, spreads from human to human. Non-specific symptoms include fever, sore throat, muscular pain and headaches, as well as gastrointestinal symptoms including vomiting and diarrhoea, and a rash. EVD has an estimated case fatality risk among confirmed cases of 60–70% (WHO Ebola Response Team, 2014). From December 2013 to March 2016, the largest ever observed Ebola epidemic occurred, with more than 28,616 confirmed, probable and suspected cases and 11,310 eventual deaths in Guinea, Liberia and Sierra Leone in West Africa (World Health Organization (WHO), 2016a, World Health Organization (WHO), 2016b). The major mode of transmission of Ebola virus is direct personal contact with blood, feces, vomit, semen or other bodily fluids. Once patients have recovered, the viral RNA is no longer detectable via ordinary blood testing, but the virus remains detectable in the semen of survivors even 9 months after the onset of illness (Deen et al., 2017). Virological and epidemiological studies demonstrated the substantial potential for sexual transmission of Ebola virus from convalescent survivors, potentially elevating the risk of re-emergence of EVD (Abbate et al., 2016, Mate et al., 2015, Kondé et al., 2017).

During the 2013–2016 epidemics, the WHO recommended the use of its original “zero Ebola” definition to declare the end of the outbreak. The definition suggested waiting for 42 days, which is derived from double the observed maximum incubation period, from the time at which the last Ebola confirmed case tested negative for the second time or the time of burial. In that definition of “zero Ebola”, the sexual transmission was not explicitly taken into account as an important factor in sustaining Ebola transmissions. After 42 days, the country was advised to maintain heightened surveillance for 90 days, anticipating recurrent cases (WHO, 2016a). Declaring the end of the epidemic results in downgrading the strengthened health system which involved screening for contact tracing and the maintenance of human resources and laboratory facilities for the immediate testing of blood samples (Elston et al., 2015, Brolin Ribacke et al., 2016). International travel and trade are considerably damaged during an epidemic (Rhymer and Speare, 2016; Centers for Disease Control and Prevention (CDC) 2016), and thus determining the appropriate time to announce the end of an epidemic has important implications for a country's legal, economic and healthcare sectors.

While the WHO criteria offer a definite fixed waiting time, the scientific basis for this may not be sufficiently robust or objective. In a modeling study that aimed to offer a more objective approach to determining the end of an epidemic, Nishiura and colleagues (Nishiura et al., 2016) derived the probability of observing additional cases at a given time by using the serial interval (i.e., the time from illness onset in a primary case to illness onset in the secondary case) and offspring distribution during the outbreak of Middle East Respiratory Syndrome (MERS) in the Republic of Korea. Using the computed probability, authors suggested that the objective determination of the end of a MERS outbreak was attainable if the probability yields less than the threshold value. Despite its successful application in the case of MERS, the extension of this methodology to other diseases including EVD has yet to be conducted.

Using the 42-day waiting period, there have been erroneous declarations of the end of Ebola epidemic (i.e. freedom from Ebola virus disease) in Guinea, Liberia and Sierra Leone from 2015 to 2016. Lee and Nishiura (2017) systematically searched the underlying mechanisms of recrudescence, identifying that many recrudescent cases were suspected to have been caused by sexual contact with survivors, implying that accounting for sexual transmission would be essential in making policy decisions on the end of an epidemic. Because sexual transmission was later identified as the cause of recrudescent events, diagnosis of infected individuals has become more challenging than before due to its potential for discrimination (WHO, 2016b). Thus, not only the existence of sexual transmission but also under-ascertainment of convalescent cases are key factors in determining the end of an EVD epidemic.

In the present study, we proposed an objective approach to determining the end of Ebola epidemic by employing a mathematical model. We formulated a model to describe the observation of cases, accounting for sexual transmission and under-ascertainment, comparing its performance against the conventionally accepted 42-day waiting period.

2. Materials and methods

First, we constructed a mathematical model, accounting for both non-sexual and sexual transmissions of EVD. Second, using the reconstructed transmission dynamics, the probability of observing additional cases in the future was computed.

2.1. Epidemiological data for illustration

We obtained weekly incidence data of confirmed and probable cases from three countries in West Africa, using the Situation Report of the WHO up until 2 May 2016 (World Health Organization (WHO), 2016b, Mayrhuber et al., 2017). The first case in Guinea and Sierra Leone from the Situation Report was reported on 15 September 2014, while the actual first confirmed case was confirmed in March 2014, Guinea and May 2014, Sierra Leone. We had to use the Situation Report, because (i) the alternative datasets, i.e., Patient Database, were subject to revisions even in the present day and (ii) the omitting the very early data in 2014 had only a negligible impact on our calculations. The first case in Liberia was reported earlier than the other two countries on 17 March 2014. We defined Week 0 of the epidemic to be the week starting 15 September 2014. The total number of cases was 2675 in Guinea, 4469 in Liberia and 7118 in Sierra Leone since 15 September 2014, excluding 1580 cases that were reported before 15 September 2014, in Liberia. In addition to epidemic weeks, we also counted weeks since the first “purported last” case (Table S1). In Liberia, this was the Week 27 since the burial of purported last case, and in Guinea and Sierra Leone, this occurred in Week 61 and Week 53 since the second negative test of the last case, respectively.

2.2. Renewal process model

We analyzed the data using the so-called renewal process model. With c _t being the number of new cases of illness onset in week t. The model intended to capture the renewal of cases according to the equation:

$$c_t=R_t\sum _{\tau =1}^{t-1}{c}_{t-\tau }{f}_{\tau }$$ (1)

where R _t is the effective reproduction number, i.e., the average number of secondary cases per single primary case in week t, and f _τ is the probability mass function (pmf) of the serial interval of length τ, defined as the time from illness onset in a primary case to illness onset in the secondary case produced by the primary case. The serial interval f _τ is modeled as a mixture distribution, $f_{\tau }=(1-p)g_{\tau }+p{h}_{\tau }$, where p is the proportional weight of sexual transmission among the total secondary transmission events and g _τ is the pmf of the serial interval through a non-sexual route which is assumed to follow a gamma distribution (see below for discretization). h _τ is the pmf of the serial interval through sexual contact. The distribution g _τ was calculated as g _τ = G(7τ)˗G(7(τ˗1)) for week τ > 0, where G(s) is the cumulative distribution function of the serial interval of direct contact during acute phase, following the gamma distribution, of length s with mean (±standard deviation) estimated at 19.0 (±11.0) days in Guinea, 13.1 (±6.6) days in Liberia and 11.6 (±5.6) days in Sierra Leone, respectively, as estimated from the line list (WHO Ebola Response Team, 2014).

h(τ) was assumed to mirror the survival length of virus positive period, assuming that the frequency of sexual contact remains unchanged over the time since recovery. Let S(x) represent the survival probability of Ebola virus RNA in semen in week x since illness onset (Eggo et al., 2015, Vinson et al., 2016), as measured by the duration of viral RNA positive period with mean m. The probability density function (pdf) (or the continuous version) of the serial interval through sexual contact, h(τ) is

$$h\left(\tau \right)={\displaystyle \frac{S\left(\tau \right)}{{\int }_0^{\infty }S\left(x\right)dx}}$$ (2)

Supposing that H(x) is the cumulative distribution of the serial interval through sexual contact, then, we calculated the pmf h _τ to be used in Eq. (1) as

$$h_{\tau }=H\left(\tau \right)-H(\tau -1).$$ (3)

Assuming that the number of new cases c _t follows a negative binomial distribution, as per published analyses of super-spreading events of Ebola (Althaus, 2015, Lau et al., 2017), with the expected value $E\left(c_t\right)=R_t{\sum }_{\tau =1}^{t-1}{c}_{t-\tau }{f}_{\tau }$, the likelihood function to estimate the effective reproduction number R _t is

$$L\left(R_t;c_t,k\right)=\prod _{t=1}^{t_{max}}{\displaystyle \frac{\Gamma \left(k+c_t\right)}{c_t!\Gamma \left(k\right)}}{\left({\displaystyle \frac{E\left(c_t\right)}{E\left(c_t\right)+k}}\right)}^{c_t}{\left(1+{\displaystyle \frac{E\left(c_t\right)}{k}}\right)}^{-k}$$ (4)

where t _max is the latest week of observation and k is the dispersion parameter assumed as 0.45 (Ajelli et al., 2015).

2.3. Probability of extinction

Here we compute the probability of observing additional cases in the future as a function of week t and compared it against the original WHO criteria with a fixed 42-day waiting period. Using the dataset of t _i, the week of illness onset of diagnosed cases was represented by i (i = 0, 1, …, M), where M is the total number of cases. X(t) represents the theoretically computed number of additional cases in week t. Then, the probability of observing at least one additional case in and after week t is

$$\mathrm{Pr}\left(X\left(t\right)\ge 1\right)=1-\prod _{i=1}^M\sum _{y=0}^{\infty }{d}_y{\left[F_{t-t_i}\right]}^y$$ (5)

where d _y is the pmf of the number of secondary cases y produced by a single primary case (referred to as the offspring distribution), which was assumed to follow a negative binomial distribution with the mean R _f and dispersion parameter k (Lloyd-Smith, 2007, Ajelli et al., 2015). F _τ represents the cumulative distribution function of the serial interval, given as the cumulative sum of f _τ. The mechanistic basis of Eq. (5) has been described elsewhere (Nishiura, 2016). The end of an outbreak is determined in the corresponding week if the probability of observing at least one additional case is less than a specified threshold value, i.e., 5% or 1%.

2.4. Computation and sensitivity analysis

We compared our model performance and the resulting data against that based on the WHO criteria, varying unknown parameters within plausible ranges (Table 1 ). First, since we did not have an empirical estimate of the mixture weight of sexual transmission among the all secondary transmissions without strict guidance to refrain from unprotected sexual contact, we varied the weight 100 × p of the mixture distribution of serial interval from 0.001% to 10%, while the most plausible value 0.12% that is derived from a published estimate on the proportion of sexual transmissions among all secondary cases in West Africa from 2014–16 (Abbate et al., 2016). The largest value 10% may be out of the plausible range, but we examined this value for two reasons: (i) we do not know what would have happened if people were not advised to refrain from sexual transmission during the 2014–16 epidemic and (ii) hypothetically we intended to present scenarios in which there were substantial number of sexual transmissions before the end of an epidemic. The parameter p constitutes the serial interval distribution as a weight of the stationary serial interval distribution, and the real time assessment of the proportion of sexual transmissions does not apply to the interpretation of p; see similar debates on the sampling of the generation time (Nishiura, 2010). The mean duration of virus persistence in semen (m) also varied from 3 to 9 months (Deen et al., 2017, Fischer and Wohl, 2016).

Table 1.

Parameter values for computing the probability of the end of an Ebola virus disease epidemic.

Category	Parameter	Description	Values	Examined range	References
Sexual transmission	100 × p	Proportion of sexual transmissions among all secondary transmissions (%)	0.12	0.001–10	Abbate et al., 2016
	m	Mean duration of testing positive for viral RNA (months)	7	3–9	Deen et al., 2017
Policy	100 × u	Relative reduction in unprotected sexual contact (%)	0	0–80	Fischer and Wohl, 2016
	100 × q	Proportion of diagnosed cases (%)	50	10–90	Houlihan et al., 2017
Epidemiological factor	Rf	Reproduction number during the late stage of the epidemic	G: 1.08	0.50–1.50	Estimated
			L: 0.74
			S: 1.28
	n	n-th declaration of the end of Ebola virus transmission	1	G:1,2	WHO, 2016a
				L:1,2,3,4
				S:1,2

G, L and S represent Guinea, Liberia and Sierra Leone, respectively.

Second, due to precautionary guidance during the course of an epidemic from the health sector, people may have refrained from unprotected sexual contact. In addition, we introduced a single fraction u that represents the proportion of people refraining from unprotected sexual contact by changing the mixture distribution of the serial interval to

$$f_{\tau }={\displaystyle \frac{\left(1-p\right)g_{\tau }+\left(1-u\right)p{h}_{\tau }}{1-p+\left(1-u\right)p}}.$$ (6)

The fraction 100 × u was assumed to broadly range from 0 to 80% (Soka et al., 2016).

Third, not all cases were ascertained during the course of the epidemic. We let q be the proportion of diagnosed Ebola patients among the total number of infected individuals. Diagnosed cases correspond to the incidence data of confirmed and probable cases (WHO, 2016b). The total number of infected individuals is calculated by (1 + λ) diagnosed cases if the number of undiagnosed cases per a diagnosed case is λ. Then, the total number of ascertained cases was calculated by the sum of diagnosed cases and undiagnosed cases. We examined how influential the imperfect diagnosis would be on the declaration of the end of an epidemic by varying 100 × q by setting 50% as the default and varying it from 10% to 90% as part of the sensitivity analysis (Houlihan et al., 2017). To examine the impact of under-ascertainment on the end of an epidemic, we recalculated the total number of cases using q and the observed epidemic curve, estimating the undiagnosed cases as (1−q)/q times the observed epidemic curve. Although the simple use of (1−q)/q could potentially inflate the actual number of cases, and whereas the issue could be overcome by using a latent variable model that separates the observation process from unobservable transmission process, we did not employ the latent modeling, because its explicit incorporation requires us to implement additional formulation that influences the derivation of Eq. (5). In addition, the Eq. (5) requires the reproduction number R _f as an input, but R _t varies with time. We examined the impact of using different R _f estimates on the probability of declaring the end of an outbreak. As the baseline setting, R _f was calculated by taking its average for the most recent 24 weeks.

2.5. Simulation-based validation

We assessed the model performance by means of random simulations, varying parameters p, m and u with an application to the setting of Guinea. First, we assumed that the observed case counts were known by Week 58 in which the first purported last case was notified to the WHO. From Week 59, the renewal process was randomly simulated for 20,000 times, using a negative binomially distributed case counts, of which the mean corresponded to the expected number of cases derived from the renewal equation in every week. The effective reproduction number during the waiting period was assumed as known and fixed at 0.05, 0.10 and 0.50, as empirically estimated during the late stage of the epidemic in three West African countries. Second, the probability of observing at least one additional case was calculated. Let A and B represent the time period of waiting time and the time after declaration of the end of epidemic, respectively. The length of waiting time, or the time period of A, denoted by t _A, was calculated from our proposed method, and the time period, B was simulated for (300- t _A) additional weeks where 300 is an arbitrary number of the final week of simulations that we consider as sufficiently large. Let X be a random variable of the number of cases in the week t ∈ {A, B}. Computing $\text{Pr}\left({\mathrm{X}}_{\mathrm{B}}>0|X_A=0\right)$ would allow us to calculate the number of realizations in which the proposed model or the WHO criteria failed to capture the recrudescent event. As an evaluation, we confirmed that the corresponding probability was smaller than the pre-defined threshold.

2.6. Cost-effectiveness analysis

We implemented a cost-effectiveness analysis to assess the economic cost of waiting time, if adhering to our modeling method and contrasting the proposed method to the WHO criteria. To do so, we calculated the cost of waiting for a certain length of time as well as the probability of reduced risk of observing additional cases due to the waiting time. First, let T _c and T _w be the number of weeks since the last case, as suggested by our computational method and the WHO, respectively. In many instances, T _c-T _w > 0. We extracted the gross domestic product (GDP) due to Ebola epidemic per week, and fixed the cost, c, as 14 million United States dollars (USD) per week (Bambery et al., 2018). Second, let Pr(T _c) and Pr(T _w) as the probability of observing at least one additional case given the waiting time T _c and T _w. We converted the risk of recrudescence into the number of Ebola deaths by assuming that one epidemic induced 10,000 deaths as approximated by the 2014–16 epidemic, and thus, 1% risk of recrudescence is assumed to be equivalent to 100 deaths. To convert the number of deaths into the number of life years lost due to Ebola, we calculated the average age of fatal cases and subtracted the average age from the life expectancy at birth. Table S2 shows the life years lost due to Ebola, y, in Guinea, Liberia and Sierra Leone. Accordingly, incremental cost-effectiveness ratio (ICER) was calculated as

$$\text{ICER}=\frac{c(T_c-T_w)}{ay\left|Pr\left(T_c\right)-Pr\left(T_w\right)\right|}\times 100,$$ (7)

where a is the conversion rate from the probability of recrudescence to the number of deaths (i.e., a = 100 deaths per 1% risk of recrudescence). During the implementation, we accounted for the uncertainty with respect to the proportion of sexual transmissions among all secondary cases, p. To address the uncertainty, we randomly sampled the value of p for 1000 times from a triangular distribution with the peak 0.0012 and minimum and maximum values at 0 and 1, respectively. This illustration was made with application to Guinea data, but univariate sensitivity analysis using (7) was also conducted for all three countries.

3. Results

Hereafter, we consistently use the “week since the last case” as defined by the number of weeks that have elapsed since the purported last case testing negative twice or burial (Table S1). Using the baseline parameter values including p = 0.0012 in Table 1, the probability of observing additional cases lowered 5% at 19, 37 and 28 weeks since the last case in Guinea, Liberia and Sierra Leone, respectively; these time points varied by country due to the different sizes and shapes of the epidemic curves. Considering that the WHO criteria imposes 6 weeks to wait since the last case, the suggested lengths of our proposed method were 13, 31 and 22 weeks longer than the WHO, but all those events were successfully captured within the waiting time (Table S3).

The first recrudescent case was reported in week 17, 14, 16 since the last case in Guinea, Liberia, Sierra Leone, respectively. It should be noted that the last observed actual recrudescent event in Guinea was in the week 20, and the gap period between the last observed recrudescence and the week of the end derived from our model (week 19) was only 1 week (Fig. 1 A). In addition, the gap period between the last declaration (week 25) and the calculated end of the epidemic from our model (week 28) was 3 weeks in Sierra Leone (Fig. 1E). The purported last case reported in week 34 in Liberia before the second declaration was 3 weeks earlier than our suggested week (week 37) in Fig. 1C.

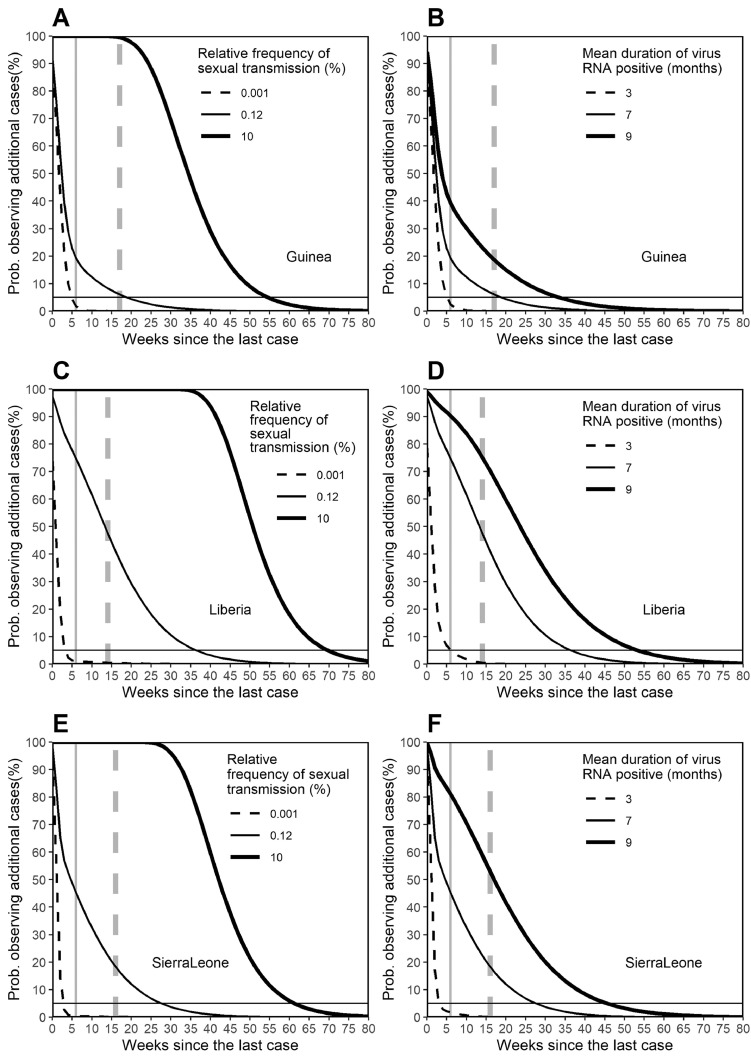
Fig. 1.

Sensitivity of the probability of the end of an Ebola epidemic to sexual transmission characteristics.

Vertical axis measures the probability of observing additional cases on or after the specified week, while the horizontal axis measures the weeks since the last case was buried or tested negative twice for Ebola virus. Panels A, C and E examine the sensitivity of the probability of the end of an epidemic to the proportion of sexual transmissions among all secondary transmissions. Of the two vertical lines, the solid line represents the week in which the end of the epidemic was declared, following a 42-day waiting period as specified by the World Health Organization. The dashed vertical line represents the week in which a recrudescent case occurred after the first erroneous declaration was recognized. The horizontal dashed line measures the probability at 5% below which one may regard that the epidemic is over. Panels B, D and F measure the sensitivity of the probability to the mean duration of detecting viral RNA.

It appears that the extent of sexual transmission among the total secondary transmission events had a profound impact on the waiting period before declaring the end of the epidemic (Fig. 1). If as many as 10% of secondary transmission events were attributed to sexual contact, it may be necessary to wait 55–81 weeks (i.e., approximately 1 year) from the purported last case to declaring the end of the Ebola epidemic. It is clear that the mean length of virus persistence also plays a role (Fig. 1B,D and F), but qualitatively, the extent of sexual transmission had a greater impact on the waiting period.

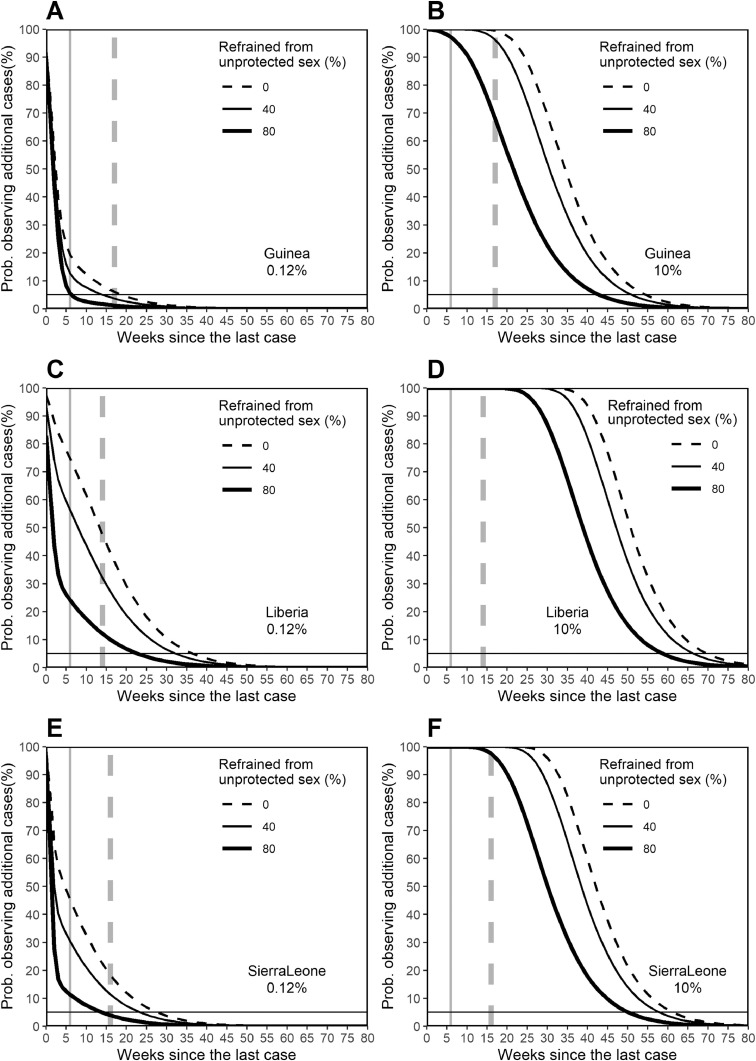
As the proportion of sexual transmission among all secondary transmission events influences the probability of observing additional cases, individual's behavior regarding unprotected sex would impact on the waiting period (Fig. 2 ). This effect is particularly visible if the extent of sexual transmission is substantial (Fig. 2B, D and F). For example, in Sierra Leone, the waiting period between the last case and declaring the end of the epidemic was 28 weeks without any interventions to avoid unprotected sex (i.e., u = 0). However, this time period can be reduced by 14 weeks if 80% of people avoid risky sexual contact (Fig. 2E). This indicates that the length of time that must elapse before declaring the end of an Ebola epidemic is highly dependent on sexual behavior.

Fig. 2.

Sensitivity of the probability of the end of the Ebola epidemic to the relative reduction in unprotected sexual contact.

Vertical axis measures the probability of observing additional cases on or after the specified week, while the horizontal axis measures the weeks since the last case was buried or tested negative twice to Ebola virus. Panels A, C and E examine the sensitivity of the probability of the end of the Ebola epidemic to the relative reduction in unprotected sexual contact, assuming that sexual transmission accounts for 0.12% of all secondary transmissions. Of the two vertical lines, the solid line represents the week in which the end of the epidemic was declared, following a 42-day waiting period as specified by the World Health Organization. The dashed vertical line represents the week in which a recrudescent case was recognized after the first erroneous declaration. The horizontal dashed line measures the probability at 5% below which one may regard that the epidemic is over. Panels B, D and F measure the sensitivity of the probability to the relative reduction in unprotected sexual contact, assuming that sexual transmission accounts for 10% of all secondary transmissions.

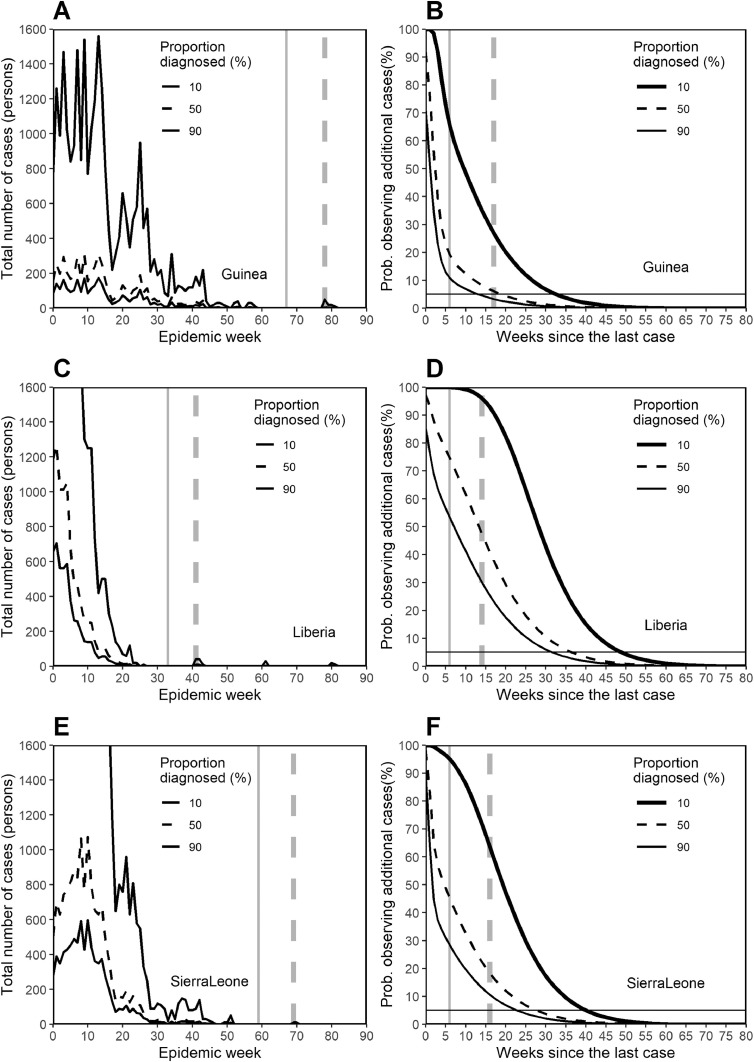
Fig. 3 examines the extent of the impact of under-ascertainment on the declaration of the end of an epidemic. As the extent of under-ascertainment is magnified by the factor of 0.1, 0.5 and 0.9, a country has to endure considerably longer waiting times to ensure that an epidemic is over (e.g. it was 19 weeks since the last case in Guinea with p = 0.0012 and q = 0.5, but it can vary from week 14 to 33 with q = 0.1 and 0.9). However, with an ascertainment rate of 10%, the impact was less than that observed with a weight of p = 0.1 (with 10% of secondary transmission events attributed to sexual transmission) in Fig. 2.

Fig. 3.

Sensitivity of the probability of the end of Ebola epidemic to case ascertainment.

Panels A, C and E show the estimated actual number of cases in the respective countries, assuming that the proportion diagnosed represents 10%, 50% and 90% of the total infected individuals. To adhere to the real time nature of the analysis, and to appropriately include recrudescent events in the epidemic data, the original data were derived from probable and confirmed cases in the Situation Report of the World Health Organization (WHO). Of the two vertical lines, the solid line represents the week in which the end of the epidemic was declared, following a 42-day waiting period as specified by the WHO. The dashed vertical line represents the week in which a recrudescent case was recognized after the first erroneous declaration. Panels B, D and F measure the sensitivity of the probability to the proportion diagnosed. The vertical axis measures the probability of observing additional cases on or after the specified week, while the horizontal axis measures the weeks since the last case was buried or tested negative twice to Ebola virus. The horizontal dashed line measures the probability at 5% below which one may regard that the epidemic is over.

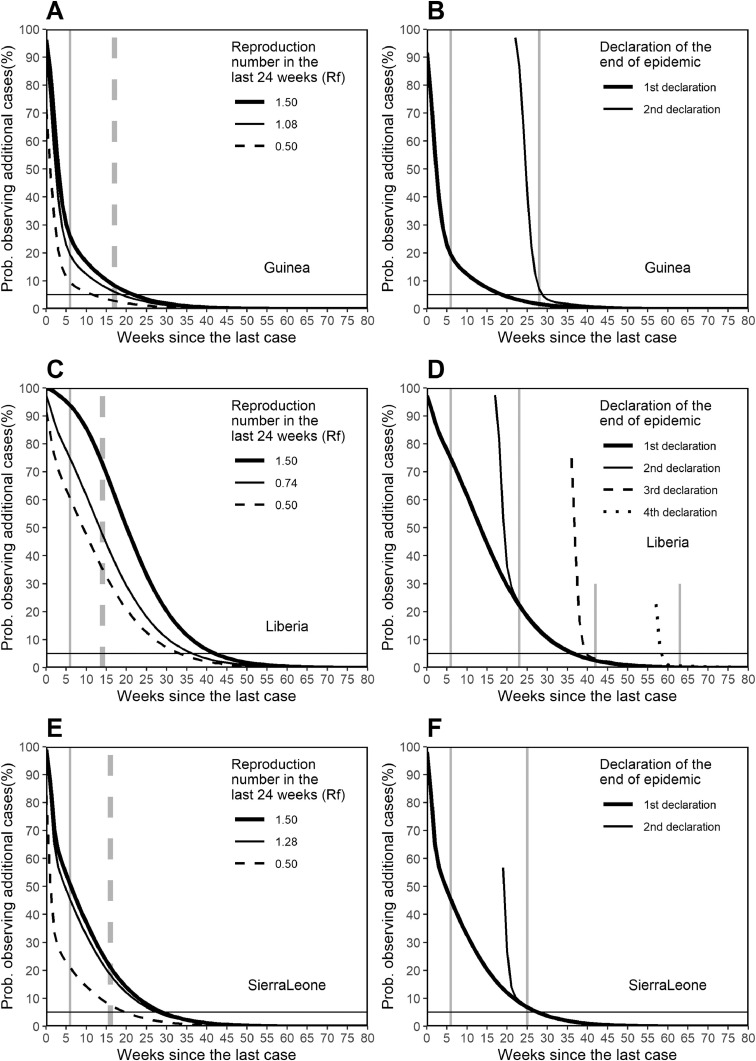
In Fig. 4 , the probability of observing additional cases is examined using the average R _f over the most recent 24 weeks, and the probability is compared against R _f = 0.5 and 1.5. The sensitivity of the waiting time to R _f varied by country due to different epidemic curves, e.g., in Liberia, there were a greater number of recent cases before the purported last case than in the other two countries, and thus, there was more variation in the week in which the end of the epidemic was declared. Fig. 4B,D and F compare our suggested week of declaration of the end of an epidemic against those adhering to the WHO criteria for all possible opportunities for declaration. In observation, declarations of the end were made twice in Guinea and Sierra Leone and four times in Liberia. Guinea declared the end of the epidemic 6 weeks after the first purported last case being buried, and subsequently, declared 28 weeks after the first purported last case testing negative twice. Liberia declared 6, 23, 42 and 63 weeks after the first purported last case testing negative twice for all possible declarations. Sierra Leone declared in weeks 6 and 25 after the first purported last case testing negative twice. Considering Week 0 of the epidemic to have commenced on 15 September 2014, the first purported last case was buried in Week 27 in Liberia and tested negative twice in Weeks 61 and 53 in Guinea and Sierra Leone, respectively. For the first declaration in all three countries, our method proposed longer waiting periods than the 42-day wait recommended by the WHO criteria. However, during the later opportunities for declaration, our method proposed earlier declaration times than those based on the WHO criteria due to the low chance of secondary transmission.

Fig. 4.

Sensitivity of the probability of the end of Ebola epidemic to the reproduction number and evaluation of the sequence of declarations.

Vertical axis measures the probability of observing additional cases on or after the specified week, while the horizontal axis measures the weeks since the last case was buried or tested negative twice to Ebola virus. Panels A, C and E examines the sensitivity of the probability to the reproduction number around the end of the epidemic. We used the reproduction numbers during the late stage of the epidemic, taking weighted means using case counts for weighting, dating back for 24 weeks from the week in which the last case was reported. Of the two types of vertical lines, the solid line represents the week in which the end of the epidemic was declared, following a 42-day waiting period as specified by the WHO. The dashed vertical line represents the week in which a recrudescent case was recognized after the first erroneous declaration. The horizontal dashed line measures the probability at 5% below which one may regard that the epidemic is over. Panels B, D and F measure the sensitivity of the probability to different timings at which the last case was observed.

We implemented random simulations of the epidemic since the purported last case, validating our proposed method. Given the absence of recrudescence during the waiting period, the probability of observing at least one additional case after declaration was below 4.9% and 1.3%, respectively, for all combinations of parameters using the cut-off values 5% and 1%, respectively. If the WHO criteria were used, highly variable results were obtained including recrudescence with the probability greater than 50%. Given those failures, the use of heightened surveillance period for 90 days following the 42-day waiting time did not help excluding the possibility of recrudescence, given large values of p or m (Table 2 ).

Table 2.

Simulation-based evaluation of the waiting time to declare the end of Ebola epidemic as applied to the dataset in Guinea, 2014–16.

			Frequency of failures (%)				Waiting time (weeks)
			Computation		WHO criteria		Computation		WHO criteria
Rf	Parameter	Value	5%	1%	42-day	90-day	5%	1%	42-day1)	90-day2)
0.05	Base	–	3.8	1.0	1.0	0.2	2	6	6	19
0.05	100 × p	0.001%	2.4	0.4	0.1	0.0	2	4	6	19
0.05	100 × p	10%	4.3	0.8	51.6	17.5	31	44	6	19
0.05	m	3	2.7	0.5	0.1	0.0	2	4	6	19
0.05	m	9	3.8	0.8	2.3	0.7	3	17	6	19
0.05	100 × u	40%	3.4	0.8	0.6	0.1	2	5	6	19
0.05	100 × u	80%	2.8	0.8	0.3	0.1	2	4	6	19
0.1	base	–	4.4	0.8	1.6	0.3	3	12	6	19
0.1	100 × p	0.001%	2.5	1.1	0.2	0.0	3	4	6	19
0.1	100 × p	10%	4.0	0.7	74.9	32.5	37	49	6	19
0.1	m	3	2.3	0.5	0.3	0.0	3	5	6	19
0.1	m	9	4.4	1.0	4.4	1.7	6	25	6	19
0.1	100 × u	40%	3.7	0.9	1.2	0.3	3	8	6	19
0.1	100 × u	80%	2.8	0.8	0.4	0.1	3	5	6	19
0.5	Base	–	4.2	0.3	8.4	1.5	12	27	6	19
0.5	100 × p	0.001%	4.6	0.6	0.6	0.0	4	6	6	19
0.5	100 × p	10%	NA	NA	100.0	NA	49	61	6	19
0.5	m	3	2.9	0.3	1.0	0.0	5	7	6	19
0.5	m	9	4.9	1.1	19.3	7.4	25	43	6	19
0.5	100 × u	40%	4.6	0.9	6.5	1.5	8	22	6	19
0.5	100 × u	80%	3.8	1.3	2.9	0.2	5	12	6	19

Base represents the baseline combination of parameters (see Table 1). Frequency of failures: the probability of observing additional cases after declaration using the specified method of determination. Waiting time 42-day¹⁾: the time elapsed from the first purported last case testing negative twice or burial to the declaration of the end of epidemic was fixed at 42 days. Waiting time 90-day²⁾: the time in which the enhanced surveillance is continued for 90 days.

Fig. 5 A,C,E and Table S3 examine the sensitivity of the weeks since the last case to various univariate changes, leading to waiting time for up to 80 weeks with p = 0.10. Even with the unrealistically large value of p, it is shown that refraining from unprotected sexual contact (large u value) can substantially reduce the length of waiting time. The resulting ICER is shown in Fig. 5B,D and F for Guinea, Liberia and Sierra Leone, respectively. As long as 5% threshold was used, the ICER indicated that the proposed method is regarded as cost effective. When 1% threshold was used, and when the number of weeks was counted from the 2nd or later purposed last cases, our analysis indicated that a large cost would be required due to too conservative decision making. Fig. 6 summarizes the results from cost-effectiveness analysis. It appeared that 50% of realizations led to declaration from week 55 to 65. The cost required to save one life year was 3000 US Dollars using the threshold 5%, indicating that the use of our modeling method would be regarded as cost effective, according to the standard in industrialized countries. However, compared with a threshold of ICER at 50,000 US Dollars in the United States (Woods et al., 2016), the acceptable total societal cost in Guinea, Liberia and Sierra Leone based on GDP per capita would range from 5929 to 18,929 US Dollars (Bartsch et al., 2015). That is, our result remains cost effective according to their countries’ criteria of cost effectiveness.

Fig. 5.

Uncertainty analysis of weeks since the last case and incremental cost effectiveness ratio (ICER) to assess the end of Ebola epidemic.

The proportion of sexual transmissions among all secondary transmissions was randomly sampled from a triangular distribution with median 0.0012 with the range from 0 to 1. A. Weeks to declare the end of Ebola epidemic since the last case testing negative twice or buried as a function of the threshold risk of observing at least 1 additional case at 5% or 1%. B. Incremental cost-effectiveness ratio calculated as US dollars per life-year as a function of the threshold risk of observing at least 1 additional case at 5% or 1%. In both panels, red diamond points the mean. Box plot shows interquartile and median values, while whiskers extend to plus/minus 1.5 times interquartile range.

Fig. 6.

Summary of sensitivity analyses of weeks since the last case and incremental cost effectiveness ratio (ICER) to univariate changes in parameter values.

Panels A, C and E show the timing of declaration of the end of Ebola epidemic obtained through the sensitivity analysis according to the threshold value 5% (black bar) or 1% (grey bar) in Guinea, Liberia and Sierra Leone, respectively. For each bar, single parameter is varied to take either minimum or maximum in the assumed range (Table 1). “0.WHO” shows the waiting time by applying the 6 weeks (42-day) criteria of the World Health Organization (WHO). “1.base” is our baseline combination of parameters in Table 1. Weeks corresponding to “2. n = 2” represent the weeks since the secondly purported cases before second declaration (n = 2). In addition, the proportion of sexual transmissions among all secondary cases (p), the mean duration of virus RNA positive period (m), the proportion of diagnosed cases among all cases (q), the proportion who refrained from unprotected sexual contact (u) and the reproduction number (R_f) were varied in the shown ranges. The parameter u is also varied while p is maintained to be a large value, 0.1 in “13.u = 0.4(0.1)” and “14.u = 0.8(0.1)”. Panels B, D and F show the incremental cost-effectiveness ratio (ICER) calculated as US dollars per life-year in Guinea, Liberia, Sierra Leone, respectively, compared to the application of WHO criteria with the fixed 42-day waiting period. In some cases, the time at which our proposed model suggest as the end of Ebola epidemic is earlier than the waiting time adhering to the WHO (i.e. 6 weeks). In such an instance, ICER can take a negative value, and was not calculated (i.e. not calculable).

4. Discussion

On many occasions, the end of an Ebola epidemic has been erroneously declared in West Africa after adhering to the WHO criteria that specify a waiting period of 42 days since the purported last case testing negative for the second time or since the burial. From a mathematical modeling point of view, the 42-day rule was not object-oriented, and moreover, did not account for the importance of sexual transmission appropriately. Motivated by a critical need to develop new science-based criteria to assist local communities with deciding when to declare the end of an epidemic, the present study employed a mathematical model (Nishiura 2016) to compute the probability of the endpoint of an epidemic. In addition to comparing the modeling results with those derived from the WHO criteria, we examined how influential relatively unknown parameters are to determining the week in which the end of an epidemic can be declared. While the relevance of sexual transmission to the overall transmission dynamics has been explored elsewhere (Abbate et al., 2016, Vinson et al., 2016), as has the extinction time of Ebola using a mathematical model (Abbate et al., 2016, Valdez et al., 2015), the present study is the first to model the end of Ebola, explicitly accounting for sexual transmission.

Our findings convey two main messages. First, the proportion of sexual transmissions among all secondary cases during the convalescent period plays a critical role in determining the risk of recrudescence of Ebola. As a result of the long persistence of the virus in semen among male survivors, we have shown that ascertaining the end of an epidemic may require up to 1 year from the purported last case. This finding should not be taken too negatively. As we have shown even with the long waiting time, refraining from unprotected sexual contact can substantially shorten the waiting time. It is striking that the adherence to refraining from unprotected sex or sexual abstinence is likely one of the key factors in determining the absence of additional cases after declaration. In future studies, the importance of sexual transmission should lead to the incorporation of heterogeneous sexual contact patterns into the modeling and decision-making process to allow for precise determination of the end of an Ebola epidemic. Moreover, despite the difficulty to statistically estimate the infectiousness during the late stage of infection (Weitz and Dushoff, 2015), an explicit estimate of the proportion of sexual transmissions among all secondary cases will be called for. The evidence of additional zoonotic sources was not reported except for a single transmission from the natural reservoir by human-to-human transmission through the genetic surveillance for the sequenced 2014 samples in Sierra Leone (Gire et al., 2014). Thus, the risk of emergence from sexual contact is far greater than the baseline risk of observing Ebola virus disease in humans transmitted from animals, given an epidemic in humans.

Second, we have shown that the waiting period to ascertain the end of an Ebola epidemic cannot be determined by a pre-fixed length of time, and rather, it can vary according to transmission dynamics, indicating that the waiting time can be highly variable according to the shape and height of the epidemic curve prior to the observation of last case, and also variable by the detailed mode of transmission including the sexual transmission. As the number of recent cases increases in a country, so does the time period before declaration of the end of the epidemic. Furthermore, the length of the waiting time can also vary depending on the ascertainment rate, which is seldom observable in real time. We have shown that the 42-day waiting period specified by the WHO is too short for the first declaration and risks unnecessary second, third and fourth declarations due to an unexpected small number of recrudescent cases.

Compared with the existing WHO criteria, our proposed method offers an objectively interpretable probability of observing additional cases in the future. Through random simulations, the proposed method was tightly validated. However, our study indicated that the computation of objective probability requires a good knowledge of sexual transmission. This finding underscores the need to conduct sexual behavior surveys during and after the Ebola virus disease epidemic (Kondé et al., 2017, Soka et al., 2016). In addition to the frequency of sexual contact and the use of condoms, it should be noted that sexual partnership structures can also vary by country and could influence the end of an epidemic. This aspect needs to be explored more in future studies to attain a more precise identification of the end of an Ebola epidemic. Moreover, the proposed method can be applied to other infectious diseases by accounting for all routes of transmission. Using this approach only via a direct transmission, Nishiura and colleagues (Nishiura et al., 2016) have investigated the end of an Middle East respiratory syndrome (MERS) outbreak in South Korea. In many infectious diseases, asymptomatic infection plays a critical role in determining the end of epidemic. For example, Zika virus infection involves 80% of asymptomatic infections (Haby et al., 2018). To objectively determine the end of outbreak, the generation time, i.e. the time from infection in a primary case to infection of the secondary case, or the serial interval needs to be mathematically derived by employing an explicitly structured mathematical model that accounts for all important routes of transmission and asymptomatic infection (Inaba and Nishiura, 2008).

Several important limitations of this study should be noted. First, the extent of sexual transmission was dealt with as a constant value throughout the course of the epidemic, but it may in fact vary during this time, potentially as a result of public health interventions. Second, while our model underscored the need to explore the importance of sexual transmission, we had to discard gender information in the dataset. It may be preferable to obtain summary data detailing gender and age (to identify sexually active people) in the future. Third, implemented control measures were not taken into account. In some cases, if contact was traced, secondary cases may not easily be produced even through the sexual route. Fourth, we did not incorporate the latent case model to separate observation process from unobservable transmission dynamics model. This simplification has introduced two critical issues to our results, i.e., (i) zero observed case did not lead to non-zero actual cases by the simple use of correction factor (1−q)/q, and (ii) potentially inflated numbers were converted to integers. However, the formulation using the latent model would require a different effort of formulation which can even change Eq. (5), and this subject is our ongoing future study.

Despite these limitations, we have successfully shown that the frequency of sexual contact during the convalescent period plays a critical role in determining the risk of recrudescence of Ebola and that the probability of the end of an epidemic can vary according to the epidemic curve and the ascertainment rate. We trust that our study identified a number of crucial points to be considered in the future to attain an improved “zero Ebola” definition.