A biologically inspired immunization strategy for network epidemiology

Abstract

Well-known immunization strategies, based on degree centrality, betweenness centrality, or closeness centrality, either neglect the structural significance of a node or require global information about the network. We propose a biologically inspired immunization strategy that circumvents both of these problems by considering the number of links of a focal node and the way the neighbors are connected among themselves. The strategy thus measures the dependence of the neighbors on the focal node, identifying the ability of this node to spread the disease. Nodes with the highest ability in the network are the first to be immunized. To test the performance of our method, we conduct numerical simulations on several computer-generated and empirical networks, using the susceptible-infected-recovered (SIR) model. The results show that the proposed strategy largely outperforms the existing well-known strategies.

Highlights

• •We study an efficient, bio-inspired immunization strategy for network epidemiology.
• •Inspiration stems from a single-celled, ameba-like organism, Physarum polycephalum.
• •Our strategy goes beyond the node degree in selecting targets for immunization.
• •The strategy performs considerably better than several well-known competitors.

1. Introduction

Infectious agents, in the broadest sense, can spread in a ‘population’ of humans, animals, and nowadays technological devices. In the case of an outbreak, the goal is to minimize the damage to the ‘population’ without violating the constraints of a limited budget. Achieving this goal in ‘populations’ other than the primitive, well-mixed ones is the main reason why the problems of (i) epidemics spreading in complex networks (Pastor-Satorras and Vespignani, 2001, Saumell-Mendiola et al., 2012, Zhou et al., 2012, Wang and Xiao, 2012, Buono et al., 2014) and (ii) the corresponding immunization strategies (Balthrop et al., 2004, Bauch and Earn, 2004, Schneider et al., 2011, Hébert-Dufresne et al., 2013) attracted considerable attention in the literature. Such a trend is further spurred by the outcomes of ineffectively controlled epidemics—exemplified by the severe acute respiratory syndrome (SARS) and the swine flu (Schneider et al., 2011)—which rapidly spread all over the world due to globalization and better means of transport (Colizza et al., 2007, Perra et al., 2012). An immediate concern, therefore, is the development of the effective countermeasures against epidemics, wherein immunization science plays an important, if not critical, role.

Multiple immunization strategies have been considered for complex networks. Uniform or random immunization (Pastor-Satorras and Vespignani, 2002) selects any node in the network with equal probability at each time step, which results in a strategy suitable for homogeneous networks, but ignores the fact that in highly heterogeneous networks eradicating an infective agent cannot be guaranteed regardless of the fraction of immunized nodes. Targeted immunization (Mirzasoleiman et al., 2012, Schneider et al., 2012) seeks to overcome this problem by selecting the nodes with the highest ability to spread the disease. Such ability is often measured in terms of degree centrality, defined as the number of ties a node has, or betweenness centrality, which indicates how often a node is located along the shortest route between two other nodes. A strategy based on degree centrality is highly effective, yet it neglects the structural significance of a node because the most connected nodes are not necessarily the ones that facilitate disease propagation from one dense cluster to another (Hébert-Dufresne et al., 2013). Betweenness centrality can be used to overcome such a shortcoming, but suffers from a considerable computational cost (Hébert-Dufresne et al., 2013). In general, targeted immunization requires global knowledge of network properties, which is impractical. Motivated by such an impracticality, so-called acquaintance immunization (Cohen et al., 2003, Gallos et al., 2007) was developed, whereby immunized nodes comprise only a small fraction of random neighbors of randomly selected nodes. Furthermore, a number of alternative and/or more specialized strategies have also been discussed (Fu et al., 2008, Lü et al., 2011, Gong et al., 2013, Wang et al., 2014, Yan et al., 2014). Owing to their immediate practical and economic implications, additional studies involving novel immunization strategies are still of considerable importance.

Herein we propose an efficient biologically inspired immunization strategy for network epidemiology. The term biologically inspired is used in the sense that we draw inspiration from a single-celled, ameba-like organism Physarum polycephalum, capable of transporting signals and nutrients through a dendritic (i.e. tree-like) network of tubular structures called pseudopodia (Nakagaki et al., 2000). Physarum is particularly interesting because of the ability to perform cellular computations of a sort, which lead to the solution of, for example, the shortest path problem. This and similar observations served as a basis for constructing a mathematical model of an adaptive transport network driven by Poiseuille flow that exhibits computational abilities much like Physarum itself (Tero et al., 2007). Subsequently, a Physarum-type algorithm has been used for solving the Steiner Minimum Tree problem (Tero et al., 2008, Tero et al., 2010), for optimizing network design (Tero et al., 2010, Watanabe et al., 2011, Liu et al., 2015, Song et al., 2014), and for a variety of other applications (Zhang et al., 2012, Zhang et al., 2013, Gao et al., 2013, Adamatzky, 2014, Adamatzky and Schubert, 2014).

The paper is organized as follows. In Section 2 we describe how to construct a Physarum model and modify it into a strategy for immunizing complex networks. Model properties and performance are examined in Section 3. In particular, we emphasize (i) the difference in functioning between the proposed strategy and other, well-known counterparts, (ii) the gain in performance by accounting for the structural importance of nodes, and (iii) the ability to capture the key attributes of a whole network based solely on the successive use of local information. Finally, in Section 4 we summarize the take-home message and discuss the potential drawbacks, as well as the future developments.

2. Methods

The proposed, biologically inspired strategy (denoted simply AS, where A stands for ameba) is constructed in three steps. First, we describe the Physarum model for the shortest path selection. We then modify the model by adding a noise factor to select the paths alternative to the shortest one along which the disease can still spread, albeit with a lower probability. Second, the original Physarum (single-source, single-sink) model is further modified to become a single-source, multi-sink model to consider the spread of the disease to multiple targets simultaneously. With these modifications, the model measures the dependence of each node in the network on the focal node. The third and final step in the construction of AS is motivated by the fact that applying the modified Physarum model to a large network is impractical due to a possible lack of information on the network structure or the high computational expense. Accordingly, for each focal node, a subnetwork consisting of the focal node itself and its R-step neighbors is separated from whole network, whereupon the model is applied to this R-local subnetwork. To test the performance of AS, we conduct numerical simulations on several computer-generated and empirical networks.

2.1. A Physarum model for the shortest paths selection

The shortest path selection by Physarum polycephalum is based on the transformations of tubular structures (pseudopodia) (Tero et al., 2007, Nakagaki et al., 2001) and a positive feedback from flow rates (Chae and Nguang, 2014, Zhang et al., 2014). Namely, high rates of the protoplasmic flow stimulate the diameter of pseudopodia to increase, whereas at low flow rates the diameter tends to decrease. The pseudopodia thickness thus adapts to the flow rate. More formally, we observe a set of nodes N, containing two end-nodes, i ₁ and i ₂ (for biological reasons also called food-source nodes), and any number of in-between nodes, $i\in N$. The edge connecting nodes $i,j\in N$ is denoted as i–j and serves as a symbolic representation of a pseudopodium. Denoting by Q _ij the flux through edge i–j (i.e. from i to j) and assuming the flow through pseudopodia to be approximately Poiseuille flow, we obtain:

$$Q_{\mathit{ij}}=\frac{\pi r_{\mathit{ij}}^4}{8\xi L_{\mathit{ij}}}(p_i-p_j)=\frac{D_{\mathit{ij}}}{L_{\mathit{ij}}}(p_i-p_j),$$ (1)

where ξ is the viscosity coefficient of the sol, $D_{\mathit{ij}}=\pi r_{\mathit{ij}}^4/8\xi$ is a measure of the conductivity of pseudopodia (with r _ij being the radius), and p_i is the pressure at node i. L _ij is the length of edge i–j. One interpretation for these lengths follows from the fact that $L_{\mathit{ij}}^{-1}$ determines the importance of edge i–j, which means that in an unweighted network $L_{\mathit{ij}}=1$ for all possible is and js.

Pressures, p_i in Eq. (1) are unknown. To obtain them, we further assume that in-between nodes are of zero capacity and that the sol conservation law is upheld, yielding at each node j, ${\sum }_{i\in \Gamma \left(j\right)}{Q}_{\mathit{ij}}=0$, $j\ne 1,2$, where i runs across the set of the nearest neighbors of j, $\Gamma \left(j\right)$. For the source node, 1, and the sink node, 2, we have ${\sum }_{i\in \Gamma \left(1\right)}{Q}_{i1}=-I_0$ and ${\sum }_{i\in \Gamma \left(2\right)}{Q}_{i2}=I_0$, respectively, where I ₀ is the influx from the source node (or into the sink node). It follows:

$$\sum _{i\in \Gamma \left(j\right)}\frac{D_{\mathit{ij}}}{L_{\mathit{ij}}}(p_i-p_j)=\{\begin{array}{cc}-1\hfill & \mathrm{for}j=1,\hfill \\ +1\hfill & \mathrm{for}j=2,\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}$$ (2)

where without any loss of generality $I_0=1$. By further setting $p_2=0$ as the basic pressure level, all p_is can be determined from the above system of equations. Finally, using Eq. (1) all flows, $Q_{\mathit{ij}}=D_{\mathit{ij}}(p_i-p_j)/L_{\mathit{ij}}$, can also be obtained.

Experiments show that pseudopodia with higher flux rates are reinforced, while those with lower flux rates degenerate (Tero et al., 2007, Nakagaki et al., 2001). To accommodate this adaptive behavior of pseudopodia, the conductivities, D _ij, are assumed to change according to the following equation:

$$\frac{d}{\mathit{dt}}{D}_{\mathit{ij}}=f\left(\right|Q_{\mathit{ij}}\left|\right)-{\mathit{aD}}_{\mathit{ij}},$$ (3)

where a is the decay rate. The functional form $f\left(\right|Q_{\mathit{ij}}\left|\right)$ is, for simplicity, set to $f\left(\right|Q_{\mathit{ij}}\left|\right)=b\left|Q_{\mathit{ij}}\right|$, where b is a constant (Tero et al., 2007). We further simplify the notation by choosing the units in which $b/a=1$, implying that flow and conductivity have the same dimensions, that pressure has the dimension of length, and that the time, $t^{\prime }=\mathit{at}$, is dimensionless (in the following, we will suppress the prime because no confusion can occur). To solve Eq. (3), a semi-implicit scheme is used as follows:

$$\frac{D_{\mathit{ij}}^{n+1}-D_{\mathit{ij}}^n}{\delta t}=\left|Q_{\mathit{ij}}^n\right|-D_{\mathit{ij}}^{n+1},$$ (4)

where $\delta t$ is a time step and the upper index, n, indicates the current moment in time. In this way, the time-varying conductivity, D _ij, degenerates to zero for every path between the end-nodes, except the shortest one.

2.2. A noise factor for irrational path selection

The described Physarum model solves the shortest path problem, but that is not where our interest lies. To formulate an immunization strategy, it is necessary to consider the paths other than the shortest one. However, in the original Physarum model, the flow Q _ij from node i to node j tends to unity if the edge i–j is lying on the shortest path or tends to zero otherwise (Bonifaci et al., 2012). To account for other pathways as well, we rewrite Eq. (4) as follows:

$$\frac{D_{\mathit{ij}}^{n+1}-D_{\mathit{ij}}^n}{\delta t}=\frac{\left|Q_{\mathit{ij}}^n\right|}{1-\gamma +\gamma \left|Q_{\mathit{ij}}^n\right|}-D_{\mathit{ij}}^{n+1},(0<\gamma \le 1)$$ (5)

where γ is a noise factor. Similar to the noise in game theory (Wang et al., 2013, Wang et al., 2013), γ is introduced to disturb the mass flow distribution through the network's edges. Using the terminology from evolutionary biology, γ permits irrational selection. The modified model approaches the original as $\gamma \to 0$.

2.3. Multi-foraging

For the purpose of devising an immunization strategy, in addition to modifying the model by a noise term, we wish to simultaneously consider the potential for the spread of the disease from a source node to multiple other nodes in the network. To achieve such a feat, we rewrite Eq. (2) as

$$\sum _{i\in \Gamma \left(j\right)}\frac{D_{\mathit{ij}}}{L_{\mathit{ij}}}(p_i-p_j)=\{\begin{array}{cc}-1\hfill & \mathrm{for}j=1,\hfill \\ {\displaystyle \frac{1}{n-1}}\hfill & \mathrm{for}j=\{2,3,\dots ,n\},\hfill \\ 0\hfill & \mathrm{otherwise},\hfill \end{array}$$ (6)

where n is the number of nodes in the network. We call this model a multi-forage model because multiple sink-nodes can “forage” on a single source-node. By applying the multi-forage model, we are in a position to derive a proxy for the ability of the focal node to spread the disease.

2.4. A biologically inspired immunization strategy (AS)

The extended Physarum model has all the desired properties for formulating an immunization strategy, yet the information on the structure of the whole network may not exist. Even if such information is available, the model may not be applicable to a very large network for computational reasons (Becchetti et al., 2013). We therefore pursue an R-local approach that considers only a subnetwork of the focal node comprised of the focal node's R-level neighbors and all the accompanying edges. Specifically, a proxy for the focal node's ability to spread the disease is obtained through the following steps:

• 1.Take ${\Gamma }_R\left(k\right)$, the set of all R-level neighbors of the focal node k.
• 2.For each $l\in {\Gamma }_R\left(k\right)$, one iteration of the model is run in which node l is the source and all other $j\in {\Gamma }_R\left(k\right)\cup \left\{k\right\}$ are the sinks. Each iteration thus generates inflows (i.e. positive flows) $Q_{\mathit{ij}}^{(k,l)}$ along all edges i–j in the selected R-local subnetwork of focal node k.
• 3.The summation across all iterations, $Q_{\mathit{ij}}^{\left(k\right)}={\sum }_{l\in {\Gamma }_R\left(k\right)}{Q}_{\mathit{ij}}^{(k,l)}$, gives the so-called flow matrix.
• 4.
  Finally, the ability of focal node k to spread the disease is quantified by a score:

  $$\mathit{AS}\left(k\right)=\sum _{i-j}{Q}_{\mathit{ij}}^{\left(k\right)},$$ (7)

  where i–j symbolizes the summation over all the edges in the R-local subnetwork of focal node k.
• 5.The focal node with the highest AS-score is the first to be immunized.

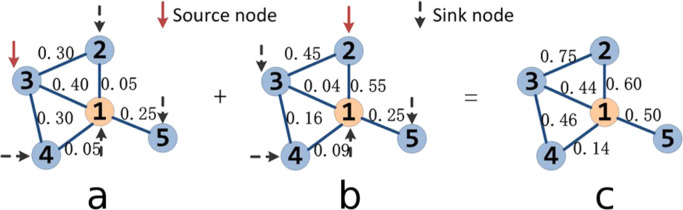
The first three steps of the described strategy may be somewhat difficult to understand using just a mathematical notation. Accordingly, these steps are illustrated in Fig. 1 . To distinguish focal node 1 from its first-level neighbors, we mark it with a wax-yellow color. The results of a single model iteration, in which node 3 is chosen as the source node, are shown in Fig. 1a. This iteration is immediately followed by another one (Fig. 1b), such that node 2 is the source node. The results are summed to produce the flow matrix in Fig. 1c. The AS-score for focal node 1 is obtained by repeating the process for all of 1's first-level neighbors and then summing the elements of the flow matrix across all edges.

Fig. 1.

Internal functioning of AS. Node 1 marked with wax-yellow color is the focal node, whereas the other nodes are its first-level neighbors. Panels a and b show the results of two model iterations in which nodes 3 and 2 are selected as the source nodes, respectively. These results are summed to produce the so-called flow matrix in panel c. Upon running all possible iterations (see the accompanying text), the AS-score for the focal node is obtained by summing the elements of the flow matrix across all edges.

3. Results and discussion

Next, we examine several interesting properties of AS and test its performance against strategies based on degree centrality (DCS), betweenness centrality (BCS), and closeness centrality (CCS). Both stylized, computer-generated networks and real-world, empirical networks are used in the performance tests. Additionally, the success of immunization is tested in conjunction with a susceptible-infectious-recovered (SIR) model.

3.1. Properties of AS

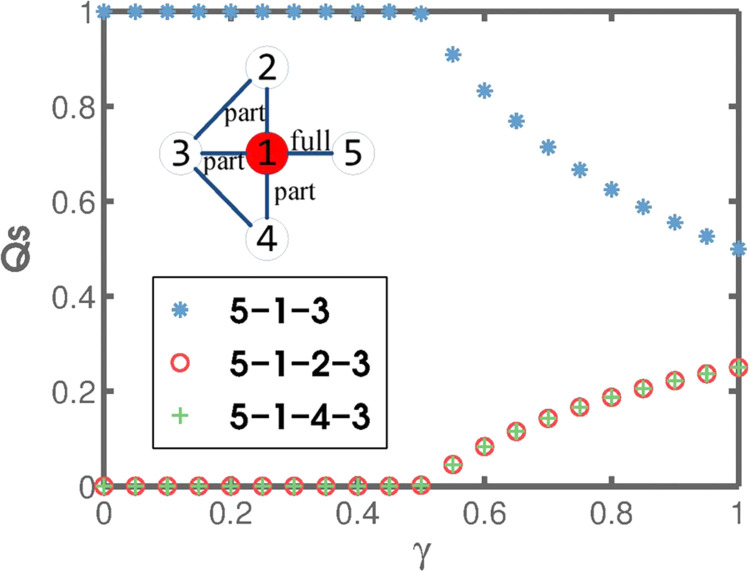
The role of the noise factor and irrational path selection. The proposed immunization strategy is designed to quantify the ability of a focal node to spread the disease through the network. Put alternatively, we want to know (i) the extent to which the neighbors depend on the focal node and (ii) the relative importance of disease spreading pathways on which the focal node lies. Nodes 2, 3, and 4 in the inset of Fig. 2 , for example, are just partially dependent on node 1 because they are, among others, connected by pathways excluding the latter node. Node 5, by contrast, is fully dependent on node 1. Furthermore, if we consider the spread of the disease from node 5 to node 3, path 5-1-3 is the most direct, but the disease can spread through alternative paths 5-1-2-3 and 5-1-4-3. Such alternatives need to be taken into account to properly determine the ability of the focal node to spread the disease. The original Physarum model cannot yield the desired result. If we imagine for a moment that the link between nodes 1 and 3 is removed and assume that path 5-1-2-3 is just a tiny bit shorter than alternative path 5-1-4-3, all flow would be assigned to the former path. Node 4 would consequently be disregarded as irrelevant for the spread of the disease, while nodes 1 and 2 would (wrongly) be considered of equal relevance. However, the possibility of having an epidemic spread via both paths (i.e. 5-1-2-3 and 5-1-4-3) would suggest that nodes 2 and 4 should be seen almost as equivalents, whereas node 1 is of more immediate concern. The role of the noise factor, γ, is to resolve the described problem. Indeed, the three paths from node 5 to node 3 are properly distinguished in Fig. 2 based on the flows, if the value of the noise factor is set to some $\gamma >0.5$.

Fig. 2.

The role of the noise factor and irrational path selection. The distribution of flows, Qs, along the different paths from node 5 to node 3 (in the inset) is shown as a function of the noise factor, γ. If $\gamma >0.5$, in addition to shortest path 5-1-3, some flow is equally distributed between the two remaining paths, 5-1-2-3 and 5-1-4-3, meaning that the relative importance of disease spreading pathways is correctly distinguished.

The advantage of AS over the other comparable strategies. To exemplify why AS should perform well at immunizing a networked population, Fig. 3 shows three networks in which the wax-yellow circle represents the focal node, whereas the other circles are its 1-step neighbors. The degree centrality strategy (DCS) fails to distinguish nodes 1 and i in Fig. 3a and b because it neglects how neighbors are connected among themselves. The betweenness centrality strategy (BCS) solves this problem, but by considering only the shortest paths, the strategy fails to distinguish nodes i and a in Fig. 3b and c. Using AS, however, we obtain $\mathit{AS}\left(1\right)=5.4$, $\mathit{AS}\left(i\right)=8.0$, and $\mathit{AS}\left(a\right)=9.2$, respectively, which highlights the capacity of the proposed strategy to classify nodes for immunization where the other comparable strategies leave us in the dark.

Fig. 3.

The advantage of AS over the other comparable strategies. Schematic network representations in which the node marked with wax-yellow color is the focal node, whereas the other nodes are its first-level neighbors. DCS fails to distinguish between the focal nodes in panels a and b. BCS fails to do the same for the focal nodes in panels b and c. AS, by contrast, does not suffer from the same problems as illustrated by displayed AS-scores.

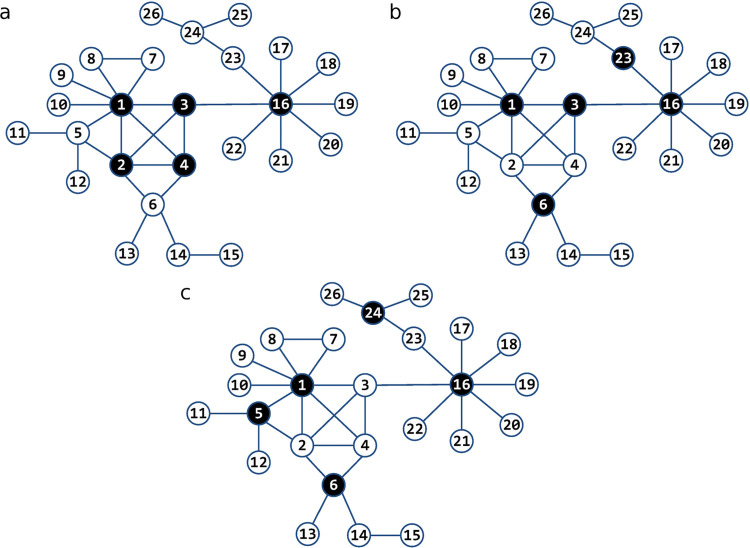
To further emphasize how different AS is from the other well-known strategies, we compare the results obtained using a simple, yet non-trivial network taken from Kitsak et al. (2010). Fig. 4 shows the first five nodes marked for immunization by each of the strategies. DCS and CCS, in fact, end up marking the same five nodes for immunization shown in Fig. 4a, albeit in a different order. Note, however, that DCS is ambiguous as to what the order should be because nodes 3–6 have the same degree. Without an additional criteria, there is no reason to prefer one node over the other (we actually followed the numbering of nodes). Although all strategies singled out nodes 1 and 16, this is where the similarities end. BCS and AS (Fig. 4b and c) go beyond the node degree to mark nodes 23 and 24, both with only two links, for immunization. Nonetheless, the best performer is AS because after the first five nodes are immunized, the biggest cluster that can get infected is of size three (containing nodes 2, 3, and 4), whereas the other strategies leave clusters of size four (DCS and CCS) and even size five (BCS) exposed.

Fig. 4.

The performance of the considered immunization strategies in a simple, yet non-trivial network taken from Kitsak et al. (2010). Nodes marked for immunization by DCS and CCS (panel a), BCS (panel b), and AS (panel c). The best performer is AS in panel c because the biggest cluster left exposed after immunization is of size three (nodes 2, 3, and 4), whereas DCS and CCS in panel a leave the cluster of size four exposed (e.g. nodes 23 to 26) and BCS in panel b leaves the cluster of size 5 (nodes 2, 4, 5, 11, and 12) exposed to a disease.

3.2. Performance testing in stylized, computer-generated networks

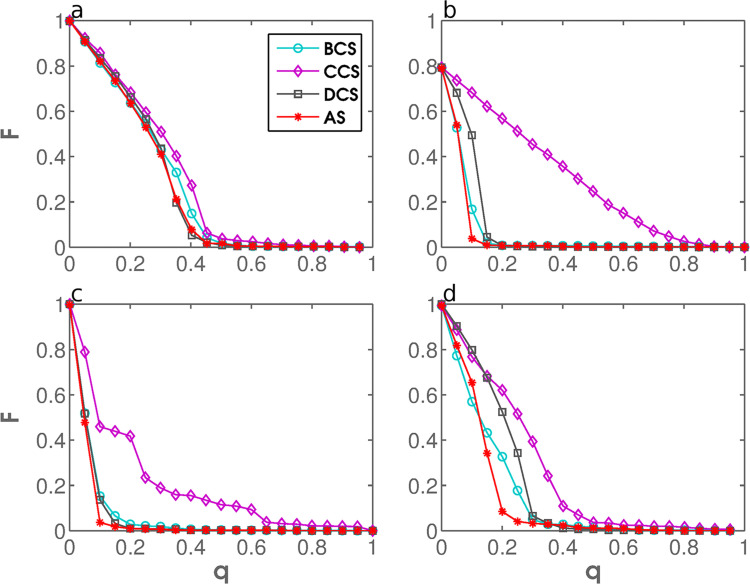
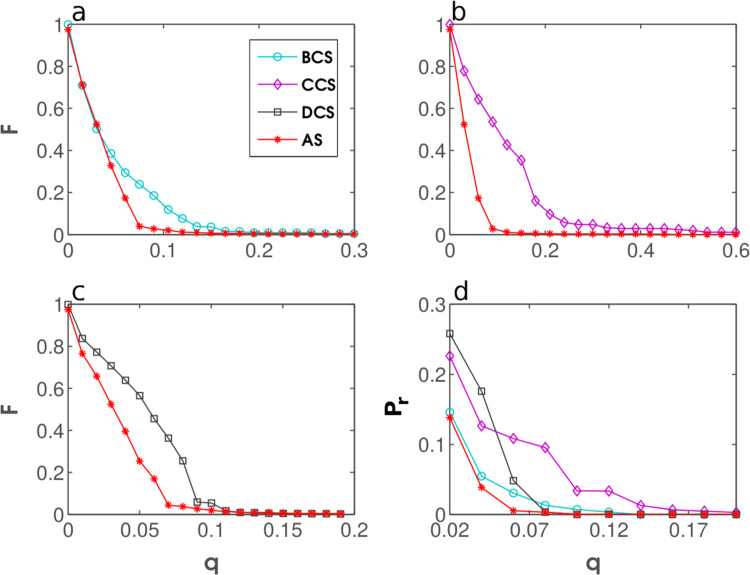
To test the performance of AS, we plot the fraction of a network that can be infected, F, against the fraction of immunized nodes, q. The tests are first performed in four stylized, computer-generated networks, the two of which are of Erdős-Rényi (ER) random type, whereas the remaining two are of Albert-Barabási scale-free (SF) type (Erdos et al., 1959, Albert and Barabási, 2002). The results are shown in Fig. 5 . Although AS performs very well, its performance is matched by DCS, which may seem surprising at first. However, random networks are not supposed to have structurally important nodes in the sense of Hébert-Dufresne et al. (2013), i.e. nodes that connect dense clusters, but do not necessarily have a high degree themselves. In scale-free networks, by contrast, structurally important nodes are most likely the ones with a high degree. These results suggest that random and scale-free networks may be overly stylized for thorough performance testing of the considered immunization strategies.

Fig. 5.

Performance testing in stylized, computer-generated networks. The fraction of the network that can be infected, F, is shown as a function of the fraction of immunized nodes, q, for DCS, BCS, CCS, and AS using ER network with $〈k〉=4.13$ (panel a), ER network with $〈k〉=4.03$ (panel b), SF network with $\alpha =2.576$ and $〈k〉=6$ (panel c), and SF network with $\alpha =2.468$ and $〈k〉=6$ (panel d). The error bars are derived from multiple realizations of the same simulation. The effectiveness of AS approximately matches that of DCS and outperforms that of BCS and CCS in random and scale-free networks likewise.

3.3. Performance testing in real-world, empirical networks

For the purpose of additional performance testing, we rely on four empirical networks as follows:

• • Email, a complex email network of an organization with over 1000 employees (Newman et al., 2002);
• • GR-QC, a collaborative scientific network between more than 5000 authors who submitted their articles to General Relativity and Quantum Cosmology category of arXiv e-print archive (Leskovec et al., 2007).
• • Power grid, a representation of connections between almost 5000 power stations in the western US (Watts and Strogatz, 1998);
• • Yeast, a protein-protein interaction network of yeast containing over 2000 proteins (Von Mering et al., 2002).

Aside from the fact that all these networks are well-documented and readily obtainable, the first two were selected for their relevance to the spread of computer viruses and the possibility of sharing some properties with the networks of human physical contacts. Power grid network is interesting in the context of the protection from cascading failures, whereby ‘immunized’ nodes should have redundant capacity to handle the extra load when another network element fails. ‘Immunizing’ Yeast network is admittedly an academic exercise, yet a useful one because the properties of empirical networks are not readily observed and analyzed in their stylized, computer-generated substitutes (Albert and Barabási, 2002). The descriptive statistics of the four selected networks are summarized in Table 1 .

Table 1.

Descriptive statistics of the four empirical networks used in performance testing.

Network	n	m	kmax	H	$〈C〉$
Email	1133	5451	71	1.9421	0.2202
GR-QC	5242	14490	81	3.0512	0.5296
Power	4941	6594	19	1.4504	0.0801
Yeast	2375	11693	118	3.4756	0.3057

Quantities: network size (n), number of edges (m), maximum degree (k_max), degree heterogeneity ($H={〈k^2〉/〈k〉}^2$), and clustering coefficient ($〈C〉$).

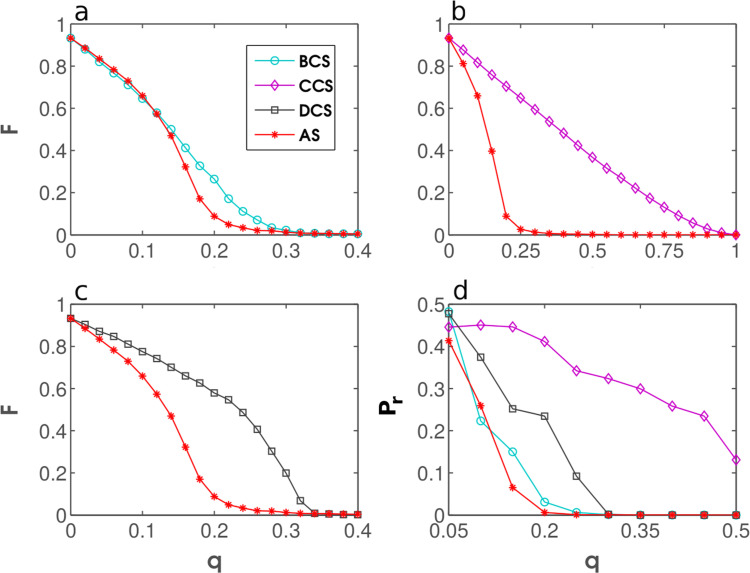
The results of performance testing in real-world, empirical networks are shown in Fig. 6 . AS is seen outperforming all three well-known strategies to which it was compared. Moreover, in Figs. 6b–d the performance of AS diverges from that of DCS, thus confirming our previous comment that random and scale-free networks are overly stylized to reveal the key properties of the considered immunization strategies necessary for a thorough evaluation. Another important point is that AS was designed to combine the qualities of DCS and BCS, meaning that AS should perform well when DCS is better than BCS (which is precisely the case in Fig. 5, for example), but also when it is the other way around (as exemplified in Fig. 6b and d). The ability of AS to perform as expected gives us some confidence that our design was successful and that AS should outperform the other strategies in an even more dramatic fashion if simulations incorporated the realistic elements of an epidemic.

Fig. 6.

Performance testing in real-world, empirical networks. Fraction of the network that can be infected, F, is shown as a function of the fraction of immunized nodes, q, for DCS, BCS, CCS, and AS using the Email network (panel a), the GR-QC network (panel b), the Power network (panel c), and the Yeast network (panel d).

3.4. Performance testing in conjunction with the susceptible-infectious-recovered model

To incorporate the realistic elements of an epidemic into performance testing, we resort to a susceptible-infectious-recovered (SIR) epidemiological model (Albert et al., 2000, Newman, 2002, Castellano and Pastor-Satorras, 2010, Xia et al., 2012) defined as follows:

• •Each node of the network can be in one of the three possible states: susceptible, infected, or recovered;
• •Initially, nodes to be immunized are determined and removed from the network, including the incident links;
• •A node from which the rest of the network can be infected is randomly selected, whereas all the other nodes start in the susceptible state;
• •At each time step, infected nodes transmit the disease to their susceptible neighbors with probability λ;
• •Infected nodes recover with probability η, whereupon they get removed from the network.

The last two steps of the process outlined above are repeated until no infected nodes remain.

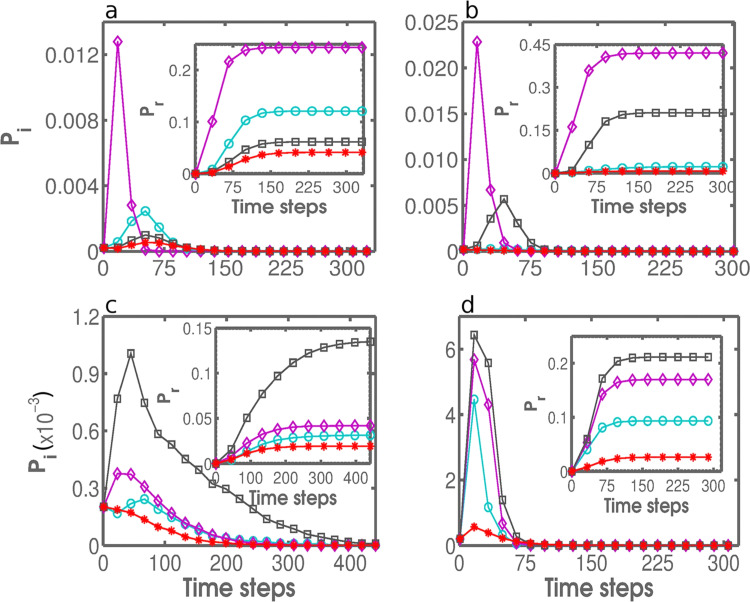
The results of performance testing in conjunction with the SIR model, where $\lambda =0.2$ and $\eta =0.05$, are shown in Fig. 7 . The performance is measured in terms of the infected fraction, P_i, and the recovered fraction, P _r, of nodes as the functions of time. The former measure is instantaneous in nature, whereas the latter quantifies the cumulative effect of an epidemic. In a scale-free network, consistent with the results in Fig. 5, DCS is an effective immunization strategy, yet AS performs considerably better (Fig. 7a). In GR-QC network, based on Fig. 6b, one might expect that BCS rather than DCS performs well. Although this is precisely the case, AS achieves an even higher effectiveness (Fig. 7b). In the power network, judging from Fig. 6c, DCS is surprisingly weak, but such a lackluster performance may have been caused by a low fraction of immunized nodes (5%) in the presented example (Fig. 7c). More importantly, AS once again emerges as a clear victor. The same is even more pronounced in the Yeast network (Fig. 7d). In summary, the maximum infected fraction and the final recovered fraction are considerably (2–20 times) lower if AS is used instead of DCS, BCS, or CCS with the same fraction of immunized nodes.

Fig. 7.

Performance testing in conjunction with SIR modeling. The infected fraction, P_i, and the recovered fraction, P_r, of nodes as the functions of time in SIR simulations. Shown are the comparisons between DCS, BCS, CCS, and AS (color coding as in Fig. 5 and Fig. 6) after having immunized fraction q=0.15 of nodes in an SF network with $〈k〉=6$ (panel a), q=0.08 of nodes in the GR-QC network (panel b), q=0.05 of nodes in the Power network (panel c), and q=0.15 of nodes in the Yeast network (panel d).

4. Conclusions and outlook

Achievements. We designed and tested a new, efficient network immunization strategy by drawing inspiration from an ameba-like organism, Physarum polycephalum. By looking at the dependence between any two nodes, we modified the original Physarum model with a noise factor for similar path finding. We then extended the model to include multi-foraging in order to obtain the dependence of other nodes on the focal one. This dependence is expressed in the form of a flow matrix, which indicates the ability of the focal node to spread the disease. Perhaps the most important properties of such a design are the ability to (i) distinguish situations that other comparable methods cannot and (ii) recognize structurally critical nodes that may not have a high degree themselves, yet they connect dense clusters of nodes.

Applicability. In the proposed strategy, immunized nodes are those with a higher ability to spread the disease as indicated by the AS-score. However, calculating such a score in reality may be difficult. The information on human physical contacts is hard to come by and even if the necessary information is available, a strong time-dependence is likely to cause erroneous assessments. The proposed method partly overcomes these difficulties by being local in the sense of Hébert-Dufresne et al. (2013). The information on a few R-local subnetworks can be used to start an immunization program, which can later be expanded in scope as the new information comes in. The results are encouraging in this context because, even if AS is applied locally, the attributes of the whole network are successfully revealed.

In view of the difficulties in applying the proposed (and any other) immunization strategy, it is important to admit that more success may be achieved in technological networks for which the relevant, structural information is more readily available. Another context in which the proposed strategy may be more applicable is the spread of a disease in a network of villages or towns, whereby an efficient immunization strategy may identify hotspots for implementing preventive measures with the most impact.

Outlook. Because the effectiveness of immunization programs may be hampered by a lack of information, perhaps the most immediate concern is to design the strategies that (i) perform well under information restrictions and (ii) can combine information from multiple sources. As for the restricted information, AS already functions locally, but achieves efficiency globally. To address the problem of combining several information sources, we may need to resort to the framework of multilayer networks (Wang et al., 2015), such that each network layer represents one type of information. Upon obtaining the AS-score in each layer separately, the results could be combined in a certain fashion to produce one overall score for the decision-making. In fact, optimizing the way in which the results are combined could be an interesting task for the field of intelligent computation (Du et al., 2016). Finally, the incentives for the different behavioral responses to an epidemic could be systematically incorporated into our framework by means of evolutionary game theory (Perc and Szolnoki, 2010, Wang et al., 2015).

Appendix A. Additional analyses

There are fundamental obstacles to analytically comparing the performance of various immunization strategies. Namely, a network's (mean–field) statistics translate into the statistics of nodes selected for immunization by each of the methods, which in turn determines the value of a common performance indicator (e.g. the largest fraction of nodes that can get infected after immunization, F). This sequence of dependencies is most easily seen by considering the workings of the degree centrality strategy, and is reflected in the fact that the simulated performance of each strategy varies greatly with the network structure. A more important consequence is that any analytical proof that one method is better than the others would have to start by assuming a mean–field statistic, and therefore would remain specific to such a statistic, largely diminishing the usefulness of this approach. Furthermore, mean–field statistics are generally known only for synthetic networks arising from the well-known (e.g. Erdős–Rényi and scale–free) algorithms, yet these networks fail to fully reveal how advantageous the proposed strategy (AS) is (Fig. 5). AS truly shines when applied to highly heterogeneous, real-world networks (Fig. 6, Fig. 7; also see below).

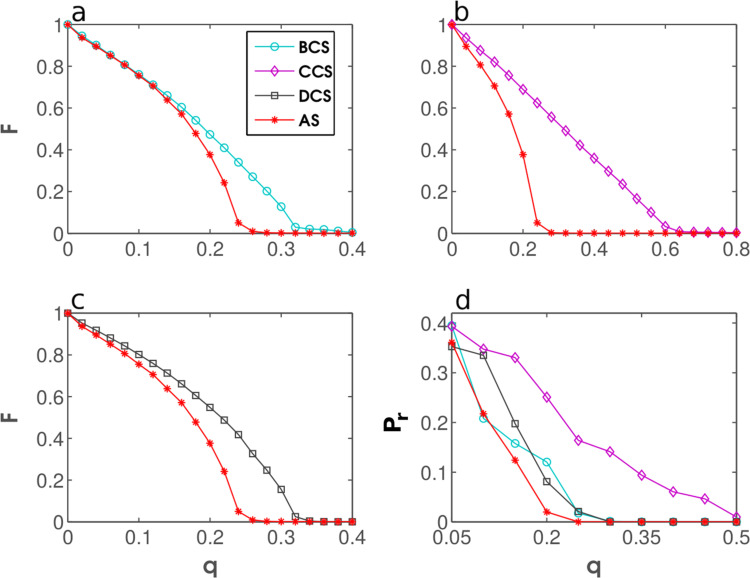
To strengthen the case for AS, we performed a number of analyses beside those found in the main text. First we compare how AS fares against a fairly recent immunization strategy called k-core (hereafter KCS) (Kitsak et al., 2010, Wei et al., 2015). A conceptual advantage of AS in comparison with KCS is that the latter strategy needs global knowledge to decompose a network and then identify the most influential nodes. AS, by contrast, relies only on local identification, meaning that the influence of each node is assessed from the information on the node's immediate neighborhood. Despite the information “handicap” of being local, AS manages to outperform KCS in all four real-world networks considered in the main text (Fig. A1 ). In addition, we provide the simulation results for the leader rank strategy (LRS) (Lü et al., 2011) which also appeared in the literature fairly recently. LRS in some instances (Fig. A2a and c) achieves almost the same efficiency as AS, yet we have not identified any examples in which the former strategy would outperform the latter.

Fig. A1.

Comparison of AS with two recent immunization strategies. Fraction of the network that can be infected, F, is shown as a function of the fraction of immunized nodes, q, for KCS (k-core strategy), LRS (leader rank strategy), and AS using the Email network (panel a), the GR-QC network (panel b), the Power network (panel c), and the Yeast network (panel d).

Fig. A2.

Performance testing in additional empirical networks: the case of the PGP network. Fraction of the network that can be infected, F (panels a–c), and the recovered fraction, P_r, of nodes in SIR simulations (panel d) are shown as the functions of the fraction of immunized nodes, q, for DCS, BCS, CCS, and AS.

To further solidify the leading position of AS, we acquired the information on three additional real-world networks and tested the performance of AS against the rival strategies. Networks used in these tests are:

• • PGP, a network of mutual trust with more than 10,500 involved parties for signing of digital documents using the Pretty Good Privacy algorithm (Boguñá et al., 2004, Duch and Arenas, 2005, Lü and Huang, 2009);
• • Ca-HepPH, a collaborative scientific network between 12,000 authors who submitted their articles to High Energy Physics category of arXiv e-print archive (Leskovec et al., 2007).
• • Twitter, a maximum component of the Twitter social network consisting of more than 65,000 users (Watts and Strogatz, 1998).

The descriptive statistics of the three additional networks are summarized in Table A1 .

Table A1.

Descriptive statistics of the three additional empirical networks used in performance testing.

Network	n	m	kmax	H	$〈C〉$
PGP	10,680	24,316	205	4.1465	0.2659
CA-HepPH	12,008	118,505	491	6.5830	0.6115
Twitter	65,911	185,737	233	2.5829	0.1823

Quantities: network size (n), number of edges (m), maximum degree (k_max), degree heterogeneity ($H={〈k^2〉/〈k〉}^2$), and clustering coefficient ($〈C〉$).

The results of numerical simulations using the networks listed in Table A1 are shown in Fig. A2, Fig. A3, Fig. A4 . After immunization, we examine the largest fraction of the network that can get infected (F) and the recovered fraction of nodes in an SIR epidemic (P _r). In all instances, the results are displayed as the functions of the fraction of immunized nodes (q). AS turns out to be a clear winner of these tests, outperforming its well-known competitors with a considerable margin. Overall, numerical tests strongly support the conclusion that AS offers new and improved power to identify nodes critical for the spread of infectious agents in network epidemiology.

Fig. A3.

Performance testing in additional empirical networks: the case of the CA-HepPH network. Fraction of the network that can be infected, F (panels a–c), and the recovered fraction, P_r, of nodes in SIR simulations (panel d) are shown as the functions of the fraction of immunized nodes, q, for DCS, BCS, CCS, and AS.

Fig. A4.

Performance testing in additional empirical networks: the case of the Twitter network. Fraction of the network that can be infected, F (panels a–c), and the recovered fraction, P_r, of nodes in SIR simulations (panel d) are shown as the functions of the fraction of immunized nodes, q, for DCS, BCS, CCS, and AS.