Increased infection severity in downstream cities in infectious disease transmission and tourists surveillance analysis

Highlights

• •Infection in downstream cities is more severe than in the source city in an outbreak.
• •Number of cities does not affect severity difference between end and source cities.
• •City-entry surveillance is more important than city-exit surveillance in a hub city.
• •Immunity strengthening on frequent travelers is inefficient in outbreak control.
• •Reducing person-to-person contacts can effectively limit infection spread.

Abstract

Infectious disease severely threatens human life. Human mobility and travel patterns influence the spread of infection between cities and countries. We find that the infection severity in downstream cities during outbreaks is related to transmission rate, recovery rate, travel rate, travel duration and the average number of person-to-person contacts per day. The peak value of the infected population in downstream cities is slightly higher than that in source cities. However, as the number of cities increases, the severity increase percentage during outbreaks between end and source cities is constant. The surveillance of important nodes connecting cities, such as airports and train stations, can help delay the occurrence time of infection outbreaks. The city-entry surveillance of hub cities is not only useful to these cities, but also to cities that are strongly connected (i.e., have a high travel rate) to them. The city-exit surveillance of hub cities contributes to other downstream cities, but only slightly to itself. Surveillance conducted in hub cities is highly efficient in controlling infection transmission. Only strengthening the individual immunity of frequent travellers is not efficient for infection control. However, reducing the number of person-to-person contacts per day effectively limits the spread of infection.

1. Introduction

Infectious disease severely threatens human life. In recent years, deaths caused by infectious diseases have remained at an annual rate of 13–15 million (WHO, 2013). The epidemic severe acute respiratory syndrome (SARS) spread to 30 countries, resulting in over 8000 cases and nearly 800 deaths in 2003 (WHO, 2003). By the end of 2009, the pandemic H1N1 virus had spread to more than 208 countries, resulting in hundreds of thousands of cases and at least 18,000 deaths (World Health Organization (WHO). Pandemic (H1N1) 2009, Massaro and Bagnoli, 2014). By June 2016, more than 28,000 Ebola cases had been reported in Guinea, Liberia and Sierra Leone, with more than 11,000 deaths (WHO, 2015). Globally, 2103 laboratory-confirmed cases of infection with the Middle East respiratory syndrome coronavirus (MERS-CoV), including at least 733 related deaths, had been reported to the WHO by 1 November 2017 (WHO, 2017). All of these infectious diseases initially occurred in a few countries and rapidly spread to others. Knowledge on the association between human mobility and infectious disease transmission is very important for infection control (Barmak et al., 2016).

Many computer simulations have been conducted on infection spread within indoor environments, such as planes (Namilae et al., 2017) and cruise ships (Zhang et al., 2016a); within buildings, such as offices (Zhang et al., 2018b, Zhang and Li, 2018), hospitals (Lau et al., 2004) and schools (Zhang et al., 2011); and within cities (Zhang et al., 2016b, Zhang et al., 2018a). Research on infection spread across cities and countries has mainly focused on human mobility based on historical data processing (Opatowski et al., 2011) and mathematical models (Charu et al., 2017). Hyman and LaForce (2003) constructed a mathematical SIPR (where P is the stage of partial immunity) infection spread model across cities and analysed long-term infection spread trends. Kim et al. (2014) developed a mathematical model of multi-city transmission and simulated the outbreaks of pandemic influenza A in Korea across cities considering transportation impacts. Gautreau et al. (2008) used the Rvachev–Longini metapopulation model to analyse the arrival times of infectious disease on a global scale. Balcan et al. (2009) used a mobility (GLEaM) model to obtain multi-scale mobility networks to simulate infection spread across countries. Travellers, including business travellers, play an important role in infection spread across cities and countries (Wang et al., 2012). In the global network of human mobility (Du et al., 2016), travellers connect all cities and countries. Therefore, knowledge on how travel behaviour affects infectious disease transmission is useful to the prevention and control of infection spread between cities or even between countries. However, the previous research was insufficient because of a lack of the quantitative comparison between the source and downstream cities, the impacts of travel patterns, and efficiency of different surveillance strategies in the transportation hubs.

In order to reveal these important questions, we develop a multi-city travel and susceptible, infected and recover (MCT-SIR) model to simulate infection spread between cities. The impacts of travel-related factors are studied. We quantitatively analyse the infection severity of the source and downstream cities under different travel patterns. We also assess the different surveillance strategies on public transportation hubs based on quantitative simulation. Moreover, some traditional prevention strategies are compared with various surveillance plans. The results offer some suggestions for infectious disease control from the travel perspective.

2. Methods

2.1. Multi-city travel SIR model

We study the difference in the severity level (peak value of the infected percentage) of source and downstream cities. To quantify the difference, we first define the severity increase percentage ($\Delta P_{c_s}^{c_d}$) to describe the difference between the source city c_s and the downstream city c_d during outbreaks (Eq. (1)).

$$\Delta P_{c_s}^{c_d}=\frac{\left(I_{c_d,max}-I_{c_s,max}\right)}{I_{c_s,max}}$$ (1)

where $I_{c_s,max}$ and $I_{c_d,max}$ are the peak values of the infected population during outbreaks in the source city c_s and the downstream city c_d, respectively. A large $\Delta P_{c_s}^{c_d}$ suggests that the severity of infectious disease in the downstream city c_d is higher than that in the source city c_s.

We also classify cities into different levels. The source city (c_s) is the city that discovers the first case. The first downstream city is the city that has direct population exchange with the source city. The second downstream city is the city that has direct population exchange with the first downstream city, but no exchange with the source city, and so on.

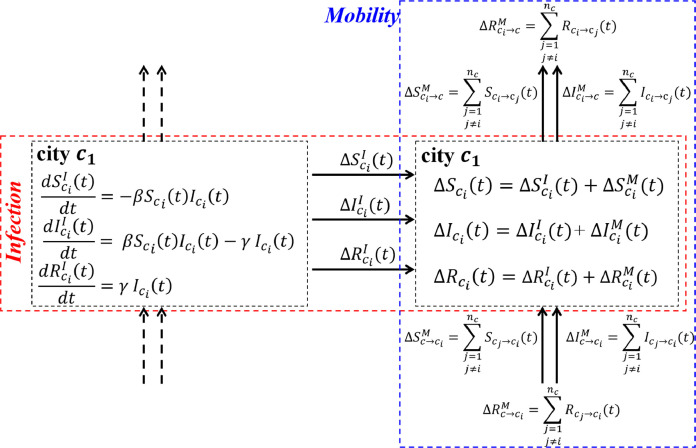
In this study, the MCT-SIR model mainly focuses on travel (human mobility) between cities. Therefore, we assume a fully mixed condition in each functional area, such as the offices, accommodations and restaurants in each city. The distribution of different functional areas is not considered. We analyse how influencing factors, such as travel rate (δ), average travel duration (t_T), the number of person-to-person contacts per day (n_p), transmission rate (β) and recovery rate (γ) affect the $\Delta P_{c_s}^{c_d}$ and outbreak occurrence times of infectious diseases. As shown in Fig. 1 , the model has two main parts: infection and mobility. Infection (red dashed frame) means that infectious disease is transmitted in a city and mobility (blue dashed frame) means that infection spreads between cities due to human mobility. It is shown in Eq. (2).

$$\{\begin{array}{c}\Delta S_{c_s}\left(t\right)=\Delta S_{c_s}^I\left(t\right)+\Delta S_{c_s}^M\left(t\right)\hfill \\ \Delta I_{c_s}\left(t\right)=\Delta I_{c_s}^I\left(t\right)+\Delta I_{c_s}^M\left(t\right)\hfill \\ \Delta R_{c_s}\left(t\right)=\Delta R_{c_s}^I\left(t\right)+\Delta R_{c_s}^M\left(t\right)\hfill \end{array}$$ (2)

where $\Delta S_{c_s}\left(t\right)$, $\Delta I_{c_s}\left(t\right)$ and $\Delta R_{c_s}\left(t\right)$ are, respectively, the variations of the total number of susceptible, infected and recovered people present in city c_s at time t; $\Delta S_{c_s}^I\left(t\right)$, $\Delta I_{c_s}^I\left(t\right)$ and $\Delta R_{c_s}^I\left(t\right)$ are, respectively, the variations of S, I and R caused by Infection at time t; and $\Delta S_{c_s}^M\left(t\right)$, $\Delta I_{c_s}^M\left(t\right)$ and $\Delta R_{c_s}^M\left(t\right)$ are, respectively, the variations of S, I and R caused by mobility at time t. In this model, different status of people caused by Infection ($\Delta S_{c_s}^I\left(t\right)$, $\Delta I_{c_s}^I\left(t\right)$, and $\Delta R_{c_s}^I\left(t\right)$) and mobility ($\Delta S_{c_s}^M\left(t\right)$, $\Delta I_{c_s}^M\left(t\right)$, and $\Delta R_{c_s}^M\left(t\right)$) are independent.

Fig. 1.

Multi-city travel SIR model.

*$S_{c_i}\left(t\right)$, $I_{c_i}\left(t\right)$ and $R_{c_i}\left(t\right)$ represent, respectively, the number of susceptible (S), infected (I) and recovered (R) people in city i at time t; β is the transmission rate; γ is the recovery rate; $\Delta S_{c_i}^I\left(t\right)$, $\Delta I_{c_i}^I\left(t\right)$ and $\Delta R_{c_i}^I\left(t\right)$ represent, respectively, the variations in S, I and R caused by infection in city i at time t; $\Delta S_{c_i}^M\left(t\right)$, $\Delta I_{c_i}^M\left(t\right)$ and $\Delta R_{c_i}^M\left(t\right)$ represent, respectively, the variations in S, I and R caused by human mobility at time t; n_c is the total number of cities; ${\sum }_{\stackrel{j=1}{j\ne i}}^{n_c}{S}_{c_j\to c_i}\left(t\right)$, ${\sum }_{\stackrel{j=1}{j\ne i}}^{n_c}{\mathrm{I}}_{c_j\to c_i}\left(t\right)$ and ${\sum }_{\stackrel{j=1}{j\ne i}}^{n_c}{R}_{c_j\to c_i}\left(t\right)$ represent, respectively, the S, I and R inflows from other cities to city i at time t; and ${\sum }_{\stackrel{j=1}{j\ne i}}^{n_c}{S}_{c_i\to c_j}\left(t\right)$, ${\sum }_{\stackrel{j=1}{j\ne i}}^{n_c}{I}_{c_i\to c_j}\left(t\right)$ and ${\sum }_{\stackrel{j=1}{j\ne i}}^{n_c}{R}_{c_i\to c_j}\left(t\right)$ represent, respectively, the S, I and R outflows from city i to other cities at time t.

In Fig. 1, the left black dashed frame shows the number of susceptible, infected and recovered people at time $t-1$. According to the SIR model (Kermack and McKendrick, 1927), the number of susceptible, infected and recovered people in city c_s can be calculated using Eq. (3). A specific calculation involving the different confined spaces is introduced in Supporting Information.

$$\begin{array}{c}\hfill \{\begin{array}{c}{\displaystyle \frac{\mathbf{d}{S}_{c_s}^I\left(t\right)}{\mathbf{d}t}=-\beta ·S_{c_s}\left(t\right)·I_{c_s}\left(t\right)}\hfill \\ {\displaystyle \frac{\mathbf{d}{I}_{c_s}^I\left(t\right)}{\mathbf{d}t}=\beta ·S_{c_s}\left(t\right)·I_{c_s}\left(t\right)-\gamma ·I_{c_s}\left(t\right)}\hfill \\ {\displaystyle \frac{\mathbf{d}{R}_{c_s}^I\left(t\right)}{\mathbf{d}t}=\gamma ·I_{c_s}\left(t\right)}\hfill \end{array}\end{array}$$ (3)

where the unit of β is ‘per person per unit time’ and the unit of γ is ‘per unit time’.

The blue dashed frame in Fig. 1 shows the variation in S, I and R caused by mobility. For a city, there are inflow and outflow populations during each time step (Eq. (4)).

$$\{\begin{array}{c}\Delta S_{c_s}^M\left(t\right)=S_{c_s,in}^M\left(t-\Delta t\right)-S_{c_s,out}^M\left(t-\Delta t\right)\hfill \\ \Delta I_{c_s}^M\left(t\right)=I_{c_s,in}^M\left(t-\Delta t\right)-I_{c_s,out}^M\left(t-\Delta t\right)\hfill \\ \Delta R_{c_s}^M\left(t\right)=R_{c_s,in}^M\left(t-\Delta t\right)-R_{c_s,out}^M\left(t-\Delta t\right)\hfill \end{array}$$ (4)

where $S_{c_s,in}^M\left(t\right)$, $I_{c_s,in}^M\left(t\right)$ and $R_{c_s,in}^M\left(t\right)$ represent, respectively, the S, I and R inflows from other cities to city c_s at time t; and $S_{c_s,out}^M\left(t\right)$, $I_{c_s,out}^M\left(t\right)$ and $R_{c_s,out}^M\left(t\right)$ represent, respectively, the S, I and R outflows from city c_s to other cities at time t. We assume that all people have the same travel rate and equal probability of travelling to each city. Therefore, the inflow and outflow population of city c_s can be calculated using Eqs. (4.1) and (4.2).

$$\{\begin{array}{c}{S}_{c_s,in}^M\left(t\right)=P_{back,\Delta t}·\sum _{i=1}^{N_C}{S}_{c_{di}\left(c_s\right)}^M\left(t\right)+P_{go,\Delta t}·\frac{1}{n_c-1}·\sum _{i=1}^{n_c}{S}_{c_{di}\left(c_{di}\right)}^M\left(t\right)\hfill \\ I_{c_s,in}^M\left(t\right)=P_{back,\Delta t}·\sum _{i=1}^{N_C}{I}_{c_{di}\left(c_s\right)}^M\left(t\right)+P_{go,\Delta t}·\frac{1}{n_c-1}·\sum _{i=1}^{n_c}{I}_{c_{di}\left(c_{di}\right)}^M\left(t\right)\hfill \\ R_{c_s,in}^M\left(t\right)=P_{back,\Delta t}·\sum _{i=1}^{N_C}{R}_{c_{di}\left(c_s\right)}^M\left(t\right)+P_{go,\Delta t}·\frac{1}{n_c-1}·\sum _{i=1}^{n_c}{R}_{c_{di}\left(c_{di}\right)}^M\left(t\right)\hfill \end{array}$$ (4.1)

$$\{\begin{array}{c}{S}_{c_s,out}^M\left(t\right)=P_{go,\Delta t}·S_{c_s\left(c_s\right)}^M\left(t\right)+P_{back,\Delta t}·\sum _{i=1}^{n_c}{S}_{c_s\left(c_{di}\right)}^M\left(t\right)\hfill \\ I_{c_s,out}^M\left(t\right)=P_{go,\Delta t}·I_{c_s\left(c_s\right)}^M\left(t\right)+P_{back,\Delta t}·\sum _{i=1}^{n_c}{I}_{c_s\left(c_{di}\right)}^M\left(t\right)\hfill \\ R_{c_s,out}^M\left(t\right)=P_{go,\Delta t}·R_{c_s\left(c_s\right)}^M\left(t\right)+P_{back,\Delta t}·\sum _{i=1}^{n_c}{R}_{c_s\left(c_{di}\right)}^M\left(t\right)\hfill \end{array}$$ (4.2)

where $S_{c_d\left(c_s\right)}^M\left(t\right)$, $I_{c_d\left(c_s\right)}^M\left(t\right)$ and $R_{c_d\left(c_s\right)}^M\left(t\right)$ are, respectively, the number of S, I and R individuals who are city c_s’s residents travelling in city c_d; $S_{c_s\left(c_d\right)}^M\left(t\right)$, $I_{c_s\left(c_d\right)}^M\left(t\right)$ and $R_{c_s\left(c_d\right)}^M\left(t\right)$ are, respectively, the number of S, I and R individuals who are city c_d’s residents travelling in city c_s; $S_{c_d\left(c_d\right)}^M\left(t\right)$, $I_{c_d\left(c_d\right)}^M\left(t\right)$ and $R_{c_d\left(c_d\right)}^M\left(t\right)$ are the number of city c_d’s residents who are not travelling; P _{go, Δt} is the probability of a resident deciding to travel to other cities after time Δt; and P _{back, Δt} is the probability of a tourist deciding to return to their home city after travel time Δt. We assume that the per-hour probability of a resident deciding to travel is P_go (h ⁻¹) and that the per-hour probability of a tourist ending travel is P_back (h ⁻¹). P _{go, Δt} and P _{back, Δt} can be calculated using Eq. (5).

$$\{\begin{array}{c}{P}_{go,\Delta t}=\sum _{t=1}^{\Delta t}{\left(1-P_{go}\right)}^{t-1}{P}_{go}\hfill \\ P_{\text{back},\Delta t}=\sum _{t=1}^{\Delta t}{\left(1-P_{back}\right)}^{t-1}{P}_{back}\hfill \end{array}$$ (5)

2.2. Parameter settings

H1N1 is used as an example to analyse infectious disease transmission between cities. According to previous studies on H1N1, default parameters used in our study are listed in Table 1 . According to previous studies on H1N1, the basic reproductive number (R ₀) of H1N1 is approximately 1.8 (Balcan et al., 2009, Lessler et al., 2009, Merler et al., 2011), which means on average 1.8 new cases (i.e., infections) arise from a single primary case (Fraser et al., 2009). In a city, a person on average contacts 400 people per day (Hyman and LaForce, 2003). To keep $R_0=1.8$, the transfer rate from the susceptible to the infected (β), is set to 1.56 × 10⁻³. As the infectious period is from 1.1 to 4.69 days (Balcan et al., 2009, Merler et al., 2011), we set the mean value of 2.89 days (69 h). The recovery rate, γ (the transition rate from susceptible to recovered), is calculated ($\gamma =0.014{\mathrm{h}}^{-1}$).

Table 1.

Default parameters in the study.

Symbol	Value	Definition
R0	1.8 (Balcan et al., 2009, Lessler et al., 2009, Merler et al., 2011)	Basic reproductive number: the average new cases (i.e., infections) arise from a single primary case (Fraser et al., 2009)
β	1.56 × 10−3 person−1 · h−1	Transfer rate: average infection probability of a susceptible individual contact with an infected individual
γ	0.014 h−1	Recovery rate: the transition rate from susceptible to recovered
δ	2.34% (CNTA (China National Tourism Administration) 2017, National Bureau of Statistics of China (NBSC) 2018)	Travel rate: the ratio of tourists in a city to citizens of the city
N	400 people/day (Hyman and LaForce, 2003)	Interpersonal contact number per day: the number of people that a person contacts on average per day
Nr	N/50	Number of confined spaces in a city
Pgo, Δt	–	The probability of a resident deciding to travel to other cities after time Δt
Pback, Δt	1.57 × 10−2 h−1	The probability of a tourist deciding to return to their home city after travel time Δt

We set the time step to 3 h. There are eight steps per day. A person contacts on average 50 people per time step. We assume that all cities have the same population (N) and number of confined spaces (N_r). People randomly distribute into different rooms per step. Therefore, a person contacts N/N_r people per step. When N ≫ N_r, it is considered that there is no repeated contact between any pair of people during a day.

Travel rate (δ) is the percentage of tourists in a city to citizens of the city. It is expressed by Eq. (6).

$${\delta }_{c_s}=\frac{{\sum }_{i=1}^{n_c}{N}_{c_{di}\left(c_s\right)}}{N_{c_s}}=\frac{{\sum }_{i=1}^{n_c}{N}_{c_{di}\left(c_s\right)}}{N_{c_s\left(c_s\right)}+{\sum }_{i=1}^{n_c}{N}_{c_{di}\left(c_s\right)}}$$ (6)

where $N_{c_s}$ is the total number of city c_s’s citizens; n_c is the total number of cities; $N_{c_d\left(c_s\right)}$ is the number of city c_s’s tourists in city c_d; and $N_{c_s\left(c_s\right)}$ represents the number of non-travelling residents of city c_s.

Each city has a population of N. The tourist population in each city is δ · N. To balance the population in a city (e.g., c_s), Eq. (7) should be satisfied.

$$\sum _{i=1}^{n_c}{N}_{c_s\left(c_s\right)\to c_{di}}=\left(1-{\delta }_{c_s}\right)N·P_{go,\Delta t}=\sum _{i=1}^{n_c}{N}_{c_{di}\left(c_s\right)\to c_s}={\delta }_{c_s}N·P_{back,\Delta t}$$ (7)

where $N_{c_s\left(c_s\right)\to c_d}$ is the total number of new tourists from city c_s to city c_d during each step; $N_{c_d\left(c_s\right)\to c_s}$ is the total number of tourists travelling in city c_d who are returning to city c_s; and ${\delta }_{c_s}$ is the travel rate of city c_s. P _go,Δt is expressed by Eq. (8).

$$P_{go,\Delta t}=\frac{{\delta }_{c_s}}{1-{\delta }_{c_s}}{P}_{back,\Delta t}$$ (8)

Using China as an example, the Chinese Tourism Statistics Bulletin showed that there were 4.44 billion trips taken in 2016 with an average travel duration of 2.66 days (CNTA, 2016). Considering that the population at the time was 1.38 billion (NBSC, 2018), the average travel rate of China can be calculated as $\delta =\frac{4.44\left(\text{billion}\text{people}/\text{year}\right)\times 2.66\left(\text{day}\right)}{365\left(\text{day}/\text{year}\right)\times 1.38\left(\text{billion}\text{people}\right)}=2.34\%$.

When the average travel duration is 2.66 days (64.84 h), $P_{back}=1.57\times {10}^{-2}{\mathrm{h}}^{-1}$ is obtained by Eq. (9).

$$\sum _{t=1}^{\infty }t\times P_{back}\times {\left(1-P_{back}\right)}^{t-1}=64.84$$ (9)

where t is the travel duration for a tourist.

The per-hour probability of a resident deciding to travel (P_go) can be calculated when travel rate (δ) is known.

3. Results

3.1. Factor analysis of the severity increase percentage between the source and downstream cities

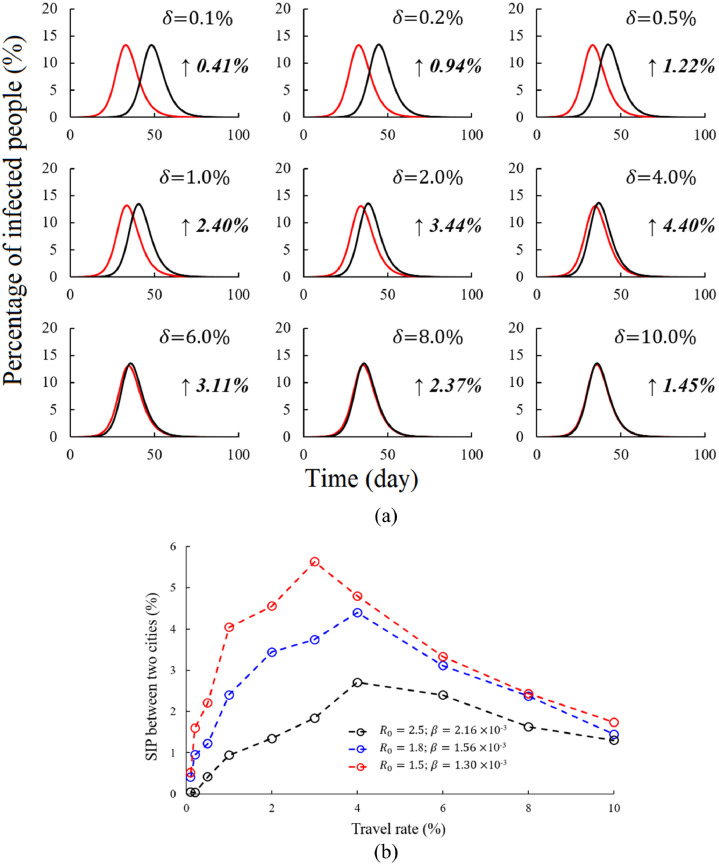
Influencing factors, such as travel rate (δ), average travel duration (t_T), basic reproductive number (R ₀); transfer rate (β), recovery rate (γ) and the average number of person-to-person contacts per day (n_p) and total population per city (N), affect the severity increase percentage (∆P) between a source city (c_s) and its downstream cities (c_d), which is expressed by $\Delta P_{c_s}^{c_d}$. Using H1N1 as an example, infectious disease transmission between only two cities (i.e., $N_c=2$) is simulated based on the MCT-SIR model (Fig. 2 ).

Fig. 2.

Infectious disease transmission at different travel rates. (a) $R_0=1.8$. The red line depicts the source city and the black line depicts the downstream city; the x-axis shows the time (day); the y-axis shows the percentage of infected people; and the number on the right side of the figure is the value of $\Delta P_{c_s}^{c_d}$. (b) Different values of R₀ (1.5, 1.8 and 2.5)*.

* With different values of R₀, n_p and γ remain constant and only β changes.

Generally, the shape of the infection spread curves in the source city and the downstream city are almost the same when δ → 0 and $\delta =50\%$. As shown in Fig. 2(a), when $\delta =4\%$, $\Delta P_{c_s}^{c_d}$ reaches the largest value of 4.40%. As δ increases, the ∆P between the source city and the downstream city first increases and then decreases after the peak. Furthermore, the peak arrives earlier when R ₀ is small. When $R_0=1.5$, $\Delta P_{c_s}^{c_d}$ reaches the largest value of 5.63% when $\delta =4\%$. However, when $R_0=2.5$, $\Delta P_{c_s}^{c_d}$ reaches the largest value of 2.70% when $\delta =3\%$. Therefore, the lower R ₀ is, the higher the peak value of the ∆P between the source city and the downstream city is (Fig. 2(b)).

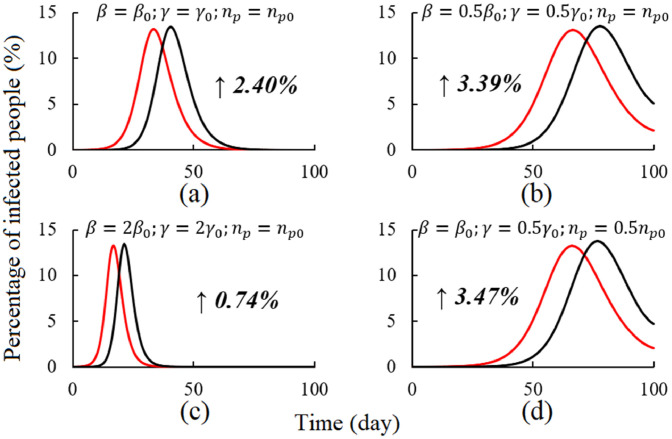
Fig. 3 shows how transfer rate (β), recovery rate (γ) and the average number of person-to-person contacts per day (n_p) influence the ∆P between the source city and the downstream city. Fig. 3(a) shows infectious disease transmission between two cities according to basic settings. Comparing Fig. 3(b) and (c) to (a), $\Delta P_{c_s}^{c_d}$ increases when β and γ decrease. Comparing Fig. 3(b) and (d), when the population of a city is large enough, $\Delta P_{c_s}^{c_d}$ remains almost unchanged if the product of β and n_p is a constant. We also find that $\Delta P_{c_s}^{c_d}$ is not influenced by the total population of the city.

Fig. 3.

Infectious disease transmission at different transmission rate (β), recovery rates (γ) and average number of person-to-person contacts per day (n_p) under $R_0=1.8$. (a) $\beta ={\beta }_0$, $\gamma ={\gamma }_0$and $n_p=n_{p0}$. (b) $\beta =0.5{\beta }_0$, $\gamma =0.5{\gamma }_0$and $n_p=n_{p0}$. (c) $\beta =2{\beta }_0$, $\gamma =2{\gamma }_0$and $n_p=n_{p0}$. (d) $\beta ={\beta }_0$, $\gamma =0.5{\gamma }_0$and $n_p=0.5n_{p0}$. The red line depicts the source city and the black line depicts the downstream city; the x-axis shows the time (day); the y-axis shows the percentage of infected people; and the number on the right side of the figure is the value of $\Delta P_{c_s}^{c_d}$.

*β₀, γ₀ and n_p0 are the defaults (${\beta }_0=1.56\times {10}^{-3}$, ${\gamma }_0=4.17\times {10}^{-2}$ and $n_{p0}=400$, respectively). Detailed information is provided in Section 2.2.

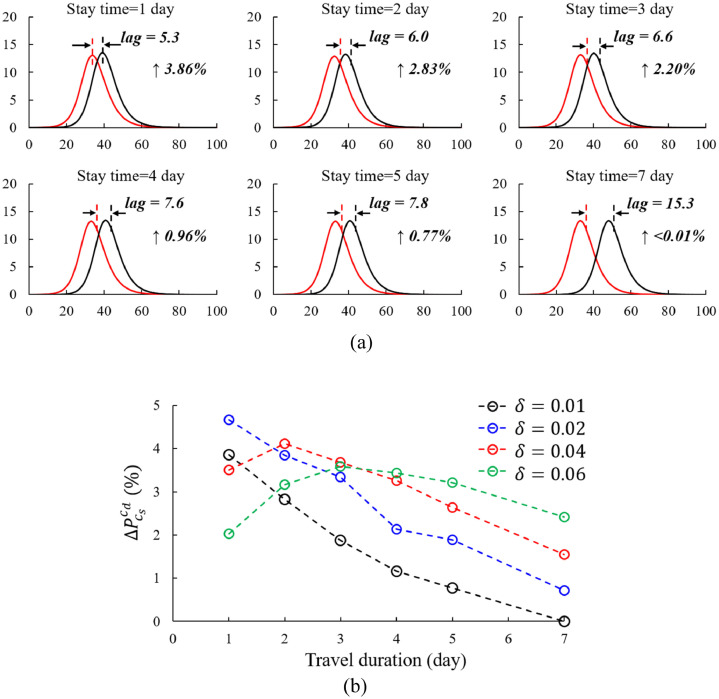
The ∆P between the source and the downstream city changes with travel duration (Fig. 4 (a)). Under a constant travel rate ($\delta =1\%$) and R ₀ (1.8), when the average travel duration changes from 1 to 7 days, the time delay for outbreak between the downstream city and the source city increases from 5.3 to 15.3 days. In addition, $\Delta P_{c_s}^{c_d}$ decreases from 3.86% to <0.01% with travel duration expansion. When travel duration increases, the population exchange rate between two cities decreases because the travel rate is constant. The impact of the source city on the downstream city is weakened.

Fig. 4.

Infectious disease transmission with different travel durations (t_T) under (a) $\delta =1\%$ and (b) $\delta =1-6\%$.

Fig. 4(a) shows that $\Delta P_{c_s}^{c_d}$ monotonically decreases as travel duration increases (1–7 days) when $\delta =1\%$. A negative correlation between $\Delta P_{c_s}^{c_d}$ and travel duration (1 to 7 days) still exists when $\delta =2\%$ (Fig. 4(b)). In reality, δ ≥ 4% is possible when certain festivals arrive. As shown by the red and green dashed lines in Fig. 4(b), $\Delta P_{c_s}^{c_d}$ does not monotonically decrease as travel duration increases. The peak value occurs at $t_T=2$ when $\delta =4\%$ and at $t_T=3$ when $\delta =6\%$, respectively. A too high or too low population exchange rate between two cities leads to a low $\Delta P_{c_s}^{c_d}$. Therefore, a high travel rate with a low travel duration or a low travel rate with a high travel duration decreases $\Delta P_{c_s}^{c_d}$. Based on our default settings ($R_0=1.8$, $\beta =1.56\times {10}^{-3}$, $\gamma =0.014{\mathrm{h}}^{-1}$ and $n_p=400$), $\Delta P_{c_s}^{c_d}$ peaks when $t_T/\delta =50$.

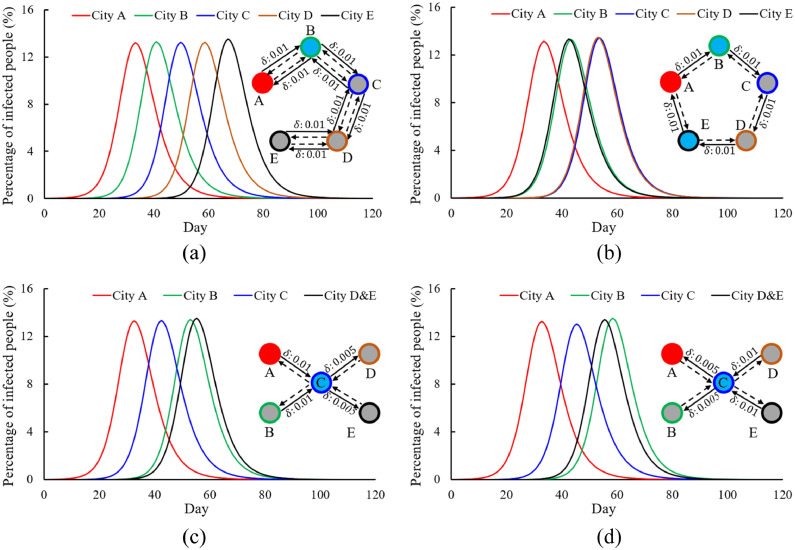
3.2. Infectious disease transmission in five cities

Fig. 5 shows how the travel patterns between five cities influence infectious disease transmission (the ∆P between five cities, the severity of infection outbreak and the outbreak occurrence time). In Fig. 5(a), infectious disease transmits from source city A to end city E city by city (i.e., A→B→C→D→E). To maintain a constant population in each city at all times, $\delta =1\%$ is set in cities A and E and $\delta =2\%$ is set in cities B, C and D. The peak value of infected individuals during outbreaks is the same in cities B, C and D, with an average $\Delta P_A^{BCD}=0.50\%$ (Fig. 5(a)). The ∆P between the middle cities is close to 0. City E is the end city and $\Delta P_A^E=2.33\%$. Comparing $\Delta P_A^E$ to the $\Delta P_{c_s}^{c_d}$ with only two cities (Fig. 2(a)), the ∆P between the source city and the end city is almost the same ($\Delta P_A^E\approx \Delta P_{c_s}^{c_d}$). In Fig. 5(a), city B receives infected tourists from source city A during the infection rising period and delivers infected people to city C at the same time. City A, B, and C like three bottles of solution. City B receives a highly concentrated solution from city A, but is also diluted by city C. However, $\Delta P_D^E$ is high because the end city (E) only absorbs the highly concentrated solution from city D without any dilution caused by the other cities. Therefore, $\Delta P_D^E$ and $\Delta P_A^B$ are big, whereas $\Delta P_B^C$ and $\Delta P_C^D$ are very small.

Fig. 5.

Impacts of the travel patterns between five cities on infectious disease transmission. The red round border represents source city A. The green, blue, brown and black round borders represent cities B, C, D and E, respectively. The black solid lines represent the flow of tourists from their home cities to other cities and the black dashed lines represent the flow of tourists returning from other cities to their home cities. The red solid circles represent the source city, the sky blue solid circles represent the first downstream cities that are directly linked to the source city and the grey circles represent the second or higher-level downstream cities that are indirectly linked to the source city. (a) Unidirectional travel (A→B→C→D→E). (b) Circular travel (A→B→C→D→E→A). (c) A/B→C→D/E*. (d) D/E→C→A/B.

* When cities D and E have the same infectious disease transmission characteristics, the black curves are used to show the average value of infected people in cities D and E.

In Fig. 5(b), the travel pattern from city A to E is circular (A→B→C→D→E→A) and the tourist flow in each city is unidirectional with $\delta =1\%$. The peak value of the infected population during the outbreaks in the second downstream cities (C and D) is higher than the first downstream cities (B and E) and the source city, A ($\Delta P_A^{BE}=1.36\%$, $\Delta P_A^{CD}=2.41\%$). This is consistent with the law that the ∆P between the source city (C_s) and the end city (C_e) is constant ($\Delta P_{c_s}^{c_e}\approx 2.4\%$). In the circular travel pattern, both cities B and E are the first downstream cities. The only difference between city B and city E is the direction of travel (A→B vs. E→A). The infected tourists from city A can spread infection to city B. Tourists from city E are probably infected when they travel to city A and then take the virus back to city E, thereby spreading infection. The infection spread curves under both conditions are almost the same. When the time step is small, we can consider the percentage of the infected individuals in city A’s tourist population who travel to city B and in city E’s tourist population who return to their home cities from city A to be the same. The population exchange rate between cities A and B during each time step equals that between cities E and A (${\delta }_{AB}={\delta }_{EA}$). Therefore, the infectious disease transmission curves of cities B and E are similar. This pattern can also be seen by comparing the results of cities C and D.

In Fig. 5(c), the residents of cities A and B can travel to city C. In city C, they can travel to cities D and E (A/B→C→D/E). City C is the first downstream city and cities B, D and E are the second downstream cities. As the travel rate from city B to city C is higher than that from city C to city D/E (${\delta }_{BC}=2{\delta }_{CD}=2{\delta }_{CE}$), the infectious disease outbreak occurs earlier in city B. Fig. 5(d) shows the reversed travel pattern of Fig. 5(c) (D/E→C→A/B). The severity of infection outbreak in city C is slightly lower than that in other cities. The travel rate from city A to C is low, but cities B, D and E have strong dilution impacts during the rising period of infection of city C. Comparing city B to cities D and E, the peak value of the infected population is the same. However, the outbreak occurrence time (when the infected population reaches the peak) in city B occurs later than that in cities D and E.

3.3. Efficiency analysis of travel-related intervention strategies

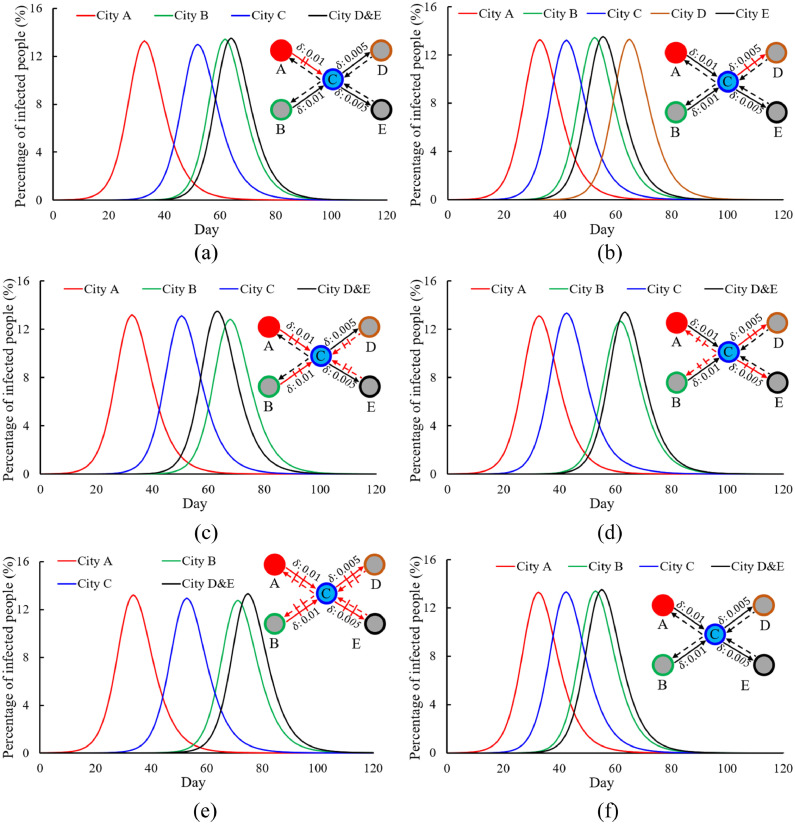
3.3.1. Human mobility surveillance between cities

Human mobility surveillance between cities influences infectious disease transmission (Fig. 6 ). We assume that surveillance strategies can help monitor infected tourists with an efficiency of 90%. Therefore, 90% of infected tourists would be monitored when moving from one city to another and sent to hospital for isolation. Comparing Fig. 6(a) and (f), when people who leave city A are monitored, the outbreak occurrence time in the first downstream city, C, is delayed from day 42.5 to 52 and the peak value of the infected population increases by 2.56%. The outbreak occurrence time in cities B, D and E is also delayed. Monitoring tourists who leave city A does not influence the relative relationship between cities B, D and E. Comparing Fig. 6(c) and (a), the relative positions of the curves of cities B, D and E remain almost constant.

Fig. 6.

Infectious disease transmission between five cities under a specific travel pattern (A/B→C→D/E)^*1 with different surveillance strategies (surveillance rate^⁎2 = 90%). The black solid lines represent the flow of tourists from their home cities to other cities and the black dashed lines represent the flow of tourists returning from other cities to their home cities. The red solid/dashed lines show the monitored route. (a) Source city A exit surveillance. (b) Second downstream city D entry surveillance. (c) Hub city C entry surveillance. (d) Hub city C exit surveillance. (e) Both hub city C entry and exit surveillance. (f) No surveillance.

^*1${\delta }_{AC}={\delta }_{BC}=1\%$; ${\delta }_{CD}={\delta }_{CE}=0.5\%$.

^⁎2 A 90% surveillance rate means that 90% of infected tourists are monitored when they move between cities. These people are isolated in hospitals and then leave from the hospital upon recovery.

When people who enter city D are monitored (Fig. 6(b)), comparing it with city A-exit surveillance (Fig. 6(a)), occurrence time for outbreaks of cities B to E is advanced. Cities A, B, C and E are not strongly influenced by this strategy, and infectious disease transmission curves are similar with them under no-control condition (Fig. 6(f)). However, the occurrence time for outbreaks of city D is delayed about 9.5 days compared with city E, and the peak value of the infected during outbreaks is decreased by 1.50%.

City C is the only first downstream city in this travel pattern, and it directly links with the source city A and the second downstream cities B, D, and E. City C can be seen as a hub, and every tourist has correlation with city C. Hub usually plays an important role in a network. As shown in Fig. 6(c), when tourists who enter city C are monitored, the outbreak occurrence time in city C is the same as that under the condition of city A exit surveillance. However, the second downstream cities, B, D and E, are strongly influenced. If there is no surveillance, the outbreak in city B occurs earlier than in cities D and E. After monitoring tourists who enter city C, the outbreak occurrence time of city B is delayed and the outbreak severity decreases by 4.72%. When infected tourists return from city C to city B, 90% of them are sent to hospital for isolation. Only 10% of infected tourists can take the virus back, strongly weakening the efficiency of infection spread. City C acts as a filter and reduces the impacts caused by infected city B’s tourists who return from city C. Infected residents in city D are never monitored because none of city D’s tourists go to city C, but a few infected tourists do go to city D from city C. In general, as a hub city, city-entry surveillance is not only useful to city C, but also to cities with a high rate of population exchange with city C.

Fig. 6(d) shows the infection spread under hub city C exit surveillance. Infected tourists leaving source city A cannot be monitored. Compared to city C entry surveillance, the outbreak occurrence time in cities B, C, D and E is advanced in city C exit surveillance. For city B, city C acts as a filter regardless of which of the two strategies is chosen. Therefore, the impact on city B is the same. Focusing on cities D and E, city C exit surveillance helps reduce negative effects and delays outbreak occurrence time. In general, city C exit surveillance contributes to three second downstream cities (B, D and E), but only slightly to its own city.

When both city C entry and exit surveillance are conducted, all eight routes between cities A, B, D and E and city C are monitored (Fig. 6(e)). However, it takes more manpower and material resources. In this situation, the outbreak occurrence time is delayed in all cities. Compared to no strategy (Fig. 6(f)), the outbreak occurrence time in city C is delayed by 10.4 days, in city B by 18.3 days and in cities D and E by 19.4 days.

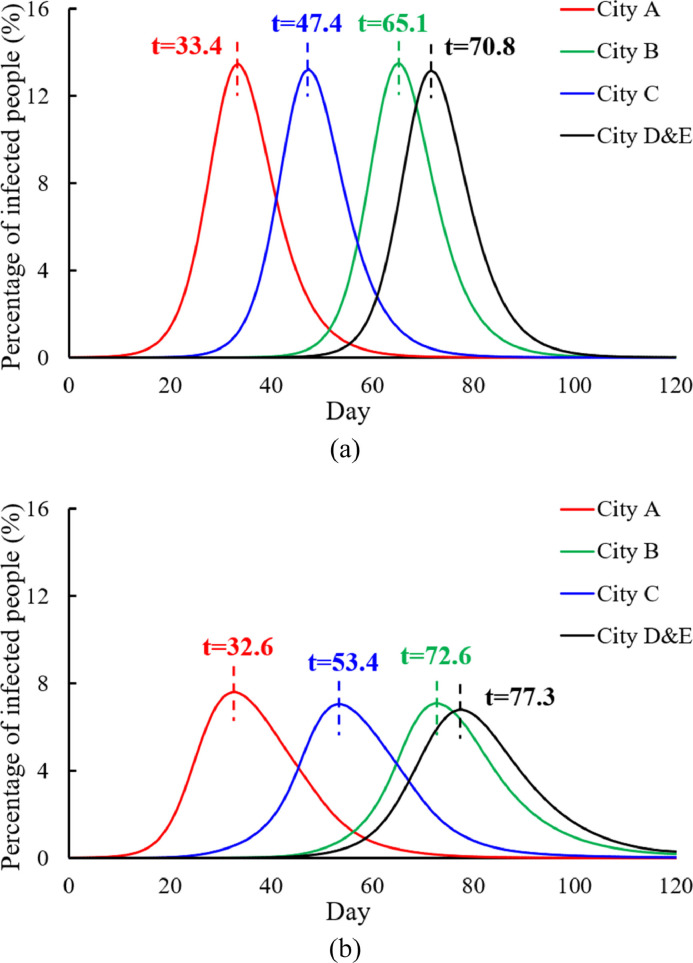
3.3.2. Restriction on travel and person-to-person contact

During infectious disease epidemics, the local government usually requests residents to reduce travel to prevent cross infection with people from other cities. In reality, when the severity of infectious disease increases, travel rate is likely to decrease. Comparing Figs. 7 (a) and 6(f), when travel rate decreases as infection severity increases, the efficiency of infectious disease control is limited because human mobility in cities is not controlled. However, the outbreak occurrence time is delayed in downstream cities. For example, the outbreak occurrence time in city C is delayed by 5 days, in city B by 12 days and in cities D and E by 15.4 days. This strategy cannot reduce the severity of outbreaks, but it can delay the outbreak occurrence time. This gives the government more time to make emergency plans. The local government usually requests individuals to avoid densely populated areas, such as shopping malls, to reduce the number of person-to-person contacts per day during infection outbreaks (Fig. 7(b)). When infectious disease is very serious, some strategies, such as work stoppage, school closure and shopping mall closure, are implemented. In this situation, the probability of person-to-person contact is decreased. Even the probability of tourists spreading infection or becoming infected decreases. The severity of infectious disease outbreak is strongly reduced and the peak value of the infected population in all cities is controlled below 7.7%.

Fig. 7.

Dynamic intervention strategies under the travel pattern A/B→C→D/E. (a) Travel rate control^*1. (b) Person-to-person contact control^⁎2.

^*1 The travel rate changes with the severity of infectious disease and agrees with $\delta \left(t\right)=0.01-0.1\times \frac{I_{c,max}\left(t\right)}{N_c\left(t\right)}$, where I_{c, max} is the maximum number of infected people in one city out of all cities at time t, N_c is the current population in the city that has the maximum number of infected people at time t and δ(t) is the travel rate at time t. The travel rate monotonically linearly decreases from 1% to 0% when the percentage of the infected population in the most severely affected city increases from 0% to 10%. When $\frac{I_{c,max}\left(t\right)}{N_c\left(t\right)}>0.1$, no people travel ($\delta \left(t\right)=0$).

^⁎2 The average number of person-to-person contacts per day (n_p) changes with the severity of infectious disease and agrees with $n_p\left(t\right)=n_p^{\prime }\times \frac{\left[0.29-\frac{I_{c,max}\left(t\right)}{N_c\left(t\right)}\right]}{0.28}$, $0.01\le \frac{I_{c,max}\left(t\right)}{N_c\left(t\right)}\le 0.15$, where $n_p^{\prime }$ is the default number of person-to-person contacts per day (400 in this study). When more than 1% of people are infected in a city, the contact behaviour between people is limited. n_P is halved when more than 15% of people are infected in the most severely affected city. n_P monotonically linearly decreases from $n_p^{\prime }$ to $n_p^{\prime }/2$ when $\frac{I_{c,max}\left(t\right)}{N_c\left(t\right)}$ increases from 0.01 to 0.15.

4. Discussion

We define the ∆P between downstream and source cities ($\Delta P_{c_s}^{c_d}$) as the ratio of the peak value of infected populations. We mainly study how travel-related factors and intervention strategies affect infection spread (∆P, outbreak severity and outbreak occurrence time) between cities.

Infection spreads quickly between cities. The phase 5 pandemic H1N1 virus (WHO, 2009b) spread to more than 208 countries, resulting in hundreds of thousands of cases and at least 18,000 deaths (World Health Organization (WHO). Pandemic (H1N1) 2009, Centers for Disease Control and Prevention (CDC) 2009). On 21 April 2009, the CDC reported that the first two cases of illness in Southern California had been caused by infection with genetically similar H1N1 viruses; Texas also reported two cases then (CDC, 2009). By the end of July 2009, Wisconsin, Hawaii and Connecticut had the highest percentages of H1N1 patients (CDC, 2010). This conforms to our results that some downstream cities are more serious than the source city in an infection outbreak. In addition to inter-city travel, population density, environment, human behaviour and other factors also influence infection spread.

Infectious diseases have different basic reproductive ratios (R ₀). For example, that for H1N1 is approximately 1.8 (De Silva et al., 2009), that for H7N9 is between 0.6 and 2.5 (Yang et al., 2015) and that for norovirus is between 5.3 and 9.3 (Lee et al., 2011). R ₀ influences not only infection spread in a city, but also the infection severity between the downstream city and the source city. The lower R ₀ is, the higher the peak value of the ∆P between the source city and the downstream city becomes. $\Delta P_{c_s}^{c_d}$ was mainly caused by mobility other than infection (Fig. 1). And increasing R ₀ leads to enhancement of the impact brought by infection, therefore, the $\Delta P_{c_s}^{c_d}$ will decrease because of weaker impact by mobility. Moreover, the higher R ₀ is, the higher the travel rate must be to reach the highest $\Delta P_{c_s}^{c_d}$. With an increasing travel rate, the $\Delta P_{c_s}^{c_d}$ increases first then goes down. For example, if there is only one infected traveller going to the downstream city and only one resident in the downstream city is infected (travel rate → 0), the trend of the number of the infected would be the same for both the source and the downstream cities (all of them are caused by only one infected person), and there is no difference between the peak value of the infected ($\Delta P_{c_s}^{c_d}$==0). When the travel rate is 0.5, which means residents in the source and downstream cities are sufficiently mixed, two cities would have the same curves of number of infected people (($\Delta P_{c_s}^{c_d}$==0). Therefore, there is a specific value of travel rate can lead to the highest $\Delta P_{c_s}^{c_d}$. The average travel rate in China is 2.34% (CNTA, 2016). When H1N1 spreads ($R_0=1.8$), $\Delta P_{c_s}^{c_d}$ reaches a maximum when the travel rate is 4%. During normal periods, the travel rate is generally lower than 4%. However, the travel rate rapidly increases when certain festivals, such as the Spring Festival (the most important festival in China), arrive. At such times, governments should also focus on infectious disease prevention and control in downstream cities rather than only in source cities.

Transmission rate (β), recovery rate (γ) and the average number of person-to-person contacts per day (n_p) influence $\Delta P_{c_s}^{c_d}$. For infectious diseases with low transfer rate (β↓) but a high infectious period (γ↓), downstream cities are strongly influenced by the associated source city ($\Delta P_{c_s}^{c_d}\uparrow$). When the infectious period increases, there is a longer time to spread disease when tourists from the source city travel to downstream cities. The severity of infection in downstream cities is strengthened. In addition, under a travel rate of 1%, with increasing travel duration (from 1 to 7 days), the population exchange rate between two cities reduces and the impacts of the source city on downstream cities weaken. In reality, the average travel duration is decided by vacation arrangements. For example, only 1–2 days of travel can occur on weekends, but the average travel duration can be between 5 and 7 days when the Spring Festival or National Day arrives. We find that when the quotient of travel duration (t_T) and travel rate (δ) is a constant ($t_T/\delta =50$ in this study), $\Delta P_{c_s}^{c_d}$ reaches a maximum. Governments may consider different emergency plans based on the characteristics of travel patterns. $\Delta P_{c_s}^{c_d}$ reaches a maximum of 4.40% when the travel rate is 4.0% and the travel duration is 2.66 days. The increased severity of the downstream city is slight. In reality, this influence is ignored because it is easily covered by other impacts caused by environmental differences (e.g., temperature and humidity), cultural differences and individual characteristics between cities. Our results are obtained for the same settings in all cities.

By simulating infection spread in five cities with different travel patterns, we can conclude that when there are many cities, the ∆P between the source city and the end city ($\Delta P_{c_s}^{c_e}$) is almost the same as between just two cities ($\Delta P_{c_s}^{c_e}=\Delta P_{c_s}^{c_d}$). $\Delta P_{c_s}^{c_e}$ is not strongly related to the total number of cities. In general, travel-related factors influence infection spread between cities, but the impacts are limited. In the study, we found that the infection enhancement in downstream cities brought by travel is much weaker than those by some environmental factors such as temperature and humidity. Normally, travel can only bring no more than 4% infection enhancement in downstream cities and the impact is relatively low compared with environment factors. However, downstream cities should be paid more attention because infection intensity in downstream cities is no weaker than the source city.

Tourist surveillance is used to control infection spread in many situations (Memish et al., 2014, Petersen et al., 2015). Our simulation shows that the severity of infectious disease transmission is difficult to control if only tourist surveillance between cities is used. This strategy can help delay the outbreak occurrence time and provide governments more time to prepare efficient emergency plans. City-entry surveillance of non-hub cities is only useful to the target city that measures tourist surveillance. The positive impacts on other cities can be ignored. City-entry surveillance of hub cities is not only useful to the hub cities, but also to cities with strong connections (i.e., a high travel rate) to them. However, for cities with little or no tourist exchange with hub cities, the positive impacts of hub city entry surveillance are weak. The city-exit surveillance of hub cities contributes to downstream cities, but only slightly to above said hub cities. Both the city-entry and -exit surveillance of hub cities are the most effective for infection control, although requiring more manpower and consuming more resources. Tourist surveillance of hub cities is much more efficient than of other cities and can provide local governments more time to prepare emergency plans to reduce the threat of infectious disease.

Infection risk can also be reduced by some other strategies, such as wearing a mask and getting vaccinated (Sobolev et al., 2016). Strengthening the individual immunity of either frequent travellers or randomly selected individuals yields little difference. The efficiency of strategies that only improve the individual immunity of frequent travellers is limited. However, the outbreak occurrence time can be slightly delayed in downstream cities. Individuals can either wear a mask or get vaccinated to reduce infection risk. Governments can limit the travel rate between cities and the probability of person-to-person contact via work stoppage (Zhang et al., 2018a) and school closure (Gemmetto et al., 2014) to reduce infection risk. Comparing the two government strategies, controlling the amount of person-to-person contact per day is obviously effective in infectious disease control.

Our study on infection spread between cities provides some suggestions for governments to control infectious disease transmission based on travel-related factors and strategies. Various limitations exist. We mainly consider the travel patterns between cities and hypothesise the random movement of residents in a city. This may affect the precision of the results. In addition, all cities in this study have the same settings in terms of population scale and the average number of person-to-person contacts per day. Moreover, the MCT-SIR model is established based on the SIR model. Lastly, the increased severity phenomenon may require observation using more sophisticated models, such as multi-agent models.