Probabilistic differential diagnosis of Middle East respiratory syndrome (MERS) using the time from immigration to illness onset among imported cases

Abstract

Middle East respiratory syndrome (MERS) has spread worldwide since 2012. As the clinical symptoms of MERS tend to be non-specific, the incubation period has been shown to complement differential diagnosis, especially to rule out influenza. However, because an infection event is seldom directly observable, the present study aims to construct a diagnostic model that predicts the probability of MERS diagnosis given the time from immigration to illness onset among imported cases which are suspected of MERS. Addressing censoring by considering the transmission dynamics in an exporting country, we demonstrate that the illness onset within 2 days from immigration is suggestive of influenza. Two exceptions to suspect MERS even for those with illness onset within 2 days since immigration are (i) when we observe substantial community transmissions of MERS and (ii) when the cases are at high risk of MERS (e.g. cases with close contact in hospital or household). It is vital to collect the information of the incubation period upon emergence of a novel infectious disease, and moreover, in our model, the fundamental transmission dynamics including the initial growth rate has to be explored to differentiate the disease diagnoses with non-specific symptoms.

Highlights

• •Clinical symptoms of MERS tend to be non-specific.
• •The incubation period complements differential diagnosis, ruling out influenza.
• •The time from immigration to illness in imported cases also informs diagnosis.
• •Illness onset within 2 days from immigration is suggestive of influenza.

1. Introduction

Middle East respiratory syndrome (MERS), caused by the novel MERS coronavirus (MERS-CoV), has been reported since March 2012 (Cauchemez et al., 2014). MERS-CoV has not caused substantial human-to-human transmissions yet, but the extent of geographic distribution of this disease has gradually expanded from Middle East countries (e.g. Jordan and Saudi Arabia) to other countries, including Europe. Recent studies have suggested that mildly symptomatic cases are common (Cauchemez et al., 2014, Fisman and Tuite, 2014, Assiri et al., 2013a), while hospitalized cases tended to exhibit severe respiratory symptoms (Assiri et al., 2013b, , 2013).

In October 2012, a Saudi boy was suspected of MERS in Hong Kong and was admitted to a hospital which is equipped with an isolation ward (South China Morning Post, 2012). Two days in advance, his father had developed fever and coughing, and the boy followed similar symptoms to his father. One day after admission to the hospital in Hong Kong, the boy was tested positive to influenza A (H1N1) virus, while testing negative to MERS-CoV. The similar suspected cases caused by influenza have been also reported from other countries (Nishiura et al., 2012). Not only influenza but also many other respiratory viruses induce only non-specific clinical signs and symptoms. Thus, it is difficult to selectively detect and differentially diagnose only MERS among imported cases with upper respiratory symptoms (e.g. by screening febrile individuals at an international border (Nishiura and Kamiya, 2011)). Laboratory diagnosis such as PCR takes time and cost, and there would be a substantial number of suspected imported cases to be tested and isolated in hospital if we intend to test and intervene all suspected febrile individuals arriving from affected countries.

As complimentary information to partly resolve this problem, a probabilistic model has been proposed to help differential diagnosis based on a known incubation period (Nishiura et al., 2012). Employing a Bayesian approach, and assuming that the incubation period distribution and the prior probability (or the population risks) of all suspected respiratory viruses are known, the model has permitted us to calculate the probability of MERS given a certain length of the incubation period. Nevertheless, it has been recognized as a core issue of infectious disease epidemiology that an infection event of non-sexual directly transmitted diseases is seldom directly observable (Clancy and O’Neill, 2008). Thus, the exact length of the incubation period is seldom known for each individual case. Nevertheless, it is frequently the case that the time of illness onset is remembered among cases, and the time from immigration to illness onset among imported cases is readily available and can be useful for demonstrating the practical usefulness of the probabilistic model to assist clinical diagnosis.

The present study aims to construct a statistical model that predicts the probability of MERS diagnosis given a certain length of the time from immigration to illness onset among imported cases. Through this exercise, we also aim to assess practical and theoretical importance of the proposed model and identify associated data gaps in epidemiological observations.

2. Materials and methods

2.1. Epidemiological setting

Further to the present study, Nishiura and Inaba (2011) proposed an estimation framework of the incubation period based on the time from immigration to illness onset among imported cases of influenza A (H1N1-2009) in Japan. While that study aimed to estimate the incubation period distribution, the present study extends the model structure in the earlier study to predict the probability of MERS diagnosis. In particular, the present study focuses on the distinction between influenza and MERS. During the early stages of the epidemic, the epidemiological parameters of MERS had yet to be estimated based on the empirical data. Thus, we also examine the corresponding estimates of the severe acute respiratory syndrome (SARS) as a substitute for MERS during the early stages.

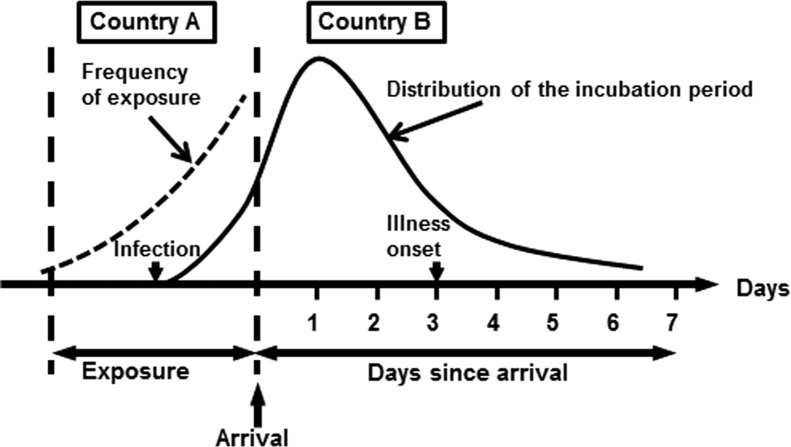
Let t be the time from immigration to illness onset in an imported case which developed a disease in country B at time t≥0 (where t=0 stands for the time of immigration; Fig. 1). Suppose that he or she traveled to country A (where MERS has spread) for k days. In the case of resident of country A, we may drop the data or assume that k→∞. We consider two different patterns of spread in country A: (i) an endemic state (i.e. the risk of infection is in a stationary state) and (ii) an epidemic state. In the case of the latter, we assume that the epidemic of novel coronavirus is in an early stage with an approximately exponential growth of infections. The frequency of exposure among imported cases during their travel is assumed as proportional to the incidence in country A. The exponential growth rate of incidence is known to be characterized by the basic reproduction number R ₀ and the mean generation time T _g (Wallinga and Lipsitch, 2007). If the generation time is exponentially distributed, the growth rate r is calculated as r=(R ₀−1)/T _g, while we have r=ln(R ₀)/T _g for a constant generation time (Wallinga and Lipsitch, 2007). Given identical values of R ₀ and T _g, the exponential distribution is known to yield the largest value of r among all the possible distributions of the generation time, while a constant T _g gives the smallest r (Roberts and Heesterbeek, 2007).

Fig. 1.

Predicting influenza among imported cases based on the time since immigration. The mechanism and timing of importation: spending k days for travel, an exposure occurs in country A with a risk proportional to the incidence. Entering country B, the exposed individual develops illness at t days since immigration. Since an infection event is not directly observable, the exact length of the incubation period has to be inferred by addressing censoring and using an explicitly infection-age structured model.

Here we briefly describe the time from immigration to illness onset among imported cases (Nishiura and Inaba, 2011). Let i(t,τ) be the number of incubating individuals at time t after immigration and at infection-age τ (i.e. the time since infection). Supposing that the rate of illness onset at infection-age τ is γ(τ), the dynamics of the density of incubating individuals are described by

$$\frac{\partial i(t,\tau )}{\partial t}+\frac{\partial i(t,\tau )}{\partial \tau }=-\gamma (\tau )i(t,\tau ),$$ (1)

with boundary conditions

$$i(t,0)=0\text{for}t>0,i(0,\tau )=j(\tau ).$$ (2)

here j(τ)=i(0,τ) represents the density of incubating population at an infection-age τ at the time of immigration t=0 (i.e. the initial age distribution). i(t,τ) can be integrated as

$$i(t,\tau )=j(\tau -t)\frac{L(\tau )}{L(\tau -t)},$$ (3)

for τ−t>0, where L(τ) represents the survival probability of incubating individuals at infection-age τ. The survival probability is calculated by using the rate of illness onset at infection-age τ, γ(τ) as follows:

$$L(\tau )=\exp \left(-{\int }_0^{\tau }\gamma (s)ds\right),$$ (4)

and, based on survival analysis, the probability density of the incubation period f(τ) is given as

$$f(\tau )=\gamma (\tau )L(\tau ).$$ (5)

Note that L(τ) is also written as 1−F(τ) where F(τ) is the cumulative distribution of the incubation period. Let c(t) be the number of new symptomatic cases (illness onsets) at time t after immigration. Supposing that the duration of travel is k days, then

$$c(t)={\int }_t^{k+t}\gamma (\tau )i(t,\tau )d\tau ={\int }_t^{k+t}\gamma (\tau )L(\tau )\frac{j(\tau -t)}{L(\tau -t)}d\tau ,$$ (6)

which can be rearranged as

$$c(t)={\int }_0^{k}f(t+s)\frac{j(s)}{L(s)}ds.$$ (7)

The frequency of illness onset is obtained by normalizing c(t) over t.

2.2. Statistical model

Hereafter, we focus on differential diagnosis of two specific diseases, influenza and MERS. Suppose that both diseases are growing in a similar manner (i.e., both in an endemic state or both in an exponential growth phase with different growth rates due to different R ₀ and T _g). As was discussed by Nishiura and Inaba (2011), the frequency of exposure in an epidemic case is written as

$$j(\tau |r)=\frac{\exp (-r\tau )L(\tau |\theta )}{{\int }_0^k\exp (-rs)L(s|\theta )ds}$$ (8)

for τ>k. In the endemic case, we have r=0, and thus, (8) is simplified as

$$j(\tau |r)=\frac{L(\tau |\theta )}{{\int }_0^{k}L(s|\theta )ds}.$$ (9)

Let i represent a label for disease i and θ _i be the population parameter of the incubation period of disease i. The probability density of observing the illness onset at t days from immigration, g _i(t), is written as

$$g_i(t|r_i,{\theta }_i)={\int }_0^k{f}_i(t+\tau |{\theta }_i)\frac{j_i(\tau |r_i,{\theta }_i)}{L_i(\tau |{\theta }_i)}d\tau .$$ (10)

The function g _i(t) is the normalized version of c(t) in Eq. (7). Let q _i be the prior probability of disease i in country A that may be derived from cause-specific prevalence such as those based on viral etiological study. As was discussed by Nishiura et al. (2012), a Bayesian approach is employed, and the present study uses the following formula for the differential diagnosis:

$$\mathrm{Pr}(\text{novel}\text{coronavirus}|t)=\frac{q_0{g}_0(t|r_0,{\theta }_0)}{\sum _i{q}_i{g}_i(t|r_i,{\theta }_i)},$$ (11)

where i=0 denotes MERS.

In practical instances, the exact time of illness onset may not be precisely known for all suspected cases due to coarsely recorded data, and we may only know that the illness onset occurred at time t from immigration where 0≤t≤t _m, where t _m is the possible maximum incubation period. In such an instance, we use a doubly interval censored likelihood (Reich et al., 2009), i.e.,

$$h_i(t,t_m|r_i,{\theta }_i):=\mathrm{Pr}(0\le t\le t_m|r_i,{\theta }_i)={\int }_0^{t_m}{\int }_0^k{f}_i(t+\tau |{\theta }_i)\frac{j_i(\tau |r_i,{\theta }_i)}{L_i(\tau |{\theta }_i)}d\tau dt,$$ (12)

which we use to compute the following crude model for prediction:

$$\mathrm{Pr}(\text{novel}\text{coronavirus}|0\le t\le t_m)=\frac{q_0{h}_0(t,t_m|r_0,{\theta }_0)}{\sum _i{q}_i{h}_i(t,t_m|r_i,{\theta }_i)}.$$ (13)

It should be noted that Eq. (13) investigates the cumulative probability of MERS from time 0 to t _m (and thus, the interpretation is different from (11)), but the consistent discrete version of (11) can be obtained by alternatively integrating time from (t _m−1) to t _m in (12).

2.3. Parameters and computational scenarios

For illustration of the proposed predictive model, we consider the differential diagnosis between two diseases, using influenza and MERS as the case study. In addition, we consider SARS and compare it against influenza, because SARS share many clinical, virological and epidemiological features in common with MERS and the empirical data of the incubation period and epidemiological parameters were available during the early stages of MERS outbreaks (Wallinga and Lipsitch, 2007, Donnelly et al., 2003). Let R ₀ and T _g of influenza be 1.5 and 3.0 days, respectively. According to recent studies, R ₀ and T _g of MERS are assumed as 0.6 and 10.7 days, respectively (Cauchemez et al., 2014, Breban et al., 2013). Similarly, R ₀ and T _g of SARS are assumed as 3.0 and 7.0 days, respectively (Donnelly et al., 2003). The incubation period was assumed to follow a lognormal distribution with the scale parameter (or the median incubation period), exp(μ)=1.6, 5.0 and 4.0 days and shape parameter σ ²=0.21, 0.19 and 0.37 for influenza, MERS and SARS, respectively (Cauchemez et al., 2014, Nishiura and Inaba, 2011, Reich et al., 2009, Donnelly et al., 2003). For illustration, we assumed that the length of travel was k=5 days (which is consistent with the empirical best estimate (Cauchemez et al., 2014)) and also that a prior probability for each disease was 0.50. To compare against influenza, a common disease, the equal prior yields a conservative result when the diagnosis involves a novel infectious disease without known q _i (Nishiura et al., 2012).

For the exposition of our proposed method, we first compare MERS against influenza, using both continuous and discrete models (i.e. Eqs. (11), (13)), and examine the possible time from immigration to illness onset as ranging from 0 to 10 days. As mentioned above, as an alternative to MERS during the early stages of pandemic, we also compare influenza against SARS. In both comparisons, we assume endemic and epidemic scenarios, and the latter is restricted to the early exponential growth phase. In the epidemic scenario, we use two different exponential growth rates, i.e., one assuming that the generation time is a constant, and the other assumes that the generation time follows an exponential distribution. As the sensitivity analysis, we compute the probability of influenza (in comparison with MERS) given the time from immigration to illness onset, by varying the length of travel (from 0 to 20 days), prior probability of influenza (from 0.1 to 0.9), and R ₀ of MERS (from 0.6 to 3.0) (Cauchemez et al., 2013).

3. Results

Fig. 2A shows the probability of influenza given the exact time from immigration to illness onset (computed by Eq. (11)). One minus the probability of influenza gives the posterior probability of MERS. Since the median incubation of influenza is 3.4 days shorter than that of the MERS, the probability of influenza is high if the cases develop the disease shortly after immigration. However, as time goes by since immigration, the probability of influenza lowers 50% at day 2, and the probability of MERS exceeds that of influenza thereafter. Exponential growth of cases during the travel yielded higher probability of influenza than the case of uniformly distributed risk, although the difference was hardly visible on day 3 since immigration and later. If the growth rate was much greater, the probability of infection shortly before immigration would be elevated, increasing the probability of influenza. A similar qualitative pattern was seen in the comparison between influenza and SARS (Fig. 2B). In this comparison, the posterior probability of influenza again appeared to be greater than 50% given that a case develops illness within 2 days since immigration.

Fig. 2.

Posterior probability of influenza in comparison with two different coronavirus infections. (A and B) The posterior probability of influenza given illness onset at t days since immigration (as compared to Middle East respiratory syndrome (MERS) and severe acute respiratory syndrome (SARS)), calculated by using Eq. (11). We assumed that the travelers stay in country A for 5 days with two different rates of exponential growth (where exponential 1 corresponds to exponentially distributed generation time, while exponential 2 corresponds a constant generation time) or the uniformly distributed risk over time. The prior probability of influenza was assumed as 0.50. R₀ of MERS was assumed to be 0.63. (C and D) The average probability of influenza given illness onset from 0 to t days since immigration (as compared to Middle East respiratory syndrome (MERS) and severe acute respiratory syndrome (SARS)), calculated by using Eq. (13). Only the results that assumed exponential growth with exponentially distributed generation time are shown, but other assumption yielded quantitatively similar estimates. Other parameters are identical to those adopted in panels A and B.

Fig. 2C and D shows the average probability of influenza, as compared with MERS and SARS, respectively, given that the case developed a disease between day 0 and day t since immigration (computed by Eq. (13)). Although the prediction becomes crude as compared to those based on the exact length of time in Fig. 2A and B, it clearly indicates that the average posterior probability of influenza is greater than 70% as long as the case develops the disease within 2 days since immigration. The probability is gradually lowered thereafter eventually reaching to 50%, i.e., the prior probability. Again, comparison between influenza and SARS yielded very similar results to that between influenza and MERS.

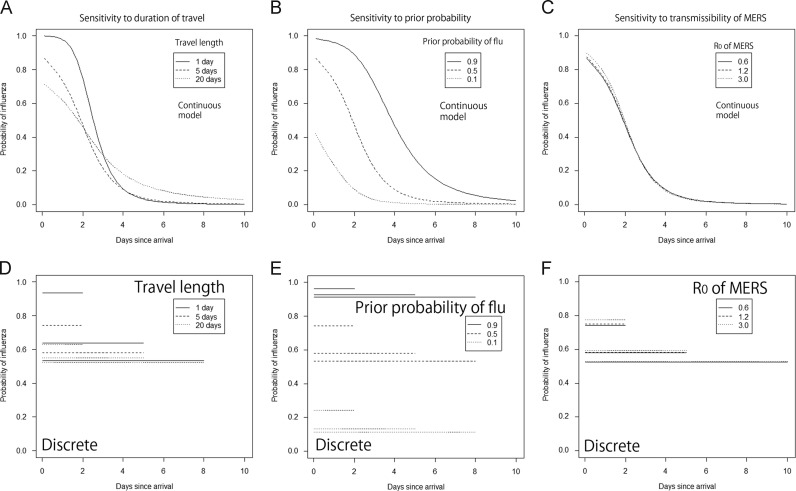
Fig. 3A–C examines the sensitivity of the posterior probability of influenza to the duration of travel, the prior probability of influenza and R ₀ of MERS, respectively. Fig. 3D–F shows the corresponding results of the average probability of influenza using Eq. (13). As the duration of travel was extended, it appeared that the posterior probability of influenza decreased for the early days from immigration (Fig. 3A and D). Since the incubation period of influenza is short (on the order of a few days at most), the long travel indirectly increased the likelihood of MERS. Short travel (e.g. 1 day) led us to have the high probability of influenza for those developing illness within 2 days since immigration, because the distribution of time from immigration to illness onset becomes closer to the incubation period distribution.

Fig. 3.

Sensitivity of the probability of influenza to three different model variables during comparison with the Middle East respiratory syndrome (MERS). (A, B and C) Sensitivity of the posterior probability of influenza to the duration of travel, the prior probability of influenza and R₀ of MERS, respectively (Eq. (11)). (D, E and F) Sensitivity of the average probability of influenza to the duration of travel, the prior probability of influenza and R₀ of MERS, respectively (Eq. (13)). A & D vary the duration of travel, B & E vary the prior probability of influenza, and C & F vary the R₀ of MERS. Unless varied in the corresponding univariate analysis, the duration of travel was 5 days, the prior probability of influenza was assumed as 0.50, and R₀ of MERS was assumed to be 0.63. Only the results that assumed exponential growth with exponentially distributed generation time are shown, but other assumption yielded quantitatively similar estimates.

The posterior probability of influenza appeared to be very sensitive to prior probability of influenza (Fig. 3B and E). Especially, if the prior probability of MERS was high (e.g., 90% due to widespread community transmission of MERS or if we have to examine cases at high risk such as those following close contact), the posterior probability of influenza was apparently smaller than 50% for those developing illness within 2 days since immigration. In the realistic situation with much greater endemicity of influenza than MERS for general travelers, the illness onset within 2 days from immigration was clearly suggestive of influenza. R ₀ of MERS had little impact on the prediction of influenza diagnosis (Fig. 3C and F), which is in line with the limited sensitivity of the posterior probability to the growth rate of infection in Fig. 2.

The findings are summarized in Table 1. It appeared that the posterior probability of influenza for those developing illness within 2 days since immigration is strongly influenced by the prior probability of influenza. This indicates that the high probability of influenza would not be the case even for those developing illness in 2 days if MERS transmission was more widespread than influenza or if the cases were at high risk of MERS (e.g. with suspected exposure to camels or other MERS cases in hospital) (Assiri et al., 2013b, Reusken et al., 2013a, Reusken et al., 2013b).

Table 1.

Sensitivity of differential diagnosis to four different variables.

Key variables	Baseline assumption	Sensitivity of diagnosis to the increase in assumed value	How sensitive within assumed parameter range?
Growth rate of infection	Exponential growth or endemic steady state	(Unrealistically) large increase in the growth rate results in increase in the posterior probability of influenza	Little impact
Duration of travel	5 days	Longer travel yields smaller posterior probability of influenza	Moderate impact
Prior probability of influenza	50%	Greater prior probability of influenza yields greater posterior probability of influenza	High impact
R0 of MERS (yielding the growth rate)	0.63	Greater transmissibility of MERS yields greater posterior probability of influenza	Little impact

4. Discussion

The present study proposed a probabilistic model that permits us to estimate the posterior probability of a specific infectious disease given the time from immigration to illness onset among imported cases. The estimation requires us to assume that we know not only the incubation period and the prior probability but also the length of travel and the transmission dynamics of exporting country. We have shown that the illness onset within 2 days from immigration is suggestive of influenza rather than MERS or SARS, which is consistent with a simpler model based on the known exact length of the incubation period (Nishiura et al., 2012). The results of using SARS data were similar to those obtained using MERS data, which were consistent with similar viral etiology and common clinical characteristics between two diseases (Assiri et al., 2013a, , 2013, Cotten et al., 2013, de Wit et al., 2013). Moreover, we have demonstrated that our approach to doubly interval censored data can correspond to common practical settings in which the exact length from immigration to illness onset is not known. Assuming that the risk of MERS is likely much smaller than 0.50, the illness onset within 2 days can be said to be strongly suggestive of influenza as compared to novel coronavirus infection. Nevertheless, this predictive statement is not applicable to suspected cases at high risk of MERS-CoV infection, such as those previously exposed to camels or other confirmed cases in household or hospital (Assiri et al., 2013b, Reusken et al., 2013a, Reusken et al., 2013b); a high weight should be given to the prior probability of MERS among these cases.

To the best of our knowledge, the present study is the first to explicitly relate the observable time length (i.e. the time from immigration to illness onset) to the differential diagnosis of infectious diseases, examining the sensitivity of the prediction model to key model variables. By doing so, we have theoretically shown that accounting for such delay mechanism is critical not only for quantifying the natural history (Nishiura and Inaba, 2011), but also for utilizing and interpreting the observable information among imported cases. Moreover, the applicability of the model is not limited to imported cases. The proposed statistical framework is widely applicable to other settings in interpreting the observable epidemiological data: the most typical application may be the distinction between nosocomial and community infections in hospitals by using the time from hospitalization to illness onset among hospitalized cases with an infectious disease (Lessler et al., 2007, Lessler et al., 2010, Ejima et al., 2013). The formulation on this subject is our ongoing research.

In practical terms, our proposed model not only predicts the posterior probability of influenza but also suggests that various data gaps have to be filled in empirical observation. As discussed in an earlier study (Nishiura et al., 2012), it is vital to collect the information of the incubation period upon emergence of a novel infectious disease. It should also be emphasized that the viral etiological study is valuable to directly quantify q _i based on empirical data, although such data may be only applicable to general travelers (and not the travelers with close contact with other MERS cases or animals (Nishiura et al., 2014)). In addition, the present study identified that addressing censored information of exposure at an exporting country requires us to understand the transmission dynamics at a global scale (and not at the country level) (Lam et al., 2011). Namely, at least, either the exponential growth rate of infection, or a combination of the estimates of R ₀ and T _g has to be derived from epidemiological data (Nishiura et al., 2013, Nishiura, 2010). If we have a disease with similar etiology and characteristics (e.g. SARS as a substitute of MERS), R ₀, T _g and the incubation period of the substitute disease could complement the uncertainty by the time these estimates become available for the novel disease.

Two specific limitations have to be noted. First, our assumed exposure rests on a homogeneous population model, and the heterogeneous transmissions as well as the heterogeneous incubation period have yet to be explored extensively. Second, if the transmission dynamics is dependent on the illness onset mechanism (Ejima et al., 2013, Klinkenberg and Nishiura, 2011), the dependence structure has to be addressed within the model system, requiring us to account for this matter explicitly in the process of model building.

Since the proposed clinical prediction solely relied on the incubation period and assumed transmission dynamics, improvements have to be made with a broader scope. Our ongoing future study includes an explicit assessment of the diagnostic performance of the proposed prediction system (i.e. assessment of validity and reliability), and also an inclusion of additional exposure variables other than the incubation period in the model (e.g. the presence of risky contact behavior during travel). Despite the need to drastically improve the model structure to fully achieve the practical modeling exercise, we believe that the present study successfully improved the applicability of our modeling approach to empirically observable dataset, identifying data gaps and modeling needs to be addressed in the future.