The impacts of simultaneous disease intervention decisions on epidemic outcomes

Abstract

Mathematical models of the interplay between disease dynamics and human behavioural dynamics can improve our understanding of how diseases spread when individuals adapt their behaviour in response to an epidemic. Accounting for behavioural mechanisms that determine uptake of infectious disease interventions such as vaccination and non-pharmaceutical interventions (NPIs) can significantly alter predicted health outcomes in a population. However, most previous approaches that model interactions between human behaviour and disease dynamics have modelled behaviour of these two interventions separately. Here, we develop and analyze an agent based network model to gain insights into how behaviour toward both interventions interact adaptively with disease dynamics (and therefore, indirectly, with one another) during the course of a single epidemic where an SIRV infection spreads through a contact network. In the model, individuals decide to become vaccinated and/or practice NPIs based on perceived infection prevalence (locally or globally) and on what other individuals in the network are doing. We find that introducing adaptive NPI behaviour lowers vaccine uptake on account of behavioural feedbacks, and also decreases epidemic final size. When transmission rates are low, NPIs alone are as effective in reducing epidemic final size as NPIs and vaccination combined. Also, NPIs can compensate for delays in vaccine availability by hindering early disease spread, decreasing epidemic size significantly compared to the case where NPI behaviour does not adapt to mitigate early surges in infection prevalence. We also find that including adaptive NPI behaviour strongly mitigates the vaccine behavioural feedbacks that would otherwise result in higher vaccine uptake at lower vaccine efficacy as predicted by most previous models, and the same feedbacks cause epidemic final size to remain approximately constant across a broad range of values for vaccine efficacy. Finally, when individuals use local information about others’ behaviour and infection prevalence, instead of population-level information, infection is controlled more efficiently through ring vaccination, and this is reflected in the time evolution of pair correlations on the network. This model shows that accounting for both adaptive NPI behaviour and adaptive vaccinating behaviour regarding social effects and infection prevalence can result in qualitatively different predictions than if only one type of adaptive behaviour is modelled.

Highlights

• •We create an agent based network model that simulates an epidemic.
• •We combine population decisions for vaccination and non-pharmaceutical interventions.
• •Vaccination mitigates epidemic final size effectively for high transmission rates.
• •Non-pharmaceutical interventions compensate for delays in vaccine availability.
• •Non-pharmaceutical interventions can lower vaccine uptake and reduce epidemic size.

1. Introduction

Infectious disease outbreaks have the potential to cause unexpected burdens and panic in societies. For example, the outbreak of severe acute respiratory syndrome (SARS) in 2003 caused significant economic impacts across the world, despite lasting only six months (Lee et al., 2002). Occurring unexpectedly, outbreaks such as the aforementioned SARS outbreak (Lee et al., 2002, Pearson et al., 2003), the Middle East respiratory syndrome outbreak in 2012 (Balkhair et al., 2013), Ebola outbreak in 2014 (WHO Ebola Response Team, 2014), or an influenza pandemic, which has happened as recently as 2009 (Girard et al., 2010), can be difficult to predict and can spread locally or globally and last anywhere from months to years.

Human behaviour can have a large impact on the spread of infectious diseases (Funk et al., 2010). People have been observed to change their regular social routines in response to an epidemic, in order to reduce their risk of becoming infected (Lau et al.,, Philipson,, Ahituv et al.,). The infection prevalence or incidence of a disease in a community serves to drive these behavioural changes, as an individual׳s perceived susceptibility generally rises along with these disease measures (Funk et al., 2010, Durham and Casman, 2012, De Zwart et al., 2009, Koh et al., 2005). There are two primary self protective intervention strategies susceptible members of a population can utilize to reduce their chances of contracting a disease. These are pharmaceutical interventions, such as vaccination, and non-pharmaceutical interventions (NPIs), such as social distancing and increased hand washing (Centers for Disease Control and Prevention, 2012). The usage of these intervention strategies are voluntary in many health jurisdictions, and so perceived risks play an important role in how often they are utilized (Chapman and Coups, 1999).

Coupled disease-behaviour models combine human decision making behaviour with traditional transmission dynamics, helping to capture an additional, and often important, aspect of disease spread (Funk et al., 2010, Bauch et al., 2013, Wang et al.,). Behaviourally based models that incorporate NPIs and social distancing during an outbreak show that these practices can lower the attack rate of a disease (Del Valle et al., 2005, Reluga,, Funk et al., 2008, Rizzo et al.,, Bagnoli et al.,, Fenichel et al., 2011, Poletti et al., 2009, Poletti et al., 2012). Suppressing an outbreak using these means can be very critical, as vaccines may not always be immediately available to the general population (Check, 2005). Modelling how NPIs are utilized can be approached in various ways by mathematical models. For example, Funk et al. (2008) allow an individual׳s level of awareness to the presence of a disease shape their usage of self-protective measures. Rizzo et al. (2014) model a population where susceptible individuals base their activity rates on the infection prevalence of a disease in the population or the infection incidence over a time step. Similarly, Bagnoli et al. 2007, and Del Valle et al. (2005) have individuals lower their susceptibility according to the proportion of their contacts in a transmission network that are infectious, and to the infection prevalence, respectively. Poletti et al., 2009, Poletti et al., 2012 incorporate imitation dynamics to model the behavioural changes of the population. Finally, Fenichel et al. and Chen et al. (2011) study models where individuals derive utility from engaging in social contact, but raise their risk of infection when doing so. In these aforementioned models, each individual׳s behaviour is shaped by the information they gather about the disease status of those around them. Thus, in these models, transmission dynamics depend heavily on the perceived risks that drive contact patterns.

Further approaches to mathematical models that integrate self protective behaviour into disease transmission utilize adaptive and multiplex networks. An adaptive network is a network whose edges between contacts change dynamically over time. Using these, Gross et al., (2006), Shaw and Schwartz, 2007, Shaw and Schwartz, 2010 and Zanette and Risau-Gusman (2008) allow susceptible nodes to rewire their existing connections away from infectious nodes at a given rate. The approach of multiplex networks helps to model the many types of social networks individuals may use to acquire information, and Granell et al. (2013) and Cozzo et al. (2013) use these to study the impact of different information flows on the spread of epidemics. On the other hand, Glass et al. (2006) and Kelso et al., (2009) use contact networks which include families, schools, and workplaces to study the effects of various NPIs such as school closures and staying at home while infectious.

Additionally, vaccines (if available) play a major role in reducing infection rates during an epidemic. Some mathematical models have shown that under voluntary vaccination, populations may not reach sufficient uptake levels to stop an epidemic (Vardavas et al., 2007; Bauch et al., 2003). However, under voluntary policies in a network, Zhang et al. (2010) demonstrate that nodes with high degree can help to suppress disease spread through their increased desires to vaccinate (Zhang et al., 2010). During an outbreak, complications may arise when there are delays in vaccination. As a result of a delay, epidemic final size can increase significantly (Yang et al., 2009), especially as the delay lengthens (Gojovic et al., 2009). When considering the efficacy of a vaccine, Wu et al. (2011) suggest through their model that a less effective vaccine causes vaccine uptake to increase (to an effectiveness of about 50%), especially for more serious diseases (Wu et al., 2011). Insights from the models discussed above, as well as more empirically based research (Brewer et al., 2007), have shown that perceived risks play an important factor in an individual׳s decision to protect themselves through vaccination. These risks include perceived susceptibility to the illness and perceived risks associated with vaccinating (due to potential side effects) (Roberts et al., 1995, Streefland, 2001). Much like NPIs, members of a population will base their vaccination decisions on information they are able to gather about the disease during an outbreak.

Perceived risks surrounding a disease play a crucial role in vaccination and NPI decisions. Information that shapes these perceptions is gathered by individuals in a population and may be derived from local information (Ahituv et al.,, Philipson,, Klein et al., 2007) (such as social contact networks), or through global information such as media reports about the population as a whole (Klein et al., 2007, Berry et al.,). We note that disease-behaviour models like those discussed above do not typically consider the intervention strategies of vaccination and NPIs simultaneously. However, it is clear that both are important factors in the spread of a disease. Andrews and Bauch have studied the interactions of these two disease interventions with a utility based decision framework model in the context of seasonal influenza. In contrast to our previous work that considers long-term, year-to-year dynamics, here we develop a disease-behaviour individual based network simulation model to study interactions between vaccinating behaviour and NPI behaviour and their impact on health outcomes during the course of a single, and sudden, epidemic outbreak of a novel, self limiting infection, where perceived risks and social influence serve as the primary drivers of individual behaviour. Moreover, we include parameters that allow controlling the relative influence of local versus global information on behaviour. Our main objective is to compare how our model predictions differ from predictions of models that capture behaviour for only one of the two interventions, under various assumptions for (1) transmission probabilities, (2) timing of vaccine introduction, and (3) vaccine efficacy, and how efficacy influences vaccine uptake. Furthermore, we explore how the utilization of local versus global information regarding disease spread and vaccine uptake can alter network wide outcomes.

2. Methods

2.1. Disease dynamics

We consider a disease with a susceptible – infectious – recovered – vaccinated (SIRV) natural history. Susceptible individuals may become infected by their infectious neighbours with probability $P\left(N_{\mathit{Inf}}\right)=1-{(1-\beta )}^{N_{\mathit{Inf}}}$ per day, where N _Inf is the number of infectious network neighbours, and β is the transmission rate. Infectious individuals move to a recovered (and immune) state for the remainder of the epidemic in a number of days sampled from a Poisson distribution with a mean of 7 days. Finally, susceptible individuals may choose to vaccinate and thus become immune for the duration of the epidemic. Baseline parameter values were calibrated to obtain epidemic final size and vaccine uptake trends within the plausible ranges of the corresponding measures in the United States for the 2009 H1N1 influenza pandemic (Shrestha et al., 2011, Centers for Disease Control and Prevention, 2015), although we emphasize that we are not modelling influenza in particular, but rather we intend our disease represent a hypothetical self-limiting, acute infection where individuals only lose natural immunity on a time scale of years. We also assume that this is a novel strain of a disease, and individuals have no prior immunity – either natural or vaccine conferred. Full details regarding network structure, transmission dynamics, and decision modelling appear in the following subsections.

2.2. Contact network

The disease is transmitted on a network consisting of 10,000 nodes which was constructed by sampling from a large contact network derived from empirical contact data in Portland, Oregon (Network Dynamics and Simulation Science Laboratory, 2008). Previous research has shown that the subnetwork is a good approximation to the full network (Wells and Bauch, 2012). This network׳s structure (see Supplementary Information (SI) Fig. 1) remains static throughout an epidemic, and we assume that the edges in the network provide sufficient contact between individuals to allow potential disease transmission. We also run simulations testing our primary results on two other types of networks: random networks and power law networks. For details regarding these results, we direct the reader to the SI.

2.3. Non-pharmaceutical interventions and vaccination

Susceptible individuals in the population may engage in self-protective behaviour in response to a growing epidemic. Their self-protecting activity is governed by both the presence and fear of the disease itself (Sadique et al., 2007, Henrich and Holmes, 2009, Uscher-Pines and Harris, 2010, Brown et al., 2010, Harvard School of Public Health, 2009) and by the social influence of their contacts and the population as a whole (Poletti et al., 2009, Bauch, 2005). To model this intervention use, we begin by allowing an individual to reduce their susceptibility to ${\beta }_{\mathit{NPI}}=\left(e^{-(\Phi +{\Gamma }_{\mathit{NPI}})}\right)\beta$. Firstly, Φ is an individual׳s risk perception of the disease, given by

$$\Phi =\sigma f\left(\lambda ,\frac{I_{\mathit{Net}}}{k}\right)+(1-\sigma )f\left(\lambda ,\frac{I_{\mathit{Pop}}}{N_{\mathit{Pop}}}\right),$$ (1)

where I _Net is the number of a given individual׳s contacts that have been infected, k is the node degree of the individual on the network, I _Pop is the number of individuals in the population that have been infected, N _Pop is the population size, and σ dictates how members of the population weigh information gathered from their contacts and the population as a whole. Finally, f is a function that determines an individual׳s response level to increasing infection incidence, given by

$$f(x,y)=1-\exp (-\mathit{xy}),$$ (2)

where x is a proportionality constant that governs the response dynamic (λ in (1)). Since perceived risks only increase in our model (due to the relatively small timespan of one epidemic), we use this functional form. Also, it is an increasing function bounded between 0 and 1 whose shape (or response of increasing perceived risk to incidence) can be governed by a single parameter. Similar functions have been used in the literature surrounding disease spread and self-protective behaviour, for example, see Funk et al. (2008). Secondly, ${\Gamma }_{{\mathit{NPI}}_j}$ measures an individual j׳s imitation of others who are utilizing self-protective NPI practices, given by

$${\Gamma }_{{\mathit{NPI}}_j}=\sigma f\left(\gamma ,\frac{\sum _{i=1}^{k_j^{\mathit{Vuln}}}1-\exp (-({\Phi }_i+{\Gamma }_{{\mathit{NPI}}_i}\left)\right)}{k_j^{\mathit{Vuln}}}\right)+(1-\sigma )f\left(\gamma ,\frac{\sum _{i\ne j=1}^{N_{\mathit{Pop}}^{\mathit{Vuln}}}1-\exp (-({\Phi }_i+{\Gamma }_{{\mathit{NPI}}_i}\left)\right)}{N_{\mathit{Pop}}^{\mathit{Vuln}}-1}\right),$$ (3)

where N ^Vuln _Pop is the number of susceptible or vaccinated (potentially vulnerable) individuals in the population, k ^Vuln _j is the number of susceptible or vaccinated neighbours individual j has, $\frac{\sum _{i=1}^{k_j^{\mathit{Vuln}}}1-\exp (-({\Phi }_i+{\Gamma }_{{\mathit{NPI}}_i}\left)\right)}{k_{\mathit{Vuln}}}$ is the average amount of transmission rate reduction caused by self-protective behaviour amongst an individual׳s susceptible neighbours, $\frac{\sum _{i\ne j=1}^{N_{\mathit{Pop}}^{\mathit{Vuln}}}1-\exp (-({\Phi }_i+{\Gamma }_{{\mathit{NPI}}_i}\left)\right)}{N_{\mathit{Pop}}^{\mathit{Vuln}}-1}$ is the similar average reduction induced by the susceptible population as a whole, and γ is a parameter that governs the response strength of imitation behaviour. Eq. (3) captures how individuals reduce their probabilities of becoming infected through observations of others doing the same. This includes imitation of both network neighbours (σ), and imitation of how the entire population is behaving $(1-\sigma )$. Thus, $0<\exp (-(\Phi +{\Gamma }_{\mathit{NPI}}\left)\right)\le 1$ dictates how individuals lower their probabilities of becoming infected as they gain awareness of the epidemic by witnessing the disease spread throughout the population. In our simulations, NPI use for each individual is updated non-synchronously in a random order at the beginning of each day. That is, an individual׳s NPI use will be updated using both information of infection levels and the NPI levels of others from the end of the previous day. Also, we observed from the simulations we ran that the transmission rate reduction through NPI use will typically be $\le 50\%$ for any given individual, which is consistent with the available literature regarding the efficacy of NPIs (Larson et al., 2010, Sheehan et al., 2007).

If vaccines are available, members of the population may also choose to protect themselves from infection by receiving a vaccine. The decision to vaccinate becomes a more attractive option as vaccine uptake increases (Bhattacharyya and Bauch, 2011), and thus an individual׳s vaccination decision will depend both on their perceived risk of the disease as well as the decisions of others to vaccinate. We represent this as

$$\sigma \left(f\left(\lambda ,\frac{I_{\mathit{Net}}}{k}\right)+f\left(\gamma ,\frac{V_{\mathit{Net}}}{k}\right)\right)+(1-\sigma )\left(f\left(\lambda ,\frac{I_{\mathit{Pop}}}{N_{\mathit{Pop}}}\right)+f\left(\gamma ,\frac{V_{\mathit{Pop}}}{N_{\mathit{Pop}}}\right)\right),$$ (4)

where V _Net and V _Pop are the numbers of a given individual׳s contacts and total number of individuals that have been vaccinated, respectively. If we define ${\Gamma }_V=\sigma f\left(\gamma ,\frac{V_{\mathit{Net}}}{k}\right)+(1-\sigma )f\left(\gamma ,\frac{V_{\mathit{Pop}}}{N_{\mathit{Pop}}}\right)$, then (4) can simply be written as

$$\Phi +{\Gamma }_V.$$ (5)

Eq. (5) combines an individual׳s risk perception of becoming infected, which is based on local and global information of disease incidence, with an individual׳s imitation of self protective behaviour, which also based on local and global information.

If on any day a susceptible individual׳s preference towards vaccinating, which we set as $\exp (-(\Phi +{\Gamma }_V\left)\right)$, exceeds a given threshold, θ, then that individual will be transferred to the vaccinated compartment. Otherwise, this is interpreted as an individual being undecided, and they therefore remain susceptible. This process is similar to methods from decision field theory (Busemeyer and Townsend, 1993), where individuals update their preferences towards making certain decisions based on available information. If their preference toward making an action reaches a pre-defined level, a decision is then subsequently made.

3. Results

3.1. Baseline dynamics

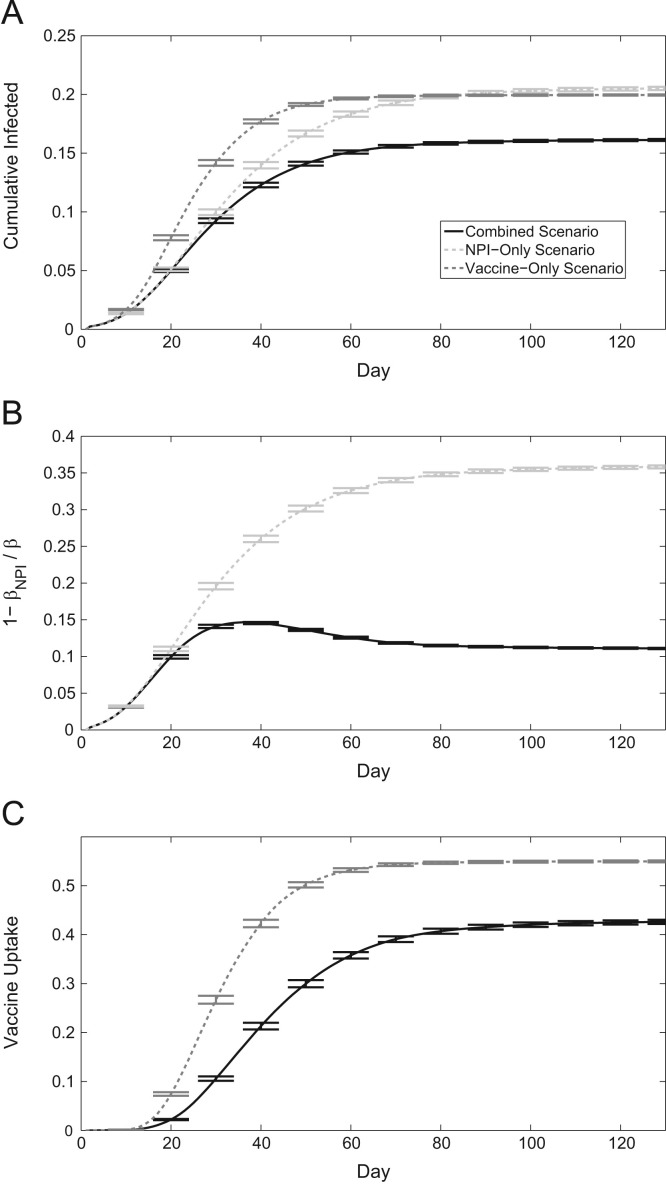
The baseline scenario of our model (Table 1 ) simulates an outbreak in a population whose individuals may protect themselves from infection using NPIs or vaccination. We call this the baseline scenario as it was calibrated to achieve plausible epidemic outcomes under the realistic assumption that both vaccination and NPIs are available simultaneously. Henceforth, we will refer to this scenario as the “combined scenario”, as both interventions may be used. If both intervention options are available, the final size of the epidemic is lowest compared to when only one of the two interventions are used, as expected (Fig. 1 a). We also compare the epidemic time series of the combined scenario to hypothetical scenarios where there is no vaccine available over the course of the outbreak (“NPI-only scenario”), or self-protective behaviour is completely ineffective (“vaccine-only scenario”). We note that the NPI-only scenario gives similar infection rates as the combined scenario for the first 3 weeks of the epidemic. This occurs because vaccine uptake in the combined scenario is close to zero in the first few weeks, due to low perceived risks of becoming infected while infection prevalence is still minimal, and therefore the differences between scenarios with and without vaccination are small during this period of time. The implication of this is that delays in vaccine availability in the first few weeks of an epidemic may not hinder vaccine uptake under a voluntary vaccination policy. After this initial period, we observe consistently higher cumulative infected for the NPI-only scenario over the combined scenario for the remainder of the epidemic. The NPI-only simulations yield the greatest average cumulative infection incidence, as the response from solely NPIs amongst susceptible individuals cannot match the disease mitigation of a perfectly efficacious vaccine, in the long term (however, we note that the difference in cumulative incidence is relatively small). In the vaccine-only scenario, infection incidence spikes rapidly but the epidemic lasts a shorter amount of time than in the NPI-only scenario. The relatively rapid early spike in total infected individuals is due to the lack of vaccine uptake in the first weeks of the epidemic, as vaccination decisions are not activated until the perceived threat of becoming infected is sufficiently high. In all these cases, self-protective behaviour serves to slow the spread of an epidemic, but does not successfully reduce the final attack rate as significantly compared to when it is aided by vaccination.

Table 1.

Baseline parameter values.

Parameter	Description	Value
λ	Constant governing awareness/risk perception of disease	1.5
γ	Constant governing behaviour imitation	0.5
θ	Vaccinating threshold	0.35
σ	Weighting for global versus local information	0.8
β	Transmission rate	0.005
NPop	Population size	10,000
I0	Initial number of infectious persons	20
η	Mean infectious period, in days	7

Fig. 1.

Time series of an epidemic, 95% confidence intervals shown every 10 days around the mean of 500 realizations. (a) Cumulative infection incidence. (b) Transmission rate reduction due to self-protective behaviour (NPIs) amongst the susceptible population. (c) Cumulative vaccine coverage.

In the NPI-only scenario, NPI uptake amongst susceptible individuals is much more pronounced than when vaccination is also an option (Fig. 1b). This occurs for two reasons. Firstly, if vaccination can occur, those that practice the strongest self protective behaviour due to having high levels of perceived risk will be amongst the first to vaccinate. In turn, this will lower the average NPI uptake amongst the remaining susceptible population. Secondly, if members of the population are vaccinating, the spread of the disease will be suppressed causing perceived risks of becoming infected to be lower. Thus, resulting NPI use will be less prominent. In the absence of vaccination, transmission reduction through NPI use simply continues to rise along with the infection incidence seen in Fig. 1a. In the final vaccine-only scenario, total vaccine uptake is increased on average (Fig. 1c). Moreover, vaccine coverage begins to rise earlier in response to the rapid spike in infection incidence that is observed when no transmission reduction is present through NPIs. Thus, when NPI effects are not considered, predicted vaccine uptake is significantly higher.

3.2. Transmission rate

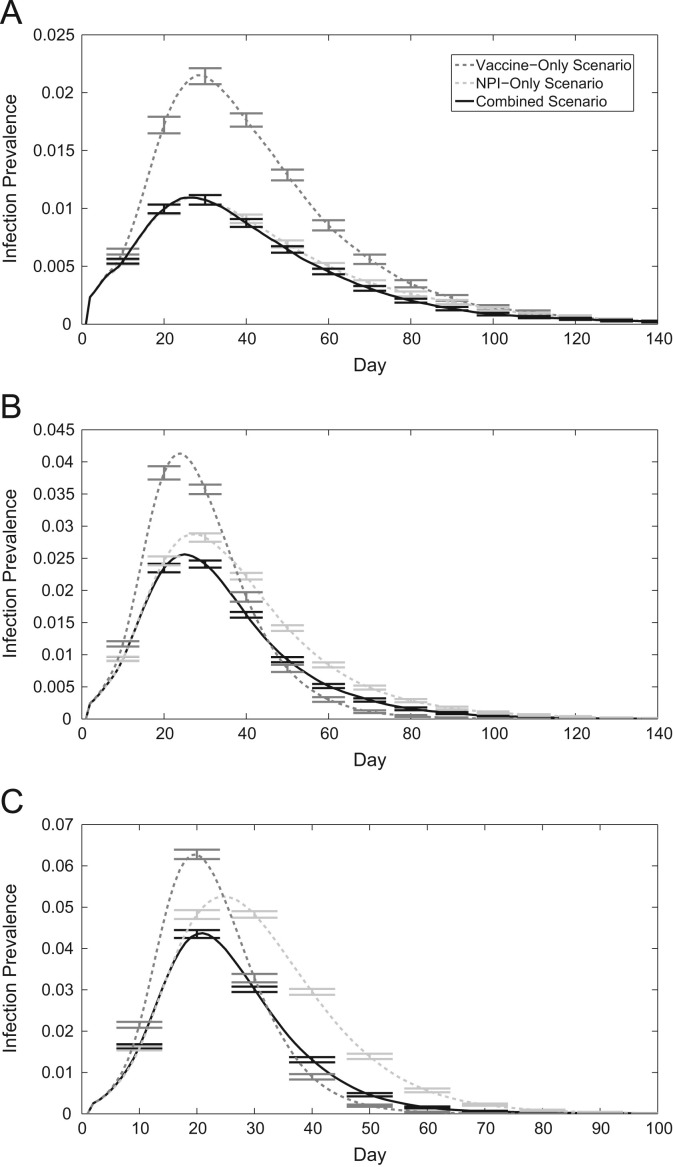
Time series of infection prevalence corresponding to different transmission rates can help us understand epidemic spread in our 3 scenarios (Fig. 2 ). When the transmission rate is low, NPIs alone are relatively effective at hindering the growth of the epidemic, lowering the peak infection prevalence compared to the vaccine-only case (Fig. 2a). For a transmission rate of $\beta =0.00493$ per infectious contact per day, simulations that utilize NPIs only or vaccination only result in the same epidemic final size (Fig. 2b). Although the peak infection prevalence in this scenario is larger for vaccine-only simulations, the epidemic dies out more quickly compared to the NPI-only scenario, resulting in the same cumulative infection incidence over the epidemic duration. For higher transmission rates, the vaccine only scenario outperforms the NPI only scenario (Fig. 2c). Although NPIs delay the peak of the epidemic, infection prevalence dies out more slowly than when the population uses solely vaccination instead. However, this highlights the importance of NPIs in epidemics where vaccination may not be immediately available. Considering the combined scenario data in Fig. 2(c), which indicates infection prevalence in simulations utilizing both NPIs and vaccination, the initial disease spread is very similar to that of the NPI-only scenario. Only when individuals begin to vaccinate does the infection prevalence in the combined scenario show quantitative difference to the infection prevalence in the NPI-only scenario. Thus, as long as a vaccine is made available within a given time frame, the final size can be expected to be the same due to the early activation of NPIs.

Fig. 2.

Time series of infection prevalence with the vaccine-only scenario, the NPI-only scenario, and the combined scenario. 95% confidence intervals shown every 10 days around the mean of 500 realizations. (a) $\beta =0.004$ (b) $\beta =0.00493$ (c) $\beta =0.006$.

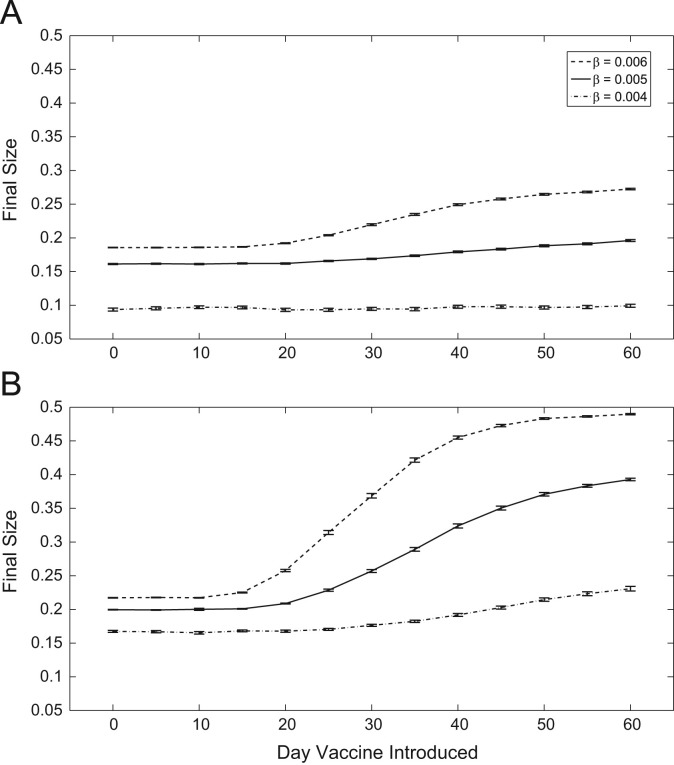
Vaccine timing plays a critical role in the health outcomes of the population during an epidemic, across a range transmission rates (Fig. 3 ). In the combined scenario (Fig. 3a), a vaccine can be introduced up to 20 days after the start of an epidemic for the epidemic final size to be roughly the same as the scenario when a vaccine is available from day one, for baseline transmission rates. If we disregard the use of NPIs (Fig. 3b), the vaccine must be made available within 15 days before we begin to observe larger epidemic final sizes. This effect is similar for $\beta =0.006$ per infectious contact per day. In the combined scenario, a vaccine must be made available within 15 days before epidemic sizes increase. However, in the vaccine-only case, vaccine availability must occur within just 10 days. Finally, for lower disease transmission, vaccine introduction timing has little impact on infection incidence in the combined scenario. However, in the vaccine-only scenario, we see final sizes begin to increase when availability occurs after 20 days. From these results, we also notice that the rate of increase of epidemic final sizes corresponding to the timing of vaccine introduction are much greater. For example, given the baseline transmission rate, the difference in infection incidence between immediate vaccine availability and availability beginning on day 60 is $\approx 20\%$ in the vaccine-only case. However, the same measure in the combined case is only $\approx 4\%$. Thus, the prediction from these two modelling approaches of epidemic size induced by vaccine timing introduction differs by about 16% of the entire population size.

Fig. 3.

Epidemic final sizes with respect to when vaccination is made available. (a) With NPIs. (b) Without NPIs.

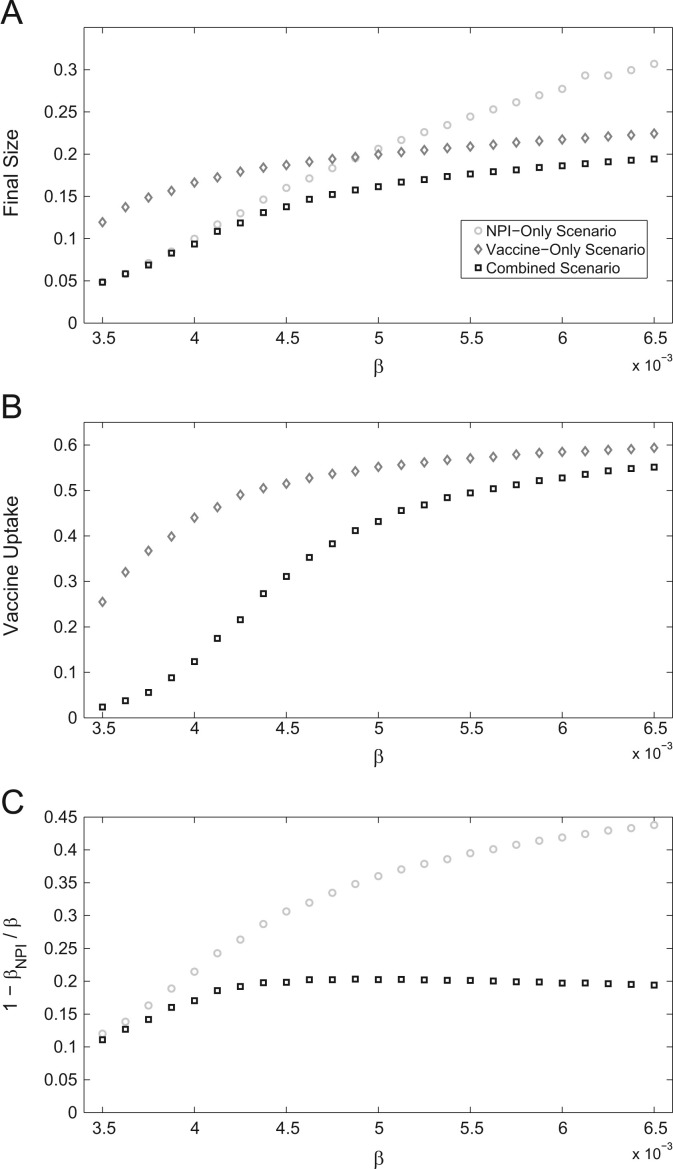
Finally, we also consider measures for epidemic final size (Fig. 4 ). When the transmission rate is low, the final size is the same for the combined scenario as for the NPI-only scenario, but much higher for the vaccine-only scenario (Fig. 4a). Hence, for low transmission rates, NPIs on their own can reduce final size as much as combined use of NPIs and vaccines, although the same is not true for vaccines on their own. This is due to individuals promptly adopting NPIs, which are targeted at the leading edge of the epidemic and quick to implement, curbing disease spread immediately. Also, vaccine uptake is much larger in the vaccine-only scenario than in the combined scenario (Fig. 4b). In contrast, when the transmission rate is high, the final size is almost (but not quite) the same for the combined scenario as for the vaccine-only scenario, but much higher for the NPI-only scenario. Moreover, vaccine uptake is also nearly the same for both of the scenarios that include vaccination. Hence, for high transmission rates, vaccines on their own can reduce final size almost as much as combined use of NPIs and vaccines, although the same is not true for NPIs on their own. In the case of NPIs, the NPI uptake amongst susceptible individuals does not change for $\beta >~0.0045$, due to the adoption of vaccination (Fig. 4c). However, in the NPI-only scenario, susceptibility reduction through NPIs continues to rise along with the transmission rate.

Fig. 4.

Epidemic measures with respect to transmission rate. (a) Epidemic final size. (b) Vaccine uptake. (c) Transmission rate reduction amongst susceptible individuals.

In summary, when transmission rates are sufficiently low, NPIs alone can be almost as effective as having both vaccines and NPIs (whereas vaccination alone is relatively less effective), but when transmission rates are sufficiently high, vaccines alone can be almost as effective as having both interventions (whereas NPIs alone are relatively less effective).

3.3. Vaccine efficacy

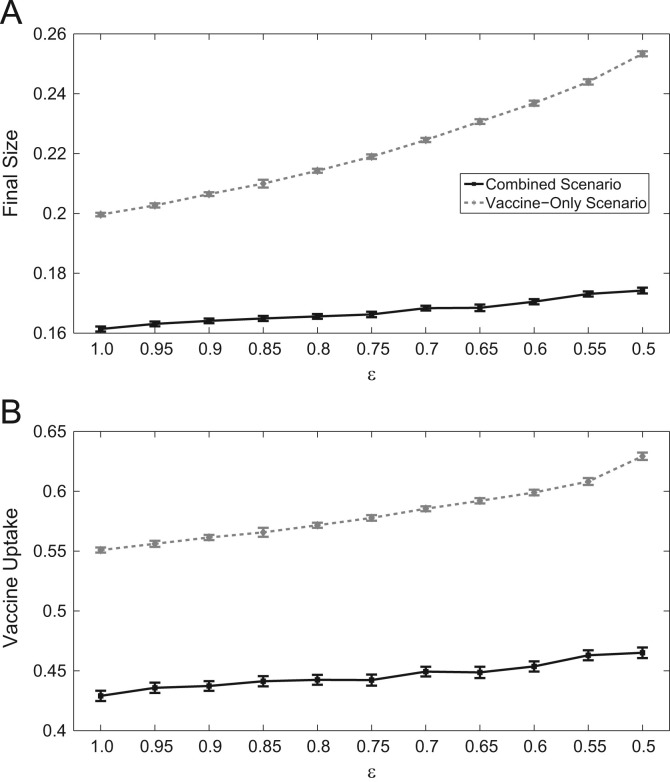
Vaccines are never 100% efficacious. For less effective vaccines, we can expect infection incidence and vaccination coverage to change as individuals in the population adapt to the quality of interventions available to them. Thus, we explore the dynamics under various vaccine efficacies (denoted ϵ), and how they relate to vaccine coverage and epidemic final size with and without the additional impacts of NPIs (Fig. 5 ). We note that in our simulations, vaccines give full protection with probability ϵ, and no additional protection with probability $1-ϵ$.

Fig. 5.

Effects of vaccine efficacy between scenarios with and without NPIs on (a) Vaccine uptake, and (b) final epidemic size.

As vaccine efficacy decreases, the vaccine-only scenario overestimates the amount of vaccine uptake demanded by up to 16.5% of the population size relative to the combined scenario. We also observe that as vaccine efficacy decreases, the subsequent increase in vaccine coverage of the population is larger when NPI effects are not incorporated. For example, between efficacies of 100%–50%, the combined scenario of the model predicts $~3.5\%$ more of the population vaccinating, whereas with the vaccine-only scenario, simulations predict an $~8\%$ increase. This effect is also seen with epidemic final size (Fig. 5a). Across all efficacies, final size increase is only $~1.5\%$ of the entire population size with combined NPI and vaccine utilization, and $~5.5\%$ with only vaccination. Thus, we see that disregarding the impact of NPIs may lead to an overestimation of the population׳s vaccine demand and final epidemic size. Moreover, the increases in vaccine uptake and final size with decreasing vaccine efficacy may be less significant than what previous predictions which disregard NPI effects show (Wu et al., 2011). Finally, when incorporating vaccination decisions and self protective behaviour simultaneously into the model, we observe that predicted levels of vaccine uptake are much smaller than when no NPIs are implemented (Fig. 5b).

3.4. Pairwise correlations

As an epidemic unfolds across a network, the status of the nodes will develop while the disease spreads and intervention decisions are made. As a result, the spatial structure of infected and susceptible individuals on the networks will evolve over time as well. The correlation between these pairs can offer insight on the vulnerability of the network to disease spread and how individuals react to infection prevalence according to the information available to them, which we control with the parameter σ. To measure the correlation between node pairs, we follow Keeling and Eames (2005):

$$C_{\mathit{AB}}=\frac{N_{\mathit{Pop}}}{k_{\mathit{avg}}}\frac{\left[\mathit{AB}\right]}{\left[A\right]\left[B\right]},$$ (6)

where k _avg is the average node degree on the network. With this formulation, an increase in C _AB indicates an increase in correlation as the number of $\left[\mathit{AB}\right]$ pairs in the network relative to the number of type $\left[A\right]$ nodes and type $\left[B\right]$ nodes also increases. A value of $C_{\mathit{AB}}=1$ indicates no correlation (Keeling and Eames, 2005).

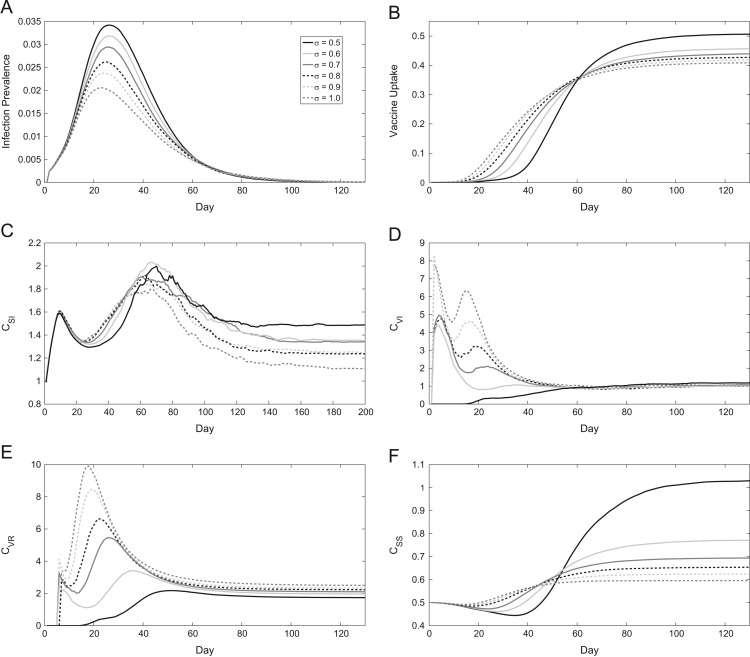
Considering the correlation between susceptible-infected ([SI]) pairs (Fig. 6 c), we observe a rapid initial spike in the network. This early increase is due to the first infected individuals spreading the disease to their network contacts, enabling more opportunities for transmission. As infection prevalence begins to peak (Fig. 6a), infected individuals have a higher probability of being connected to a non-susceptible node, which results in the decline of C _SI in the network, as distinct clusters of infected and other infected, recovered or vaccinated individuals develop. However, the correlation rises again as infectious nodes recover and only a final few clusters of infected and susceptible nodes remain, more so for lower σ as those who vaccinated are less likely to be connected to an infectious node. Correlations of vaccinated nodes with nodes that are or have been infected, [VI] and [VR], respectively, also show how network dynamics respond to different levels of σ (Fig. 6d,e). When individuals base their decisions on local information, that is, on the basis of the number of infectious neighbours $(\sigma =1.0)$, C _VI and C _VR are higher. This indicates successful ring vaccination occurring in proximity to the infectious individuals. Under strong influence of local information, neighbours of infectious individuals develop a high perceived risk and decide to vaccinate earlier. Then, social influences reinforce this vaccinating behaviour, resulting in clusters of vaccinated individuals around infectious individuals. However, when decisions are made more strongly based on population level infection prevalence $(\sigma =0.5)$, [VI] and [VR] pairs become less common in proportion to all vaccinated and infected/recovered nodes since vaccinations do not always occur on the epidemic front. The cumulative vaccine uptake under global information is higher than under local information, however, vaccine uptake increases more rapidly in the early stages of the epidemic under local information (Fig. 6b). This reflects the efficiency of targeted vaccination under local information, where vaccines are administered to the contacts of infectious individuals so that infection spread is efficiently prevented. Finally, as the epidemic dies out and infectious nodes become rare, [VI] and [VR] correlations across varying levels of σ converge to similar values.

Fig. 6.

Time series of epidemics over different values of σ, the weighting for global versus local information. (a) Infection prevalence, (b) vaccine uptake, (c) correlation between SS pairs, (d) SI pairs, (e) VI pairs, and (f) VR pairs. Lines show the average values over 500 realizations.

As σ decreases in our model, [SS] pairs become more common relative to the total number of susceptible nodes towards the end of an epidemic, increasing C _SS (Fig. 6f). On the other hand, with higher σ, final values of C _SS continue to decrease. However, we note that during an epidemic, the opposite is true, albeit to a lesser extent. When $\sigma =0.5$, vaccination occurs in locations other than the epidemic front, in turn decreasing C _SS compared to higher values of σ. Nonetheless, the ring vaccination observed with increased σ is more efficient than the more random vaccine allocation seen when $\sigma =0.5$, for example, due to the disease only being able to spread along the network edges.

4. Discussion

We have developed and analyzed a model that simulates a population׳s adaptive self protective behaviour (use of NPIs and vaccination) in the face of a disease outbreak, in contrast to most previous approaches that model only vaccinating behaviour or only NPI behaviour. We allow an individual׳s actions to depend both on their perceived risk of infection developed from their experiences with the disease on the network (both from their network neighbours and from the population as a whole), as well as imitation of the behaviour of others in the population.

Surprisingly, when transmission rates are low, the NPI-only scenario offers comparable disease mitigation effectiveness to the combined scenario, while the vaccine-only scenario results in relatively larger epidemic sizes than either the NPI-only scenario or the combined scenario. For higher transmission rates, the opposite becomes true. That is, the vaccine-only scenario is almost as effective as the combined scenario for reducing infection incidence, but the NPI-only scenario fares worse. If a vaccine is not available immediately to the population at the start of an epidemic, epidemic mitigation through adaptive NPI behaviour can curb the growth of an epidemic. Thus, if vaccination is made available to the population within a given time frame, health outcomes will be very similar to situations where a vaccine was always available. If, however, the effects of NPIs are not incorporated, then these time frames are comparatively shorter. Moreover, the increases in infection incidence for the vaccine-only scenarios are significantly higher the later the vaccine is introduced, resulting in increasingly higher predictions of epidemic final size. Finally, the impact of varying vaccine efficacy on both vaccine uptake and epidemic final size varies significantly between scenarios with and without adaptive NPI behaviour. The increases in both final size and vaccine uptake when vaccine efficacy is decreased are much higher for the vaccine-only scenario than the combined scenario. Hence, a model of adaptive vaccinating behaviour that does not also account for adaptive NPI behaviour will make very different predictions than a model that accounts for adaptive behaviour toward both interventions. This again highlights the positive benefits of epidemic mitigation through adaptive NPI behaviour.

From a network perspective, individuals basing their decisions to practice NPIs or become vaccinated based on the infection prevalence and behaviour in their infection contact network leads to the most effective disease control. Pairwise correlations between vaccinated and infected nodes are highest when this information gathering is possible, as those that vaccinate are typically connected to infected nodes. We also tested the main results with two additional types of networks: random networks and power law networks (see SI). While the dynamics are qualitatively the same, the amount of change in epidemic final size or vaccine uptake with differing vaccine delays or vaccine efficacies can depend on the specific network type. Assumptions about network structure and transmission are an important consideration – particularly when modelling a specific disease. For example, a transmission network for influenza likely has a different structure than one that would be used to model HIV transmission.

In the combined scenario, epidemic final size is suppressed most effectively compared to when only single interventions are possible. Also, when the effects of NPIs are not considered in our vaccine-only scenario (an assumption which is common in previous behaviour-disease models focusing on vaccinating behaviour), vaccine uptake predictions are higher compared to when these effects are considered by our model, on account of counteractive feedbacks from NPI behaviour.

Our model includes some simplifying assumptions about behaviour-disease dynamics. For example, NPI efficacy is poorly quantified in the epidemiological literature, and it is not always known in what situations individuals may practice them most often. Thus, we assume that NPIs for the spreading disease are not used initially, but in reality there may be some baseline level of NPIs used in the population due to other circulating diseases. Moreover, we do not model the effects of NPI practices that infectious individuals may utilize, such as self isolation. Instead, we make the assumption that infectious NPI use is absorbed into the transmission rate. Also, the network we used in our simulations could be extended to distinguish family, friend, and work structures, where transmission rates to an individual can vary depending on what category certain network contacts fall in. Similarly, age structure can be introduced into the model. As children will be much less likely to effectively practice NPIs, disease transmission in these groups may be more rapid than our model predicts. Finally, we did not include the impact of asymptomatic infections, and assumed all cases were identifiable in our main results. However, we also considered a scenario where 50% of cases were asymptomatic (see SI), and the primary results regarding vaccine efficacy and vaccine availability delays across various transmission rates are qualitatively the same. Although the main results are similar, in future work that aims to model a specific disease, accounting for asymptomatic infections is an important factor.

Through these experiments, we see that predictions of health outcomes and vaccine uptake in a population can vary significantly when NPI use is, or is not, considered. It is important for behaviourally based epidemiological models to incorporate the effects of transmission reduction through this adaptive behaviour, as perceived risks of a disease will in turn be shaped by them – subsequently altering the outcomes of an epidemic. The same is also true of models that focus on modelling NPI behaviour, in populations where adaptive vaccinating behaviour could significantly alter model predictions of NPI practices.