Influence of temporary migration on the transmission of infectious diseases in a migrants' home village

Abstract

The number of temporary migrant workers from rural areas to urban areas in emerging market economies like China has increased dramatically since the early 1980s. Temporary migrant workers have been labeled as the major driving force for the rising incidence of infectious diseases in cities. However, it has not been well recognized that temporary migration indeed may have tremendous impacts on the spread of infectious diseases in migrants' home villages. In this paper, by proposing a delay differential equation model, we provide a framework to study the influence of temporary migration on the transmission of infectious diseases in a migrant workers' home village. The model is shown to admit a unique positive equilibrium which is locally asymptotically stable and is globally asymptotically stable under certain conditions. This implies that the disease always persists at a constant level. Considering tuberculosis as an example, we explore various disease prevention and control strategies numerically to demonstrate how migration related parameters affect the early outbreak of the disease. We find that a single control strategy, such as reducing the migration time period alone, has little effect on reducing the disease endemic level. For disease prevention and control, temporary migrant workers should be identified as the top target group, and a combination of several prevention strategies should be implemented.

Highlights

► A new model is proposed to study the influence of temporary migration on disease transmission in a migrants' home village. ► We find that the disease persists at a constant level. ► A single control strategy such as reducing the migration time period alone has little effect on reducing the disease endemic level. ► Temporary migrant workers should be identified as the top target group for disease control. ► A combination of several prevention strategies should be implemented for disease control.

1. Introduction

Emergence and re-emergence of infectious diseases is very complex, and many factors contribute to this complexity (Wilson, 1995). Among those frequently identified are mobility and travel, for which there are many examples: the proportion of new tuberculosis (TB) cases and HIV cases has been increasing recently in China in migrants who have complex mobility (Jia et al., 2008, Strand et al., 2007, Wang and Shen, 2009); severe acute respiratory syndrome (SARS) was introduced into Canada by a visitor to Hong Kong who returned to Toronto (Varia et al., 2003); air travel was blamed as the major risk factor for the introduction of measles in a highly vaccinated population (van Binnendijk et al., 2008).

In emerging market economies like China, there has been increasing population mobility, especially among a special group of people called migrant workers. Migrant workers (also called the floating population) emerged in China in the early 1980s when rural residents were allowed to seek employment in urban areas. Since then the number of migrant workers in China has been increasing dramatically. A report from the National Bureau of Statistics of China shows that there were a total of 145.33 million migrant workers in 2009, while the number in 1989 was only about 30 million. Migrant workers make a huge contribution to China's development, but they also bring many societal problems.

According to the 2009 report, among those 145.33 million migrant workers, 61.6% were young people (aged between 16 and 30), 76.5% did not finish their high school education and 51.1% received no occupational skills training. At a young age, lacking education and professional skills, most temporary migrant workers have to work in construction sites, restaurants, or crowded factories that require no or little experience. Temporary employment and China's current existing household registration system make it very difficult for migrant workers to settle down permanently in urban cities. Thus they usually cannot access the social welfare benefits and health care available to urban residents (Zhang, 2001). Unstable living and working conditions, being away from sexual partners, economic pressure, and limited awareness of infectious diseases all contribute to a high incidence of infectious diseases among migrant workers.

It is commonly believed that migrant workers, in contrast to non-migrant workers, are much more vulnerable to infectious diseases such as TB, HIV and sexually transmitted diseases (STDs) (Strand et al., 2007). For example, two-thirds of the 176 HIV cases reported by the Shanxi Province Epidemiological Station, were migrant workers (U.S. Embassy Beijing AIDS in China, 2000). It is reported that in 2006, the migrant population accounted for 1638 of 4088 TB cases in Beijing (Jia et al., 2008). Due to migrant workers' increasing mobility, there was a tenfold increase in the total incidence of syphilis over the past decade (Chen et al., 2007). For studies on migrant workers' vulnerability to infectious diseases, see Li et al., 2004, Yang, 2006 and references cited therein.

The link between temporary migration (especially the rural-to-urban migration) and the rising incidence of HIV/AIDS and other infectious diseases is well recognized by the Chinese government and the scholarly community (Yang, 2004). However, to the best of our knowledge, no work yet has focused on the spread of infectious diseases in the migrants' home village. Influenced by the Chinese traditional culture, migrant workers regularly return home for holiday family gatherings (especially during the period of Chinese New Year). This mobility pattern may cause an epidemic outbreak in their home village if some of the returning migrant workers were infected with an infectious disease while they were away from their home. For instance, returning migrants with the AIDS virus can unknowingly pass it onto their sexual partners (Lau and Thomas, 2001). In the meantime, migrant workers may also serve as a major vector for bringing the diseases to the urban areas when they return to work from their home village. Movement back and forth between rural and urban areas by temporary migrant workers is believed to be a key factor for the emergence and re-emergence of infectious diseases including TB and HIV/AIDS in China (Jia et al., 2008, Strand et al., 2007, Wang and Shen, 2009).

Due to the complex mobility patterns among migrant workers, it is very difficult to construct a mathematical model to study the overall influence of migration on the spread of infectious diseases. It is almost impossible to track each migrant worker's working place. However, it is certain that migrant workers return home regularly. In this paper, we focus on modeling the spread of infectious diseases in a migrants' home village. By proposing a new mathematical model, we aim to investigate the influence of temporary migration on the spread of infectious diseases in a migrant workers' home village assuming some migrant workers return home with an infection.

There has been some related work concerning special mobility patterns in disease modeling; see Arino and van den Driessche, 2006, Hsieh et al., 2007 and Wang and Zhao (2004) for disease models concerning movements between patches and Brauer and van den Driessche (2001) and Jia et al. (2008) for models considering immigration. In Brauer and van den Driessche (2001) some theoretical immigration models are proposed, and in Jia et al. (2008) an ordinary differential equation model is formulated to study how TB spreads among local residents and immigrants. Our model is given by a system of delay differential equations. For models using delay differential equations in ecology and disease modeling, see Klepac et al. (2007) and Wang, 2009, Wang, 2007 and references cited therein. We should point out that our general model can also be used to explore how international travel by tourists can initiate an epidemic when the tourists return to their home country.

The rest of the paper is organized as follows. Model formulation and main results are given in Section 2; numerical simulations are presented in Section 3; in Section 4 we discuss some of our analytical and numerical findings. The proofs of our main results are given in the Appendix.

2. Model formulation and main results

As in any compartmental disease transmission model (Brauer et al., 2008), we divide the total population in a migrants' home village (with size N(t)) into three disjoint classes of individuals: namely, susceptible, infectious and recovered, with class sizes denoted by S(t), I(t) and R(t), respectively. It is assumed that recruitment into the susceptible class is at a constant rate $\Lambda$. Let $\beta$ be the transmission coefficient, ${\mu }_S,{\mu }_I,{\mu }_R$ be the natural death rates for susceptible, infectious and recovered individuals, respectively, and $\gamma$ be the rate at which infectious individuals recover. Let d denote the death rate of migrants, and let m _S and m _R denote the rates at which susceptible and recovered individuals migrate, respectively. Let $\tau$ be the average time a migrant worker spends working away from home. It is also assumed that infectious individuals do not migrate. The flow diagram of our model is presented in Fig. 1 .

Fig. 1.

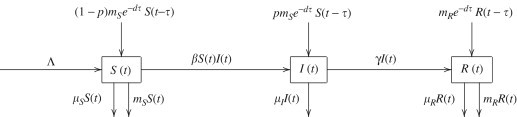
Flow diagram of an SIR model.

Assume that recovered individuals have permanent immunity. Let $p(\tau )$ denote the probability that a susceptible migrant worker returns home with an infection. Throughout, we assume that $p(\tau )$ is either a constant or satisfies the assumption (H): $p:[0,+\infty )\to [\mathrm{0,1})$ is nondecreasing and continuous. For example, we may take $p(\tau )=10\tau /(1000+\tau )$.

Assume that the force of infection is given by mass action, which is appropriate since the population in a village is relatively small (McCallum et al., 2001). Then the model is governed by the following system of delay differential equations:

$$\left\{\begin{array}{c}S\prime (t)=\Lambda -{\mu }_{S}S(t)-\beta S(t)I(t)-m_{S}S(t)+(1-p)m_S{e}^{-d\tau }S(t-\tau ),\hfill \\ I\prime (t)=\beta S(t)I(t)-\gamma I(t)-{\mu }_{I}I(t)+{\mathit{pm}}_S{e}^{-d\tau }S(t-\tau ),\hfill \\ R\prime (t)=\gamma I(t)-{\mu }_{R}R(t)-m_{R}R(t)+m_R{e}^{-d\tau }R(t-\tau ).\hfill \end{array}\right)$$ (2.1)

The associated initial conditions are $S(\theta )=\phi (\theta )\ge 0$ for $\theta \in [-\tau ,0]$, $I(0)>0$ and $R(\theta )\ge 0$ for $\theta \in [-\tau ,0]$. As the variable R does not appear in the first two equations, we can just consider the first two equations

$$\left\{\begin{array}{c}S\prime (t)=\Lambda -{\mu }_{S}S(t)-\beta S(t)I(t)-m_{S}S(t)+(1-p)m_S{e}^{-d\tau }S(t-\tau ),\hfill \\ I\prime (t)=\beta S(t)I(t)-\gamma I(t)-{\mu }_{I}I(t)+{\mathit{pm}}_S{e}^{-d\tau }S(t-\tau ),\hfill \end{array}\right)$$ (2.2)

with their associated initial conditions.

Our main results are given in the following theorem with the proofs postponed to the Appendix.

Theorem 2.1

Consider model (2.2) with the associated initial conditions. The model is well posed, i.e., there is a unique solution $(S(t),I(t))$ which exists globally, and S(t) and I(t) are positive and bounded for all $t>0$. There exists a unique positive equilibrium, $E=(S^{⁎},I^{⁎})$, which is locally asymptotically stable. Moreover, if

$$\frac{\beta \Lambda }{({\mu }_S+m_S-(1-p)m_S{e}^{-d\tau })(\gamma +{\mu }_I)}<1,$$ (2.3)

then the equilibrium E is globally asymptotically stable.

Remark 2.1

The above theorem implies that the disease always persists and the number of infectious individuals stabilizes at a constant level I ^⁎ as long as the probability of migrant workers returning home with an infection is not zero.

3. Numerical simulations and control strategies

As currently there is no data that can be directly applied to our model, we take parameter values from various sources.

3.1. Demographic parameters

Consider a typical village in western China with a total population of 1000 in 1999. Using China's natural population growth rates data from the World Bank, we can construct a population time series of this village as 1000, 1008, 1015, 1022, 1028, 1034, 1040, 1046, 1051, 1056 and 1062 from year 1999 to year 2009. Note that, without considering migration and disease induced death, the total population N(t) follows the differential equation

$$N\prime (t)=\Lambda -{\mu }_{S}N(t).$$ (3.1)

According to the World Bank data, the average life expectancy in China is about 72 years, which suggests ${\mu }_S=\frac{1}{72}=0.0139$ per year. Using the least-square method to fit the above population time series to (3.1) yields $\Lambda =20.69$. According to a report from the (China National Bureau of Statistics), on average, a temporary migrant worker works outside his/her home village for about 9.4 months, so we take $\tau =\frac{9.4}{12}=0.7833$ years. The death rate d during migration is assumed to be slightly larger than ${\mu }_S$ with d=0.016 per year (the parameter d could be much higher than ${\mu }_S$ in reality).

3.2. Disease related parameters

As TB is one of the major infectious diseases in rural areas of China (Wang and Shen, 2009), we select parameter values for TB from Blower et al. (1995) to demonstrate the influence of migration parameters and control strategies on the transmission of infectious disease in a migrants' home village. The time unit is one year. The parameters are: $\gamma =0.058$ per year, ${\mu }_I=0.1439$ per year.

3.3. Numerical simulations

We use the Matlab package DDE23 to obtain numerical solutions to system (2.2). We take m _S=0.3567 per year, which implies every year $1-e^{-m_S}\approx 30\%$ of the population from the village seeks temporary employment in other places. The proportion ranges from 10% to 40% in rural areas (China National Bureau of Statistics), so $m_S\in [0.10,0.51]$. With parameters $\beta =0.001$ per year per person, $p=10\tau /(1000+\tau )$, the resulting equilibrium level of infection is $I^{⁎}=84.71$. Fig. 2 indicates that $I(t)\to I^{⁎}$ as $t\to \infty$ and the equilibrium $E=(S^{⁎},I^{⁎})$ is stable.

Fig. 2.

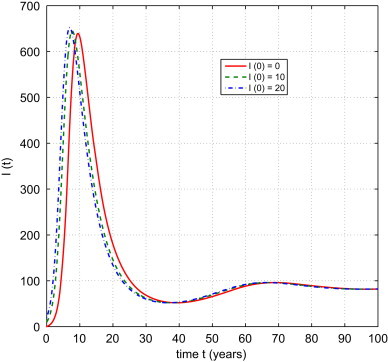
The I component of numerical solutions of (2.2). Three sets of initial conditions are used: (1) $S(\theta )=\varphi (\theta )$, $I(0)=0$; (2) $S(\theta )=\varphi (\theta ),I(0)=10$; (3) $S(\theta )=\varphi (\theta )$, $I(0)=20$; where $\varphi (\theta )=(\Lambda /{\mu }_S)-((\Lambda /{\mu }_S)-1000)e^{-{\mu }_S(\theta +\tau )}=1488.5-488.5e^{-0.0139(\theta +0.7833)}$ for $\theta \in [-0.7833,0]$.

3.4. Control strategies: numerical exploration

In this subsection we numerically evaluate several possible control strategies. It is reasonable to focus on the transient behavior (solution behavior during a relatively short time period) rather than the long time behavior. This is mainly because the control strategies may not be the same throughout a long time period and some model parameters may also have different values if the time period is too long. For example, more effective drugs may be developed, which will increase the value of $\gamma$, or the migration patterns could change with the development of the economy, which would change the values of m _S and $\tau$. In particular, we mainly examine the two transient numbers: $I_{\mathit{max}}≔\max \{I(t),t\ge 0\}$ (we use t _max to denote the peak time at which I _max is reached) and I(5), based on the following arguments:

• • I _max is certainly a very important indicator for any infectious disease as it gives the largest number of infectious individuals and describes the worst possible situation. It is of importance to examine how different strategies will affect I _max.
• •We evaluate the value of I(5) for different control strategies because in China, the government always comes up with 5-year plans. During those 5 years, there are no sudden policy changes. We compare the outcome of year 5 for each strategy, with the aim of providing public health authorities some theoretical guidance on designing their 5-year plans.

In what follows, to explore several possible control strategies, we use the same type of initial conditions: $S(\theta )=\varphi (\theta )=1488.5-488.5e^{-0.0139(\theta +\tau )}$ for $\theta \in [-\tau ,0]$ and I(0)=0. To have a comparison between different strategies, we take the solution of (2.2) with $\tau =0.7833,m_S=0.3567,\beta =0.001,p=p_{\mathit{ref}}=10\tau /(1000+\tau )$ as the reference solution. For the reference solution, $I_{\mathit{max}}\approx 639.28$, $I(5)\approx 157.65$, $t_{\mathit{max}}\approx 9.42$ and $I^{⁎}\approx 84.71$. These four numbers are listed in Table 1 for different representative strategies discussed below.

Table 1.

Comparison between different control strategies on transient numbers I_max, t_max, I(5) and the equilibrium level of infection I^⁎.

Representative strategy (ST)	Imax	tmax	I(5)	I⁎
ST I: $\tau =0.5$	604.49	9.84	108.31	86.07
ST II: mS=0.2	595.50	9.98	97.05	86.37
ST III: $p={\displaystyle \frac{1}{10}}{p}_{\mathit{ref}}$	639.25	12.29	18.74	84.19
ST IV: $\beta =0.0005$	351.93	17.91	31.54	68.52
ST V: q=0.5	630.30	10.34	85.43	83.07
ST VI: $q=0.2,\beta =0.0005,p={\displaystyle \frac{1}{10}}{p}_{\mathit{ref}}$	345.44	30.68	0.65	65.41
Reference solution:	639.28	9.42	157.65	84.71

Strategy I: Reduce the average migration period $\tau$. We fix $\beta =0.001,m_S=0.3567$ and vary $\tau$ with $p=10\tau /(1000+\tau )$. Fig. 3 shows that both I _max and $I(5)$ will be reduced under this control strategy, while I ^⁎ and t _max will be increased. In particular, compared to the reference solution, if $\tau$ drops from 0.7833 to 0.5, then I _max has a slight drop by $5.44\%$, t _max is increased by 0.42 years (about 5 months) and $I(5)$ drops by $31.3\%$, while in the long run, the equilibrium level of infection I ^⁎ is slightly increased by $1.61\%$.

Fig. 3.

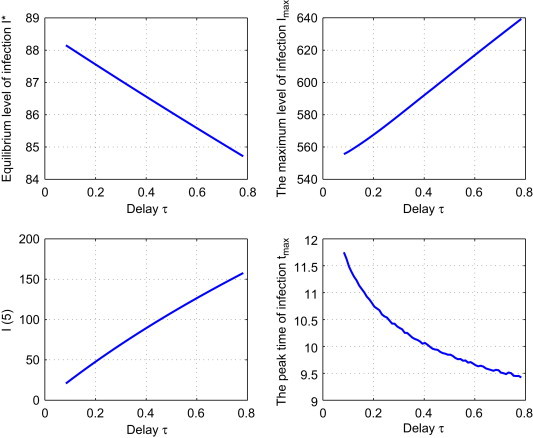
Effect of strategy I: the dependence of $I^{⁎}$, $I_{\mathit{max}}$, $I(5)$ and t_max on the control parameter $\tau$.

Strategy II: Reduce the migration rate m _S. We fix $\beta =0.001,\tau =0.7833,p=10\tau /(1000+\tau )$ and vary m _S. Fig. 4 shows that this strategy has the similar effect on I _max and I(5) as Strategy I does: as we decrease m _S, both I _max and I(5) decrease, while I ^⁎ and t _max increase. In comparison with the reference solution, if m _S drops to 0.2, then this results in a 6.85% decrease in I _max, a 1.5% increase in t _max, and a 38.44% decrease in I(5). In the long run, the equilibrium level of infection I ^⁎ is increased by 1.96%.

Fig. 4.

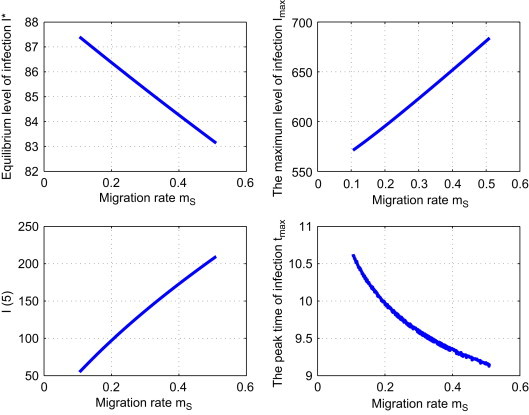
Effect of strategy II: the dependence of $I^{⁎}$, $I_{\mathit{max}}$, $I(5)$ and t_max on the control parameter m_S.

Strategy III: Reduce the probability p of having an infection for returning migrant workers. We fix $\beta =0.001$, m _S=0.3567 and $\tau =0.7833$. Let $p=p_k\tau /(1000+\tau )$ with p _k varying from 1 to 10. Fig. 5 shows that I _max will drop first and then increase, but the variation is very small. As p decreases, both I(5) and I ^⁎ decrease and t _max increases. If p drops 90% to $\tau /(1000+\tau )$, then the value of I _max remains almost the same but buys 2.87 additional years to attain I _max, while I(5) drops from 157.65 to 18.74, i.e., 88.1%. In the long run, the equilibrium level of infection I ^⁎ drops only 0.61%.

Fig. 5.

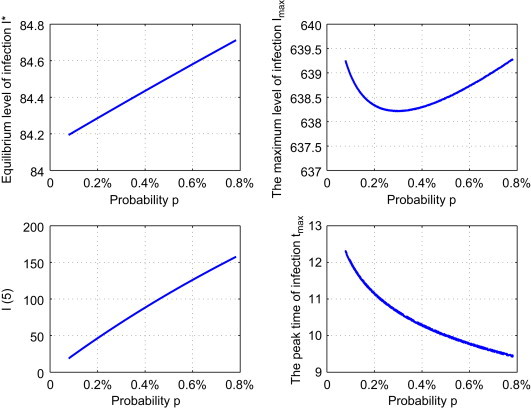
Effect of strategy III: the dependence of $I^{⁎}$, $I_{\mathit{max}}$, $I(5)$ and t_max on the control parameter p.

Strategy IV: Reduce the transmission rate $\beta$. We fix $\tau =0.7833,m_S=0.3567$, and $p=10\tau /(1000+\tau )$. We vary $\beta$ to get Fig. 6 . It is seen in Fig. 6 that I _max, I(5) and I ^⁎ all decrease and t _max increases as we decrease $\beta$. If $\beta$ is reduced by 50%, then I _max, I(5) and I ^⁎ will be reduced by 44.95%, 79.99%, 19.11%, respectively, and t _max will be increased by 8.49 years.

Fig. 6.

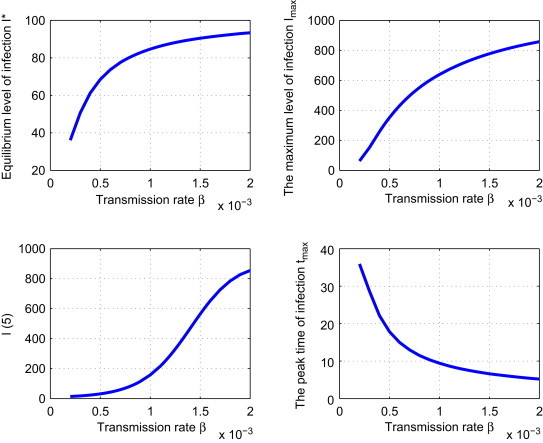
Effect of strategy IV: the dependence of $I^{⁎}$, $I_{\mathit{max}}$, $I(5)$ and t_max on the control parameter $\beta$.

Strategy V: Encourage returning migrant workers to have a medical examination and apply quarantine/isolation to confirmed infectious cases. Let Q stand for the number of returning migrant workers who are confirmed with infection and are placed in quarantine/isolation, and let $1-q$ be the success rate of confirming infectious cases. Then model (2.2) reduces to the following model:

$$\left\{\begin{array}{c}S\prime (t)=\Lambda -{\mu }_{S}S(t)-\beta S(t)I(t)-m_{S}S(t)+(1-p)m_S{e}^{-d\tau }S(t-\tau ),\hfill \\ I\prime (t)=\beta S(t)I(t)-\gamma I(t)-{\mu }_{I}I(t)+{\mathit{qpm}}_S{e}^{-d\tau }S(t-\tau ),\hfill \\ Q\prime (t)=(1-q){\mathit{pm}}_S{e}^{-d\tau }S(t-\tau )-{\mu }_{I}Q(t).\hfill \end{array}\right)$$ (3.2)

We fix $\tau =0.7833,m_S=0.3567,\beta =0.001$, and $p=10\tau /(1000+\tau )$. Varying q in (3.2), we obtain Fig. 7 . The impact of this strategy is similar to that of Strategy IV: as $1-q$ increases, I _max, I(5) and I ^⁎ all decrease and t _max increases. If q=0.5, then $I_{\mathit{max}},I(5),I^{⁎}$ will drop 1.4%, 45.81%, 1.94% and t _max is increased to 10.34 years.

Fig. 7.

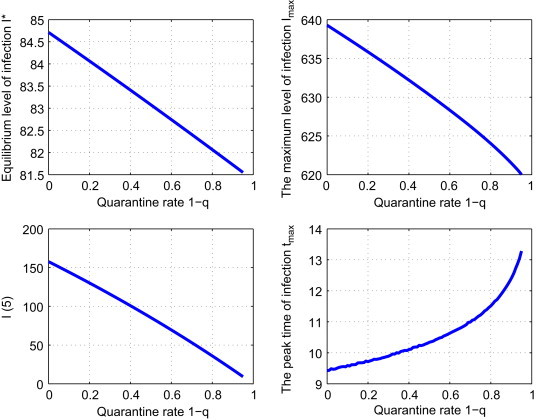
Effect of strategy V: the dependence of $I^{⁎}$, $I_{\mathit{max}}$, $I(5)$ and t_max on the control parameter $1-q$.

Strategy VI: Combine Strategies III, IV and V. In Fig. 8 , the success quarantine/isolation rate is $1-q=80\%$, the disease transmission coefficient is $\beta =0.0005$, the probability of returning migrants being infected is $p=\tau /(1000+\tau )$. Compared to the reference solution, the disease transmission rate is reduced by 50%, the probability of returning migrants being infectious drops 90%. Under these efforts, I _max drops 46% (changes from 639.28 to 345.44), and t _max is increased from 9.42 to 30.68. I(5) drops dramatically from 157.65 to 0.65, while I ^⁎ experiences a 23% drop (see Table 1).

Fig. 8.

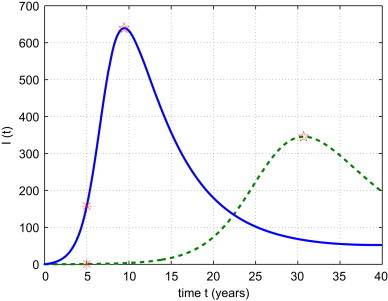
Solid curve is the reference solution from (2.2) with $\tau =0.7833,m_S=0.3567,\beta =0.001,p=10\tau /(1000+\tau )$, the dashed curve is the solution of model (3.2) with a combined prevention strategy: $\tau =0.7833,m_S=0.3567,q=0.2,\beta =0.0005$ and $p=\tau /(1000+\tau )$.

4. Discussion and conclusion

In this paper, we have proposed a delay differential equation model to study the influence of temporary migration on disease transmission in a migrant workers’ home village. In the model, we have assumed that a fraction of returning migrant workers acquired infection when they were away from their home village. This model particularly applies to the huge migrant worker population in China. There has been evidence that migrant workers are more vulnerable to infectious diseases especially TB, HIV/AIDs and STDs because of migrant workers' high risk behaviors (Grusky et al., 2002, Li et al., 2004, Yang, 2006, Yang, 2004).

Theorem 2.1 shows that there is a unique equilibrium E in our model, which is locally asymptotically stable and globally asymptotically stable if (2.3) is satisfied (see Remark A.1 for a weaker condition). This indicates that there is no disease free equilibrium and the disease remains endemic as long as there are cases in temporary migrants. The fact is that the proportion of new cases in migrants has been increasing year by year. It is reported that in 2006, the migrant population accounted for 1638 of 4088 TB cases in Beijing (Jia et al., 2008). Numerical simulations using parameter values derived from available data and TB-related parameters from the literature confirmed that returning infectious migrant workers can cause huge outbreaks in their home village.

To control the spread of infectious diseases in a migrants' home village, our numerical simulations (Fig. 3, Fig. 4) indicate that reducing the temporary migration period $\tau$, or limiting the migration rate m _S, is not very effective. Indeed these two strategies (Strategies I and II) are not practical as the government cannot have a regulation determining the period $\tau$ that a migrant worker can work, and it is not possible to control the migration rate by any regulation. The fact is that both $\tau$ and m _S seem to have an increasing trend. The most effective measure is a combination of Strategies III, IV and V, that is to reduce three key parameters: p, $\beta$, and q in (3.2). To this end, the following efforts should be encouraged:

• •The government should improve migrant workers' working and living conditions, offer free or affordable health care, educate them with knowledge of infectious diseases, and encourage their employers to offer free and regular medical examinations as well as suitable medical coverage. This will reduce the value of p.
• •The local government should encourage returning migrant workers to have medical examinations, offer needed help for quarantine/isolation processes, and have regular education campaigns on basic knowledge and awareness of infectious diseases such as TB, HIV/AIDS and STDs. This will reduce the values of $\beta$ and q.

It is assumed in our model that infectious individuals do not migrate but stay at home for treatment. Either due to economic pressure, or due to not knowing infection status, some infectious individuals may still migrate to urban areas. This may lead to re-emergence of rather under controlled diseases or emergence of new diseases in urban areas. But because of the current existing household registration system, different jobs and working conditions and different backgrounds, many temporary migrant workers are isolated, not only residentially, but also socially and culturally, from the “mainstream” society in the place where they temporarily live and work (Yang, 2006). A report from the Beijing Municipal Health Bureau shows that the total annual new registered active TB cases increased dramatically from 2000 through 2006, but the cases among the permanent residents only increased slightly (Beijing Research Institute for TB Control Work on the prevention of TB in Beijing). Thus, from a disease prevention and control point of view, temporary migrants should be identified as the target group. Due to migrants' high mobility, lack of knowledge about infectious diseases, poor living and working conditions, and increased (sexual) risk behaviors, a combination of several effective interventions should be implemented.

It is worth pointing out that it is extremely useful for the government to collect related data for temporary migration. Each village can easily collect information about each migrant worker such as age, gender, health status (from medical examinations before leaving and after returning), education level, leaving dates and returning dates, cities he/she has been, working conditions, etc. Only with accurate data can modelers provide more accurate modeling and analysis and thus advise the government on more effective control strategies.

This framework can also be employed to study how temporary cross-border travel can influence the spread of infectious diseases in a travelers' home community. It is possible for some travelers to become infected when they return home and there could be a spread among people who had close contacts with the infectious returning travelers. For example, all 28 confirmed measles cases reported between 1 January and 30 April 2008 in Canada were either imported or import-related (Lipskie and Varughese, 2008). One Ontario case had arrived from Pakistan 10 days prior to rash onset. Two other cases detected in Ontario were un-immunized siblings visiting from Switzerland where there was an ongoing measles outbreak. Our model analysis suggests that the prevention of a local disease outbreak is helped if each traveler has a medical examination after returning home.

Appendix A. Proof of Theorem 2.1

To prove our main result, we first introduce a lemma which can be easily derived from the result of Example 2.6 in Hale and Verduyn Lunel (1993, p. 134).

Lemma A.1

Consider the linear delay differential equation

$$x\prime (t)=\lambda -{\delta }_{1}x(t)+{\delta }_{2}x(t-\tau ).$$

If $\left|{\delta }_2\right|<{\delta }_1$, then

$$\underset{t\to \infty }{\lim }x(t)=x^{⁎}=\frac{\lambda }{{\delta }_1-{\delta }_2}.$$

A.1. Well posedness of the model

The existence and uniqueness of the solution follows directly from the step method for delay differential equations (Hale and Verduyn Lunel, 1993). Next we show that S(t) and I(t) are positive for $t\in (0,\tau ]$. Suppose not, then there must be a first time $t_1\in (0,\tau ]$ such that $S(t_1)I(t_1)=0$, which yields either (i), $I(t_1)=0$ and $S(t)\ge 0$ for $t\in [0,t_1]$ or (ii), $S(t_1)=0$ and $I(t)\ge 0$ for $t\in [0,t_1]$. For case (i), $I\prime (t)\ge -(\gamma +{\mu }_I)I(t)$ for $t\in [0,t_1]$. Thus, $I(t_1)\ge I(0)e^{-(\gamma +{\mu }_I)t_1}$ which is in contradiction with $I(t_1)=0$. For case (ii), $S\prime (t_1)=\Lambda +(1-p)m_S{e}^{-d\tau }S(t_1-\tau )\ge \Lambda >0$. On the other hand, to have $S(t_1)=0$, $S\prime (t_1)\le 0$ must be true as $S(0)>0$. This is a contradiction. In a similar fashion, we can show S(t) and I(t) are positive for $t>0$.

Next we show both S(t) and I(t) are bounded. Note that $S(t)>0$ and $I(t)>0$ for $t>0$. Then the first equation of system (2.2) gives

$$S\prime (t)\le \Lambda -({\mu }_S+m_S)S(t)+(1-p)m_S{e}^{-d\tau }S(t-\tau ).$$

Let z(t) be the solution of

$$z\prime (t)=\Lambda -({\mu }_S+m_S)z(t)+(1-p)m_S{e}^{-d\tau }z(t-\tau ),$$

with the initial condition $z(\theta )=S(\theta )$ for $\theta \in [-\tau ,0],$ then $S(t)\le z(t)$ for $t\ge 0$ by the standard comparison theorem for delay differential equations (Smith, 1995). Clearly, ${\mu }_S+m_S>(1-p)m_S{e}^{-d\tau }$ and it follows from Lemma A.1 that

$$\underset{t\to \infty }{\lim }z(t)=\frac{\Lambda }{{\mu }_S+m_S-(1-p)m_S{e}^{-d\tau }}:=U_1^S.$$

This implies that

$$\underset{t\to \infty }{\lim \sup }S(t)\le \underset{t\to \infty }{\lim \sup }z(t)=U_1^S$$ (A.1)

and thus S(t) is bounded. For any $ϵ>0$, there exists $T_1>\tau$ such that

$$S(t)\le U_1^S+ϵ\mathrm{for}t\ge T_1.$$ (A.2)

Let $n(t)=S(t)+I(t)$. It then follows from (2.2) and (A.2) that

$$n\prime (t)=\Lambda -{\mu }_{S}S(t)-m_{S}S(t)-\gamma I(t)-{\mu }_{I}I(t)+m_S{e}^{-d\tau }S(t-\tau )\le \Lambda -\min ({\mu }_S+m_S,\gamma +{\mu }_I)n(t)+m_S{e}^{-d\tau }(U_1^S+ϵ)\mathrm{for}t\ge T_1.$$

By the same argument used to show the boundedness of S(t), one can show that

$$\underset{t\to \infty }{\lim \sup }n(t)\le \frac{\Lambda +m_S{e}^{-d\tau }{U}_1^S}{\min ({\mu }_S+m_S,\gamma +{\mu }_I)}≔n^{⁎}.$$ (A.3)

This shows that n(t) is bounded and hence I(t) is bounded.

A.2. Existence and uniqueness of the equilibrium

For convenience, we let $a=\gamma +{\mu }_I,k={\mu }_S+m_S-m_S{e}^{-d\tau },b={\mathit{pm}}_S{e}^{-d\tau },c=(1-p)m_S{e}^{-d\tau }$, then $a>0,k>0,b\ge 0,c>0$ and $\Delta =[\Lambda \beta -a(b+k){]}^2+4\Lambda \beta \mathit{ab}>0$. It follows from system (2.2) that the equilibrium $(S^{⁎},I^{⁎})$ satisfies

$$\beta I·\frac{\Lambda -\mathit{aI}}{k}-\mathit{aI}+b·\frac{\Lambda -\mathit{aI}}{k}=0,$$

which gives

$$a\beta I^2-[\Lambda \beta -a(b+k)]I-\Lambda b=0.$$ (A.4)

Note that since $\Delta =[\Lambda \beta -a(b+k){]}^2+4\Lambda \beta \mathit{ab}>0$, Eq. (A.4) has only one positive real root denoted by

$$I^{⁎}=\frac{\Lambda \beta -a(b+k)+\sqrt{\Delta }}{2a\beta },$$

which immediately yields

$$S^{⁎}=\frac{\Lambda -{\mathit{aI}}^{⁎}}{k}=\frac{\Lambda \beta +a(b+k)-\sqrt{\Delta }}{2k\beta }.$$

A.3. Local stability

Let $S(t)=x(t)+S^{⁎}$ and $I(t)=y(t)+I^{⁎}$, then x(t) and y(t) satisfy the following equations:

$$\left\{\begin{array}{c}x\prime (t)=-({\mu }_S+m_S)x(t)-\beta (I^{⁎}+y(t))x(t)+(1-p)m_S{e}^{-d\tau }x(t-\tau )-\beta {\mathit{aS}}^{⁎}y(t),\hfill \\ y\prime (t)=\beta (I^{⁎}+y(t))x(t)+{\mathit{pm}}_S{e}^{-d\tau }x(t-\tau )+(\beta S^{⁎}-a)y(t).\hfill \end{array}\right)$$ (A.5)

Linearizing the Eq. (A.5) about (0,0) yields

$$\left\{\begin{array}{c}x\prime (t)=-({\mu }_S+m_S+\beta I^{⁎})x(t)+(1-p)m_S{e}^{-d\tau }x(t-\tau )-\beta S^{⁎}y(t),\hfill \\ y\prime (t)=\beta I^{⁎}x(t)+m_S{\mathit{pe}}^{-d\tau }x(t-\tau )+(\beta S^{⁎}-a)y(t).\hfill \end{array}\right)$$ (A.6)

Thus, the characteristic equation of (A.6) is

$$h(z)=z^2+a_{1}z+a_2+(a_3+a_{4}z)e^{-\tau z}=0,$$ (A.7)

where $a_1={\mu }_S+m_S+\beta I^{⁎}+(a-\beta S^{⁎}),a_2=({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})+{\beta }^2{I}^{⁎}{S}^{⁎},a_3=b\beta S^{⁎}-c(a-\beta S^{⁎})$ and $a_4=-c$.

We first consider the special case with $\tau =0$. In this case $b=c=0$, $a_3=a_4=0$ and Eq. (A.7) reduces to

$$z^2+a_{1}z+a_2=0.$$ (A.8)

It is easy to compute two roots of (A.8) and both have negative real parts. Notice that the assumption (ii) of Beretta and Kuang (2002, p. 1146) holds, and hence no zero emerges from infinity. That is, $\mathrm{Re}(z)<+\infty$ for any zero of h(z). Therefore, as the delay $\tau$ increases, the zeros of h(z) can cross the imaginary axis only through a pair of nonzero purely imaginary zeros. Let $z=i\omega$ with $\omega >0$ be a purely imaginary zero of h(z), then

$${\omega }^2-{\mathit{ia}}_1\omega -a_2=(a_3+{\mathit{ia}}_4\omega )e^{-i\tau \omega }.$$

Taking the modules of both sides of the above equation gives

$$|{\omega }^2-{\mathit{ia}}_1\omega -a_2|=|(a_3+{\mathit{ia}}_4\omega )|,$$

which yields

$$({\omega }^2-a_2{)}^2+a_1^2{\omega }^2=a_3^2+a_4^2{\omega }^2.$$

Let $y={\omega }^2$, then y satisfies

$$y^2+b_{1}y+b_2=0,$$ (A.9)

with $b_1=a_1^2-a_4^2-2a_2$ and $b_2=a_2^2-a_3^2$.

If Eq. (A.9) has no positive root, then $h(z)=0$ has no nonzero purely imaginary roots, which implies that all roots of $h(z)=0$ have negative real parts for all $\tau \ge 0$ and the equilibrium is locally asymptotically stable. Thus the local stability of the equilibrium E follows from the following two lemmas.

Lemma A.2

Assume $b_2\ge 0$, then the equilibrium E is locally asymptotically stable provided one of the following conditions holds:

• (i) $b_1\ge 0$;
• (ii)
  $b_1<0$ and the inequality

  $$b_1^2<4b_2$$ (A.10)

  holds, where b ₁ and b ₂ are as in Eq. (A.9).

Proof

The inequalities $b_1\ge 0$ and $b_2>0$ imply that Eq. (A.9) has no positive real roots. If $b_1<0$ and inequality (A.10) is true, then all roots of Eq. (A.9) are complex with positive real parts. Therefore, $h(z)=0$ has no nonzero purely imaginary roots, which implies that all roots of $h(z)=0$ have negative real parts for all $\tau \ge 0$ and the equilibrium E is locally asymptotically stable. □

Lemma A.3

The following statements hold:

• (iii) $b_2>0$;
• (iv) If $b_1<0$, then $b_1^2<4b_2$.

Proof

Direct calculations give

$$a_3^2=b^2{\beta }^2{S^{⁎}}^2+c^2(a-\beta S^{⁎}{)}^2-2\mathit{bc}(a-\beta S^{⁎})$$

and

$$a_2^2=[({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})+{\beta }^2{I}^{⁎}{S}^{⁎}{]}^2=({\mu }_S+m_S+\beta I^{⁎}{)}^2(a-\beta S^{⁎}{)}^2+{\beta }^4{I^{⁎}}^2{S^{⁎}}^2+2{\beta }^2{I}^{⁎}{S}^{⁎}({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎}).$$

Thus

$$b_2=a_2^2-a_3^2=2\mathit{bc}(a-\beta S^{⁎})+{\beta }^4{I^{⁎}}^2{S^{⁎}}^2+{\beta }^2{I}^{⁎}{S}^{⁎}({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})+[({\mu }_S+m_S+\beta I^{⁎}{)}^2-c^2](a-\beta S^{⁎}{)}^2+{\beta }^2{S}^{⁎}[({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})I^{⁎}-b^2{S}^{⁎}]>{\beta }^2{S}^{⁎}[({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})I^{⁎}-b^2{S}^{⁎}].$$

To show $b_2>0$, one only needs to show

$$({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})I^{⁎}-b^2{S}^{⁎}>0.$$ (A.11)

Note that $S^{⁎}={\mathit{aI}}^{⁎}/(\beta I^{⁎}+b)$ and $b={\mathit{pm}}_S{e}^{-d\tau }<m_S$, thus

$$({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})I^{⁎}-b^2{S}^{⁎}=({\mu }_S+m_S+\beta I^{⁎})I^{⁎}·\frac{\mathit{ab}}{\beta I^{⁎}+b}-\frac{b^2{\mathit{aI}}^{⁎}}{\beta I^{⁎}+b}=\frac{{\mathit{abI}}^{⁎}}{\beta I^{⁎}+b}[{\mu }_S+m_S+\beta I^{⁎}-b]>0.$$

For (iv), condition $b_1<0$ implies $a_1^2-a_4^2-2a_2<0$. Obviously, $a_1^2-a_4^2>0$ and $(a_1^2-a_4^2)(a_1^2-a_4^2-2a_2)<0$. Thus

$$b_1^2-4b_2=(a_1^2-a_4^2-2a_2{)}^2-4a_2^2+4a_3^2=(a_1^2-a_4^2{)}^2-4a_2(a_1^2-a_4^2)+4a_3^2=(a_1^2-a_4^2)(a_1^2-a_4^2-2a_2)+2[2a_3^2-a_2(a_1^2-a_4^2)]<2[2a_3^2-a_2(a_1^2-a_4^2)].$$

It then suffices to show that $2a_3^2-a_2(a_1^2-a_4^2)\le 0$. Since

$$a_1^2-a_4^2=({\mu }_S+m_S+\beta I^{⁎}+a-\beta S{)}^2-c^2=({\mu }_S+m_S+\beta I^{⁎}{)}^2+(a-\beta S^{⁎}{)}^2-c^2+2({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})$$

and

$$a_2(a_1^2-a_4^2)=({\mu }_S+m_S+\beta I^{⁎}{)}^3(a-\beta S^{⁎})+({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎}{)}^3+2({\mu }_S+m_S+\beta I^{⁎}{)}^2(a-\beta S^{⁎}{)}^2+({\mu }_S+m_S+\beta I^{⁎}{)}^2{\beta }^2{S}^{⁎}{I}^{⁎}+{\beta }^2{S}^{⁎}{I}^{⁎}(a-\beta S^{⁎}{)}^2+2({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎}){\beta }^2{S}^{⁎}{I}^{⁎}-c^2{\beta }^2({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})-c^2{\beta }^2{S}^{⁎}{I}^{⁎},$$

we obtain

$$2a_3^2-a_2(a_1^2-a_4^2)=-4\mathit{bc}\beta S^{⁎}(a-\beta S^{⁎})-{\beta }^2{S}^{⁎}{I}^{⁎}(a-\beta S^{⁎}{)}^2-({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎}{)}^2+2(a-\beta S^{⁎}{)}^2[c^2-({\mu }_S+m_S+\beta I^{⁎}{)}^2]+{\beta }^2{S}^{⁎}{I}^{⁎}[c^2-({\mu }_S+m_S+\beta I^{⁎}{)}^2]+(a-\beta S^{⁎})({\mu }_S+m_S+\beta I^{⁎})[c^2-({\mu }_S+m_S+\beta I^{⁎}{)}^2]+2{\beta }^2{S}^{⁎}[b^2{S}^{⁎}-({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})I^{⁎}]<[c^2-({\mu }_S+m_S+\beta I^{⁎}{)}^2][2(a-\beta S^{⁎}{)}^2+{\beta }^2{S}^{⁎}{I}^{⁎}+(a-\beta S^{⁎})({\mu }_S+m_S+\beta I^{⁎})]+2{\beta }^2{S}^{⁎}[b^2{S}^{⁎}-({\mu }_S+m_S+\beta I^{⁎})(a-\beta S^{⁎})I^{⁎}]<0.\square$$

A.4. Global stability

It is shown in (A.1) that

$$\underset{t\to \infty }{\lim \sup }S(t)\le U_1^S=\frac{\Lambda }{{\mu }_S+m_S-c},$$

and for any $ϵ>0$, there exists $T_1>\tau$ such that $S(t)\le U_1^S+ϵ$ for $t\ge T_1$. This, together with the second equation of system (2.2), yields

$$I\prime (t)\le \beta (U_1^S+ϵ)I(t)-\gamma I(t)-{\mu }_{I}I(t)+{\mathit{pm}}_S{e}^{-d\tau }(U_1^S+ϵ),t\ge T_1+\tau =-(\gamma +{\mu }_I-\beta (U_1^S+ϵ))I(t)+b(U_1^S+ϵ).$$

If follows from condition (2.3) that $\gamma +{\mu }_I-\beta (U_1^S+ϵ)>0,\mathrm{for}\mathrm{small}ϵ$. Thus, by comparison, we have

$$\underset{t\to \infty }{\lim \sup }I(t)\le \frac{b(U_1^S+ϵ)}{\gamma +{\mu }_I-\beta (U_1^S+ϵ)}.$$

Since $ϵ$ can be arbitrarily small, we then have

$$\underset{t\to \infty }{\lim \sup }I(t)\le \frac{{\mathit{bU}}_1^S}{\gamma +{\mu }_I-\beta U_1^S}≔U_1^I.$$

For small $ϵ>0$, there exists $T_2>T_1+\tau$ such that $I(t)\le U_1^I+ϵ$ for $t\ge T_2$. It follows from this fact and the first equation of system (2.2) that for $t\ge T_2$

$$S\prime (t)\ge \Lambda -{\mu }_{S}S(t)-\beta (U_1^I+ϵ)S(t)-m_{S}S(t)+(1-p){\mathit{me}}^{-d\tau }S(t-\tau )=\Lambda -({\mu }_S+m_S+\beta (U_1^I+ϵ))S(t)+\mathit{cS}(t-\tau ).$$

Again, by comparison and Lemma A.1, and noting that $ϵ$ can be arbitrarily small, we have

$$\underset{t\to \infty }{\lim \inf }S(t)\ge \frac{\Lambda }{{\mu }_S+m_S-c+\beta U_1^I}≔L_1^S.$$

Thus, there exists $T_3>T_2+\tau$, such that $S(t)\ge L_1^S-ϵ$ for $t\ge T_3$. This, together with the second equation of system (2.2), gives

$$I\prime (t)\ge -(\gamma +{\mu }_I-\beta (L_1^S-ϵ))I(t)+b(L_1^S-ϵ),t\ge T_3+\tau ,$$

which implies that

$$\underset{t\to \infty }{\lim \inf }I(t)\ge \frac{{\mathit{bL}}_1^S}{\gamma +{\mu }_I-\beta L_1^S}≔L_1^I>0.$$

Hence for a small $ϵ>0$, there exists $T_4>T_3$ such that $I(t)\ge L_1^I-ϵ$ for $t\ge T_4$. It then follows from the first equation of system (2.2) that

$$S\prime (t)\le \Lambda -({\mu }_S+m_S+\beta (L_1^I-ϵ))S(t)+\mathit{cS}(t-\tau ),$$

which yields

$$\underset{t\to \infty }{\lim \sup }S(t)\le U_2^S≔\frac{\Lambda }{{\mu }_S+m_S-c+\beta L_1^I}<U_1^S.$$

In a similar fashion, we can show that

$$\underset{t\to \infty }{\lim \sup }I(t)\le U_2^I≔\frac{{\mathit{bU}}_2^S}{\gamma +{\mu }_I-\beta U_2^S}<U_1^I,$$

$$\underset{t\to \infty }{\lim \inf }S(t)\ge L_2^S≔\frac{\Lambda }{{\mu }_S+m_S-c+\beta U_2^I}>L_1^S$$

and

$$\underset{t\to \infty }{\lim \inf }I(t)\ge L_2^I≔\frac{{\mathit{bL}}_2^S}{\gamma +{\mu }_I-\beta L_2^S}>L_1^I.$$

Repeating this procedure, we obtain four sequences $\{U_k^S,U_k^I,L_k^S,L_k^I\},k=\mathrm{2,3},\dots$ with

$$U_{k+1}^S≔\frac{\Lambda }{{\mu }_S+m_S-c+\beta L_k^I}<U_k^S,$$

$$U_{k+1}^I≔\frac{{\mathit{bU}}_{k+1}^S}{\gamma +{\mu }_I-\beta U_{k+1}^S}<U_k^I,$$

$$L_{k+1}^S≔\frac{\Lambda }{{\mu }_S+m_S-c+\beta U_{k+1}^I}>L_k^S,$$

$$L_{k+1}^I=\frac{{\mathit{bL}}_{k+1}^S}{\gamma +{\mu }_I-\beta L_{k+1}^S}>L_k^I$$ (A.12)

and

$$L_k^S\le \underset{t\to \infty }{\lim \inf }S(t)\le \underset{t\to \infty }{\lim \sup }S(t)\le U_k^S,$$

$$L_k^I\le \underset{t\to \infty }{\lim \inf }I(t)\le \underset{t\to \infty }{\lim \sup }I(t)\le U_k^I.$$ (A.13)

This shows that these four sequences are all bounded and monotone, hence

$$\underset{t\to \infty }{\lim }{U}_k^S=U^S,\underset{t\to \infty }{\lim }{U}_k^I=U^I,\underset{t\to \infty }{\lim }{L}_k^S=L^S,\underset{t\to \infty }{\lim }{L}_k^I=L^I,$$

exist. It then follows from (A.12) that

$$U^S=\frac{\Lambda }{{\mu }_S+m_S-c+\beta L^I},$$

$$U^I=\frac{{\mathit{bU}}^S}{\gamma +{\mu }_I-\beta U^S},$$

$$L^S=\frac{\Lambda }{{\mu }_S+m_S-c+\beta U^I},$$

$$L^I=\frac{{\mathit{bL}}^S}{\gamma +{\mu }_I-\beta L^S}.$$ (A.14)

Solving the above system, we obtain

$$U^S=L^S=S^{⁎},U^I=L^I=I^{⁎},$$

which yields

$$\underset{t\to \infty }{\lim }I(t)=I^{⁎},\underset{t\to \infty }{\lim }S(t)=S^{⁎}.$$

Remark A.1

Note that condition (2.3) is equivalent to

$$\gamma +{\mu }_I>\beta U_1^S.$$

If we replace $U_1^I$ by n ^⁎ defined in (A.3) in the proof, then condition (2.3) can be improved by a weaker condition

$$\gamma +{\mu }_I>\beta U_2^S,$$ (A.15)

where

$$U_2^S=\frac{\Lambda }{{\mu }_S+m_S-c+\beta L_1^I},$$

with

$$L_1^I=\frac{{\mathit{bL}}_1^S}{\gamma +{\mu }_I-\beta L_1^S},L_1^S=\frac{\Lambda }{{\mu }_S+m_S-c+\beta U_1^I},U_1^I=n^{⁎}.$$