Superinfection and cell regeneration can lead to chronic viral coinfections

Highlights

• •Clinical researchers have found that coinfection of the respiratory tract can cause distinct disease outcome, sometimes leading to long-lasting infection, compared to single viral infection.
• •The impact of coinfections in human respiratory tract have not yet been evaluated in either theoretical or experimental studies on a large scale.
• •A few experiments confirm that different respiratory viruses can infect the same cell (superinfection).
• •Superinfection alone cannot cause long-lasting viral coinfections.
• •The combined mechanism of superinfection and cell regeneration provides a plausible mechanism for chronic viral coinfections.

Abstract

Molecular diagnostic techniques have revealed that approximately 43% of the patients hospitalized with influenza-like illness are infected by more than one viral pathogen, sometimes leading to long-lasting infections. It is not clear how the heterologous viruses interact within the respiratory tract of the infected host to lengthen the duration of what are usually short, self-limiting infections. We develop a mathematical model which allows for single cells to be infected simultaneously with two different respiratory viruses (superinfection) to investigate the possibility of chronic coinfections. We find that a model with superinfection and cell regeneration has a stable chronic coinfection fixed point, while superinfection without cell regeneration produces only acute infections. This analysis suggests that both superinfection and cell regeneration are required to sustain chronic coinfection via this mechanism since coinfection is maintained by superinfected cells that allow slow-growing infections a chance to infect cells and continue replicating. This model provides a possible mechanism for chronic coinfection independent of any viral interactions via the immune response.

1. Introduction

Viral infections are responsible for almost 80% of acute respiratory tract diseases (Malekshahi et al., 2017). While the growth dynamics of single viruses have been well-characterized through both mathematical modeling and experimental studies for several viral diseases (Baccam, Beauchemin, Macken, Hayden, Perelson, 2006, González-Parra, Dobrovolny, 2015, González-Parra, Dobrovolny, Aranda, Chen-Charpentier, RAG, 2018, Neumann, Lam, Dahari, Gretch, Wiley, Layden, et al., 1998, Perelson, Neumann, Markowitz, Leonard, Ho, 1996), little is known about the kinetics of coinfection, i.e. simultaneous infection with more than one type of virus. Prevalence of viral coinfections has been identified in many studies, reporting a highly variable detection level of 14–70% in hospitalized patients with respiratory infectious viruses such as influenza A virus (IAV), influenza B virus (IBV), respiratory syncytial virus (RSV), human rhinovirus (hRV), adenovirus (AdV), human enterovirus (hEV), human metapneumovirus (hMPV), coronavirus (CoV), parainfluenza virus (PIV), and human bocavirus (hBoV) (Achten, Wu, Bont, Blanken, Gebretsadik, Chappell, et al., 2017, Asner, Rose, Petrich, Richardson, Tran, 2015, Kenmoe, Tchendjou, Vernet, Tetang, Mossus, Ripa, et al., 2016, Pretorius, Madhi, Cohen, Naidoo, Groome, Moyes, et al., 2012, Scotta, Chakr, de Moura, Becker, de Souza, Jones, et al., 2016).

Although the prognostic significance of coinfection is still poorly understood, there is growing evidence in clinical studies that respiratory tract coinfection affects severity of the infectious disease (Costa, DAO, da Silveira, Neto, de Paula, TFMS, et al., 2014, Mazur, Bont, Cohen, Cohen, von Gottberg, Groome, et al., 2017, Scotta, Chakr, de Moura, Becker, de Souza, Jones, et al., 2016). Many clinical surveys on respiratory coinfections find that the presence of more than one viral infection at the same time causes not only increased disease severity compared to single viral infections (Aberle, Aberle, Pracher, Hutter, Kundi, Popow-Kraupp, 2005, Choi, Chung, Kim, 2015) but also contributes to acute exacerbation and longer hospital stay among patients with pulmonary diseases such as asthma (GGM et al., 2017), chronic obstructive pulmonary disease (COPD) (Dai et al., 2015) and bronchiolitis (Richard et al., 2008). For example, several studies on pediatric coinfections with RSV, IAV, AdV and HRV find that children with lower respiratory tract coinfection stay longer in hospital (Aberle, Aberle, Pracher, Hutter, Kundi, Popow-Kraupp, 2005, Costa, DAO, da Silveira, Neto, de Paula, TFMS, et al., 2014, Martin, Fairchok, Stednick, Kuypers, Englund, 2013, Mazur, Bont, Cohen, Cohen, von Gottberg, Groome, et al., 2017), suffer higher incidence of fever (Calvo et al., 2008) and require life threatening disease supports like mechanical ventilation and ICU admission (Mazur et al., 2017) in comparison to children infected singly with RSV, IAV, AdV or HRV. Besides children, there is evidence that coinfections can be more severe in adults. One study finds that hospitalized adult patients experience chronic lung disease when infected with multiple respiratory viruses (Choi et al., 2015). There is some evidence that respiratory infections can be particularly long-lasting, over a year in some cases, in immunocompromised patients (Dobrovolny, Reddy, Kamal, Rayner, CAA, 2013, Egli, Bucher, Dumoulin, Stern, Buser, Bubendorf, et al., 2012, Loubet, Voiriot, Houhou-Fidouh, Neuville, Bouadma, Lescure, et al., 2017), with more recent studies indicating that at least some of these long-lasting infections are viral coinfections (Egli, Bucher, Dumoulin, Stern, Buser, Bubendorf, et al., 2012, Loubet, Voiriot, Houhou-Fidouh, Neuville, Bouadma, Lescure, et al., 2017). Respiratory viruses interact in unique ways within different age groups and with different viral combinations which can result in altered disease severity compared to how they behave in single infections.

To our knowledge, few experimental studies on coinfection are conducted in vivo or in vitro with different respiratory infectious viruses. Existing studies of coinfection have been mostly done with parasites such as bacteria (Smith et al., 2013), human malaria (Taylor et al., 1997), mosquito-borne dengue strains (Pepin and Hanley, 2008), animal viruses (Klemme et al., 2016), plant viruses (Susi et al., 2015) or non respiratory viruses such as human immunodeficiency virus, Hepatitis C virus and Hepatitis B virus (Bellecave et al., 2009) in laboratories. Shinjoh et al. (2000) were the first to design an in vitro experimental study to determine the growth interference ability of IAV and RSV in a single cell. Their study showed that simultaneous infection with RSV and IAV in Madin Darby Canine Kidney (MDCK) cells led to growth suppression of RSV infection due to the faster growing IAV infection; however the suppression of RSV infection was overcome by initiating IAV infection a few days after the initiation of RSV infection. Using immunofluorescence and scanning electron microscopy, they also observed IAV-RSV interactions at the level of viral protein synthesis where both viruses were found to replicate independently and release their surface antigens selectively from the infected cell during the budding period. They argued that the growth inhibition of RSV was due to the reduced cellular capacity for viral production, since both viruses competed for intracellular resources such as proteins or amino acids for their maturation. Another recent study of quantum dot (QD) nanoparticles as viral detection probes within cells has shown that not only different strains of the same virus, but also different respiratory viruses can infect the same cell (Fayyadh et al., 2017). Using the proposed QD probe, researchers detected AdV and IAV at different subcellular levels of the same infected human bronchial epithelial (A549) cell and found similar growth inhibition of one virus due to the presence of the other virus as the Shinjoh et al. (2000) experiment. An in vivo study observed a similar kind of blocking interaction with avian influenza virus and new castle disease virus in poultry (Shengqiang et al., 2012). Additionally, other in vivo studies also noticed a sequential combination of viruses can control viral activities during coinfection (Laurie, Guarnaccia, Carolan, AWC, Aban, Petrie, et al., 2015, Shengqiang, Zheng, Zhao, Liu, Liu, Sun, et al., 2012). Thus coinfection can lead to complex infection dynamics for two or more viruses.

Some mathematical models have investigated the interactions of simultaneous infection with two viruses, although they have been applied to different strains of the same virus (Petrie, Butler, Barr, McVernon, Hurt, McCaw, 2015, Pinilla, Holder, Abed, Boivin, CAA, 2012, Simeonov, Gong, Kim, Poss, Chiaromonte, Fricks, 2010). For example, Pinilla et al. (2012) proposed a two virus model to quantify competitive mixed-infection experiments in order to compare the relative in vivo replication characteristics of pandemic A/H1N1 influenza with its H275Y mutant strain. Petrie et al. (2015) used a similar model to examine coinfection of the same two strains of influenza virus. Simeonov et al. (2010) considered spatial associations to explain in vitro cellular susceptibility due to the simultaneous presence of RSV A2 and RSV B by applying empirical and statistical approaches. In our previous work (Pinky, Dobrovolny, 2016, Pinky, Dobrovolny, 2017), we investigated a coinfection model with distinct respiratory viruses that share the same type of target cells but not the same cell. All of these different studies, including ours, have assumed that coinfecting viruses interact with the host by means of resource exploitation.

Unfortunately, none of models studied so far have predicted long-lasting or chronic coinfections. According to classical ecological principle, coexistence of two species competing for the same resource is governed by the competitive exclusion principle (Hardin, 1960), which states that one species will ultimately drive the other to extinction. However, some mechanisms of species interaction have been shown to lead to coexistence of two species (Bashey, 2015), although these ideas have not yet been applied to the investigation of chronic coinfections.

In this paper, our aim is to construct a mathematical model to better explain coinfection dynamics of the respiratory tract in an effort to explore disease outcomes due to viral coinfection, looking particularly for chronic coinfections. In order to understand the effects of coinfection at the within host cellular level, it is critical to know the mechanisms of interaction between the viruses and cells. Since viruses are known to infect the same cell during coinfection (Fayyadh, Ma, Qin, Zhang, Li, Zhang, et al., 2017, Shinjoh, Omoe, Saito, Matsuo, Nerome, 2000), we integrate superinfection, i.e. simultaneous infection of two different viruses in the same cell, and cellular regeneration as potential mechanisms of interaction in the model. Our model shows that these interactions alter the effect of coinfection on disease outcomes in the human respiratory tract. We find that having superinfection along with cellular regeneration can lead to chronic coinfection, which cannot occur with either mechanism alone.

2. Methods

In our previous work (Pinky and Dobrovolny, 2016), we presented a two virus model to reproduce experimental data of coinfection taken from Shinjoh et al. (2000). As some studies have shown that coinfection is associated with long-lasting disease (Aberle, Aberle, Pracher, Hutter, Kundi, Popow-Kraupp, 2005, Choi, Chung, Kim, 2015, Costa, DAO, da Silveira, Neto, de Paula, TFMS, et al., 2014, Martin, Fairchok, Stednick, Kuypers, Englund, 2013, Mazur, Bont, Cohen, Cohen, von Gottberg, Groome, et al., 2017), we extend our model to be more biologically relevant and at the same time to examine possible mechanisms for chronic disease conditions. Our previous study exploring the effect of cell regeneration in coinfection models indicated that cell regeneration alone could lead to chronic infection, but only with a single virus (Pinky and Dobrovolny, 2017). Here, we will explore the phenomenon of superinfection, where a single cell can be infected by both types of viruses at the same time, both with and without constant regeneration of cells and cell death.

2.1. Superinfection model

The deterministic model presented here is an extension of the basic coinfection model from our previous work (Pinky and Dobrovolny, 2016) where now we introduce possible infection of single cells by both types of virus; we call this superinfection mechanism. The model presented here is the most general form of all the events we are interested in investigating. The model is represented by the following ordinary differential equations,

$$\begin{array}{ccc}\hfill \mathrm{Target}\text{cell}:\dot{T}& =& r-aT-\sum _i{\beta }_{i}T{V}_i\hfill \\ \hfill \mathrm{Eclipse}\text{cell}:\dot{E_i}& =& {\beta }_{i}T{V}_i-k_i{E}_i-{\beta }_{ji}{E}_i{V}_j\hfill \\ \hfill \mathrm{Superinfected}\text{eclipse}\text{cell}:\dot{E_3}& =& \sum _{i,j}{\beta }_{ji}{E}_i{V}_j-k_3{E}_3\hfill \\ \hfill \mathrm{Infectious}\text{cell}:\dot{I_i}& =& k_i{E}_i-{\delta }_i{I}_i\hfill \\ \hfill \mathrm{Superinfected}\text{infectious}\text{cell}:\dot{I_3}& =& k_3{E}_3-{\delta }_3{I}_3\hfill \\ \hfill \mathrm{Virus}:\dot{V_i}& =& p_i{I}_i+p_{ij}{I}_3-c_i{V}_i,\hfill \end{array}$$ (1)

where $i,j=1,2$ and ${\beta }_{ij}=p_{ij}=0$ when $i=j,$ and all the derivatives are taken with respect to time, t.

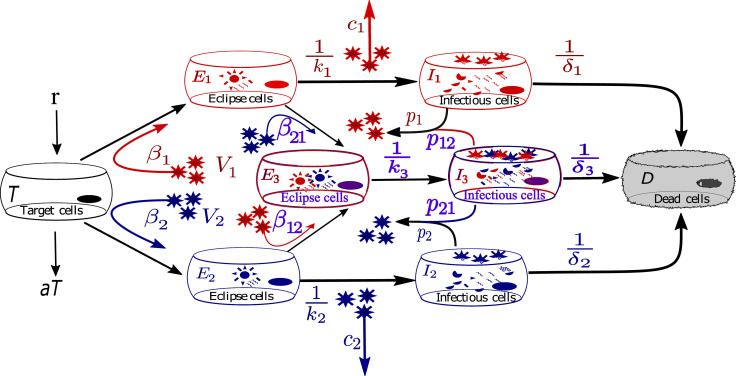
A schematic of the model is shown in Fig. 1 . Susceptible target cells, T, are infected by virus, V_i, at a rate β_iV_i. In addition, target cells regenerate at a constant rate, r, and decay naturally at a rate, a. Both kinds of infected target cells undergo eclipse phases where viruses exhibit intra-cellular activities to take over the host’s cellular mechanisms to produce viral genomes (RNA). We assume that the second virus can still infect the cells in eclipse phases such that E ₁ get infected with the second virus, V ₂, at a rate β ₂₁ and E ₂ get infected by the first virus, V ₁, at a rate β ₁₂. Thus cells in the eclipse phases become functional target cells for the other virus and these dually infected eclipse cells are called superinfected eclipse cells, E ₃. We further assume that once cells are infectious, they can no longer be infected by another virus. As soon as the eclipse phases are ready to produce viruses after the time durations of $\frac{1}{k_1},$ $\frac{1}{k_2}$ and $\frac{1}{k_3},$ they become infectious cells, I ₁, I ₂ and I ₃. I ₁ and I ₂ produce viruses at rates, p ₁ and p ₂ while the superinfected infectious cells, I ₃, produce viruses of both types V ₁ and V ₂, at rates p ₁₂ and p ₂₁ respectively. These infectious cells produce viruses throughout their lifespans of $\frac{1}{{\delta }_1},$ $\frac{1}{{\delta }_2}$ and $\frac{1}{{\delta }_3}$. Viruses of both types, V ₁ and V ₂, decay at rates c ₁ and c ₂ respectively. Table 1 describes the model variables and parameters with values used for our simulations. All parameters are positive.

Fig. 1.

Model diagram for virus-virus coinfection with superinfection mechanism. Two different viruses infect the susceptible target cells simultaneously. Target cells regenerate at a constant rate and decay according to available target cells. Once infected by one type of virus, some of the infected cells are additionally infected by the other type of virus. Infection is established once the viruses successfully hack the cellular mechanisms for their own replication during the eclipse phase, eventually becoming infectious. Viruses replicate by infecting not only susceptible target cells but also the singly infected cells with a different virus type.

Table 1.

Definition of model variables and parameter values for model simulations.

Variable	Definition			Units
T	number of susceptible target cells			cell counts
Ei	number of cells in eclipse phase with virus i			cell counts
E3	number of cells in eclipse phase with both viruses			cell counts
Ii	number of infectious cells with virus i			cell counts
I3	number of infectious cells with both viruses			cell counts
Vi	infectious viral titer of virus i			PFU/mL
Parameter	Definition	IAVa(i=1)	RSVa(i=2)	Units
T0	number of initial target cell	1.0	1.0	cell counts
V0i	initial viral titer of virus i	1.0	1.0	PFU/mL
βi	infection rate of virus i	$8.27\times {10}^{-6}$	$3.08\times {10}^{-2}$	(PFU/mL)${}^{-1}$ d${}^{-1}$
βij	infection rate of superinfected cell	varied	varied	(PFU/mL)${}^{-1}$ d${}^{-1}$
$\frac{1}{k_i}$	transition rate of eclipse phase cell by virus i	4.2	1.27	d${}^{-1}$
$\frac{1}{{\delta }_i}$	death rate of infectious cell of virus i	4.2	1.27	d${}^{-1}$
$\frac{1}{k_3}$	time duration of superinfected eclipse phase	varied	varied	d${}^{-1}$
$\frac{1}{{\delta }_3}$	life span of superinfected infectious cell	varied	varied	d${}^{-1}$
pi	production rate of virus i	1.2 × 108	7.64 × 103	PFU/mL d${}^{-1}$
pij	virus production rate of superinfected cell	varied	varied	PFU/mL d${}^{-1}$
ci	clearance rate of virus i	4.03	1.27	d${}^{-1}$
r	regeneration rate of target cell	0.033b		d${}^{-1}$
a	natural death rate of target cell	0.005 (6 months)c		d${}^{-1}$

^aIAV and RSV parameter values are taken from (Pinky and Dobrovolny, 2016) and $i,j=1,2$ and i ≠ j.

^bTaken from (Beauchemin, Handel, 2011, Beers, Morrisey, 2011).

^cTaken from (Rawlins and BLM, 2008).

We have not included an explicit immune response in our model for a number of reasons. We are interested in studying the mechanisms behind chronic coinfections, which occur more often in immunocompromised patients. Thus a complete lack of explicit immune response makes sense. Second, since we do not have any experimental data that explains immune response with respect to coinfection of two different viruses, our model does not explicitly account for any immune responses, however, this can be incorporated implicitly in the superinfection parameters, i.e. death rates of dually infected cells, $\frac{1}{{\delta }_3},$ superinfectivity rates, β_ij, and viral production rates from superinfected cells, p_ij, in the model. Moreover, studies show superinfection may cause both enhanced (Mosquera, Adler, 1998, Nowak, May, 1994) and reduced (Brown et al., 2002) production of viruses; we assume that superinfected infectious cells produce each type of virus at different rates, p ₁₂ and p ₂₁, than that of the singly infected cells so that we can explore the pathological consequences due to the different replication rates. Also it is reported that the susceptibility of target cells changes due to the occurrence of earlier infection (Anestad, Vainio, Hungnes, 2007, Laurie, Guarnaccia, Carolan, AWC, Aban, Petrie, et al., 2015, Simeonov, Gong, Kim, Poss, Chiaromonte, Fricks, 2010). For example, infection by one virus may increase the probability of being subsequently infected by other types since the first infection may weaken a host’s immunity or resistance (Soares et al., 2016). Another study showed that primary infection evokes an immune response which reduces the chance for secondary infection (Devevey, Dang, Graves, Murray, Brisson, 2015, Klemme, Louhi, Karvonen, 2016, Susi, Barrès, Vale, Laine, 2015). So we consider different infection rates for superinfection to explore the possible outcomes. Lastly, we also allow the transition rate of superinfected eclipse phases and death rate of superinfected infectious cells to vary across a range of acceptable parameter values for both viruses based. While there is no direct experimental examination of eclipse phases or infectious cell lifespans during coinfection, since viruses are sharing the cell’s resources (Shinjoh et al., 2000), it seems possible that the speed at which virions are produced is altered. On a larger scale, the observation by Laurie et al. (2015) that in a ferret model of human influenza, subsequent influenza infections with different strains (H1N1, H3N2, IBV) limits the time duration of virus replication also suggests that these transition rates are altered.

The terms of disease severity, superinfection and coinfection have ambiguous meanings in literature as there are no standard definitions for them in general (Sofonea et al., 2017). In this paper, coinfection refers to infection caused by two different viruses in the respiratory tract at the same time, though not necessarily sharing the same target cells, while superinfection refers to infection of a single cell with two different viruses. In our case, we define disease severity by the two factors defined as viral load and duration of infection where two viruses coexist. Other than these two, order of inoculation, initial viral inoculum, number of coinfecting pathogens, virus specific interactions, host defense mechanisms can also influence disease severity.

2.2. Numerical simulation

To present numerical simulations of coinfection dynamics we choose IAV and RSV because they are the leading etiologic agents for respiratory illness and are a common coinfection pair in clinical studies (Rotzén-Östlund et al., 2014). Parameter values of IAV and RSV are estimated from in vitro experimental studies, performed in human epithelial cell cultures. Details are given in our previous work (Pinky and Dobrovolny, 2016). Parameter definitions along with their values for computer simulation are given in Table 1. Simulations are performed using Octave 3.6.4 lsode function to solve the system of equations. Octave codes are given in the supplemental file [see Additional file].

3. Results

Previously, we tested the mechanism of target cell replenishment in the basic coinfection model (Pinky and Dobrovolny, 2016) and confirmed that addition of a renewable supply of cells was necessary for chronic infection. However, that model could not produce long-lasting infections with both viruses (Pinky and Dobrovolny, 2017). The basic coinfection model did not consider superinfection mechanism, so here we aim to determine whether allowing single cells to be infected by both viruses (superinfection) can lead to chronic coinfection.

3.1. Superinfection with target cell regeneration and death

We first investigate the most general case of the superinfection model (Eq. (1)) which includes superinfection along with target cell regeneration and natural cell death. The average lifespan of airway epithelial cells ranges from 6–18 months, which is much longer than the average time it takes to infect a target cell by a respiratory virus (Rawlins and BLM, 2008). Although there is negligible natural target cell death before the cells are infected, we include this rate to make the model more biologically appropriate. We look for a steady state with non-zero values for both V ₁ and V ₂, since this is the chronic coinfection equilibrium. Then we evaluate the stability of the equilibrium to determine whether there are parameter values for which it is a stable steady state. Finally, we confirm the theoretical results of the stability study by applying numerical simulations with one of the common coinfection pairs reported in clinical studies. Sensitivity analysis of this model is also shown in a supplemental document [see Additional file].

The superinfection model given by Eq. (1) is characterized by two different types of long term dynamics that are presented by the equilibria of the forms $Q_1^{*}=(T^{*},$0,0,0,0,0,0,0,0) known as infection free equilibrium, and $Q_2^{*}=(T^{*},E_1^{*},E_2^{*},E_3^{*},I_1^{*},I_2^{*},I_3^{*},V_1^{*},V_2^{*})$ known as chronic equilibrium. The full expressions for the equilibria are

$$\begin{array}{ccc}\hfill {\displaystyle Q_1^{*}}& {\displaystyle =}& {\displaystyle (T^{*},0,0,0,0,0,0,0,0),\text{where}{T}^{*}\in {\mathbb{R}}_{\ge }\text{or}}\hfill \\ & & {\displaystyle \{T^{*}\in \mathbb{R}|T^{*}\ge 0\}\text{and}}\hfill \\ \hfill {\displaystyle Q_2^{*}}& {\displaystyle =}& {\displaystyle (T^{*},E_1^{*},E_2^{*},E_3^{*},I_1^{*},I_2^{*},I_3^{*},V_1^{*},V_2^{*}),\text{where}}\hfill \\ \hfill {\displaystyle T^{*}}& {\displaystyle =}& {\displaystyle \frac{r}{{\beta }_1{V}_1^{*}+{\beta }_2{V}_2^{*}+a},E_1^{*}=\frac{{\beta }_1{T}^{*}{V}_1^{*}}{k_1+{\beta }_{21}{V}_2^{*}},}\hfill \\ \hfill {\displaystyle E_2^{*}}& {\displaystyle =}& {\displaystyle \frac{{\beta }_2{T}^{*}{V}_2^{*}}{k_2+{\beta }_{12}{V}_1^{*}},E_3^{*}=\frac{1}{k_3}({\beta }_{12}{E}_2^{*}{V}_1^{*}+{\beta }_{21}{E}_1^{*}{V}_2^{*}),}\hfill \\ \hfill {\displaystyle I_1^{*}}& {\displaystyle =}& {\displaystyle \frac{k_1}{{\delta }_1}{E}_1^{*},I_2^{*}=\frac{k_2}{{\delta }_2}{E}_2^{*},I_3^{*}=\frac{k_3}{{\delta }_3}{E}_3^{*},V_i^{*}=\frac{-B_i\pm \sqrt{B_i^2-4A_i{C}_i}}{2A_i},}\hfill \\ & & {\displaystyle \text{where}{A}_i={\beta }_i{\beta }_{\mathit{ij}}{c}_i{\delta }_i{\delta }_3(k_i+{\beta }_{\mathit{ji}}{V}_j^{*}),}\hfill \\ \hfill {\displaystyle B_i}& {\displaystyle =}& {\displaystyle c_i{\delta }_i{\delta }_3(k_i+{\beta }_{\mathit{ji}}{V}_j^{*})({\beta }_i{k}_j+{\beta }_j{\beta }_{\mathit{ij}}{V}_j+a{\beta }_{\mathit{ij}})}\hfill \\ & & {\displaystyle -r{\beta }_i{\beta }_{\mathit{ij}}(p_i{k}_i{\delta }_3+p_{\mathit{ij}}{\delta }_i{V}_j)\text{and}}\hfill \\ \hfill {\displaystyle C_i}& {\displaystyle =}& {\displaystyle c_i{\delta }_i{\delta }_3(k_i+{\beta }_{\mathit{ji}}{V}_j^{*})({\beta }_j{k}_j{V}_j^{*}+a{k}_j)-r{\delta }_i{\beta }_j{V}_j^{*}{p}_{\mathit{ij}}{\beta }_{\mathit{ij}}(k_i+{\beta }_{\mathit{ji}}{V}_j^{*})}\hfill \\ & & {\displaystyle -r{\beta }_i{k}_j(p_i{k}_i{\delta }_3+p_{\mathit{ij}}{\beta }_{\mathit{ji}}{\delta }_i{V}_j),\text{for}i,j=1,2.}\hfill \end{array}$$

Since the coefficient A_i is always positive, for different combinations of B_i and C_i and given that the discriminant is always positive, there exist four unique solutions for $V_i^{*}$ where $i,j=1,2$ for the equilibrium, $Q_2^{*}$. All four solutions for each virus are given in the supplemental document in more detail [see Additional file]. Putting $i,j=1,2,$ the viral steady states become

$$\begin{array}{ccc}\hfill V_1^{*}& =& {\displaystyle \frac{1}{2{\beta }_1{\beta }_{12}{c}_1{\delta }_1{\delta }_3(k_1+{\beta }_{21}{V}_2^{*})}\left[\right\{r{\beta }_1{\beta }_{12}(p_1{k}_1{\delta }_3+p_{12}{\delta }_1{V}_2^{*})}\hfill \\ & & {\displaystyle -c_1{\delta }_1{\delta }_3(k_1+{\beta }_{21}{V}_2^{*})({\beta }_1{k}_2+{\beta }_2{\beta }_{12}{V}_2^{*}+a{\beta }_{12})\}}\hfill \\ & & {\displaystyle \pm \sqrt{[{\left\{c_1{\delta }_1{\delta }_3(k_1+{\beta }_{21}{V}_2^{*})({\beta }_1{k}_2+{\beta }_2{\beta }_{12}{V}_2^{*}+a{\beta }_{12})\right\}}^2}}\hfill \\ & & {\displaystyle +{\left\{r{\beta }_1{\beta }_{12}(p_1{k}_1{\delta }_3+p_{12}{\delta }_1{V}_2^{*})\right\}}^2}\hfill \\ & & {\displaystyle +4r{\beta }_2{V}_2^{*}{p}_{12}{\beta }_1{\beta }_{12}^2{c}_1{\delta }_1^2{\delta }_3{(k_1+{\beta }_{21}{V}_2^{*})}^2}\hfill \\ & & {\displaystyle +4r{\beta }_1^2{k}_2{\beta }_{12}{c}_1{\delta }_1{\delta }_3(k_1+{\beta }_{21}{V}_2^{*})(p_1{k}_1{\delta }_3+p_{12}{\beta }_{21}{\delta }_1{V}_2^{*})}\hfill \\ & & {\displaystyle -(4{\beta }_1{\beta }_{12}{c}_1^2{\delta }_1^2{\delta }_3^2{(k_1+{\beta }_{21}{V}_2^{*})}^2({\beta }_2{k}_2{V}_2^{*}+a{k}_2)}\hfill \\ & & {\displaystyle +2r{c}_1{\delta }_1{\delta }_3{\beta }_1{\beta }_{12}(k_1+{\beta }_{21}{V}_2^{*})({\beta }_1{k}_2+{\beta }_2{\beta }_{12}{V}_2^{*}+a{\beta }_{12})}\hfill \\ & & {\displaystyle (p_1{k}_1{\delta }_3+p_{12}{\delta }_1{V}_2^{*})})\left]\right],\hfill \\ \hfill {\displaystyle V_2^{*}}& =& {\displaystyle \frac{1}{2{\beta }_2{\beta }_{21}{c}_2{\delta }_2{\delta }_3(k_2+{\beta }_{12}{V}_1^{*})}\left[\right\{r{\beta }_2{\beta }_{21}(p_2{k}_2{\delta }_3+p_{21}{\delta }_2{V}_1^{*})}\hfill \\ & & {\displaystyle -c_2{\delta }_2{\delta }_3(k_2+{\beta }_{12}{V}_1^{*})({\beta }_2{k}_1+{\beta }_1{\beta }_{21}{V}_1^{*}+a{\beta }_{21})\}}\hfill \\ & & {\displaystyle \pm \sqrt{[{\left\{c_2{\delta }_2{\delta }_3(k_2+{\beta }_{12}{V}_1^{*})({\beta }_2{k}_1+{\beta }_1{\beta }_{21}{V}_1^{*}+a{\beta }_{21})\right\}}^2}}\hfill \\ & & {\displaystyle +{\left\{r{\beta }_2{\beta }_{21}(p_2{k}_2{\delta }_3+p_{21}{\delta }_2{V}_1^{*})\right\}}^2}\hfill \\ & & {\displaystyle +4r{\beta }_1{V}_1^{*}{p}_{21}{\beta }_2{\beta }_{21}^2{c}_2{\delta }_2^2{\delta }_3{(k_2+{\beta }_{12}{V}_1^{*})}^2}\hfill \\ & & {\displaystyle +4r{\beta }_2^2{k}_1{\beta }_{21}{c}_2{\delta }_2{\delta }_3(k_2+{\beta }_{12}{V}_1^{*})(p_2{k}_2{\delta }_3+p_{21}{\beta }_{12}{\delta }_2{V}_1^{*})}\hfill \\ & & {\displaystyle -(4{\beta }_2{\beta }_{21}{c}_2^2{\delta }_2^2{\delta }_3^2{(k_2+{\beta }_{12}{V}_1^{*})}^2({\beta }_1{k}_1{V}_1^{*}+a{k}_1)}\hfill \\ & & {\displaystyle +2r{c}_2{\delta }_2{\delta }_3{\beta }_2{\beta }_{21}(k_2+{\beta }_{12}{V}_1^{*})({\beta }_2{k}_1+{\beta }_1{\beta }_{21}{V}_1^{*}+a{\beta }_{21})}\hfill \\ & & {\displaystyle (p_2{k}_2{\delta }_3+p_{21}{\delta }_2{V}_1^{*})})\left]\right].\hfill \end{array}$$

The chronic equilibria, $Q_2^{*},$ are biologically feasible when both viral steady states possess real positive values. According to this constraint the parameters must maintain the following two conditions to avoid generating imaginary viral equilibria.

$$\begin{array}{ccc}& & {\displaystyle {\left(c_1{\delta }_1{\delta }_3({\beta }_1{k}_2+{\beta }_2{\beta }_{12}{V}_2^{*}+a{\beta }_{12})\right)}^2}\hfill \\ & & {\displaystyle +{\left(r{\beta }_1{\beta }_{12}\frac{(p_1{k}_1{\delta }_3+p_{12}{\delta }_1{V}_2^{*})}{(k_1+{\beta }_{21}{V}_2^{*})}\right)}^2+4r{\beta }_2{V}_2^{*}{p}_{12}{\beta }_1{\beta }_{12}^2{c}_1{\delta }_1^2{\delta }_3}\hfill \\ & & {\displaystyle +4r{\beta }_1^2{k}_2{\beta }_{12}{c}_1{\delta }_1{\delta }_3\frac{(p_1{k}_1{\delta }_3+p_{12}{\beta }_{21}{\delta }_1{V}_2^{*})}{(k_1+{\beta }_{21}{V}_2^{*})}}\hfill \\ & & {\displaystyle \ge 4{\beta }_1{\beta }_{12}{c}_1^2{\delta }_1^2{\delta }_3^2({\beta }_2{k}_2{V}_2^{*}+a{k}_2)}\hfill \\ & & {\displaystyle +2r{c}_1{\delta }_1{\delta }_3{\beta }_1{\beta }_{12}({\beta }_1{k}_2+{\beta }_2{\beta }_{12}{V}_2^{*}+a{\beta }_{12})}\hfill \\ & & {\displaystyle \frac{(p_1{k}_1{\delta }_3+p_{12}{\delta }_1{V}_2^{*})}{(k_1+{\beta }_{21}{V}_2^{*})},\text{and}}\hfill \\ & & {\displaystyle {\left(c_2{\delta }_2{\delta }_3({\beta }_2{k}_1+{\beta }_1{\beta }_{21}{V}_1^{*}+a{\beta }_{21})\right)}^2}\hfill \\ & & {\displaystyle +{\left(r{\beta }_2{\beta }_{21}\frac{(p_2{k}_2{\delta }_3+p_{21}{\delta }_2{V}_1^{*})}{(k_2+{\beta }_{12}{V}_1^{*})}\right)}^2+4r{\beta }_1{V}_1^{*}{p}_{21}{\beta }_2{\beta }_{21}^2{c}_2{\delta }_2^2{\delta }_3}\hfill \\ & & {\displaystyle +4r{\beta }_2^2{k}_1{\beta }_{21}{c}_2{\delta }_2{\delta }_3\frac{(p_2{k}_2{\delta }_3+p_{21}{\beta }_{12}{\delta }_2{V}_1^{*})}{(k_2+{\beta }_{12}{V}_1^{*})}}\hfill \\ & & {\displaystyle \ge 4{\beta }_2{\beta }_{21}{c}_2^2{\delta }_2^2{\delta }_3^2({\beta }_1{k}_1{V}_1^{*}+a{k}_1)}\hfill \\ & & {\displaystyle +2r{c}_2{\delta }_2{\delta }_3{\beta }_2{\beta }_{21}({\beta }_2{k}_1+{\beta }_1{\beta }_{21}{V}_1^{*}+a{\beta }_{21})\frac{(p_2{k}_2{\delta }_3+p_{21}{\delta }_2{V}_1^{*})}{(k_2+{\beta }_{12}{V}_1^{*})}.}\hfill \end{array}$$

The system converges towards either of the equilibria, $Q_1^{*}$ or $Q_2^{*},$ depending on the virus specific parameter values or on the basic reproductive number, ${\mathcal{R}}_0$. ${\mathcal{R}}_0$ can be found from the spectral radius (largest eigenvalue) of the next generation matrix (Diekmann et al., 1990), i.e. $\left({\mathcal{FV}}^{-1}\right),$ where $\mathcal{F}$ is the infection matrix and $\mathcal{V}$ is the transition matrix obtained by the model (1) and evaluated at the infection free steady state, $Q_1^{*}$. The next generation matrix, $\left({\mathcal{FV}}^{-1}\right),$ of model (1) is

$$\begin{array}{cc}\hfill {\mathcal{FV}}^{-1}=& \left(\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& {\displaystyle \frac{{\beta }_{1}T}{c_1}}& 0\\ 0& 0& 0& 0& 0& 0& 0& {\displaystyle \frac{{\beta }_{2}T}{c_2}}\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ {\displaystyle \frac{p_1}{{\delta }_1}}& 0& {\displaystyle \frac{p_{12}}{{\delta }_3}}& {\displaystyle \frac{p_1}{{\delta }_1}}& 0& {\displaystyle \frac{p_{12}}{{\delta }_3}}& 0& 0\\ 0& {\displaystyle \frac{p_2}{{\delta }_2}}& {\displaystyle \frac{p_{21}}{{\delta }_3}}& 0& {\displaystyle \frac{p_2}{{\delta }_2}}& {\displaystyle \frac{p_{21}}{{\delta }_3}}& 0& 0\end{array}\right)\end{array}$$

and the eigenvalues of ${\mathcal{FV}}^{-1}$ are $(0,0,0,0,-\sqrt{{\mathcal{R}}_{01}},\sqrt{{\mathcal{R}}_{01}},-\sqrt{{\mathcal{R}}_{02}},\sqrt{{\mathcal{R}}_{02}})$. The dominant eigenvalue of the matrix ${\mathcal{FV}}^{-1}$ is equal to ${\mathcal{R}}_0,$ and the expression is

$${\mathcal{R}}_0=\max (\sqrt{{\mathcal{R}}_{01}},\sqrt{{\mathcal{R}}_{02}}),\text{where}{\mathcal{R}}_{0i}=\frac{{\beta }_i{p}_{i}T}{c_i{\delta }_i}\text{for}i=1,2.$$

For the values of ${\mathcal{R}}_0>1,$ the infection free equilibrium, $Q_1^{*},$ is unstable, i.e. infection grows and converges to the chronic coinfection state, $Q_2^{*}$. On the other hand, for ${\mathcal{R}}_0<1,$ the infection free state, $Q_1^{*},$ will be globally asymptotically stable. An additional file shows all the possible equilibria individually with corresponding parameter constraints [see Additional file].

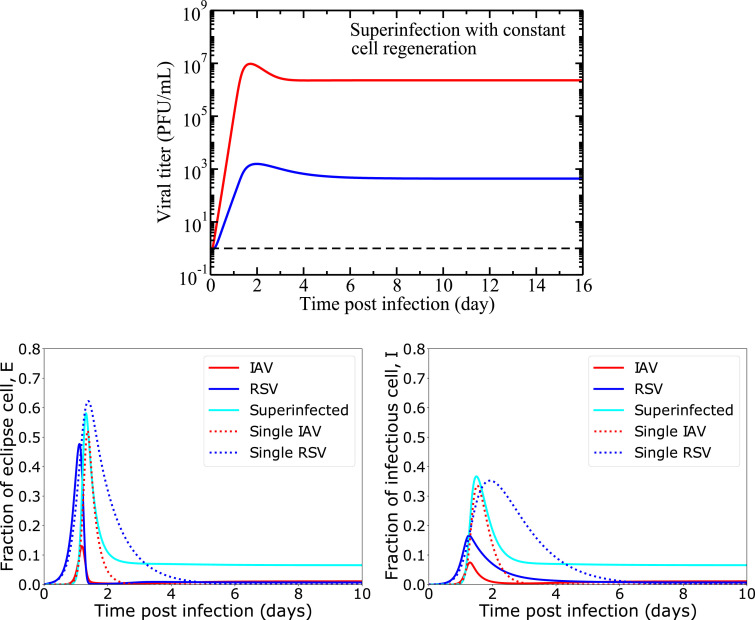
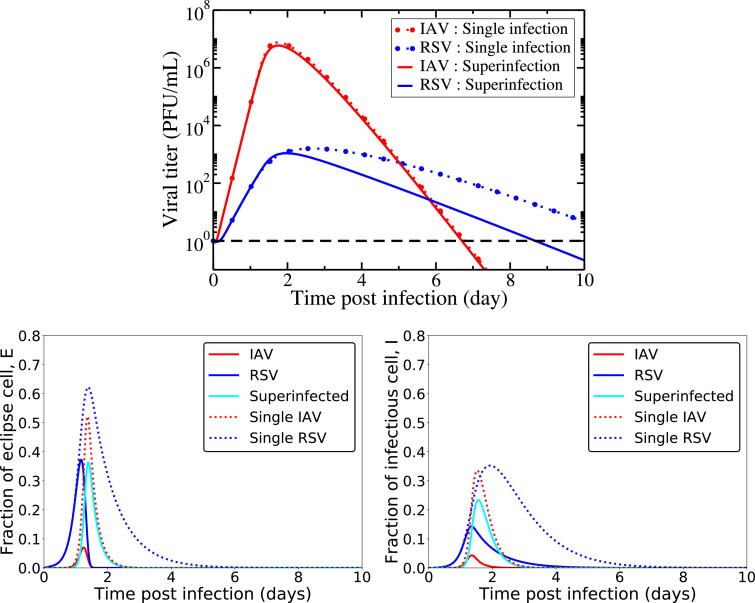
Simulations of the full model are presented in Fig. 2, using the initial conditions and parameter values given in Table 1. All viral infections are initiated with the same initial conditions (viral inoculum and infection initiation time) for ease of comparison. Since we have six unknown parameters to characterize superinfection mechanisms in our model, we initially set them equal to parameters of single virus such that ${\beta }_{12}={\beta }_1,{\beta }_{21}={\beta }_2,p_{12}=p_1,p_{21}=p_2,k_3=k_1\text{and}{\delta }_3={\delta }_1$. Biologically, it means that there is no change in cell capacity due to infections with more than one virus simultaneously. A detailed sensitivity analysis of this model is also given in the supplemental document [see Additional file]. Fig. 2 shows that the infections persist for a long time for each virus, leading to a chronic coinfection. The cells have a high probability of being superinfected with two viruses for a longer period of time. Both viruses produce a viral peak viral, similar to an acute infection and both of them decrease slightly after their viral peaks to maintain constant viral loads thereafter. The cellular dynamics are also shown in the bottom row of Fig. 2, where we see that the coinfection is maintained primarily by the superinfected cells.

Fig. 2.

Viral and cellular dynamics during superinfection with target cell regeneration and natural death (model(1)). We show the viral load, eclipse cells and infectious cells dynamics over the course of infection considering no change in cell capacity due to superinfection, i.e. setting superinfection parameters equal to the single IAV infection according to Table 1. The horizontal dashed black line (top row) indicates the virus detection limit. In both rows, solid lines show superinfection model predictions and the broken lines show single viral and their cell dynamics during single IAV and RSV infections.

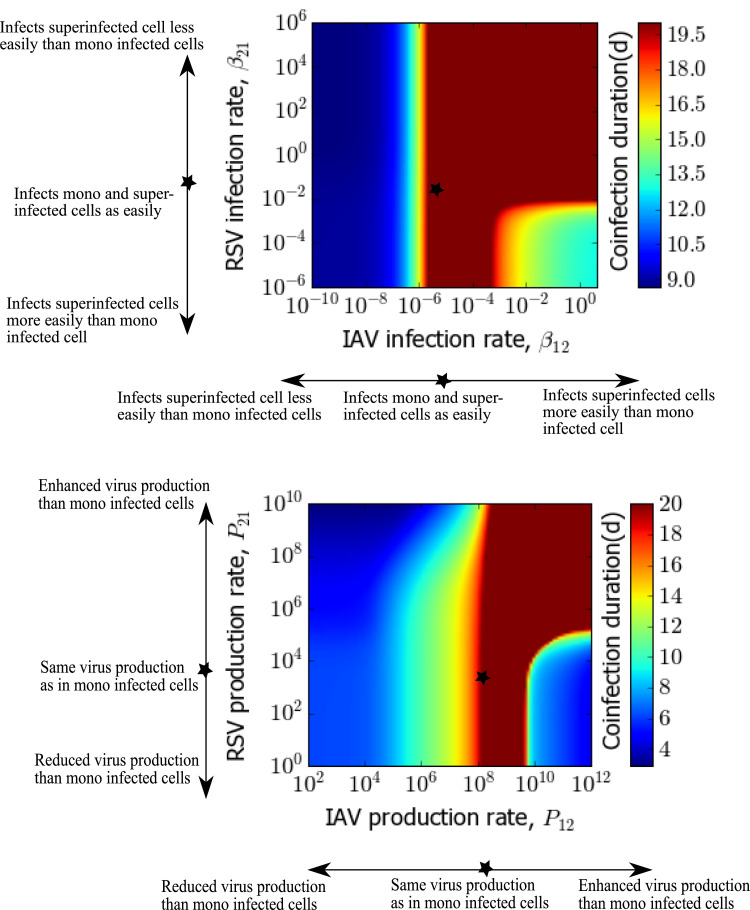
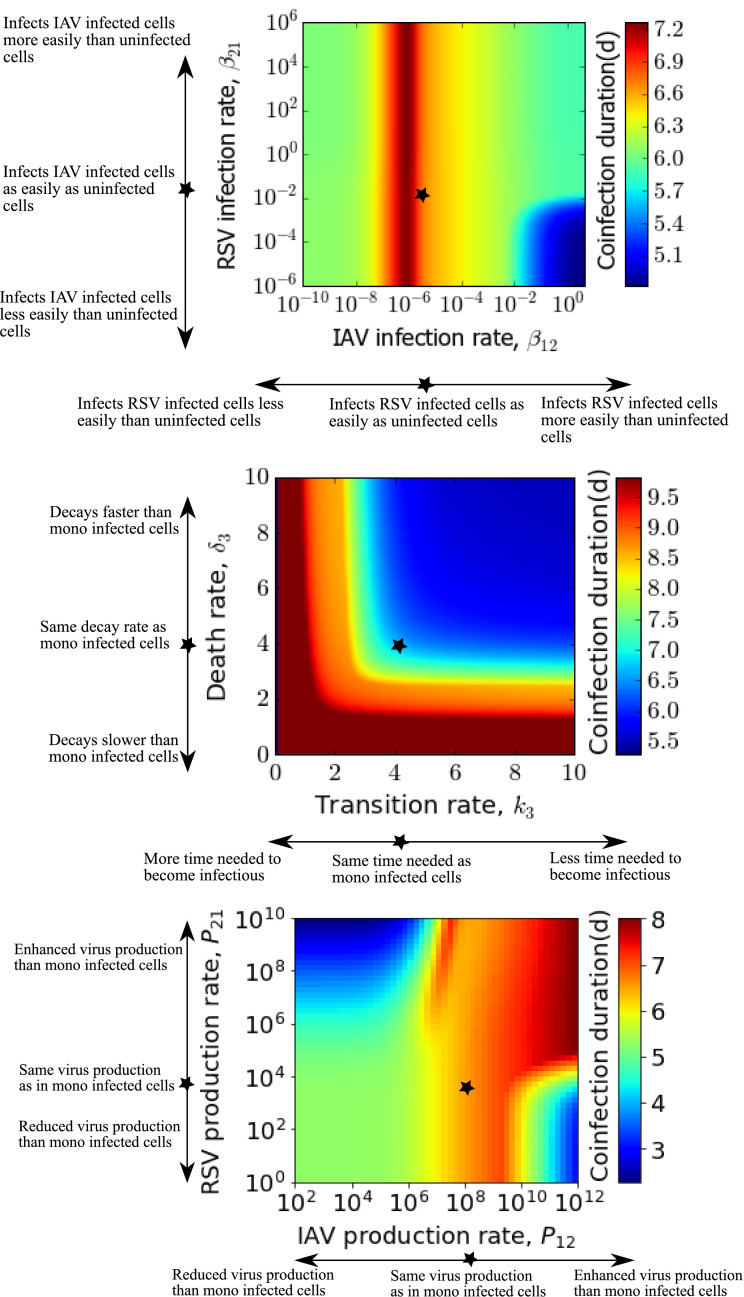
We also examine the variation in coinfection duration due to various superinfection parameters in Fig. 3 . Coinfection duration is defined as the time during which both infections are above the detection threshold (virus load greater than 1.0 PFU/mL). When IAV can superinfect RSV infected cells more easily than uninfected cells (preferential infection), chronic coinfection of more than two weeks is possible for a wider range of RSV’s susceptibility to reinfect IAV infected cells. The blue region in Fig. 3 (top) represents when RSV becomes a single chronic infection due to significantly higher infectiousness than IAV. On the other hand, according to Fig. 3 (bottom), if the superinfected cells produce more IAV than singly IAV infected cells, for RSV being produced at any level from the superinfected cells, chronic coinfection longer than 20 days can be found. At higher RSV superinfection production rates ( >  ∼ 10³), the range of IAV superinfection production rates that lead to chronic coinfection are broader. There is no change in coinfection duration due to variations in superinfected eclipse cell’s capacity to become infectious, i.e. k ₃ and superinfected infectious cell life span, i.e. ${\displaystyle \frac{1}{{\delta }_3}}$.

Fig. 3.

Coinfection duration as a function of superinfection parameters for IAV-RSV coinfection. Coinfection duration as a function of superinfection infection rates (left) (baseline rates of IAV and RSV are $8.27\times {10}^{-6}$ and $3.08\times {10}^{-2}$ (PFU/mL)${}^{-1}$ d${}^{-1}$ respectively) and superinfection production rates (right) (baseline rates are 1.2 × 10⁸ and 7.64 × 10³ PFU/mL d${}^{-1}$ respectively). Other parameters are fixed to virus specific single infection parameters, as given in Table 1. Star on the images indicates the baseline values used in Fig. 2.

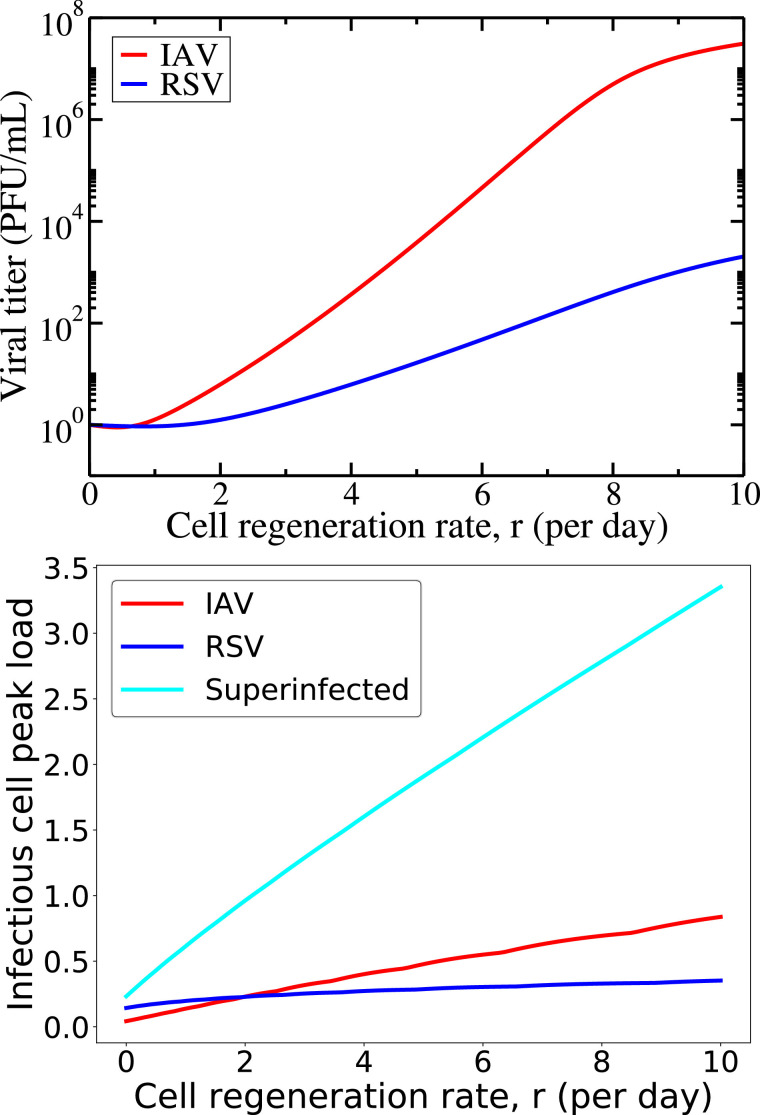
To explore the impact of cell regeneration rate on coinfection dynamics, we examine the steady-state viral load as a function of regeneration rate, r (Fig. 4 , top) sampling on day 20. The viral titer increases with increasing regeneration rates; the more rapidly cells are being regenerated, the larger the sustained viral load. This dependence is stronger for IAV than for RSV, suggesting that as cells become available more rapidly, IAV infects the cells more effectively. We also investigate the variation in peak load of infected cells by varying regeneration rate, r (Fig. 4, bottom). While singly infected infectious cells slightly increase with increasing regeneration for both viruses, the superinfected infectious population increases much more rapidly. This is further evidence that the chronic coinfection is maintained by the superinfected cell population rather than singly infected cells.

Fig. 4.

Variation in steady-state viral load and infectious cell peak load for varying regeneration rate,r, during superinfection with cell regeneration and no death. Sustained viral load for IAV and RSV (top) and infectious cell populations (bottom) are found for varying regeneration rate, r, during coinfection.

3.2. Superinfection with no target cell regeneration or death

Cell regeneration is a natural process which can allow secondary infection to take hold even if primary infection has infected the initial supply of target cells. However, this mechanism is usually neglected during acute respiratory infection because these infections are short, 1–2 weeks in length compared to the average regeneration time of the epithelial cells ( ∼ 30 days (Beauchemin, Handel, 2011, Beers, Morrisey, 2011)). Here, we examine the implications of this assumption in the context of superinfection.

$$\begin{array}{cc}\hfill \mathrm{Target}\text{cell}:\dot{T}& =-{\beta }_{1}T{V}_1-{\beta }_{2}T{V}_2,\hfill \end{array}$$ (2)

in model (1) we set the cell regeneration rate, r, and natural cell death rate, a, equal to zero. We will call this special case of model (1) model (2). In this case, we find only the infection free equilibrium, $Q_1^{*}=(T^{*},0,0,0,0,0,0,0,0)$. The equilibrium point, $Q_1^{*},$ represents two possible scenarios: (a) the system does not have an infection at all, but rather all the target cells remain uninfected (equal to the initial value, T ₀) with any initial virus clearing before an infection starts; (b) an acute infection when target cells, T*, are equal to zero, meaning all the susceptible cells of the system have been infected and killed by the two viruses. We will call this second scenario $Q_{11}^{*}$. As there are no more resources left for the viruses to infect, both of the viruses die eventually and the system becomes free of infection. To determine the stability of the infection free equilibrium, we linearize the model about the equilibrium points, $Q_1^{*}$ and $Q_{11}^{*},$ then calculate the eigenvalues of the characteristic equation of the linearized system. We find that the eigenvalues of the equilibrium point, $Q_{11}^{*},$ are $0,-c_1,-c_2,-{\delta }_1,-{\delta }_2,-{\delta }_3,-k_1,-k_2$ and $-k_3$. For this trivial equilibrium point, $Q_{11}^{*},$ all the eigenvalues are negative or zero indicating that the point is locally stable. The eigenvector corresponding to the zero eigenvalue lies along the target cell, T, axis where we have a continuum of equilibrium points. The eigenvalues of the other infection free equilibrium, $Q_1^{*}$ are $0,-{\delta }_3,-k_3,$ and roots of functions F_i(λ), where F_i(λ) is given by

$$\begin{array}{ccc}\hfill F_i\left(\lambda \right)& =& {\lambda }^3+{\lambda }^2(c_i+{\delta }_i+k_i)+\lambda (c_i{\delta }_i+{\delta }_i{k}_i+c_i{k}_i)\hfill \\ & & +(c_i{\delta }_i{k}_i-{\beta }_i{p}_i{k}_{i}T),\hfill \end{array}$$

for $i=1,2$. The infection free equilibrium, $Q_1^{*},$ is stable only if the following inequality is satisfied so that the roots of both F ₁ and F ₂ are negative;

$$\begin{array}{c}\hfill {\mathcal{R}}_{0i}<1,\text{where}{\mathcal{R}}_{0i}={\displaystyle \frac{{\beta }_i{p}_{i}T}{c_i{\delta }_i}}.\end{array}$$

Simulations of this reduced model are presented in Fig. 5 where superinfection dynamics for IAV and RSV are presented along with IAV and RSV single viral dynamics. In Fig. 5 (top), we see that the superinfection model cannot produce chronic coinfection for the choice of parameters mentioned above. Superinfection with two viruses of different virulence results in faster cell consumption than single viral infection (Fig. 5, bottom left). During superinfection, target cells are consumed rapidly compared to single viral infection but maintain almost the same viral load for IAV and reduced viral load for RSV forcing it to decay faster; since now viruses are not only competing for target cells at the extracellular level but also at the intracellular level. Superinfected cell kinetics for both the eclipse phase and the infectious phase are also shown in Fig. 5 (bottom middle and right). Note that there are very few superinfected cells, in contrast to the model with cell regeneration.

Fig. 5.

Viral and cellular dynamics during superinfection without target cell regeneration and natural death (model(2)). We show the viral load, eclipse cell and infectious cell dynamics over the course of an infection considering no change in cell capacity due to superinfection, i.e. setting superinfection parameters equal to the single IAV infection as in Table 1. The horizontal dashed black line (top row) indicates the virus detection limit. In both rows, solid lines show superinfection model predictions and the broken lines show single viral and their cell dynamics during single IAV and RSV infections.

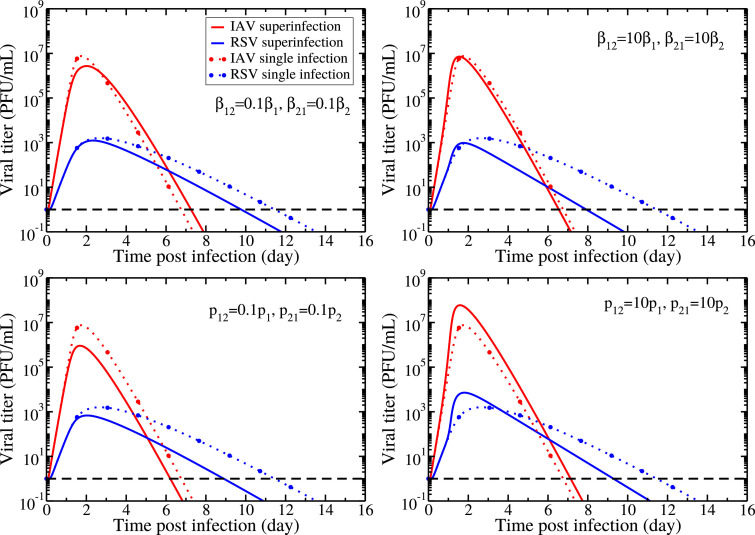
We again investigate the effect of the superinfection parameters by changing the superinfected cells’ capacity, varying the infection (Fig. 6, top) and production (Fig. 6, bottom) rates of the dually infected cells. While changing superinfection parameters doesn’t result in chronic coinfection, it can change both the peak viral load and the duration of the infection (time spent above the level of detection) which are both measures of the severity of the disease.

Fig. 6.

Comparison of the dynamics of single viral infections and superinfection model applied to IAV and RSV coinfection under different conditions of cell capacity changed due to superinfection. Variation of viral load is shown by varying superinfection infection rates, β_ij, (top row) and superinfection production rates, p_ij, (bottom row), and keeping all other parameters fixed according to Table 1. Solid lines show superinfection model predictions and the broken lines show single IAV and RSV infections. The horizontal dashed black line indicates the viral detection limit.

To more thoroughly explore the effect of superinfection parameters on disease severity, we examine the coinfection duration, varying the superinfection parameters k ₃, δ ₃, β_ij, and p_ij. Fig. 7 shows the coinfection duration as a function of pairs of the superinfection parameters. Considering the single infection rates as baseline values (given in Table 1 and indicated by star on the images) for superinfection, we vary the superinfection parameters on either side of the baseline to account for possible enhanced or diminished biological properties due to superinfection. The top graph shows the dependence on superinfection rates; the middle graph shows the dependence on k ₃ and δ ₃; and the bottom graph shows the dependence on superinfection production rates. In the figure, the blue region indicates parameter values for which one viral infection is suppressed by the other viral infection; thus showing reduced duration, while the red region represents prolonged duration of coinfection. According to the top graph, both lower and higher values of superinfection rates give shorter coinfection duration than the single RSV or IAV infection duration. If IAV can reinfect the RSV infected cells as easily as it can infect the uninfected cells, duration of coinfection can be as long as about 1 week irrespective of RSV’s ability to superinfect, although coinfection duration seems to be less sensitive to changes in superinfection rates than the other parameters. In the middle graph, we see that different combinations of k ₃ and δ ₃ give different coinfection durations with coinfection duration increasing as both k ₃ and δ ₃ decrease. Biologically this means that if superinfection causes viruses to utilize more time for intracellular activities (attachment, entry, uncoating, biosynthesis) and causes superinfected infectious cells to have a longer life span compared to single viral infections, duration of coinfection can prolong beyond 9 days. In the last graph, superinfection production rates have the most complex effect on coinfection duration with IAV superinfection production rate increases leading to longer coinfection durations, but RSV superinfection production rate increases having the opposite effect.

Fig. 7.

Coinfection duration as a function of superinfection parameters when both target cell regeneration and death are absent. Coinfection duration dependence on superinfection infection rates varied from single virus infection rates (baseline rates) of IAV and RSV, i.e. $8.27\times {10}^{-6}$ and $3.08\times {10}^{-2}$ (PFU/mL)${}^{-1}$ d${}^{-1}$ respectively (top), superinfected transition rate of eclipse cells and death rate of infectious cells varied from the baseline rates, i.e. 4.2 d${}^{-1}$ for both (IAV parameter) (middle), and superinfection production rates varied from the baseline rates of IAV and RSV, i.e. 1.2 × 10⁸ and 7.64 × 10³ PFU/mL d${}^{-1}$ respectively (bottom). Other parameters are fixed to respective single virus parameters according to Table 1. Star on the images indicates the baseline values 5.

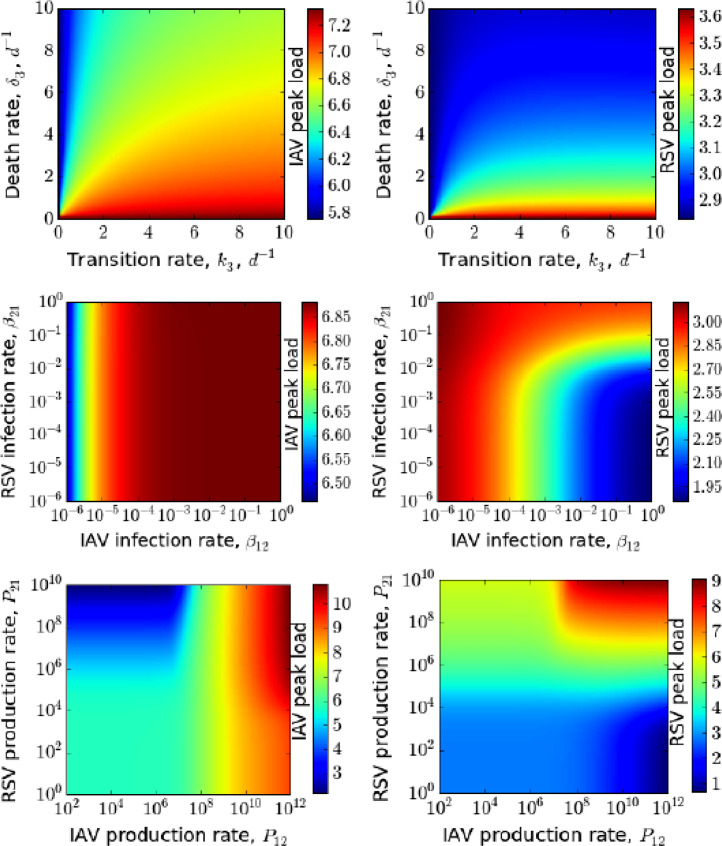
Another measure of disease severity is the peak viral load. In Fig. 8 , we examine how changes in superinfection parameters affect the peak viral loads of IAV and RSV in coinfection. We see that the production rates of superinfected cells influence peak viral load more than other superinfection parameters. Peak viral load for IAV and RSV are not, respectively, more than 10^7.2 and 10^3.6 PFU/mL even if the average transition time of superinfected eclipse cells to infectious cells and the death rate are short ( ∼ 2.4 hours) along with the slowest death rate of infectious cells. Similarly, a large variation in superinfection rates of IAV and RSV does not produce peak viral load higher than production rates from superinfected cells. Conversely, the peak viral loads can be as high as 10⁹ PFU/mL due to superinfection if virus production rates are as high as 10¹⁰ PFU/mL d${}^{-1}$. Although IAV produces almost similar peak viral load to RSV for a wider range of production rates ($1-{10}^{10}$ PFU/mL d${}^{-1}$), RSV only reaches higher peak viral load when both of them produce more than 10⁸ PFU/mL d${}^{-1}$. Thus, if superinfection production rates are higher than production rates in singly infected cells, the peak loads of each virus can be increased. This is not a likely scenario, however, since viruses are competing for intracellular resources (Fayyadh, Ma, Qin, Zhang, Li, Zhang, et al., 2017, Shinjoh, Omoe, Saito, Matsuo, Nerome, 2000), so it is more likely that superinfected cells will produce less of a particular virus than singly infected cells. A detailed sensitivity analysis for this model (2) is also given in the supplemental document [see Additional file]

Fig. 8.

Peak viral load (log₁₀PFU/mL) of IAV and RSV as a function of superinfection parameters when both target cell regeneration and death are absent. Variation in peak viral load of IAV (left column) and RSV (right column) are shown by varying transition rate of superinfected eclipse cell and death rate of superinfected cell (top row), superinfection infection rates of IAV and RSV (middle row) and superinfection production rates of IAV and RSV (bottom row). All other parameters are from Table 1.

3.3. Delayed initiation of coinfection

Here, we study the conditions of coexistence by studying invasion of the second virus into a system where the first virus is at a steady state. To do so, we perform the steady state analysis for the single virus system setting the second virus system equal to zero. For which the model (1) reduces to

$$\begin{array}{cc}\hfill \mathrm{Target}\text{cells}:\dot{T}& =r-aT-{\beta }_{1}T{V}_1\hfill \\ \hfill \mathrm{Eclipse}\text{cells}:\dot{E_1}& ={\beta }_{1}T{V}_1-k_1{E}_1\hfill \\ \hfill \mathrm{Infectious}\text{cells}:\dot{I_1}& =k_1{E}_1-{\delta }_1{I}_1\hfill \\ \hfill \mathrm{Virus}:\dot{V_1}& =p_1{I}_1-c_1{V}_1.\hfill \end{array}$$

There are now two different equilibria; an infection free equilibrium, $Q_1^{*},$ and a chronic single viral infection equilibrium, $Q_2^{*}$. Their expressions are

$$\begin{array}{ccc}\hfill Q_1^{*}& =& (\overline{T},{\overline{E}}_1,{\overline{I}}_1,{\overline{V}}_1)=(\frac{r}{a},0,0,0)\text{and}\hfill \\ \hfill Q_2^{*}& =& (\frac{c_1{\delta }_1}{{\beta }_1{p}_1},\frac{1}{k_1}\{\frac{{\beta }_1{p}_{1}r-a{c}_1{\delta }_1}{{\beta }_1{p}_1}\},\frac{1}{{\delta }_1}\{\frac{{\beta }_1{p}_{1}r-a{c}_1{\delta }_1}{{\beta }_1{p}_1}\},\hfill \\ & & \frac{1}{{\beta }_1}\left\{\frac{{\beta }_1{p}_{1}r-a{c}_1{\delta }_1}{c_1{\delta }_1}\right\}).\hfill \end{array}$$

The chronic single infection equilibrium exists if the following condition holds true.

$$\begin{array}{c}\hfill \frac{{\beta }_1{p}_1}{c_1{\delta }_1}>\frac{a}{r}\text{or}{\mathcal{R}}_{01}>\frac{a}{r}.\end{array}$$

3.3.1. Stability analysis

The eigenvalues of the infection free equilibrium, $Q_1^{*},$ are (${\lambda }_1\to -a,{\lambda }_2,{\lambda }_3,{\lambda }_4)$. Here λ ₂, λ ₃ and λ ₄ are the roots of function F ₁(λ _{2, 3, 4}), where the function F_i(λ _{2, 3, 4}) is

$$\begin{array}{ccc}& & {\lambda }_{2,3,4}^3+{\lambda }_{2,3,4}^{2}a(c_1+{\delta }_1+k_1)+{\lambda }_{2,3,4}{a}^2(c_1{\delta }_1+{\delta }_1{k}_1+c_1{k}_1)\hfill \\ & & +a^2{k}_1(a{c}_1{\delta }_1-r{\beta }_1{p}_1).\hfill \end{array}$$

For ${\displaystyle \frac{{\beta }_1{p}_1}{c_1{\delta }_1}}<{\displaystyle \frac{a}{r}}$ or ${\mathcal{R}}_{01}<{\displaystyle \frac{a}{r}},$ the function F ₁(λ _{2, 3, 4}) generates one negative real root and two imaginary roots with negative real parts. This implies that under the condition, ${\mathcal{R}}_{01}<{\displaystyle \frac{a}{r}},$ the infection free equilibrium is asymptotically stable and the system oscillates around this steady state. On the other hand, the eigenvalues of the chronic single infection equilibrium, $Q_2^{*},$ are the roots of the function, F ₂(λ _{1, 2, 3, 4}). Function F ₂(λ _{1, 2, 3, 4}) is

$$\begin{array}{cc}\hfill A{\lambda }_{1,2,3,4}^4+& B{\lambda }_{1,2,3,4}^3+C{\lambda }_{1,2,3,4}^2+D{\lambda }_{1,2,3,4}+E,\text{where}\hfill \\ \hfill A=& 1,\hfill \\ \hfill B=& c_1{\delta }_1{p}_1(c_1{\delta }_1+{\delta }_1^2+{\delta }_1{k}_1)+{\beta }_1{\delta }_1{p}_1^{2}r,\hfill \\ \hfill C=& c_1^2{\delta }_1^4{p}_1^2(c_1{\delta }_1+c_1{k}_1+{\delta }_1{k}_1)+{\beta }_1{c}_1{\delta }_1^3{p}_1^{3}r(c_1+{\delta }_1+k_1),\hfill \\ \hfill D=& {\beta }_1{c}_1^2{\delta }_1^5{p}_1^{4}r(c_1{\delta }_1+c_1{k}_1+{\delta }_1{k}_1),\hfill \\ \hfill E=& c_1^4{\delta }_1^8{k}_1{p}_1^4({\beta }_1{p}_{1}r-a{c}_1{\delta }_1).\hfill \end{array}$$

Now for ${\displaystyle \frac{{\beta }_1{p}_1}{c_1{\delta }_1}}>{\displaystyle \frac{a}{r}}$ or ${\mathcal{R}}_{01}>{\displaystyle \frac{a}{r}},$ the function F ₂(λ _{1, 2, 3, 4}) generates no positive roots (according to Descartes’ rule of sign). This implies that the chronic infection equilibrium is asymptotically stable under the condition, ${\mathcal{R}}_{01}>{\displaystyle \frac{a}{r}}$.

3.3.2. Secondary infection

Next, we assume that the first virus initially remains at this equilibrium ($V_1^{*}$) when the second virus, V ₂, is introduced in the system. Thus the system of superinfection becomes

$$\begin{array}{cc}\hfill \mathrm{Target}\text{cell}:\dot{T}& =r-aT-{\beta }_{1}T{V}_1^{*}-{\beta }_{2}T{V}_2\hfill \\ \hfill \mathrm{Eclipse}\text{cell}:\dot{E_2}& ={\beta }_{2}T{V}_2-{\beta }_{12}{E}_2{V}_1^{*}-k_2{E}_2\hfill \\ \hfill \mathrm{Superinfected}\text{eclipse}\text{cells}:\dot{E_3}& ={\beta }_{21}{E}_1^{*}{V}_2+{\beta }_{12}{E}_2{V}_1^{*}-k_3{E}_3\hfill \\ \hfill \mathrm{Infectious}\text{cell}:\dot{I_2}& =k_2{E}_2-{\delta }_2{I}_2\hfill \\ \hfill \mathrm{Superinfected}\text{infectious}\text{cell}:\dot{I_3}& =k_3{E}_3-{\delta }_3{I}_3\hfill \\ \hfill \mathrm{Second}\text{virus}:\dot{V_2}& =p_2{I}_2+p_{21}{I}_3-c_2{V}_2.\hfill \end{array}$$ (3)

The model (3) gives the following steady state solutions. They are

$$\begin{array}{ccc}\hfill Q_1^{*}& =& (\frac{r}{a+{\beta }_1{\overline{V}}_1},0,0,0,0,0)\text{and}\hfill \\ \hfill Q_2^{*}& =& (T^{*},E_2^{*},E_3^{*},I_2^{*},I_3^{*},V_2^{*})\text{where}\hfill \\ \hfill T^{*}& =& \frac{r}{{\beta }_1{\overline{V}}_1+{\beta }_2{V}_2^{*}+a},\hfill \\ \hfill E_2^{*}& =& \frac{{\beta }_2{T}^{*}{V}_2^{*}}{k_2+{\beta }_{12}{\overline{V}}_1},E_3^{*}=\frac{1}{k_3}({\beta }_{21}{\overline{E}}_1{V}_2^{*}+{\beta }_{12}{E}_2^{*}{\overline{V}}_1),\hfill \\ \hfill I_2^{*}& =& \frac{k_2}{{\delta }_2}{E}_2^{*},I_3^{*}=\frac{k_3}{{\delta }_3}{E}_3^{*},\hfill \\ \hfill V_2^{*}& =& \frac{r(p_2{\beta }_2{k}_2{\delta }_3+p_3{\beta }_{12}{\delta }_2{\beta }_1{\overline{V}}_1)-{\delta }_2(a+{\beta }_2{\overline{V}}_1)(c_2{\delta }_3-p_3{\beta }_{21}{\overline{E}}_1)(k_2+{\beta }_{12}{\overline{V}}_1)}{{\beta }_2{\delta }_2(c_2{\delta }_3-p_3{\beta }_{21}{\overline{E}}_1)(k_2+{\beta }_{12}{\overline{V}}_1)}.\hfill \end{array}$$

In addition to the primary chronic single infection, this secondary chronic single infection equilibrium exists if the following conditions hold true, i.e

$$\begin{array}{ccc}& & r(p_2{\beta }_2{k}_2{\delta }_3+p_3{\beta }_{12}{\delta }_2{\beta }_1{\overline{V}}_1)>{\delta }_2(a+{\beta }_2{\overline{V}}_1)\hfill \\ & & (c_2{\delta }_3-p_3{\beta }_{21}{\overline{E}}_1)(k_2+{\beta }_{12}{\overline{V}}_1),\text{and}\hfill \\ & & \frac{p_3{\beta }_{21}}{c_2{\delta }_3}>{\overline{E}}_1,\text{or}\frac{p_3{\beta }_{21}}{c_2{\delta }_3}>\frac{a}{k_1}(\frac{r}{a}-\frac{1}{{\mathcal{R}}_{01}}),\text{where}{\mathcal{R}}_{01}>\frac{a}{r}.\hfill \end{array}$$

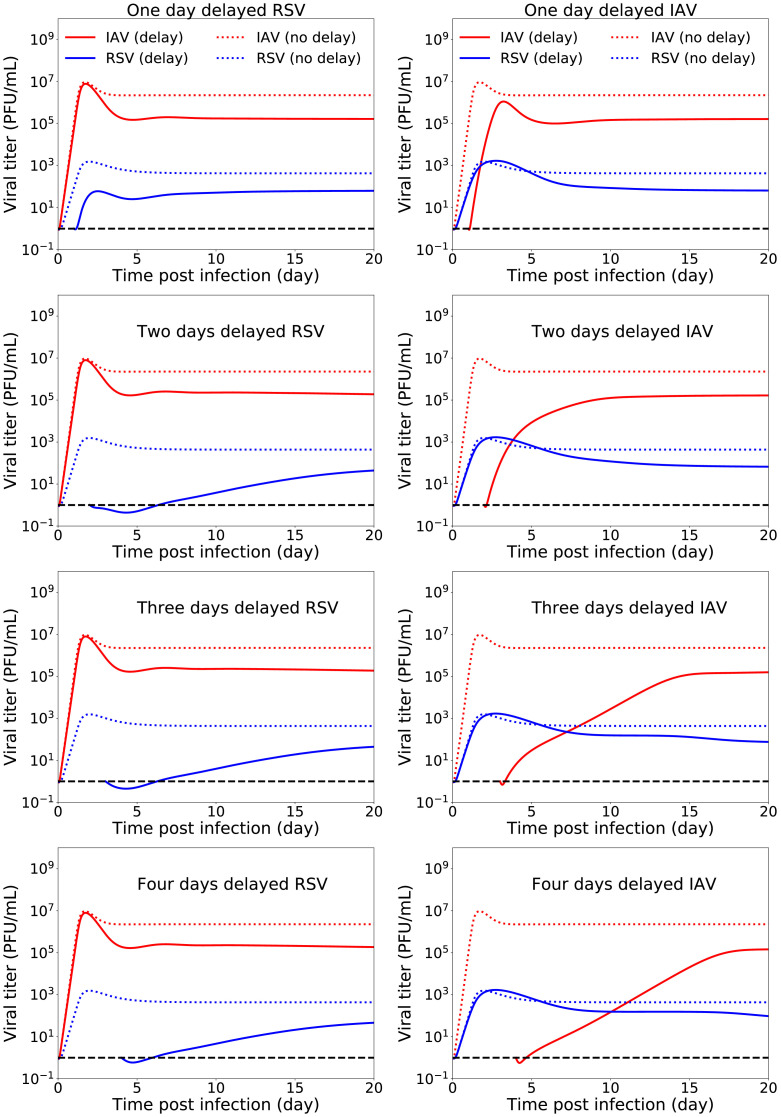
Here, if there is no regeneration, i.e. $r=0,$ the chronic infection steady states become the infection free steady state. Numerical simulation of this delayed infection model (Fig. 9 ) shows that for a time interval of the length 1 to 4 days between two infections, IAV as a primary infection suppresses the growth of RSV as a secondary infection while RSV being the primary does not affect the growth of IAV. Note that when the infections are not started simultaneously, the chronic virus titers are lowered from simultaneous infection for both viruses.

Fig. 9.

Effects of inter-exposure intervals on IAV-RSV coinfection dynamics (model(3)). The first and second column represent coinfection dynamics when RSV infection and IAV infection are delayed respectively. The superinfection parameters are fixed to single virus parameters (Table 1). The dotted red and blue lines show the infection dynamics of IAV and RSV in case of no delay respectively. The horizontal dashed black line indicates the virus detection limit. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

4. Discussion

In this paper, we have shown that superinfection can result in chronic coinfection if cell regeneration is also considered in the model. Our previous work showed that while cell regeneration is necessary for producing chronic infection, it is not sufficient for chronic coinfections (Pinky and Dobrovolny, 2017). This work shows that superinfection alone is also not sufficient for chronic coinfections. When new cells are available for both viruses during the course of coinfection, the virus with the higher growth rate will infect more of the available cells than the slower-growing virus. On the other hand, the slower-growing virus which infected fewer cells in the previous cycle will infect even fewer cells in every subsequent cycle of infection, eventually disappearing. However, if there is superinfection, the slower-growing virus does not have to be the first to infect a particular cell — it can infect a particular cell after the faster-growing virus has already infected the cell. In this way, replication of both viruses can be maintained indefinitely. This is supported by our observation that chronic coinfection is maintained by the superinfected cells.

While our model suggests one possible mechanism for chronic coinfections, particularly suitable for immunocompromised patients, the model is simple and neglects many of the complex biological process underlying virus-cell and virus-virus interactions. These processes can give rise to other mechanisms that could possibly lead to chronic coinfections. Perhaps the most glaring omission in the model is the lack of an immune response, which can be an important mechanism for interaction between the two viruses (Hodgson et al., 2004). A suggested mechanism for chronic coinfection via immune interaction is through the innate immune response. When a pathogen invades a host for the first time, a nonspecific innate immune response is immediately elicited. During subsequent infection it can be weakened enough due to the primary infection to let the nearby cells be more susceptible to a secondary viral infection (Simeonov et al., 2010). This antagonistic effect on the primary virus can facilitate access for another viral infection which can persist at the same time (Mideo, 2009). Introducing the immune responses to the model will allow for exploration of these mechanisms of virus-cell interactions. Unfortunately, the inclusion of additional parameters to address immune responses in the model has to be calibrated with a sufficient amount of experimental data that is not readily available. Another possible mechanism for chronic coinfections is cell tropism. Respiratory viruses are reported to show cell tropism, which is a viral preference for certain types of cells (Matrosovich et al., 2015). So two different viruses may infect different respiratory cell types, limiting competition for host cells because of resource partitioning (Hodgson et al., 2004). Thus both viruses may coexist in the respiratory tract for longer times and might also contribute to more virus production since now they have exclusive access to certain cells. Again, a mathematical model extended to include two distinct cell populations would allow exploration of the conditions necessary for chronic viral coinfections in this scenario.

The model also makes a number of assumptions about the superinfection process. Since experimental observations of this process are still in the early stages, there is not much known about the details. For example, we limit a cell’s susceptibility to a second infection to the eclipse phase of the first virus. There is, as yet, no experimental evidence to inform us of how long an infected cell remains susceptible to a secondary infection. We also allow for the infectious lifespan and eclipse phase duration of superinfected cells to differ from singly infected cells. This is motivated by the idea that viruses share internal resources (Shinjoh et al., 2000), which might slow production of proteins and RNA, thereby lengthening the eclipse phase duration. But other mechanisms might alter the rates of internal protein and RNA production. Infection of a cell induces cellular responses that inhibit the replication of the virus (Tang, Na, Zhu, Shen, Yang, Fu, et al., 2014, Tian, Guo, Wei, Yang, He, Wang, 2012, Xue, Fu, Ma, Zhang, Li, Feng, et al., 2018) while viruses have developed mechanisms to prevent these responses (Wang et al., 2014). Thus, if one of the viruses involved in the superinfection can inhibit a cellular response that suppresses viral replication, the other virus can be produced more quickly than it would if it were infecting the cell alone. Finally, we assumed that a superinfected cell starts producing both viruses and stops producing both viruses at the same time. In all likelihood, the time at which a cell starts and stops producing virus is determined by the time elapsed since the cell was infected by a particular virus. Since individual cells are not infected with both viruses simultaneously, they will not start producing virus simultaneously. Addition of age-structure to within host models does not alter the long-term dynamics of the model (Browne, 2015, Browne, Pilyugin, 2013, Holder, Simon, Liao, Abed, Bouhy, CAA, et al., 2011), but does change the duration of the infection, so addition of more accurate age structure will likely alter the coinfection duration. These details will need to be explored experimentally so that they can be added to more detailed models of coinfection.

It is important to understand the conditions that lead to chronic coinfections since chronic respiratory tract virus infections can, if severe, exacerbate, or alter lung function for an extended period and can lead to chronic pulmonary inflammatory diseases such as asthma and COPD (Pelaia et al., 2006). Additionally, chronic coinfections have the potential to spread viral infections broadly within the human population since one person is shedding two different viruses over a long period of time. In such cases, treatment becomes an important consideration. Treatment of only one of the viruses could result in growth of a potentially harmful virus that was suppressed to some extent by the presence of the other virus. Antiviral treatment can be more efficient in treating superinfecting viruses if a broad spectrum antiviral is used, allowing for simultaneous treatment of both viruses (Calenda et al., 2017).

Our work was motivated by the fact that the impact of coinfections in human respiratory tract have not yet been evaluated in either theoretical or experimental studies on a large scale even though there is evidence of a substantial number of hospitalized patients suffering from severe disease outcomes due to coinfections (Malekshahi, Shafiei-Jandaghi, Yavarian, Shadab, Naseri, Azad, 2017, Mazur, Bont, Cohen, Cohen, von Gottberg, Groome, et al., 2017). Here, we have shown with our model that the combined mechanism of superinfection and cell regeneration can lead to chronic coinfections. Since a few experiments (Fayyadh, Ma, Qin, Zhang, Li, Zhang, et al., 2017, Shinjoh, Omoe, Saito, Matsuo, Nerome, 2000) confirm that different viruses can infect the same cell, this provides a plausible mechanism for chronic viral coinfections.

Conflicts of interest

Hana M. Dobrovolny received funding from Janssen R&D Belgium, and Gilberto Gonzalez-Parra’s salary was paid by a grant from Janssen R&D Belgium.

Author’s contributions

L.P., G.G.P. and H.M.D conceived the experiments, L.P. conducted the experiments, L.P. analyzed the results. L.P. and H.M.D. wrote the paper. All authors reviewed the manuscript.

Appendix A. Supplementary materials

Supplementary Data S1

Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/