Interplay between epidemic spread and information propagation on metapopulation networks

Abstract

The spread of an infectious disease has been widely found to evolve with the propagation of information. Many seminal works have demonstrated the impact of information propagation on the epidemic spreading, assuming that individuals are static and no mobility is involved. Inspired by the recent observation of diverse mobility patterns, we incorporate the information propagation into a metapopulation model based on the mobility patterns and contagion process, which significantly alters the epidemic threshold. In more details, we find that both the information efficiency and the mobility patterns have essential impacts on the epidemic spread. We obtain different scenarios leading to the mitigation of the outbreak by appropriately integrating the mobility patterns and the information efficiency as well. The inclusion of the impacts of the information propagation into the epidemiological model is expected to provide an support to public health implications for the suppression of epidemics.

Highlights

• •A model of epidemiological metapopulation combined with the information propagation is proposed.
• •Both information propagation and human mobility patterns coeffect the epidemic spread.
• •Scenarios of mitigation of outbreaks by considering information propagation and human mobility patterns are proposed.

1. Introduction

Infectious diseases are transmitted through social contacts between individuals. The modeling of epidemic spreading among human beings has been extensively studied in mathematical epidemiology and network science. The developments of transportation system have enabled people to travel more globally. Consequently, epidemics starting from a local patch can spread to the entire network in a very short time. Recently, the metapopulation modeling approach has been broadly applied to study infectious disease spreading among the spatial structure of populations with well-defined social units (Colizza et al., 2007, Colizza and Vespignani, 2007, Balcan et al., 2010). Then the metapopulation network model has been greatly developed by considering a number of factors such as the network structure (Watts et al., 2005, Cao et al., 2011, Wang et al., 2014), human mobility patterns (Belik et al., 2011a, Belik et al., 2011b, Balcan and Vespignani, 2011, Balcan and Vespignani, 2012, Poletto et al., 2012), human behavior (Meloni et al., 2011, Wang et al., 2012), and human contact patterns (Wang et al., 2013, Yang et al., 2011, Iribarren, 2009). It has been shown that the substrate network structure (Watts et al., 2005, Cao et al., 2011, Wang et al., 2014) plays an essential role in the spatial spread of epidemics. In real-world networks, human mobility patterns vary in a very complicated way, e.g., recurrent visits of patches (Belik et al., 2011a, Belik et al., 2011b, Balcan and Vespignani, 2011, Balcan and Vespignani, 2012), diverse staying period in patches (Poletto et al., 2012), etc. Human behavioral responses to the epidemics have also been found to be able to delay the epidemic spread (Meloni et al., 2011, Wang et al., 2012). With regard to human contact patterns, location-specific contact patterns have been investigated (Wang et al., 2013). Recently, since human contact patterns are temporal, the nature of burstiness and heterogeneity in human activities has been found in empirical studies, and it has striking effects on the speed of spreading (Yang et al., 2011, Iribarren, 2009, Masuda and Holme, 2013). For instance, heterogeneity of human activity is responsible for the slow dynamics of information propagation (Iribarren, 2009).

Human beings often react to the presence of an infectious disease by changing their behavior. The perception of the risk associated with the infection and countermeasures are usually accompanied with the behavior like cutting the connection with infectious contacts to form adaptive rewiring (Gross et al., 2008, Wang et al., 2011, Belik et al., ), accepting vaccination (Bauch and Earn, 2004), wearing face-masks, reducing travel range (Lima et al., 2015), etc. Within the epidemic-related game, the change of human behavior such as tradeoff between cost and risk often results in the decision-making process like vaccination via a game-theoretic framework (Basu et al., 2008, Perisic and Bauch, 2009, Zhang et al., 2013).

Many works have focused on the impact of information propagation on separating a non-epidemic state and an epidemic state. With the progression of the outbreak, messages on the epidemics, such as fears of the disease and self-initiated awareness, may be passed from one individual to another (Epstein et al., 2008, Perra et al., 2011). Following the seminal work in Ref. (Funk et al., 2009), the source of information (e.g., local or global awareness) and the pattern of information dissemination have been widely studied (Funk et al., 2010, Wu et al., 2012, Granell et al., 2013, Sahneh et al., 2013, Yuan et al., 2013, Zhang et al., 2014). Depending on the path of information propagation, there are several types of information. For instance, people obtain information from broadcasting and the Internet, which could be taken as a kind of global information. People can also exchange information by face-to-face contacts, which is a kind of contact-based information (Funk et al., 2009). So far, the study of the impacts of information propagation on the epidemic spread has been restricted to individual-based networks, where one node corresponds to one individual (Zhang et al., 2014).

Under the framework of metapopulation model, people may get infected by contacting with infectious individuals within the same patch; they may exchange information related to the presence of an infectious disease through face-to-face contacts (Funk et al., 2009, Funk et al., 2010). Information carriers may pass the message of the epidemic situation to uninformed individuals, which may potentially alter their future mobility patterns, thus, affecting the epidemic spread. This has been observed in real-world situations, where people are usually reluctant to visit infected areas (Bajardi et al., 2011, Camitz and Liljeros, 2006). The diameter of human mobility during the H1N1 epidemic has been found to reduce significantly with the progression of alert campaign, which verifies the fact that human beings indeed alter their movements when being exposed to the presence of the information during the outbreak of epidemics (Bajardi et al., 2011).

In this paper, we present a metapopulation framework to explore the interplay between epidemic dynamics and information dynamics based on diverse mobility patterns. With a mean-field approximation of the metapopulation model, we find that both the information efficiency and the mobility patterns jointly affect the epidemic spread in terms of both the outbreak size and the epidemic threshold. When the information efficiency is low, mobility to the patch with more healthy individuals facilitates the epidemic spread with an increased outbreak size and an decreased epidemic threshold, even though more individuals get informed; on the contrary, when the information efficiency is high enough to cause people's attention, mobility to the patch with more healthy individuals, suppresses the epidemic outbreak by informing more individuals. In order to highlight the role of mobility, we apply a simplistic model of information dynamics to that of the disease dynamics; the incorporation of passing messages among mobile individuals in the metapopulation model gives us a new perspective on the countermeasure of epidemics, which is different from the previous studies on the contact-based networks. It suggests a possible way to suppress the epidemic spread by guiding individual mobility patterns in accordance with the evaluation of the risk perception and the information efficiency as well.

2. Model definitions

Before introducing the model, we briefly demonstrate the mobility patterns and information propagation, respectively. Usually, a random mobility pattern is often used for the convenience of theoretical analysis. To be more realistic, we consider that the mobility pattern is driven by the safety level at destination. In facing the outbreak, people usually prefer to visit safer patches in order to avoid infection, i.e., the safer the destination is, the higher the probability that individuals move to it is (Wang et al., 2012).

In the context of information, we regard it to be only accessible by contacting with information carriers as opposed to the general knowledge obtained through multi-media (global awareness) and self-initiated awareness as well. Thus, we focus on the interplay between mobility patterns and information propagation. The role of information in reducing the infection risk is described by the information efficiency, which is classified into two major types: (i) the information that is highly efficient to warn people to take measures in the face of a fatal flu, such as severe acute respiratory syndrome (SARS); (ii) the information that cannot cause people's sufficient attention to take measures in the face of an infectious disease, such as seasonal influenza. As a result, the exchange of information on the risk perception may potentially alter human behavior, e.g., contact structures or travel patterns, which in turn influences the spreading process.

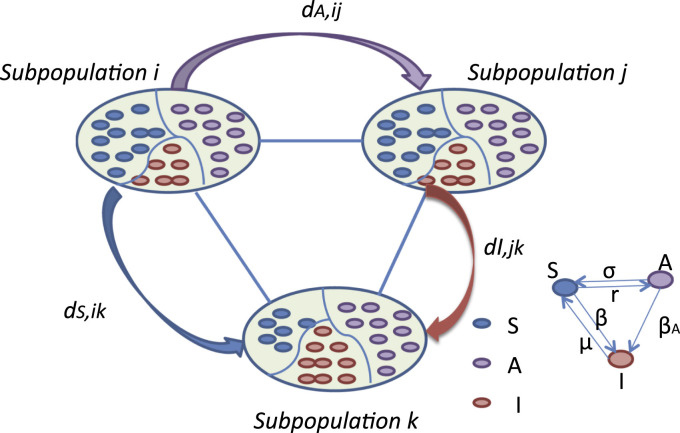
The metapopulation approach describes the spatially structured interacting patches, which are connected by the movement of individuals. Inside each patch, individuals are divided into classes that represent their states according to the infection dynamics. To demonstrate the role of information propagation in the epidemic dynamics, we couple a mathematical model similar to the susceptible-infectious-susceptible (SIS) model for the epidemic dynamics with a model for the information propagation. Due to the information propagation, susceptible individuals are further classified into two types: Uninformed susceptible (S) and informed susceptible (A) individuals. Uninformed susceptible individuals are those who have not yet received the information on the epidemic and may get infected by contacting with infectious individuals at transmission rate β, while informed susceptible individuals (A) may get infected with a reduced transmission rate β _A with ${\beta }_A<\beta$. This is supported by the fact that people may reduce the number of contacts as a defensive response (Poletti et al., 2009) and they also may get infected with a reduced infection transmission rate by self-awareness, such as wearing face-masks or washing hands frequently (Can et al., 2015, Zhang et al., 2015, Zhang et al., 2016). For convenience, we represent the reduced transmission rate as ${\beta }_A=(1-\alpha )\beta$, where α denotes the information efficiency for reduction of infection risk. Infectious individuals may get recovered at rate μ. Here, we assume the nonlimited transmission, where the infection rate is not divided by the total population in the patch. The propagation of information is analogous to that of an infectious disease, often called “information contagion”: information is passed from information carriers to uninformed individuals through contact at rate σ, and information carriers may lose the information at rate r as time goes by. We assume that information is passed by contact instead of self-awareness, and for simplicity, we also assume that infectious individuals are ignorant to the information. In fact, it is more realistic to assume that infectious individuals know the infectious status and they may reduce their contact number by being detected or quarantined, however, it is out of the range of this paper and may be investigated in the future. Fig. 1 illustrates the interplay between the information propagation and the disease spread on metapopulation networks.

Fig. 1.

Schematic illustration of the model of the epidemical spread and the information propagation (SAIS). In this model, each individual falls into one of the three states: uninformed (S), informed (A), and infectious (I). All types of individuals move from patch i to patch j with probability $d_{\theta ,\mathit{ij}}$ for $\theta =S,A,I$. For example, informed individuals in patch i may move to patch j with probability $d_{A,\mathit{ij}}$; susceptible individuals in patch i may move to patch k with probability $d_{S,\mathit{ik}}$. The mobility probability of infectious individuals $d_{I,\mathit{jk}}$ can be defined in a similar way.

Connected patches as a force of infection result from the movement of individuals. Next, let us consider the diffusion process (Colizza and Vespignani, 2008, Saldaña, 2008, Juher et al., 2009). Parallel to the contagion process, simultaneously all the individuals move from one patch to another at rate D. In more details, uninformed, informed, and infectious individuals leave the patch at rates D _S, D _A, and D _I, respectively. Considering the heterogeneity in the real-world networks, individuals in state θ ($\theta =S,A,I$) at patch $k\prime$ (patch with degree $k\prime$ is briefly denoted by patch $k\prime$) move to the neighboring patch k with probability $d_{\theta ,k\prime k}$. Human mobility shows diverse patterns depending on individual's gender, age, and native or non-native (Salon and Gulyani, 2010, Yan et al., 2013, Yang et al., 2017). An explicit expression of $d_{\theta ,k\prime k}$ relies on the knowledge of the empirical data on traveling patterns of human beings (Brockmann et al., 2006, Brockmann and Theis, 2008, González et al., 2008, Song et al., 2010a, Song et al., 2010b). In the following, we use $d_{\theta ,k\prime k}$ as a general expression for mobility probability in the determined reaction-diffusion equations to describe the dynamics of the epidemic and that of the information in the metapopulation system.

By incorporating the contagion process and the information propagation into the diffusion processes, the dynamics of the subpopulation of uninformed, informed, and infectious individuals at patch k, ${\rho }_{S,k}$, ${\rho }_{A,k}$, and ${\rho }_{I,k}$, respectively, are approximated with the mean-field approximation as follows:

$$\frac{d{\rho }_{S,k}}{\mathit{dt}}=-\beta {\rho }_{S,k}{\rho }_{I,k}-\sigma {\rho }_{S,k}{\rho }_{A,k}+\mathrm{\mu }{\rho }_{I,k}+r{\rho }_{A,k}-D_S{\rho }_{S,k}+{\mathit{kD}}_S\sum _{k\prime }{\rho }_{S,k\prime }P(k\prime |k)d_{S,k\prime k},\frac{d{\rho }_{A,k}}{\mathit{dt}}=\sigma {\rho }_{S,k}{\rho }_{A,k}-{\beta }_A{\rho }_{A,k}{\rho }_{I,k}-r{\rho }_{A,k}-D_A{\rho }_{A,k}+{\mathit{kD}}_A\sum _{k\prime }{\rho }_{A,k\prime }P(k\prime |k)d_{A,k\prime k},\frac{d{\rho }_{I,k}}{\mathit{dt}}=\beta {\rho }_{S,k}{\rho }_{I,k}+{\beta }_A{\rho }_{A,k}{\rho }_{I,k}-\mathrm{\mu }{\rho }_{I,k}-D_I{\rho }_{I,k}+{\mathit{kD}}_I\sum _{k\prime }{\rho }_{I,k\prime }P(k\prime |k)d_{I,k\prime k},$$ (1)

for $k_{\mathit{min}}\le k\le k_{\mathit{max}}$, where k _min and k _max are the minimum and maximum degrees of the patches, respectively; $P(k\prime |k)$ is the conditional probability that a patch k connects with a patch $k\prime$. For simplicity of calculation, we assume that the patches connect in an uncorrelated way in the sense that they connect at random, i.e., $P(k\prime |k)=\frac{k\prime P(k\prime )}{〈k〉}$, where $〈k〉={\sum }_k\mathit{kP}(k)$ is the average degree of the network (Newman, 2003) and P(k) is the degree distribution of the network.

Since the information propagation affects the epidemic spread by informing more individuals of the disease and thereby reducing their risk of infection, mobility patterns of the informed susceptible individuals play a fundamental role in the effectiveness of the information propagation, and thus, affect the epidemic spread. To understand the role of mobility patterns in both the dynamics of epidemic spread and that of the information propagation, we investigate the mobility probability from patch $k\prime$ to patch k by assuming the detailed functional form of $d_{\theta ,k\prime k}$ for $\theta =S,A,I$. Intuitively, the more healthy individuals a patch contains, the safer the patch is, and individuals usually prefer to move to safer patches, or in other words, in order to prevent infection they attempt to avoid visiting infected patches. To reflect this effect, following Ref. (Wang et al., 2012), we assume that all the individuals move in accordance with the safety level at the destination, which is mathematically expressed by

$$d_{\theta ,\mathit{kk}\prime }=\frac{{({\rho }_{S,k\prime })}^{{\gamma }_{\theta }}}{k{\sum }_{k″}P(k″|k){({\rho }_{S,k″})}^{{\gamma }_{\theta }}}\mathrm{for}\theta =S,A,I,$$ (2)

for $k_{\mathit{min}}\le k,k\prime \le k_{\mathit{max}}$, where the parameter ${\gamma }_{\theta }$ controls the dependency on the safety level at the patch. By tuning ${\gamma }_{\theta }$, diverse mobility patterns can be observed. For instance, if ${\gamma }_{\theta }>0$, the safer the patch is, the more likely it is that individuals move to the patch; this is consistent with the phenomenon that people attempt to bypass infected areas; in order to deploy a systematic study, we also consider the opposite case with ${\gamma }_{\theta }<0$, which means that the safer the patch is, the less likely it is that people travel to the patch. This may correspond to the situation that people receive incorrect information. If ${\gamma }_{\theta }=0$, the model is reduced to the case of random mobility and Eq. (2) is simplified as follows:

$$\frac{d{\rho }_{S,k}}{\mathit{dt}}=-\beta {\rho }_{S,k}{\rho }_{I,k}-\sigma {\rho }_{S,k}{\rho }_{A,k}+\mathrm{\mu }{\rho }_{I,k}+r{\rho }_{A,k}-D_S{\rho }_{S,k}+D_S\frac{k}{〈k〉}{\rho }_S,\frac{d{\rho }_{A,k}}{\mathit{dt}}=\sigma {\rho }_{S,k}{\rho }_{A,k}-{\beta }_A{\rho }_{A,k}{\rho }_{I,k}-r{\rho }_{A,k}-D_A{\rho }_{A,k}+D_A\frac{k}{〈k〉}{\rho }_A,\frac{d{\rho }_{I,k}}{\mathit{dt}}=\beta {\rho }_{S,k}{\rho }_{I,k}+{\beta }_A{\rho }_{A,k}{\rho }_{I,k}-\mathrm{\mu }{\rho }_{I,k}-D_I{\rho }_{I,k}+D_I\frac{k}{〈k〉}{\rho }_I,$$ (3)

for $k_{\mathit{min}}\le k\le k_{\mathit{max}}$. In the following, we will explore how mobility patterns influence the information propagation and the epidemic process as well.

3. The invasion thresholds for disease dynamics and information dynamics

3.1. The equilibrium point $({\overline{\rho }}_{S,k},{\overline{\rho }}_{A,k},{\overline{\rho }}_{I,k})=({\overline{\rho }}_{S,k},0,0)$

We investigate the ability that a disease or information can survive in the network by analyzing the stability of the disease-free and information-free state at the equilibrium point $({\overline{\rho }}_{S,k},{\overline{\rho }}_{A,k},{\overline{\rho }}_{I,k})=({\overline{\rho }}_{S,k},0,0)$. By inserting Eq. (2) into Eq. (1), the uninformed susceptible individuals at patch k, ${\overline{\rho }}_{S,k}$, at the equilibrium state is given by

$${\overline{\rho }}_{S,k}=\frac{k}{〈k〉}\sum _{k\prime }P(k\prime ){\overline{\rho }}_{S,k\prime }\frac{{({\overline{\rho }}_{S,k})}^{{\gamma }_S}}{{\sum }_{k″}P(k″|k\prime ){({\overline{\rho }}_{S,k″})}^{{\gamma }_S}},$$ (4)

for $k_{\mathit{min}}\le k\le k_{\mathit{max}}$, which is rewritten using $P(k″|k\prime )=\frac{k″P(k″)}{〈k\prime 〉}$ as follows:

$${\overline{\rho }}_{S,k}=\frac{k{\rho }^0{({\overline{\rho }}_{S,k})}^{{\gamma }_S}}{{\sum }_{k″}k″P(k″){({\overline{\rho }}_{S,k″})}^{{\gamma }_S}}=\frac{k{\rho }^0{({\overline{\rho }}_{S,k})}^{{\gamma }_S}}{〈{({\overline{\rho }}_S)}^{1,{\gamma }_S}〉},$$ (5)

where $〈{({\overline{\rho }}_S)}^{.,{\gamma }_S}〉$ denotes an arbitrary order moment of ${({\overline{\rho }}_S)}^{{\gamma }_S}$ and ρ ⁰ is the total population density in the network and the parameter γ _S controls the susceptible population at the equilibrium. The exact solution of ${\overline{\rho }}_{S,k}$ can be numerically solved with the fixed-point iteration with Eq. (5).

The linearized matrix of Eq. (1) around the disease-free and information-free equilibrium is given by

$${\mathbf{J}}_{\mathit{DF}}=\left[\begin{array}{ccc}\hfill D_S(\mathbf{C}-\mathbf{I})\hfill & \hfill -\mathit{diag}(\sigma {\overline{\rho }}_{S,k}-r)\hfill & \hfill -\mathit{diag}(\beta {\overline{\rho }}_{S,k}-\mu )\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathit{diag}(\sigma {\overline{\rho }}_{S,k}-(r+D_A))+D_A\mathbf{C}\hfill & \hfill 0\hfill \\ \hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill & \hfill \mathit{diag}(\beta {\overline{\rho }}_{S,k}-\mu )+D_I(\mathbf{C}-\mathbf{I}),\hfill \end{array}\right],$$ (6)

where each block is a $(k_{\mathit{max}}-k_{\mathit{min}})$ matrix; $\mathbf{0}$ is the null matrix; $\mathbf{I}$ is the identity matrix; $\mathit{diag}(x_k)$ is a diagonal matrix with kth component as x _k; the matrix $\mathbf{C}$ is given by

$${\mathbf{C}}_{\mathit{kk}\prime }=\frac{\mathit{kP}(k\prime )}{〈k〉}.$$ (7)

Since $\mathbf{C}$ is a rank-one matrix, it has an eigenvalue $\lambda =0$ with multiplicity $k_{\mathit{max}}-1$ and an eigenvalue $\lambda =1$. The characteristic equation of ${\mathbf{J}}_{\mathit{DF}}$ is given by $f(\lambda )=f_1(\lambda )f_2(\lambda )f_3(\lambda )$, where $f_1(\lambda )$ is the characteristic equation of $D_S(\mathbf{C}-\mathbf{I})$, $f_2(\lambda )$ is the characteristic equation of $\mathit{diag}(\sigma {\overline{\rho }}_{S,k}-(r+D_A))+D_A\mathbf{C}$, and $f_3(\lambda )$ is the characteristic equation of $\mathit{diag}(\beta {\overline{\rho }}_{S,k}-\mu )+D_I(\mathbf{C}-\mathbf{I})$. The set of eigenvalues of ${\mathbf{J}}_{\mathit{DF}}$ is the union of the solutions $f_1(\lambda )=0$ and those of $f_2(\lambda )=0$ and $f_3(\lambda )=0$. Because $f_1(\lambda )=-\lambda (-{(\lambda +D_S))}^{k_{\mathit{max}}-k_{\mathit{min}}-1}$, the largest eigenvalue of $D_S(\mathbf{C}-\mathbf{I})$ is 0. From a general interlacing theorem of eigenvalues for perturbations of a diagonal matrix by rank-one matrices, the largest eigenvalue ${\lambda }_{\mathit{max},A}$ of $\mathit{diag}(\sigma {\overline{\rho }}_{S,k}-(r+D_A))+D_A\mathbf{C}$ satisfies ${\lambda }_{\mathit{max},A}>{\rho }^0\sigma \frac{k_{\mathit{max}}}{〈k〉}-(r+D_A)$, while the largest eigenvalue ${\lambda }_{\mathit{max},I}$ of $\mathit{diag}(\beta {\overline{\rho }}_{S,k}-(\mu +D_I))+D_I\mathbf{C}$ satisfies ${\lambda }_{\mathit{max},I}>{\rho }^0\beta \frac{k_{\mathit{max}}}{〈k〉}-(\mu +D_I)$. The largest eigenvalue of ${\mathbf{J}}_{\mathit{DF}}$ is given by $\max \{0,{\lambda }_{\mathit{max},A},{\lambda }_{\mathit{max},I}\}$. Therefore, the sufficient condition for the disease-free equilibrium to be unstable is given by

$${\rho }_{c,I}^0\ge \frac{〈k〉}{k_{\mathit{max}}}\frac{\mu +D_I}{\beta },$$ (8)

or the sufficient condition for the information-free equilibrium to be unstable is given by:

$${\rho }_{c,A}^0\ge \frac{〈k〉}{k_{\mathit{max}}}\frac{r+D_A}{\sigma }.$$ (9)

3.2. The equilibrium point $({\overline{\rho }}_{S,k},{\overline{\rho }}_{A,k},{\overline{\rho }}_{I,k},)=({\overline{\rho }}_{S,k},{\overline{\rho }}_{A,k},0)$

Except for the equilibrium point of the disease- and information-free state $({\overline{\rho }}_{S,k},{\overline{\rho }}_{A,k},{\overline{\rho }}_{I,k})=({\overline{\rho }}_{S,k},0,0)$, we have to note that there exists the second equilibrium point $({\overline{\rho }}_{S,k},{\overline{\rho }}_{A,k},{\overline{\rho }}_{I,k})=({\overline{\rho }}_{S,k},{\overline{\rho }}_{A,k},0)$ with ${\overline{\rho }}_{A,k}>0$. Let us start with a simplistic assumption that individuals in all the states move at random, i.e., ${\gamma }_S={\gamma }_A={\gamma }_I=0$ and D _S=D _A. By solving Eq. (1), the population density at patch k, ${\overline{\rho }}_k$, at the equilibrium is given by

$${\overline{\rho }}_k={\overline{\rho }}_{S,k}+{\overline{\rho }}_{A,k}=\frac{k}{〈k〉}{\rho }^0.$$ (10)

With Eq. (1), the informed populations at the equilibrium state, ${\overline{\rho }}_{A,k}$, is obtained by solving the following equation:

$$0=\sigma {\overline{\rho }}_{A,k}^2+(r+D_A-\sigma {\overline{\rho }}_k){\overline{\rho }}_{A,k}-\frac{k}{〈k〉}{\overline{\rho }}_A,$$ (11)

where ${\overline{\rho }}_A={\sum }_{k}P(k){\overline{\rho }}_{A,k}$ is the total informed population at the equilibrium state in the network.

By setting ${\omega }_k=\frac{k}{〈k〉}{\rho }^0-\frac{r+D_A}{\sigma }$, the informed and uninformed susceptible populations at patch k, ${\overline{\rho }}_{A,k}$ and ${\overline{\rho }}_{S,k}$, respectively, at the equilibrium are given by

$${\overline{\rho }}_{A,k}=\frac{{\omega }_k+\sqrt{{\omega }_k^2+4{\displaystyle \frac{k}{〈k〉}}{\overline{\rho }}_A\frac{1}{\sigma }}}{2},$$ (12)

$${\overline{\rho }}_{S,k}=\frac{k}{〈k〉}{\rho }^0-\frac{{\omega }_k+\sqrt{{\omega }_k^2+4{\displaystyle \frac{k}{〈k〉}}{\overline{\rho }}_A\frac{1}{\sigma }}}{2},$$ (13)

where the equilibrium solution ${\overline{\rho }}_{A,k}$ can be solved with the fixed point iteration.

The equilibrium becomes unstable if the uninformed susceptible and informed susceptible individuals become infected before the infected individuals get recovered, that is,

$$\frac{\beta {\overline{\rho }}_{S,k}+{\beta }_A{\overline{\rho }}_{A,k}}{\mu +D_I}\ge 1,$$ (14)

which is rewritten as

$$\frac{{\displaystyle \frac{2k}{〈k〉}}{\rho }^0-\alpha \sqrt{{\omega }_k^2+4{\displaystyle \frac{k}{〈k〉}}{\overline{\rho }}_A\frac{D_A}{\sigma }}}{2{\displaystyle \frac{\mu +D_I}{\beta }}}\ge 1,$$ (15)

where $0\le \alpha \le 1$, ${\overline{\rho }}_A$ can be obtained from Eq. (11). In order to trigger an epidemic outbreak, there exists a third invasion threshold, ${\rho }_{c,\mathit{AI}}^0$, such that the unformed and informed susceptible individuals get infected by contacting with the infectious individuals. Regarding ${\overline{\rho }}_A$ as a parameter, ${\rho }_{c,\mathit{AI}}^0$ is such ρ ⁰ that satisfies the condition (15). The exact value of ${\rho }_{c,\mathit{AI}}^0$ can be obtained numerically.

If ${\rho }^0\le {\rho }_{c,I}^0$ and ${\rho }^0\ge \max \{{\rho }_{c,A}^0,{\rho }_{c,\mathit{AI}}^0\}$, then the epidemic occurs by infecting more informed individuals instead of infecting uninformed individuals. If ${\rho }^0\ge {\rho }_{c,I}^0$ and ${\rho }_{c,A}^0\le {\rho }^0\le {\rho }_{c,\mathit{AI}}^0$, then the epidemic occurs by infecting more uninformed individuals instead of infecting informed individuals.

Let us see some specific cases. When $\alpha =0$, all the informed individuals get infected at the same infection rate as the uninformed individuals do, and ${\rho }_{c,\mathit{AI}}^0={\rho }_{c,I}^0$; when $\alpha =1$, all the informed individuals get full immunity to the disease with the infection rate ${\beta }_A=0$; hence, the threshold condition is given by ${\overline{\rho }}_{S,k}\frac{\beta }{\mu +D_I}=1$, where ${\overline{\rho }}_{S,k}$ satisfies the condition ${\overline{\rho }}_S={\sum }_{k}P(k){\overline{\rho }}_{S,k}$ and ${\overline{\rho }}_S={\rho }^0-{\overline{\rho }}_A$, which is consistent with Eq. (8); when $0<\alpha <1$, if ${\rho }_{c,\mathit{AI}}^0>{\rho }^0>{\rho }_{c,A}^0$, it indicates that the population density ρ ⁰ is large enough to inform a quantitative size of susceptible individuals but it is not large enough to infect them, whereas it is possible that the outbreak occurs by infecting the informed individuals if ${\rho }^0>{\rho }_{c,\mathit{AI}}^0$.

4. Numerical results

4.1. Impacts of mobility patterns on the final prevalence of the epidemic

In order to take the safety movement patterns into account, in the following, we investigate three representative types of mobility patterns: (i) ${\gamma }_{\theta }>0$: individuals in state θ ($\theta =S,A,I$) prefer to move to safer patches; (ii) ${\gamma }_{\theta }<0$: individuals in state θ prefer to move to less safe patches; (iii) ${\gamma }_{\theta }=0$: individuals in state θ move at random. We take case (iii) as a standard criterion for comparison with cases (i) and (ii). In a more detailed way, we investigate the situation that both the uninformed and informed individuals follow the same mobility patterns with ${\gamma }_S={\gamma }_A$ and the situation that they follow opposite mobility patterns with ${\gamma }_S>0$ and ${\gamma }_A<0$ or vice versa. Networks of patches are generated with the configuration network model (Molloy and Reed 1995) with size N=2000 following the degree distribution $P(k)\sim k^{-2.5}$ with $k_{\mathit{min}}=2$. Simulation results are based on averaging over more than 100 results for different initial conditions and network structures. Without specification, all the infectious individuals are assumed to move at random with ${\gamma }_I=0$. We randomly seed 0.1% of the total population for each of the dynamics of infectious disease and information propagation. This condition ensures that the outbreak for each dynamics is started separately.

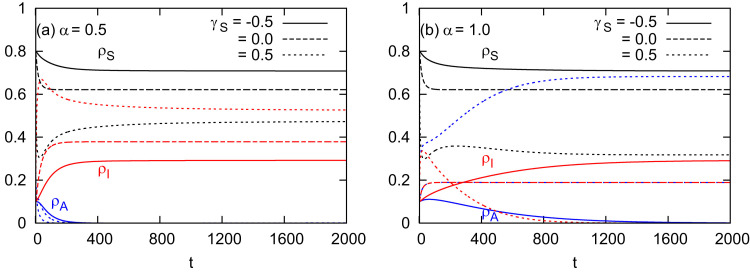
Time courses of the uninformed, informed, and infectious populations for different combinations of α and mobility patterns γ _S (γ _A) are shown in Fig. 2 . When α is at a medium level, that is, the informed individuals get infected with a half risk of infection ($\alpha =0.5$, Fig. 2 (a)), the informed population (the blue curves) firstly grows and then reduces to zero due to the infection by infectious individuals, leaving the uninformed and infectious populations at the stable state. The final prevalence of infection also depends on mobility patterns. For instance, moving to safer patches (${\gamma }_S={\gamma }_A=0.5>0$, the dotted curve) causes a relatively higher prevalence, while, on the contrary, moving to less safe patches (${\gamma }_S={\gamma }_A=-0.5<0$, the solid curve) causes a lower prevalence.

Fig. 2.

Time courses of the prevalences for different combinations of α and mobility patterns controlled by γ_S. (a) $\alpha =0.5$; (b) $\alpha =1.0$. Informed and uninformed individuals are assumed to move in the same way (${\gamma }_A={\gamma }_S$). Uninformed susceptible population (the black curve); informed susceptible population (the blue curve); infectious population (the red curve). The mobility parameters are set at ${\gamma }_S=-0.5$ (the solid curve), ${\gamma }_S=0$ (the dashed curve), and ${\gamma }_S=0.5$ (the dotted curve). The population density is set at ${\rho }^0=2$ and the epidemiological parameters are set at $\beta =\sigma =0.1$ and $\mu =r=0.2$. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

4.2. Impacts of information efficiency on the final prevalence of epidemics

In the case of an extremely perfect information efficiency with $\alpha =1.0$ (Fig. 2 (b)), where the informed individuals become totally immune to the infectious disease, the informed population sustains a non-zero value only if people move to safer patches (${\gamma }_S=0.5$, the blue dotted curve). In this case, mobility patterns play a role different from that at a lower α (Fig. 2 (a)). Since informed individuals get full immunity to the infection, the more individuals get informed, the less individuals get infected. Hence, moving to the patch that contains more susceptible individuals will inform more and make them immune to the infectious disease. As a result, mobility patterns with ${\gamma }_S={\gamma }_A=0.5>0$ inform individuals most (the blue dotted curve) and yield the lowest prevalence of infection (the red dotted curve).

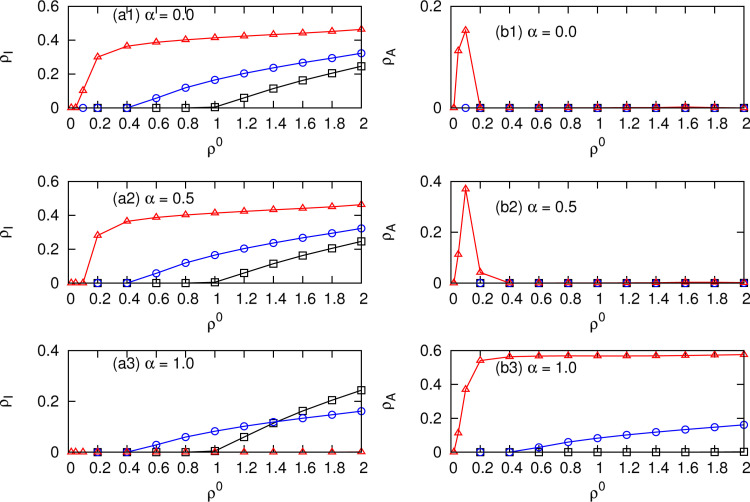
The final prevalence of infection and that of the informed individuals for different choices of α can be further observed in Fig. 3 . The final prevalence depends on the combined role of the information efficiency and mobility patterns. For instance, when $\alpha =0$, the informed individuals get the same infection rate as the uninformed individuals do. We firstly observe that moving to the less safe patch can cause a higher epidemic threshold and a lower prevalence irrespective of the information efficiency α (Fig. 3 (a1), the black squares). Conversely, moving to the safer patches causes a smaller epidemic threshold and a higher prevalence (Fig. 3 (a1), the red triangles). The informed population firstly grows by informing susceptible individuals, and then it ceases to grow and reduces to zero due to the infection by contacting with infectious individuals (Fig. 3 (b1)).

Fig. 3.

Final prevalences of the infectious population ρ_I ((a)) and that of the informed population ρ_A ((b)) for different combinations of α and the mobility patterns γ_S (γ_A). (a1) and (b1), $\alpha =0.0$; (a2) and (b2), $\alpha =0.5$; (a3) and (b3), $\alpha =1.0$. The mobility parameters are set at ${\gamma }_S={\gamma }_A=-0.5$ (the black squares); ${\gamma }_S={\gamma }_A=0$ (the blue circles), and ${\gamma }_S={\gamma }_A=0.5$ (the red triangles). The other parameters are the same as in Fig. 2. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

With the increase of the information efficiency such as $\alpha =0.5$, the informed individuals get a reduced risk of infection. We find that even if the infection rate is reduced to half, the final prevalence of infection does not obviously decrease for all the mobility patterns that we tested (Fig. 3 (a2)). With further increase of α, such as $\alpha =1$, the informed individuals get full immunity to the infectious disease. When individuals prefer to move to safer patches with ${\gamma }_S=0.5$, we find that the more susceptible individuals get informed (Fig. 3 (b3)), the smaller the outbreak size will be (Fig. 3 (a3)). For instance, with ${\gamma }_S=0.5$, infection disappears from the network while keeping a non-zero quantity of individuals being informed.

From the above analysis, we find that a medium value of α cannot change the contagion process in terms of both the final prevalence and the epidemic threshold. Although moving to the safer patches can inform more individuals, it increases the probability of infection as well.

4.3. The interaction of mobility patterns and information efficiency on the final prevalence of epidemics

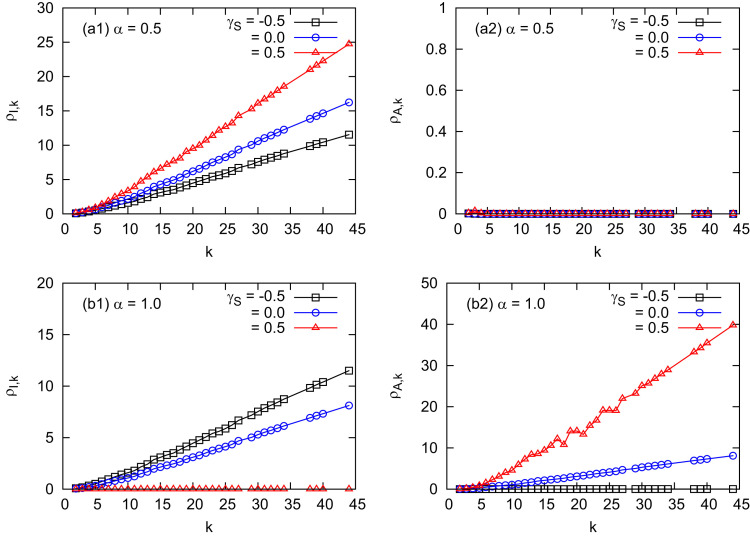
The interaction of individuals' mobility patterns and the information efficiency can be further verified by observing the final prevalences of the infectious and informed individuals at patches k, ${\rho }_{I,k}$ and ${\rho }_{A,k}$, as shown in Fig. 4 . It shows that the larger the patch degree k is, the more infectious individuals are contained in it, roughly following a linear increase form. Moreover, for a medium level of α, moving to the patches with more healthy population will infect more; while moving to the patches with less healthy population, infect less due to the dissemination of individuals at high degree patches (Figs. 4 (a1) and (a2)). With the increase in α, moving to the patch with high degrees can inform more individuals (Fig. 4 (b2), the red triangles), thus, less individuals at the patch get infected (Fig. 4 (b1)).

Fig. 4.

Final prevalences of the infectious population ${\rho }_{I,k}$ and the informed population ${\rho }_{A,k}$ at patch k. (a1) and (a2) $\alpha =0.5$; (b1) and (b2) $\alpha =1$. ${\gamma }_S={\gamma }_A=-0.5$ (the black squares); ${\gamma }_S={\gamma }_A=0$ (the blue circles), and ${\gamma }_S={\gamma }_A=0.5$ (the red triangles). The epidemiological parameters are set at the same values as in Fig. 2. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

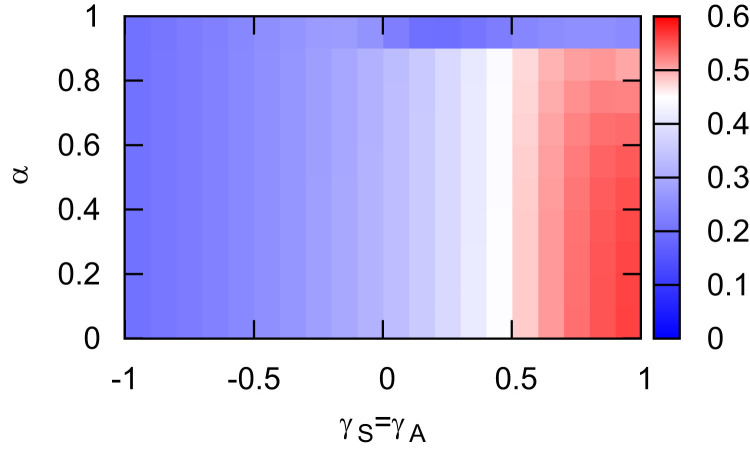
The detailed interplay between α and mobility patterns for the epidemic spread is shown in Fig. 5 . We find that for all possible values of α, moving to the patches that contain more susceptible individuals, increases the risk of outbreak, except for an extremely information efficiency α ($\alpha >0.9$), where the prevalence of infection can be significantly reduced by increasing the contact probability between information carriers and uninformed susceptible individuals (${\gamma }_S>0$). When α is a medium value, reducing the contact probability between information carries and uninformed susceptible individuals (${\gamma }_S<0$) can efficiently prevent the epidemic spread.

Fig. 5.

Final prevalence of the infectious individuals versus γ_S ($={\gamma }_A$) and α. The informed individuals move with the same pattern as the uninformed individuals do with ${\gamma }_A={\gamma }_S$. The total population density is set at ${\rho }^0=2$. The other parameters are the same as in Fig. 2.

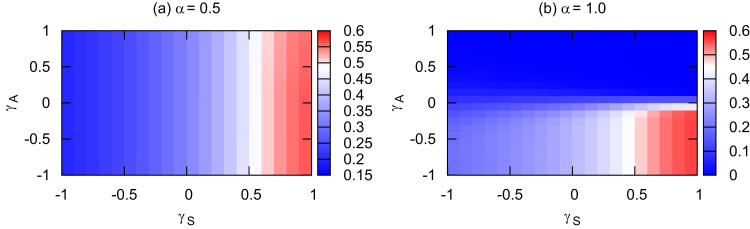
In the above analysis, we have assumed that both the informed and uninformed individuals follow the same types of mobility patterns with “${\gamma }_S>0$ and ${\gamma }_A>0$” or “${\gamma }_S<0$ and ${\gamma }_A<0$”. In order to make the analysis consistent, in the following, we investigate the case that the informed and uninformed susceptible individuals take different types of mobility patterns by tuning the parameters ${\gamma }_S>0$ and ${\gamma }_A<0$ or vice versa, and we explore their impacts on the final prevalence of infection (Fig. 6 ). For a medium value of α, the more uninformed individuals move to the safer patches (${\gamma }_S>0$), the higher the prevalence is. This is irrelevant to the mobility patterns of the informed individuals and is independent of whether they approach the safer patches or not (${\gamma }_A>0$ or ${\gamma }_A<0$). With an extremely high efficiency ($\alpha =1$, Fig. 6 (b)), we find two opposite results. The highest contact probability between information carriers and uninformed susceptible individuals yields the lowest prevalence (“${\gamma }_A>0$ and ${\gamma }_S>0$” or “${\gamma }_A<0$ and ${\gamma }_S<0$”), while the separation of them promotes the epidemic spread (${\gamma }_S>0$ and ${\gamma }_A<0$).

Fig. 6.

Final prevalence of the infected population versus γ_A and γ_S for different α. (a) $\alpha =0.5$; (b) $\alpha =1.0$. The total population density is set at ${\rho }^0=2$. The other parameters are the same as in Fig. 2.

From the above results, we conclude that information propagation is vital to the epidemic spread. The role of information propagation has to be evaluated by taking the information efficiency α into account. On the one hand, information may help mitigate the epidemic spread as long as it is highly efficient enough to reduce the risk of infection (a high value of α). Under this circumstance, mobility to safer patches may strengthen the role of information by informing more individuals. On the other hand, when the information on the disease cannot cause people's attention to reduce the risk of infection (a medium or lower value of α), informing more individuals by moving to the safer patches can only promote the epidemic spread by gathering more susceptible individuals in one patch.

4.4. Impacts of the information efficiency α and mobility patterns on the epidemic threshold

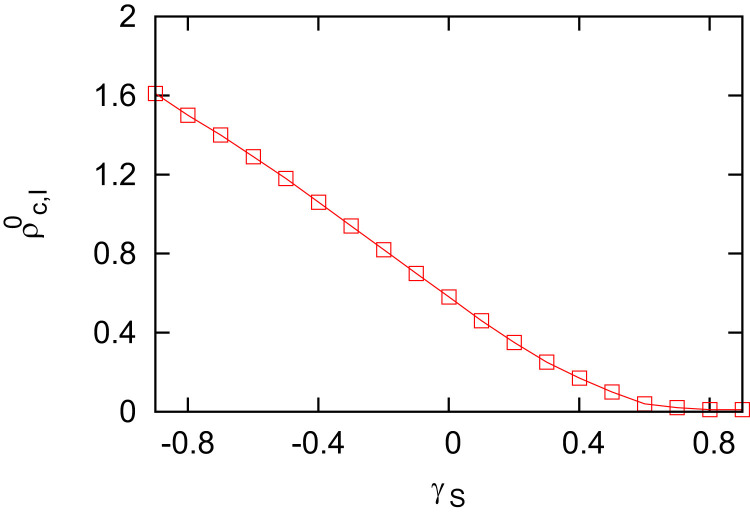
Next, we explore how mobility patterns affect the epidemic threshold ${\rho }_{c,I}^0$ with Eq. (8) as shown in Fig. 7 , where we assume that the informed individuals follow the same mobility patterns as the uninformed susceptible individuals do. It shows that ${\rho }_{c,I}^0$ decreases with γ _S, indicating that the more susceptible individuals move to the safer patches, the smaller the epidemic threshold will be. In other words, moving to the safer patches promotes the epidemic spread.

Fig. 7.

The epidemic threshold ${\rho }_{c,I}^0$ versus γ_S. The epidemiological parameters are set at $\beta =0.1$ and $\mu =0.2$. The mobility rates are set the same at $D_S=D_A=D_I=1$. The other parameters are the same as in Fig. 2.

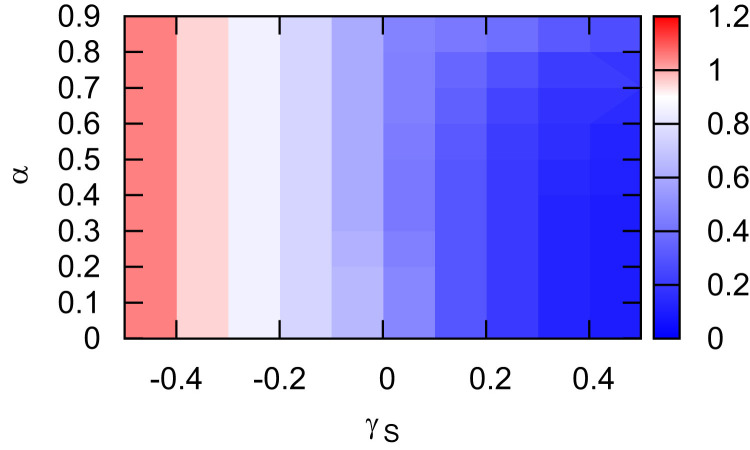
To further reveal the impacts of the information efficiency and mobility patterns on the epidemic process, we show the dependence of the epidemic threshold ${\rho }_{c,I}^0$ on α and γ _S in Fig. 8 . It shows that for a lower α, moving to safer patches promotes the disease spread with a reduced epidemic threshold (bottom-right); while for a higher α, moving to the safer patches informs more individuals and thus protects them from infection yielding a higher invasion threshold (top-right). This result is consistent with the analysis of the epidemic prevalence as shown in Fig. 5.

Fig. 8.

The epidemic threshold ${\rho }_{c,I}^0$ versus α and γ_S. The informed individuals move in the same pattern as the uninformed individuals do with ${\gamma }_A={\gamma }_S$. The epidemiological parameters are set at $\beta =0.2$ and $\mu =0.2$. The mobility rates are set at $D_I=D_S=D_A=1$. The other parameters are the same as in Fig. 2.

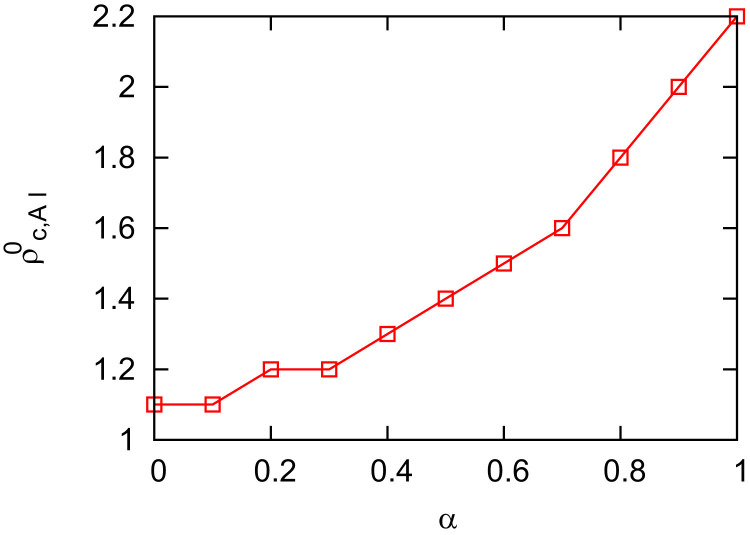
The dependence of the third epidemic threshold ${\rho }_{c,\mathit{AI}}^0$ on the information efficiency α can be found in Fig. 9 . We find that with the increase of information efficiency, α, the informed individuals get immunity to infection and it mitigates the disease spread in the network, yielding a higher critical invasion threshold ${\rho }_{c,\mathit{AI}}^0$.

Fig. 9.

The epidemic threshold ${\rho }_{c,\mathit{AI}}^0$ versus α. The uninformed susceptible, informed susceptible, and infectious individuals are assumed to move with the same pattern i.e. ${\gamma }_A={\gamma }_S={\gamma }_I=0$. The epidemiological parameters are set at $\beta =0.1$ and $\mu =0.2$. The mobility rates are set at $D_I=D_S=D_A=1$. The other parameters are the same as in Fig. 2.

5. Discussion

Whenever the outbreak of an infectious disease occurs, it is inevitably accompanied with the propagation of the information that is related to the progression of the infectious disease. In this work, we have investigated the interplay between the disease spread and the information propagation by focusing on the role of the information efficiency in reducing the risk of infection, and that of mobility patterns. The mobility pattern is mainly driven by the risk perception expressed by the safety level at the destination patch. The more healthy individuals a patch contains, the safer it is. Although the model we have proposed is simplistic and more realistic scenarios with detailed mobility patterns are determined by the availability of data, our model captures basic characteristics of the dynamics of information propagation and that of epidemic spread. We find that appropriately incorporating the knowledge of the information efficiency with the guidance of human mobility may effectively mitigate the epidemic outbreak by decreasing the outbreak size and increasing the epidemic threshold. Changing mobility patterns in accordance with the evaluation of the information efficiency could strengthen the role of information propagation in preventing the outbreak.

Information carriers play a role of double sides of swords. Our results suggest that mobility to the patches that contain more healthy individuals can mitigate the epidemic outbreak only if the information can efficiently appeal people's attention to reduce the risk of infection; otherwise, informing more individuals can promote the epidemic spread with a larger outbreak size. Thus, in addition to the usual intervention measurements (e.g., vaccinations), guiding mobility patterns or controlling the traffic flow between patches based on the proper evaluation of the information efficiency may be useful in preventing an epidemic.