Numerical simulation of virus diffusion in facemask during breathing cycles

Abstract

The recent SARS outbreak has spawned a major controversy concerning the protective performance of facemasks. The objective of this paper is to establish a mathematical model for describing the mechanism of viruses diffusion in a facemask during breathing cycles. In this model the mechanisms of the water vapor molecular diffusion, evaporation/condensation, sorption/desorption of moisture by fibers, Brownian diffusion of the virus, filtration of virus, capillary penetration of the viruses with the liquid water and latent heat generation due to phase change are considered. Meanwhile, the theoretical predictions are compared with experimental data, and good agreement is observed between the two, indicating that the model is satisfactory. Also, the effects of structural and materials properties on virus transfer are investigated.

Nomenclature

c

experiment constant

(c_v)_m

volumetric heat capacity of the fabric (J/m³)

C_a

water vapor concentration in the air filling the inter-fiber void spaces of the fabric (kg/m³)

$C_{\mathrm{a}}^{\ast }(T)$

saturated water vapor concentration (kg/m³)

C_ab

ambient water vapor concentration (kg/m³)

C_f

water vapor concentration in the fibers of the fabric (kg/m³)

C_s

gas concentration in the air filling the inter-fiber void spaces of the fabric (kg/m³)

C_v

virus concentration in the liquid water of the fabric (kg/m³)

d_c

effective radius of pore in fabrics (m)

D_B

Brownian diffusivity (m²/s)

D_f(w_c, t)

diffusion coefficient of water vapor in the fibers (m²/s)

D_M

molecular diffusivity (m²/s)

h_c

convection mass transfer coefficient (m/s)

h_l↔g

mass transfer coefficient (m/s)

h_t

combined heat transfer coefficient (J/m²  K)

k_mix

thermal conductivity of the fabric (W/m K)

K

intrinsic permeability (m²)

K_rl

relative permeability of liquid water

K_rs

relative permeability of gas

L

thickness of fabric (m)

M_s

mole mass of gas (kg/mol)

p_c

capillary pressure (kg/m s²)

p_s

pressure of gas phase (kg/m s²)

Q₁

evaporation rate of liquid water (kg/m³  s)

r

radius (m)

R

gas constant (J/mol K)

S_v

specific area of the fabric (1/m)

t

time (s)

T

temperature of the fabric (K)

V_l

intrinsical velocity of liquid water (m/s)

V_s

intrinsical velocity of gas (m/s)

x

X-coordinate

Greek symbols

ρ_l

density of liquid water (kg/m³)

ρ_v

density of virus (kg/m³)

ε

porosity of fabric

ε_f

volume fraction of fibers

ε_l

volume fraction of liquid water

ε_s

volume fraction of gas

ε_v

volume fraction of virus in deposition

λ

heat of sorption or water or vapor by fibers (J/kg)

λ_l

heat of sorption or desorption of liquid water by fibers (J/kg)

λ_v

heat of sorption or desorption of water vapor by fibers (J/kg)

ϕ

contact angle (°)

σ

surface tension (N/m)

β

average angle of the capillaries in fabrics (°)

μ_l

dynamic viscosity of water (kg/(ms))

μ_s

dynamic viscosity of gas (kg/(ms))

Superscripts

n

previous time

n + 1

present time

Subscript

0

initial value

1. Introduction

Since the breakout of SARS, the infection rate of front-line healthcare workers was very high. Even though they were equipped in the later stage with the best protective devices available on the market, a number of healthcare workers were still reported infected [1]. WHO announced that the primary route of SARS infection is thought to be via droplets through the mouth, nose and eyes. Therefore, it is critical to develop sound scientific understanding on how viruses can penetrate facemasks and infect the wearer during breathing.

Chen et al. [2] reported a study on the evaluation of single-use masks and respirators for protection of health care workers against mycobacterial aerosols by measuring the filtration efficiencies of a sub-micron surgical mask and three different types of respirators. They found that mean efficiencies were 97% for the surgical mask and a dusk/mist respirator, and more than 99.9% for the high-efficiency particulate air respirator. Willekem et al. [3] investigated bacterial penetration of different bacterial shapes, aerodynamic sizes, and flow rates through a surgical mask and a dust/mist respirator. The authors found that the spherical corn oil particles and spherical bacteria have the same penetration in size range from 0.9 to 1.7 μm, while rod-shaped bacteria penetrate less, depending on the aspect ratio of bacteria. Qian et al. [4] further studied the penetration efficiency of N95 respirators for airborne microbial and inert particles. Using laboratory tests with NaCl certification aerosols and measurements with particle-size spectrometers, N95 respirators were found to have higher filtration efficiency than DM and DFM respirators and non-certified surgical masks. The authors concluded that N95 respirators provide excellent protection against airborne particles when there is good face seal.

These findings provide good scientific evidences and guidelines for practical usages in terms of penetration efficiency. However, it is questionable whether filtration alone is able to provide enough protection against viruses. For instance, Qian et al. [4] found that N95 respirators made by different companies have different filtration efficiencies for the most penetrating particle size (0.1–0.3 μm), above which the filtration efficiency increases with size and reaches 99.5% or higher at about 0.75 μm.

When the droplets contaminated with viruses reach a surface such as that on a mask, they can stick to the mask if its outer surface is not strongly water repellent or be absorbed by the mask if its surface is water absorbent. A N95 mask that can filter out particles down to 0.3 μm can obviously filter out droplets greater in size. However, SARS corona viruses are irregularly shaped and are about 60–120 nm in diameter. Therefore, viruses may be able to penetrate or spread through the mask in the form of liquid diffusion by a capillary effect, particularly since the expired air will most likely wet the mask. The high moisture content and high temperature in the expired air can cause water vapor to condense in the mask due to the temperature difference between the air and the mask. The droplets that are expelled when speaking will accelerate the wetting process. The action of breathing will mechanically reinforce the penetration. During repeated breathing actions, a mask also becomes a collector of viruses, particularly when its outer surface is exposed to contaminated droplets. This process is a typical physical process of coupled heat and mass transfer in porous materials such as non-woven textile materials. As viruses and bacteria can stay on the surface and in the masks for significantly long time period during wear, it is obviously dangerous and undesirable if they can live comfortably and stay active in the warm and humid microenvironment in the masks. In order to avoid these phenomena, it is necessary to study the transfer mechanisms of the virus or bacteria in the mask and to supervise the design and usage of the mask according to these mechanisms.

Heat and mass transfer in porous textiles is a complicated process involving simultaneous coupled multi-field change. There are many references for utilized mathematical model to describe the heat and mass transfer mechanisms in porous media. Ogniewicz and Tien [5] reported an analysis with assumption that heat is transported by conduction and convection, the condensate is in pendular state. Motakef and El-Masri [6] and Shapiro and Motakef [7] extended the analysis to consider mobile condensates. More recently, heat and mass transfer in wet porous media in presence of evaporation–condensation was recently revisited analytically by Bouddour et al. [8] using the homogenization method of asymptotic for periodic structure. The inertia effects and boundary on flow and heat transfer in porous media were investigated by Vafai and Tien [9]. They discovered the Darcy model is not valid at high flow velocity. Amiri and Vafai [10] studied the dispersion effects of forced convection on heat transfer. In these studies, the researchers focused mainly on materials that do not absorb moisture vapor.

For textile materials, the majority of textile fibers have a certain degree of moisture absorption capability (called hygroscopicity). The moisture absorption influences the heat and moisture transfer processes. In order to describe the simultaneous heat and moisture transfer in porous textiles Li and Holcombe [11] introduced a new two-stage absorption model to better describe the coupled heat and moisture transport in fabrics. Li and Luo [12] improved the sorption rate equation by assuming that the moisture sorption by a wool fiber can be generally described as a uniform-diffusion equation for both stages of sorption. Luo et al. [13] presented a dynamic model of heat and moisture transfer with sorption and condensation in porous clothing assemblies. Their model considers the effect of water content in the porous fibrous batting on the effective thermal conductivity as well as radiative heat transfer. But the above-mentioned models ignored the effect of liquid water movement.

Fan and Wen [14] reported a model, in which evaporation and mobile condensates are considered. Li and Zhu [15] reported a new model that takes into account the condensation/evaporation and liquid diffusion by capillary actions, which is a function of fiber surface energy, contact angle and fabric pore size distributions. However in above Refs. [11], [12], [13], [14], [15], the models were based on the mass diffusion only due to the concentration gradient, the effect of the atmospheric pressure gradient on heat and moisture transfer in porous materials was ignored. In order to investigate the influence of atmospheric pressure gradient on heat and mass transfer within hygroscopic textile materials, and to provide insights on the functional design of clothing for windy conditions and active sportswear in outdoor, Li et al. [16] reported a new model by introducing new equations/terms and integrating them. They investigated the effect of atmospheric pressure on heat and moisture transfer.

All the above models did not consider the particle transfer processes in liquid water. For the transport in the porous media, Khilar and Fogler [17] originally proposed mathematical models describing the migration of fines in porous media are based on the release and capture mechanisms. For the pollutant transfer, Jiang and Corapcioglu [18] presented a hybrid equilibrium model of solute transport in porous media in the presence of colloids. But these models are established on the liquid water saturated porous media. The velocity of liquid water is assumed being constant. These assumptions may not be true in many situations. For instance, the heat and mass transfer in in vivo worn facemasks during breathing cycles, the liquid water is not saturated and the velocity is not a constant. The purpose of this paper is to report the development of a mathematical model to describe the complicated and coupled physical mechanisms, the numerical solution and validation of the model with experimental data.

2. Physical mechanisms of heat and mass transfer in the masks

We focus on the coupled processes of droplets contaminated with viruses transfer with other mass transfer in this paper. The liquid water contaminated with SARS viruses is propelled by surface tension force and breathing action. During the capillary action and breathing the water evaporation/condensation, sorption/desorption, virus deposition/release, and virus Brownian diffusion take place at the same time, as shown in Fig. 1 .

Fig. 1.

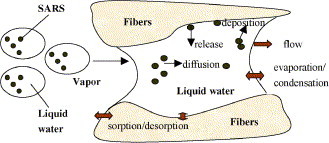
The schematic map of SARS viruses transfer in the mask.

We have made the following assumption: first, a local thermal equilibrium exists among all phases due to the small dimensions of the constituting fibers and the particles. Therefore, all phases have an identical temperature at a point in space. Second, swelling of the fibers due to changing moisture content is neglected. Third, the droplets transferred by capillary action, and the viruses in the droplets move and diffuse with the droplets due to concentration gradient. The gas in void space between fibers includes: dry air, and water vapor. Fourth, the gas is assumed to satisfy the partial pressure law and the sate equation of the perfect gas. Fifth, the SARS viruses are sphere form with uniform size.

Let x denote the coordinate across the layer of the mask; x  = 0 and x  =  L indicate the positions at the inner and the outer surface of the mask. The t denotes time. According to the mass and energy balance laws, we can list the following balance equations: for water vapor:

$$\frac{\mathrm{\partial }({\epsilon }_{\mathrm{s}}{C}_{\mathrm{a}})}{\mathrm{\partial }t}=\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[(D_{\mathrm{M}}){\epsilon }_{\mathrm{s}}\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }x}\right]-\frac{\mathrm{\partial }({\epsilon }_{\mathrm{s}}{V}_{\mathrm{s}}{C}_{\mathrm{a}})}{\mathrm{\partial }x}-{\varpi }_1{\epsilon }_{\mathrm{f}}\frac{\mathrm{\partial }{C}_{\mathrm{f}}}{\mathrm{\partial }t}+Q_1$$ (1)

for whole gas:

$$\frac{\mathrm{\partial }({\epsilon }_{\mathrm{s}}{C}_{\mathrm{s}})}{\mathrm{\partial }t}=-\frac{\mathrm{\partial }({\epsilon }_{\mathrm{s}}{V}_{\mathrm{s}}{C}_{\mathrm{s}})}{\mathrm{\partial }x}-{\varpi }_1{\epsilon }_{\mathrm{f}}\frac{\mathrm{\partial }{C}_{\mathrm{f}}}{\mathrm{\partial }t}+Q_1$$ (2)

for liquid water:

$$\frac{\mathrm{\partial }({\epsilon }_{\mathrm{l}}{\rho }_{\mathrm{l}})}{\mathrm{\partial }t}=-\frac{\mathrm{\partial }({\epsilon }_{\mathrm{l}}{V}_{\mathrm{l}}{\rho }_{\mathrm{l}})}{\mathrm{\partial }x}-{\varpi }_2{\epsilon }_{\mathrm{f}}\frac{\mathrm{\partial }{C}_{\mathrm{f}}}{\mathrm{\partial }t}-Q_1$$ (3)

for virus in the liquid water:

$$\frac{\mathrm{\partial }({\epsilon }_{\mathrm{l}}{C}_{\mathrm{v}})}{\mathrm{\partial }t}=\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[(D_{\mathrm{B}}){\epsilon }_{\mathrm{l}}\frac{\mathrm{\partial }(C_{\mathrm{v}})}{\mathrm{\partial }x}\right]-\frac{\mathrm{\partial }({\epsilon }_{\mathrm{l}}{V}_{\mathrm{l}}{C}_{\mathrm{v}})}{\mathrm{\partial }x}-\frac{\mathrm{\partial }({\rho }_{\mathrm{v}}{\epsilon }_{\mathrm{v}})}{\mathrm{\partial }t}$$ (4)

for energy:

$$(c_v{)}_m\frac{\mathrm{\partial }T}{\mathrm{\partial }t}-{\lambda }_{\mathrm{v}}{\epsilon }_{\mathrm{f}}{\varpi }_1\frac{\mathrm{\partial }{C}_{\mathrm{f}}}{\mathrm{\partial }t}-{\lambda }_{\mathrm{l}}{\epsilon }_{\mathrm{f}}{\varpi }_2\frac{\mathrm{\partial }{C}_{\mathrm{f}}}{\mathrm{\partial }t}+\lambda (Q_1)+[(C_{\mathrm{a}}{c}_{p\text{,}\mathrm{a}}+C_{\mathrm{d}}{c}_{p\text{,}\mathrm{d}}){\epsilon }_{\mathrm{s}}{V}_{\mathrm{s}}+{\rho }_{\mathrm{l}}{c}_{\mathrm{l}}{\epsilon }_{\mathrm{l}}{V}_{\mathrm{l}}]\frac{\mathrm{\partial }T}{\mathrm{\partial }x}=\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(k_{\mathrm{mix}}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)$$ (5)

for deposition viruses on the fiber surface:

$$\frac{\mathrm{\partial }({\rho }_{\mathrm{v}}{\epsilon }_{\mathrm{v}})}{\mathrm{\partial }t}=K_1{\epsilon }_{\mathrm{l}}{C}_{\mathrm{v}}-K_2{\rho }_{\mathrm{v}}{\epsilon }_{\mathrm{v}}$$ (6)

where ε _s is the volume fraction of gas, ε _s  = 1 −  ε _f  −  ε _l  −  ε _v, ε _f is the volume fraction of the fiber in the fabrics, ε _l is the volume of liquid water in a unit volume element, ε _v is the volume of virus in deposition on surface of fibers in a unit volume. C _a and C _v represent the concentration of water vapor in gas and virus concentration in liquid water respectively. C _s denotes the concentration of the whole gas. V _s and V _l are the intrinsical velocity of gas and liquid water respectively. ρ _l is the density of the liquid water. D _M is the molecular diffusion coefficient of the water vapor. $D_{\mathrm{B}}=\frac{k_{\mathrm{B}}T}{6\mathrm{\pi }{\mu }_{\mathrm{l}}{r}_{\mathrm{v}}\tau }$ [19] is the Brownian diffusion coefficient of virus in liquid water, which is a function of temperature T, r _v is the radius of viruses and μ _l is the dynamic viscosity of liquid water, τ is correction coefficient for bend diffusion way and effect of non-continuity of liquid water droplets. k _B is the Boltzmann constant. ϖ ₁ denotes the proportion of the sorption of water vapor by fibers, and ϖ ₂ denotes the proportion of liquid water by fibers. Q ₁ represents the evaporation rate of liquid water on the fibers. C _f is the water vapor concentration in the fiber. λ _v, λ _l, λ represent the sorption latent heat coefficients of the water vapor, liquid water and evaporation latent coefficient of liquid water respectively. (c _v)_m is effective volume heat capacity, and k _mix is the effective thermal conductivity of fabric. In the present study, the dispersion phenomenon is treated as an additional diffusive term added to the stagnant component. The empirical equation employed by Amiri and Vafai [10] is employed as:

$$k_{\mathrm{mix}}=\sum _{i=\mathrm{a}\text{,}\mathrm{d}\text{,}\mathrm{l}\text{,}\mathrm{f}}{\epsilon }_i{k}_i+0\text{.}5\sum _{j=\mathrm{s}\text{,}\mathrm{l}}[P_{\mathrm{r}}{R}_{\mathrm{e}}{]}_j{k}_j$$ (7)

In Eq. (1), the term on the left side represents vapor storage within the void space of the inter-fiber, the first term on the right side represent the molecular diffusion of the water vapor, the second term represents the water vapor flow with the whole gas, the third term represents water vapor accumulation rate within the fiber, i.e. the sorption rate of fibers, whereas the fourth term is evaporation flux of the liquid water in the inter-fibers void space. The meanings of the terms in Eqs. (2), (3), (4) are similar as those in Eq. (1). Eq. (5) represents the energy balance. The first term on the left side of Eq. (5) represents energy storage, the second and third term represent sorption latent heat of water vapor by fibers and the latent heat of liquid water within inter-fibers respectively; the fourth term represents the latent heat of evaporation of liquid water, and the fifth term represents the convective heat transfer. The right side represents the heat conduct ion. When the viruses are stable, in other words, when they do not deposit on collector (matrix) surfaces, they can migrate in the liquid water. However, when they are unstable, they can deposit and attach to solid surface. Both types of phenomenon can be observed simultaneously. The first-order rate Eq. (6) provides the kinetic expression for simultaneous virus capture/release mechanisms. The deposition rate coefficient K ₁ can be calculated by making use of the collector approach. Gruesbeck and Collins [20] proposed a two-parameters rate expression for spherical collectors. Here, we consider the fibrous collectors and give below [20]:

$$K_1=(c_{\mathrm{e}}{S}_{\mathrm{v}}E+b{\epsilon }_{\mathrm{v}})V_{\mathrm{l}}$$ (8)

where c _e is effective capture area coefficient of the collectors, S _v is the specific area of fabrics, E is the retention efficiency, b is the adjustable parameter. The second term gives the additional capture of viruses due to bridging, which increases with the amount of viruses deposited. The release coefficient K ₂ is a function of velocity of liquid water [20]:

$$K_2=\left\{\begin{array}{cc}{c}_{\mathrm{r}}(V_{\mathrm{l}}-V_{\mathrm{c}}){\epsilon }_{\mathrm{l}}\hfill & V_{\mathrm{l}}>V_{\mathrm{c}}\hfill \\ 0\hfill & V_{\mathrm{l}}⩽V_{\mathrm{c}}\hfill \end{array}\right)$$ (9)

where c _r is the release coefficient of the virus, V _c is the critical velocity.

Evaporation rate of liquid water on the fibers can express as following [15]:

$$Q_1={\epsilon }_{\mathrm{s}}{h}_{\mathrm{l}\leftrightarrow \mathrm{g}}{S}_{\mathrm{v}}(C_{\mathrm{a}}^{\ast }(T)-C_{\mathrm{a}})$$ (10)

where S _v denotes the specific volume of fabric. $C_{\mathrm{a}}^{\ast }(T)$ is the saturated water vapor concentration and solely determined by the temperature.

Sorption and desorption of moisture by the fibers obey the Fickian law [12]:

$$\frac{\mathrm{\partial }{C}_{\mathrm{f}}(x\text{,}r\text{,}t)}{\mathrm{\partial }t}=\frac{1}{r}\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left[{\mathit{rD}}_{\mathrm{f}}(x\text{,}t)\frac{\mathrm{\partial }{C}_{\mathrm{f}}(x\text{,}r\text{,}t)}{\mathrm{\partial }r}\right]$$ (11)

where D _f(x,  t) is the diffusion coefficient of water vapor in the fiber, r is the radial coordinate in a fiber. The boundary condition is determined by the relative humidity of the air surrounding a fiber at x.

It is known that in flow through a porous medium the pressure drop caused by frictional drag is directly proportional to velocity for low speed flow. At higher velocities, inertial effects become appreciable, causing an increase in the form drag. As Vafai and Tien [9] pointed that the pressure drop in the bulk of porous medium is proportional to a linear combination of flow velocity and square of the flow velocity. The square term is caused by the inertial effects offered through the solid matrix, it is a function of Reynolds number and geometry of porous media. In the present case, the gas velocity during normal breathing cycles is small and the pore size of mask N95 and fiber radius are small, so the Reynolds number is small (Re _max is about 3). Therefore, the inertial effects can be ignored. Therefore, we can assume the relationship of pressure drop and velocity satisfies the Darcy’s law:

$${\epsilon }_{\mathrm{s}}{V}_{\mathrm{s}}=-\frac{{\mathit{KK}}_{\mathrm{rs}}}{{\mu }_{\mathrm{s}}}\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}$$ (12)

$${\epsilon }_{\mathrm{l}}{V}_{\mathrm{l}}=-\frac{{\mathit{KK}}_{\mathrm{rl}}}{{\mu }_{\mathrm{l}}}\left(\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}-\frac{\mathrm{\partial }{p}_{\mathrm{c}}}{\mathrm{\partial }x}\right)$$ (13)

where p _s is the pressure of gas. p _c is capillary pressure. μ _s and μ _l are the dynamic viscosity of gas and liquid water respectively. Extending the results of Ref. [15], we can obtain:

$$K=\frac{3\epsilon {\sin }^2\beta d_{\mathrm{c}}^2}{80}$$ (14)

where K is the intrinsical permeability, β is the average angle of the capillaries in the material, d _c is effective radius of the pores in material, ε is the porosity of material. The relative permeability of liquid water [15]:

$$K_{\mathrm{rl}}=({\epsilon }_{\mathrm{l}}/\epsilon {)}^3$$ (15)

The relative permeability of the gas [21]:

$$K_{\mathrm{rs}}=1-K_{\mathrm{rl}}$$ (16)

The relation of capillary pressure p _c and the volume fraction of liquid water ε _l [15]:

$$\frac{\mathrm{\partial }{p}_{\mathrm{c}}}{\mathrm{\partial }x}=-\frac{2\sigma \cos \varphi \epsilon }{{\epsilon }_{\mathrm{l}}^2{d}_{\mathrm{c}}}\frac{\mathrm{\partial }{\epsilon }_{\mathrm{l}}}{\mathrm{\partial }x}$$ (17)

where σ is the surface tension and ϕ is the contact angle.

According to the basic assumption of the perfect gas, we have:

$$C_{\mathrm{s}}=\frac{M_{\mathrm{s}}{p}_{\mathrm{s}}}{\mathit{RT}}$$ (18)

Then,

$$\frac{\mathrm{\partial }({\epsilon }_{\mathrm{s}}{C}_{\mathrm{s}})}{\mathrm{\partial }t}=\frac{M_{\mathrm{s}}{\epsilon }_{\mathrm{s}}}{\mathit{RT}}\frac{\mathrm{\partial }(p_{\mathrm{s}})}{\mathrm{\partial }t}-p_{\mathrm{s}}\frac{{\epsilon }_{\mathrm{s}}{M}_{\mathrm{s}}}{{\mathit{RT}}^2}\frac{\mathrm{\partial }T}{\mathrm{\partial }t}-\frac{M_{\mathrm{s}}{p}_{\mathrm{s}}}{\mathit{RT}}\frac{\mathrm{\partial }{\epsilon }_{\mathrm{l}}}{\mathrm{\partial }t}-\frac{M_{\mathrm{s}}{p}_{\mathrm{s}}}{\mathit{RT}}\frac{\mathrm{\partial }{\epsilon }_{\mathrm{v}}}{\mathrm{\partial }t}$$ (19)

Substitution of Eqs. (8), (9), (10), (11), (12), (13), (14), (15), (16), (17), (18), (19) into Eqs. (1), (2), (3), (4), (5), (6) yields:

$$\begin{array}{cc}\hfill & {\epsilon }_{\mathrm{s}}\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }t}-C_{\mathrm{a}}\frac{\mathrm{\partial }({\epsilon }_{\mathrm{l}})}{\mathrm{\partial }t}\hfill \\ \hfill & =\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[D\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }x}\right]+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[G\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right]-C+Q_1+C_{\mathrm{a}}\frac{\mathrm{\partial }({\epsilon }_{\mathrm{v}})}{\mathrm{\partial }t}\hfill \end{array}$$ (20)

$$\begin{array}{cc}\hfill & A_3\frac{\mathrm{\partial }(p_{\mathrm{s}})}{\mathrm{\partial }t}+A_4\frac{\mathrm{\partial }T}{\mathrm{\partial }t}+A_5\frac{\mathrm{\partial }{\epsilon }_{\mathrm{l}}}{\mathrm{\partial }t}\hfill \\ \hfill & =\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[\mathit{GS}\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right]-C+Q_1-A_5\frac{\mathrm{\partial }{\epsilon }_{\mathrm{v}}}{\mathrm{\partial }t}\hfill \end{array}$$ (21)

$${\rho }_{\mathrm{l}}\frac{\mathrm{\partial }({\epsilon }_{\mathrm{l}})}{\mathrm{\partial }t}=\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[\mathit{GL}\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right]+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[(\mathit{DL})\frac{\mathrm{\partial }{\epsilon }_{\mathrm{l}}}{\mathrm{\partial }x}\right]-C_1-Q_1$$ (22)

$$\begin{array}{cc}\hfill & {\epsilon }_{\mathrm{l}}\frac{\mathrm{\partial }(C_{\mathrm{v}})}{\mathrm{\partial }t}+C_{\mathrm{v}}\frac{\mathrm{\partial }({\epsilon }_{\mathrm{l}})}{\mathrm{\partial }t}=\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[\mathit{DV}\frac{\mathrm{\partial }(C_{\mathrm{v}})}{\mathrm{\partial }x}\right]+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[\mathit{GV}\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right]\hfill \\ \hfill & +\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left((\mathit{DLV})\frac{\mathrm{\partial }{\epsilon }_{\mathrm{l}}}{\mathrm{\partial }x}\right)-\frac{\mathrm{\partial }({\rho }_{\mathrm{v}}{\epsilon }_{\mathrm{v}})}{\mathrm{\partial }t}\hfill \end{array}$$ (23)

$$\begin{array}{cc}\hfill & (c_v{)}_m\frac{\mathrm{\partial }T}{\mathrm{\partial }t}-{\lambda }_{\mathrm{v}}C-{\lambda }_{\mathrm{l}}{C}_1+\lambda (Q_1)\hfill \\ \hfill & +[(C_{\mathrm{a}}{c}_{p\text{,}\mathrm{a}}+C_{\mathrm{d}}{c}_{p\text{,}\mathrm{d}}){\epsilon }_{\mathrm{s}}{V}_{\mathrm{s}}+{\rho }_{\mathrm{l}}{c}_{\mathrm{l}}{\epsilon }_{\mathrm{l}}{V}_{\mathrm{l}}]\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\hfill \\ \hfill & =\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left(k_{\mathrm{mix}}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right)\hfill \end{array}$$ (24)

$$\frac{\mathrm{\partial }({\epsilon }_{\mathrm{v}})}{\mathrm{\partial }t}=\frac{1}{{\rho }_{\mathrm{v}}}{K}_1{\epsilon }_{\mathrm{l}}{C}_{\mathrm{v}}-K_2{\epsilon }_{\mathrm{v}}$$ (25)

where ε _s  = 1 −  ε _f  −  ε _l  −  ε _v, D  =  DMε _s, ε  =  ε ₀  −  ε _v, $G=C_{\mathrm{a}}\frac{3\epsilon {\sin }^2\beta d_{\mathrm{c}}^2}{80{\mu }_{\mathrm{s}}}(1-(\frac{{\epsilon }_{\mathrm{l}}}{\epsilon }{)}^3)$,

$$\begin{array}{cc}\hfill & C={\varpi }_1(1-\epsilon )\frac{\mathrm{\partial }{C}_{\mathrm{f}}}{\mathrm{\partial }t}\text{,}{A}_3=\frac{M_{\mathrm{s}}(1-{\epsilon }_{\mathrm{f}}-{\epsilon }_{\mathrm{l}}-{\epsilon }_{\mathrm{v}})}{\mathit{RT}}\text{,}\hfill \\ \hfill & A_4=-p_{\mathrm{s}}\frac{(1-{\epsilon }_{\mathrm{f}}-{\epsilon }_{\mathrm{l}}-{\epsilon }_{\mathrm{v}})M_{\mathrm{s}}}{{\mathit{RT}}^2}\hfill \\ \hfill & \mathit{GS}=\frac{M_{\mathrm{s}}{p}_{\mathrm{s}}}{\mathit{RT}}\frac{3\epsilon {\sin }^2\beta d_{\mathrm{c}}^2}{80{\mu }_{\mathrm{s}}}\left(1-{\left(\frac{{\epsilon }_{\mathrm{l}}}{\epsilon }\right)}^3\right)\text{,}{A}_5=-\frac{M_{\mathrm{s}}{p}_{\mathrm{s}}}{\mathit{RT}}\text{,}\hfill \\ \hfill & \mathit{GL}={\rho }_{\mathrm{l}}\frac{3\epsilon {\sin }^2\beta d_{\mathrm{c}}^2}{80{\mu }_{\mathrm{l}}}{\left(\frac{{\epsilon }_{\mathrm{l}}}{\epsilon }\right)}^3\hfill \\ \hfill & \mathit{DL}={\rho }_{\mathrm{l}}\frac{3{\sin }^2\beta d_{\mathrm{c}}\sigma \cos \varphi {\epsilon }_{\mathrm{l}}}{40\epsilon {\mu }_{\mathrm{l}}}\text{,}{C}_1={\varpi }_2(1-\epsilon )\frac{\mathrm{\partial }{C}_{\mathrm{f}}}{\mathrm{\partial }t}\text{,}\hfill \\ \hfill & \mathit{DV}=(D_{\mathrm{B}}){\epsilon }_{\mathrm{l}}\hfill \\ \hfill & \mathit{GV}=C_{\mathrm{v}}\frac{3{\sin }^2\beta d_{\mathrm{c}}^2}{80{\epsilon }^2{\mu }_{\mathrm{l}}}{\epsilon }_{\mathrm{l}}^3\text{,}\mathit{DLV}=C_{\mathrm{v}}\frac{3{\sin }^2\beta d_{\mathrm{c}}\sigma \cos \varphi {\epsilon }_{\mathrm{l}}}{40\epsilon {\mu }_{\mathrm{l}}}\hfill \end{array}$$

2.1. Initial and boundary conditions

In order to generate a solution to above mentioned equations, we need to specify an initial condition and boundary conditions at the mask surfaces in terms of humidity, temperature, vapor content, liquid water content, the concentration of virus in the liquid water and temperature respectively. Fig. 2 is a schematic diagram to show the initial and boundary conditions of facemask. Initially, a mask is equilibrated to a given atmosphere of temperature and humidity, the temperature, moisture content and virus concentration are uniform throughout the mask at known values.

$$\begin{array}{cc}\hfill & T(x\text{,}0)=T_0\hfill \\ \hfill & C_{\mathrm{v}}(x\text{,}0)=C_{\mathrm{v}0}\hfill \\ \hfill & {\epsilon }_{\mathrm{l}}(x\text{,}0)={\epsilon }_{\mathrm{l}0}\hfill \\ \hfill & p_{\mathrm{s}}(x\text{,}0)=p_{\mathrm{s}0}\hfill \\ \hfill & C_{\mathrm{f}}(x\text{,}0)=f({\mathit{RH}}_0\text{,}{T}_0)\hfill \\ \hfill & C_{\mathrm{a}}(x\text{,}0)=C_{\mathrm{a}0}\hfill \end{array}$$ (26)

Then, the boundaries of the mask are exposed to two different environments:

For simulation the breathing process, at x  = 0 (the mask inner surface), we have

$$\begin{array}{cc}\hfill & {\left(\left(D\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }x}+G\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right)\right|}_{x=0}=-{\epsilon }_{\mathrm{s}}\kappa (C_{\mathrm{ab}1}v)\hfill \\ \hfill & {\left(\left(\mathit{GS}\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right)\right|}_{x=0}=-{\epsilon }_{\mathrm{s}}\kappa (C_{\mathit{sb}1}v)\hfill \\ \hfill & {\left(\left(\mathit{GL}\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}+(\mathit{DL})\frac{\mathrm{\partial }{\epsilon }_{\mathrm{l}}}{\mathrm{\partial }x}\right)\right|}_{x=0}=-h_{\mathrm{l}\leftrightarrow \mathrm{g}}{\epsilon }_{\mathrm{l}}(C_{\mathrm{a}}^{\ast }(T)-C_{\mathrm{ab}1})\hfill \\ \hfill & {\left(\left(\mathit{DV}\frac{\mathrm{\partial }(C_{\mathrm{v}})}{\mathrm{\partial }x}+\mathit{GV}\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}+(\mathit{DLV})\frac{\mathrm{\partial }{\epsilon }_{\mathrm{l}}}{\mathrm{\partial }x}\right)\right|}_{x=0}=0\hfill \\ \hfill & {\left(k_{\mathrm{mix}}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right|}_{x=0}=-h_{\mathrm{t}1}(T-T_{\mathrm{ab}1})-\lambda h_{\mathrm{l}\leftrightarrow \mathrm{g}}{\epsilon }_{\mathrm{l}}(C_{\mathrm{a}}^{\ast }(T)-C_{\mathrm{ab}1})\hfill \end{array}$$ (27)

where v is the velocity of the breathing out. $v=v_0\sin (\frac{\pi }{2}t)$, v ₀ is the peak value of breathing velocity. κ is the ratio of area of nares to effective ventilation area of the mask. C _ab1, C _sb1 denote the concentration of water vapor and whole gas. If person breath out C _ab1, C _sb1 are ambient values, else they are taken values on position x  = 0. h _t1 is the combined heat exchange coefficient. It is the sum of radiation heat exchange coefficient and convective heat exchange coefficient, which is a function of the flow velocity.

Fig. 2.

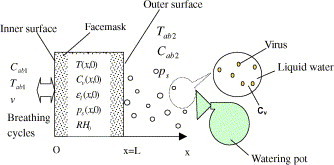
Schematic diagram of initial and boundary conditions of facemask.

At x  =  L (the mask outer surface), we have the following boundary conditions to take into account the convective of the boundary air layer:

$$\begin{array}{cc}\hfill & {\left(\left(D\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }x}+G\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right)\right|}_{x=L}=-h_{\mathrm{c}}{\epsilon }_{\mathrm{s}}(C_{\mathrm{a}}-C_{\mathrm{ab}2})\hfill \\ \hfill & {\left(k_{\mathrm{mix}}\frac{\mathrm{\partial }T}{\mathrm{\partial }x}\right|}_{x=L}=-h_{\mathrm{t}2}(T-T_{\mathrm{ab}2})-\lambda h_{\mathrm{l}\leftrightarrow \mathrm{g}}{\epsilon }_{\mathrm{l}}(C_{\mathrm{a}}^{\ast }(T)-C_{\mathrm{ab}2})\hfill \\ \hfill & {\left(\left(\mathit{GL}\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}+(\mathit{DL})\frac{\mathrm{\partial }{\epsilon }_{\mathrm{l}}}{\mathrm{\partial }x}\right)\right|}_{x=L}=-h_{\mathrm{l}\leftrightarrow \mathrm{g}}{\epsilon }_{\mathrm{l}}(C_{\mathrm{a}}^{\ast }(T)-C_{\mathrm{ab}2})\hfill \\ \hfill & p_{\mathrm{s}}(L\text{,}t)=p_{\mathrm{s}b2}\hfill \\ \hfill & {\left(\left(\mathit{DV}\frac{\mathrm{\partial }(C_{\mathrm{v}})}{\mathrm{\partial }x}+\mathit{GV}\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}+(\mathit{DLV})\frac{\mathrm{\partial }{\epsilon }_{\mathrm{l}}}{\mathrm{\partial }x}\right)\right|}_{x=L}=0\hfill \end{array}$$ (28)

where h _c is the convection mass transfer coefficient, h _t2 is the combined heat exchange coefficient.

3. Numerical method of the model

To derive a numerical solution for Eqs. (20), (21), (22), (23), (24), (25), (26), (27), (28) by using the finite volume method, we select a control volume, as shown in Fig. 3 .

Fig. 3.

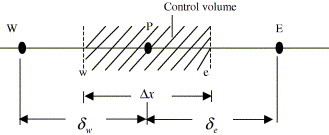
Schematic map of control volume.

For example, a simplified integral form is used for Eq. (20) in a control volume P.

$${\int }_{{\Omega }_P}\left({\epsilon }_{\mathrm{s}}\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }t}-C_{\mathrm{a}}\frac{\mathrm{\partial }({\epsilon }_{\mathrm{l}})}{\mathrm{\partial }t}-C_{\mathrm{a}}\frac{\mathrm{\partial }({\epsilon }_{\mathrm{v}})}{\mathrm{\partial }t}+C-Q_1\right)\mathrm{d}x={\int }_{{\Omega }_P}\left(\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[D\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }x}\right]+\frac{\mathrm{\partial }}{\mathrm{\partial }x}\left[G\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right]\right)\mathrm{d}x$$ (29)

Then,

$$\frac{({\epsilon }_{\mathrm{s}}{)}_P^n[(C_{\mathrm{a}}{)}_P^{n+1}-(C_{\mathrm{a}}{)}_P^n]}{\mathrm{\Delta }t}\mathrm{\Delta }x-\frac{(C_{\mathrm{a}}{)}_P^n[({\epsilon }_{\mathrm{l}}{)}_P^{n+1}-({\epsilon }_{\mathrm{l}}{)}_P^n]}{\mathrm{\Delta }t}\mathrm{\Delta }x+C_P^n\mathrm{\Delta }x-Q_{1P}^n\mathrm{\Delta }x-{\left[C_{\mathrm{a}}\frac{\mathrm{\partial }({\epsilon }_{\mathrm{v}})}{\mathrm{\partial }t}\right]}_P^n\mathrm{\Delta }x={\left[D\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }x}\right]}_{\mathrm{e}}-{\left[D\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }x}\right]}_{\mathrm{w}}+{\left[G\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right]}_{\mathrm{e}}-{\left[G\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right]}_{\mathrm{w}}$$ (30)

The right terms of Eq. (30) can write as following:

$${\left[D\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }x}\right]}_{\mathrm{e}}-{\left[D\frac{\mathrm{\partial }(C_{\mathrm{a}})}{\mathrm{\partial }x}\right]}_{\mathrm{w}}+{\left[G\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right]}_{\mathrm{e}}-{\left[G\frac{\mathrm{\partial }{p}_{\mathrm{s}}}{\mathrm{\partial }x}\right]}_{\mathrm{w}}=D_{\mathrm{e}}^n\frac{(C_{\mathrm{a}}{)}_{\mathrm{e}}^{n+1}-(C_{\mathrm{a}}{)}_P^{n+1}}{{\delta }_{\mathrm{e}}}-D_{\mathrm{w}}^n\frac{(C_{\mathrm{a}}{)}_P^{n+1}-(C_{\mathrm{a}}{)}_W^{n+1}}{{\delta }_{\mathrm{w}}}+G_{\mathrm{e}}^n\frac{(p_{\mathrm{s}}{)}_{\mathrm{e}}^{n+1}-(p_{\mathrm{s}}{)}_P^{n+1}}{{\delta }_{\mathrm{e}}}-G_{\mathrm{w}}^n\frac{(p_{\mathrm{s}}{)}_P^{n+1}-(p_{\mathrm{s}}{)}_W^{n+1}}{{\delta }_{\mathrm{w}}}$$ (31)

Substitution of Eq. (31) into Eq. (30) yields:

$$K_1(C_{\mathrm{a}}{)}_W^{n+1}+K_2(p_{\mathrm{s}}{)}_W^{n+1}+K_3(C_{\mathrm{a}}{)}_P^{n+1}+K_4(p_{\mathrm{s}}{)}_P^{n+1}+K_5(C_{\mathrm{a}}{)}_{\mathrm{e}}^{n+1}+K_6(p_{\mathrm{s}}{)}_{\mathrm{e}}^{n+1}+K_7({\epsilon }_{\mathrm{l}}{)}_P^{n+1}=R_1$$ (32)

Let ${\mu }_{\mathrm{w}}=\frac{\mathrm{\Delta }t}{\mathrm{\Delta }x{\delta }_{\mathrm{w}}}$, ${\mu }_{\mathrm{e}}=\frac{\mathrm{\Delta }t}{\mathrm{\Delta }x{\delta }_{\mathrm{e}}}$ where

$$K_1={\mu }_{\mathrm{w}}{D}_{\mathrm{w}}^n\text{,}{K}_2={\mu }_{\mathrm{w}}{G}_{\mathrm{w}}^n\text{,}{K}_3=-({\mu }_{\mathrm{w}}{D}_{\mathrm{w}}^n+{\mu }_{\mathrm{e}}{D}_{\mathrm{e}}^n+({\epsilon }_{\mathrm{s}}{)}_P^n)\text{,}{K}_4=-({\mu }_{\mathrm{w}}{G}_{\mathrm{w}}^n+{\mu }_{\mathrm{e}}{G}_{\mathrm{e}}^n)\text{,}{K}_5={\mu }_{\mathrm{e}}{D}_{\mathrm{e}}^n\text{,}{K}_6={\mu }_{\mathrm{e}}{G}_{\mathrm{e}}^n\text{,}{K}_7=(C_{\mathrm{a}}{)}_P^n$$

$$R_1=-({\epsilon }_{\mathrm{s}}{C}_{\mathrm{a}}{)}_P^n+({\epsilon }_{\mathrm{l}}{C}_{\mathrm{a}}{)}_P^n+C_P^n\mathrm{\Delta }t-Q_{1P}^n\mathrm{\Delta }t-{\left[C_{\mathrm{a}}\frac{\mathrm{\partial }({\epsilon }_{\mathrm{v}})}{\mathrm{\partial }t}\right]}_P^n\mathrm{\Delta }t$$

At x  =  L,

$$\left[D_{N-1/2}^n\frac{(C_{\mathrm{a}}{)}_N^{n+1}-(C_{\mathrm{a}}{)}_{N-1}^{n+1}}{{\delta }_{N\mathrm{w}}}\right]+\left[G_{N-1/2}^n\frac{(p_{\mathrm{s}}{)}_N^{n+1}-(p_{\mathrm{s}}{)}_{N-1}^{n+1}}{{\delta }_{N\mathrm{w}}}\right]=-h_{\mathrm{c}}({\epsilon }_{\mathrm{s}}{)}_N^n(C_{\mathrm{a}N}^{n+1}-C_{\mathrm{ab}2})$$ (33)

At x  = 0,

$$\left[D_{1+1/2}^n\frac{(C_{\mathrm{a}}{)}_2^{n+1}-(C_{\mathrm{a}}{)}_1^{n+1}}{{\delta }_{1\mathrm{e}}}\right]+\left[G_{1+1/2}^n\frac{(p_{\mathrm{s}}{)}_2^{n+1}-(p_{\mathrm{s}}{)}_1^{n+1}}{{\delta }_{1\mathrm{e}}}\right]=-({\epsilon }_{\mathrm{s}}{)}_N^n\kappa (C_{\mathrm{ab}}v)$$ (34)

Following the same procedure as for the water vapor mass conservation, we can derive the discretization equations for liquid water, energy, whole gas and virus. By specifying initial conditions we can calculate the coefficient of the discretization and its right term, the values of water vapor concentration, liquid water fraction, temperature and atmospheric pressure and concentration of virus at next time can be obtained.

4. Numerical solutions and discussion

4.1. Experimental validation and simulation

In order to investigate the prediction ability of the present model, we compare the predictions from the model with the experimental observations reported else by Li et al. [23]. Briefly, an in vivo wear filtration efficiency trial was carried by using human subjects. In the trial, each subject was asked to put on a N95 facemask and started to perform walking exercise. The researcher sprayed the simulated viral solution onto the facemask once at a distance 1 m every 10 min. The simulated viral solution was sprayed on the mask seven times during the walking in total. The average weight of the splash in one stroke of spray was 2 ml. The simulated viral solution was made up with KCl (potassium chloride) water solution, in which the K⁺ concentration is 0.02 g/cm³. Seventy minutes later K⁺ content of each layer was obtained. Further, the relative K⁺ content of each layer to K⁺ content of the whole mask was calculated by dividing the K⁺ content of each layer with the sum of K⁺ content of all layers for each mask. All the percentages were used as the basis for analysis of the test results for four layers of N95 masks. The initial and boundary’s conditions in simulation are listed in Table 1 . The computation parameters are listed in Table 2 .

Table 1.

The initial and boundary’s conditions in simulation

Initial condition	Boundary’s conditions at the mask inner surface (x = 0)	Boundary’s conditions at the mask outer surface (x = L)
T(x, 0) = 25 °C	In Eq. (27):	In Eq. (28):
Cv(x, 0) = (1.0e–10)%	$C_{\mathrm{ab}1}(0\text{,}t)=C_{\mathrm{a}}^{\ast }(T_{\mathrm{ab}1})$	Tab2 = 25 °C
εl(x, 0) = 1.0e−3	Tab1 = 37 °C	$C_{\mathrm{ab}2}=C_{\mathrm{a}}^{\ast }(T_{\mathrm{ab}2})\times 65\%$
ps(x, 0) = 1.01325e5 Pa	v0 = 0.2 m/s	ps(L, t) = 1.01325e5 Pa
RH0 = 65%		Additional conditions:
		If t = 0, 600, 1200, …, 3600 s
		Change:
		Cv(L, t) = [0.02 × 103 × 0.5 + εl(L, t − Δt)  × Cv(L, t − Δt)]/0.5
		εl(L, t) = 0.5

Table 2.

The computation parameters

Parameters	Symbol	Unit	Value and reference
Density of a fiber	ρf	kg/m3	910 [12]
Volumetric heat capacity of fabric	Cvf	kJ/m3 K	1715 [12]
Thermal conductivity of fabric	kfab	W/m2 K	5.18e–2 [12]
Heat of sorption of water vapor by fibers	λ	kJ/kg	2522 [15]
Heat of sorption or desorption of liquid water by fibers	λl	kJ/kg	2522 [15]
Heat of sorption or desorption of water vapor by fibers	λv	kJ/kg	2260 [15]
Convection mass transfer coefficient	hc2	m/s	1.37e–2
Mass transfer coefficient	hl↔g	m/s	1.37e–2
Combined heat transfer coefficient	ht	W/m2 K	81.6
Diffusion coefficient of water vapor in fiber	Df(wc, t)	m2/s	1.3e–13 [15]
Dynamic viscosity of gas	μs	kg/m s	1.83e–5 [22]
Dynamic viscosity of liquid water	μl	kg/m s	1.0e–3 [22]
Contact angle	ϕ	°C	80
Effective radius of pore in fabrics	dc	m	5.0e–7
Surface tension	σ	N/m	31
Average angle of the capillaries in fabrics	β	°C	20
Molecular diffusion coefficient	Da	m2/s	2.5e–5
Thickness of N95 mask	LN95	m	5.1e–3
Special surface	Sv	1/m	10 000
Effective capture area coefficient of the collectors	ce	–	0.1
Retention efficiency	E	–	0.01
Critical velocity	Vc	m/s	1.0e–7
Release coefficient of the virus	cr	–	0.3

We simulated above progress and the comparisons of the simulation and the experimental results of the N95 mask in the relative K⁺ content in each layer are shown in Fig. 4 .

Fig. 4.

Comparison of measured relative K⁺ content with predictions from the model.

As Fig. 4 shows, the layer 1 (the outer layer of the masks) has the highest K⁺ contents, as they were exposed to the simulated viral loading, followed by the second layer and third layer, as well as the fourth layer of N95 masks. We can also see that the simulated relative K⁺ content of the outer layer is slightly lower than the experiment data, and a little higher in the second layer. It is because that the effect of layer gap is not considered. However, it can be seen that the trend predicted by the model agrees well with that of the experiment.

Using above condition, we can also obtain the transfer progresses of the K⁺ concentration, liquid water, water vapor concentration, pressure and temperature during breathing cycles.

Fig. 5 shows the distribution of the K⁺ concentration in liquid water variation in the fabric with the time. The K⁺ concentration in liquid water of outer layer (x  =  L) decreases after every splash and increases with the evaporation of liquid water and then decreases again due to the K⁺ diffusion from high to low concentration areas.

Fig. 5.

Distribution of the K⁺ concentration in liquid water.

The fraction of deposition K⁺ on the surface of fibers is shown in Fig. 6 . The fraction of deposition K⁺ on the surface of fibers of the outer surface increases gradually with the progress of splash on the outer surface. But K⁺ deposits very little in the deeper layers as the liquid water does not diffuse into the mask very far.

Fig. 6.

Distribution of the fraction of deposition K⁺ on the fibers surface.

From Fig. 7 we can see the distribution of the liquid water in the mask with the time in 600 s, which is enlarged to show the dynamic transfer processes. We can see the variation progress of the liquid water fraction by the capillary pressure and evaporation. Since the contact angle is large and the effective radius of the capillary is small, the diffusion velocity of the liquid water is slow. The liquid water of outer surface evaporates quickly since the relative humidity of the environment is slow. Liquid water appears on the inner surface due to the condensation from high humidity of air breathed out.

Fig. 7.

Distribution of the liquid water.

Fig. 8 shows the K⁺ content in the liquid water. We can see the K⁺ content on outer surface is the highest at the beginning of the splash, gradually diffuses in wards.

Fig. 8.

K⁺ content in the liquid water.

Fig. 9 shows the distribution of atmospheric pressure during breathing. The pressure increases quickly in the process of breathing out because the effect of resistance of the mask to air flow and opposite trend can be seen during the process of breathing in. The pressure changes periodically with the breathing cycles.

Fig. 9.

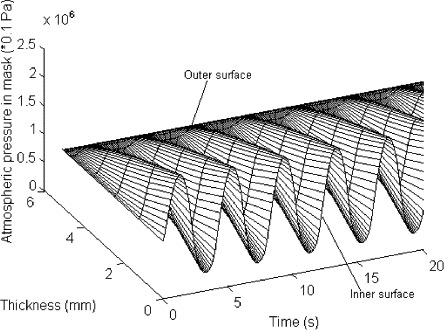
Distribution of atmospheric pressure.

As shown in Fig. 10 , the concentration of water vapor varies periodically with the breathing cycles. When a person breathes out the air, the water vapor concentration increases, and then, the water vapor concentration decreases during the breathing in process.

Fig. 10.

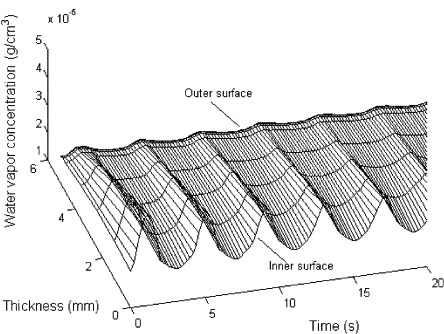
Distribution of water vapor concentration.

Fig. 11 shows the temperature distribution. The temperature change is controlled by convective heat transfer and the evaporation/condensation of water. The temperature on the inner surface increases gradually, as the body temperature is higher than that of mask. The temperature on the outer surface decreases as the liquid water evaporates and heat is adsorbed. Meanwhile, the temperature changes periodically with the breathing cycles. When a person breathes out the air, the water vapor concentration on the surface of the fibers is increased and the relative humidity of air is increase, so that water vapor condenses and releases the latent heat. Also, the air convective heat transfer occurs during breathing cycles. When the person breathes in the air, the opposite occurs.

Fig. 11.

Temperature distribution.

4.2. Effects of the structures and materials properties on virus content

In order to investigate the effects of structures and materials properties on virus content(i.e. ε _l  ×  C _v) transferred to the mask inner surface, we simulate masks with different effective capillary radius, thickness and contact angle and compare the simulation results. The simulation conditions are the same described in Section 4.1.

Fig. 12 shows the effect of the effective capillary radius on virus content on the facemask inner surface. The larger effective capillary is, the more viruses are deposited on the facemask inner surface becomes.

Fig. 12.

Effect of the effective capillary radius on virus content on the facemask inner surface.

Fig. 13 shows the effect of the thickness of facemask on virus content on the inner surface. The virus content on the inner surface of mask with small thickness is more than that with large thickness.

Fig. 13.

Effect of the thickness on virus content on the facemask inner surface.

Fig. 14 shows the effect of the contact angle on virus content on the facemask inner surface. The larger contact angle is, the smaller amount of viruses on the spread to facemask inner surface during breathing cycles.

Fig. 14.

Effect of the contact angle on virus content on the facemask inner surface.

5. Conclusion

In order to provide the critical theoretical analysis on mask thermal and moisture comfort and protective performance during wear, we report the development of a coupled heat and mass transfer model to describe the virus diffusion in the mask during breathing cycles. From the simulation, we can conclude that:

• 1.The predictions given by the model agree well with that of the experiment, indicating that the model has good prediction ability.
• 2.For material with large contact angle and small pore size such as N95 mask, the effect of breathing cycles on liquid water diffusion is small, but that on water vapor concentration and gas pressure is large. The viruses transfer in the mask mainly by diffusion in liquid water, and the evaporation of liquid water increases the virus concentration in liquid water. The virus mass in liquid water is larger than that on the surface of fibers in deposition because of small penetration velocity of liquid water.
• 3.The concentration of water vapor and pressure of the gas in the mask change periodically with the breathing cycles. The temperature of mask also changes periodically with the breathing cycles.
• 4.Decrease the effective capillary radius, increase the thickness and contact angle can restrain the virus transfer from outer surface to inner surface of the facemask.