Highlights
-
•
Human rabies is one of the major public-health problems in China.
-
•
Propose various models for the spread of rabies among dogs and from dogs to humans.
-
•
Roles of domestic and dogs, seasonality, spatial spread, inter-provincial spread were considered.
-
•
Use the models to simulate various rabies data in China.
-
•
Derive different control and prevention measures for rabies in China.
Keywords: Mathematical modeling, Transmission dynamics, Rabies, Basic reproduction number, Seasonality, Geographic spread
Abstract
Human rabies was first recorded in ancient China in about 556 BC and is still one of the major public-health problems in China. From 1950 to 2015, 130,494 human rabies cases were reported in Mainland China with an average of 1977 cases per year. It is estimated that 95% of these human rabies cases are due to dog bites. The purpose of this article is to provide a review about the models, results, and simulations that we have obtained recently on studying the transmission of rabies in China. We first construct a basic susceptible, exposed, infectious, and recovered (SEIR) type model for the spread of rabies virus among dogs and from dogs to humans and use the model to simulate the human rabies data in China from 1996 to 2010. Then we modify the basic model by including both domestic and stray dogs and apply the model to simulate the human rabies data from Guangdong Province, China. To study the seasonality of rabies, in Section 4 we further propose a SEIR model with periodic transmission rates and employ the model to simulate the monthly data of human rabies cases reported by the Chinese Ministry of Health from January 2004 to December 2010. To understand the spatial spread of rabies, in Section 5 we add diffusion to the dog population in the basic SEIR model to obtain a reaction–diffusion equation model and determine the minimum wave speed connecting the disease-free equilibrium to the endemic equilibrium. Finally, in order to investigate how the movement of dogs affects the geographically inter-provincial spread of rabies in Mainland China, in Section 6 we propose a multi-patch model to describe the transmission dynamics of rabies between dogs and humans and use the two-patch submodel to investigate the rabies virus clades lineages and to simulate the human rabies data from Guizhou and Guangxi, Hebei and Fujian, and Sichuan and Shaanxi, respectively. Some discussions are provided in Section 7.
1. Introduction
Rabies, an acute and fatal zoonotic disease, remains one of the most feared and important threats to public health around the world [29], [103]. It is most often transmitted through the bite or scratch of a rabid animal [87], [101]. All species of mammals are susceptible to rabies virus infection, but dogs remain the main carrier of rabies and are responsible for most of the human rabies deaths worldwide [13]. The rabies virus infects the central nervous system, ultimately causing disease in the brain and death. Once the symptoms of rabies have developed, its mortality rate is almost 100%. Rabies causes almost 60,000 deaths worldwide per year [29], [53], [92], [105], more than 95% of which occur in Asia and Africa [50]. More human deaths from rabies occur in Asia than anywhere else in the world [101], where India and China have the most and second most reported cases, respectively [90].
Rabies was first recorded in ancient China in about 556 BC [97] and nowadays it is still a very serious public-health problem in China. It has been classified as a class II infectious disease in the National Stationary Notifiable Communicable Diseases [45], [115] and the annual data of human rabies have been archived by the Chinese Center for Disease Control and Prevention since 1950. From 1950 to 2015, 130,494 human rabies cases were reported in China [60], [67], [84], [115], an average of 1977 cases per year. It is estimated that 95% of human rabies cases are due to dog bites in mainland China [60], [100].
In the last 60 years, China experienced a few major epidemics of human rabies. The first peak occurred from 1956 to 1957 with about 2000 cases in both years, followed by substantial decreases in the early 1960s. The number of cases reached 2000 again in 1969 and increased to the historical record of 7037 cases in 1981. During the 1980s, more then 5000 cases were reported annually. In the 1990s, the number of cases declined rapidly from 3520 in 1990 to 159 in 1996 [60], [115]. Since then, the number of human rabies case has increased steadily again and reached another peak in 2007 with 3300 cases [60], [84]. From 1996 to 2015, 30,300 human rabies cases were reported [59], [60], [61]. Though human rabies were reported in almost all provinces in China [45], nearly 60% of the total rabies cases in China were reported in the southern Guangdong, Guangxi, Guizhou, Hunan, and Sichuan provinces [60]. It is believed that the increase of rabies deaths results from a major increase in dog ownership and a very low rate of rabies vaccination [60]. In rural areas, about 70 percent of households have dogs and vaccination coverage of dogs is very low, largely because of poor awareness of rabies and the high cost of vaccination. Moreover, owned dogs usually have not been registered and the number of dogs is estimated at 80–200 millions [87].
Although the recent reemergence of human rabies in China has attracted enormous attention of many researchers, the transmission dynamics of rabies in China is still poorly understood. Zhang et al. [115] analyzed the 108,412 human rabies cases in China from 1950 to 2004. They suggested that the rabies epidemics in China may be explained by dog population dynamics, untimely and inappropriate postexposure prophylaxis (PEP) treatment, and the existence of healthy carrier dogs. Si et al. [79] examined the 22,527 human rabies cases from January 1990 to July 2007 and the details of 244 rabies patients, including their anti-rabies treatment of injuries or related incidents. They concluded that the failure to receive PEP was a major factor for the increase of human cases in China. Song et al. [84] investigated the status and characteristics of human rabies in China between 1996 and 2008 to identify the potential factors involved in the emergence of rabies. Yin et al. [107] compiled all published articles and official documents on rabies in mainland China to examine challenges and needs to eliminate rabies in the country.
Mathematical modeling has become an important tool in analyzing the epidemiological characteristics of infectious diseases and can provide useful control measures. Various models have been used to study different aspects of rabies in wild animals. Anderson et al. [3] pioneered a deterministic model consisting of three subclasses, susceptible, infectious and recovered, to explain epidemiological features of rabies in fox populations in Europe. A susceptible, exposed, infectious, and recovered (SEIR) model was proposed by Coyne et al. [19], and lately was also used by Childs et al. [14], to predict the local dynamics of rabies among raccoons in the United States. Dimitrov et al. [24] presented a model for the immune responses to a rabies virus in bats. Clayton et al. [17] considered the optimal control of an SEIRS model which describes the population dynamics of a rabies epidemic in raccoons with seasonal birth pulse. Besides these deterministic models, discrete deterministic and stochastic models [2], [7], continuous spatial models [48], and stochastic spatial models [75], [81] have also been employed to study the transmission dynamics of rabies. See also [27], [33], [38], [73], [82], [83]. We refer to reviews by Sterner and Smith [86] and Panjeti and Real [70] for more detailed discussions and references on different rabies models. Note that all these modeling studies focused on rabies in wildlife [55].
Recently there have been some studies on modeling canine and human rabies. Hampson et al. [39] observed rabies epidemics cycles with a period of 3–6 years in dog populations in Africa, built a susceptible, exposed, infectious, and vaccinated model with an intervention response variable, and showed significant synchrony. Carroll et al. [11] created a continuous compartmental model to describe rabies epidemiology in dog populations and explored three control methods: vaccination, vaccination plus fertility control, and culling. Wang and Lou [96] and Yang and Lou [109] used ordinary differential equation models to characterize the transmission dynamics of rabies between humans and dogs. Zinsstag et al. [117] extended existing models on rabies transmission between dogs to include dog-to-human transmission and concluded that combining human PEP with a dog-vaccination campaign is more cost-effective in the long run.
In the last a few years, our team have been trying to model the transmission dynamics of rabies in China by considering different characters and aspects. In Zhang et al. [113] we constructed a basic susceptible, exposed, infectious, and recovered (SEIR) type model for the spread of rabies virus among dogs and from dogs to humans and used the model to simulate the human rabies data in China from 1996 to 2010. In Hou et al. [43] we modified the basic model in Zhang et al. [113] by including both domestic and stray dogs and applied the model to simulated the human rabies data from Guangdong Province, China. Observing that the monthly data of human rabies cases reported by the Chinese Ministry of Health from January 2004 exhibit a periodic pattern on an annual base, in Zhang et al. [111] we proposed a SEIR model with periodic transmission rates to investigate the seasonal rabies epidemics and used the model to simulate the monthly data of human rabies cases reported by the Chinese Ministry of Health from January 2004 to December 2010. To understand the spatial spread of rabies, in Zhang et al. [112] we added diffusion to the dog population in the SEIR model considered by Zhang et al. [113] to obtain a reaction–diffusion equation model, determined the minimum wave speed connecting the disease-free equilibrium to the endemic equilibrium and illustrated the existence of traveling waves by numerical simulations. In order to investigate how the movement of dogs affects the geographically inter-provincial spread of rabies in Mainland China, in Chen et al. [12] we proposed a multi-patch model to describe the transmission dynamics of rabies between dogs and humans and used the two-patch submodel to investigate the rabies virus clades lineages and to simulate the human rabies data from Guizhou and Guangxi, Hebei and Fujian, and Sichuan and Shaanxi, respectively. The purpose of this article is to provide a review about the models, results, and simulations that we have obtained in these papers on studying the transmission of rabies in China. We also summarize the prevention and control measures for the spread of rabies in mainlan China that were proposed based on these studies. Finally we discuss some topics for future study.
2. A SEIR rabies model for dog–human interactions [113]
We consider both dogs and humans and classify each of them into four subclasses: susceptible, exposed, infectious and recovered, with dog sizes denoted by Sd(t), Ed(t), Id(t), and Rd(t), and human sizes denoted by Sh(t), Eh(t), Ih(t), and Rh(t), respectively. When a susceptible human individual is bitten by an infectious dog, this human individual is now exposed. Data [51] indicate that the incubation period ranges from 5 days to 3 years, with a median of 41 days and a mean of 70 days. About 15–20% of those bitten by infected dogs progress to illness and become infectious [9]. Since more and more bitten people are seeking for PEP, the recovered rate of infected humans has been increasing in China [15].
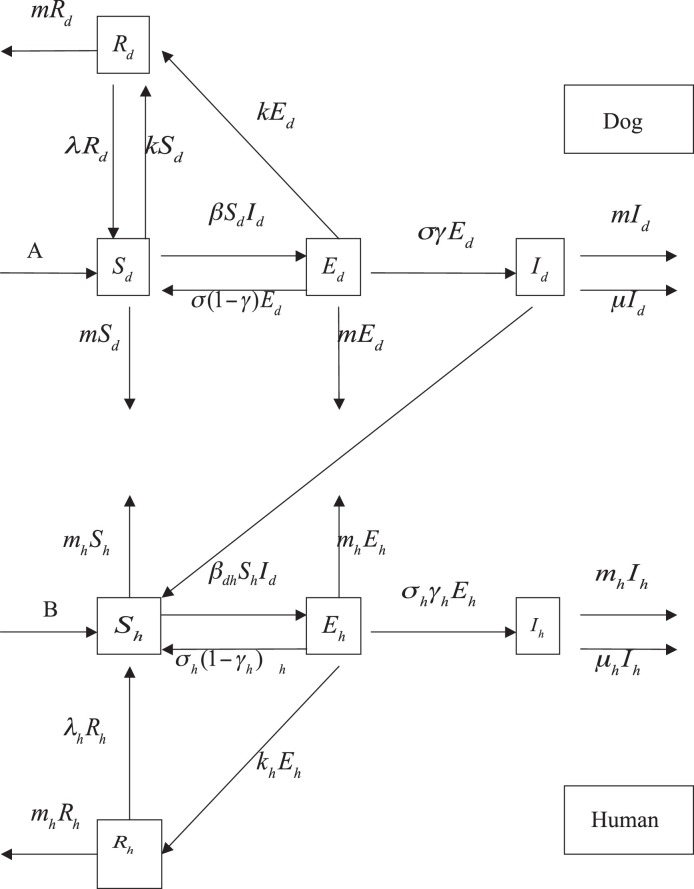
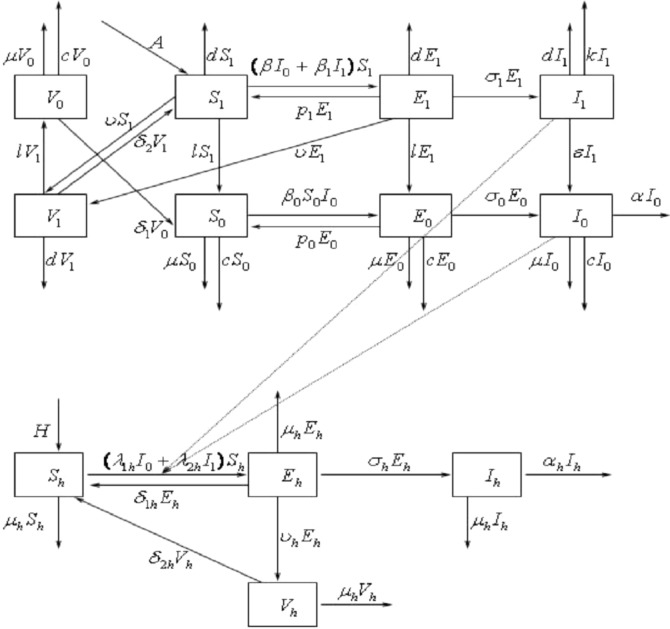
Our assumptions on the dynamical transmission of rabies among dogs and from dogs to humans are demonstrated in the flowchart (Fig. 2.1 ). The model is a system of eight ordinary differential equations:
| (2.1) |
where all parameters are positive. For the dog population, A describes the annual birth rate; λ denotes the loss rate of vaccination immunity; i represents the incubation period of infected dogs so that is the time duration in which infected dogs remain infectious; γ is the risk factor of clinical outcome of exposed dogs, so σγE represents those exposed dogs that develop clinical rabies and denotes those that do not develop clinical rabies and return to the susceptible class; m is the natural death rate; k is the vaccination rate; μ is the disease-related death rate; βSI describes the transmission of rabies by interactions between infectious dogs and susceptible dogs. For the human population, B is the annual birth rate; λh represents the loss rate of vaccination immunity; ih denotes the incubation period of infected individuals so is the time duration of infectiousness of infected persons; γh is the risk factor of clinical outcome of exposed humans, so σhγhEh represents those exposed individuals develop into the infectious class and the rest return to the susceptible class; mh is the natural death rate; k 1 is the vaccination rate; μ 1 is the disease-related death rate. The term βdhShId describes the transmission of rabies from infectious dogs to susceptible humans.
Fig. 2.1.
Transmission diagram of rabies among dogs and from dogs to humans. Sd(t), Ed(t), Id(t), Rd(t), and Sh(t), Eh(t), Ih(t), Rh(t) represent susceptible, exposed, infectious and recovered dogs and humans, respectively.
2.1. Basic reproduction number and stability of equilibria
Define the basic reproduction number by (see [23], [93])
| (2.2) |
There is a disease-free equilibrium given by
| (2.3) |
where
| (2.4) |
If R 0 > 1, we can derive the unique endemic equilibrium:
| (2.5) |
where
| (2.6) |
in which
For the stability of the disease-free and endemic equilibria, we have the following results.
Theorem 2.1 [113] —
(a) If R 0 < 1, then the disease-free equilibrium E 0 of system (2.1) is locally asymptotically stable and is globally asymptotically stable in the region
(b) If R 0 > 1, then the endemic equilibrium E * of system (2.1) is locally asymptotically stable in the region and all solutions in tend toward the disease-free equilibrium E 0 .
2.2. Estimation of epidemiological parameters
In order to carry out numerical simulations, we need to estimate the model parameters. The data concerning human rabies from 1996 to 2010 are obtained mainly from epidemiological bulletins published by the Chinese Ministry of Health [60], [61]. To obtain the data involving dogs, we rely on online news, our estimation or data fitting. The values of parameters are listed in Table 1 and are explained as follows: (a) The number of dogs was estimated to be 30 millions in 1996 and 75 millions in 2009 [60]. (b) The incubation period of rabies is 1–3 months. We select the medium value: 2 months. So . According to the protection period of rabies vaccine, we assume that . The probability of clinical outcome of the exposed is 30–70%. Here, we assume that it is 40%. So . (c) The rate of vaccination is the product of efficiency and the coverage rate of rabies vaccine. Efficiency of rabies vaccine is about 90%. However, the rates of vaccine coverage for dogs and humans are low. Considering a large number of stray dogs and the poor awareness of people in rural areas, we assume that they are equal to 10% and 60%, respectively. (d) The transmission rates β and βdh are obtained by fitting in simulations.
Table 2.1.
Description of parameters in model (2.1).
| Parameters | Value | Unit | Comments | Source |
|---|---|---|---|---|
| A | 3 × 106 | Annual crop of newborn puppies | Fitting | |
| λ | 1 | Dog loss rate of vaccination immunity | Assumption | |
| γ | 0.4 | Risk of clinical outcome of exposed dogs | [9] | |
| σ | 6 | The reciprocal of the dog incubation period | Assumption | |
| 1/6 | year | Dog incubation period | Assumption | |
| m | 0.08 | Dog natural mortality rate | Assumption | |
| β | Dog-to-dog transmission rate | Fitting | ||
| k | 0.09 | Dog vaccination rate | [60] | |
| μ | 1 | Dog disease-related death rate | [60] | |
| B | 1.54 × 107 | Human annual birth population | [30] | |
| λh | 1 | Human loss of vaccination immunity | Assumption | |
| γh | 0.4 | Risk of clinical outcome of exposed humans | [9] | |
| σh | 6 | The reciprocal of the human incubation period | [9] | |
| 1/6 | year | Human incubation period | [9] | |
| mh | 0.0066 | Human natural mortality rate | [65] | |
| βdh | Dog-to-human transmission rate | Fitting | ||
| kh | 0.54 | Human vaccination rate | [60] | |
| μh | 1 | Human disease-related death rate | [60] |
2.3. Numerical simulations
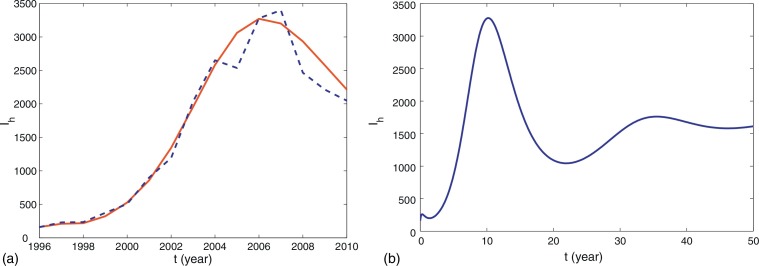
The numerical simulation of human rabies cases in China from 1996 to 2010 is shown in Fig. 2.2 (a), indicating that our model provides a good match to the reported data. The awareness of rabies for people in recent years has been enhanced gradually. This may explain why the number of human rabies cases decreased in most recent years. This demonstrates further that our model has certain rationality. Moreover, our model indicates the tendency of the rabies epidemics with the current control and prevention measures, which is presented in Fig. 2.2(b). It shows that the number of human rabies cases will decrease steadily in the next 7 or 8 years, then increase again and reach another peak (about 1750) in 2030, and finally become stable. Therefore, if no further effective prevention and control measures are taken, the disease will not vanish.
Fig. 2.2.
(a) The comparison between the reported human rabies cases in mainland China from 1996 to 2010 and the simulation of Ih(t) from the model. The dashed curve represents the data reported by the Chinese Ministry of Health while the solid curve is simulated by using our model. The values of parameters are given in Table 2.1. The initial values used in the simulations were (b) The predition of human rabies cases Ih(t) in 50 years (1996–2045) with the current control and prevention measures.
2.4. Basic reproductive number for rabies in China
Based on the parameter values given in Table 2.1, we estimate that the basic reproduction number for rabies transmission in China. For rabies in Africa, Hampson et al. [40] obtained that according to the data from 2002 to 2007 when the peak of animal rabies cases was less than 30 weekly, which is far less than 393 the peak of monthly human rabies cases in China. Zinsstag et al. [117] also estimated the effective reproductive ratio to be 1.01 through a research framework for rabies in an African city. Also for the rabies in USA in the 1940s when the annual reported cases varied from 42 to 113 and sharply increased in 1948, it was estimated that [18]. From these, it can be seen that our estimate of is reasonable. More discussions of R 0 for outbreaks of rabies around the world can be found in [18], [40].
2.5. Sensitivity analysis
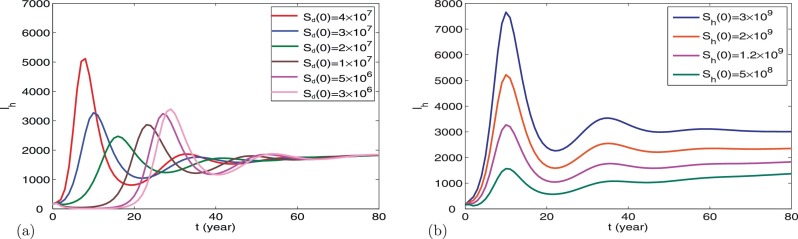
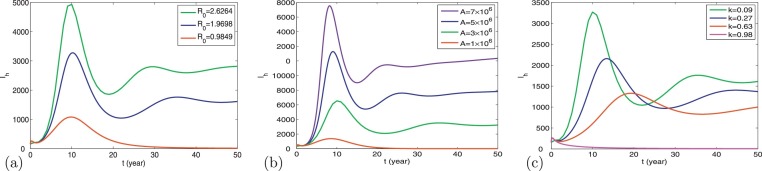
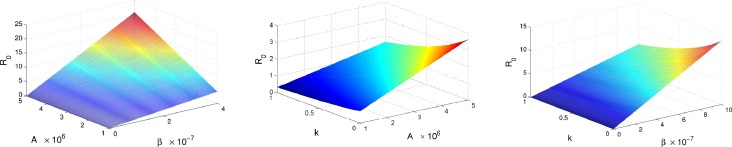
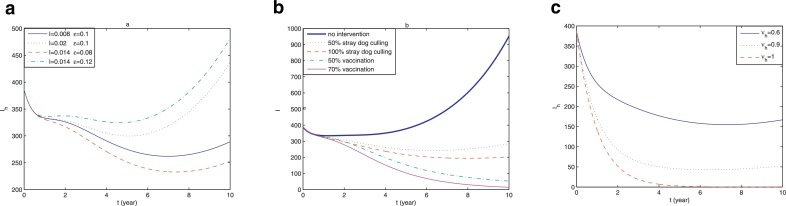
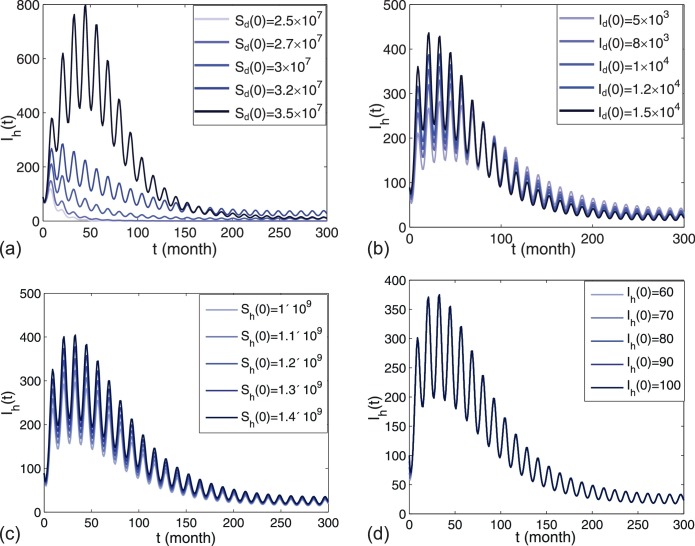
Firstly, we examine the influence of initial conditions on the number of infected human rabies cases Ih(t). From Fig. 2.3 , we can see that the initial population sizes of both dogs and humans effect on Ih(t). Moreover, the initial conditions of dogs can influence not only the number of human rabies cases but also the time of rabies case peak. The initial conditions of humans do not have such effects. We also observe that the peak of the initial outbreak would be postponed if Sd(0) is decreasing. Next, to find better control strategies for rabies infection, we perform some sensitivity analysis of Ih(t) and the basic reproduction number R 0 in terms of the model parameters. First, we show variations of Ih(t) with time for different values of R 0 in Fig. 2.4 . We can see that R 0 is really the threshold for the establishment of the disease in the susceptible pool and the number of infections increases with the increase of R 0 (Fig. 2.4(A)). The influences of A and k on Ih(t) are shown in Fig. 2.4(B)(C). It can be observed that Ih(t) decreases as A is declining or k is increasing. When and the disease can die out. Moreover, we find that the decrease of A cannot delay the time of the first peak while an increase of k can. Furthermore, the influences of A, β, k on R 0 are given in Fig. 2.5 . It is clear that R 0 changes more quickly when both A and β vary. When β is very small, the disease can be eliminated even if . When the disease cannot be eliminated even if . From (B) and (C) in Fig. 2.5, it is clear that when A or β is very small, the disease can disappear even if . When A > 3 × 106 or the disease cannot be eliminated even if . Hence, it indicates that the influence of A and β on the basic reproduction number R 0 is greater. Fig. 2.5 reflects that whatever dog vaccination rate is, when the annual crop of newborn puppies is greater than 3 million and dog-to-dog transmission rate is greater than R 0 cannot be below 1. However, it is difficult to control β. Currently, in China the annual crop of newborn puppies can exceed 5 million and the proportion of immunized dogs is only about 10%, which is too low. With the current incidence rate we know that if the annual crop of newborn puppies A(5 × 106) is not reduced, it is impossible to have R 0 below 1; if it is necessary to keep k ≥ 0.95; if it is necessary to keep k ≥ 0.39.
Fig. 2.3.
The influence of initial conditions on the number of human rabies cases Ih(t). (a) For different initial values of susceptible dog population Sd(0). (b) For different values of susceptible huamns Sh(0).
Fig. 2.4.
The effects of parameters on the number infected human rabies cases Ih(t). (a) Ih(t) in terms of different values of R0; (b) Ih(t) in terms of different values of A and (c) Ih(t) in terms of different values of k.
Fig. 2.5.
The combined influence of parameters on R0. (a) R0 in terms of A and β. (b) R0 in terms of A and k. (c) R0 in terms of β and k.
The above analysis demonstrates that human rabies can be controlled with two strategies: reducing the annual crop of newborn puppies and increasing the dog immunization rate at the same time, which can also reduce the incidence rate β.
3. SEIV rabies models with both domestic and stray dogs [43]
The population of dogs has increased gradually in China since the late 1990s. Now most households in Guangdong, Guangxi, Guizhou, and Hunan Provinces, where most of the rabies cases were recorded in recent years, have at least one dog. However, dog rabies surveillance often has not been carried out and most people are unaware of the risk of rabies in China. Domestic dog vaccination rate remains 2.8–6.4% [44], and only 30% or less of infected patients seek medical services or receive adequate post-exposure prophylaxis (PEP, which consists of local treatment of the wound, followed by vaccine therapy with or without rabies immunoglobulin) [79], [84], [114]. In Guangdong Province, there are more than three million domestic dogs and many stray dogs, but only about four hundred thousand rabies vaccines are sold every year. In particular, some infected domestic dogs are not treated properly and are abandoned by their hosts or run away from their hosts. From 2003 to 2004, 66.5% of the human rabies cases were caused by domestic dogs and at least 18.2% by stray dogs and others [79]. Between 2006 and 2010, a total of 1671 human rabies cases were reported in Guangdong Province, the average outbreak rate is about 0.40/100,000, accounting for 12.7% of the total cases of China [20], [61], see Table 3.1 . After Guangxi and Hunan Provinces, Guangdong has the third most rabies cases in China [79].
Table 3.1.
Reported human rabies cases in Guangdong Province and China, 2006–2010.
| Year | 2006 | 2007 | 2008 | 2009 | 2010 |
|---|---|---|---|---|---|
| Guangdong | 387 | 334 | 319 | 330 | 301 |
| China | 3279 | 3300 | 2246 | 2213 | 2049 |
| Percentage | 11.8% | 10.2% | 14.2% | 14.9% | 14.7% |
In this section, taking into account some specific characteristics of rabies transmission in Guangdong Province of China, we propose a susceptible-exposed-infectious-vaccinated (SEIV) model for the dog–human transmission of rabies taking both domestic and stray dogs into consideration. We classify each of the stray dog, domestic dog, and human populations into four subclasses: susceptible, exposed, infective and vaccinated. Let S 0(t), E 0(t), I 0(t), V 0(t), and S 1(t), E 1(t), I 1(t), V 1(t) denote the densities of susceptible, exposed, infective and vaccinated stray dog and domestic dog populations; Sh(t), Eh(t), Ih(t), Vh(t) denote the densities of susceptible, exposed, infective and vaccinated human populations at time t, respectively. The twelve compartments and model variables are given in Fig. 3.1 .
Fig. 3.1.
Flowchart of rabies transmission between domestic and stray dogs and humans.
There are some assumptions for the dog–human model. (i) The annual human birth population is constant; (ii) the infection of rabies virus are divided into three stages: prodromal, furious (or excitative) and paralytic. Once infected with rabies virus, dogs first experience the Symptoms of Prodromal stage, including lethargy, shyness and the desire to be alone, etc., lasting about 2 days, and then enter the furious stage (rabid domestic dogs leave their hosts to be stray dogs), so we assume that the transmission rate from domestic dogs to stray dogs is zero; (iii) the birth rate of stray dog is zero since newborn stray dogs are not taken care of by people and do not survive well in stray, and hence their survival rate is assumed to be almost zero. The mathematical model is governed by twelve ordinary differential equations.
| (3.1) |
The parameters are described in Table 3.2 . One can show that the region
is positively invariant for model (3.1).
Table 3.2.
Parameters and their values for model (3.1) (unit: ).
| Parameter | Value | Interpretation | Source |
|---|---|---|---|
| A | 7.7 × 105 | Domestic dog recruitment rate | Fitting |
| l | 0.014 | Rate of domestic dog abandoned | Fitting |
| μ | 0.24 | Stray dog mortality rate | Assumption |
| c | 0.06 | Stray dog culling rate | Assumption |
| δ1 | 0.5 | Stray dog loss of vaccination immunity rate | Assumption |
| δ2 | 0.5 | Domestic dog loss of vaccination immunity rate | assumzption |
| σ0 | 0.35 | Rate of clinical outcome of exposed stray dogs | [A] |
| σ1 | 0.37 | Rate of clinical outcome of exposed domestic dogs | [A] |
| p0 | 0.35 | Rate of no clinical outcome of exposed stray dogs | [A] |
| p1 | 0.37 | Rate of no clinical outcome of exposed domestic dogs | [A] |
| ϵ( > l) | 0.1 | Transfer rate from rabid dogs to stray dogs | Fitting |
| α | 1 | Rabid dog mortality rate | [60] |
| β0 | Transmission rate from stray dogs to stray dogs | Fitting | |
| β | Transmission rate from stray dogs to domestic dogs | Fitting | |
| β1 | Transmission rate from domestic dogs to domestic dogs | Fitting | |
| d | 0.11 | Domestic dog mortality rate | Assumption |
| ν | 0.133 | Domestic dog vaccination rate | [80] |
| k | 0.79 | Domestic rabid dog culling rate | [B] |
| H | 106 | Annual human birth population | [35] |
| μh | Human mortality rate | [34] | |
| λ1h | Transmission rate from stray dogs to humans | Fitting | |
| λ2h | Transmission rate from domestic dogs to humans | Fitting | |
| δ1h | 0.33 | Rate of no clinical outcome of exposed humans | [A] |
| δ2h | 1 | Human loss of vaccination immunity rate | [B] |
| σh | 0.33 | Rate of clinical outcome of exposed humans | [A] |
| νh | 0.328 | Human vaccination rate | [79] |
| αh | 1 | Rabid human mortality rate | [60] |
Notes: [A] The probability of clinical outcome of the exposed dogs is about 30–70% [16]. Here, we estimate that it is 50%, so the probability of stray dog survival and clinical outbreak is . Similarly, the probability of domestic dog (human) survival and clinical outbreak is about 0.37(0.33). [B] . In China, the valid time of rabies vaccination for humans is six months to one year, so we have .
3.1. Basic reproduction number, extinction and persistence of the disease
Now we derive the basic reproduction number of the model by the next generation matrix formulated in Diekmann et al. [22] and van den Driessche and Watmough [93]. It is easy to see that model (3.1) always has a disease-free equilibrium where
and
We define the basic reproduction number by
| (3.2) |
where
Note that
we have the following results.
Theorem 3.1 [43] —
If R 0 < 1, then the disease-free equilibrium P 0 of model (3.1) is globally asymptotically stable.
Let be the continuous flow on X generated by the solution x(t) of model (3.1) with initial condition x(0) ∈ X. ∂X is the boundary of X, and Ω is the maximal invariant set of Φt(x) on ∂X. We have the following result.
Theorem 3.2 [43] —
If R 0 > 1, then the flow Φt(x) on X is uniformly persistent for any solution x(t) of system (3.1) with and E 0(0), I 0(0) > 0 or E 1(0), I 1(0) > 0.
Remark 3.3
The semiflow Φt(x) we defined above is point dissipative, all the solutions of the system are ultimately bounded in X, and disease is uniformly persistent if R 0 > 1 from Theorem 3.2. Thus, by a well known result in persistence theory (see [46], [116]) we know that the system has at least one positive equilibrium However, since there are 12 equations in the model, we are unable to express P* explicitly and determine its stability.
3.2. Data simulations and sensitivity analysis
From the Department of Health of Guangdong Province, we can obtain the data on human rabies cases. However, there are very few published studies on the population dynamics of dogs. Thus we rely on reality to make some rational assumptions or data fitting to estimate some parameters related to dogs. The values of parameters are listed in Table 3.2. In Guangdong Province, there are 2 million dogs on rabies exposure every year [41], the vaccination rate is only 32.8% or less, hence we estimate that the number of vaccinated dogs is 0.6 million, so . we make the data fitting to obtain that then [35]; there are about three million dogs and four hundred thousand rabies vaccines every year [80], thus we estimate and assume and data fitting gives .
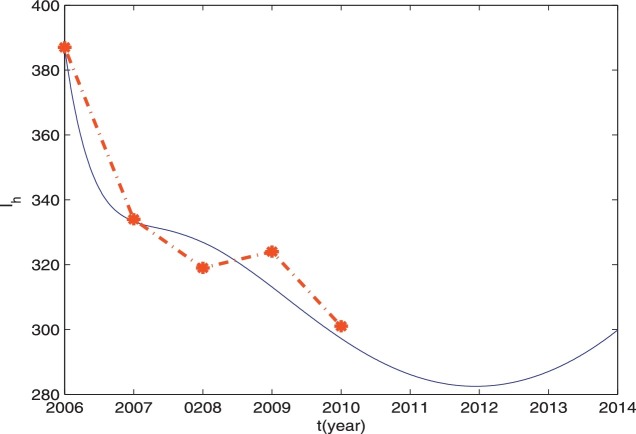
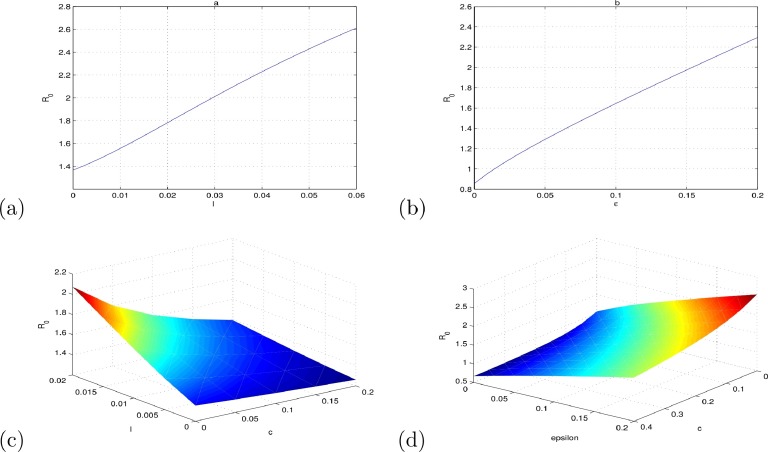
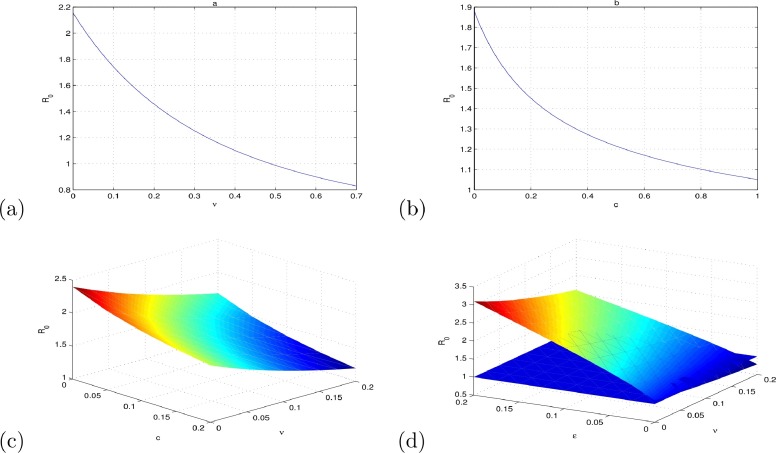
Using model (3.1), we simulate the data from 2006 to 2010 and predict the trend of human rabies infection in Guangdong Province. Fig. 3.2 shows that the simulation of our model with reasonable parameters values provides a good match to the data on infected human rabies cases in Guangdong Province from 2006 to 2010. With the current control measures, our model predicts that the human rabies infection cases would continue decreasing in the next a couple of years and then may increase slightly afterward. With the simulated parameter values, we estimate that Thus, human rabies will persist in Guangdong Province under the current control and prevention measures. If we fix all parameters except l (the rate at which domestic dogs are abandoned) and ϵ (the rate rabid domestic dogs become stray dogs), the basic reproduction number R 0 increases as l and ϵ increase. Fig. 3.3 (a) and (b) represents the relationship between R 0 and the quantity of stray dogs. We can see that the influence of parameter ϵ on the basic reproduction number R 0 is greater than that of parameter l, thus culling domestic infected dogs at the right time can effectively decrease R 0. From Fig. 3.3(c) and (d), we can also see that culling stray dog population (increasing c) can reduce R 0. Moreover, in order to control rabies, the larger ϵ is, the more important it is to target culling stray dogs. Though both vaccinating susceptible dogs and culling stray dogs are effective control measures, comparing Fig. 3.4 (a) and (b), we find that R 0 can become less than one if vaccination rate ν is greater than 50% but cannot become less than one even though the culling rate is 100%. Thus, culling stray dogs alone is not a good control measure while vaccination is a more effective one. Fig. 3.4(c) and (d) depicts the plots of R 0 in terms of (ν, c) and (ν, ϵ), respectively. We can see that increasing the vaccination rate and the culling rate of rabid domestic dogs are more effective than increasing the vaccination rate and the culling rate of stray dogs. Therefore, culling of infected dogs and vaccination are most important and effective means to control rabies infection. From Fig. 3.5 (a), we can see that the acute infection in humans in Guangdong Province would be reduced evidently through the decrease of the stray dog population. Moreover, reducing the transfer from infected domestic dogs to stray dogs is more effective than decreasing domestic dogs that are abandoned. According to WHO, as long as victims bitten by animals receive proper PEP timely, human rabies can be prevented [98]. Fig. 3.5(c) indicates that the rabies infection rate can be reduced with the increase of using PEP. Thus, publicity and education on the risk and prevention of rabies is necessary and important to control the epidemic and should be strengthen in endemic areas, especially in rural areas.
Fig. 3.2.
Simulation of human rabies infection cases over time for Guangdong Province of China. The smooth curve represents the solution Ih of model (3.1) and the stars are the reported data on human cases.
Fig. 3.3.
Plots of R0 in terms of (a) l (abandoned rate of domestic dogs), (b) ϵ (transfer rate from rabid dogs to stray dogs), (c) l and c (culling rate of stray dogs), and (d) ϵ and c.
Fig. 3.4.
Plots of R0 in terms of (a) ν (vaccination rate of domestic dogs), (b) c (culling rate of stray dogs), (c) ν and c, and (d) ν and ϵ (transfer rate from rabid dogs to stray dogs).
Fig. 3.5.
Simulations of infected human rabies cases Ih in Guangdong Province of China on different parameters. (a) l and ϵ, (b) c and ν, and (c) νh.
4. Seasonal rabies models [111]
After the outbreaks of Severe Acute Respiratory Syndromes (SARS) in 2003, the Chinese Ministry of Health started to publish reported cases about the National Stationary Notifiable Communicable Diseases, including rabies, every month. We observe that the monthly data of human rabies cases reported by the Chinese Ministry of Health from January 2004 exhibit a periodic pattern on an annual base. The cases in the summer and autumn are significantly higher than in the spring and winter [60], [61]. It was also reported that the main seasons for rabies epidemics in China are summer and fall [84]. Moreover, the infected areas are mainly distributed in the south provinces such as Sichuan, Hunan, Guangxi, Guangdong, Anhui, Fujian [84], which demonstrates that rabies transmission depends on the weather.
It is well-known that many diseases exhibit seasonal fluctuations, such as whooping cough, measles, influenza, polio, chickenpox, mumps, etc.[10], [25], [32], [52], [62], [99], [102], [110]. Seasonally effective contact rate [78], periodic changing in the birth rate [54] and vaccination program are often regarded as sources of periodicity. In this section, we take periodic transmission rate into account based on the following facts: (i) In the summer and fall, people wear light clothing and are lack of protection for the bites or scratches of dogs. Also, in summer and fall people, in particular farmers, have more frequent outdoor activities which increase chance of human–dog interact. (ii) In these seasons, dogs are more maniacal and apt to attack each other and humans. (iii) From July to September schools are closed for summer vacations and children are out of supervision and enjoy tantalizing dogs. In fact, it was reported [84] that 25.7% of human rabies cases in China are students and unattended children. (iv) In addition, temperature may be related to the fluctuation of diseases. Under high temperature in summer, rabies virus can survive easily and its infectivity is stronger.
4.1. Model formulation
We denote the total numbers of dogs and humans by Nd(t) and Nh(t), respectively, and classify each of them into four subclasses: susceptible, exposed, infectious and recovered, with the number of dogs denoted by Sd(t), Ed(t), Id(t), and Rd(t), and human sizes denoted by Sh(t), Eh(t), Ih(t), and Rh(t), respectively. The transmission dynamics associated with these subpopulations are illustrated in Fig. 2.1. The transmission rate between Sd(t) and Id(t) is β(t), the transmission rate between Sh(t) and Id(t) is βdh(t), and humans do not spread rabies to each other. We can write transmission rate β(t) in the general form where Nd is the total number of dogs, is the number of dogs that a susceptible dog comes across per unit time, is the probability of getting bitten after interacting with the susceptible dog, and λ 0 is the probability of being infected after bitten for the susceptible dog. We can express βdh(t) similarly. As discussed in the introduction, in the summer and fall there are more frequent interacts among dogs and between dogs and humans and these coefficients are more likely to change as season changes. Thus we use the periodic functions and proposed by [76] to describe the transmission rates among dogs and from dogs to humans, where a and a 1 are the baseline contact rates and b and b 1 are the magnitudes of forcing.
The birth numbers of dogs and humans per unit time are constant. Vaccination is often applied to seemingly healthy dogs (Sd(t) and Ed(t)) and people bitten by dogs (Eh(t)). Particularly, we need to interpret that kh and k are the products of the vaccination coverage rate and the vaccination effective rate. However, there is a protection period for rabies vaccine. Thus, we introduce loss rates of immunity λ and λh. Because not all the exposeds will develop clinical outbreak, clinical outcome rates γ and γh are presented. Natural death rates are m and mh, and disease-related death rates are μ and μh, respectively. The model takes the following form:
| (4.1) |
where all parameters are positive, the interpretations and values of parameters are described in Table 4.1 , and .
Table 4.1.
Descriptions and values of parameters in model (4.1).
| Para. | Value | Unit | Interpretation | Source |
|---|---|---|---|---|
| A | 2.34 × 105 | Dog birth population | Estimation | |
| λ | Dog loss rate of immunity | Assumption | ||
| i | 1.045 | month | Dog incubation period | [117] |
| σ | 1/i | [117] | ||
| γ | 0.49 | Clinical outcome rate of exposed dogs | [117] | |
| m | 0.0064 | Dog natural mortality rate | Assumption | |
| a | none | The baseline contact rate | Estimation | |
| b | 0.41 | none | The magnitude of forcing | Estimation |
| k | 0.09 | Dog vaccination rate | [60] | |
| μ | 1 | Dog disease-related death rate | [60] | |
| B | 1.34 × 106 | Human birth population | [65] | |
| λh | Human loss rate of immunity | [16] | ||
| ih | 2 | month | Human incubation period | [16] |
| σh | 1/i1 | [16] | ||
| γh | 0.5 | clinical outcome rate of exposed humans | [5] | |
| mh | 0.00057 | Human natural mortality rate | [65] | |
| ah | none | The baseline contact rate | Estimation | |
| bh | 0.23 | none | The magnitude of forcing | Estimation |
| kh | 0.54 | Human vaccination rate | [60] | |
| μh | 1 | Human disease-related death rate | [60] |
4.2. Disease-free equilibrium and positive periodic solutions
Notice that from the equations in model (4.1), we have
| (4.2) |
Let
Theorem 4.1 [111] —
The region X is positively invariant with respect to system (4.1) .
It is easy to see that system (4.1) has one disease-free equilibrium
where
We calculate the basic reproduction number R 0 for system (4.1) following the definition of [8] and the general calculation procedure in [95], which is defined as z 0 such that where W(ω, 0, z 0) is the evolution operator of the linearized periodic system. Rewriter the variables of system (4.1) as a vector Following [95], we have
Thus we obtain that
and
Let Y(t, s), t ≥ s, be the evolution operator of the linear system
That is, the 4 × 4 matrix Y(t, s) satisfies
for any where I is the 4 × 4 identity matrix. Now we introduce the linear ω-periodic system
| (4.3) |
with parameter . Let W(t, s, z), t ≥ s, be the evolution operator of system (16) on . Clearly,
Following the method in [95], let ϕ(s) be periodic in s and the initial distribution of infectious individuals. So F(s)ϕ(s) is the rate of new infections produced by the infected individuals who were introduced at time s. When t ≥ s, Y(t, s)F(s)ϕ(s) gives the distribution of those infected individuals who were newly infected by ϕ(s) and remain in the infected compartments at time t. Naturally,
is the distribution of accumulative new infections at time t produced by all those infected individuals ϕ(s) introduced at time previous to t.
Let Cω be the ordered Banach space of all periodic functions from to which is equipped with the maximum norm ∥ · ∥ and the positive cone . Then we can define a linear operator L: Cω → Cω by
L is called the next infection operator and the spectral radius of L is defined as the basic reproduction number
for the periodic epidemic model (4.1).
To determine the threshold dynamics of model (4.1), applying Theorem 2.2 in [95], we have the following result.
Theorem 4.2 [111] —
The disease-free equilibrium P 0 is globally asymptotically stable when R 0 < 1.
Define
and Denote u(t, x 0) as the unique solution of system (4.1) with the initial value . Let P: X → X be the Poincaré map associated with system (4.1), i.e., where ω is the period. Applying the fundamental existence-uniqueness theorem [71], we know that u(t, x 0) is the unique solution of system (4.1) with From Theorem 4.1, we know that X is positively invariant and P is point dissipative. Moreover, we can show that is an isolated invariant set in X and so P is uniformly persistent with respect to (X 0, ∂X 0) (Theorem 1.3.1 and Remark 1.3.1 in [116]). Thus, Theorem 1.3.6 in [116] implies that there is a periodic solution.
Theorem 4.3 [111] —
System (4.1) has at least one positive periodic solution.
4.3. Simulations and sensitivity analysis
We now use model (4.1) to simulate the reported human rabies data of China from January 2004 to December 2010, predict the trend of the disease and seek for some control and prevention measures. The data, concerning human rabies from 2004 to 2010, are obtained mainly from epidemiologic bulletins published by the Chinese Ministry of Health [61]. We need to estimate the parameters of model (4.1), most of which can be obtained from the literature or assumed on the basis of common sense. However, we have to estimate β(t), βdh(t) and A by using the least-square fitting of Ih(ti) through discretizing the ordinary differential system (4.1) as follows:
| (4.4) |
The least-square fitting is to minimize the objective function
| (4.5) |
which is implemented by the instruction lsqnonlin, a part of the optimization toolbox in MATLAB.
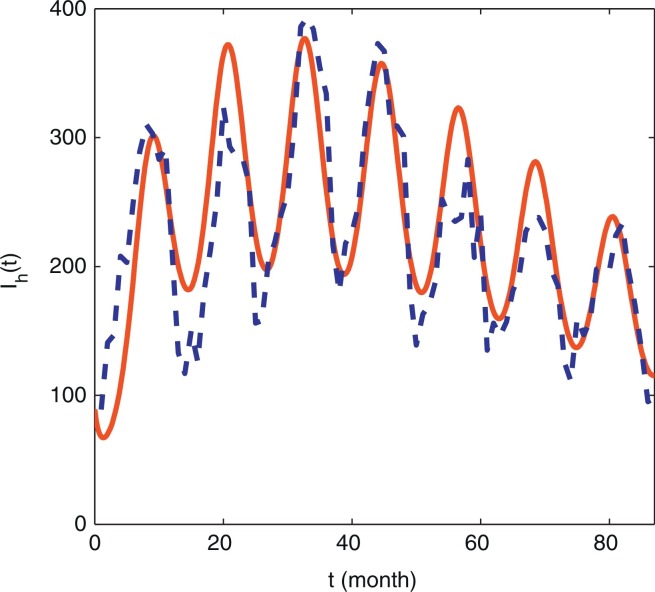
The values of parameters are listed in Table 4.1. We obtain the annual number of human population using the annual birth and death data from the National Bureau of Statistics of China [65]. Then we calculate the average and divide it by 12 to derive the monthly human birth population We need the initial values to perform the numerical simulations of the model. The number of the initial susceptible human population at the end of 2003, Sh(0), is obtained from the China Statistical Yearbook and the number of the initial infective humans Ih(0) is from epidemiological bulletins published by the Chinese Ministry of Health. However, the numbers of the initial exposed humans Eh(0) and the recovered humans Rh(0) cannot be obtained. We derive Eh(0) reversely by the parameter γ and R 1(0) is estimated roughly. Regarding the initial values for dogs, we only know that there are about 75 millions dogs in 2009 from online news. So, Sd(0), Ed(0), Id(0), and Rd(0) are calculated reversely by the corresponding parameters rh, kh and data fitting. The numerical simulation of the model on the number of human rabies cases is shown in Fig. 4.1.
Fig. 4.1.
The comparison between the reported human rabies data in mainland China from January 2004 to December 2010 and the simulation of our model. The dashed curve represents the monthly data reported by Ministry of Health of China while the solid curve is simulated by using our model. The values of parameters are given in Table 4.1. The initial values used in the simulations were
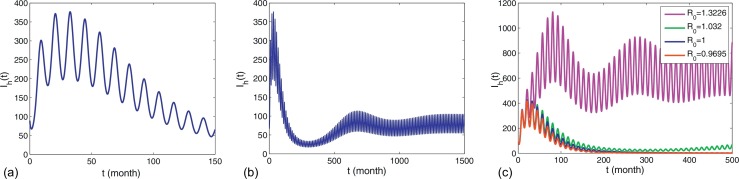
We observe that the data of 2005, 2008 and 2009 are slightly different from the solution as observed in [113]. We think this is because of large scale culling of dogs in these years. However, culling of dogs is not considered in model (4.1). We can also predict the general tendency of the epidemic in a long term according to the current situation, which is presented in Fig. 4.2. From these figures we can see that the epidemic of rabies can be relieved in a short time (Fig. 4.2(a)), but cannot be eradicated with the current prevention and control measures (Fig. 4.2(b)). Moreover, with these parameter values, we can roughly estimate that the basic reproduction number under the current circumstances in China. From Fig. 4.2(c), we can see that when R 0 < 1, the number of infected humans Ih(t) tends to 0. On the contrary, when R 0 > 1, Ih(t) tends to a stable periodic solution.
Fig. 4.2.
The tendency of the human rabies infectious cases Ih(t) in (a) a short time, (b) a long time, and (c) a long time with different values of R0. Here and the values of other parameters are given in Table 4.1.
The initial conditions adopted in model fitting are mostly assumed and back-extrapolated by parameters. So it is necessary to study the influence of initial conditions on the rabies epidemics which are showed in Fig. 4.3. From Fig. 4.3, we can see that the initial susceptible dog population Sd(0) has a stronger influence on Ih(t) and other initial conditions have little or almost no effect on Ih(t). It implies that the increasing number of dogs is really an important factor for the prevalence and persistence of rabies in China.
Fig. 4.3.
The influence of initial conditions on the number of human rabies cases Ih(t). (a) Different initial susceptible dog populations Sd(0); (b) Different initial infectious dog populations Id(0); (c) Different initial susceptible human populations Sh(0); and (d) Different initial infectious human populations Ih(0).
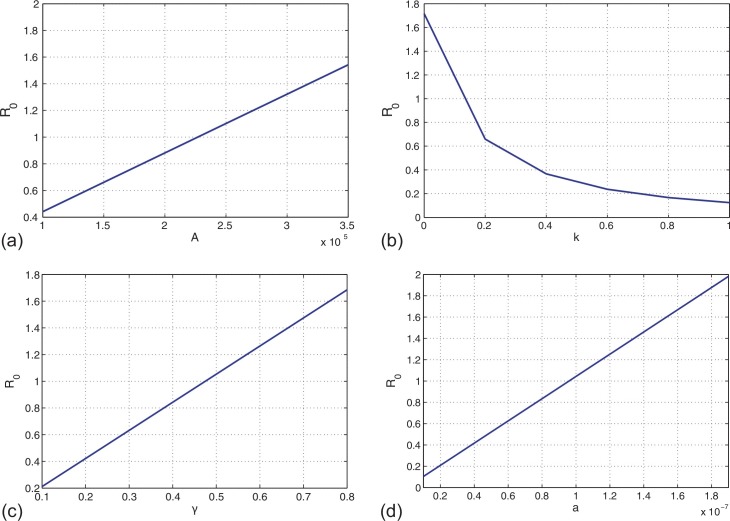
Finally, we perform some sensitivity analysis to determine the influence of parameters A, k, γ and a on R 0. From Fig. 4.4(a), it is obvious that when A is less then 226,890, R 0 can be less than 1. However, the annual birth population of dogs can achieve 400,000 or more in China. This indicates that human rabies in China cannot be eradicated if the birth number of dogs cannot be controlled under 2 million.
Fig. 4.4.
The influence of parameters on R0. (a) versus A; (b) versus k; (c) versus γ; and (d) versus a. Other parameter values are given in Table 4.1.
The postexposure prophylaxis (PEP) is used for most situations for human rabies. In model (4.1), it is embodied in the terms k and kh and it can affect γ and γh. We observe that R 0 is a concave function of k from Fig. 4.4(b). So k has an obvious effect on R 0. We also know that immunization is an effective measure to control rabies. Next, we consider the dependence of R 0 on γ and observe that it is linear in γ, which is depicted in Fig. 4.4(c). Most people, especially in the rural and remote areas, have little knowledge about rabies and even do not know what to do after being bitten by dogs. It was reported in [84] that 66.3% of rabies victims did not seek medical services at all and 27.6% of the cases received inadequate PEP. Although the effect of γ on R 0 is less than k, in order to decrease the rate of clinical outbreak to rabies we can enhance people the awareness and knowledge about rabies and the emergency measure and treatment after they are bitten and scratched by dogs.
Now we discuss how a effects R 0 in Fig. 4.4(d). Although R 0 in linear in a,, a slight change of a can lead to large variations of R 0. Since we can manage a by controlling i.e., the number of dogs a susceptible dog runs into per unit time, which is to strengthen the management of dogs, especially stray dogs, in case they run wild and bite each other and humans.
5. Modeling spatial spread of rabies by reaction–diffusion equations [112]
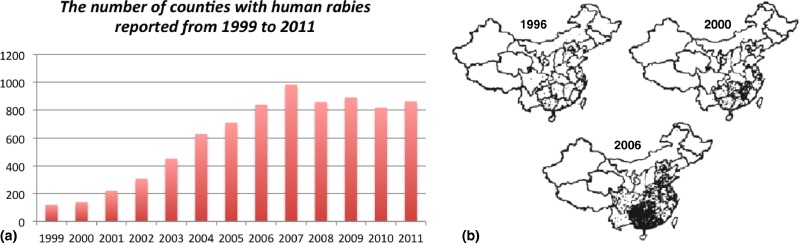
In recent years, rural communities and areas in China invaded by rabies are gradually enlarged. Fig. 5.1 (a) shows that there were only 120 counties reporting human rabies cases in 1999. However, the number of infected counties in 2008 was nearly seven times as that in 1999. Moreover, we can see the tendency of rabies diffusion from Fig. 5.1(b). In 1996, the 160 infected cases were sporadically distributed in the south provinces. As time goes on, the situation of rabies in south provinces has become more serious and it has spread to central and north provinces.
Fig. 5.1.
(a) The data on the numbers of counties reported rabies cases in Mainland China from 1999 to 2011. The figure is derived from [60]. (b) Geographic distributions of human rabies in Mainland China in 1996, 2000 and 2006. The figures are derived from [84].
Now we want to explore the factors behind the spatial spread of rabies in Mainland China. There are some studies on investigating animals rabies and using partial differential equations by adding diffusion terms to ordinary differential equations. Kallen [47] studied rabies transmission in fox population by differential equations with diffusion. He used the deterministic model to simulate rabies epizootic in foxes crossing continental Europe and proved the existence of traveling waves. Murray et al. [63], [64] also considered foxes rabies, calculated the speed of propagation of the epizootic front and the threshold for the existence of an epidemic and quantified a mean to control the spatial spread of the disease. Artois et al. [7] employed a one-dimensional discrete deterministic model to analyze the evolution of a given population which is infected by rabies. Ou and Wu [69] considered the spatio-temporal patterns of rabies spread involving structured fox populations and delayed nonlocal interaction on the disease spread. See also Ruan and Wu [74].
We add diffusion to the dog population in the SEIR model (2.1) to obtain a reaction–diffusion equation model. For reaction–diffusion equations, the asymptotic speed and traveling waves are attracting more attention and usually need to be investigated and discussed in order to understand the dynamics. The concept of asymptotic speeds of spread was first introduced in [6] for reaction–diffusion equations. There is an intuitive interpretation for the spreading speed c* in a spatial epidemic model: if one runs at a speed c > c*, then one will leave the epidemic behind; whereas if one runs at a speed c < c*, then one will eventually be surrounded by the epidemic [21]. Following the method adopted by [56], [57], we determine the minimum wave speed connecting the disease-free equilibrium to the endemic equilibrium and illustrate the existence of traveling waves by numerical simulations. In Section 2 it was shown that the endemic equilibrium of the ODE model (2.1) is stable. Here we study the diffusive model by linear analysis to see whether the endemic equilibrium is still stable and whether spatial patterns can appear. Moreover, we carry out some sensitivity analysis on parameters to determine factors that affect the spatial spread of rabies in Mainland China.
5.1. Reaction–diffusion equations for rabies
Let Sd(x, t), Ed(x, t), Id(x, t), and Rd(x, t) to denote the density of susceptible, exposed, infectious, and recovered dogs at location x and time t, respectively. The corresponding human sub-populations are denoted by Sh(x, t), Eh(x, t), Ih(x, t), and Rh(x, t), respectively. Suppose that the spatial diffusion of rabies is a result of the movement of dogs. So we add the diffusion of dogs to system (2.1) and obtain the following reaction–diffusion equation model:
| (5.1) |
for t > 0, x ∈ Ω with null Neumann conditions:
| (5.2) |
where, and d 1, d 2, d 3, d 4 are the non-negative diffusion rates whose values are given in Table 5.1 .
Table 5.1.
Description of parameters in model (5.1).
| Parameters | Value | Unit | Comments | |
|---|---|---|---|---|
| A | 3 × 106 | Dog birth population | ||
| λ | 1 | Dog loss rate of immunity | ||
| i | year | Dog incubation period | ||
| σ | 6 | 1/i | ||
| γ | 0.4 | Clinical outcome rate of exposed dogs | ||
| m | 0.08 | Dog natural mortality rate | ||
| βdd | none | Dog-to-dog transmission rate | ||
| k | 0.09 | Dog vaccination rate | ||
| μ | 1 | Dog disease-related death rate | ||
| B | 1.54 × 107 | Human birth population | ||
| λh | 1 | Human loss rate of immunity | ||
| ih | year | Human incubation period | ||
| σh | 6 | 1/ih | ||
| γh | 0.4 | Clinical outcome rate of exposed humans | ||
| mh | 0.0066 | Human natural mortality rate | ||
| βdh | none | Dog-to-human transmission rate | ||
| kh | 0.54 | Human vaccination rate | ||
| μh | 1 | Human disease-related death rate | ||
| d1 | 0.005 | Diffusion rate for the susceptible dogs | ||
| d2 | 0.01 | Diffusion rate for the exposed dogs | ||
| d3 | 0.01 | Diffusion rate for the infected dogs | ||
| d4 | 0.005 | Diffusion rate for the vaccinated dogs |
Since the last four equations are independent of the first four equations and only the first four equations have diffusion terms, we only need to study the subsystem:
| (5.3) |
5.2. Steady states and stability analysis
In Section 2, we presented the steady states and discussed their stability without diffusion. Now we want to know whether the endemic equilibrium E * is still stable when the system is diffusive, that is, if there appears any spatial pattern. We only need to study the steady state of the dog-only subsystem (5.3). Firstly, we linearize the subsystem about this steady state. Set
| (5.4) |
where and . We choose s(x, t), e(x, t), i(x, t) and r(x, t) as follows.
| (5.5) |
where s 0, e 0, i 0 and r 0 are constants, einx is periodic and bounded () and n is the wavenumber that indicates the wavelength of the emergent spatial pattern. The sign of the real part of α is crucially important to determine the stability of the steady state.
If Re(α) > 0, |eαt| > 1, then the linearized system will grow and there will appear spatial patterning. On the contrary, if Re(α) < 0, |eαt| < 1, then the steady state will be stable. Substituting (5.5) into (5.3) and ignoring nonlinear terms, we obtain the characteristic equation, which is a fourth order polynomial equation in α of the following form
| (5.6) |
where
| (5.7) |
and
Using the Routh–Hurwitz criterion, we know that all roots of (5.6) have negative real parts if and only if
| (5.8) |
Substituting the parameter values in Table 5.1 into (5.4) and letting we obtain that and So, under the parameter values in Table 5.1 and all roots of (5.6) have negative real parts, that is, the endemic equilibrium is stable.
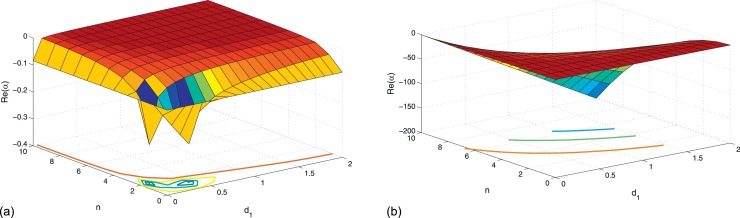
We also have the largest real parts of roots in terms of d 1, d 2, d 3, d 4 and n in the three-dimensional diagrams. Consider the conjunct influence of d 1, d 2, d 3, d 4 and n. The case when and is given in Fig. 5.2 (a). The case when and is given in Fig. 5.2(b). In both cases, we can see that the largest Re(α) < 0. So, the steady state is stable, that is, E * is stable and spatial patterns cannot appear. Moreover, in Fig. 5.3 , we can intuitively see that the endemic equilibrium with small perturbations is still stable.
Fig. 5.2.
The largest real parts of roots in term of parameters d1, d2, d3, d4 and n. (a) and and (b) and .
Fig. 5.3.
The temporal and spatial solutions of Id(x, t), Rd(x, t), Ih(x, t) and Rh(x, t) for the parameters given in Table 5.1. The initial values are the endemic equilibrium values with small perturbations.
5.3. Traveling waves
In order to investigate traveling waves, system (5.3) is rewritten in term of a coordinate frame to the right with speed c. Let we can rewrite system (5.3) as the following form:
| (5.9) |
Let We have the corresponding first-order ordinary differential equations with respect to the variable z of the above system:
| (5.10) |
Now we present some numerical results on the existence of traveling waves, sensitivity analysis of parameters about the human rabies cases and the minimum wave speed. The initial data we take in numerical simulations of system (5.2) are as follows:
If x ∈ [0, 25],
If x ∈ [25, 100],
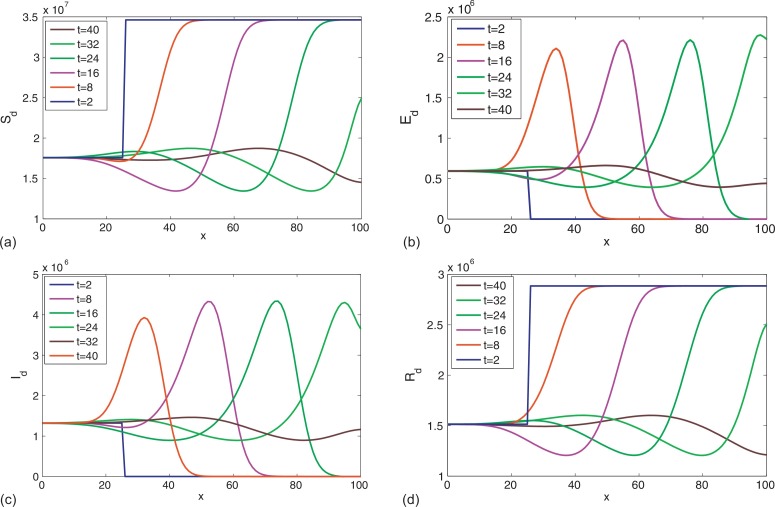
From the two-dimensional figures on the population number in every subclasses in the one-dimension space (Figs. 5.4 and 5.5 (a)), we can see that with the movement of dogs, not only there really exist traveling waves in every subclasses of dogs but also there are epidemic waves in the infected human population. Moreover, from Fig. 5.5 we can see that the diffusion of dogs not only spreads the disease to other adjacent areas but also makes the rabies situation more serious, which agrees with the fact that not only rabies has spread from the south to the central and north areas but also the situation of rabies in the south is getting more serious.
Fig. 5.4.
Traveling wave solutions of the dog population in the PDE model (5.1) with parameters given in Table 5.1. The solutions are plotted when t =2, 8, 16, 24, 32, 40.
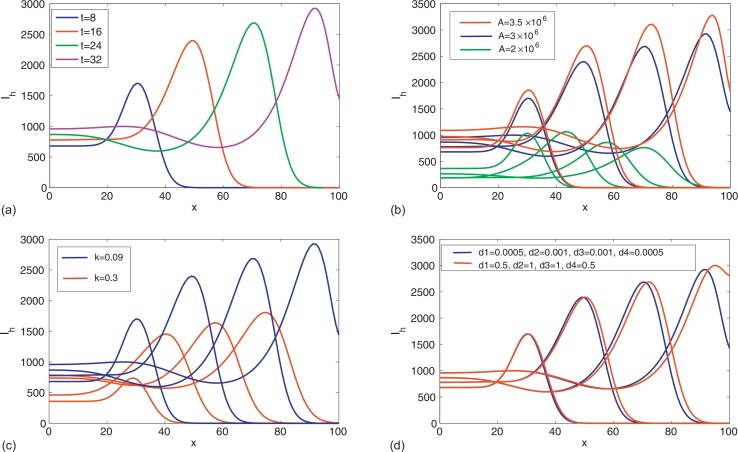
Fig. 5.5.
(a) The density of infected human Ih in the PDE model (5.1) with the diffusion condition on the dog population. The solutions are plotted when t =8, 16, 24, 32. The waves of human rabies cases Ih in term of x under different parameter values. The solutions are plotted when with (b) different A; (c) different k and (d) different d1, d2, d3, d4. (For interpretation of the references to color in this figure, the reader is referred to the web version of this article).
We knew that the traveling waves exist in the dog population. We now explore the influencing factors for the traveling waves. Taking this into account, Fig. 5.5(b)–(d) intuitively illustrates how the parameters impact the transmission and diffusion of rabies. We can visually see that the influences of d 1, d 2, d 3, d 4 are smaller than that of A and k. Moreover, d 1, d 2, d 3, d 4 only affect the speed of traveling waves, while other parameters not only affect the speed of waves but also change the magnitude of waves. This illustrates that strengthening quarantine during the dog movement only can control the diffusion spread of rabies to other areas but cannot eliminate rabies. In addition, in Fig. 5.5(b) we can observe that the bottle-green curve is convergent, which is because R 0 < 1 when .
5.4. The minimum wave speed
The purpose of this section is to determine the minimum wave speed c* connecting the spatially homogeneous disease-free equilibrium E 0 to the spatially homogeneous endemic equilibrium E * for the reaction–diffusion system (5.1). The solutions corresponding to the minimum wave speed describe the observed epidemic waves and are called traveling waves. The traveling waves, if they exist, satisfy the following conditions:
and
As for system (5.10), the minimum wave speed for traveling waves can be determined by considering the eigenvalues of the Jacobian matrix at the disease-freeequilibrium E 0. Following the calculations in [112], it follows that
Plugging the parameter values in Table 5.1 into the above formula, we obtain .
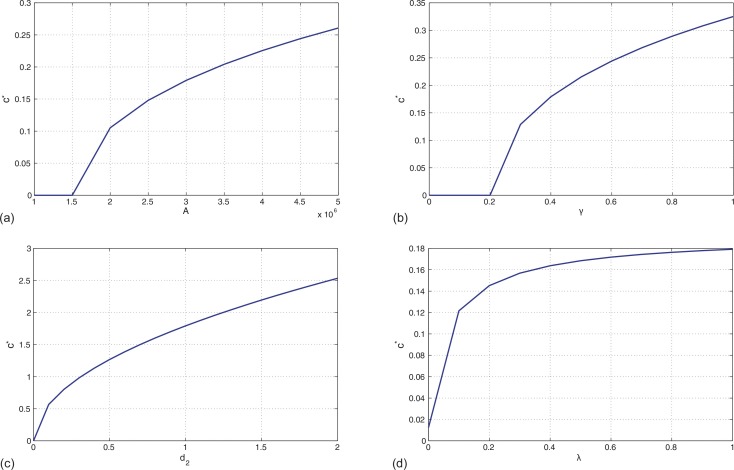
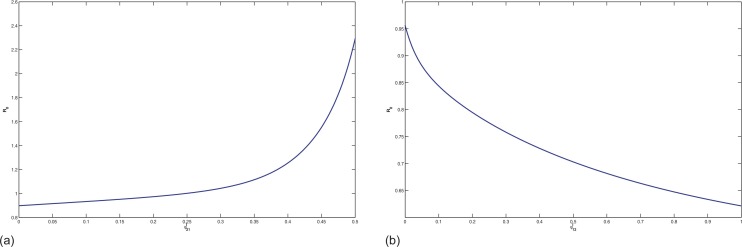
Now we consider the influence of parameters on c*. From Fig. 5.6 , we can see that the parameter d 2 has a larger influence on c* than k, A, γ, λ. c* is a convex function of A, γ, d 2 and λ, which illustrates that the influences of them are much smaller, especially λ has little influence on c* when λ > 0.5. Therefore, movement of exposed and infected dogs is indded the main factor for the geographic spread of human rabies.
Fig. 5.6.
The minimum wave speed c* in term of different parameters. (a) a; (b) γ; (c) d2; and (d) λ.
6. Modeling the geographic spread of rabies by multi-patch models [12]
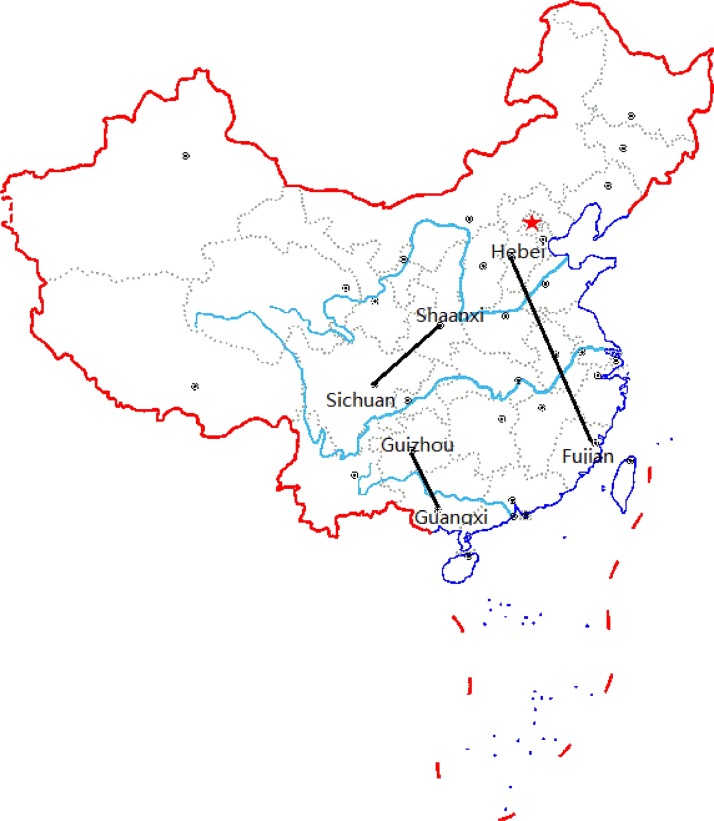
Although dogs remain the major infection source, contributing 95% of human cases in China [60], [100], there are very little scientific studies and very few data on the population dynamics of dogs, let alone diseases of dogs. In order to improve rabies control and prevention, in 2005 the Chinese government implemented a trial surveillance program to monitor rabies at the national level in an attempt to obtain a more comprehensive epidemiological dataset. In addition to recording statistics on human cases, the Institute for Viral Disease Control and Prevention of China CDC cooperated with the provincial CDC laboratories and began collecting samples from dog populations in regions where human rabies cases had been reported. The positive samples were then submitted for DNA sequencing and combined with a second subset of selected sequences from publicly available sequences. Yu et al. [108] selected a subset of samples for sequencing and investigated the history and origin of the virus in China and examined the variation from a geographical perspective. Guo et al. [36] used comprehensive spatial analysis methodology to describe the spatiotemporal variation of human rabies infections in China from 2005 to 2011, detected spatiotemporal clusters of human rabies, modeled the transmission trend of rabies, and provided a scientific basis for improved targeted human rabies control interventions in China. Guo et al. [37] collected rabies virus nucleoprotein gene sequences from different provinces and investigated their phylogenetic and phylogeographic relationship. More specifically, their phylogeographical analyses of two rabies virus clades (China I and China II) lineages identified several provinces that appear to be epidemiologically linked and China I lineage plays the dominant role in the spread of rabies in China. Moreover, their analysis indicates that east China appears to be not only epidemiologically related to adjoining provinces but also to distant provinces, and seems to act as an epidemic hub for transmission of rabies virus to other regions, which is consistent with previous results by Yu et al. [108]. Other long distance translocations of rabies virus can also be identified as well as translocation events between neighboring provinces. Their analysis demonstrates a strong epidemiological linkage between Shaanxi and Sichuan and between Sichuan and Yunnan. This is consistent with surveillance data for human rabies cases which show dissemination of the virus from southwest China to neighboring provinces and into regions such as Shaanxi in the northern part of the county that have previously been incident free for several years [106]. For both clades there appears to be a general trend of longitudinal transmission (Guangdong–Shandong, Fujian–Hebei, Zhejiang–Shandong) and latitudinal transmission (Yunnan–Shanghai, Guizhou–Shanghai, Hunan–Shanghai). That is also consistent with human rabies surveillance data which highlights a flow of cases from high incidence regions in the south of the country to medium and low incidence regions [106]. For example, discrete phylogeographic analysis for China I strain [37], [88], [89], [103], [108] indicates the linkage of rabies virus between Sichuan and Shaanxi, Guangxi and Guizhou, and Fujian and Hebei (Fig. 6.1 ).
Fig. 6.1.
The linkage of rabies virus China I strain between Sichuan and Shaanxi, Guangxi and Guizhou, and Fujian and Hebei [37], [108].
In Section 5 we used a reaction–diffusion model to study the spatial spread of rabies in China. However, reaction–diffusion equations are based on the mathematical assumptions that the spatial domain is connected and the movement of dogs is a continuous process in the domain. While the phylogeographical analyses of rabies virus indicate that there are long-distance inter-provincial spreads of rabies in China, in order to investigate how the movement of dogs affects the geographic spread, we propose a multi-patch model to study the spatial transmission of rabies between dogs and from dogs to humans (see [31] for a multi-patch malaria model). We will describe the model in details, discuss the existence of the disease-free equilibrium, calculate the basic reproduction number, and study how the moving rates between patches affect the basic reproduction number. To investigate the epidemiological linkage (such as Guizhou and Guangxi, Hebei and Fujian, and Sichuan and Shaanxi) observed in Guo et al. [37], we will use the two-patch submodel to simulate the human rabies data to understand the inter-provincial spread of rabies in China.
6.1. Multi-patch rabies model
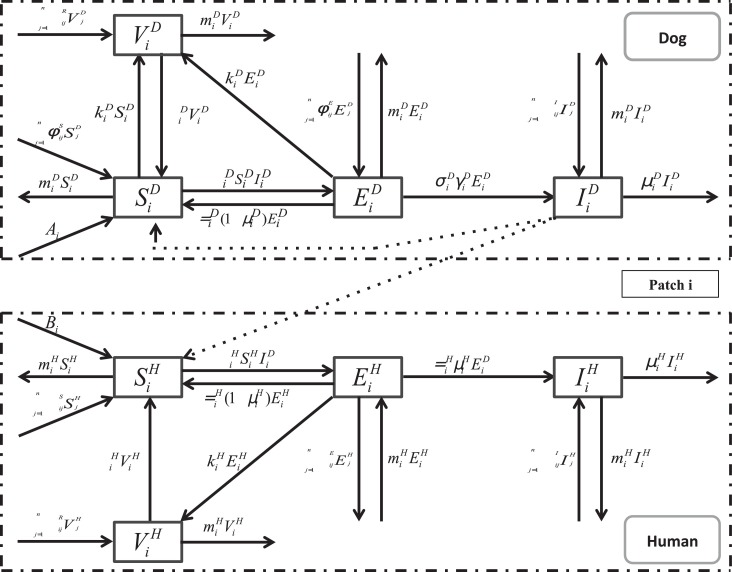
Since the data on human rabies in mainland China are reported to the China CDC by provinces, we regard each province as a single patch and, in each patch, the submodel structure follows the SEIR model (2.1) (see Fig. 6.2 ). We use superscripts H and D to represent human and dog, respectively, and a subscript i to denote the ith-patch. For patch i, the dog population is divided into four subclasses: and which denote the populations of susceptible, exposed infectious and vaccinated dogs at time t, respectively. Similarly, the human population in patch i is classified into and which denote the populations of susceptible, exposed, infectious and vaccinated humans at time t, respectively. Our assumptions on the dynamical transmission of rabies between dogs and from dogs to humans are presented in the flowchart (Fig. 6.2). The model in patch i is described by the following differential equations:
| (6.1) |
Fig. 6.2.
Flow chart for the transmission of rabies virus between dogs and from infectious dogs to humans within patches and from patches to patches via transportation of dogs.
All parameters and their interpretations are listed in Table 6.1 .
Table 6.1.
Parameters and descriptions.
| Parameter | Description | Reference |
|---|---|---|
| Ai | The annual birth rate of dogs in patch i | Estimation |
| The loss rate of vaccination immunity for dogs in patch i | [77] | |
| The time duration in which infected dogs in patch i remain infectious | [91] | |
| The risk factor of clinical outcome of exposed dogs in patch i | [60] | |
| The non-disease related death rate for dogs in patch i | [117] | |
| The vaccination rate of dogs in patch i | [60] | |
| The disease-related death rate for dogs in patch i | [60] | |
| The transmission coefficient of infectious dogs to susceptible dogs in patch i | Fitting | |
| Bi | The annual birth rate of humans in patch i | [66] |
| The loss rate of vaccination immunity of humans in patch i | [15] | |
| The time duration of infectiousness of infected humans in patch i | [101] | |
| The risk factor of clinical outcome of exposed humans in patch i | [42] | |
| The natural death rate of humans in patch i | [66] | |
| The vaccination rate of humans in patch i | [60] | |
| The disease-related death rate of humans in patch i | [60] | |
| The transmission coefficient of infectious dogs to susceptible humans in patch i | fitzting | |
| () | The immigration rate from patch j to patch i for i ≠ j of susceptible (exposed, infectious, and vaccinated) dogs | Fitting |
| () | thze immigration rate from patch j to patch i for i ≠ j of susceptible (exposed, infectious, and vaccinated) humans | Fitting |
Ai describes the annual birth rate of the dog population in patch i; denotes the transmission coefficient between dogs in patch i and describes the transmission of rabies from infectious dogs to susceptible dogs in this patch; represents the incubation period of infected dogs in patch i; is the risk factor of clinical outcome of exposed dogs in patch i. Therefore, denotes dogs that develop clinical rabies and enter the susceptible class and the rest denotes the exposed dogs that do not develop clinical rabies; is the non-disease related death rate for dogs in patch i; is the vaccination rate of dogs and denotes the loss rate of vaccination immunity for dogs in patch i; is the disease-related death rate for dogs in patch i.
For the human population, similarly Bi describes the annual birth rate of the human population in patch i; denotes the transmission coefficient from dogs to humans in patch i and describes the transmission of rabies from infectious dogs to susceptible dogs in this patch; represents the incubation period of infected humans in patch i; describes exposed people that become infectious and describes the exposed people that return to be susceptible; is the non-disease related death rate for humans in patch i; is the vaccination rate of dogs and denotes the loss rate of vaccination immunity for huamns in patch i; is the disease-related death rate for humans in patch i.
() is the immigration rate from patch j to patch i for i ≠ j of susceptible, exposed, infectious, and vaccinated dogs, respectively; () is the immigration rate from patch j to patch i for i ≠ j of susceptible, exposed, infectious, and vaccinated humans, respectively. Then () describes the corresponding subclass of the dog population that enter into patch i from other patches and denotes the corresponding subclass dog population that leave patch i. Meanwhile, the immigrations of humans are described in the same way by (K=S, E, I, V).
Ignoring the deaths and births during transportation, for we have
Assume that the travel rate matrices for and for are irreducible.
Consider the case that then the positive equilibria of the subsystem satisfy the following:
| (6.2) |
and
| (6.3) |
By adding the equations in (6.3) from to n, we have
which leads to for and It follows that there exists such that since the matrix is strictly diagonal dominant.
Let Then equation (6.2) is equivalent to where and
here
Consider the i-th column of matrix M, we can show that
After showing the similar properties for the i-th column where we can see that M is strictly diagonal dominant. Therefore, the inverse of M exists. Denote where
We thus obtain the disease-free equilibrium for model (6.1)
6.2. Data and parameters
We used a two-patch submodel to simulate the data of human rabies from 2004 to 2012 in three pairs of provinces: Guangxi and Guizhou, Fujian and Hebei, and Sichuan and Shaanxi (see Fig. 6.1). Data were obtained from the Data-Center of China Public Health Science reported by China CDC. Each province is regarded as a patch in the model (). The parameters about humans including the annual birth rate and natural death rate of humans in each province are adopted from the “China Health Statistical Yearbook 2012” [66]. The incubation period for rabies is typically 1–3 months [101], we assume that it is 2 months on average, thus . Similarly, we also have [91]. The disease induced death rates of humans and dogs are assumed to be 1 [60]. According to [60], the vaccination rate of humans in China is about 0.5 and the risk factor of clinical outcome of exposed dogs is 0.4. Based on studies the minimum duration of immunity for canine is 3 years [77], we assume that the loss rate of vaccination immunity for dogs in patch i is . Rabies mortality after untreated bites by rabid dogs varies from 38% to 57% [42], thus we take the average 47.5% as the risk factor of clinical outcome of exposed humans.
The difficulty in parameter estimations is that there is no scientifically or officially reported data on dogs in China. So the values of Ai used in simulations are estimated based on the dog density from the household survey [85], the total areas of provinces, the density of human population and other research results [43], [111], [112]. Now we assume that the immigration rates of susceptible, exposed, infectious and vaccinated dogs are same. Additionally, susceptible, exposed and vaccinated humans also move at the same rate but infectious humans do not move inter-provincially, so . All other parameters are left to be unknown and estimated through simulating the model by the data.
6.3. Basic reproduction number
The basic reproduction number of rabies which reflects the expected number of dogs infected by a single infected dog, is derived by following the method in [93]. We have
where
Since Aii is a strictly diagonally dominant matrix for they are all non-singular. Therefore, exists. This leads to the inverse of V:
Thus, the spectral radius of matrix
| (6.4) |
is the basic reproduction number.
The isolated basic reproduction number,
| (6.5) |
is the basic reproduction number in one single patch (patch i here) when all the immigration rates are zero. For the two-patch submodel, R 0 can be expressed as
| (6.6) |
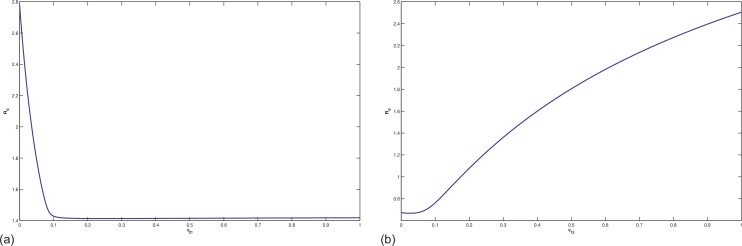
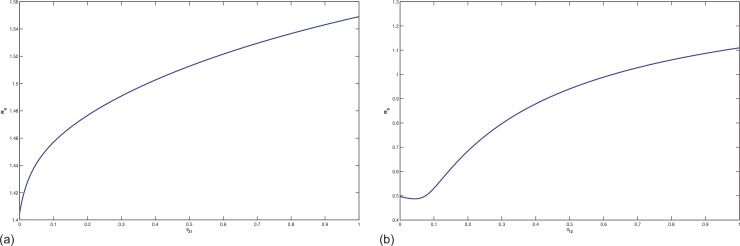
Even for a two-patch model the expression of is very complicated and it is almost impossible to analyze the relationship between the parameters and . We will perform sensitivity analysis to determine how each parameter quantitatively affects R 0. In particular, we will study how the immigration rate affect the basic reproduction numbers of the whole system and the isolated patch by performing some sensitivity analyses.
6.4. Numerical simulations
In this section, we use the two-patch submodel to simulate the reported human rabies data from three pairs of provinces, Guangxi and Guizhou, Sichuan and Shaanxi, and Fujian and Hebei, respectively.
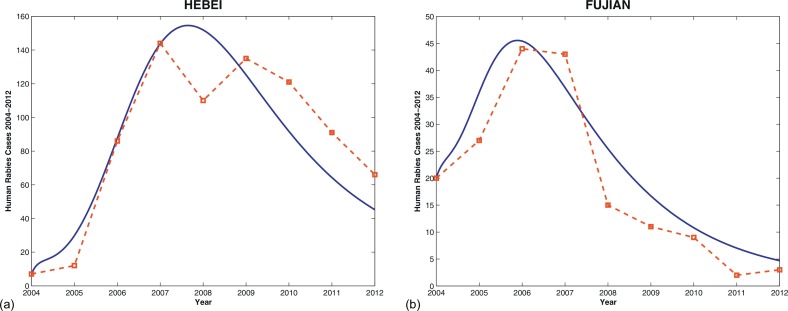
(a) Hebei and Fujian. The data from Guo et al. [37] indicate that Hebei and Fujian are epidemiologically linked. In Hebei, there was only one human rabies case reported in 2000 [60], while it is now one of the 15 provinces having more than 1000 cumulative cases and is included in “Mid-to-long-term Animal Disease Eradication Plan for 2012–2020” project. We take Hebei and Fujian as the two patches in model (6.1) (when ) and simulate the numbers of human cases from 2004 to 2012 by using the model. In Fig. 6.3 , the solid blue curves represent simulation results and the dashed red curves are reported numbers of human rabies cases from 2004 to 2012, which show a reasonable match between the simulation results and reported data from China CDC. Based on the values of parameters in the simulations and the formula of the basic reproduction number in the two-patch model, it is calculated that . That means the disease will not die out in this two-patch system.
Fig. 6.3.
Simulations of the numbers of reported human rabies cases in Hebei and Fujian from 2004 to 2012. The solid blue curves are simulation results by our model and the dashed red curves are the numbers of reported cases by China CDC [15]. Values of parameters: . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
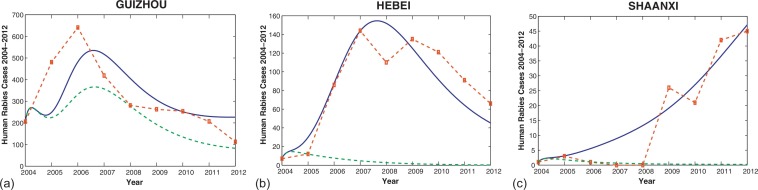
If we assume that there is no immigration of both dogs and humans in this system, then the isolated basic reproduction numbers for Hebei and Fujian are and respectively. Under this assumption the disease would die out in both provinces since their isolated basic reproduction numbers are less than one. This example theoretically shows the possibility that the immigration of dogs can lead the disease to a worse scenario even it could be eliminated in each isolated patch. It is remarkable that we only mentioned the dog immigration here because a simple observation to the formula of the basic reproduction number shows that only the immigration rates of dogs ( for ) can affect it. In fact, only dogs can carry the rabies virus and then spread it to humans and other dogs. This transmission feature supports our mathematical analysis. Furthermore, Fig. 6.6(b) shows a direct comparison of numerical simulations on the number of human cases from the model with immigration and without immigration. The additional green curve represents simulations of the human cases without any immigration in Hebei and the human infectious population size goes to zero faster which is consistent with the fact that the isolated basic reproduction number (0.5477) in Hebei is less than one.
Fig. 6.6.
Simulations of the numbers of reported human rabies cases in Guizhou, Hebei, and Shaanxi with dog immigration and without dog immigration. The dashed red curves are reported cases by China CDC; the solid blue curves correspond to simulations with immigration and the dashed green curves correspond to simulations without immigration ( for ). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
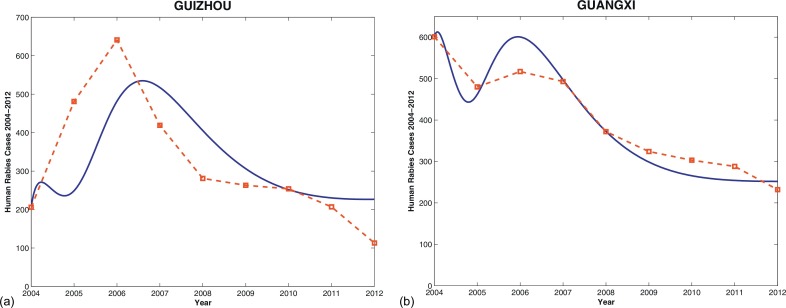
(b) Guizhou and Guangxi. Yu et al. [108] reported that there is a statistically significant translocation event between Guizhou and Guangxi. Fig. 6.4 shows that both Guizhou and Guangxi have large numbers of human rabies cases (both are in top 5 endemic provinces in China) in recent years. Particularly, the number of human deaths caused by rabies virus in Guangxi is ranked the highest in China. Similar simulations were carried out for these two provinces and results are shown in Fig. 6.4. The isolated basic reproduction numbers for Guizhou and Guangxi are calculated as and respectively, while the basic reproduction number for the linked system is estimated to be . To eliminate rabies we need some effective control strategies that can reduce significantly. Thus it is even more challenging to control and prevent the disease in Guangxi and Guizhou from a numerical perspective. In Fig. 6.6(a), we compare the human rabies in Guizhou having dog immigration with that having no dog immigration. It is obvious that if there is no dog immigration between Guizhou and Guangxi, the number of human rabies in Guizhou would be less than the reported numbers, and also much less than the simulation results with dog immigration.
Fig. 6.4.
Simulations of the numbers of reported human rabies cases in Guizhou and Guangxi from 2004 to 2012. The solid blue curves are simulation results by our model and the dashed red curves are the numbers of reported cases by China CDC [15]. Values of parameters: . (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
(c) Sichuan and Shaanxi. Shaanxi had only 15 cumulative human cases from 2000 to 2006 (only 2–3 cases every year on average), but is now an alarming province for rabies in China with more and more reported human cases. Rabies was found to spread along the road network [36]. With the parameters in Fig. 6.5 , the isolated basic reproduction numbers for Sichuan and Shaanxi are and respectively, while the basic reproduction number for the two-province model with immigration is which is greater than both of these two isolated ones. Numerically, that means more efforts are needed to reduce the human cases if immigration is involved. Fig. 6.6(c) shows that if there is no dog immigration for Shaanxi, the human rabies cases would decrease fast while it increased fast in reality.
Fig. 6.5.
Simulations of the numbers of reported human rabies cases in Sichuan and Shaanxi from 2004 to 2012. The solid blue curves are simulation results by our model and the dashed red curves are the numbers of reported cases by China CDC [15]. Values of parameters: (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
6.5. Sensitivity analysis
Now we carry out some sensitivity analyses of the basic reproduction number in terms of some parameters of dogs, especially the immigration rates between provinces. For the sake of implicity, we consider the two-patch submodel and study how depends on parameters of dogs, especially the immigration rates where . We consider the following three cases.
(i) Immigration of dogs between patches with different transmission rates. Suppose and where . the remaining parameters of dogs in patch 2 are the same as the corresponding parameters of dogs in patch 1. Here the only difference between the two patches in that the transmission coefficients of infectious dogs to susceptible dogs are different. Then the isolated basic production numbers satisfy the inequality: . So rabies is endemic in patch 1 and will die out in patch 2. First, let (the immigration rate of dogs from patch 1 to patch 2) . It is shown in Fig. 6.7 that decreases as ϕ 21 (the immigration rate of dogs from patch 2 to patch 1) increases. Then, let increases as ϕ 12 increases. Furthermore, if ϕ 21 is small and ϕ 12 is large, is greater than both and . To reduce we need to control ϕ 12 small enough. For example, let then we obtain that . If then which is smaller than but greater than . Thus, if the immigration rates of dogs are controlled in an appropriate range, the endemic level will be lower.
Fig. 6.7.
Plots of in terms of (a) the immigration rate of dogs from patch 1 to patch 2 (ϕ21) and (b) the immigration rate of dogs from patch 2 to patch 1 (ϕ12) when patch 1 has a higher transmission coefficient than patch 2 (). Values of other parameters: .
(ii) Immigration of dogs between patches with different vaccination rates. We assume that dogs move at the same rate regardless of their subclasses ( and for ). Then let dogs in patch 1 have a higher vaccination rate than those in patch 2: . All the remaining parameters of dogs in patch 2 are the same as the corresponding parameters of dogs in patch 1. Fig. 6.8 presents the basic reproduction number in terms of the immigration rates. Firstly, increases as the immigration rates increase at most of the time. This is consistent with our previous simulation results: the dog movements bring difficulties to rabies control. Secondly, a detailed observation in the range of indicates that it is more sensitive in ϕ 12. Therefore, we conclude that immigration of dogs from the patch with lower vaccination rate to a patch with higher vaccination rate is more harmful.
Fig. 6.8.
Plots of in terms of (a) the immigration rate of dogs from patch 1 to patch 2 (ϕ21) and (b) the immigration rate of dogs from patch 2 to patch 1 (ϕ12) when patch 1 has a higher vaccination rate than patch 2 (). We assume immigration rates of susceptible, exposed, infectious and vaccinated dogs are same, that is, and . Values of other parameters: .
It is notable that might be greater than both isolated basic reproduction numbers. For example, let and and all other parameters be the same as in Case (ii). Then . That is, the immigration of dogs might lead to a more serious situation.
(iii) Immigration of infective dogs between patches. Now we fix all immigration rates of dogs to 0.2 except (the immigration rate of infective dogs from patch 1 to patch 2), then increases quickly as increases, as it is shown in Fig. 6.9 (a). On the other hand we fix all immigration rates of dogs to 0.2 except (the immigration rate of infective dogs from patch 2 to patch 1), then decreases as increases, as it is shown in Fig. 6.9 (b). Interestingly, compare with Case (ii), we found that immigration of infectious dogs from the patch with a high vaccination rate to a patch with a low vaccination rate is more dangerous. The patch with a low vaccination rate actually has a week protection from the virus, thus infectious dogs from another patch may spread the disease faster.
Fig. 6.9.
Plots of in terms of (a) immigration rate of infectious dogs from patch 1 to patch 2 () and (b) the immigration rate of infectious dogs from patch 2 to patch 1 () when patch 1 has a higher vaccination rate than patch 2 (). Fix the immigration rates of susceptible, exposed and vaccinated dogs, that is, . Values of other parameters: .
7. Discussions
Rabies is one of the biggest public health threats in China. Facing up to the epidemic situation, both the central and local governments have been seeking forceful methods to reduce rabies transmission. Various prevention and control measures have been proposed by many researchers which include: (i) strengthening the postexposure prophylaxis (PEP) schedules delivered to rabies patients [79], [84]; (ii) culling of dogs, in particular stray dogs [51]; (iii) increasing the vaccination coverage in dogs [104]. Some researches suggest that combining these methods can be more effective in controlling the rabies. For example, Hu et al. [45] came up with strategies to control and prevent human rabies that include public education and awareness about rabies, pet vaccination programs, culling of stray animals, and enhancing PEP for infected patients. However, the large-scale culling of dogs, criticized by pet owners and animal protection activists, is controversial and there is a lack of evidence of its effectiveness in controlling dog population or rabies [100]. In fact, culling may remove vaccinated dogs, increase immigration, disrupt social organization, and lose public support, which make rabies control more difficult [11].
7.1. Modeling dog–human interactions
In order to explore effective control and prevention measures, in Section 2 we proposed a susceptible, exposed, infectious, and recovered model to study the transmission dynamics of rabies in China. The model describes the transmission of rabies among dogs and from dogs to humans. The model simulations agreed with the human rabies data reported by the Chinese Ministry of Health and gave an estimate of the basic reproduction number R 0 ≈ 2. The sensitivity analysis of R 0 in terms of the model parameters and the comparison of the effects of culling and immunization of dogs demonstrate that (i) controlling dog birth rate and increasing dog immunization coverage rate are the most effective methods for controlling rabies in China; and (ii) large scale culling of susceptible dogs can be replaced by immunization of them.
The characteristics of rabies epidemics in China include the large size of the dog population, the extremely low dog vaccination rate, poor understanding of the transmission dynamics of rabies, inadequate treatment of the infected patients, and the countrywide scale of the disease [60]. WHO recommends that 70% of dogs in a population should be immunized in order to eliminate or prevent outbreaks of rabies. However, the dog immunization rate in China has yet reached 10%, which is even lower in the countryside [60]. So increasing dog vaccination coverage rate is necessary and crucial in control rabies transmission in China. We suggest decreasing the dog birth rate in order to reduce the dog population and stop culling dogs and try to vaccinate these dogs instead. For pet dogs, registration and immunization should be mandatory; the price of vaccine should be reduced; the awareness of prevention rabies for dog owners should be enhanced; and contraception measures should be taken.
7.2. Including both domestic and stray dogs
A very important fact that was not considered in Section 2 is that there is a very large number of stray dogs in China. It was reported that at least 18.2% of the human rabies cases in Guangdong Province are caused by stray dogs [79]. In Section 3, taking this fact into consideration and using rabies data from Guangdong Province, we proposed a SEIV model for the dog–human transmission of rabies in which both domestic and stray dogs are considered. By the analysis of the model, we concluded that the cases of rabies in Guangdong would decrease gradually in the next a few year and increase slightly afterward, which indicates that rabies cannot be controlled or eradicated under the current strategies. By carrying out some sensitivity analysis of the basic reproduction number in terms of various parameters, we found that the vaccination rate of domestic dogs, the recruitment rate of domestic dogs, the number of stray dogs and the valid time of the immunity play very important roles for the transmission of rabies. From Fig. 3.5(a), we can see that the acute infection in humans in Guangdong Province would be reduced evidently through the decrease of the stray dog population. Moreover, reducing the transfer from infected domestic dogs to stray dogs is more effective than decreasing domestic dogs that are abandoned. As shown in Fig. 3.4(a) and Fig. 3.5(b), rabies can be controlled with the vaccination coverage rate over 75% which is a little bit higher than the recommended vaccination rate by WHO, the main reason is that a large number of stray dogs exists in most areas of Guangdong Province. However, from Fig. 3.5(b), although acute infection cases can be reduced by culling stray dogs, rabies cannot be eventually eradicated by this measure alone. Therefore, culling stray dogs is not a good strategy in controlling rabies. To prevent and control rabies in stray dogs, as suggested in Section 2, fostering of stray dogs could be introduced and encouraged, food baits containing abortifacient oral vaccine in capsules could be distributed in order to reduce the stray dog population and vaccinate stray dogs.
The differences between model (2.1) and model (3.1) are that only domestic dogs were considered in (2.1) while both domestic and stray dogs are included in model (3.1); model (2.1) was used to simulate the human rabies data from the whole country from 1996 to 2010 while model (3.1) was used to simulate the human rabies data from Guangdong Province from 2006 to 1010. It should be pointed out that the latter is the reason that the basic reproduction number for rabies in China was estimated to be in Section 2 while it is estimated that for Guangdong Province in this section. Indeed, the human rabies cases increased continuously and dramatically in China from 1996 to 2006 and then started to decrease steadily (see Fig. 2.2). In Section 3 we used the data from 2004 to 2010 for the whole country and it was estimated that the “average” basic reproduction number for China for this time period is These results indicate that human rabies in Guangdong Province is more severe than the average in China.
According to WHO, as long as victims bitten by animals receive proper PEP timely, human rabies can be prevented [98]. Fig. 3.5(c) indicates that the rabies infection rate can be reduced with the increase of using PEP. Thus, publicity and education on the risk and prevention of rabies is necessary and important to control the epidemic and should be strengthen in endemic areas, especially in rural areas.
7.3. Seasonal rabies epidemics
The monthly data of human rabies cases reported by the Chinese Ministry of Health exhibits seasonal characteristics that the morbidity rates in the summer and autumn are much higher than in the winter and spring. In order to study the transmission dynamics of rabies in China, in Section 4, seasonality of the spreading of the rabies was incorporated into the SEIR model (2.1) with periodic transmission rates. Firstly, we calculated the basic reproduction number R 0 and analyzed the dynamics of the model including the global stability of the disease-free equilibrium and the existence of periodic solutions. We then used our model to simulate the monthly data on the number of infected human cases from January 2004 to December 2010 in China reported by the Chinese Ministry of Health and predicted the general tendency of disease in China. Moreover, we carried out some sensitivity analysis of parameters on R 0. The demographic data were estimated from National Bureau of Statistics of China [65]. The values of most parameters in our model were obtained from the literature or by assumptions. The values of β(t), βdh(t) and A were estimated through least-square fitting of Ih(ti) by discretizing the ordinary differential system.
We would like to point out that in Section 2 it was estimated that the basic reproduction number while in Section 4 we calculated that with a similar model structure. This can be explained as follows. In Section 2, the data adopted by model fitting were from 1996 to 2010. In Section 4 we only used the data from 2004 to 2010. From Fig. 2.2, we can see that the numbers of infected human cases increased dramatically from 159 cases in 1996 and were fierce from 1996 to 2004. After 2004, the spread of rabies began to slow down. Moreover, the data in 2005 and after 2007 decreased. So the fact that R 0 in Section 4 is less than in Section 2 is reasonable.
Controlling the population of dogs, reducing the birth rate of dogs, increasing the immunization rate of dogs, improve the management of dogs, enhancing the awareness of people about rabies, and combining these measures are effective measures to control rabies in China. In addition, because the monthly data of human rabies cases exhibits a periodic pattern on an annual base and the human rabies cases in the summer and autumn are higher, it will be useful to take extra measures from May to July every year before the infection peaks, such as extra supervision of children and students out of school.
7.4. Spatial spread of rabies
To investigate how the movement of dogs leads to and impacts the spatial spread speed of rabies, in Section 5 we constructed a reaction–diffusion equation model to describe the interactions between dogs and humans, where dogs can disperse. We calculated the minimum wave speed and considered the existence of traveling wave by numerical simulations. Moreover, we discussed the stability of the endemic equilibrium with diffusion to illustrate that the spatial pattern cannot appear. The key is to check the magnitude of influence of parameters on human rabies cases and the minimal wave speed c*. From the formula of c*, we can see that only can influence c*, but d 1, d 4 do not. Therefore, only the movement of exposed and infected dogs affects the spatial spread of rabies. From Fig. 5.6(b), we know that the influence of d 2, d 3 on c* is larger which illustrates that quarantine of dogs during movement is important to control the spatial spread of rabies.
The existence of traveling waves in the model indicates that the spatial spread of rabies in both dogs and humans is caused by the dispersal of dogs. Thus, management of dogs and dog movement is important to reduce and prevent such spread of rabies.
7.5. Multi-patch rabies models
In Section 6, a multi-patch model was proposed to describe the spatial transmission dynamics of rabies in China and to investigate how the immigration of dogs affects the geographical spread of rabies. The expression and sensitivity analysis of the basic reproduction number indicates that the movement of dogs plays an essential role in the spatial transmission of rabies. As mentioned in the previsous sections, reducing dog birth rate and increasing dog immunization coverage rate are the most effective methods in controlling human rabies infections in China. They also play important roles in controlling the spatial spread of rabies based on the multi-patch model. WHO recommends that 70% of dogs in a population should be immunized to eliminate the rabies. Unfortunately, this rate is still lower than 10% in most regions in China. Therefore, efforts to bring the awareness of the importance of treatments and enhance the vaccination coverage in dogs are important to control the disease in China.
We also performed some numerical simulations to study the effects of the immigration rate in three pairs of provinces in China: Guizhou and Guangxi, Hebei and Fujian, Sichuan and Shaanxi, as shown in Fig. 6.1. First of all, the immigration may lead a basic reproduction number to be larger than one even if the isolated basic reproduction numbers are all less than one. Therefore, the immigration of dogs is the main factor for the long-distance inter-provincial spread of rabies. We note that the transportation of dogs even between non-endemic provinces, such as Fujian and Hebei, can cause human rabies in Hebei to increase greatly. Additionally, the movement of dogs from regions with a low vaccination rate also makes the situation worse. Attention should be paid not only to the provinces with more reported cases but also to the provinces with low vaccination rates. In those extremely poor areas, where dogs have a low vaccination coverage, the dog trade business and transportation to other areas will contribute to the geographical spread of rabies significantly. To control the disease at a national level, more efforts are needed in these regions.
The primary purpose of the transportation of dogs in China is believed to be related to food business. In some areas, such as the endemic provinces Guizhou and Guangxi, people eat dogs due to minority culture or harsh climate. There is no open market for selling and buying dogs for business purpose, however the black market always exists. It is frequently reported that trucks sometimes full of dogs are intercepted by animal lovers in the inter-provincial highway. Sometimes more than one thousand dogs were crammed into many tiny cages in one truck. The efficiency of such dog transportation has been enhanced by the fast development and expansion of the highway system in China in the past ten years. Chinese law requires that the transported animals must be certified as vaccinated for rabies and other diseases. However, dog traders are found to falsify the paperwork for most of the dogs in the truck to reduce their cost. Thus it would be important to regulate the market and implement certain policies on dogs (such as vaccine records) and the dog traders (such as licenses). During our research, we found that it was very difficult to find the information on dog population in China due to the lack of dog registration management. Since a large number of dogs are transported from provinces to provinces, it is necessary to register and manage such transportation properly. In particular, dogs carrying rabies viruses can easily spread the virus to other dogs when they are crowded into a small space during the trip. The last case of our sensitivity analysis shows the oblivious dangers resulted from the transportation of infectious dogs that has a destination with a low vaccination rate. We suggest creating strict and uniform procedures to test the dogs that will be transported.
7.6. Further studies
We used deterministic models to study the spread of rabies and simulated the reported data in either in the whole country or in some provinces in China. If local regions and small towns are concerned, then stochastic models are preferable [[1], [2], [4]]. Stochastic models are also advantageous when the contact structure in the community contains small complete graphs and households and other local social networks need to be considered.
In Section 6, we only applied two-patch model to simulate the data in pairs of two provices. As the highway system has been advance so dramatically in China in the last decade, long-distance and inter-provincial transportation becomes much more frequent and easier, a more general case on the complex transmission among three or more provinces is interesting to study.
In the interactions between dogs and humans, if the number of contacts each individual has is considerably smaller than the population size, then network structured models [49], [68] may be helpful, which assign to each individual a finite set of permanent contacts to whom they can transmit infection and from whom they can be infected.
We only considered the interactions between dogs and humans in our models. It has been reported that the number of wildlife rabies and wildlife-associated human and livestock rabies cases has increased in recent years, particularly in the southeast and northeast regions of mainland China [94]. It would be very interesting and important to take into account both dogs and wild animals in studying the transmission dynamics of rabies in China.
Local and central Chinese governments have devoted a large amount of financial resource to the control of rabies, particularly in vaccinations. Remarkably, vaccines for dogs are less expensive than that for humans, but the dog vaccination implementation requires a continuously huge human, material and financial resources. It will be interesting to investigate how to optimize the resources and efforts and how to take the socioeconomic factors into consideration in order to pursue the control and elimination of rabies virus in humans.
Since China has the second most reported human rabies cases in the world, we believe that the models, results and simulations can be modified to study the transmission dynamics of rabies in other countries, such as Ethiopia [26], India [28], Nepal [58], Tanzania [40], Zimbabwe [72], and some other Asian countries [90].
Acknowledgments
I would like to thank my collaborators Jing Chen, Qiang Hou, Zhen Jin, Qui-Quan Sun, Juan Zhang and Lan Zou for their contributions to this project on modeling the transmission dynamics of rabies in China.
Footnotes
Research was partially supported by National Science Foundation (DMS-1412454).
References
- 1.Allen L.J.S. 2nd ed. Chapman and Hall/CRC; Boca Raton, FL: 2010. An Introduction to Stochastic Processes with Applications to Biology. [Google Scholar]
- 2.Allen L.J.S., Flores D.A., Ratnayake R.K., Herbold J.R. Discrete-time deterministic and stochastic models for the spread of rabies. Appl. Math. Comput. 2002;132:271–292. [Google Scholar]
- 3.Anderson R.M., Jackson H.C., May R.M., Smith A.M. Population dynamics of fox rabies in Europe. Nature. 1981;289:765–771. doi: 10.1038/289765a0. [DOI] [PubMed] [Google Scholar]
- 4.Andersson H., Britton T. Springer Verlag; New York: 2000. Stochastic Epidemic Models and their Statistical Analysis. [Google Scholar]
- 5.C.D.C. Anshan, Rabies Knowledge for 20 Questiones, 2011, http://www.ascdc.com.cn/newscontent.asp?lsh=5.
- 6.Aronson D.G., Weinberger H.F. Nonlinear diffusion in population genetics, combustion, and nerve pulse propagation. In: Goldstein J.A., editor. Partial Differential Equations and Related Topics. Springer-Verlag; Berlin: 1975. pp. 5–49. [Google Scholar]; Lecture Notes in Mathematics 446.
- 7.Artois M., Langlais M., Suppo C. Simulation of rabies control within an increasing fox population. Ecol. Model. 1997;97:23–34. [Google Scholar]
- 8.Bacaer N., Guernaoui S. The epidemic threshold of vector-borne diseases with seasonality. J. Math. Biol. 2006;53:421–436. doi: 10.1007/s00285-006-0015-0. [DOI] [PubMed] [Google Scholar]
- 9.B. Baike, Rabies, http://baike.baidu.com/view/10630.htm.
- 10.Bjornstad O.N., Finkenstadt B.F., Grenfell B.T. Dynamics of measles epidemics: estimating scaling of transmission rates using a time series SIR model. Ecol. Monogr. 2002;72:169–184. [Google Scholar]
- 11.Carroll M.J., Singer A., Smith G.C., Cowan D.P., Massei G. The use of immunocontraception to improve rabies eradication in urban dog populations. Wildl. Res. 2010;37:676–687. [Google Scholar]
- 12.Chen J., Zou L., Jin Z., Ruan S. Modeling the geographic spread of rabies in China. PLoS Negl. Trop. Dis. 2015;9(5):e0003772. doi: 10.1371/journal.pntd.0003772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Center for Disease Control and Provention (CDC), 2011, Rabies. http://www.cdc.gov/rabies/. Accessed June 1.
- 14.Childs J.E., Curns A.T., Dey M.E., Real L.A., Feinstein L. Predicting the local dynamics of epizootic rabies among raccoons in the United States. Proc. Natl. Acad. Sci. USA. 2000;97:13666–13671. doi: 10.1073/pnas.240326697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chinese Center for Disease Control and Prevention (CCDC), National Public Health Statistical Data. 2012. http://www.chinacdc.cn/tjsj/gjwstjsj.
- 16.Chinese Center for Disease Control and Provention (CCDC), Questions and Answers About Rabies, 2011, http://www.chinacdc.cn/jkzt/crb/zl/kqb/kqbzstd/201109/t20110922_52966.html.
- 17.Clayton T., Duke-Sylvester S., Gross L.J., Lenhart S., Real L.A. Optimal control of a rabies epidemic model with a birth pulse. J. Biol. Dyn. 2010;4:43–58. doi: 10.1080/17513750902935216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Coleman P.G., Dye C. Immunization coverage required to prevent outbreaks of dog rabies. Vaccine. 1996;14:185–186. doi: 10.1016/0264-410x(95)00197-9. [DOI] [PubMed] [Google Scholar]
- 19.Coyne M.J., Smith G., McAllister F.E. Mathematic model for the population biology of rabies in raccoons in the Mid-Atlantic states. Am. J. Vet. Res. 1989;50:2148–2154. [PubMed] [Google Scholar]
- 20.Department of Health of Guangdong Province (DOHG), Bulletins, 2010, http://www.gdwst.gov.cn/a/yiqingxx/.
- 21.Diekmann O. Run for your life. A note on the asymptotic speed of propagation of an epidemic. J. Differ. Equ. 1979;33:58–73. [Google Scholar]
- 22.Diekmann O., Heesterbeek J.A.P., Roberts M.G. On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- 23.Diekmann O., Heesterbeek J.A.P., Roberts M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface. 2010;7:873–885. doi: 10.1098/rsif.2009.0386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dimitrov D.T., Hallam T.G., Rupprecht C.E., Turmelle A.S., McCracken G.F. Integrative models of bat rabies immunology, epizootiology and disease demography. J. Theor. Biol. 2007;245:498–509. doi: 10.1016/j.jtbi.2006.11.001. [DOI] [PubMed] [Google Scholar]
- 25.Dowell S.F. Seasonal variation in host susceptibility and cycles of certain infectious diseases. Emerg. Infect. Dis. 2001;7:369–374. doi: 10.3201/eid0703.010301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ega T.T., Luboobi L.S., Kuznetsov D., Kidane A.H. Sensitivity analysis and numerical simulations for the mathematical model of rabies in human and animal within and around Addis Ababa. Asian J. Math. Appl. 2015;4:23. [Google Scholar]; Article ID ama0271.
- 27.Evans N.D., Pritchard A.J. A control theoretic approach to containing the spread of rabies. IMA J. Math. Appl. Med. Biol. 2001;18:1–23. [PubMed] [Google Scholar]
- 28.Fitzpatrick M.C., Shah H.A., Pandey A. One health approach to cost-effective rabies control in India. Proc. Natl. Acad. Sci. USA. 2016;113:14574–14581. doi: 10.1073/pnas.1604975113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Fooks A.R., Banyard A.C., Horton D.L. Current status of rabies and prospects for elimination. Lancet. 2014;384:1389–1399. doi: 10.1016/S0140-6736(13)62707-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Fxxue, Statistics on Annual Birth Populations in China, 2010. http://fxxue.blog.hexun.com/44596551_d.html.
- 31.Gao D., Ruan S. A multipatch malaria model with logistic growth populations. SIAM J. Appl. Math. 2012;72:819–841. doi: 10.1137/110850761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Greenhalgh D., Moneim I.A. SIRS epidemic model and simulations using different types of seasonal contact rate. Syst. Anal. Model. Simul. 2003;43:573–600. [Google Scholar]
- 33.Grenfell B. Rivers dam waves of rabies. Proc. Natl. Acad. Sci. USA. 2002;99:3365–3367. doi: 10.1073/pnas.062049599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Guangdong Statistical Yearbook (GSY), Main Population Indicators, 2010a, http://www.gdstats.gov.cn/tjnj/2010/table/4/c4_1.htm.
- 35.Guangdong Statistical Yearbook (GSY), Status of Natural Population Changes, 2010b, http://www.gdstats.gov.cn/tjnj/2010/table/4/c4_3.htm.
- 36.Guo D., Zhou H., Zou Y. Geographical analysis of the distribution and spread of human rabies in China from 2005 to 2011. PLoS One. 2013;8(8):e72352. doi: 10.1371/journal.pone.0072351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Guo Z., Tao X., Yin C. National borders effectively halt the spread of rabies: the current rabies epidemic in China is dislocated from cases in neighboring countries. PLoS Negl. Trop. Dis. 2013;7(1):e2039. doi: 10.11/journal.pntd.0002039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hampson K., Coudeville L., Lembo T. Estimating the global burden of endemic canine rabies. PLoS Negl. Trop. Dis. 2015;9(4):e0003709. doi: 10.1371/journal.pntd.0003709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Hampson K., Dushoff J., Bingham J., Bruckner G., Ali Y.H. Synchronous cycles of domestic dog rabies in sub-Saharan Africa and the impact of control effort. Proc. Natl. Acad. Sci. USA. 2007;104:7717–7722. doi: 10.1073/pnas.0609122104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hampson K., Dushoff J., Cleaveland S., Haydon D.T., Kaare M. Transmission dynamics and prospects for the elimination of canine rabies. PLoS Biol. 2009;7:0462–0471. doi: 10.1371/journal.pbio.1000053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.He J.-F., Kang M., Li L.-H., Liang W.-J. Exposure to human rabies and the related risk factors in Guangdong. Chin. J. Epidemiol. 2009;30:532–533. [PubMed] [Google Scholar]
- 42.Hemachudha T., Laothamatas J., Rupprecht C.E. Human rabies: a disease of complex neuropathogenetic mechanisms and diagnostic challenges. Lancet Neurol. 2002;1:101–109. doi: 10.1016/s1474-4422(02)00041-8. [DOI] [PubMed] [Google Scholar]
- 43.Hou Q., Jin Z., Ruan S. Dynamics of rabies epidemics and the impact of control efforts in Guangdong Province, China. J. Theor. Biol. 2012;300:39–47. doi: 10.1016/j.jtbi.2012.01.006. [DOI] [PubMed] [Google Scholar]
- 44.Hu R.-L., Fooks A.R., Zhang S.-F., Liu Y., Zhang F. Inferior rabies vaccine quality and low immunization coverage in dogs (canis familiaris) in China. Epidemiol. Infect. 2008;136:1556–1563. doi: 10.1017/S0950268807000131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Hu R.-L., Tang Q., Tang J.R., Fooks A.R. Rabies in China: an update. Vector-borne Zoonotic Dis. 2009;9:1–11. doi: 10.1089/vbz.2008.0046. [DOI] [PubMed] [Google Scholar]
- 46.Hutson V., Schmitt K. Permanence and the dynamics of biological systems. Math. Biosci. 1992;111:1–71. doi: 10.1016/0025-5564(92)90078-b. [DOI] [PubMed] [Google Scholar]
- 47.Kallen A. Thresholda and travelling waves in an epidemic model for rabies. Nonlinear Anal. 1984;8:851–856. [Google Scholar]
- 48.Kallen A., Arcuri P., Murray J.D. A simple model for the spatial spread and control of rabies. J. Theor. Biol. 1985;116:377–393. doi: 10.1016/s0022-5193(85)80276-9. [DOI] [PubMed] [Google Scholar]
- 49.Keeling M.J., Eames K.T.D. Networks and epidemic models. J. R. Soc. Interface. 2005;2:295–307. doi: 10.1098/rsif.2005.0051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Knobel D.L., Cleaveland S., Coleman P.G. Re-evaluating the burden of rabies in Africa and Asia. Bull. WHO. 2005;83:360–368. [PMC free article] [PubMed] [Google Scholar]
- 51.Kureishi A., Xu L.Z., Stiver H.G. Rabies in China: recommendations for control. Bull. WHO. 1992;70:443–450. [PMC free article] [PubMed] [Google Scholar]
- 52.London W., Yorke J.A. Recurrent outbreaks of measles, chickenpox and mumps. I. Seasonal variation in contact rates. Am. J. Epidemiol. 1973;98:453–468. doi: 10.1093/oxfordjournals.aje.a121575. [DOI] [PubMed] [Google Scholar]
- 53.Lozano R., Naghavi M., Foreman K. Global and regional mortality from 235 causes of death for 20 age groups in 1990 and 2010: a systematic analysis for the global burden of disease study 2010. Lancent. 2012;380:2095–2128. doi: 10.1016/S0140-6736(12)61728-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ma J., Ma Z. Epidemic threshold conditions for seasonally forced SEIR models. Math. Biosci. Eng. 2006;3:161–172. doi: 10.3934/mbe.2006.3.161. [DOI] [PubMed] [Google Scholar]
- 55.MacDonald D.W. Oxford University Press; Oxford: 1980. Rabies and Wildlife: A Biologist’s Perspective. [Google Scholar]
- 56.Maidana N.A., Yang H.M. Describing the geographic spread of degue disease by traveling waves. Math. Biosci. 2008;215:64–77. doi: 10.1016/j.mbs.2008.05.008. [DOI] [PubMed] [Google Scholar]
- 57.Maidana N.A., Yang H.M. Spatial spreading of west nile virus described by traveling waves. J. Theor. Biol. 2009;258:403–417. doi: 10.1016/j.jtbi.2008.12.032. [DOI] [PubMed] [Google Scholar]
- 58.Massei G., Fooks A.R., Horton D.L. Free-roaming dogs in Nepal: demographics, health and public knowledge, attitudes and practices. Zoonose Public Health. 2017;64:29–40. doi: 10.1111/zph.12280. [DOI] [PubMed] [Google Scholar]
- 59.Meng S.L., Xu G.L., Wu X.F. Transmission dynamics of rabies in China over the last 40 years: 1969–2009. J. Clin. Virol. 2010;49:47–52. doi: 10.1016/j.jcv.2010.06.014. [DOI] [PubMed] [Google Scholar]
- 60.Ministry of Health of the People’s Republic of China (MOHC), The Status of Prevention and Control of Rabies in China (Zhongguo Kuangquanbing Fangzhi Xiankuang), 2009, http://www.moh.gov.cn/publicfiles/business/htmlfiles/mohbgt/s9513/200909/42937.htm.
- 61.Ministry of Health of the People’s Republic of China (MOHC), Bulletins, 2010, http://www.moh.gov.cn/publicfiles/business/htmlfiles/mohbgt/pwsbgb/index.htm. Accessed June 1, 2011.
- 62.Moneim I. The effect of using different types of periodic contact rate on the behaviour of infectious diseases: a simulation study. Comput. Biol. Med. 2007;37:1582–1590. doi: 10.1016/j.compbiomed.2007.02.007. [DOI] [PubMed] [Google Scholar]
- 63.Murray J.D., Seward W.L. On the spatial spread of rabies among foxes with immunity. J. Theor. Biol. 1992;156:327–348. [Google Scholar]
- 64.Murray J.D., Stanle E.A., Brown D.L. On the spatial spread of rabies among foxes. Proc. R. Soc. Lond. B. 1986;229:111–150. doi: 10.1098/rspb.1986.0078. [DOI] [PubMed] [Google Scholar]
- 65.National Bureau of Statistics of China (NBSC), China Demographic Yearbook of 2009, 2011, http://www.stats.gov.cn/tjsj/ndsj/2009/indexch.htm. Accessed June 1.
- 66.National Health and Family Planning Commission of the People’s Republic of China (NHFPC), China Health Statistical Yearbook 2012, 2014, http://www.nhfpc.gov.cn/htmlfiles/zwgkzt/ptjnj/year2012/index2012.html. Accessed July 17.
- 67.National Health and Family Planning Commission of the People’s Republic of China (NHFPC), Bulletins, 2014, http://www.nhfpc.gov.cn/jkj/s3578/list.shtml. Accessed July 17, 2014.
- 68.Newman M.E.J. Spread of epidemic disease on networks. Phys. Rev. E. 2002;66:016128. doi: 10.1103/PhysRevE.66.016128. [DOI] [PubMed] [Google Scholar]
- 69.Ou C., Wu J. Spatial spread on nonlinear dynamics. SIAM J. Appl. Math. 2006;67:138–163. [Google Scholar]
- 70.Panjeti V.G., Real L.A. Mathematical models for rabies. Adv. Virus Res. 2011;79:377–395. doi: 10.1016/B978-0-12-387040-7.00018-4. [DOI] [PubMed] [Google Scholar]
- 71.Perko L. Springer-Verlag; New York: 2000. Differential Equations and Dynamical Systems. [Google Scholar]
- 72.Rhodes C.J., Atkinson R.P.D., Anderson R.M., Macdonald D.W. Rabies in Zimbabwe: reservoir dogs and the implications for disease control. Philos. Trans. R. Soc. Lond. B. 1998;353:999–1010. doi: 10.1098/rstb.1998.0263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Roberts M.G., Aubert M.F.A. A model for the control of echinococcus multilocularis in France. Vet. Parasitol. 1995;56:67–74. doi: 10.1016/0304-4017(94)00655-v. [DOI] [PubMed] [Google Scholar]
- 74.Ruan S., Wu J. Modeling spatial spread of communicable diseases involving animal hosts. In: Cantrell S., Cosner C., Ruan S., editors. Spatial Ecology. Chapman Hall/CRC; Boca Raton, FL: 2009. pp. 293–316. [Google Scholar]
- 75.Russell C.A., Real L.A., Smith D.L. Spatial control of rabies on heterogeneous landscapes. PLoS One. 2006;1:e27. doi: 10.1371/journal.pone.0000027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Schenzle D. An age-structured model of pre- and pose-vaccination measles transmission. Math. Med. Biol. 1984;1:169–191. doi: 10.1093/imammb/1.2.169. [DOI] [PubMed] [Google Scholar]
- 77.Schultz R.D. Duration of immunity for canine and feline vaccines: a review. Vet. Microbiol. 2006;117:75–79. doi: 10.1016/j.vetmic.2006.04.013. [DOI] [PubMed] [Google Scholar]
- 78.Schwartz I. Small amplitude, long periodic out breaks in seasonally driven epidemics. J. Math. Biol. 1992;30:473–491. doi: 10.1007/BF00160532. [DOI] [PubMed] [Google Scholar]
- 79.Si H., Guo Z.M., Hao Y.T., Liu Y.G., Zhang D.M. Rabies trend in China (1990–2007) and post-exposure prophylaxis in the Guangdong province. BMC Infect. Dis. 2008;8:113. doi: 10.1186/1471-2334-8-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Si H., Liu Y.-G., Li G.-W., Liu Z.-Y., Lu J.-H. Analysis on the characteristic of rabies epidemiology in Guangdong Province from 1990 to 2005. J. Sun Yat-Sen Univ. 2007;28:263–264. [Google Scholar]
- 81.Smith D.L., Lucey B., Waller L.A., Childs J.E., Real L.A. Predicting the spatial dynamics of rabies epidemic on heterogeneous landscapes. Proc. Natl. Acad. Sci. USA. 2002;99:3668–3672. doi: 10.1073/pnas.042400799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Smith G.C., Cheeseman C.L. A mathematical model for the control of diseases in wildlife populations: culling, vaccination and fertility control. Ecol. Model. 2002;150:45–53. [Google Scholar]
- 83.Smith G.C., Harris S. The control of rabies in urban fox populations. In: Putman R.J., editor. Mammals as Pests. Chapman & Hall; London: 1989. pp. 209–224. [Google Scholar]
- 84.Song M., Tang Q., Wang D.M., Mo Z.J., Guo S.H. Epidemiological investigations of human rabies in China. BMC Infect. Dis. 2009;9:210. doi: 10.1186/1471-2334-9-210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Song M., Tang Q., Rayner S. Human rabies surveillance and control in China. BMC Infect. Dis. 2014;14:212. doi: 10.1186/1471-2334-14-212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Sterner R.T., Smith G.C. Modelling wildlife rabies: transmission, economics, and conservation. Biol. Conserv. 2006;131:163–179. [Google Scholar]
- 87.Tang X.C., Luo M., Zhang S.Y., Anthony R.F., Hu R.L. Pivotal role of dogs in rabies transmission, China. Emerg. Infect. Dis. 2005;11:1970–1972. doi: 10.3201/eid1112.050271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Tao X.Y., Tang Q., Li H. Molecular epidemiology of rabies in southern People’s Republic of China. Emerg. Infect. Dis. 2009;15:1192–1198. doi: 10.3201/eid1508.081551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Tao X.-Y., Tang Q., Yayner S. Molecular phylodynamic analysis indicates lineage displacement occurred in Chinese rabies epidemics between 1949 to 2010. PLoS Negl. Trop. Dis. 2013;7(7):e2294. doi: 10.1371/journal.pntd.0002294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Tenzin, Ward M.P. Review of rabies epidemiology and control in south, south east and east Asia: past, present and prospects for elimination. Zoonoses Public Health. 2012;59:451–467. doi: 10.1111/j.1863-2378.2012.01489.x. [DOI] [PubMed] [Google Scholar]
- 91.Tierkel E.S. Canine rabies. In: Baer G.M., editor. The Natural History of Rabies. Academic Press; London: 1975. [Google Scholar]
- 92.Torill M., Pal P. Arctic rabies – a review. Acta Vet. Scand. 2004;45:1–9. doi: 10.1186/1751-0147-45-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.van den Driessche P., Watmough J. Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math. Biosci. 2002;180:29–48. doi: 10.1016/s0025-5564(02)00108-6. [DOI] [PubMed] [Google Scholar]
- 94.Wang L., Tang Q., Liang G. Rabies and rabies virus in wildlife in Mainland China, 1990–2013. Int. J. Infect. Dis. 2014;25:122–129. doi: 10.1016/j.ijid.2014.04.016. [DOI] [PubMed] [Google Scholar]
- 95.Wang W., Zhao X.-Q. Threshold dynamics for compartmental epidemic models in periodic environments. J. Dyn. Differ. Equ.. 2008;20:699–717. [Google Scholar]
- 96.Wang X., Lou J. Two dynamic models about rabies between dogs and human. J. Biol. Syst. 2008;16:519–529. [Google Scholar]
- 97.Wang X.J., Huang J.T. Epidemiology. In: Yu Y.X., editor. Rabies and Rabies Vaccine. Chinese Medicine Technology Press; Beijing: 2001. pp. 127–144. [Google Scholar]
- 98.Wang Z.-X. WHO position on rabies vaccine. Int. J. Biol. 2002;25:245–248. [Google Scholar]
- 99.Wesley C., Allen L. The basic reproduction number in epidemic models with periodic demographics. J. Biol. Dyn. 2009;3:116–129. doi: 10.1080/17513750802304893. [DOI] [PubMed] [Google Scholar]
- 100.World Health Organization (WHO), 2004, WHO Expert Consultation on Rabies: First Report. Geneva.
- 101.World Health Organization (WHO), 2010, Rabies. http://www.who.int/mediacentre/factsheets/fs099/en/. Updated.
- 102.Williams B. Infectious disease persistence when transmission varies seasonally. Math. Biosci. 1997;145:77–88. doi: 10.1016/s0025-5564(97)00039-4. [DOI] [PubMed] [Google Scholar]
- 103.Wu H., Wang L., Tao X. Genetic diversity and molecular evolution of the rabies virus matrix protein gene in China. Infect. Genet. Evol. 2013;16:248–253. doi: 10.1016/j.meegid.2013.02.009. [DOI] [PubMed] [Google Scholar]
- 104.Wu X.F., Hu R.L., Zhang Y.Z., Dong G.M., Rupprecht C.E. Reemerging rabies and lack of systemic surveillance in People’s Republic of China. Emerg. Infect. Dis. 2009;15:1159–1164. doi: 10.3201/eid1508.081426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Wunner W.H., Briggs D.J. Rabies in the 21st century. PLoS Negl. Trop. Dis. 2010;4(3):e591. doi: 10.1371/journal.pntd.0000591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Yin C., Zhou H., Wu H. Analysis on factors related to rabies epidemic in China from 2007–2011. Virol. Sin. 2012;27:132–143. doi: 10.1007/s12250-012-3244-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Yin W., Dong J., Tu C. Challenges and needs for China to eliminate rabies. Infect. Dis. Poverty. 2013;2:23. doi: 10.1186/2049-9957-2-23. [DOI] [PMC free article] [PubMed] [Google Scholar]; http://www.idpjournal.com/content/2/1/23.
- 108.Yu J., Hao L., Tang Q. The spatial and temporal dynamics of rabies in China. PLoS Negl. Trop. Dis. 2012;6:e1640. doi: 10.1371/journal.pntd.0001640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Yang W., Lou L. The dynamics of an interactional model of rabies transmitted between human and dogs. Boll. UMI. 2009;(3):591–605. [Google Scholar]
- 110.Zhang F., Zhao X.-Q. A periodic epidemic model in a patchy environment. J. Math. Anal. Appl. 2007;325:496–516. [Google Scholar]
- 111.Zhang J., Jin Z., Sun G., Sun X., Ruan S. Modeling seasonal rabies epidemics in China. Bull. Math. Biol. 2012;74:1226–1251. doi: 10.1007/s11538-012-9720-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Zhang J., Jin Z., Sun G., Sun X., Ruan S. Spatial spread of rabies in China. J. Appl. Anal. Comput. 2012;2:111–126. [Google Scholar]
- 113.Zhang J., Jin Z., Sun G., Zhou T., Ruan S. Analysis of rabies in China: transmission dynamics and control. PLoS One. 2011;6:e20891. doi: 10.1371/journal.pone.0020891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Zhang Y.-Z., Xiao D.-L., Sun Y.-H., Yang X.-R., Yan Y.-Z. The epidemic situation of human rabies from 1984 to 2002 and its preventive measures in China. Chin. J. Epidemiol. 2003;24:883–886. [PubMed] [Google Scholar]
- 115.Zhang Y.-Z., Xiong C.-L., Xiao D.-L. Human rabies in China. Emerg. Infect. Dis. 2005;11:1983–1984. doi: 10.3201/eid1112.040775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Zhao X.-Q. Springer-Verlag; New York: 2003. Dynamical Systems in Population Biology. [Google Scholar]
- 117.Zinsstag J., Durr S., Penny M.A., Mindekem R., Roth F. Transmission dynamic and economics of rabies control in dogs and humans in an African city. Proc. Natl. Acad. Sci. USA. 2009;106:14996–15001. doi: 10.1073/pnas.0904740106. [DOI] [PMC free article] [PubMed] [Google Scholar]