Coronavirus phylogeny based on triplets of nucleic acids bases

Abstract

We considered the fully overlapping triplets of nucleotide bases and proposed a 2D graphical representation of protein sequences consisting of 20 amino acids and a stop code. Based on this 2D graphical representation, we outlined a new approach to analyze the phylogenetic relationships of coronaviruses by constructing a covariance matrix. The evolutionary distances are obtained through measuring the differences among the two-dimensional curves.

1. Introduction

Compilation of DNA primary sequence data continues unabated and tends to overwhelm us with voluminous outputs that increase daily. Comparison of primary sequences of different DNA strands remains one of the important aspect of the analysis of DNA data banks. Mathematical analysis of the large volume genomic DNA sequence data is one of the challenges for bio-scientists. There are three class methods for the analysis of DNA sequences: (i) Alignment [1], [2]. (ii) Matrices: (1) matrices in which an individual entry corresponds to an individual pair of bases [3], [6], [7] and (2) matrices in which entries summarize information of different X–Y pairs of bases [4], [5], [7]. (iii) Graphical representation: Graphical representation of DNA sequence provides a simple way of viewing, sorting and comparing various gene structures. Graphical techniques have emerged as a very powerful tool for the visualization and analysis of long DNA sequences. These techniques provide useful insights into local and global characteristics and the occurrences, variations and repetition of the nucleotides along a sequence which are not as easily obtainable by other methods. In recent years several authors outlined different graphical representation of DNA sequences based on 2D, 3D or 4D [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20]. Based on these graphical representation, several authors outlined some approaches to make comparison of DNA sequences [21], [22], [23], [24], [25].

All this methods are based on the (four letter alphabet, A, C, G, and T standing for nucleotide bases adenine, cytosine, guanine, and thymine, respectively). We will change to consider the fully overlapping triplets of nucleotide bases. Consideration of triplets of nucleotide bases instead of individual nucleotide bases has several reasons and advantages. There are three of them: (i) The genetic code consists of triplets (codons) of DNA (or RNA in some virus) nucleotides. (ii) The second advantage is that one can easily find the open reading frame as the longest sequence of triplets that contains no stop codons when read in a single reading frame. (iii) The computation will become more simple.

In this Letter, we proposed a 2D graphical representation of the protein sequences consisting of 20 amino acids and a stop code. Based on this 2D graphical representation, we outlined a new approach to analyze the phylogenetic relationships of coronaviruses. The evolutionary distances are obtained through measuring the differences among the two-dimensional curves. Unlike most existing phylogeny construction methods [26], [27], [28], [29], [30], [31], the proposed method does not require multiple alignment.

2. 2D graphical representation of protein sequences and properties

As is known, all of the 64 triplets of nucleotide bases correspond 20 amino acids and a stop code. There are three reading frame start at position 1, 2 and 3, respectively. Using the translate tool, we can obtain three protein sequences consisting of 20 amino acids and a stop code. The 20 amino acids found in proteins can be grouped according to the chemistry of their R groups as in [32]: amino acids A,V,F,P,M,I,L belong to the hydrophobic chemical group; amino acids D,E,K,R belong to charged chemical group; amino acids S,T,Y,H,C,N,Q,W belong to polar chemical group; amino acid belong to glycine chemical group. Then for any DNA sequence, we will transform it into three new sequences defined over alphabet $\{\overline{H}\text{,}\overline{C}\text{,}\overline{P}\text{,}\overline{G}\}$. The rule is as follows:

$\varphi (g(3i-2\text{,}3i-1\text{,}3i))=\left\{\begin{array}{cc}\overline{H}\hfill & \text{if}g(3i-2\text{,}3i-1\text{,}3i)=A\text{,}V\text{,}F\text{,}P\text{,}M\text{,}I\text{,}L\hfill \\ \overline{C}\hfill & \text{if}g(3i-2\text{,}3i-1\text{,}3i)=D\text{,}E\text{,}K\text{,}R\hfill \\ \overline{P}\hfill & \text{if}g(3i-2\text{,}3i-1\text{,}3i)=S\text{,}T\text{,}Y\text{,}H\text{,}C\text{,}N\text{,}G\text{,}W\hfill \\ \overline{G}\hfill & \text{if}g(3i-2\text{,}3i-1\text{,}3i)=G\text{,}-\hfill \end{array}\right)$

As shown in Fig. 1 , we construct a pyrimidine–purine graph on two quadrants of the cartesian coordinate system, with pyrimidines ($\overline{P}$ and $\overline{C}$) in the first quadrant and purines ($\overline{H}$ and $\overline{G}$) in the fourth quadrant. The unit vectors representing four alphabets $\overline{H}\text{,}\overline{G}\text{,}\overline{C}$ and $\overline{P}$ are as follows:

$(m\text{,}-\sqrt{n})\to \overline{H}\text{,}(\sqrt{n}\text{,}m)\to \overline{G}\text{,}(\sqrt{n}\text{,}m)\to \overline{C}\text{,}(m\text{,}\sqrt{n})\to \overline{P}$

where m is a real number and $m\ne \sqrt{n}$, n is a positive real number but not a perfect square number. So that we will reduce a DNA sequence into a series of nodes P ₀,P ₁,P ₂, … ,P _⌊N/3⌋, whose coordinates x _i, y _i (i  = 0,1, 2, … , ⌊N/3⌋, where N is the length of the DNA sequence being studied) satisfy

$\left\{\begin{array}{c}{x}_i={\overline{h}}_{i}m+{\overline{g}}_i\sqrt{n}+{\overline{c}}_i\sqrt{n}+{\overline{p}}_{i}m\hfill \\ y_i=-{\overline{h}}_i\sqrt{n}-{\overline{g}}_{i}m+{\overline{c}}_{i}m+{\overline{p}}_i\sqrt{n}\hfill \end{array}\right)$ (1)

${\overline{h}}_i\text{,}{\overline{c}}_i\text{,}{\overline{g}}_i$ and ${\overline{p}}_i$ satisfy

$\left\{\begin{array}{c}{\overline{h}}_i=A_i+\sqrt{s_1}{V}_i+\sqrt{s_2}{F}_i+\sqrt{s_3}{P}_i\hfill \\ +\sqrt{s_4}{M}_i+\sqrt{s_5}{I}_i+\sqrt{s_6}{L}_i\hfill \\ {\overline{c}}_i=D_i+\sqrt{s_7}{E}_i+\sqrt{s_8}{K}_i+\sqrt{s_9}{R}_i\hfill \\ {\overline{g}}_i=S_i+\sqrt{s_{10}}{T}_i+\sqrt{s_{11}}{Y}_i+\sqrt{s_{12}}{H}_i\hfill \\ +\sqrt{13}{C}_i+\sqrt{s_{14}}{N}_i+\sqrt{s_{15}}{Q}_i+\sqrt{s_{16}}{W}_i\hfill \\ {\overline{p}}_i=G_i+\sqrt{s_{17}}{\Omega }_i\hfill \end{array}\right)$ (2)

Fig. 1.

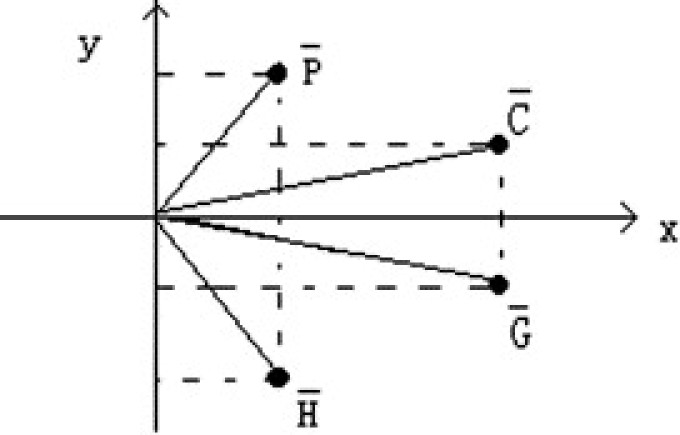
Pyrimidine–purine graph.

where A _i,V _i,F _i,P _i,M _i,I _i,L _i,D _i,E _i,K _i,R _i,S _i,T _i,Y _i,H _i,C _i, N _i Q _i W _i,G _i,Ω _i; are the cumulative occurrence numbers of A, V,F,P,M,I,L,D,E,K,R,S,T,Y,H,C,N,Q,W,G and −(or stop code), respectively, in the subsequence from the 1st base to the ith base in the sequence. And s _k,k  = 1, … ,17 are positive real number but not perfect square number, s _i  ≠  s _j,i,j  = 1, … ,17, and $m\ne \sqrt{s_k}\text{,}m\ne \sqrt{{\mathit{ns}}_k}\text{,}m\sqrt{s_k}\ne \sqrt{n}\text{,}1\text{,}\dots \text{,}17$. We define A ₀  =  V ₀  =  F ₀  =  P ₀  =  M ₀  =  I ₀  =  L ₀  =  D ₀  =  E ₀  =  K ₀  =  R ₀  =  S ₀  =  T ₀  =  Y ₀  =  H ₀  =  C ₀  =  N ₀  =  Q ₀  =  W ₀  =  G ₀  =  Ω ₀  = 0.

We called the corresponding plot set be characteristic plot set. The curve connected all plots of the characteristic plot set in turn is called characteristic curve, which is determined by m, n, that satisfy above mentioned condition. In Fig. 2, Fig. 3, Fig. 4 , we show the SARS corresponding curves with different parameters n and m, where s ₁  = 2/3;s ₂  = 3/4; s ₃  = 4/5;s ₄  = 5/6;s ₅  = 6/7;s ₆  = 7/8;s ₇  = 8/9;s ₈  = 9/10;s ₉  = 10/11; s ₁₀  = 11/12;s ₁₁  = 12/13;s ₁₂  = 13/14;s ₁₃  = 14/15;s ₁₄  = 15/16;s ₁₅  =  16/17;s ₁₆  = 17/18;s ₁₇  = 18/19. Observing Fig. 2, Fig. 3, Fig. 4, we find SARS have similar curves despite with different parameters n and m.

Property 1

For a given DNA sequence there are three 2D representations corresponding to it.

Proof

Using the translate tool, one can obtain three protein sequences consisting of 20 amino acids and a stop code corresponding three reading frame start at position 1, 2 and 3. In a single reading frame, let (x _i, y _i) be the coordinates of the ith amino acid of protein sequence, then we have

${\overline{h}}_i(m\text{,}-\sqrt{n})+{\overline{g}}_i(\sqrt{n}\text{,}-m)+{\overline{c}}_i(\sqrt{n}\text{,}m)+{\overline{p}}_i(m\text{,}\sqrt{n})=(x_i\text{,}{y}_i)$

i.e.,

$\left\{\begin{array}{c}{\overline{h}}_{i}m+{\overline{g}}_i\sqrt{n}+{\overline{c}}_i\sqrt{n}+{\overline{p}}_{i}m=x_i\hfill \\ -{\overline{h}}_i\sqrt{n}-{\overline{g}}_{i}m+{\overline{c}}_{i}m+{\overline{p}}_i\sqrt{n}=y_i\hfill \end{array}\right)$ (3)

 □

Obviously, x _i and y _i are irrational numbers of form $\mathit{sm}+k\sqrt{n}$, where s and k are integers. We suppose

$\begin{array}{cc}\hfill & x_i=s_{x}m+k_x\sqrt{n}\hfill \\ \hfill & y_i=s_{y}m+k_y\sqrt{n}\hfill \end{array}$

then we have

$\left\{\begin{array}{c}{\overline{h}}_i+{\overline{p}}_i=s_x\hfill \\ {\overline{g}}_i+{\overline{c}}_i=k_x\hfill \\ -{\overline{g}}_i+{\overline{c}}_i=s_y\hfill \\ -{\overline{h}}_i+{\overline{p}}_i=k_y\hfill \end{array}\right)$ (4)

So, for given x-projection and y-projection of any point P  = (x, y) on the sequence, after uniquely determining s _x,k _x,s _y,k _y from x and y, the number A _p,V _p,F _p,P _p,M _p,I _p,L _p,D _p,E _p,K _p,R _p,S _p,T _p,Y _p,H _p,C _p,N _p,Q _p,W _p,G _p,Ω _p of A,V,F,P,M,I,L,D,E,K,R,S,T,Y,H,C,N,Q,W,G and −(or stop code) from the beginning of the sequence to the point P can be found by solving linear system (2), (4).

Fig. 2.

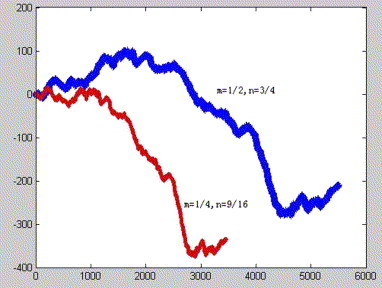
SARS corresponding curve with different parameters n and m based on the first reading frame.

Fig. 3.

SARS corresponding curve with different parameters n and m based on the second reading frame.

Fig. 4.

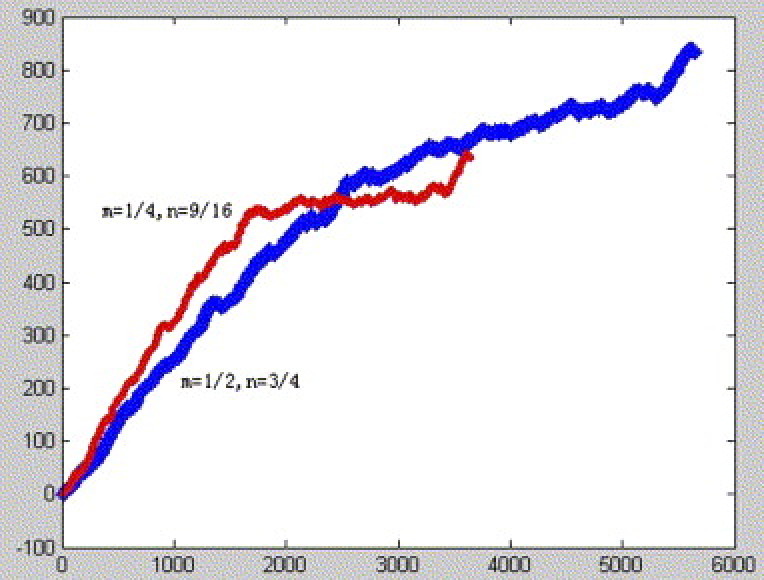
SARS corresponding curve with different parameters n and m based on the third reading frame.

The vector pointing to the point P _i from the origin O is denoted by r _i. The component of r _i, i.e. x _i and y _i are calculated by Eqs. (1), (2). Let Δr _i  =  r _i  −  r _i − 1, then we have Property 2.

Property 2

For any i  = 1, 2, … ,  N′, where N′is the length of protein sequence corresponding the studied DNA sequence, the vector Δr _i has only twenty one possible direction. Furthermore, the length of Δr _i, i.e.,∣Δ r _i∣, is always equal to s _k(m ²  +  n), for any i  = 1, 2, … ,  N, k  = 0,1, … ,17,s ₀  = 1.

Proof

Actually, the components of Δr _i, i.e., Δx _i and Δy _i can be calculated for each possible residue (A, V,F,P,M,I,L,D,E,K,R,S,T,Y,H,C,N,Q,W,G and −) at the ith position of the protein sequence by using Eqs. (1), (2). For example, when the ith residue is A, we find Δx _i  =  m and $\mathrm{\Delta }{y}_i=-\sqrt{n}$. This result is independent of the conformation state of the (i  − 1)th residue. The two numbers $(m\text{,}-\sqrt{n})$ are called the direction of Δr _i. The direction number and the length of Δr _i for each possible residue type at the ith position are summarized. □

Property 3

There is no circuit or degeneracy in our two-dimensional graphical representation.

Proof

We assume that: (1) the number of amino acid forming a circuit is l; (2) the number of A,V,F,P,M,I,L,D,E,K,R,S, T,Y,H,C,N,Q,W,G and −(or stop code) in a circuit is a′,v′,f′,p′,m′,i′,l′,d′,e′,k′,r′,s′,t′,y′,h′,c′,n′,q′,w′,g′ and δ′, respectively. So a′ +  v′ +  f′ +  p′ +  m′ +  i′ +  l′ +  d′ + e′ +  k′ +  r′ +  s′ +  t′ +  y′ +  h′ +  c′ +  n′ +  q′ +  w′ +  g′ +  δ′ =  l. Because a′A,v′V,f′F,p′P,m′M,i′I,l′L,d′D,e′E,k′K,r′R,s′S,t′T,y′Y,h′H,c′C,n′N,q′Q,w′W,g′G and δ′ −(or stop code) form a circuit, the following equation holds:

$\left\{\begin{array}{c}{\overline{h}}^{\prime }=a^{\prime }+\sqrt{s_1}{v}^{\prime }+\sqrt{s_2}{f}^{\prime }+\sqrt{s_3}{p}^{\prime }+\sqrt{s_4}{m}^{\prime }+\sqrt{s_5}{i}^{\prime }+\sqrt{s_6}{l}^{\prime }\hfill \\ \overline{c^{\prime }}=d^{\prime }+\sqrt{s_7}{e}^{\prime }+\sqrt{s_8}{k}^{\prime }+\sqrt{s_9}{r}^{\prime }\hfill \\ \overline{g^{\prime }}=s^{\prime }+\sqrt{s_{10}}{t}^{\prime }+\sqrt{s_{11}}{y}^{\prime }+\sqrt{s_{12}}{h}^{\prime }+\sqrt{13}{c}^{\prime }+\sqrt{s_{14}}{n}^{\prime }\hfill \\ +\sqrt{s_{15}}{q}^{\prime }+\sqrt{s_{16}}{w}^{\prime }\hfill \\ \overline{p^{\prime }}=g^{\prime }+\sqrt{s_{17}}{\delta }^{\prime }\hfill \end{array}\right)$ (5)

$\overline{h^{\prime }}(m\text{,}-\sqrt{n})+\overline{g^{\prime }}(\sqrt{n}\text{,}-m)+\overline{c^{\prime }}(\sqrt{n}\text{,}m)+\overline{p^{\prime }}(m\text{,}\sqrt{n})=(0\text{,}0)$

i.e.,

$\left\{\begin{array}{c}\overline{h^{\prime }}m+\overline{g^{\prime }}\sqrt{n}+\overline{c^{\prime }}\sqrt{n}+\overline{p^{\prime }}m=0\hfill \\ -\overline{h^{\prime }}\sqrt{n}-\overline{g^{\prime }}m+\overline{c^{\prime }}m+\overline{t^{\prime }}\sqrt{n}=0\hfill \end{array}\right)$ (6)

Clearly Eqs. (5), (6) hold if, and only if a′ =  v′ =  f′ =  p′ =  m′ =  i′ =  l′ =  d′ = e′ =  k′ =  r′ =  s′ =  t′ =  y′ =  h′ =  c′ =  n′ =  q′ =  w′ =  g′ =  δ′ = 0. Therefore, l  = 0, which means no circuit exists in this graphical representation. □

Property 4

The 2D representation possesses the reflection symmetry.

Proof

usually the sequence is expressed in the order from 5′ to 3′. Suppose that the 2D representation for protein sequence is described by (x _i, y _i),i  = 0,1, 2, … ,  N. Suppose again that the 2D representation for the reverse sequence, i.e, the same sequence but from 3′ to 5′ is described by $({\hat{x}}_i\text{,}{\hat{y}}_i)$, we find

$\left\{\begin{array}{c}\widehat{x_i}=x_N-x_{N-i}\hfill \\ \widehat{y_i}=y_N-y_{N-i}\hfill \end{array}\right)$ (7)

 □

3. Phylogenetic tree of coronaviruses

For any DNA sequence, we have three translating protein sequences. For any protein sequence, we have a set of points (x _i, y _i),i  =  1,2,3, … ,N, where N is the length of the sequence. The coordinates of the geometrical center of the points, denoted by x ⁰ and y ⁰, may be calculated as follows:

$x^0=\frac{1}{N}\sum _{i=1}^N{x}_i\text{,}{y}^0=\frac{1}{N}\sum _{i=1}^N{y}_i$ (8)

The element of covariance matrix CM of the points are defined:

$\left\{\begin{array}{c}{\mathit{CM}}_{\mathit{xx}}=\frac{1}{N}\sum _1^N(x_i-x^0)(x_i-x^0)\hfill \\ {\mathit{CM}}_{\mathit{xy}}=\frac{1}{N}\sum _1^N(x_i-x^0)(y_i-y^0)={\mathit{CM}}_{\mathit{yx}}\hfill \\ {\mathit{CM}}_{\mathit{yy}}=\frac{1}{N}\sum _1^N(y_i-y^0)(y_i-y^0)\hfill \end{array}\right)$ (9)

(See Table 1 )The above four numbers give a quantitative description of a set of point (x _i, y _i),i  = 1, 2, … ,  N, scattering in a two-dimensional space. Obviously, the matrix is a real symmetric 2 × 2 one. There is a leading eigenvalue for a matrix CM. So that there are three geometrical centers and three leading eigenvalue corresponding a DNA sequence. In Table 2 , we list the geometrical centers $(x_k^0\text{,}{y}_k^0)\text{,}k=1\text{,}2\text{,}3$ and leading eigenvalues belonging to 24 species with parameter $m=\frac{1}{2}\text{,}n=\frac{3}{4}\text{,}{s}_1=2/3\text{;}{s}_2=3/4\text{;}{s}_3=4/5\text{;}{s}_4=5/6\text{;}{s}_5=6/7\text{;}{s}_6=7/8\text{;}{s}_7=8/9\text{;}{s}_8=9/10\text{;}{s}_9=10/11\text{;}{s}_{10}=11/12\text{;}{s}_{11}=12/13\text{;}{s}_{12}=13/14\text{;}{s}_{13}=14/15\text{;}{s}_{14}=15/16\text{;}{s}_{15}=16/17\text{;}{s}_{16}=17/18\text{;}{s}_{17}=18/19$ (See Table 3 ).

Table 1.

The accession number, abbreviation, name and length for the 24 coronavirus geneomes

No.	Accession	Abbreviation	Genome	Length (nt)
l	NC_002645	HCoV_229E	Human coronavirus 229E	27 317
2	NC_002306	TGEV	Transmissible gastroenteritis virus	28 586
3	NC_003436	PEDV	Porcine epidemic diarrhea virus	28 033
4	U00735	BCoVM	Bovine coronavirus strain Mebus	31 032
5	AF391542	BCoVL	Bovine coronavirus isolate BCoV-LUN	31 028
6	AF220295	BCoVQ	Bovine coronavirus Quebec	31 100
7	NC_003045	BCoV	Bovine coronavirus	31 028
8	AF208067	MHVM	Murine hepatitis virus strain ML-10	31 233
9	AF101929	MHV2	Murine hepatitis virus strain 2	31 276
10	AF208066	MHVP	Murine hepatitis virus strain Penn 97-1	31 112
11	NC_001846	MHV	Murine hepatitis virus	31 357
12	NC_001451	IBV	Avian infectious bronchitis virus	27 608
13	AY278488	BJ01	SARS coronavirus BJ01	29 725
14	AY278741	Urbani	SARS coronavirus Urbani	29 727
15	AY278491	HKU-39849	SARS coronavirus HKU-39849	29 742
16	AY278554	CUHK-W1	SARS coronavirus CUHK-W1	29 736
17	AY282752	CUHK-Su10	SARS coronavirus CUHK-SulO	29,736
18	AY283794	SIN2500	SARS coronavirus Sin2500	29 711
19	AY283795	SIN2677	SARS coronavirus Sin2677	29 705
20	AY283796	SIN2679	SARS coronavirus Sin2679	29 711
21	AY283797	SIN2748	SARS coronavirus Sin2748	29 706
22	AY283798	SIN2774	SARS coronavirus Sin2774	29 711
23	AY291451	TW1	SARS coronavirus TW1	29 729
24	NC_004718	TOR2	SARS coronavirus	29 751

Table 2.

Twenty one possible direction

	Δxn	Δyn	∣Δrn∣
A	m	$-\sqrt{n}$	m2 + n
D	$\sqrt{n}$	m	m2 + n
S	$\sqrt{n}$	−m	m2 + n
G	m	$\sqrt{n}$	m2 + n
V	$m\sqrt{s_1}$	$\sqrt{s_{1}n}$	s1(m2 + n)
F	$m\sqrt{s_2}$	$\sqrt{s_{2}n}$	s2(m2 + n)
P	$m\sqrt{s_3}$	$\sqrt{s_{3}n}$	s3(m2 + n)
M	$m\sqrt{s_4}$	$\sqrt{s_{4}n}$	s4(m2 + n)
I	$m\sqrt{s_5}$	$\sqrt{s_{5}n}$	s5(m2 + n)
L	$m\sqrt{s_6}$	$\sqrt{s_{6}n}$	s6(m2 + n)
E	$\sqrt{{\mathit{ns}}_7}$	$m\sqrt{s_7}$	s7(m2 + n)
K	$\sqrt{{\mathit{ns}}_8}$	$m\sqrt{s_8}$	s8(m2 + n)
R	$\sqrt{{\mathit{ns}}_9}$	$m\sqrt{s_9}$	s9(m2 + n)
T	$\sqrt{{\mathit{ns}}_{10}}$	$-m\sqrt{s_{10}}$	s10(m2 + n)
Y	$\sqrt{{\mathit{ns}}_{11}}$	$-m\sqrt{s_{11}}$	s11(m2 + n)
H	$\sqrt{{\mathit{ns}}_{12}}$	$-m\sqrt{s_{12}}$	s12(m2 + n)
C	$\sqrt{{\mathit{ns}}_{13}}$	$-m\sqrt{s_{13}}$	s13(m2 + n)
N	$\sqrt{{\mathit{ns}}_{14}}$	$-m\sqrt{s_{14}}$	s14(m2 + n)
Q	$\sqrt{{\mathit{ns}}_{15}}$	$-m\sqrt{s_{15}}$	s15(m2 + n)
w	$\sqrt{{\mathit{ns}}_{16}}$	$-m\sqrt{s_{16}}$	s16(m2 + n)
–	$m\sqrt{s_{17}}$	$\sqrt{{\mathit{ns}}_{17}}$	s17(m2 + n)

Table 3.

The geometric centers and three leading eigenvalues for each of the 24 coronavirus genomes

i	$x_1^0$	$y_1^0$	$x_2^0$	$y_2^0$	$x_3^0$	$y_3^0$	λ1	λ2	λ3
1	2.5692e + 003	−159.0439	2.5566e + 003	−342.5873	2.6794e + 003	389.8249	2.1520	2.2321	2.3707
2	2.8619e + 003	−230.4309	2.8245e + 003	−723.2605	2.9971e + 003	128.9913	2.6999	2.8393	2.9157
3	2.8626e + 003	−233.0932	2.8231e + 003	−724.5553	2.9976e + 003	130.5104	2.7034	2.8386	2.9178
4	2.8602e + 003	−245.6989	2.8245e + 003	−743.4898	2.9985e + 003	133.2708	2.7056	2.8453	2.9209
5	2.8688e + 003	−294.6379	2.8364e + 003	−709.6245	3.0012e + 003	146.3851	2.7519	2.8561	2.9158
6	2.6263e + 003	415.1362	2.5204e + 003	−204.5027	2.4666e + 003	−516.9428	2.2817	2.0813	2.1269
7	2.8773e + 003	−476.9658	2.8773e + 003	−476.9658	2.9006e + 003	−252.7994	2.8910	2.8910	2.7932
8	2.8902e + 003	−446.8927	2.8902e + 003	−446.8927	2.9139e + 003	−227.7537	2.9004	2.9004	2.8179
9	2.8853e + 003	−459.6862	3.0344e + 003	82.5446	2.8912e + 003	−273.7115	2.9146	2.9739	2.7829
10	2.8582e + 003	−528.7428	3.0320e + 003	34.9426	2.8807e + 003	−253.2886	2.8697	2.9882	2.7408
11	2.5137e + 003	−415.8854	2.6893e + 003	244.2464	2.5817e + 003	−222.8666	2.2271	2.3287	2.1831
12	2.7670e + 003	−48.3996	2.7276e + 003	−34.7759	2.8570e + 003	524.7574	2.4705	2.5740	2.6849
13	2.7255e + 003	−35.7080	2.8550e + 003	526.4976	2.7646e + 003	−43.8066	2.5698	2.6804	2.4654
14	2.7656e + 003	−45.9837	2.7262e + 003	−35.1151	2.8557e + 003	528.0186	2.4675	2.5711	2.6821
15	2.7659e + 003	−45.2775	2.7260e + 003	−36.4889	2.8558e + 003	530.0127	2.4680	2.5710	2.6828
16	2.7656e + 003	−47.8004	2.7267e + 003	−33.6628	2.8560e + 003	527.4290	2.4680	2.5725	2.6838
17	2.7239e + 003	−35.1426	2.8535e + 003	527.3351	2.7632e + 003	−45.2702	2.5669	2.6777	2.4630
18	2.7233e + 003	−36.1921	2.8529e + 003	527.2583	2.7627e + 003	−45.4289	2.5657	2.6766	2.4620
19	2.7239e + 003	−34.4434	2.8535e + 003	527.8162	2.7633e + 003	−45.2775	2.5667	2.6780	2.4630
20	2.7239e + 003	−35.6707	2.8525e + 003	525.5247	2.7621e + 003	−43.2715	2.5678	2.6737	2.4587
21	2.7241e + 003	−35.5425	2.8535e + 003	527.2287	2.7634e + 003	−45.5734	2.5675	2.6777	2.4636
22	2.7647e + 003	−48.0684	2.7258e + 003	−35.7184	2.8553e + 003	523.7099	2.4661	2.5700	2.6815
23	2.7647e + 003	−47.8421	2.7252e + 003	−35.8263	2.8547e + 003	524.8910	2.4661	2.5692	2.6808
24	2.6110e + 003	−251.1068	2.7585e + 003	459.3175	2.6727e + 003	−97.0235	2.3573	2.4587	2.3322

In order to facilitate the quantitative comparison of different species in terms of their collective parameters, we introduce a distance scale as defined below. Suppose that there are two species i and j, the parameters are ${\lambda }_1^i\text{,}{\lambda }_2^i\text{,}{\lambda }_3^i\text{,}{\lambda }_1^j\text{,}{\lambda }_2^i\text{,}{\lambda }_3^j$, respectively, where ${\lambda }_1^i\text{,}{\lambda }_2^i\text{,}{\lambda }_3^i$ are the three leading eigenvalues of matrix CM _i corresponding to species i. The distance d _ij between the two points is

$d_{\mathit{ij}}\sqrt{({\lambda }_1^i-{\lambda }_1^j{)}^2+({\lambda }_2^i-{\lambda }_2^j{)}^2+({\lambda }_3^i-{\lambda }_3^j{)}^2}\text{,}i\text{,}j=1\text{,}2\text{,}\dots \text{,}M$ (10)

where d _ij denotes the distance between the geometric centers of the ith and the jth genomes, and M is the total number of all genomes (M  = 24, here). Then we obtain a real M  ×  M symmetric matrix whose elements are d _ij.

Accordingly, a real symmetric M  ×  M matrix D _ij is obtained and used to reflect the evolutionary distance between the species i and j. The clustering tree is constructed using the UPGMA method in Phylip package (http://evolution.genetics.washington.edu/phylip.html). The final phylogenetic tree is drawn using the Drawgram program in the Phylip package. In Fig. 5 , we present the phylogenetic tree belonging to 24 species.

Fig. 5.

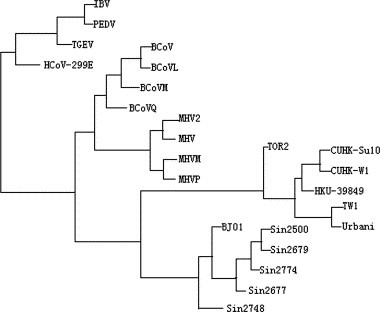
Phylogenetic tree.

4. Conclusion

We made a analysis of DNA sequences by considering the fully overlapping triplets of nucleotide bases. The presented graphical representation can be recaptured mathematically without loss of textual information. And our representation provides a direct plotting method to denote DNA sequences without degeneracy.

Most existing approaches for phylogenetic inference use multiple alignment of sequences and assume some sort of an evolutionary model. The multiple alignment strategy does not work for all types of data, e.g., whole genome phylogeny, and the evolutionary models may not always be correct. The current two-dimensional graphical representation of DNA sequences provides different approach for constructing phylogenetic tree. Unlike most existing phylogeny construction methods, the proposed method does not require multiple alignment. Also, both computational scientists and molecular biologists can use it to analysis protein sequences efficiently. We can obtain some graphical representation of protein sequence based on 2D, 3D and 4D using the following transform: $a_i\to {\overline{h}}_i\text{,}{g}_i\to {\overline{g}}_i\text{,}{c}_i\to {\overline{c}}_i\text{,}{t}_i\to {\overline{P}}_i$. ${\overline{h}}_i\text{,}{\overline{c}}_i\text{,}{\overline{g}}_i$ and ${\overline{p}}_i$ satisfy Eq. (2). a _i,c _i,g _i and t _i are the cumulative occurrence numbers of A, C, G and T, respectively, in the subsequence from the 1st base to the ith base in the sequence.