Effect of media-induced social distancing on disease transmission in a two patch setting

Abstract

We formulate an SIS epidemic model on two patches. In each patch, media coverage about the cases present in the local population leads individuals to limit the number of contacts they have with others, inducing a reduction in the rate of transmission of the infection. A global qualitative analysis is carried out, showing that the typical threshold behavior holds, with solutions either tending to an equilibrium without disease, or the system being persistent and solutions converging to an endemic equilibrium. Numerical analysis is employed to gain insight in both the analytically tractable and intractable cases; these simulations indicate that media coverage can reduce the burden of the epidemic and shorten the duration of the disease outbreak.

1. Introduction

The severe acute respiratory syndrome (SARS), which spread around the globe in 2003, was one of the first novel infectious diseases to emerge in the twenty-first century. It was not, as far as the magnitude of the event, a major epidemic: 8096 and 774 people are known to have been infected and killed by SARS, respectively. However, the amount of media coverage garnered by this event was colossal. For example, in Britain, a study found that 3 tabloids and 2 broadsheets ran a total of 1153 news stories mentioning SARS from March to July 2003 [27]; the New Zealand Herald ran 261 articles from March 13 to June 11, 2003 [28]. In fact, media coverage of health related events has become so important that several surveillance systems now rely on active trolling of Internet news media and blogs to detect emerging disease threats [8], [19].

The effect of media in infectious disease spread has long been under investigation, for example in the case of HIV/AIDS [17], [24]. Media coverage of an infectious outbreak can be seen as following two major routes. The first route is when the media report directly to the public on facts that they (the media) observe; the second has public health authorities using mass media or the Internet to communicate about the outbreak [1]. Because information is widely available and that it is difficult for public health authorities to arrange a permanent flow of information, it is frequent that during a crisis, the media try to create ‘value’ from very sparse information, thus following the first route rather than the second. This can be detrimental. For example, a study conducted after the SARS outbreak shows that students from Ontario, Canada were aware that the risk of becoming infected by the SARS coronavirus was low, but they also predominantly had misconceptions about the virus [5]. It is therefore important for public health authorities to communicate accurate and timely information to the public about infectious disease outbreaks. Communication is also extremely important in determining vaccine uptake [13], [21], [22].

Because it gives a sense about the risk level and the relative need for precautions in risk areas, media coverage about an epidemic can encourage the public to take precautionary measures against the disease such as wearing masks, avoiding public places, avoiding travel when sick, frequent hand washing, etc. [6]. This in turn reduces the frequency of potentially infecting contacts and helps lower the probability of disease transmission among the well-informed population. This is extremely important in the early stages of an epidemic, when pharmaceutical interventions are not often possible because treatment or vaccination options have not yet been developed.

In view of the discussion above, it is not surprising that a communication aspect was included in the pandemic influenza plans of many countries. At the international level, the WHO guidance document [23] breaks down the actions to be taken when in Influenza Phases 5–6 into five categories: Planning and coordination, Situation monitoring and assessment, Reducing the spread of disease, Continuity of health care and provision and Communications. In the Reducing the spread of disease category, many actions to be taken at the national level require the use of media. More significantly, the Communications category discusses actions to circulate information between national public health authorities but also with the public. The WHO must ‘Update national authorities, other partners and stakeholders, and the public on global situation, trends, epidemiological characteristics, and recommended measures’, while member nations must ‘Regularly update the public on what is known and unknown about the pandemic disease, including transmission patterns, clinical severity, treatment, and prophylaxis options’, ‘Provide regular communications to address societal concerns, such as the disruption to travel, border closures, schools, or the economy or society in general’ and ‘Regularly update the public on sources of emergency medical care, resources for dealing with urgent non-pandemic health care needs, and resources for self-care of medical conditions’.

The use of media in the context of an infectious disease outbreak is therefore well accepted. However, the precise functioning of media coverage of epidemics is not well understood. Mathematical modeling can therefore play an important role in helping understand the potential effects of media coverage on infectious disease transmission.

Several modeling articles address this problem. Xiao and Ruan [29] formulated an SIR (susceptible, infectious and recovered) model and proposed a non-linear incidence rate

$$g(I)S=\frac{\mathit{kSI}}{1+\alpha I^2}\text{,}$$ (1.1)

to describe the effect of mass media coverage. They showed that in this case, media coverage did not have any obvious effect on disease dynamics. Liu et al. [18] emphasized media impact in an EIH model, where H denotes hospitalized individuals, and assumed a transmission coefficient of the form

$${\beta }_0=\beta e^{-{\alpha }_{1}E-{\alpha }_{2}I-{\alpha }_{3}H}\text{.}$$ (1.2)

Possible multiple outbreaks and even sustained periodic oscillations of the infection were found. Zhu et al. [10] used a similar function as (1.2) and studied an SIR model. Numerical simulations in [10] suggested that the media impact was stronger when the basic reproduction number ${\mathcal{R}}_0>1$, and the model exhibited multiple endemic equilibria. Cui et al. [11] presented an SIS epidemic model incorporating media coverage and held the contact rate to be a function of the number of infectives in the population of the form

$$c(I)=c_1-c_{2}f(I)\text{.}$$ (1.3)

They observed a classic threshold-type behavior, with the disease becoming extinct when ${\mathcal{R}}_0<1$ and going to a globally asymptotically stable equilibrium when ${\mathcal{R}}_0>1$. They concluded that media coverage was critical in disease eradication.

All the mathematical models referenced above assume that space is homogeneous and investigations are confined to a population. However, infectious diseases spread geographically over time. For example, West Nile virus arrived in New York in the late 1990s and later on spread all the way to the west coast of North America. People also travel more frequently, which no doubt speeds up disease transmission through transportation. Two illustrations are SARS spreading from China to the rest of the world in 2002–2003 and Swine Flu (pH1N1) from Mexico to other countries in the world in 2009 [16]. Therefore, incorporating spatial heterogeneity in epidemic models is important (see, e.g. [2], [3], [4] and the references therein). The question we ask here is the following: does the addition of space perturb the results previously obtained? In the case of classical epidemic models, it is generally true that the addition of space by means of linearly interconnected patches does not lead to a change of behavior. However, restricting contacts when the incidence rises introduces effects that could lead to differences with the classical cases. We show here that such is not the case and that, at least in the model considered, which is a modification of [11], the addition of space is inconsequential as far as the dynamics is concerned.

2. Model formulation

We consider two patches connected by population movement. The population in each patch is divided into two compartments, depending on the epidemiological status of individuals: susceptible to $(S)$ or infectious with $(I)$ the disease. Infectious individuals become susceptible again as soon as they recover from the disease, with no immune period. Each patch is thus equipped with an SIS epidemic model, where the only difference with classic SIS models on several patches [2] lies in the nature of the incidence function used.

In the absence of media effect, we assume a classic standard (or proportional) incidence, with the rate at which new infections arise in patch i given by ${\beta }_i{S}_i{I}_i/N_i\text{,}{\beta }_i$ being the infection coefficient in patch i. When media coverage is present, social distancing mechanisms come into effect. The reporting by media is assumed to be an increasing function of the number of infectious cases present in a patch, and as a consequence, the contact rate between susceptible and infectious individuals there is a decreasing function of the number of infectious cases present. We take similar non-linear functions as in [11] and denote the effective contact rate as

$${\beta }_i(I_i)=a_i-b_i{f}_i(I_i)\text{,}$$ (2.1)

where $a_i$ is the maximal effective contact rate between the susceptibles and infectives in patch i and $b_i$ is the maximal reduced effective contact rate due to mass media alert in the presence of infectives. We here assume that $a_i⩾b_i$ and

$$f_i(0)=0\text{,}\underset{I_i\to \infty }{\lim }{f}_i(I_i)=1\text{,}0<f_i^{\prime }(I_i)⩽1\text{,}{f}_i^{″}(I_i)<0\text{.}$$ (2.2)

The basic SIS metapopulation system under consideration is then

$$\frac{{\mathit{dS}}_1}{\mathit{dt}}={\Lambda }_1-{\beta }_1(I_1)\frac{S_1{I}_1}{S_1+I_1}+{\gamma }_1{I}_1-d_1{S}_1-m_{12}{S}_1+m_{21}{S}_2\text{,}$$ (2.3a)

$$\frac{{\mathit{dI}}_1}{\mathit{dt}}={\beta }_1(I_1)\frac{S_1{I}_1}{S_1+I_1}-({\gamma }_1+d_1)I_1-m_{12}{I}_1+m_{21}{I}_2\text{,}$$ (2.3b)

$$\frac{{\mathit{dS}}_2}{\mathit{dt}}={\Lambda }_2-{\beta }_2(I_2)\frac{S_2{I}_2}{S_2+I_2}+{\gamma }_2{I}_2-d_2{S}_2+m_{12}{S}_1-m_{21}{S}_2\text{,}$$ (2.3c)

$$\frac{{\mathit{dI}}_2}{\mathit{dt}}={\beta }_2(I_2)\frac{S_2{I}_2}{S_2+I_2}-({\gamma }_2+d_2)I_2+m_{12}{I}_1-m_{21}{I}_2\text{,}$$ (2.3d)

under initial conditions

$$S_1(0)+S_2(0)>0\text{,}{I}_1(0)\text{,}{I}_2(0)⩾0\text{,}{I}_1(0)+I_2(0)>0\text{.}$$ (2.4)

In system (2.3a), (2.3b), (2.3c), (2.3d), ${\Lambda }_i$ is the (constant) recruitment into patch $i=1\text{,}2$. The parameter $m_{\mathit{ij}}(i\text{,}j=1\text{,}2\text{,}i\ne j)$ is the travel rate from patch i to patch j; here we assume that the travel rates for susceptible and infective individuals are the same, i.e., the disease is not severe enough to impede travel. ${\gamma }_i$ is the individuals’ rate of recovery due to natural causes or treatment, and $d_i$ is the natural death rate. Because most diseases that fit within the framework of an SIS model are benign, we ignore disease-caused death. The population in patch i is denoted by $N_i=S_i+I_i$ and the total population is $N=N_1+N_2$.

3. Mathematical analysis

3.1. Basic results

Model (2.3a), (2.3b), (2.3c), (2.3d) is well posed, as established by the following theorem.

Theorem 3.1

Consider system (2.3a), (2.3b), (2.3c), (2.3d) with initial conditions (2.4). The positive orthant ${\mathbb{R}}_{+}^4$ is invariant under the flow of (2.3a), (2.3b), (2.3c), (2.3d), with $S_i(i=1\text{,}2)$ remaining positive. The total population within each patch converges to a steady state as $t\to \infty$ and solutions are bounded.

Proof

Under initial conditions (2.4), if for instance $I_1$ becomes zero at some time $t_1$ before $I_2$ becomes zero, then from (2.3b), ${\mathit{dI}}_1/\mathit{dt}=m_{21}{I}_2⩾0$ at $t_1$, which shows that $I_1$ is a non-decreasing function of t at $t_1$. Hence, $I_1$ stays non-negative. Similarly, so does $I_2$. Suppose now that at some time $t_2\text{,}{S}_1(t_2)=0$ before $S_2$ goes to zero. Then at $t=t_2$, from (2.3a), (2.3b), (2.3c), (2.3d), ${\mathit{dS}}_1/\mathit{dt}={\Lambda }_1+m_{21}{S}_2+{\gamma }_1{I}_1>0$, which implies that ${\mathit{dS}}_1/\mathit{dt}>0$ when $S_1$ is positive and small. Thus, there is no time $t_2$ such that $S_1(t_2)=0$. Therefore, $S_1$ stays positive for $t>0$ when the initial condition $S_1(0)>0$. By a similar argument, we obtain the positivity of $S_2$.

From system (2.3a), (2.3b), (2.3c), (2.3d), the differential equations governing the evolution of $N_1$ and $N_2$ are

$$\frac{{\mathit{dN}}_1}{\mathit{dt}}={\Lambda }_1-(m_{12}+d_1)N_1+m_{21}{N}_2\text{,}$$ (3.1a)

$$\frac{{\mathit{dN}}_2}{\mathit{dt}}={\Lambda }_2+m_{12}{N}_1-(m_{21}+d_2)N_2\text{.}$$ (3.1b)

A simple calculation shows that the positive equilibrium $(N_1^{\ast }\text{,}{N}_2^{\ast })$ is the unique equilibrium of (3.1a), (3.1b) and is a stable node, with

$$N_1^{\ast }=\frac{{\Lambda }_1(d_2+m_{21})+{\Lambda }_2{m}_{21}}{m_{12}{d}_2+m_{21}{d}_1+d_1{d}_2}\text{,}$$ (3.2a)

$$N_2^{\ast }=\frac{{\Lambda }_2(d_1+m_{12})+{\Lambda }_1{m}_{12}}{m_{12}{d}_2+m_{21}{d}_1+d_1{d}_2}\text{.}$$ (3.2b)

Since the positive orthant ${\mathbb{R}}_{+}^{\mathbb{4}}$ is invariant under (2.3a), (2.3b), (2.3c), (2.3d) and that the total population is bounded, the individual components are also bounded. □

3.2. Local properties of the disease-free equilibrium

Setting the right-hand side of system (2.3a), (2.3b), (2.3c), (2.3d) to zero, there always exists the disease-free equilibrium $E^0≔(I_{10}\text{,}{I}_{20}\text{,}{S}_{10}\text{,}{S}_{20})=(0\text{,}0\text{,}{N}_1^{\ast }\text{,}{N}_2^{\ast })$. Following the next generation matrix method [12], [26] for deterministic compartmental models, we calculate the basic reproduction number ${\mathcal{R}}_0$ at $E^0$. Using the same notations as in [26], we write

$$\mathcal{F}=\left(\begin{array}{c}\hfill (a_1-b_1{f}_1(I_1))\frac{S_1{I}_1}{(S_1+I_1)}\hfill \\ \hfill (a_2-b_2{f}_2(I_2))\frac{S_2{I}_2}{(S_2+I_2)}\hfill \end{array}\right)\text{,}\mathcal{V}=\left(\begin{array}{c}\hfill (m_{12}+{\gamma }_1+d_1)I_1-m_{21}{I}_2\hfill \\ \hfill -m_{12}{I}_1+(m_{21}+{\gamma }_2+d_2)I_2\hfill \end{array}\right)\text{.}$$

Taking the Fréchet derivatives of $\mathcal{F}$ and $\mathcal{V}$ and evaluating them at the disease free equilibrium, we find

$$F=\left(\begin{array}{cc}\hfill a_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill a_2\hfill \end{array}\right)\text{,}V=\left(\begin{array}{cc}\hfill m_{12}+{\gamma }_1+d_1\hfill & \hfill -m_{21}\hfill \\ \hfill -m_{12}\hfill & \hfill m_{21}+{\gamma }_2+d_2\hfill \end{array}\right)\text{,}$$

where F is non-negative and V is a non-singular M-matrix. Denote $\mathrm{\Delta }≔(m_{12}+{\gamma }_1+d_1)(m_{21}+{\gamma }_2+d_2)-m_{12}{m}_{21}$. Then

$${\mathit{FV}}^{-1}=\frac{1}{\mathrm{\Delta }}\left(\begin{array}{cc}\hfill a_1(m_{21}+{\gamma }_2+d_2)\hfill & \hfill a_1{m}_{21}\hfill \\ \hfill a_2{m}_{12}\hfill & \hfill a_2(m_{12}+{\gamma }_1+d_1)\hfill \end{array}\right)\text{.}$$

Therefore, ${\mathit{FV}}^{-1}$ is non-negative and

$${\mathcal{R}}_0≔\rho ({\mathit{FV}}^{-1})\text{,}$$

where $\rho (X)$ is the spectral radius of matrix X. Note that media coverage does not play a role in the basic reproduction number since ${\beta }_i(0)=a_i$. From [26, Theorem 2], we then have the following.

Lemma 3.1

The disease-free equilibrium $E^0$ of (2.3a), (2.3b), (2.3c), (2.3d) is locally asymptotically stable if ${\mathcal{R}}_0<1$ and unstable if ${\mathcal{R}}_0>1$ .

3.3. Global dynamics

In fact, the threshold behavior established in Lemma 3.1 is sharp and distinguishes between the global stability of the disease-free equilibrium and of a unique endemic equilibrium. To show this, we start by considering the global stability of the disease-free equilibrium when ${\mathcal{R}}_0<1$.

Theorem 3.2

The disease-free equilibrium $E^0$ of (2.3a), (2.3b), (2.3c), (2.3d) is globally asymptotically stable if ${\mathcal{R}}_0<1$ .

Proof

Since for $i=1\text{,}2\text{,}{S}_i/(S_i+I_i)⩽1$ and ${\beta }_i(I_i)⩽a_i$, ((2.3b), (2.3d)) satisfy

$$\frac{{\mathit{dI}}_1}{\mathit{dt}}⩽[a_1-(m_{12}+{\gamma }_1+d_1)]I_1+m_{21}{I}_2\text{,}$$ (3.3a)

$$\frac{{\mathit{dI}}_2}{\mathit{dt}}⩽m_{12}{I}_1+[a_2-(m_{21}+{\gamma }_2+d_2)]I_2\text{.}$$ (3.3b)

Define an auxiliary linear system using the right hand side of (3.3a), (3.3b):

$$\frac{d{\overline{I}}_1}{\mathit{dt}}=[a_1-(m_{12}+{\gamma }_1+d_1)]{\overline{I}}_1+m_{21}{\overline{I}}_2\text{,}$$

$$\frac{d{\overline{I}}_2}{\mathit{dt}}=m_{12}{\overline{I}}_1+[a_2-(m_{21}+{\gamma }_2+d_2)]{\overline{I}}_2\text{,}$$

or, in other words,

$$\frac{d}{\mathit{dt}}\left(\begin{array}{c}\hfill {\overline{I}}_1\hfill \\ \hfill {\overline{I}}_2\hfill \end{array}\right)=(F-V)\left(\begin{array}{c}\hfill {\overline{I}}_1\hfill \\ \hfill {\overline{I}}_2\hfill \end{array}.\right)$$ (3.4)

We have ${\mathcal{R}}_0<1\iff \sigma (F-V)<0$, where $\sigma (X)$ is the stability modulus (or spectral abscissa) of matrix X (see the proof of [26, Theorem 2]). So, when ${\mathcal{R}}_0<1$, both eigenvalues of $F-V$ are with negative real parts. Thus all non-negative solutions of (3.4) are such that ${\lim }_{t\to \infty }{\overline{I}}_i=0\text{,}i=1\text{,}2$. By a standard comparison principle [25, Theorem B.1] and the non-negativity of $I_i$, we conclude that when ${\mathcal{R}}_0<1$, all non-negative solutions of (2.3a), (2.3b), (2.3c), (2.3d) satisfy ${\lim }_{t\to \infty }{I}_i=0\text{,}i=1\text{,}2$.

Since $I_i$ tends to zero as $t\to \infty$, (2.3a), (2.3b), (2.3c), (2.3d) is an asymptotically autonomous system [9, Theorem 2.5] with limit affine system

$$\frac{{\mathit{dS}}_1}{\mathit{dt}}={\Lambda }_1-(m_{12}+d_1)S_1+m_{21}{S}_2\text{,}$$ (3.5a)

$$\frac{{\mathit{dS}}_2}{\mathit{dt}}={\Lambda }_2+m_{12}{S}_1-(m_{21}+d_2)S_2\text{.}$$ (3.5b)

It is known from (3.1a), (3.1b) that the positive equilibrium $(N_1^{\ast }\text{,}{N}_2^{\ast })$ of (3.5a), (3.5b) is (globally) asymptotically stable. The proof is complete. □

Following the proof of Theorem 3.2, when ${\mathcal{R}}_0<1$, there does not exist any endemic equilibrium. We now turn to the case where ${\mathcal{R}}_0>1$. We first establish the uniform persistence for (2.3a), (2.3b), (2.3c), (2.3d) when ${\mathcal{R}}_0>1$, by applying the following result of Zhao [30].

Lemma 3.2 [30] —

Let ${\varphi }_t:X\to X$ be a semiflow and $X_0\subset X$ an open set. Define $\partial X_0=X⧹X_0$ , and $M_{\partial }=\{x\in \partial X_0:{\varphi }_{t}x\in \partial X_0\text{,}t⩾0\}$ . Assume that

• $({\mathbf{C}}_1)$ ${\varphi }_t{X}_0\subset X_0$ and ${\varphi }_t$ has a global attractor A;
• $({\mathbf{C}}_2)$
  there exists a finite sequence $\mathcal{M}=\{M_1\text{,}\dots \text{,}{M}_k\}$ of disjoint, compact, and isolated invariant sets in $\partial X_0$ such that

  • (a)
    $\Omega (M_{\partial })≔{\cup }_{x\in M_{\partial }}\omega (x)\subset {\cup }_{i=1}^k{M}_i$ ;
  • (b)
    no subset of $\mathcal{M}$ forms a cycle in $\partial X_0$ ;
  • (c)
    $M_i$ is isolated in X;
  • (d)
    $W^s(M_i)\cap X_0=\varnothing$ , where $W^s(M_i)=\{x\in X_0:\omega (x)\subset M_i\}$ , for each $1⩽i⩽k$ .

Then ${\varphi }_t$ is uniformly persistent with respect to $(X_0\text{,}\partial X_0)$ , i.e., there exists $\eta >0$ , such that ${\mathrm{liminf}}_{t\to +\infty }d({\varphi }_{t}x\text{,}\partial X_0)⩾\eta$ for $x\in X_0$ .

Theorem 3.3

If ${\mathcal{R}}_0>1$ , then system (2.3a), (2.3b), (2.3c), (2.3d) is uniformly persistent, namely, there exists $\eta >0$ , such that $\underset{t\to \infty }{\mathrm{liminf}}\{S_i(t)\text{,}{I}_i(t)\}⩾\eta$ for initial conditions $S_i(0)\text{,}{I}_i(0)>0(i=1\text{,}2)$ .

Proof

Choose $X={\mathbb{R}}_{+}^4\text{,}{X}_0=\{(I_1\text{,}{I}_2\text{,}{S}_1\text{,}{S}_2)\in X\text{,}{I}_1+I_2>0\}$, and $\partial X_0=X⧹X_0=\{(I_1\text{,}{I}_2\text{,}{S}_1\text{,}{S}_2)\in X\text{,}{I}_1=I_2=0\}\text{.}$ Let ${\varphi }_t$ be the semiflow induced by the solutions of system (2.3a), (2.3b), (2.3c), (2.3d). We have proved in Theorem 3.1 that ${\varphi }_t{X}_0\subset X_0$ and ${\varphi }_t$ is ultimately bounded in $X_0$; so there always exists a global attractor for ${\varphi }_t$. It is obvious that $E^0$ is the unique boundary equilibrium on $\partial X_0$, which implies that $E^0$ is globally stable on $\partial X_0$. Moreover, $(S_1\text{,}{S}_2)$ converges to $(N_1^{\ast }\text{,}{N}_2^{\ast })$ on $\partial X_0$. Let $M_1=\{E^0\}$ and $\mathcal{M}=\{M_1\}$. Then ${\cup }_{x\in M_{\partial }}\omega (x)=M_1$ and no subset of $\mathcal{M}$ forms a cycle in $\partial X_0$. If ${\mathcal{R}}_0>1$, then $E^0$ is unstable in $X_0$. Therefore, conditions (c) and (d) are satisfied and the proof is complete. □

We have thus shown that if ${\mathcal{R}}_0>1$ then the disease is endemic. We now use another result of Zhao [30] to show that endemicity is in fact at an equilibrium level.

Lemma 3.3 [30] —

Let ${\varphi }_t:X\to X\text{,}t⩾0$ , be an autonomous semiflow with ${\varphi }_t{X}_0\subset X_0$ for all $t⩾0$ . Assume that

• (1) ${\varphi }_t:X\to X$ is point dissipative;
• (2) ${\varphi }_t$ is compact for each $t>0$ ; or alternatively, ${\varphi }_t$ is an $\alpha$ -contraction with its contracting function $k(t)\in [0\text{,}1)\text{,}\forall t>0$ , and ${\gamma }^{+}(U)$ is strongly bounded in $X_0$ if $X_0$ is strongly bounded in $X_0$ ;
• (3) ${\varphi }_t$ is uniformly persistent with respect to $(X_0\text{,}\partial X_0)$ .

Then there exists a global attractor $A_0$ for ${\varphi }_t$ in $X_0$ that attracts strongly bounded sets in $X_0$ , and ${\varphi }_t$ has a stationary coexistence state $x_0$ in $A_0$ , $i.e.\text{,}{x}_0\in X_0$ and ${\varphi }_t{x}_0=x_0$ for all $t⩾0$ .

A continuous mapping $f:X\to X$ is point dissipative if there is a bounded set $B_0$ in X such that $B_0$ attracts each point in X. Thus the semiflow ${\varphi }_t$ we choose above is point dissipative, all the solutions are ultimately bounded in $X_0$, which also implies the satisfaction of condition (2) in Lemma 3.3. Therefore, we have the following result.

Theorem 3.4

If ${\mathcal{R}}_0>1$ , then (2.3a), (2.3b), (2.3c), (2.3d) has at least one endemic equilibrium.

Next, we consider the uniqueness of the endemic equilibrium. Note that system (2.3a), (2.3b), (2.3c), (2.3d) can be rewritten as follows.

$$\frac{{\mathit{dI}}_1}{\mathit{dt}}=(a_1-b_1{f}_1(I_1))\frac{(N_1-I_1)I_1}{N_1}+m_{21}{I}_2-m_{12}{I}_1-({\gamma }_1+d_1)I_1\text{,}$$ (3.6a)

$$\frac{{\mathit{dN}}_1}{\mathit{dt}}={\Lambda }_1-(m_{12}+d_1)N_1+m_{21}{N}_2\text{,}$$ (3.6b)

$$\frac{{\mathit{dI}}_2}{\mathit{dt}}=(a_2-b_2{f}_2(I_2))\frac{(N_2-I_2)I_2}{N_2}-m_{21}{I}_2+m_{12}{I}_1-({\gamma }_2+d_2)I_2\text{,}$$ (3.6c)

$$\frac{{\mathit{dN}}_2}{\mathit{dt}}={\Lambda }_2+m_{12}{N}_1-(m_{21}+d_2)N_2\text{,}$$ (3.6d)

For subsystem ((3.6b), (3.6d)), the unique positive equilibrium $(N_1^{\ast }\text{,}{N}_2^{\ast })$ is asymptotically stable, from the discussion in the proof of Theorem 3.1. Substituting $N_i^{\ast }(i=1\text{,}2)$ into the asymptotically autonomous planar system ((3.6a), (3.6c)) gives the limit system

$$\frac{{\mathit{dI}}_1}{\mathit{dt}}=(a_1-b_1{f}_1(I_1))\frac{(N_1^{\ast }-I_1)I_1}{N_1^{\ast }}+m_{21}{I}_2-m_{12}{I}_1-({\gamma }_1+d_1)I_1≕P(I_1\text{,}{I}_2)\text{,}$$ (3.7a)

$$\frac{{\mathit{dI}}_2}{\mathit{dt}}=(a_2-b_2{f}_2(I_2))\frac{(N_2^{\ast }-I_2)I_2}{N_2^{\ast }}-m_{21}{I}_2+m_{12}{I}_1-({\gamma }_2+d_2)I_2≕Q(I_1\text{,}{I}_2)\text{.}$$ (3.7b)

In the limit system (3.7a), (3.7b), we have $I_1<N_1^{\ast }$ and $I_2<N_2^{\ast }$. Indeed, from Theorem 3.1, for $i=1\text{,}2$ we have ${\lim }_{t\to \infty }{S}_i(t)+I_i(t)=N_i^{\ast }$ and $S_i(t)>0$ for all $t>0$; therefore, there exists $\tau ⩾0$ such that $I_i(t)<N_i^{\ast }$ for all $t⩾\tau$ and this is true in particular for (3.7a), (3.7b).

Theorem 3.5

If ${\mathcal{R}}_0>1$ , (3.6a), (3.6b), (3.6c), (3.6d) has a unique endemic equilibrium $E^{\ast }(I_1^{\ast }\text{,}{I}_2^{\ast }\text{,}{N}_1^{\ast }\text{,}{N}_2^{\ast })$ .

Proof

Suppose $E^{\ast }(I_1^{\ast }\text{,}{I}_2^{\ast })$ is the endemic equilibrium of (3.7a), (3.7b). Then $I_1^{\ast }\text{,}{I}_2^{\ast }$ are the positive solutions of the following equations:

$$I_2=\frac{1}{m_{21}}\left\{({\gamma }_1+d_1+m_{12})-(a_1-b_1{f}_1(I_1))\frac{N_1^{\ast }-I_1}{N_1^{\ast }}\right\}{I}_1≕g_1(I_1)\text{,}$$ (3.8a)

$$I_1=\frac{1}{m_{12}}\left\{({\gamma }_2+d_2+m_{21})-(a_2-b_2{f}_2(I_2))\frac{N_2^{\ast }-I_2}{N_2^{\ast }}\right\}{I}_2≕g_2(I_2)\text{.}$$ (3.8b)

Denote

$${\varphi }_1(I_1)≔({\gamma }_1+d_1+m_{12})-(a_1-b_1{f}_1(I_1))\frac{N_1^{\ast }-I_1}{N_1^{\ast }}\text{,}$$ (3.9a)

$${\varphi }_2(I_2)≔({\gamma }_2+d_2+m_{21})-(a_2-b_2{f}_2(I_2))\frac{N_2^{\ast }-I_2}{N_2^{\ast }}\text{.}$$ (3.9b)

The derivatives of ${\varphi }_1(I_1)$ and ${\varphi }_2(I_2)$ with respect to $I_1$ and $I_2$ are:

$$\frac{d{\varphi }_1(I_1)}{{\mathit{dI}}_1}=b_1{f}_1^{\prime }(I_1)\frac{N_1^{\ast }-I_1}{N_1^{\ast }}+\frac{a_1-b_1{f}_1(I_1)}{N_1^{\ast }}>0\text{,}$$ (3.10a)

$$\frac{d{\varphi }_2(I_2)}{{\mathit{dI}}_2}=b_2{f}_2^{\prime }(I_1)\frac{N_2^{\ast }-I_2}{N_2^{\ast }}+\frac{a_2-b_2{f}_2(I_2)}{N_2^{\ast }}>0\text{,}$$ (3.10b)

since $I_1<N_1^{\ast }$ and $I_2<N_2^{\ast }$ in system (3.7a), (3.7b).

Differentiating $g_1(I_1)$ and $g_2(I_2)$ with respect to $I_1$ and $I_2$, respectively, gives

$$\frac{{\mathit{dg}}_1(I_1)}{{\mathit{dI}}_1}=\frac{1}{m_{21}}\left[\frac{b_1(N_1^{\ast }-I_1)(f_1+I_1{f}_1^{\prime })}{N_1^{\ast }}+\frac{a_1{I}_1+I_1(a_1-b_1{f}_1)}{N_1^{\ast }}+{\gamma }_1+d_1+m_{12}-a_1\right]=\frac{1}{m_{21}}\left(\frac{d{\varphi }_1(I_1)}{{\mathit{dI}}_1}{I}_1+{\varphi }_1(I_1)\right)\text{,}$$

$$\frac{{\mathit{dg}}_2(I_2)}{{\mathit{dI}}_2}=\frac{1}{m_{12}}\left[\frac{b_2(N_2^{\ast }-I_2)(f_2+I_2{f}_2^{\prime })}{N_2^{\ast }}+\frac{a_2{I}_2+I_2(a_2-b_2{f}_2)}{N_2^{\ast }}+{\gamma }_2+d_2+m_{21}-a_2\right]=\frac{1}{m_{12}}\left(\frac{d{\varphi }_2(I_2)}{{\mathit{dI}}_2}{I}_2+{\varphi }_2(I_2)\right)\text{.}$$

Assume that system (3.7a), (3.7b) has multiple endemic equilibria when ${\mathcal{R}}_0>1$. Suppose that ${\overline{E}}^{\ast }=\left({\overline{I}}_1^{\ast }\text{,}{\overline{I}}_2^{\ast }\right)$ is the one with the smallest $I_1$ component, namely, if there is another equilibrium, say, ${\widehat{E}}^{\ast }=\left({\widehat{I}}_1^{\ast }\text{,}{\widehat{I}}_2^{\ast }\right)$, then ${\overline{I}}_1^{\ast }⩽{\widehat{I}}_1^{\ast }$. It follows from (3.9a), (3.9b) that ${\varphi }_1\left({\overline{I}}_1^{\ast }\right)\text{,}{\varphi }_2\left({\overline{I}}_2^{\ast }\right)>0$. Moreover, ${\varphi }_1(I_1)>0$ and $\frac{{\mathit{dg}}_1(I_1)}{{\mathit{dI}}_1}>0$, if ${\overline{I}}_1^{\ast }⩽I_1⩽N_1^{\ast }$. Then there is no such equilibrium as $\left({\widehat{I}}_1^{\ast }\text{,}{\widehat{I}}_2^{\ast }\right)$, such that ${\widehat{I}}_1^{\ast }>{\overline{I}}_1^{\ast }$ and ${\widehat{I}}_2^{\ast }<{\overline{I}}_2^{\ast }$, namely, if ${\widehat{I}}_1^{\ast }>{\overline{I}}_1^{\ast }$, then ${\widehat{I}}_2^{\ast }>{\overline{I}}_2^{\ast }$. Therefore, ${\varphi }_2(I_2)>0$ and $\frac{{\mathit{dg}}_2(I_2)}{{\mathit{dI}}_2}>0$, if ${\overline{I}}_2^{\ast }⩽I_2⩽N_2^{\ast }$. Thus, the following inequality holds.

$$\frac{{\mathit{dg}}_1(I_1)}{{\mathit{dI}}_1}\frac{{\mathit{dg}}_2(I_2)}{{\mathit{dI}}_2}=\frac{1}{m_{21}}\left(\frac{d{\varphi }_1(I_1)}{{\mathit{dI}}_1}{I}_1+{\varphi }_1(I_1)\right)\frac{1}{m_{12}}\left(\frac{d{\varphi }_2(I_2)}{{\mathit{dI}}_2}{I}_2+{\varphi }_2(I_2)\right)>\frac{1}{m_{12}{m}_{21}}{\varphi }_1(I_1){\varphi }_2(I_2)⩾\frac{1}{m_{12}{m}_{21}}{\varphi }_1\left({\overline{I}}_1^{\ast }\right){\varphi }_2\left({\overline{I}}_2^{\ast }\right)\text{.}$$ (3.11)

From (3.8a), (3.8b),

$${\overline{I}}_2^{\ast }={\varphi }_1\left({\overline{I}}_1^{\ast }\right){\overline{I}}_1^{\ast }/m_{21}\text{,}{\overline{I}}_1^{\ast }={\varphi }_2\left({\overline{I}}_2^{\ast }\right){\overline{I}}_2^{\ast }/m_{12}\text{.}$$ (3.12)

Substituting (3.12) into (3.11) gives

$$\frac{{\mathit{dg}}_1(I_1)}{{\mathit{dI}}_1}\frac{{\mathit{dg}}_2(I_2)}{{\mathit{dI}}_2}>1\text{.}$$

Therefore, since $\frac{{\mathit{dg}}_1(I_1)}{{\mathit{dI}}_1}>1\left./\left(\frac{{\mathit{dg}}_2(I_2)}{{\mathit{dI}}_2}\right)\right)$, starting from the point ${\overline{E}}_{\ast }$, the curve determined by $I_2=g_1(I_1)$ is always above the curve determined by $I_1=g_2(I_2)$. So, in the $I_1-I_2$ plane, the two curves can only intersect once at ${\overline{E}}^{\ast }$ in the interval $\{I_1|0<I_1<N_1^{\ast }\}$. This implies that (3.6a), (3.6b), (3.6c), (3.6d) has a unique endemic equilibrium $E^{\ast }$.

To show that the unique endemic equilibrium in fact is globally asymptotically stable, we need first show that there are no closed orbits for (3.7a), (3.7b). To do this, take as Dulac function the function $D=1/(I_1{I}_2)$. Then

$$\frac{\partial (\mathit{DP})}{\partial I_1}(I_1\text{,}{I}_2)=-b_1{f}_1^{\prime }(I_1)\frac{N_1^{\ast }-I_1}{N_1^{\ast }{I}_2}-(a_1-b_1{f}_1(I_1))\frac{1}{N_1^{\ast }{I}_2}-\frac{m_{21}}{I_1^2}\text{,}$$

$$\frac{\partial (\mathit{DQ})}{\partial I_2}(I_1\text{,}{I}_2)=-b_2{f}_2^{\prime }(I_2)\frac{N_2^{\ast }-I_2}{N_2^{\ast }{I}_1}-(a_2-b_2{f}_2(I_2))\frac{1}{N_2^{\ast }{I}_1}-\frac{m_{12}}{I_2^2}\text{,}$$

Under the assumption $a_i>b_i$ and the properties of $f_i$ in (2.2), it follows that

$$\frac{\partial (\mathit{DP})}{\partial I_1}(I_1\text{,}{I}_2)+\frac{\partial (\mathit{DQ})}{\partial I_2}(I_1\text{,}{I}_2)<0\text{.}$$

From the Bendixson–Dulac criterion [20], we have the result.

Theorem 3.6

System (3.7a), (3.7b) does not admit any cycle in the positively invariant region $\Gamma ≔\{(I_1\text{,}{I}_2)|0<I_i⩽N_i^{\ast }\text{,}i=1\text{,}2\}$ .

Note that this result holds true throughout parameter space under the assumptions on the media coverage effect function.

Theorem 3.7

If ${\mathcal{R}}_0>1$ , then the unique endemic equilibrium of (3.6a), (3.6b), (3.6c), (3.6d) is globally asymptotically stable.

Proof

When ${\mathcal{R}}_0>1$, by Lemma 3.1, $E^0$ is a hyperbolic unstable saddle point or a node and repels solutions in its neighborhood. Due to the hyperbolicity of $E^0$, it is not part of any cycle chain in $\Gamma$. Following Theorem 3.6, and also by Castillo-Chavez and Thieme [9], every bounded forward orbit of (3.7a), (3.7b) in $\Gamma$ converges towards $(I_1^{\ast }\text{,}{I}_2^{\ast })$, which is globally asymptotically stable. Therefore, the unique endemic equilibrium $E^{\ast }$ of (3.6a), (3.6b), (3.6c), (3.6d) is globally asymptotically stable. The proof is complete. □

Since systems (2.3a), (2.3b), (2.3c), (2.3d) and (3.6a), (3.6b), (3.6c), (3.6d) are equivalent, Theorems Theorem 3.2, Theorem 3.5, Theorem 3.7 yield the following result, which completely characterizes the dynamics of system (2.3a), (2.3b), (2.3c), (2.3d).

Theorem 3.8

If ${\mathcal{R}}_0<1$, then all solutions to (2.3a), (2.3b), (2.3c), (2.3d) with initial conditions (2.4) tend to the disease-free equilibrium. If ${\mathcal{R}}_0>1$, then (2.3a), (2.3b), (2.3c), (2.3d) has the unique globally asymptotically stable endemic equilibrium $E^{\ast }$.

4. Simulation study

To complement the mathematical analysis carried out in the previous section, we now investigate some of the numerical properties of system (2.3a), (2.3b), (2.3c), (2.3d). We choose parameters characteristic of the common cold, as detailed in Table 1 .

Table 1.

Parameter values used in simulations.

Parameter	Value or range	Unit	Interpretation
$N_1^{\ast }$	95,000	Individuals	Population size in patch 1
$N_2^{\ast }$	105,000	Individuals	Population size in patch 2
$m_{12}$	0.008	${\text{Day}}^{-1}$	Travel rate from patch 1 to patch 2
$m_{21}$	0.009	${\text{Day}}^{-1}$	Travel rate from patch 2 to patch 1
$d_1$	$1/(78\times 365)$	${\text{Day}}^{-1}$	Average life expectancy in patch 1 is 78 years
$d_2$	$1/(70\times 365)$	${\text{Day}}^{-1}$	Average life expectancy in patch 2 is 70 years
${\gamma }_1$	1/10	${\text{Day}}^{-1}$	Average infectious period 10 days
${\gamma }_2$	1/12	${\text{Day}}^{-1}$	Average infectious period 12 days
$a_1$	0.09 or 0.12	${\text{Day}}^{-1}$	Maximal effective contact rate in patch 1
$a_2$	0.08 or 0.11	${\text{Day}}^{-1}$	Maximal effective contact rate in patch 2
$b_1$	0.02 to 0.05	${\text{Day}}^{-1}$	Maximal reduced effective contact rate in patch 1
$b_2$	0.02 to 0.05	${\text{Day}}^{-1}$	Maximal reduced effective contact rate in patch 2

Note that in the simulations, the variables $N_i^{\ast }$ are considered as parameters and are set once and for all. The parameters ${\Lambda }_i\text{,}i=1\text{,}2$, are determined using (3.2a), (3.2b), i.e.,

$${\Lambda }_1=(m_{12}+d_1)N_1^{\ast }-m_{21}{N}_2^{\ast }$$

$${\Lambda }_2=-m_{12}{N}_1^{\ast }+(m_{21}+d_2)N_2^{\ast }\text{,}$$

in order to maintain constant populations. Carrying capacities (and other parameters) are chosen to be slightly different, in order to study the effect of varying parameters: a common problem in the numerical study of metapopulation systems stems from the use of equal parameters in the different patches, which tends to reduce or completely hide the effect of coupling [2]. Demographic and disease parameters are chosen to illustrate the situation that would prevail if the two patches had very different health systems: patch 1 is a wealthy nation or city, with higher mean life expectancy and better care for infectious individuals than patch 2. Here, we assume a non-fatal disease and therefore that ‘better care’ implies a shorter recovery time. In the case of diseases that cause mortality, it could be necessary to nuance this hypothesis for individuals with severe infections; for instance, influenza patients put under respirators can spend a long time before recovering, whereas patients in poorer settings with no access to respirators who would be subject to an influenza infection of similar severity, generally die.

Finally, we choose a very simple ‘media coverage function’: for $i=1\text{,}2$,

$$f(I_i)=\frac{I_i}{1+I_i}\text{.}$$

First, let us illustrate the situation that occurs about the endemic equilibrium. Fig. 1 shows the curves $g_1(I_1)$ and $g_2(I_2)$ defined by (3.8a), (3.8b). For parameter values corresponding to $\mathcal{R}<1$, as in Fig. 1, the only point of intersection between the curves is the origin, and there is no endemic equilibrium. When $\mathcal{R}>1$, as in Fig. 1, there is an additional point of intersection, the (unique) endemic equilibrium.

Fig. 1.

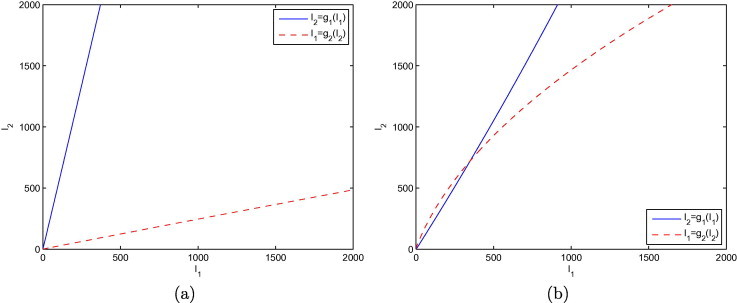
Illustration of the nature of the intersections in the $(I_1\text{,}{I}_2)$-plane of the curves $g_1(I_1)$ and $g_2(I_2)$ defined by (3.8a), (3.8b), when (a) ${\mathcal{R}}_0<1$ and (b) ${\mathcal{R}}_0>1$.

Next, we investigate in Fig. 2 the effect of media coverage on the time that it takes for an epidemic to go extinct, in the case where $\mathcal{R}<1$. Note that this is an hypothetical situation: when $\mathcal{R}<1$, there is no transient increase of the infected population, only a steady decrease to 0. Therefore, a situation such as the one shown in Fig. 2 implies that the situation would have had to change drastically before the beginning of simulations, with $\mathcal{R}$ brought from a value larger than 1 to a value smaller than 1. But if such were the case, it is clear from Fig. 2 that media coverage would lead to a large reduction in the time to extinction of the disease.

Fig. 2.

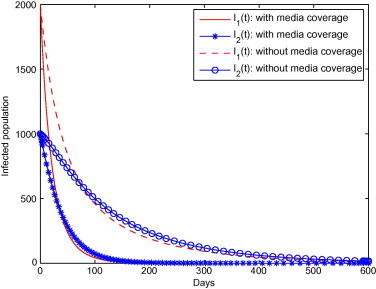
Effect of media coverage on the time to extinction of a pre-existing epidemic, when $\mathcal{R}<1$.

We now consider the effect of media coverage on the system. Fig. 3 shows the equilibrium values of $I_1^{\ast }$ and $I_2^{\ast }$ as the intensity of the effect of media coverage, $b_1$ and $b_2$, are varied, in a situation where $\mathcal{R}>1$. Recall from the derivation of $\mathcal{R}$ in Section 3.2 that $\mathcal{R}$ does not depend on the effect of media coverage. However, while increasing the intensity of the effect cannot bring $\mathcal{R}$ down to a value less than 1, it is clear from Fig. 3 that it can contribute to a considerable reduction of the burden of the disease. The curvature of the iso-infection curves differs between the patches; it is more pronounced for patch 2. This is a consequence of the different conditions that prevail in the patches.

Fig. 3.

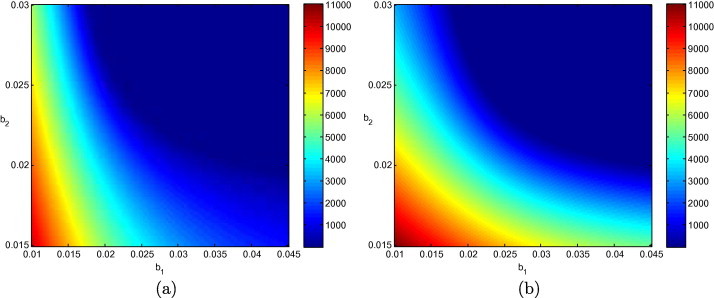
Equilibrium values of (a) $I_1^{\ast }$ and (b) $I_2^{\ast }$, as $b_1$ and $b_2$ are varied, with other parameters as in Table 1 such that $\mathcal{R}>1$.

In Fig. 4 , we show the value of $I_1^{\ast }$ at the endemic equilibrium, when $\mathcal{R}$ and the intensity of the effect of media coverage $b_1$ are varied. The variation of $\mathcal{R}$ is obtained by varying the value of $a_1$. The region to the left has positive values of $I_1^{\ast }$, but they are small and thus appear as zero because of the scale of the color bar. We see that there seems to exist a linear relationship between the value of $I_1^{\ast }$ and the values of $\mathcal{R}$ and $b_1$. For low values of $\mathcal{R}$, it is possible to greatly reduce the burden of disease in patch 1 by using media coverage. As $\mathcal{R}$ becomes larger, it becomes increasingly difficult to bring the infection down to the same type of values.

Fig. 4.

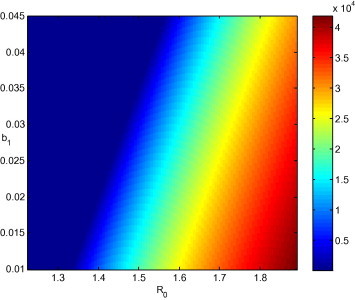
Equilibrium value of $I_1^{\ast }$ as a function of $\mathcal{R}$ and $b_1$, with other parameters as in Table 1 such that $\mathcal{R}>1$.

Finally, Fig. 5 presents a sensitivity analysis of the value of ${\mathcal{R}}_0$ to the variation of parameters. Parameters are made to vary in the following ranges: $m_{\mathit{ij}}\in [0.001\text{,}0.01]$, $d_i\in [1/90\text{,}1/45]$ (1/years), ${\gamma }_i\in [1/30\text{,}1/4]$ (1/days), $a_i\in [0.02\text{,}0.2]$ and $b_i\in [0.01\text{,}0.05]$. Sample points are chosen within this range using Latin hypercube sampling. Fig. 5 shows the range of values obtained for $\mathcal{R}$ when 10,000 such sample points are chosen. The red bar shows the median value of $\mathcal{R}$, the box indicates the interquartile range, while the whiskers show the extent of values not considered to be outlying. Outlying values are not shown here.

Fig. 5.

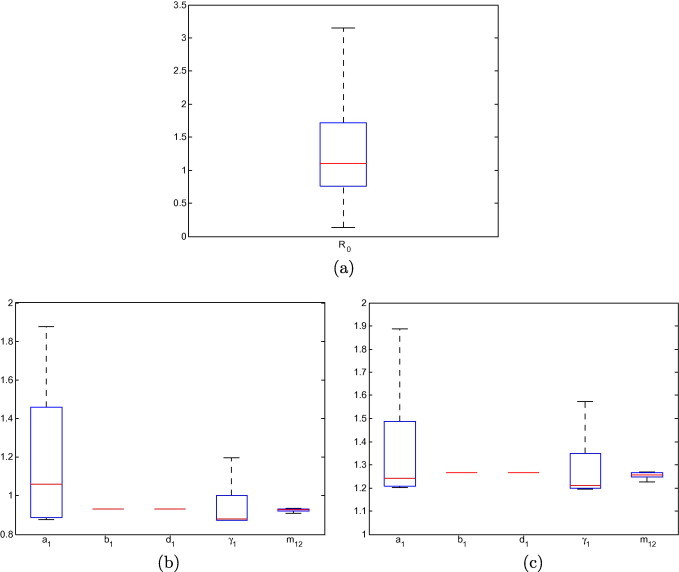
(a) Sensitivity of ${\mathcal{R}}_0$ to the variation of parameters, for 10,000 sample points in the parameter region indicated in the text. Sensitivity of ${\mathcal{R}}_0$ to the variation of individual parameters. In the absence of variation of any parameter, (b) $\mathcal{R}<1$ and (c) $\mathcal{R}>1$.

In Figs. 5(b) and (5c), the role of individual parameters is investigated. In order to do so, all parameter values are fixed to the values in Table 1, and each of $m_{12}\text{,}{d}_1\text{,}{\gamma }_1\text{,}{a}_1$ and $b_1$ is successively made to vary 10,000 times in the ranges indicated above.

5. Discussion

In this paper, we study an SIS model on two patches that takes into account a reduction of interpersonal contacts as a result of media coverage about the disease. Media coverage is described in patch $i=1\text{,}2$ by a general non-linear function $b_i{f}_i(I_i)$, which is assumed to be an increasing but saturating function of the number of infectious individuals present in a given patch; its effect is to reduce the contact rate between individuals. The global dynamics of the model is analyzed. It is found that when the basic reproduction number ${\mathcal{R}}_0<1$, system (2.3a), (2.3b), (2.3c), (2.3d) has only one disease free equilibrium point $E^0$, which is globally asymptotically stable. When ${\mathcal{R}}_0>1$, system (2.3a), (2.3b), (2.3c), (2.3d) is uniformly persistent, and in addition, there exists a unique globally asymptotically stable endemic equilibrium $E^{\ast }$.

Because media coverage is assumed to have no effect in the absence of disease and that the basic reproduction number is evaluated in the absence of disease, media coverage does not play a role in ${\mathcal{R}}_0$. This feature is of course also present in [11], from which our model is derived. Hence, changing the intensity of media coverage cannot be used to trigger the passage of $\mathcal{R}$ from values larger to values smaller than 1. Increasing the intensity of media coverage can however greatly reduce the number of infectious individuals at the endemic equilibrium in an endemic situation, i.e., if $\mathcal{R}>1$. On the other hand, if other means are used to bring $\mathcal{R}$ to values less than 1, then media coverage can help speed up the extinction of the epidemic.

This work is just a preliminary exploration of the consequences of media coverage on the spatial spread of an infectious disease, and there are many ways in which it could be improved. The first limitation of the system is that it uses a very simple SIS model, whereas a lot of the diseases that would be relevant are expected to follow an SEIRS-type progression. However, this distinction is not as important here as it would be should we have considered problems related to the control of the spread of the infection. In the latter case, the presence of a class of incubating individuals makes controlling the infection hard (since E individuals might travel undetected). In the case of media-induced social distancing, the presence of an E class simply delays the ‘birth’ of new infectives, so we expect similar results to the ones obtained here. The system should be studied with an arbitrary number of patches. It can be expected, though, that the global results we were able to establish here, in particular about the endemic equilibrium, will be hard to carry through to higher dimensionality. Also, while media coverage can help curtail an epidemic, it can also have negative consequences. The WHO guidance document [23] states, among the Communications actions to be taken in the event of a pandemic, that the WHO should ‘Continue to work with partners to promote consistent messages’. We have assumed in our model that communication is always beneficial in mitigating the spread of disease. However it is possible that some forms of messaging could be counterproductive from a public health standpoint (e.g. messages inciting fears over vaccine safety). Therefore, more elaborate forms of the ‘media coverage effect function’ should be considered. This would be a very interesting problem on many different levels: the interaction of patches with different media coverage effect functions, some decreasing, some increasing, would most likely pose difficult and interesting mathematical problems. There are additional temporal effects in social distancing that are important but not taken into consideration here. For example, [7] found that social distancing was generally well accepted, but only insofar as it did not have major economic consequences for the individuals involved. During the 2009 pandemic influenza outbreak, [14] found that after initially experiencing high anxiety about getting infected by the virus, individuals were becoming less and less concerned. There is, therefore, a waning of the effect at the individual level that could be taken into account. Finally, knowledge of the presence of a disease could also lead to modification of the rate of travel between locations. During the 2009 H1N1 pandemic, it was for instance observed [15] that air traffic to Mexico was affected in the early stages of the epidemic, although the effect on the overall global air transportation network was less evident. Work is in progress to incorporate such effects to our model.