Skip to main content
PMC home page
F1000Research logoLink to F1000Research
. 2020 Apr 27;9:Chem Inf Sci-113. Originally published 2020 Feb 13. [Version 2] doi: 10.12688/f1000research.22090.2

Machine learning meets pK a

Marcel Baltruschat 1, Paul Czodrowski 1,a
PMCID: PMC7096188  PMID: 32226607

Version Changes

Revised. Amendments from Version 1

We have made the following changes from version1 to version2:

  • Figure1 is now Figure3 (requested by Reviewer1)

  • Figure2 is now Figure4 (requested by Reviewer1)

  • Figure2(A) and Figure 2(B) are new (requested by Reviewer2)

  • Figure3 is now Figure1 (requested by Reviewer1)

  We have transformed the text to the past tense (requested by Reviewer1). We also included text and Figure2A/Figure2B about the composition of the external Novartis test set. As requested by Reviewer1: In the discussion section, the developed method are now discussed first before discussing its performance relative to other methods.

Abstract

We present a small molecule pK a prediction tool entirely written in Python. It predicts the macroscopic pK a value and is trained on a literature compilation of monoprotic compounds. Different machine learning models were tested and random forest performed best given a five-fold cross-validation (mean absolute error=0.682, root mean squared error=1.032, correlation coefficient r 2 =0.82). We test our model on two external validation sets, where our model performs comparable to Marvin and is better than a recently published open source model. Our Python tool and all data is freely available at https://github.com/czodrowskilab/Machine-learning-meets-pKa.

Keywords: machine learning, pKa value, protonation, dissociation

Introduction

The acid-base dissociation constant (pK a) of a drug has a far-reaching influence on pharmacokinetics by altering the solubility, membrane permeability and protein binding affinity of the drug. Several publications summarize these findings in a very comprehensive manner 1– 7. An accurate estimation of pK a values is therefore of utmost importance for successful drug design. Several (commercial and non-commercial) tools and approaches for small molecule pK a prediction are available: MoKa 8 uses molecular interaction fields, whereas ACD/Labs Percepta Classic 9, Marvin 10 and Epik 11 make use of the Hammet-Taft equation. By means of Jaguar 12, a quantum-mechanical approach to pK a prediction becomes possible. Recently, the usage of neural nets for pK a prediction became prominent 13– 15. In particular, the publication by Williams et al. 15 makes use of a publicly available data set provided by the application DataWarrior 16 and provides a freely available pK a prediction tool called OPERA.

As this article is part of a Python collection issue, we provide a pK a prediction method entirely written in Python 17 and make it available open source (including all data). Our tool computes the macroscopic pK a value for a monoprotic compound. Our model solely differentiates between a base and acid based on the predicted pK a value; i.e., we do not offer separate models for acids and bases. In addition to pK a data from DataWarrior 16, we also employ pK a data from ChEMBL 18. As external validation sets, we use compound data provided by Novartis 19 and a manually curated data set compiled from literature 20– 24, which are not part of the training data.

Methods

Data set preparation

A ChEMBL 18 web search was performed to find all assays containing pK a measurement data. The following restrictions were made: it must be a physicochemical assay, the measurements must be taken from scientific literature, the assay must be in “small-molecule physicochemical format” and the organism taxonomy must be set to “N/A”. This results in a list of 1140 ChEMBL assays downloaded as CSV file. Using a Python script, the CSV file was read in and processed further, extracting all additional information required from an internally hosted copy of the ChEMBL database via SQL. Only pK a measurements, i.e. ChEMBL activities, were taken into account that were specified as exact (“standard_relation” equals “=”) and for which one of the following names was specified as “standard_type”: “pka”, “pka value”, “pka1”, “pka2”, “pka3” or “pka4” (case-insensitive). Measured values for which the molecular structure was not available were also sorted out. The resulting 8111 pK a measured values were saved as SDF file.

A flat file from DataWarrior 16 named “pKaInWater.dwar” was used in addition. In this case, the file was converted to an SDF file only and contains 7911 entries with valid molecular structures.

These data sets were concatenated for the purpose of this study and preprocessed as follows:

  • Removal of all salts from molecules

  • Removal of molecules containing nitro groups, Boron, Selenium or Silicium

  • Filtering by Lipinski‘s rule of five (one violation allowed)

  • Keeping only pK a data points between 2 and 12

  • Tautomer standardization of all molecules

  • Protonation of all molecules at pH 7.4

  • Keeping only monoprotic molecules regarding the specified pK a range

  • Combination of data points from duplicated structures while removing outliers

All steps up to filtering out all pK a values outside the range of 2 to 12 were performed with Python and RDKit 25. The QuacPac 26 Tautomers tool from OpenEye was used for tautomer standardization and setting the protonation state to pH 7.4. The Marvin 10 tool from ChemAxon was used to filter out the multiprotic compounds. It predicted the pK a values of all molecules in the range 2 to 12 and then retained only those molecules where Marvin did not predict more than one pK a in that range.

The removal of the outliers is performed in two steps. First, before combining multiple measurements for the same molecules, all entries where the pK a predicted by ChemAxon's Tool Marvin differs from the experimental value by more than four log units are removed. All molecules were then combined on the basis of the canonical isomeric SMILES. In the second step, when combining several measured values of a molecule, all those values that deviate from the mean value by more than two standard deviations are removed. The remaining values are arithmetically averaged.

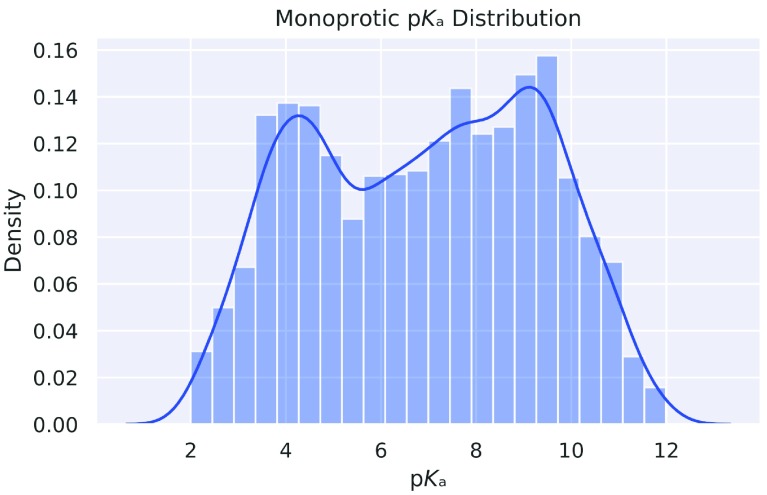
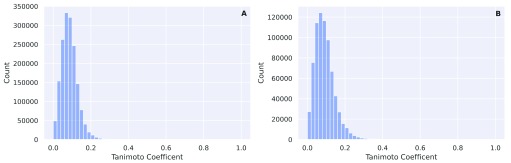
After all, 5994 unique monoprotic molecules with experimental pK a values remained. The distribution of pK a values is given in Figure 1. The same preprocessing steps were also performed on an external test data set provided to us by Novartis 19 (280 molecules) and a manual curation (123 molecules) from literature 20– 24. The Novartis data set consists of 280 unique molecules with a molecular weight between 129 and 670 daltons (mean value 348.68, standard deviation 94.17). The calculated LogP values vary between -1.54 and 6.30 (mean value 3.01, standard deviation 1.41). The 280 molecules spread over 228 unique Murcko Scaffolds. The ten most common murcko scaffolds cover 15% of the molecules of the total data set (42/280). A histogram of the pairwise comparison between the training set and the two external test sets (Fingerprint: 4096 bit MorganFeatures radius=3) is given in Figure 2(A) and Figure 2(B)

Figure 1. Distribution of the individual pK a values.

Figure 1.

Open in a new tab

Figure 2.

Figure 2.

Open in a new tab

( A) Pairwise comparison between the training set and the Novartis test set (Fingerprint: 4096 bit MorganFeatures radius=3). ( B) Pairwise comparison between the training set and the test set compiled by manual curation (Fingerprint: 4096 bit MorganFeatures radius=3).

Learning

First, to simplify cross-validation, a class “CVRegressor” was defined, which can serve as a wrapper for any regressor implementing the Scikit-Learn 27 interface. This class simplifies cross-validation itself, training and prediction with the cross-validated model. Next, 196 of the 200 available RDKit descriptors (“MaxPartialCharge”, “MinPartialCharge”, “MaxAbsPartialCharge” and “MinAbsPartialCharge” were not used because they are computed as “NaN” for many molecules), and a 4096-bit long MorganFeature fingerprint with radius 3 were calculated for the training data set. Random forest (RF), support vector regression (SVR, two configurations), multilayer perceptron (MLP, three configurations) and XGradientBoost (XGB) were used as basic regressors. Unless otherwise specified, the Scikit-Learn default parameters (version 0.22.1) were used. For the RF model, only the number of trees was increased to 1000. For SVR the size of the cache was increased to 4096 megabytes in the first configuration, but this only increases the training speed and has no influence on the model quality. In the second configuration the parameter “gamma” was additionally set to the value “auto”. For MLP in the first configuration the number of hidden layers was increased to two and the number of neurons per layer to 500. In the second configuration, early stopping was additionally activated, where 10% of the training data was separated as validation data. If the error of the validation data did not improve by more than 0.001 over ten training epochs, the training is stopped early to avoid overtraining. In the third configuration three hidden layers with a size of 250 neurons each were used with early stopping still activated. For XGB the default parameters of the used library XGBoost (version 0.90) 28 were applied. The training of RF, MLP and XGB was parallelized on 12 CPU cores and the generation of the folds for cross-validation as well as the training itself were random seeded to a value of 24 to ensure reproducibility. This resulted in a total of seven different machine learning configurations.

Six different descriptor/fingerprint combinations were also tested. First only the RDKit descriptors, followed by only the fingerprints and finally both combined. Additionally, all three combinations were tested again in a standardized form (z-transformed). As a result, 42 combinations of regressor and training data configurations were compared.

A 5-fold cross-validation was performed for all configurations, which were evaluated using the MAE, RMSE and the empirical coefficient of determination (r 2). After training was completed for all configurations, two external test data sets, which do not contain training data, were used to re-validate each trained cross-validated model. Here, MAE, RMSE, and r 2 were also calculated as statistical quality measures. To ensure that no training data was contained in the test data sets, the conical isomeric SMILES were checked for matches in both training and test data sets and corresponding hits were removed from the test data sets.

Implementation

The following Python dependencies have to be met: Python >= 3.7, NumPy >= 1.18, Scikit-Learn >= 0.22, RDKit >= 2019.09.3, Pandas >= 0.25, XGBoost >= 0.90, JupyterLab >= 1.2, Matplotlib >= 3.1, Seaborn >= 0.9

For the data preparation pipeline, ChemAxon Marvin 10 and OpenEye QUACPAC/Tautomers 26 are required. To use the provided prediction model with the included Python script, ChemAxon Marvin 10 is not required.

First of all a working Miniconda/Anaconda installation is needed. Miniconda can be downloaded at https://conda.io/en/latest/miniconda.html.

Now an environment named "ml_pka" with all needed dependencies can be created and activated with:

conda env create -f environment.yml
conda activate ml_pka

Alternatively, a new environment can be created manually without the environment.yml file:

conda create -n ml_pka python=3.7
conda activate ml_pka

In case of Linux or macOS:

conda install -c defaults -c rdkit -c conda-forge scikit-learn rdkit xgboost jupyterlab matplotlib seaborn

In case of Windows:

conda install -c defaults -c rdkit scikit-learn rdkit jupyterlab matplotlib seaborn
pip install xgboost

Operation

Prediction pipeline. To use the data preparation pipeline the repository folder hast to be entered and the created conda environment must be activated. Additionally the Marvin 10 commandline tool cxcalc and the QUACPAC 26 commandline tool tautomers have to be added to the PATH variable.

Also the environment variables OE_LICENSE (containing the path to the OpenEye license file) and JAVA_HOME (referring to the Java installation folder, which is needed for cxcalc) have to be set.

After preparation a small usage information can be displayed with bash run_pipeline.sh -h. Examplary call:

bash run_pipeline.sh --train datasets/chembl25.sdf --test datasets/novartis_cleaned_mono_unique_notraindata.sdf

Prediction tool. First of all the repository folder has to be entered and the created conda environment must be activated. To use the prediction tool the machine learning model has to be retrained. To do so the training script should be called, it will train the 5-fold cross-validated Random Forest machine learning model using 12 cpu cores. If the number of cores has to be adjusted the train_model.py can be edited by changing the value of the variable EST_JOBS.

python train_model.py

To use the prediction tool with the trained model QUACPAC/Tautomers have to be available as mentioned in the section above.

Now the python script can be called with an SDF file and an output path:

python predict_sdf.py my_test_file.sdf my_output_file.sdf

It should be noted that this model was built for monoprotic structures regarding a pH range of 2 to 12. If the model is used with multiprotic structures, the predicted values will probably not be correct.

Results

Different experimental methods

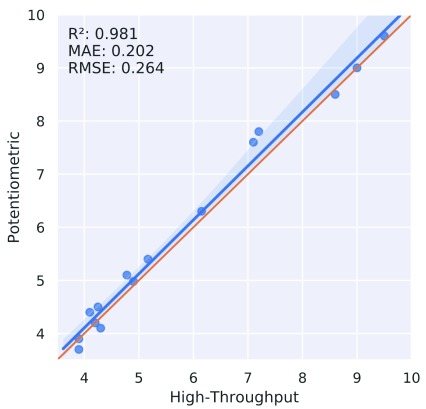
One crucial point in the field of pK a measurements (and its usage for pK a predictions) was linked to the different experimental methods 25, 30. Based on the Novartis set, the correlation between capillary electrophoresis and potentiometric measurements (for 15 data points) was convincing enough (mean absolute error (MAE)=0.202, root mean squared error (RMSE)=0.264, correlation coefficient r 2=0.981) for us to combine pK a measurements from these different experimental methods (see Figure 3).

Figure 3. Correlation of Novartis compounds measured in potentiometric and high-throughput (capillary electrophoresis) set-up.

Figure 3.

Open in a new tab

MAE, mean absolute error; RMSE, root mean square error.

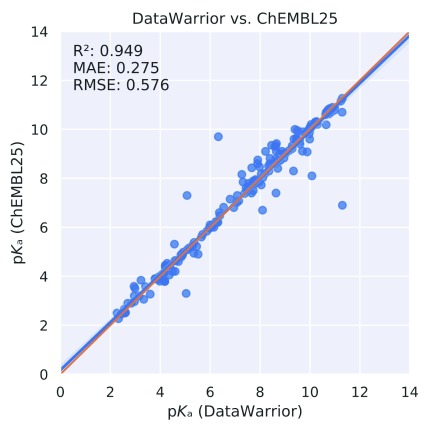
We also compared the pK a values of 187 monoprotic molecules contained in both the ChEMBL and DataWarrior data sets. Due to the missing annotation, it remained unclear if different experimental methods were used or multiple measurements with the same experimental method have been performed (or a mixture of both). Either way, this comparison was an additional proof-of-concept that the ChEMBL and DataWarrior pK a data sources can be combined after careful curation. The aforementioned intersection is given in Figure 4. The correlation coefficient between the annotated pK a values for these two data sets r 2 was 0.949, the MAE was 0.275, and the RMSE was 0.576.

Figure 4. Intersection between ChEMBL and DataWarrior data sets.

Figure 4.

Open in a new tab

MAE, mean absolute error; RMSE, root mean square error.

The compounds for which the pK a values between the different sources deviate by more than two units are as follows:

  • -

    Hydralazine:

    • -

      pK a (DataWarrior) 5.075

    • -

      pK a (ChEMBL25) 7.3

  • -

    Edaravone:

    • -

      pK a (DataWarrior) 11.3

    • -

      pK a (ChEMBL25) 6.9

  • -

    Trifluoromethanesulfonamide:

    • -

      pK a (DataWarrior) 6.33

    • -

      pK a (ChEMBL25) 9.7

Since the annotation about the experimental settings is not given in the DataWarrior file, we can only hypothesize that these differences are due to the different experimental settings.

Machine Learning

The statistics for a five-fold cross-validation are given in Table 1. In terms of the mean absolute error, a random forest with scaled MorganFeatures (radius=3) and descriptors gave the best performing model (MAE=0.682, RMSE=1.032, r 2=0.82). For the two external test sets (see Table 2), a random forest with FeatureMorgan (radius=3) gave the best model

Table 1. Statistics of the five-fold cross-validation of the machine learning models.

The two best and worst performing models are highlighted in green and red. For those neural networks where the values were specified as "not available" (“#NA”), the weights could not be optimized properly due to the large value range of the RDKit descriptors, so training failed here.

Cross-Validation
Modell (seed=24) Train Configuration MAE
(mean)		 MAE
(std)		 RMSE
(mean)		 RMSE
(std)		 R 2
(mean)		 R 2
(std)
Random Forest (n_estimators=1000) Desc (196 RDKit) 0,718 0,022 1,077 0,021 0,804 0,01
FCFP6 (4096 bit) 0,708 0,021 1,094 0,029 0,797 0,008
Desc + FCFP6 0,683 0,017 1,032 0,013 0,82 0,005
Desc (196 RDKit) (scaled) 0,717 0,022 1,076 0,022 0,804 0,011
FCFP6 (4096 bit) (scaled) 0,708 0,021 1,094 0,029 0,797 0,008
Desc + FCFP6 (scaled) 0,682 0,017 1,032 0,013 0,82 0,005
Support Vector Machine Desc (196 RDKit) 2,1 0,037 2,436 0,035 -0,004 0,004
FCFP6 (4096 bit) 0,851 0,025 1,24 0,035 0,74 0,012
Desc + FCFP6 2,1 0,037 2,436 0,035 -0,004 0,004
Desc (196 RDKit) (scaled) 0,876 0,033 1,282 0,047 0,722 0,015
FCFP6 (4096 bit) (scaled) 1,09 0,034 1,466 0,041 0,637 0,014
Desc + FCFP6 (scaled) 1,02 0,037 1,4 0,047 0,668 0,016
Support Vector Machine (gamma='auto') Desc (196 RDKit) 2,016 0,042 2,362 0,039 0,056 0,009
FCFP6 (4096 bit) 1,612 0,031 1,926 0,033 0,373 0,007
Desc + FCFP6 1,642 0,061 2,052 0,06 0,288 0,027
Desc (196 RDKit) (scaled) 0,882 0,035 1,288 0,048 0,719 0,016
FCFP6 (4096 bit) (scaled) 1,09 0,034 1,465 0,041 0,637 0,014
Desc + FCFP6 (scaled) 1,019 0,037 1,4 0,047 0,669 0,016
Multilayer Perceptron (hidden_layer_
sizes=(500, 500)) 		Desc (196 RDKit) #NA #NA #NA #NA #NA #NA
FCFP6 (4096 bit) 0,866 0,025 1,27 0,047 0,727 0,019
Desc + FCFP6 #NA #NA #NA #NA #NA #NA
Desc (196 RDKit) (scaled) 0,726 0,018 1,102 0,05 0,794 0,022
FCFP6 (4096 bit) (scaled) 1,037 0,045 1,457 0,057 0,64 0,024
Desc + FCFP6 (scaled) 0,968 0,032 1,383 0,04 0,677 0,014
Multilayer Perceptron (hidden_layer_
sizes=(500, 500),
early_stopping=True) 		Desc (196 RDKit) #NA #NA #NA #NA #NA #NA
FCFP6 (4096 bit) 0,894 0,024 1,297 0,04 0,715 0,016
Desc + FCFP6 #NA #NA #NA #NA #NA #NA
Desc (196 RDKit) (scaled) 0,768 0,034 1,161 0,09 0,77 0,038
FCFP6 (4096 bit) (scaled) 1,031 0,037 1,447 0,057 0,645 0,026
Desc + FCFP6 (scaled) 0,984 0,029 1,404 0,035 0,666 0,017
Multilayer Perceptron (hidden_layer_
sizes=(250, 250, 250),
early_stopping=True) 		Desc (196 RDKit) #NA #NA #NA #NA #NA #NA
FCFP6 (4096 bit) 0,869 0,023 1,265 0,039 0,729 0,016
Desc + FCFP6 #NA #NA #NA #NA #NA #NA
Desc (196 RDKit) (scaled) 0,775 0,008 1,158 0,033 0,773 0,013
FCFP6 (4096 bit) (scaled) 1,026 0,038 1,455 0,053 0,642 0,022
Desc + FCFP6 (scaled) 0,973 0,035 1,388 0,053 0,674 0,023
XGBoost Desc (196 RDKit) 1,02 0,014 1,353 0,021 0,691 0,007
FCFP6 (4096 bit) 1,094 0,027 1,423 0,036 0,657 0,011
Desc + FCFP6 1,018 0,01 1,346 0,022 0,694 0,005
Desc (196 RDKit) (scaled) 1,02 0,014 1,353 0,021 0,691 0,007
FCFP6 (4096 bit) (scaled) 1,094 0,027 1,423 0,036 0,657 0,011
Desc + FCFP6 (scaled) 1,018 0,01 1,346 0,022 0,694 0,005
Open in a new tab

MAE, mean absolute error; RMSE, root mean square error.

Table 2. Predictive performance of the machine learning models the on the two external test sets.

The two best and worst performing models are highlighted in green and red. For those neural networks where the values were specified as "not available" (“#NA”), the weights could not be optimized properly due to the large value range of the RDKit descriptors, so training failed here.

Novartis AvLiLuMoVe
Modell (seed=24) Train Configuration MAE RMSE R 2 MAE RMSE R 2
Random Forest (n_estimators=1000) Desc (196 RDKit) 1,259 1,607 0,513 0,689 0,979 0,828
FCFP6 (4096 bit) 1,147 1,513 0,569 0,532 0,785 0,889
Desc + FCFP6 1,2 1,532 0,558 0,628 0,884 0,86
Desc (196 RDKit) (scaled) 1,259 1,607 0,513 0,688 0,979 0,828
FCFP6 (4096 bit) (scaled) 1,147 1,513 0,569 0,532 0,785 0,889
Desc + FCFP6 (scaled) 1,198 1,531 0,558 0,628 0,884 0,86
Support Vector Machine Desc (196 RDKit) 2,177 2,451 -0,132 2,18 2,441 -0,07
FCFP6 (4096 bit) 1,423 1,732 0,435 0,688 0,981 0,827
Desc + FCFP6 2,177 2,451 -0,132 2,18 2,441 -0,07
Desc (196 RDKit) (scaled) 1,382 1,735 0,433 0,772 1,058 0,799
FCFP6 (4096 bit) (scaled) 1,771 2,035 0,219 1,115 1,422 0,637
Desc + FCFP6 (scaled) 1,746 2,015 0,235 1,044 1,345 0,675
Support Vector Machine (gamma='auto') Desc (196 RDKit) 2,162 2,428 -0,111 1,921 2,242 0,097
FCFP6 (4096 bit) 1,686 1,932 0,297 1,429 1,67 0,499
Desc + FCFP6 2,161 2,442 -0,124 1,611 2,004 0,279
Desc (196 RDKit) (scaled) 1,378 1,732 0,435 0,766 1,049 0,802
FCFP6 (4096 bit) (scaled) 1,77 2,034 0,22 1,114 1,421 0,637
Desc + FCFP6 (scaled) 1,744 2,013 0,236 1,043 1,343 0,676
Multilayer Perceptron (hidden_layer_
sizes=(500, 500)) 		Desc (196 RDKit) #NV #NV #NV #NV #NV #NV
FCFP6 (4096 bit) 1,414 1,773 0,407 0,852 1,169 0,755
Desc + FCFP6 #NV #NV #NV #NV #NV #NV
Desc (196 RDKit) (scaled) 1,318 1,634 0,497 0,688 0,942 0,841
FCFP6 (4096 bit) (scaled) 1,627 2,033 0,221 1,102 1,569 0,558
Desc + FCFP6 (scaled) 1,542 1,941 0,29 1,001 1,427 0,634
Multilayer Perceptron (hidden_layer_
sizes=(500, 500), early_stopping=True) 		Desc (196 RDKit) #NV #NV #NV #NV #NV #NV
FCFP6 (4096 bit) 1,404 1,772 0,408 0,846 1,154 0,761
Desc + FCFP6 #NV #NV #NV #NV #NV #NV
Desc (196 RDKit) (scaled) 1,298 1,626 0,502 0,701 0,936 0,843
FCFP6 (4096 bit) (scaled) 1,611 2,028 0,225 1,141 1,575 0,554
Desc + FCFP6 (scaled) 1,605 1,998 0,248 0,987 1,365 0,665
Multilayer Perceptron (hidden_layer_
sizes=(250, 250, 250), early_stopping=True) 		Desc (196 RDKit) #NV #NV #NV #NV #NV #NV
FCFP6 (4096 bit) 1,363 1,717 0,445 0,86 1,164 0,757
Desc + FCFP6 #NV #NV #NV #NV #NV #NV
Desc (196 RDKit) (scaled) 1,354 1,705 0,452 0,777 1,057 0,799
FCFP6 (4096 bit) (scaled) 1,584 1,989 0,254 1,053 1,468 0,613
Desc + FCFP6 (scaled) 1,581 1,963 0,274 0,953 1,352 0,672
XGBoost Desc (196 RDKit) 1,367 0,453 1,704 0,819 0,806 1,04
FCFP6 (4096 bit) 1,28 0,503 1,624 0,782 0,823 0,992
Desc + FCFP6 1,293 0,495 1,637 0,774 0,822 0,995
Desc (196 RDKit) (scaled) 1,367 0,453 1,704 0,819 0,806 1,04
FCFP6 (4096 bit) (scaled) 1,28 0,503 1,624 0,782 0,823 0,992
Desc + FCFP6 (scaled) 1,293 0,495 1,637 0,774 0,822 0,995
ChemAxon Marvin (V20.1.0) 0,856 1,166 0,744 0,566 0,865 0,866
OPERA (V2.5) * 2,274 3,059 -0,754 1,737 2,182 0,124
Open in a new tab

*For OPERA 6 molecules from AvLiLuMoVe and 31 molecules from Novartis were left out because OPERA predicted either two or zero pK a values.

MAE, mean absolute error; RMSE, root mean square error.

  • -

    Novartis: MAE=1.147, RMSE=1.513, r 2=0.569

  • -

    LiteratureCompilation: MAE=0.532, RMSE=0.785, r 2=0.889)

The predictive performance for Marvin 10 and the OPERA tool 15 were as follows:

  • -

    Novartis

    • -

      Marvin: MAE=0.856, RMSE=1.166, r 2=0.744

    • -

      OPERA: MAE= 2.274, RMSE= 3.059, r 2= -0.754

  • -

    LiteratureComplation 20– 24

    • -

      Marvin: MAE= 0.566, RMSE= 0.865, r 2= 0.866

    • -

      OPERA: MAE= 1.737, RMSE= 2.182, r 2= 0.124.

This showed that our model had a slightly better performance than Marvin for the LiteratureCompilation, but Marvin performed better for the Novartis dataset. For both data sets, our models 17 had a better predictive performance than the OPERA tool. Since some molecules had to be omitted for prediction with OPERA due to none or multiple predicted pK a values, no consistent significance test could be performed for all comparisons.

Discussion and conclusions

The developed model offers the possibility to predict pK a values for monoprotic molecules with good accuracy. However, since the model has been trained exclusively with monoprotic molecules, only monoprotic molecules can be predicted properly. In this respect the model is limited. Nevertheless, the results show that the performance for monoprotic molecules can compete with the performance of existing prediction tools. The good performance of Marvin on the Novartis set is interesting to note: the RMSE was almost 0.4 units better than our top performing model. This could be because Marvin’s training set is much larger than our own training set. This provides a better foundation for the training of the Marvin model. In contrast, Marvin performed slightly worse than our top model on the LiteratureCompilation. The OPERA tool performed significantly worse than our model on both external test sets. We assume that the addition of 2470 ChEMBL pK a – datapoints to our training set which were not part of the OPERA training set led to this drop in predictive performance. In addition, the pre-processing of the data was performed differently by OPERA in comparison to our pre-processing procedure.

As next step for the enhancement and improvement of our pK a prediction model 17, we are currently expanding it to multiprotic molecules. We are also investigating the impact of different neural net architectures and types (such as graph neural nets) and the development of individual models for acids and bases. From a chemistry perspective, an analysis of pK a effects of different functional groups (e.g. by means of matched molecular pairs analysis) is an on-going effort for a future publication.

Data availability

Source data

Zenodo: czodrowskilab/Machine-learning-meets-pKa article. https://doi.org/10.5281/zenodo.3662245 17.

The following data sets were used in this study:

  • AvLiLuMoVe.sdf - Manually combined literature pK a data.

  • chembl25.sdf - Experimental pK a data extracted from ChEMBL25.

  • datawarrior.sdf - pK a data shipped with DataWarrior.

  • combined_training_datasets_unique.sdf - Preprocessed and combined data from datasets chembl25.sdf and datawarrior.sdf, used as training dataset.

  • AvLiLuMoVe_cleaned_mono_unique_notraindata.sdf - used as external testset.

  • novartis_cleaned_mono_unique_notraindata.sdf - inhouse dataset provided by Novartis 19, used as external testset.

The data sets are also available at https://github.com/czodrowskilab/Machine-learning-meets-pKa.

License: MIT license.

Software availability

The source code is available at https://github.com/czodrowskilab/Machine-learning-meets-pKa.

Archived source code at time of publication: https://doi.org/10.5281/zenodo.3662245 17.

License: MIT license.

Acknowledgments

Ed Griffen (MedChemica) is acknowledged for his investigations on our initial data set which revealed some wrongly annotated data points. We thank Bob Clark, Eric Jamois and Michael Lawless (Simulations Plus) for their support and advise in terms of data curation. Alpha Lee and Matt Robinson (Cambridge University) are appreciated for fruitful discussions.

Funding Statement

The author(s) declared that no grants were involved in supporting this work.

[version 2; peer review: 2 approved]

References

  • 1. Manallack DT: The P K a Distribution of Drugs: Application to Drug Discovery. Perspect Medicin Chem. 2007;1:25–38. 10.1177/1177391x0700100003 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2. Manallack DT, Yuriev E, Chalmers DK: The influence and manipulation of acid/base properties in drug discovery. Drug Discov Today Technol. 2018;27:41–47. 10.1016/j.ddtec.2018.04.003 [DOI] [PubMed] [Google Scholar]
  • 3. Manallack DT, Prankerd RJ, Yuriev E, et al. : The significance of acid/base properties in drug discovery. Chem Soc Rev. 2013;42(2):485–496. 10.1039/c2cs35348b [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4. Meanwell NA: Improving drug candidates by design: a focus on physicochemical properties as a means of improving compound disposition and safety. Chem Res Toxicol. 2011;24(9):1420–1456. 10.1021/tx200211v [DOI] [PubMed] [Google Scholar]
  • 5. Gleeson MP: Generation of a set of simple, interpretable ADMET rules of thumb. J Med Chem. 2008;51(4):817–834. 10.1021/jm701122q [DOI] [PubMed] [Google Scholar]
  • 6. Leeson PD, St-Gallay SA, Wenlock MC: Impact of Ion Class and Time on Oral Drug Molecular Properties. Med Chem Commun. 2011;2(2):91–105. 10.1039/c0md00157k [DOI] [Google Scholar]
  • 7. Charifson PS, Walters WP: Acidic and basic drugs in medicinal chemistry: a perspective. J Med Chem. 2014;57(23):9701–9717. 10.1021/jm501000a [DOI] [PubMed] [Google Scholar]
  • 8. Milletti F, Storchi L, Sforna G, et al. : New and original p K a prediction method using grid molecular interaction fields. J Chem Inf Model. 2007;47(6):2172–2181. 10.1021/ci700018y [DOI] [PubMed] [Google Scholar]
  • 9. ACD/Percepta, Advanced Chemistry Development, Inc. Toronto, On Canada, Www.Acdlabs.Com,2019. Reference Source [Google Scholar]
  • 10. Marvin 20.1.0.2020. ChemAxon. Reference Source [Google Scholar]
  • 11. Shelley JC, Cholleti A, Frye LL, et al. : Epik: a software program for pK a prediction and protonation state generation for drug-like molecules. J Comput Aided Mol Des. 2007;21(12):681–691. 10.1007/s10822-007-9133-z [DOI] [PubMed] [Google Scholar]
  • 12. Bochevarov AD, Watson MA, Greenwood JR, et al. : Multiconformation, Density Functional Theory-Based p K a Prediction in Application to Large, Flexible Organic Molecules with Diverse Functional Groups. J Chem Theory Comput. 2016;12(12):6001–6019. 10.1021/acs.jctc.6b00805 [DOI] [PubMed] [Google Scholar]
  • 13. Fraczkiewicz R, Lobell M, Göller AH, et al. : Best of both worlds: combining pharma data and state of the art modeling technology to improve in Silico p K a prediction. J Chem Inf Model. 2015;55(2):389–397. 10.1021/ci500585w [DOI] [PubMed] [Google Scholar]
  • 14. Roszak R, Beker W, Molga K, et al. : Rapid and Accurate Prediction of p K a Values of C-H Acids Using Graph Convolutional Neural Networks. J Am Chem Soc. 2019;141(43):17142–17149. 10.1021/jacs.9b05895 [DOI] [PubMed] [Google Scholar]
  • 15. Mansouri K, Cariello NF, Korotcov A, et al. : Open-Source QSAR Models for PKa Prediction Using Multiple Machine Learning Approaches. J Cheminform. 2019;11(1):60 10.1186/s13321-019-0384-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16. Sander T, Freyss J, von Korff M, et al. : DataWarrior: an open-source program for chemistry aware data visualization and analysis. J Chem Inf Model. 2015;55(2):460–473. 10.1021/ci500588j [DOI] [PubMed] [Google Scholar]
  • 17. Lewis RA, Rodde S: Novartis Pharma AG.Basel, Switzerland.
  • 18. Settimo L, Bellman K, Knegtel RM: Comparison of the accuracy of experimental and predicted pKa values of basic and acidic compounds. Pharm Res. 2014;31(4):1082–1095. 10.1007/s11095-013-1232-z [DOI] [PubMed] [Google Scholar]
  • 19. Liao C, Nicklaus MC: Comparison of nine programs predicting p K a values of pharmaceutical substances. J Chem Inf Model. 2009;49(12):2801–2812. 10.1021/ci900289x [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20. Avdeef A: Absorption and Drug Development: Solubility, Permeability, and Charge State. John Wiley & Sons, Inc.: Hoboken, NJ, USA,2012. 10.1002/9781118286067 [DOI] [Google Scholar]
  • 21. Morgenthaler M, Schweizer E, Hoffmann-Röder A, et al. : Predicting and tuning physicochemical properties in lead optimization: amine basicities. ChemMedChem. 2007;2(8):1100–1115. 10.1002/cmdc.200700059 [DOI] [PubMed] [Google Scholar]
  • 22. Luan F, Ma W, Zhang H, et al. : Prediction of p K a for neutral and basic drugs based on radial basis function Neural networks and the heuristic method. Pharm Res. 2005;22(9):1454–1460. 10.1007/s11095-005-6246-8 [DOI] [PubMed] [Google Scholar]
  • 23. Dardonville C: Automated techniques in p K a determination: low medium and high-throughput screening methods. Drug Discov Today Technol. 2018;27:49–58. 10.1016/j.ddtec.2018.04.001 [DOI] [PubMed] [Google Scholar]
  • 24. Reijenga J, van Hoof A, van Loon A, et al. : Development of Methods for the Determination of pK a Values. Anal Chem Insights. 2013;8(1):53–71. 10.4137/ACI.S12304 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25. RDKit, Open-Source Chemiformatics. Reference Source [Google Scholar]
  • 26. QUACPAC 2.0.2.2: OpenEye Scientific Software. Santa Fe, NM. Reference Source [Google Scholar]
  • 27. Pedregosa F, Weiss R, Brucher M: Scikit-Learn: Machine Learning in Python. J Mach Learn Res. 2011;12:2825–2830. Reference Source [Google Scholar]
  • 28. Chen T, Guestrin C: XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining - KDD ’ 16; ACM Press: New York, New York, USA.2016;785–794. 10.1145/2939672.2939785 [DOI] [Google Scholar]
  • 29. Baltruschat M, Czodrowski P: czodrowskilab/Machine-learning-meets-pKa article (Version article). Zenodo. 2020. 10.5281/zenodo.3662245 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30. Gaulton A, Hersey A, Nowotka M, et al. : The ChEMBL database in 2017. Nucleic Acids Res. 2017;45(D1):D945–D954. 10.1093/nar/gkw1074 [DOI] [PMC free article] [PubMed] [Google Scholar]
F1000Res. 2020 Mar 24. doi: 10.5256/f1000research.24362.r61511

Reviewer response for version 1

Johannes Kirchmair 1

Baltruschat and Czodrowski report on the development of a Python-based tool for the prediction of pk a values. The tool is made available open source and will certainly be useful to the scientific community.

  • Could the authors please comment on the structural relationship between the training and the test data (how far apart are these datasets, e.g. measured by the distribution of pairwise Tanimoto coefficients based on molecular fingerprints)?

  • Could the authors please confirm statistical significance of the key statements made in the first paragraph of the Results section, starting with "This shows that our model slightly outcompetes..."?

  • In the Abstract, please name the open source model that was tested as part of the comparative performance analysis.

  • It is not clear from the manuscript text whether capillary electrophoresis and potentiometric measurements were the only two experimental methods considered in this work (or, for the Novartis dataset only).

  • Please revise the sentence starting with "We also compare the overlap...".

  • "make use of a" should be replaced by "makes use of a".

  • Please explain where DataWarrior's data originates from.

  • Please comment on the outliers observed in Figure 2.

  • Please explain the procedure that was followed to ensure that there was no overlap between the training data and the external validation sets (the Novartis dataset in particular).

  • "isomeric SMILES": is it canonical as well?

  • Avoid using "you" in the Implementation section (use "one [can]..." instead).

  • The part starting with "For the two external test sets..." is difficult to read. Could the authors find a more simple way to describe this and enable readers to compare the individual values more easily?

Is the work clearly and accurately presented and does it cite the current literature?

Yes

If applicable, is the statistical analysis and its interpretation appropriate?

Partly

Are all the source data underlying the results available to ensure full reproducibility?

Yes

Is the study design appropriate and is the work technically sound?

Yes

Are the conclusions drawn adequately supported by the results?

Yes

Are sufficient details of methods and analysis provided to allow replication by others?

Yes

Reviewer Expertise:

cheminformatics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

F1000Res. 2020 Apr 15.
Paul Czodrowski 1

Could the authors please comment on the structural relationship between the training and the test data (how far apart are these datasets, e.g. measured by the distribution of pairwise Tanimoto coefficients based on molecular fingerprints)?

We have included new figures (2A and 2B) with pairwise Tanimoto coefficients (4096 bit MorganFeatures radius=3).

Could the authors please confirm statistical significance of the key statements made in the first paragraph of the Results section, starting with "This shows that our model slightly outcompetes..."?

A thorough test of the statistical significance is hindered by the fact the external open source tool OPERA cannot process all molecules of our external test sets. We therefore decided to rephrase “This showed that our model slightly outcompeted Marvin for the LiteratureCompilation” to “his showed that our model has a slightly better performance than Marvin for the LiteratureCompilation”.

In the Abstract, please name the open source model that was tested as part of the comparative performance analysis.

The open source model is now mentioned in the abstract.

It is not clear from the manuscript text whether capillary electrophoresis and potentiometric measurements were the only two experimental methods considered in this work (or, for the Novartis dataset only).

We mention this already in the section “Different experimental methods” :“Due to the missing annotation, it remained unclear if different experimental methods were used or multiple measurements with the same experimental method have been performed (or a mixture of both)”.

Please revise the sentence starting with "We also compare the overlap...".

Changed "We also compared the overlap of the filtered (see next section) ChEMBL and DataWarrior data sets, 187 monoprotic molecules could be identified in both sources." To "We also compared the pKa values of 187 monoprotic molecules contained in both the ChEMBL and DataWarrior data sets."

"make use of a" should be replaced by "makes use of a".

Done

Please explain where DataWarrior's data originates from.

We cannot make any statement about the origin, because it is not included in the DataWarrior file.

Please comment on the outliers observed in Figure 2.

We include the name of the outliers and the different pKa values originating from different data sources, if they differ by more than two log units.

Please explain the procedure that was followed to ensure that there was no overlap between the training data and the external validation sets (the Novartis dataset in particular).

To ensure that no training data was contained in the test data sets, the canonical isomeric SMILES were checked for matches in both training and test data sets and corresponding hits were removed from the test data sets. Chirality was not included in this comparison.

"isomeric SMILES": is it canonical as well?

Yes, it is the canonical isomeric SMILES generated by RDKit.

Avoid using "you" in the Implementation section (use "one [can]..." instead).

Done

The part starting with "For the two external test sets..." is difficult to read. Could the authors find a more simple way to describe this and enable readers to compare the individual values more easily?

We have pulled most of the numbers apart and included bullet points which improves the readability and makes a comparison more feasible.

F1000Res. 2020 Feb 25. doi: 10.5256/f1000research.24362.r60011

Reviewer response for version 1

Ruth Brenk 1

The article describes a machine learning method for pkA prediction. The presented method and results are scientifically solid. Therefore, I recommend the article for indexing. However, the methods and results should be presented more clearly before the article is indexed.

The following points should be addressed:

  1. Past tense should be used consistently to describe the methods and results.

  2. The “different experimental methods” should be moved to the results part as it contains results.

  3. A short description of the molecules in the self-compiled data set and the Novartis set should be added. What type of molecules are contained in these sets?

  4. Why does the user need to train the model before making predictions? Could the trained model be provided to make the developed tool easier to use?

  5. In the discussion section, the developed method should be first discussed before discussing its performance relative to other methods.

Is the work clearly and accurately presented and does it cite the current literature?

Partly

If applicable, is the statistical analysis and its interpretation appropriate?

Not applicable

Are all the source data underlying the results available to ensure full reproducibility?

Yes

Is the study design appropriate and is the work technically sound?

Yes

Are the conclusions drawn adequately supported by the results?

Yes

Are sufficient details of methods and analysis provided to allow replication by others?

Yes

Reviewer Expertise:

chemoinformatics

I confirm that I have read this submission and believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

F1000Res. 2020 Mar 5.
Paul Czodrowski 1

  1. Past tense should be used consistently to describe the methods and results. We have used past tense throughout the entire document.

  2. The “different experimental methods” should be moved to the results part as it contains results. This part was moved accordingly.

  3. A short description of the molecules in the self-compiled data set and the Novartis set should be added. What type of molecules are contained in these sets? We have added this information in the manuscript: "The Novartis data set consists of 280 unique molecules with a molecular weight between 129 and 670 daltons (mean value 348.68, standard deviation 94.17). The calculated LogP values vary between -1.54 and 6.30 (mean value 3.01, standard deviation 1.41). The 280 molecules spread over 228 unique Murcko Scaffolds. The ten most common murcko scaffolds cover 15% of the molecules of the total data set (42/280)."

  4. Why does the user need to train the model before making predictions? Could the trained model be provided to make the developed tool easier to use? The user has to train the model again by himself or herself, because the model is larger than 1.7 GB as a file and therefore cannot be offered for download without paid services. Even with the best possible bzip2 compression, the file is still over 250 MB in size and thus larger than the 100 MB limit at GitHub. In addition, if the model is provided as a file, you must use exactly the same versions of the Python libraries used for training to load the model, otherwise inconsistencies may occur. However, if the model is trained again by yourself, only the minimum library requirements have to be met.

  5. In the discussion section, the developed method should be first discussed before discussing its performance relative to other methods. This was done and is reflected in the new manuscript version.

Associated Data

    This section collects any data citations, data availability statements, or supplementary materials included in this article.

    Data Citations

    1. Lewis RA, Rodde S: Novartis Pharma AG.Basel, Switzerland.

    Data Availability Statement

    Source data

    Zenodo: czodrowskilab/Machine-learning-meets-pKa article. https://doi.org/10.5281/zenodo.3662245 17.

    The following data sets were used in this study:

    • AvLiLuMoVe.sdf - Manually combined literature pK a data.

    • chembl25.sdf - Experimental pK a data extracted from ChEMBL25.

    • datawarrior.sdf - pK a data shipped with DataWarrior.

    • combined_training_datasets_unique.sdf - Preprocessed and combined data from datasets chembl25.sdf and datawarrior.sdf, used as training dataset.

    • AvLiLuMoVe_cleaned_mono_unique_notraindata.sdf - used as external testset.

    • novartis_cleaned_mono_unique_notraindata.sdf - inhouse dataset provided by Novartis 19, used as external testset.

    The data sets are also available at https://github.com/czodrowskilab/Machine-learning-meets-pKa.

    License: MIT license.

    Software availability

    The source code is available at https://github.com/czodrowskilab/Machine-learning-meets-pKa.

    Archived source code at time of publication: https://doi.org/10.5281/zenodo.3662245 17.

    License: MIT license.

    Articles from F1000Research are provided here courtesy of F1000 Research Ltd

    RESOURCES