Assessment of MC-PDFT excitation energies for a set of QM/MM models of rhodopsins

Abstract

A methodology for the automatic production of quantum mechanical/molecular mechanical (QM/MM) models of retinal-containing rhodopsin proteins and subsequent prediction of their spectroscopic properties has been proposed recently by some of the authors. The technology employed for the evaluation of the excitation energies is called Automatic Rhodopsin Modeling (ARM), and it involves the use of the complete active space self-consistent field (CASSCF) method followed by a multi-configuration second- order perturbation theory (in particular, CASPT2) calculation of external correlation energies. Although it was shown that ARM is capable of successfully reproducing and predicting spectroscopic property trends in chromophore-embedding protein sets, practical applications of such technology are limited by the high computational costs of the multi-configuration perturbation theory calculations. In the present work we benchmark the more affordable multi-configuration pair-density functional theory (MC-PDFT) method whose accuracy has been recently validated for retinal chromophores in the gas phase, indicating that MC-PDFT could potentially be used to analyze large (e.g., few hundreds) sets of rhodopsin proteins. Here, we test this theory for a set of rhodopsin QM/MM models whose experimental absorption maxima (λ^a_max) have been measured. The results indicate that MC-PDFT may be employed to calculate λ^a_max values for this important class of photoresponsive proteins.

Graphical Abstract

1. Introduction

Until recently, computational chemists working on photoresponsive proteins, have developed their methods with the primary aim of uncovering the mechanisms underlying proteins function.¹ However, more recent research is opening the possibility that chemists can use computations to design novel protein functions.² This process is fostered by the expanding fields of synthetic biology^3,4 and, more specifically, optogenetics,⁵ where both experimental and computational screenings of many proteins are carried out to search for specific properties, such as absorption wavelengths. The rhodopsin family of proteins (see Figure 1A) represents one of the major subjects of such technological advances, especially in the case of optogenetics.^6,7 Computational protocols⁸ aimed at the automated and parallel construction of combined quantum mechanical/molecular mechanical models of rhodopsins can play an important role in synthetic biology.

Figure 1:

(A) Crystallographic structure of Bovine rhodopsin (Rh) (PDB ID 1U19)¹⁶ and (B) 11-cis (top) and all-trans (bottom) retinal configurations, as a generic example of a rhodopsin and its corresponding retinal photo-isomerization.

Computational approaches have the advantage of being much less expensive and requiring much less manpower than wet-lab experiments. However, to be most useful, computational methods should not only be accurate but also should exceed the speed of their experimental counterparts. Then it will be possible to computationally analyze very large sets of protein mutants for fast and accurate in silico screening and to guide, drive, and focus the more expensive and time-consuming wet-lab activity.

In order to carry out systematic studies of light-responsive proteins, some of the authors have recently proposed the Automatic Rhodopsin Modeling (ARM)⁸ protocol for the fast generation of combined quantum mechanical and molecular mechanical (QM/MM)^9–11 models of rhodopsin-like photoreceptors.^12,13 For a given rhodopsin, either from a crystallographic structure or produced through homology modeling, ARM generates its charge-neutral, gas- phase monomer QM/MM model in about two days. Subsequently, ARM predicts the ab- sorption maximum of the rhodopsin model as an average of ten conformation samples. ARM is designed to reproduce trends in excitation energies (ΔE_S1–S0) rather than absolute spectroscopic properties, and it has been demonstrated that its vertical excitation energies agree well with excitation energies calculated from the maxima of the absorption spectra of a set of wild-type and mutant rhodopsins.^14,15

In the previously published work-flow of the ARM protocol, as briefly described in section S1 of the Supporting Information, the vertical excitation energies of the first (S₁ ) and second (S₂) singlet excited states (ΔE_S1–S0 and ΔE_S2–S0) of the protein-embedded retinal chromophore are computed using complete active space second-order perturbation theory (CASPT2).^17,18 However, this methodology is computationally expensive. When applied to a wide (e.g., few hundreds) set of rhodopsins, it is difficult to obtain results within a reasonable amount of time. Therefore, we decided to investigate a less expensive alternative to CASPT2 to see how it compares in terms of both accuracy and required computational time. In particular, in the present work, we assess the performance of multiconfiguration pair-density functional theory (MC-PDFT)^19,20 as an alternative to CASPT2 for the calculation of excitation energies of rhodopsins.

The photo-induced isomerization of the retinal chromophore (see Figure 1B) is associated with an excitation that has charge transfer (CT) character. Therefore, an accurate description of such character is necessary when computing excitation energies. One alternative is multi-reference perturbation theory methods such as CASPT2 that are suitable to describe CT excitations, and in case of strong mixing of electronic states (e.g., S1–S2) the multi-state CASPT2^21–23 (MS-CASPT2) method can be employed. However such methods are computationally expensive. Another alternative is Kohn-Sham (KS) density functional theory (DFT), which is faster, but it has difficulty describing charge transfer excitation correctly,²⁴ and excitations involving long-range CT character have proven especially difficult for most time-dependent DFT methods. Although tuned range-separated hybrid exchange-correlation functionals can describe CT excitations more accurately, they require additional calculations to determine the value of the tuning parameter for each system.²⁵ An alternative that is less expensive than CASPT2 and that does not require tuning is the recently developed MC-PDFT method.^19,20

CASPT2, MS-CASPT2, and MC-PDFT each begin with a complete active space self-consistent field (CASSCF)^26,27 calculation. For CASPT2 and MS-CASPT2, perturbation theory follows CASSCF to estimate the remainder of the dynamic correlation energy, which is called the external correlation energy. MC-PDFT also involves a post-SCF energy calculation, but it is much less expensive.^28–30 In particular, MC-PDFT calculates (i) the kinetic energy, the density, and the on-top pair density from the CASSCF reference wave function; (ii) the electron-nuclear attraction energy and the classical electron-electron interaction energy from the density, and (iii) uses an on-top density functional to estimate the rest of the electronic energy, including dynamic correlation energy. Because MC-PDFT is faster than the CASPT2 and MS-CASPT2 methods, it may represent a useful alternative for extensive screening of rhodopsin proteins. The present work tests whether this is the case and also evaluates the effect of varying the basis set and CASSCF active space on the computed vertical excitation energies. We consider the 6–31G(d)³¹ and TZVP³² basis sets with (12,12) and (10,10) active spaces in the following combinations: (12,12)/6–31G(d), (10,10)/6–31G(d), and (10,10)/TZVP). As compared to the previous ARM work,⁸ in the present work we also consider a different approach to the QM/MM geometry optimization of the rhodopsin models by employing DFT with the M06–2X ^33,34 functional instead of CASSCF. The goal is to learn if we can find combinations of methods that are faster and/or more accurate than the previously published ARM protocol.

2. Computational Methods

2.1. Rhodopsin Benchmark

Our rhodopsin benchmark set comprises ten rhodopsins from vertebrates, invertebrates, and microbial, with excitation energies estimated from experimental maximum absorption wavelengths (λ^a_max) (see Table 1). Specifically, we use all-trans and 13-cis isomers of anabaena sensory rhodopsin (ASR_AT and ASR₁₃c, microbial, sensorial) and bacteriorhodosin (BR_AT and BR_13C, Archea proton pump); bovine rhodopsin (Rh, vertebrate, visual pigment); squid rhodopsin (SqRh, invertebrate, visual pigment); human melanopsin (hMeOp, vertebrate, nonvisual pigment); blue-proteorhodopsin (PRh, a eubacterial proton pump) and the chimera channelrhodopsin (CRh_C1C2, a lab construction of microbial eukaryotic light-gated ion channels from the green alga Chlamydomonas reinhardtii) and the primary photocycle intermediate’s Rh, bathorhodopsin (bathoRh). The geometries to build each QM/MM model using the ARM protocol were obtained from corresponding PDB crystallographic structures, whereas for hMeOp a comparative model was employed.⁵⁰ Optimized structures can be found in the Supporting Information of Melaccio et al.⁸

Table 1:

Excitation energies ΔE_S1–S0 (kcal/mol) corresponding to maximum absorption wavelengths λ^a_max (nm)) for a benchmark set of ten wild-type rhodopsins. Protein code, Protein Data Base ID, retinal conformation, and organism are also listed.

Protein(a)	Code	PDB ID	Conformation	Organism	Exp. ΔES1–S0 (λamax)
X-Ray
Squid rhodopsin (I)	SqRh	2Z7335	11-cis	Todarodes pacificus	58.6 (488)36
Blue-Proteorhodopsin (M)	PRh	4JQ637	all-trans	Excherichia coli	58.3 (490)38
Bovine rhodopsin (V)	Rh	1U1916	11-cis	Bos taurus	57.4 (498)39
Bathorhodopsin (V)	bathoRh	2G8740	all-trans	Bos taurus	54.0 (529)41
Anabaena sensory rhodopsin (M)	ASR13C	1XIO42	13-cis	Cyanobacterium anabaena PCC7120	53.2 (537)15
	ASRAT		all-trans		52.0 (550)15
Bacteriorhodopsin (M)	BR13C	1X0S43	13-cis	Halobacterium salinarum	52.3 (547)44
	BRAT	6G7H45	all-trans		50.3 (568)44
Channelrhodopsin (M)	CRhC1C2	3UG946	all-trans	Chlamydomonas reinhardtii	62.4 (458)47
Homology Model
Human Melanopsin (V)	hMeOp	2Z73(b)	11-cis	Todarodes pacificus	60.1 (473)(c)

^(a)Vertebrate (V), invertebrate (I), and microbial (M)

^(b)Template model

^(c)Average of available values from references 48,49.

2.2. QM/MM Model Structures

In this work, we will consider two different sets of geometries (CASSCF Set and DFT Set) to evaluate excitation energies. The CASSCF Set includes ten QM/MM sample structures for each of the ten benchmark rhodopsins (100 QM/MM structures in total) and is dis- cussed in subsection 3.1. The DFT Set involves ten QM/MM sample structures for just one rhodopsin (and thus, it contains only 10 QM/MM structures), namely bovine rhodopsin, and is discussed in subsection 3.2.

2.2.1. CASSCF Set

To obtain the QM/MM geometries for the CASSCF Set, we employed the previously described ARM protocol,⁸ which utilizes single-state CASSCF(12,12)/6–31G(d)/Amber calculations to obtain optimized ground-state geometries. The MM part of the calculation is carried out using the force field of Cornell et al.⁵¹ All QM/MM calculations were performed with Gromacs 4.5.4,⁵² Molcas 8.1.⁵³ and Tinker 6.3.⁵⁴

2.2.2. DFT Set

The QM/MM structures for the DFT Set were obtained in the same way as described in section 2.2.1 except for the employed QM method. For this set, QM/MM structures for bovine rhodopsin were optimized using Kohn-Sham density functional theory (DFT) with the M06–2X exchange-correlation functional^33,34 and the 6–31G(d,p) basis set for the QM part of the QM/MM calculation. We selected the M06–2X functional because it has been shown to generate reliable ground state geometries of retinal analogs for studying their vertical excitation energies in the gas phase.^24,28,29 Although Dong et al.²⁸ used a 6–31+G(d,p) basis set, we decided here to employ the smaller 6–31G(d,p) basis set in order to reduce the overall computational costs.

2.3. Excitation Energy Computation

To compute the vertical excitation energies of each rhodopsin, with the aim of comparing them with the experimental absorption spectra, we run in parallel N molecular dynamics (N = 10), each run being 1 ns long, on the whole protein structure. From these ten runs, we have ten structures, from each of which, after a QM/MM optimization of the chromophore, we compute the vertical excitation energies, again in a QM/MM fashion. This gives ten values of each vertical excitation energy for each rhodopsin, and we calculate the average of these ten values to obtain the computational value to compare to the experimental one. Further details of the molecular dynamics simulations (i.e., which parts are movable), of how the rhodopsin protein is divided into a QM and a MM part, and of how each part is treated can be found in the Supporting Information and in Melaccio et al.⁸

In the present work, excitation energies were computed using CASSCF, CASPT2, MS-CASPT2, and MC-PDFT methods. All of them started with a CASSCF calculation averaged over three states (ground and two first excited singlet states), and the MS-CASPT2 calculations involved a 3 × 3 model space in the perturbation theory calculation. We carried out the CASPT2 and MS-CASPT2 calculations with an imaginary shift⁵⁵ of 0.2 hartrees and no IPEA shift.⁵⁶ A zero IPEA shift was chosen because it was previously found to give vertical excitation energy of rhodopsins closest to the experimental maximal-absorption wavelength.⁸ We also note that a recent systematic study of CASPT2 calculations led to the recommendation that the IPEA shift should not be used to calculate excited states.⁵⁷ The MC-PDFT vertical excitation energies were obtained with the tPBE^20,58 on-top density functional (see Supporting Information for Molcas implementation details). It was previously shown by Dong et al.²⁸ that the selection of on-top density functionals does not significantly affect the vertical excitation energies for the molecular systems considered in that study (i.e., retinals). All excitation energies were computed in the electrostatic field of the protein point charges.

We first chose a (12,12) active space that includes the full set of π and π* orbitals and 12 electrons of the chromophore. To ensures that the whole n system is well represented the initial orbitals (guess orbitals) for the CASSCF iterations were chosen as the six highest occupied and six lowest unoccupied Hartree-Fock orbitals. As previously described in section 1, the effect of active space and basis set on vertical excitation energies was tested using (12,12) and (10,10) active spaces and 6–31G(d) and TZVP^59,60 basis sets in the following combina- tions: (12,12)/6–31G(d), (10,10)/6–31G(d) and (10,10)/TZVP. The (10,10) active space was obtained by removing the most and least occupied orbitals from the active space of a previous (12,12) calculation. We also tested second-order Møller-Plesset perturbation theory (MP2)-based HOMO-LUMO energies gaps, as a cheap way to estimate excitation energies, which provided trends of lesser quality (see Section S7 in the Supporting Information).

The CASPT2 oscillator strengths were computed using CASSCF transition dipole moments extracted from the RASSI module of Molcas combined with CASPT2 energy values, and the MC-PDFT oscillator strengths were computed using the same transition dipole moments and MC-PDFT energy values. All single-point energy evaluations were computed using Molcas 8.2.⁵³

Excitation energies were obtained for all possible combinations of CASSCF, CASPT2, MS-CASPT2, and MC-PDFT with the (12,12)/6–31G(d),(10,10)/6–31G(d), and (10,10)/TZVP active space/basis set combinations, for a total of 1200 excitation energies for the CASSCF Set and 120 for the DFT Set. For each rhodopsin in the CASSCF Set, the absolute difference between computed and experimental excitation energies was evaluated. The mean and standard deviations were then computed by averaging over the results for the 10 rhodopsins.

We also tested the various methods for their ability to predict excitation energy changes (i.e., trends) from one rhodopsin to another. For this test, we considered bovine rhodopsin as the standard against which to compare all other rhodopsins; in these comparisons, for each rhodopsin and for each method, we evaluated the absolute difference between experimental and computed values against the same difference for bovine rhodopsin, and we report the mean and standard deviations. The mean and standard deviations for each method were computed by averaging over the comparisons of the nine other rhodopsins (see Table 2 and Supporting Information).

Table 2:

Absolute mean deviations and uncertainties between computed and experimental excitation energies for each method and combination of basis set and active space. In parenthesis, there are mean absolute errors (MAE) and deviation (MAD) of ||Trend Dev.||, as defined in Section S5.1 of the Supporting Information. All values are in kcal/mol; for comparison purposes, the same data is also provided in eV in Table S9 in the Supporting Information. These values were obtained using the data of Tables S10, S11 and S12 in the Supporting Information.

Active Space/Basis Set	CASSCF	CASPT2	MS-CASPT2	MC-PDFT
(12,12)/6-31G(d)	29.8±2.0 (1.8±0.9)	1.2±0.9 (1.5±0.9)	3.8±1.6 (2.4±0.8)	10.1 ±1.4 (3.0±1.1)
(10,10)/6-31G(d)	30.3±2.2 (2.0±1.1)	2.6±2.0 (1.3±0.7)	5.1±2.0 (1.5±1.0)	5.4±2.0 (2.4±1.1)
(10,10)/TZVP	16.2±5.8 (4.9±3.4)	0.9±0.8 (1.3±1.1)	1.7±1.3 (1.6±1.2)	7.2±4.3 (3.3±2.9)

3. Results and Discussion

3.1. Excitation Energy Trends

In this section, we compare the CASSCF, CASPT2, MS-CASPT2, MC-PDFT, and experimental excitation energies (ΔE_S1–S0 and ΔE_S2–S0) by using three combinations of active space and basis set. There is no experimental data available for ΔE_S2-S0, so for S₂ singlet state, we compare just the four theoretical methods. The results are presented in Figure 2, where each ΔE_S1–S0 and ΔE_S2-S0 value is computed as an average of ten samples as explained above.

Figure 2:

Excitation energies of rhodopsins. (A, C, and E) ΔE_S1–S0; (B, D, and E) ΔE_S1–S0. (A and B) Vertical excitation energies by (12,12)/6–31G(d) are shown as circles. (C and D) Vertical excitation energies by (10,10)/6–31G(d) are shown as diamonds. (E and F) Vertical excitation energies by (10,10)/TZVP are shown as triangles. (A, C, and E) Experimental excitation energies corresponding the maxima in the absorption spectra are shown in black. The corresponding ΔE values are reported in Tables S3, S4 and S5. Also, absolute energies for the 10 samples of Rh using the (12,12)/6–31G(d) methodology are reported in Table S7.

3.1.1. (12,12) active space and 6–31G(d) basis set data

We first analyze the trend in ΔE_S1–S0 generated by (12,12)/6–31G(d). These results are reported in Table S3 and plotted in Figure 2A. As expected based on previous results,⁸ the CASPT2 method reproduces not only qualitatively but also semiquantitatively the ΔE_S1–S0 experimental trend. The quantitative success of CASPT2 is due in part to various error-cancellation effects introduced by CASSCF geometries and small basis sets.⁶¹ MS-CASPT2 shows a similar behavior, although there is an inversion of the trend in the case of SqRh and PRh rhodopsins.

Although the MC-PDFT method reproduces the CASTP2 trend, it is in less quantitative agreement with the values corresponding to the wavelength peaks in the experimental spectra, and the MC-PDFT results are red-shifted with respect to the experiment. However, one can see that the individual deviations are more or less constant, which indicates a correlation between the computed and experimental data. A comparison between the average deviations of the various methods for the excitation energy (ΔE_S1–S0), is given in the first two rows of Table 2. In interpreting this comparison, one has to remember that, due to Franck-Condon factors and vibronic effects, the computed quantities, which are vertical excitation energies, are not the same as the experimental excitation energies, which are computed from maxima in the spectra as functions of wavelength.^62,63 With this caveat in mind, we note that CASPT2 method features the smallest absolute deviation between computed and experimental excitation energies (1.2 ± 0.9 kcal/mol) due, again, in part to error cancellations.⁶¹

CASPT2 is the best method when considering the reproduction of experimental trends. Only the CASPT2 level of theory reproduces the experimental values with a computational uncertainty of less than 2 kcal/mol. MS-CASPT2 does not present any significant improvement over CASPT2. Although CASSCF is poor in reproducing excitation energies, it performs comparably well when predicting general trends, with a mean deviation for trend evaluation of only 1.8 ± 0.9 kcal/mol.

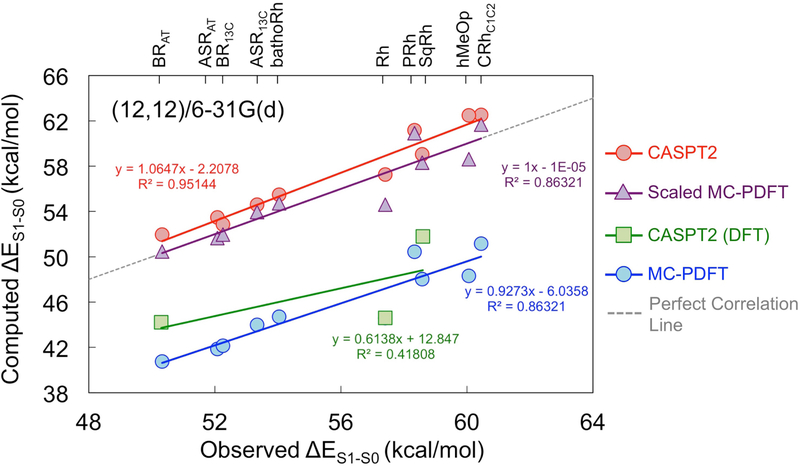
The standard deviations of excitation energies found with MC-PDFT are larger than those found with CASPT2. However, MC-PDFT is capable of reproducing trends with an accuracy similar to that of MS-CASPT2. As depicted in Figure 3, and as described in the Supporting Information, a set of semiquantitative results can be obtained from a linear regression based on MC-PDFT data (Table S13). Such a linear regression can be useful when trying to predict the excitation energies of novel rhodopsins. CASPT2 single-point calculations require threefold more compute time than MC-PDFT for the present systems. Therefore these results indicate the usefulness of employing the MC-PDFT methodology to compute trends in vertical excitation energy at a lower cost. Linear regression can also be based on the CASSCF data (see Table S13 and Figure S5 in the Supporting Information). The more scattered energies seen for Rh, PRh and SqRh are interpreted in terms of a more flexible chromophore cavity for these rhodopsins with respect to microbial rhodopsins, which may cause a greater uncertainty of the retinal geometries.

Figure 3:

Comparison of observed and vertical excitation energies (ΔE_S1–S0) computed with CASPT2 (red circles), MC-PDFT (blue circles) and the scaled MC-PDFT (violet triangles), where all calculations use CASSCF geometries, the (12,12) active space, and the 6–31G(d) basis set. Also, CASPT2 vertical excitation energies for BR_AT, Rh and SqRh rhodopsins using DFT (M06–2X) geometries are shown in green squares (see Section 3.2). The computed excitation energies are vertical excitation energies, and the abscissa of this plot is the excitation energy computed from the wavelength maximum in the absorption spectrum. The method used to obtain the linear regression is described in the Supporting Information.

An alternative way to lower the cost and overcome the red shift, would be to use an on-top functional that predicts larger excitation energies. For example, it would be interesting in future work to evaluate the use of an on-top functional obtained by translating the HLE17⁶⁴ exchange-correlation functional.

3.1.2. (10,10) active space and 6–31G(d) basis set data

Using the (10,10)/6–31G(d) combination of active space and basis set (Figure 2C and D and Table S4), CASPT2 and MS-CASPT2 methods reproduce qualitatively and semiquantitatively the experimental trend. Remarkably, unlike the (12,12)/6–31G(d) methodology, there is no inversion of energy trends for SqRh, PRh and Rh rhodopsins. However, using this approach the trend is inverted for ASR_AT and BR_13C. Encouragingly, MC-PDFT reproduces the observed trend without any inversion, although it again shows red-shifted values with respect to the experimental values. The ΔE_S2–S0 (Figure 2D) trend is reproduced by all methods, but the vertical excitation energies obtained at the MC-PDFT levels the (10,10)/6–31G(d) combination are much closer than those of obtained with the (12,12)/6–31G(d) combination.

A quantitative comparison of the vertical excitation energy (ΔE_S1–S0) between the four employed methods can be carried out by looking at the third and fourth rows of Table 2. CASPT2 shows, again, the smallest absolute deviation between computed and experimental excitation energies (2.6 ± 2.0 kcal/mol). Clearly, for the selected benchmark set and protocol of comparing 6–31G(d) vertical excitation energies to experimental excitation energies computed from absorption maxima, CASPT2 is the method of choice. CASPT2 is also the best method when considering trends, with an estimated deviation of 1.3 ± 0.7 kcal/mol. MS-CASPT2 does not present any significant improvement over CASPT2. MC-PDFT data is in line with MS-CASPT2, for both mean deviations and trends. As opposed to CASPT2, MC-PDFT with (10,10)/6–31G(d) methodology performs better than using (12,12)/6–31G(d) methodology. The decision as to which active space is best balanced remains a difficult issue without a definitive means of settlement. From the computational costs point of view, the reduction of the active space is translated into a reduction of only about 10 minutes in computational time for each method.

3.1.3. (10,10) active space and TZVP basis set data

The data obtained using the (10,10)/TZVP combination are plotted in Figures 2E and 2F, and the corresponding numerical values are reported in Table S5. Upon enlarging the basis set size from 6–31G(d) to TZVP, we observe that the agreement of theory and experiment for both vertical excitation energies (ΔE_S1–S0) and excitation energies trends increases for all the methods that we tested. This is illustrated by the fifth and sixth rows of Table 2, which show an overall improvement for all methodologies. However, there is less correlation between the various methodologies for ΔE_S2–S0, as seen in Figure 2F.

Although TZVP-based results for ΔE_S1–S0 are in better agreement with the experimental data, the use of this basis set increases the computational time by a factor of three relative to 6–31G(d). Therefore, we deem that the slightly improved agreement between experimental and computed data due to TZVP is not sufficient to justify its general usage in the ARM protocol.

3.2. Effect of the Geometrical Structure

In Dong et al.,²⁸ gas-phase retinal chromophores were optimized with the M06–2X exchange-correlation functional and the 6–31+G(d,p) basis set. In the analysis of previous sections, our QM/MM models were optimized by CASSCF(12,12)/6–31G(d) (see section 2.2.1), and this raises the question of how the retinal geometry impacts the computed vertical excitation energies. To explore this, we carried out QM/MM ground state geometry optimizations with the M06–2X functional (see section 2.2.2) for one rhodopsin of our benchmark set (in particular bovine rhodopsin, Rh). In order to enlarge the M06–2X geometry optimization set, we benchmarked other two rhodopsins. Indeed, we choose an invertebrate (SqRh) and a microbial (BR_AT) rhodopsins to have representative cases with very different amino acid sequences (see Figure S3 and Table S6 in the Supporting Information.)

We start by comparing the geometrical parameters (i.e., bond lengths and dihedral angles) of the CASSCF(12,12)/6–31G(d) and M06–2X/6–31G(d,p) optimized geometries (see Figure 4). To insure conformational consistency, we started both sets of calculations from the same guess structure obtained through the ARM protocol (see Supporting Information) by a geometry optimization at the Hartree-Fock (HF) level with the 3–21G basis set. Since we have ten QM/MM models in each ARM cycle, the comparison in Figure 4 is for the representative structure defined as the one with the vertical excitation energy closest to the value averaged over all ten vertical excitation energies.

Figure 4:

11-cis retinal chromophore of Bovine rhodopsin. Comparison of the values for (A) bonds and (B) dihedral angles of CASSCF(12,12)/6–31G(d) (blue) and DFT/M06–2X/6–31G(d,p) (red) optimized geometries. Among the ten samples, we chose the one with computed excitation energy closest to the average ΔE_S1–S0.

Figure 4A shows that the representative M06–2X/6–31G(d,p) geometry (in red) has shorter single and longer double bonds than the representative CASSCF(12,12)/6–31G(d) structure (in blue). Thus, the bond length alternation^30,65–68 (BLA, as computed from the three central single bonds and their flanking double bonds) is smaller for M06–2X (0.06 Å) than for CASSCF (0.11 Å), and there is more delocalization.

In addition, these retinal geometries, which were optimized inside the protein cavity, deviate from the retinal geometries calculated in gas-phase quite significantly. ²⁸ In the gas phase, the lowest-energy geometry of retinal optimized by M06–2X/6–31+G(d,p) has its chain nearly planar (deviation within 2 degrees). However, both CASSCF and DFT geometries optimized in the protein cavity have several dihedral angles in the chain deviating from being planar by about 10 degrees, including the torsion around some double bonds (Figure 4B). This difference between the retinal geometry in the protein and that in the gas phase may explain in part the deviation in the quality of the performance of the MC-PDFT vertical excitation energy reported in this study from those in Dong et al.²⁸ Moreover, for the DFT-optimized geometry (Figure 4), the torsion angle around the C₁₁=C₁₂ bond is −9.4 degrees, far from being planar, while for the CASSCF optimized geometry, this angle is −4.7 degrees, slightly closer to being planar. It is possible that, the electrostatic field provided by the protein as calculated from the MM charges provides an extra source of error cancellation for the CASSCF geometry to perform better than DFT geometry. As in the previous section, we computed the ΔE_S0–S1 and ΔE_S0–S2 energy differences relative to DFT Set geometries employing the various methods, active spaces, and basis sets (see Figure 5 and Table S6). As shown in Figure 5, the three possible methodologies give the same behavior: all vertical excitation energies based on DFT geometries are red-shifted compared to those calculated with CASSCF geometries; the difference is between 10 and 25 kcal/mol, depending on the employed method. Due to this red shift, CASSCF values, in DFT geometries, become closer to the experimental values, but we interpret this as resulting from unphysical cancellation of errors.

Figure 5:

Comparison of vertical excitation energies (ΔE_S1–S0) of Bovine rhodopsin for (12,12)/6–31G(d) (circles), (10,10)/6–31G(d) (diamonds) and (10,10)/TZVP (triangles) methodologies for geometries optimized by CASSCF(12,12)/6–31(d) (CASSCF) and geometries optimized by M06–2X/6–31G(d,p) (DFT). The corresponding ΔE values are reported in Table S6.

4. Conclusions

In this work, we have evaluated the effects of different active spaces and basis sets on vertical excitation energies and oscillator strengths by using the CASSCF, CASPT2, MS-CASPT2, and MC-PDFT methods for QM/MM models generated with the ARM protocol. All excitation energies are computed in the electrostatic field of the protein point charges.

The use of CASPT2 with a (12,12) active space, 6–31G(d) basis set, and CASSCF optimized geometries was confirmed to be the most successful method for reproducing both experimental excitation energies and trends (Table 2). The CASPT2/CASSCF method also works well due to cancellation of errors from the geometry and basis set.⁶¹

However, if faster calculations are a necessity, the MC-PDFT level of theory with a smaller active space (10,10), CASSCF-optimized geometries, and the 6–31G(d) basis set, represents a useful alternative, even if it has larger deviations than CASPT2 from the available experimental data (Table 2); these results reproduce qualitatively the CASPT2 trend, while the computer time is reduced by a factor of 3. Both CASPT2 and MC-PDFT methods performed best when applied to rhodopsins whose geometry have been optimized at the CASSCF level of theory. The use of a (10,10) active space saves about 10 minutes of compute time; nevertheless, such an active space choice raises nontrivial problems in choosing which π orbitals (section 2.3) to include. Therefore, we do not see any practical advantage in choosing a (10,10) over a (12,12) active space.

The added computational costs due to enlarging the basis set (from 6–31G(d) to TVZP) is not accompanied by a much higher degree of agreement with experimental data (Table 2, bottom row), but we must keep in mind that the theoretical results are vertical excitation energies and the experimental results are excitation energies computed from the wavelength maxima in the absorption spectra.

Finally, we note in Table 2 that the MC-PDFT method is capable of obtaining qualitatively good trends, in spite of the computed excitation energies being red-shifted. It is possible to take advantage of the successful prediction of the trend by applying linear regression to fit a predictive model using the MC-PDFT data (Figure 3). With such a scheme, we foresee the opportunity to study large sets of rhodopsins, and obtain reliable trends for excitation energies at a reasonable computational costs, in terms of both time and resources, by applying the MC-PDFT method with CASSCF optimized geometries. We foresee that future releases of the ARM protocol will include the possibility to choose which method (CASPT2 or MC-PDFT) to employ to compute excitation energies.