Abstract
Background
Isolation of cases and contact tracing is used to control outbreaks of infectious diseases, and has been used for coronavirus disease 2019 (COVID-19). Whether this strategy will achieve control depends on characteristics of both the pathogen and the response. Here we use a mathematical model to assess if isolation and contact tracing are able to control onwards transmission from imported cases of COVID-19.
Methods
We developed a stochastic transmission model, parameterised to the COVID-19 outbreak. We used the model to quantify the potential effectiveness of contact tracing and isolation of cases at controlling a severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2)-like pathogen. We considered scenarios that varied in the number of initial cases, the basic reproduction number (R0), the delay from symptom onset to isolation, the probability that contacts were traced, the proportion of transmission that occurred before symptom onset, and the proportion of subclinical infections. We assumed isolation prevented all further transmission in the model. Outbreaks were deemed controlled if transmission ended within 12 weeks or before 5000 cases in total. We measured the success of controlling outbreaks using isolation and contact tracing, and quantified the weekly maximum number of cases traced to measure feasibility of public health effort.
Findings
Simulated outbreaks starting with five initial cases, an R0 of 1·5, and 0% transmission before symptom onset could be controlled even with low contact tracing probability; however, the probability of controlling an outbreak decreased with the number of initial cases, when R0 was 2·5 or 3·5 and with more transmission before symptom onset. Across different initial numbers of cases, the majority of scenarios with an R0 of 1·5 were controllable with less than 50% of contacts successfully traced. To control the majority of outbreaks, for R0 of 2·5 more than 70% of contacts had to be traced, and for an R0 of 3·5 more than 90% of contacts had to be traced. The delay between symptom onset and isolation had the largest role in determining whether an outbreak was controllable when R0 was 1·5. For R0 values of 2·5 or 3·5, if there were 40 initial cases, contact tracing and isolation were only potentially feasible when less than 1% of transmission occurred before symptom onset.
Interpretation
In most scenarios, highly effective contact tracing and case isolation is enough to control a new outbreak of COVID-19 within 3 months. The probability of control decreases with long delays from symptom onset to isolation, fewer cases ascertained by contact tracing, and increasing transmission before symptoms. This model can be modified to reflect updated transmission characteristics and more specific definitions of outbreak control to assess the potential success of local response efforts.
Funding
Wellcome Trust, Global Challenges Research Fund, and Health Data Research UK.
Introduction
As of Feb 5, 2020, more than 24 550 cases of coronavirus disease 2019 (COVID-19) had been confirmed, including more than 190 cases outside of China, and more than 490 reported deaths globally.1 Control measures have been implemented within China to try to contain the outbreak.2 As people with the infection arrive in countries or areas without ongoing transmission, efforts are being made to halt transmission, and prevent potential outbreaks.3, 4 Isolation of confirmed and suspected cases, and identification of contacts are a crucial part of these control efforts; however, whether these efforts will achieve control of transmission of COVID-19 is unclear.
Isolation of cases and contact tracing becomes less effective if infectiousness begins before the onset of symptoms.5, 6 For example, the severe acute respiratory syndrome (SARS) outbreak that began in southern China in 2003, was eventually able to be controlled through tracing contacts of suspected cases and isolating confirmed cases because the majority of transmission occurred after symptom onset.7 These interventions also play a major role in response to outbreaks where onset of symptoms and infectiousness are concurrent—eg, Ebola virus disease,8, 9 Middle East respiratory syndrome (MERS),10, 11 and many other infections.12, 13
Research in context.
Evidence before this study
Contact tracing and isolation of cases is a common intervention for controlling infectious disease outbreaks. It can be effective but might require intensive public health effort and cooperation to effectively reach and monitor all contacts. Previous work has shown that when the pathogen has infectiousness before symptom onset, control of outbreaks using contact tracing and isolation is more challenging. Further introduction of coronavirus disease 2019 (COVID-19) to new territories is likely in the coming days and weeks, and interventions to prevent an outbreak following these introductions are a key mitigating strategy. Current planning is focused on tracing of contacts of introduced cases, and rapid isolation. These methods have been used previously for other novel outbreaks, but it is not clear if they will be effective for COVID-19.
Added value of this study
We use a mathematical model to assess the feasibility of contact tracing and case isolation to control outbreaks of COVID-19. We used disease transmission characteristics specific to the pathogen and give the best available evidence if contact tracing and isolation can achieve control of outbreaks. We simulated new outbreaks starting from 5, 20, or 40 introduced cases. Contact tracing and isolation might not contain outbreaks of COVID-19 unless very high levels of contact tracing are achieved. Even in this case, if there is subclinical transmission, or a high fraction of transmission before onset of symptoms, this strategy might not achieve control within 3 months.
Implications of all the available evidence
The effectiveness of isolation of cases and contacts to control outbreaks of COVID-19 depends on the precise characteristics of transmission, which remain unclear at the present time. Using the current best understanding, around 80% of symptomatic contacts must be traced and isolated to control over 80% of outbreaks in the model. Future research on the transmission characteristics could improve precision on control estimates.
The effectiveness of isolation and contact-tracing methods hinges on two key epidemiological parameters: the number of secondary infections generated by each new infection and the proportion of transmission that occurs before symptom onset.5 In addition, successful contact tracing and reducing the delay between symptom onset and isolation are crucial, because, during this time, cases remain in the community where they can infect others until isolation.6, 14 Transmission before symptom onset could only be prevented by tracing contacts of confirmed cases and testing (and quarantining) those contacts. Cases that do not seek care, potentially because of subclinical infection, are a further challenge to control.
If COVID-19 can be controlled by isolation and contact tracing, then public health efforts should be focused on this strategy; however, if this is not enough to control outbreaks, then additional resources might be needed for additional interventions. Several key characteristics of the transmissibility and natural history of COVID-19 are currently unknown—eg, whether transmission can occur before symptom onset. Therefore, we explored a range of epidemiological scenarios that represent potential transmission properties based on current information about COVID-19 transmission. We assessed the ability of isolation and contact tracing to control disease outbreaks in areas without widespread transmission using a mathematical model.6, 15, 16, 17 By varying the efficacy of contact-tracing efforts, the size of the outbreak when detected, and the promptness of isolation after symptom onset, we show how viable it is for countries at risk of imported cases to use contact tracing and isolation as a containment strategy.
Methods
Model structure
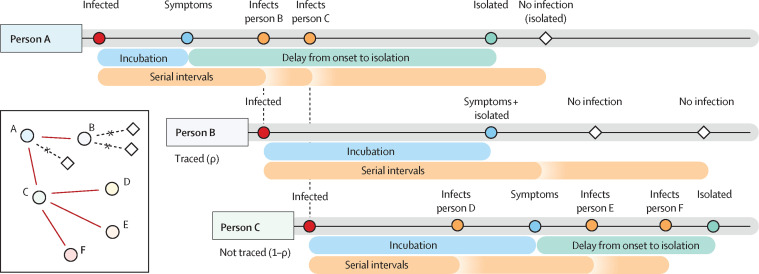
We implemented a branching process model, in which the number of potential secondary cases produced by each individual is drawn from a negative binomial distribution with a mean equal to the reproduction number, and heterogeneity in the number of new infections produced by each individual.6, 15, 17, 18, 19 Each potential new infection was assigned a time of infection drawn from the serial interval distribution. Secondary cases were only created if the person with the infection had not been isolated by the time of infection. As an example (figure 1 ), a person infected with the virus could potentially produce three secondary infections (because three is drawn from the negative binomial distribution), but only two transmissions might occur before the case is isolated. Thus, in the model, a reduced delay from onset to isolation would reduce the average number of secondary cases.
Figure 1.
Example of the simulated process that starts with person A being infected
After an incubation period, person A shows symptoms and is isolated at a time drawn from the delay distribution (table). A draw from the negative binomial distribution with mean reproduction number (R0) and distribution parameter determines how many people person A potentially infects. For each of those, a serial interval is drawn. Two of these exposures occur before the time person A is isolated. Each contact is traced with probability ρ, with probability 1–ρ they are missed by contact tracing. Person B is successfully traced, which means that they will be isolated without delay when they develop symptoms. They could, however, still infect others before they are isolated. Person C is missed by contact tracing. This means that they are only detected if and when symptomatic, and are isolated after a delay from symptom onset. Because person C was not traced, they infected two more people (E and F), in addition to person D, than if they had been isolated at symptom onset. A version with subclinical transmission is given in the appendix appendix (p 12).
We initialised the branching process with five, 20, or 40 cases to represent a newly detected outbreak of varying size. Initial symptomatic cases were then isolated after symptom onset with a delay drawn from the onset-to-isolation distribution (table ). Isolation was assumed to be 100% effective at preventing further transmission; therefore, in the model, failure to control the outbreak resulted from the incomplete contact tracing and the delays in isolating cases rather than the inability of isolation to prevent further transmission. Either 100% or 90% of cases became symptomatic, and all symptomatic cases were eventually reported.
Table.
Parameter values for the model
| Value | Reference | |
|---|---|---|
| Sampled | ||
| Delay from onset to isolation (short) | 3·43 days (2·02–5·23) | Donnelly et al20 |
| Delay from onset to isolation (long) | 8·09 days (5·52–10·93) | Li et al21 |
| Incubation period | 5·8 days (2·6) | Backer et al22 |
| Serial interval | Incubation period (2) | Assumed |
| Fixed | ||
| Initial cases | 5, 20, and 40 | Public Health England11 and Klinkenberg and colleagues14 |
| Percentage of contacts traced | 0%, 20%, 40%, 60%, 80%, 100% | Tested |
| Reproduction number (R0; low, central, high estimate) | 1·5, 2·5, 3·5 | Kucharski et al17 and Imai et al18 |
| Overdispersion in R0 (SARS-like) | 0·16 | Lloyd-Smith et al19 |
| R0 after isolation | 0 | Assumed |
| Cases isolated once identified | 100% | Assumed |
| Isolation effectiveness | 100% | Assumed |
| Subclinical infection percentage | 0%, 10% | Tested |
Data are median (IQR) or mean (SD), n, or %. Sampled values are probabilistically sampled during the simulation, and fixed values remain constant during the simulation. The mean of the short and long delays are 3·83 and 9·1, respectively. SARS=severe acute respiratory syndrome.
Each newly infected case was identified through contact tracing with probability ρ. Secondary cases that had been traced were isolated immediately on becoming symptomatic. Cases that were missed by contact tracing (probability 1–ρ) were isolated when they became symptomatic, with a delay drawn from the onset-to-isolation distribution.
In addition, each case had an independent probability of being subclinical, and was therefore not detected either by self-report or contact tracing. New secondary cases caused by a subclinical case were missed by contact tracing and could only be isolated on the basis of symptoms. The model included isolation of symptomatic individuals only—ie, no quarantine, so isolation could not prevent transmission before symptom onset. In the model, subclinical cases were never isolated, whereas symptomatic cases might transmit before symptoms appear, but were eventually isolated. Quarantining contacts of cases (ie, individuals who are not yet symptomatic, and might not be infected) requires a considerable investment in public health resources, and has not been widely implemented for all contacts of cases.3 However, some countries have adopted a quarantine or self-quarantine policy for airline travellers who have returned from countries with confirmed COVID-19 transmission.23
Transmission scenarios
We ran 1000 simulations of each combination of R 0, the proportion of transmission before symptom onset, onset-to-isolation delay, the number of initial cases, and the probability that a contact was traced (table).
We explored two scenarios of delay (short and long) between symptom onset and isolation (figure 2 ). The short delay was estimated during the late stages of the 2003 SARS outbreak in Singapore,18 and the long delay was an empirical distribution calculated from the early phase of the COVID-19 outbreak in Wuhan.23 We varied the percentage of contacts traced from 0% to 100%, at 20% intervals, to quantify the effectiveness of contact tracing.
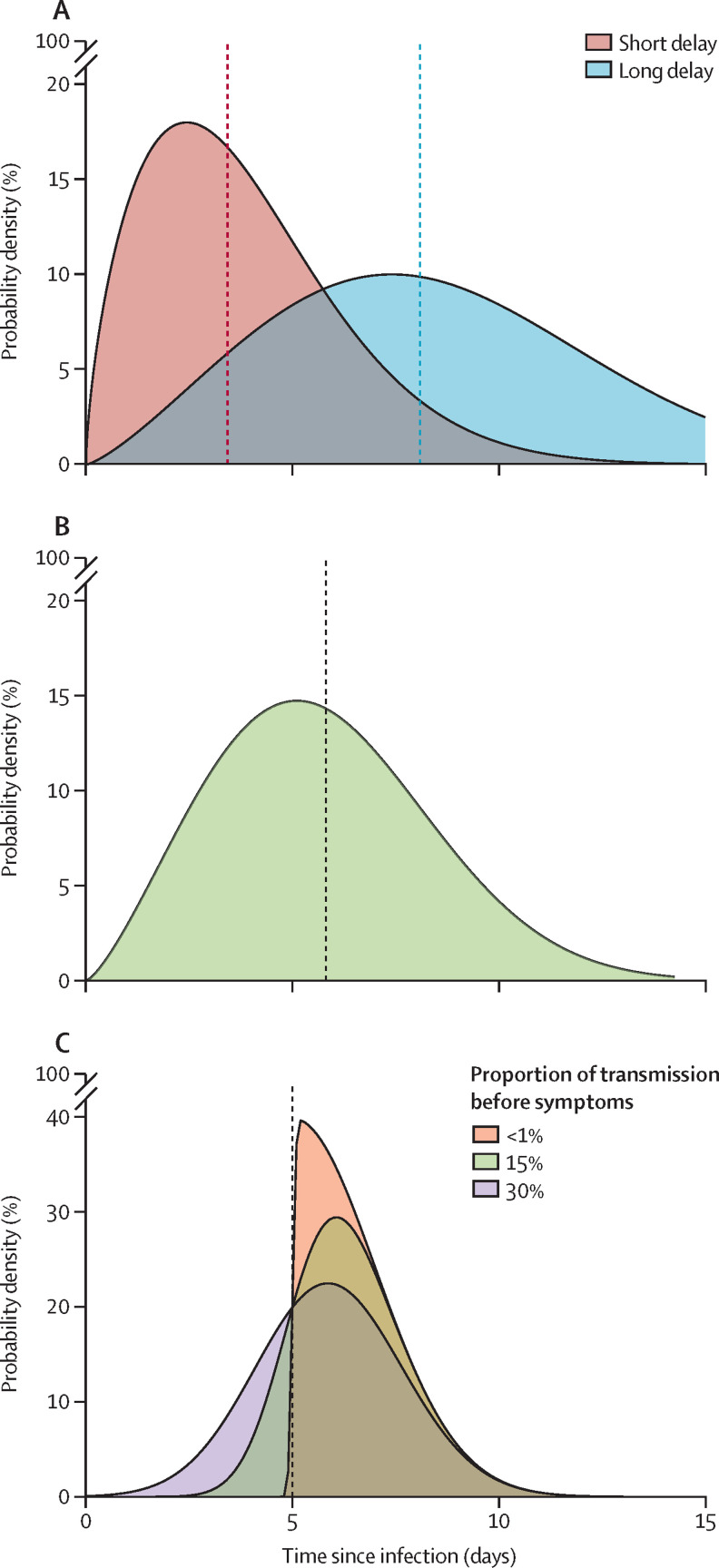
Figure 2.
Probability distributions used in simulations
(A) The short and long delay distributions between the onset of symptoms and isolation (median marked by line). Parameter values and references are given in the table. (B) The incubation distribution estimate fitted to data from the Wuhan outbreak by Backer and colleagues.22 (C) An example of the method used to sample the serial interval for a case that has an incubation period of 5 days. Each case has an incubation period drawn from the distribution in (B), their serial interval is then drawn from a skewed normal distribution with the mean set to the incubation period of the case. In (C), the incubation period was 5 days. The skew parameter of the skewed normal distribution controls the proportion of transmission that occurs before symptom onset; the three scenarios explored are less than 1%, 15%, and 30% of transmission before onset.
The incubation period for each case was drawn from a Weibull distribution. A corresponding serial interval for each case was then drawn from a skewed normal distribution with the mean parameter of the distribution set to the incubation period for that case, an SD of 2, and a skew parameter chosen such that a set proportion of serial intervals were shorter than the incubation period (meaning that a set proportion of transmission happened before symptom onset; figure 2). This sampling approach ensured that the serial interval and incubation period for each case was correlated, and prevented biologically implausible scenarios where a case could develop symptoms soon after exposure, but not become infectious until very late after exposure and vice versa.
There are many estimates of the reproduction number for the early phase of the COVID-19 outbreak in Wuhan, China,15, 17, 18, 21, 24, 25, 26, 27, 28 and therefore we used the values 1·5, 2·5, and 3·5, which span most of the range of current estimates (table). We used the secondary case distribution from the 2003 SARS outbreak,19 and tested the effect of lower heterogeneity in the number of secondary cases29 as a sensitivity analysis (appendix pp 2–5). We calculated the effective reproduction number (R eff) of the simulation as the average number of secondary cases produced by each infected person in the presence of isolation and contact tracing. We present results in relation to the baseline scenario of R 0 of 2·5,21 20 initial cases, a short delay to isolation,20 15% of transmission before symptom onset,30 and 0% subclinical infection.31 Values of the natural history represent the current best understanding of COVID-19 transmission, and we used 20 index cases and a short delay to isolation to represent a relatively large influx into a setting of high awareness of possible infection.23
Definition of outbreak control
Outbreak control was defined as no new infections between 12 and 16 weeks after the initial cases. Outbreaks that reached 5000 cumulative cases were assumed to be too large to control within 12–16 weeks, and were categorised as uncontrolled outbreaks. Based on this definition, we reported the probability that an outbreak of a severe acute respiratory syndrome coronavirus 2-like pathogen would be controlled within 12 weeks for each scenario, assuming that the basic reproduction number remained constant and no other interventions were implemented.
The probability that an outbreak is controlled gives a one-dimensional understanding of the difficulty of achieving control, because the model placed no constraints on the number of cases and contacts that could be traced and isolated. In reality, the feasibility of contact tracing and isolation is likely to be determined both by the probability of achieving control, and the resources needed to trace and isolate infected cases.32 We therefore reported the weekly maximum number of cases undergoing contact tracing and isolation for each scenario that resulted in outbreak control. New cases require their contacts to be traced, and if these numbers are high, it can overwhelm the contact-tracing system and affect the quality of the contact-tracing effort.33 It is likely that the upper limit on contacts to trace varies from country to country.
All code is available as an R package.
Role of the funding source
The funders of the study had no role in study design, data collection, data analysis, data interpretation, writing of the Article, or the decision to submit for publication. All authors had full access to all the data in the study and were responsible for the decision to submit the Article for publication.
Results
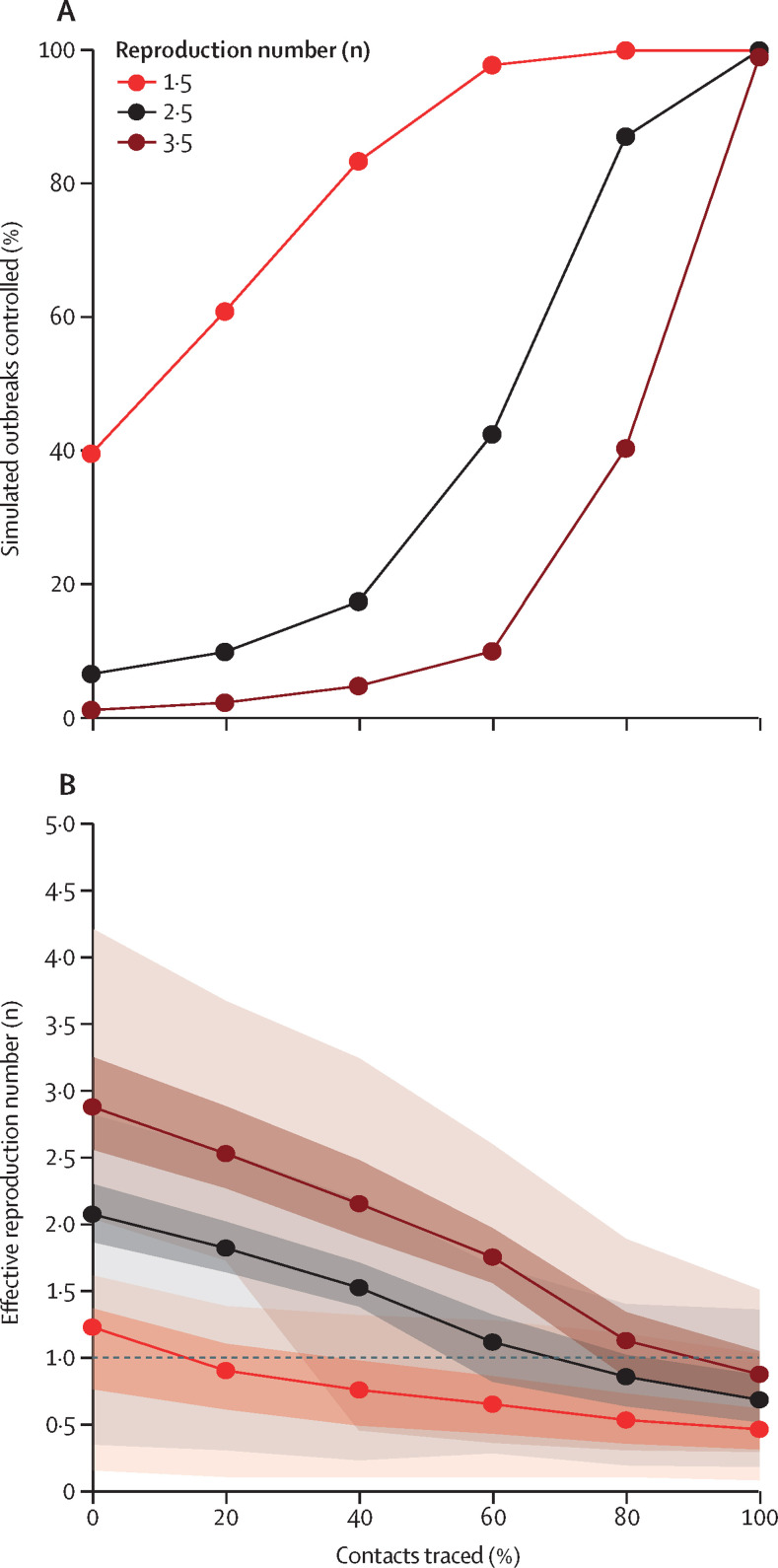
To achieve control of 90% of outbreaks, 80% of contacts needed to be traced and isolated for scenarios with a reproduction number of 2·5 (figure 3 ). The probability of control was higher at all levels of contact tracing when the reproduction number was 1·5, and fell rapidly for a reproduction number of 3·5. At a reproduction number of 1·5, the effect of isolation was coupled with the chance of stochastic extinction resulting from overdispersion,19 which is why some outbreaks were controlled even at 0% contacts traced.
Figure 3.
Effect of isolation and contact tracing on controlling outbreaks and on the effective reproduction number
(A) The percentage of outbreaks that are controlled for scenarios with varying reproduction number (R0), at each value of contacts traced. The baseline scenario is R0 of 2·5, 20 initial cases, a short delay to isolation, 15% of transmission before symptom onset, and 0% subclinical infection. A simulated outbreak is defined as controlled if there are no cases between weeks 12 and 16 after the initial cases. Other scenarios are presented in the appendix (p 2). (B) Effective reproduction number in the presence of case isolation and contact tracing. Median, and 50% and 95% intervals are shown.
Isolation and contact tracing decreased transmission, as shown by a decrease in the effective reproduction number (figure 3). When the basic reproduction number was 1·5, the median estimate rapidly fell below 1, which indicated that control was probable. For the higher transmission scenarios, a higher level of contact tracing was needed to bring the median effective reproduction number below 1. The effect of isolation without contact tracing can be seen at 0%, where the effective reproduction number was lower than the simulated basic reproduction number because of rapid isolation (and ceasing transmission) of cases.
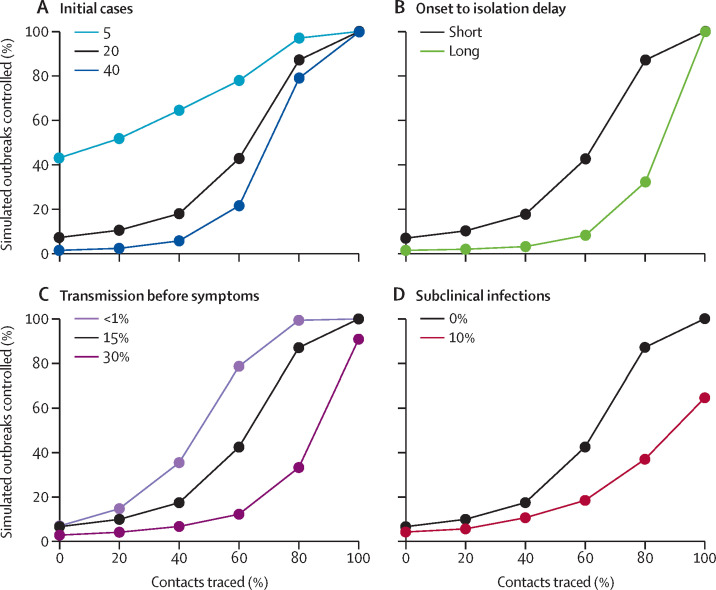
The number of initial cases had a large effect on the probability of achieving control. With five initial cases, there was a greater than 50% chance of achieving control in 3 months, even at modest contact-tracing levels (figure 4 ). More than 40% of these outbreaks were controlled with no contact tracing because of the combined effects of isolation of symptomatic cases and stochastic extinction. The probability of control dropped as the number of initial cases increased—eg, for 40 initial cases, 80% contact tracing did not lead to 80% of simulations controlled within 3 months.
Figure 4.
Achieving control of simulated outbreaks under different transmission scenarios
The percentage of outbreaks controlled for the baseline scenario, and varied number of initial cases (A), time from onset to isolation (B), percentage of transmission before symptoms (C), and proportion of subclinical (asymptomatic) cases (D). The baseline scenario is a basic reproduction number (R0) of 2·5, 20 initial cases, a short delay to isolation, 15% of transmission before symptom onset, and 0% subclinical infection. Results for R0=1·5 and 3·5 are given in the appendix. A simulated outbreak is defined as controlled if there are no cases between weeks 12 and 16 after the initial cases.
The delay from symptom onset to isolation had a major role in achieving control of outbreaks (figure 4). At 80% of contacts traced, the probability of achieving control fell from 89% to 31%, with a long delay from onset to isolation. If no transmission occurred before symptom onset, then the probability of achieving control was higher for all values of contacts traced (figure 4). The difference between 15% and 30% of transmission before symptoms had a marked effect on probability to control. We found this effect in all scenarios tested (appendix p 5). In scenarios in which only 10% of cases were asymptomatic, the probability that simulations were controlled by isolation and contact tracing for all values of contact tracing decreased (figure 4). For 80% of contacts traced, only 37% of outbreaks were controlled, compared with 89% without subclinical infection. These figures show the effect of changing one model assumption at a time; all combinations are given in the appendix, in comparison to the baseline scenario (appendix pp 2–5).
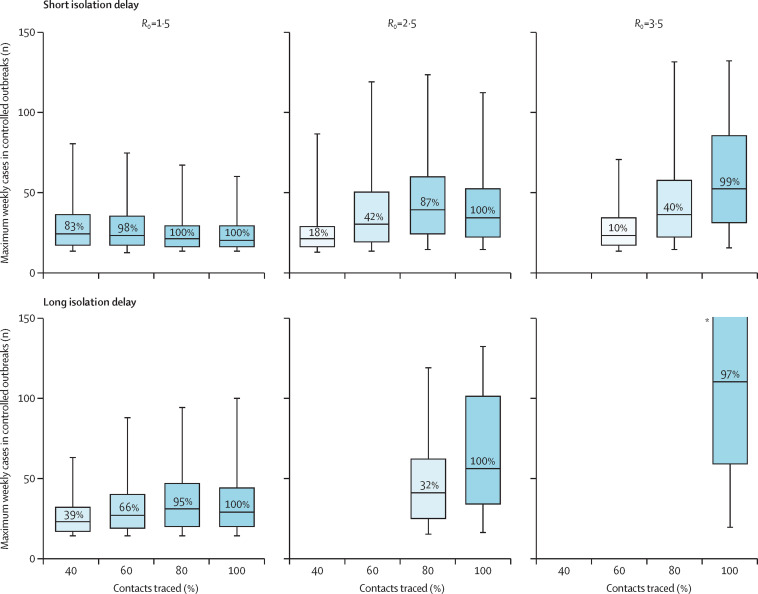
In many scenarios, between 25 and 100 symptomatic cases occurred in a week at the peak of the simulated outbreak (figure 5 ). All of these cases, and their contacts, would need to be isolated. Large numbers of new cases can overwhelm isolation facilities, and the more contacts that need to be traced, the greater the logistical task of following them up. In the 2014 Ebola epidemic in Liberia, each case reported between six and 20 contacts,8 and the number of contacts seen in MERS outbreaks is often higher than that.10 20 contacts for each of 100 cases means 2000 contacts traced to achieve control. Uncontrolled outbreaks typically had higher numbers of cases (appendix p 13). The maximum numbers of weekly cases in figure 5 might appear counterintuitive, because a lower maximum number of weekly cases is not associated with higher outbreak control. This occurs because with better contact tracing it becomes possible to control outbreaks with higher numbers of weekly cases.
Figure 5.
The maximum weekly cases requiring contact tracing and isolation in scenarios with 20 index cases that achieved control within 3 months
Scenarios vary by reproduction number and the mean delay from onset to isolation. 15% of transmission occurred before symptom onset, and 0% subclinical infection. The percentage of simulations that achieved control is shown in the boxplot. This illustrates the potential size of the eventually controlled simulated outbreaks, which would need to be managed through contact tracing and isolation. *The interval extends out of the plotting region.
Discussion
We determined conditions in which case isolation, contact tracing, and preventing transmission by contacts who are infected would be sufficient to control a new COVID-19 outbreak in the absence of other control measures. We found that in some plausible scenarios, case isolation alone would be unlikely to control transmission within 3 months. Case isolation was more effective when there was little transmission before symptom onset and when the delay from symptom onset to isolation was short. Preventing transmission by tracing and isolating a larger proportion of contacts, thereby decreasing the effective reproduction number, improved the number of scenarios in which control was likely to be achieved. However, these outbreaks required a large number of cases to be contact traced and isolated each week, which is of concern when assessing the feasibility of this strategy. Subclinical infection markedly decreased the probability of controlling outbreaks within 3 months.
In scenarios in which the reproduction number was 2·5, 15% of transmission occurred before symptom onset, and there was a short delay to isolation, at least 80% of infected contacts needed to be traced and isolated to give a probability of control of 90% or more. This scenario echoes other suggestions that highly effective contact tracing will be necessary to control outbreaks in other countries.16 In scenarios in which the delay from onset to isolation was long, similar to the delays in the early phase of the outbreak in Wuhan, the same contact tracing success of 80% achieved a probability of containing an outbreak of less than 40%. Higher presymptomatic transmission decreases the probability that the outbreaks were controlled, under all reproduction numbers and isolation delay distributions tested.
Our model did not include other control measures that might decrease the reproduction number and therefore also increase the probability of achieving control of an outbreak. At the same time, it assumed that isolation of cases and contacts is completely effective, and that all symptomatic cases are eventually reported. Relaxing these assumptions would decrease the probability that control is achieved. We also make the assumption that contact is required for transmission between two individuals, but transmission via fomites might be possible. This type of transmission would make effective contact tracing challenging, and good respiratory and hand hygiene would be crucial to reduce this route of transmission, coupled with environmental decontamination in health-care settings. For this reason, we used contact-tracing percentage intervals of 20% to avoid indicating more precision in the corresponding probability of control than the model could support.
We simplified our model to determine the effect of contact tracing and isolation on the control of outbreaks under different scenarios of transmission; however, as more data becomes available, the model can be updated or tailored to particular public health contexts. The robustness of control measures is likely to be affected both by differences in transmission between countries, but also by the concurrent number of cases that require contact tracing in each scenario. Practically, there is likely to be an upper bound on the number of cases that can be traced, which might vary by country, and case isolation is likely to be imperfect.34 We reported the maximum number of weekly cases during controlled outbreaks, but the capacity of response efforts might vary. In addition to the number of contacts, other factors could decrease the percentage of contacts that can be traced, such as cooperation of the community with the public health response.
We explored a range of scenarios informed by the latest evidence on transmission of COVID-19. Similar analyses using branching models have already been used to analyse the Wuhan outbreak to find plausible ranges for the initial exposure event size and the basic reproduction number.15, 18 Our analysis expands on this work by including infectiousness before the onset of symptoms, case isolation, explicit modelling of case incubation periods, and time to infectiousness. A key area of uncertainty is whether, and for how long, individuals are infectious before symptom onset, and whether subclinical infection occurs; both are likely to make the outbreak harder to control.22 Whether, and how much, transmission occurs before symptoms is difficult to quantify. Under-reporting of prodromal symptoms, such as fatigue and mild fever, is possible; thus, transmission might not truly be occurring before symptoms, but before noticeable symptoms. There is evidence of transmission before onset,30 and so we used 15%. Increased awareness of prodromal symptoms, and therefore short delays until isolation—as seen in the SARS outbreak in Beijing in 200335—would increase control of outbreaks in our model. If contact tracing included testing of non-symptomatic contacts, those contacts could be quarantined without symptoms, which would decrease transmission in the model. Costs associated with additional testing might not be possible in all contexts.
The model could be modified to include some transmission after isolation (such as in hospitals), which would decrease the probability of achieving control. In addition, we defined an outbreak as controlled if it reached extinction by 3 months, regardless of outbreak size or number of weekly cases. This definition might be narrowed where the goal is to keep the overall caseload of the outbreak low. This might be of concern to local authorities for reducing the health-care surges, and might limit geographical spread.
Our study indicates that in most plausible outbreak scenarios, case isolation and contact tracing alone is insufficient to control outbreaks, and that in some scenarios even near perfect contact tracing will still be insufficient, and further interventions would be required to achieve control. Rapid and effective contact tracing can reduce the initial number of cases, which would make the outbreak easier to control overall. Effective contact tracing and isolation could contribute to reducing the overall size of an outbreak or bringing it under control over a longer time period.
This online publication has been corrected. The corrected version first appeared at thelancet.com/lancetgh on March 5, 2020
Data sharing
No data were used in this study. The R code for the work is available at https://github.com/cmmid/ringbp.
Acknowledgments
Acknowledgments
JH, SA, JDM, and SF were funded by the Wellcome Trust (grant number 210758/Z/18/Z), AG and CIJ were funded by the Global Challenges Research Fund (grant number ES/P010873/1), TWR and AJK were funded by the Wellcome Trust (grant number 206250/Z/17/Z), and RME was funded by HDR UK (grant number MR/S003975/1). This research was partly funded by the National Institute for Health Research (NIHR) (16/137/109) using UK aid from the UK Government to support global health research. The views expressed in this publication are those of the authors and not necessarily those of the NIHR or the UK Department of Health and Social Care. This research was partly funded by the Bill & Melinda Gates Foundation (INV-003174). This research was also partly funded by the Global Challenges Research Fund project RECAP managed through Research Councils UK and Economic and Social Research Council (ES/P010873/1). We would like to acknowledge (in a randomised order) the other members of the London School of Hygiene & Tropical Medicine COVID-19 modelling group, who contributed to this work: Stefan Flasche, Mark Jit, Nicholas Davies, Sam Clifford, Billy J Quilty, Yang Liu, Charlie Diamond, Petra Klepac, and Hamish Gibbs. Their funding sources are as follows: Stefan Flasche and Sam Clifford (Sir Henry Dale Fellowship [grant number 208812/Z/17/Z]); Mark Jit, Yang Liu, and Petra Klepac (BMGF [grant number INV-003174]); Nicholas Davies (NIHR [grant number HPRU-2012–10096]); Billy J Quilty (grant number NIHR [16/137/109]); Charlie Diamond and Yang Liu (NIHR [grant number 16/137/109]); and Hamish Gibbs (Department of Health and Social Care [grant number ITCRZ 03010]).
Contributors
RME conceived the study. JH, AG, SA, WJE, SF, and RME designed the model. CIJ, TWR, and NIB worked on statistical aspects of the study. JH, AG, SA, and NIB programmed the model, and, with RME, made the figures. AJK and JDM consulted on the code. All authors interpreted the results, contributed to writing the Article, and approved the final version for submission.
Declaration of interests
We declare no competing interests.
Contributor Information
Centre for the Mathematical Modelling of Infectious Diseases COVID-19 Working Group:
Fiona Sun, Stefan Flasche, Billy J Quilty, Nicholas Davies, Yang Liu, Samuel Clifford, Petra Klepac, Mark Jit, Charlie Diamond, Hamish Gibbs, and Kevin van Zandvoort
Supplementary Material
References
- 1.WHO . World Health Organization; 2020. Novel coronavirus (2019-nCoV) situation report 16.https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200205-sitrep-16-ncov.pdf?sfvrsn=23af287f_2 [Google Scholar]
- 2.WHO . World Health Organization; 2020. Novel coronavirus (2019-nCoV) situation report 2.https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200122-sitrep-2-2019-ncov.pdf?sfvrsn=4d5bcbca_2 [Google Scholar]
- 3.European Centre for Disease Prevention and Control . European Centre for Disease Prevention and Control; 2020. Public health management of persons having had contact with novel coronavirus cases in the European Union.https://www.ecdc.europa.eu/en/publications-data/public-health-management-persons-having-had-contact-novel-coronavirus-cases [Google Scholar]
- 4.Quilty B, Clifford S, CCMID nCoV working group. Flasche S, Eggo RM. Effectiveness of airport screening at detecting travellers infected with 2019-nCoV. 2020. https://cmmid.github.io/ncov/airport_screening_report/airport_screening_preprint_2020_01_30.pdf [DOI] [PMC free article] [PubMed]
- 5.Fraser C, Riley S, Anderson RM, Ferguson NM. Factors that make an infectious disease outbreak controllable. Proc Natl Acad Sci USA. 2004;101:6146–6151. doi: 10.1073/pnas.0307506101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Peak CM, Childs LM, Grad YH, Buckee CO. Comparing nonpharmaceutical interventions for containing emerging epidemics. Proc Natl Acad Sci USA. 2017;114:4023–4028. doi: 10.1073/pnas.1616438114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Glasser JW, Hupert N, McCauley MM, Hatchett R. Modeling and public health emergency responses: lessons from SARS. Epidemics. 2011;3:32–37. doi: 10.1016/j.epidem.2011.01.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Swanson KC, Altare C, Wesseh CS, et al. Contact tracing performance during the Ebola epidemic in Liberia, 2014–2015. PLoS Negl Trop Dis. 2018;12 doi: 10.1371/journal.pntd.0006762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.WHO . World Health Organization; 2015. Implementation and management of contact tracing for Ebola virus disease.http://www.who.int/csr/resources/publications/ebola/contact-tracing/en/ [Google Scholar]
- 10.Kang M, Song T, Zhong H, et al. Contact tracing for imported case of Middle East respiratory syndrome, China, 2015. Emerging Infect Dis. 2016;22:9. doi: 10.3201/eid2209.152116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Public Health England MERS-CoV close contact algorithm. Public health investigation and management of close contacts of Middle East Respiratory Coronavirus (MERS-CoV) cases (v17 29 January 2019) 2019. https://assets.publishing.service.gov.uk/government/uploads/system/uploads/attachment_data/file/776218/MERS-CoV_Close_contacts_algorithm.pdf
- 12.European Centre for Disease Prevention and Control Risk assessment guidelines for diseases transmitted on aircraft. Part 2: Operational guidelines for assisting in the evaluation of risk for transmission by disease. 2011. https://www.ecdc.europa.eu/sites/default/files/media/en/publications/Publications/1012_GUI_RAGIDA_2.pdf
- 13.Hoang TTT, Nguyen VN, Dinh NS, et al. Active contact tracing beyond the household in multidrug resistant tuberculosis in Vietnam: a cohort study. BMC Public Health. 2019;19:241. doi: 10.1186/s12889-019-6573-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Klinkenberg D, Fraser C, Heesterbeek H. The effectiveness of contact tracing in emerging epidemics. PLoS One. 2006;1:e12. doi: 10.1371/journal.pone.0000012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Abbott S, Hellewell J, Munday J, CMMID nCoV working group. Funk S. The transmissibility of novel coronavirus in the early stages of the 2019–20 outbreak in Wuhan: exploring initial point-source exposure sizes and durations using scenario analysis. Wellcome Open Res. 2020;5:17. doi: 10.12688/wellcomeopenres.15718.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Imai N, Cori A, Dorigatti I, et al. Report 3: transmissibility of 2019-nCov. 2020. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-2019-nCoV-transmissibility.pdf
- 17.Kucharski AJ, Eggo RM, Watson CH, Camacho A, Funk S, Edmunds WJ. Effectiveness of ring vaccination as control strategy for Ebola virus disease. Emerg Infect Dis. 2016;22:105–108. doi: 10.3201/eid2201.151410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Imai N, Dorigatti I, Cori A, Riley S, Ferguson NM. Estimating the potential total number of novel coronavirus cases in Wuhan City, China. 2020. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/2019-nCoV-outbreak-report-22-01-2020.pdf
- 19.Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz WM. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438:355–359. doi: 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Donnelly CA, Ghani AC, Leung GM, et al. Epidemiological determinants of spread of causal agent of severe acute respiratory syndrome in Hong Kong. Lancet. 2003;361:1761–1766. doi: 10.1016/S0140-6736(03)13410-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Li Q, Guan X, Wu P, et al. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N Engl J Med. 2020 doi: 10.1056/NEJMoa2001316. published online Jan 29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Backer JA, Klinkenberg D, Wallinga J. The incubation period of 2019-nCoV infections among travellers from Wuhan, China. medRxiv. 2020 doi: 10.1101/2020.01.27.20018986. published online Jan 28. (preprint). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.BBC News Coronavirus patient is University of York student. Feb 1, 2020. https://www.bbc.com/news/health-51337400
- 24.Riou J, Althaus CL. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Eurosurveillance. 2020;25 doi: 10.2807/1560-7917.ES.2020.25.4.2000058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Bedford T, Neher R, Hadfield J, Hodcroft E, Ilcisin M, Müller N. Genomic analysis of nCoV spread. Situation report 2020-01-30. 2020. https://nextstrain.org/narratives/ncov/sit-rep/2020-01-30
- 26.Majumder M, Mandl KD. Social Science Research Network; Rochester, NY: 2020. Early transmissibility assessment of a novel coronavirus in Wuhan, China.https://papers.ssrn.com/abstract=3524675 [Google Scholar]
- 27.Read JM, Bridgen JR, Cummings DA, Ho A, Jewell CP. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions. medRxiv. 2020 doi: 10.1101/2020.01.23.20018549. published online Jan 28. (preprint). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zhao S, Ran J, Musa SS, et al. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak. Int J Infect Dis. 2020;92:214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Dugas AF, Jalalpour M, Gel Y, et al. Influenza forecasting with Google Flu Trends. PLoS One. 2013;8 doi: 10.1371/journal.pone.0056176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yu P, Zhu J, Zhang Z, Han Y, Huang L. A familial cluster of infection associated with the 2019 novel coronavirus indicating potential person-to-person transmission during the incubation period. J Infect Dis. 2020 doi: 10.1093/infdis/jiaa077. published online Feb 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Heymann DL, Shindo N. COVID-19: what is next for public health? Lancet. 2020;395:542–545. doi: 10.1016/S0140-6736(20)30374-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dhillon RS, Srikrishna D. When is contact tracing not enough to stop an outbreak? Lancet Infect Dis. 2018;18:1302–1304. doi: 10.1016/S1473-3099(18)30656-X. [DOI] [PubMed] [Google Scholar]
- 33.Olu OO, Lamunu M, Nanyunja M, et al. Contact tracing during an outbreak of Ebola virus disease in the Western area districts of Sierra Leone: lessons for future Ebola outbreak response. Front Public Health. 2016;4:130. doi: 10.3389/fpubh.2016.00130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Huang C, Wang Y, Li X, et al. Clinical features of patients infected with 2019 novel coronavirus in Wuhan, China. Lancet. 2020;395:497–506. doi: 10.1016/S0140-6736(20)30183-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pang X, Zhu Z, Xu F, et al. Evaluation of control measures implemented in the severe acute respiratory syndrome outbreak in Beijing, 2003. JAMA. 2003;290:3215–3221. doi: 10.1001/jama.290.24.3215. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
No data were used in this study. The R code for the work is available at https://github.com/cmmid/ringbp.