Abstract
Kinesin is a typical molecular motor that can step processively on microtubules powered by hydrolysis of adenosine triphosphate (ATP) molecules, playing a critical role in intracellular transports. Its dynamical properties such as its velocity, stepping ratio, run length, dissociation rate, etc. as well as the load dependencies of these quantities have been well documented through single-molecule experimental methods. In particular, the run length shows a dramatic asymmetry with respect to the direction of the load, and the dissociation rate exhibits a slip–catch–slip bond behavior under the backward load. Here, an analytic theory was provided for the dynamics of kinesin motors under both forward and backward loads, explaining consistently and quantitatively the diverse available experimental results.
1. Introduction
The kinesin protein is a typical biological molecular motor that performs mechanical work powered by the free energy released from the chemical reaction.1−6 Kinesin (concretely kinesin-1) constitutes two identical motor domains (heads) connected together by a coiled-coil stalk through their neck linkers (NLs).7 It can step processively on microtubules (MTs) toward the plus end by hydrolyzing adenosine triphosphate (ATP) molecules, which play a critical role in intracellular transports. To dissect the biophysical mechanism of the kinesin movement, many of the quantities that characterize the motor dynamics have been well documented through different experimental methods. For example, with single-molecule optical tweezer techniques, the dependencies of quantities such as the velocity, forward-to-backward stepping ratio (abbreviated to stepping ratio), dwell time between two successive mechanical steps, etc. on the external force or load in both the backward and forward directions were determined.8−17 In particular, the single-molecule results,17,18 which were reproduced by computational simulations,19,20 showed interestingly that the run length is dramatically asymmetric with respect to the direction of the external force acting on the coiled-coil stalk with the run length under a moderate forward force being much smaller than under a moderate backward force.
Apart from the abovementioned quantities, the dissociation rate of the motor from its track during its processive motion is another important quantity to characterize its dynamic behaviors. Particularly, to study theoretically and computationally the cooperative transports by multiple molecular motors, besides the velocity versus force relations of the single motors, their dissociation rate versus force relations are also indispensable.21−31 Following the concept of Kramers theory, the dissociation rate of a motor is usually argued to be an exponential function of the force. However, the available experimental evidence indicated that the dissociation rate of the kinesin motor exhibits a slip–catch–slip bond behavior: as the backward force increases, the dissociation rate first increases then decreases and then increases again.22 Recent computational simulations also showed that the dissociation rate exhibits the slip–catch–slip bond behavior.32
Although a lot of analytical and/or computational studies have been presented on the dynamics of kinesin molecular motors,19,20,33−42 an analytical theory is still lacking, which can give consistent and quantitative explanations of the dependencies of the quantities such as the velocity, stepping ratio, run length, dissociation rate, etc. upon both forward and backward forces and particularly the dramatic asymmetry of the run length with respect to the force direction as well as the slip–catch–slip bond behavior for the dissociation rate under the backward force. The purpose of this work is to present such an analytical theory.
2. Model
2.1. Chemomechanical Coupling Pathway
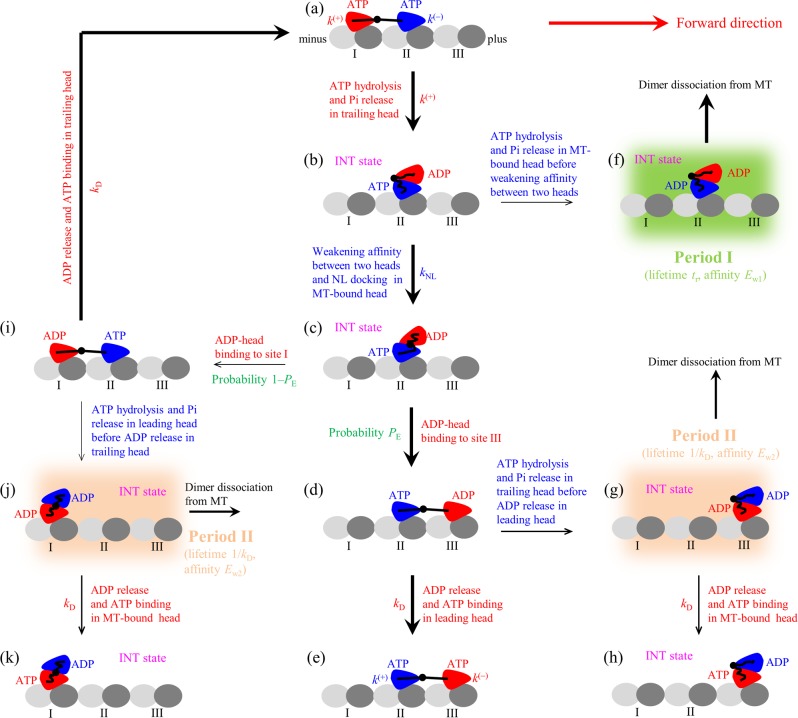
The model for the chemomechanical coupling pathway of the kinesin at saturating concentrations of ATP is schematically shown in Figure 1, which is modified slightly from that presented before.19,20,41,42 It is set up based mainly on the following three elements: (i) A kinesin head in an empty (ϕ), ATP, or ADP·Pi state has a strong interaction with an MT-tubulin heterodimer,43 inducing conformational changes in the MT tubulin.44 After the MT-bound ADP·Pi head releases Pi, it temporally has a much lower binding energy (Ew1) to the local MT tubulin (with the conformational changes) than the weak binding energy (Ew2) to other MT tubulins (without the conformational changes).45 Since the weak interaction of the ADP head with the MT tubulin induces nearly no conformational change in the MT tubulin,45 in a time period tr of the order of microseconds after the head releases Pi, the local MT tubulin restores elastically to its normally unchanged conformation with the binding energy between the ADP head and the local MT tubulin changing from Ew1 to Ew2. (ii) When the MT-bound head is in the ATP or ADP·Pi state, a large conformational change of the head can take place,46 enabling the NL to dock into the head,15,46,47 while in the ϕ or ADP state, the large conformational change cannot take place46 with the NL docking unable to occur.15,46,47 (iii) The MT-bound head without the large conformational change has a strong affinity for the ADP head while with the conformational change has a much weaker affinity, as atomistic MD simulations indicated.48 The detailed correlations among the ATPase activity, reduction of the affinity between two heads, and NL docking are described in the Supporting Information (Section S2).
Figure 1.
Model of kinesin chemomechanical coupling. (a–k) Pathway of kinesin stepping at saturating ATP and occurrence of weak MT-binding periods (including periods I and II) when the dimer binds weakly to MT (see text for detailed descriptions). The thickness of the arrow denotes the magnitude of the transition rate or probability under no load. For simplicity, ATP hydrolysis and Pi release are treated here as one step with the symbol ATP representing both ATP and ADP·Pi states, because in both ATP and ADP·Pi states the head binds strongly to the MT. As a result, the change of ATP to ADP shown here consists of two sequential transitions including the transition of ATP to ADP·Pi and that of ADP·Pi to ADP. Since at saturating ATP after ATP release from the leading head, another ATP molecule can bind immediately, and the lifetime of the nucleotide-free state is so short that the nucleotide-free state is neglected here.
Let us begin the chemomechanical coupling cycle of the kinesin dimer with its two heads in the ATP state bound strongly to the MT with the nucleotide-binding pocket (NBP) of the trailing head closed while the NBP of the leading head open (see Section S2) (Figure 1a). The trailing head has a much higher rate of ATP hydrolysis and Pi release than that of the leading head (see the next section or Section S2). After ATP hydrolysis and Pi release taking place in the trailing head (opening its NBP), the head dissociates easily from binding site I on the MT by overcoming Ew1 and diffuses rapidly to the intermediate (INT) position relative to the MT-bound head where the two heads have a high binding energy (Figure 1b). Then, the closing of the NBP and large conformational change of the MT-bound ATP head can take place, weakening greatly its affinity for the ADP head and inducing its NL docking (Section S2) (Figure 1c). With a probability PE, the ADP head can diffuse forward rapidly and bind to site III with affinity Ew2 (Figure 1d). Then, ADP release occurs in the leading head followed immediately by ATP binding (Figure 1e). Figure 1e is the same as Figure 1a except that the dimer took a forward step of size d = 8.2 nm, the distance between two successive binding sites on an MT filament.
From Figure 1b, ATP hydrolysis and Pi release in the MT-bound head can also take place occasionally before weakening of its affinity for the ADP head occurs (Figure 1f). During the time period tr (called period I) before the affinity of the ADP head for the local MT tubulin changes from Ew1 to Ew2, the kinesin dimer (with the two heads bound together by high affinity) can easily detach from the MT by overcoming Ew1. From Figure 1d, ATP hydrolysis and Pi release can also take place occasionally in the trailing head before ADP release occurs in the leading head. The trailing ADP head then detaches from site II and diffuses to the INT position where the two ADP heads have a large binding energy (Figure 1g). During the time period (called period II) before ADP release occurs in the MT-bound head, the kinesin dimer can detach from the MT by overcoming Ew2 with high probability. If the dimer has not detached until ADP release occurs in the MT-bound head, after ATP binding, the dimer becomes the state of Figure 1h that is the same as Figure 1b except that the dimer took a forward step.
From Figure 1c, with the probability 1 – PE, the detached ADP head can also diffuse backward and bind to site I with affinity Ew2 (noting that, after detaching from site I, the affinity of the ADP head for site I changes rapidly to Ew2 in the time tr of the order of microseconds) (Figure 1i). It is noted that, in Figure 1i, due to the effect of the NL in the backward and horizontal direction, the reverse conformational change of the leading head takes place and its NBP becomes open (see Section S2). From Figure 1i, after ADP release occurs in the trailing head and then ATP binds, the system returns to Figure 1a. From Figure 1i, ATP hydrolysis and Pi release in the leading head can also take place occasionally before ADP release occurs in the trailing head. The leading ADP head then detaches from site II and diffuses to the INT position where the two ADP heads have a large binding energy (Figure 1j). During the time period (period II) before ADP release occurs in the MT-bound head, the dimer can detach from MT by overcoming Ew2 with high probability. If the dimer has not detached until ADP release occurs in the MT-bound head, after ATP binding, the dimer becomes the state of Figure 1k that is the same as Figure 1b except that the dimer took a backward step.
It is mentioned that, in Figure 1a, ATP hydrolysis and Pi release can also take place occasionally in the leading head before taking place in the trailing head, which is not drawn here. As discussed elsewhere,41,42 if this case occurs, the leading head easily detaches from site II by overcoming Ew1 and diffuses to the INT position. From the INT position with the probability 1 – PE, the detached ADP head can diffuse toward the minus end of the MT and bind to the site next to site I with affinity Ew2. This leads to the dimer taking a backward step. From the INT position with the probability PE, the detached ADP head can also diffuse toward the plus end of the MT and rebind to site II with affinity Ew2. This leads to a futile chemomechanical coupling.
2.2. Force-Independent but NL-Orientation-Dependent ATPase Rate of the Kinesin Head
Consider an external force, F, acting on the coiled-coil stalk connecting the two NLs as done in the single-molecule optical tweezer experiments.8−18 The previous experimental results indicated that the extension of the NL in each head of the kinesin dimer has little influence on the ATPase rate of the kinesin dimer during its processive motion.49 Because varying the NL length varies significantly the internally elastic force on the NLs of the two heads bound to MT,39 the experimental results hence mean that the force on the NL has little influence on the ATPase rate of the kinesin head (at least the rate of the rate-limiting step of the ATPase activity, namely, ATP hydrolysis and Pi release). As a consequence, it is proposed that the rate of ATP hydrolysis and Pi release of the kinesin head is independent of the force on its NL.39−42 However, the rate of ATP hydrolysis and Pi release depends sensitively on the orientation of the NL: the head with its NL in the forward orientation has a much larger rate than the head with its NL not in the forward orientation.39−42 This can be explained as follows. The interaction of the NL in the forward orientation with the head enhances the rate of ATP hydrolysis and Pi release (see also Section S2). This is in accordance with the experimental evidence in that the deletion of the NL in the kinesin head reduced greatly its ATPase rate while having no influence on its ADP release rate50 because, after ATP binding and before Pi release, the docked NL is in the forward orientation. For simplicity, we treat here that the rate of ADP release from the MT-bound head (the non-rate-limiting step of the ATPase activity) is a constant independent of the force on and orientation of its NL. When the head is detached from the MT, the rate of ADP release is zero.
3. Results and Discussion
In this work, it is defined that the force F in the backward direction has a positive value. Since F acts on the coiled-coil stalk connecting the two NLs that are flexible, it is reasonably considered that, during the movement of the detached head relative to the other MT-bound head, a backward force (F > 0) acts solely on the NL of the head in the front position while a forward force (F < 0) acts solely on the NL of the head in the rear position.41,42 Thus, after the trailing head releases Pi and detaches from site I, the backward force has no influence on and the forward force facilitates the diffusion of the ADP head to the INT position with the ADP head arriving at the INT position (i.e., Figure 1a transitioning to Figure 1b) within time tr with a probability nearly equal to 1. After the leading head releases Pi and detaches from site II, the backward force facilitates and the forward force has no influence on the diffusion of the ADP head to the INT position with the ADP head arriving at the INT position within time tr with a probability nearly equal to 1. On the other hand, in the INT state after the affinity between the two heads is reduced, the ADP head can move to the forward binding site on the MT with probability PE or move to the backward binding site with probability 1 – PE (see Figure 1). Consequently, it is noted that, if Pi release occurs in the trailing head, the motor either takes a forward step of size d = 8.2 nm with probability PE or does not move with probability 1 – PE and, if Pi release occurs in the leading head, the motor either does not move with probability PE or takes a backward step of size d = 8.2 nm with probability 1 – PE.
We denote by k(+) the rate of ATP hydrolysis and Pi release in the trailing head with its NL in the forward orientation, k(−) the rate of ATP hydrolysis and Pi release in the leading head with its NL not in the forward orientation, and kD the rate of ADP release from the ADP head after binding to the MT. Considering that, in the INT state, the affinity between the two heads is reduced with a rate (which is equal to the NL docking rate, kNL, under no load) much higher than k(+) ≫ k(−) (see Table 1) and the two weak MT-binding periods (periods I and II) occur with very low probabilities in a chemomechanical coupling cycle, for a good approximation, we can neglect the occurrences of the INT state and the two weak MT-binding periods in calculations of the overall ATPase rates. From the model, it is noted that, during the processive motion, the state of the dimer with the trailing head bound to ATP and the leading head bound to ADP (e.g., Figure 1d) occurs with probability PE, while the state of the dimer with the trailing head bound to ADP and the leading head bound to ATP (e.g., Figure 1i) occurs with probability 1 – PE. Consequently, the overall ATPase rates of the trailing and leading heads can be calculated as
| 1 |
| 2 |
where kT and kL are ATPase rates of the trailing and leading heads, respectively. The motor steps forward and backward with the overall rates PEkT and (1 – PE)kL, respectively. Therefore, the pathway of Figure 1 can be simplified to the one shown in Figure 2. The total ATPase rate of the motor is k = kT + kL. Substituting eqs 1 and 2 into the above expression, we obtain
| 3 |
Table 1. Values of Parameters Used in the Calculation.
| parameter | Drosophila kinesin | squid optic lobe kinesin |
|---|---|---|
| k(+) (s–1) | 95 | 102 |
| k(−) (s–1) | 3 | 3 |
| ENL (kBT) | 3.34 | 4 |
| d(+) (nm) | 3.2 | 3.1 |
| kD (s–1) | 250 | 250 |
| kNL (s–1) | 1500 | 1500 |
| kw0 (s–1) | 5 | 5 |
| δw (nm) | 2.2 | 1.6 |
Figure 2.
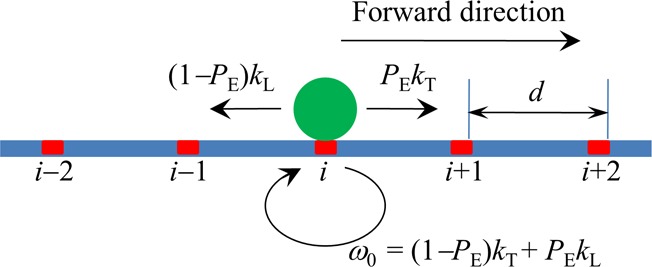
Simplified model of stepping of the kinesin dimer at saturating ATP. The simplified model is derived from the pathway illustrated in Figure 1 where the two weak MT-binding periods (including periods I and II) that can only occur with very low probabilities in a chemomechanical coupling cycle can be neglected. The green circle denotes the kinesin dimer. The binding sites on the MT filament are indicated by ..., (i – 1), i, (i + 1), .... The kinesin dimer steps forward with the rate PEkT and backward with the rate (1 – PE)kL where PE is the effective chemomechanical coupling probability, kT is the ATPase rate of the trailing head, and kL is the ATPase rate of the leading head.
It is noted that, for kD ≫ k(+) ≫ k(−), eqs 1–3 become kT = k(+), kL = k(−), and k = k(+) + k(−), which are identical to those studied before.41,42
3.1. Stepping Ratio and Velocity
To derive the expressions for force dependencies of the stepping ratio and velocity, we first derive the expression for the force dependence of probability PE. Let us consider the backward force (F > 0) and forward force (F < 0) separately.
First, focus on F > 0. Since F > 0 resists the forward motion of the detached ADP head from the INT to leading position (see above), the force dependence of the rate for the ADP head to change from the INT state to the state binding to the forward binding site on the MT can be written as kFwd = C1 exp ( – βFd( + )) where C1 is a constant independent of F, d(+) is the characteristic distance for the motion from the INT position to the forward binding site, and β–1 = kBT is the thermal energy. Since F > 0 has no influence on the motion of the detached ADP head from the INT to the trailing position (see above), the rate for the ADP head to change from the INT state to the state binding to the backward binding site on MT can be written as kBwd = C1 exp ( – βENL) where ENL is the NL-docking energy (more precisely, ENL is the free energy change associated with both the NL docking and large conformational change induced by ATP binding).42 The probability PE can be calculated with PE = kFwd/(kFwd + kBwd). Substituting kFwd and kBwd into the above expression, we obtain
| 4 |
In the above derivation of eq 4, we have considered that the NL docking has no effect on the forward motion of the ADP head from the INT position to the forward binding site on the MT while having a resistant effect on the backward motion to the backward binding site. Alternatively, we consider that the NL docking facilitates the forward motion of the ADP head to the forward binding site while having no effect on the backward motion to the backward binding site. Then, the force dependencies of the rate for the forward and backward motions can be written as kFwd = C1 exp (βENL) exp ( – βFd( + )) and kBwd = C1, respectively. Thus, from PE = kFwd/(kFwd + kBwd), we obtain the same eq 4. This implies that shifting along the horizontal direction the potential characterizing the effect of NL docking on the motion of the detached ADP head has no influence on PE, which has been checked numerically by using Brownian dynamics simulations used in Guo et al.39
Second, focus on F < 0, which has no influence on the motion of the ADP head from the INT to leading position and resists the motion to the trailing position (see above). Thus, for the case that the NL docking has no effect on the forward motion of the ADP head from the INT position to the forward binding site, the rates for the ADP head to change from the INT state to the state binding to the forward and backward sites on MT can be written as kFwd = C2 and kBwd = C2 exp ( – βENL) exp (βFd( – )), respectively, where C2 is a constant independent of F and d(−) is the characteristic distance for the motion from the INT position to the backward binding site. Approximating d(−) = d(+), we obtain that PE = kFwd/(kFwd + kBwd) under F < 0 can still be written in the form of eq 4. Similarly, for the case that NL docking facilitates the forward motion of the ADP head from the INT position to the forward binding site on the MT, PE under F < 0 still has the form of eq 4.
From Figure 2, the stepping ratio can be calculated with r = (PEkT)/[(1 – PE)kL]. Substituting eqs 1, 2, and 4 into the above expression, we obtain
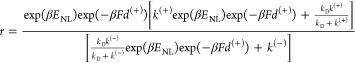 |
5 |
From eq 5, the stepping ratio under no force or at F = 0 can be written as
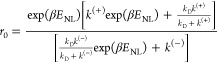 |
6 |
From Figure 2, the motor’s velocity can be calculated with v = [PEkT – (1 – PE)kL]d. Substituting eqs 1 and 2 into the above expression, we obtain
| 7 |
where d = 8.2 nm.
It is noted that, for kD ≫ k(+) ≫ k(−), eqs 5–7 become
| 8 |
| 9 |
| 10 |
With eq 9, eq 8 can be written in another form
| 11 |
where the stall force FS = log (r0)/(βd( + )). With eqs 4, 8, and 11, eq 10 can be rewritten as
| 12 |
As expected, eqs 9, 11, and 12 are identical to those derived before.41,42 As shown before,41 these equations for the stepping ratio and velocity are consistent with the numerical results of Monte Carlo simulations.
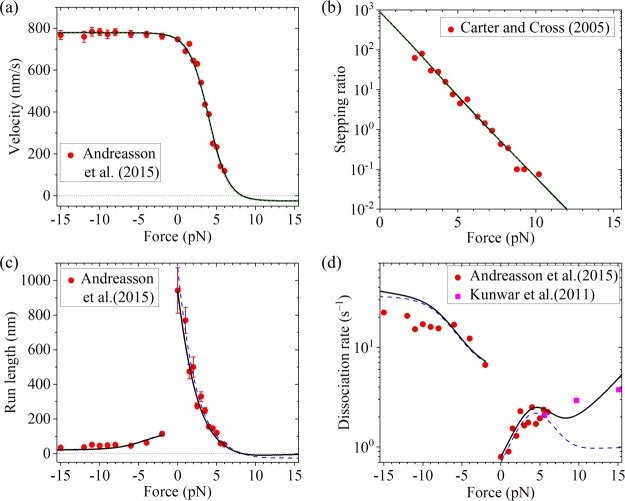
As shown before, with simpler eqs 11 and 12 and by adjusting the values of four parameters, k(+), k(−), r0, and FS, the available single-molecule results about force dependencies of the stepping ratio and velocity can be reproduced well.41,42 Alternatively, the available single-molecule results can also be reproduced well with eqs 4, 8, and 10 and by adjusting values of the four parameters k(+), k(−), ENL, and d(+). For example, by adjusting k(+) = 95 s–1, k(−) = 3 s–1, ENL = 3.34kBT, and d(+) = 3.5 nm, the theoretical results about the force dependence of velocity (Figure 3a, green dashed line) are in good agreement with the single-molecule results of Andreasson et al.17 for Drosophila kinesin. The sensitivity of the four fitting parameters can be seen in Figure S1 (see the Supporting Information). With the same values of k(+) = 95 s–1, k(−) = 3 s–1, and ENL = 3.34kBT as given above and adjusting d(+) = 3.95 nm, the theoretical results about the force dependence of the stepping ratio (Figure 3b, green dashed line) are in good agreement with the single-molecule results of Carter and Cross16 for Drosophila kinesin. Note that the slight difference in the value of d(+) in Figure 3a,b could be due to different conditions in the two experiments. For example, the characteristic distances of the interaction between the head and MT tubulin along the MT filament under different conditions could be slightly different, resulting in the slight difference in the value of d(+).
Figure 3.
Results for Drosophila kinesin at saturating ATP. (a) Velocity vs external force. The black solid line denotes the theoretical results calculated with more precise eq 7, and the green dashed line denotes the theoretical results calculated with simpler eq 10. Since the green dashed line is almost coincident with the black solid line, the two lines are almost indistinguishable. Symbols denote experimental data from Andreasson et al.17 (b) Stepping ratio vs external force. The black solid line denotes the theoretical results calculated with more precise eq 5, and the green dashed line denotes the theoretical results calculated with simpler eq 8. Since the green dashed line is almost coincident with the black solid line, the two lines are almost indistinguishable. Symbols denote experimental data from Carter and Cross16 (adapted with permission from Springer Nature). (c) Run length vs external force. The dashed blue line denotes the theoretical results calculated by considering that the motor can only dissociate in the weak MT-binding state, and the black solid line denotes the theoretical results calculated by considering that the motor can dissociate in both the weak and strong MT-binding states with εs0 = 0.1 s–1. Since the dashed blue line is almost coincident with the black solid line at F < −2 pN, the two lines at F < −2 pN are almost indistinguishable. Symbols denote experimental data from Andreasson et al.17 (d) Dissociation rate vs external force. The dashed blue line denotes the theoretical results calculated by considering that the motor can only dissociate in the weak MT-binding state, and the black solid line denotes the theoretical results calculated by considering that the motor can dissociate in both the weak and strong MT-binding states with εs0 = 0.1 s–1. Symbols denote experimental data from Andreasson et al.17 (circles) and from Kunwar et al.22 (squares).
The single molecule results can also be reproduced well using more precise eqs 4, 5, and 7 and with the five parameters k(+), k(−), ENL, d(+), and kD. As shown above, we still take k(+) = 95 s–1, k(−) = 3 s–1, and ENL = 3.34kBT for Drosophila kinesin (see Table 1). To be consistent with the biochemical data of approximately 250 s–1 for the rate constant of ADP release,51 we take kD = 250 s–1 (see Table 1). Then, by adjusting d(+) = 3.2 nm (see Table 1), the theoretical results about the force dependence of velocity (Figure 3a, black solid line) are in good agreement with the single-molecule results of Andreasson et al.17 for Drosophila kinesin. Still with k(+) = 95 s–1, k(−) = 3 s–1, ENL = 3.34kBT, and kD = 250 s–1, by adjusting d(+) = 3.8 nm, the theoretical results about the force dependence of the stepping ratio (Figure 3b, black solid line) are in good agreement with the single-molecule results of Carter and Cross16 for Drosophila kinesin. As mentioned just above, the slight difference in the value of d(+) in Figure 3a, b could be due to different conditions in the two experiments.
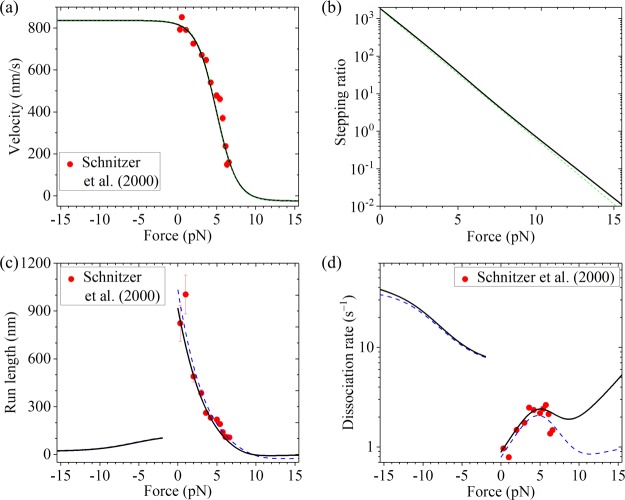
Then, we focus on squid optic lobe kinesin. With k(+) = 102 s–1, k(−) = 3 s–1, ENL = 4kBT, kD = 250 s–1, and d(+) = 3.1 nm (see Table 1), the theoretical results about the force dependence of velocity (Figure 4a, black solid line) calculated using more precise eqs 4 and 7 are in agreement with the single-molecule results of Schnitzer et al.33 The theoretical results about the force dependence of the stepping ratio calculated using eq 5 are shown in Figure 4b (black solid line). For comparison, with k(+) = 102 s–1, k(−) = 3 s–1, ENL = 4kBT, and d(+) = 3.28 nm, the single-molecule results of Schnitzer et al.33 can also be reproduced by using simpler eqs 4 and 10 (Figure 4a, green dashed line). With k(+) = 102 s–1, k(−) = 3 s–1, ENL = 4kBT, and d(+) = 3.28 nm, the theoretical results about the force dependence of the stepping ratio calculated by using simpler eq 8 (Figure 4b, green dashed line) are also close to those calculated using more precise eq 5 and with parameter values given in Table 1.
Figure 4.
Results for squid optic lobe kinesin at saturating ATP. Lines denote theoretical results, and symbols denote experimental data from Schnitzer et al.33 (adapted with permission from Springer Nature). (a) Velocity vs external force. The black solid line denotes the theoretical results calculated with more precise eq 7, and the green dashed line denotes the theoretical results calculated with simpler eq 10. Since the green dashed line is almost coincident with the black solid line, the two lines are almost indistinguishable. (b) Stepping ratio vs external force. The black solid line denotes the theoretical results calculated with more precise eq 5, and the green dashed line denotes the theoretical results calculated with simpler eq 8. (c) Run length vs external force. The dashed blue line denotes the theoretical results calculated by considering that the motor can only dissociate in the weak MT-binding state, and the black solid line denotes the theoretical results calculated by considering that the motor can dissociate in both the weak and strong MT-binding states with εs0 = 0.1 s–1. Since the dashed blue line is almost coincident with the black solid line at F < −2 pN, the two lines at F < −2 pN are almost indistinguishable. (d) Dissociation rate vs external force. The dashed blue line denotes the theoretical results calculated by considering that the motor can only dissociate in the weak MT-binding state, and the black solid line denotes the theoretical results calculated by considering that the motor can dissociate in both the weak and strong MT-binding states with εs0 = 0.1 s–1.
3.2. Run Length and Dissociation Rate When Dissociation Only in the Weak MT-Binding State Is Considered
If the dissociation cannot occur in the strong MT-binding state, based on the model (Figure 1), the dissociation can only occur during two periods of the weak MT-binding state, periods I and II. Period I occurs under the case that, in the INT state, ATP hydrolysis and Pi release in the MT-bound head take place before the weakening of the affinity between the two heads takes place (Figure 1f). Under no or a backward load, the NL of the MT-bound head in the INT state before NL docking is not in the forward orientation. Thus, the rate of ATP hydrolysis and Pi release of the MT-bound head is equal to k(−) (see Section 2.2). Denoting by kNL the NL-docking rate of the MT-bound head under no load (which is equal to the rate of the reduction of the affinity between the two heads under any load) in the INT state, the probability of period I occurring after ATP hydrolysis and Pi release in the trailing head can be calculated with
| 13 |
Under the forward load with the magnitude larger than 2 pN, it is argued here that the NL of the MT-bound head in the INT state before NL docking is driven in the forward orientation that can enhance the rate of ATP hydrolysis and Pi release of the head with the rate being equal to k(+) (see Section 2.2). As a result, the probability of period I occurring after ATP hydrolysis and Pi release in the trailing head can be calculated with
| 14 |
Considering that period I cannot occur after ATP hydrolysis and Pi release in the leading head and with the trailing head in ATP state, the occurrence rate of period I can then be calculated with
| 15 |
Period II occurs under the following two cases. (i) ATP hydrolysis and Pi release take place in the trailing head before ADP release from the leading head (Figure 1g). (ii) ATP hydrolysis and Pi release take place in the leading head before ADP release from the trailing head (Figure 1j). In one ATPase cycle, the occurrence probability of case i can be calculated with PEk( + )/(k( + ) + kD), while the occurrence probability of case ii can be calculated with (1 – PE)k( – )/(k( – ) + kD). Thus, the occurrence probability of period II in one ATPase cycle can be calculated with
| 16 |
The occurrence rate of period II can then be calculated with
| 17 |
where k is calculated with eq 3.
On the basis of Kramers theory, the dissociation rate in period II can be approximately calculated with
| 18 |
where kw0 is the dissociation rate in period II under no external force and δw is the characteristic distance. Note here that, in eq 18, for simplicity but without loss of generality, it has been assumed implicitly that the potential of the weak interaction between the kinesin head and an MT-tubulin dimer is symmetric in the forward and backward directions. Considering the lifetime of 1/kD for period II, the dissociation probability in period II can then be calculated with
| 19 |
Since Ew1 in period I is very small, the motor is considered to be dissociated from the MT in period I with a probability of PdI ≈ 1. Thus, the dissociation rate during processive motion of the motor when dissociation only in the weak MT-binding state is considered can be calculated with εw = ωIPdI + ωIIPdII ≈ ωI + ωIIPdII which with eqs 15 and 17 can be rewritten as
| 20 |
The run length can then be calculated with
| 21 |
As it is seen above, using eqs 1–4, 7, 13, 14, 16, and 18–21, we can calculate the force-dependent dissociation rate and run length where values of parameters k(+), k(−), ENL, d(+), kD, kNL, kw0, and δw are required. As shown in the above section, values of parameters k(+), k(−), ENL, d(+), and kD have been determined (see Table 1). Thus, only values of the remaining three parameters kNL, kw0, and δw are required to be determined.
First, we focus on Drosophila kinesin. With k(+), k(−), ENL, d(+), and kD given in Table 1 and by adjusting kNL = 1500 s–1, kw0 = 5 s–1, and δw = 2.2 nm (see Table 1), the theoretical results about the dependence of the run length upon both backward and forward forces (Figure 3c, dashed blue line) reproduce quantitatively the single-molecule results of Andreasson et al.17 Note that the value of kNL = 1500 s–1 taken here is consistent with the available experimental data.52 The sensitivity of the three fitting parameters can be seen in Figure S2 (see the Supporting Information). In particular, the dramatically asymmetric characteristic of the run length with respect to the direction of the external force is explained well. By comparison, in the previous theoretical and numerical studies,33,34,53 although the dependence of the run length on the backward load can be fitted, the dependence of the run length on the forward load has not been explained. Our theoretical results about the dependence of the dissociation rate upon both backward and forward forces (Figure 3d, dashed blue line) are also in accordance with the single-molecule results of Andreasson et al.17 (red circles) where the single-molecule results of Andreasson et al.17 are obtained by dividing data of velocity in Figure 3a by corresponding data of the run length in Figure 3c.
Then, we focus on squid optic lobe kinesin. With k(+), k(−), ENL, d(+), and kD given in Table 1 and by adjusting kNL = 1500 s–1, kw0 = 5 s–1, and δw = 1.6 nm (see Table 1), the theoretical results about the dependence of the run length upon backward force (Figure 4c, dashed blue line) reproduce well the single-molecule results of Schnitzer et al.33 As for the case of Drosophila kinesin, the theoretical results predict that the run length of squid optic lobe kinesin is also dramatically asymmetric with respect to the direction of the external force. The theoretical results about the force dependence of the dissociation rate (Figure 4d, dashed blue line) are also in agreement with the single-molecule results of Schnitzer et al.33 where the single molecule data are obtained by dividing data of velocity in Figure 4a by corresponding data of the run length in Figure 4c. Both the experimental and theoretical results show that in the range of approximately 0 < F < 4 pN, the dissociation rate increases almost exponentially as the backward force increases, and in the range of approximately 5 < F < 7 pN, the dissociation rate decreases as the backward force increases.
3.3. Run Length and Dissociation Rate When Dissociations in Both the Weak and Strong MT-Binding States Are Considered
In the above section, we have not considered the dissociation of the motor in the strong MT-binding state, which is approximately applicable to the case of small magnitudes of the external force. However, when the external force has a large magnitude, the dissociation of the dimer in the strong MT-binding state must be taken into account. Thus, in this section, we consider the dissociation in both the weak MT-binding state, as studied in the above section, and strong MT-binding state.
During the processive motion of the kinesin dimer, the periods of the weak MT-binding state, including periods I and II, can only occur occasionally in one chemomechanical coupling cycle, and if they occur, they only make up a small percent of the whole period of the chemomechanical coupling cycle. That is, during the processive motion, the kinesin motor is nearly always in the strong MT-binding state. Thus, on the basis of Kramers theory, the dissociation rate of the motor when dissociation only in the strong MT-binding state is considered can be approximately calculated with
| 22 |
where εs0 is the dissociation rate under F = 0 and δs is the interaction distance. Here, it was also implicitly assumed that the potential of the strong interaction between the kinesin head and MT-tubulin dimer is symmetric in the forward and backward directions. It is noted that the potential of the kinesin head in the strong MT-binding state could have a different form from that in the weak MT-binding state, and thus δs could have a value different from δw.
The total rate of dissociation of the motor during its processive motion can be calculated with
| 23 |
The run length can then be calculated with
| 24 |
From eqs 22–24, it is seen that two additional parameters εs0 and δs are required to calculate the dissociation rate and run length when the dissociations occurring at both the weak and strong MT-binding states are considered. To be consistent with the measured dissociation rate of approximately 45 s–1 under very large backward force of F = 25 pN by Andreasson et al.,17 from eqs 22 and 23, we see that only one parameter, for example, εs0 is adjustable, while the other parameter δs can be determined. Here, we take two values of εs0 for the calculations.
In the main text, we take εs0 = 0.1 s–1. Then, with values of other parameters given in Table 1, we calculate the force-dependent run length when dissociations in both the weak and strong MT-binding states are considered with the results being shown in Figures 3c and 4c (black solid lines) for Drosophila and squid optic lobe kinesin motors, respectively. As expected, the inclusion of the dissociation that can occur in the strong MT-binding state has only a slight effect on the run length in the range of F < 9 pN. The theoretical results of the run length versus external force when dissociations in both the weak and strong MT-binding states are considered are also in quantitative agreement with the available experimental results.
With inclusion of the dissociation that can occur in the strong MT-binding state, the theoretical results of the dissociation rate upon the external force (black solid lines) are shown in Figures 3d and 4d for Drosophila and squid optic lobe kinesin motors, respectively. From Figure 3d, it is seen that the theoretical results are consistent with both the single-molecule results of Andreasson et al.17 and those of Kunwar et al.22Figure 4d shows that the theoretical results are also consistent with the single-molecule results of Schnitzer et al.33 The theoretical results in both Figures 3d and 4d show the slip–catch–slip bond behavior for the interaction between kinesin and MTs during the processive motion of the motor on MTs under the backward external force, as indicated by experimental evidence22 and used in a lot of works to study the cooperative transports by multiple kinesin and/or dynein molecular motors.22,28−30 In the range of a small backward force (approximately 0 < F < 4 pN), as the backward force increases, the dissociation rate increases almost exponentially. After reaching the maximum, the dissociation rate decreases as the backward force increases further. After reaching the minimum, the dissociation rate increases again as the backward force increases further. By comparison, in the previous theoretical and numerical studies,33,34,53 the slip–catch–slip bond behavior for the dissociation rate under the backward has not been explained.
In the Supporting Information (Figures S3 and S4), we take εs0 = 0.01 s–1. With values of other parameters given in Table 1, the theoretical results about the force dependencies of the run length and dissociation rate for Drosophila and squid optic lobe kinesin motors are shown in Figures S3 and S4, respectively. It can be seen that the theoretical results also agree well with the available single-molecule results, and the dissociate rate versus F (>0) also shows the slip–catch–slip bond behavior.
4. Concluding Remarks
Analytical theory on dynamics of kinesin molecular motors under both forward and backward external forces reproduces quantitatively the previous single-molecule results about force dependencies of the velocity, stepping ratio, run length, dissociation rate, etc. Particularly, the dramatic asymmetry of the run length with respect to the direction of the external force is well explained. Moreover, the theory shows that under the backward force, the dissociation rate of the motor during its processive motion exhibits the slip–catch–slip bond behavior with the dissociation rate increasing first with the backward force then decreasing with the backward force and then increasing again with the backward force.
Finally, it is mentioned that, in the main text, we only present the analytical studies at saturating ATP. The approximate analytical studies at nonsaturating ATP are presented in the Supporting Information (see Sections S1–S6 and Figures S5–S8). The theoretical results about the force dependencies of the velocity, stepping ratio, and dwell time at different ATP concentrations are also in quantitative agreement with the available single-molecule results (Figure S6). The theoretical results show that if the dissociation can only occur in the weak MT-binding state, the run length is nearly independent on ATP concentration and the dependence of the run length on the ATP concentration arises almost solely from the dissociation in the strong MT-binding state (Figure S7). For the case of εw ≫ εs, for example, under a low forward force (see Figures 3d and 4d), the change of ATP concentration has only a slight effect on the run length (Figure S7), consistent with the single-molecule results of Andreasson et al.17 By contrast, for the case of εw comparable to or smaller than εs, for example, under no or a backward force (see Figures 3d and 4d), the change of ATP concentration has a large effect on the run length (Figures S7 and S8), consistent with the single-molecule results of Schnitzer et al.33
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b03738.
Analytical studies of dynamics of kinesin molecular motors at nonsaturating ATP (Sections S1–S6) and Figures S1–S8 (PDF)
The research is supported by the National Natural Science Foundation of China (grant no. 11775301).
The author declares no competing financial interest.
Supplementary Material
References
- Vale R. D.; Reese T. S.; Sheetz M. P. Identification of a Novel Force-generating Protein, Kinesin, Involved in Microtubule-based Motility. Cell 1985, 42, 39–50. 10.1016/s0092-8674(85)80099-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirokawa N. Kinesin and Dynein Superfamily Proteins and the Mechanism of Organelle Transport. Science 1998, 279, 519–526. 10.1126/science.279.5350.519. [DOI] [PubMed] [Google Scholar]
- Vale R. D.; Milligan R. A. The Way Things Move: Looking Under the Hood of Molecular Motor Proteins. Science 2000, 288, 88–95. 10.1126/science.288.5463.88. [DOI] [PubMed] [Google Scholar]
- Asbury C. L. Kinesin: World’s Tiniest Biped. Curr. Opin. Cell Biol. 2005, 17, 89–97. 10.1016/j.ceb.2004.12.002. [DOI] [PubMed] [Google Scholar]
- Kolomeisky A. B.; Fisher M. E. Molecular Motors: A Theorist’s Perspective. Annu. Rev. Phys. Chem. 2007, 58, 675–695. 10.1146/annurev.physchem.58.032806.104532. [DOI] [PubMed] [Google Scholar]
- Xie P. Mechanism of Processive Movement of Monomeric and Dimeric Kinesin Molecules. Int. J. Biol. Sci. 2010, 6, 665–674. 10.7150/ijbs.6.665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozielski F.; Sack S.; Marx A.; Thormählen M.; Schönbrunn E.; Biou V.; Thompson A.; Mandelkow E. M.; Mandelkow E. The Crystal Structure of Dimeric Kinesin and Implications for Microtubule-dependent Motility. Cell 1997, 91, 985–994. 10.1016/S0092-8674(00)80489-4. [DOI] [PubMed] [Google Scholar]
- Schnitzer M. J.; Block S. M. Kinesin Hydrolyses One ATP per 8-nm Step. Nature 1997, 388, 386–390. 10.1038/41111. [DOI] [PubMed] [Google Scholar]
- Svoboda K.; Schmidt C. F.; Schnapp B. J.; Block S. M. Direct Observation of Kinesin Stepping by Optical Trapping Interferometry. Nature 1993, 365, 721–727. 10.1038/365721a0. [DOI] [PubMed] [Google Scholar]
- Coppin C. M.; Pierce D. W.; Hsu L.; Vale R. D. The Load Dependence of Kinesin’s Mechanical Cycle. Proc.Natl. Acad. Sci. U. S. A. 1997, 94, 8539–8544. 10.1073/pnas.94.16.8539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kojima H.; Muto E.; Higuchi H.; Yanagida T. Mechanics of Single Kinesin Molecules Measured by Optical Trapping Nanometry. Biophys. J. 1997, 73, 2012–2022. 10.1016/S0006-3495(97)78231-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher K.; Schnitzer M. J.; Block S. M. Single Kinesin Molecules Studied with a Molecular Force Clamp. Nature 1999, 400, 184–189. 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- Nishiyama M.; Higuchi H.; Yanagida T. Chemomechanical coupling of the forward and backward steps of single kinesin molecules. Nat. Cell Biol. 2002, 4, 790–797. 10.1038/ncb857. [DOI] [PubMed] [Google Scholar]
- Asbury C. L.; Fehr A. N.; Block S. M. Kinesin Moves by an Asymmetric Hand-Over-Hand Mechanism. Science 2003, 302, 2130. 10.1126/science.1092985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khalil A. S.; Appleyard D. C.; Labno A. K.; Georges A.; Karplus M.; Belcher A. M.; Hwang W.; Lang M. J. Kinesin’s Cover-neck Bundle Folds Forward to Generate Force. Proc.Natl. Acad. Sci. U. S. A. 2008, 105, 19247–19252. 10.1073/pnas.0805147105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter N. J.; Cross R. A. Mechanics of the kinesin step. Nature 2005, 435, 308–312. 10.1038/nature03528. [DOI] [PubMed] [Google Scholar]
- Andreasson J. O. L.; Milic B.; Chen G.-Y.; Guydosh N. R.; Hancock W. O.; Block S. M. Examining kinesin processivity within a general gating framework. eLife 2015, 4, e07403 10.7554/eLife.07403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milic B.; Andreasson J. O. L.; Hancock W. O.; Block S. M. Kinesin processivity is gated by phosphate release. Proc.Natl. Acad. Sci. U. S. A. 2014, 111, 14136–14140. 10.1073/pnas.1410943111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo S.-K.; Shi X.-X.; Wang P.-Y.; Xie P. Processivity of dimeric kinesin-1 molecular motors. FEBS Open Bio 2018, 8, 1332–1351. 10.1002/2211-5463.12486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo S.-K.; Wang W.-C.; Wang P.-Y.; Xie P. Force dependence of velocity and run length of kinesin-1, kinesin-2 and kinesin-5 family molecular motors. Molecules 2019, 24, 287. 10.3390/molecules24020287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouzat S.; Falo F. The influence of direct motor-motor interaction in models for cargo transport by a single team of motors. Phys. Biol. 2010, 7, 046009 10.1088/1478-3975/7/4/046009. [DOI] [PubMed] [Google Scholar]
- Kunwar A.; Tripathy S. K.; Xu J.; Mattson M. K.; Anand P.; Sigua R.; Vershinin M.; McKenney R. J.; Yu C. C.; Mogilner A.; Gross S. P. Mechanical stochastic tug-of-war models cannot explain bidirectional lipid-droplet transport. Proc.Natl. Acad. Sci. U. S. A. 2011, 108, 18960–18965. 10.1073/pnas.1107841108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger F.; Keller C.; Lipowsky R.; Klumpp S. Elastic coupling effects in cooperative transport by a pair of molecular motors. Cell. Mol. Bioeng. 2013, 6, 48–64. 10.1007/s12195-012-0258-3. [DOI] [Google Scholar]
- Arpaǧ G.; Shastry S.; Hancock W. O.; Tüzel E. Transport by Populations of Fast and Slow Kinesins Uncovers Novel Family-Dependent Motor Characteristics Important for In Vivo Function. Biophys. J. 2014, 107, 1896–1904. 10.1016/j.bpj.2014.09.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reddy B. J. N.; Tripathy S.; Vershinin M.; Tanenbaum M. E.; Xu J.; Mattson-Hoss M.; Arabi K.; Chapman D.; Doolin T.; Hyeon C.; Gross S. P. Heterogeneity in kinesin function. Traffic 2017, 18, 658–671. 10.1111/tra.12504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fu Y.-B.; Guo S.-K.; Wang P.-Y.; Xie P. Dynamics of cooperative cargo transport by two elastically coupled kinesin motors. Eur. Phys. J. E: Soft Matter Biol. Phys. 2019, 42, 41. 10.1140/epje/i2019-11801-4. [DOI] [PubMed] [Google Scholar]
- Arpaǧ G.; Norris S. R.; Mousavi S. I.; Soppina V.; Verhey K. J.; Hancock W. O.; Tüzel E. Motor Dynamics Underlying Cargo Transport by Pairs of Kinesin-1 and Kinesin-3 Motors. Biophys. J. 2019, 116, 1115–1126. 10.1016/j.bpj.2019.01.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takshak A.; Mishra N.; Kulkarni A.; Kunwar A. Effect of fuel concentration on cargo transport by a team of kinesin motors. Phys. A 2017, 467, 395–406. 10.1016/j.physa.2016.10.022. [DOI] [Google Scholar]
- Bouzat S. Models for microtubule cargo transport coupling the Langevin equation to stochastic stepping motor dynamics: Caring about fluctuations. Phys. Rev. E 2016, 93, 012401 10.1103/PhysRevE.93.012401. [DOI] [PubMed] [Google Scholar]
- Dallon J. C.; Leduc C.; Etienne-Manneville S.; Portet S. Stochastic modeling reveals how motor protein and filament properties affect intermediate filament transport. J. Theor. Biol. 2019, 464, 132–148. 10.1016/j.jtbi.2018.12.022. [DOI] [PubMed] [Google Scholar]
- Khataee H.; Howard J. Force Generated by Two Kinesin Motors Depends on the Load Direction and Intermolecular Coupling. Phys. Rev. Lett. 2019, 122, 188101. 10.1103/PhysRevLett.122.188101. [DOI] [PubMed] [Google Scholar]
- Guo S.-K.; Shi X.-X.; Wang P.-Y.; Xie P. Force dependence of unbinding rate of kinesin motor during its processive movement on microtubule. Biophys. Chem. 2019, 253, 106216. 10.1016/j.bpc.2019.106216. [DOI] [PubMed] [Google Scholar]
- Schnitzer M. J.; Visscher K.; Block S. M. Force production by single kinesin motors. Nat. Cell Biol. 2000, 2, 718–723. 10.1038/35036345. [DOI] [PubMed] [Google Scholar]
- Fisher M. E.; Kolomeisky A. B. Simple mechanochemistry describes the dynamics of kinesin molecules. Proc.Natl. Acad. Sci. U. S. A. 2001, 98, 7748–7753. 10.1073/pnas.141080498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyeon C.; Onuchic J. N. Internal strain regulates the nucleotide binding site of the kinesin leading head. Proc.Natl. Acad. Sci. U. S. A. 2007, 104, 2175–2180. 10.1073/pnas.0610939104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liepelt S.; Lipowsky R. Kinesin’s Network of Chemomechanical Motor Cycles. Phys. Rev. Lett. 2007, 98, 258102. 10.1103/PhysRevLett.98.258102. [DOI] [PubMed] [Google Scholar]
- Khataee H.; Wee-Chung Liew A. A mathematical model describing the mechanical kinetics of kinesin stepping. Bioinformatics 2014, 30, 353–359. 10.1093/bioinformatics/btt698. [DOI] [PubMed] [Google Scholar]
- Sumi T. Design principles governing chemomechanical coupling of kinesin. Sci. Rep. 2017, 7, 1163. 10.1038/s41598-017-01328-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo S.-K.; Wang P.-Y.; Xie P. A model of processive movement of dimeric kinesin. J. Theor. Biol. 2017, 414, 62–75. 10.1016/j.jtbi.2016.11.023. [DOI] [PubMed] [Google Scholar]
- Xie P.; Chen H. A non-tight chemomechanical coupling model for force-dependence of movement dynamics of molecular motors. Phys. Chem. Chem. Phys. 2018, 20, 4752–4759. 10.1039/C7CP05557A. [DOI] [PubMed] [Google Scholar]
- Xie P.; Guo S.-K.; Chen H. ATP-concentration- and force-dependent chemomechanical coupling of kinesin molecular motors. J. Chem. Inf. Model. 2018, 59, 360–372. 10.1021/acs.jcim.8b00577. [DOI] [PubMed] [Google Scholar]
- Xie P.; Guo S.-K.; Chen H. A generalized kinetic model for coupling between stepping and ATP hydrolysis of kinesin molecular motors. Int. J. Mol. Sci. 2019, 20, 4911. 10.3390/ijms20194911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cross R. A. Review: Mechanochemistry of the kinesin-1 ATPase. Biopolymers 2016, 105, 476–482. 10.1002/bip.22862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morikawa M.; Yajima H.; Nitta R.; Inoue S.; Ogura T.; Sato C.; Hirokawa N. X-ray and Cryo-EM structures reveal mutual conformational changes of Kinesin and GTP-state microtubules upon binding. EMBO J. 2015, 34, 1270–1286. 10.15252/embj.201490588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi X.-X.; Fu Y.-B.; Guo S.-K.; Wang P.-Y.; Chen H.; Xie P. Investigating role of conformational changes of microtubule in regulating its binding affinity to kinesin by all-atom molecular dynamics simulation. Proteins 2018, 86, 1127–1139. 10.1002/prot.25592. [DOI] [PubMed] [Google Scholar]
- Sindelar C. V.; Downing K. H. An atomic-level mechanism for activation of the kinesin molecular motors. Proc. Natl. Acad. Sci. U. S. A. 2010, 107, 4111–4116. 10.1073/pnas.0911208107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rice S.; Lin A. W.; Safer D.; Hart C. L.; Naber N.; Carragher B. O.; Cain S. M.; Pechatnikova E.; Wilson-Kubalek E. M.; Whittaker M.; Pate E.; Cooke R.; Taylor E. W.; Milligan R. A.; Vale R. D. A structural change in the kinesin motor protein that drives motility. Nature 1999, 402, 778–784. 10.1038/45483. [DOI] [PubMed] [Google Scholar]
- Shi X.-X.; Guo S.-K.; Wang P.-Y.; Chen H.; Xie P. All-atom molecular dynamics simulations reveal how kinesin transits from one-head-bound to two-heads-bound state. Proteins 2019, 10.1002/prot.25833. [DOI] [PubMed] [Google Scholar]
- Yildiz A.; Tomishige M.; Gennerich A.; Vale R. D. Intramolecular strain coordinates kinesin stepping behavior along microtubules. Cell 2008, 134, 1030–1041. 10.1016/j.cell.2008.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cao L.; Wang W.; Jiang Q.; Wang C.; Knossow M.; Gigant B. The structure of apo-kinesin bound to tubulin links the nucleotide cycle to movement. Nat. Commun. 2014, 5, 5364. 10.1038/ncomms6364. [DOI] [PubMed] [Google Scholar]
- Moyer M. L.; Gilbert S. P.; Johnson K. A. Pathway of ATP hydrolysis by monomeric and dimeric kinesin. Biochemistry 1998, 37, 800–813. 10.1021/bi9711184. [DOI] [PubMed] [Google Scholar]
- Rosenfeld S. S.; Jefferson G. M.; King P. H. ATP reorients the neck linker of kinesin in two sequential steps. J. Biol. Chem. 2001, 276, 40167–40174. 10.1074/jbc.M103899200. [DOI] [PubMed] [Google Scholar]
- Maes C.; van Wieren M. H. A Markov model for kinesin. J. Stat. Phys. 2003, 112, 329–355. 10.1023/A:1023691923564. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.