Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Mar 10;5(11):5951–5958. doi: 10.1021/acsomega.9b04302

In Silico Rational Design and Virtual Screening of Bioactive Peptides Based on QSAR Modeling

Mehri Mahmoodi-Reihani †, Fatemeh Abbasitabar ‡,*, Vahid Zare-Shahabadi †
PMCID: PMC7097998  PMID: 32226875

Abstract

graphic file with name ao9b04302_0004.jpg

Predicting the bioactivity of peptides is an important challenge in drug development and peptide research. In this study, numerical descriptive vectors (NDVs) for peptide sequences were calculated based on the physicochemical properties of amino acids (AAs) and principal component analysis (PCA). The resulted NDV had the same length as the peptide sequence, so that each entry of NDV corresponded to one AA in the sequence. They were then applied to quantitative structure–activity relationship (QSAR) analysis of angiotensin-converting enzyme (ACE) inhibitor dipeptides, bitter-tasting dipeptides, and nonameric binding peptides of the human leukocyte antigens (HLA-A*0201). Multiple linear regression was used to construct the QSAR models. For each peptide set, a proper subset of physicochemical properties was chosen by the ant colony optimization algorithm. The leave-one-out cross-validation (qloo2) values were 0.855, 0.936, and 0.642 and the root-mean-square errors (RMSEs) were 0.450, 0.149, and 0.461. Our results revealed that the new numerical descriptive vector can afford extensive characterization of peptide sequence so that it can be easily employed in peptide QSAR studies. Moreover, the proposed numerical descriptive vectors were able to determine hot spot residues in the peptides under study.

Introduction

Peptides play crucial roles in biological systems and are therefore recognized as an important target group for pharmaceutical, nutritional, and cosmetic applications.1 As a result, thousands of peptides are designed, synthesized, and screened for different pharmacological systems. In this regard, design and prediction of bioactivities of peptides remain one of the most challenging areas in the life science because it is impossible to test all of the peptides to find the most bioactive among them when considering a large number of theoretical possible peptides.2 Bioinformatic studies have become more and more popular in peptide’s design, particularly the quantitative structure–activity relationship (QSAR) study. QSAR models utilize a mathematical function to summarize the relationship between biological activities of a set of compounds and their structural characteristics.3−6 So far, QSAR models have been successfully established for angiotensin-converting enzyme (ACE)-inhibitory peptides,7 antioxidant peptides,8 antimicrobial peptides,9 bitter peptides,10 antitumor peptides,11 etc.12−16 To develop a QSAR model, a set of numerical descriptors is generated to characterize the structure of interest, e.g., amino acids, which serves as independent variables, while the biological activities are the dependent variables. Since the activities of peptides are determined by the amino acid compositions, sequences, and structures, a proper encoding technique should be employed for representing the sequence of amino acids.

Several encoding approaches have been proposed for representing the sequence of amino acids. Some of them are based on the amino acid sequence. For example, in orthonormal encoding,17 each amino acid of the sequence is represented by a 20 bit vector having all entries equal to zero except for that corresponding to the considered amino acid which is set to one. Consequently, a peptide sequence with M amino acids is represented by the concatenation of M × 20 features. The 2 g representation is another example.18 In this approach, a peptide is represented by a set of 202 pairs of values of νi and ci, in which νi is a couple of amino acids and ci is the counts of the appearance of that couple in the sequence. The other encoding approaches are calculated from the physicochemical information. For this category, a set of descriptors is calculated for each amino acid and they are concatenated to produce a descriptor data matrix for a set of peptides. An example is weighted physicochemical encoding: in this method, instead of considering the composition of the sequence in its natural order, it is represented by concatenating alphabetically features of amino acids that have been weighted according to the frequency of amino acids in the sequence. Therefore, the resulted numerical vector is composed by 20 × F features.19 Hemmateenejad et al. used quantum topological molecular similarity parameters of each amino acid instead of their physicochemical properties.20 In most of the amino acid indices defined so far, there is more than one feature for each amino acid in the resulting numerical descriptor vector and, consequently, the length of the obtained numerical descriptor vector is much longer than the length of the sequence. In this specific situation, the introduction of a new peptide representation that can be utilized in QSAR studies is the frontier of the peptide research.

Recently, we introduced a new numerical descriptive vector for proteins and applied it to reveal the similarities between proteins. This numerical descriptive vector had the same length as the original sequence. It was calculated based on the physicochemical properties and principal component analysis. We suggested here the applicability of our numerical descriptive vector (NDV) for peptide representation and its usefulness in peptide QSAR research.

Results and Discussion

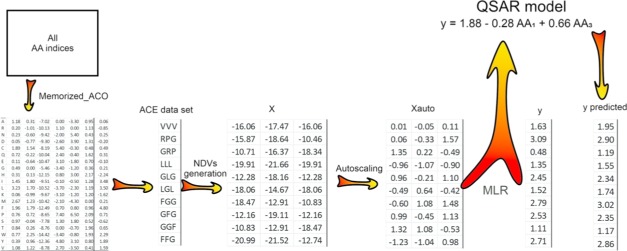
Five hundred fifty-three physicochemical properties of AAs were extracted from the AAindex1 database. For a given peptide sequence, a numerical descriptive vector with the same size of the sequence length is calculated based on a set of physicochemical properties of AAs and PCA.21 For example, if a data set containing n hexapeptides was considered, a descriptor data matrix with the number of rows and columns of n and 6, respectively, would be obtained (Figure 1). The values of the numerical descriptive vector are dependent on the types of the AA indices used in the computation step. Since the number of AA indices provided in the AAindex1 database was large, it was necessary to employ a variable selection method such as the Memorized_ACO algorithm for selecting the most convenient subset of AA indices in a specified data set.

Figure 1.

Figure 1

Open in a new tab

Graphical representation of the NDV calculation and QSAR modeling for the ACE data set.

QSAR Models of ACE Inhibitors

ACE data set is composed of 55 tripeptides as inhibitors of the angiotensin-converting enzyme (ACE), among which 45 molecules were selected as a training set and the remainders were used as an external test set to validate the constructed QSAR model (Table 1).

Table 1. Characteristics of the Data Sets Used in This Paper.

        size
  
groups name no. of peptides no. of sequences training set test set refs
data set 1 ACE 55 3 45 10 (30)
data set 2 bitter tasting 48 2 40 8 (26)
data set 3 HLA 177 9 131 46 (20, 34)
Open in a new tab

Several subsets of AA indices with the different sizes were selected by the Memorized_ACO algorithm. For each chosen subset, a specific descriptor data matrix was calculated and used in the QSAR model development. The resulting models based on the use of different subsets of AA indices are summarized in Table 2. The ability of the NDV to represent the peptide sequences can be judged from Table 2. The QSAR model based on the NDM computed using only two AA indices had correlation coefficients of 0.83 and 0.80 for the training and test sets, respectively. However, the quality of the QSAR model was improved by considering more AA indices up to seven. Consequently, seven physicochemical properties of AA were used in the construction of the final QSAR model. A list of these AA indices is given in Table S1 (Supporting Information). The calculated NDM for ACE data set together with the experimental and predicted biological activities is also presented in Table S2.

Table 2. QSAR Models of the Peptides as ACE Inhibitors Obtained Using Different Sets of the AA Indices.

number of used AA indices Rtraining2 Rtest2 qloo2 qlmo2 RSMEtraining RSMEtest RMP2a
2 0.829 0.801 0.797 0.788 0.266 0.376 0.150
3 0.830 0.826 0.806 0.803 0.265 0.341 0.217
4 0.843 0.852 0.814 0.814 0.255 0.265 0.121
5 0.849 0.842 0.822 0.819 0.250 0.317 0.176
6 0.845 0.844 0.818 0.816 0.253 0.314 0.104
7 0.855 0.859 0.831 0.830 0.245 0.302 0.160
8 0.855 0.861 0.831 0.829 0.245 0.295 0.099
Open in a new tab
a

Maximum Rtraining2 for the Y-randomization test.

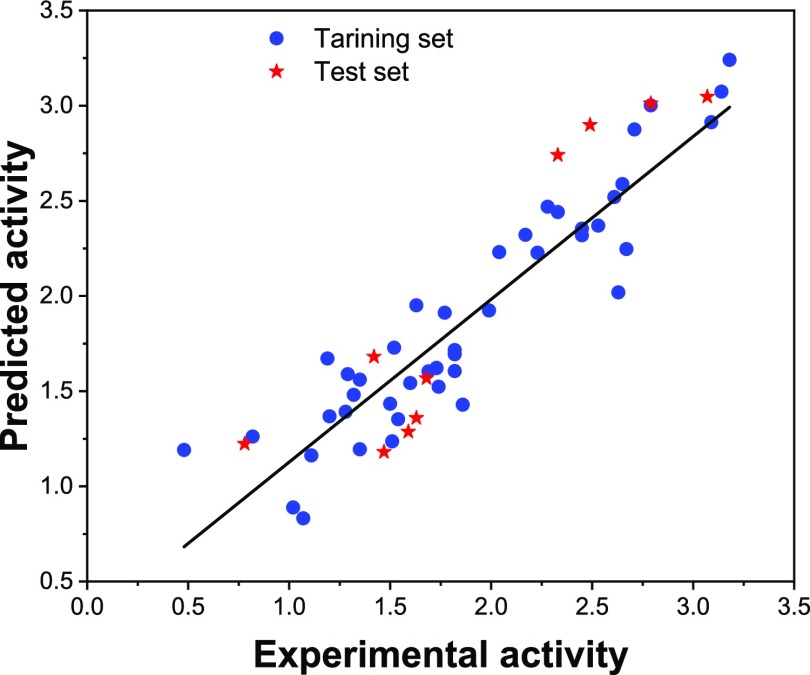
The plot of the predicted activities against the experimental activities for both training and test sets, for the ACE inhibitor tripeptides, is shown in Figure 2. The squared correlation coefficient for the training set was calculated as 0.86. With the purpose of confirming the reliability of the model, leave-one-out and leave-m-out (for example, leave-5-out) cross validation was applied on the training set and the corresponding qloo2 and qlmo of 0.831 and 0.830 were obtained. The closeness of these statistical parameters to each other and to that of Rtraining2 confirms that the constructed model is stable. The R2 value for the test set (Rtest = 0.859) was also very close to those for training and cross validation, which revealed the good prediction power of the QSAR model without the presence of significant overfitting. In addition, the model possessed a very low value of the chance correlation of RMP2 (Table 2), highlighting that the model was not chancy and the resulted relationship was systematic. Table 3 summarizes the consequences of different past QSAR models of the ACE peptides alongside those obtained in this investigation. Clearly, the QSAR model derived in this work for the ACE data set has better quality in regard to all previous models. The results of cross validation also approve the efficiency of the model in comparison to the previous works.

Figure 2.

Figure 2

Open in a new tab

Plot of predicted versus experimental pIC50 values of ACE tripeptides.

Table 3. Comparison between QSAR Models for the ACE Data Seta.

descriptors model variables/LVs Rtraining2 RSMEtraining qloo2 Rtest2 refs
1 z scale PLS 2 0.770 NR NR NR Hellberg et al.22
2 GRID PP PLS 1 0.744 NR NR NR Cocchi and Johansson23
3 ISA-ECI PLS 2 0.700 NR NR NR Collantes and Dunn24
4 MS-WHIM (extended) PLS 2 0.708 NR 0.637 NR Zaliani and Gancia25
5 MS-WHIM (rotameric) PLS 6 0.657 NR 0.541 NR Zaliani and Gancia25
6 VHSE PLS 1 0.770 0.48 0.745 0.688 Mei et al.27
7 T scale PLS 2 0.845 0.39 0.786 0.798 Tian et al.28
8 VSW PLS 2 0.868 0.37 0.784 0.871 Tong et al.26
9 ATS–QTMS PLS 3 0.868 0.36 0.812 0.702 Yousefinejad et al.29
10 NDV MLR 3 0.855 0.245 0.831 0.861 this work
Open in a new tab
a

NR, not reported.

One key ergonomic advantage of our QSAR model is its easy understanding and interpretation. To determine the position of the anchor residues in the peptides binding to ACE, it is enough to check which ones of residues are significant in the QSAR model. Moreover, the quantitative contributions for each position reveal, directly, the importance of these positions.

Table 4 summarizes the statistical analysis of the selected QSAR model for ACE peptide inhibitors. It is clear from Table 4 that the regression coefficient associated with the second AA in the peptide sequence is not significant. The following equation shows the final QSAR model after removing the nonsignificant term for the ACE inhibitor tripeptides

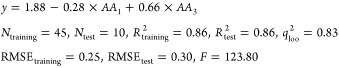graphic file with name ao9b04302_m001.jpg 1

It means that the anchor positions for ACE peptide inhibitors are the first and third positions. In other words, the amino acids located at the two ends of the considered tripeptides would have more impact on the ACE inhibition. This is in accordance with the previous studies.20,30 It is also possible to check if there is a peptide having activity more than the most bioactive peptide in the ACE data set. The most activity value was measured for the following sequence: “PPG”. By changing the type of AA at each position of the peptide sequence, we found that the most bioactive peptide was that previously recognized (i.e., PPG). Preferred amino acids at each position were recognized, as well. The preferred amino acids at position 1 were found to be Pro, Trp, and Tyr and for the third position to be just Gly.

Table 4. Statistical Analysis of the Selected QSAR Model for ACE Data Set.

regression coefficient SE t-value P-value
1.88 0.038 49.25 4.17 × 10–38
–0.27 0.046 –5.87 6.59 × 10–7
–0.02 0.046 –0.35 0.73
0.66 0.044 15.01 2.97 × 10–18
Open in a new tab

QSAR Study on Bitter Peptide

Bitter sensitivity, as one of the gustatory sensitivities, shields humans and organisms from damage by toxic substances. Studies demonstrate that the conduction of taste signal in taste receptor cells includes a series of complicated processes intervened by G protein-coupled receptors.31 Bitter-tasting thresholds (BTTs) of 48 dipeptides and their activities as the negative logarithm of concentration (pT) were chosen by Collantes et al.24 This data set is frequently utilized to approve the efficiency of amino acid descriptors. Forty samples out of 48 dipeptides were treated as the training set that was used to construct the QSAR model, and the remaining were regarded as the test set.

Statistical parameters of QSAR models constructed with different subsets of AA indices are given in Table 5. The results showed the proficiency of NDV in QSAR modeling of the peptide sequences. As can be seen in Table 5, even with two AA indices, the obtained QSAR model had good quality. However, the best QSAR model was constructed using eight AA indices (Table 5). These AA indices are listed in Table S3. The resulted NDM for BTT is given in Table S4. The resulted multiple linear regression (MLR) model was

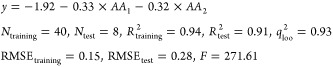graphic file with name ao9b04302_m002.jpg 2

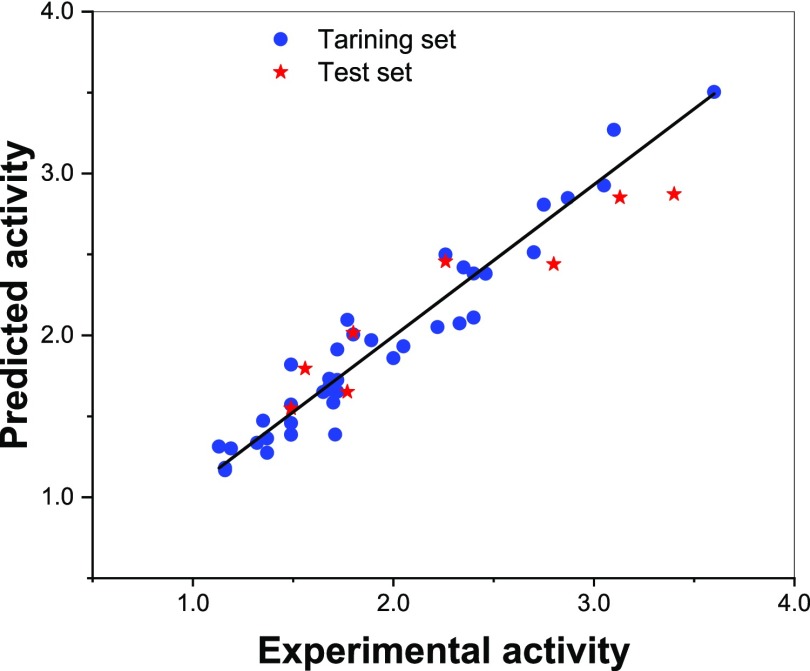
As shown in eq 2, the best QSAR model yielded a squared correlation coefficient (R2) of 0.936 and a root-mean-square error (RMSE) of 0.149 for the training set. The squared correlation coefficient calculated via leave-one-out cross validation (q2) was found to be 0.926. Further validation of the model was carried out on the basis of the external test set, and a good result was obtained (Rtest2 = 0.907, RMSE = 0.283). The experimental and predicted biological activities for the BTT data set are given in Table S4. The relationship between predicted and experimental activities is shown in Figure 3. The NDV-QSAR model developed in this study for the BTT data set is compared with the previously reported QSAR models in Table 6. Analysis of variance (ANOVA) of the final QSAR models showed that both amino acids in the peptide sequence have a significant impact on the BTT peptide set (Table S5).

Table 5. QSAR Models of BTT Obtained Using Different Sets of the AA Indices.

number of used AA indices Rtraining2 Rtest2 qloo2 qlmo2 RSMEtraining RSMEtest RMP2a
2 0.850 0.855 0.828 0.813 0.228 0.343 0.166
3 0.905 0.903 0.890 0.890 0.182 0.302 0.126
4 0.878 0.898 0.858 0.856 0.206 0.280 0.084
5 0.900 0.899 0.877 0.882 0.186 0.339 0.073
6 0.901 0.902 0.877 0.883 0.186 0.337 0.179
7 0.917 0.899 0.903 0.899 0.170 0.309 0.136
8 0.936 0.907 0.926 0.924 0.149 0.283 0.133
9 0.909 0.909 0.893 0.892 0.178 0.303 0.146
Open in a new tab
a

Maximum Rtraining2 for the Y-randomization test.

Figure 3.

Figure 3

Open in a new tab

Plot of predicted versus experimental activities for the BTT data set.

Table 6. Comparison between QSAR Models for the BTT Data Set.

descriptors model variables/LVs Rtraining2 RSMEtraining qloo2 Rtest2 refs
1 VSW PLS 2 0.873 0.23 0.751 0.713 Tong et al.26
2 z scale PLS 2 0.824 0.26 NR NR Hellberg et al.22
3 ISA-ECI PLS 2 0.8480 0.245 NR 0.245 Collantes and Dunn24
4 MS-WHIM (extended) PLS 3 0.754 NR 0.710 NR Zaliani and Gancia25
5 MS-WHIM (rotameric) PLS 3 0.704 NR 0.633 NR Zaliani and Gancia25
6 VHSE PLS 3 0.910 0.20 0.816 0.883 Mie et al.27
7 ATS/QTMS GA–PLS 2 0.872 0.22 0.826 0.770 Yousefinejad et al.29
8 NDV MLR 2 0.936 0.149 0.926 0.907 this work
Open in a new tab

QSAR Model for the HLA Data Set

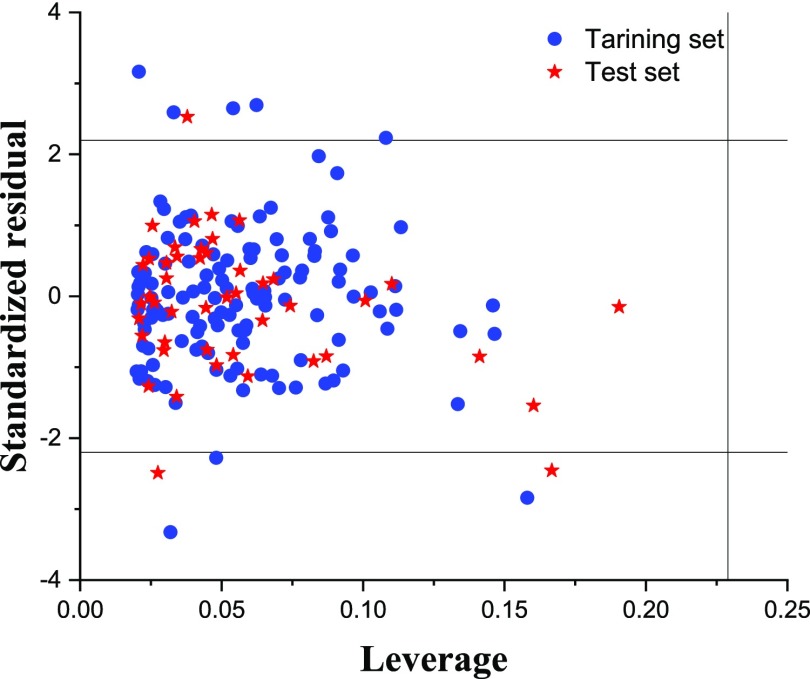
This data set comprises of 177 nonameric binding peptides of the HLA-A*0201. Each peptide has nine residues. Several QSAR models using different subsets of AA indices were built, and the results are summarized in Table S6. The best NDV-QSAR model was obtained using six AA indices. In total, 54.0% of variance in the dependent variable was explained by this selected model, while 40.7 and 46.1% of variances were reproduced in leave-one-out and leave-five-out cross validations, respectively. Although the quality of this model is not as good as those obtained for two later data sets, it is still comparable to those reported previously for the HLA data set (row 6 in Table 7). The presence of outliers was checked using the Williams plot. This plot utilizes simultaneously the concepts of standardized residual and leverage to show visually the applicability domain of the model.6Figure 4 depicts the Williams plot for the HLA data set, indicating that there are several outliers. To obtain a stable QSAR model, these outliers were removed and the MLR model was reconstructed and rechecked for the presence of outliers. Eleven peptides from the training set and three peptides from the test set were found to be outliers. The resulted QSAR model after removing the detected outliers had better quality compared to that of the original model. Features of this model are given in row 7 of Table 7. The obtained QSAR model had better prediction ability in comparison to those in all of the previous reports. The root-mean-squared errors for the training and test sets (RSMEtraining and RSMEtest) were 0.45 and 0.46, respectively. The RMSE–CV was calculated as 0.50, which is as good as the RSMEtest. The squared correlation coefficients for the prediction of activities in the training and test sets were found to be 0.70 and 0.71, respectively. Statistical parameters of the model are tabulated in Table 8. From the results in Table 8, it was found that some regression coefficients associated to residuals 1, 5, 6, and 7 were not significant. The calculated t-values for these coefficients were more than 0.05, and the corresponding p-values for these coefficients were high. Omitting these nonsignificant variables resulted in a QSAR model with Rtraining2 and Rtest of 0.69 and 0.71, respectively. RSMEtraining and RSMEtest were both calculated to be 0.46. Based on these results, it was found that the final QSAR model could explain the variance in the training set as well as predict the affinities of the test set accurately. On the other hand, based on the variables remaining in the final QSAR model, it could be concluded that the anchor positions are 2, 3, 4, 8, and 9. The final QSAR model for the HLA data set was as follows

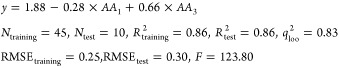graphic file with name ao9b04302_m003.jpg 3

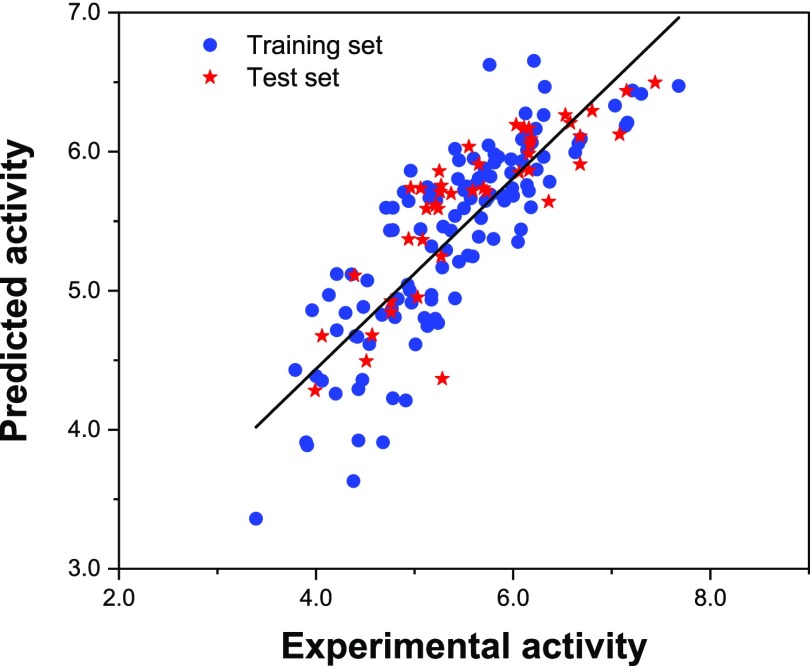
The relationship between predicted and experimental activities is depicted in Figure 5. Searching for AAs for each anchor point to find favored amino acids at each position led to find sequence “VVPPEEEPV” with a maximum pBL50 of 7.41. It is worth noting again that entries of the calculated NDV for each sequence are influential by the AA appeared at each position, the neighbors of the AA in the sequence, and the types of AA indices used in the calculation. Consequently, although positions 1, 5, 6, and 7 were not recognized as the anchor positions, they could affect the entries of the NDV. However, changing of AAs at positions 1, 5, 6, and 7 of the best sequence had a small variation on the binding affinity and the minimum and maximum pBL50 values were found to be 6.96 and 7.41, respectively. It should be noticed that the most active peptide in the original data set is “ILDPFPVTV” with a pBL50 of 8.65. This sequence was detected as outlier and removed before the model construction. Our model predicted pBL50 of 6.49 for this sequence. The other most active peptides along with the experimental and predicted activities are listed in Table 9. To find favored AAs for each position, a list of suggested peptides by pBL50 values greater than 7.30 was provided by the replacement method (Table 10). Inspection the results of Table 10 indicated that preferred amino acids at position 1 are valine, leucine, alanine, methionine, and isoleucine; at position 2 are valine and alanine; at position 3 are proline and aspartic acid; at position 4 is just proline; at position 5 is just glutamic acid; at positions 6 and 7 are glutamic acid, valine, leucine, methionine, and isoleucine; at position 8 is just proline; and at position 9 are valine and alanine.

Table 7. Comparison between QSAR Models for the HLA Data Set.

descriptors model variables/LVs Rtraining2 RSMEtraining qloo2 Rtest2 refs
1 QTMS–ADFQ GA–PLS 3 0.648 0.59 0.561 0.50 Hemmateenejad et al.20
2 ATS/QTMS GA–PLS 6 0.782 0.47 0.682 0.50 Yousefinejad et al.29
3 additive PLS 3 0.85 NR 0.54 0.64 Doytchinova et al.33
4 global GA–MLR   0.43 0.75a NR 0.42 Doytchinova et al.33
5 z scales GA–MLR   0.67 0.59a NR 0.50 Doytchinova et al.33
6 NDV MLR 9 0.540 0.664 0.407 0.535 this work
7 NDV MLR (after removing outliers) 9 0.702 0.452 0.632 0.712 this work
8 NDV MLR (after removing outliers and omitting nonsignificant variables) 5 0.690 0.461 0.642 0.713 this work
Open in a new tab
a

Standard error of estimate (SEE).

Figure 4.

Figure 4

Open in a new tab

Williams plot (standardized residual versus leverage) for the HLA data set. Critical values of standardized residual and leverage are shown by horizontal and vertical dashed lines, respectively.

Table 8. Statistics for the Best QSAR Model for the HLA Data Set.

AA no. β SE t-value P-value VIF
intercept 5.381 0.043 124.810 <10–11  
1 0.002 0.049 0.049 0.96 1.26
2 –0.381 0.048 –7.878 <10–11 1.25
3 0.233 0.066 3.536 5.95 × 10–4 2.31
4 0.372 0.063 5.935 3.48 × 10–8 2.10
5 0.032 0.051 0.636 0.53 1.38
6 0.071 0.066 1.078 0.28 2.30
7 0.084 0.046 1.829 0.07 1.12
8 0.216 0.055 3.965 1.31 × 10–4 1.58
9 –0.281 0.048 –5.894 4.20 × 10–8 1.22
Open in a new tab

Figure 5.

Figure 5

Open in a new tab

Plot of predicted versus experimental activities for the HLA data set.

Table 9. Most Active Peptides along with the Experimental and Predicted Activitiesa.

peptide sequence experimental pBL50 predicted pBL50
ILDPFPVTV 8.65 6.4927
ILDPFPPTV 8.17 6.3781
ILDPFPPEV 7.68 6.4713
ILDPFPITV 8.14 6.4678
ILDPFPPPV 7.44 6.4911
ILDPLPPTV 7.15 6.4363
VVPPEEEPV   7.4082
Open in a new tab
a

The peptide in the last row is that introduced by the QSAR model.

Table 10. List of 50 Sequences with High Activities Suggested by the QSAR Model.

  sequence predicted pBL50   sequence predicted pBL50
1 AVPPEEEPV 7.38 26 VVPPEVMPV 7.31
2 IVPPEEEPV 7.34 27 VVPPEEMPV 7.35
3 LVPPEEEPV 7.38 28 VVPPELMPV 7.30
4 MVPPEEEPV 7.37 29 VVPPELEPV 7.36
5 VVPPEEEPV 7.41 30 VVPPELEPA 7.32
6 VAPPEEEPV 7.36 31 VVPPEEEPA 7.36
7 VADPEEEPV 7.31 32 VVPPEMEPA 7.31
8 VVDPEEEPV 7.36 33 VVPPEVEPA 7.33
9 VVDPEIEPV 7.31 34 AVPPEVEPA 7.30
10 VVDPELEPV 7.32 35 LVPPEVEPA 7.30
11 VVDPEMEPV 7.31 36 LVPPEEEPA 7.34
12 VVDPEVEPV 7.34 37 LVPPEEVPA 7.30
13 VVDPEVVPV 7.30 38 LVPPEEVPV 7.35
14 VVPPEVVPV 7.34 39 AVPPEEVPV 7.34
15 VVPPEEVPV 7.37 40 IVPPEEVPV 7.31
16 VVPPEIVPV 7.31 41 MVPPEEVPV 7.33
17 VVPPELVPV 7.33 42 MVPPEVVPV 7.30
18 VVPPEMVPV 7.32 43 MVPPEVEPV 7.34
19 VVPPEMEPV 7.35 44 AVPPEVEPV 7.35
20 VVPPEMLPV 7.30 45 IVPPEVEPV 7.31
21 VVPPEELPV 7.36 46 LVPPEVEPV 7.35
22 VVPPELLPV 7.31 47 LAPPEVEPV 7.30
23 VVPPEVLPV 7.32 48 LAPPEEEPV 7.33
24 VVPPEVEPV 7.38 49 LAPPEEVPV 7.30
25 VVPPEVIPV 7.30 50 AAPPEEVPV 7.30
Open in a new tab

In the derived model, each anchor position has a regression coefficient accounting for its contribution to the affinity. Thus, positions 2 and 9 with negative coefficients decrease the affinity because of their negative contributions and positions 3, 4, and 8 make positive contributions to the affinity.

Conclusions

A new numerical descriptive vector was introduced for peptide QSAR analysis. Physicochemical properties of AAs and principal component analysis were used in the calculation of NDVs of peptide sequences. The application of the proposed NDV on three peptide sets showed that this new peptide descriptor is useful in bioactive peptide QSAR analysis. The resulted QSAR models not only showed good self-prediction ability but also exhibited sufficient prediction power for samples in the test sets. On the other hand, since our proposed numerical descriptive vector has the same length as the peptide sequence, the interpretation of the resulted QSAR models is straightforward and it seems that we can easily use them to have a hot spot analysis for different kinds of biologically and pharmaceutically peptides. Indeed, the active parts of the considered peptides correspond to those AAs having statistically significant regression coefficients in the resulted QSAR model.

Computational Methods

Data Sets and Descriptors

Three peptide data sets with known biological activity were used to investigate the performances of the suggested AA indices. They were as follows: data set 1 contained a set of 55 angiotensin-converting enzyme (ACE) inhibitors; data set 2 contained a set of 12 bactericidal peptides, data set 3 comprised a set of 177 nonameric peptides binding to the HLA-A*0201 molecule, and data set 4 contained a set of 48 bitter dipeptides. The data sets were picked up from the literature.20,26,30,32−34 To ensure a fair comparison, the same training and test sets were used for each considered data set. Table 1 presents details of all data sets.

Descriptor Extraction and Model Development

One of the essential steps in structure–activity relationship studies is the extraction of some numerical descriptors from the desired compounds that can be useful in describing the structural properties.

In the current research, for each peptide sequence, a numerical descriptive vector is calculated based on a set of physicochemical properties of AAs and PCA.21 Consider a residue with n AAs. For each amino acid in the residue a numerical matrix Xi with a size of N × L is created, where L is the number of considered physicochemical indices. For a residue of length N, subsequently, N numerical matrices are created. The entries of the ith X matrix are calculated by the following equation

graphic file with name ao9b04302_m004.jpg 4

where ai is a vector containing the physicochemical properties of the ith AA and dij is

graphic file with name ao9b04302_m005.jpg 5

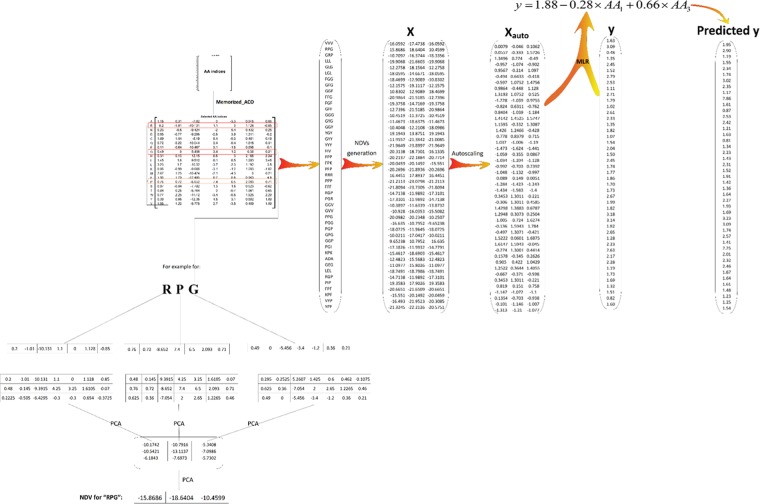
Here, the distance between the two AA in the residue is calculated as the Euclidean distance. The first eigenvector of each Xi matrix is computed. No pretreatment is carried out on the Xi matrix prior to PCA. The resulted eigenvector vectors from all X matrices are collected in a matrix Y (N × N). The first eigenvector of the Y matrix is considered as the numerical descriptive vector of the residue. Figure 1 describes graphically all of the above calculation steps for a tripeptide “RPG”, as an example. For more information, the reader should refer to our previous paper.21

The physicochemical properties of AAs were extracted from the AAindex database. This database contains various physicochemical and biochemical properties of amino acids and pairs of amino acids.35,36 The AAindex database is divided into three parts: AAindex1 for the amino acid indices of 20 numerical values, AAindex2 for amino acid substitution matrices, and AAindex3 for amino acid contact potential matrices.37 For the purpose of peptide descriptor calculation, we considered only the 553 amino acid indices in AAindex1.

Keeping in the mind that the calculated numerical descriptive vector for a peptide sequence is highly dependent on the AA indices used in the calculation, a proper set of AA indices was chosen by the Memorized_ACO algorithm38−40 for each data set. The ACO algorithm is inspired by the behavior of real ants that are able to find the shortest path from a food to their nest. An ant deposits pheromone while moving. Ants explore the space randomly, but a route with more pheromone deposited by previous ants that have already passed is more likely to be chosen by the future ants. The ACO algorithm is an iterative algorithm. In this algorithm, equal pheromone values are initially assigned to all AA indices. As time proceeds, the level of pheromone deposited on the best AA indices increases, while that for other variables decreases. The best AA indices are those yielding a highly predictive power QSAR model. A graphical representation of the process is given in Figure 1. The Memorized_ACO algorithm employs an external memory in which knowledge incorporated from the previous ACO iterations is deposited. It fills by running a simple ACO algorithm several times.

Another advantage of our proposed method is that modeling of the relationship between the calculated numerical descriptive vectors and the biological activities of peptides was simply achieved by utilizing multiple linear regression (MLR) without requiring variable selection. Assessment of the importance of each residue, in the peptide sequence, in the biological activity is carried out by considering the regression coefficients of the resulted model.

To test the predictive power of the models, different cross-validation approaches were applied. The correlation coefficient of the test set (Rtest2) was also computed. A Y-randomization test was performed to assess the risk of chance correlation of the model. All necessary programs were written in MATLAB (MathWorks). The method is available for the research community.

Acknowledgments

This manuscript was extracted from the Ph.D. thesis of Mehri Mahmoodi-Reihani. The financial support to this work from Islamic Azad University, Mahshahr Branch, is greatly appreciated.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b04302.

  • Tables S1 and S3, AA indices used in the construction of the ACE and BBT QSAR models, respectively; Tables S2 and S4, calculated NDM for ACE and BBT data sets, respectively; Table S5, statistical analysis of the selected QSAR model for BTT data set; Table S6, QSAR models for HLA data set obtained using different sets of the AA indices (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao9b04302_si_001.pdf (159.7KB, pdf)

References

  1. Yazawa K.; Numata K. Recent advances in chemoenzymatic peptide syntheses. Molecules 2014, 19, 13755–13774. 10.3390/molecules190913755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Deng B.; Long H.; Tang T.; Ni X.; Chen J.; Yang G.; Zhang F.; Cao R.; Cao D.; Zeng M. Quantitative structure-activity relationship study of antioxidant tripeptides based on model population analysis. Int. J. Mol. Sci. 2019, 20, 995. 10.3390/ijms20040995. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Abbasitabar F.; Zare-Shahabadi V. Development predictive QSAR models for artemisinin analogues by various feature selection methods: A comparative study. SAR QSAR Environ. Res. 2012, 23, 1–15. 10.1080/1062936X.2011.623316. [DOI] [PubMed] [Google Scholar]
  4. Abbasitabar F.; Zare-Shahabadi V. In silico prediction of toxicity of phenols to Tetrahymena pyriformis by using genetic algorithm and decision tree-based modeling approach. Chemosphere 2017, 172, 249–259. 10.1016/j.chemosphere.2016.12.095. [DOI] [PubMed] [Google Scholar]
  5. Zare-Shahabadi V. Quantitative structure–activity relationships of dihydrofolatereductase inhibitors. Med. Chem. Res. 2016, 25, 2787–2797. 10.1007/s00044-016-1666-z. [DOI] [Google Scholar]
  6. Abbasitabar F.; Zare-Shahabadi V. QSAR study of artemisinin analogues as antimalarial drugs by neural network and replacement method. Drug Res. 2017, 67, 476–484. 10.1055/s-0043-108553. [DOI] [PubMed] [Google Scholar]
  7. Deng B.; Ni X.; Zhai Z.; Tang T.; Tan C.; Yan Y.; Deng J.; Yin Y. New quantitative structure–activity relationship model for angiotensin-converting enzyme inhibitory dipeptides based on integrated descriptors. J. Agric. Food. Chem. 2017, 65, 9774–9781. 10.1021/acs.jafc.7b03367. [DOI] [PubMed] [Google Scholar]
  8. Chen N.; Chen J.; Yao B.; Li Z. QSAR study on antioxidant tripeptides and the antioxidant activity of the designed tripeptides in free radical systems. Molecules 2018, 23, 1407. 10.3390/molecules23061407. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Vishnepolsky B.; Gabrielian A.; Rosenthal A.; Hurt D. E.; Tartakovsky M.; Managadze G.; Grigolava M.; Makhatadze G. I.; Pirtskhalava M. Predictive model of linear antimicrobial peptides active against gram-negative bacteria. J. Chem. Inf. Model. 2018, 58, 1141–1151. 10.1021/acs.jcim.8b00118. [DOI] [PubMed] [Google Scholar]
  10. Wu S.; Qi W.; Su R.; Li T.; Lu D.; He Z. CoMFA and CoMSIA analysis of ACE-inhibitory, antimicrobial and bitter-tasting peptides. Eur. J. Med. Chem. 2014, 84, 100–106. 10.1016/j.ejmech.2014.07.015. [DOI] [PubMed] [Google Scholar]
  11. Radman A.; Gredičak M.; Kopriva I.; Jerić I. Predicting antitumor activity of peptides by consensus of regression models trained on a small data sample. Int. J. Mol. Sci. 2011, 12, 8415–8430. 10.3390/ijms12128415. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Bahadori M.; Hemmateenejad B.; Yousefinejad S. Quantitative sequence-activity modeling of ACE peptide originated from milk using ACC–QTMS amino acid indices. Amino Acids 2019, 51, 1209–1220. 10.1007/s00726-019-02761-y. [DOI] [PubMed] [Google Scholar]
  13. Li Z.; Miao Q.; Yan F.; Meng Y.; Zhou P. Machine learning in quantitative protein–peptide affinity prediction: Implications for therapeutic peptide design. Curr. Drug Metab. 2019, 20, 170–176. 10.2174/1389200219666181012151944. [DOI] [PubMed] [Google Scholar]
  14. Xu B.; Chung H. Y. J. M. Quantitative structure–activity relationship study of bitter di-, tri-and tetrapeptides using integrated descriptors. Molecules 2019, 24, 2846. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Toropova A. P.; Toropov A. A. Application of the monte carlo method for the prediction of behavior of peptides. Curr. Protein Pept. Sci. 2019, 20, 1151–1157. 10.2174/1389203720666190123163907. [DOI] [PubMed] [Google Scholar]
  16. Guan X.; Liu J. QSAR study of angiotensin i-converting enzyme inhibitory peptides using svhehs descriptor and osc-svm. Int. J. Pept. Res. Ther. 2019, 25, 247–256. 10.1007/s10989-017-9661-x. [DOI] [Google Scholar]
  17. Qian N.; Sejnowski T. J. Predicting the secondary structure of globular proteins using neural network models. J. Mol. Biol. 1988, 202, 865–884. 10.1016/0022-2836(88)90564-5. [DOI] [PubMed] [Google Scholar]
  18. Wu C.; Whitson G.; McLarty J.; Ermongkonchai A.; Chang T. C. Protein classification artificial neural system. Protein Sci. 1992, 1, 667–677. 10.1002/pro.5560010512. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Mundra P.; Kumar M.; Kumar K. K.; Jayaraman V. K.; Kulkarni B. D. Using pseudo amino acid composition to predict protein subnuclear localization: Approached with PSSM. Pattern Recognit. Lett. 2007, 28, 1610–1615. 10.1016/j.patrec.2007.04.001. [DOI] [Google Scholar]
  20. Hemmateenejad B.; Yousefinejad S.; Mehdipour A. R. Novel amino acids indices based on quantum topological molecular similarity and their application to QSAR study of peptides. Amino Acids 2011, 40, 1169–1183. 10.1007/s00726-010-0741-x. [DOI] [PubMed] [Google Scholar]
  21. Mahmoodi-Reihani M.; Abbasitabar F.; Zare-Shahabadi V. A novel graphical representation and similarity analysis of protein sequences based on physicochemical properties. Phys. A 2018, 510, 477–485. 10.1016/j.physa.2018.07.011. [DOI] [Google Scholar]
  22. Hellberg S.; Eriksson L.; Jonsson J.; Lindgren F.; Sjöström M.; Skagerberg B.; Wold S.; Andrews P. Minimum analogue peptide sets (maps) for quantitative structure-activity relationships. Int. J. Pept. Protein Res. 1991, 37, 414–424. 10.1111/j.1399-3011.1991.tb00756.x. [DOI] [PubMed] [Google Scholar]
  23. Cocchi M.; Johansson E. Amino acids characterization by grid and multivariate data analysis. Quant. Struct.-Act. Relat. 1993, 12, 1–8. 10.1002/qsar.19930120102. [DOI] [Google Scholar]
  24. Collantes E. R.; Dunn W. J. III Amino acid side chain descriptors for quantitative structure-activity relationship studies of peptide analogs. J. Med. Chem. 1995, 38, 2705–2713. 10.1021/jm00014a022. [DOI] [PubMed] [Google Scholar]
  25. Zaliani A.; Gancia E. MS-WHIM scores for amino acids: A new 3D-description for peptide QSAR and QSPR studies. J. Chem. Inf. Comput. Sci. 1999, 39, 525–533. 10.1021/ci980211b. [DOI] [Google Scholar]
  26. Tong J.; Liu S.; Zhou P.; Wu B.; Li Z. A novel descriptor of amino acids and its application in peptide QSAR. J. Theor. Biol. 2008, 253, 90–97. 10.1016/j.jtbi.2008.02.030. [DOI] [PubMed] [Google Scholar]
  27. Mei H.; Liao Z. H.; Zhou Y.; Li S. Z. A new set of amino acid descriptors and its application in peptide QSARs. Biopolymers 2005, 80, 775–786. 10.1002/bip.20296. [DOI] [PubMed] [Google Scholar]
  28. Tian F.; Zhou P.; Li Z. T-scale as a novel vector of topological descriptors for amino acids and its application in QSARs of peptides. J. Mol. Struct. 2007, 830, 106–115. 10.1016/j.molstruc.2006.07.004. [DOI] [Google Scholar]
  29. Yousefinejad S.; Hemmateenejad B.; Mehdipour A. New autocorrelation QTMS-based descriptors for use in QSAM of peptides. J. Iran. Chem. Soc. 2012, 9, 569–577. 10.1007/s13738-012-0070-y. [DOI] [Google Scholar]
  30. Lin Z.-h.; Long H.-x.; Bo Z.; Wang Y.-q.; Wu Y.-z. New descriptors of amino acids and their application to peptide QSAR study. Peptides 2008, 29, 1798–1805. 10.1016/j.peptides.2008.06.004. [DOI] [PubMed] [Google Scholar]
  31. de Armas R. R.; Díaz H. G.; Molina R.; González M. P.; Uriarte E. Stochastic-based descriptors studying peptides biological properties: Modeling the bitter tasting threshold of dipeptides. Bioorg. Med. Chem. 2004, 12, 4815–4822. 10.1016/j.bmc.2004.07.017. [DOI] [PubMed] [Google Scholar]
  32. Mei H.; Zhou Y.; Sun L.-L.; Li Z.-L. A new descriptor of amino acids and its application in peptide QSAR. Acta Phys.-Chim. Sin. 2004, 20, 821–825. [Google Scholar]
  33. Doytchinova I. A.; Walshe V.; Borrow P.; Flower D. R. Towards the chemometric dissection of peptide–HLA-a* 0201 binding affinity: Comparison of local and global QSAR models. J. Comput.-Aided Mol. Des. 2005, 19, 203–212. 10.1007/s10822-005-3993-x. [DOI] [PubMed] [Google Scholar]
  34. Guan P.; Doytchinova I. A.; Walshe V. A.; Borrow P.; Flower D. R. Analysis of peptide–protein binding using amino acid descriptors: Prediction and experimental verification for human histocompatibility complex HLA-a*0201. J. Med. Chem. 2005, 48, 7418–7425. 10.1021/jm0505258. [DOI] [PubMed] [Google Scholar]
  35. Kawashima S.; Ogata H.; Kanehisa M. Aaindex: Amino acid index database. Nucleic Acids Res. 1999, 27, 368–369. 10.1093/nar/27.1.368. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Kawashima S.; Kanehisa M. Aaindex: Amino acid index database. Nucleic Acids Res. 2000, 28, 374 10.1093/nar/28.1.374. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Han G. S.; Anh V.; Krishnajith A. P.; Tian Y.-C.; et al. An ensemble method for predicting subnuclear localizations from primary protein structures. PLoS One 2013, 8, e57225 10.1371/journal.pone.0057225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Shamsipur M.; Zare-Shahabadi V.; Hemmateenejad B.; Akhond M. An efficient variable selection method based on the use of external memory in ant colony optimization. Application to QSAR/QSPR studies. Anal. Chim. Acta 2009, 646, 39–46. 10.1016/j.aca.2009.05.005. [DOI] [PubMed] [Google Scholar]
  39. Zare-Shahabadi V.; Abbasitabar F. Application of ant colony optimization in development of models for prediction of anti-HIV-1 activity of HEPT derivatives. J. Comput. Chem. 2010, 31, 2354–2362. 10.1002/jcc.21529. [DOI] [PubMed] [Google Scholar]
  40. Zare-Shahabadi V.; Lotfizadeh M.; Gandomani A. R. A.; Papari M. M. Determination of boiling points of azeotropic mixtures using quantitative structure–property relationship (QSPR) strategy. J. Mol. Liq. 2013, 188, 222–229. 10.1016/j.molliq.2013.09.037. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b04302_si_001.pdf (159.7KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES