Automatic PET Cervical Tumor Segmentation by Combining Deep Learning and Anatomic Prior

Abstract

Cervical tumor segmentation on 3D ¹⁸FDG PET images is a challenging task because of the proximity between cervix and bladder, both of which can uptake ¹⁸FDG tracers. This problem makes traditional segmentation based on intensity variation methods ineffective and reduces overall accuracy. Based on anatomy knowledge, including “roundness” of the cervical tumor and relative positioning between the bladder and cervix, we propose a supervised machine learning method that integrates convolutional neural network (CNN) with this prior information to segment cervical tumors. First, we constructed a spatial information embedded CNN model (S-CNN) that maps the PET image to its corresponding label map, in which bladder, other normal tissue, and cervical tumor pixels are labeled as −1, 0, and 1, respectively. Then, we obtained the final segmentation from the output of the network by a prior information constrained (PIC) thresholding method. We evaluated the performance of the PIC-S-CNN method on PET images from 50 cervical cancer patients. The PIC-S-CNN method achieved a mean Dice similarity coefficient (DSC) of 0.84 while region-growing, Chan-Vese, graph-cut, fully convolutional neural networks (FCN) based FCN-8 stride, and FCN-2 stride, and U-net achieved 0.55, 0.64, 0.67, 0.71, 0.77, and 0.80 mean DSC, respectively. The proposed PIC-S-CNN provides a more accurate way for segmenting cervical tumors on 3D PET images. Our results suggest that combining deep learning and anatomic prior information may improve segmentation accuracy for cervical tumors.

1. INTRODUCTION

In 2015, cervical cancer was the second leading cause of death due to cancer in women aged 20 to 39 years. Moreover, 13,240 new cases with cervical cancer are predicted for 2018 resulting in an estimated 4,170 deaths (Rebecca L. Siegel, 2018). Positron emission tomography (PET) employing radiopharmaceutical ¹⁸fludeoxyglucose (¹⁸FDG) is a valuable imaging modality for staging, treatment planning, and follow-up in cervical cancer. Besides providing important complementary information for target volume delineation in radiation treatment planning, PET imaging is also essential in evaluating treatment response and outcome. An essential step in these applications is cervical tumor segmentation on 3D PET images. In the clinic, manual segmentation is routinely used by radiation oncologists, but it is time-consuming and observer-dependent. Automatic or semi-automatic methods for segmenting cervical tumor on PET are needed to ensure more consistent tumor segmentation.

While many automatic segmentation techniques (Zhu and Jiang, 2003; Zaidi and El Naqa, 2010; Zaidi et al., 2012; Erdi et al., 1997; Abdoli et al., 2013; Daisne et al., 2003; Miller et al., 2003; Mu et al., 2015; Roman-Jimenez et al., 2016; Roman-Jimenez et al., 2012; Crivellaro et al., 2012; Sironi et al., 2006; Bagci et al., 2013; Weina Xu, 2017) have been investigated for PET imaging, accurate automatic cervical tumor segmentation is still a challenging task because of the proximity between cervix and bladder. Traditional automatic segmentation methods including automatic thresholding and region growing are mainly based on the difference in the activity value (intensity value in image) between the lesion and normal tissues. However, because the bladder retains a large amount of ¹⁸FDG tracer, bladder intensity may be similar to cervical tumor intensity. Because the cervix is so close to the bladder, region growing-based methods often misclassify the bladder as a tumor. The same situation is expected for gradient-based (Geets et al., 2007) and active-contour (Li et al., 2008) methods, which primarily rely on variations in intensity values. Based on the graph-cut algorithm, a two-stage segmentation scheme that considers tumor position and area between adjacent slices was proposed earlier (Chen et al., 2018). Although the segmentation accuracy of cervical tumors was improved, this semi-automatic method needs manual contouring of the cervical tumor on a given slice. In addition to these unsupervised or semi-supervised methods for PET image segmentation, learning atlas-based methods have been proven to be effective to segment organs in medical images (Aljabar et al., 2009; Xue et al., 2006; Wu et al., 2014) (Kalinić, 2009). Deep convolutional neural networks (CNN) have also shown great promise in tumor segmentation (Rouhi et al., 2015; Havaei et al., 2017; Arbabshirani et al., 2017; Zhu et al., 2017; Gibson et al., 2017; Cheng et al., 2016; Frederick, 1990; Pereira et al., 2016; Ronneberger et al., 2015; Kamnitsas et al., 2017). CNN-based tumor segmentation can be summarized into two categories: patch-to-patch (pixel) and image-to-image strategies. Redundancy and training efficiency are two major issues in the patch-to-patch (pixel) strategy because each patch overlaps and is predicted separately (Çiçek et al., 2016; Ronneberger et al., 2015). Moreover, because cervical tumors and bladder are so close and have similar intensities, extracting patches has been challenging for the patch-to-patch strategy so that the bladder pixel patch can be differentiated from the cervical tumor pixel patch. The fully convolutional networks (FCN) (Long et al., 2015; Shelhamer et al., 2017) and U-net (Ronneberger et al., 2015) aim to resolve the segmentation problem by using the whole image as the input. In these methods, the max-pooling layer is used to reduce image resolution and obtain global features, while up-sampling layer is added to guarantee that the output image size is the same as the input image size. Multiple modified networks based on FCN and U-net have been investigated and have shown to be promising to solve tumor and organ segmentation in magnetic resonance (MR) and computed tomography (CT) images (Pereira et al., 2016) (Zhu et al., 2017).

As CNN-based segmentation methods learn and extract features only based on the images, they may not effectively learn some prior anatomical knowledge (ie, the bladder is always anterior relative to cervix). Integrating such prior anatomical knowledge into a CNN-based model can potentially enhance its ability to differentiate cervical tumors from the bladder. In addition to the relative anatomical position between bladder and cervix, round shape has previously been characterized as a feature for cervical tumors (Paiziev, 2014; Yang et al., 2000; Fukuya et al., 1995; Liyuan Chen, 2018; Bourgioti et al., 2016; Liyanage et al., 2010). Thus cervical tumors are “rounder” than the bladder. We propose to integrate a CNN model with such prior anatomical information constrained post-processing procedure to segment cervical tumors in PET.

2. Materials and methods

2.1. Patient Dataset

The study includes ¹⁸FDG PET images from 50 cervical cancer patients (1176 slices in total). As reference we used cervical tumor contours delineated by a radiation oncologist with 4 years of experience and reviewed by another radiation oncologist with 19 years of experience. Bladder contours were drawn by a physicist using ITK-SNAP software slice by slice and reviewed in 3D by a radiation oncologist with 4 years of experience. Bladder contours were only used during the training process. The experiments were conducted by five rounds of five-fold cross validation. For each round, we randomly shuffle the dataset into five equal size subsets. Of the five subsets, a single subset (PET images from 10 patients) is retained as the validation data for testing the model, and the remaining four subsets (PET images from another 40 patients~900 slices) are used as the training dataset. The cross-validation process is then repeated five times, with each of the five subsets used exactly once as the validation data. The validation results are combined (e.g. averaged) over five rounds to give an estimate of the model’s segmentation performance.

2.2. Overview

The proposed segmentation method integrates a convolutional neural network with prior anatomy information of cervical tumor including cervical tumor shape and anatomy location. Specifically, in this prior information constraint spatial information embedded CNN (PIC-S-CNN) method, we first constructed a convolutional neural network based on the relative positioning information between bladder and cervical tumor to map PET image to its corresponding label map, in which the bladder, other normal tissues, and cervical tumors are labeled as −1, 0, and 1, respectively. This enlarges the difference between cervical tumors and bladder such that bladder pixels have lower probabilities to be classified as cervical tumors. Based on the prior information including roundness of cervical tumors and relative anatomic positioning information between cervix and bladder, we derive the final segmentation result by applying an auto-thresholding method on the output probability map of S-CNN.

The pipeline of the proposed PIC-S-CNN method is shown in Fig. 1 and involves three main steps: 1) pre-processing including image normalization and region-of-interest (ROI) patch extraction; 2) spatial information embedded CNN-based initial segmentation; and 3) post-processing based on prior information constrained thresholding. These three steps are introduced in Sections 2.3, 2.4, and 2.5, respectively. The parameter such as the thresholding value in post-processing is also learned from the training dataset. Therefore, the proposed PIC-S-CNN method is completely automatic.

Fig. 1:

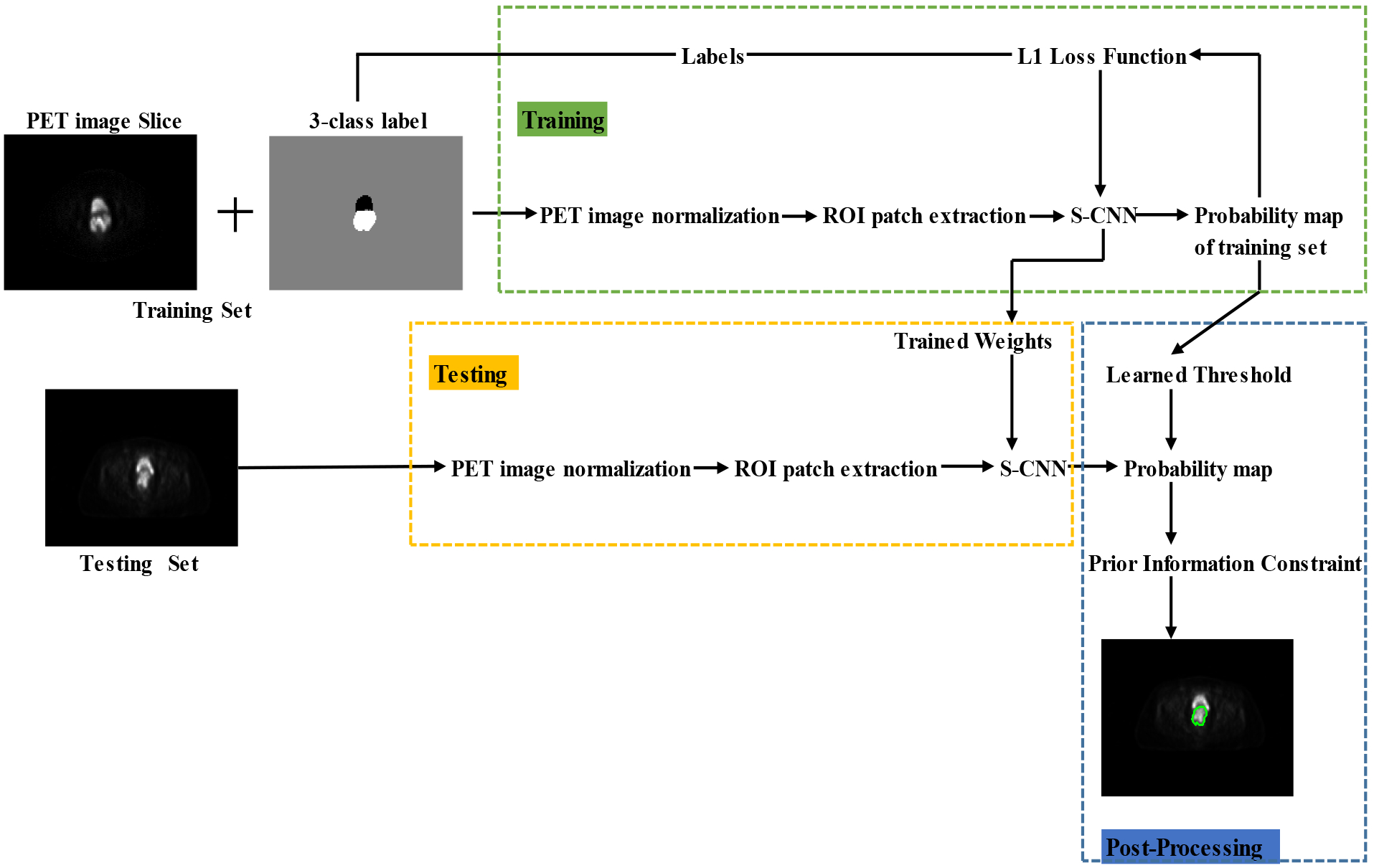
The pipeline of the proposed PIC-CNN method.

2.3. Preprocessing Procedure

Building an effective neural network model requires careful consideration of the network architecture as well as the input data format. Before introducing the proposed S-CNN architecture, we present several data preprocessing steps for the presented segmentation problem. The data preprocessing steps mainly include image intensity normalization, region of interest (ROI) patch extraction, and reference labelling.

2.3.1. Image Intensity Normalization

The intensity value for each pixel in the PET image is related to its FDG uptake. Like in the other CNN-based image processing techniques, we first apply intensity normalization for each patient’s PET image to ensure the same intensity range for each input. This makes convergence faster during network training. For each patient’s 3D PET image I, we use unity-based normalization strategy to bring all the intensity values in the image I into the range [0, 1]. The unity-based normalization formula is as follows:

$$I^{\text{'}}= \frac{I-I_{min}}{I_{max}-I_{min}},$$ (1)

where I_min and I_max are corresponding to the minimum and maximum intensity value of the image I. This normalization strategy is applied to both training and testing images.

2.3.2. ROI Patch Extraction

The distribution of the training data affects the performance of CNN (Hensman and Masko, 2015). A balanced number of samples of each label is desired during the training process. Hence, we exclude background and part of normal tissues with low intensity values from training data by extracting a region-of-interest (ROI) for each slice of PET images that covers both bladder and cervix. We extracted a 56×56 ROI patch from each slice of all the patients’ PET images, which is sufficient to include all the tumors and bladders. The reduced dimension of the input also significantly decreases the training time of the network. An example of an extracted ROI patch for one PET image slice is shown in Fig. 2. Bladder and cervical tumor were both included in the ROI patch. Meanwhile, most of background and other normal tissues were excluded.

Fig. 2:

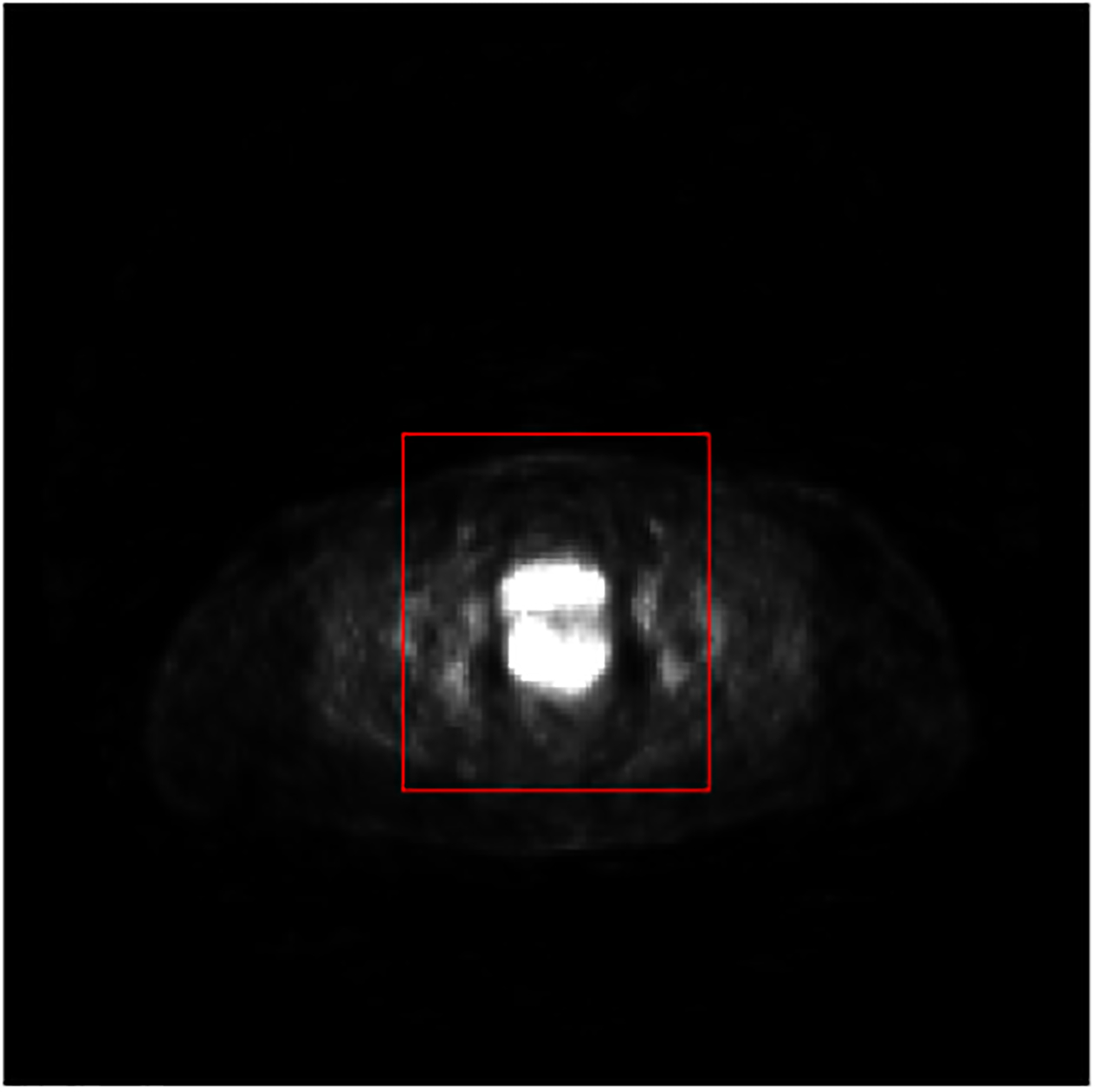
An example of ROI extracted from an original 2D slice of a PET image. The red rectangle indicates the ROI boundary.

2.3.3. Reference Label for Each Slice

A main challenge of our segmentation problem is to differentiate bladder from cervical tumors these organs are anatomically close and share similar FDG activity values. To sufficiently differentiate between bladder and tumor in the labeled image, we label each pixel as follows: bladder with −1, cervical tumor with 1, and other background normal tissue with 0. Using this labeling, the output probability map of a multi-class neural network trained in this work will have better separate between bladder and cervical tumor. An example of the generated label map for network training is shown in Fig. 3.

Fig. 3:

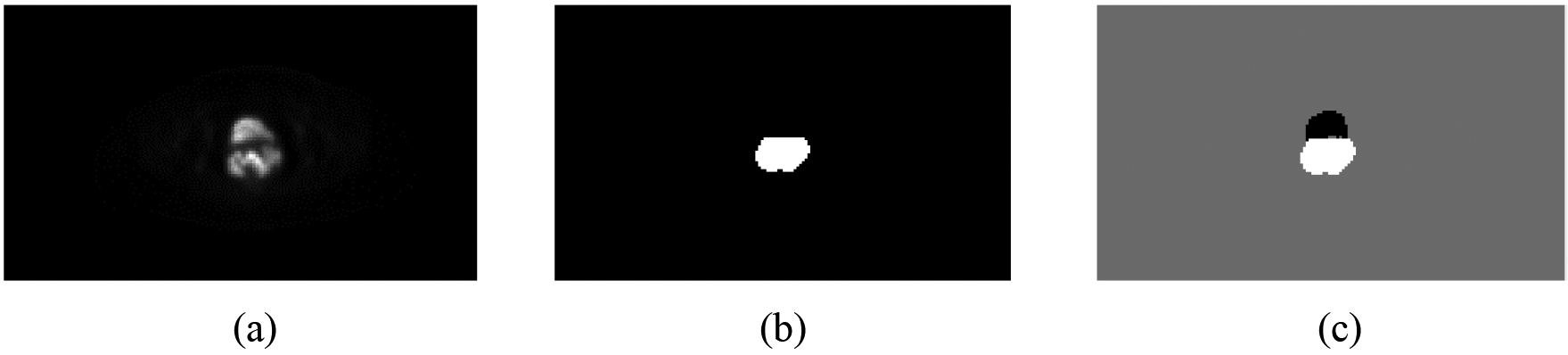
One example showing the generated input image label: (a) original PET slice image; (b) cervical tumor label of (a); and (c) generated label map for the network training.

2.4. Spatial Information Embedded Convolutional Neural Network (S-CNN)

A convolutional neural network is usually composed of several convolution, activation, pooling, up-sampling, and fully connected layers. In each convolutional layer, a set of learnable kernels are included. After several stacked convolutional layers, the extracted features become more and more abstract and will be used for the final prediction or segmentation. Each convolution layer is followed by an activation layer, which is controlled by a non-linear function to make the network complex, representing real complications. Different CNN architectures can capture different kinds of image features, generating different outputs. Because the bladder is always in front of cervical tumors, we designed the following spatial information embedded CNN (S-CNN) architecture to fully consider the global spatial information to differentiate between bladder and cervical tumor.

2.4.1. Proposed S-CNN Architecture

The architecture of the proposed S-CNN is summarized in Table 1. For each convolutional layer in the proposed S-CNN model, we first assigned zero around each feature map from the previous layer and then conduct the convolution to make the output image size the same as the input image size. For example, for the first convolutional layer with a kernel size of 7×7, the input within that layer will be expanded by 3 pixels along all four borders, which is presented as padding [3, 3, 3, 3] in Table 1. For the fourth convolutional layer with a kernel size of 5×1, the input within that layer will be expanded by 2 pixels along the left and right borders, which is presented as padding [2, 2, 0, 0] in Table 1. The activation function that we used in the activation-layer after each convolutional layer (Table 1) is rectifier linear units (ReLU). Its definition is f(x) = max(0, x) This function is non-linear to ensure complexity (that is, nonlinearity) of the CNN model. In addition, ReLU has been shown to propagate the gradient and compute more efficiently than the logistic sigmoid and hyperbolic tangent activation function.

Table 1:

Architecture of the proposed S-CNN model

Layer	Kernel Size	Padding	Features Patches
Input	-		1
Conv1	7×7	[3 3 3 3]	32
Conv2	3×3	[1 1 1 1]	32
Conv3	1×31	[0 0 15 15]	32
Conv4	5×1	[2 2 0 0]	32
Conv5	25×25	[12 12 12 12]	32
Prediction	3×3	[1 1 1 1]	1

^*Conv indicates Convolution layer + activation layer

The input of the proposed S-CNN model is equivalent to the extracted ROI patches (Sec. 2.3.2). Then, the first two convolutional layers (Table 1) are used to capture the local features for each pixel. The third and fourth convolutional layers are designed to learn the features along the y-axis and x-axis directions for each slice, respectively. Because the bladder is located in front of the cervix, we utilize large 1×31 kernels to learn the globally relative positioning information between the bladder and cervix along the y-axis. The 1×31 kernels along the y-axis were chosen because 31 can cover the maximum total length of the cervical tumor and bladder. The last convolutional layer with 25×25 kernels is used to further seek for global spatial features. The final prediction layer is constructed by a convolution layer with 3×3 kernels and generates the final output, in which bladder, other normal tissue, and cervical tumor pixel values approach −1, 0, and 1, respectively. We denote the output of the proposed S-CNN model as the probability map for each input patch.

2.4.2. Train the Proposed S-CNN Model

To train the proposed S-CNN model, several key steps were followed:

Initialization:

Initialization of the network weights will affect the network convergence. In our S-CNN model, we used the Xavier initialization method (Glorot and Bengio, 2010). The Xavier initialization assigns the network weights from a Gaussian distribution with zero mean and a variance of 1/N where N specifies the number of input neurons. Through Xavier initialization, we can guarantee the variance of input and output for each layer to be same to prevent back-propagated gradients from vanishing or exploding and allow activation functions to work normally.

Loss Function:

Differently from mostly used soft-max function for segmentation, the loss function that we used to train the proposed S-CNN model is L1 norm, which is defined as:

$${\mathcal{L}}^{{\mathcal{l}}_1}\left(P\right)=\frac{1}{N}{\sum }_{p\in P}\left|x\left(p\right)-y\left(p\right)\right|,$$ (2)

where p is the index of the pixel and P is the input patch; x(p) and y(p) are the values of the pixels in the predicted output and reference, respectively. L1 norm loss function is less sensitive to the outliers than the L2 norm loss function (Ke and Kanade, 2005) and it has been widely used to solve CNN-based image restoration problems (Zhao et al., 2017). Additionally, the L1 norm is more suitable than the L2 norm segmenting bladder and cervical tumor regions out (relatively small to the region of background) because it can produce sparser solutions.

Optimization algorithm:

We used the stochastic gradient descent (SGD) algorithm to train the proposed CNN model. The learning rate and momentum are set as 0.01 and 0.9, respectively. The maximum epoch for training is set as 200.

2.5. Post-processing by Thresholding with Prior Information

The output of S-CNN will be finally processed by a thresholding method combined with prior information. The threshold used in this step is learned from the training samples. By measuring changes in segmentation accuracy according to different thresholds, we obtain an optimized threshold value from the training dataset. Here, the accuracy refers to the mean value of the Dice Similarity Coefficients (DSC) and all the possible thresholds were selected in the range of [0, 1] with a step-size of 0.05. Then, we use this optimized threshold value to determine the initial label of each pixel of the images from the output probability map of CNN for testing images. The change in mean-DSC values with different thresholding applied to the output probability map from S-CNN during one round cross-validation is illustrated in Fig. 4. In this example, the optimal threshold value is 0.4 under which the mean-DSC value for the training dataset is 0.902. In our experiments, the optimal threshold was selected for each cross-validation round. The selected optimal values for all five rounds of cross-validation are within a range of 0.35–0.45 (Table 2). When the thresholds are within this range, the mean-DSC values do not change much (Fig. 4). For future applications, the optimal threshold of the finally trained CNN model can be selected according to the whole training dataset.

Fig. 4:

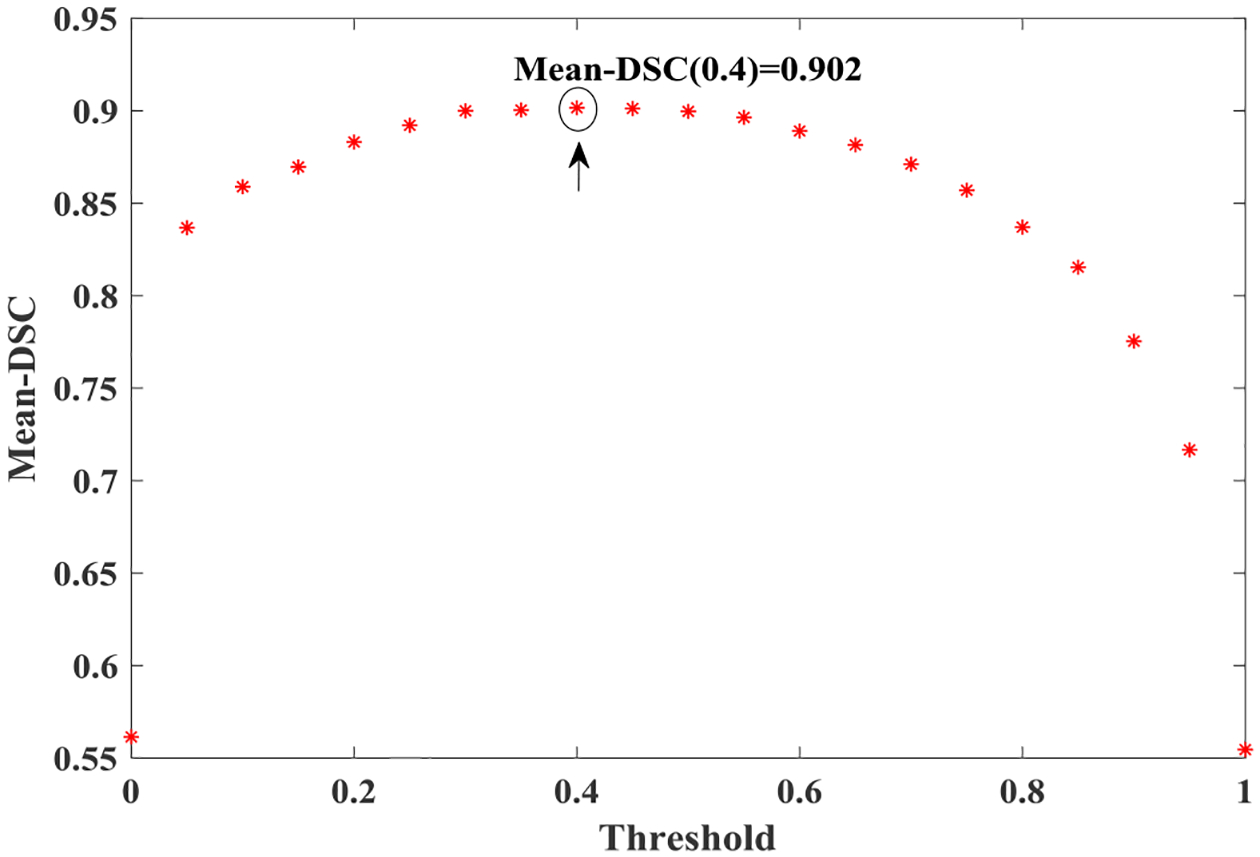
Threshold-accuracy (Mean-DSC) V.S. threshold for one training dataset. The optimal threshold in this example is 0.4.

Table 2:

The optimal threshold values for the five rounds of cross-validation. The step-size used in threshold selection is 0.05.

	R1	R2	R3	R4	R5
F1	0.40	0.40	0.35	0.35	0.40
F2	0.35	0.40	0.45	0.35	0.35
F3	0.45	0.35	0.35	0.40	0.40
F4	0.35	0.45	0.40	0.45	0.45
F5	0.40	0.45	0.35	0.35	0.35

In addition to the thresholding used in post-processing, we also consider the relative anatomy positioning of bladder and cervix and the roundness of cervical tumors. Based on the anatomical prior knowledge, a more anterior object should be considered as bladder rather than cervical tumor. After applying the optimal threshold to the S-CNN output probability map, if more than one connected object is present, we first find the central pixel of each connected object. By denoting the position of the central pixel for each object i as${ c}^i=\mathrm{ }[c_x^i,c_y^i]$, the object with the largest c_y value ($c_y^{\mathit{\text{max}}}$) is treated as the initial cervical tumor. Additionally, if the center of another object $c_y^j$ is within two pixels of the initially identified object (i.e., $c_y^j$ in the range of [$c_y^{\mathit{\text{max}}}-2$,$c_y^{\mathit{\text{max}}}$]), this object is also included as the initial cervical tumor to take the uncertainty of determining central position into account.

Cervical tumors are quantified as “rounder” than the bladder (Liyanage et al., 2010) (Bourgioti et al., 2016) (Paiziev, 2014; Yang et al., 2000; Fukuya et al., 1995). For any object i in a binary image, we estimate its area Dⁱ and perimeter Pⁱ first. Then, the roundness R of this object i is estimated by the following formula:

$$R\left(i\right)=\frac{4\pi D^i}{{\left(P^i\right)}^2}$$ (3)

The roundness value R is closer to 1 if the object is closer to a circle. After applying the optimal threshold to the S-CNN output probability map, the object with the roundness R value closer to 1 is considered as the cervical tumor. Several calculated roundness R values of cervical tumors and bladders are listed in Fig. 5, demonstrating that R values of cervical tumors are much closer to 1 than those of bladders.

Fig. 5:

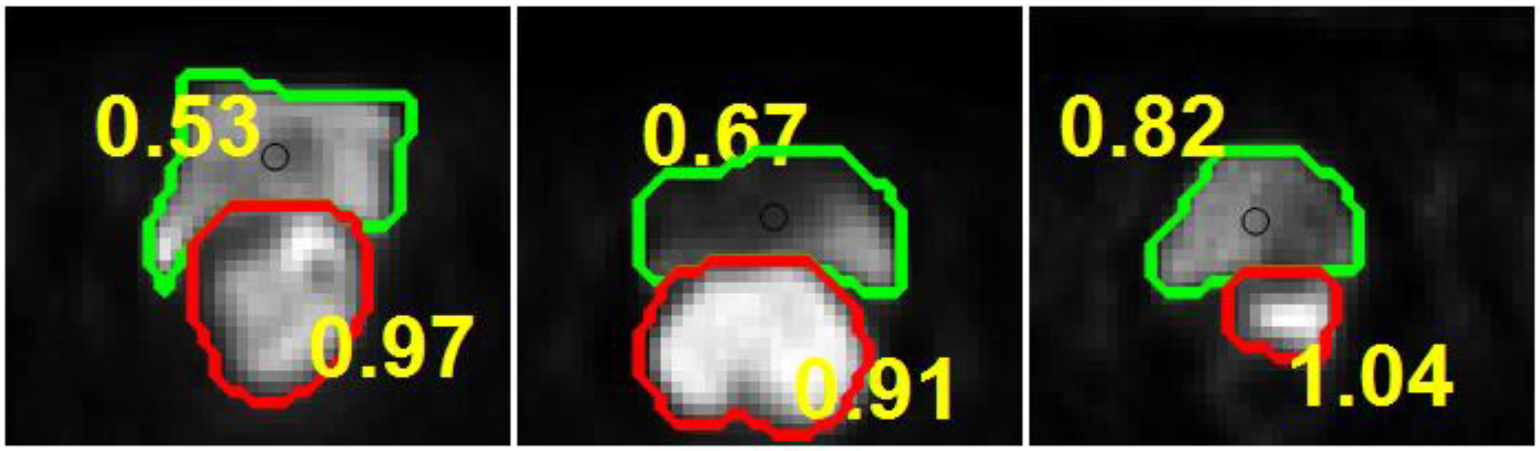
List of roundness values R of bladder and cervical tumor from different patients.

By integrating all the above information, we obtain the final segmentation result. The post-processing steps are summarized in Fig. 6. The only object present after thresholding the network output is considered as cervical tumor; otherwise, we will calculate the central position of each object i and determine whether the object belongs to the initial cervical tumor based on the value of$c_y^i$. If two or more objects are included in the initial cervical tumor, we will calculate the roundness of each object and select the one with largest roundness value as the final cervical tumor. In our dataset, 23 slices out of 1176 slices need to calculate the roundness of the objects to differentiate the tumor from other misclassified objects.

Fig. 6:

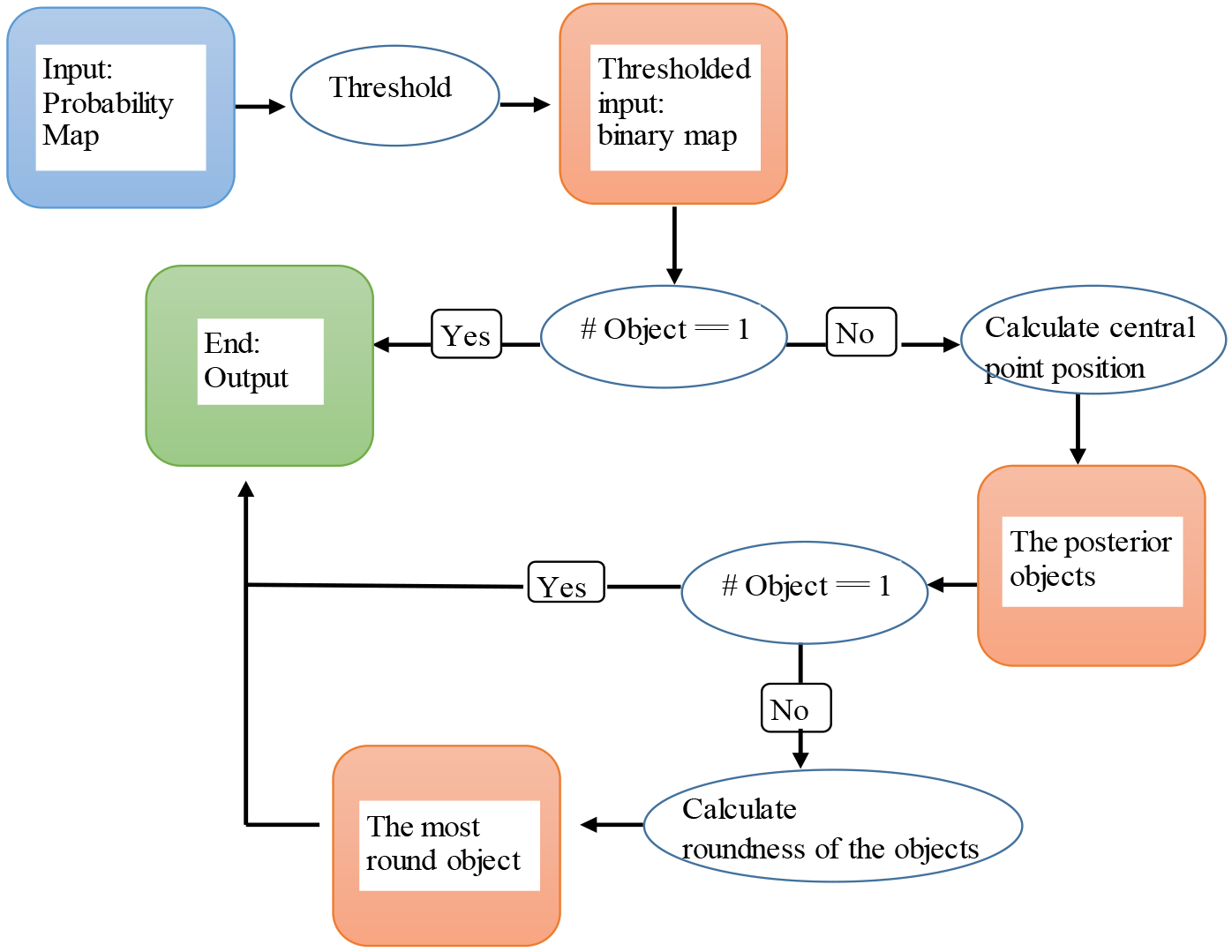
Flowchart for the post-processing procedure.

2.6. Influence of zero-padding during convolution

For the proposed S-CNN model, we use zero-padding during the convolution process to preserve the output size. If we don’t use zero-padding during convolution, the predicted output size will be smaller than the input size by a constant border width, which is determined by the convolutional kernel size and number of convolution layers in the CNN-based models. A larger input size is required for the unpadded convolution-based CNN model to obtain the segmentation result of an image with given size. To investigate the influence of zero-padding during convolution on the final cervical tumor segmentation result, we designed two different set-ups for the popular U-net-based (Ronneberger et al., 2015) medical image segmentation scheme as follows:

Set-up 1:

Set-up 1 for U-net (U-net-S1) uses unpadded convolutions, and the input image is a 96×96 patch containing the ROI (56×56) patch from the original PET image slice. Based on the input size, only two 2×2 max-pooling layers can be applied to this set-up so that the final output of U-net is exactly the same size as that of the ROI patch. Otherwise, a larger patch that includes more background pixels is needed so that more max-pooling layers can be applied. In this case, the numbers of each label pixel are more imbalanced.

Set-up 2:

Set-up 2 for U-net (U-net-S2) uses padded convolutions to ensure that enough max-pooling layers can be applied. The output size can be the same as the input size if the input size is selected so that all 2×2 max-pooling operations are applied to a layer with an even x- and y-size. In this set-up, we extended the ROI patch to a 64×64 patch cropped from the original PET image. Then, we can use up to five 2×2 max-pooling layers in the U-net to capture global and spatial information. Through our testing, we found that four 2×2 max-pooling yielded the most accurate segmentation results.

2.7. Influence of different types of labelling

In both U-net-S1 and U-net-S2, the output contains three probability maps (bladder, cervical tumor, and background) following the standard U-net implementation. In our proposed S-CNN model, instead of generating three output maps, we generate only one output map in which background, cervical tumor, and bladder should be labelled with 0, 1, and -1 respectively. To fairly compare the performance of the proposed network with that of U-net, we also train a U-net with the same as that of the proposed PIC-S-CNN method, denoted as U-net-S3. In U-net-S3, while the architecture is same as that of U-net-S2 with padded convolution, the output contains one map (i.e., -1 for bladder, 0 for background, and 1 for cervical tumor) instead of three probability maps for each category.

2.8. Comparison methods

To evaluate the performance of the proposed PIC-S-CNN method, we compare it with region-growing, Chan-Vese (Chan and Vese, 2001; Vese and Chan, 2002), and graph-cut (Bağci et al., 2011), which are traditional segmentation methods for PET image. We also compared our method with two widely used deep learning methods: fully convolution network (FCN) (Long et al., 2015; Noh et al., 2015; Arbabshirani et al., 2017; Shelhamer et al., 2017) and U-net (Ronneberger et al., 2015). Roundness and relative positioning information constraint were applied to the region-growing method, Chan-Vese, and graph-cut methods to obtain the final segmentation results. FCN-8s (8 pixel stride net) generates more accurate segmentation results than other FCN-based methods (Shelhamer et al., 2017). We compared the proposed PIC-S-CNN model with FCN-8s as previously described (Shelhamer et al., 2017). In addition, PET resolution is low and the cervical tumor in some slices can be small. The use of an 8-stride may skip some small cervical tumors and obtain segmentation boundaries in coarse resolution. Thus, we modify the FCN-8s into a FCN-2s net in which the last 8× up-sampling layer is replaced by three 2× up-sampling layers to obtain results at finer scale. Meanwhile, the detailed information from pool 1 and 2 layers are preserved. This FCN-2s net is also compared with the proposed PIC-S-CNN method. The post-processing procedure (introduced in Section 2.5) was also applied to all the FCN-based methods. Furthermore, because we implemented U-net with three different set-ups, the U-net with the set-up, which achieved the best segmentation result, was chosen as the comparison method. The final segmentation results of the U-net were also obtained by applying the post-processing procedure (introduced in Section 2.5) to the probability maps of U-net. All the parameters of the comparison methods in this study were fine tuned to achieve the highest average DSC values.

2.9. Evaluation criteria

Five criteria were used to quantitatively evaluate the segmentation accuracy including DSC, positive predictive value (PPV), intersection over union value (IoU), sensitivity (SEN), and specificity (SPC). The formulas for these five criteria are listed in Table 3.

Table 3:

Five criteria for quantitatively evaluating the segmentation accuracy.

Criteria	Formula
DSC	DSC = 2TP/(2TP+FP+FN)
PPV	PPV = TP/(TP+FP)
IoU	IoU = TP/(TP+FP+FN)
SEN	SEN = TP/(TP+FN)
SPC	SPC = TN/(TN+FP)

Note: TP (true positive) is the number of correctly classified tumor pixels; FN (false negative) is the number of tumor pixels labeled as normal pixels; TN (true negative) is the number of correctly classified normal pixels; FP (false positive) is the number of normal pixels labeled as tumor pixels.

3. Results

3.1. Illustration of Learning Process of PIC-S-CNN

Several randomly selected 7×7 small filters and 25×25 large filters are shown in Fig. 7, and their corresponding captured local and global features are shown in Fig. 8. Edge information is illustrated in Fig. 8 (a) while spatial and localization information is illustrated in Fig. 8 (b).

Fig. 7:

(a) and (b) contain several convolution kernels with size 7×7 and 25×25, respectively.

Fig. 8:

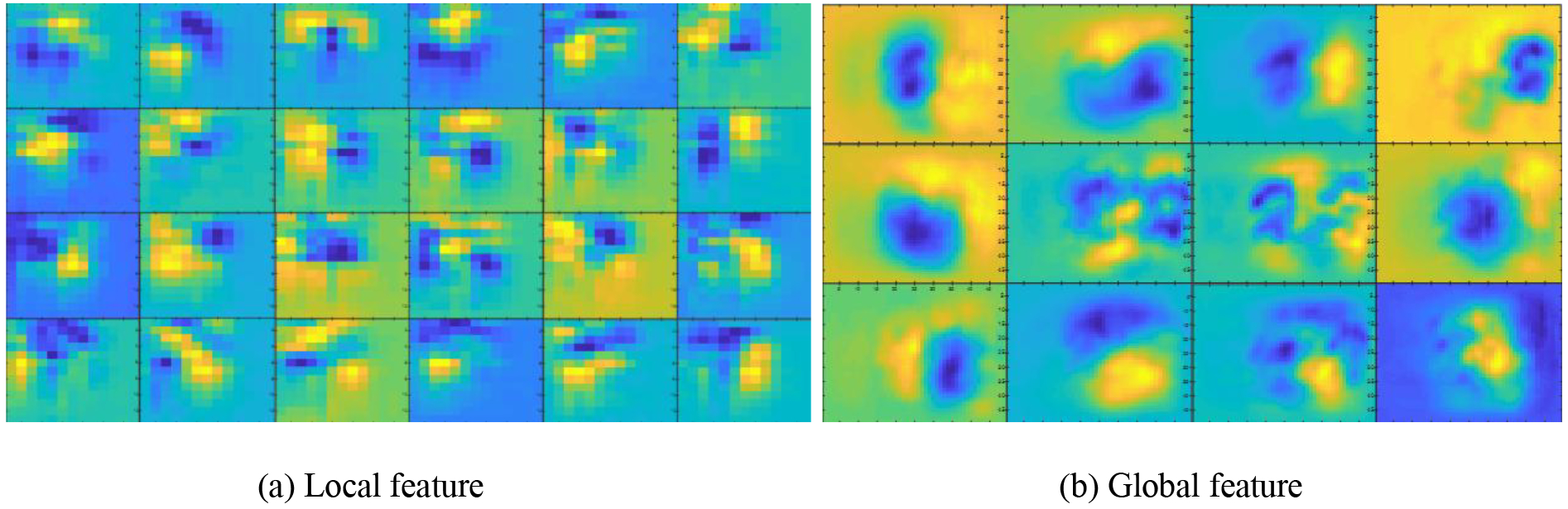
Some local features (a) from the first convolution layer with 7×7 kernels and global features (b) from the fifth convolution layer with 25×25 kernels.

To better understand the learning process of the proposed S-CNN architecture, we show the learning progression during the training process (Fig. 9). The first column includes the original PET images and the second column gives the reference label of the cervical tumor. Columns three to eight show the outputs of the network by different epochs (1, 5,20,30,50, and 200). More accurate probability maps were obtained as the epoch number increased. The probability maps obtained by epoch=200 distinguished the boundaries between bladder and cervical tumor. By applying the post-processing procedure described in Section 2.5 on these probability maps, we obtain the final segmentation results of cervical tumor.

Fig. 9:

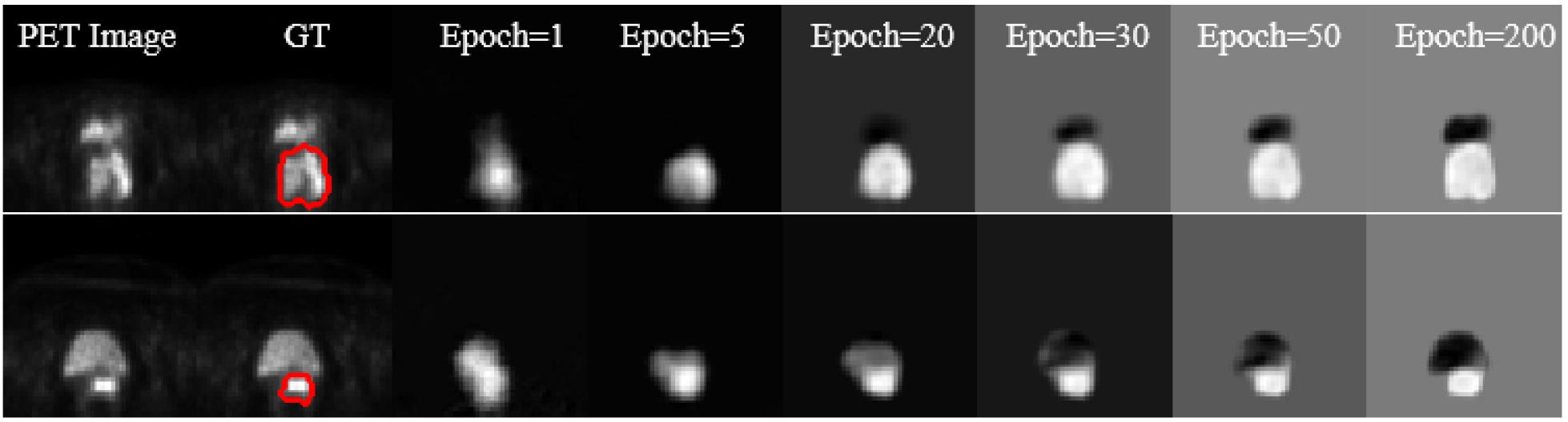
Progression of learning in the proposed CNN. The first two columns contain the original PET images and the reference labels of cervical tumor. The other columns list the outputs of the network by different epochs.

After showing the probability maps obtained from the proposed S-CNN model (Fig. 9), we provide an example that illustrates the role of the proposed post-processing procedure (Fig. 10). The boundary between cervical tumor and bladder is unclear in the original PET image. Meanwhile, the intensity values of cervical tumor and bladder are similar (Fig. 10(a)). Even though most of bladder pixels were mapped approximately to -1 by the proposed S-CNN model, some bladder pixels were still mapped to values which are larger than 0. After thresholding the output of the S-CNN model, we obtained a binary image (Fig. 10(d)), which includes two objects. After calculating the distance norms for these two objects, we can determine the final segmentation result in (e).

Fig. 10:

Illustration of post-processing to obtain final segmentation results: (a) original PET image; (b) cervical tumor with reference label; (c) predicted probability map from CNN; (d) initial label with threshold = 0.4 applied on (c); and (e) the final segmentation result based on the prior information.

3.2. Comparison among Different Set-ups of U-net

3.2.1. Influence of Zero-padding during Convolution

The values of the five evaluation criteria obtained by U-net-S1 and U-net-S2 are shown in Fig. 11. Four of the five evaluation criteria values obtained by U-net-S2 are equal to or greater than those obtained by U-net-S1. Using padded convolution with more max-pooling layers equipped can capture better global features than using unpadded convolution with less max-pooling layers, yielding better segmentation results.

Fig. 11:

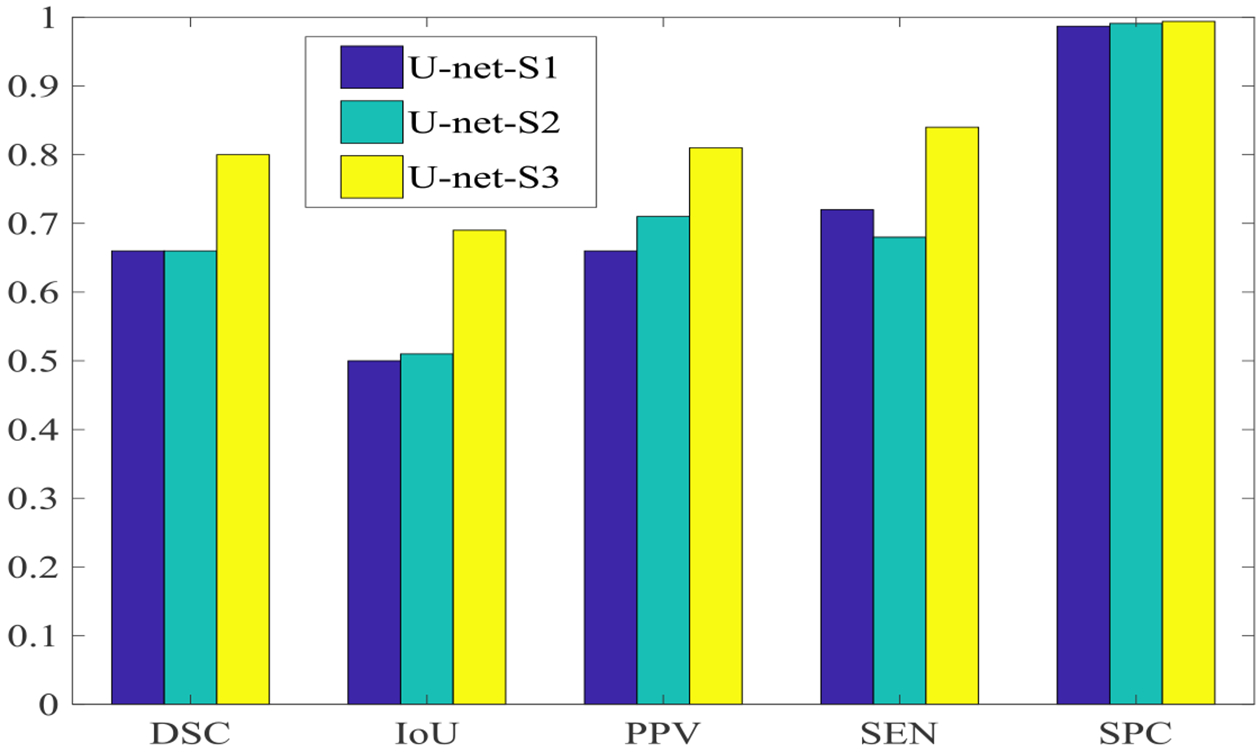
Values of five evaluation criteria obtained by U-net for three different set-ups.

3.2.2. Influence of Different Types of Labeling

U-net-S3 shows better segmentation results (average DSC of 0.80) than U-net-S2 (average DSC of 0.66). Segmentation results obtained from three set-ups of U-net for two PET image slices from two different patients are illustrated in Fig. 12. The red and green contours represent reference contours given by the radiation oncologists and the segmentation results obtained by U-net, respectively (Fig. 12). For each set-up, we show segmentation results from U-net with and without the post-processing procedure. Segmentation results were improved by the post-processing procedure for both U-net-S1 and U-net-S2 because post-processing considers the lower object as cervical tumor based on the anatomy location of the bladder and cervix. For U-net-S3, the segmentation result was not affected greatly because there was only one object left after thresholding. For all patient data, the segmentation accuracy of U-net-S1, 2, and 3 measured by DSC increases by 0.02, 0.02, and 0.01 on average, respectively, through the post-processing procedure. Overall, U-net-S3 outperforms the other two methods in terms of quantitative and visual aspects. In the following comparisons, the segmentation results of U-net were obtained from U-net-S3 with the post-processing procedure.

Fig. 12:

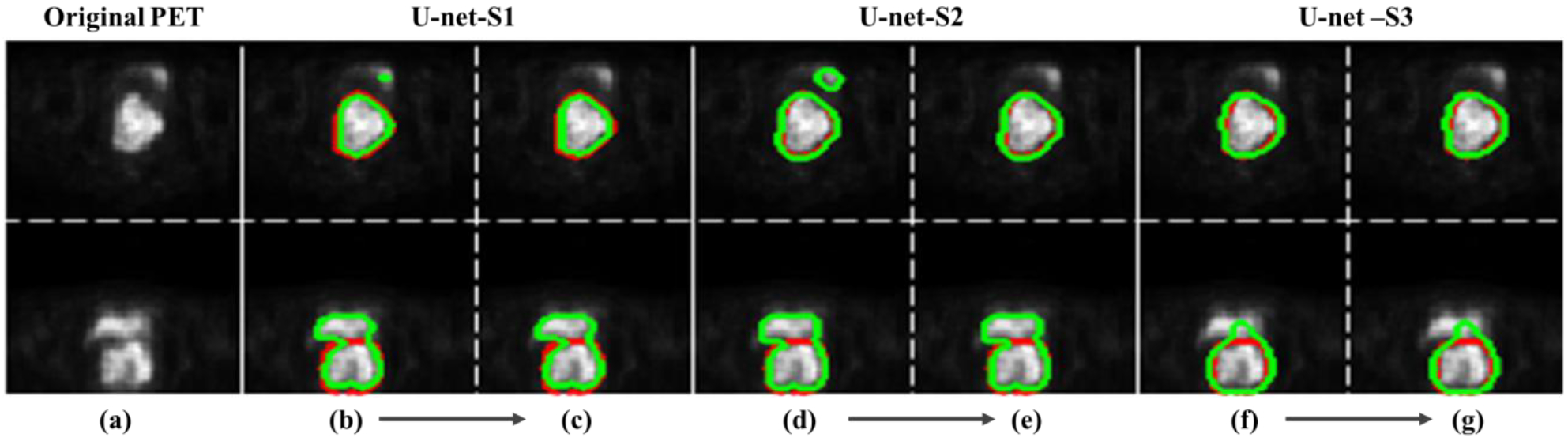
Segmentation results (green contour) obtained from three setups of U-net for two PET images from two different patients. Red contour is the reference. (a) Original PET images; (b)-(d)-(f) are segmentation results directly from the U-net probability maps; (c)-(e)-(g) are segmentation results which were obtained after the post-procedure.

3.3. Qualitative Evaluation

Upon comparing our proposed PIC-S-CNN method with region growing, Chan-Vese, graph-cut, U-net, and FCN based methods, we show segmentation results from six different patients obtained by seven methods in Fig. 13. The PET images in Fig. 13 can be divided into three categories: (1) bladder intensity is lower than cervical tumor intensity (Row 1–2); (2) bladder intensity is similar to cervical tumor intensity (Row 3–4); and (3) bladder intensity is higher than cervical tumor intensity (Row 5–6).

Fig. 13:

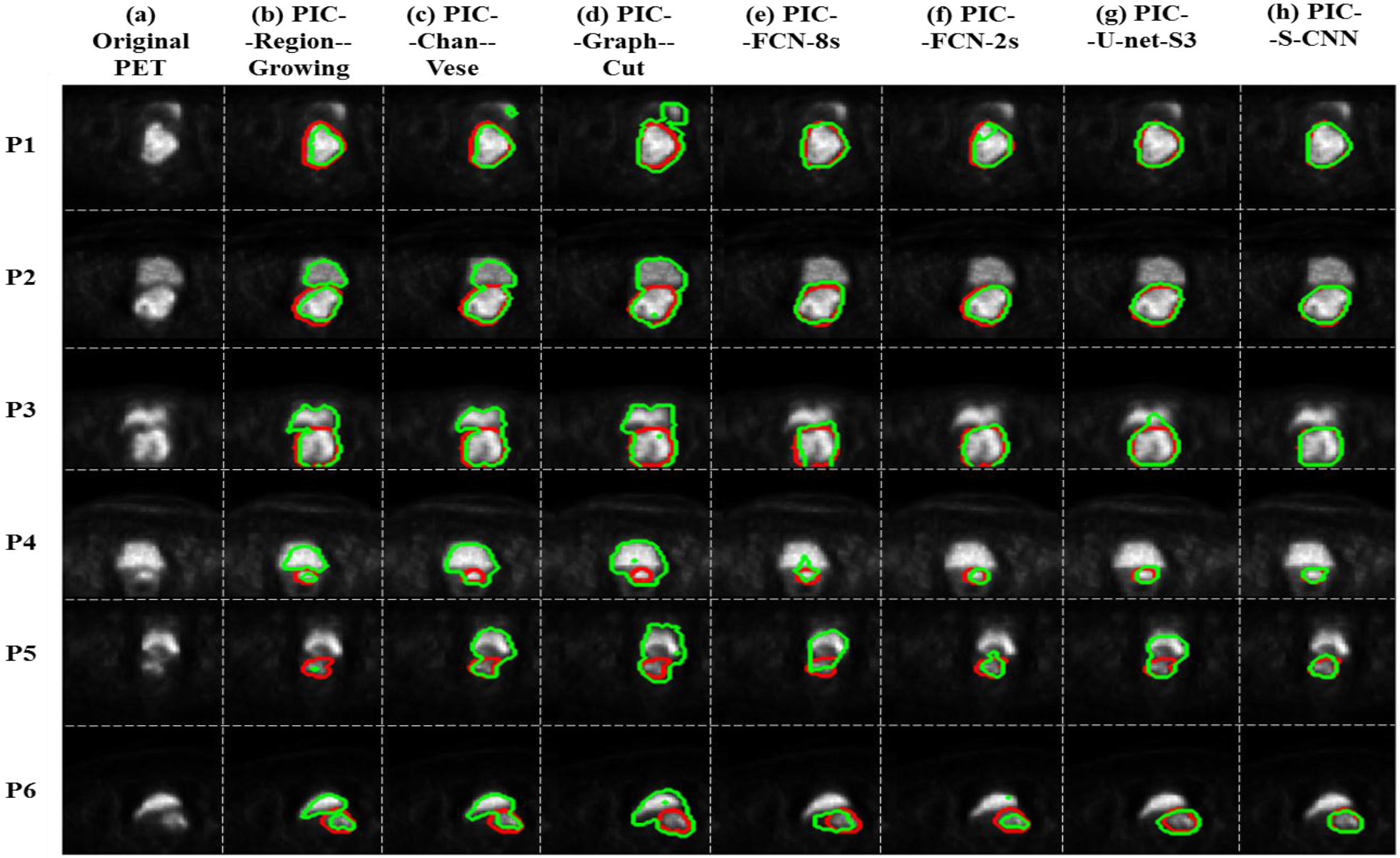
(a) Original PET image; blue arrow indicates bladder and yellow arrow indicates cervical tumor; (b)-(h) Predicted cervical tumor contours (green contour) obtained by PIC-Region-growing, PIC-Chan-Vese, PIC-Graph-cut, PIC-FCN-8s, PIC-FCN-2s, PIC-U-net-S3 and PIC-S-CNN methods, respectively. Red contour is the reference.

For PET images from category (1) in which cervical tumor intensity value is higher than bladder intensity value, region-growing, Chan-Vese and graph-cut methods sometimes can segment the correct part of the image as cervical tumor, but sometimes can misclassify the bladder as tumor. FCN-8s, FCN-2s, and U-net can all segment the correct part of the image as cervical tumor. Because of the inhomogeneity of cervical tumor intensity, the boundary of segmented cervical tumor obtained by these methods is not as accurate as PIC-S-CNN. The segmentation results obtained by the proposed PIC-S-CNN method are closer to those of the reference. For PET images from category (2), region-growing, Chan-Vese, and graph-cut methods cannot differentiate bladder from cervical tumor as they mostly misclassify bladder pixels into cervical tumor pixels. Although FCN-8s, FCN-2s, and U-net methods can distinguish between bladder and cervical tumor to some extent, the cervical tumor contours obtained by these three methods are not accurate enough. For example, the shape of the segmented cervical tumors obtained by FCN-8s or U-net is close to rectangular or irregular, respectively, while the reference is close to the circle (row 3). The PIC-S-CNN method generates almost same the segmentation results as those of the reference contour. Overall, the PIC-S-CNN method outperforms the other methods for patients from category (2). For PET images from category (3) where cervical tumor intensity is much lower than bladder intensity (Row 5–6), the region-growing method may misclassify bladder as cervical tumor or may not detect cervical tumors because cervical tumor intensity is closer to that of the background. The Chan-Vese, graph-cut, FCN-8s, FCN-2s, and U-net methods sometimes misclassify bladder pixels into cervical tumor pixels. In this circumstance, the PIC-S-CNN method can segment cervical tumor accurately. Overall, the proposed PIC-S-CNN method can generate more accurate segmentation results than the other methods in any circumstance. For small tumors in the top or bottom slices, the proposed PIC-S-CNN model can also generate accurate segmentation (Fig. 14).

Fig. 14:

All the slices containing cervical tumor from one patient’s PET image. Row 1: Original PET slices; Row 2: Reference segmentation of cervical tumor; Row 3: Segmentation results of cervical tumor obtained by the proposed PIC-S-CNN method.

3.4. Quantitative Evaluation

Other than visually, we also compared the proposed PIC-S-CNN method quantitatively with region-growing, Chan-Vese, graph-cut, U-net, and FCN-based methods. We list the (average ± std) values of DSC, PPV, IoU, SEN and SPC obtained from these different methods in Table 4. The higher the values, the better are the segmentation results. Region-growing, Chan-Vese, and graph-cut methods can only achieve 0.55, 0.64, and 0.67 DSC values on average because they cannot differentiate between bladder and cervical tumor in some cases. Because FCN-8s uses 8 pixels stride in the last up-sampling layer, cervical tumor location and boundary are not accurate enough because less detailed features are incorporated. The average DSC value for the FCN-8s method is 0.71. FCN-2s replacing the last ×8 up-sampling layer by three ×2 up-sampling layers of FCN-8s detects location and boundary information more accurately, and achieves an average DSC value of 0.77. U-net-S3 performs better than region-growing, FCN-8s, and FCN-2s methods, achieving an average DSC value of 0.80. The DSC value obtained by our proposed PIC-S-CNN method yielded the highest value with an average DSC value of 0.80 0.84. The PIC-S-CNN method generates more accurate segmentation result for cervical tumor than region-growing, FCN-8s, FCN-2s, and U-net methods. Moreover, we also list the evaluation criteria values obtained by the S-CNN model without using the post-processing procedure in Table 4. The average DSC value obtained by using the S-CNN model only is 0.82, while the post-processing procedure can further increase DSC values by 0.02 on average. Such increase is smaller than the difference between different models (e.g., the difference of DSC between PIC-U-Net-S3 and PIC-S-CNN is 0.04). These results suggest that network architecture plays a more important role in improving the segmentation accuracy for the whole algorithm.

Table 4:

Values of five evaluation criteria obtained by different methods.

	DSC	PPV	IoU	SEN	SPC
PIC-Region-growing	0.55	0.60	0.40	0.74	0.985
PIC-Chan-Vese	0.64	0.82	0.48	0.55	0.993
PIC-Graph-Cut	0.67	0.82	0.52	0.54	0.993
PIC-FCN-8s	0.71 ± 0.009	0.65 ± 0.018	0.57 ± 0.009	0.84 ± 0.010	0.988 ± 0.0005
PIC-FCN-2s	0.77 ± 0.013	0.71 ± 0.018	0.64 ± 0.017	0.88 ± 0.014	0.989 ± 0.0007
U-net-S3	0.79 ± 0.011	0.80 ± 0.010	0.67 ± 0.013	0.83 ± 0.011	0.994 ± 0.0002
PIC-U-net-S3	0.80 ± 0.011	0.81 ± 0.010	0.69 ± 0.032	0.84 ± 0.011	0.994 ± 0.0002
S-CNN	0.82 ± 0.008	0.78 ± 0.010	0.71 ± 0.010	0.92 ± 0.005	0.991 ± 0.0004
PIC-S-CNN	0.84 ± 0.007	0.82 ± 0.005	0.73 ± 0.010	0.89 ± 0.011	0.993 ± 0.0002

4. Discussion

We didn’t include any pooling layer in the S-CNN architecture to preserve output image size. Although pooling layer can help to achieve positional and translational invariance and to discard irrelevant details, it can also eliminate important details, potentially leading to losing a precise sense of tumor location. In our S-CNN architecture, spatial and global features were captured by using large size convolution kernels in the convolutional layer. In addition, even though we didn’t include any dropout layer, which is usually used to avoid overfitting, we alleviated the overfitting concern by balancing the parameters of the network with number of training samples. In summary, all the processing conducted by the S-CNN model was completed by convolution and activation layers. Additionally, we investigated the influence of class labelling order by designing a different class labelling way in which bladder, other normal tissue, and cervical tumor were labelled as 0, -1, and 1, respectively. Under this labelling way, DSC decreased by 0.03. This illustrates that the labelling way described in Section 2.3.3, which makes bladder class and tumor class sufficient different, can generate more accurate segmentation results.

The post-processing procedure we developed is mainly used to exclude some separated regions that are incorrectly labelled as tumor after the output thresholding. If only one object area is present after thresholding the network output and this area contains both cervical tumor and bladder, the presented post-processing procedure will not help to improve the segmentation results further. However, in our dataset, only 19 slices out of 1176 could connect bladder and tumor after thresholding. In most of these 19 slices, only a small part of bladder was connected to tumor after thresholding. Additionally, if more than one tumor region is present in a slice, the proposed post-processing procedure will exclude the upper region and select the lower region as the cervical tumor. This is a limitation of the proposed post-processing procedure for some irregular tumors in images of higher resolution, although we have not observed this situation for all the 1176 slices of the cervix PET.

Because of the limited number of samples from real patients, the proposed PIC-S-CNN method is a 2D convolutional neural network. Three-dimensional convolutional neural networks need more training samples than 2D convolutional neural network. Thus, for fair comparison, we didn’t compare the proposed method with the 3D U-net (Çiçek et al., 2016) and V-net (Milletari et al., 2016) methods. We can modify the proposed PIC-S-CNN method into a 3D convolutional neural network once we have accumulated a sufficient number of patient images. We can then compare the proposed 3D PIC-S-CNN method with the 3D U-net and V-net methods. Since the 3D convolutional neural network can take advantage of the 3D nature of objects in the images, more accurate segmentation results are expected.

Another limitation of our current study is that the proposed segmentation scheme strongly depends of the quality of PET images, which could be affected by different factors such as patient motion, bladder filling change during the scan, and spill-in counts from bladder to cervical tumor. Advanced motion correction strategies (Rahmim et al., 2007) or PET scanner design (Zhang et al., 2017) with limited scanning time could help alleviate the influence of patient motion and bladder filling change during the scan. The spill-in counts from the bladder can introduce bias in quantifying small regions such as cervical tumor in PET images (Silva-Rodríguez et al., 2016). The effect of spill-over effect from the bladder to cervical regions was not considered in our neural network design. To correct the spill-over effect, advanced reconstruction algorithms should be used to reconstruct cervical PET images by removing the contribution of the bladder to the final image (Silva-Rodríguez et al., 2016). Alternatively, we can design a neural network that considers the partial volume effect (Rousset et al., 2007) during segmentation, where one voxel can have contributions from both bladder spill-over and cervical tumor. To train such a neural network, simulation or phantom studies are needed to obtain the ground truth of cervical tumors.

5. Conclusion

We propose a prior information constraint spatial information embedded convolutional neural network (PIC-S-CNN) to segment cervical tumors on 3D PET images. Since CNN has shown great promise in capturing image features, combining it with some prior information (roundness of cervical tumor and relative positioning information between cervix and bladder) can help resolve the cervical tumor segmentation problem. First, an S-CNN model should be used to map the original PET image into a classification map in which bladder, other normal tissue, and cervical tumor are labelled as -1, 0, and 1, respectively. In designing the S-CNN architecture, prior positioning information between cervical tumor and bladder has been considered by using different kernel sizes along the x- and y-directions and relatively large kernel size in the final convolutional layer to exploit global spatial information. Then, the final segmentation result is obtained via an auto-thresholding technique which is, again, constrained by the known prior information. Experimental results have shown that the proposed PIC-S-CNN provides a more accurate way for segmenting cervical tumors on 3D PET images.