Abstract
Purpose:
The ability to register image data to a common coordinate system is a critical feature of virtually all imaging studies. However, in spite of the abundance of literature on the subject and the existence of several variants of registration algorithms, their practical utility remains problematic, as commonly acknowledged even by developers of these methods.
Methods:
A new registration method is presented that utilizes a Hamiltonian formalism and constructs registration as a sequence of symplectomorphic maps in conjunction with a novel phase space regularization. For validation of the framework a panel of deformations expressed in analytical form is developed that includes deformations based on known physical processes in MRI and reproduces various distortions and artifacts typically present in images collected using these different MRI modalities.
Results:
The method is demonstrated on the three different magnetic resonance imaging (MRI) modalities by mapping between high resolution anatomical (HRA) volumes, medium resolution diffusion weighted MRI (DW-MRI) and HRA volumes, and low resolution functional MRI (fMRI) and HRA volumes.
Conclusions:
The method has shown an excellent performance and the panel of deformations was instrumental to quantify its repeatability and reproducibility in comparison to several available alternative approaches.
Keywords: diffeomorphic mapping, diffusion tensor imaging, functional MRI, non-linear registration, symplectomorphic mapping
1 |. INTRODUCTION
Modern imaging systems are increasingly capable of acquiring data sensitive to a wide range of physical parameters at multiple resolutions, thus offering greater sensitivity to structural and dynamical information in complex biological systems. However, these technological advancements present the increasingly important theoretical and computational challenge of how to rigorously and efficiently combine, or register, such data in order to be able to accurately detect and quantify subtle and complex system characteristics.
An important example of this problem, and our motivation for the current paper, is presented by the application of magnetic resonance imaging (MRI) methods to human neuroimaging (neuro-MRI). MRI is an exceedingly flexible technology for measuring various characteristics of water in biological systems and three major techniques have emerged as the cornerstone of neuro-MRI: high resolution anatomical acquisitions (HRA) that facilitates the characterization of brain morphology, diffusion weighted MRI (DW-MRI) that allows the characterization of focal alterations in tissue diffusion as well as the reconstruction of neural fiber pathways critical to brain function, and functional MRI (FMRI) which is capable of detecting spatial-temporal variations in brain activity, even if the subject is “at rest” and not performing a task in the magnet (called resting state fMRI, or rsFMRI). Each of these modalities is typically acquired at different spatial resolution and possess unique contrast characteristics.
The ability to register image data to a common coordinate system is not only important for combining different modalities, but is also for combining data across subjects. It is thus a critical feature of virtually all imaging studies that require quantitative statistical analysis of group populations. Consequently, this subject has been the focus of a great deal of research. This has been a focus in computational neuroanatomy which has motivated the developed of diffeomorphic registrations methods1–5 for which faster and more efficient algorithms continue to be developed,6–10 as well as various regularizations11,12 and addition enhancements such as local-global mixture, contrast changes, multichannel mapping, etc,13–15 and the use of probabilistic diffeomorphic registration methods.16,17 These registration advancements are important to group analyses and the development of standard atlases18–24 which serve a critical role in the standardization of studies. The emergence of diffusion tensor imaging (DTI) methods and their variants for connectivity studies required the extension of diffeomorphic registration methods to accommodate tensor data.25–38 These methods have had a profound effect on the success of numerous scientific studies on important clinical issues such as Alzheimer’s and traumatic brain injury,39–44 as well as studies in other organs (cardiac, lungs, etc).45–49
In spite of the abundance of literature and the existence of several variants of diffeomorphic algorithms their practical appeal are still rather limited (possibly due to an interplay of a variety of reasons—speed, accuracy, robustness, complexity, repeatability, etc), as commonly acknowledged even by developers of these registration methods. For example citing the developer of one of the relatively broadly used approach—Large Deformation Diffeomorphic Metric Mapping30,34,35,37,44,50 “applications of the LDDMM framework on volumetric 3D medical images still remain limited for practical reasons”.51 Two large and thorough comparison studies (i.e.52,53) also confirm that although currently available methods are in general able to perform the registration task with varying degrees of success (although some are exceedingly slow and some are not particular accurate), the practical use limitations seem to drive an interest in improvements at least in terms of speed and accuracy.
To address these issues we present in this paper a new method that is similar in spirit to diffeomorphic mapping, but is more general and flexible. The transformation is developed within a Hamiltonian formalism54–56 in which not just the spatial coordinates are considered, but the entirety of phase space, which is a called a symplectomorphism. This theoretical construct enables a novel flexible, accurate, and robust computational method based on a sequence of energy shell transformations. The approach adds a novel phase space regularization based on the powerful entropy spectrum pathways framework.61 The framework provides a unique opportunity to tailor image details into the regularization scheme by choosing an image derived regularization kernel. The incorporation of phase space constraints allows us to use the same simple metric on the space of diffeomorphisms that remains valid even with image dependent regularization, something that is missing in currently available methods. A spherical wave decomposition is applied as a powerful preconditioning tool in the position domain to allow accurate and fast interpolation, resampling and estimation of fixed shape rotation and scale. The result is an efficient and versatile method capable of fast and accurate registration of a variety of volumetric images of different modalities and resolutions.
2 |. METHODS
2.1 |. Symplectomorphic mapping
We introduce the Hamiltonian function on a fixed Cartesian grid x as
| (1) |
Here I0 and I1 are two multidimensional images defined on the same fixed Cartesian grid x, V is the measure (volume) of the reference I0 image domain , and (q(x, t), p(x, t)) is a set of canonical coordinates, that define a time dependent mapping from Cartesian grid x to a new curvilinear grid y ≡ q(x, t), such that initially at t = 0 the grids are identical, i.e. (q(x, 0), p(x, 0)) ≡ (x, 0).
The Hamiltonian Equation 1 defines a flow at each location on a fixed grid through a system of Hamilton’s equations
| (2) |
| (3) |
where denotes variational (or functional) derivative.
We should emphasize that a simple squared image difference is used as a measure of the distance between the reference and original images in Equation 1 for the clarity of notation. Any expression for the image distance can be substituted in general functional form as resulting in a replacement of image difference term (I0−I1) by in the momentum Equation 3.
The flow defined by Equations 2 and 3 is called a Hamiltonian flow and takes place in the space of the coordinates (q, p), which is called phase space. Diffeomorphisms in this phase space are called Hamiltonian diffeomorphisms or symplectomorphisms since a phase space is a symplectic manifold. Thus symplectomorphisms preserve the symplectic structure (including the volume) of phase space. This is a very important feature that will allow the generation of a shell-like sequence of transformations suitable for volumetric measurements and quantifications.
Because the Hamiltonian function Equation 1 and the reference image I0 are defined on a Cartesian grid x we do not calculate the curvilinear gradient directly. Instead we express I1(q) as a function on a Cartesian grid I1(q(x, t)) and use the chain rule to evaluate the curvilinear gradient through a gradient on Cartesian grid and Jacobian .
An evolution of the Jacobian with time can be obtained by differentiating the position Equation 2 on a fixed grid, giving a closed set of equations
| (4) |
| (5) |
| (6) |
Integrating these equations with initial conditions q(x, 0) = x, p(x, 0) = 0, and generates a symplectomorphic transformation x→q(x, t). A new metric can be defined for the position part q of the canonical coordinates by introducing the metric tensor G ≡ {gij} = (J−1)TJ−1, where indices i and j correspond to derivatives over qi and qj components of the curvilinear coordinates q such that in Euclidean space gij = δij where δij is the Kronecker delta. The metric tensor is important for providing accurate measures of line and surface properties using the curvilinear coordinate system q. For example, a length of a curve parameterized by x(s) with a parameter s between zero and one in Cartesian space can be expressed using the metric tensor and curvilinear mapping as
| (7) |
where repeated indices i and j represent summation.
To ensure that the transformation is symplectomorphic at every location on a fixed grid x during numerical integration we set a small constant ε and impose a requirement that both the Jacobian and the inverse Jacobian are bounded by this constant, i.e.
| (8) |
For the majority of the results presented in the paper a value of ε = 0.01 was used. When the Jacobian becomes sufficiently close to zero the further integration does not make sense as it will not be able to guarantee either the symplectomorphic or diffeomorphic properties of the flow (even numerical stability of the solution can be compromised). Therefore, when the condition of Equation 8 is violated we stop numerical integration, freeze the flow, and restart the integration (i.e., setting t = 0) beginning at a new set of phase space coordinate {q(n)(x, 0), p(n)(x, 0)} where n is the number of restart times. Since the Hamiltonian is an operator that describes the “energy” of a system, we refer to these n different sets of initial conditions as energy shells. Each restart of the integration therefore represents the initiation of a new energy shell.
The new initial conditions that define the energy shells are related to the stopping point of the coordinates in the previous energy shell by the following conditions:
| (9) |
| (10) |
| (11) |
Repeating this sequence of initial conditions therefore generates a set of shell-embedded symplectomorphic transformations such that the total transformation is diffeomorphic with the Jacobian defined as a product of J(n)
| (12) |
It is worth noting that this updating equation for the Jacobian effectively results in an updating of the metric tensor G = (J−1)TJ−1 that characterizes the local geometry and assures volume preservation.
The similarities between the Hamilton function Equation 1 and the traditional objective function of nonlinear registration (either diffeomorphic4,57,58 or non-diffeomorphic59) can be cast by viewing the first momentum part as the regularity term which assures the smoothness of velocity field, and the second part as the fitting term which guides the displacement field. But the Hamiltonian formalism provides a number of important advantages, e.g., it allows the use of different spatially varying regularization strategies for momentum and displacement parts and at the same time includes those terms as a part of the Hamiltonian function itself rather than applying them at a post processing step.
We would also like to emphasize that our use of Hamiltonian framework provides a major advantage over conventional approaches in both efficiency and accuracy. For example, similar considerations for limiting the Jacobian were employed in60 where Euler equations of viscous flow were used to describe the displacement field on a fixed grid. The introduction of fixed Eulerian reference frame resulted in frequent use of costly and inaccurate template regridding procedure that is completely avoided by our formulation.
An important practical implementation issue is that the number of shells n does not have to be introduced in advance and can be determined based on overall convergence (or even devised from running time constraints). In our numerical implementation the shells were terminated as soon as I1 → I0 convergence condition
| (13) |
2.2 |. Entropy spectrum pathways as a phase space regularization
The form of Hamiltonian function used in Equation 1 assumes only local input from difference between I0 and I1 images to the flow momentum p at every point on the fixed grid x. A more reasonable assumption would be an inclusion of some information relevant to the structure of I0 and I1 images. One possible (and by far the most straightforward) way to provide this structure based preconditioning is the entropy spectrum pathways (ESP) approach61 that takes into account nearest neighbor coupling between adjacent grid locations.
The ESP approach starts with generating the coupling density Q(x, x′) which can be as simple and trivial as just the adjacency matrix
| (14) |
or may in general include a strength of coupling through some kind of coupling potentials that may depend on the grid positions. The ESP approach solves the generalized eigenvalue problem
| (15) |
finding the largest eigenvalue λ and corresponding eigenvector ψ(x) and then constructs the quantity
| (16) |
calling it the transition probability density for transition between grid locations x and x′. The square of the eigenvector ψ(x) is called the equilibrium probability μ(x) in the sense that it represents the stationary solution that satisfies the stationary point condition
| (17) |
Equation 16 can be included in Equation 1 to take into account nonlocal effects and provide a way of regularization by defining a non-local Hamiltonian
| (18) |
here δ(x, x′) is Dirac delta function, q ≡ q(x′, t) and p ≡ p(x′, t). This nonlocal expression for the Hamiltonian function produces non-local Hamilton’s equations
| (19) |
| (20) |
| (21) |
where the momentum Equation 20 is the non-local version of Equation 5 that now includes the convolution of a local potential (gradient of squared image difference in our case) with a kernel ρ(x, x′) that depends on the coupling between grid locations.
Alternatively the non-local Hamiltonian function can be specified as
| (22) |
providing alternative non-local form for the coordinate Equation 4 as well
| (23) |
Assuming that the coupling density Q(x, x′) does not depend on position x but depends only on a difference between them (i.e. Q(x, x′) ≡ Q(x−x′)), the ESP scheme can provide a variety of position independent regularization kernels often used as convolution filters in image registration.2 As a trivial example, an eigenvalue problem (15) for position independent Gaussian coupling density Q(x−x′) = exp(−(x−x′)TS(x−x′))) in infinite n-dimensional domain has maximum eigenvalue and a trivial eigenvector ψ(x) = const, resulting in the commonly used Gaussian regularization kernel. This simple illustration is merely meant to demonstrate that the commonly used Gaussian kernel is naturally derived from our very general procedure. In practice, more complex coupling schemes can provide more informative prior information, resulting in more robust warping schemes.
We would like to emphasize the significant advantages that ESP regularization provides. Its general formulation61 is probabilistic in nature and provides a framework for the incorporation of available information. In the present context of image registration it naturally provides a mechanism to incorporate information from either or both of the I0 and I1 images. The position dependent coupling naturally creates image dependent regularization. Moreover, the ESP approach can also include any information that is not present in the images themselves but known a priori and related to images in some quantitative way can be easily included into the coupling scheme with some sort of linear or nonlinear parameterization. We have recently demonstrated this ability to incorporate multiple priors in ESP coupling in the related problem of multi-modal parameter estimation,62 where the symplectomorphic registration method of this paper was used for registration of multiple modalities. Additionally, incorporation of the ESP method into the Hamiltonian formalism provides a simple and efficient way for introduction of different image matching terms by modification of the position–based part of either local or nonlocal Hamiltonian function. This provides great flexibility for tailoring the method to specific applications.
2.3 |. Spherical waves decomposition as a position domain preconditioning
The set of Hamilton’s Equations 19–21 used in the previous sections to generate a sequence of energy shell-embedded symplectomorphic transformations (12) requires equal dimensionality of images I0 and I1. However, in many cases the images to be registered are of different spatial resolutions so that some form of interpolation is required. To provide an effective way to do position domain resampling, interpolation, filtering and estimation of the best orthogonal transform in a single step we used the spherical waves decomposition (SWD) approach.63 The SWD is based on fast FFT–based algorithms to expand images in spherical wave modes and therefore allows image resampling, scaling, rotating and filtering with the highest possible order of polynomial accuracy (much more accurately than nearest neighbors, tri-linear or tri-spline used by all other methods), but at a fraction of the time.
The SWD approach uses fast algorithms to expand both I0 and I1 images in spherical wave modes
| (24) |
where are the spherical harmonics, and Rnl(r) can be expressed through the spherical Bessel function
| (25) |
with an appropriate choice of normalization constants and the discrete spectrum wave numbers kln determined by the boundary conditions. The number of modes (l, m = 0…Lmax and n = 1…Nmax) are determined by the highest image resolution. The details of definitions of the spherical harmonics and spherical Bessel Functions jl(r) can be found in.63 The interpolation and resampling are then implemented as fast inverse spherical wave transform
| (26) |
using appropriate grid locations (r, θ, ϕ) and assigning flmn to zeros for modes with n > Nmax or l, m > Lmax. A variety of low/band/high pass filters can be used for frequency domain filter following the standard image processing techniques.
The scale and the amount of rigid rotation between images can be easily and effectively estimated using the decomposition of the radial and spherical parts with the partial transforms
| (27) |
| (28) |
and finding the parameters of the similarity transformation (scale sr and rotation angles θr and ϕr) by solving the two (one and two dimensional) minimization problems
| (29) |
| (30) |
using a small number of modes (L < Lmax and N < Nmax) for initial coarse search and increasing them to refine the estimate, thus avoiding being trapped in local minimums and at the same time creating computationally efficient approach. Criteria similar to the considerations about optimal order of SWD transform expressed in63 can be used as a stopping condition for this scale refinement procedure. A similar scale refinement procedure was also used for the calculation of the symplectomorphic mapping.
2.4 |. Algorithm implementation
The processing workflow of symplectomorphic registration involves the following steps:
Computing SWD transforms Equation 24 for both the reference (I0) and the source (I1) volumes;
- Finding best similarity transformation starting with low radial (Nmin) and angular (Lmin) scales and repeating the following steps with higher scales (L > Lmin, N > Nmin) as needed:
- Reconstructing radial Equation 27 and angular Equation 28 parts;
- Estimating scale (sr) and rotation (θr, ϕr) from Equations 29 and 30 respectively;
Applying the final similarity transformation ((sr)–(θr, ϕr) to the source volume;
Interpolating and resampling both the reference and the source volumes using Equation 26 again starting with low radial (Nmin) and angular (Lmin) scales and improving the scales as needed;
Integrating the non-local Hamiltonian Equations 19–21 or Equations 20–23 using symplectic scheme64,65;
- Generating the transitional probability ρ(x′, x) Equation 16 based on the select coupling density Q(x, x′) for the current scales;
- Propagating the momentum p, the position q and the Jacobian J to the new time t;
- Verifying the invertibility condition Equation 8;
- Reinitializing the p, q flow and the Jacobian J with Equations 9–11 if the Jacobian is out of bounds;
Repeating the integration updating the scales as needed until the convergence condition Equation 13 is not satisfied.
3 |. RESULTS
All results shown below were coded in standard C/C++ and parallelized using POSIX threads.
3.1 |. Phantom data registration
To test the approach we first applied it to 3D extension of a classical “toy” example commonly used to show the performance of non-linear registration approaches—the registration of the “C” shape to the ”circle” shape. The original 200 × 200 × 200 3D “C” and ”circle” volumes are shown in Figure 1A and B. Panels C and D show 3D view and central slices for the forward and inverse maps. Panels E and F show grid lines for a subset of points selected from three groups of orthogonal planes. The overall performance of our approach seems to be very good, with nearly perfect forward map of the “circle” to the “C” shape, and only a slight signature of the original hole in the inverse map of “C” shape to the “circle”. No SWD preconditioning was used in this example and simple adjacency type matrix was used for phase space coupling.
FIGURE 1.
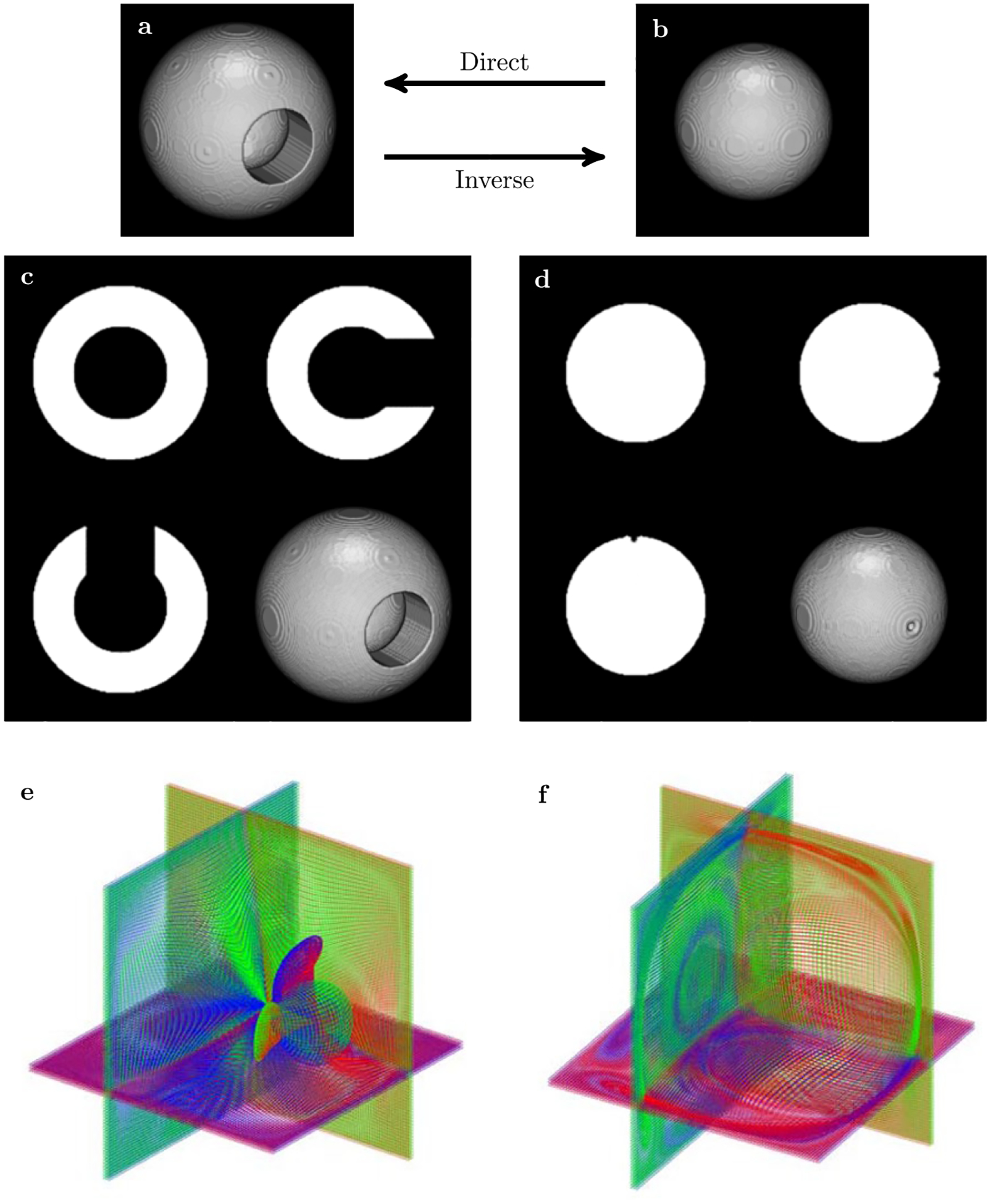
3D extension of the classical “toy” example used for benchmarking of diffeomorphic registration: fitting “circle”—sphere in (B)—to “C”—spherical shell with a hole in (A). Results of direct (C) and inverse (D) maps obtained in 8 embedded energy shells. Subset of curvilinear grid lines plotted for three neighboring layers selected from three orthogonal planes for direct (E) and inverse (F) maps. The different colors were used to distinguish between the anterior-posterior grid lines (blue), the dorsal-ventral grid lines (green) and the right-left lateral grid lines (red). Both inverse and direct maps were obtained in a single run, the processing time for 200 × 200 × 200 volumetric datasets was just above 30 s on 12 cores Intel ® CoreTM i7–4930K CPU 3.40 GHz
The second stage of our evaluation procedure was the comparison with some of the existing state-of-the-art nonlinear registration methods commonly used. As it is clearly beyond the scope of our paper to conduct a comprehensive evaluation using all possible variations of nonlinear deformation algorithms versus all possible variations of accuracy metrics (such as is done in evaluation studies, like e.g.,52 we decided to report here just the simplest and the most straightforward type of metrics and have restricted our choice of registration tools to those commonly used at our institution. Following the recommendation from52 concerning the speed and accuracy, we processed the phantom registration using Diffeomorphic Demons (which is reported as one of the fastest) and symmetric diffeomorphic image registration SyN (reported as one of the most accurate), both from the Advanced Normalization Tools (ANTs) package,66 as well as using FNIRT non-linear registration utility from the FSL67 and 3dQwarp non-linear warping utility from AFNI.58
As noted above, our quantitative comparison of accuracy and efficiency are based on two simple and well-understood metrics: The time is used as a practical measure of efficiency and a simple root mean square deviation between the reference and the registered image is used as a measure of accuracy. The evaluation results are summarized in Table 1 and demonstrate the enhanced accuracy and efficiency of our symplectomorphic registration approach in comparison with some well established non-linear registration techniques for these two simple metrics and a well-defined standard numerical phantom.
TABLE 1.
Comparison of accuracy and efficiency of phantom registration between three commonly used packages (ANTs, FSL and AFNI) and our symplectomorphic registration (SYM-REG) Approach
| ANTsa,c | ANTsb,c | FSLd | AFNIe | SYM-REG | |
|---|---|---|---|---|---|
| RMSD | 156.4 | 81.0 | 448.2 | 234.3 | 54.0 |
| Time | 10 min 15 s | 1 h 21 min | 12 min 43 s | 45 min 50 s | 38 s |
 |
 |
 |
 |
 |
 |
Notes: Simple Root-Mean-Square Deviation (RMSD) between reference and registered images are used as an accuracy metric and time is reported to characterize an efficiency. One of the center slices of registered images is also included to provide visual insights into correspondent registration artifacts.
GreedyExp—We used −t GreedyExp option to produce Diffeomorphic Demons style exponential mapping. It was required to increase number of iterations using −i 400 × 160 × 80 as the default (-i 10×10×5) choice produced unacceptable results with RMSD = 326.
SyN[0.3]—This was the best result we were able to achieve using native ANTs diffeomorphic registration with −t SyN[0.3] parameter. The number of iterations was again increased to 400 × 160 × 80. It may be possible to improve this results by further increasing the number of iterations, but we decided that going beyond 1h 30 min for this simple 2003 phantom would not justify the improvement.
MSD—We used −m MSD (mean square difference) similarity model for both of ANTs methods as the rest of the models (cross-correlation—CC, mutual information—MI, and probability mapping—PR) appeared to be both less accurate and more slow for this numerical phantom registration.
FNIRT—We used the default (−miter = 5, 5, 5, 5) number of iterations and it produced the unacceptable results shown here. Increasing the number of iterations to 100, 100, 20, 5 increased the runtime to over an hour with virtually no improvement in accuracy.
3dQWarp—We used −penfac 0.02-workhard options for 3dQwarp to allow larger grid deformations and extra iterations to find better alignment (the default settings produced unacceptable results after 30 min with RMSD = 418).
3.2 |. High resolution anatomical MR data registration
3.2.1 |. Multi-subject registration
For our first test of the method on actual data, we addressed the most common usage of registration algorithms: to register a set of high resolution anatomical (HRA) images to a common reference image. This is a typical multi subject analysis task appearing in a variety of group studies that involve morphometry based comparison between different subjects or subject groups. We utilized HRA data collected on the 3T GE Discovery MR750 whole body system at the UCSD Functional MRI (CFMRI) using a 32 channel head coil for ten different subjects previously collected in a study to determine the effects of caffeine on the resting state brain activity.69 However, only high resolution T1 data (all having 290 × 262 × 262 voxel resolution) were used for registration test described in the current subsection. Further details are available in.69 Normalized T1 intensities were used as matching terms I0 and I1 in symplectomorphic registration.
Figure 2 shows the collage of images related to this registration test. The central plane from anatomical volume used as reference is shown in (A) panel. The same location planes for randomly selected four volumes out of ten subjects are shown in (B). Panel (D) shows the result of SWD preconditioning step equivalent to rigidly fitting each volume to reference with orthogonal transform that includes rotation and uniform scaling for the same four volumes. Panel (C) shows image obtained by averaging of SWD preconditioned volumes for all ten subjects. The next four panels show results of symplectomorphic transforms using 5 (F) and 15 (H) embedded energy shells again with correspondent all subject averages in (E) and (G) respectively. Plots of RMSD as a function of a number of shells (convergence plots), as well as illustrative plots of curvilinear grids for the same randomly chosen four subjects are available in Supporting Information Figure S1 and S2.
FIGURE 2.
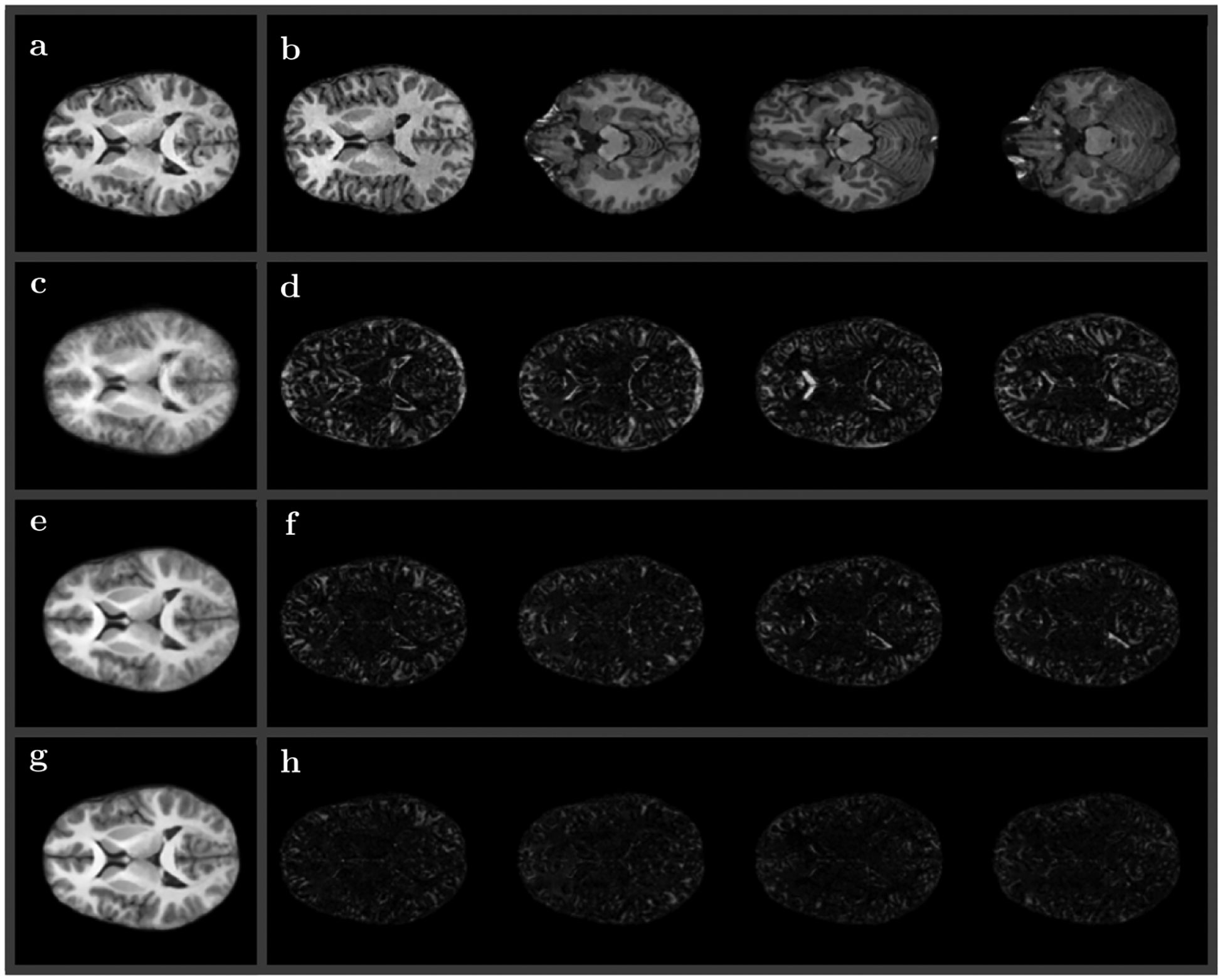
Results of high resolution anatomical (HRA) mapping to the same anatomical reference volume (shown in A). (B) Central planes for four volumes out of ten subjects used for mapping. (D) Residual images of SWD preconditioning (fitted with orthogonal transform) for the same four volumes, (C) all ten volumes averaged. Residual images of symplectomorphic transforms using 5 (F) and 15 (H) embedded shells with all ten subject averages in (E) and (G) respectively
Overall, as would be expected, the symplectomorphic registration shows significant improvement over rigidly fitted volumes, with additional improvement due to increase of a number of energy shells used in registration. In general, there is no obvious relationship between the number of shells and the accuracy, although practically, as the number of shells is determined by selected limits of Jacobian range (ε) (and indirectly can be affected by a selected policy of time step adjustments), symplectomorphic registration with increased number of shells may allow to obtain better overall accuracy. The total processing time for all ten subject fitting ranges from 15 to 40 minutes based on the selected quality (this is time measured by running the registration on 12 cores Intel ® CoreTM i7–4930K CPU 3.40 GHz).
We note, while the quality of the fit is measured here by RMSD, the most advantageous implementation in any particular clinical or research scenario of course depends on several parameters, including the desired quality of the fit, the type of regularization, the type of coupling in ESP step, aggressiveness of time step updating, etc. These trade-offs necessarily depend on the specific desires of the user in any particular application.
3.2.2 |. Synthetic deformation maps
An important practical aspect of non-linear registration methods in their application to MRI is their robustness to image distortions produced in the MRI procedure. The dependence of the spatial encoding process in MRI on magnet field gradient linearity results, in practice, in a wide range of complex non-linear distortions due to gradient non-linearities induced by both machine dependent factors (e.g. imperfect gradients) and subject morphological variations (e.g. susceptibility effects). To add to the complexity of this problem, the machine dependent variations can depend not only on the scanner vendor, but on the scanner software revision as well. And the subject morphological variations certainly differ between subjects.
Therefore, in order to provide a quantitative assessment of the symplectomorphic registration using HRA data under more realistic conditions encountered in practical applications, we took several T1 brains acquired on different hardware (Siemens and GE scanners) at different resolutions using different acquisition sequences and subjected them to artificially generated distortions designed to mimic some of the most prominent non-linear distortions common to MRI acquisitions.
We utilized 5 different high resolution datasets: (1) MNI152 T1 2 mm with 91×109×91 voxels, (2) T1 MPRAGE 1.2 mm with 160 × 200 × 200 voxels, (3) T1 MPRAGE 1 mm with 212 × 240 × 256 voxels, (4) T1 1 mm with 290 × 262 × 262 voxels, and (5) T1 1 mm with 256 × 176 × 176 voxels. All subjects were resampled into MNI152 space (to provide the same accuracy and required workload for all subjects) and then were distorted several times using five different types of warpage (see Figure 3). The different types of warpage include nonlinear or differential rotation, nonlinear stretching, nonlinear compression, etc, and Figure 3 shows one of the subjects (MNI152 T1 2 mm with 91 × 109 × 91 voxels) with all five warpage types applied to this subject.
FIGURE 3.
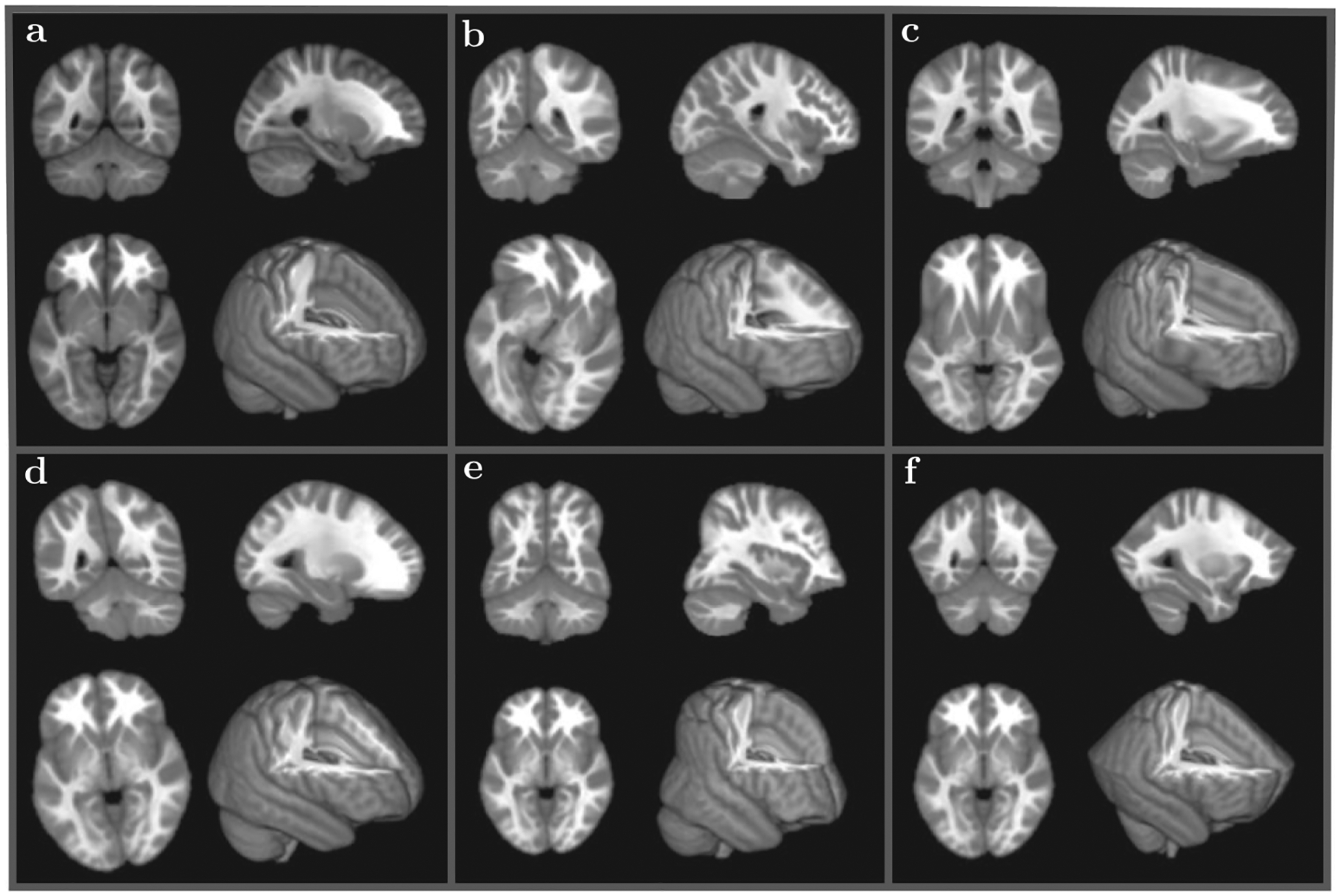
Different nonlinear warpage types applied to 5 different subjects (only one subject is shown for each warpage type—MNI152 T1 2 mm with 91 × 109 × 91 voxels): (A) an original subject; (B) differential rotation with the amount of rotation proportional to the distance from the center in the axial plane (whirl); (C) differential stretch in the anterior direction; (D) differential rotation with the amount of rotation proportional to the distance from the axial plane in the longitudinal direction (twist); (E) nonuniform compression in the axial plane proportional to the the longitudinal distance; (F) nonuniform compression in the longitudinal direction relative to the position in the axial plane
The idea of generation and use of synthetic deformation maps for validation is not new. A somewhat similar procedure of synthetic Gaussian 2D deformations was used recently for registration validation in.70 The important difference of our deformation panel is that it includes a variety of more complex deformation modes observed and frequently present in various MRI acquisition protocols and modalities.
The 25 warped volumes were then processed using the two non-linear registration methods most commonly used at our institution – ANTs SyN and AFNI 3dQwarp, in addition to SYM-REG, and compared the restored volumes with the original unwarped datasets. The results are summarized in Table 2 showing mean values for the RMSD as well as mean execution times for all subjects (top) and for all warpage types (bottom). The complete processing took 976, 3414 and 1223 s for SYM-REG, AFNI and ANTs respectively giving 304.6, 358.5 and 584.0 for the RMSD values with SYM-REG providing both the lowest RMSD error and the lowest execution time (the default processing options were used for all packages). Supporting Information Figures S8–S12 show Matlab listings for each of the five different types of warpage used in Figure 3 and in Table 2.
TABLE 2.
Comparison of accuracy and efficiency of HRA registration between ANTs SyN, AFNI and our symplectomorphic registration (SYM-REG) approach
| Method | Mean RMSD/time (s) across subjects | ||||
|---|---|---|---|---|---|
| AFNI 3dQwarp | 402.2/130.8 | 363.8/139.4 | 371.6/130.0 | 316.5/137.8 | 338.1/144.8 |
| ANTs SyN | 578.2/38.2 | 606.0/47.0 | 586.2/43.2 | 581.1/60.0 | 568.5/56.2 |
| SYM-REG | 298.2/54.8 | 312.4/37.0 | 311.8/34.2 | 300.7/33.4 | 299.8/35.8 |
| Mean RMSD/time (s) across warpage types | |||||
| AFNI 3dQwarp | 162.9/134.0 | 373.5/137.2 | 482.7/135.6 | 404.6/130.0 | 368.6/146.0 |
| ANTs SyN | 140.8/50.6 | 705.0/47.4 | 602.9/53.6 | 781.9/51.0 | 689.4/42.0 |
| SYM-REG | 87.0/38.4 | 331.6/46.8 | 438.7/36.2 | 351.8/38.6 | 313.9/35.2 |
Notes:.
Five different subjects and five different warpage types were used for the comparison. Two subtables include mean RMSD values and mean execution times calculated across subject (top) and across warpage types (bottom). The average of all subjects and warpage types gives RMSD of 304.6, 348.5 and 584.0 for SYM-REG, AFNI and ANTs respectively with 976, 3414 and 1223 s required to finish the processing for each method.
3.3 |. Diffusion weighed MR image registration
The second important application we investigated was the registration of diffusion-weighted images (DWI) to the HRA image of the same subject. This is a critical step required for collocation of diffusion tractography based quantities with high resolution anatomical morphometry. Registration of DWI to HRA is generally a more complicated problem than registering HRA to HRA because DWI images are typically acquired with echo-planar imaging (EPI) acquisitions that are not only prone to more severe non-linear susceptibility distortions than HRA images but are invariably acquired at lower spatial resolution than the HRA for the same subject.
The data used for this example were again collected at the UCSD Center for Functional MRI (CFMRI) using 3T GE Discovery MR750 whole body system to study the effects of traumatic brain injuries (TBI). The HRA T1 volume has 168 × 256 × 256 voxel size with 1.2 × 0.9375 × 0.9375 mm resolution. The DWI data has 100 × 100 × 72 voxel size with 2 mm3 resolution. The normalized HRA T1 intensity was used for the reference image matching term I0 and the equilibrium probability map (see71) was used as a moving image matching term I1.
Figure 4 shows a central slice and a 3D view of the reference volume A, DWI b = 0 volume B, DWI equilibrium probability volume that has the same resolution as b = 0 volume C, and the final symplectomorphic registration of the DWI equilibrium probability volume D. The details about the equilibrium probability and how it is obtained can be found in.71 The last two panels E and F show enlarged side by side comparison of the HRA reference and transformed DWI with the same resolution.
FIGURE 4.
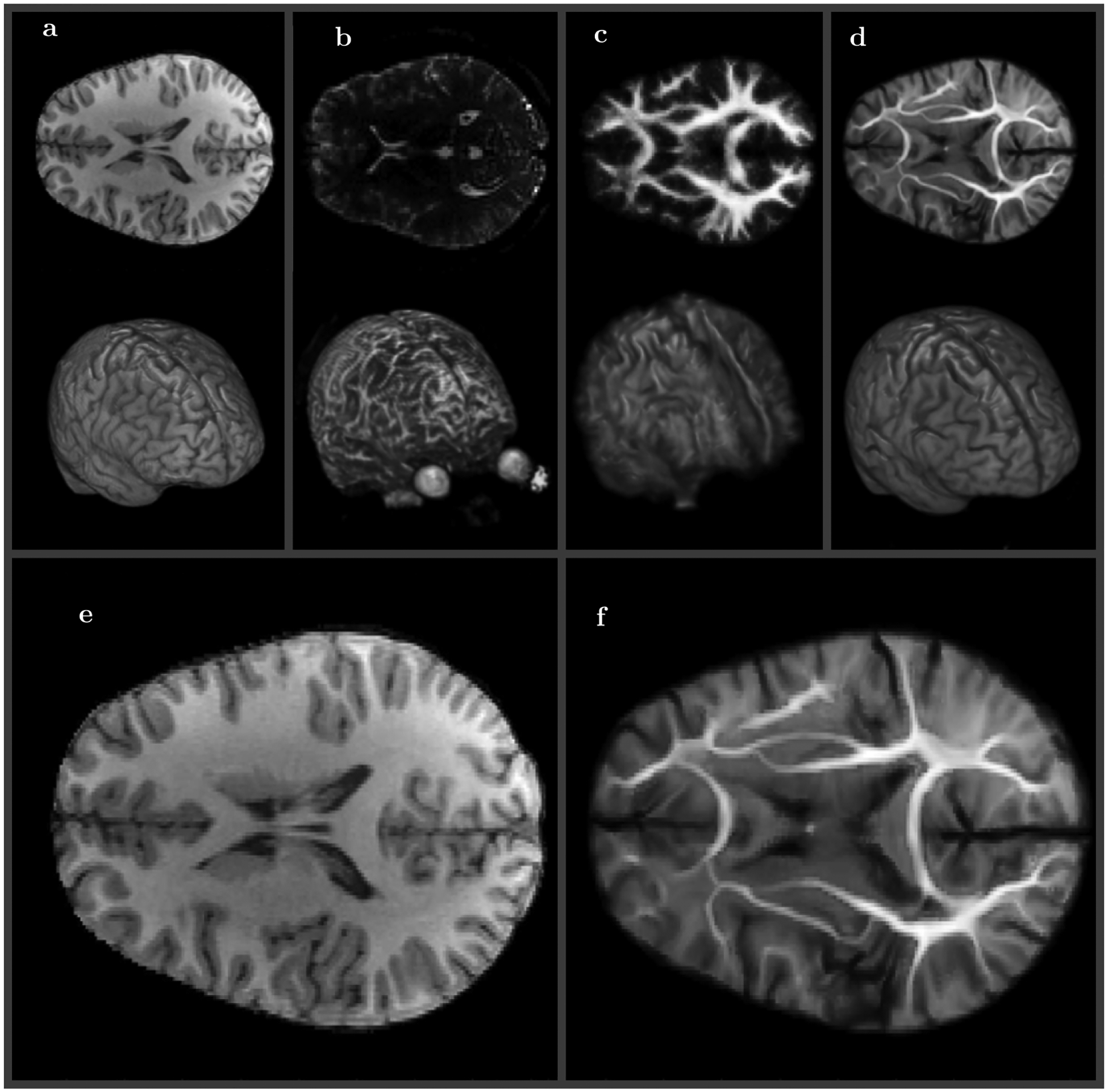
Medium resolution (100 × 100 × 72) diffusion weighted (DWI) volume registration to high resolution (168 × 256 × 256) T1 reference. A, Reference T1 MRI image (2D center slice top and 3D view bottom), B, DWI b0 MRI image, C, equilibrium probability DWI image (same resolution as b0 image), D, DWI image SWD preconditioned and registered to T1 image (same resolution as T1 image). Side by side comparison of reference E, and symplectomorphic registration of DWI volume F (enlarged versions of A and D)
Figure 5 shows a comparison of registration and its effects on tractography performance for the same non-linear registration methods used in registration validation with synthetic deformation maps of spin echo HRA images in the previous Section 3.2. These diffusion weighted EPI acquisitions have clinically relevant SNR differences, which could have a big impact on the accuracy and speed of the registration, but was not addressed in the 5 simulated analytical warpage types of the previous section.
FIGURE 5.
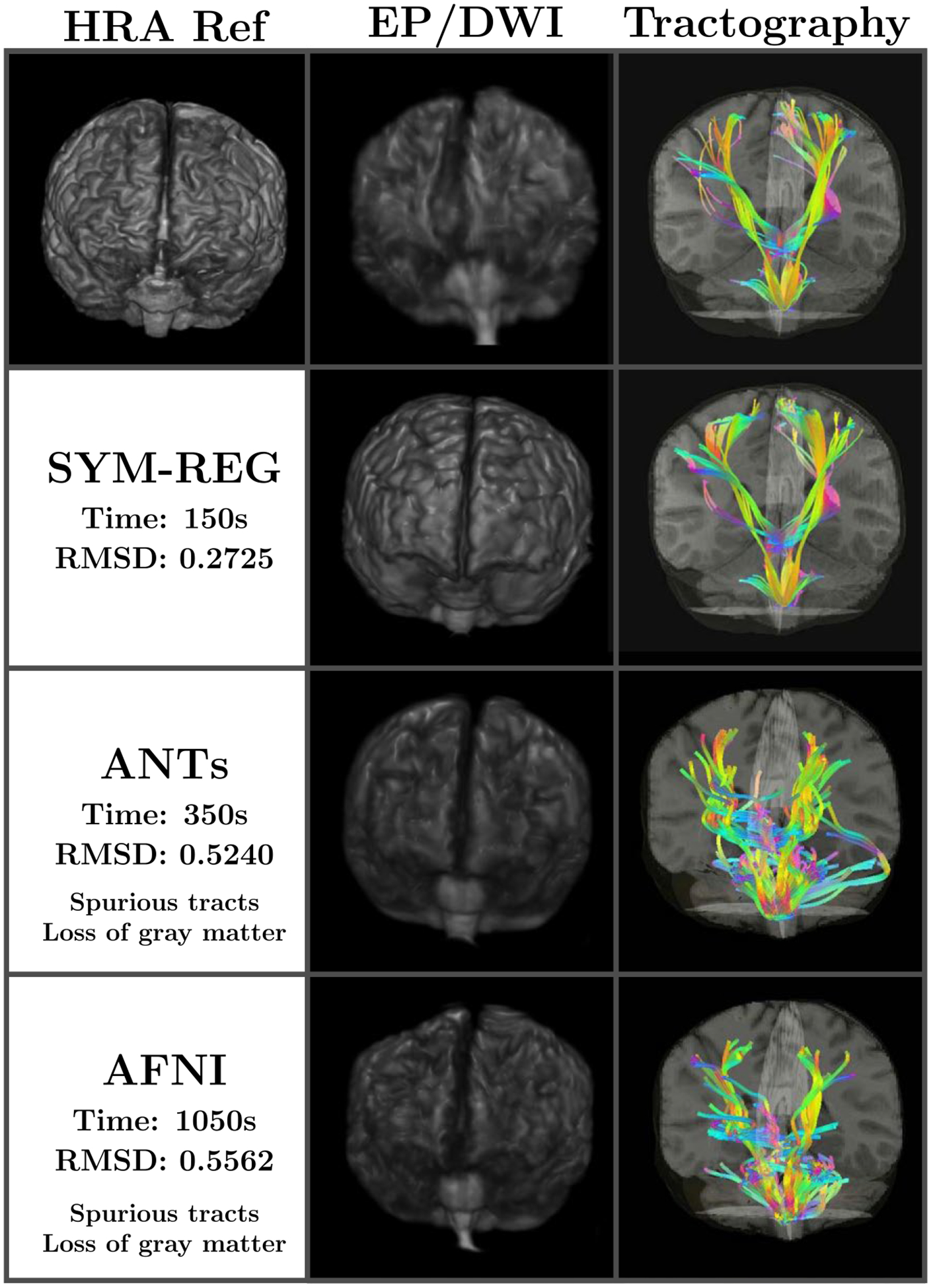
Comparison of registration and diffusion weighted tractography using the original DWI volume space (100 × 100 × 72) (top row) and the warped HRA space (168 × 256 × 256) using the symplectomorphic registration (second row), the ANTs SyN method (third row) and the AFNI’s 3dQwarp (bottom row). The SYM-REG requires less time and results in largest overall quality improvements both in term of equilibrium probability (second column) and the details of tracts (third column). The latero–lateral (left to right and right to left), anterior–posterior, and dorsal–ventral tracts are shown in cyan, magenta and yellow respectively
The comparison of SYM-REG with ANTs SyN and AFNI 3dQwarp clearly show that SYM-REG is capable to achieve the best speed of registration (150 s vs 350 s/1050 s) and RMSD accuracy (0.27 vs 0.52/0.56) on the spin echo/EPI registration with the real life distortions and noise. The figure also shows that the symplectomorphic registration method allows very accurate localization of diffusion derived tracts with the high resolution anatomical features. More details that include a SYM-REG based tractography implementation as well as multi-modal estimation in general are not relevant to this paper and are reported in.62
We would like to mention one important consideration here. A considerable amount of work has been spent recently not just on spatial registration of diffusion imaged volumes, but also on devising techniques for local reorientation of diffusion tensors that would be consistent with the new deformed spatial grid [see e.g25–27,29,30]. These methods are both time consuming and an unnecessary intermediate step from our viewpoint. An important feature of our method is that we can directly import the diffeomorphic maps together with the high resolution data into our diffusion estimation and tractography technique GO-ESP,71 so that both the estimation of local diffusion properties and the generation of tracts are performed in the locally warped space characterized by the spatially dependent metric tensor, thereby obviating the need to use any ad hoc proceed to impose geometric consistency, which in our method is guaranteed by the symplectomorphic nature of transformation. The result is a method that provides a fast and effective way of adding a new level of details to relatively low resolution output available from diffusion weighted tractography.
3.4 |. Registration of functional MR images
The third and final important application we investigated was the registration of low spatial resolution functional resting state FMRI (rs-FMRI) data to HRA data from a single subject. As in DWI, FMRI data is typically acquired using EPI acquisitions that, as previously mentioned, are more prone to non-linear geometric distortions than HRA acquisitions, and are of lower spatial resolution.
The data used for this test were from the same caffeine study dataset69 used in Section. Registration of functional rs-FMRI data to anatomical images is required to establish an accurate localization of activation regions in the high resolution maps of gray matter.
Figure 6 shows side by side comparison for 3D views of rs-FMRI A, T1 B and rs-FMRI mapped to T1 C volumes. The processing was carried through 30 energy embedded shells and required about 5 minutes of waiting time from the start to the finish, with a subset of the final grid shown in D. The work is currently underway to include flexible mapping grids directly to our rs-FMRI mode detection approach.72,73 Figure 7 shows comparison of original and registered images for several of the resting state functional modes obtained using our entropy field decomposition (EFD) technique.72,73 The default mode A and D, the visual lateral B and E, and the visual occipital C and F modes are shown for some of the subjects from Figure 2. The symplectomorphically mapped images overlayed over correspondent HRA slices D, E, and F show very accurate localization of functional modes in the appropriate regions of HRA volumes.
FIGURE 6.
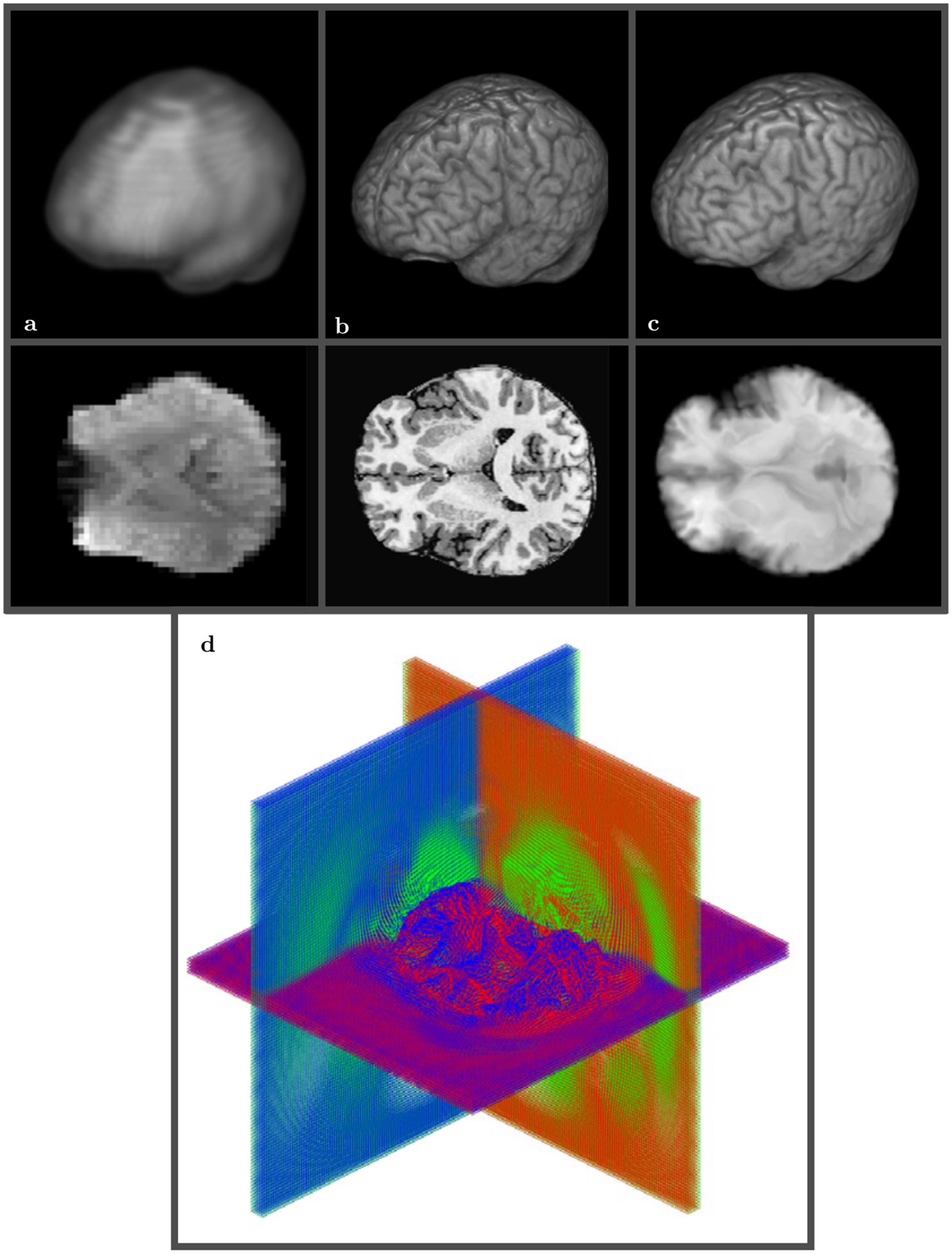
3D view of low resolution (64 × 64 × 30) rs-FMRI volume A vs T1 high resolution (290 × 262 × 262) anatomical volume B. SWD preconditioned rs-FMRI volume after registration to high resolution T1 template C. The final mapping grid used 30 shells D and took about 5 minutes on 12 cores Intel ® CoreTM i7–4930K CPU 3.40 GHz. The same color scheme is used for the displacement field with blue corresponding to the anterior-posterior grid lines, green to the dorsal-ventral grid lines, and red to the right-left lateral grid lines
FIGURE 7.
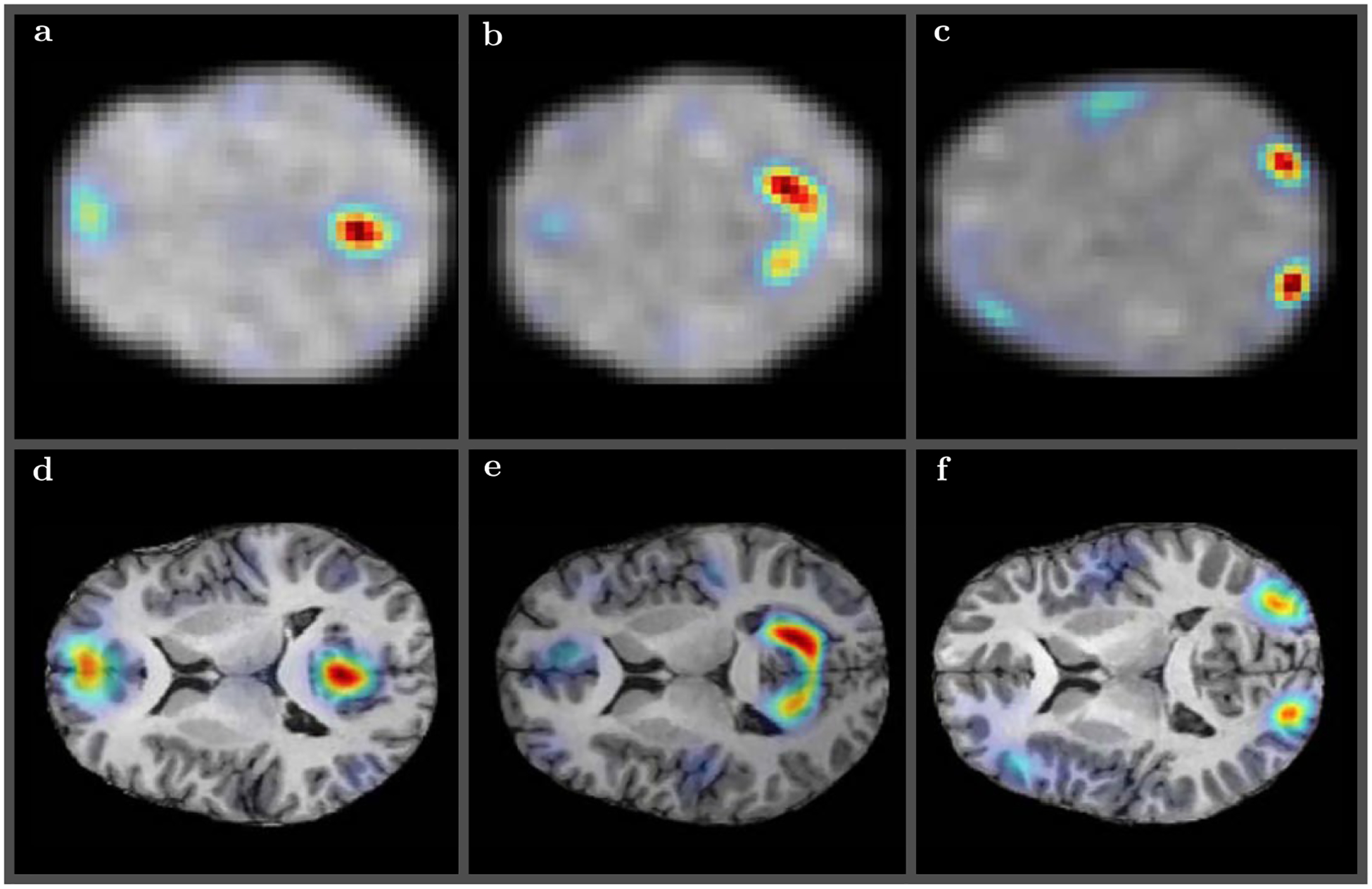
Several randomly selected resting state modes obtained using low resolution (64 × 64 × 30) rs-FMRI volume registered to T1 high resolution (290 × 262 × 262) anatomical volume—default mode A and D, visual lateral B and E, and visual occipital C and F—for some of the subjects from Figure 2. The upper panels A, B, and C show the original low resolution rs-FMRI modes. The symplectomorphic maps in lower panels D–F show accurate localizations of functional modes in the appropriate regions of HRA volumes
4 |. DISCUSSION
The recent review paper74 conducted a retrospective analysis of the past two decades of the field of medical image registration since publication of the original review.75 It is of concern that the main conclusion of this twenty years retrospective is that, in spite of all the progress in the field of registration, “the two major problems mentioned in75 validation of registration methods and translation of these to the clinic—are major problems still, which have even been aggravated by the elaboration of registration methods.”
In this paper we have presented a new flexible multidimensional image registration approach that is based on the Hamiltonian formalism. The method generates a set of Hamilton’s equations capable of producing a symplectomorphic transformation for mapping between Cartesian and curvilinear grids that minimizes some predefined image difference metric. The final diffeomorphic mapping is constructed as a multiplicative sequence of symplectomorphic transforms with gradually diminishing levels of total energy, thus providing a sequence of energy embedded symplectomorphic shells. For demonstration purposes, we used both a simple local squared difference, as well as a more complicated non-local image squared difference, as a Hamilton function.
An application of the powerful and versatile ESP approach61 to the phase space domain resulted in a non-local form of Hamilton’s equations. The non-local form represents an efficient and relatively straight forward way to introduce regularization that is capable of taking into account some image specific details or even additional knowledge based parameterizations. More generally, the Hamiltonian formalism allows easy adaptation of custom and possibly more complex forms of image difference metrics, and at the same time allows the metric in the diffeomorphism space to be kept the same, which facilitates the comparison and validation between different techniques and regularization approaches.
By “resetting” of the Hamiltonian (or “freezing” the flow) our approach provides an effective way to move those singular points outside of the domain of interest creating a final diffeomorphic map as a composition of symplectomorphisms. Some methods (like LDDMM) employ a trick to remove some of the singular points (zeros in Jacobian) by using exponential mapping (at the expense of effectiveness, in particular due to limiting a space of available updates), but it still has to deal with other singular points (infinities in Jacobian) to ensure the invertibility. We employed a different trick by freezing the flow and thus moving the singularities in an image specific manner.
Hence overall shell-like sequence of transformations provides more flexibility and may potentially allow to reach better overall fits than fixed number of steps and fixed exponential mapping methods.
The resolution differences between images as well as rigid shape alignment is addressed using the preconditioning step based on the SWD technique63 This efficient volumetric decomposition computes a set of fast spherical harmonics and spherical Bessel transforms and is able to produce accurate interpolation, filtering and fitting of rigid shapes.
One of the major hurdles in the translation of registration methods to clinical practice74 is the difficulty in validation of these methods in the face of the exceedingly complex interplay of the many pulse sequence details, the scanner hardware, and the anatomical variations that interact with the magnetic fields. To this end, we have developed a panel of analytically defined deformations based on known physical effects present in MR acquisitions. While these certainly do not constitute an exhaustive list of possible effects, they are a fair representation of the major distortions in the major MR image acquisition schemes. This deformation panel was used to validate our method and quantitatively demonstrate its robustness to a wide range of different types of distortions that regularly plaque MR studies. The deformations from the panel can be applied to images of different modalities and acquisition conditions and potentially can be appropriate for quick and robust validation in clinical settings. This validation approach is somewhat similar to 2D Gaussian deformations used in,70 but our panel includes deformations that can be attributed to a variety of real physical processes present in different acquisition protocols and modalities (i.e. twist, whirl, stretch, etc).
We should emphasize that although the use of the synthetic distortion data is a great test tool for the registration algorithm; however it can not be used as a substitute for a comprehensive study of effects of real SNR, pulse sequence and motion induced distortions, etc, in practical medical imaging. Therefore, for each and every application of any of the available registration methods to translational and more clinically relevant MRI data such test/retest/validation studies will surely be required and reserved for future work.
Overall the symplectomorphic registration approach is both accurate and fast and is capable of processing of a variety of volumetric images of different modalities and resolutions. In the tests reported in this paper we were able to handle all three of the major neuro-MRI modalities routinely used for human neuroimaging applications, including mapping between high-resolution anatomical volumes, medium resolution diffusion weighted volumes and high-resolution anatomicals, and low resolution functional MRI images and high-resolution anatomicals. The typical processing time for high quality mapping ranges from less than a minute to several minutes on a modern multi-core CPU for a typical high resolution anatomical MRI volumes. The speed, accuracy, and flexibility of this new method has the potential to play an important role in the quantitative assessment of neuroimaging data in a wide range of both basic research and clinical applications.
Supplementary Material
FIGURE S1 Convergence plots for the four subjects of Figure 2 as a function of a number of shells (red/green/blue and magenta colors correspond to the first, second, third and forth subject shown in Figure 2B)
FIGURE S2 Illustrative plots of curvilinear grids for the same four subjects of Figure 2, using blue color for the anterior-posterior grid lines, green for the dorsal-ventral grid lines, and red for the right-left lateral grid lines
FIGURE S3 Slices of AFNI 3dQwarp registration of 5 subjects × 5 warpages. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5×5 panel of slices show the final AFNI 3dQwart registration results with timings and accuracy reported in Table 3(A)
FIGURE S4 Slices of ANTs SyN registration of 5 subjects × 5 warpages. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5×5 panel of slices show the final ANTs SyN registration results with timings and accuracy reported in Table 3B
FIGURE S5 Slices of SYM-REG registration of 5 subjects × 5 warpages. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5×5 panel of slices show the final SYM-REG registration results with timings and accuracy reported in Table 3C. Full regularization (Equations (19), (20) and (23)) was used for grid updates
FIGURE S6 Slices of SYM-REG registration of 5 subjects × 5 warpages obtained without regularization. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5 × 5 panel of slices show the final SYM-REG registration results without regularization, i.e. using Equations (4)–(6) for updating grid (with sufficiently small time step to ensure at least some convergence)
FIGURE S7 Slices of SYM-REG registration of 5 subjects × 5 warpages obtained with momentum-only regularization. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5 × 5 panel of slices show the final SYM-REG registration results with momentum-only regularization, i.e. using Equations (19), (20) and (21) for grid updates
FIGURE S8 Listing of warpage 1—differential rotation with the amount of rotation proportional to the distance from the center in the axial plane (whirl). Applied to undeformed grid mesh and then used to warp each of the five subjects
FIGURE S9 Listing of warpage 2—differential stretch in the anterior direction. Applied to undeformed grid mesh and then used to warp each of the five subjects
FIGURE S10 Listing of warpage 3—differential rotation with the amount of rotation proportional to the distance from the axial plane in the longitudinal direction (twist). Applied to undeformed grid mesh and then used to warp each of the five subjects
FIGURE S11 Listing of warpage 4—nonuniform compression in the axial plane proportional to the the longitudinal distance. Applied to undeformed grid mesh and then used to warp each of the five subjects FIGURE S12 Listing of warpage 5—nonuniform compression in the longitudinal direction relative to the position in the axial plane. Applied to undeformed grid mesh and then used to warp each of the five subjects.
ACKNOWLEDGMENTS
The authors thank Dr Alec Wong and Dr Tom Liu at the UCSD CFMRI for providing the resting state data and Dr Scott Sorg at the VA San Diego Health Care System for providing the diffusion weighted imaging data. LRF and VLG were supported by NSF grants DBI-1143389, DBI-1147260, EF-0850369, PHY-1201238, ACI-1440412, ACI-1550405 and NIH grants R01 MH096100 and R01 AG054049-02.
Funding information
NSF, Grant/Award Number: DBI-1143389, DBI-1147260, EF-0850369, PHY-1201238, ACI-1440412 and ACI-1550405; NIH, Grant/Award Number: R01 MH096100 and R01 AG054049-02.
APPENDIX: Individual subject and warpage accuracy and timings
Table 3 provides values of RMSD and wall execution time for all subjects and all warpage types after processing by AFNI 3dQwarp, ANTs SyN, and SYM-REG respectively and supporting Information Figures S3–S5 show corresponding image registration results.
TABLE 3.
RMSD and time (s) for registration of five different subjects and five different warpage types for AFNI 3dQwarp (a), ANTs SyN (b) and SYM-REG (c)
| Subject/Warpage | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| (a) AFNI 3dQwarp | 1 | 225.2192/129 | 161.0997/130 | 185.5213/123 | 107.5805/132 | 134.8321/156 |
| 2 | 411.3067/136 | 380.6455/126 | 380.4736/123 | 335.5967/157 | 359.5755/144 | |
| 3 | 520.8890/119 | 483.1769/167 | 497.8304/128 | 452.3812/123 | 459.2277/141 | |
| 4 | 445.6333/117 | 417.0812/132 | 414.8282/125 | 363.8450/145 | 381.5591/131 | |
| 5 | 408.1614/153 | 376.9296/142 | 379.3344/151 | 323.2617/132 | 355.3540/152 | |
| (b) ANTs SyN | 1 | 144.2440/40 | 123.9576/46 | 165.7479/45 | 129.8583/60 | 140.0372/62 |
| 2 | 685.4163/31 | 741.1117/48 | 668.2548/44 | 714.8960/59 | 715.1198/55 | |
| 3 | 595.7664/52 | 626.0091/46 | 611.8217/46 | 583.2656/63 | 597.7054/61 | |
| 4 | 783.7732/34 | 812.4037/53 | 784.9238/39 | 774.4482/69 | 754.1112/60 | |
| 5 | 681.7424/34 | 726.7434/42 | 700.0624/42 | 703.2313/49 | 635.3843/43 | |
| (c) SYM-REG | 1 | 81.4292/51 | 99.6207/50 | 105.7807/29 | 76.3845/31 | 71.5707/31 |
| 2 | 331.0654/52 | 339.2126/29 | 334.6728/52 | 320.4282/50 | 332.5362/51 | |
| 3 | 420.8638/58 | 436.0106/30 | 429.0045/29 | 482.7290/28 | 424.9221/36 | |
| 4 | 349.0831/50 | 363.1338/51 | 362.9932/31 | 325.4440/28 | 358.1071/33 | |
| 5 | 308.6141/63 | 324.2186/25 | 326.5479/30 | 298.3141/30 | 311.8945/28 |
Supporting Information Figures S6 and S7 show image registration results for the SYMREG method with no regularization and momentum only regularization.
Supporting Information Figures S8–S12 show Matlab listings for each of the five different types of warpage used in Figure 3 and in Tables 2 and 3.
REFERENCES
- 1.Christensen GE, Rabbitt RD, Miller MI. 3D brain mapping using a deformable neuroanatomy. Phys Med Biol. 1994;39:609–618. [DOI] [PubMed] [Google Scholar]
- 2.Ashburner J A fast diffeomorphic image registration algorithm. Neuroimage. 2007;38:95–113. [DOI] [PubMed] [Google Scholar]
- 3.Narayanan R, Fessler JA, Park H, Meyerl CR. Diffeomorphic nonlinear transformations: a local parametric approach for image registration. Inf Process Med Imaging. 2005;19:174–185. [DOI] [PubMed] [Google Scholar]
- 4.Vercauteren T, Pennec X, Perchant A, Ayache N. Symmetric log-domain diffeomorphic Registration: a demonsbased approach. Med Image Comput Comput Assist Interv. 2008;11:754–761. [DOI] [PubMed] [Google Scholar]
- 5.Li X, Long X, Laurienti P, Wyatt C. Registration of images with varying topology using embedded maps. IEEE Trans Med Imaging. 2012;31:749–765. [DOI] [PubMed] [Google Scholar]
- 6.Zhang M, Fletcher PT. Finite-dimensional lie algebras for fast diffeomorphic image registration. Inf Process Med Imaging. 2015;24:249–259. [DOI] [PubMed] [Google Scholar]
- 7.Gruslys A, Acosta-Cabronero J, Nestor PJ, Williams GB, Ansorge RE. A new fast accurate nonlinear medical image registration program including surface preserving regularization. IEEE Trans Med Imaging. 2014;33:2118–2127. [DOI] [PubMed] [Google Scholar]
- 8.Yeo BT, Sabuncu MR, Vercauteren T, Ayache N, Fischl B, Golland P. Spherical demons: fast diffeomorphic landmark-free surface registration. IEEE Trans Med Imaging. 2010;29:650–668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yeo BT, Sabuncu M, Vercauteren T, Ayache N, Fischl B, Golland P. Spherical demons: fast surface registration. Med Image Comput Comput Assist Interv. 2008;11:745–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lorenzi M, Ayache N, Frisoni GB, Pennec X. LCC-Demons: a robust and accurate symmetric diffeomorphic registration algorithm. Neuroimage. 2013;81:470–483. [DOI] [PubMed] [Google Scholar]
- 11.Tustison NJ, Avants BB. Explicit B-spline regularization in diffeomorphic image registration. Front Neuroinform. 2013;7:39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mansi T, Pennec X, Sermesant M, Delingette H, Ayache N. LogDemons revisited: consistent regularisation and incompressibility constraint for soft tissue tracking in medical images. Med Image Comput Comput Assist Interv. 2010;13:652–659. [DOI] [PubMed] [Google Scholar]
- 13.Liu X, Yuan Z, Zhu J, Xu D. Medical image registration by combining global and local information: a chain-type diffeomorphic demons algorithm. Phys Med Biol. 2013;58:8359–8378. [DOI] [PubMed] [Google Scholar]
- 14.Janssens G, Jacques L, Orban de Xivry J, Geets X, Macq B. Diffeomorphic registration of images with variable contrast enhancement. Int J Biomed Imaging. 2011;2011:891585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Djamanakova A, Faria AV, Hsu J, Ceritoglu C, Oishi K, Miller MI, et al. Diffeomorphic brain mapping based on T1-weighted images: improvement of registration accuracy by multichannel mapping. J Magn Reson Imaging. 2013;37:76–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Zhang M, Fletcher PT. Bayesian principal geodesic analysis in diffeomorphic image registration. Med Image Comput Comput Assist Interv. 2014;17:121–128. [DOI] [PubMed] [Google Scholar]
- 17.Ha L, Prastawa M, Gerig G, Gilmore JH, Silva CT, Joshi S. Image registration driven by combined probabilistic and geometric descriptors. Med Image Comput Comput Assist Interv. 2010;13:602–609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ashburner J, Kloppel S. Multivariate models of inter-subject anatomical variability. Neuroimage. 2011;56:422–439. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bieth M, Lombaert H, Reader AJ, Siddiqi K. Atlas construction for dynamic (4D) PET using diffeomorphic transformations. Med Image Comput Comput Assist Interv. 2013;16:35–42. [DOI] [PubMed] [Google Scholar]
- 20.Joshi S, Davis B, Jomier M, Gerig G. Unbiased diffeomorphic atlas construction for computational anatomy. Neuroimage. 2004;23:S151–S160. [DOI] [PubMed] [Google Scholar]
- 21.Lim IA, Faria AV, Li X, Hsu JT, Airan RD, Mori S, et al. Human brain atlas for automated region of interest selection in quantitative susceptibility mapping: application to determine iron content in deep gray matter structures. Neuroimage. 2013;82:449–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dhollander T, Veraart J, Van Hecke W, Maes F, Sunaert S, Sijbers J, et al. Feasibility and advantages of diffusion weighted imaging atlas construction in Q-space. Med Image Comput Comput Assist Interv. 2011;14:166–173. [DOI] [PubMed] [Google Scholar]
- 23.Oishi K, Mori S, Donohue PK, Ernst T, Anderson L, Buchthal S, et al. Multi-contrast human neonatal brain atlas: application to normal neonate development analysis. Neuroimage. 2011;56:8–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Goodlett C, Davis B, Jean R, Gilmore J, Gerig G. Improved correspondence for DTI population studies via unbiased atlas building. Med Image Comput Comput Assist Interv. 2006;9:260–267. [DOI] [PubMed] [Google Scholar]
- 25.Li J, Shi Y, Tran G, Dinov I, Wang DJ, Toga A. Fast local trust region technique for diffusion tensor registration using exact reorientation and regularization. IEEE Trans Med Imaging. 2014;33:1005–1022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ruthotto L, Kugel H, Olesch J, Fischer B, Modersitzki J, Burger M, et al. Diffeomorphic susceptibility artifact correction of diffusion-weighted magnetic resonance images. Phys Med Biol. 2012;57:5715–5731. [DOI] [PubMed] [Google Scholar]
- 27.Xue Z, Li H, Guo L, Wong ST. A local fast marching-based diffusion tensor image registration algorithm by simultaneously considering spatial deformation and tensor orientation. Neuroimage. 2010;52:119–130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li H, Xue Z, Guo L, Wong ST. Simultaneous consideration of spatial deformation and tensor orientation in diffusion tensor image registration using local fast marching patterns. Inf Process Med Imaging. 2009;21:63–75. [DOI] [PubMed] [Google Scholar]
- 29.Geng X, Ross TJ, Gu H, Shin W, Zhan W, Chao YP, et al. Diffeomorphic image registration of diffusion MRI using spherical harmonics. IEEE Trans Med Imaging. 2011;30:747–758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ceritoglu C, Oishi K, Li X, Chou MC, Younes L, Albert M, et al. Multi-contrast large deformation diffeomorphic metric mapping for diffusion tensor imaging. Neuroimage. 2009;47: 618–627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Raffelt D, Tournier JD, Fripp J, Crozier S, Connelly A, Salvado O. Symmetric diffeomorphic registration of fibre orientation distributions. Neuroimage. 2011;56:1171–1180. [DOI] [PubMed] [Google Scholar]
- 32.Irfanoglu MO, Modi P, Nayak A, Hutchinson EB, Sarlls J, Pierpaoli C. DR-BUDDI (Diffeomorphic Registration for Blip-Up blip-Down Diffusion Imaging) method for correcting echo planar imaging distortions. Neuroimage. 2015;106:284–299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Irfanoglu MO, Modi P, Nayak A, Knutsen A, Sarlls J, Pierpaoli C. DR-BUDDI: diffeomorphic registration for blip up-down diffusion imaging. Med Image Comput Comput Assist Interv. 2014;17:218–226. [DOI] [PubMed] [Google Scholar]
- 34.Zhang P, Niethammer M, Shen D, Yap PT. Large deformation diffeomorphic registration of diffusion-weighted images with explicit orientation optimization. Med Image Comput Comput Assist Interv. 2013;16:27–34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zhang P, Niethammer M, Shen D, Yap PT. Large deformation diffeomorphic registration of diffusion-weighted images. Med Image Comput Comput Assist Interv. 2012;15:171–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Du J, Goh A, Qiu A. Diffeomorphic metric mapping of high angular resolution diffusion imaging based on Riemannian structure of orientation distribution functions. IEEE Trans Med Imaging. 2012;31:1021–1033. [DOI] [PubMed] [Google Scholar]
- 37.Du J, Goh A, Qiu A. Large deformation diffeomorphic metric mapping of orientation distribution functions. Inf Process Med Imaging. 2011;22:448–462. [DOI] [PubMed] [Google Scholar]
- 38.Chiang MC, Leow AD, Klunder AD, Dutton RA, Barysheva M, Rose SE, et al. Fluid registration of diffusion tensor images using information theory. IEEE Trans Med Imaging. 2008;27:442–456. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Adluru N, Destiche DJ, Lu SY, Doran ST, Birdsill AC, Melah KE, et al. White matter microstructure in late middle-age: effects of apolipoprotein E4 and parental family history of Alzheimerʼs disease. Neuroimage Clin. 2014;4:730–742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ota M, Sato N, Matsuo J, Kinoshita Y, Kawamoto Y, Hori H, et al. Multimodal image analysis of sensorimotor gating in healthy women. Brain Res. 2013;1499:61–68. [DOI] [PubMed] [Google Scholar]
- 41.Nakatsuka T, Imabayashi E, Matsuda H, Sakakibara R, Inaoka T, Terada H. Discrimination of dementia with Lewy bodies from Alzheimerʼs disease using voxel-based morphometry of white matter by statistical parametric mapping 8 plus diffeomorphic anatomic registration through exponentiated Lie algebra. Neuroradiology. 2013;55:559–566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Sparks R, Madabhushi A. Novel morphometric based classification via diffeomorphic based shape representation using manifold learning. Med Image Comput Comput Assist Interv. 2010;13:658–665. [DOI] [PubMed] [Google Scholar]
- 43.Bossa M, Zacur E, Olmos S. Tensor-based morphometry with stationary velocity field diffeomorphic registration: application to ADNI. Neuroimage. 2010;51:956–969. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Kim J, Avants B, Patel S, Whyte J, Coslett BH, Pluta J, et al. Structural consequences of diffuse traumatic brain injury: a large deformation tensor-based morphometry study. Neuroimage. 2008;39:1014–1026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhang Z, Sahn DJ, Song X. Cardiac motion estimation by optimizing transmural homogeneity of the myofiber strain and its validation with multimodal sequences. Med Image Comput Comput Assist Interv. 2013;16:493–500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Lombaert H, Peyrat JM, Croisille P, Rapacchi S, Fanton L, Cheriet F, et al. Human atlas of the cardiac fiber architecture: study on a healthy population. IEEE Trans Med Imaging. 2012;31:1436–1447. [DOI] [PubMed] [Google Scholar]
- 47.Helm P, Beg MF, Miller MI, Winslow RL. Measuring and mapping cardiac fiber and laminar architecture using diffusion tensor MR imaging. Ann N Y Acad Sci. 2005;1047:296–307. [DOI] [PubMed] [Google Scholar]
- 48.Beg MF, Helm PA, McVeigh E, Miller MI, Winslow RL. Computational cardiac anatomy using MRI. Magn Reson Med. 2004;52:1167–1174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Sofka M, Stewart CV. Location registration and recognition (LRR) for serial analysis of nodules in lung CT scans. Med Image Anal. 2010;14:407–428. [DOI] [PubMed] [Google Scholar]
- 50.Risser L, Vialard FX, Wolz R, Murgasova M, Holm DD, Rueckert D, et al. Simultaneous multi-scale registration using large deformation diffeomorphic metric mapping. IEEE Trans Med Imaging. 2011;30:1746–1759. [DOI] [PubMed] [Google Scholar]
- 51.Risser L Image registration; 2016. Accessed: 2016-02-09 http://laurent.risser.free.fr/IMPERIAL/menuImperialEng.html.
- 52.Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang MC, et al. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage. 2009;46:786–802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Ribeiro AS, Nutt DJ, McGonigle J. Which Metrics Should Be Used in Non-linear Registration Evaluation? In Navab N, Hornegger J, Wells MW, Frangi FA (Eds). Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015: 18th International Conference, Munich, Germany, October 5–9, 2015, Proceedings, Part II Cham: Springer International Publishing; 2015. p. 388–395. [Google Scholar]
- 54.Vialard FX. Hamiltonian Approach to Shape Spaces in a Diffeomorphic Framework: from the Discontinuous Image Matching Problem to a Stochastic Growth Model. Theses, École normale supérieure de Cachan—ENS Cachan; 2009. [Google Scholar]
- 55.Miller MI, Trouve A, Younes L. Hamiltonian systems and optimal control in computational anatomy: 100 years since D’Arcy Thompson. Annu Rev Biomed Eng. 2015;17:447–509. [DOI] [PubMed] [Google Scholar]
- 56.Younes L, Arrate F, Miller MI. Evolutions equations in computational anatomy. Neuroimage. 2009;45:40–50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Beg MF, Miller MI, Trouvé A, Younes L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. International Journal of Computer Vision 2005;61:139–157. [Google Scholar]
- 58.Vercauteren T, Pennec X, Perchant A, Ayache N. Diffeomorphic demons: efficient non-parametric image registration. Neuroimage. 2009;45:61–72. [DOI] [PubMed] [Google Scholar]
- 59.Shen D, Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Trans Med Imaging. 2002;21:1421–1439. [DOI] [PubMed] [Google Scholar]
- 60.Christensen GE, Rabbitt RD, Miller MI. Deformable templates using large deformation kinematics. IEEE Trans Image Process. 1996;5:1435–1447. [DOI] [PubMed] [Google Scholar]
- 61.Frank LR, Galinsky VL. Information pathways in a disordered lattice. Phys Rev E. 2014;89:032142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Galinsky VL, Frank LR. A unified theory of neuro-MRI data shows scale–free nature of connectivity modes. Neural Comput. 2017:1–27. Early access, March 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Galinsky VL, Frank LR. Automated segmentation and shape characterization of volumetric data. NeuroImage. 2014;92:156–168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Sanz-Serna JM. Runge-kutta schemes for Hamiltonian systems. BIT Numer Math. 1988;28:877–883. [Google Scholar]
- 65.Sanz-Serna JM. Symplectic Runge-Kutta and related methods: recent results. Physica D Nonlinear Phenomena. 1992;60:293–302. [Google Scholar]
- 66.Avants BB, Epstein CL, Grossman M, Gee JC. Symmetric diffeomorphic image registration with crosscorrelation: evaluating automated labeling of elderly and neurodegenerative brain. Med Image Anal. 2008;12:26–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Andersson JLR, Jenkinson M, Smith S, Non-linear registration AKA spatial normalisation; 2016. Accessed: 2016-02-09 FMRIB Technial Report TR07JA2 http://www.fmrib.ox.ac.uk/analysis/techrep/tr07ja2/tr07ja2.pdf.
- 68.Cox RW. AFNI: software for analysis and visualization of functional magnetic resonance neuroimages. Comput Biomed Res. 1996;29:162–173. [DOI] [PubMed] [Google Scholar]
- 69.Wong CW, Olafsson V, Tal O, Liu TT. The amplitude of the resting-state fMRI global signal is related to EEG vigilance measures. Neuroimage. 2013;83:983–990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Rogelj P, Kovacic S. Symmetric image registration. Med Image Anal. 2006;10:484–493. [DOI] [PubMed] [Google Scholar]
- 71.Galinsky VL, Frank LR. Simultaneous multi-scale diffusion estimation and tractography guided by entropy spectrum pathways. IEEE Trans Med Imaging. 2015;34:1177–1193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Frank LR, Galinsky VL. Detecting spatio-temporal modes in multivariate data by entropy field decomposition. J Phys A Math General. 2016;49:395001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Frank LR, Galinsky VL. Dynamic Multiscale Modes of Resting State Brain Activity Detected by Entropy Field Decomposition. Neural Comput. 2016;28:1769–1811. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Viergever MA, Maintz JB, Klein S, Murphy K, Staring M, Pluim JP. A survey of medical image registration—under review. Med Image Anal. 2016;33:140–144. [DOI] [PubMed] [Google Scholar]
- 75.Maintz JB, Viergever MA. A survey of medical image registration. Med Image Anal. 1998;2:1–36. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
FIGURE S1 Convergence plots for the four subjects of Figure 2 as a function of a number of shells (red/green/blue and magenta colors correspond to the first, second, third and forth subject shown in Figure 2B)
FIGURE S2 Illustrative plots of curvilinear grids for the same four subjects of Figure 2, using blue color for the anterior-posterior grid lines, green for the dorsal-ventral grid lines, and red for the right-left lateral grid lines
FIGURE S3 Slices of AFNI 3dQwarp registration of 5 subjects × 5 warpages. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5×5 panel of slices show the final AFNI 3dQwart registration results with timings and accuracy reported in Table 3(A)
FIGURE S4 Slices of ANTs SyN registration of 5 subjects × 5 warpages. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5×5 panel of slices show the final ANTs SyN registration results with timings and accuracy reported in Table 3B
FIGURE S5 Slices of SYM-REG registration of 5 subjects × 5 warpages. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5×5 panel of slices show the final SYM-REG registration results with timings and accuracy reported in Table 3C. Full regularization (Equations (19), (20) and (23)) was used for grid updates
FIGURE S6 Slices of SYM-REG registration of 5 subjects × 5 warpages obtained without regularization. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5 × 5 panel of slices show the final SYM-REG registration results without regularization, i.e. using Equations (4)–(6) for updating grid (with sufficiently small time step to ensure at least some convergence)
FIGURE S7 Slices of SYM-REG registration of 5 subjects × 5 warpages obtained with momentum-only regularization. Five slices in the top row show 5 different deformation applied to each of 5 subjects. Five slices in the left column show the original 5 subjects. The remaining 5 × 5 panel of slices show the final SYM-REG registration results with momentum-only regularization, i.e. using Equations (19), (20) and (21) for grid updates
FIGURE S8 Listing of warpage 1—differential rotation with the amount of rotation proportional to the distance from the center in the axial plane (whirl). Applied to undeformed grid mesh and then used to warp each of the five subjects
FIGURE S9 Listing of warpage 2—differential stretch in the anterior direction. Applied to undeformed grid mesh and then used to warp each of the five subjects
FIGURE S10 Listing of warpage 3—differential rotation with the amount of rotation proportional to the distance from the axial plane in the longitudinal direction (twist). Applied to undeformed grid mesh and then used to warp each of the five subjects
FIGURE S11 Listing of warpage 4—nonuniform compression in the axial plane proportional to the the longitudinal distance. Applied to undeformed grid mesh and then used to warp each of the five subjects FIGURE S12 Listing of warpage 5—nonuniform compression in the longitudinal direction relative to the position in the axial plane. Applied to undeformed grid mesh and then used to warp each of the five subjects.


