Avascular tumour growth models based on anomalous diffusion

Abstract

In this study, we model avascular tumour growth in epithelial tissue. This can help us to understand that how an avascular tumour interacts with its microenvironment and what type of physical changes can be observed within the tumour spheroid before angiogenesis. This understanding is likely to assist in the development of better diagnostics, improved therapies, and prognostics. In biological systems, most of the diffusive processes are through cellular membranes which are porous in nature. Due to its porous nature, diffusion in biological systems are heterogeneous. The fractional diffusion equation is well suited to model heterogeneous biological systems, though most of the early studies did not use this fact. They described tumour growth with simple diffusion-based model. We have developed a spherical model based on simple diffusion initially, and then the model is upgraded with fractional diffusion equations to express the anomalous nature of biological system. In this study, two types of fractional models are developed: one of fixed order and the other of variable order. The memory formalism technique is also included in these anomalous diffusion models. These three models are investigated from phenomenological point view by measuring some parameters for characterizing avascular tumour growth over time. Tumour microenvironment is very complex in nature due to several concurrent molecular mechanisms. Diffusion with memory (fixed as well as variable) formation may be an oversimplified technique, and does not reflect the detailed view of the tumour microenvironment. However, it is found that all the models offer realistic and insightful information of the tumour microenvironment at the macroscopic level, and approximate well the physical phenomena. Also, it is observed that the anomalous diffusion based models offer a closer description to clinical facts than the simple model. As the simulation parameters get modified due to different biochemical and biophysical processes, the robustness of the model is determined. It is found that the anomalous diffusion models are moderately sensitive to the parameters.

Introduction

A tumor is a group of cells with genetic or epigenetic defects, growing uncontrollably and in uncoordinated manner. It can be categorized into malignant and benign. Malignant tumours have the ability to penetrate into the surrounding tissues. This quality makes it more dangerous than the benign one. After the formation of a lump of cells, tumour depends upon the surrounding microenvironment for absorbing glucose, oxygen (nutrients) and growth factors (GFs) as it does not have direct blood vessels support. In avascular stage, the growth of a tumour is restricted due to limited supply of nutrients and GFs. To grow further, it needs direct blood vessel support for having sufficient nutrients and GFs. Hence, it must undergo angiogenesis (vascularization) [1–3]. During angiogenesis, tumour-induced capillaries grow from the nearby existing blood vessels towards the tumour, and form a local vascular network for supplying nutrients and GFs. Direct access to nutrients and GFs helps the tumour to expand unboundedly, which becomes fatal to the host over the time. Unbounded growth helps the tumour to penetrate into the nearby blood vessels or organs to disturb their functionalities (invasion). During this phase, tumour cells might become detached from their source singly or collectively, and enter into nearby blood vessels (intravasation) [4] through which they spread into different body parts. The circulating tumour cells which are able to survive from the immune surveillance, blood flow, etc. may get arrested to the vascular endothelium within the vessels at the distant sites of the body. These arrested cells may form secondary colonies (metastasis) [4] and penetrate into other organs thereby threatening the host.

Many biochemical processes and biophysical stresses work in a coordinated manner in this phase. The tumour takes necessary nutrients and GFs (such as epidermal growth factor (EGF) frequently found in non-small lung tumour [5, 6] and breast cancer [7, 8], and it is secreted by the surrounding stromal cells [9]) from the nearby blood vessels through the extracellular matrix (ECM). As a result, a fluid flux is generated within the tumour towards its centre due to the movement of nutrients and GFs molecules from the surrounding microenvironment. The tumour cells absorb these molecules to persist its growth. Hence, a cell flux has been formed in the outward direction throughout the tumour to expand its volume (Fig. 1(a)). Due to over-metabolism, requirement of nutrients and GFs among the tumour cells gradually increases with tumour volume, but it can absorb necessary substances proportional to its surface area [10].

Fig. 1.

Cell flux and fluid flux in different phases a early b intermediate and c long-time of avascular tumour growth (flux schema inspired by those described by Macklin [12])

Due to over-consumption of nutrients and GFs, their levels gradually decrease inside the tumour cells, especially in the innermost area of the tumour [11]. The deficiency level increases with the distance from the outer surface of the tumour towards its centre. At the centre, the deficiency level will be the maximum (below the threshold level). Also, the tumour has an upper bound in size (critical size) up to which it can grow before it experiences nutrients deficiency (hypoxia). This situation creates a layer of proliferative cells at the outer surface and a core of hypoxic cells at the centre of the tumour (Fig. 1(b)). If deficiency is further increased, some portions of the hypoxic cells near the tumour centre become necrotic and develop a core of dead cells. On the other hand, hypoxic cells release some chemical substrates (tumour angiogenic factors, growth inhibitory factors, etc.) to reduce the tumour volume [12]. This creates another fluid flux to the outward direction. These opposite fluxes decrease the mechanical stress on the necrotic core and help it to expand further.

These synchronized processes divide the tumour into different cellular layers: the outer layer mostly consists of proliferative cells, and the innermost layer contains only the dead cells due to necrosis. The layer existing in-between is called the quiescent layer (Fig. 1(c)). The boundaries among these layers are not clearly distinguishable (Fig. 2) [13]. As the volume of tumour grows, the volume of its necrotic core also increases. Once the tumour reaches its critical size, the cell flux and the fluid flux balance each other, and the avascular spheroid reaches a steady state. It cannot grow further without absorbing nutrients and GFs directly from the blood vessel (vascularization). The cells belonging to the quiescent layer are alive but do not divide; however, they become proliferative again if the surrounding microenvironment is suitable for them [14]. In this phase, an avascular tumour spheroid grows up to 2 mm in diameter before it experience angiogenesis [11, 15–17] and it consists of approximately 10⁶–10⁷ number of cells [16, 18].

Fig. 2.

2-D view of avascular tumour at different time intervals (black, green and blue coloured cells are indicating necrotic quiescent and proliferative cells, respectively)

Avascular tumours have great clinical importance. Tumour volume and volume doubling time (VDT) are the important parameters from clinical point of view. VDT refers to the time a tumour takes to double its volume. Shorter VDT indicates the aggressiveness of the tumour [19]. VDT not only may vary between different types of tumours but also it may vary for the same type of tumours in different entities. As an example, for the lung tumours, VDT may vary between 150 to 400 days, whereas for small cell lung tumour VDT is less than 100 days [20]. But there are exceptions too, i.e., the tumour spheroid which remains stable for the last 2 years does not guarantee that it is a benign tumour as some of the malignant tumours have a long VDT [20]. It is clinically said that the cancer patients whose VDT are over 200 days have a better prognosis. Oncologists have estimated that almost 30 VDTs are required for a tumour to grow up to 2 mm in diameter (See, for example, https://notesofoncologist.com/2018/02/26/how-fast-do-tumours-grow/.)

Tumour growth modelling over the last two decades has become a growing field of research. Intricacies of most of the biochemical and biophysical phenomena regarding tumour growth and its progression are less understood. Researchers have developed various models to explain avascular tumour growth from different perspectives. Greenspan [21] has developed the first-ever tumour growth model with proliferative, quiescent and necrotic cell layers that were regulated by mitotic inhibitors and necrotic decomposition. The model incorporated various phases of growth leading to saturation. Later, many researchers have adapted this framework and tried different modifications and advancements on it.

Ward and King [22] have developed a model for avascular tumour growth that is based on diffusion theory. In this model, the tumour growth is directly influenced by the nutrient concentrations in the microenvironment. The model considered that cell death is a gradual process, and it does not depend on the local nutrients level. The tumour volume changes with the growth of its cells. Cell death creates a velocity field in the continuum of live cells. In another study, Ward and King [23] have extended the previous work [22] by including a physical mechanism for growth saturation. In this work, authors have assumed that, for reproduction, a tumour cell depends on cellular materials such as proteins, DNA, lipid (due to the breakdown of necrosis or external tissue in vivo) and nutrients and other growth factors (in vitro). Two mechanisms have been proposed for the reduction of cellular materials, and loss of the volumes: first, the leakage of cellular material by diffusion to the ECM, and second, the consumption of cellular materials for constructing new cells. Sherratt and Chaplain [24] have developed a 1-D spatio-temporal model for avascular tumour which grows in epithelium. The model was developed in terms of different cell densities like proliferative, quiescent and necrotic with contact inhibition. The tumour growth is driven by the cell movements due to nutrient concentrations. The model considered that the different cell-layer boundaries are not sharply distinguishable.

Smallbone et al. [25], Kiran et al. [26], Grimes et al. [27], and Grimes et al. [28] have considered that different cell layers in the tumour are distinctly identifiable. Smallbone et al. [25] have developed a three-dimensional model to examine the effect of acidosis on avascular tumour cell populations. Kiran et al. [26] have established a continuum model based on diffusion. They have considered that the tumour is spherical in shape and its growth depends on the diffusive nutrients across the contiguous tissue. Tumour cells die due to apoptosis as well as necrosis. The authors have also measured the radii of quiescent and necrotic zones and validated the measurement with the available data in vitro and Gompertzian empirical relationship parameters. Grimes et al. [27] have built reaction-diffusion models to study the effect of oxygen consumption rates in tumour cells at different oxygen tensions. In another study, Grimes et al. [28] have examined the oxygen dynamics within the tumour spheroids, and concluded that the cell doubling time and oxygen consumption rate can be enough to define tumour growth.

Transportation in biological system is a critical issue in biophysics because of the structural porosity of cellular membranes [29–32] and the ECM [33]. Transport process through biological membranes and the ECM are governed by their structural heterogeneity rather than the external concentrations. Researchers deal with it by determining the concentration profile within the cellular membrane while the concentration of flowing solute outside of the membrane itself, either on both sides or on a simple face of the membrane [34]. In general, researchers have been using Fick’s law of diffusion with a constant diffusion coefficient. But this consideration is not always correct due to porous in nature of the medium [35]. Further, the memory of the concentration profile may vary over the time and is also a relevant issue in biological transportation [34].

In this study, we focus on avascular tumour in epithelial tissue, and consider that it is spherical in shape. Nutrients, EGF and fibronectin (component of ECM) in the microenvironment synthesize the structural support of the tumour cells and stimulate the tumour cells to proliferate and migrate. Therefore, tumour cell migration is influenced by the diffusive (analogous to molecular diffusion), chemotactic (in response to the gradient created by EGF) and haptotactic (in response to the gradient created by fibronectin) fluxes. In this research, initially, we develop a continuum spherical model based on the diffusion equation depending on the above consideration by allowing overlapped boundaries between different cell layers in the Section 2.

Transportation across the biological membrane is anomalous due to its structural heterogeneity and porosity [35]. Jiang et al. [36] have found different migratory patterns from the clinical images of the tumours. They have observed different types of diffusion in tumour cells like sub-diffusion, super-diffusion or even ballistic diffusion. In this study, we try to exploit this anomalous feature of diffusion which is responsible for transporting nutrients, growth factors and different proteins [37] across the cell membranes and the ECM. The fractional diffusion equation (FDE) is one of the popular techniques to model anomalous diffusion [38, 39]. The advantages of this approach to model the transport processes in complex systems are discussed in [40]. Caputo and Cametti [34] have proposed an extension (diffusion with memory) based on Fick’s diffusion equation from phenomenological point of view to handle the transport process in biological system without considering the internal structure. In this study, we adopt the memory formalism technique, and modify our simple model in the sub-section 3.1 to encounter anomalousness in the diffusion. In order to simulate the memory formalism, partial differential equations of fractional order space derivatives are included [41].

It is found that fixed order-FDE (FO-FDE) have received wonderful success in case of anomalous transportation in heterogeneous environment [42]. However, Kobelev et al. [43] have illustrated that systems with anomalous diffusion have multi-fractal properties, and the memory in certain physical systems vary with special and temporal domains. Therefore, Kobelev et al. [43] and Atangana and Secer [42] have suggested to use VO-FDE to model anomalous diffusion phenomena in biological medium. Hence, the modifications of FO-FDE model are developed by including VO-FDE in the sub-section 3.2. A suitable parameter is also included to capture skewness in the anomalous diffusive process in the fractional models (FO-FDE and VO-FDE). We study all of these three models (simple diffusion model, FO-FDE model and VO-FDE model) from phenomenological and clinical point of views by measuring parameters like tumour radius, tumour volume and VDT.

This paper is organized as follows: Section 2 describes a simple diffusion-based spherical model; Section 3 describes fractional models to capture the anomalous behaviour in tumour microenvironment. Parameter estimation, simulation and results of these three models are described in Section 4. Section 5 illustrates different characteristics, clinical effectiveness and robustness of these models. Section 6 concludes the paper.

Simple diffusion model

In this study, our focus is on the avascular tumour growth in the epithelium tissue. In this section, we develop a 3-D model in terms of three different cell densities. We use P(x, y, z, t), Q(x, y, z, t) and N(x, y, z, t) to denote the concentration of proliferative, quiescent and necrotic cells, respectively. Here, t denotes the time and x, y and z are the spatial coordinates in three-dimensional domain. The centre of the tumour is at x = 0, y = 0, and z = 0. Tumour-cell migration is influenced by diffusive, chemotactic, and haptotactic fluxes. The proliferative and quiescent cells both have motile abilities and it is assumed that both are equally sensitive to the chemosensory and haptotactic signals. The interplay among the proliferative and quiescent cells is triggered due to the changes in the nutrients and EGF concentrations. It is considered that boundaries of different cell layers are not clearly distinguishable. Transformation rates of proliferative cells into the quiescent and the quiescent cells into necrotic are influenced by the nutrients (C) and EGF (E) concentration levels. Proliferative and quiescent cells are both alive but only the proliferative cells have mitosis abilities. Hence, it is assumed that the proliferative cells consume more nutrients and GFs than the quiescent cells. When the nutrients and EGF concentrations reduce below a certain level within the tumour, hypoxic cells near the centre become necrotic gradually. As the necrotic cells are the dead cells with no motile ability hence, no flux effects are considered. Moreover, it is created from the quiescent cells due to hypoxia; therefore, only source term in the equation of necrotic cell is sufficient [24]. We also assume that proliferative and quiescent cells have the same apoptosis (programmed cell death) rate, i.e. d_P = d_Q. The model ignores the fact that hypoxic cells release a number of chemical substrates to reduce tumour volume and also does not consider that proliferative cells secrets matrix metalloproteinases (MMPs) to degrade and remodel the ECM. Hence, the governing PDEs for proliferative, quiescent, and necrotic cells are as follows:

1a

1b

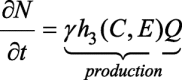1c

In the above Eqs. (1a)–(1c), D_P and D_Q are the diffusion coefficients of proliferative and quiescent cells; α, β and γ are the scalars controlling the production and loss terms of proliferative, quiescent and necrotic cells, respectively. η and ρ are the chemotactic and haptotactic coefficients used in (1a) and (1b) as we assume that chemosensory signal and haptotactic adhesiveness equally effect on the proliferative and quiescent cells.

In the above equations, we need to define functions h₁(.), h₂(.) and h₃(.) which are associated with the source and the loss term of proliferative, quiescent, and necrotic cell concentrations, respectively. These three functions should vary with nutrients and EGF concentration. If either nutrients or EGF or both reduce to 0 (i.e. either C = 0 or E = 0 or C = 0 and E = 0), then proliferative cell would not grow (Fig. 3(a)) (source term of Eq. (1a) will be 0). On the other hand, the functions h₂(.) and h₃(.) will be decreasing gradually and reaches to 0 with nutrient or EGF or both increase to + ∞ (Fig. 3(b) [24]. The definitions of the functions are represented below,

$$h_1\left(C,E\right)=C\times E;h_2\left(C,E\right)=h_3\left(C,E\right)=\frac{exp\left(-\frac{C\times E}{0.25}\right)}{1+exp\left(-\frac{C\times E}{0.25}\right)}.$$

Fig. 3.

Nature of the functions ah1(.) and bh2(.) with respect to (C.E)

In this model, we consider nutrients (C(x, y, z, t)) and EGF (E(x, y, z, t)) concentration diffuse through the ECM from the nearby blood vessels towards the tumour. As the tumour is assumed to be spherical in shape, nutrients and GFs move through all the cells from the outer surface towards the centre of the tumour hence, the PDEs corresponding to the nutrients and EGF are the following:

1d

1e

In the above Eqs. (1d) and (1e), D_C and D_E are the diffusion coefficients of nutrients and EGF, respectively; μ_C and μ_E are the production rates of nutrients and EGF, respectively, in the microenvironment. k₁, k₂, k₃ and w₁, w₂, w₃ are positive constant represent the uptake coefficient of nutrients and EGF.

During the tumour growth, tumour cells migrate through the ECM which is a collection of interstitial tissue, collagen fibres, fibronectin and etc. [44, 45]. Fibronectin can be found as insoluble form in the ECM and the basement membrane of cells (cellular fibronectin) [46]. The cellular fibronectin does not diffuse but bound to the ECM [46, 47], and its main function is to increase the cell-matrix adhesion [48, 49]. Tumour cells use the fibronectin to attach to the ECM with integrins (haptotaxis) [46, 50, 51].

Smith et al. [52], have found fibronectin predominantly in primary carcinomas during epithelial cell culture. In this research, it is considered that both proliferative and quiescent cells produce and secrete fibronectin. However, the rates of productions are different. It is considered that the fibronectin production rate of proliferative cells is higher than the quiescent cells. As the secreted fibronectin does not diffuse [46, 47], the diffusion term is not required in the equation. There is some uptake and binding of fibronectin to the proliferative and quiescent cells. Hence, the equation is as follows:

1f

In the above Eq. (1f), μ_FP and μ_FQ are the production rates of fibronection in the microenvironment and μ_FP > μ_FQ. Uptake coefficient z₁ and z₂ are positive constants.

Using spherical symmetry, Eqs. (1a) – (1f) are reduced to Eq. (2). Hence, proliferative cells, quiescent cells, necrotic cells, nutrients and EGF concentration, and fibronectin are represented as P(r, t), Q(r, t), N(r, t), C(r, t), E(r, t), and F(r, t), respectively, where r represents radius of the sphere, and t represents time.

$$\left(\begin{array}{c}\frac{\partial P}{\partial t}=\frac{\partial }{\partial r}\left(D_P\frac{\partial P}{\partial r}-\mathit{\eta P}\frac{\partial E}{\partial r}-\mathit{\rho P}\frac{\partial F}{\partial r}\right)+\frac{2}{r}\left(D_P\frac{\partial P}{\partial r}-\mathit{\eta P}\frac{\partial E}{\partial r}-\mathit{\rho P}\frac{\partial F}{\partial r}\right)+\alpha h_1\left(C,E\right)P-\beta h_2\left(C,E\right)P-d_{P}P\\ \frac{\partial Q}{\partial t}=\frac{\partial }{\partial r}\left(D_Q\frac{\partial Q}{\partial r}-\mathit{\eta Q}\frac{\partial E}{\partial r}-\mathit{\rho Q}\frac{\partial F}{\partial r}\right)+\frac{2}{r}\left(D_Q\frac{\partial Q}{\partial r}-\mathit{\eta Q}\frac{\partial E}{\partial r}-\mathit{\rho Q}\frac{\partial F}{\partial r}\right)+\beta h_2\left(C,E\right)P-\gamma h_3\left(C,E\right)Q-d_{Q}Q\\ \frac{\partial N}{\partial t}=\gamma h_3\left(C,E\right)Q\\ \frac{\partial C}{\partial t}=\frac{\partial }{\partial r}\left(D_C\frac{\partial C}{\partial r}\right)+\frac{2}{r}\left(D_C\frac{\partial C}{\partial r}\right)+{\mu }_{C}C-k_{1}C-k_2\mathit{CP}-k_3\mathit{CQ}\\ \frac{\partial E}{\partial t}=\frac{\partial }{\partial r}\left(D_E\frac{\partial E}{\partial r}\right)+\frac{2}{r}\left(D_E\frac{\partial E}{\partial r}\right)+{\mu }_{E}E-w_{1}E-w_2\mathit{EP}-w_3\mathit{EQ}\\ \frac{\partial F}{\partial t}={\mu }_{\mathit{FP}}P+{\mu }_{\mathit{FQ}}Q-z_1\mathit{FP}-z_2\mathit{FQ}\end{array}\right\}$$ 2

We assume that the minimum distance from the tumour centre (r = 0) to the nearest blood vessel is l. Hence, a sphere of radius l is considered as the domain of our study in which the tumour has grown. Here, r is the radial direction from the centre (r = 0) towards the boundary (r = l) of the spherical-shaped domain. The tumour cells and the fluid concentrations within the spherical domain from r = 0 to r = l is under consideration. We non-dimensionalize Eq. (2) by rescaling the distance l with time τ = l²/D_C. Proliferative cell, quiescent cell, necrotic cell, nutrients and EGF concentrations, and fibronectin are rescaled with P₀, Q₀, N₀, C₀, E₀, and F₀, respectively (where P₀, Q₀, N₀, C₀, E₀, and F₀ are the appropriate reference variables). After the non-dimensionalization (the non-dimensionalization process is described in Appendix A), we get a new system of Eq. (3).

$$\left(\begin{array}{c}\frac{\partial P}{\partial t}=\frac{\partial }{\partial r}\left(D_{\mathit{PC}}\frac{\partial P}{\partial r}-\mathit{\eta P}\frac{\partial E}{\partial r}-\mathit{\rho P}\frac{\partial F}{\partial r}\right)+\frac{2}{r}\left(D_{\mathit{PC}}\frac{\partial P}{\partial r}-\mathit{\eta P}\frac{\partial E}{\partial r}-\mathit{\rho P}\frac{\partial F}{\partial r}\right)+\alpha h_1\left(C,E\right)P-\beta h_2\left(C,E\right)P-d_{P}P\\ \frac{\partial Q}{\partial t}=\frac{\partial }{\partial r}\left(D_{\mathit{QC}}\frac{\partial Q}{\partial r}-\mathit{\eta Q}\frac{\partial E}{\partial r}-\mathit{\rho Q}\frac{\partial F}{\partial r}\right)+\frac{2}{r}\left(D_{\mathit{QC}}\frac{\partial Q}{\partial r}-\mathit{\eta Q}\frac{\partial E}{\partial r}-\mathit{\rho Q}\frac{\partial F}{\partial r}\right)+\omega h_2\left(C,E\right)P-\gamma h_3\left(C,E\right)Q-d_{Q}Q\\ \frac{\partial N}{\partial t}=\lambda h_3\left(C,E\right)Q\\ \frac{\partial C}{\partial t}=\frac{{\partial }^{2}C}{\partial r^2}+\frac{2}{r}\frac{\partial C}{\partial r}+{\mu }_{C}C-k_{1}C-k_2\mathit{CP}-k_3\mathit{CQ}\\ \frac{\partial E}{\partial t}=\frac{\partial }{\partial r}\left(D_{\mathit{EC}}\frac{\partial E}{\partial r}\right)+\frac{2}{r}\left(D_{\mathit{EC}}\frac{\partial E}{\partial r}\right)+{\mu }_{E}E-w_{1}E-w_2\mathit{EP}-w_3\mathit{EQ}\\ \frac{\partial F}{\partial t}={\mu }_{\mathit{FP}}P+{\mu }_{\mathit{FQ}}Q-z_1\mathit{FP}-z_2\mathit{FQ}\end{array}\right\}$$ 3

Anomalous diffusion

Diffusion is one of the main transport mechanisms in the evolution of many non-equilibrium systems towards equilibrium [53]. In diffusion, particles are displaced from the high-concentration area to the low-concentration area. The underlying process of diffusion is the Brownian motion. The probability density function which controls the Brownian motion of a particle, follow the Gaussian curve, and the mean squared displacement (MSD) or variance (σ²) is proportional to the first power of time (linear relationship) (Fig. 4). However, in case of complex (anomalous) domain, the variance is no longer proportional to the first power of time (anomalous diffusion) [53, 54] rather proportional to the fractional power of time (non-linear relationship) (Fig. 4).

Fig. 4.

Variance (σ2) for different types of anomalous diffusion

Biological systems are very complex and dynamic. As noted in the paragraph above, in biological systems, diffusion is one of the crucial transport mechanisms to transport nutrients and other proteins [37] through the cell membrane. Cellular membranes govern the sorption, desorption or translocation of selective particles from one place to another. Moreover, it ensures the transport and balance of essential molecules and ions (important for maintaining life) between its inner and outer regions [55, 56]. Investigation of diffusive processes in biological system reveal that cell membranes are porous in nature [29–32, 35] Gal and Weihs [35]). Structural heterogeneity and porosity of biological membrane are the main causes of the anomalous behaviour [57]. Transport of nutrients and other essential molecules across the cell membrane are sensitive to the porosity in all scales, and this can affect the behaviour at larger scales [58].

Researchers commonly use Fick’s law-based diffusion or advection-diffusion equation (ADE) to describe the transportation process across porous medium [58, 59]. But recent research outcomes [35, 36] show that transportation through the porous media (cellular membrane) is anomalous or non-Fickian with skewness [60–64]. Jiang et al. [36] have identified different migratory patterns from the clinical images of the tumours, which were collected in Sun Yat-sen University Cancer Center. They have observed that the invasive liver tumour spread in faster rate (characteristic of super-diffusion or even ballistic diffusion) than the adrenal tumour (characteristic of sub-diffusion). From this phenomena, they have concluded that the rate of tumour expansion is varied rapidly depending upon its niche.

The simple diffusion is not suitable to model these types of phenomena as it converges faster to the support than what is expected [65–67]. Moreover, the memory of concentration profile changes over the time, which is also a relevant issue in biological transportation [34, 43]. Diffusion with memory denotes that the function considers the past behaviour of itself by adding the initial value with the corresponding weighted increments over the time [34, 43]. Simple diffusion model cannot address this issue.

Scientists use nonlinear modelling to model anomalous diffusion, though it is very difficult to analyse and computationally expensive [54]. Fractals or fractional derivatives are used as an alternative approaches to handle anomalous diffusive phenomena [54, 68] because its rate of convergence to the support is varied with the order of the derivative. Also, it can describe the inherent abnormal-exponentials or heavy tail decay processes (skewness). Moreover, the parameters of the fractional derivative models have physical significance. Though it is computationally expensive like nonlinear equations, there are several methods available based on fractional derivative to model anomalous diffusion like the continuous-time random walk [57, 69], non-local stochastic transport theories [70, 71], fractional advection-diffusion equation (FADE) or FDE [38, 39] and etc.

Diffusion coefficient can be considered a constant in ideal conditions in which (a) diameter and shape of the molecules are similar for the diffusing components, (b) the molecular interactions between diffusing components are negligible (no attraction or repulsive forces are present) and (c) environment is non-reacting [72]. But the transportation processes across porous medium like cell membranes and ECM are governed by the complex structures of the surroundings. These phenomena illustrate that the diffusion processes through the cell membranes and ECM are medium dependent, indicating a space as well as time-dependant diffusion coefficient [34, 43].

In this paper, we adopt memory-based diffusion process [34, 43] by including fractional order space derivative in our model and also assume that diffusion coefficient of tumour cells are nutrients dependent, and the diffusion coefficients nutrients and EGF are fibronectin (ECM) dependent. Therefore, we modify the system of Eq. (3) based on the above considerations, and present the FO-FDE (fixed memory based) as well as the VO-FDE (variable memory based) model in sub-sections 3.1 and 3.2, respectively.

Fixed order fractional diffusion model

In this sub-section, a continuum model with coupled FO-FDE is presented (with fractional order φ and ξ where 1 < φ ≤ 2 and 0 < ξ ≤ 1) from the phenomenological point of view for different types of tumour cells (proliferative, quiescent and necrotic), nutrients and EGF concentration and fibronectin. In this case, space fractional derivatives are included. A suitable parameter (θ) is also incorporated in the anomalous model to handle the skewness in the diffusion.

We assume diffusion coefficients of proliferative and quiescent cells are varied with nutrient concentrations in the porous medium. In Brownian motion, movement of a particle depends on its energy like in tumour microenvironment, nutrients is one of the sources that supplies energy to the tumour cells. From this analogy, we assume that if the domain is full of nutrients then the cell diffusion coefficient would be as high as the value of ‘e’. With the reduction of nutrient in the domain, the diffusion coefficients of proliferative and quiescent cells gradually decrease, and it reduces to 1 in non-linear fashion (Fig. 5(a)). On the other hand, we consider that diffusion coefficients of nutrients and EGF are varied with the fibronectin (a component of the ECM). At the initial phase when no fibronectin are present in the domain, the diffusion coefficients of nutrients and EGF will be as high as the value of ‘e’. With the increment of fibronectin in the domain, the coefficients reduce to 1 non-linearly when fibronectin increases to 1 and beyond that (Fig. 5(b)). From these assumptions, we consider,

$$\left(\begin{array}{c}\text{Diffusion coefficient of cells}\propto h\left(C\right)\\ \text{Diffusion coefficient of fluids}\propto f\left(F\right)\end{array}\right\}$$ 4

Fig. 5.

Nature of the function ah(.) with respect to C and bf(.) with respect to F for different values of ψ

According to (4), we consider

$$\left(\begin{array}{c}{D}_{\mathit{PC}}^{\prime }=D_{\mathit{PC}}h\left(C\right);\text{and}{D}_{\mathit{QC}}^{\prime }=D_{\mathit{QC}}h\left(C\right)\\ D_{\mathit{CC}}^{\prime }=D_{\mathit{CC}}f\left(F\right);\text{and}{D}_{\mathit{EC}}^{\prime }=D_{\mathit{EC}}f\left(F\right)\end{array}\right\}$$ 5

$$\begin{array}{c}\left(\begin{array}{c}\text{where},h\left(C\right)=\left\{\begin{array}{c}exp\left(C\right)\text{if}C\le 1\\ exp\left(1\right)\text{Otherwise}\end{array}\right)\\ \text{and}f\left(F\right)=\left\{\begin{array}{c}exp{\left(1-F\right)}^{\psi }\text{if}F\le 1\\ exp\left(0\right)\text{Otherwiese}\end{array}\right)\end{array}\right\}\\ \text{where}1\le \psi \le 2\end{array}$$ 6

In Eq. (5), D_PC, D_QC, D_CC, and D_EC are the constant coefficients described in Appendix A1.

Anomalous diffusion is one of the primary transport processes across the biological membrane [37]. In this sub-section, we modify the proposed simple diffusion model (Eq. (3)) and develop a fixed memory-based model to handle anomalous diffusion. Memory formalism technique has been adopted and included in the model by using PDEs of fractional order space derivative [41]. Zhang et al. [73, 74], system of Eq. (3) can be modified with the fractional flux DE and variable diffusion coefficients (Eq. (5)) in spherical domain as,

$$\frac{\partial P}{\partial t}=D_{\mathit{PC}}\left\{h\left(\frac{{\partial }^{\phi }P}{\partial r^{\phi }}+\frac{2}{r}\frac{{\partial }^{\xi }P}{\partial r^{\xi }}\right)+A_1\left(\frac{{\partial }^{\xi }P}{\partial r^{\xi }}+\frac{2}{r}P\right)\right\}-\left\{\frac{{\partial }^{\xi }P}{\partial r^{\xi }}{A}_2+\frac{2}{r}P{A}_2+P{A}_3\right\}+\alpha h_1\left(C,E\right)P-\beta h_2\left(C,E\right)P-d_{P}P$$ 7a

$$\frac{\partial Q}{\partial t}=D_{\mathit{QC}}\left\{h\left(\frac{{\partial }^{\phi }Q}{\partial r^{\phi }}+\frac{2}{r}\frac{{\partial }^{\xi }Q}{\partial r^{\xi }}\right)+A_1\left(\frac{{\partial }^{\xi }Q}{\partial r^{\xi }}+\frac{2}{r}Q\right)\right\}-\left\{\frac{{\partial }^{\xi }Q}{\partial r^{\xi }}{A}_2+\frac{2}{r}Q{A}_2+Q{A}_3\right\}+\omega h_2\left(C,E\right)P-\gamma h_3\left(C,E\right)Q-d_{Q}Q$$ 7b

$$\frac{\partial N}{\partial t}=\lambda h_3\left(C,E\right)Q$$ 7c

$$\frac{\partial C}{\partial t}=f\left(\frac{{\partial }^{\phi }C}{\partial r^{\phi }}+\frac{2}{r}\frac{{\partial }^{\xi }C}{\partial r^{\xi }}\right)+A_4\left(\frac{{\partial }^{\xi }C}{\partial r^{\xi }}+\frac{2}{r}C\right)+{\mu }_{C}C-k_{1}C-k_2\mathit{CP}-k_3\mathit{CQ}$$ 7d

$$\frac{\partial E}{\partial t}=D_{\mathit{EC}}\left\{f\left(\frac{{\partial }^{\phi }E}{\partial r^{\phi }}+\frac{2}{r}\frac{{\partial }^{\xi }E}{\partial r^{\xi }}\right)+A_4\left(\frac{{\partial }^{\xi }E}{\partial r^{\xi }}+\frac{2}{r}E\right)\right\}+{\mu }_{E}E-w_{1}E-w_2\mathit{EP}-w_3\mathit{EQ}$$ 7e

$$\frac{\partial F}{\partial t}={\mu }_{\mathit{FP}}P+{\mu }_{\mathit{FQ}}Q-z_1\mathit{FP}-z_2\mathit{FQ}$$ 7f

$$\begin{array}{c}\text{where}{A}_1=\left(\frac{{\partial }^{\xi }h}{\partial C^{\xi }}\frac{{\partial }^{\xi }C}{\partial r^{\xi }}\right),A_2=\left(\eta \frac{{\partial }^{\xi }E}{\partial r^{\xi }}+\rho \frac{{\partial }^{\xi }F}{\partial r^{\xi }}\right),A_3=\left(\eta \frac{{\partial }^{\phi }E}{\partial r^{\phi }}+\rho \frac{{\partial }^{\phi }F}{\partial r^{\phi }}\right)\\ \text{and}{A}_4=\left(\frac{{\partial }^{\xi }f}{\partial F^{\xi }}\frac{{\partial }^{\xi }F}{\partial r^{\xi }}\right).\end{array}$$

In Eq. (7a)–(7f), all the parameters are in non-dimensionalized form, and has been described in the Section 2. In Section 2, h₁, h₂ and h₃ are also defined. Here, we use h instead of h (C) and f instead of f (F) .

In (7a), $\frac{{\partial }^{\phi }P}{\partial r^{\phi }}\text{and}\frac{{\partial }^{\xi }P}{\partial r^{\xi }}$are the fractional derivatives with respect to r and 1 < φ ≤ 2 and 0 < ξ ≤ 1 (where ξ = φ – 1) are the fractional orders. The derivatives have been approximated by [38, 58] as shown in Eq. (8).

$$\left(\begin{array}{c}\frac{{\partial }^{\phi }P}{\partial r^{\phi }}\approx \left(\frac{1+\theta }{2}\right)D_L^{\phi }\left(P\right)+\left(\frac{1-\theta }{2}\right)D_R^{\phi }\left(P\right),1<\phi \le 2\\ \frac{{\partial }^{\xi }P}{\partial r^{\xi }}\approx \left(\frac{1+\theta }{2}\right)D_L^{\xi }\left(P\right)-\left(\frac{1-\theta }{2}\right)D_R^{\xi }\left(P\right),0<\xi \le 1\end{array}\right\}$$ 8

In Eq. (8), θ (− 1 ≤ θ ≤ 1) is the skewness parameter which controls the bias of the diffusion. It reflects the relative weight of forward versus backward transition probability. If φ = 2 and θ = 0, then it indicates no skewness exists in the diffusion (i.e. Fick’s law of diffusion). If θ < 0, then, the dispersion will be skewed backward, a slow evolving contaminant plume followed by a heavy tail, whereas θ > 0 indicates a forward dispersion, a fast evolving contaminant plume followed by a light tail.

In (8), $D_L^{\phi }\text{and}{D}_R^{\phi }\left(D_L^{\xi }\text{and}{D}_R^{\xi }\right)$ are the left- and right-handed fractional derivatives, respectively. L = 1 and R = 2 $\left(D_L^{\phi }\text{and}{D}_R^{\phi }\right)$ are the corresponding lower and upper bounds of φ. L = 0 and R = 1 $\left(D_L^{\xi }\text{and}{D}_R^{\xi }\right)$are the corresponding lower and upper bounds of ξ.

Variable order fractional diffusion model

FO-FDE-based model present a non-Markov process with fixed memory [43]. Memory defines a system whose state at particular time depends on its previous behaviour. Memory in certain anomalous system changes with the spatial and temporal domain [34, 43]. Though FO-FDE model shows some advantages over the simple diffusion to model transportation across porous media [34, 70, 71, 75], experimental data indicate that fixed memory-based system (FO-FDE) does not capture the multi-fractal nature of porous media [43]. Therefore, in the case of biological phenomena, it has been suggested to use variable memory-based VO-FDE model [42, 43] for heterogeneous biological media. Hence, we modify our proposed model by including VO-FDE. In this context, we assume that φ = φ(r, t) and ξ = ξ(r, t) in Eq. (7a–f). Now, the space fractional derivative is included in the model from [76],

$$\left(\begin{array}{c}\frac{{\partial }^{\phi \left(r_i,t_k\right)}P}{\partial r^{\phi \left(r_i,t_k\right)}}=\frac{{\partial }^{{\phi }_i^k}P}{\partial r^{{\phi }_i^k}}\approx \left(\frac{1+\theta }{2}\right)D_L^{{\phi }_i^k}\left(P\right)+\left(\frac{1-\theta }{2}\right)D_R^{{\phi }_i^k}\left(P\right),1<\phi \left(r_i,t_k\right)\le 2\\ \frac{{\partial }^{\xi \left(r_i,t_k\right)}P}{\partial r^{\xi \left(r_i,t_k\right)}}=\frac{{\partial }^{{\xi }_i^k}P}{\partial r^{{\xi }_i^k}}\approx \left(\frac{1+\theta }{2}\right)D_L^{{\xi }_i^k}\left(P\right)-\left(\frac{1-\theta }{2}\right)D_R^{{\xi }_i^k}\left(P\right),0<\xi \left(r_i,t_k\right)\le 1\end{array}\right\}$$ 9

In Eq. (9), φ(r_i, t_k) and ξ(r_i, t_k) are the corresponding fractional orders at the i^th radial point at k^th time instance, and θ (−1 ≤ θ ≤ 1) is the skewness parameter. $D_L^{{\phi }_i^k}\text{and}{D}_R^{{\phi }_i^k}\left(D_L^{{\xi }_i^k}\text{and}{D}_R^{{\xi }_i^k}\right)$ are the left- and right-handed fractional derivatives of φ(r_i, t_k) and ξ(r_i, t_k), respectively. L and R are the corresponding lower and upper bounds of φ(r_i, t_k) and ξ(r_i, t_k) like the FO-FDE.

Simulation

We simulate all the models (simple diffusion, FO-FDE and VO-FDE) using the same set of parameters (discussed in the sub-section 4.1) with proper initial and boundary conditions. Then the results of these three models are discussed briefly in the sub-section 4.2.

To solve the simple as well as anomalous diffusion models, proper initial and boundary conditions are required. We assume that, at t = 0, tumour microenvironment is full of nutrients and EGF. The quiescent and necrotic cells are not found in the domain of interest initially except the proliferative cells. In this model, it is assumed that the proliferative and quiescent cells are the only producers of fibronectin. Hence, at t = 0, quantity of fibronectin present in the spatial domain is same as the quantity of proliferative cells. With the above assumptions the following initial conditions are found:

$$\left(\begin{array}{c}P\left(r=i,t=0\right)=\frac{exp\left(-\frac{i}{10}\right)}{100},1\le i\le l;Q\left(r,t=0\right)=0;N\left(r,t=0\right)=0;C\left(r,t=0\right)=1;\\ E\left(r,t=0\right)=1;\text{and}F\left(r=i,t=0\right)=\frac{exp\left(-\frac{i}{10}\right)}{100},1\le i\le l;\text{where}r\in \left[0,l\right]\end{array}\right\}$$ 10

We further consider that, at any time, there is no cell flux at the boundary (at r = 0 and r = l) of the domain of interest, but the boundaries are full of nutrient and EGF concentrations. Fibronectin is produced only by proliferative and quiescent cells (according to our model). Therefore, no fibronectin exists at the boundaries. From these assumptions, we find the boundary conditions:

$$\left(\begin{array}{c}P\left(r=0,t\right)=P\left(r=l,t\right)=0;Q\left(r=0,t\right)=Q\left(r=l,t\right)=0;\\ N\left(r=0,t\right)=N\left(r=l,t\right)=0;C\left(r=0,t\right)=C\left(r=l,t\right)=1;\\ E\left(r=0,t\right)=E\left(r=l,t\right)=1;\text{and}F\left(r=0,t\right)=F\left(r=l,t\right)=0;\end{array}\right\}$$ 11

where t∈(0, T). T is the total simulation time.

Estimation of parameters

For the purpose of simulation, we consider that at the very beginning, nutrients and EGF levels throughout the domain of interest remain uniform. That is at every point in the spherical domain receive equal amount of nutrients and EGF from the source (nearby blood vessels). We simulate the simple diffusion, FO-FDE and VO-FDE-based models with the initial (10) and boundary conditions (11). The values of the used parameters are summarized in Table 1.

Table 1.

Parameter values

Parameter	Meaning	Suggested value	Used values	Reference
DP	Diffusivity of proliferative cells	6.90 × 10−9 cm2 s−1 to 3.50 × 10−11 cm2 s−1	3.50 × 10−11 cm2 s−1	Sherratt and Murray [77]
DQ	Diffusivity of quiescent cells	6.90 × 10−9 cm2 s−1 to 3.50 × 10−11 cm2 s−1	3.50 × 10−11 cm2 s−1	Sherratt and Murray [77]
DC	Diffusivity of nutrients	1.10 × 10−6 cm2 s−1	1.10 × 10−6 cm2 s−1	Casciari et al. [78]
DE	Diffusivity of EGF		1.82 × 10−5 cm2 s−1
dP	Proliferative cell apoptosis rate	4.00 × 10−10 s−1	4.00 × 10−10 s−1	Busini et al. [79]
dQ	Quiescent cell apoptosis rate	4.00 × 10−10 s−1	4.00 × 10−10 s−1	Busini et al. [79]
α	Proliferative cell production rate	1.38 × 10−6 s−1 to 5.92 × 10−5 s−1	1.50 × 10−5 s−1	Burton [80]
β	Proliferative to quiescent transformation rate		1.70 × 10−4 s−1
γ	Quiescent to necrotic transformation rate	3.80 × 10−6 s−1	3.40 × 10−5 s−1	Busini et al. [79]
η	Chemotactic coefficient	2600 cm2 s−1	2600 cm2 s−1	Anderson and Chaplain [81]
ρ	Haptotactic coefficient	2600 cm2 s−1	2600 cm2 s−1	Anderson and Chaplain [81]
μC	Nutrients production rate		1.73 × 10−5 s−1
μE	EGF production rate		1.73 × 10−5 s−1
μFP	Fibronection production rate (proliferative)		1.0 × 10−5 s−1
μFQ	Fibronection production rate (quiescent)		1.15 × 10−6 s−1
w1	Positive parameter		1.0 × 10−5 s−1
w2	Positive parameter		9.25 × 10−4 s−1
w3	Positive parameter		1.15 × 10−4 s−1
k1	Positive parameter		1.0 × 10−5 s−1
k2	Positive parameter		9.25 × 10−4 s−1
k3	Positive parameter		1.15 × 10−4 s−1
z1	Positive parameter		9.25 × 10−4 s−1
z2	Positive parameter		1.15 × 10−4 s−1
l	Radius of spherical domain		2 mm	Anderson and Chaplain [81]
P0	Reference variable (proliferative)		10−10
Q0	Reference variable (quiescent)		2.25 × 10−10
N0	Reference variable (necrotic)		3.375 × 10−10
C0	Reference variable (nutrients)		10−10
E0	Reference variable (EGF)	10−10	10−10	Anderson and Chaplain [81]
F0	Reference variable (fibronectin)	10−10	10−10	Anderson and Chaplain [81]

We have tried to use the values for different parameters from the available data in the literature, as indicated in Table 1. For some parameters, the values were not available. Their values are fixed through trial and error. We have done our computer experiment with spatial scale of 10⁻² mm. For an avascular tumour, the maximum possible radius is 1 mm before it experience angiogenesis. We have considered l = 2 mm (the distance between the tumour centre to the nearest blood vessel) [81]. It is assumed that the diffusivity of living tumour cells (either proliferative or quiescent) is the same as the diffusivity of epithelial cells. In case of avascular tumour, cells migrate due to the nutrients and EGF present in the fluid. Sherratt and Murray [77] have estimated the diffusivity of proliferative cells to be in the range of 6.9 × 10⁻⁹ cm² s⁻¹ to 3.5 × 10⁻¹¹ cm² s⁻¹ in the presence of growth molecules. Also, we take D_P = D_Q = 3.5 × 10⁻¹¹ cm² s⁻¹. The diffusivity of nutrients is taken as D_C = 1.1 × 10⁻⁶ cm² s⁻¹ [78] and EGF concentration as D_E = 1.82 × 10⁻⁶ cm² s⁻¹.

Burton [80] suggested that the tumour proliferation rate should be in the range of 1.38 × 10⁻⁶ s⁻¹ to 5.92 × 10⁻⁵ s⁻¹. Busini et al. [79] suggested the rate of transformation from quiescent to necrotic to be 3.80 × 10⁻⁶ s⁻¹. For this simulation, we have taken proliferation rate (α) to be 9.8 × 10⁻⁶ s⁻¹, and quiescent to necrotic transformation rate (γ) to be 3.4 × 10⁻⁵ s⁻¹. The transformation rate from proliferative to quiescent (β) cell has been taken as (1.70 × 10⁻⁴ s⁻¹) through trial and error as no reference for β is available. The apoptosis rate of proliferative (d_P) and quiescent (d_Q) cells are 4 × 10⁻¹⁰ s⁻¹ [79]. In this study, the values of chemotactic and haptotactic coefficients are taken as 2600 cm² s⁻¹ [81].

Estimation of other parameters like production rates of nutrients (μ_C), EGF (μ_E), fibronectin (μ_FP and μ_FQ) and positive parameters (w₁, w₂, w₃, k₁, k₂, k₃, z₁ and z₂) are very difficult to find clinically. We use production rates of nutrients, EGF and fibronectin as μ_C = μ_E = 1.73 × 10⁻⁵ s⁻¹; and μ_FP = 1.73 × 10⁻⁵ s⁻¹; μ_FQ = 1.15 × 10⁻⁶ s⁻¹. We also take the values of w₁ = k₁ = 1 × 10⁻⁵ s⁻¹; w₂ = k₂ = 9.25 × 10⁻⁶ s⁻¹; w₃ = k₃ = 1.15 × 10⁻⁶ s⁻¹; z₁ = 9.25 × 10⁻⁶ s⁻¹ and z₂ = 1.15 × 10⁻⁶ s⁻¹.

Results

We solve the system of Eqs. (7(a)–7(f)) numerically by combining Eq. (8) with the initial and boundary conditions (10, 11, respectively). We assume t_k = kΔt, 0 ≤ t_k ≤ T, where k = 0, 1, 2, …, n_t$\left(\text{where},n_t=\frac{{\rm T}}{\mathit{\Delta t}}\right)$ and r_i = iΔr, 0 ≤ r_i ≤ l, where i = 0, 1, 2, …, n_r$\left(\text{where},n_r=\frac{l}{\mathit{\Delta r}}\right)$. Grünwald approximated the left-handed as well as the right-handed fractional derivatives in Eq. (8) [82, 83]. By using the discretization rule we get from the Eq. (8),

$$\left(\begin{array}{c}{D}_L^{\phi }\left(P\right)=\frac{{\partial }^{\phi }P}{\partial {\left(r\right)}^{\phi }}=\frac{1}{{\left(\mathit{\Delta r}\right)}^{\phi }}\sum _{\chi =0}^{i+1}{g}_{\chi }{P}_{i-\chi +1}\text{and}{D}_R^{\phi }\left(P\right)=\frac{{\partial }^{\phi }P}{\partial {\left(-r\right)}^{\phi }}=\frac{1}{{\left(\mathit{\Delta r}\right)}^{\phi }}\sum _{\chi =0}^{\chi -i+1}{g}_{\chi }{P}_{i+\chi -1}\\ D_L^{\xi }\left(P\right)=\frac{{\partial }^{\xi }P}{\partial {\left(r\right)}^{\xi }}=\frac{1}{{\left(\mathit{\Delta r}\right)}^{\xi }}\sum _{\delta =0}^{i+1}{g}_{\delta }{P}_{i-\delta +1}\text{and}{D}_R^{\xi }\left(P\right)=\frac{{\partial }^{\xi }P}{\partial {\left(-r\right)}^{\xi }}=\frac{1}{{\left(\mathit{\Delta r}\right)}^{\xi }}\sum _{\kappa =0}^{\delta -i+1}{g}_{\delta }{P}_{i+\delta -1}\end{array}\right\}$$ 12

In Equation (12),

$$g_{\chi }={\left(-1\right)}^{\chi }\frac{\Gamma \left(\phi +1\right)}{\Gamma \left(\chi +1\right)\Gamma \left(\phi -\chi +1\right)}\text{and}{g}_{\delta }={\left(-1\right)}^{\delta }\frac{\Gamma \left(\xi +1\right)}{\Gamma \left(\delta +1\right)\Gamma \left(\xi -\delta +1\right)}$$ 13

${\mathrm{g}}_{\mathrm{\chi }}=\frac{\mathrm{\Gamma }\left(\mathrm{\varphi }+1\right)}{\mathrm{\Gamma }\left(\mathrm{\chi }+1\right)\mathrm{\Gamma }\left(\mathrm{\varphi }-\mathrm{\chi }+1\right)}$Γ(.) Γ(.) in (13) is the Euler gamma function, and Δr is the uniform size of the intervals into which the spatial axis is divided. We have included the fractional derivative on the spatial domain only, and applied forward differencing method for the time domain. The step sizes are considered as Δt = 0.004 and Δr = 1, so that, diffusion stability condition $\left(\frac{\mathit{\Delta t}}{\Delta r^2}\le \frac{1}{2}\right)$ is satisfied for the models.

According to Oncologist's Note [84: https://notesofoncologist.com/2018/02/26/how-fast-do-tumours-grow/], avascular tumours in epithelial tissue grow up to 2 mm in diameter (approx.) over 6 years. In this simulation, we consider, an iteration is equivalent to 1 day. Also, we iterate this process for 2190 times (2190 days = 6 years), and collect the results at the duration of 365 days or 1 year. The models are simulated with θ = 0.5 and ψ = 1.50.

At the initial phase (up to the 2nd year) of the simulation, proliferative cells are mostly concentrated near the centre (Fig. 6(a)). After that, the cells gradually move in the forward direction, and at the end of the simulation (after 6th year of time), the tumor reaches 1.10 mm (approx.) from the centre (values up to 0.01 are considered). This indicates that after 6 years, the radius of the tumour will be 1.10 mm (approx.). With proliferative cells, fibronectin also increases in the tumour microenvironment (Fig. 7(b)). Up to 1 year, there is no sign of quiescent cells. From the 2nd year and onwards, the quiescent cells gradually increase (Fig. 6(b)) due to a steady decrease of nutrients (Fig. 8(a)) and EGF concentration (Fig. 8(b)) within the tumour cells nearer to the centre. After 4 years of time, nutrients and EGF levels further decrease sharply near the centre of the tumour. As a result, quiescent cells (hypoxic) near the centre are transformed into necrotic cells. With time the necrotic core increases rapidly and reaches approximately 0.80 mm (Fig. 7(a)) in radius, whereas the quiescent cells grow approximately 1.02 mm from the tumour centre (Fig. 6(b)). The outer surface of the tumour always contains proliferative cells with higher concentrations. The volume of the necrotic core increases with the radius of the tumour. The overlapping areas (Fig. 9) between different cell layers indicate that boundaries between these layers are not distinguishable. Tumour regression cannot be seen in its life time. The above simulation is done with φ = 1.75, ξ = 0.75 and θ = 0.5.

Fig. 6.

a Proliferative (P/P₀) and b quiescent (Q/Q₀) cell concentration waves at different time intervals with respect to the distance from the tumour centre

Fig. 7.

a Necrotic (N/N₀) cell concentration and b fibronectin (F/F₀) waves at different time intervals with respect to the distance from tumour centre

Fig. 8.

a Nutrients (C/C₀) and b EGF (E/E0) waves at different time intervals with respect to the distance from tumour centre

Fig. 9.

Proliferative, quiescent and necrotic cell concentration waves in the fixed-order fractional diffusion model

We also solve this model (7a) – 7f)) by including VO-FDE numerically using Eq. (9) with the initial (10) and boundary conditions (11). Here, we also assume t_k = kΔt, 0 ≤ t_k ≤ T, where k = 0, 1, 2, …, n_t$\left(\text{where},n_t=\frac{{\rm T}}{\mathit{\Delta t}}\right)$ and r_i = iΔr, 0 ≤ r_i ≤ l, where i = 0, 1, 2, …, n_r$\left(\text{where},n_r=\frac{l}{\mathit{\Delta r}}\right)$. We discretize Eq. (9) using [76],

$$\left(\begin{array}{c}{D}_L^{{\phi }_i^k}\left(P\right)=\frac{{\partial }^{{\phi }_i^k}P}{\partial {\left(r\right)}^{{\phi }_i^k}}=\frac{1}{{\left(\mathit{\Delta r}\right)}^{{\phi }_i^k}}\sum _{\chi =0}^{i+1}{g}_{{\phi }_i^k}^{\left(\chi \right)}{P}_{i-\chi +1}\\ D_R^{{\phi }_i^k}\left(P\right)=\frac{{\partial }^{{\phi }_i^k}P}{\partial {\left(-r\right)}^{{\phi }_i^k}}=\frac{1}{{\left(\mathit{\Delta r}\right)}^{{\phi }_i^k}}\sum _{\chi =0}^{n_r-i+1}{g}_{{\phi }_i^k}^{\left(\chi \right)}{P}_{i+\chi -1}\\ D_L^{{\xi }_i^k}\left(P\right)=\frac{{\partial }^{{\xi }_i^k}P}{\partial {\left(r\right)}^{{\xi }_i^k}}=\frac{1}{{\left(\mathit{\Delta r}\right)}^{{\xi }_i^k}}\sum _{\delta =0}^{i+1}{g}_{{\xi }_i^k}^{\left(\delta \right)}{P}_{i-\delta +1}\\ D_R^{{\xi }_i^k}\left(P\right)=\frac{{\partial }^{{\xi }_i^k}P}{\partial {\left(-r\right)}^{{\xi }_i^k}}=\frac{1}{{\left(\mathit{\Delta r}\right)}^{{\xi }_i^k}}\sum _{\delta =0}^{n_r-i+1}{g}_{{\xi }_i^k}^{\left(\delta \right)}{P}_{i+\delta -1}\end{array}\right\}$$ 14

$$\text{In Equation}\left(14\right),g_{{\phi }_i^k}^{\left(\chi \right)}={\left(-1\right)}^{\chi }\frac{\Gamma \left({\phi }_i^k+1\right)}{\Gamma \left(\chi +1\right)\Gamma \left({\phi }_i^k-\chi +1\right)}\text{and}{g}_{{\xi }_i^k}^{\left(\delta \right)}={\left(-1\right)}^{\delta }\frac{\Gamma \left({\xi }_i^k+1\right)}{\Gamma \left(\delta +1\right)\Gamma \left({\xi }_i^k-\delta +1\right)}$$ 15

In variable order simulation, the order of the equation is restricted. Therefore, we use the value of φ which varies in between$\left(1.55\le {\phi }_i^k\le 1.95\right)$ for the simulation. Therefore, we assume that ${\phi }_i^k=1.75+0.2\times sin\left(\frac{\pi }{2}{r}_i{t}_k\right),$ and ${\xi }_i^k=0.75+0.2\times sin\left(\frac{\pi }{2}{r}_i{t}_k\right).$_.We have applied the fractional derivative on the spatial domain only. The previously used parameter values (described in the sub-section 4.1) are also used for this simulation. We have iterated the simulation process for 6-year times (2190 times) and collect the result at the interval of 365 days.

Figure 10(a) describes that after 2 years of time the proliferative cells wave grows up to 0.3 mm. and within 6 years it reaches up to 1.09 mm (approx.) (value up to 0.01 is considered). With proliferative cells, fibronectin also increases in the tumour microenvironment (Fig. 11(b)). On the other hand, quiescent cells gradually increase after 3 years (Fig. 10(b)) due to the steady fall of nutrients (Fig. 12(a)) and EGF concentrations (Fig. 12(b)) within the tumour cells. After 4 years, nutrients and EGF concentration levels decrease significantly among the tumour cells; as a result quiescent cells nearer to the tumour centre are transformed into necrotic cells in a rapid speed. With time, the necrotic core reaches approximately 0.78 mm (Fig. 11(a)) in radius, whereas quiescent cells grow approximately 1.02 mm from the tumour centre (Fig. 10(b)). The outer surface of the tumour always contains proliferative cells with higher concentration. The overlapping areas in Fig. 13 indicate that boundary among these cellular layers are not distinguishable. Tumour regression cannot be seen in its life time. All the simulations have been carried out in MATLAB R2017a on Intel i5 processor.

Fig. 10.

a Proliferative (P/P₀) and b quiescent (Q/Q₀) cell concentration waves at different time intervals with respect to the distance from the tumour centre

Fig. 11.

a Necrotic (N/N₀) cell concentration and b fibronectin (F/F₀) waves at different time intervals with respect to the distance from tumour centre

Fig. 12.

a Nutrients (C/C₀) and b EGF (E/E0) waves at different time intervals with respect to the distance from tumour centre

Fig. 13.

Proliferative, quiescent and necrotic cell concentration waves in the variable-order fractional diffusion model

We study the behaviour of FO-FDE model by changing its order (φ = 1.55, through 1.95 at a step of 0.1 by keeping skewness θ = 0.5 fixed) and plot the results (only for 6th year) with the simple as well as the variable order models for the proliferative (Fig. 14(a)), quiescent (Fig. 14(b)) and necrotic cells (Fig. 14(c)). From these figures, we can conclude that the amplitude of the curves decrease with the order of FO-FDE models, but no significant changes are visible in terms of radial direction. Simple model overestimates in all three cases, whereas the outcomes of VO-FDE model always lie in between the outcomes of FO-FDE with φ = 1.75 and φ = 1.65.

Fig. 14.

a Proliferative b quiescent and c necrotic cell concentration waves for simple, FO-FDE and VO-FDE models in the sixth year of simulated time

The results for the anomalous models are also observed by changing the skewness parameter (θ is 0.5, 0.95, −0.95 and by keeping φ = 1.75 fixed for FO-FDE). In all the occasions, no significant changes can be seen in the radial direction.

Discussion

We compare all the models from phenomenological point of view. The tumour radius of the FO-FDE model is 1.10 mm, and the VO-FDE model is 1.09 mm whereas, the simple model produces tumour radius as 1.16 mm. We also determine the tumour volume at different time intervals for all the models (Fig. 15). It is observed that the outcomes of all the anomalous models (FO-FDE and VO-FDE) are very close to each other whereas the simple model always overestimate tumour volume.

Fig. 15.

Tumour volume (in mm³) different time intervals for simple, FO-FDE and VO-FDE-based models

We also determine the avg. VDT for all the models and plotted in Fig. 16. It can be seen that outcomes of all the models lie in between 250 and 300 days which justifies the clinical fact (150 to 400 days [20]). At the macroscopic level, all of these models approximate the physical phenomena well and in consonance with the clinical facts. Though the simple model overestimates the computed parameters (tumour radius, and tumour volume) than the anomalous models whereas, the outcome of VO-FDE in all cases lie in between the outcomes of FO-FDE models with φ = 1.75 and φ = 1.65. Measured parameter values from the results are summarized in Table 2. The outcomes of all the FO-FDE models are very close to each other hence, we keep only the outcomes with φ = 1.75.

Fig. 16.

VDT for simple, FO-FDE and VO-FDE-based models

Table 2.

Tumour variables outcome in the FO-FADE and the VO-FADE model

Tumour parameters	Simple model	FO-FDE (φ = 1.75)	VO-FDE	Clinical observation
Radius	1.16 mm	1.10 mm	1.09 mm	Up to 1 mm [15, 17]
Volume	6.51 mm3	5.55 mm3	5.40 mm3	4.17 mm3 [15, 17]
VDT	267 days	264 days	264 days	150 to 400 days [20]

For model validation, one of the popular schemes is sensitivity analysis [85]. It is used to study the robustness of a model by changing one or more of the input parameters. If the outcome of the model changes significantly with the input parameter values [86–89], the model is strongly sensitive to the parameter values indicating scope for refinement of the model’s underlying assumptions. There are various types of sensitivity analysis methods available like mathematical, statistical and graphical methods. These methods are different in term of applicability, computational issues, complexity of their applications and representations.

Here, we make a partial sensitivity analysis (Table 3) by calculating the effect of the model outcome through changing some input parameters, while other parameters are kept fixed. The sensitiveness of both the models are represented by the root mean squared deviation (RMSD) percentage with respect to the mean output value of the model. The analysis is repeated for a couple of times by changing the values of the parameters α, β, γ, μ_E, μ_C, μ_FP, μ_FQ, w₁, w₂, w₃, k₁, k₂, k₃, z₁ and z₂ by changing them ±5%, ±10% by keeping the other parameter values fixed. The growth waves for proliferative, quiescent and necrotic cells are neither distorted nor any significant changes are visible in their patterns after changing the values of the parameters α, β, γ, μ_E, μ_C, μ_FP, μ_FQ, w₁, w₂, w₃, k₁, k₂, k₃, z₁ and z₂ by ±5%, ±10%. In the simple model, the RMSD percentage for radius is 3.26, for volume 9.84 and average VDT 0.23. In the FO-FDE model, RMSD percentage for radius is 11.64, for volume 11.48 and average VDT 0.59. On the other hand, in the VO-FDE model, the RMSD percentage for radius is 11.58, volume 11.31 and average VDT 0.23. The RMSD percentages indicate that the anomalous models (FO-FDE and VO-FDE) are moderately sensitive to the parameter values than the simple model.

Table 3.

Measuring RMSD for simple, FO-FDE (φ = 1.75) and VO-FDE models by changing variables

Model	Tumour parameters	5% increment	10% increment	Without changing parameters	5% decrement	10% decrement	RMSD	RMSD (in %)
Simple	Radius (mm)	1.23	1.29	1.16	1.11	1.05	0.0381	3.26
FO-FDE		1.21	1.27	1.10	1.09	1.04	0.1330	11.64
VO-FDE		1.19	1.25	1.09	1.07	1.01	0.1300	11.58
Simple DE	Volume (mm3)	7.77	8.96	6.51	5.71	4.83	0.6649	9.84
FO-FDE		7.39	8.55	5.55	5.40	4.69	0.7251	11.48
VO-FDE		7.03	8.15	5.40	5.11	4.30	0.6786	11.31
Simple DE	Avg. VDT (in days)	268	269	267	266	265	0.6324	0.23
FO-FDE		266	267	264	263	271	1.5874	0.59
VO-FDE		265	266	264	263	262	0.6324	0.23

Conclusions

Over the decades there has been growing interest in using mathematical modelling for refining our understanding of tumour microenvironment. Diffusion is an important transportation process in this complex phenomena. Diffusion processes in tumour microenvironment are anomalous in nature due to heterogeneity and porosity of cellular membranes and the ECM. Scientists have advocated for using FDE-based model over the simple diffusion to model heterogeneous biological systems. Though most of the researchers neglect this fact and use simple ADE or simple DE to model tumour growth process.

In this paper, we have developed three models: simple diffusion-based, FO-FDE-based and VO-FDE-based for avascular tumour growth. We study all the models from phenomenological and clinical point of views by measuring tumour radius, tumour volume and also determine tumour VDT. We find that both of the anomalous models offer realistic and insightful information for tumour growth at the macroscopic level and will approximate the physical phenomena. Simple diffusion-based model always overestimate the clinical facts like tumour radius and tumour volume, whereas the outcomes of anomalous models are very close to the clinical facts in the tumour growth phenomena. As the simulation parameters may change due to different biochemical and biophysical processes, the robustness of the model is determined by changing the values of the important parameters. It is found that the anomalous diffusion-based model are moderately sensitive than the simple model.

Appendix

A. Non-dimensionalization of Eq. (2)

Non-dimensionalize Eq. (2) by rescaling the distance l with time τ = l²/D_C. Proliferative cell, quiescent cell, necrotic cell, nutrients and EGF concentrations, and fibronectin are rescaled with P₀, Q₀, N₀, C₀, E₀, and F₀ respectively, where P₀, Q₀, N₀, C₀, E₀, and F₀ are the appropriate reference variables. Therefore,

$$P^{\ast }=\frac{P}{P_0},Q^{\ast }=\frac{Q}{Q_0},N^{\ast }=\frac{N}{N_0},C^{\ast }=\frac{C}{C_0},E^{\ast }=\frac{E}{E_0},F^{\ast }=\frac{F}{F_0},t^{\ast }=\frac{t}{\tau }$$

We obtain the new system of Eqs. (3) (by dropping the stars), where,

$$\begin{array}{c}{\eta }^{\ast }=\frac{\eta E_0}{D_C},{\rho }^{\ast }=\frac{\rho F_0}{D_C},{\alpha }^{\ast }=\frac{\alpha l^2}{D_C},{\beta }^{\ast }=\frac{\beta l^2}{D_C},d_P^{\ast }=\frac{d_P{l}^2}{D_C},{\omega }^{\ast }=\frac{\beta l^2{P}_0}{D_C{Q}_0},{\gamma }^{\ast }=\frac{\gamma l^2}{D_C},d_Q^{\ast }=\frac{d_Q{l}^2}{D_C},{\lambda }^{\ast }=\frac{\gamma l^2{Q}_0}{D_C{N}_0},\\ \begin{array}{cccccccc}{\mu }_C^{\ast }=\frac{{\mu }_C{l}^2}{D_C},& w_1^{\ast }=\frac{w_1{l}^2}{D_C},& w_2^{\ast }=\frac{w_2{l}^2{P}_0}{D_C},& w_3^{\ast }=\frac{w_3{l}^2{Q}_0}{D_C},& {\mu }_E^{\ast }=\frac{{\mu }_E{l}^2}{D_C},& k_1^{\ast }=\frac{k_1{l}^2}{D_C},& k_2^{\ast }=\frac{k_2{l}^2{P}_0}{D_C},& k_3^{\ast }=\frac{k_3{l}^2{Q}_0}{D_C},\end{array}\\ \begin{array}{cccccccc}{\mu }_{\mathit{FP}}^{\ast }=\frac{{\mu }_{\mathit{FP}}{l}^2{P}_0}{D_C{F}_0},& {\mu }_{\mathit{FQ}}^{\ast }=\frac{{\mu }_{\mathit{FQ}}{l}^2{Q}_0}{D_C{F}_0},& z_1^{\ast }=\frac{z_1{l}^2{P}_0}{D_C},& z_2^{\ast }=\frac{z_2{l}^2{P}_0}{D_C},& D_{\mathit{PC}}=\frac{D_P}{D_C},& D_{\mathit{QC}}=\frac{D_Q}{D_C},& D_{\mathit{CC}}=\frac{D_C}{D_C},& \text{and}\end{array}\\ D_{\mathit{EC}}=\frac{D_E}{D_C}\end{array}$$