Abstract
Control and manipulation of objects with underactuated dynamics remains a challenge for robots. Due to their typically nonlinear dynamics, it is computationally taxing to implement model-based planning and control techniques. Yet humans can skillfully manipulate such objects, seemingly with ease. More insight into human control strategies may inform how to enhance control strategies in robots. This study examined human control of objects that exhibit complex - underactuated and nonlinear - dynamics. We hypothesized that humans seek to make their trajectories exponentially stable to achieve robustness in the face of external perturbations. A stable trajectory is also robust to the high levels of noise in the human neuromotor system. Motivated by the task of carrying a cup of coffee, a virtual implementation of transporting a cart-pendulum system was developed. Subjects interacted with the virtual system via a robotic manipulandum that provided a haptic and visual interface. Human subjects were instructed to transport this simplified system to a target position as fast as possible without ‘spilling coffee’, while accommodating different visible perturbations that could be anticipated. To test the hypothesis of exponential convergence, tools from the framework of control contraction metrics were leveraged to analyze human trajectories. Results showed that with practice the trajectories indeed became exponentially stable, selectively around the perturbation. While these findings are agnostic about the involvement of feedback and feedforward control, they do support the hypothesis that humans learn to make trajectories stable, consistent with achieving predictability.
Keywords: Physical Human-Robot Interaction, Dexterous Manipulation, Biologically-Inspired Robots, Virtual Reality and Interfaces
I. Introduction
PHYSICAL interaction with everyday objects and tools is a hallmark of human behavior. Despite their limited actuator bandwidth and information transmission speed compared to robots, humans still outperform robots in dexterous behavior, especially in physical interaction and object manipulation. This disparity in performance raises the question of how humans achieve their remarkable skill. A better understanding of the human sensorimotor control system may lead to advances in robotic manipulation and control.
Insights gained from biological motor control have already inspired several new approaches to the control of robot motion. These include central pattern generators for robot locomotion [1], feedback control of postural balance with different time delays [2], and Dynamic Movement Primitives (DMP) inspired by discrete and rhythmic behaviors in humans [3] [4]. Most of the bio-inspired control approaches have been in locomotion and balance; considerably less work has been on manipulation and how human dexterity may inspire robot control. A deeper understanding of human motor control may also lead to more efficient and collaborative human-robot interaction. A recent study showed that when following a robot trajectory that shared the same velocity-curvature relation as human movements, the human actor exerted less force on the robot [5].
The current study examined the control strategies that humans employ when physically (and skillfully) interacting with a dynamically complex object. Specifically, the experimental task was motivated by the everyday action of transporting a cup of coffee. A cup filled with coffee exemplifies a dynamically complex object that is underactuated and nonlinear, and the interaction forces can exhibit chaotic dynamics depending on the applied external force [6]–[8].
Several studies on unconstrained movements have suggested that humans utilize internal forward and inverse models that map hand movements and muscle forces to object movements[9]–[13]. However, control based on precise internal models of objects with underactuated and nonlinear dynamics seems daunting for the human. Furthermore, only relying on feedback corrections is not plausible as the feedback delays in the human neuromotor system are astonishingly long and in the order of 120ms [14]. We therefore hypothesized that humans use control strategies that make interactions predictable. Predictability implies that uncertainties and their effects are minimized.
In previous studies investigating the control of a complex object, specifically the “cup-of-coffee” system, predictability was quantified by mutual information between the input to the system (force) and its output (cup trajectory) when continuously moving the cup [15]. Results showed that with practice humans indeed made the dynamically complex system simpler to predict as quantified by increased mutual information [8] [16]. Higher mutual information indicated less uncertainty in the long-term evolution of the cup trajectory if the force input was known, i.e., more predictability.
To extend these previous findings, the present study examined transporting the cup of coffee in the face of perturbations. Here, predictability was operationalized in terms of stability: A stable system rejects small perturbations and returns to its attractor, which is predictable. A stable trajectory provides robustness to external perturbations. We define robustness as the ability to exponentially decay bounded external disturbances. We hypothesized that when faced with perturbations, humans seek exponential convergence since this guarantees robustness and a fast recovery rate from disturbances.
To assess exponential stability in human trajectories, this study applied contraction analysis [17], a method that evaluates the dynamics of infinitesimal displacements between neighboring trajectories of dynamical systems. This differential dynamics is approximately linear and hence admits application of several techniques from linear systems theory. A favorable property of contraction analysis is that it does not require knowledge of the stable solution. This is especially useful for studying dynamically complex physical interactions where the task is not at steady state but rather in a transient state.
A previous study on the same model system showed that humans exploited contraction regions to compensate for perturbations during complex physical interactions [18] [19]. The identified contraction regions were those of the unforced system, which implied that humans guided the system to regions where it was naturally contracting without the need for any external control effort. In this paper, we extended this work to address the question of whether the human controller actively seeks to stabilize the trajectories and make them contracting. The added challenge was that the analysis had to take the forces applied by the subjects into account. To address this, we leveraged the concept of control contraction metrics (CCMs) [20] to test whether humans employed exponentially stabilizing controllers when manipulating dynamically complex objects. In order to challenge the human controller, we presented perturbations. However, the perturbations were visible and always present so that humans could learn how to encounter them. We hypothesized that humans would develop exponentially stable trajectories to mitigate the effect of the perturbations.
The existence of a CCM guarantees the existence of an exponentially stabilizing controller. Unlike previous work in robotics that used this metric for the design of a controller, this is the first study that adapted the concept of CCMs for the analysis of human movements. The first step was to find a CCM and deduce the conditions that the control input had to meet to be exponentially stabilizing. Next, we tested whether the force applied by the subject met those conditions. If it did, then the resulting human trajectory, or segments of it, could be regarded as exponentially stable or contracting.
The contributions of this paper are as follows: 1) The control contraction metrics framework was adapted such that it can be used not only as a framework for the synthesis of a controller, but also as a tool for the analysis of stability in human data. 2) This framework was validated by assessing stability in a complex human physical interaction task. Note that existing tools in the human movement literature were not applicable to such complex tasks. 3) The results provided support to our hypothesis that humans seek to exponentially stabilize their trajectories in this interactive task.
II. Preliminaries, Definitions, and Problem Statement
Let denote the set of symmetric positive definite matrices in . For a given matrix Q, let . The non-negative reals are denoted by . Given a smooth matrix-valued function M(x, t) and vector field defined for , , the directional derivative is defined as . The time-derivative is . For simplicity, all matrix-valued functions considered in this paper will not be explicit functions of time t, so that the time-derivative reduces to . All subsequent matrix inequalities are to be understood in Loewner ordering.
The following notations and definitions from Riemannian geometry are used: The inner product on the tangent space of a smooth manifold endows the manifold with a Riemannian metric according to the metric tensor M(x, t). The norm induced by this inner product is . A metric tensor is uniformly bounded if ∃ 0 < α1 ≤ α2 such that α1I ≤ M(x, t) ≤ α2I ∀ x, t. For a smooth parameterized curve r(s), s ∈ [0, 1], the Riemannian length l and energy are defined as
| (1) |
where . The Riemannian distance between two points x1 and x2 is the Riemannian length of the geodesic (the shortest path) joining them, where μ(0, t) = x2 and μ(1, t) = x1. If the manifold is and the metric tensor M is flat, i.e., independent of x, then all geodesics are straight lines and the expression for the Riemannian distance reduces to .
Consider a control-affine nonlinear system described by the following differential equation:
| (2) |
where and are the state and control input, respectively, at time , and f and B are smooth functions. The ith column of B(x(t)) is denoted as bi(x(t)) where i = 1, 2, …, m.
The control input is assumed to be generated by a state-feedback policy π parameterized as the sum of an open-loop input u* and a feedback term uf designed to track a desired feasible state trajectory x* (achieved by u* in the absence of disturbances, noise, etc.) [21]:
| (3) |
A trajectory x(t) is said to be incrementally exponentially stable (IES) [21] with respect to a desired trajectory x*(t), with rate λ and overshoot R if there exists a state-feedback controller of the form (3) such that
| (4) |
where λ, R > 0 are constants independent of initial conditions. A controller that achieves this behavior is said to be an incrementally exponentially stabilizing controller.
Two sets of conditions need to be satisfied to guarantee the exponential stability expressed in (4): 1) Conditions on the system’s dynamics (2) which guarantee the existence of an incrementally exponentially stabilizing controller. 2) Conditions which the controller must meet in order to be incrementally exponentially stabilizing. These conditions have been derived previously using the framework of control contraction metrics (CCMs) [20], and will be presented in the next section.
The hypothesis in this paper was that, when manipulating dynamically complex objects, humans seek exponential stability, especially when encountering perturbations. To test this hypothesis, we evaluated whether the human trajectories, or segments of them, became exponentially stable, i.e. contracting, with practice. The analysis was conducted by combining experimental data with model-based calculations. Using a model of the system of the form (2), the experimentally collected force measurements were used as the control input u(t). Each sample of the data was evaluated whether it met the conditions for an exponentially stabilizing controller and, hence, whether the trajectory was contracting at that point.
III. Contraction Analysis
Contraction analysis [17] is a method for assessing stability of nonlinear systems by studying convergence of neighboring trajectories. The analysis examines the dynamics of infinitesimal displacements of the system, i.e., expressing system (2) in its variational or differential dynamics form:
| (5) |
where and δx is an infinitesimal displacement.
The central result of [17] is that if there exists a uniformly bounded metric tensor such that , the system is contracting with respect to that metric with contraction rate λ, i.e., .
A. Control contraction metrics
As an extension, Manchester and Slotine [20] subsequently introduced the concept of control contraction metrics. A CCM is a uniformly bounded metric tensor that guarantees the existence of an incrementally exponentially stabilizing controller for any desired feasible trajectory. A CCM is one that satisfies:
| (6) |
| (7) |
for a constant λ > 0, ∀ x, and ∀ δx ≠ 0 such that . The proof that the existence of a CCM guarantees the existence of an incrementally exponentially stabilizing controller is provided in Lemma 2 in [20].
The first condition (6) ensures that the vector fields bi are Killing vector fields (vector fields that preserve the metric) [22] for the metric M. This ensures that for displacements along the actuated directions the metric remains invariant and hence distances are preserved and no expansion (to be understood as the opposite of contraction) occurs. Condition (7) ensures that the system is contracting in the directions orthogonal to the span of the control inputs, i.e., that the uncontrolled manifold is naturally contracting.
CCMs are a generalization of control Lyapunov functions (CLFs) [23] [24]. The CCM guarantees that the Riemannian energy of the geodesics E(μ) between the actual and desired trajectories can be decreased exponentially, i.e., can be used as a CLF for the desired trajectory [21].
B. Dual control contraction metrics
A favorable feature of the contraction analysis framework is that, unlike CLFs, the search for a CCM can be written as a convex optimization problem. This is achieved by searching for the dual metric W(x) := M(x)−1. For the dual metric, conditions (6) and (7) are equivalent to:
| (8) |
| (9) |
where B⊥ satisfies . A computationally tractable finite-dimensional approximation of this CCM feasibility problem can be obtained by casting it as a Sums-of-Squares (SOS) program, whereby W(x) is parameterized as a matrix of polynomials, and the Linear-Matrix-Inequality (LMI) (9) is relaxed and expressed as a SOS constraint [25].
C. Incrementally exponentially stabilizing controllers
A uniformly bounded CCM α1I ≤ M (x) ≤ α2I guarantees the existence of an incrementally exponentially stabilizing controller for any desired feasible trajectory, with contraction rate λ and overshoot . Specifically, the controller has the form u* + uf and satisfies:
| (10) |
where , , and .
Note how the controller enforces contraction tangent to the geodesic between the two trajectories.
Given force measurements collected from subjects performing a task, the inequality (10) was evaluated in a point-by-point manner to assess whether the human trajectories were IES/contracting.
IV. The Experimental Task and The Model
Transporting a cup filled with coffee is an example of a physical interaction with a dynamically complex object. Motivated by this real-life example, subjects maneuvered an underactuated object from a starting point to a target position as fast as possible without “spilling the coffee”.
A. The dynamical model
Simulating a realistic 3-dimensional cup with sloshing coffee governed by nonlinear equations from fluid dynamics is computationally taxing [6] [7]. This computational complexity was undesirable as the study employed a virtual setup where real-time simulations of the system dynamics were required. The cup of coffee was therefore simplified to a semicircular 2-dimensional arc, the cup, with a ball rolling inside, the coffee; the motion of the 2D cup was limited to the horizontal axis only. Restricting the ball to only slide along the cup without rolling or friction, the system was reduced to the well-known cart-and-pendulum system with no damping. Fig. 1(a) illustrates the real and simplified task, while Fig. 1(b) displays the mechanical model of the simplified system.
Fig. 1.
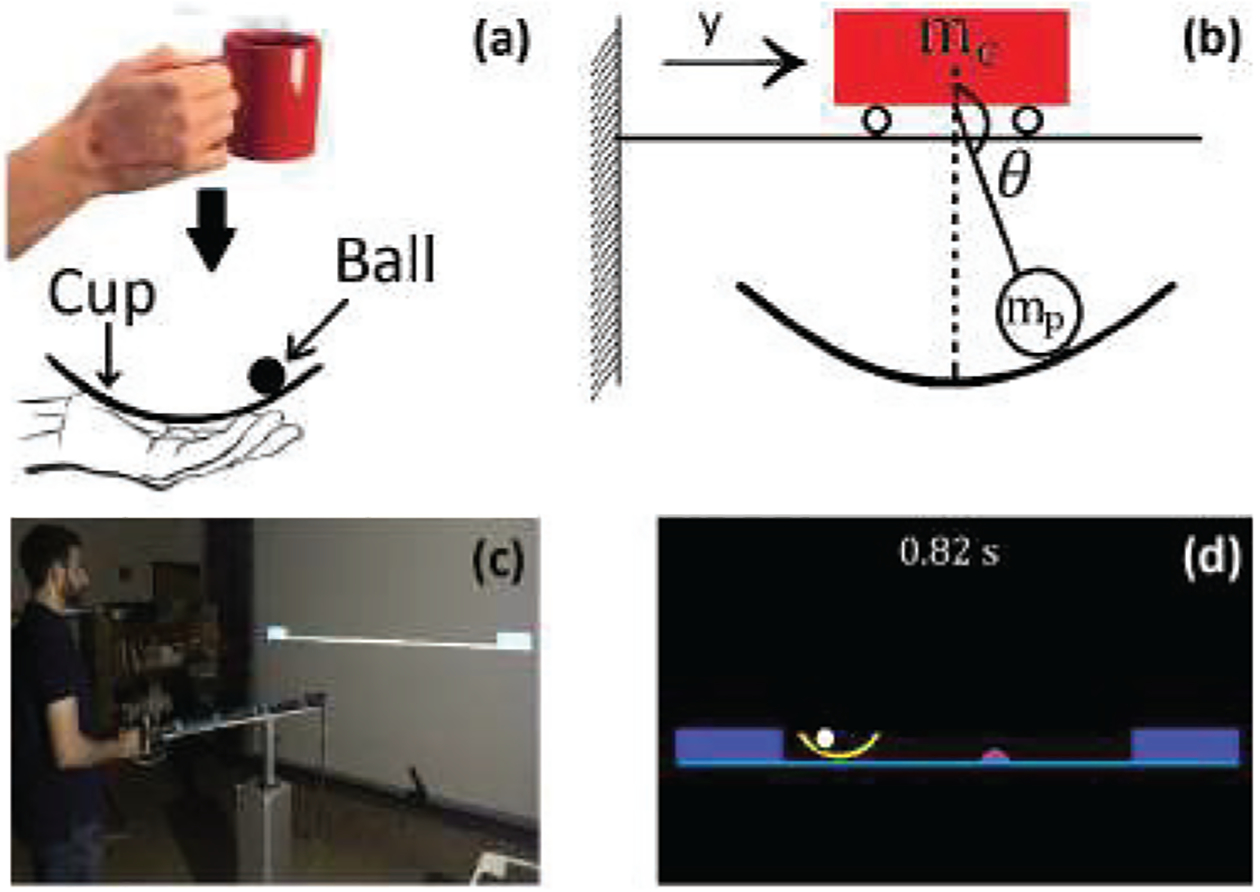
(a) Real and simplified task. (b) Mechanical model. (c) Virtual environment with a subject operating the HapticMaster robot to manipulate the virtual cup. (d) Screen display.
Taking the state variables to be , the equations of motion of the simplified system were
| (11) |
| (12) |
where y denoted the position of the cart, θ denoted the pendulum angle with a clockwise positive convention, mp was the mass of the pendulum bob, mc was the mass of the cart, l was the length of the massless pendulum rod, and g denoted gravitational acceleration. To make the task more challenging, the simulated dynamics in the virtual environment incorporated a gain G for the cup acceleration ÿ. This was added to make the ball more “agile” and thereby the task more difficult. The force exerted by the human subject was u. The parameters used to simulate this system in the virtual environment were: mc = 3.5 kg, mp = 0.3 kg, l = 0.35 m, G = 5, and g = 9.8 m/s2.
Expressing the dynamics in the form shown in (2), the equations became
| (13) |
where P = mc + mp (1 − G cos2(θ)). Note that the resulting input matrix B was a function of the state variable θ. It was desirable to have B independent of the state variables, to allow for the possibility of the dual metric W being independent of the state variables as well. A flat metric was favored since that would greatly simplify the calculation of geodesics in inequality (10). Therefore, using the partial feedback linearization of [26] and borrowing a coordinate transformation from [27], the new state vector was and the resulting dynamics were
| (14) |
where and the resulting B was now independent of x. The resulting differential dynamics were
| (15) |
B. The virtual experiment
This simplified mechanical model was simulated in a virtual environment with visual and haptic feedback interfaced via a robotic manipulandum (Fig. 1(c)). The projection screen displayed the cup as a 2D arc and a rolling ball (corresponding to the pendulum bob), moving between a start and target box, separated by a distance of 0.4 m (Fig. 1(d)). Subjects were instructed to move the cup from the start box on the left to the target box on the right as fast as possible without losing the ball. At the end of each trial the duration of the movement was displayed on the screen as feedback. For the trial to end, the cup had to be completely inside the box and at rest, otherwise, the timer would keep running. Therefore, only generating faster movements did not necessarily lead to better performance since a fast cup displacement could result in larger ball oscillations. The resulting larger ball forces could impede the subject from bringing the cup to a complete stop inside the target box.
In each trial, a perturbation of magnitude 40 N, duration 20 ms, was presented at 60% of the travel distance. This perturbation was either in the direction of motion of the cup, i.e., assistive, or against it, i.e., resistive. Note that the label ‘assistive’ did not imply that the perturbation was helpful. It was an unwanted disturbance in the direction of the cup movement, while the resistive perturbation opposed the direction of movement. The position of the perturbation was visually displayed as a small bump (Fig. 1(d)). The subject knew the magnitude and direction of the perturbation and had the opportunity to learn how to navigate it without losing the ball. For simplicity, the virtual cup moved through the (virtual) bump and remained on the horizontal line. Seven subjects participated and gave informed written consent before the experiment. The protocol was approved by the Institutional Review Board of Northeastern University.
The experiment consisted of 4 blocks. Block 1 comprised 60 trials without any perturbation to allow subjects to familiarize themselves with the task. Blocks 2 and 4 comprised 60 trials each and involved a series of assistive or resistive perturbations respectively. The order of resistive and assistive blocks was counter-balanced between subjects. Block 3 presented 10 unperturbed trials to separate the two perturbation conditions. At the beginning of each trial, the cup was centered in the start box and the ball rested at the bottom of the cup.
C. Apparatus and data acquisition
Subjects were seated about 2 m in front of a large back-projection screen (2.4 × 2.4 m). Physical interaction with the virtual environment occurred via a 3-degree-of-freedom admittance-controlled robotic manipulandum (HapticMaster, Motekforce, NL [28]). By applying a force to the handle of the robotic arm, participants controlled the horizontal y-position of the virtual cup. The robotic arm was restricted to move only in the horizontal direction in the subject’s frontal plane to ensure a linear horizontal motion of the cup, consistent with the model. The robotic arm provided haptic feedback, allowing participants to sense the system’s inertia, the force of the ball on the cup, and the perturbations. The force applied by the participants to the manipulandum (u) and the kinematics of the cup and the ball were recorded at 120 Hz.
V. Experimental Results
Representative assistive and resistive trials are shown in Fig. 2. The resistive perturbation opposed the cup’s motion and caused a sharp decrease in the velocity. The opposite effect is seen for the assistive perturbation. For blocks with a resistive perturbation 78% of the trials were successful (the ball was not lost), whereas for assistive trials the success rate was 84%. Failed trials had a uniform distribution across trial number and perturbation type, with no tendency for the second perturbation block to have more failed trials than the first.
Fig. 2.
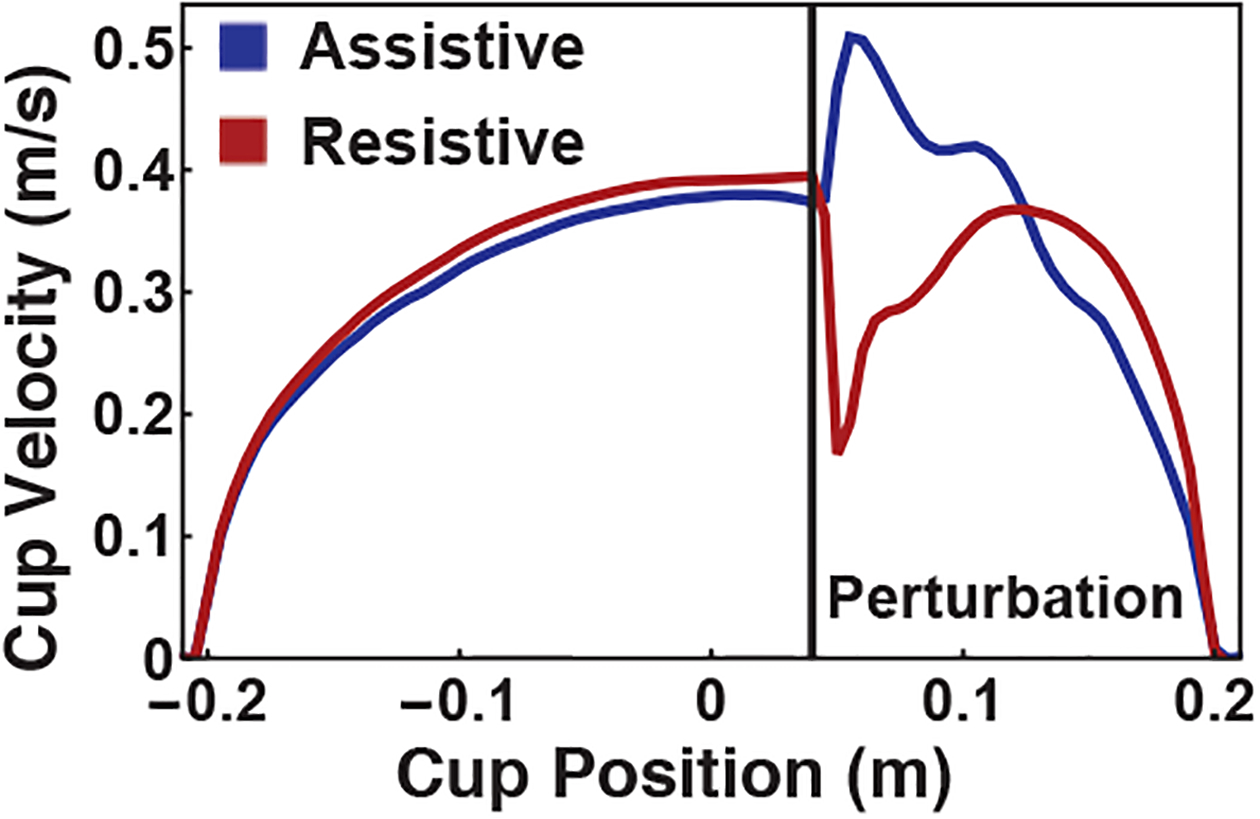
One representative assistive and one resistive cup displacement eliciting the expected different effect.
A. Trial duration
Subjects’ performance improved with practice; the mean duration of successful trials across all subjects became shorter for both resistive and assistive perturbations, as can be seen in Fig. 3(a). Two observations are worth noting: 1) While both perturbation conditions started with similar performance in the first few trials, performance dropped sharply in the assistive trials in less than 10 trials and then approached a plateau relatively fast. In contrast, in the resistive trials the performance improved in an approximately continuous manner, with no abrupt changes. Fig. 3(b) displays the exponential fit for both curves (R2 = 0.99 for both fits). The time constant was −0.03 for the resistive trials and −0.48 for the assistive trials. This indicated that it was easier to achieve better performance in a shorter period of practice for the assistive perturbation as opposed to the resistive perturbation. 2) Despite this different time course in the two perturbation types, there was no significant difference in performance at the end of practice. A paired t-test on the last 10 trials in each perturbation condition did not reach significance (t(9) = −0.27, p = 0.79). This indicated that perturbation type had no effect on the best attainable performance.
Fig. 3.
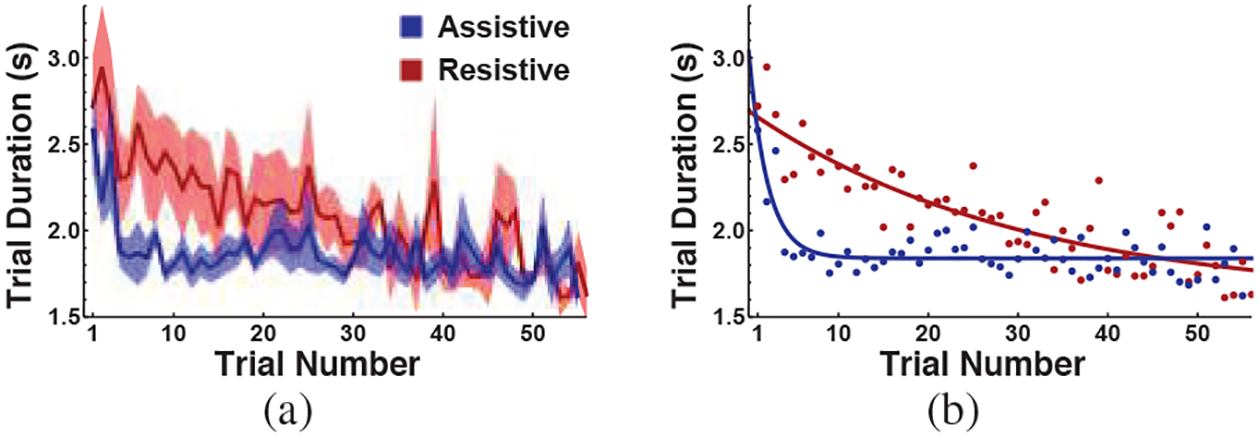
(a) Mean trial durations of successful trials across all subjects. The shaded bands denote ± one standard error. (b) Exponential fits of subject means for each perturbation across trials.
B. The contraction rate
The SOS program expressed in (8) and (9) was solved for W using the LMI parser Yalmip [29] [30] and the solver Mosek. In this case, condition (8) required that the dual metric was not a function of η or . The dual metric that was found was indeed flat, thereby simplifying the computation of the geodesics. Note that before solving the SOS program, the differential dynamics A(x) in (15) were Taylor expanded to degree 3 to obtain a polynomial vector field.
The data collected from the subjects was post-processed and converted to the frame to make it compatible with the model. Next, for each trial, the inequality that rendered the controller u* + uf incrementally exponentially stabilizing (10) was checked. If it was satisfied at a given sample, this meant that the force applied by the subject at that instance was generated by an incrementally exponentially stabilizing controller with a convergence rate of at least λ. The following substitutions were made in the inequality:
was the state vector of the experimental data.
x*(t) was the state vector resulting from a minimum-jerk trajectory in the y-direction. It was assumed that the subjects’ desired trajectory was a minimum-jerk y(t) and the resulting θ and η from such a movement were used. The assumption was motivated by previous work that showed that a minimum-trajectory was an accurate description of unconstrained arm reaching movement [31]. While several models for control of non-rigid objects have been proposed [32] [33] [34], these are only applicable to movements that bring the internal degree of freedom (in this case the ball) to rest at the end of the movement. In this experiment, the instruction was to move the system as fast as possible without the specification to bring the ball to rest.
. Since the metric was flat, the geodesic between any two points was just the straight line between them.
To arrive at a unique solution for the SOS program in (8) and (9), one had to specify the exponential convergence rate λ. For the purpose of calculating the contraction metric, we solved the feasibility problem, i.e., we chose λ = 1. However, when contraction analysis was conducted and the inequality (10) was checked, a different λ was chosen as explained below.
u* +uf was set equal to the measured force applied by the subject.
At first, the inequality (10) was assessed with λ = 1 for all successful trials. In this case, the segments that satisfied the inequality, i.e. the contracting segments, had a contraction rate that was at least equal to the one guaranteed by the metric. Fig. 4(a) displays the results obtained for the assistive block of one of the subjects. However, given the movement durations within which the subjects completed the task, a contraction rate equal to 1 would not have been sufficient for attenuating the perturbation’s effect. Post-processing of the data revealed that, on average, subjects had ≈ 0.4 s to stabilize the system after the perturbation. The required contraction rate for a time constant τ = 0.4 s is . Therefore, the data was tested again, but this time the contraction rate was set to λ = 3. We chose a slightly larger contraction rate than the minimum sufficient one as a conservative measure. The results for the same set of trials evaluated with λ = 1 and λ = 3 are displayed in Fig. 4(a) and 4(b) respectively.
Fig. 4.
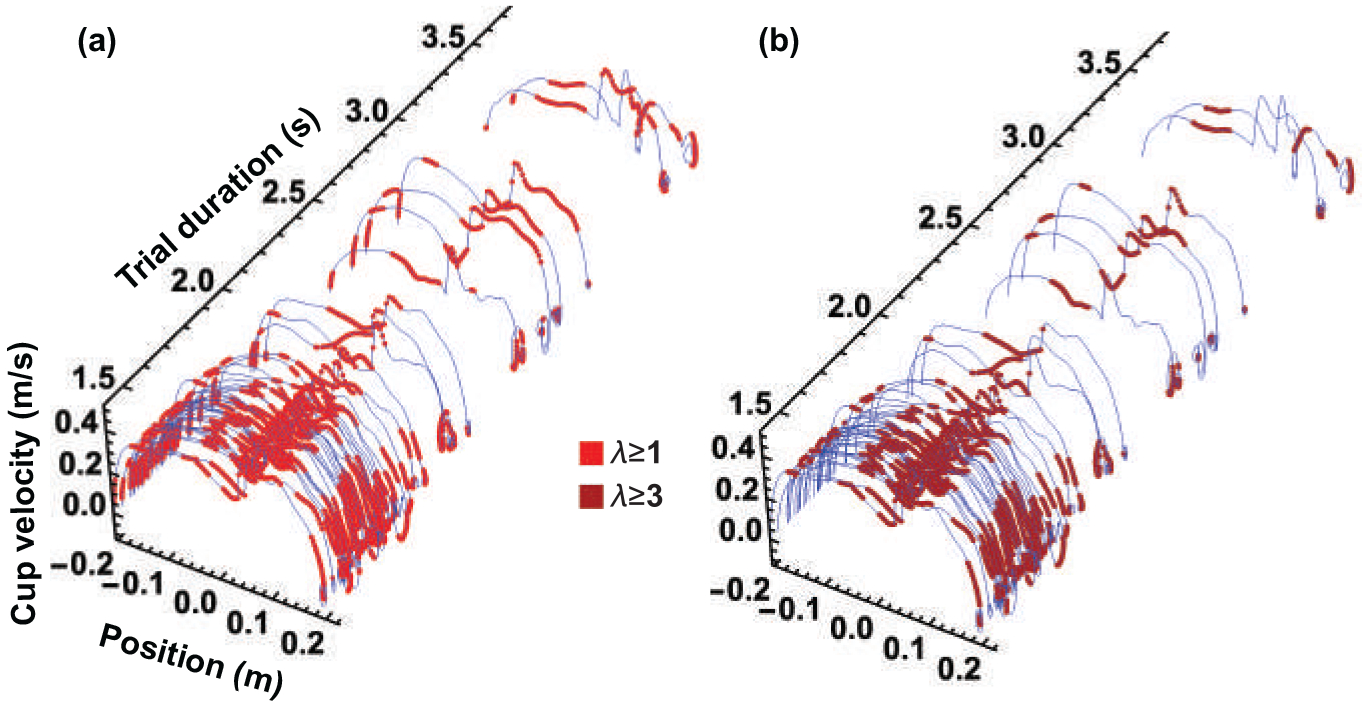
All successful trials for one representative subject in an assistive perturbation block. Trajectories are ordered by trial duration, not trial number. To enable better alignment with the perturbation onset, they are plotted over position, not time.
Fig. 4 shows that trials with shorter durations have longer contracting segments for both λ values. Moreover, when a stronger contraction rate was imposed, the slower trials exhibited an even smaller number of contracting segments, as seen in Fig. 4(b). This observation was consistent among all 7 subjects. This observation led to three conclusions: 1) Using the slowest contraction rate guaranteed by the contraction metric falsely identified large segments of the trajectories as contracting, specifically in the slower trials. 2) The faster trajectories retained more of their contraction segments with the higher contraction rate. 3) For faster trajectories, the contracting segments were specifically in the vicinity of the perturbation, where contraction was functionally useful.
These results provided evidence that faster movements, i.e., better performance was correlated with more and longer segments with higher contraction rates.
C. Contraction ratio
Returning to the main hypothesis - contracting trajectories can withstand perturbations better - a contraction ratio was calculated for every successful trial and averaged across all subjects. The contraction ratio was defined as the ratio of the duration of the contracting segments in a given trial to the duration of the trial. Fig. 5 shows that, qualitatively, the contraction ratio evolved with practice in a very similar manner as the trial duration. For resistive perturbations the contraction ratio continuously increased with practice, whereas for assistive perturbations the contraction ratio increased only in the first 10 trials and then plateaued. This correlated well with task performance as quantified by the Pearson correlation coefficient to be −0.73 (p = 2.4 × 10−10) for assistive perturbations and −0.80 (p = 8.0 × 10−14) for resistive perturbations (Fig. 6). This result provided further evidence for the hypothesis that subjects achieved better performance by exponentially stabilizing (contracting) their trajectories.
Fig. 5.
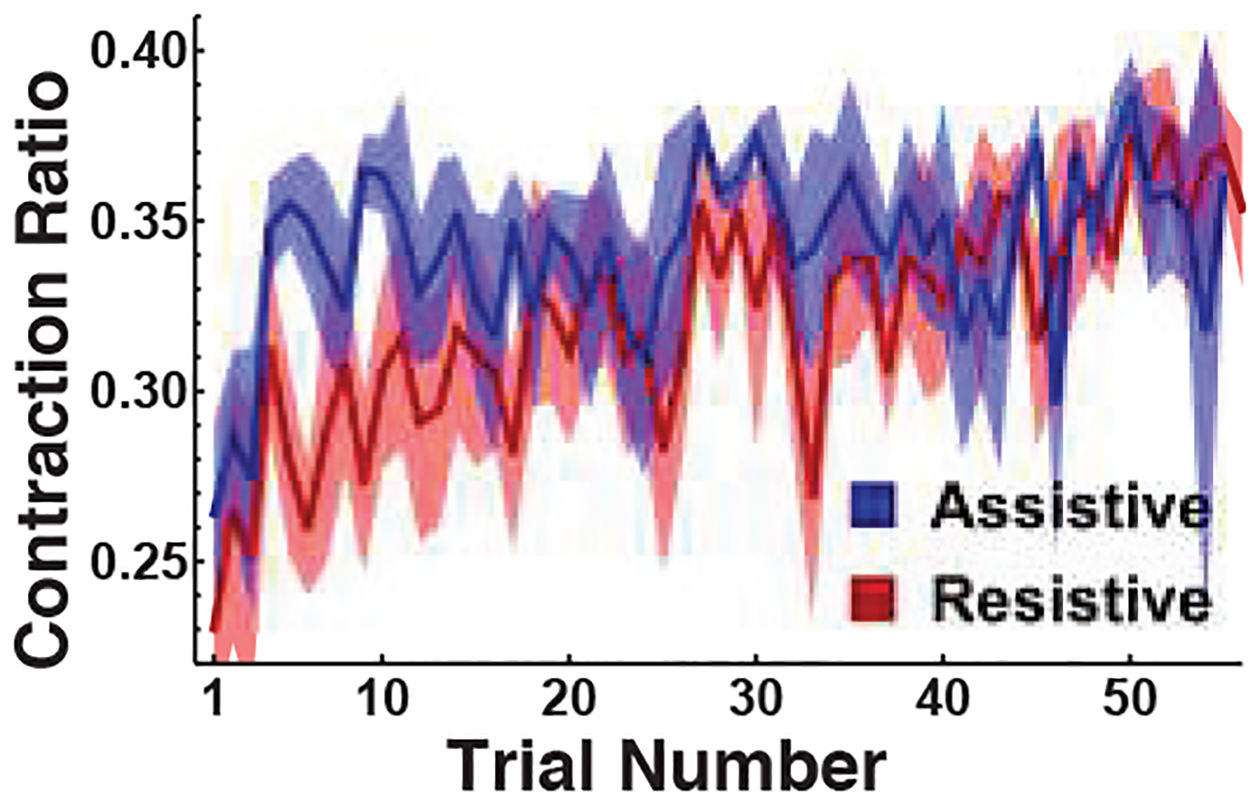
Mean contraction ratios of successful trials across all subjects. The shaded bands denote ± one standard error.
Fig. 6.
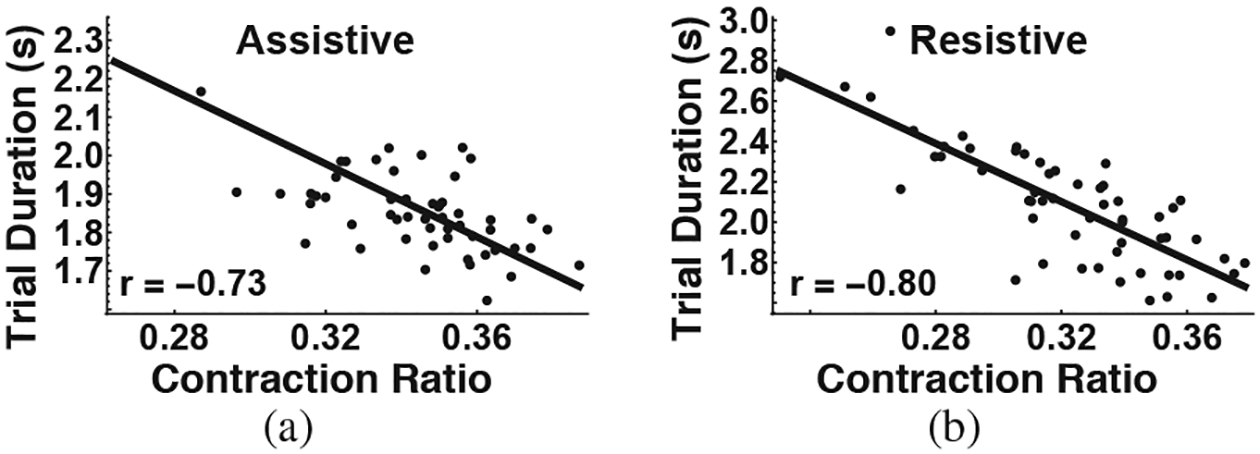
A negative correlation between trial duration and contraction ratio for the (a) assistive perturbations (b) resistive perturbations.
D. Average contracting segments
To further examine whether better performance correlated with more contraction, the successful trials of each subject for each perturbation type were split into two categories: fast trials and slow trials. Trials were classified as ‘fast’ if they were below the respective average, and ‘slow’ if above the respective average. The average successful trial duration across all subjects was 2.14 s for resistive blocks, and 1.89 s for assistive blocks. The trials were then averaged, including the contracting segments. Fig. 7 displays the average fast and slow trials in each perturbation block across all 7 subjects. The color gradient represents the percentage of trials for each sample (across all subjects) that were contracting.
Fig. 7.
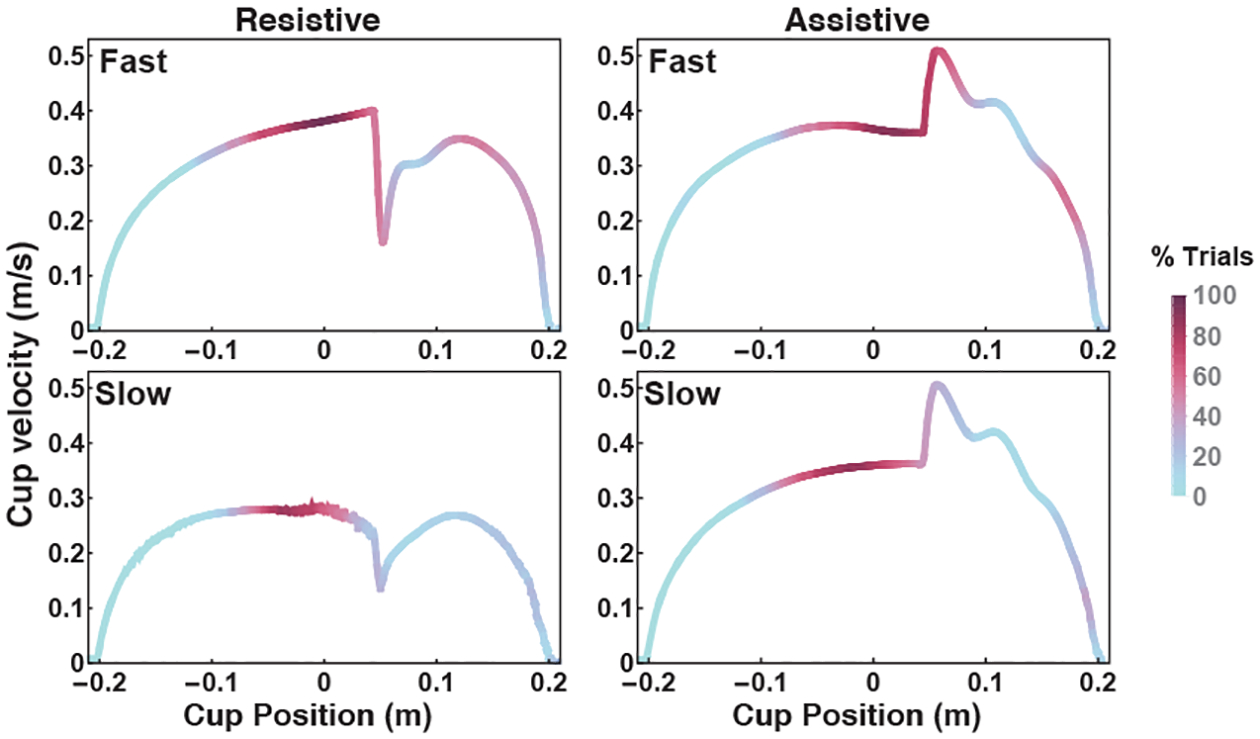
Average fast and slow trajectories and their contracting segments across all 7 subjects in the respective perturbation blocks. The color code represents the percentage of trials that were contracting at a given position.
The following observations can be drawn from Fig. 7:
For fast trials, a larger proportion of the trajectory was contracting than for slow trials.
For fast trials, there were more contracting segments at the perturbation onset and immediately after it.
For the fast resistive trials, subjects used a strategy that combined both faster movements and more contracting segments. For assistive trials, there was no significant difference in the peak velocity between the fast and the slow trials. In fact, the velocity profiles look almost identical, yet they resulted in different trial durations due to the differences in contracting segments.
Looking at the assistive trials, one would expect that trials with the same velocity profile should have the same trial duration. However, as mentioned above, the trial only stopped when the cup was completely at rest inside the target box. In both slow and fast trials in the assistive block, the cup took the same amount of time to arrive at the box, however the shorter trial duration meant that fast trials required a shorter amount of time to get to a complete rest after entering the box. The key to achieving these shorter trial durations was contraction, as can be seen in Fig. 7. Subjects used a robust control strategy and changed their control/force input (which affected the left-hand side of inequality (10)) to render the trajectories more contracting directly before and after the perturbations. This resulted in the effective attenuation of the perturbation effects on the ball, allowing the cup to reach the target box with small residual ball oscillations. This, in turn, resulted in less time to get the cup to a complete stop after reaching the target.
VI. Discussion and Conclusions
This work examined the interactive task of transporting an underactuated object with nonlinear dynamics, like a cup of coffee. We tested the hypothesis that humans stabilize their trajectories to withstand perturbations, both external and internal. We proposed and validated a new method for assessing stability of human trajectories using recently developed tools in contraction theory. The results were consistent with the hypothesis that humans enhance the robustness of their trajectories by seeking exponential convergence, especially in the face of perturbations.
The results revealed what the human controller seeks. Note that this ‘higher-level’ strategy provides no indication about whether this is achieved by feedforward and/or feedback control. We reason that pure feedback control is unlikely given the long feedback delays in the neuromotor system, the dynamical complexity of the object, the short duration of a single trial, and the task instruction to be as fast as possible. Further, the experiment was explicitly set up to make the perturbations predictable (the perturbations were present and visible in every trial of a block and had constant magnitude, direction, and duration). Therefore, subjects could learn to anticipate, rather than react and correct. We speculate that the subjects most probably learned a feedforward strategy, specifically one that makes the system exonentially stable and thereby predictable. Our study contrasts with a recent study that examined how humans deal with unpredictable perturbations in reaching movements [35]. The authors showed that humans developed a strategy that resembled robust H∞ control. It would be interesting to study the cup-and-ball task where perturbations are invisible and unpredictable, and investigate whether subjects developed a similar strategy.
We posit that the results presented here are an important first step towards addressing the questions about the structure of the controller. As argued before, given the complexity of the underactuated object, an exponentially stable strategy may be possible even when the internal model of the object is only approximate. One option to realize such a strategy may be by modulating impedance of the limb as has been shown before [16]. To further address the structure of the controller and how humans actually implement their exponentially stabilizing strategy, different experimental manipulations are required. More insights into the underlying structure of the human controller may inspire the development of more robust control strategies for robotic manipulation.
Acknowledgments
This paper was recommended for publication by Editor Allison M. Okamura upon evaluation of the Associate Editor and Reviewers’ comments. Dagmar Sternad was supported by the following grants: NIH R01-HD087089, NSFNRI 1637854, NSF-M3X-1825942.
References
- [1].Righetti L and Ijspeert AJ, “Programmable central pattern generators: an application to biped locomotion control,” in IEEE International Conference on Robotics and Automation, 2006, pp. 1585–1590. [Google Scholar]
- [2].Ott C, Henze B, Hettich G, Seyde TN, Roa MA, Lippi V, and Mergner T, “Good posture, good balance: comparison of bioinspired and model-based approaches for posture control of humanoid robots,” IEEE Robotics & Automation Magazine (RAM), vol. 23, no. 1, pp. 22–33, 2016. [Google Scholar]
- [3].Sternad D, Dean WJ, and Schaal S, “Interaction of rhythmic and discrete pattern generators in single-joint movements,” Human Movement Science, vol. 19, no. 4, pp. 627–664, 2000. [Google Scholar]
- [4].Schaal S, Mohajerian P, and Ijspeert A, “Dynamics systems vs. optimal controla unifying view,” Progress in Brain Research, vol. 165, pp. 425–445, 2007. [DOI] [PubMed] [Google Scholar]
- [5].Maurice P, Huber ME, Hogan N, and Sternad D, “Velocity-curvature patterns limit human–robot physical interaction,” IEEE Robotics and Automation Letters (RA-L), vol. 3, no. 1, pp. 249–256, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Mayer HC and Krechetnikov R, “Walking with coffee: Why does it spill?” Physical Review E, vol. 85, no. 4, p. 046117, 2012. [DOI] [PubMed] [Google Scholar]
- [7].Han J, “A study on the coffee spilling phenomena in the low impulse regime,” Achievements in the Life Sciences, vol. 10, no. 1, pp. 87–101, 2016. [Google Scholar]
- [8].Nasseroleslami B, Hasson CJ, and Sternad D, “Rhythmic manipulation of objects with complex dynamics: predictability over chaos,” PLoS Computational Biology, vol. 10, no. 10, p. e1003900, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Kawato M, “Internal models for motor control and trajectory planning,” Current Opinion in Neurobiology, vol. 9, no. 6, pp. 718–727, 1999. [DOI] [PubMed] [Google Scholar]
- [10].Takahashi C, Scheidt RA, and Reinkensmeyer D, “Impedance control and internal model formation when reaching in a randomly varying dynamical environment,” Journal of Neurophysiology, vol. 86, no. 2, pp. 1047–1051, 2001. [DOI] [PubMed] [Google Scholar]
- [11].Flanagan JR, Nakano E, Imamizu H, Osu R, Yoshioka T, and Kawato M, “Composition and decomposition of internal models in motor learning under altered kinematic and dynamic environments,” Journal of Neuroscience, vol. 19, no. 20, pp. RC34–RC34, 1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Flanagan JR, Vetter P, Johansson RS, and Wolpert DM, “Prediction precedes control in motor learning,” Current Biology, vol. 13, no. 2, pp. 146–150, 2003. [DOI] [PubMed] [Google Scholar]
- [13].Mehta B and Schaal S, “Forward models in visuomotor control,” Journal of Neurophysiology, vol. 88, no. 2, pp. 942–953, 2002. [DOI] [PubMed] [Google Scholar]
- [14].Kandel ER, Schwartz JH, and Jessell TM, Principles of Neural Science. McGraw-hill; New York, 2000, vol. 4. [Google Scholar]
- [15].Cover TM and Thomas JA, Elements of information theory. John Wiley & Sons, 2012. [Google Scholar]
- [16].Maurice P, Hogan N, and Sternad D, “Predictability, force and (anti-) resonance in complex object control,” Journal of Neurophysiology, vol. 120, no. 2, pp. 765–780, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [17].Lohmiller W and Slotine J-JE, “On contraction analysis for nonlinear systems,” Automatica, vol. 34, no. 6, pp. 683–696, 1998. [Google Scholar]
- [18].Bazzi S, Ebert J, Hogan N, and Sternad D, “Stability and predictability in dynamically complex physical interactions,” in IEEE International Conference on Robotics and Automation (ICRA), 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Bazzi S, Ebert J, Hogan N, and Sternad D, “Stability and predictability in human control of complex objects,” Chaos: An Interdisciplinary Journal of Nonlinear Science, vol. 28, no. 10, p. 103103, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Manchester IR and Slotine J-JE, “Control contraction metrics: Convex and intrinsic criteria for nonlinear feedback design,” IEEE Transactions on Automatic Control, vol. 62, no. 6, pp. 3046–3053, 2017. [Google Scholar]
- [21].Singh S, Majumdar A, Slotine J-J, and Pavone M, “Robust online motion planning via contraction theory and convex optimization,” in IEEE International Conference on Robotics and Automation (ICRA), 2017, pp. 5883–5890. [Google Scholar]
- [22].Carroll SM, An introduction to general relativity: spacetime and geometry. Addison Wesley, 2004. [Google Scholar]
- [23].Artstein Z, “Stabilization with relaxed controls,” Nonlinear Analysis: Theory, Methods & Applications, vol. 7, no. 11, pp. 1163–1173, 1983. [Google Scholar]
- [24].Sontag ED, “A Lyapunov-like characterization of asymptotic controllability,” SIAM Journal on Control and Optimization, vol. 21, no. 3, pp. 462–471, 1983. [Google Scholar]
- [25].Parrilo PA, “Semidefinite programming relaxations for semialgebraic problems,” Mathematical Programming, vol. 96, no. 2, pp. 293–320, 2003. [Google Scholar]
- [26].Spong MW, “Energy based control of a class of underactuated mechanical systems,” IFAC Proceedings Volumes, vol. 29, no. 1, pp. 2828–2832, 1996. [Google Scholar]
- [27].Manchester IR, Tang JZ, and Slotine J-JE, “Unifying robot trajectory tracking with control contraction metrics,” in Robotics Research. Springer, 2018, pp. 403–418. [Google Scholar]
- [28].van der Linde RQ and Lammertse P, “Hapticmaster–a generic force controlled robot for human interaction,” Industrial Robot: An International Journal, vol. 30, no. 6, pp. 515–524, 2003. [Google Scholar]
- [29].Lofberg J, “Yalmip: A toolbox for modeling and optimization in matlab,” in IEEE International Symposium on Computer Aided Control Systems Design, 2004, pp. 284–289. [Google Scholar]
- [30].Löfberg J, “Pre- and post-processing sum-of-squares programs in practice,” IEEE Transactions on Automatic Control, vol. 54, no. 5, pp. 1007–1011, 2009. [Google Scholar]
- [31].Flash T and Hogan N, “The coordination of arm movements: an experimentally confirmed mathematical model,” Journal of Neuroscience, vol. 5, no. 7, pp. 1688–1703, 1985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Dingwell JB, Mah CD, and Mussa-Ivaldi FA, “An experimentally confirmed mathematical model for human control of a non-rigid object,” Journal of Neurophysiology, 2004. [DOI] [PubMed] [Google Scholar]
- [33].Svinin M, Goncharenko I, Luo Z-W, and Hosoe S, “Reaching movements in dynamic environments: How do we move flexible objects?” IEEE Transactions on Robotics, vol. 22, no. 4, pp. 724–739, 2006. [Google Scholar]
- [34].Svinin M, Goncharenko I, Kryssanov V, and Magid E, “Motion planning strategies in human control of non-rigid objects with internal degrees of freedom,” Human Movement Science, vol. 63, pp. 209–230, 2019. [DOI] [PubMed] [Google Scholar]
- [35].Crevecoeur F, Scott SH, and Cluff T, “Robust control in human reaching movements: a model-free strategy to compensate for unpredictable disturbances,” Journal of Neuroscience, vol. 39, no. 41, pp. 8135–8148, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]


