Abstract
Background:
Sholl analysis has been used to analyze neuronal morphometry and dendritic branching and complexity for many years. While the process has become semi-automated in recent years, existing software packages are still dependent on user tracing and hence are subject to observer bias, variability, and increased user times for analyses. Commercial software packages have the same issues as they also rely on user tracing. In addition, these packages are also expensive and require extensive user training.
New Method:
To address these issues, we have developed a broadly applicable, no-cost ImageJ plugin, we call AutoSholl, to perform Sholl analysis on pre-processed and ‘thresholded’ images. This algorithm extends the already existing plugin in Fiji ImageJ for Sholl analysis by allowing for secondary analysis techniques, such as determining number and length of root, intermediate, and terminal dendrites; functions not currently supported in the existing Sholl Analysis plugin in Fiji ImageJ.
Results:
The algorithm allows for rapid Sholl analysis in both 2-dimensional and 3-dimensional data sets independent of user tracing.
Comparison with Existing Methods:
We validated the performance of AutoSholl against pre-existing software packages using trained human observers and images of neurons. We found that our algorithm outputs similar results as available software (i.e., Bonfire), but allows for faster analysis times and unbiased quantification.
Conclusions:
As such, AutoSholl allows inexperienced observers to output results like more trained observers efficiently, thereby increasing the consistency, speed, and reliability of Sholl analyses.
Keywords: Morphometry, Sholl analysis, Dendritic field, Dendrite
Introduction
Sholl analysis is an analytical technique for the investigation of neuronal dendritic morphometry (Binley et al., 2014; Sholl, 1953). It involves tracing the morphology of a neuron, and then placing a series of concentric circles on the traced image to analyze the number of dendritic intersections at a given radius from the center of the neuronal cell body (Sholl, 1953). This serves as a surrogate measure for neuronal surface area and allows for quantification of dendritic arbor complexity (Binley et al., 2014; Sholl, 1953). While the process has become semi-automated in recent years, existing commercial software (i.e., Neurolucida) and open-source packages (i.e., Bonfire) still rely on user tracings of dendritic morphology (Langhammer et al., 2010; Yang et al., 2013). Moreover, these analysis software packages require specifying the cell soma center, in addition to identifying primary, secondary, and higher order dendrites during the tracing process (Langhammer et al., 2010; Yang et al., 2013). Such necessary involvement of users can make Sholl analyses subject to observer bias and variability, in addition to being very time consuming. Developing more automated software programs for Sholl analysis, and in general for imaging analysis, will allow for faster analyses with higher reproducibility and rigor.
Since previously published work has made it possible to trace 2-dimensional (2D) and 3-dimensional (3D) structures (Arganda-Carreras et al., 2010; Dougherty and Kunzelmann, 2007; Srinivasan et al., 2018), we built on these studies to automate Sholl analysis in 2D and 3D neuronal image sets. These new features allow for Sholl analysis, independent of user tracing, and without the need to specify the somal center and dendrite order. While the standard distribution of Fiji ImageJ comes with a plugin, termed Sholl Analysis (Ferreira et al., 2014), this plugin is unable to perform secondary analyses such as dendritic root, intermediate, and terminal counts, thickness (diameter), and length that are found in software that employ user tracing. We validated our algorithm using neurons in 2D images (low-density neuronal cultures) in addition to 3D data sets. Together, these analyses show both the precision and efficiency of the algorithm, as compared to semi-automated analyses, utilizing multiple test models with varying dendritic branching morphologies.
Materials and Methods
All experimental protocols were performed under approval from the Institutional Animal Care and Use Committees of Albany Medical College and complied with the National Institutes of Health “Guide for the Care and Use of Laboratory Animals”
Tissue dissociation and neuron culture
Timed pregnant mice with day 17.5 embryos were euthanized and cerebral cortices dissected as described previously (Tuz et al., 2013). Briefly, tissue was incubated in 100 μL of a 0.25% trypsin-EDTA solution (Gibco 25209-056) at 37°C for 7 min. The trypsin solution was then removed and 100 μL of a trypsin inhibitor solution added (1 mg/mL soybean trypsin inhibitor, Sigma SLBR01181). The tissue was incubated with the trypsin inhibitor solution for 5 min at room temperature. The trypsin inhibitor solution was then removed and replaced with 500 μL of Neurobasal media supplemented with 2 mM glutamine, 40 μg/mL gentamicin, 1x B27 supplement, 0.5% glucose). Tissue was mechanically dissociated by triturating 20 times using a 1 mL micropipette. The samples were then allowed to settle and 200 μL of cell suspension from the cortical preparation was added to 500 μL of Neurobasal media (supplemented as previously described). Suspensions were further mechanically dissociated 20 times using a 200 μL micropipette.
Four hours prior to plating cells, glass coverslips (18 mm diameter; ThermoFisher, Cat #18CIR-1.5) were coated with poly-D-lysine (Sigma-Aldrich, Cat #A-003-E; 1 h at 37°C), washed twice using sterile deionized water, and allowed to air dry in a culture hood. Cells (6000 cells) were added to each coverslip with 500 μL of fresh supplemented Neurobasal media. Following a 2 h incubation period, allowing for cell adherence, all media was removed and 500 μL of fresh supplemented Neurobasal media was added. Coverslips were then inverted above a confluent astrocyte layer (Kaech and Banker, 2006; Srivastava et al., 2011). Cultures were maintained in a 37°C, 5% CO2 atmosphere incubator for 21 days in vitro (DIV). Cells were fixed at 21 DIV and processed for immunostaining and imaging.
Neuronal immunostaining and image acquisition
Low-density primary cultured neurons were fixed using 4% paraformaldehyde (PFA) made in phosphate-buffered saline (PBS) and sucrose (Kaech and Banker, 2006; Srivastava et al., 2011). For immunocytochemistry analysis, nonspecific antigen sites were blocked with 1% bovine serum albumin (BSA; Sigma, Cat #A7030) in PBS at room temperature for 1 h. Cells were then incubated with an anti-MAP2 antibody (1:500; EMD-Millipore, AB5622) in 1% BSA overnight at 4°C. On the next day, cells were washed with PBS followed by the addition of an anti-rabbit Alexa Fluor 488 antibody (1:1000; Molecular Probes, Cat #A11055), and incubated for 1 h at room temperature. Cells were then washed with PBS and incubated with Hoescht 33342 (1:10000; ThermoFisher, Cat #H3570) for 1 min at room temperature. Cells were then mounted using Fluoromount (Southern Biotech, Cat #0100-01) and imaged with a Zeiss Imager.M2 microscope with a 40x objective (Zeiss Plan-Achromat 40x/0.75). Neurons were chosen, with no specific criterion, to test the algorithm’s performance across a wide variety of conditions with variable noise. Images of neuronal stacks (for 3D testing) were obtained from the Gold166_v1 release from the BigNeuron database (https://github.com/BigNeuron/Data/releases/tag/Gold166_v1))(Peng et al., 2015).
Explanation of the algorithm
The algorithm presented here requires two parts – skeletonization of a segmented neuron and determination of thickness. Skeletonization can be accomplished using an adapted version of the medial axis transform presented previously (Lee et al., 1994). Local thickness can be correlated to this skeletonized structure by defining the thickness of the structure of interest as the distance map of all non-overlapping circles via: ΩR = {p ∈ Ω|sph(p, Dmap(p)) ⊄ sph(x, Dmap(x)), p ≠ x, x ∈ Ω} where Dmap is the distance map, and p is set as the center points of all non-overlapping circles. The radii of the circles defined here gives the local thickness (a more detailed description is presented in Hildebrand and Rüegsegger, 1997; Srinivasan et al., 2018).
The center was defined as the branch point with the maximal number of neighbors. For secondary analysis of the dendritic arbor, a root-intermediate-terminal method was used due to its ease of definition based on classification of branch points. Root or primary dendrites were defined as dendrites with one end point as the center, and the second end point as a branch point. Intermediate dendrites were defined as having both end points being branch points. Terminal dendrites were defined as having one end point as a branch point and the other end point as an end point.
Algorithm development
The algorithm was developed using the Integrated Design Environment Eclipse Neon v3.0 (The Eclipse Foundation) with Java version 1.8.0.11. To determine inter-observer variability, image data sets were analyzed by two trained observers (Obs. A and B). To determine intra-observer variability, one observer analyzed images on separate days (Obs. A1 and A2).
Code availability
The source code and compiled version of the AutoSholl algorithm are available on GitHub (https://github.com/ferlandlab). A ReadMe file is included with the source code and compiled algorithm.
Algorithm workflow
A flowchart of the algorithm workflow is provided (Fig. 1) – the image is converted to a binary black and white image before being inputted into AutoSholl for analysis (2D example output is presented in Table 1, 3D example output is presented in Table 2 – from a single human neuron within the Gold166_v1 release from the BigNeuron database (https://github.com/BigNeuron/Data/releases/tag/Gold166_v1; Peng et al., 2015). We also processed the example ‘thresholded’ image of a Drosophila neuron provided in ImageJ (Schindelin et al., 2012; Ferreira et al., 2014) using AutoSholl to show the algorithm’s ability to effectively process very complex dendritic fields (Fig. 2; example output provided in Supplementary Table 1) as well as process simpler dendritic fields.
Figure 1. Schematic of algorithm workflow.
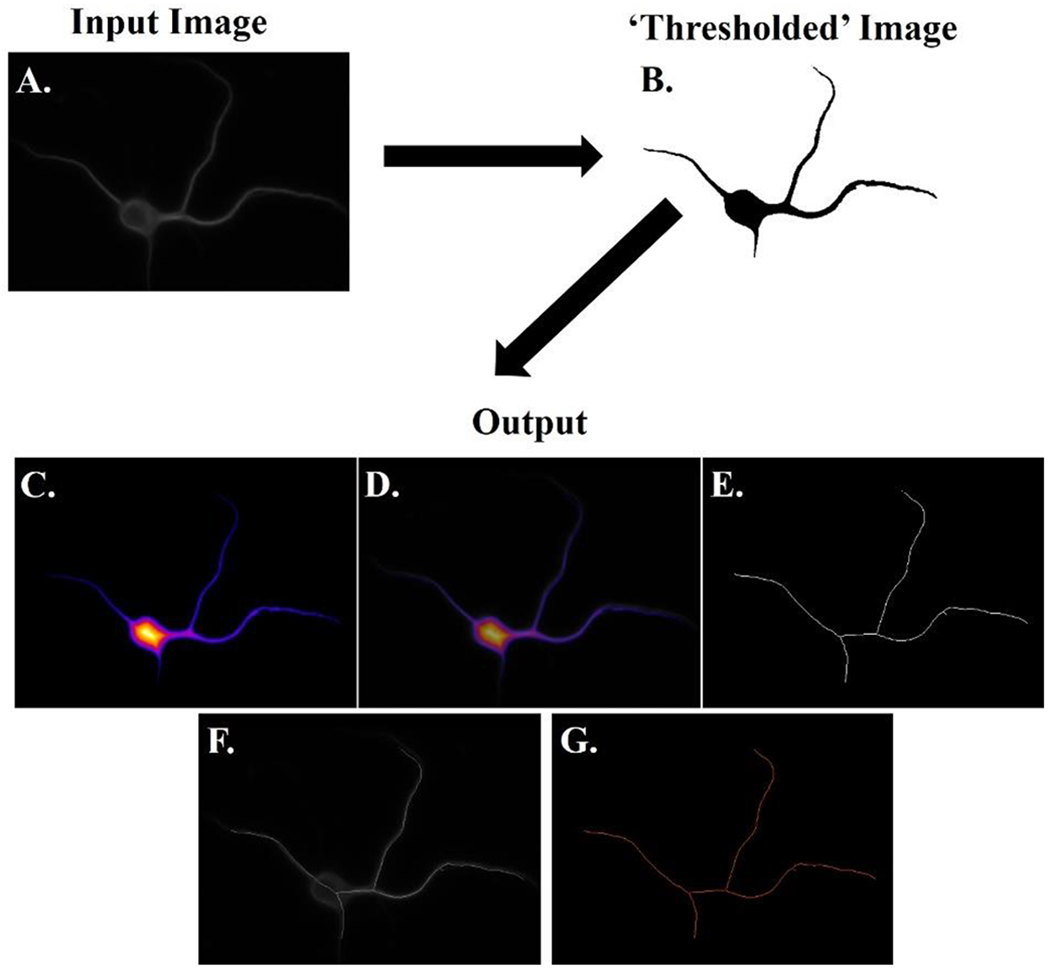
A simplified explanation of the algorithm workflow is presented. The user manually pre-processes the input image into a ‘thresholded’ binary image. This binary image is then used as the input for AutoSholl, which then returns the results of the analysis (termed output). The output shows the original image (A) followed by the ‘thresholded’ binary image (B). The local thickness heat map (darker colors correspond to smaller thicknesses) (C) is overlaid onto the original image (D) for comparison. The optimal skeleton is presented (E) and is overlaid onto the original image (F). The tagged skeleton is shown with branch points labeled in purple and all dendrites in orange (G). Overlaid images are not part of the algorithm output, but are presented here to allow for visual confirmation of results. This figure was enhanced with Photoshop for better visualization purposes by enhancing the color levels within the linear range.
Table 1. Example 2D neuronal Sholl output.
Classification of a dendrite as primary, intermediate, or terminal, independent of user tracing, is not currently supported in ImageJ. Analyses were performed on the input image presented in Figure 1. (V1x, V1y, V1z) and (V2x, V2y, V2z) are the (x, y, z) position of the starting and ending voxel of each branch, respectively. Branch length and thickness are in microns. Branch (Dendrite) Type: TER – terminal, INT – intermediate, PRI – primary.
| Skeleton ID | Branch Length | V1x | V1y | V1z | V2x | V2y | V2z | Branch Type | Euclidean Distance | Running Avg. Length | Max Thickness | Avg. Thickness | Avg. Intensity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 4.423 | 5.958 | 7.281 | 0 | 6.198 | 4.125 | 0 | TER | 3.165 | 4.197 | 7 | 2.434 | 255 |
| 2 | 1 | 3.63 | 7.302 | 8.312 | 0 | 7.146 | 5.188 | 0 | TER | 3.129 | 3.451 | 4 | 2.395 | 255 |
| 3 | 1 | 3.453 | 9.104 | 7.271 | 0 | 7.135 | 4.719 | 0 | TER | 3.223 | 3.306 | 9.22 | 3.849 | 255 |
| 4 | 1 | 2.558 | 1.542 | 3.51 | 0 | 3.677 | 3.885 | 0 | TER | 2.168 | 2.4 | 4 | 2.306 | 255 |
| 5 | 1 | 2.471 | 5.125 | 5.875 | 0 | 7 | 4.51 | 0 | TER | 2.319 | 2.352 | 18.682 | 2.858 | 255 |
| 6 | 1 | 2.174 | 7.073 | 2.302 | 0 | 6.719 | 4.208 | 0 | TER | 1.939 | 2.041 | 11.402 | 2.917 | 255 |
| 7 | 1 | 2.058 | 3.677 | 3.885 | 0 | 5.552 | 3.542 | 0 | INT | 1.906 | 1.922 | 5.831 | 3.904 | 255 |
| 8 | 1 | 1.871 | 4.771 | 2.031 | 0 | 5.552 | 3.542 | 0 | TER | 1.701 | 1.771 | 5.831 | 2.142 | 255 |
| 9 | 1 | 0.555 | 6.198 | 4.125 | 0 | 6.719 | 4.208 | 0 | INT | 0.527 | 0.499 | 11.402 | 8.084 | 255 |
| 10 | 1 | 0.533 | 3.385 | 4.292 | 0 | 3.677 | 3.885 | 0 | TER | 0.5 | 0.505 | 4 | 1.471 | 255 |
| 11 | 1 | 0.532 | 7.854 | 4.031 | 0 | 7.396 | 4.188 | 0 | TER | 0.484 | 0.497 | 2 | 1.225 | 255 |
| 12 | 1 | 0.527 | 7.688 | 4.417 | 0 | 7.208 | 4.385 | 0 | TER | 0.48 | 0.502 | 12 | 3.694 | 255 |
| 13 | 1 | 0.502 | 5.938 | 3.74 | 0 | 6.198 | 4.125 | 0 | INT | 0.465 | 0.456 | 7.071 | 6.12 | 255 |
| 14 | 1 | 0.467 | 5.552 | 3.542 | 0 | 5.938 | 3.74 | 0 | INT | 0.433 | 0.415 | 6.325 | 5.438 | 255 |
| 15 | 1 | 0.288 | 7.208 | 4.385 | 0 | 7.396 | 4.188 | 0 | INT | 0.273 | 0.273 | 12 | 5.982 | 255 |
| 16 | 1 | 0.287 | 6.927 | 4.052 | 0 | 6.833 | 4.292 | 0 | TER | 0.257 | 0.272 | 15.297 | 5.708 | 255 |
| 17 | 1 | 0.286 | 7.094 | 4.979 | 0 | 7.135 | 4.719 | 0 | INT | 0.264 | 0.242 | 9.22 | 4.288 | 255 |
| 18 | 1 | 0.285 | 5.979 | 3.49 | 0 | 5.938 | 3.74 | 0 | TER | 0.253 | 0.27 | 6.083 | 2.203 | 255 |
| 19 | 1 | 0.271 | 7 | 4.51 | 0 | 7.135 | 4.719 | 0 | INT | 0.248 | 0.241 | 18.682 | 12.058 | 255 |
| 20 | 1 | 0.242 | 6.833 | 4.292 | 0 | 7 | 4.458 | 0 | PRI | 0.236 | 0.229 | 25 | 21.332 | 255 |
| 21 | 1 | 0.239 | 7 | 4.458 | 0 | 7.208 | 4.385 | 0 | PRI | 0.221 | 0.201 | 23.537 | 16.295 | 255 |
| 22 | 1 | 0.23 | 7.094 | 4.979 | 0 | 7.146 | 5.188 | 0 | INT | 0.215 | 0.2 | 4.123 | 3.405 | 255 |
| 23 | 1 | 0.149 | 6.719 | 4.208 | 0 | 6.833 | 4.292 | 0 | INT | 0.142 | 0.105 | 15.297 | 14.318 | 255 |
| 24 | 1 | 0.107 | 7.24 | 5.219 | 0 | 7.146 | 5.188 | 0 | TER | 0.099 | 0.103 | 5 | 2.89 | 255 |
| 25 | 1 | 0.065 | 7.042 | 5.01 | 0 | 7.094 | 4.979 | 0 | TER | 0.061 | 0.066 | 4.123 | 2.198 | 255 |
| 26 | 1 | 0.061 | 7 | 4.458 | 0 | 7 | 4.51 | 0 | PRI | 0.052 | 0.036 | 23.537 | 21.235 | 255 |
| 27 | 1 | 0.056 | 7.406 | 4.135 | 0 | 7.396 | 4.188 | 0 | TER | 0.053 | 0.054 | 2 | 1.236 | 255 |
Table 2. Example 3D neuronal Sholl output.
Classification of a dendrite as primary, intermediate, or terminal, independent of user tracing, is not currently supported in ImageJ. Analyses were performed on a test 3D image (not shown). (V1x, V1y, V1z) and (V2x, V2y, V2z) are the (x, y, z) position of the starting and ending voxel of each branch, respectively. Branch length and thickness are in microns. Branch (Dendrite) Type: TER – terminal, INT – intermediate, PRI – primary.
| Skeleton ID | Branch Length | V1x | V1y | V1z | V2x | V2y | V2z | Branch Type | Euclidean Distance | Running Avg. Length | Max Thickness | Avg. Thickness | Avg. Intensity | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 14.41344 | 214.08 | 261.44 | 28 | 225.28 | 255.04 | 11 | INT | 21.3401 | 13.0496 | 0.90496 | 0.58016 | 255 |
| 2 | 1 | 9.32544 | 202.56 | 271.04 | 35 | 209.92 | 267.2 | 30 | INT | 9.690986 | 8.14912 | 1.15392 | 0.64672 | 255 |
| 3 | 1 | 9.21568 | 189.44 | 283.2 | 13 | 195.2 | 277.12 | 32 | INT | 20.76401 | 8.35104 | 1.01184 | 0.6368 | 255 |
| 4 | 1 | 8.7632 | 167.04 | 302.4 | 66 | 173.44 | 297.6 | 78 | TER | 14.42221 | 8.21696 | 1.15392 | 0.62528 | 255 |
| 5 | 1 | 8.63072 | 183.68 | 288.32 | 27 | 189.44 | 283.2 | 31 | INT | 8.682857 | 6.5152 | 1.43104 | 0.88224 | 255 |
| 6 | 1 | 7.85792 | 231.36 | 250.56 | 2 | 236.8 | 246.08 | 32 | INT | 30.81662 | 6.50496 | 0.90496 | 0.49824 | 255 |
| 7 | 1 | 7.8032 | 178.88 | 293.12 | 8 | 183.68 | 288.32 | 31 | INT | 23.98083 | 6.81152 | 1.35776 | 0.88416 | 255 |
| 8 | 1 | 7.67072 | 209.92 | 267.2 | 21 | 214.08 | 261.44 | 21 | INT | 7.105153 | 5.98944 | 0.71552 | 0.50752 | 255 |
| 9 | 1 | 7.27296 | 281.6 | 214.4 | 36 | 287.68 | 211.52 | 36 | PRI | 6.727615 | 5.76128 | 0.64 | 0.41536 | 255 |
| 10 | 1 | 6.95296 | 197.44 | 274.56 | 46 | 202.56 | 271.04 | 37 | PRI | 10.9364 | 5.5104 | 1.01184 | 0.6528 | 255 |
| 11 | 1 | 6.5552 | 273.92 | 216.96 | 45 | 279.68 | 215.04 | 47 | PRI | 6.392496 | 5.6672 | 0.71552 | 0.47936 | 255 |
| 12 | 1 | 5.80544 | 174.72 | 296.64 | 3 | 178.88 | 293.12 | 9 | INT | 8.105307 | 5.05984 | 0.96 | 0.45472 | 255 |
| 13 | 1 | 5.78272 | 260.16 | 223.68 | 20 | 264.96 | 221.76 | 2 | INT | 18.72769 | 3.84768 | 0.64 | 0.41056 | 255 |
| 14 | 1 | 5.2752 | 255.68 | 226.24 | 38 | 259.2 | 223.36 | 46 | PRI | 9.202434 | 4.32896 | 0.64 | 0.44416 | 255 |
| 15 | 1 | 5.19456 | 243.52 | 235.84 | 44 | 247.36 | 233.92 | 47 | PRI | 5.237557 | 3.62752 | 0.64 | 0.50848 | 255 |
| 16 | 1 | 5.08768 | 225.28 | 255.04 | 40 | 228.8 | 252.16 | 48 | PRI | 9.202434 | 3.96832 | 0.96 | 0.68384 | 255 |
| 17 | 1 | 4.76768 | 228.8 | 252.16 | 44 | 230.08 | 249.28 | 36 | PRI | 8.598418 | 3.29312 | 0.96 | 0.55904 | 255 |
| 18 | 1 | 4.50272 | 266.24 | 220.8 | 38 | 269.76 | 218.88 | 49 | PRI | 11.70798 | 3.78944 | 0.64 | 0.4864 | 255 |
| 19 | 1 | 3.9952 | 240 | 241.28 | 40 | 242.56 | 238.72 | 41 | PRI | 3.755955 | 3.10688 | 0.64 | 0.51424 | 255 |
| 20 | 1 | 3.9952 | 242.56 | 238.72 | 1 | 243.52 | 235.84 | 25 | INT | 24.19124 | 3.03104 | 0.64 | 0.55328 | 255 |
| 21 | 1 | 3.6752 | 195.2 | 277.12 | 15 | 197.44 | 274.56 | 18 | INT | 4.535548 | 2.82944 | 0.96 | 0.56256 | 255 |
| 22 | 1 | 3.6752 | 251.84 | 229.44 | 1 | 254.4 | 227.2 | 11 | INT | 10.56273 | 2.76704 | 0.71552 | 0.6736 | 255 |
| 23 | 1 | 3.28384 | 236.8 | 246.08 | 15 | 238.72 | 243.52 | 24 | INT | 9.551963 | 1.35776 | 0.64 | 0.4176 | 255 |
| 24 | 1 | 2.95776 | 247.36 | 233.92 | 17 | 248 | 231.68 | 1 | INT | 16.16871 | 2.25632 | 0.64 | 0.4224 | 255 |
| 25 | 1 | 2.95776 | 270.72 | 219.2 | 34 | 273.28 | 218.24 | 9 | INT | 25.14906 | 1.6336 | 0.90496 | 0.5296 | 255 |
| 26 | 1 | 2.50496 | 292.48 | 209.28 | 73 | 290.24 | 209.92 | 64 | TER | 9.296623 | 2.2992 | 0.64 | 0.38464 | 255 |
| 27 | 1 | 2.45024 | 236.8 | 246.08 | 44 | 236.8 | 246.08 | 43 | PRI | 1 | 1.35776 | 0.45248 | 0.40832 | 255 |
| 28 | 1 | 2.39328 | 230.08 | 249.28 | 46 | 231.36 | 250.56 | 38 | PRI | 8.202244 | 1.35776 | 0.71552 | 0.45216 | 255 |
| 29 | 1 | 2.31776 | 260.48 | 221.76 | 52 | 260.16 | 223.68 | 72 | TER | 20.0945 | 2.19488 | 0.64 | 0.41056 | 255 |
| 30 | 1 | 2.26048 | 228.8 | 252.16 | 6 | 230.4 | 250.88 | 30 | INT | 24.08731 | 0.99776 | 0.96 | 0.69216 | 255 |
| 31 | 1 | 2.18496 | 241.6 | 243.52 | 72 | 239.68 | 242.88 | 58 | TER | 14.14553 | 2.0096 | 0.45248 | 0.34208 | 255 |
| 32 | 1 | 2.18496 | 279.68 | 215.04 | 28 | 281.6 | 214.4 | 32 | INT | 4.482856 | 1.01504 | 0.71552 | 0.45216 | 255 |
| 33 | 1 | 2.10432 | 183.68 | 286.4 | 71 | 183.68 | 288.32 | 65 | TER | 6.299714 | 2.15968 | 0.96 | 0.54624 | 255 |
| 34 | 1 | 1.99776 | 239.68 | 242.88 | 21 | 240 | 241.28 | 18 | INT | 3.415026 | 1.26272 | 0.64 | 0.46624 | 255 |
| 35 | 1 | 1.99776 | 250.24 | 230.4 | 20 | 251.84 | 229.44 | 33 | INT | 13.13323 | 1.42016 | 0.64 | 0.54624 | 255 |
| 36 | 1 | 1.86496 | 173.44 | 297.6 | 3 | 174.72 | 296.64 | 6 | INT | 3.4 | 0.97952 | 1.31936 | 1.07072 | 255 |
| 37 | 1 | 1.86496 | 254.4 | 227.2 | 34 | 255.68 | 226.24 | 19 | INT | 15.08509 | 0.99776 | 0.71552 | 0.57888 | 255 |
| 38 | 1 | 1.73248 | 211.52 | 266.88 | 66 | 209.92 | 267.2 | 46 | TER | 20.06645 | 1.78752 | 0.45248 | 0.38624 | 255 |
| 39 | 1 | 1.73248 | 288.96 | 210.56 | 11 | 290.24 | 209.92 | 8 | INT | 3.323853 | 1.29728 | 0.64 | 0.576 | 255 |
| 40 | 1 | 1.67776 | 264.96 | 221.76 | 7 | 266.24 | 220.8 | 29 | INT | 22.05811 | 0.90496 | 0.71552 | 0.6176 | 255 |
| 41 | 1 | 1.67776 | 249.28 | 231.68 | 33 | 250.24 | 230.4 | 35 | INT | 2.56125 | 0.45248 | 0.71552 | 0.65888 | 255 |
| 42 | 1 | 1.67552 | 230.08 | 249.28 | 31 | 230.4 | 250.88 | 20 | INT | 11.12036 | 0.64 | 0.71552 | 0.45216 | 255 |
| 44 | 1 | 1.54496 | 230.4 | 250.88 | 29 | 231.36 | 250.56 | 26 | INT | 3.16607 | 0.77248 | 0.45248 | 0.36416 | 255 |
| 45 | 1 | 1.54496 | 273.28 | 218.24 | 28 | 273.92 | 216.96 | 23 | INT | 5.200769 | 0.99776 | 0.90496 | 0.54624 | 255 |
| 46 | 1 | 1.488 | 232.64 | 251.2 | 74 | 231.36 | 250.56 | 73 | TER | 1.745852 | 1.39328 | 0.32 | 0.32 | 255 |
| 47 | 1 | 1.41248 | 260.48 | 224.96 | 60 | 260.16 | 223.68 | 66 | TER | 6.143354 | 1.41248 | 0.64 | 0.43328 | 255 |
| 48 | 1 | 1.35776 | 237.76 | 242.56 | 61 | 238.72 | 243.52 | 51 | TER | 10.09174 | 1.35776 | 0.64 | 0.43328 | 255 |
| 49 | 1 | 1.35776 | 264 | 220.8 | 57 | 264.96 | 221.76 | 44 | TER | 13.0707 | 1.35776 | 0.64 | 0.4 | 255 |
| 50 | 1 | 1.35776 | 279.36 | 214.08 | 59 | 279.68 | 215.04 | 65 | TER | 6.084735 | 1.35776 | 0.71552 | 0.45184 | 255 |
| 51 | 1 | 1.35552 | 229.12 | 250.88 | 77 | 228.8 | 252.16 | 56 | TER | 21.04141 | 1.35552 | 0.96 | 0.53344 | 255 |
| 52 | 1 | 1.28 | 248 | 231.68 | 2 | 249.28 | 231.68 | 26 | INT | 24.03411 | 0.32 | 0.64 | 0.47072 | 255 |
| 53 | 1 | 1.22496 | 196.16 | 277.76 | 43 | 195.2 | 277.12 | 45 | TER | 2.308939 | 1.22496 | 0.96 | 0.70944 | 255 |
| 54 | 1 | 1.22496 | 243.52 | 239.36 | 61 | 242.56 | 238.72 | 81 | TER | 20.03325 | 1.22496 | 0.64 | 0.42656 | 255 |
| 55 | 1 | 1.22496 | 238.72 | 243.52 | 18 | 239.68 | 242.88 | 5 | INT | 13.0511 | 0.90496 | 0.71552 | 0.61216 | 255 |
| 56 | 1 | 1.22496 | 172.48 | 296.96 | 62 | 173.44 | 297.6 | 50 | TER | 12.05534 | 1.0624 | 0.96 | 0.57888 | 255 |
| 57 | 1 | 1.22496 | 175.68 | 297.28 | 73 | 174.72 | 296.64 | 50 | TER | 23.02892 | 1.13024 | 0.96 | 0.53344 | 255 |
| 58 | 1 | 1.22496 | 182.72 | 287.68 | 70 | 183.68 | 288.32 | 76 | TER | 6.109926 | 1.0624 | 0.96 | 0.56 | 255 |
| 59 | 1 | 1.22496 | 188.8 | 282.24 | 61 | 189.44 | 283.2 | 46 | TER | 15.04431 | 1.0624 | 1.01184 | 0.57312 | 255 |
| 60 | 1 | 1.22496 | 203.2 | 272 | 57 | 202.56 | 271.04 | 81 | TER | 24.02772 | 1.0624 | 1.01184 | 0.75232 | 255 |
| 61 | 1 | 1.22496 | 252.48 | 230.4 | 65 | 251.84 | 229.44 | 69 | TER | 4.163076 | 1.13024 | 0.64 | 0.42656 | 255 |
| 62 | 1 | 1.22496 | 272.96 | 216.32 | 81 | 273.92 | 216.96 | 63 | TER | 18.03694 | 1.0624 | 0.32 | 0.32 | 255 |
| 63 | 1 | 1.168 | 288.64 | 212.16 | 74 | 287.68 | 211.52 | 49 | TER | 25.02661 | 1.168 | 0.32 | 0.32 | 255 |
| 64 | 1 | 1.09248 | 179.84 | 293.44 | 82 | 178.88 | 293.12 | 74 | TER | 8.063746 | 0.99776 | 0.45248 | 0.36416 | 255 |
| 65 | 1 | 1.09248 | 225.92 | 255.68 | 53 | 225.28 | 255.04 | 48 | TER | 5.08126 | 0.99776 | 0.90496 | 0.60352 | 255 |
| 66 | 1 | 1.09248 | 288.64 | 209.6 | 65 | 288.96 | 210.56 | 46 | TER | 19.02693 | 0.97728 | 0.64 | 0.4 | 255 |
| 67 | 1 | 1.09248 | 249.28 | 231.68 | 23 | 249.28 | 231.68 | 18 | INT | 5 | 0.77248 | 0.64 | 0.53344 | 255 |
| 68 | 1 | 1.09248 | 259.2 | 223.36 | 21 | 260.16 | 223.68 | 20 | INT | 1.422674 | 0.32 | 0.64 | 0.5776 | 255 |
| 69 | 1 | 1.09248 | 269.76 | 218.88 | 10 | 270.72 | 219.2 | 22 | INT | 12.04259 | 0.32 | 0.64 | 0.64 | 255 |
| 70 | 1 | 0.90496 | 265.6 | 220.16 | 47 | 266.24 | 220.8 | 67 | TER | 20.02047 | 0.90496 | 0.64 | 0.47072 | 255 |
| 71 | 1 | 0.90496 | 287.04 | 210.88 | 59 | 287.68 | 211.52 | 46 | TER | 13.03147 | 0.90496 | 0.32 | 0.32 | 255 |
| 72 | 1 | 0.77248 | 197.12 | 273.92 | 81 | 197.44 | 274.56 | 48 | TER | 33.00776 | 0.67776 | 0.64 | 0.42656 | 255 |
| 73 | 1 | 0.77248 | 213.76 | 260.8 | 49 | 214.08 | 261.44 | 84 | TER | 35.00731 | 0.67776 | 0.64 | 0.42656 | 255 |
| 74 | 1 | 0.77248 | 230.4 | 248.64 | 43 | 230.08 | 249.28 | 74 | TER | 31.00826 | 0.81024 | 0.71552 | 0.496 | 255 |
| 75 | 1 | 0.77248 | 249.92 | 229.76 | 49 | 250.24 | 230.4 | 66 | TER | 17.01505 | 0.67776 | 0.64 | 0.42656 | 255 |
| 76 | 1 | 0.77248 | 269.44 | 218.24 | 45 | 269.76 | 218.88 | 44 | TER | 1.229634 | 0.67776 | 0.64 | 0.42656 | 255 |
| 77 | 1 | 0.77248 | 271.04 | 219.84 | 68 | 270.72 | 219.2 | 69 | TER | 1.229634 | 0.77248 | 0.64 | 0.48 | 255 |
| 78 | 1 | 0.77248 | 273.6 | 218.88 | 65 | 273.28 | 218.24 | 49 | TER | 16.01599 | 0.67776 | 0.90496 | 0.72832 | 255 |
| 79 | 1 | 0.77248 | 281.92 | 215.04 | 44 | 281.6 | 214.4 | 81 | TER | 37.00692 | 0.77248 | 0.45248 | 0.38624 | 255 |
| 80 | 1 | 0.64 | 239.36 | 241.28 | 78 | 240 | 241.28 | 60 | TER | 18.01137 | 0.64 | 0.45248 | 0.36416 | 255 |
| 81 | 1 | 0.45248 | 255.36 | 225.92 | 71 | 255.68 | 226.24 | 70 | TER | 1.097634 | 0.45248 | 0.32 | 0.32 | 255 |
| 82 | 1 | 0.45248 | 258.88 | 223.04 | 73 | 259.2 | 223.36 | 56 | TER | 17.00602 | 0.45248 | 0.45248 | 0.38624 | 255 |
| 83 | 1 | 0.45248 | 289.92 | 209.6 | 78 | 290.24 | 209.92 | 72 | TER | 6.017042 | 0.45248 | 0.32 | 0.32 | 255 |
| 84 | 1 | 0.32 | 243.2 | 235.84 | 83 | 243.52 | 235.84 | 58 | TER | 25.00205 | 0.32 | 0.64 | 0.48 | 255 |
| 85 | 1 | 0.32 | 247.68 | 231.68 | 74 | 248 | 231.68 | 50 | TER | 24.00213 | 0.32 | 0.32 | 0.32 | 255 |
Figure 2. Algorithm outputs for a complex dendritic field.
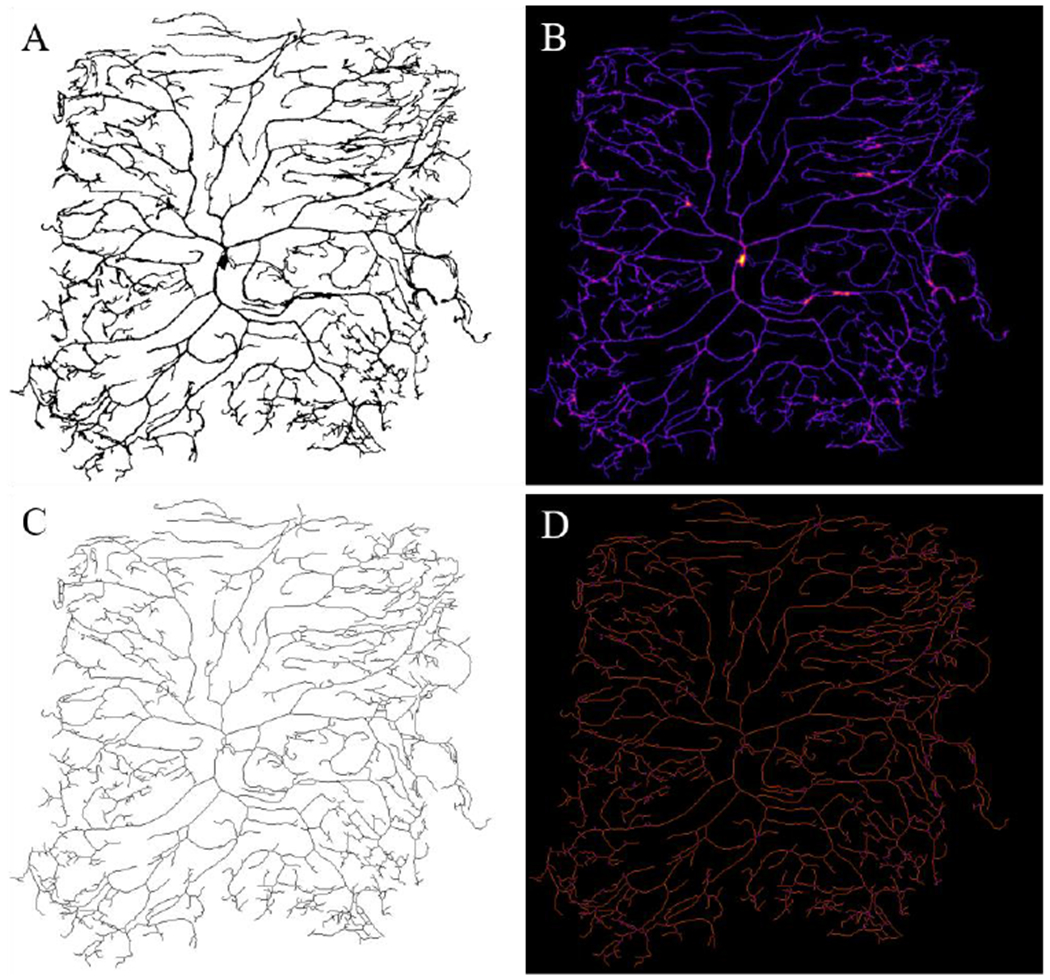
The thresholding process was previously performed, since the input image is a Drosophila neuron sample, provided with the Sholl Analysis plugin found in the standard distribution of Fiji ImageJ (Schindelin et al., 2012; Ferreira et al., 2014). The output shows the ‘thresholded’ binary image (A). The local thickness heat map (darker colors correspond to smaller thicknesses) (B) and optimal skeleton is presented (C) for the sample image. The tagged skeleton is shown with branch points labeled in purple and all dendrites in orange (D). This figure was enhanced with Photoshop for better visualization purposes by enhancing the color levels within the linear range.
Image Analysis
Observers performed Sholl analysis using the open-source algorithm Bonfire, which requires manual tracing, against AutoSholl. Two trained observers performed the analysis (Observer A (Obs. A) and Observer B (Obs. B)) as described above. The results were examined for significance using one-way ANOVA (Statistica). The average time of analysis per image, including pre-processing steps, was measured by each observer performing the analysis using Bonfire and using our AutoSholl algorithm. Analysis times were measured using a computer with an Intel Core i7-4500U, 1.80 GHz processor.
Results
The algorithm’s performance was validated against BonFire using 5 test neurons (Table 3). AutoSholl was found to output similar root (F3,16 = 0.48, p = 0.7007), intermediate (F3,16 = 0.02, p = 0.9960), and terminal dendrite (F3,16 = 0.03, p = 0.9927) counts and lengths (F3,16 = 0.17, p = 0.9151; F3,16 = 0.63, p = 0.6062; F3,16 = 0.42, p = 0.7411, respectively) as users performing the analysis using BonFire.
Table 3. AutoSholl outputs similar results as human observers, but requires less time.
Values represent mean ± SEM. Dendrite lengths are in microns. Image Count: n2D = 5, n3D = 7.
| Observer A, Day 1 | Observer A, Day 2 | Observer B | Algorithm | |
|---|---|---|---|---|
| 2D Data | ||||
| Root Dendrite Count | 3.4 ± 0.2191 | 3.2 ± 0.1788 | 3.6 ± 0.2191 | 3.4 ± 0.2191 |
| Root Dendrite Length (μm) | 34.1807 ± 12.9296 | 35.2384 ± 12.6224 | 33.1338 ± 12.3609 | 22.9979 ± 11.2710 |
| Intermediate Dendrite Count | 2 ± 1.3856 | 2.4 ± 1.5126 | 2.4 ± 1.7111 | 2 ± 1.5748 |
| Intermediate Dendrite Length (μm) | 4.0109 ± 2.3496 | 4.2164 ± 1.9798 | 9.0545 ± 2.5783 | 2.5870 ± 1.4982 |
| Terminal Dendrite Count | 7 ± 1.5811 | 7.25 ± 1.8268 | 7.5 ± 2.2913 | 8 ± 1.8708 |
| Terminal Dendrite Length (μm) | 30.7466 ± 6.1412 | 27.7633 ± 6.1114 | 35.4112 ± 4.3202 | 30.01749 ± 3.8029 |
| Analysis Time (min) | 22.4833 ± 2.4009 | 22.6433 ± 2.6852 | 23.8033 ± 2.1885 | 0.6233 ± 0.0498* |
| 3D Data | ||||
| Root Dendrite Count | 8.4286 ± 1.0853 | 8.8571 ± 1.2194 | 8.4286 ± 1.1039 | 7.1429 ± 0.7403 |
| Root Dendrite Length (μm) | 6.4701 ± 0.8445 | 5.5941 ± 1.1697 | 5.2609 ± 1.0022 | 5.1681 ± 0.8709 |
| Intermediate Dendrite Count | 22.2857 ± 3.6181 | 21.2857 ± 4.4845 | 19.7143 ± 3.5669 | 20.1429 ± 3.3651 |
| Intermediate Dendrite Length (μm) | 4.0433 ± 0.5377 | 5.0214 ± 0.7517 | 4.5185 ± 0.5635 | 4.618 ± 0.6116 |
| Terminal Dendrite Count | 26.2857 ± 3.3728 | 24.7143 ± 2.9604 | 25.1429 ± 2.7362 | 24.7143 ± 3.3728 |
| Terminal Dendrite Length (μm) | 2.6478 ± 0.3114 | 2.7384 ± 0.3537 | 2.7363 ± 0.4445 | 2.3346 ± 0.4629 |
| Analysis Time (min) | 22.4264 ± 1.4904 | 24.7623 ± 1.7124 | 23.8888 ± 1.3271 | 12.2157 ± 0.6633* |
indicates significant differences from observers (p < 0.01).
Similar results were obtained in testing 3D data sets for root dendrite count (F3,24 = 0.42, p = 0.7333) and length (F3,24 = 0.31, p = 0.8179), intermediate dendrite count (F3,24 = 0.08, p = 0.9702) and length (F3,24 = 0.36, p = 0.7824), and terminal dendrite count (F3,24 = 0.05, p = 0.9849) and length (F3,24 = 0.2, p = 0.8953).
AutoSholl was significantly faster in performance speed, as compared with users interfacing with BonFire, in both 2D neuronal data sets (F3,16 = 22.56, p < 0.01) and in the 3D neuronal data sets (F3,24 = 15.78, p < 0.01).
Discussion
Though multiple software packages exist for morphometric analyses, we have developed an easier to use analysis algorithm, designed for pre-processed image input, made available as an open-source ImageJ plugin. The current ImageJ Sholl Analysis plugin does not support secondary analyses, which our AutoSholl algorithm does (Schindelin et al., 2012; Ferreira et al., 2014). Other software packages such as NeuronJ or BonFire are only able to handle 2D data sets (Langhammer et al., 2010), while commercial software packages such as Neurolucida are limited, since they are not open source projects and require extensive user training prior to use (Dickstein et al., 2001). Since most Sholl analyses are currently conducted in 2D image sets, our AutoSholl algorithm offers the possibility of performing these analyses in 3D image sets.
AutoSholl is an extension of BranchAnalysis2D/3D and thus is subject to the same errors described previously (Srinivasan et al., 2018). Briefly, both algorithms perform their comparisons at a pixel/voxel level considering the unit as a discrete quantity. As the pixel/voxel is a continuous function, it is possible to compute morphometric measures at a sub-pixel/sub-voxel level by profiling the curve intensity using different methods. Most commercial packages do not perform this analysis (Yang et al., 2013), but consideration of these measures would be important for future algorithm development as they could provide biologically relevant information for image processing. Given that observers using our algorithm outputted similar results to already existing open-source software, the errors present within our algorithm are clearly not enough to bias the results with the sample images used, indicating AutoSholl is as precise as existing methodologies.
An interesting error to note, found within the algorithm, occurs when determining the center of a neuron. As a skeletonization algorithm was employed to convert the neuron image into a single pixel skeleton, the skeletonization algorithm used here has an error of 1 pixel/voxel. During the skeletonization process, this can lead to converting the soma into a structure not represented by a point, but two points. This typically occurs with very abnormally shaped neuronal soma (not the typically occurring triangular shape of pyramidal neurons or ellipsoid shapes seen in other neuron types). Such an error, leads to fewer primary dendrites, but more secondary dendrites. While this did not significantly bias our results using various types of neurons, including pyramidal and ellipsoid soma shapes, it may become an error when more precision is required. Future work could focus on introducing an error to the determination of the center point, thereby correcting for the error introduced by the skeletonization algorithm.
In the future, automating the thresholding process with AutoSholl will increase its potential functionality by removing any user interaction with input images further reducing user bias, while also significantly increasing the processing speed. Thus, AutoSholl provides advantages to trained and untrained observers performing Sholl analysis, since it is a fast, accurate, and reliable algorithm producing equivalent results as current software packages. Finally, this AutoSholl plugin would be an appropriate tool to extend the analyses performed in the original Sholl Analysis plugin in ImageJ (Ferreira et al., 2014).
Supplementary Material
Supplementary Table 1. Example Sholl output. Classification of a dendrite as primary, intermediate, or terminal, independent of user tracing, is not currently supported in ImageJ. Analyses were performed on the input image presented in Figure 2. (V1x, V1y, V1z) and (V2x, V2y, V2z) are the (x, y, z) position of the starting and ending voxel of each branch, respectively. Branch length and thickness are in microns. Branch (Dendrite) Type: TER – terminal, INT – intermediate, PRI – primary.
Highlights.
An open-source algorithm for analysis of morphometry and dendritic branching is presented
Algorithm output performs similarly to output from human observers using existing analysis tools
The algorithm is faster than human observers using other tools
AutoSholl decreases investigator bias given that it is automated
Acknowledgments
The authors would like to thank SV Sangameswara for his guidance and insights during the development of this algorithm. This work was supported by the National Institutes of Health (R01NS064283 to R.J.F., R01NS092062 to R.J.F.). The authors report no conflicts of interest.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Arganda-Carreras I, Fernández-González R, Muñoz-Barrutia A, Ortiz-De-Solorzano C, 2010. 3D reconstruction of histological sections: Application to mammary gland tissue. Microsc. Res. Tech 73, 1019–1029. 10.1002/jemt.20829 [DOI] [PubMed] [Google Scholar]
- Binley KE, Ng WS, Tribble JR, Song B, Morgan JE, 2014. Sholl analysis: A quantitative comparison of semi-automated methods. J. Neurosci. Methods 225, 65–70. 10.1016/j.jneumeth.2014.01.017 [DOI] [PubMed] [Google Scholar]
- Dickstein DL, Dickstein DR, Janssen WGM, Hof PR, Glaser JR, Rodriguez A, O’Connor N, Angstman P, Tappan SJ, 2001. Automatic Dendritic Spine Quantification from Confocal Data with Neurolucida 360, in: Current Protocols in Neuroscience. John Wiley & Sons, Inc. 10.1002/cpns.16 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dougherty R, Kunzelmann K-H, 2007. Computing Local Thickness of 3D Structures with ImageJ. Microsc. Microanal 13, 1678–1679. 10.1017/S1431927607074430 [DOI] [Google Scholar]
- Ferreira TA, Blackman AV, Oyrer J, Jayabal S, Chung AJ, Watt AJ, Sjöström PJ, van Meyel DJ, 2014. Neuronal morphometry directly from bitmap images. Nat. Methods 11, 982–984. 10.1038/nmeth.3125 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hildebrand T, Rüegsegger P, 1997. A new method for the model-independent assessment of thickness in three-dimensional images. J. Microsc 185, 67–75. 10.1046/j.1365-2818.1997.1340694.x [DOI] [Google Scholar]
- Kaech S, Banker G, 2006. Culturing hippocampal neurons. Nat. Protoc 1, 2406–2415. 10.1038/nprot.2006.356 [DOI] [PubMed] [Google Scholar]
- Langhammer CG, Previtera ML, Sweet ES, Sran SS, Chen M, Firestein BL, 2010. Automated Sholl analysis of digitized neuronal morphology at multiple scales: Whole cell Sholl analysis versus Sholl analysis of arbor subregions. Cytom. Part J. Int. Soc. Anal. Cytol 77, 1160–1168. 10.1002/cyto.a.20954 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee TC, Kashyap RL, Chu CN, 1994. Building Skeleton Models via 3-D Medial Surface Axis Thinning Algorithms. CVGIP Graph. Models Image Process 56, 462–478. 10.1006/cgip.1994.1042 [DOI] [Google Scholar]
- Peng H, Hawrylycz M, Roskams J, Hill S, Spruston N, Meijering E, Ascoli GA, 2015. BigNeuron: Large-Scale 3D Neuron Reconstruction from Optical Microscopy Images. Neuron 87, 252–256. 10.1016/j.neuron.2015.06.036 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schindelin J, Arganda-Carreras I, Frise E, Kaynig V, Longair M, Pietzsch T, Preibisch S, Rueden C, Saalfeld S, Schmid B, Tinevez J-Y, White DJ, Hartenstein V, Eliceiri K, Tomancak P, Cardona A, 2012. Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682. 10.1038/nmeth.2019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sholl DA, 1953. Dendritic organization in the neurons of the visual and motor cortices of the cat. J. Anat 87, 387–406. [PMC free article] [PubMed] [Google Scholar]
- Srinivasan A, Muñoz-Estrada J, Bourgeois JR, Nalwalk JW, Pumiglia KM, Sheen VL, Ferland RJ, 2018. BranchAnalysis2D/3D automates morphometry analyses of branching structures. J. Neurosci. Methods 294, 1–6. 10.1016/j.jneumeth.2017.10.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Srivastava DP, Woolfrey KM, Penzes P, 2011. Analysis of Dendritic Spine Morphology in Cultured CNS Neurons. J. Vis. Exp. JoVE. 10.3791/2794 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tuz K, Hsiao Y-C, Juárez O, Shi B, Harmon EY, Phelps IG, Lennartz MR, Glass IA, Doherty D, Ferland RJ, 2013. The Joubert Syndrome-associated Missense Mutation (V443D) in the Abelson-helper Integration Site 1 (AHI1) Protein Alters Its Localization and Protein-Protein Interactions. J. Biol. Chem 288, 13676–13694. doi: 10.1074/jbc.M112.420786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Gonzalez-Bellido PT, Peng H, 2013. A distance-field based automatic neuron tracing method. BMC Bioinformatics 14, 93 10.1186/1471-2105-14-93 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table 1. Example Sholl output. Classification of a dendrite as primary, intermediate, or terminal, independent of user tracing, is not currently supported in ImageJ. Analyses were performed on the input image presented in Figure 2. (V1x, V1y, V1z) and (V2x, V2y, V2z) are the (x, y, z) position of the starting and ending voxel of each branch, respectively. Branch length and thickness are in microns. Branch (Dendrite) Type: TER – terminal, INT – intermediate, PRI – primary.


